State-transition analysis of time-sequential gene expression identifies critical points that predict development of acute myeloid leukemia

Abstract

Temporal dynamics of gene expression inform cellular and molecular perturbations associated with disease development and evolution. Given the complexity of high-dimensional temporal genomic data, an analytical framework guided by a robust theory is needed to interpret time-sequential changes and to predict system dynamics. Here we model temporal dynamics of the transcriptome of peripheral blood mononuclear cells in a two-dimensional state-space representing states of health and leukemia using time-sequential bulk RNA-seq data from a murine model of acute myeloid leukemia (AML). The state-transition model identified critical points which accurately predict AML development and identifies step-wise transcriptomic perturbations that drive leukemia progression. The geometry of the transcriptome state-space provided a biological interpretation of gene dynamics, aligned gene signals that are not synchronized in time across mice, and allowed quantification of gene and pathway contributions to leukemia development. Our state-transition model synthesizes information from multiple cell types in the peripheral blood and identifies critical points in the transition from health to leukemia to guide interpretation of changes in the transcriptome as a whole to predict disease progression.

Introduction

Acute myeloid leukemia (AML) is a devastating malignancy of the hematopoietic system that can rapidly lead to bone marrow failure and death. Approximately 21,000 new patients are diagnosed with AML each year in the United States, and the latest 5-year overall survival rate remains at only 28% (https://seer.cancer.gov)(1). Thus, novel diagnostic and therapeutic approaches are highly needed.

AML comprises multiple distinct biological and clinical entities characterized by gene mutations and chromosomal abnormalities that drive leukemogenesis and predict prognosis and treatment response. Genomic studies such as the cancer genome atlas have revealed mutational landscapes in AML, highlighting patterns of cooperation and exclusivity among the gene mutations in the ontogenesis of the disease(2). These various genetic mutations ultimately alter the expression of downstream genes and are therefore associated with unique gene expression profiles representing functional networks in leukemic cell biology. Identification of genomic alterations including gene mutations, epigenetic changes, and gene expression profiles, obtained by high-throughput sequencing assays are becoming a part of the routine clinical assessment of AML patients at diagnosis and subsequent follow-ups.

As a biologically complex disease with genomic alterations and expression, AML can be viewed as an evolving, dynamic system wherein multiple interconnected inputs produce changes in the disease state that correspond to specific clinical phenotype. However, with the plethora of non-synchronized genomic alterations (e.g., gene mutations, deletions, epigenetic changes) and differentially expressed genes that can be detected at any given time point in patient’s peripheral blood (PB) or bone marrow (BM), it is challenging to quantitatively determine which of these changes are biologically and clinically relevant to predict disease evolution (e.g., malignant cell transformation, treatment response or resistance, disease relapse). Although methods have been proposed to analyze time-series genomic data(3–5), it remains critical to develop novel approaches that improve the accuracy of predicting disease evolution and treatment response. Thus, a framework guided by a robust theory is needed to interpret and predict a system’s dynamics. To this end, a central challenge for interpretation of dynamic data is the identification and prioritization of the genomic alterations and gene expression changes that at defined time-points, and to integrate all available information to accurately predict disease evolution.

Here, we propose that AML initiation and progression can be viewed as a state change of the transcriptome of BM or PB cells. To support this hypothesis, we apply concepts from state-transition theory to identify time-dependent critical transcriptomic perturbations that predict disease initiation and progression. To this end, we use a well-established conditional knock-in mouse model that mimics a subset of human AML driven by the fusion gene CBFB-MYH11 (CM), corresponding to the cytogenetic rearrangement inv(16)(p13.1q22) or t(16;16)(p13.1;q22) [henceforth inv(16)] in the human disease. Inv(16) is one of the most common recurrent cytogenetic aberrations and is found in approximately 5–12% of all patients with AML. The selection of this model was motivated by the possibility to select a common starting time given that the CM gene can be pharmacologically induced, the reliability of the mouse model to develop AML stochastically over time, and the feasibility to follow disease evolution from a state of health to a state of leukemia through time-series sampling of PB mononuclear cells (PBMCs) of each individual mouse. Induction of CM expression disrupts normal hematopoietic differentiation, resulting in perturbed hematopoiesis in the BM and an increased probability of state-transition from health to leukemia.

We show here that temporal dynamics of the PBMC transcriptome from CM mice are predictive of state-transition from health to leukemia. We represent the transcriptome as a particle moving in a two-dimensional state-space (i.e., normal hematopoiesis and leukemia) and identify state-transition critical points that correspond to specific states of the disease evolution, and associate with changes in the expression of individual genes and pathways that contribute to leukemogenesis.

Materials and Methods

State-transition model to describe transcriptome dynamics and development of AML

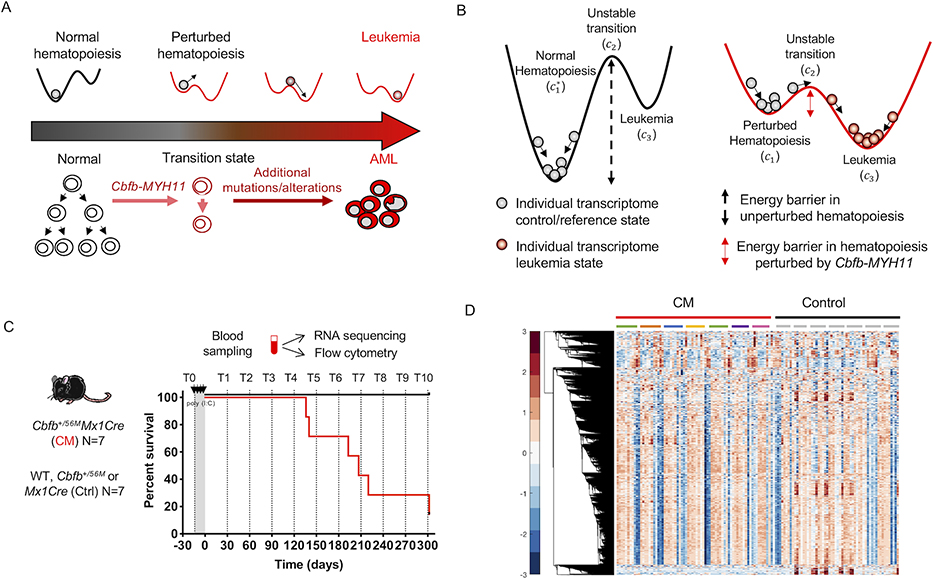
State-transition theory has a rich mathematical foundation(6) and has been broadly applied in various scientific fields, from chemistry, to physics, and biology(7–12) (see Yuan et al(13) for a thorough review of applications to cancer). We applied state-transition theory to model AML development and evolution, starting with the observation that the cellular composition of BM and PBMCs changes over time in relation to disease state (Figure 1A). To this end, therefore, we expect gene expression profiles of the BM and PBMCs to change over time during leukemia development and progression. Thus, we reasoned that we could use changes in the transcriptome to model disease evolution, i.e. from health to leukemia. Following state-transition theory, we postulated that in a state of health, a large energy barrier exists which reduces the probability of the system (i.e., a mouse or a patient) to transition from a state of normal hematopoiesis to a state of leukemia. Once hematopoiesis is perturbed by the expression of one or more leukemogenic events and the transcriptome changes, the energy barrier is reduced, and the probability of transition from normal hematopoiesis to leukemia increases, but not vice versa, because the system will tend to the lowest energy state. A state of leukemia is defined here as greater than 20% circulating blasts, based on the established AML diagnostic guideline(14).

Figure 1. Leukemia as a state-transition of the transcriptome.

State-transition theory is applied to model transcriptional states over time and to identify critical points in the transition from health to leukemia, and to compute the probability of leukemia development. A) The scheme represents the temporal evolution of the transcriptome of the blood from a healthy state to a leukemia state in a longitudinal study in an AML model induced by the Cbfb-MYH11 (CM) oncogene. In the conditional CM knock-in mouse model (Cbfb^+/56M/Mx1Cre), expression of CM in the adult bone marrow alters normal hematopoietic differentiation creating aberrant pre-leukemic progenitor cells which with time acquire additional genetic, epigenetic alterations needed for malignant transformation and AML development. B) We model the action of oncogenic events as a reduction in the energy barrier required to cause state-transition, and thus increase the probability of leukemia development. In unperturbed—normal—hematopoiesis, a large energy barrier between the reference state c₁ and unstable transition c₂ result in low probability of the state-transitioning to leukemia c₃. In hematopoiesis perturbed by an AML oncogene CM, the energy barrier is reduced and therefore increases the probability of transition from c₁ to c₃ to a leukemia state. The * marker indicates normal hematopoiesis unperturbed by Cbfb-MYH11. C) In a cohort of CM mice (Cbfb^+/56M/Mx1Cre; N=7) and littermate controls (Ctrl; N=7) lacking one or both transgenes (Cbfb^+/56M or Mx1Cre), PB was sampled prior to and following CM induction (by poly (I:C) treatment) monthly for up to 10 months (timepoints T0-T10), or when mice were moribund with leukemia. Blood samples were subjected to bulk RNA-seq and flow cytometry analysis. Survival curve of CM (red line) and Ctrl (black line) mice corresponding to blood sampling time point (dashed line) are shown. D) Hierarchical clustering of row normalized (mean zero, standard deviation one) log2 transformed counts per million (cpm) reads time-series RNA-seq data for all blood samples (N= 132). Color bar shows standard deviation from the mean. Each column represents a timepoint sample, which are ordered sequentially in time and grouped by condition (CM red, Control black) and individual mice, indicated by colored bars or grey bars, respectively. Hierarchical clustering reveals similar leukemia transcriptional profiles over time which is not uniform across all mice.

To translate these concepts into a state-transition model, we represent the transcriptome as a particle undergoing Brownian motion in a double-well quasi-potential (denoted U_p) with two stable states (see Table 1 glossary of terms). Leukemogenic events alter the quasi-potential so that the energy barrier is lowered and the probability of the transcriptome particle moving from one stable state to another, i.e. from health to leukemia, is increased. The motivation for this double-well model is the underlying hypothesis that there are two states in this experimental system: health and leukemia. This is because if a mouse is healthy it will remain healthy without an oncogenic alteration, and if a mouse has leukemia, it will remain with leukemia until moribund without a treatment. We note that in our model, the existence of a transition state between health and leukemia follows directly from modeling the motion of a particle in a potential energy landscape; between two stable states (i.e. valleys) there must be an unstable state (i.e. peak).

Table 1.

Glossary of terms

Term	Meaning
State variable	A state variable is one of a minimal set of variables that describe the mathematical “state” of a dynamic system. In this work, the state variable is the transcriptome derived from RNA-seq of peripheral blood mononuclear cells.
State-space	A state-space is a mathematical representation of all possible configurations of a system defined by the state variables. In this work, the state-space is constructed with principal component analysis of time-series RNA-seq data of peripheral blood mononuclear cells over the course of leukemia progression in a mouse model.
State-transition	A state-transition is the dynamic process of a system changing from one state to another. In this work, the state-transition of interest is the transition of the transcriptome from a reference state of hematopoiesis to leukemia.
Probability density	The probability density gives the probability of finding the system in a given state (position in the state-space) at a given time. The probability density takes values between zero and one. The sum of the probability density over the entire state-space is one. The probability density is given by the solution of the Fokker-Planck equation.
Double-well quasi-potential	A double-well potential is an energy function which has two local minima, and a local maxima, similar to a “w” shape. In this work, the double-well potential is derived from the transcriptome state-space. The potential is referred to as a “quasi-potential” because the state-space does not have physical units, and therefore the potential energy function does not have a clearly defined physical analog. The wells of the potential correspond to stable states of the transcriptome, whereas the peak corresponds to an unstable transition state.
Eigengene	Eigengene refers to the coefficient weights (or loadings) of a given gene computed with principal component analysis. In this work, a “leukemia eigengene” refers to the weight of a given gene in the principal component analysis of gene expression data associated with leukemia.

The states in our model are identified with critical points denoted as ${c_1^{*},c}_1,c_2,c_3$ corresponding to local minima and maxima of the quasi-potential U_p (Figure 1B). The critical point c₁ represents the reference state of perturbed hematopoiesis; a stable state with no evidence of disease that occurs upon activation of an initial leukemogenic event (i.e. CM). We differentiate c₁ from $c_1^{*}$, which is a critical point that represents the reference stable state of normal hematopoiesis in control mice. The critical point c₃ represents a state of overt leukemia. The critical point c₂ represents an unstable transition state between the states of health and leukemia, i.e. between c₁ and c₃. Because the critical point c₂ is an unstable transition state, the model predicts that it would be unlikely to observe the system precisely at or very near this state. Thus, the model predicts that when the system crosses the unstable critical point c₂, the development of leukemia becomes inevitable and the velocity of the transcriptome particle will increase toward c₃. This can be interpreted biologically as an acceleration of leukemia progression following a critical change in the transcriptional state of the system as observed from the peripheral blood.

We tested the double-well state-transition model by performing a time-series gene expression study using a well-established, conditional knock-in mouse model (Cbfb^+/56M/Mx1-Cre; C57BL/6) and observe the transcriptome over disease initiation and progression. The Cbfb^+/56M/Mx1-Cre mouse recapitulates the human inv(16) AML that is also driven by the CM fusion gene. In this mouse, CM expression is induced via the activation of Cre-mediated recombination by intravenous administration of synthetic double-stranded RNA polyinosinic–polycytidylic acid [poly (I:C)] (supplemental Figure S1)(15,16). We collected PBMC samples from a cohort of CM-induced mice (n = 7) and similarly treated littermate control mice lacking the transgene (n = 7) before induction (T0) and at one-month intervals after induction up to 10 months (T1-T10) or when the mouse was diseased and moribund. All mice were maintained in an AAALAC-accredited animal facility, and all experimental procedures were performed in accordance with federal and state government guidelines and established institutional guidelines and protocols approved by the Institutional Animal Care and Use Committee (IACUC) at the Beckman Research Institute of City of Hope. We collected blood at one-month intervals because this was the most frequent sampling allowed under IACUC guidelines given the volume of blood required to perform flow cytometry and RNA-seq analyses. All the CM-induced mice developed AML within the 10-month duration of the experiment (Figure 1C), except for one mouse that exhibited CM-perturbed pre-leukemic expansion of progenitor populations in the BM but evidence of circulating leukemic blasts by the end of experiment. All the collected PBMC samples were analyzed by RNA-seq (heatmap of RNA-seq samples shown in Figure 1D) and flow cytometry to assess the percentage of circulating leukemia blasts (supplemental Figures S1C,S2), which is used to define disease state.

Construction of the transcriptome state-space and quasi-potentials

In order to follow changes in the state of the PBMC transcriptome over time during the course of AML initiation and progression, we constructed a two-dimensional state-space utilizing dimension reduction analysis on the time-series bulk RNA-seq data. We constructed a data matrix (X) so that each row corresponds to a sample and each column corresponds to a gene transcript level in log2 transformed counts per million (cpm) reads(17). We then performed principal component analysis (PCA) on the matrix X and identified the principal components for variance that most clearly associated with leukemia progression. Principal components (PCs) were computed via singular value decomposition (supplemental Figure S3A), which is one of several matrix factorization methods that can be used to deconvolve genomic data(18–21). The singular value decomposition is given by $\widehat{X}=U\mathrm{\Sigma }{V}^{*}$ where $\widehat{X}$ is column mean centered data and * denotes the conjugate transpose. The columns of the unitary matrix U, not to be confused with the quasi-potential U_p, form an orthonormal basis for the sample space (i.e., the temporal dynamics of the transcriptome), the diagonal matrix Σ contains the singular values, and the columns of the matrix V* correspond to the eigengenes(20) (see Table 1 glossary of terms), or loadings, of each gene in the transcriptome per PC.

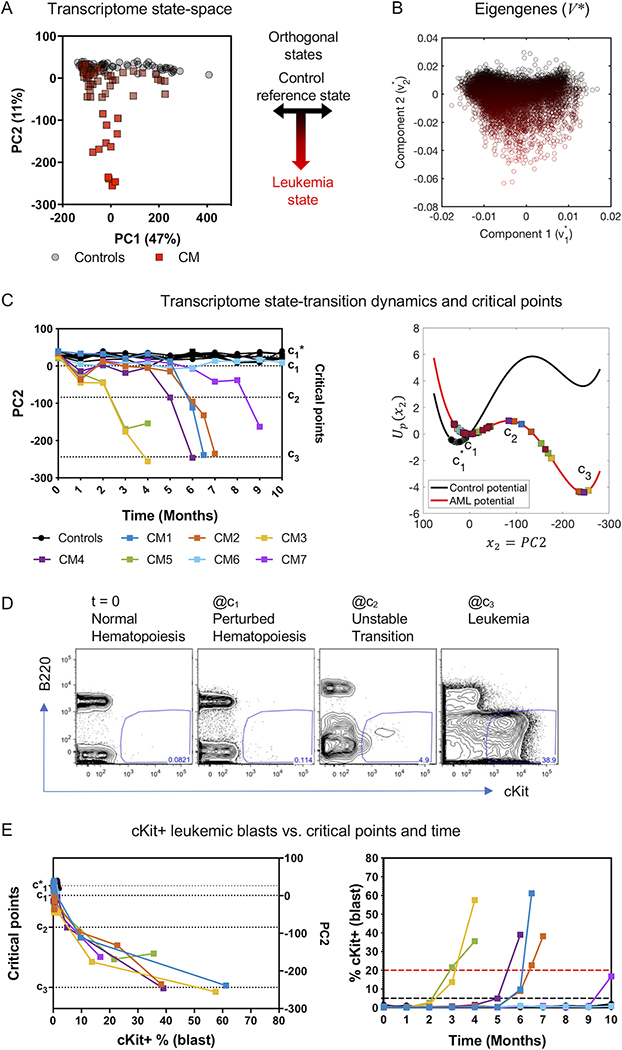
We found the “elbow” in the PC spectrum was captured in the first 4 components, representing a 66% of the total variation in the data (supplemental Figure S3B). An analysis of the first 4 components revealed that the first component (PC1) was correlated with time for all control and CM mice, suggesting transcriptional changes associated with aging. The second component (PC2) strongly correlated with the appearance of differentially expressed Kit (supplemental FigureS3C), which in this mouse model is a surrogate immunophenotypic marker for leukemic cells (blasts). The third and fourth principal components (PC3,PC4) were not interpretable (supplemental Figure S3D). We therefore constructed a 2-dimensional state-space with the first (denoted as non-leukemic) and second (denoted as leukemic) principal components, labeled (x₁,x₂) = (PC1,PC2) in order to study two orthogonal, mutually exclusive states; health and leukemia, so that each data point represents the transcriptome as a particle, which creates a trajectory through the 2D principal component space over time. We note that PCs are eigenvectors of the data matrix X and are orthogonal by construction. We therefore could have used any other component as a non-leukemic coordinate axis, for example (PC3, PC2). We chose PC1 for convenience and simplicity. We also examined other dimension reduction methods to construct the state-space, but found them to be sub-optimal due to free parameters (e.g., diffusion mapping(22)) or the inability to isolate leukemia trajectories with default settings (e.g., t-SNE(23), hierarchical clustering) (see supplemental methods, Figure S4-S5). We note that PCA is a parameter-free, linear method and these properties are advantageous because they simplify and make more objective the construction of the state-space.

We identified a geometric orientation of the transcriptome state-space such that the mean position of the reference (non-leukemic) state was located at PC2 = 0 and smoothly increased toward a leukemic state from north to south in the space along the PC2 axis (Figure 2A). This geometric interpretation allowed use to identify PC2 as a leukemic axis and model the contribution of each gene to the transition to leukemia state, by considering the loading matrix V*. The columns of the matrix V* represent the eigengenes corresponding to principal components so that each gene can be represented as a 2-dimensional vector with components $\overrightarrow{g}=(v_1^{*},v_2^{*})$ for the principal component state-space (x₁,x₂) = (PC1,PC2) (Figure 2B). This representation enables the decomposition of each gene into non-leukemic ($v_1^{*}$) and leukemic ($v_2^{*}$) components, and therefore the interpretation of the leukemic component of genes based on the contribution to the leukemia state ($v_2^{*}$) in differential expression analysis. We then mapped the trajectory of each mouse along the leukemic axis in the state-space (PC2) over time and computed the shape of the double-well quasi-potentials used to model state-transition along the leukemic axis PC2 (U_p(x₂)) via estimation of the critical points $c_1^{*}$, c₁, c₂, c₃ (Figure 2C, supplemental Figure S6A-B).

Figure 2. Construction of the transcriptome state-space and estimation of state-transition critical points.

A) The first two principal components (PCs) representing 58% of the variance in the data, and gene weights (eigengenes) corresponding to PCs are shown. The first principal component correlates with time and is likely due to the aging process (supplemental Figure S3D) and explains 47% of the variance in the data. The second principal component (PC2) explains 11% of the variance and shows a strong correlation with the appearance of differentially expressed Kit, which in this mouse model is a surrogate immunophenotypic marker for leukemic cells (supplemental Figure S3C) and encodes transition from health to leukemia. Therefore PC1 and PC2 are used create a 2D orthogonal transcriptome state-space where each dot is an individual transcriptome from control (circles) and CM (squares) mice at different time points. B) The PCA weights for all sequenced genes corresponding to the first two PCs from the loading matrix (V*). The points in A) and B) are pseudo-colored from black to red, from north to south to indicate transition to leukemia. C) Temporal dynamics and state-transition critical points. Left: Transcriptome state-space trajectories of individual mice along PC2 plotted over time (controls in black; CM induced mice in colors). Right: state-transition critical points and dynamics of PC2 mapped onto the quasi-potential energy (U_p(x₂)) for control and CM mice. Controls remain at the reference state ($c_1^{*}$) and CM induced mice transition from the reference state of perturbed hematopoiesis (c₁) to the leukemic state (c₃). D) Representative flow cytometry plots of leukemia blasts (cKit⁺) frequency detected in the blood before induction and at each critical point. B220 is a B cell lineage marker and is not expressed on leukemia blasts. E) The frequency of cKit⁺ leukemia blasts increases rapidly after crossing c₂ transition point and increase over time as the mice develop leukemia.

Results

Transcriptome dynamics precede detection of leukemic blasts

As early as one month following induction of CM and despite the absence of any circulating leukemic (cKit⁺) blasts, we detected initial changes of the transcriptome position toward the leukemia state (p<0.01, supplemental Figure 6C), likely representing the early CM-driven hematopoietic perturbations that we have previously reported(15,16,24). Leukemic blasts were initially detected (>5% by flow cytometry) once the transcriptome-particle approached the unstable critical point c₂ in the state-space. Once the transcriptome crossed c₂, consistent with the predicted acceleration of transition toward the leukemia state c₃, we observed a rapid increase of leukemic blasts and manifestation of overt disease (Figure 2D). The acceleration after crossing c₂ was also supported by increasing velocity calculated between each pair of time-sequential points in the state-space (supplemental Figure S6D). Of note, levels of Kit expression in the transcriptome correlated with the number of PB cKit+ cells (blasts) and the PC2 position only after the mice began to develop leukemia (Figure 2E, supplemental Figure S7A,B), implying that expression changes of genes other than Kit contributed to the variance in the data and thus to the initial movement of the transcriptome in the state-space before any sign of disease was detectable.

Biological interpretation of the critical points in the transcriptome state-space

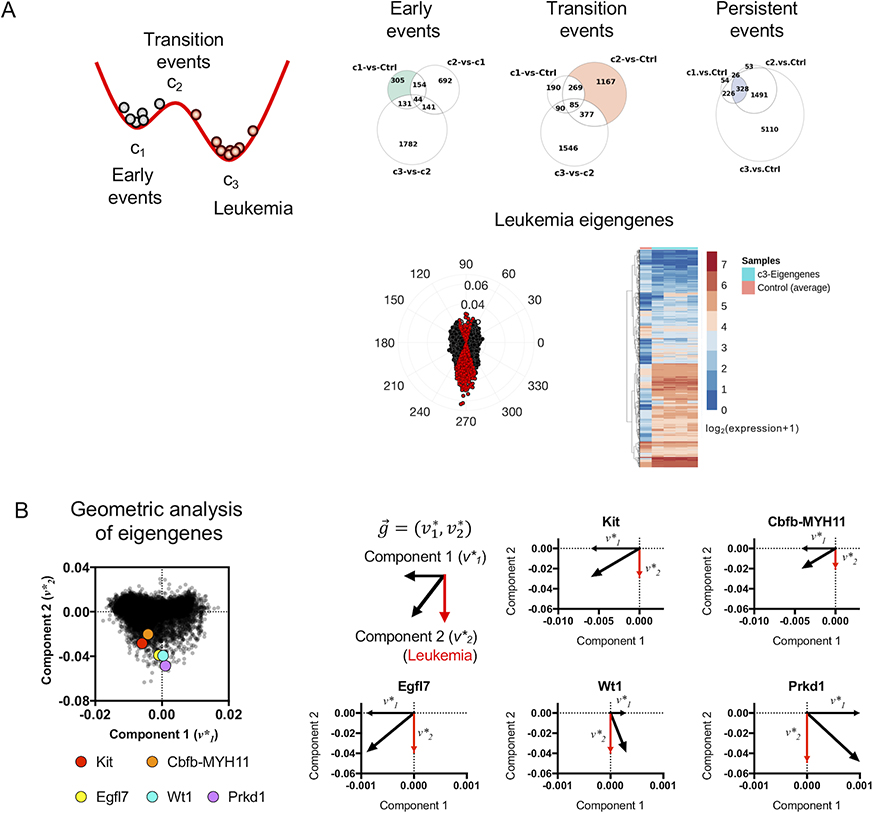
Because state-transition theory enables the interpretation of time-series genomic data in terms of critical points, we hypothesized that the transcriptome changes [differentially expressed genes (DEGs)] occurring at each critical point ($c_1^{*},c_1,c_2,c_3$) also represented critical biological alterations that drive the evolution of the disease (Figure 3A). To identify these alterations, we partitioned the data such that each sample was associated with a unique critical point with the smallest distance in the state-space (Figure 3A). We then identified DEGs by performing pairwise comparisons of gene expression at each of the critical points with that of the reference state (i.e., c₁ vs $c_1^{*}$; c₂ vs $c_1^{*}$; c₃ vs $c_1^{*}$) and with that of other critical points (c₂ vs c₁; c₃ vs c₁; c₃ vs c₂) using edgeR and a false discovery rate of 0.05 (Table 2, supplemental Figure S8, Tables S1-6). We then categorized the DEGs at each critical point as early events (c₁ vs. $c_1^{*}$, ~c₂ vs. c₁; ~c₃ vs. c₂), transition events (c₂ vs. $c_1^{*}$, ~c₁ vs. $c_1^{*}$; ~c₃ vs. c₂), and persistent events, genes that remained as DEGs at all three of the critical points (c₁ vs. $c_1^{*}$; c₂ vs. $c_1^{*}$; c₃ vs. $c_1^{*}$) where ~ denotes the exclusion of genes from that comparison (Fig. 3A; supplemental Figure S8, Tables S7-S10).

Figure 3. State-transition critical point-based analysis of gene expression in leukemia progression.

A) The state-transition model is used to group samples relative to critical points. Early, transition, and persistent events in leukemia progression are defined relative to critical points. Leukemia eigengenes are a subset of eigengenes shown in Figure 2B, and are defined geometrically in the state-space (see supplemental Figure S10). Leukemia eigengenes are plotted in red in a radial histogram along with the other eigengenes in black. Leukemia eigengene expression is shown in a heatmap as compared to the average expression in control samples. B) Geometric representation and decomposition of eigengenes. Eigengene weights (V*, see Figure 2B, supplemental Figure S3A) for the first two components are plotted for all genes (black). Selected genes (Kit, CM, Egfl7, Wt1, Prkd1) are shown in colors and are oriented south in the space indicating relative contribution to state-transition to leukemia. The larger the magnitude, and more south is the red portion of the gene vector component ($v_2^{*}$), the stronger is the relative contribution of that gene to the variance associated with leukemia.

Table 2. Differentially expressed genes based on critical points.

Thousands of genes are differentially expressed across critical points in the transcriptome state-transition from health to leukemia (q<0.05, |log2(FC)|>1).

Test vs. reference	#genes down	#genes up	#genes total
c1 vs control (${\mathit{c}}_{\mathbf{1}}^{*}$)	2,305	1,859	4,164
c2 vs control (${\mathit{c}}_{\mathbf{1}}^{*}$)	4,421	4,126	8,547
c3 vs control (${\mathit{c}}_{\mathbf{1}}^{*}$)	6,119	5,515	11,634
c2 vs c1	3,560	3,772	7,332
c3 vs c1	5,744	5,565	11,309
c3 vs c1	3,602	3,274	6,876

Gene Ontology (GO) analysis revealed insights into the biological and functional impact of DEGs associated with each critical point in the transition from normal hematopoiesis to leukemia (supplemental Table S11-S14). For transcriptional early events at c₁, the top three GO terms ranked by q-value (multiple-test corrected p-value) included extracellular matrix organization (GO-0030198), cellular response to cytokine stimulus (GO-0071345) and cytokine-mediated signaling pathway (GO-0070098) (Figure 3A; Figure S9A; Table S11). For the transition events at ~c₂, the top three ranked GO terms included DNA metabolic processes (GO-0006259), DNA replication (GO-0006260), and G1-S transition of mitotic cell cycle (GO-0000082) (Figure 3A; Figure S9B; Table S12). For the persistent events at c₁, which are the DEGs that continued to be differentially expressed also at the critical points c₂ and c₃, the top three ranked GO terms included positive regulation of phosphatidylinositol 3-kinase activity (GO-0043552), positive regulation of phospholipid metabolic process (GO-1903727), and positive regulation of lipid kinase activity (GO-0090218) (Figure 3A; Figure S9C; Table S13). Interestingly, consistent with increasing leukemic blasts, Kit up-regulation was observed among the persistent events.

Quantification of individual genes and pathways contribution to leukemia progression

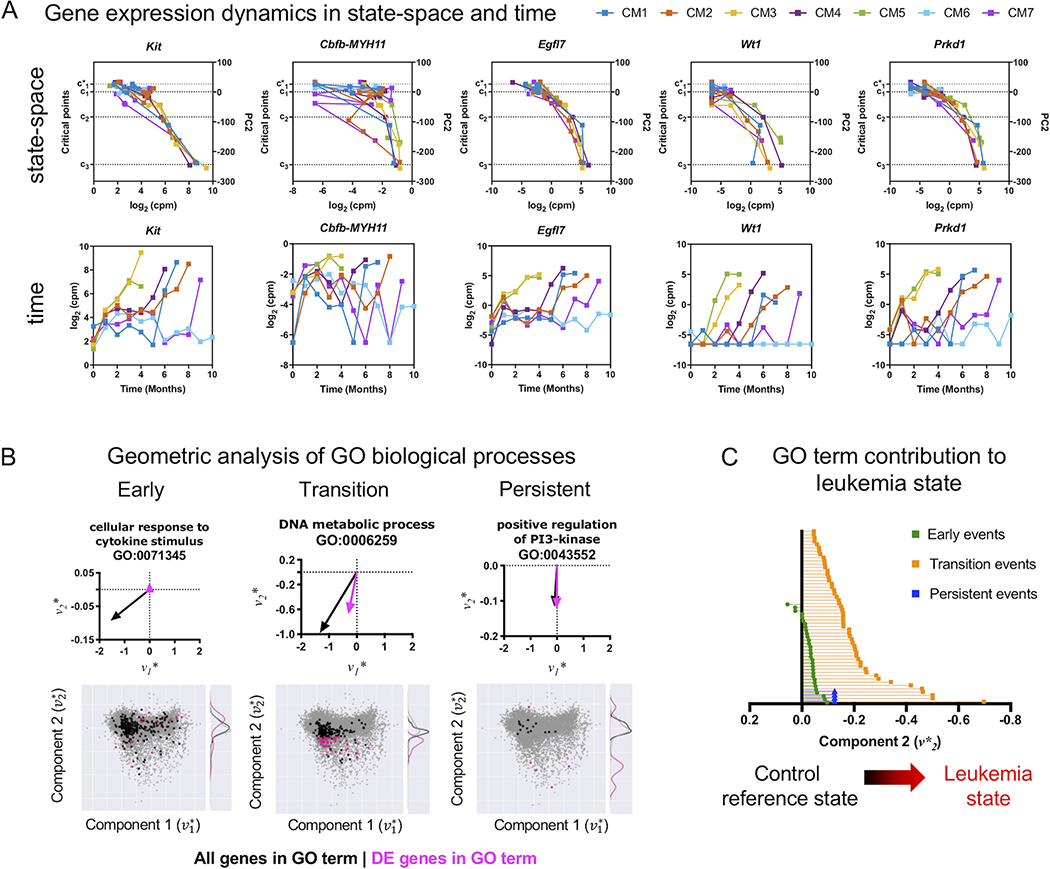
Given the 2-dimensional geometry of the transcriptome state-space, as demonstrated in Figure 2B, we were also able to decompose the contribution of each gene to leukemia progression by considering the second component ($v_2^{*}$) of the eigengene vector $\overrightarrow{g}=(v_1^{*},v_2^{*})$. For instance, considering the expression of leukemia marker Kit and the leukemogenic CM genes, we showed that the magnitude of the second component of both genes was negative ($v_2^{*}<0$) and therefore pointing south in the state-space, contributing to the variance in the transcriptome associated with leukemia, with $\overrightarrow{kit}=(-0.0060,-0.0284)$ and $\overrightarrow{CM}=(-0.0042,-0.0202)$ (Figure 3B). Analysis of the top 1% of eigengenes (Table S15) which were also identified as persistent events showed strong contribution to leukemia. To illustrate quantification of leukemia contribution and state-space trajectory, we selected several of these genes based on known functions in AML (Egfl7, Wt1) (25–29) or cancer progression (Prkd1) (30–32). Indeed, the proangiogenic factor Egfl7 [$\overrightarrow{Egfl7}=(-0.0009,-0.0390)$], leukemia-associated antigen Wt1 [$\overrightarrow{Wt1}=(0.0003,-0.0395)$] and the protein kinase Prkd1 [$\overrightarrow{Prkd1}=(0.0010,-0.0486)$] were among the genes showing the strongest contributions toward leukemia (Figure 3B; see supplemental Table S7-10 for decomposition of each gene). Accordingly, all CM mice that developed leukemia (CM1–5, CM7) showed increasing expression of these leukemia eigengenes (Kit, CM, Egfl7, Wt1, Prkd1) and reproducible trajectories in the state-space as they move from perturbed hematopoiesis (c₁) to leukemia (c₃) (Figure 4A). The trajectories of the leukemia eigengenes, determined by plotting eigengene expression in the state-space, were remarkably concordant for all CM leukemia mice (Figure 4A, top), in contrast to the nonsynchronous changes observed over time (Figure 4A, bottom). In other words, the transcriptomic state—as defined by location in the state-space—consistently aligned leukemia eigengene dynamics across all CM mice despite the fact that mice develop overt leukemia stochastically at different times. Therefore, analysis of gene expression dynamics with the transcriptome state-space provided a meaningful approach to align gene expression dynamics and to quantify the leukemogenic contribution of individual genes as well as the collective contribution of a set of genes.

Figure 4. Geometric analysis of gene expression and quantification of pathways contribution to leukemia progression.

A) Gene expression dynamics in state-space and time. Expression levels for selected leukemia eigengenes Kit, CM, Egfl7, Wt1, Prkd1 are plotted against the state-space (PC2) (top) or plotted against time (bottom) for CM mice. Increasing expression of these genes are concordant with movement from normal hematopoiesis ($c_1^{*}$) to leukemia (c₃) in the state-space despite the variability of expression over time. Representing gene expression dynamics in the state-space reveals alignment of gene dynamics by disease state, rather than the passage of time, which is more variable depending on when each mouse stochastically develops leukemia. B) Top: Geometric and vector analysis of GO terms overall (black) and genes (pink) that are differentially expressed (DE). The sum total of genes in a GO term (black vector) and the portion which is differentially expressed (pink vector) are used to geometrically interpret the contribution of the step-wise contribution of each GO term towards leukemia progression. Bottom: The eigengene state-space is used to represent genes and biological pathways identified through pathway enrichment analysis as vectors. Subsets of genes in a given pathway which are differentially expressed are shown in pink and the distribution along the second component is shown as a kernel density. As with the gene analysis, the larger the magnitude and more south is the pink portion of the vector, the stronger is the relative contribution of the pathway to the variance in the transcriptome associated with transition to a state of leukemia. Selected pathways for early, transition, and persistent events are shown. C) The leukemia component of the vector representation of each GO term enriched in the early, transition, and persistent events is shown. Biological pathways represented as vectors demonstrate increasing orientation in the state-space towards the state of leukemia ($v_2^{*}$), with some early events pointing away from leukemia, suggesting a restorative homeostatic effect in the variance of the transcriptome. Few early events show a contribution away from the leukemia state, suggesting a homeostatic restorative force attempting to counteract the action of the leukemogenic perturbation caused by CM.

With this geometric interpretation in hand, we could also quantify the contribution of gene pathways, defined by GO terms, as the vector sum of each constituent eigengene, so that $\overrightarrow{G}=(G_1,G_2)=({\sum }_{i=1}^n{g}_1^i,{\sum }_{j=1}^n{g}_2^j)$. The second component of the summed vector, G₂ represents the maximum contribution of an individual GO term pathway G to leukemogenesis (Figure 4B; black vector). To this end, of the all of the constituent genes for a GO term (black dots), we considered only those that were DEGs (pink dots) and thus active contributors in each pathway to leukemogenesis (Figure 4B; pink vector). As such, each significantly enriched GO term could be quantitatively analyzed for its relative contribution to leukemogenesis as the sum total $v_2^{*}$ contributions of the DEGs in that particular GO term.

To evaluate the step-wise contribution of the GO terms, we then performed vector analysis of the GO pathways enriched in early, transition, and persistent events and represented them as vectors in the state-space (Figure 4B). Notably, our analysis of early events that characterize c₁ revealed some GO pathways that exhibited contributions away from leukemia (i.e. north, $\overrightarrow{G_2^i}>0$)(Figure 4C), suggesting the presence of a restorative force that attempted to counteract the initially CM-driven hematopoietic perturbation and restore the system to a reference state of normal hematopoiesis. On the other hand, analysis of GO terms that characterized transition and persistent events demonstrated an increasing magnitude and direction (angle) toward the leukemic state (Figure 4B). Evaluation of all early, transition, and persistent GO terms revealed a strong overall leukemogenic contribution (Figure 4C), underscoring the unique biological insights that could be gained by an analytical approach based on critical points of the transcriptome state-space.

Analysis of the leukemic transcriptome at c₃ showed dysregulation of a large number (11,634) of genes (Table 2, supplemental Figure S8, Table S5), making it difficult to perform pathway enrichment or to interpret in terms of contribution to leukemia. Thus, we filtered genes with a geometric criteria to include genes within a range of angles in the state-space that were most strongly associated with leukemia (Figure 3A; supplemental Figure S10). This approach identified differentially expressed leukemia eigengenes (leukemia eigenDEG; supplemental Table S10). The top three GO terms for leukemia eigenDEG ranked by q-value included mitotic spindle organization (GO-0007052), centromere complex assembly (GO-0034508), and microtubule cytoskeleton organization involved in mitosis (GO-1902850) (supplemental Table S14), consistent with the hyper-proliferative phenotype, leukemic cell trafficking, and extramedullary tissue infiltration associated with late-stage disease.

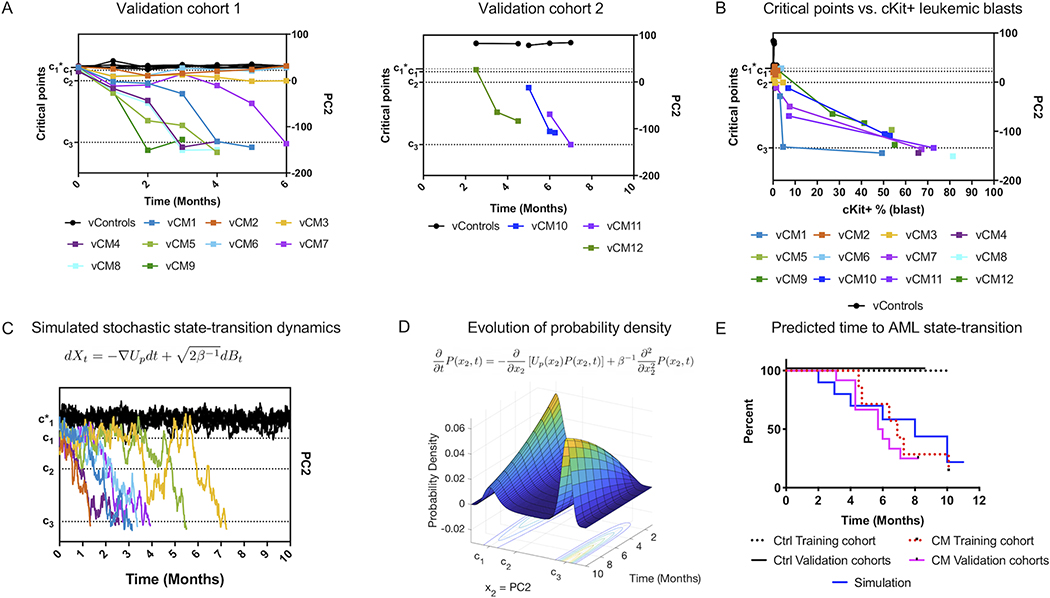
Validation studies in independent cohorts of mice

To validate our state-transition model, state-space, and analytical approach, we performed independent experiments to collect PBMC bulk RNA-seq data from two additional validation (v) cohorts of control (vControl) and CM (vCM) mice which were similarly induced with poly (I:C) as described for the training cohort. We collected validation cohort 1 samples (vControl1–7; vCM1–9) monthly for up to 6 months; and collected validation cohort 2 samples (vControl8–9; vCM10–12) sparsely at 3 randomly selected timepoints during leukemia progression. We performed principal component analysis of the validation cohort 1 and 2 data, which again demonstrated that the majority of the variance was encoded in the first 4 PCs (supplemental Figure S11A-C) and the leukemia-related variance was again encoded in PC2 (Figure 5A). We then evaluated our ability to map state-transition trajectories and predict leukemia development in the validation cohorts by projecting the data from the validation cohorts into the state-space constructed using the training cohort (see supplemental methods). The trajectories of vControls in both validation cohorts remained at $c_1^{*}$, whereas vCM mice that developed leukemia in both validation cohorts progressed toward the leukemia state at c₃. Of note, three CM-induced mice in the validation cohort 1 (vCM2, 3, 6) did not develop leukemia during the 6-month study period, and were mapped to positions in the state-space between c₁ and c₂ but did not cross the transition point c₂ (Figure 5A; S11D), consistent with a delayed onset of leukemia. These mice showed pre-leukemic states in the bone marrow (i.e., expansion of pre-leukemic progenitor populations) at the end of the study, indicating leukemia progression was taking place but had not yet manifested (supplemental Figure S2). As in the original analysis and similar to the initial dataset, we detected early movement of the transcriptome-particles representing CM mice at c₁, 1 month (T1) after induction of CM expression (supplemental Figures S11E). We also observed similar state-space trajectories, in that acceleration of the transcriptome-particle toward the leukemia state occurred once it crossed the unstable critical point c₂, which also corresponded to a rapid increase in cKit+ cells detected in the peripheral blood (Figure 5B).

Figure 5. Validation and prediction of leukemia development in independent cohorts.

As a validation of the state-transition mathematical model, critical points, and state-space geometry, we mapped data from two additional independent experiments into the state-space: cohort 1 and cohort 2. Cohort 1 consists of 7 controls and 9 CM mice (vCM1–9) sampled at the same frequency as the training cohort. Cohort 2 consists of 2 controls and 3 CM mice (vCM10–12) sampled sparsely in time. A) Leukemia trajectories (PC2) of validation cohorts projected into the state-space constructed with the training cohort. Critical points were estimated with the same procedure as the training data set. The locations in the transcriptome state-space correctly identify controls and states of leukemia, even in cohort 2 which does not include timepoints prior to CM induction. B) The frequency of cKit⁺ leukemia blasts increases rapidly after crossing c₂ transition point. C) The equation of motion of the transcriptome-particle in the quasi-potential is a stochastic differential equation which predicts trajectories of state-transition. One realization of a stochastic simulation is shown (controls black, CM induced mice in colors). Controls remain at the reference state ($c_1^{*}$) and CM induced mice transition from the reference state of perturbed hematopoiesis (c₁) to the leukemic state (c₃). D) Due to the stochastic nature of the biological processes and variability in RNA-seq data, we predict state-transition by considering the spatial-temporal evolution of the probability density (P(x₂,t)) given by numerically solving the Fokker-Planck equation with initial conditions and simulation parameters determined by the training cohort. E) The predicted (simulated) time to state-transition is calculated by integrating the probability density. The predicted time to develop leukemia is compared to the observed time to leukemia with a survival analysis for validation cohorts (cohort 1 and 2; CM n=12; Ctrl n=9). Survival curves for the training cohort is also shown (red dashed lines, CM=7; black dashed lines, Ctrl n=7). The observed and simulated time to AML are not statistically different from each other (p >> 0.05).

Prediction of leukemia development and progression

Mathematically, we model the transcriptional state of the system as a particle in a quasi-potential with a Langevin equation of motion given by the stochastic differential equation $d{X}_t=-\nabla U_{p}dt+\sqrt{2{\beta }^{-1}}d{B}_t$ where X_t denotes the state of the transcriptome at time t, U_p is the quasi-potential, and dB_t is a Brownian motion that is uncorrelated in time $<B_{t_i},B_{t_j}>={\delta }_{i,j}$, with δ_i,j being the Dirac delta function and β⁻¹ is the diffusion coefficient. An example realization of the stochastic equation of motion for control and CM mice is shown in Figure 5C. Because of the stochasticity due to biological, experimental, technical, or time-sampling variations, transcriptome trajectories cannot be precisely predicted with this approach.

In order to calculate the mean expected behavior of the stochastic dynamics of a transcriptome-particle, we consider the evolution of the probability density function. The spatial and temporal evolution of the probability density for the position of a particle P(x₂,t) is given by the solution of the Fokker-Planck (FP) equation based on the shape of the potential (U_p(x₂)) and equation of motion as:

$$\frac{\partial }{\partial t}P(x_2,t)=-\frac{\partial }{\partial x_2}\left(U_p(x_2)P(x_2,t)\right)+\frac{{\partial }^2}{\partial x_2^2}({\beta }^{-1}P(x_2,t))$$ (1)

where x₂ is the spatial coordinate (PC2) and β⁻¹ is the diffusion coefficient, which we estimated with a mean-squared displacement analysis of state-space trajectories (supplemental Figure S12A)(6). Solution of the FP permits the direct calculation of the expected first arrival time from an initial point (e.g., perturbed hematopoiesis c₁) in the state-space to a final point (e.g., leukemia c₃).

In order to predict the time to develop leukemia in the validation cohorts, we numerically solved the FP equation using the parameters estimated from the training cohort with initial conditions derived from the validation cohorts 1 and 2 and integrate the probability density (Eq. 1, Figure 5D). The simulation accurately predicted the time to leukemia for all CM mice (n=9) that eventually developed leukemia during the study period (p>>0.05, Figure 5E). Parameters used in the simulations are given in supplemental material (Figure S12B,C). Of note, the model correctly predicted the delayed onset of overt leukemia in the three CM-induced mice in the validation cohort 1 (vCM2, 3, 6) that did not develop leukemia during the 6-month study period.

Discussion

Here we report the application of state-transition theory to interpret temporal genomic data and accurately predict leukemia development in a murine model of AML. As a proof of principle, we obtained time-sequential RNA-seq data from a well-characterized orthotopic mouse model of inv(16) AML and modelled state-transition from health to leukemia. We demonstrate the feasibility of predicting state-transition dynamics and time to leukemia using these time-sequential genomic data collected at sparse timepoints. Our results show that movement of the transcriptome, represented as a particle in a state-space, can be understood in terms of critical points—mathematically-derived inflection points—which provide a framework to predict the development of leukemia at any point in the space, at any timepoint, without the presence of detectable leukemic blasts.

One of the greatest challenges in analyzing time-sequential genomic data is the fact that multiple signal(s) of interest (i.e., genes relevant to leukemia) often are not synchronized in time. Although methods exist to perform time realignment or estimate parameters of a predictive probability density function(33–37), these methods often require prior knowledge of the system dynamics or have not been experimentally validated in a cancer model. Here, we modeled the development of AML as state-transition of the transcriptome-particle in a leukemia state-space with a double-well quasi-potential. This method does not require a priori information, and allows for a wide range of nonlinear dynamics, including transient changes of the genes due to stochastic variations or biological fluctuations, for example environmental conditions that may be random. Furthermore, our approach guides interpretation of temporal genomic data even when data are incomplete or sparse—as is often the case with longitudinal human data from the clinic.

Through the analysis of DEGs based on state-transition critical points, we identified early, transition, and persistent transcriptional events, and identified perturbations of gene expression associated with critical step-wise development of leukemia, which we refer to as eigengenes. Early events are enriched for cellular response to cytokine stimulus and cytokine-mediated signaling pathway, consistent with previously reported altered cell signaling and impaired lineage differentiation induced by the CM oncogene(16,24). Notably, our results revealed that early perturbations associated with critical point c₁ are not necessarily contributing positively to leukemogenesis but may instead represent a counteracting homeostatic response. The transition events associated with the unstable critical point c₂ were characterized by aberrant expression of many genes involved in DNA damage and DNA repair, consistent with the notion that additional cooperating mutations or epigenetic alterations are required for a full leukemia development (15,16). Furthermore, we identified genes that, although not uniquely associated with individual critical points, were persistently and differentially expressed at all critical points c₁, c₂ and c₃ during the leukemia state-transition. These genes are mainly involved in signaling pathways that support cell proliferation and survival, and vector analyses demonstrated a direction of strong contribution to the variance associated with leukemia. These persistent events can be interpreted as a force cooperating with the CM oncogene to propel the change of the system’s transcriptional state from the reference state to the leukemia state. Based on this analysis, we postulate that AML and perhaps cancer in general, can be considered an eigenstate of the transcriptome; that is to say that AML is an energetically favorable configuration of the transcriptome as a whole, that evolves in parallel to clonal expansion of malignant cells.

Furthermore, the location and trajectory of individual genes in the state-space allows assessment of the direction and the magnitude with which individual genes contribute to the transition to leukemia. For example, among the persistent events Egfl7, Wt1 and Prkd1 showed a strong selectivity in the direction toward leukemia and their expression level consistently increased during transition toward leukemia, particularly between c₁ and c₂ in the state-space. Indeed, the human homolog of these genes have been implicated in leukemia or cancer pathobiology. The angiogenic factor EGFL7 is known to be highly expressed and predict poor prognosis in AML patients (25), and is also a host gene of miR-126, which is a miRNA signature associated with inv(16) AML(38) and leukemia stem cell quiescence and drug resistance(39). The Wilms’ tumor gene WT1 is overexpressed and plays an oncogenic role in leukemia and various solid tumors. In AML, overexpression of WT1 has been found to predict poor prognosis and minimal residual disease(26,27,29). Prkd1 encodes a serine/threonine protein kinase and is part of all top 3 ranked GO terms enriched for persistent events. The specific role of PRKD1 in AML has not been described, however, it is known to promote invasion, cancer stemness and drug resistance in several solid tumors(30–32). In addition to these genes, our approach identified many other genes showing a strong contribution to leukemia development (Table S8-S11). Many of these genes have not been previously linked to leukemia, highlighting that the state-transition based approach offers novel biological insights and hypotheses for further investigation.

State-transition theory and corresponding mathematical models have been applied to other systems and to other omics data platforms (e.g., epigenomics, miRomics)(7,40,41). However, our application to the interpretation of leukemia evolution is novel in the use of time-series bulk RNA-seq data collected from the peripheral blood. We chose to use PB as a tissue of interest because changes in the cellular composition of PBMCs are obvious once AML is clinically present and it is much more accessible for frequent sequential sampling than BM, and therefore this approach could potentially be more easily applied to patients with leukemia and other hematopoietic malignancies in the clinical setting. Nevertheless, with the development of more sensitive approaches that include “liquid biopsies” for solid tumors, it is possible that this approach could be also be extended to patients with solid tumors. Meanwhile, future studies will examine the relationships between the changes in the transcriptomic states of the BM and PBMCs, and to estimate more precisely the magnitude of perturbations detectable in the transcriptome. Notably, our state-transition model allowed us to derive useful information about the state of the system as a whole, without concern for heterogeneity related to additional mutations, clonal dynamics, or composition of cells within the sample. To our knowledge, other approaches currently available to analyze time-series genomic data such as those that use concepts of thermodynamic (non)equilibrium and statistical mechanics(42) may be useful tools for analyzing cellular state transitions (e.g., epithelial to mesenchymal transition(41) and early stages of carcinogenesis(43)), but they do not provide similar geometric- or critical point-based interpretation of genes or pathways as we report herein. Our approach builds on these works and offers an opportunity to anticipate critical transitions in cancer initiation and progression as proposed by Scheffer et al in their seminal work(44).

Recent studies have interrogated the clonal architecture of AML over time(45), and shown that somatic mutations may precede diagnosis of AML by months or years(46) and that deep sequencing of mutations can be used to differentiate age-related clonal hematopoiesis from pre-AML and predict AML risk in otherwise healthy individuals(47). Our approach detects system-wide perturbation before any leukemic blasts are seen in the blood, or differential expression of known leukemogenic marker genes, suggesting the signal detected by bulk RNA-seq is not driven solely by the presence of leukemic cells. Our model presents a view of cancer as a change in transcriptional state of the system as a whole, which occurs in parallel with, and in addition to, DNA mutations and clonal evolution of malignant cells. Our model provides a predictive mathematical framework to identify a transition point (c₂) in leukemia development. Notably, this transition point also marks a point of accelerated leukemia progression manifested on the level of leukemia blast counts as well as the transcriptome movement. Importantly, although data from a relatively simple mouse model of AML were used to develop this theoretical framework, we demonstrated that the results are reproducible in multiple cohorts (i.e., one training cohort and two validation cohorts) and that the robustness of this approach is not affected by variability in sampling time, frequency, sample preparation, or data normalization methods (supplemental Figure S13–S14). Moreover, we show that the transcriptome data from independent validation cohorts can be mapped into a previously built leukemia state-space, suggesting that our approach robustly isolated leukemia related signals in the context of a defined genetic mouse model.

We expect that in the future, state-transition dynamical models could be applied in the clinic to support proactive monitoring to detect transcriptional perturbations away from a reference state of health or complete remission after treatment to a state of disease or vice versa(48). However, applications to humans possess challenges. Because of the background genomic variability across humans, it may be that the leukemia trajectories are encoded in multiple principle components. As we have done with the mice, a careful examination of all PCs may be required to extract the signal associated with leukemia in humans. Given the enormous number of changes in the genome over the course of leukemia progression, we expect variability driven by leukemia processes will be encoded in a single principal component despite the variance due to genomic background and disease etiology across individuals. If this is not the case, signal amplification techniques may be required such as contrastive PCA(49) or gene filtering based on information criteria such as mutual information. An alternative approach may be to utilize pseudotime methods to construct trajectories across patients with similar disease states(50). Our expectation is that in the near future, our state-transition dynamical model could be tested in the clinic as a monitoring tool to detect transcriptome perturbations and predict changes in the state of the disease thereby providing useful information for therapeutic intervention by targeting pathways at or before critical points in state-transition(48).

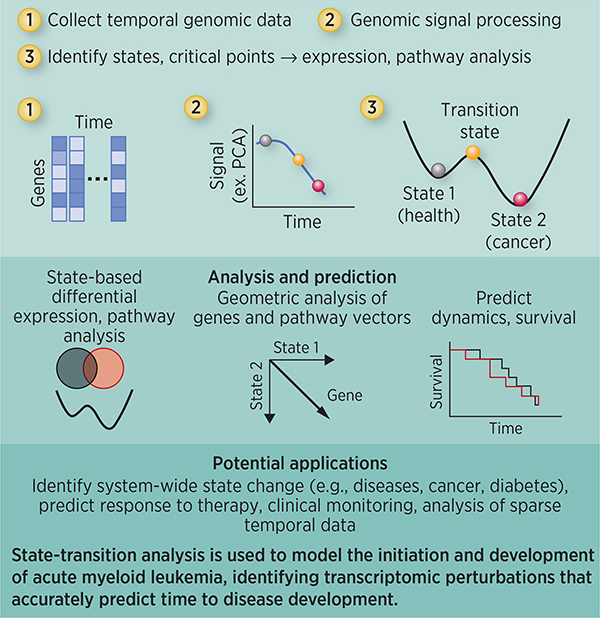
State-transition theory identifies critical points and predicts leukemia development

Statement of Significance.

Findings apply the theory of state transitions to model the initiation and development of acute myeloid leukemia, identifying transcriptomic perturbations that accurately predict time to disease development.