Abstract
Coronavirus Disease 2019 (COVID-19) may spread through respiratory droplets released by infected individuals during coughing, sneezing, or speaking. Given the limited supply of professional respirators and face masks, the U.S. Centers for Disease Control and Prevention (CDC) has recommended home-made cloth face coverings for use by the general public. While there have been several studies on aerosol filtration performance of household fabrics, their effectiveness at blocking larger droplets has not been investigated. Here, we ascertained the performance of 11 common household fabrics at blocking large, high-velocity droplets, using a commercial medical mask as a benchmark. We also assessed the breathability (air permeability), texture, fiber composition, and water absorption properties of the fabrics. We found that most fabrics have substantial blocking efficiency (median values >70%). In particular, two layers of highly permeable fabric, such as T-shirt cloth, blocks droplets with an efficiency (>94%) similar to that of medical masks, while being approximately twice as breathable. The first layer allows about 17% of the droplet volume to transmit, but it significantly reduces their velocity. This allows the second layer to trap the transmitted droplets resulting in high blocking efficacy. Overall, our study suggests that cloth face coverings, especially with multiple layers, may help reduce droplet transmission of respiratory infections. Furthermore, face coverings made from materials such as cotton fabrics allow washing and reusing, and can help reduce the adverse environmental effects of widespread use of commercial disposable and non-biodegradable facemasks.
Keywords: Cloth face covering, Face mask, SARS-CoV-2, COVID-19, Respiratory droplets, Droplet blocking, Breathability
Respiratory infections caused by novel pathogenic agents (e.g., a novel virus) can lead to epidemics or pandemics. Existing knowledge from respiratory infections such as influenza, SARS-1, and MERS indicates three major routes of transmission, namely, droplets, aerosols, and contact [1], [2], [3]. Although the mechanism of spread of the current novel coronavirus (SARS-CoV-2) is not clearly understood, it is thought that spread can occur through respiratory droplets containing virus particles that are released by infected persons when they sneeze, cough, or speak [4], [5]. Larger droplets tend to fall nearby by gravity, and the sufficiently smaller ones can stay in the air and travel longer [1], [6], [7]. Droplets containing viruses may be shed by symptomatic as well as pre-symptomatic and asymptomatic individuals [8], [9], [10], [11]. If inhaled by a healthy individual, droplets allow the virus to enter the respiratory system and cause infection. Face coverings offer a physical barrier against virus transmission, and can be especially useful as a method of source control. For example, medical masks have recently been shown to be highly effective in reducing the dissemination of droplets of all sizes from COVID patients [12].
During the COVID-19 pandemic, the supply of commercially manufactured respirators and facemasks has not been able to meet the demand. The U.S. CDC has therefore provided guidance for the public to use alternatives such as cloth face coverings to slow the spread of COVID-19 [13]. However, it is not yet clear what kind of fabric would be the most efficient material or how many layers of cloth would protect against both spreading and contracting the virus. Existing literature on cloth masks have mostly focused on the filtration efficiency of household materials against dry or liquid aerosols with particle/droplet sizes within the range of 10 nm to [14], [15], [16], [17], [18], [19]. Such studies are based on the well-established theoretical and experimental foundations of aerosol filtration by fibrous media. However, when an individual coughs, sneezes, or speaks, the droplets that are released typically have a size distribution that includes larger droplets (up to 1 mm in size) in addition to the aerosolized fraction (< size) [20], [21], [22], [23]. Established knowledge from aerosol science may not be immediately applicable to determine the efficiency of mask materials at blocking larger droplets carrying virus particles. How effective cloth face coverings can be at reducing transmission via large droplets therefore remains elusive.
To address this issue in the current context of COVID-19, we developed a method of quantifying the effectiveness of fabrics at blocking large droplets containing 100 nm-diameter nanoparticles which serve as a mimic for viruses in terms of size. We considered a wide range of regular household fabrics using a commercial medical mask as a benchmark. Our work is meant to complement existing information on the aerosol filtration efficiency of household fabrics [14], [15], [16], [17], [18], [19] and offer insight into the possible mechanisms of how fabrics may block virus transmission via large respiratory droplets.
In this study, we did not consider methods for producing a facemask, e.g., how they should be stitched, how their boundaries should be designed, how to attach them to the face, and how they should be used or decontaminated. For detailed information on how to make, use, and decontaminate cloth face coverings, we refer the reader to guidelines provided by the U.S. CDC and World Health Organization [13], [24].
1. Results and discussion
1.1. Problem definition
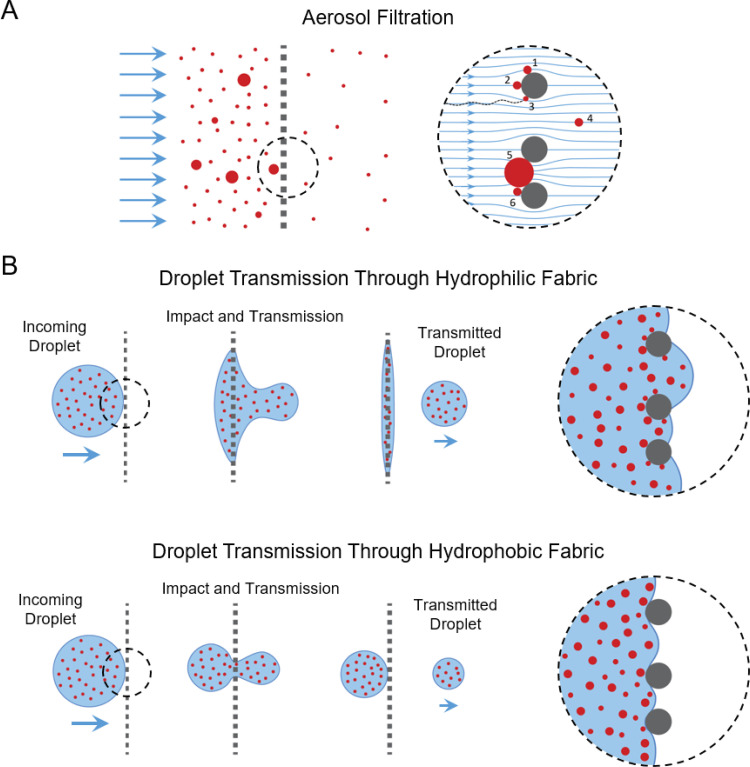
Aerosol Filtration versus droplet blocking: We first illustrate the key distinctions between filtering aerosol particles and blocking larger droplets by fabrics (Fig. 1). There is a well-established theoretical and experimental body of literature on aerosol filtration by fibrous materials [25], [26], [27], [28], [29], [30], [31]. For aerosols, particle sizes considered are often within the 10 nm to 5– range, smaller than or comparable to the fiber diameter and inter-fiber spacing of the fibrous filter. Typically, the particles are treated as solids. This holds naturally for dry aerosols, but it is also a reasonable assumption for liquid aerosols since, at the small scale, surface tension dominates and droplets behave as solid particles. Such particles can be captured by fibers of the filter via mechanisms such as direct impaction, interception, and diffusion (Fig. 1A). Some particles can pass through the inter-fiber spaces (i.e. pores) as projectiles or be carried across by bulk fluid flow. Particles that are larger than the pores are simply blocked by straining or settling/caking. This is where the key distinction between established aerosol filtration models and blocking of large droplets emerges: While large solid particles will simply be blocked, a large droplet with sufficient momentum can squeeze through the pores of the fabric against shear stress and surface tension barriers (Fig. 1B). This is a complex phenomenon involving non-equilibrium processes, interface energies, and short time-scale events. Existing models of aerosol filtration may therefore not be sufficient in predicting outcomes. This reveals a gap in the understanding of the potential effectiveness of cloth face coverings in blocking virus particles carried by large droplets. Our goal here is to close this gap, at least partially, through experimental studies with 11 different household fabrics and commercial medical mask. We first identify the essential parameters for droplet blocking outlined below.
Fig. 1.
Distinction between aerosol filtration and large droplet blocking by fabrics. (A) Typical mechanisms of particle capture and transport during aerosol filtration: Particles 1, 2, and 3 are captured by the fiber via interception, impaction, and diffusion, respectively. Particle 4 is smaller than the inter-fiber spacing and is transmitted through the fabric, carried by air flow. Particle 5, being larger than the inter-fiber spacing, is captured by straining. Particle 6 is subsequently captured by settling/caking. (B) Blocking of nanoparticles carried by large droplets. Top and bottom rows represent transmission through hydrophilic and hydrophobic fabrics, respectively. Droplets impact the fabric with high velocity, squeeze through the pores, and part of the volume can transmit. This process involves energy costs associated with interfacial energies and shear stresses, which may be influenced by fabric porosity, fabric type, and viscosity of the droplet. Energy barriers for transmission increase with decreasing pore size, increasing droplet viscosity, as well as hydrophobicity of the fabric. For example, interfacial energy barrier for transmission through hydrophobic fabric is much higher than that for hydrophilic one.
Breathability and droplet blocking efficiency — the two key parameters for face coverings: Any mask material must offer sufficient breathability (i.e., air permeability) and yet efficiently block virus particles carried by droplets. In contrast to fit-tested respirators, medical masks or cloth face coverings typically cannot ensure tight sealing against the contours of the face. As a result, a significant portion of the air released during breathing, sneezing, and coughing may escape through the gaps, potentially carrying some of the respiratory droplets with virus particles with it [32]. A mask material with low breathability (high resistance to air flow across the mask) will result in relatively large leakage, defeating the purpose of the mask, and providing a false sense of protection — even if the mask material itself is highly efficient at filtering respiratory droplets. Higher breathability can lead to less leakage as more air will pass through the mask material which can block some of the droplets. However, higher air permeability may also correspond to lower blocking efficiency. The problem of finding an appropriate material for a home-made mask therefore involves a trade-off between breathability, , and efficiency, , of blocking virus particles carried by droplets. Hence, we consider and as the two critical parameters for mask materials. Throughout the rest of the manuscript, we refer to as “droplet blocking efficiency” for short.
Here, we considered a diverse set of 11 common household fabrics, and used a medical mask as our benchmark (Fig. 2). The household fabrics were selected from new and used garments, quilt cloths, bed sheet, and dishcloth, and characterized in terms of their fabric construction (woven, knit, or napped), fiber content (cotton, polyester, polyamide, silk), weight, thread count, porosity, and water absorption rate (see Methods). Sample descriptions and parameter values are listed in Table 1. We measured the droplet blocking efficiency and breathability of the fabrics in a laboratory setting and empirically assessed the relationship between these two critical parameters.
Fig. 2.
Samples used in this study. (A) Image of a medical/dental quality FM-EL style face mask with (B) 3-layer construction, which was used as a benchmark. (C) Microscopic texture of the outer surface of the medical mask and the 11 different home fabric samples. All scale bars: 1 mm.
Table 1.
Characterization of fabrics used in the study.
| Sample Description | Fiber Content [Fabric Construction] |
Weight (g/m) |
Thread Count (threads per inch) | Porosity (%), mean SD, n 9 |
Water Soaking Speed (mm/s) |
|---|---|---|---|---|---|
| Medical Mask: | polypropylene | 53.9 | n/a | n/a | 0 |
| FM-EL style | [non-woven] | ||||
| Fabric 1: | 100% cotton | 114.2 | 200 | 0.7 ± 0.1 | 10.0 |
| Used shirt | [knit] | ||||
| Fabric 2: | 100% cotton | 111.5 | 45 | 4.5 ± 0.1 | 0 |
| New undershirt | [knit] | ||||
| Fabric 3: | 100% cotton | 89.1 | 150 | 10.8 ± 0.2 | 10.1 |
| New quilt cloth | [woven] | ||||
| Fabric 4: | 75% cotton, | 148.2 | 85 | 5.5 ± 0.2 | 160.7 |
| Used undershirt | 25% polyester | ||||
| [knit] | |||||
| Fabric 5: | 70% cotton, | 107.5 | 200 | 0.1 ± 0.1 | 1.6 |
| Used shirt | 30% polyester | ||||
| [woven] | |||||
| Fabric 6: | 60% cotton, | 183.2 | 75 | 1.1 ± 0.3 | 72.4 |
| New T-shirt | 40% polyester | ||||
| [knit] | |||||
| Fabric 7: | 35% cotton, | 95.4 | 180 | 4.8 ± 0.2 | 23.6 |
| New quilt cloth | 65% polyester | ||||
| [woven] | |||||
| Fabric 8: | 100% polyester | 81.1 | 180 | 5.8 ± 0.8 | 28.5 |
| new bedsheet | [woven] | ||||
| Fabric 9: | 80% polyester, | 380.5 | n/a | n/a | 6.2 |
| New dishcloth | 20% polyamide | ||||
| [napped] | |||||
| Fabric 10: | silk | 49.9 | 220 | 4.3 ± 0.1 | 6.7 |
| Used shirt | [woven] | ||||
| Fabric 11: | silk | 49.4 | 200 | 2.2 ± 0.5 | 5.8 |
| Used shirt | [woven] | ||||
1.2. Droplet blocking efficiency
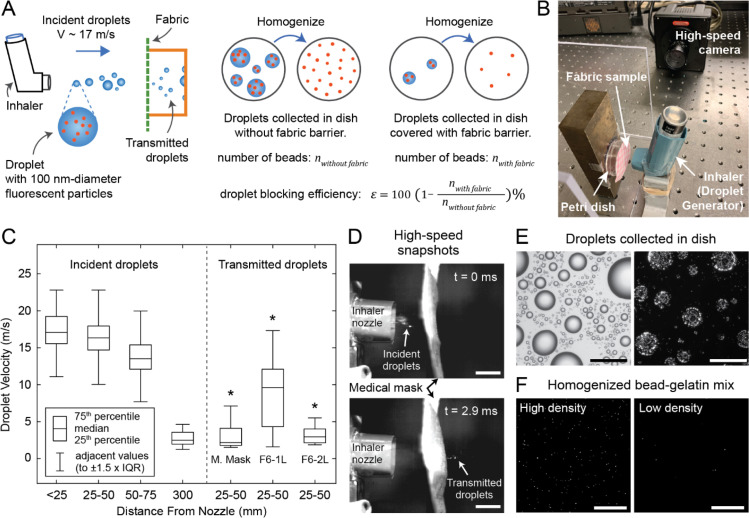
We developed a method to challenge the fabrics with large droplets and to quantify their droplet blocking efficiency. A schematic of our experimental method is shown in Fig. 3A. To generate large droplets with high initial velocity, we repurposed a metered-dose inhaler. Such inhalers, when pressed, generate sprays with consistent ejection pressure and duration [33], [34]. We loaded the nozzle of the inhaler with a suspension of 100 nm-diameter fluorescent nanoparticles (beads) in distilled water. The fluorescent beads mimic SARS-CoV-2 virus (70–100 nm-diameter) [35], [36] in terms of size, and allow to quantify the efficiency of the fabric samples at reducing the transmission of 100 nm-size particles carried by water. When the inhaler is pressed, the internal pressure of the inhaler ejects the bead suspension out of the nozzle, creating high-speed droplets (Video S1). The droplets then hit the fabric sample that is placed in front of the inhaler (Fig. 3B).
Fig. 3.
Droplet challenge tests. (A) Schematic of the experimental method and (B) image of lab set-up. (C) Box plots showing incident droplet velocities at various distances from the inhaler nozzle, and exit velocities of droplets that penetrate medical mask and single and double-layered T-shirt fabric (fabric 6). *p<0.001, two-sample t-test comparing exit velocities of penetrating droplets to incident velocity (measured within 25 mm from the nozzle, i.e., leftmost box plot). (D) High-speed snapshots of droplets hitting and penetrating the medical mask. Scale bars: 10 mm. (E) Brightfield and fluorescence images of droplets collected on a petri dish. Scale bars: . (F) Confocal images of homogenized bead collection; representative images from samples with high and low bead density. Scale bars: .
We recorded high-speed videos of the ejected droplets and performed image analysis to estimate droplet size and velocity (see Methods for details). We detected droplets with diameters in the 0.1 mm to 1 mm range within the spray ejected by the inhaler (Figure S1). Droplets released by sneezing, coughing, and speaking typically have size distributions within the range of to 1 mm [20], [21], [22], [23]. Our experimental platform thus offers a way to test blocking efficiency against large droplets which fall within the size range of droplets released by respiratory events, thereby complementing previous studies on aerosol filtration efficiency which considered particles smaller than in size [14], [15], [16], [17], [18], [19]. Analysis of high-speed videos also revealed that droplets exit the inhaler with a median velocity of 17.1 m/s, measured within 25 mm (1 inch) from the nozzle, and gradually slow down as they travel through the air. Median droplet velocity reduces to 2.7 m/s after they travel 300 mm (12 inch) from the inhaler nozzle (Fig. 3C). Droplets released by coughing and sneezing typically have velocities within the ranges of 10 to 20 m/s, [23], [37], [38] and 10 to 40 m/s, [39], [40], [41] respectively. We chose to place fabric samples 25 mm from the inhaler nozzle to challenge them with droplets with a median velocity of 17.1 m/s (high-momentum droplets), which mimic, in terms of velocity, the droplets released by coughing and sneezing that would impact the inside of the mask. Droplets released during speaking have velocities in the range of 1 to 5 m/s, [23], [37]. Thus, we placed samples at 300 mm from the inhaler nozzle to challenge them with low-momentum droplets (median velocity 2.7 m/s), mimicking droplets released during speaking.
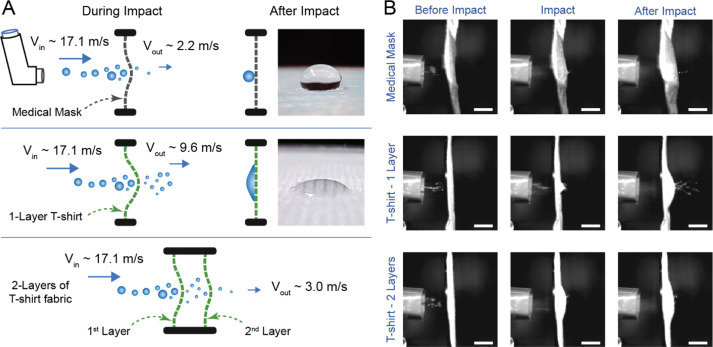
High-speed video recordings verify that high-momentum droplets can penetrate the medical mask and T-shirt fabric (Fabric 6 in Table 1) with 1 or 2 layers (Fig. 3D, Videos S2–S4). Droplets penetrating a single layer of T-shirt fabric had a median exit velocity of 9.6 m/s. In contrast, droplets penetrating a medical mask and 2 layers of T-shirt fabric had median exit velocities of 2.2 m/s and 3.0 m/s, respectively (Fig. 3C). In all three of these cases, exit velocities of the droplets that penetrated the fabric barriers were significantly lower than the incident velocity of 17.1 m/s (p < 0.001 for all, two-sample t-test).
To collect the droplets that were transmitted through the fabrics, we placed a petri dish behind the fabric samples (Fig. 3A,B). Similarly, petri dish without a fabric barrier was used at the same location to collect incident droplets for comparison. Fig. 3E shows brightfield and fluorescence images of droplets that were collected in the petri dish without a fabric barrier. Since fluorescent beads are uniformly dispersed in the solution that is loaded into the inhaler nozzle, we can use the number of fluorescent beads collected with and without a fabric barrier to measure the droplet blocking efficiency. However, the droplet images in Fig. 3E cannot be used to count the beads because many beads are clustered together and cannot be counted separately. To solve this problem, we developed a method to disperse and homogenize the beads collected in the petri dish. We achieved homogenization by first collecting the droplets on petri dishes coated with a layer of gelatin hydrogel, then melting the gelatin at 37 °C, mixing the beads with liquid gelatin, and re-gelling. We used a confocal microscope to image the gelatin hydrogels containing fluorescent beads (Fig. 3F). For each test, 100 to 150 images were taken from separate locations of the hydrogel and the average number of beads per image, , was computed by image analysis. We carried out control measurements to validate our method and found that can be used as an accurate predictor of the bead density in the gelatin mixture within the range of (Figure S2, see Methods for details of bead mixture homogenization, confocal imaging, analysis, and validation).
To measure droplet blocking efficiency, we need to compute a ratio of the total number of beads transmitted through the fabric and collected in the gelatin-coated dish, , to the total number of beads collected without a fabric barrier, . To compute this ratio, we also took into account the total volume of gelatin solution, , that the fluorescent beads were dispersed in for each test. Since the average number of beads per image, , correlates with bead density (i.e., number of beads per unit volume), we use as a predictor of the total number of beads collected in the petri dish. Droplet blocking efficiency, , of the fabric is thus computed as:
| (1) |
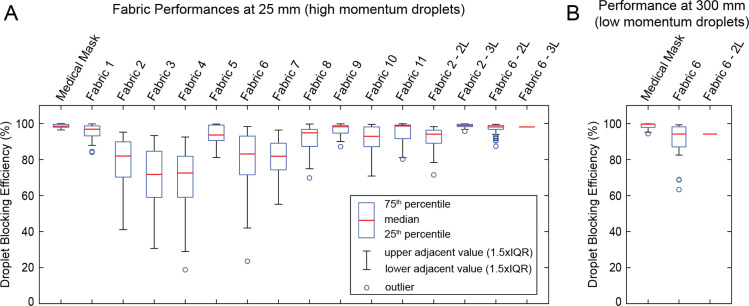
We performed independent measurements of without any fabric barrier (15 separate measurements, 100–150 images each), as well as with the medical mask, all 11 household fabrics with a single layer, and fabric 2 and fabric 6 (see Table 1) with 2 and 3 layers (6 or 7 separate sample measurements for each fabric, 100–150 images per measurement). We then computed the droplet blocking efficiency, , using Eq. (1), for all possible combinations of and . Distributions of droplet blocking efficiency values for all tests are shown in Fig. 4. The minimum, median, and maximum values are provided in Table 2.
Fig. 4.
Droplet blocking efficiency. Box plots showing the distribution of droplet blocking efficiencies for different fabrics at (A) 25 mm and (B) 300 mm from the nozzle, representing efficiencies against high velocity and low velocity droplets, respectively. For 3 layers of fabric 6 at 25 mm and 2 layers of fabric 6 at 300 mm, measurements were below detection limit, therefore, only a line corresponding to the estimated lower bound is presented for these samples.
Table 2.
Results of droplet blocking efficiency () and breathability () measurements.
| Sample description |
(%) at 25 mm (high momentum droplets) |
(mm/Pa s) | ||
|---|---|---|---|---|
| Minimuma | Median | Maximum | Mean SD, n 3 | |
| Medical Mask | 96.4 | 98.5 | 99.9 | 1.83 ± 0.15 |
|
Fabric 1: Used shirt, knit, 100% C |
87.9 | 96.8 | 99.8 | 1.37 ± 0.06 |
|
Fabric 2: New undershirt, knit, 100% C |
41.1 | 81.9 | 95.2 | 10.70 ± 0.66 |
|
Fabric 3: New quilt cloth, woven, 100% C |
30.6 | 71.7 | 93.3 | 8.67 ± 0.12 |
|
Fabric 4: Used undershirt, knit, 75% C - 25% PE |
28.9 | 72.5 | 92.5 | 11.97 ± 0.25 |
|
Fabric 5: Used shirt, woven, 70% C - 30% PE |
81.2 | 93.6 | 99.7 | 1.80 ± 0.00 |
|
Fabric 6: New T-shirt, knit, 60% C - 40% PE |
42.0 | 83.1 | 98.3 | 7.23 ± 0.55 |
|
Fabric 7: New quilt cloth, woven, 35% C - 65% PE |
55.2 | 81.8 | 96.4 | 5.07 ± 0.21 |
|
Fabric 8: New bedsheet, woven, 100% PE |
74.9 | 94.8 | 99.7 | 3.23 ± 0.06 |
|
Fabric 9: New dishcloth, napped, 80% PE - 20% PA |
90.0 | 98.2 | 99.8 | 6.53 ± 0.21 |
|
Fabric 10: Used shirt, woven, 100% S |
70.8 | 92.9 | 99.5 | 3.90 ± 0.36 |
|
Fabric 11: Used shirt, woven, 100% S |
81.1 | 98.7 | 99.8 | 2.10 ± 0.61 |
| Fabric 2 - 2 Layers | 78.3 | 94.1 | 98.3 | 5.53 ± 0.35 |
| Fabric 2 - 3 Layers | 96.8 | 98.9 | 99.8 | 3.77 ± 0.06 |
| Fabric 6 - 2 Layers | 94.0 | 98.1 | 99.6 | 3.87 ± 0.06 |
| Fabric 6 - 3 Layersb | >98.1 | 2.63 ± 0.06 | ||
| Sample description |
(%) at 300 mm (low momentum droplets) |
|||
| Minimuma | Median | Maximum | ||
| Medical Mask | 95.2 | 99.7 | 99.9 | |
| Fabric 6 | 82.5 | 94.2 | 99.3 | |
| Fabric 6 - 2 Layersb | >94.2 | |||
C: cotton, PE: polyester, PA: polyamide, S: silk.
Outliers (see Fig. 3) are ignored. Minimum values tabulated correspond to the lower ends of whiskers in the box plots of Fig. 3. (Maximum values are data maxima. There were no outliers in the upper quartiles.)
For these tests, the average number of fluorescent beads per image was below the detection limit. Hence, the expected value based on the median efficiency of one fewer layer of the same fabric is reported.
The tests at 25 mm from the inhaler nozzle represent the case of mask users releasing droplets with high-velocity onto the mask by sneezing or coughing. At this range, we found that most fabrics with a single layer have relatively high droplet blocking efficiencies (median values > 70%) (Fig. 4A, Table 2). The median droplet blocking efficiency was 98.5% (minimum 96.4%) for the medical mask. For single layers of fabrics 2 and 6, median droplet blocking efficiency was 81.9% (minimum 41.1%) and 83.1% (minimum 42.0%), respectively. The addition of second and third layers increased the efficiency, with median values exceeding 94% (Table 2). Note, however, that for 3 layers of fabric 6, the average number of beads per image was below the detection limit (). We assume that the droplet blocking efficiency of 3 layers of fabric will be at least as high as the efficiency of 2 layers (median 98.1% for fabric 6), and hence report the median efficiency for 3 layers of fabric 6 as >98.1% (Table 2). For all other tests at 25 mm, was within the accurate detection range ().
Next, we measured droplet blocking efficiency for low-momentum droplets (300 mm away from the inhaler nozzle), which represents the case of users releasing droplets with low velocity onto the mask during speaking. Droplets released during respiratory events decrease in velocity and size as they travel through air [6], [7]. Hence, our low-momentum droplet challenge can also represent the case of a mask user receiving droplets released by a nearby individual. We measured for the medical mask and 1 and 2 layers of fabric 6 at a distance of 300 mm from the inhaler nozzle (6 separate sample measurements for medical mask, and fabric 6 with 1 and 2 layers). At this distance, high-speed imaging of the droplets shows a median velocity of 2.7 m/s (Fig. 3C, Video S5). The droplet sizes at this distance are also smaller (Figure S1). Thus, the impact of the droplets has decreased. At 300 mm, median values of for the medical mask and single layer of fabric 6 were 99.7% and 94.2%, respectively (Fig. 4B, Table 2), i.e., at 300 mm is higher compared to that at 25 mm. For 2 layers of fabric 6 at 300 mm, the average number of beads per image was below the detection limit (); Hence, as above, we report the median efficiency as >94.2% (i.e., efficiency of 2 layers at least as high as the efficiency of a single layer).
1.3. Fabric breathability
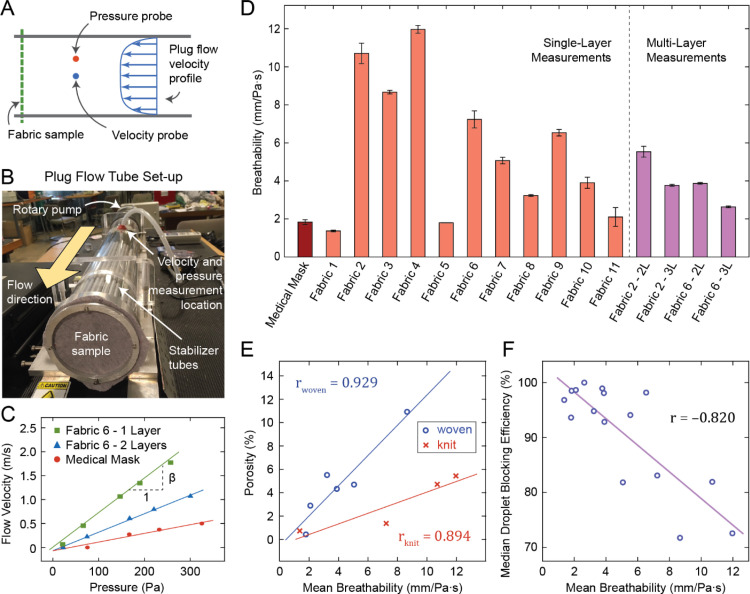
We define breathability, , of a fabric as, , where is a change in the flow rate of air through unit area of fabric, and is the corresponding change in the pressure differential across the sample that is required to induce . We used a plug flow tube [42], [43] to measure . Here, the sample fabric seals the opening of a plug flow tube (Fig. 5A,B). Pressurized air was pumped through the tube. Pressure outside the tube is atmospheric and the pressure inside the tube was measured with respect to the atmosphere. Thus, air was forced through the fabric by the gauge pressure, . Since the area of the fabric sample subjected to air flow is the same as the cross-sectional area of the plug flow tube, the change in flow rate through unit area of fabric, , is equivalent to the change in average flow velocity, inside the tube. Hence, breathability can be written as . Note that this expression of breathability or air permeability is general and allows linear as well as non-linear velocity–pressure relationships. Linearity is a special case (Darcy’s Law) at low Reynolds number flow regimes. However, deviations from linearity may still arise while flow is laminar [44]. We did not assume linearity a priori and we measured as a function of to assess the relationship.
Fig. 5.
Fabric breathability measurement. (A) Schematic of the experimental method and (B) image of plug flow tube set-up. (C) Flow velocity vs. pressure plots for selected samples. (D) Breathability measurement results for all samples. (E) Fabric porosity vs. breathability for woven and knit fabrics, and (F) droplet blocking efficiency vs. breathability plots with regression lines.
In a short plug tube, pressure is uniform and flow velocity is approximately uniform across any cross section [43], [45]. Also, pressure changes negligibly along the length of the short tube (small pressure gradient). Most of the pressure drop occurs across the sample fabric. We measured and at the same cross-section at mid length of the tube. Fig. 5C shows velocity vs. pressure measured at various pump speeds for a single and double layered T-shirt (fabric 6) and the medical mask. These measurements were made for the medical mask, single layers of all 11 household fabrics, as well as 2 and 3 layers of fabric 2 and fabric 6 (3 independent samples tested for each case). In all cases, velocity vs. pressure showed a highly linear relationship, i.e., following Darcy’s Law. Hence, we computed breathability, , as the slope of the least-squares fit line to the velocity–pressure data. Results are shown Fig. 5D and Table 2.
We found that, for household fabrics, breathability depends strongly on porosity (correlation coefficient, r = 0.929 for woven fabrics, r = 0.894 for knit fabrics). Although the correlation between breathability and porosity was high for both woven and knit fabrics, the slopes of the regression lines were different. For the same porosity, knit fabrics had higher breathability than woven fabrics (Fig. 5E). This is due to the porosity being measured under static conditions, whereas breathability measurement involved applying air pressure across the fabrics. In the latter case, fabrics can stretch due to air pressure. Knit fabrics are overall more stretchable than woven fabrics, and therefore have higher breathability for a given static porosity.
Furthermore, in aerosol science, air permeability of a fibrous filter usually anti-correlates with aerosol filtration efficiency, i.e., the higher the air permeability, the lower the filtration efficiency [46]. To assess whether this relationship also holds for blocking of large droplets, we plotted droplet blocking efficiency against breathability, and found that they are indeed anti-correlated (r = 0.820, Fig. 5F). For example, a single layer of T-shirt (fabric 6) had high breathability (7.23 ± 0.55 mm/Pa s) and relatively low blocking efficiency (median 83.1%, minimum 42.0%). The addition of a second layer increased droplet blocking efficiency (median 98.1%, minimum 94%) while reducing breathability (to 3.87 ± 0.06 mm/Pa s, see Table 2).
A corollary of the porosity–breathability and efficiency-breathability relationships shown in Fig. 5E and 5F is that droplet blocking efficiency should also anti-correlate with porosity. Indeed, we found this to be the case (efficiency vs. porosity: r = 0.796 for woven fabrics, r = 0.822 for knit fabrics). Similar to the porosity–breathability relationship, the slopes of the regression lines in efficiency vs. porosity plots were different for woven and knit fabrics (Figure S3). For the same porosity (measured in static conditions), knit fabrics tend to have lower droplet blocking efficiency than woven fabrics. High-speed recordings show that fabric samples can deform and stretch as a result of the impact from high-velocity droplets (see Video S3). Since knit fabrics are overall more stretchable, their effective porosity may increase during impact, leading to lower droplet blocking efficiency.
1.4. Possible mechanisms of droplet blocking by home fabrics
The data presented so far demonstrates that most home fabrics with one layer can block both high and low impact droplets reasonably well. With 2 or 3 layers, their blocking efficiency becomes comparable to that of medical masks while still having similar or higher breathability. However, the materials of the medical mask and that of the home fabrics are very different. How do the home fabrics achieve their blocking efficiency? While porosity plays a role, as discussed above, we also observed differences between the medical mask material and home fabrics in terms of wetting and water soaking behavior. Commercially manufactured medical masks (Fig. 2A,B) use 3 layers of hydrophobic fabric (non-woven plastic material, e.g., polypropylene) with a high contact angle (Fig. 6A, Video S6). They do not wet. This hydrophobicity may be one of the factors that offer them high droplet blocking efficiency. Most home fabrics, on the other hand, are hydrophilic to different degrees. They soak water (Table 1, Video S6).
Fig. 6.
Analysis of high impact droplet resistance by T-shirt fabric and medical mask. (A) Schematic representation of the processes during high-speed impact of droplets on medical mask and cotton T-shirt fabric (fabric 6). Note that the gap between the 2-layered fabric is exaggerated to highlight the droplets between the layers. Images show water droplets on medical mask and T-shirt fabric. While the mask is highly hydrophobic, T-shirt fabric is hydrophilic. (B) Impact response of various samples. Top row: medical mask, middle row: 1 layer of T-shirt fabric, bottom row: 2 layers of T-shirt fabric. It is apparent that mask material does not bend much, compared to the T-shirt fabric samples that undergo extensive bending deformation due to impact. Scale bars: 10 mm.
To better understand the underlying mechanism of droplet blocking by hydrophilic home fabrics, we recorded high-speed videos of the incident droplets from the inhaler and subsequent transmission through the medical mask, as well as 1 and 2 layers of T-shirt (fabric 6) (Fig. 6B, Videos S2–S4). In all cases, the samples were attached to a 40 mm-diameter wire ring which was placed 25 mm from the inhaler nozzle. Image analysis reveals that the large droplets impact and push on the fabric (medical mask or T-shirt fabric) with a median velocity of 17.1 m/s. They also stretch the fabrics. A few droplets squeeze through small pores of the fabrics and split into smaller droplets as they exit within few milliseconds (Fig. 6B, Videos S2–S4). Thus, the droplets deform during transmission through the pores of the fabric against surface tension (Fig. 1B). The kinetic energy of the incident droplets is spent deforming the fabric (bending and stretching), overcoming surface tension barriers and splitting into smaller droplets (Figures 1B, 6A). Energy needed to overcome surface tension barriers will be higher for hydrophobic fabrics compared to hydrophilic fabrics (Fig. 1B).
Transmission through fabric reduces kinetic energy of the droplets. The median exit velocity of droplets penetrating a single layer of T-shirt fabric was 9.6 m/s, significantly lower than the incident velocity of 17.1 m/s (Fig. 3C, p < 0.001, two-sample t-test). These transmitted droplets therefore have much lower momentum with which they would impact a second layer, if present. Indeed, high-speed imaging reveals very few droplets exiting the 2-layered T-shirt fabric sample (Fig. 6B, Video S4). This reduction of momentum of large droplets by first layer followed by the trapping of the lower-momentum droplets by the second layer may explain the high blocking efficiency of 2-layered T-shirt fabric sample (median 98.1%, minimum 94.0%). Thus, energy dissipation appears to be a key mechanism that contributes to the high droplet blocking efficiency of multi-layered home fabrics. After completion of the impact and partial transmission, the T-shirt fabric may soak and retain the remaining droplet volume, whereas hydrophobic medical mask does not absorb any liquid (Figures 1 and 6A). Large droplets may just roll down the medical mask by gravity.
The above scenarios involve high-speed impact and represent droplets released by users coughing and sneezing onto the mask. Droplets released by speaking onto a mask, as well as droplets received on the outside surface of the mask, have low momentum. Hence they may not have enough energy to overcome surface tension barriers and squeeze through the fabric. This may explain our measurements of higher blocking efficiency against low-momentum droplets compared to those with high-momentum (for medical mask and 1–2 layers of T-shirt Fabric, see Table 2, Fig. 4).
1.5. Home test of water permeability
The techniques we developed and used in this study to measure breathability and droplet blocking efficiency involved specialized laboratory equipment not available to the general public. We therefore sought a simple method that could be used at home to help compare different fabric choices. Here, we describe a simple test of water permeability and assess correlations between its result and breathability and droplet blocking efficiency (Figure S4).
We pre-wetted the fabrics with water (medical mask was not used here since it did not wet), placed them onto the mouth of a bottle and tied in place with a rubber band. The bottle contained a cup (250 ml) of water and had a small hole punched at mid-height to equilibrate pressure inside the bottle to atmospheric pressure. Next, we gently flipped the bottle to allow water to drain through the wetted fabric (Figure S4A). We used a stopwatch to record the time that it takes water to drain, , stopping when water stops streaming and begins to drip. Water drains faster through fabrics with higher water permeability. Thus, the inverse of the draining time, , offers a measure of water permeability. We found that correlates strongly with breathability, which is a measure of air permeability (r = 0.943, Figure S4B). This strong correlation implies that both measures (water and air permeability) dependent on the same fabric properties, among which porosity is most likely a dominant one. Given that breathability and droplet blocking efficiency were anti-correlated (Fig. 5F), we expect that water permeability should also anti-correlate with droplet blocking efficiency. Indeed, a comparison of median droplet blocking efficiency and revealed this to be the case (r = 0.828, Figure S4C).
The simplicity and availability of this water draining test – requiring only a water bottle, rubber band, and stopwatch – provides a means by which individuals at home can assess their choices of household fabrics for masks. The result of this test, , correlates (or anti-correlates) reasonably strongly with breathability and droplet blocking efficiency that were measured in a laboratory setting (Figure S4B,C). Nonetheless, due to the approximate nature of the method, we suggest that those who choose to perform the water draining test at home to indirectly estimate breathability and droplet blocking efficiency should use it only to evaluate relative measures between fabrics and not to determine absolute values of breathability or efficiency.
1.6. Remarks
Regarding the practical use of home-made face coverings, the properties of home fabrics have several important implications aside from breathability and droplet blocking efficiency. Microscale and nanoscale properties, such as microstructure and surface chemistry, of the fabrics contribute to their wetting behavior, which can be modified by engineering these properties [47]. Home fabrics can be washed and reused, as opposed to medical masks that are disposable. Medical masks are typically made of non-biodegradable plastics such as polypropylene. Their widespread use during a pandemic can therefore pose an environmental burden. The ability to wash and reuse home-made face coverings offers an advantage in terms of reducing waste and pollution. Washing home-made face covering is also necessary for decontamination. As we have discussed above, most home fabrics are hydrophilic (water soaking). In contrast to the highly hydrophobic medical mask material, home fabrics can soak and hold the droplets. While this holding ability of hydrophilic fabrics may accrue possible benefits in terms of droplet blocking performance of home-made masks, it also means that the fabrics can retain the viruses that were in the soaked droplets. Home-made masks must therefore be washed regularly to decontaminate, either by laundry machine at warmest temperature setting, or by hand using water and household disinfectants such as bleach [13].
The results of droplet blocking efficiency we have presented here complement the existing knowledge from studies on the aerosol filtration efficiency of household fabrics [14], [15], [16], [17], [18], [19]. The method commonly employed in these studies, as well as in the standard testing of commercial facemasks and respirators, involves challenging the sample by a pressure-driven airflow containing aerosols with particle sizes usually within the 10 nm to range, and using a particle counter to measure and compare the number of particles upstream and downstream of the fabric [48]. A recent study on the performance of common household fabrics against aerosols with particle sizes within 10 nm to range reported several findings that align with ours: Fabrics with lower porosity (tighter weave) performed better than those with higher porosity. Multiple layers of fabric were highly effective (>90% filtration efficiency in most cases) [19]. In our experiments, the fabrics were challenged with large droplets (up to 1 mm in size), significantly larger than the particles used in aerosol filtration studies. As our results indicate, household fabrics can also be effective at blocking such large droplets, especially with multiple layers.
Blocking of both small aerosol particles and large droplets by fabrics can be considered within the general theoretical framework of advective–diffusive transport through a porous barrier. The performance of the barrier can depend on which mode of transport dominates. In our experiments, the motion of droplets towards the fabric samples can be described as projectile motion with relatively high velocity. Similarly, in the previous aerosol filtration studies, aerosol particles travel towards the fabric with momentum imparted upon them by pressure-driven bulk airflow. Thus, in both cases, advective transport plays a dominant role, as opposed to diffuse transport which may occur, for instance, due to osmotic pressure. In most practical situations of facemask use, advective transport is dominant. Droplets or aerosols released by a mask wearer during sneezing, coughing, or speaking will impact the mask with high velocity. In situations where a facemask is intended for blocking incoming droplets or aerosol particles, advective motion is also expected due to ambient airflow or flow generated by inhalation. We therefore expect our results, and the findings of previous aerosol filtration studies, to be applicable in these scenarios. Situations where diffusive transport dominates may arise in confined spaces with high concentration of airborne particles but with minimal ambient airflow, thereby creating osmotic pressure across the mask. Future studies are required to assess the performance of facemasks in such situations involving predominantly diffusive transport.
While fabric porosity appears to play a role in the blocking of both aerosols and larger droplets, the mechanisms of penetration may be different. Aerosols with particles in the nanometer to micrometer range may pass through the fabric pores without interacting with the fabric (Fig. 1A). Thus, lower porosity (as a fraction of the total fabric are (a) will result in higher filtration efficiency. With multiple layers of fabric, the net effective porosity is likely to decrease significantly due to misalignment of the pores of the separate layers. This can significantly increase filtration efficiency against small particles. Droplets, on the other hand, can squeeze and flow through the pores. Lower porosity can still be advantageous since squeezing through smaller pores is more energy consuming due to higher shear stresses and surface tension barrier originating from the interfacial energies of air, water and the fabric material (Fig. 1B). As we have discussed above, household fabrics can vary in their degree of hydrophilicity and water absorption properties. A more hydrophilic fabric may impose less activation barrier against droplets squeezing through the pores compared to that of a hydrophobic fabric. A multi-layered fabric barrier will likely misalign the pores of the separate layers, decreasing the effective porosity, and significantly increasing the blocking efficiency.
The droplet blocking efficiency of the fabrics reported here is based on the count of 100 nm-diameter nanoparticles transported through the fabric, , compared to the total number of incident particles, , both carried by water droplets. Thus, the efficiency is really a measure of the ability of the fabrics to block the nanoparticles carried by water droplets. On the other hand, SARS-CoV-2 (approximately 100 nm in size [35], [36]) are carried by saliva droplets released during respiratory events [49], [50]. Saliva typically has much higher viscosity than water, even under high shear rates [51], [52]. Transmission of large droplets of saliva would therefore require higher energy to squeeze through fabric pores due to higher shear stresses. Hence, the blocking efficiency values that we measured, using water droplets, provide a conservative estimate of the efficiency of fabrics to block transmission of viruses carried by saliva droplets.
We would like to stress that the efficiency values we report here are indicative of the ability of the fabric materials to block 100 nm-sized particles carried by droplets, and are not meant to reflect the net performance of a cloth facemask. The performance of a facemask would also depend on how it is worn, and how much air leaks through the gaps between the mask and face contours. Net efficiency of the facemask can be significantly lower than the efficiency of the fabric material itself, due to leakage through gaps [32]. Cloth face coverings could therefore be made more effective by ensuring proper sealing against the face contour. For example, a recent study reported that adding a layer of nylon stocking over the masks minimized the air flow around the edges of the masks and improved particle filtration efficiency for both home-made and commercial masks [53]. As an alternative measure to ensure a better fit, an elastomeric net or half-mask can be used over the mask [54].
Although the relative contributions of aerosols and larger droplets to the spread of COVID-19 are not fully understood, our results, taken together with those of aerosol filtration studies, suggest that home-made face coverings may have considerable efficacy in blocking both. Furthermore, a recent modeling study suggests that extensive adoption of even relatively ineffective face masks may meaningfully reduce community transmission of COVID-19 and decrease peak hospitalizations and deaths [55]. Mask use reduces transmission rate in a nearly linear proportion to the product of mask effectiveness (as a fraction of potentially infectious contacts blocked) and coverage rate (as a fraction of the general population), while the impact on epidemiologic outcomes (death, hospitalizations) is highly nonlinear [55]. As a result, it is anticipated that face coverings made from household fabrics can play a vital role as a mitigating strategy.
2. Conclusions
In this study, we asked whether face coverings made from home fabrics can be effective against the dissemination of droplets carrying 100 nm size infectious viruses, such as SARS-CoV-2, and if so, will their droplet blocking efficiency be comparable to that of a commercial medical mask. We studied a diverse set of 11 common household fabrics with varying fiber types and constructions. We quantified their breathability, and their ability to block 100 nm-diameter nanoparticles carried by high-velocity droplets similar to those that may be released by sneezing or coughing. We found that all of these fabrics have considerable efficiency at blocking high-velocity droplets, even as a single layer. With 2 or 3 layers, even highly permeable fabrics, such as T-shirt cloth, achieve droplet blocking efficiency that is similar to that of a medical mask, while still maintaining comparable breathability.
For low-velocity droplets, which mimic droplets released during speaking, we found that blocking efficiency of T-shirt fabric is much higher compared to that for high-velocity droplets. A scenario involving low-velocity droplets may also arise when a mask user receives droplets released by an infected individual nearby. It thus follows that a 2 or 3-layered home-made mask with most common fabrics may help prevent the dissemination of droplets by infected individuals, and protect healthy individuals from inhaling droplets, with efficiencies similar to that of commercial medical masks.
Considering our results within the context of recent literature on aerosol filtration efficiency of home fabrics and epidemiological modeling of the potential impacts of mask use, we conclude that during pandemics and mask shortages, home-made face coverings with multiple layers can be effective against transmission of respiratory infection through droplets. Mask wearing by all individuals, supported by proper education and training of mask making and appropriate usage, can be an effective strategy in conjunction with social distancing, testing and contact tracing, and other interventions to reduce disease transmission.
3. Methods
3.1. Fabric characterization
To quantify fabric weight (mass per unit area), rectangular samples of known area were cut from each fabric and medical mask using a paper trimmer and their masses were measured using a high precision lab scale. Fabric construction (woven, knit, or napped) was determined by visual inspection. Fiber contents were noted from the cloth labels. To measure thread count, close-up views of the fabric samples (see Fig. 2) were imaged using a digital camera (MS100 USB Microscope, Teslong), and the thread count was calculated as the sum of the number of threads per unit length in weft and warp directions. Thread count measurement was not applicable to the medical mask and dishcloth due to their non-woven and napped fabric construction, respectively. To measure fabric porosity, a digital image analysis method was used (see Figure S5), adapted from previous studies [56], [57]. Samples of woven and knit fabrics were imaged while being illuminated from the backside by diffused light. Light that passed through the fabric was used to identify the pores. Backside illumination intensity was kept constant and 9 samples were imaged for each fabric. Images were then analyzed in MATLAB as follows: Images were converted to grayscale. A median filter was applied to reduce noise. Filtered images were converted to binary by applying a threshold at 90% intensity; hence, pores were identified as pixels with intensity values in the top 10th percentile. Binarized images were analyzed to calculate porosity as the ratio of the number of bright pixels to the total number of pixels in the image (Figure S5). For the medical mask and dishcloth, this method did not produce images with sufficient contrast; therefore porosity measurement for these fabrics was omitted. To quantify the water absorption behavior of fabrics (Figure S4), a small droplet (100 l) of water was dispensed on dry fabric samples, and video of the soaking process was recorded using a digital camera (MS100 USB Microscope, Teslong). Food coloring was added to the water to provide contrast and allow us to visualize the soaked area. Images were converted to binary and analyzed to measure the soaked fabric area as a function of time. Water soaking speed was then computed as the time derivative of the soaked area. We note that there are a wide variety of standardized tests available to characterize fabrics, listed as ISO 9073, for industrial applications.
3.2. Droplet generation and characterization
We used a metered-dose inhaler (HFA-propelled, 210 sprays, GlaxoSmithKline) and loaded its nozzle with 10 l of distilled water to generate droplets. To measure droplet velocity, we recorded videos of the ejected droplets at 10,000 frames per second (fps) using a high-speed camera (FASTCAM-ultima APX, Photron). Videos of 4 separate sprays were recorded and analyzed in ImageJ. Droplet positions were tracked manually across consecutive frames and velocity was calculated by dividing the distance traveled by the elapsed time. To estimate ejected droplet size, we used a separate imaging setup (4MP 25601600 CMOS camera, Phantom) which offered higher spatial resolution with a lower frame rate (400 fps). Droplets were illuminated with a laser (50 mJ Terra PIV dual cavity YLF laser, Amplitude) for clear visualization. Images of ejected droplets from 3 separate sprays were analyzed using ImageJ and MATLAB. Captured images were converted to binary and droplets were identified as objects (8-connected components) in the binary image. Droplet diameter was calculated as the ‘equivalent diameter’ of a circle with the same area as that of the imaged droplet. Using this imaging and analysis method, we were able to detect droplets with diameters greater than 0.1 mm (Figure S1). For measurement of droplet size at 300 mm from the inhaler nozzle (low momentum droplets), the droplets were collected on a polystyrene dish placed perpendicular to the spray direction. The dish was then imaged immediately using brightfield microscopy. ImageJ and MATLAB were used as before to convert images to binary and measure the equivalent diameter of the landed droplets. Since water contact angle on polystyrene is about 87° [58], we approximated the landed droplets as half-spheres, and calculated the diameters of corresponding incoming droplets using volume conservation (Figure S1).
3.3. Droplet challenge tests
To challenge the fabric samples with droplets, we placed the inhaler at mid-height of an acrylic channel open at both ends. The channel prevents air flow within the room from interfering with the tests. Droplets were generated using a suspension of 100 nm-diameter red fluorescent beads (ex/em 580/605 nm, Invitrogen, catalog #F8801) diluted in distilled water. For testing the fabric samples, we first coated the bottom of a petri dish with 1 ml of warm gelatin solution (5% wt/v) which was prepared by dissolving powdered gelatin (Sigma Aldrich, catalog #G9391) in distilled water. Gelatin forms a hydrogel at and below room temperature and melts at higher temperatures [59]. We let the gelatin solution gel inside the petri dishes at 4 °C, then covered the dishes by attaching the fabric cut-outs to the rim of the dish using double-sided tape. We placed samples inside the acrylic channel, at mid-height, 25 mm or 300 mm away from the inhaler nozzle, to challenge with high or low-velocity droplets, respectively. In each test, after the inhaler was pressed and droplets containing fluorescent beads impacted the fabric samples, droplets that penetrated the fabric samples were collected on the gelatin layer. Similarly, droplets were collected on separate gelatin-covered petri dishes without any fabric barrier, as control. Next, we warmed the samples to 37 °C in an incubator to liquefy the gelatin layer and allow the beads to dissolve into the gelatin solution. This mixture was transferred to a vial, vortexed for 20 s, and then sonicated for at least 30 min to uniformly disperse the fluorescent beads in solution. This homogenized bead-gelatin mixture was re-gelled at 4 °C. The beads were thus frozen in place in the hydrogel.
3.4. Fluorescent bead counting and validation
We imaged the gels containing fluorescent beads on a confocal laser scanning microscope (LSM 710, Zeiss) using a 40X water-immersion lens (NA = 1.2). For each sample, we picked five random fields of view and took z-stacks with spacing (to ensure the same set of beads were not imaged twice) and 20 to 30 slices, resulting in 100 to 150 images per sample. The bead distribution was reasonably uniform in plane and across the gel thickness. Confocal microscopy images were analyzed in MATLAB. Images were converted to binary by applying a threshold at 50% intensity. Beads were identified as objects (8-connected components) in binary images, and the average number of beads per image, , was calculated from the 100–150 images for each separate test. To validate that can be used as an accurate predictor of the bead density in the gelatin mixture, we prepared gelatin mixtures with known bead densities by serial dilution of the original bead solution (known bead density provided by vendor). We then gelled these solutions, performed confocal imaging, and computed , averaged over 100 images for each density tested. For samples with , the average number of beads per image, , correlated very strongly with the known bead density in the mixture. Bead densities corresponding to were not tested. For , there was significant deviation from the regression model (Figure S2). Thus, for all droplet blocking efficiency measurements, we took and as our upper and lower detection limits, respectively.
3.5. Breathability measurement
Our plug flow apparatus (Fig. 5B) consists of an acrylic tube with 100 mm inner diameter, a pump on one end, and a set of long aluminum tubes aligned within the acrylic tube on the other end which help stabilize the flow [42], [43], [45]. Flow through the tube can be controlled by varying the pump speed with an analog dial. We measured the air flow velocity, , and the gauge pressure, , at the same cross-section at mid-length of the tube ( was measured at the center of the cross-section). A pressure gauge (Magnehelic) and a hot-wire anemometer (Omega) were used to measure pressure and velocity, respectively. A small hole in the acrylic tube was used to insert the pressure probe and the anemometer and the hole was sealed with clay dough. An O-ring at the open end of the tube was used to seal the sample fabric, ensuring that the pumped air flows through the fabric only.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We thank Dr. Blake Johnson of the University of Illinois at Urbana-Champaign (UIUC) for helping us with the use of the plug tube apparatus to measure breathability of the fabrics, Dr. Sivaguru Mayandi and Dr. Austin Cyphersmith of Carl R. Woese Institute for Genomic Biology, UIUC for their help with using the confocal imaging facility. Finally, we thank Dr. Faruque Ahmed of CDC for providing valuable guidance in conducting the research.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.eml.2020.100924.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
Supporting information.
Droplets ejected by the metered-dose inhaler, followed by the cloud of aerosolized medicine from the inhaler.
Droplet challenge of commercial medical mask material at 25 mm from the inhaler nozzle.
Droplet challenge of single layer of T-shirt fabric at 25 mm from the inhaler nozzle.
Droplet challenge of 2 layers of T-shirt fabric at 25 mm from the inhaler nozzle.
Incident droplets against a sample placed 300 mm from the inhaler nozzle.
Wetting and water absorption behavior of medical mask (non-soaking), fabric 1 (used shirt fabric, slow soaking), and fabric 4 (used undershirt fabric, fast soaking).
References
- 1.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: Emission of respirable pathogens. J. Occup. Environ. Hyg. 2005;2(3):143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Killingley B., Nguyen-Van-Tam J. Routes of influenza transmission. Influenza Other Respi. Viruses. 2013;7:42–51. doi: 10.1111/irv.12080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tellier R. Review of aerosol transmission of influenza a virus. Emerg. Infect. Diseases. 2006;12(11):1657–1662. doi: 10.3201/eid1211.060426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.V. Stadnytskyi, Bax C.E., Bax A., Anfinrud P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. Proc. Natl. Acad. Sci. 2020;117(22):11875–11877. doi: 10.1073/pnas.2006874117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.US Centers for Disease Control and Prevention How COVID-19 Spreads. https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/how-covid-spreads.html (Accessed 23 July 2020).
- 6.Bourouiba L., Dehandschoewercker E., Bush J.W.M. Violent expiratory events: On coughing and sneezing. J. Fluid Mech. 2014;745:537–563. [Google Scholar]
- 7.Wei J., Li Y. Human cough as a two-stage jet and its role in particle transport. PLoS One. 2017;12(1) doi: 10.1371/journal.pone.0169235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hu Z., Song C., Xu C., Jin G., Chen Y., Xu X., Ma H., Chen W., Lin Y., Zheng Y., Wang J., Hu Z., Yi Y., Shen H. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing. China. Sci. China Life Sci. 2020;63(5):706–711. doi: 10.1007/s11427-020-1661-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zou L., Ruan F., Huang M., Liang L., Huang H., Hong Z., Yu J., Kang M., Song Y., Xia J., Guo Q., Song T., He J., Yen H.-L., Peiris M., Wu J. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N. Engl. J. Med. 2020;382(12):1177–1179. doi: 10.1056/NEJMc2001737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rothe C., Schunk M., Sothmann P., Bretzel G., Froeschl G., Wallrauch C., Zimmer T., Thiel V., Janke C., Guggemos W., Seilmaier M., Drosten C., Vollmar P., Zwirglmaier K., Zange S., Wölfel R., Hoelscher M. Transmission of 2019-NCoV infection from an asymptomatic contact in Germany. N. Engl. J. Med. 2020;382(10):970–971. doi: 10.1056/NEJMc2001468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pan X., Chen D., Xia Y., Wu X., Li T., Ou X., Zhou L., Liu J. Asymptomatic cases in a family cluster with SARS-CoV-2 infection. Lancet Infect. Dis. 2020;20(4):410–411. doi: 10.1016/S1473-3099(20)30114-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Leung N.H.L., Chu D.K.W., Shiu E.Y.C., Chan K.-H., McDevitt J.J., Hau B.J.P., Yen H.-L., Li Y., Ip D.K.M., Peiris J.S.M., Seto W.-H., Leung G.M., Milton D.K., Cowling B.J. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 2020;26:676–680. doi: 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.US Centers for Disease Control and Prevention Use of Cloth Face Coverings to Help Slow the Spread of COVID-19. https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/diy-cloth-face-coverings.html (Accessed 23 July 2020).
- 14.Chughtai A.A., Seale H., MacIntyre C.R. Use of cloth masks in the practice of infection control - evidence and policy gaps. Int. J. Infect. Control. 2013;9(3) [Google Scholar]
- 15.van der Sande M., Teunis P., Sabel R. Professional and home-made face masks reduce exposure to respiratory infections among the general population. PLoS One. 2008;3(7) doi: 10.1371/journal.pone.0002618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shakya K.M., Noyes A., Kallin R., Peltier R.E. Evaluating the efficacy of cloth facemasks in reducing particulate matter exposure. J. Expo. Sci. Environ. Epidemiol. 2017;27:352–357. doi: 10.1038/jes.2016.42. [DOI] [PubMed] [Google Scholar]
- 17.Davies A., Thompson K.-A., Giri K., Kafatos G., Walker J., Bennett A. Testing the efficacy of homemade masks: Would they protect in an influenza pandemic? Disaster med. Public Health Prep. 2013;7:413–418. doi: 10.1017/dmp.2013.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rengasamy S., Eimer B., Shaffer R.E. Simple respiratory protection—Evaluation of the filtration performance of cloth masks and common fabric materials against 20–1000 Nm size particles. Ann. Occup. Hyg. 2010;54(7):789–798. doi: 10.1093/annhyg/meq044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Konda A., Prakash A., Moss G.A., Schmoldt M., Grant G.D., Guha S. Aerosol filtration efficiency of common fabrics used in respiratory cloth masks. ACS Nano. 2020;14(5):6339–6347. doi: 10.1021/acsnano.0c03252. [DOI] [PubMed] [Google Scholar]
- 20.Duguid J.P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiol. Infect. 1946;44(6):471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Loudon R.G., Roberts R.M. Droplet expulsion from the respiratory tract. Am. Rev. Respir. Dis. 1967;95(3):435–442. doi: 10.1164/arrd.1967.95.3.435. [DOI] [PubMed] [Google Scholar]
- 22.Han Z.Y., Weng W.G., Huang Q.Y. Characterizations of particle size distribution of the droplets exhaled by sneeze. J. R. Soc. Interface. 2013;10 doi: 10.1098/rsif.2013.0560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. Aerosol Sci. 2009;40:122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.World Health Organization Advice on the use of masks in the context of COVID-19. https://www.who.int/publications/i/item/advice-on-the-use-of-masks-in-the-community-during-home-care-and-in-healthcare-settings-in-the-context-of-the-novel-coronavirus-(2019-ncov)-outbreak (Accessed 23 July 2020).
- 25.Chen C.Y. Filtration of aerosols by fibrous media. Chem. Rev. 1955;55(3):595–623. [Google Scholar]
- 26.Friedlander S.K. Theory of aerosol filtration. Ind. Eng. Chem. 1958;50(8):1161–1164. [Google Scholar]
- 27.C.N. Davies. Filtration of aerosols. J. Aerosol Sci. 1983;14(2):147–161. [Google Scholar]
- 28.Lee K.W., Liu B.Y.H. Theoretical study of aerosol filtration by fibrous filters. Aerosol Sci. Technol. 1982;1:147–161. [Google Scholar]
- 29.K.W. Lee, Liu B.Y.H. Experimental study of aerosol filtration by fibrous filters. Aerosol Sci. Technol. 1982;1:35–46. [Google Scholar]
- 30.Yeh H.-C., Liu B.Y.H. Aerosol filtration by fibrous filters - I. Theor. Aerosol Sci. 1974;5:191–204. [Google Scholar]
- 31.Yeh H.-C., Liu B.Y.H. Aerosol filtration by fibrous filters - II. Exp. Aerosol Sci. 1974;5:205–217. [Google Scholar]
- 32.Grinshpun S.A., Haruta H., Eninger R.M., Reponen T., McKay R.T., Lee S.-A. Performance of an n95 filtering facepiece particulate respirator and a surgical mask during human breathing: Two pathways for particle penetration. J. Occup. Environ. Hyg. 2009;6:593–603. doi: 10.1080/15459620903120086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Xu Z., Hickey A.J. Controlled Pulmonary Drug Delivery. Springer; New York: 2011. The physics of aerosol droplet and particle generation from inhalers; pp. 75–100. [Google Scholar]
- 34.Dal Negro R.W., Longo P., Ziani O.V., Bonadiman L., Turco P. Instant velocity and consistency of emitted cloud change by the different levels of canister filling with metered dose inhalers (MDIs), but not with soft mist inhalers (SMIs): A bench study. Multidiscip. Respir. Med. 2017;12(1):13. doi: 10.1186/s40248-017-0096-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bar-On Y.M., Flamholz A., Phillips R., Milo R. SARS-Cov-2 (COVID-19) by the numbers. Elife. 2020;9 doi: 10.7554/eLife.57309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kim J.-M., Chung Y.-S., Jo H.J., Lee N.-J., Kim M.S., Woo S.H., Park S., Kim J.W., Kim H.M., Han M.-G. Identification of coronavirus isolated from a patient in Korea with COVID-19. Osong Public Heal. Res. Perspect. 2020;11(1):3–7. doi: 10.24171/j.phrp.2020.11.1.02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kwon S.-B., Park J., Jang J., Cho Y., Park D.-S., Kim C., Bae G.-N., Jang A. Study on the initial velocity distribution of exhaled air from coughing and speaking. Chemosphere. 2012;87:1260–1264. doi: 10.1016/j.chemosphere.2012.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhu S., Kato S., Yang J.-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build. Environ. 2006;41:1691–1702. [Google Scholar]
- 39.Jennison M.W., Edgerton H.E. Droplet infection of air: High-speed photography of droplet production by sneezing. Proc. Soc. Exp. Biol. Med. 1940;43(3):455–458. [Google Scholar]
- 40.Turner C.E., Jennison M.W., Edgerton H.E. Public health applications of high-speed photography. Am. J. Public Heal. Nations Heal. 1941;31(4):319–324. doi: 10.2105/ajph.31.4.319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Scharfman B.E., Techet A.H., Bush J.W.M., Bourouiba L. Visualization of sneeze ejecta: Steps of fluid fragmentation leading to respiratory droplets. Exp. Fluids. 2016;57(2):24. doi: 10.1007/s00348-015-2078-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mikhailova N.P., Repik E.U., Sosedko Y.P. Optimal control of free-stream turbulence intensity by means of honeycombs. Fluid Dyn. 1994;29(3):429–437. [Google Scholar]
- 43.Loehrke R.I., Nagib H.M. 1972. Experiments on Management of Free-Stream Turbulence. [Google Scholar]
- 44.Hlushkou D., Tallarek U. Transition from creeping via viscous-inertial to turbulent flow in fixed beds. J. Chromatogr. A. 2006;1126:70–85. doi: 10.1016/j.chroma.2006.06.011. [DOI] [PubMed] [Google Scholar]
- 45.Scheiman J., Brooks J.D. Comparison of experimental and theoretical turbulence reduction from screens, honeycomb, and honeycomb-screen combinations. J. Aircr. 1981;18(8):638–643. [Google Scholar]
- 46.Lawrence C.A., Liu P. Relation of structure, properties and performance of fibrous media for gas filtration. Chem. Eng. Technol. 2006;29(8):957–967. [Google Scholar]
- 47.Park S., Kim J., Park C.H. Superhydrophobic textiles: Review of theoretical definitions, fabrication and functional evaluation. J. Eng. Fiber. Fabr. 2015;10(4) [Google Scholar]
- 48.Rengasamy S., Shaffer R., Williams B., Smit S. A comparison of facemask and respirator filtration test methods. J. Occup. Environ. Hyg. 2017;14(2):92–103. doi: 10.1080/15459624.2016.1225157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Han P., Ivanovski S. Saliva — friend and foe in the COVID-19 outbreak. Diagnostics. 2020;10:290. doi: 10.3390/diagnostics10050290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.D.R.E. Ranoa, R.L. Holland, F.G. Alnaji, K.J. Green, L. Wang, C.B. Brooke, M.D. Burke, T.M. Fan, P.J. Hergenrother, Saliva-based molecular testing for SARS-CoV-2 that bypasses RNA Extraction. bioRxiv 2020.
- 51.Davis S.S. The rheological properties of saliva. Rheol. Acta. 1971;10:28–35. [Google Scholar]
- 52.Roberts B.J. A study of the viscosity of saliva at different shear rates in dentate and edentulous patients. J. Dent. 1977;5(4):303–309. doi: 10.1016/0300-5712(77)90122-1. [DOI] [PubMed] [Google Scholar]
- 53.A.V. Mueller, Eden M.J., Oakes J.M., Bellini C., Fernandez L.A. Quantitative method for comparative assessment of particle removal efficiency of fabric masks as alternatives to standard surgical masks for ppe. Matter. 2020 doi: 10.1016/j.matt.2020.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Han D.-H., Park Y., Woo J.-J. Effect of the tight fitting net on fit performance in single-use filtering facepieces for Koreans. Ind. Health. 2018;56:78–84. doi: 10.2486/indhealth.2017-0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Eikenberry S.E., Mancuso M., Iboi E., Phan T., Eikenberry K., Kuang Y., Kostelich E., Gumel A.B. To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 2020;5:293–308. doi: 10.1016/j.idm.2020.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ragab A., Fouda A., El-Deeb H., Abou-Taleb H. Determination of pore size, porosity and pore size distribution of woven structures by image analysis techniques. J. Text. Sci. Eng. 2017;7(5) [Google Scholar]
- 57.Benltoufa S., Fayala F., Cheikhrouhou M., Nasrallah S.B. Porosity determination of jersey structure. AUTEX Res. J. 2007;7(1):63–69. [Google Scholar]
- 58.Li Y., Pham J.Q., Johnston K.P., Green P.F. Contact angle of water on polystyrene thin films: Effects of CO2 environment and film thickness. Langmuir. 2007;23:9785–9793. doi: 10.1021/la0636311. [DOI] [PubMed] [Google Scholar]
- 59.Osorio F.A., Bilbao E., Bustos R., Alvarez F. Effects of concentration, bloom degree, and PH on gelatin melting and gelling temperatures using small amplitude oscillatory rheology. Int. J. Food Prop. 2007;10:841–851. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting information.
Droplets ejected by the metered-dose inhaler, followed by the cloud of aerosolized medicine from the inhaler.
Droplet challenge of commercial medical mask material at 25 mm from the inhaler nozzle.
Droplet challenge of single layer of T-shirt fabric at 25 mm from the inhaler nozzle.
Droplet challenge of 2 layers of T-shirt fabric at 25 mm from the inhaler nozzle.
Incident droplets against a sample placed 300 mm from the inhaler nozzle.
Wetting and water absorption behavior of medical mask (non-soaking), fabric 1 (used shirt fabric, slow soaking), and fabric 4 (used undershirt fabric, fast soaking).