Abstract
In this paper, we propose a quadtree based approach to capture the spatial information of medical images for explaining nonlinear SVM prediction. In medical image classification, interpretability becomes important to understand why the adopted model works. Explaining an SVM prediction is difficult due to implicit mapping done in kernel classification is uninformative about the position of data points in the feature space and the nature of the separating hyperplane in the original space. The proposed method finds ROIs which contain the discriminative regions behind the prediction. Localization of the discriminative region in small boxes can help in interpreting the prediction by SVM. Quadtree decomposition is applied recursively before applying SVMs on sub images and model identified ROIs are highlighted. Pictorial results of experiments on various medical image datasets prove the effectiveness of this approach. We validate the correctness of our method by applying occlusion methods.
Keywords: Non linear classification, Interpretability, Localization, Quadtree
Introduction
Machine learning models are required not only to be optimized for task performance but also to fulfil other auxiliary criteria like interpretability. If a model can explain its prediction which can be converted into knowledge giving the insight of the domain, the model is considered to be interpretable [14].
SVM classifies the linearly separable datasets with high accuracy, but if the nonlinear dataset needs to be classified, we apply kernel trick to transform the data into another dimension. These kernel SVMs use implicit mapping making it challenge to have an institutive understanding of the prediction.Though the model classifies the data with high accuracy, the separating hyperplane is unknown. The hyperplane can be used to classify a new instance, but the nature of the hyperplane is not known in the feature space. The explanation of instances becoming support vectors is also unexplainable. Hence, to explain the predictions of nonlinear SVM is a challenge, and the model behaves like a black-box.
The interpretation of the results becomes vital in the case of medical image classification. The diagnosis of a medical condition without determining the association of the underlying disease with the manifestation is unacceptable. However, we can observe that in medical image classification, the manifestation of the disease is a global function of the entire space and depends on specific local phenomena. These regions of interest may be identified and associated with the disease and can be used as a pointer and explanation of a particular medical condition.
When we apply SVMs as a decision-support tool in medical image classification, the model needs to be human interpretable, so that the decisions taken by an expert on the basis of the model becomes acceptable and credible [10, 19]. A Quadtree decomposition approach may be used with SVMs to localize those ROIs to explain the decisions. When SVM is applied on these ROIs, the classification results are predicted on the basis of the local phenomenon captured by these discriminative regions and hence more interpretable.
In this paper, we propose a deductive-nomological model using quadtree to interpret the SVMs classification for medical image datasets. We apply the quadtree decomposition recursively before applying SVMs in a hierarchical manner on images and sub images and highlight various discriminative regions which are predicted as malignant according to our SVM based model. These model identified ROIs are compared with the given ROIs to check the correctness of the interpretability model. These regions support an expert to understand the cause of prediction. The primary contributions of this work are as follows:
A quad-tree based image decomposition method to interpret the prediction made by SVM. The decomposition allows localization of the discriminative regions in small boxes, which contain the information needed to explain the SVM prediction. The ensemble based decision trained at every tree height enables discard spurious predictions, which in turn allows better interpretability of the classifier.
In the upcoming sections the contents are structured as follows: In Section 2, we have explained nonlinear SVM and its opaqueness. In Section 3, we have proposed our approach of using a quadtree to interpret SVMs in medical image datasets. Section 4 highlights the results on medical image datasets. Finally, Section 5 contains our conclusion.
Related work
Interpretability requires that the models which are made should be simple, which can help to explain their decisions. The existing relationship between model accuracy, its complexity and interpretability does not allow a transparent decision process. Even the existing model interpretation methods extract parallel mathematical rules which remain semi-human interpretable.
The approaches to make black-box nature of SVMs interpretable can largely be divided into two categories; rule extraction and visualization. In [5], rule extraction techniques have been categorized into four sections; (i) closed-box, (ii) using support vectors, (iii) using support vector and decision boundaries in combination, and (iv) using training data along with hyperplane. For rule extraction, we can prioritize features and find fuzzy rules or generate a decision tree to interpret the model [25]. Fuzzy rules have a syntax similar to familiar languages which are quite simple to make decisions. Sequential covering algorithm can be modified to generate rules using the support vectors of a tuned SVM. The feature which has more discriminative power will have a higher priority in the ordering of rules[7]. Another approach in [26] combines the rules with hyper-rectangular boundaries. Support vectors are used to find cross points between the lines along each axis extended from support vector of a class and decision boundary. The hyper-rectangular rules are derived from the cross-points. Cross-points also detect the support vectors of other class and a set of rules is made using the tuned hyper-rectangular rules which exclude these support vectors. The problem with this approach is time, as rule generation takes far longer than SVM training and time is one of the prime concerns for on-line data streams. In [17] SVMs are collaborated with decision trees for rule generation to predict the protein secondary structure. Decision trees are constructed using a resulting training set which is generated by training the SVM using original training set. In this approach number of rules would be very high, which is also difficult to comprehend. In [6] an iterative learning approach is used to extract the rules, but it requires a domain expert to verify the correctness of final rules.
The rules extraction approaches are good measures of interpretability for numeric data, but in the case of non-numeric data, i.e., image, audio, or video, a visualization approach is required. In [20] trained SVMs are visualized using nomograms, which represent the entire model graphically on a sheet regardless of the number of features. After training the SVM, univariate logistic regression is employed to obtain the effect vector and the intercept on the log-odds scale. The terms of effect vector give an effect function which is visualized in nomograms with the intercept. They gave the idea of a decomposable kernel for visualization. In [30], the idea of projecting the data on the direction of decision boundary is used for feature selection. In [40] input data is projected onto a two-dimensional self-organizing map nonlinearly, giving a SVM visualization algorithm. In [9], data is projected onto a two-dimensional plane. The location of support vectors on this plane is used to identify the importance of the plane and the variables forming this plane. But this approach is interactive and requires domain expertise if the data is high dimensional and thus not interpretable intuitively.
There are various semi-supervised learning methods which use SVMs to classify the images. These methods assume that if two images are close enough, they would induce similar conditional distribution. So to classify an unlabeled image, it becomes important to analyze the local geometry of that image. In [38] hessian regularization is used with SVMs to deal with image annotation problem on the cloud. This method works well when the distribution of unlabeled data is estimated precisely. Thus a large number of unlabeled data is required which in turn requires huge storage and computing capabilities for better performance. In [22], a graph p-laplacian regularization is used with SVMs for scene recognition. This approach preserves local similarity of data and reduces the cost of computation using approximation algorithm. In [23] hypergraphs and p-laplacian regularization are used for image recognition. The methods exploit the local geometry of the data distribution and improves the computational efficiency. All these manifold regularization methods used with SVM improve the accuracy of classification but do not explain the visual interpretability aspect of classification.
SVMs have been used to classify various types of medical images like MRIs, WSIs, X-rays, CT scans to diagnose brain tumors, breast cancer, diabetic retinopathy, tuberculosis and COVID-19 etc. In [1, 8, 24, 28, 32] brain MRIs are used to diagnose brain cancer, brain tumor and Alzheimer. In [1, 28] wavelet transform is applied on the data and then SVM is used for binary classification. In [8], SVM classification along with CRF-based hierarchical regularization is used to enhance the accuracy of tumor prediction. In [24] skull masking is used as a preprocessing step before applying SVMs. In [32] Alzheimer is diagnosed by applying linear SVMs along with classification trees on the brain images. In [18, 35] mammography images are classified using SVMs for benign and malignant masses, but in [18] ROIs are passed as input to the model. In [2, 16, 43] chest X-Ray images are used to predict tuberculosis and covid-19 using SVM classifier but do not focus on interpretability.
Various medical image classification models proposed in the past highlighting ROIs, use various diverse algorithms but mostly they don’t exploit the power of SVM. In [42] CNNs are used for mammograms segmentation in a pre-processed image to detect the suspicious regions. This approach tries to classify the mammograms using texture and shape features but to achieve better segmentation results, CNN parameters need to be optimized. In [41], regression activation map is applied after pooling layer of CNN model to interpret the classification of diabetic retinopathy. These regression activation maps highlight the ROIs on the basis of severity. In [37], a linear SVM is used with special-anatomical regularization to classify Cuingnet’s Alzheimer’s disease vs. cognitive normals dataset. In addition to this, a group lasso penalty is used to induce structural penalty for identifying ROIs. In [13] curvelet level moments-based feature extraction technique has been used for mammogram classification which does not loose any information of the original space. These features were computed on limited ROIs, which contain the prospective abnormality. The method does not use a nonlinear feature reduction approach. In [27] classification of dense ROIs is done using taxonomic indices. After extracting texture regions, SVM classifier was used to classify the mass regions but does not deal with interpretability of results. In [4] a hybrid bag-of-visual-words based classifier as an ensemble of Gaussian mixture model and support vector machine is applied on diabetic retinopathy (DR) images. The system is measured using various performance parameters such as specificity, accuracy, sensitivity, etc. for statistical implementation. In [33] a unified DR-lesion detector has been proposed by introducing discrimination of bright lesions by extracting local feature descriptors and color histogram features from local image patches. In [3] multiscale AM-FM based decomposition is used to discriminate normal and DR images. In this technique, the lesion map is inferred by a set of frequency-domain based features which describe the image as a whole.
SVM interpretability
Interpretability of the SVM classification requires explanation of its prediction through textual or visual artifacts that provide qualitative or quantitative understanding of the relationship between salient input constituents and the prediction. SVM defines a hyperplane separation boundary using (1):
| 1 |
where is data, yi is label, is the vector that subtends a 90∘ angle on the hyperplane and b is bias.
| 2 |
Solving the above optimization problem for and b shall give us the classifier. The maximum-margin hyperplane is completely decided by the points that lie nearest to it and these data points are known as support vectors.
In Kernel SVM, we have a kernel function k which satisfies . It is known that satisfies (3) in the transformed space.
| 3 |
where ci is obtained by solving (4)
| 4 |
For computing the class of the new points, (5) is used:
| 5 |
Kernel trick transforms the data into another dimension and the features which play the vital role in prediction, may not correspond to any of the features in original space. The separating hyperplane is also unknown in original space. In case of medical image data, where each pixel represents one dimension, an SVM considers almost all the attributes to interpret the prediction results, making it complicated for human consumption. This non-interpretability persists even if the contribution of all the attributes can be determined. In these cases, various salient components can be used to explain the results, which may not be actual input attributes.
Proposed ROI-stitching algorithm
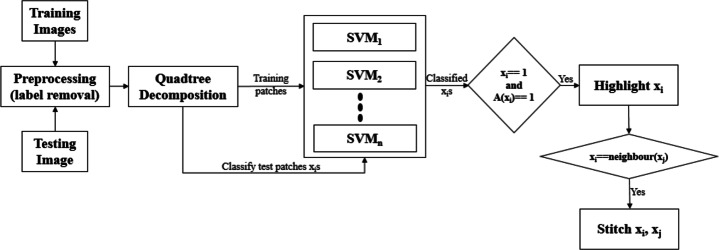
In medical image classification, diseases like cancer, diabetic retinopathy, etc., the prediction of disease is not a global function of the entire space, rather the disease manifests locally and has a spatially localized phenomenon. The presence of disease can be observed by multiple local regions in the image, which may co-occur in isolation. Various CNN based algorithms focus on most distinguishable ROIs and overlook other important parts of image [34, 44]. To visually perceive the image’s classification we need to find a relationship between the prediction model and input image. It is important to localize the ROIs to understand the cause of prediction. We can segment the image to localize the discriminative regions causing the prediction. When we segment an image, we divide it into more meaningful regions, where neighboring pixels bear similar characteristics and hence making it easier to analyze the prediction. In medical image classification, when we apply nonlinear SVMs, the cause of prediction may not apparently be human interpretable. If we segment an image hierarchically and then apply SVMs in a cascaded manner, we can localize the lesions and explain the predictions. The idea is to apply SVM again on the segmented portions of an image if the image itself is predicted as disease prone and hence to distinguish the ROIs from neighboring segments which may reflect significantly different characteristics. In the proposed method, we employ Quadtree decomposition to localize those regions which influence and explain model’s decision. Through Quadtree decomposition, the model processes a relatively smaller data region which contains crucial features and highlights the ROIs in the image. We use following steps to find the ROIs:
Decompose the images using quadtree approach up to certain levels of tree.
Train SVMs, an SVM for each level of tree except the root level.
For a test image, predict the result for each node in each level by its own SVM.
Mark only those nodes in the final result which have (l - 1) fold fortification of their decision towards being a malignant region.
Finally, connect all the nodes which are marked using 4-connectivity in order to unearth the underlying ROI.
All these steps are depicted in Fig. 1.
Fig. 1.
Flowchart of the proposed method. A(xi) indicates all the ancestors of xi
This approach helps to preserve the spatial correlation between the features. The model is unsupervised in a sense that it predicts the ROIs without any prior information of probable candidate regions.
Quadtree decomposition
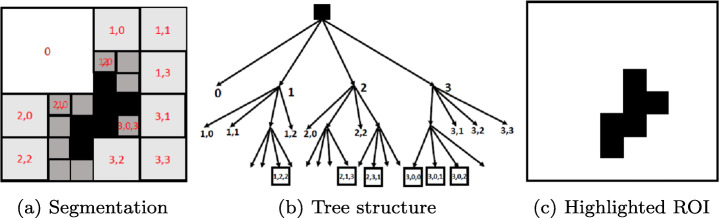
Quadtree is a region splitting and merging based segmentation method. This approach partitions an image into multiple regions having similarity on the basis of predefined criteria[31]. In Quadtree each node has exactly four branches except the leaf nodes (Fig. 2) [36] [21]. One need not to keep all the nodes at any levels (Fig. 3) and can further sub divide only those nodes which are essential for prediction (Fig. 2b). Quadtree decomposition has following steps:
Start to split a region into four branches.
When adjacent regions are found similar, merge by dissolving the common edges.
Fig. 2.
Quadtree
Fig. 3.
A quadtree constructed from an image
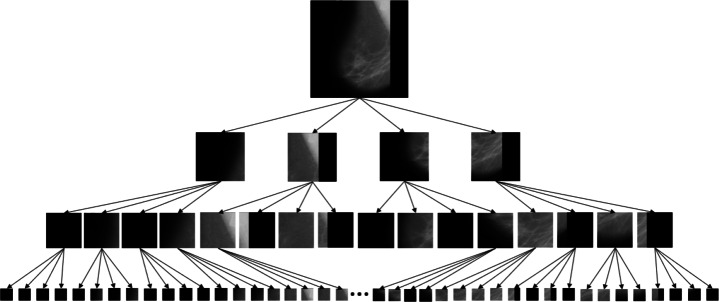
Quadtree decomposition has a feature-preserving capability [11] and it can extract the details of images, thus more feature information can be extracted from the visual important ROIs than from the monotone areas of the image[39]. For instance, let X be the original image and we divide X up to p levels using quadtree decomposition. X is divided into ni sub images at level i, i.e.
| 6 |
When SVM is applied on each sub image of X up to p levels, we get a vector DX
| 7 |
where is defined as prediction on the sub image ; and the set for level i corresponds to the prediction of ith level of representation. When SVM predicts class C = {+ 1,− 1} for image X and using quad tree the feature vector also predicts the same class C from level 1 to p consistently, it signifies that sub image or collection of sub images at level p, on which predicts same class C, are the spatially localized regions causing such prediction. All the steps of Algorithm 1 are explained using figures depicting the effects on mammography images.
Pre-processing
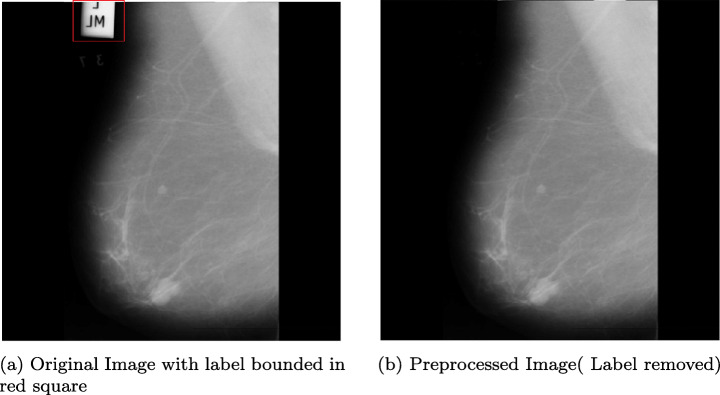
Any medical image contains patient specific information such as watermark, name, technology used etc. The actual decision from SVM should not be influenced with such details, hence in the first step, all these informations are eliminated by finding the connected components and discarding the smaller one (Fig. 4) by employing (8):
| 8 |
where xk is the kth image. By using (8), the smaller connected component is discarded, giving a clean image by removing labels that adversely affect SVMs’ decision ability. Each image is divided into ni patches at level i up to level p; where p is application and domain expert dependent. All the patches having irrelevant data beyond threshold are labeled as benign.
Fig. 4.
Preprocessing
Training and testing of SVMs
After preprocessing, images are decomposed using quadtree up to p levels using (6). For training of SVMs, patches of training images from each level’s nodes are extracted and corresponding SVMs for each level have been trained. RBF SVM has been used for classification.
| 9 |
where is the jth patch of the image at ith level, Xi,l is lth support vector of SVM corresponding to ith level, sp is number of support vectors at that level, α is weight and σ is a free parameter. For each level of quadtree, a separate SVM has been trained. When testing our method, the respective SVMs are used at each level for prediction of malignancy in the node’s image. The predictions of all the nodes are agglomerated by (10):
| 10 |
where is the decision for jth node in ith level. As median is a better centrality measure than mean and it is robust to outliers, the threshold for deciding if a lesion is present in the test image or not, (11) is used:
| 11 |
where N is the number of training samples and dk represents the decision taken for training image k. As we focus on early detection of disease, the size of the lesion should be invariate to the results. Ignoring the smaller ROIs would allow to leave such patches out, which can be detrimental for the patient for a long run. The regions that are more relevant and valued most in the classification need to be examined further. By segmenting such patches using quadtree we cover the bases as much as we can.
ROI highlighting
For highlighting the ROI, nodes in the lowest level which were predicted as malignant, were taken and only those of them, whose ancestors except root were all predicted as malignant, were chosen and highlighted. This condition can also be represented as follows:
| 12 |
where Dj represents the decision of corresponding node and Ai − root represents the ancestors of the corresponding node excluding root. The output of this step is shown in Fig. 5a for a mammography image.
Fig. 5.
ROI identification
ROI stitching
The results in the previous step may have multiple adjacent highlighted ROIs. In order to find the arbitrary shape of affected regions we use the concept of four-connectivity [15]. If two ROIs are four-connected then the common edge between them is removed. Formally,
| 13 |
This connectivity algorithm provides us the result as shown in Fig. 5b. Through ROI highlighting technique, the proposed method is able to identify each isolated local region responsible for underlying model’s prediction however, few common regions present in the image remain unknown. The ROI stitching method illustrated here joins such regions to provide a better understanding of the localized region. It also captures the proliferation disease and assess how discriminating region may grow.

Experiment and results
In classification, the reason behind the prediction is must for acceptance of the model and this makes interpretability an inseparable measure behind model’s utilization. Medical images are not readily interpretable. In case of medical image classification, the ROIs are not highlighted by default in the images. Thus, domain experts are required to find localized regions which are affected by disease based on their experience and lead to the justification of the treatment given to the patient. When SVM is employed for the similar task of medical image classification, images annotated by domain experts are used to train the model. Once the model is trained, it gives prediction for images other than training by identifying features similar to what it has learned during training phase.
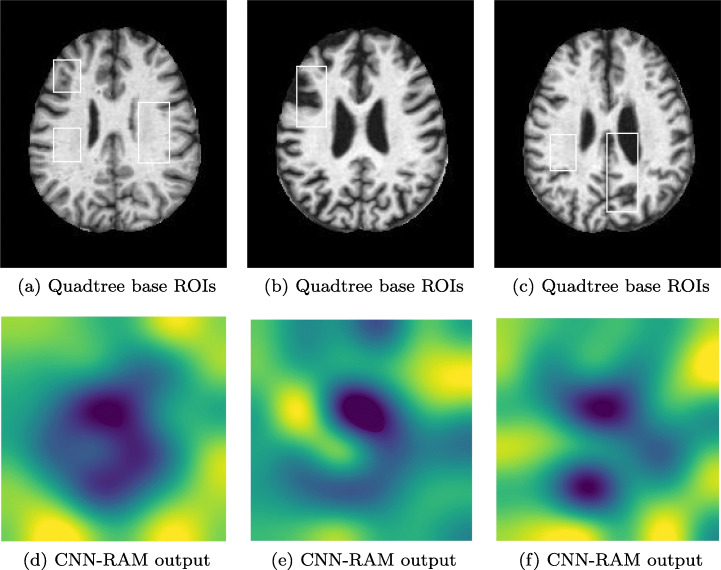
To validate the prediction of SVM for medical image classification, we had applied our algorithm on various medical image datasets consisting of mammography images, diabetic retinopathy images, COVID-19 X-rays and CT-Scans and Alzheimer’s MRI images. We applied our algorithm on a diverse medical datasets to establish its generality and capacity of localizing the discriminative regions for any image classification application. In the algorithm, SVM was backed by highlighting ROIs which motivated the SVM to classify a whole image to be malignant. The adjacent highlighted ROIs were merged using four-connectivity to reveal the true shape of the affected area. The algorithm’s performance was assessed by matching the sensitive areas according to the experts without losing the spatial correlation. The Quadtree approach has been further compared with state-of-the-art discriminative localization using regression activation map (CNN-RAM) model.1 The base model of CNN-RAM for diabetic retinopathy was used with prior trained weights and features as available. On other benchmark medical data sets, the CNN-RAM was trained on three levels (128, 256, and 512) as recommended. Further, we compared our model with You Look Only Once (YOLO), a CNN based supervised model. YOLO needs candidate regions of images before getting trained. This process requires human intervention, which may lead to errors. Mammographic images dataset contains the original ROIs, hence results obtained from YOLO have been analyzed extensively in case of mammography images only. As an outcome, the proposed method gives prediction with readily available annotated(ROIs) image, which supports the prediction.
Experimental setup
The experimental results were obtained using python 3.7 on a server equipped with 2 Intel Xeon CPUs with 16 cores each accompanied by 64 GB of RAM, 2TB of disk space, and a 4GB Nvidia Quadro K2200 GPU.
Mammographic images Dataset
The first dataset we have taken is mammography images dataset from Mammographic Image Analysis Society (Mini-MIAS)2 to classify them using quadtree-backed SVMs. Mammography is used to screen the breast cancer but their interpretation is difficult without domain expert and may lead to misclassification [29]. The classification requires an additional supportive opinion. The dataset consisted of 322 mammography images having 1024x1024 dimensions each. A quadtree is constructed till level 3 i.e.; nodes have images with dimensions 128 x 128. For training, the images from all the nodes in the first 200 quadtrees are extracted and then, the corresponding 3 SVMs (512x512, 256x256, and 128x128) are trained using the corresponding images extracted from the nodes of quadtree’s 3 levels. For testing, the labels for each node’s image in quadtree are predicted using the corresponding SVMs, and then, ROIs are highlighted. A node is only highlighted in the output image iff it is predicted as cancerous and all its ancestors excluding the root node in image’s quadtree decomposition are also predicted as cancerous.
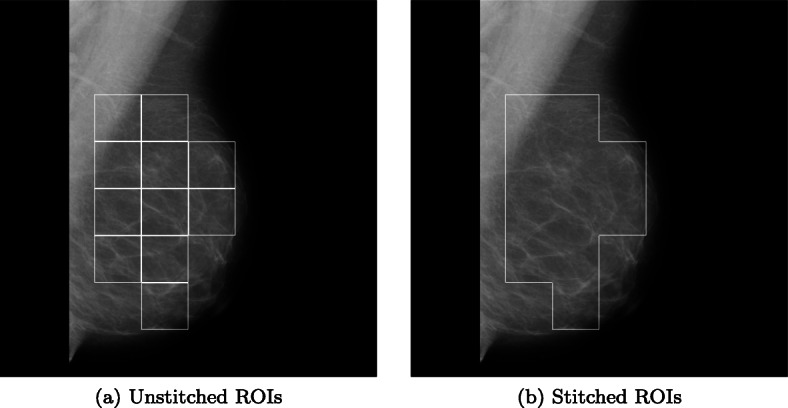
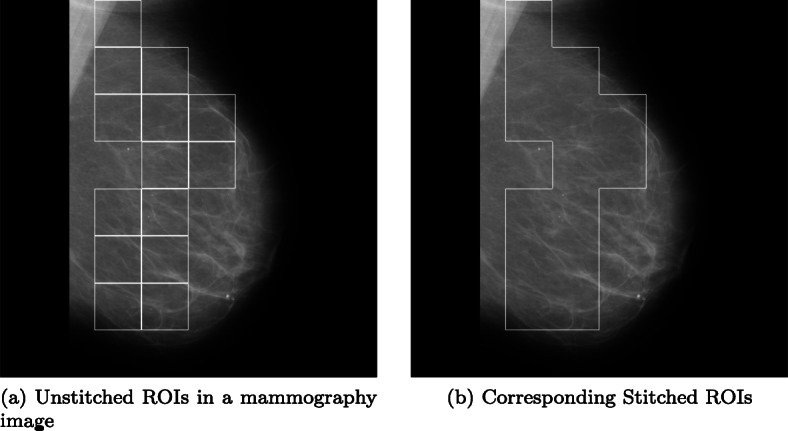
The image in Fig. 6a shows an output of mammography image before ROI stitching. The image in Fig. 6b shows the corresponding stitched ROI output. Figure 7 validates the effectiveness of our algorithm where Fig. 7a and e highlight the actual ROIs in two cancerous images, whereas Figs. 7b and f are the results of corresponding images from our algorithm.
Fig. 6.
A Mammography image showing output of the algorithm
Fig. 7.
Comparison of Highlighed region with actual ROIs of 2 Mammographic images, a, b, c and d are results on same image and e, f, g and h are results on another image
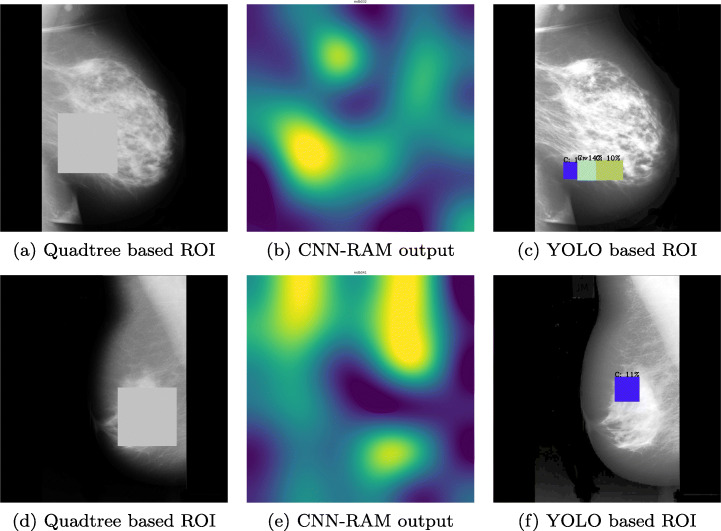
To compare our approach of finding ROIs in mammograms using quadtree, we had applied CNN-RAM and YOLO algorithms for classification. YOLO sees the whole image at once and the CNN gives predictions of bounding boxes and class probabilities for these boxes. Due to the low contrast of the images, histogram equalization was applied to the dataset. Input dataset to the network consisted of annotation files containing the bounding regions of the cancer cells given in data. Of all the 322 images 70% images were passed as training images and the remaining were used for testing. To train the model using YOLO we had provided the bounding regions in training images. The test image corresponding to image in Fig. 7a is classified with multiple highlighted ROIs of varying confidence shown in Fig. 7d. Figure 7h could not find the ROIs in the image corresponding to image shown in Fig. 7e and misclassified it as normal. The results of YOLO based model were only 63.93% accurate, whereas our Quadtree based approach has given 77.86% accuracy. The biggest concern with YOLO is providing bounding boxes to supervise the training. Quadtree approach finds the ROIs without prior supervision and does not need the probable ROIs for training.
To verify the correctness of our Quadtree based classification, we applied ROI occlusion on all the test images. Figure 8a and d are the images tested after occluding the ROIs predicted using Quadtree. Figure 8c and f are the results of images tested after occluding the ROIs predicted using YOLO. All the positive test images whether true or false, both Quadtree and YOLO methods predicted them as normal images and do not find any other ROIs after occluding the previously found ROIs.
Fig. 8.
Classifying Mammographic images with new ROIs using Quadtree and YOLO models with existing ROI occlusion, a, b and c are results for same image and d, e and f are results on another image
Diabetic Retinopathy images Dataset
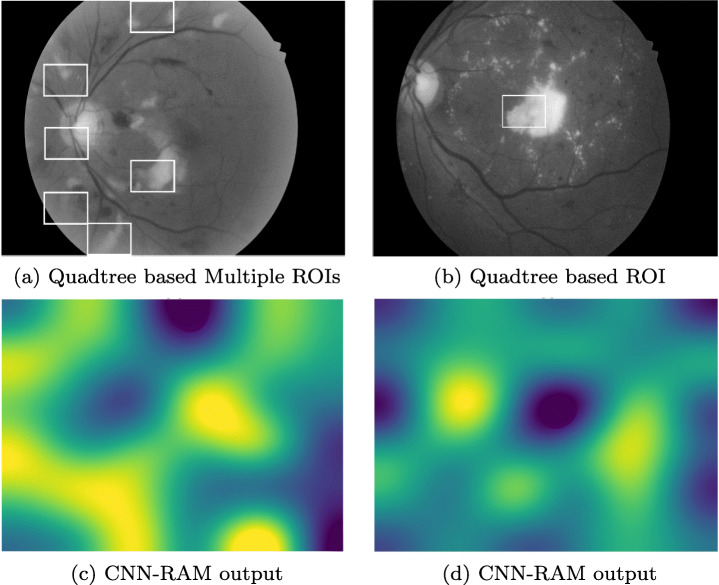
In our second experiment, a dataset containing diabetic retinopathy images, has been taken from Indian Diabetic Retinopathy Image Dataset (IDRiD) website3. This abnormality of eyes affects the retina of patients by increasing the amount of insulin in their blood. In this experiment, a subset containing 516 images was used, where each image is of resolution 4288x2848 pixels. Expert markups of typical diabetic retinopathy lesions and normal retinal structures were also provided. The training set consisted of 344 images. After decomposing images to size 2144x1424, 1072x712, and 536x356, respectively, the SVMs were trained using the corresponding images. Remaining 172 images were tested, and lesions were highlighted in defected images. Figure 9 shows some of the results of diabetic retinopathy images which were correctly classified. We had applied the YOLO based model on this dataset as well. Since we don’t have prior information of ROIs in training images, the results found using YOLO were very poor. Either the whole image was predicted as ROI or misclassified.
Fig. 9.
Highlighted ROI(s) in Malignant Diabetic Retinopathy Images, a and c are results on same image and b and d are results on another image
COVID X-RAY Dataset
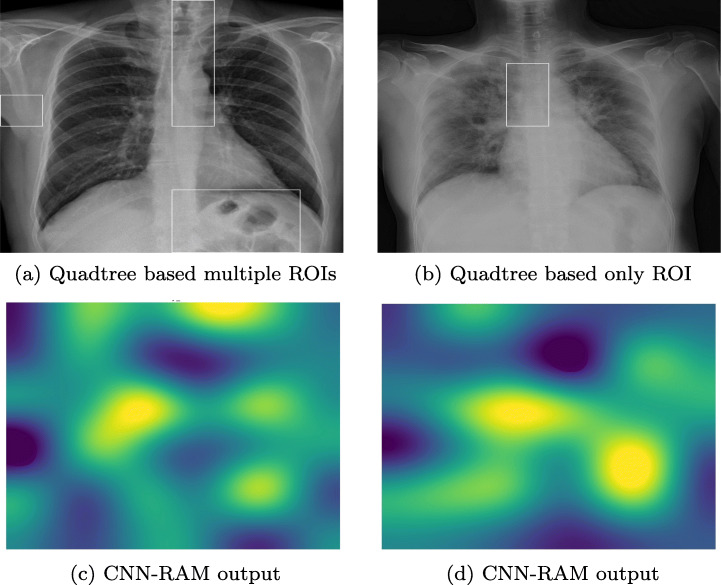
In the third experiment, a dataset containing 338 chest X-ray images,4 is used to classify data into COVID-19, SARS (Severe acute respiratory syndrome), ARDS (acute respiratory distress syndrome) and other classes[12]. Out of 422 X-ray and CT Scan images of 216 patients, we have taken only X-ray images of 194 patients, containing 272 COVID-19 positive images. Due to the varying size of images, all the images are resized to 1024x1024 pixel. We have applied the concept of one-vs-all classification using SVMs to identify the ROIs of minimum size 128x128 pixels in COVID-19 positive images. In Fig. 10 two X-ray images of COVID-19 patients with highlighted ROIs are shown. In Fig. 10a, an ROI highlights the opaqueness in trachea and a lesion on right lung. In Fig. 10b, ROI captures the hazy lung opacity on the upper lobe but does not highlight heziness in the lower lob of right lung.
Fig. 10.
Highlighted ROI(s) in COVID X-Ray Images, a and c are results on same image and b and d are results on another image
COVID CT SCAN images Dataset
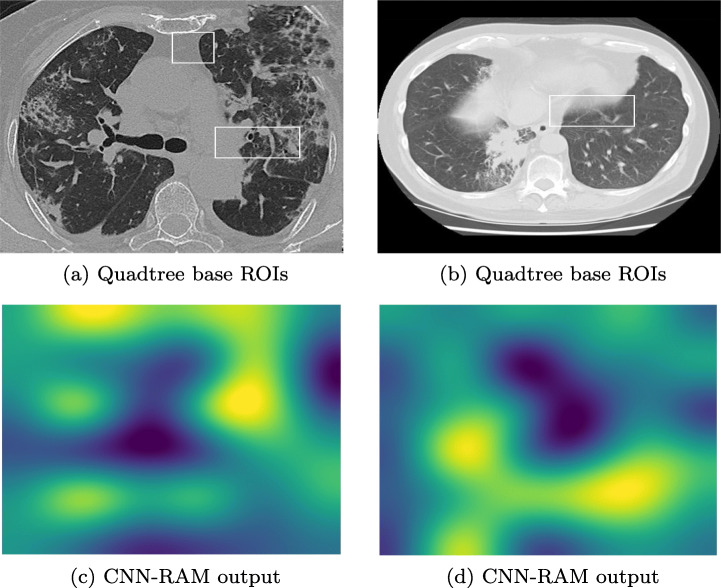
In our fourth experiment, a dataset containing COVID CT Scan images,5 is analyzed. A total of 349 images of 216 patients are COVID-positive and 397 images are non-COVID images. All the images are of different resolutions, varying from minimum 153x124 pixels to maximum of 1853x1485 pixels; averaging 491x383 pixels; we resized all the images to 512x512 pixels. After removing the labels in preprocessing, 60% images are considered in training and remaining 40% for testing. After applying the SVM up to 3 levels, we identifed the patches of size 64x64. Figure 11 shows the results of COVID CT Scan images after applying ROI stitching. In Fig. 11a, our algorithm highlights two ROIs, of which the larger ROI contains a small lesion. It is not evident to understand the significance of other ROI for a human. In Fig. 11b the ROI highlights opacity in right lung only, though we can see the opacities involved bilaterally due to thickening or partial collapse of the lung alveoli.
Fig. 11.
Highlighted ROI(s) in COVID CT Scan Images, a and c are results on same image and b and d are results on another image
Alzheimer’s Dataset
To further evaluate the proposed method, in the final experiment, we have taken a dataset containing 6400 Alzheimer’s Brain MRI images6 of resolution 176x208 pixels each. This dataset contains 5121 images for training and 1279 images for testing. In Alzheimer’s, cognitive impairment can be very mild, mild or moderate. So, the dataset has 4 classes of images namely non demented, very mild demented, mild demented and moderate demented. The model is trained using one-versus-rest strategy. The results shown in Fig. 12 with minimum ROI size equals to 22x33 prove that the algorithm is able to locate the localized regions responsible for model’s prediction in the test images. These ROIs show damage in the right frontal, temporal, and parietal lobes, including the middle frontal gyrus, inferior frontal gyrus, precentral gyrus, postcentral gyrus, superior temporal gyrus, and insula. In Fig. 12a the ROIs in a very mild demented image, capture the opaqueness in left frontal lobe and temporal lobes. In Fig. 12b the ROI captures the damage in left frontal lobe of mild demented image. In Fig. 12c the ROIs capture the damage in parietal lobes of a moderately demented image.
Fig. 12.
Highlighted ROI(s) in Alzheimer’s MRI Images, a and b are results for a very mild demented image, b and e are results for a mild demented image and c and f are results for a moderate demented image
Performance and sensitivity analysis
The main objective of our method is to explain the SVM classification results. In order to establish the completeness of the proposed Quadtree model, we have performed sensitivity analysis to compare our method with CNN-RAM and YOLO. The sensitivity of these method can be analyzed on the basis of their performance and visual correctness as well. To analyze the performance of the method, only accuracy cannot provide a complete overview. Here, we have measured the precision, sensitivity, specificity and F1 score of the method using the confusion matrix i.e. TP, FP, TN and FN. Precision provides the percentage of correctly identified positive instances out of total positively identified instances. Sensitivity or recall provides the percentage of correctly identified positives of given positive instances, whereas specificity provides the correctly identified negatives. F1 score provides the balance between precision and recall. To evaluate these measures, we use following formulas
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
Table 1 provides the details of all performance anaysis parameters in percentage. Though for mammography, COVID and Alzheimer’s images our method performs better than the rest of the methods, CNN-RAM marginally outperforms our method in case of diabetic retinopathy images. For visual sensitivity, we have compared the method generated ROIs with the readily available ROIs provided with the datasets. In our experiments, only mammography images dataset and NIH dataset have provided the original ROIs.
Table 1.
Precision, sensitivity, specificity, F1 Score and accuracy of models (in%)
| Dataset | Method | Precision | Sensitivity | Specificity | F1 Score | Accuracy |
|---|---|---|---|---|---|---|
| Mini-MIAS | Quadtree | 80.45 | 87.50 | 59.52 | 83.82 | 77.86 |
| CNN-RAM | 50.98 | 74.28 | 71.26 | 60.46 | 72.13 | |
| YOLO | 43.33 | 72.22 | 60.46 | 54.16 | 63.93 | |
| IDRiD | Quadtree | 87.69 | 93.44 | 68.0 | 90.47 | 86.04 |
| CNN-RAM | 92.43 | 90.16 | 82.0 | 91.28 | 87.79 | |
| COVID X-Ray | Quadtree | 60 | 78 | 65.54 | 67.83 | 77.61 |
| CNN-RAM | 80.95 | 68.0 | 60.0 | 74.38 | 65.71 | |
| COVID CT Scan | Quadtree | 85 | 86 | 75.6 | 85.17 | 85.92 |
| CNN-RAM | 72.97 | 77.14 | 75.0 | 74.99 | 76.0 | |
| Alzheimers MRI | Quadtree | 77.65 | 72.30 | 79.22 | 74.88 | 75.76 |
| CNN-RAM | 67.54 | 38.14 | 96.32 | 48.75 | 87.65 |
The results show that the aim of interpreting SVMs’ classification results for image datasets by segmenting them using quadtree is achieved successfully. Our method does not require prior ROI information for training the model. Hence Quadtree approach can be applied on all the datasets which don’t have information of regions to supervise the model. Quadtree method is also independent of the size of images, whereas YOLO fails in case of smaller objects in an image. We can further find more arbitrary and accurate ROIs by segmenting the smallest patches of images using further quadtree levels.
Conclusion
In this paper, we proposed an algorithm of finding regions of interest in medical images using quadtree to explain the prediction made by an SVM. The technique is based on the assumption that some diseases manifest in local regions of a medical image and localization of such discriminative regions can help in explaining the presence of the disease the also the classification made by the SVM used for prediction. We first applied quad tree reclusively on the segments of multiple levels and employed separate SVMs at each level of quadtree to identify discriminative regions at a very fine level. The regions of interest in mammography images highlighted the regions containing the actual lesions. Though many of the images in the dataset had only one lesion spot, our method could highlight additional regions in few images. The presence of regions which are not immediately discriminative might have also been responsible for the disease. For diabetic retinopathy images, our method highlighted multiple regions of interest in an image containing perforated abnormalities in isolation. These regions of interest could be related to severity of disease. Our method highlighted the opaqueness on both the sides of the trachea in COVID-19 X-ray images. By applying the SVM hierarchically, we could highlight the small lesions contributing in prediction. The high accuracy of the classifier with ability to explain the classification can be used for better understanding of the disease. For COVID-19 CT scan images, though the model predicts with 85.92% of accuracy, the highlighted regions of interest on COVID-19 CT scan dataset were not visually enhancing the model’s explainability, making it difficult to understand the factors responsible for prediction. The regions of interest of mild and moderately demented Alzheimer MRI images captured the significantly discriminative regions with high model accuracy as well. The SVM model could identify the regions of interest in mild and moderate demented images providing correct visual explanation. Sensitivity analysis of SVM classifier in the model supported the visual explainability with high accuracy on all the datasets. However, localization of regions of interest using quadtree needs to be combined with other techniques to explain the prediction of a classifier in entirety.
Footnotes
Codes were available at https://github.com/cauchyturing/kaggle diabetic RAM
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Prashant Shukla, Email: rsi2016502@iiita.ac.in.
Abhishek Verma, Email: ism2013002@iiita.ac.in.
Abhishek, Email: rsi2016006@iiita.ac.in.
Shekhar Verma, Email: sverma@iiita.ac.in.
Manish Kumar, Email: manish@iiita.ac.in.
References
- 1.Abdullah N, Ngah UK, Aziz SA (2011) Image classification of brain mri using support vector machine. In: 2011 IEEE International conference on imaging systems and techniques. IEEE, pp 242–247
- 2.Achmad A, Achmad AD, et al. (2019) Backpropagation performance against support vector machine in detecting tuberculosis based on lung x-ray image. In: First international conference on materials engineering and management-engineering section (ICMEMe 2018). Atlantis press
- 3.Agurto C, Murray V, Barriga E, Murillo S, Pattichis M, Davis H, Russell S, Abràmoff M, Soliz P. Multiscale am-fm methods for diabetic retinopathy lesion detection. IEEE Trans Med Imag. 2010;29(2):502–512. doi: 10.1109/TMI.2009.2037146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Akram MU, Khalid S, Tariq A, Khan SA, Azam F. Detection and classification of retinal lesions for grading of diabetic retinopathy. Comput Biol Med. 2014;45:161–171. doi: 10.1016/j.compbiomed.2013.11.014. [DOI] [PubMed] [Google Scholar]
- 5.Barakat N, Bradley AP. Rule extraction from support vector machines: a review. Neurocomputing. 2010;74(1):178–190. doi: 10.1016/j.neucom.2010.02.016. [DOI] [Google Scholar]
- 6.Barakat N, Diederich J (2004) Learning-based rule-extraction from support vector machines: performance on benchmark data sets. In: 3rd conference on neuro-computing and evolving intelligence (NCEI’04)
- 7.Barakat NH, Bradley AP. Rule extraction from support vector machines: a sequential covering approach. IEEE Trans Knowl Data Eng. 2007;19(6):729–741. doi: 10.1109/TKDE.2007.190610. [DOI] [Google Scholar]
- 8.Bauer S, Nolte LP, Reyes M (2011) Fully automatic segmentation of brain tumor images using support vector machine classification in combination with hierarchical conditional random field regularization. In: International conference on medical image computing and computer-assisted intervention. Springer, pp 354–361 [DOI] [PubMed]
- 9.Caragea D, Cook D, Honavar VG (2001) Gaining insights into support vector machine pattern classifiers using projection-based tour methods. In: Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, pp 251–256
- 10.Chatchinarat A, Wong KW, Fung CC (2017) Rule extraction from electroencephalogram signals using support vector machine. In: Knowledge and smart technology (KST), 2017 9th international conference on, pp. 106–110. IEEE
- 11.Chung KL, Tseng SY. New progressive image transmission based on quadtree and shading approach with resolution control. Pattern Recogn Lett. 2001;22(14):1545–1555. doi: 10.1016/S0167-8655(01)00106-4. [DOI] [Google Scholar]
- 12.Cohen JP, Morrison P, Dao L (2020) Covid-19 image data collection. arXiv:2003.11597. https://github.com/ieee8023/covid-chestxray-dataset
- 13.Dhahbi S, Barhoumi W, Zagrouba E. Breast cancer diagnosis in digitized mammograms using curvelet moments. Comput Biol Med. 2015;64:79–90. doi: 10.1016/j.compbiomed.2015.06.012. [DOI] [PubMed] [Google Scholar]
- 14.Doshi-Velez F, Kim B (2017)
- 15.Galil Z. Finding the vertex connectivity of graphs. SIAM J Comput. 1980;9(1):197–199. doi: 10.1137/0209016. [DOI] [Google Scholar]
- 16.Hassanien AE, Mahdy LN, Ezzat KA, Elmousalami HH, Ella HA (2020) Automatic x-ray covid-19 lung image classification system based on multi-level thresholding and support vector machine medRxiv
- 17.He J, Hu HJ, Harrison R, Tai PC, Pan Y. Rule generation for protein secondary structure prediction with support vector machines and decision tree. IEEE Trans Nanobiosc. 2006;5(1):46–53. doi: 10.1109/TNB.2005.864021. [DOI] [PubMed] [Google Scholar]
- 18.Hundekar S, Chakrasali S (2019) Detection and classification of breast cancer using support vector machine and artificial neural network using contourlet transform ICTACT. J Image Video Process 9(3)
- 19.Jakulin A, Možina M, Demšar J, Bratko I, Zupan B (2005) Nomograms for visualizing support vector machines. In: Proceedings of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining. ACM, pp 108–117
- 20.Jakulin A, Možina M, Demšar J, Bratko I, Zupan B (2005) Nomograms for visualizing support vector machines. In: Proceedings of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining. ACM, pp 108–117
- 21.Langote VB, Chaudhari D. Segmentation techniques for image analysis. Int J Adv Eng Res Stud. 2012;1(2):252–255. [Google Scholar]
- 22.Liu W, Ma X, Zhou Y, Tao D, Cheng J. P-laplacian regularization for scene recognition. IEEE Trans Cybern. 2018;PP:1–14. doi: 10.1109/TCYB.2018.2833843. [DOI] [PubMed] [Google Scholar]
- 23.Ma X, Liu W, Li S, Tao D, Zhou Y. Hypergraph p-laplacian regularization for remotely sensed image recognition. IEEE Trans Geosci Remote Sens. 2018;PP:1–11. [Google Scholar]
- 24.Nandpuru HB, Salankar S, Bora V (2014) Mri brain cancer classification using support vector machine. In: 2014 IEEE Students’ conference on electrical, electronics and computer science. IEEE, pp 1–6
- 25.Nguyen DH, Le MT (2014) Improving the interpretability of support vector machines-based fuzzy rules. arXiv:1408.5246
- 26.Núñez H, Angulo C, Català A (2002) Rule extraction from support vector machines. In: Esann , pp 107–112
- 27.de Oliveira FSS, de Carvalho Filho AO, Silva AC, de Paiva AC, Gattass M. Classification of breast regions as mass and non-mass based on digital mammograms using taxonomic indexes and svm. Comput Biol Med. 2015;57:42–53. doi: 10.1016/j.compbiomed.2014.11.016. [DOI] [PubMed] [Google Scholar]
- 28.Othman MFB, Abdullah NB, Kamal NFB (2011) Mri brain classification using support vector machine. In: 2011 Fourth international conference on modeling, simulation and applied optimization. IEEE , pp 1–4
- 29.Posso M, Puig T, Carles M, Rué M, Canelo-Aybar C, Bonfill X. Effectiveness and cost-effectiveness of double reading in digital mammography screening: a systematic review and meta-analysis. Eur J Radiol. 2017;96:40–49. doi: 10.1016/j.ejrad.2017.09.013. [DOI] [PubMed] [Google Scholar]
- 30.Poulet F (2004) Svm and graphical algorithms: a cooperative approach. In: Data mining, 2004. ICDM’04. Fourth IEEE international conference on. IEEE, pp 499–502
- 31.Rastgarpour M, Shanbehzadeh J (2011) Application of ai techniques in medical image segmentation and novel categorization of available methods and tool. In: Proceedings of the international multiconference of engineers and computer scientists 2011 Vol I, IMECS 2011, March 16-18, 2011, Hong Kong. Citeseer
- 32.Salas-Gonzalez D, Górriz JM, Ramírez J, López M, Álvarez I, Segovia F, Chaves R, Puntonet C. Computer-aided diagnosis of alzheimer’s disease using support vector machines and classification trees. Phys Med Biol. 2010;55(10):2807. doi: 10.1088/0031-9155/55/10/002. [DOI] [PubMed] [Google Scholar]
- 33.Sidibé D, Sadek I, Mériaudeau F. Discrimination of retinal images containing bright lesions using sparse coded features and svm. Comput Biol Med. 2015;62:175–184. doi: 10.1016/j.compbiomed.2015.04.026. [DOI] [PubMed] [Google Scholar]
- 34.Smilkov D, Thorat N, Kim B, Viégas F, Wattenberg M (2017)
- 35.Solanke A, Manjunath R, Jadhav D. Classification of masses as malignant or benign using support vector machine. Lung. 2019;20(176):61–007. [Google Scholar]
- 36.Sonka M, Hlavac V, Boyle R (2014) Image processing, analysis, and machine vision. Cengage learning
- 37.Sun Z, Qiao Y, Lelieveldt BP, Staring M, Initiative ADN, et al. Integrating spatial-anatomical regularization and structure sparsity into svm: Improving interpretation of alzheimer’s disease classification. NeuroImage. 2018;178:445–460. doi: 10.1016/j.neuroimage.2018.05.051. [DOI] [PubMed] [Google Scholar]
- 38.Tao D, Jin L, Liu W, Li X. Hessian regularized support vector machines for mobile image annotation on the cloud. IEEE Trans Multimed. 2013;15(4):833–844. doi: 10.1109/TMM.2013.2238909. [DOI] [Google Scholar]
- 39.Tseng SY, Yang ZY, Huang WH, Liu CY, Lin YH (2009) Object feature extraction for image retrieval based on quadtree segmented blocks. In: 2009 World congress on computer science and information engineering. IEEE, pp 401–405
- 40.Wang X, Wu S, Wang X, Li Q (2006) Svmv–a novel algorithm for the visualization of svm classification results. In: International symposium on neural networks. Springer, pp 968–973
- 41.Wang Z, Yang J (2018) Diabetic retinopathy detection via deep convolutional networks for discriminative localization and visual explanation. In: Workshops at the thirty-second AAAI conference on artificial intelligence
- 42.Sampaio WB, Diniz EM, Silva AC, de Paiva AC, Gattass M. Detection of masses in mammogram images using cnn, geostatistic functions and svm. Comput Biol Med. 2011;41:653–664. doi: 10.1016/j.compbiomed.2011.05.017. [DOI] [PubMed] [Google Scholar]
- 43.Yahyaoui A, Yumuṡak N (2018) Decision support system based on the support vector machines and the adaptive support vector machines algorithm for solving chest disease diagnosis problems
- 44.Zeiler MD, Fergus R (2014) Visualizing and understanding convolutional networks. In: European conference on computer vision. Springer, pp 818–833