Abstract
Social distancing and lockdown measures taken to contain the spread of COVID-19 may have distributional economic costs beyond the contraction of GDP. Here we evaluate the capacity of individuals to work under a lockdown based on a Lockdown Working Ability index which considers their teleworking capacity and whether their occupation is essential or closed. Our analysis reveals substantial and uneven potential wage losses across the distribution all around Europe and we consistently find that both poverty and wage inequality rise in all European countries. Under four different scenarios (2 months of lockdown and 2 months of lockdown plus 6 months of partial functioning of closed occupations at 80%, 70% and 60% of full capacity) we estimate for 29 European countries an average increase in the headcount poverty index that goes from 4.9 to 9.4 percentage points and a mean loss rate for poor workers between 10% and 16.2%. The average increase in the Gini coefficient ranges between 3.5% to 7.3% depending on the scenario considered. Decomposing overall wage inequality in Europe, we find that lockdown and social distance measures produce a double process of divergence: both inequality within and between countries increase.
Keywords: Wage inequality, Poverty, Teleworking, Social distancing, Europe
1. Introduction
The dramatic and unprecedented intensity of the shock due to the COVID-19 pandemic has highlighted the importance of measuring the economic consequences of “social distancing”. The lockdown measures implemented in many countries around the world will likely have a significant negative impact on their GDP. Thus, the global economy is expected to shrink by 3% this year. Asia will not have economic growth for the first time in 60 years, the economies of the US and Europe are projected to contract between 8% and 13% (IMF, 2020), and the global job losses are estimated to be over 200 million (ILO, 2020). However, the effect of the pandemic will not only take place at the aggregate level and is likely to have distributional implications (Furceri et al., 2020). The social distancing imposed by governments to limit the spread of the pandemic has caused an asymmetric effect on the labour market: discounting essential occupations like health services and food sales, only the jobs not closed by the lockdown that can be done from home (“teleworkable”) will be not impeded. This asymmetry of the supply shock implies that the economic costs of social distancing could be significant, not only in terms of negative GDP growth rates but also in terms of higher wage inequality and poverty rates. In this paper, we analyse the potential effects of social distancing on wage inequality and poverty in absence of any compensating public policy across Europe.
Recent studies have provided estimates of the supply shock caused by the emergency regulation imposed to contain the spread of COVID-19 (Dingel and Neiman, 2020; Hicks, 2020). They have evaluated the possible economic consequences of social distancing –without considering the subsequent effects that may occur on the demand side– by calculating to what extent occupations can be performed from home (teleworking). Mongey et al. (2020) find that workers with less ability to work from home have been indeed more unable to follow the ‘stay at home advice’ –using geolocation data– and that they have suffered higher unemployment increases. Studies focused on the demand side have shown that, due to fear of infection, economic activity dropped and individuals changed their consumption habits even before lockdown was formally imposed (Goolsbee and Syverson, 2020). In a more comprehensive analysis, del Rio-Chanona et al. (2020) provide quantitative predictions of supply and demand shocks associated with the COVID-19 pandemic. These studies, mainly focused on the U.S. economy, have analysed the consequences of social distancing in the job market, at the occupation and industry levels, without delving into the study of poverty and inequality. We find two exceptions. First, Irlacher and Koch (2020) obtain a substantial wage premium (higher than 10%) in a Mincer regression for German workers performing their job from home, and a lower share of teleworkable occupations in poorer German regions. Second, Brunori et al. (2020) study the short-term effects that two months of lockdown have had on the Italian income distribution. By using a static microsimulation model, they find a non-negligible increase of poverty and inequality in Italy.
To estimate the impact of social distancing on wage inequality and poverty across Europe, we concentrate on the legal restrictions (supply side) due to the closure of non-essential occupations and workers not being able to perform their activities at home during the lockdown period. Additionally, we consider a range of scenarios with further partial closures of certain activities, caused by mandatory capacity limitations and by the change in individual consumption habits to prevent contagion. Despite its relevance, our analysis does not consider additional indirect effects in supply (as shortages propagate through supply chains) and in demand (when the loss of labour income for some workers further reduces consumption). These effects are difficult to estimate at this early stage, and the legal and voluntary restrictions imposed to prevent the spread of the pandemic already provide a clear framework to study the consequences for inequality and poverty of having a particular productive structure. Under a lockdown, the asymmetry of the restrictions may affect economies in a different way just because their productive structure is not the same: countries who are specialised in outdoor and non-essential activities like tourism will, in principle, suffer more from the lockdown and the capacity limitations. We thus restrict ourselves to measuring the potential impact on wage inequality and poverty of enforced and voluntary social distancing.
In general, if occupations with higher wages are more teleworkable, we should observe an increase in wage inequality due to lockdown and the implementation of social distance measures within each country analysed. However, whether this happens, and the intensity of this change, will depend on the structure of the economy and the extent of essential and closed occupations under the lockdown. The wide set of European countries in our sample –with a variety of productive structures– will also allow us to test if different productive structures imply different potential effects on wage inequality and poverty under lockdown and social distancing. Note that if that is the case, inequality would not only increase within countries, but also between nations, which could exacerbate the problem of cohesion in Europe.
The first step to measure the changes in wage inequality and poverty across Europe due to lockdown is to calculate the index of teleworking at the occupational level. Dingel and Neiman (2020) found that 37 percent of jobs in the United States can be done entirely from home. What is the share of occupations that allow teleworking in Europe? Following these authors, we use fifteen questions from the Occupational Information Network (O*NET) database such as, ‘is the work done outdoors?’ or, ‘does it require significant physical activity?’ to calculate the probability of teleworking for each occupation. We then use the 2018 European Union Labour Force Survey (EU-LFS) occupational structure to translate these probabilities into the European context. Finally, we match the EU-LFS occupation teleworking index and the 2018 European Union Statistics on Income and Living Conditions (EU-SILC), which provides detailed information on wage at the individual level. After this process, we have for every worker in the EU-SILC database the individual index of teleworking (according to her occupation) and the wage.
A lockdown implies that some activities –like healthcare or food chain related jobs– will become essential while others will be closed. When the occupation is essential, workers will be not affected by lockdown regardless of their capacity to work from home. When a certain economic activity is closed –like hospitality– working is not at all possible. For the remaining economic activities, only teleworking is allowed. Consequently, during the lockdown we need to adjust our index of teleworking for the workers whose occupation is essential or closed, to obtain an individual measure that summarizes the capacity of each worker to keep active under the lockdown. We will call this measure Lockdown Working Ability (LWA) index.
The next step is to estimate the wage loss due to the lockdown. Because not all workers are able to perform their job at home and some activities are closed or limited (or less demanded to avoid infection), there are potential wage reductions for a significant part of the labour force. To simulate these wage losses, we consider four possible scenarios: two months of lockdown and two months of lockdown plus six months of only partial functioning of the closed activities at 80%, 70% and 60% of capacity. In addition, we consider in Appendix D another three scenarios where partial functioning of closed occupations −at 80%, 70% and 60% of full capacity− lasts for nine months. With these proposals we intend to measure not only the effect of the lockdown, but also the impact of the de-escalation period imposed to contain the spread of COVID-19. Although each European country may have followed slightly different lockdown and de-escalation strategies, the core of the social distancing enforcing policies has been similar in most of them. For that reason, and to ensure that in our analysis differences across countries are mainly due to their productive structure, we simulate the same scenarios for all European countries.
The last step is to measure the changes in wage inequality and poverty across countries, and the variation of wage inequality between and within-countries due to the lockdown. For this task, we first compute the Lockdown Incidence Curve (LIC), which represents the relative change in the wage of individuals ordered by centiles, and the related changes in the mean ‘growth’ rate of the poor (Ravallion and Chen, 2003) and headcount poverty index. Then, we use the Gini coefficient and the Mean Logarithmic Deviation (MLD) to calculate the changes in wage inequality. The first measure is a popular index of inequality which is widely used in the literature, while the second measure fulfils some properties which are necessary for our analysis of inequality decomposition. In particular, the MLD is the only inequality index that is additively decomposable into a between-group and a within-group component (Bourguignon, 1979; Shorrocks, 1980) and has a path-independent decomposition (Foster and Shneyerov, 2000).
Our results show that poverty increases for the headcount index and the mean loss rate of the poor in all countries for all simulations, although these changes vary greatly with the country and simulation under consideration. For the four simulated scenarios, we estimate for 29 European countries an average increase in the headcount poverty index that goes from 4.9 to 9.4 percentage points and a mean loss rate for the poor that goes from 10% to 16.2%. Likewise, wage inequality increases for the Gini coefficient in all countries for all simulations. For example, the average increase in the Gini coefficient varies between 3.5% and 7.3% for Europe as a whole. We thus find that poverty and inequality changes are sizeable in all countries and they increase with the duration of the lockdown and social distance measures. When we decompose overall inequality in Europe, both within countries and between countries inequality increase, producing a double process of divergence in wage inequality in Europe. But this increase in wage dispersion is not symmetric, and the within-countries inequality component increases more than the between-countries inequality component. Thus, the increase in the within-countries inequality component ranges from 5.0% to 12.1%, while the change in the between-countries inequality component goes from 2.5% to 4.0%, depending on the scenario under consideration.
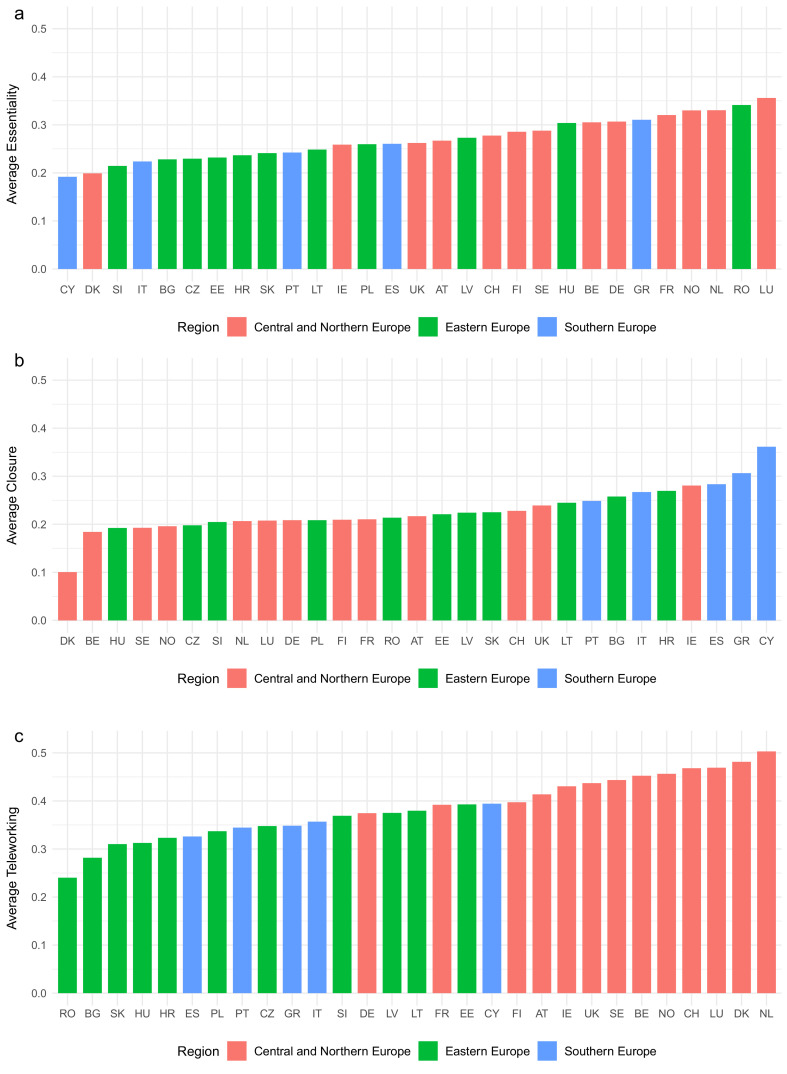
The observed increases in poverty and inequality are in general greater in Eastern and Southern countries than Central and Northern countries and are inversely related to the LWA index. To further understand these differences across European countries we need to analyse separately the three components of the LWA index: teleworking and essentiality (which increase the working ability of occupations during the lockdown), and closure (which implies a lower working ability during the lockdown and subsequent de-escalation periods). We observe that the occupational and industry structure of Eastern European countries presents, in general, medium average levels of closure, but low average levels of essentiality and teleworking. On the contrary, Northern and Central European countries show large values of essentiality and teleworking, and low average levels of closure. Meanwhile, workers in Southern European countries have medium average levels of essentiality, rather low levels of teleworking and, especially, the highest average levels of closure, due to the large preponderance in their productive sector of activities that imply the agglomeration of large groups of people like recreation or hospitality.
The rest of the paper is structured as follows. In Section 2 we present the LWA index and the methodology applied to calculate the wage losses and changes in inequality and poverty. In Section 3 we highlight the main results obtained for Europe. Finally, Section 4 concludes.
2. The lockdown working ability index and potential wage losses
2.1. The lockdown working ability index
To analyse the working ability of individuals during the lockdown, we need first to estimate occupational teleworking. For this task we use three different databases (see Appendix A). First, we make use of teleworking information acquired using key attributes and characteristics of occupations from the American O*NET database (Dingel and Neiman, 2020). Second, we use the latest 2018 wave of EU-LFS (2020 release) –with detailed employment and occupational information for European countries– to accurately obtain occupational teleworking information for the European occupational categories. Finally, this information is combined with the rich socioeconomic data –crucially, salaries– from the 2018 wave of EU-SILC (2020 release). This strategy, which is explained in detail in Appendix A, allows us to calculate the teleworking capacity of European workers.
However, teleworking capacity is not the only determinant of workers ability to effectively work and keep their wage during the lockdown period. We need to consider that some occupations are not affected by the lockdown because they are considered essential −like healthcare or agriculture− while others are fully closed to contain the spread of COVID-19, like accommodation or entertainment. Based on the decisions made by the governments in Italy and Spain, two of the earliest and most affected countries by the pandemic in the world, we have defined the essential and closed occupations at the ISCO-08 2-digit level and NACE (Rev.2) 1-digit level.1 Our classification of occupations is mainly based on the Royal Decree 463/2020 (Boletin Oficial del Estado, 14th March, 2020) approved by the government of Spain on March 14th (2020). We have also considered the Royal Decree 10/2020 (Boletin Oficial del Estado, 29th March, 2020) approved by the government of Spain on March 29th (2020), and the Decree Law 23 (Gazzetta Ufficiale della Repubblica Italiana, 23rd February, 2020) approved by the government of Italy on February 23rd (2020). The essentiality and closure values are shown in Appendix B (Table B1, Table B2, Table B3, Table B4, Table B5).
All occupations in industries A (Agriculture, forestry and fishing) and O (Public administration and defence; Compulsory social security), and occupations 22 (Health professionals) and 32 (Health associate professionals) −for all industries− are classified as entirely essential under the lockdown. For these cases, the essentiality score (E) given to the occupation of the individual is the highest (1 point). Most of the occupations in industry Q (Human health and social work activities) are also considered as completely essential since they are closely related to healthcare, therefore, they receive a value of essentiality equal to 1. Meanwhile, the majority of occupations in industries B-E (Mining and quarrying; Manufacturing; Electricity, gas, steam and air conditioning supply; Water supply, sewerage, waste management and remediation activities) receive a value of essentiality equal to 0.1 because a few of them (in particular electricity, gas, water supply and sewerage) are fundamental for the correct functioning of the economy during the lockdown.2 In the same manner, most of the occupations in industry H (Transportation and storage) receive a value of essentiality equal to 0.5 since the Royal Decree 463/2020 have declared 50% of minimum services in transportation. For most occupations in industries J (Information and communication) and K (Financial and insurance activities), the given value of essentiality is 0.25 since the Spanish decree considered that a minimum service of banking and press (part of the communication industry) was deemed essential and this is approximately the percentage of activities in these industries that keep functioning under the lockdown.
With respect to the closed occupations under the lockdown, we have that all occupations −except 22 (Health professionals) and 32 (Health associate professionals) − in industries G (Wholesale and retail trade; Repair of motor vehicles and motorcycles), I (Accomodation and food service activities) and R-T (Arts, entertainment and recreation; Other service activities; Activities of households as employers; Undifferentiated goods and services; Producing activities of households for own use) are classified as completely closed. For these cases, the closure score (C) given to the occupation of the individual is the highest (1 point). Likewise, occupations 26 (Legal, social and cultural professionals), 34 (Legal, social, cultural and related associate professionals) and 52 (Sales workers) receive a value of closure equal to 0.75 since the Royal Decree 463/2020 have declared that, among all legal activities, only the criminal legal activities should function under the lockdown, and that social and cultural activities and non-online sales are temporary forbidden to prevent people from getting together in large groups.
Having calculated the teleworking index and identified the essential and closed occupations, we construct the Lockdown Working Ability (LWA) index. This measure summarizes the capacity of individuals to work under a lockdown taking into account not only the value of their occupation's teleworking index, but also if such occupation is essential (e) or closed (c). The central idea is that workers in essential occupations can work during the lockdown regardless of whether the occupation can be teleworked or not. On the contrary, workers in closed activities cannot work at all to the extent that their overall activity has been closed. In all remaining cases, working capacity will depend on the share of that occupation that can be teleworked.
Formally, the first step in constructing the LWA index requires to split the population of n workers into three groups according to the occupation oi of each worker . If the individual has an occupation that is neither essential nor closed, the value of her LWAi index will be equal to the value of her index of teleworking, Ti ∈ [0, 1]. If the person has an essential job (), we will compute the LWA index as , where Ei ∈ (0, 1] is the essentiality score given to the occupation of the individual. Thus, for partially essential occupations (0 < Ei < 1), the non-essential share of the occupation can work during lockdown only to the extent that it is teleworkable. Finally, if the person has a job that is closed (), we will calculate the LWA index as , where Ci ∈ (0, 1] is the close score given to the closed occupation of the individual. In partially closed occupations (0 < Ci < 1), the non-closed share of the occupation can work to the extend that is teleworkable. In summary, the Lockdown Working Ability index is calculated as follows:
| (1) |
for all .
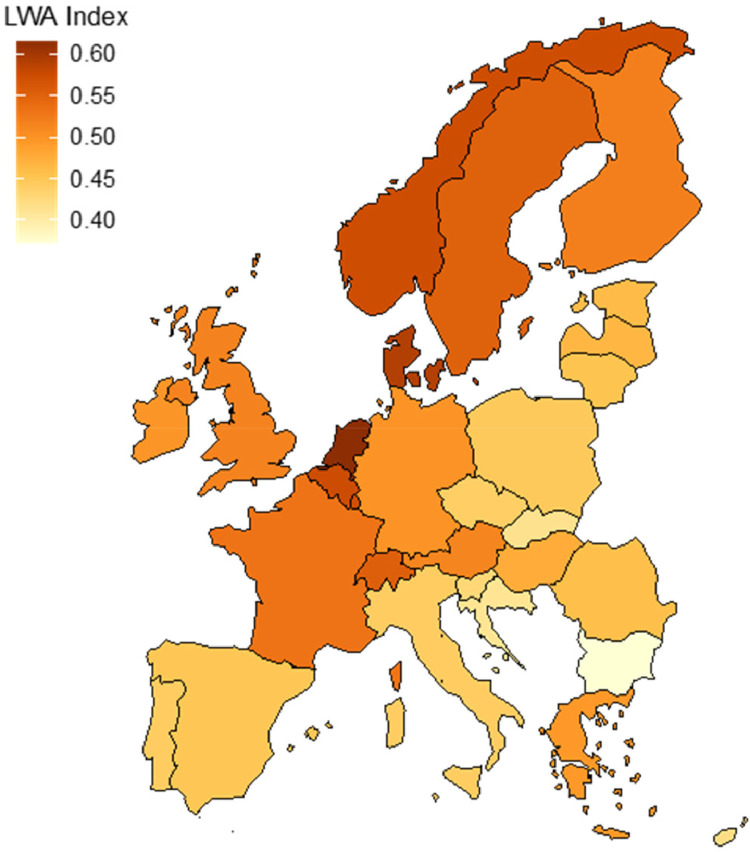
As shown in Fig. 1 , the average LWA index varies significantly across European countries: Netherlands (0.61), Denmark (0.59), Luxembourg (0.57), Norway (0.57) and Belgium (0.57) have the highest average capacity to work during the lockdown, while Bulgaria (0.37), Slovakia (0.41), Croatia (0.41), Cyprus (0.42) and Slovenia (0.43) have the lowest. It appears therefore that under a lockdown and social distance measures, occupations can be performed to a greater degree in Northern and Central Europe than in Southern Europe and, especially, than in Eastern Europe. To understand this ranking of countries, we analyse separately the average levels of essentiality, closure and teleworking across Europe (see Fig. 2 a–c). Northern and Central countries present the highest values of the LWA index because they have large average levels of essentiality and teleworking, while their average levels of closure are low. On the contrary, some Eastern European countries like Bulgaria, Croatia and Slovakia present the lowest values of the LWA index because they have low average levels of essentiality and teleworking, while their average levels of closure are high. Other Eastern European countries like Romania and Hungary show a higher LWA index because their low values of average teleworking are compensated with high values of average essentiality due to their large primary sectors. Southern European countries, with intermediate values of LWA, have intermediate levels of essentiality and higher average values of teleworking than Eastern European countries but the highest close score average values. These are the economies most penalised by additional de-escalation periods of partial closure due to their large dependence on activities that required the agglomeration of people like tourism.
Fig. 1.
Lockdown working ability index across Europe.
Fig. 2.
a. Average essentiality across Europe. b. Average closure across Europe. c. Average teleworking across Europe.
Our LWA index varies significantly not only by countries but also by gender, type of contract −permanent or temporary−, type of work −full or part time−, and level of education (see Table 1 ). According to their LWA index, women jobs are less affected by social distancing than men jobs in all European countries. Interestingly, the biggest difference between both sexes is found in the Nordic countries: Norway (23 points), Denmark (22 points), Finland (20 points) and Sweden (20 points). By type of contract, as might be expected, fixed-term contract workers tend to have a lower LWA than their permanent counterparts. Only in Austria, Denmark, Finland, Hungary, Latvia, and Norway have temporary contracts workers a higher capacity to work under a lockdown than permanent workers. Meanwhile, part-time jobs tend to be less able to work during lockdown than full-time jobs in Southern countries, but this is not so clear elsewhere in Europe. Finally, we find a strong positive relationship between the level of education and the capacity of working under a lockdown in all European countries. By levels of education, the capacity of working under a lockdown for a worker with primary education is the highest in Romania (0.66) and Greece (0.48), the two European countries with the largest primary productive sectors. For a worker with secondary education the capacity of working under a lockdown is maximum in Luxembourg (0.59) and the Netherlands (0.54). Meanwhile, the possibility of working under a lockdown for workers with tertiary education is the highest in the Nordic countries: Norway (0.76), Sweden (0.76) and Denmark (0.75).
Table 1.
Lockdown working ability in Europe.
| Country | All | Male | Female | Permanent | Temporary | Full-Time | Part-Time | Low-Edu | Mid-Edu | High-Edu |
|---|---|---|---|---|---|---|---|---|---|---|
| AT | 0.51 | 0.47 | 0.57 | 0.50 | 0.60 | 0.51 | 0.53 | 0.28 | 0.44 | 0.67 |
| BE | 0.57 | 0.49 | 0.67 | 0.59 | 0.46 | 0.56 | 0.62 | 0.33 | 0.43 | 0.74 |
| BG | 0.37 | 0.34 | 0.40 | 0.36 | 0.36 | 0.37 | 0.41 | 0.31 | 0.26 | 0.60 |
| CH | 0.55 | 0.49 | 0.62 | 0.56 | 0.52 | 0.54 | 0.58 | 0.30 | 0.50 | 0.68 |
| CY | 0.42 | 0.37 | 0.47 | 0.44 | 0.34 | 0.43 | 0.31 | 0.19 | 0.28 | 0.62 |
| CZ | 0.44 | 0.38 | 0.51 | 0.46 | 0.41 | 0.44 | 0.45 | 0.18 | 0.36 | 0.71 |
| DE | 0.50 | 0.46 | 0.54 | 0.51 | 0.45 | 0.51 | 0.46 | 0.29 | 0.46 | 0.64 |
| DK | 0.59 | 0.48 | 0.70 | 0.59 | 0.65 | 0.59 | 0.61 | 0.35 | 0.48 | 0.75 |
| EE | 0.46 | 0.40 | 0.52 | 0.46 | 0.41 | 0.46 | 0.45 | 0.23 | 0.32 | 0.65 |
| ES | 0.45 | 0.42 | 0.49 | 0.48 | 0.42 | 0.47 | 0.31 | 0.26 | 0.36 | 0.62 |
| FI | 0.52 | 0.42 | 0.62 | 0.52 | 0.56 | 0.53 | 0.42 | 0.32 | 0.39 | 0.70 |
| FR | 0.53 | 0.44 | 0.62 | 0.55 | 0.49 | 0.52 | 0.56 | 0.38 | 0.43 | 0.69 |
| GR | 0.49 | 0.46 | 0.54 | 0.53 | 0.31 | 0.50 | 0.37 | 0.48 | 0.36 | 0.66 |
| HR | 0.41 | 0.36 | 0.47 | 0.43 | 0.26 | 0.41 | 0.48 | 0.34 | 0.30 | 0.70 |
| HU | 0.47 | 0.41 | 0.55 | 0.45 | 0.67 | 0.48 | 0.35 | 0.44 | 0.36 | 0.73 |
| IE | 0.50 | 0.45 | 0.55 | 0.49 | 0.41 | 0.53 | 0.39 | 0.36 | 0.32 | 0.63 |
| IT | 0.44 | 0.40 | 0.50 | 0.48 | 0.36 | 0.45 | 0.38 | 0.26 | 0.42 | 0.72 |
| LT | 0.45 | 0.40 | 0.50 | 0.45 | 0.42 | 0.45 | 0.44 | 0.30 | 0.32 | 0.62 |
| LU | 0.57 | 0.55 | 0.59 | 0.58 | 0.45 | 0.57 | 0.56 | 0.32 | 0.59 | 0.73 |
| LV | 0.46 | 0.42 | 0.51 | 0.45 | 0.55 | 0.47 | 0.43 | 0.32 | 0.33 | 0.67 |
| NL | 0.61 | 0.56 | 0.68 | 0.64 | 0.55 | 0.59 | 0.64 | 0.37 | 0.54 | 0.74 |
| NO | 0.57 | 0.47 | 0.70 | 0.58 | 0.64 | 0.56 | 0.65 | 0.41 | 0.46 | 0.76 |
| PL | 0.44 | 0.41 | 0.49 | 0.46 | 0.30 | 0.45 | 0.39 | 0.35 | 0.32 | 0.67 |
| PT | 0.44 | 0.39 | 0.49 | 0.48 | 0.38 | 0.45 | 0.31 | 0.26 | 0.43 | 0.74 |
| RO | 0.46 | 0.43 | 0.49 | 0.36 | 0.29 | 0.43 | 0.82 | 0.66 | 0.34 | 0.64 |
| SE | 0.55 | 0.46 | 0.66 | 0.57 | 0.52 | 0.54 | 0.59 | 0.37 | 0.44 | 0.76 |
| SI | 0.43 | 0.37 | 0.49 | 0.44 | 0.35 | 0.43 | 0.37 | 0.23 | 0.30 | 0.65 |
| SK | 0.41 | 0.34 | 0.50 | 0.43 | 0.36 | 0.41 | 0.40 | 0.26 | 0.31 | 0.73 |
| UK | 0.51 | 0.46 | 0.57 | 0.55 | 0.48 | 0.54 | 0.45 | 0.33 | 0.41 | 0.65 |
| EU-AVG | 0.49 | 0.43 | 0.55 | 0.50 | 0.45 | 0.49 | 0.47 | 0.33 | 0.39 | 0.68 |
2.2. Potential wage losses of lockdown and social distancing
The next step is to calculate the potential wage loss due to the lockdown for every individual in the population. Following the facts observed in Europe during the pandemic, we adopt four possible scenarios. As a lower bound, we assume a simple scenario: two months of lockdown (case i).3 Here we suppose that occupations can be developed at full capacity (100%) after the lockdown. Next, we assume two months of lockdown and six months of partial functioning of closed occupations at 80% (case ii), 70% (case iii) and 60% (case iv) of full capacity. The rationale for these scenarios is that governments may not allow a fully functioning of closed occupations after the lockdown to avoid a new outbreak of the virus and that individuals may voluntarily choose to stay home, which reduces their consumption, to avoid infection (Goolsbee and Syverson, 2020). For example, some activities like arts, entertainment, recreation, restaurant, hotel and transportation are still under a large negative shock in production and consumption.4 Consequently, to be more informative we have adopted a range of capacity constraints that goes from 100% to 60% of full capacity for a period of six months. In addition, given the uncertainty about the duration of legal and voluntary restrictions, in Appendix D we have further replicated our results for another three scenarios where partial functioning of closed occupations −at 80%, 70% and 60% of full capacity− lasts for nine months instead of six. We simulate the same scenarios for all countries so that differences across countries are mainly due to their distinct productive structures, isolating our analysis from the influence of particular mitigation measures adopted by each European government.
Using the LWA index, we calculate the wage loss (wl) experienced by every individual during the lockdown according to the four simulated scenarios described. For the first case (i) the equation we estimate is the following:
| (2) |
where is the annual wage of individual i in period (before the lockdown) and DL represents the duration of the lockdown in annual terms, i.e., . Because LWAi measures the capacity of individual i to work under a lockdown, the term represents the incapacity of worker i to perform their job under a lockdown. Consequently, the wage loss experienced by workers under a lockdown is the proportion of annual wage they lose due to their inability to work during the shutdown period.
For the cases (ii), (iii) and (iv) we apply the same Eq. (2) unless the individual has a closed occupation, in which case, we need to additionally consider the wage loss due to the partial closure of 20%, 30% or 40% of their occupation for six (or nine) additional months. For these scenarios the relevant equation is:
| (3) |
where is the indicator function, DC represents the duration of the partial closure ( or ), and CL is the proportion of closure (0.2 for case (ii), 0.3 for case (iii) and 0.4 for case (iv)). To give the intuition of expressions (2) and (3), we provide an example.
Suppose we are interested in calculating the wage loss for three workers with different occupations under a lockdown of 2 months and a posterior partial closure of some activities of 20% (keeping 80% of capacity) for 6 months. The first worker is a physician, the second works as a clerk and the third one is a waiter. Their pre-lockdown annual salaries are , and , respectively. The occupation of the first worker is essential with so we apply Eq. (2) to calculate her wage loss: , i.e., the doctor does not lose earnings during the pandemic. The second worker has an administrative occupation that in our example is neither essential nor closed so her LWAi index is equal to the value of her index of teleworking, for example, 0.7. Then, according to Eq. (2) her wage loss will be . Finally, the occupation of the third worker is closed with so the value of her LWA index is 0. In this case, we apply Eq. (3) to calculate the wage loss: . Because , the waiter is the worker that losses the highest proportion of her salary due to the pandemic.
The estimated wage loss of each individual in the population will allow us to analyse the changes in poverty and inequality across Europe under the lockdown. A first glimpse of these changes between dates (pre-lockdown) and t can be achieved by representing the loss rate (l) in the wage of every worker caused by the lockdown, i.e., , since . For this task we first order the workers by their pre-lockdown wage and group them into centiles (q), obtaining the mean loss rate lqt at each centile. The result is the Lockdown Incidence Curve (LIC) where it is easy to appreciate which part of the wage distribution (low, middle, high) suffers the largest relative wage losses.5 It can be proved that if lqt is an increasing (decreasing) function for all q then inequality falls (rises) with the lockdown for all inequality measures satisfying the Pigou–Dalton transfer principle.6
Closely related to the LIC we have the mean loss rate for the poor, a measure that reveals the average wage loss for workers below the poverty line.7 Let H(z) denote the headcount index defined as the proportion of workers whose salary is less than z, where z is the poverty line (set at 60% of the median wage). Then, the mean loss rate for the poor (P) is defined as the area under the LIC up to the headcount index divided by the headcount measure, which can be expressed as:
| (4) |
When lq < 0 for all q < H(z) one can conclude that the lockdown was poverty-augmenting.
In addition to representing the LICs for the set of European countries and compute the above mentioned P index, we also calculate the absolute change in the headcount poverty index H(z) for the four scenarios of lockdown: , where z is the poverty line before the lockdown.
The asymmetric potential impact of the lockdown and partial closures is also likely to affect inequality, and after gaining some understanding about the changes in wage poverty, we will estimate the changes in wage inequality. Of all the possible inequality indices that fulfill the basic principles found in the literature on inequality (progressive transfers, symmetry, scale invariance and replication of the population) we adopt the popular Gini coefficient:
| (5) |
where w represents the wage distribution, wi is the salary of individual i, and μ is the mean wage of the economy. μ is the mean wage of the economy. Absolute changes in wage inequality are measured as the difference , where is the pre-lockdown wage distribution and wt is the wage distribution under a given scenario (cases i-iv). Meanwhile, relative changes in wage inequality are measured as percentages of pre-lockdown inequality, i.e., .
Unfortunately, the Gini index is not additively decomposable into a between-group and a within-group component. Its decomposition includes also a residual term which cannot be assigned to either component. For this reason, we use the MLD index in the last part of our analysis, where we decompose the overall estimated change of inequality in Europe into its between-countries and within-countries components. The MLD belongs to the Generalized Entropy class, which is the only class of inequality indices that is additively decomposable into a between-group and a within-group component (Bourguignon, 1979 and Shorrocks, 1980). Moreover, the MLD has a path-independent decomposition, so the result of the decomposition is independent of which component (between-group or within-group) is eliminated first (Foster and Shneyerov, 2000). The MLD (T) is defined as:
| (6) |
Let be a partition of wage into M groups (countries), μm the mean of the wage distribution wm and nm the population size associated with the wage distribution wm, where . Then, taking advantage of the additive decomposability property of the MLD and grouping workers by countries, the MLD index can be exactly decomposed as follows:
| (7) |
where 1n is n-coordinated vector of ones. Expression (7) provides a breakdown of overall wage inequality into between-group and within-group terms. The between-group component is the level of wage inequality that would arise if each worker in a country enjoys the mean wage of the country, and the within-group component is the weighted sum of wage inequalities within different countries.
3. Poverty and inequality changes in Europe
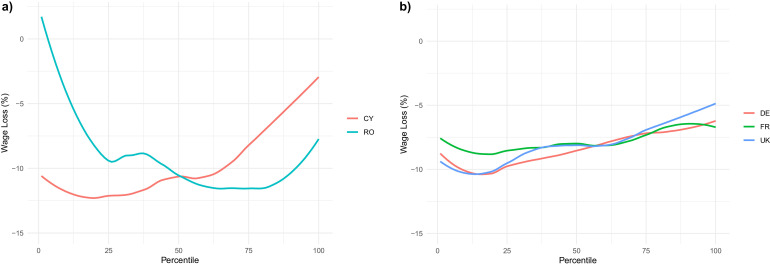
How large are the wage losses experienced by workers during the lockdown? Are they evenly distributed? A visual approximation to the wage loss across the wage distribution can be achieved by looking at the LIC curves. In Fig. 3 we represent the LICs for some European countries under two months of lockdown (case i).8 We highlight the LIC for two extreme cases, Romania, and Cyprus, where the main wage losses take place at the upper and lower part of the wage distribution (Fig. 3, panel a) and for Germany, the UK and France (Fig. 3, panel b), where wage losses tend to decrease with the percentile that the worker occupies.
Fig. 3.
Lockdown Incidence Curves in some European countries (scenario i).
In our two-month lockdown scenario, wage losses are already sizeable and can be superior to 10% at some parts of the distribution in some countries, varying significantly with the centile of the workers. Also, we find that the shape of the distribution of wage losses is similar for the rest of scenarios and the main difference lies only in the larger size of the wage drops.
3.1. Changes in poverty due to social distancing
We formally capture the potential impact of social distancing on poverty with two measures: the mean loss rate for the poor (P) and the changes in the headcount poverty index (H).9 Table 2 (columns 2 to 5) shows the values of P for the four simulations under consideration, which indicate that the lockdown is poverty-augmenting in the four scenarios for all European countries. Under the most conservative scenario, a two-month lockdown, we find a mean loss rate for the poor of 10% for Europe on average. If we consider an additional 6-month period of partial functioning of closed activities at 60% of full capacity (scenario iv), the mean loss rate for poor workers in Europe increases up to 16% (19% if the period of partial functioning lasts for nine months). By countries, the highest loss rate for the poor is found in Cyprus (between 12.3% and 22.4%), while the smallest one happens in Romania (between 3.1% and 4.0%).
Table 2.
Poverty changes in Europe.
 |
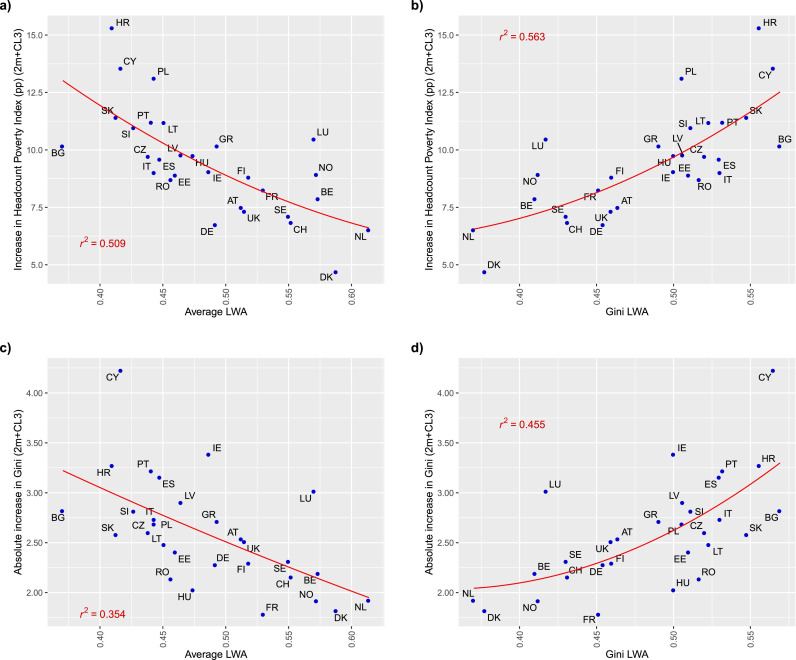
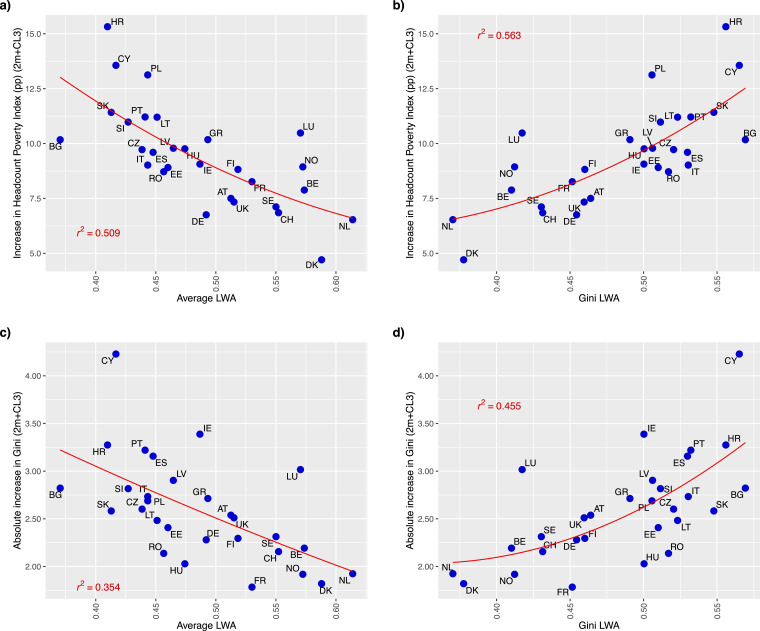
The share of workers under the poverty line H also increases significantly for the four simulated cases in all European countries (see Table 2, columns 6-14).10 For Europe on average, this increase varies between 4.9 percentage points under two months of lockdown and 9.4 percentage points if we consider an additional six months during which closed activities are partially functioning at 60%. These values imply that −in absence of compensating policies− the percentage of poor people in Europe (those with earnings below 60% of the pre-lockdown median in the country) may substantially increase even if lockdown does not last long. If closed activities are partially functioning at 60% for nine months (instead of six months) the increase of H for Europe on average is 12.1 percentage points (Table D1 in Appendix D). In general, increases are greater in Eastern and Southern countries than Central and Northern countries. Thus, we find that the highest increase in poverty according to the headcount poverty index is in Croatia (between 8.5 and 15.3 points). On the contrary, the smallest percentage increase in poverty according to the headcount index happens in Switzerland for case i (2.6 points) and Denmark for cases ii (3.7 points), iii (4.1 points) and iv (4.7 points). If we look at the relationship between these changes in the headcount poverty index and the average LWA we find a negative correlation with R 2= 0.35 for the first scenario (Fig. 4 , panel a) and R 2= 0.51 for the fourth scenario (Figure C1, panel a, in Appendix C). When we consider the Gini of LWA within countries instead of the average LWA the correlation becomes positive with R 2= 0.34 for the first scenario (Fig. 4 panel b) and R 2= 0.56 for the fourth scenario (Figure C1, panel b, in Appendix C).
Fig. 4.
Correlation between the LWA index and the changes in poverty and inequality.
Fig. C1.
Correlation between the LWA index and the changes in poverty and inequality.
Note: CL3 refers to partial closure for 6 months at 60% of full capacity and 2 m is 2 months of lockdown.
3.2. Inequality changes in Europe
The uneven distribution of potential wage losses across the distribution is prone to have an impact on wage inequality as well. European countries already have important differences in pre-lockdown inequality (Table 3 , column 2). Slovakia is the European country with the lowest pre-lockdown wage inequality (G = 25.4). Other countries with low levels of inequality before the lockdown are Sweden, Czechia, Belgium and Norway, all of them with a Gini index slightly below 0.30. On the other extreme of the spectrum, we find the countries with the highest level of pre-lockdown wage inequality: Bulgaria, Ireland, the UK and Spain, all of them with a Gini index above 0.40.
Table 3.
Wage inequality changes in Europe.
 |
When comparing wage inequality after the lockdown with the baseline, it is observed that absolute and relative changes in inequality are sizeable and increase in all countries with the duration of the partial closure of some activities (Table 3). For example, the relative increase of the Gini coefficient, at scenario (i), ranges from 2.2% (the Netherlands) to 4.9% (Cyprus). At the more severe scenario (iv), relative increases in inequality range from 4.9% in France to 10.9% in Cyprus (if the period of partial functioning lasts nine months these rates become 7% in France and 15% in Cyprus). These changes are greater if we consider a longer duration of partial closure measures (Appendix D).
A scrutiny of the absolute changes in the Gini coefficient which makes the change scale independent of the previous level of inequality reveals that Cyprus is again the European country where inequality increases the most for the four simulation cases (between 1.9 and 4.2 Gini points) followed by Ireland (between 1.7 and 3.4 points). On the other hand, the smallest absolute change in inequality is found in Norway (0.7 points) for scenario (i), in Norway and France for scenarios (ii) (1.2 points) and (iii) (1.5 points), and in France and Denmark for scenario (iv) (1.8 points). These variations in inequality also tend to be related with the LWA index. In Fig. 4 (panel c) we observe that the average LWA is negatively correlated with the increase in wage inequality under the first scenario with R 2 = 0.32 (0.35 under scenario (iv), see Figure C1, panel c, in Appendix C). When we consider the Gini of individual LWA within countries (Fig. 4, panel d), it is observed that its correlation with the increase in wage inequality is positive, with R 2 = 0.38 (0.46 under scenario (iv), Figure C1, panel d, in Appendix C).
Given the link between the values of the LWA index and the increases in wage inequality (and poverty), it is not surprising that the observed changes are in general greater in Eastern and Southern countries than Central and Northern countries. As mentioned before, Northern and Central Europe present large average levels of essentiality and teleworking, and low average levels of closure. Meanwhile, Eastern Europe shows the opposite pattern, i.e., low average levels of essentiality and teleworking, and medium-high average levels of closure. The partial closure of activities that imply the agglomeration of large groups of people like tourism significantly penalises Southern Europe, whose countries tend to have the highest average closure scores. While some tertiary jobs like administrative, programmers and accountants are not affected by partial closures, others are strongly impacted by the measures to fight COVID-19 and the fears to be infected: hospitality, restaurants, arts and entertainment. For this reason, the impact on inequality and poverty is also related to the share of these specific tertiary occupations.11
Our findings show an increase in inequality for all European countries but, would inequality changes be different enough to increase inequality between countries? The answer is yes, although they are smaller than the inequality changes occurring within countries. In Table 4 we show the results of the decomposition of wage inequality for all European workers. Our simulations show an increase in overall inequality in workers’ salary of 4.3% in Europe (0.423 to 0.441) according to the MLD index under a lockdown of two months. For the same scenario, the changes in the between- and within-countries inequality components are 2.5% (from 0.125 to 0.128) and 5.0% (from 0.298 to 0.313), respectively. For two months of lockdown and six months of partial functioning of closed activities at 60% of capacity (scenario iv) we find the following increases in inequality for Europe on average: 9.7% in overall inequality, 4.0% in between-countries inequality and 12.1% in within-countries inequality. When the period of partial functioning of closed activities at 60% of capacity lasts nine months the corresponding increases are: 14.0% in total inequality, 4.8% in between-countries inequality and 17.9% in within-countries inequality (Table D3 in Appendix D)
Table 4.
The between- and within-countries inequality components in Europe.
 |
Both components of overall inequality increase, but the within-countries inequality component increases significantly more than the between-countries inequality component in all scenarios.12 That is, cohesion between European countries decreases with the lockdown, though the main change in wage inequality happens within European countries. With the partial closure of some activities, changes get larger and the double process of wage divergence (between and within countries) deepens.
4. Conclusions
The emergency measures adopted to contain the spread of COVID-19 all around the world are largely based on social distancing and closure of high-risk productive activities. The paralysis of production imposed by the contention measures during the lockdown and the capacity limitations driven by official restrictions and by consumers precautionary behaviour will thus have an uneven impact on workers from different occupations and industries. Our analysis reveals a sizable potential increase in poverty and inequality across Europe.
Poverty will increase under our simulations in all countries. Under the most conservative scenario, a lockdown of two months, we estimate a mean loss rate for the poor of 10% and an increase in the headcount index of 4.9 percentage points on average in Europe, with the change ranging from 2.6 points (Switzerland) to 8.5 points (Croatia). Likewise, wage inequality increases under a lockdown of two months, being the change in the Gini coefficient equal to 3.5% for Europe on average, with changes ranging between 2.2% (Netherlands) and 4.9% (Cyprus). Considering a more severe scenario with 6 months of partial closure at 60% of full capacity after a two-month lockdown, we estimate a mean loss rate of 16.2% for the poor workers in overall Europe, a rise of 9.4 percentage points in the headcount poverty index and a Gini increase of 7.3% on average for Europe. Our results also highlight that lockdown measures are likely to worsen cohesion in Europe both between countries and, especially, within countries. Our decomposition exercise shows that between-countries inequality will increase in Europe between 2.5% and 4.0%, while within-countries inequality will increase between 5.0% and 12.1%.
In general, we find a greater increase of both poverty and inequality in Eastern and Southern Europe than in Northern and Central Europe. Workers tend to have a lower and more unequally distributed ability to work under the shutdown and social distancing in the economies of Eastern and Southern Europe than in the Northern and Central European countries. These differences across European areas get larger with the severity of the measures to fight and prevent COVID-19 infection.
Acknowledgement
We are grateful for the editor and referee's comments and suggestions that helped to improve the paper. We also thank participants at the INET Oxford and the ICAE Complutense Seminars for the valuable input provided. All errors remain our own. The authors acknowledge funding from Citi for the Inequality and Prosperity programme at INET at the Oxford Martin School (Palomino) and from the Ministerio de Ciencia e Innovación under project PID2019-104619RB-C42, COTEC Foundation and Comunidad de Madrid under project H2019/HUM-5793-OPINBI-CM (Rodríguez and Sebastián). The views expressed are those of the authors not the funders.
Footnotes
Given the level of disaggregation available for some particular countries, we have defined essential and closed occupations at the ISCO-08 1-digit level and NACE (Rev.2) 1-digit level for Bulgaria, Germany, Poland and Slovenia (see Tables B3 and B4 in Appendix B), and at only the ISCO-08 2-digit level for Denmark, which does not disaggregate industry information in EU-SILC (see Table B5 in Appendix B).
From the EU-LFS database, with greater industry disaggregation, we know that the ‘water supply and electricity’ share in industries B-E lies between 5% and 10% in European economies.
The duration of the lockdown in many European countries has been approximately of two months. For example, the lockdown went from the 23rd of February to the 3th of May in Italy, from the 15th of March to the 4th of May in Spain, and from the 17th of March to the 11th of May in France.
For these activities Chetty et al. (2020) have found, as of July 08th 2020, a decrease in spending compared to the pre-lockdown levels in the range of between 32.9% and 48.3% in the US. Based on weekly credit card expenditure data, BBVA Research (2020) has found, as of July 12th 2020, a negative interannual growth rate for these spending groups ranging between 20% and 40% in Spain.
This curve is an adaptation to our framework of the Growth Incidence Curve (GIC) proposed in Ravallion and Chen (2003). For a view on the literature that studies the capacity of economic growth to reduce poverty see also Kakwani and Pernia (2000), Kakwani and Son (2008) and Bluhm et al. (2018), among others.
This result comes from well-known results on tax progressivity and inequality. See, for example, Eichhorn et al. (1984).
This measure is an adaption to our context of the mean growth rate for the poor proposed in Ravallion and Chen (2003). It is equivalent to the rate of change in the Watts index of poverty (Watts, 1968) normalized by the headcount index. Zheng (1993) identifies a set of axioms for which the Watts index emerges as the unique poverty measure.
Lockdown Incidence Curves have been smoothed using local polynomial regression with span 0.5 and degree 2.
The contribution of growth and redistribution to poverty reduction over the period 1981 to 2010 in 124 countries, including Europe, is estimated in Bluhm et al. (2018). The relationship between the components of social mobility (growth, dispersion and exchange mobility) and inequality is estimated for 15 countries of the European Union in Prieto-Rodríguez et al., 2008.
The headcount poverty index gives additional relevant information about the consequences of the pandemic for poverty since this index is not necessarily consistent with the LIC (Essama-Nssah and Lambert, 2009).
While there is no empirical relationship between tertiary occupations in general and the changes in inequality and poverty (for example, the coefficient of determination R2 between the absolute changes in inequality under scenario iv and the share of tertiary occupations is 0.02), the correlation between the share of tertiary occupations that cannot be performed during the shutdown and the changes in inequality and poverty is high (the coefficient of determination R2 between the absolute changes in inequality under scenario iv and the share of tertiary occupations not workable during the lockdown is 0.69).
From the literature on global inequality (applied to all household incomes in the world) we know that between-countries inequality has fallen since 1990, while average within-countries inequality has increased (see Ravallion, 2019).
Employment –and therefore occupational shares– can be measured either by thousands of persons employed (given by the EU-LFS survey weights) or by thousands of weekly hours worked (EU-LFS survey weights multiplied by usual weekly hours), we use the former definition in our EU-LFS analysis.
For Bulgaria, Poland, and Slovenia occupations are coded at the ISCO-08 2-digit level, so we can only obtain teleworking at the 1 digit-level after applying the crosswalk with ONET-SOC (2010) maintaining country specific weights. Industries are not disaggregated for Denmark (see Table A3), so essentiality and closure scores are assigned in Denmark based only on the occupational category (ISCO-2d).
For Germany and Slovenia occupations are coded at the ISCO-08 1-digit level in EU-SILC (see Table A3).
Mongey et al. (2020) propose a variant of the teleworking index in Dingel and Neiman (2020) and a measure of low physical proximity to others at work.
The possible answers for each item are: 1 (never), 2 (once a year or more but not every month), 3 (once a month or more but not every week), 4 (once a week or more but not every day) and 5 (every day).
The possible answers for each item are: 1 (not important), 2 (somewhat important), 3 (important), 4 (Very important) and 5 (extremely important).
To use country specific occupational weights, for the countries that have information in EU-LFS at the ISCO 08 2-digit level we can obtain the teleworking index at the 1-digit level. Thus, although Poland and Bulgaria have ISCO 08 2-digit information at EU-SILC, we only have teleworking information for them at the ISCO 08 1-digit level. In our final analysis four countries (Bulgaria, Germany, Poland and Slovenia) have teleworking scores at the ISCO 1-digit level, and the essential and closure scores by ISCO 1-digit level and NACE (Rev. 2) 1-digit level (see footnotes 15 and 16).
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.euroecorev.2020.103564.
Appendix A. Databases and the index of teleworking in Europe
Before we explain the procedure followed to calculate the teleworking index, the three databases under consideration, O*NET, EU-LFS (2020) and EU-SILC (2020), are described in detail.
The databases
The O*NET database is the primary project of the O*NET program promoted by the US Department of Labour, and replaces the Dictionary of Occupational Titles (DOT), which was used for earlier research. O*NET analysts at the Department of Labour assign scores to each task according to standardized guidelines to describe their importance within each occupation. Thus, O*NET is a source of occupational information, providing data on key attributes and characteristics –from which teleworking capacity can be derived– for 968 occupations, based on the Standard Occupation Classification 2010 (ONET-SOC2010). Therefore, for this information about occupations to be used in our analysis, we will have to translate O*NET-SOC2010 data into European codification ISCO-08 used in EU-LFS (at the 3-digit level) and EU-SILC (at the 2-digit level). We describe the set of industries NACE (1-digit level) and occupations ISCO-08 (2-digit level) in Tables A1 and A2 , respectively.
Table A1.
Overview of the NACE Rev.2 codes and their description.
| NACE code | Description |
|---|---|
| A | Agriculture, Forestry and Fishing |
| B | Mining and Quarrying |
| C | Manufacturing |
| D | Electricity, Gas, Steam and Air Conditioning Supply |
| E | Water Supply; Sewerage, Waste Management and Remediation Activities |
| F | Construction |
| G | Wholesale and Retail Trade; Repair of Motor Vehicles and Motorcycles |
| H | Transportation and Storage |
| I | Accommodation and Food Service Activities |
| J | Information and Communication |
| K | Financial and Insurance Activities |
| L | Real Estate Activities |
| M | Professional, Scientific and Technical Activities |
| N | Administrative and Support Service Activities |
| O | Public Administration and Defence; Compulsory Social Security |
| P | Education |
| Q | Human Health and Social Work Activities |
| R | Arts, Entertainment and Recreation |
| S | Other Service Activities |
| T | Activities of Households as Employers; Undifferentiated Goods and Services Producing Activities of Households for Own Use |
| U | Activities of Extraterritorial Organisations and Bodies |
Note: we exclude industry U in our analysis.
Table A2.
Overview of the ISCO-08 codes and their description.
| ISCO code | Description |
|---|---|
| 11 | Chief Executives, Senior Officials and Legislators |
| 12 | Administrative and Commercial Managers |
| 13 | Production and Specialized Services Managers |
| 14 | Hospitality, Retail and Other Services Managers |
| 21 | Science and Engineering Professionals |
| 22 | Health Professionals |
| 23 | Teaching Professionals |
| 24 | Business and Administration Professionals |
| 25 | Information and Communications Technology Professionals |
| 26 | Legal, Social and Cultural Professionals |
| 31 | Science and Engineering Associate Professionals |
| 32 | Health Associate Professionals |
| 33 | Business and Administration Associate Professionals |
| 34 | Legal, Social, Cultural and Related Associate Professionals |
| 35 | Information and Communications Technicians |
| 41 | General and Keyboard Clerks |
| 42 | Customer Services Clerks |
| 43 | Numerical and Material Recording Clerks |
| 44 | Other Clerical Support Workers |
| 51 | Personal Services Workers |
| 52 | Sales Workers |
| 53 | Personal Care Workers |
| 54 | Protective Services Workers |
| 61 | Market-oriented Skilled Agricultural Workers |
| 62 | Market-oriented Skilled Forestry, Fishery and Hunting Workers |
| 63 | Subsistence Farmers, Fishers, Hunters and Gatherers |
| 71 | Building and Related Trades Workers (excluding Electricians) |
| 72 | Metal, Machinery and Related Trades Workers |
| 73 | Handicraft and Printing Workers |
| 74 | Electrical and Electronic Trades Workers |
| 75 | Food Processing, Woodworking, Garment and Other Craft and Related Trades Workers |
| 81 | Stationary Plant and Machine Operators |
| 82 | Assemblers |
| 83 | Drivers and Mobile Plant Operators |
| 91 | Cleaners and Helpers |
| 92 | Agricultural, Forestry and Fishery Labourers |
| 93 | Labourers in Mining, Construction, Manufacturing and Transport |
| 94 | Food Preparation Assistants |
| 95 | Street and Related Sales and Services Workers |
| 96 | Refuse Workers and Other Elementary Workers |
Note: we exclude occupations 63 and 95 in our analysis.
EU-LFS, which we will use to translate O*NET teleworking indices into European coding, compiles national labour force surveys carried out by the national statistical authorities and is homogenised by Eurostat. This database includes information on the labour market status of the 28 European Union countries, plus Norway, Switzerland, Iceland, Turkey, and Macedonia. These last three countries are not considered in our analysis, as they are not included in the current EU-SILC 2020 release that we use for our wage inequality analysis. Malta is also discarded because the occupation variable is only available at the International Standard Classification for Occupations (ISCO-08) 1-digit level, lacking enough precision for our analysis (see Table A3 ).
Table A3.
ISCO-08 and NACE digit levels by countries in EU-LFS and EU-SILC.
|
EU-LFS |
EU-SILC |
Indexes (EU-SILC) |
||||||
|---|---|---|---|---|---|---|---|---|
| Country | ISCO | NACE | ISCO | NACE | Teleworking | Essential | Closed | |
| AT | Austria | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| BE | Belgium | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| BG | Bulgaria | 2d | 1d | 2d | 1d | ISCO 1d | I(1d) N(1d) | I(1d) N(1d) |
| CH | Switzerland | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| CY | Cyprus | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| CZ | Czech Republic | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| DE | Germany | 3d | 1d | 1d | 1d | ISCO 2d | I(1d) N(1d) | I(1d) N(1d) |
| DK | Denmark | 3d | No info | 2d | No info | ISCO 2d | I(2d) | I(2d) |
| EE | Estonia | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| ES | Spain | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| FI | Finland | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| FR | France | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| GR | Greece | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| HR | Croatia | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| HU | Hungary | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| IE | Ireland | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| IT | Italy | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| LT | Lithuania | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| LU | Luxembourg | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| LV | Latvia | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| NL | The Netherlands | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| NO | Norway | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| PL | Poland | 2d | 1d | 2d | 1d | ISCO 1d | I(1d) N(1d) | I(1d) N(1d) |
| PT | Portugal | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| RO | Romania | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| SE | Sweden | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| SI | Slovenia | 2d | 1d | 1d | 1d | ISCO 1d | I(1d) N(1d) | I(1d) N(1d) |
| SK | Slovak Republic | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
| UK | United Kingdom | 3d | 1d | 2d | 1d | ISCO 2d | I(2d) N(1d) | I(2d) N(1d) |
Note: “d” means digit; “I” is for ISCO and “N” is for NACE in columns 8 and 9.
In this work, we use EU-LFS 2020 release where employment is measured according to the International Labour Organization (ILO) definition.13 Occupations are coded at the 3-digit level (ISCO-08) and industries are coded at the 1-digit level with the Nomenclature Statistique des Activités Economiques dans la Communauté Européenne (NACE) revision 2.14 We drop the occupation “Subsistence farmers, fishers, hunters, and gatherers” (ISCO-08 63) and the occupation “Street and related sales and services workers” (ISCO-08 95), since employment occurs only in a small number of countries (suggesting classification problems). The industry “Activities of extraterritorial organisations and bodies” (NACE. Rev.2 U) is also dropped because the number of observations is scarce and occurs only in very few countries. We also discard “Armed forces occupations” (ISCO-08 0) as O*NET does not facilitate information on those occupations and “Unpaid family workers” that has very few observations. While EU-LFS is the best database to map the occupations (and teleworking indices) from O*NET it lacks the wage information crucial for our inequality analysis. For this reason, we will merge EU-LFS teleworking indices for each ISCO-08 occupation with the EU-SILC database which provides detailed microdata on wages.
EU-SILC encompasses homogeneous surveys on living conditions implemented by the national institutes of statistics under the coordination of Eurostat. Collected data contains information on a wide range of socioeconomic items, including occupation, industry and salary at the personal level. Taking advantage of this information, we will sample active workers −employees and self-employed– who declare to be working at least part time at the time, and who have a greater than zero salary during the reference year. This excludes unemployed and retired workers, and people under the legal working age of 16. For our salary variable, for each individual we have aggregated yearly cash and in-kind gross employee income and gross self-employed income. Employee income is defined as ‘the total remuneration payable by an employer to an employee in return for work done by the latter during the income reference period’, while self-employed income is the gross income received during the reference year as a result of their current or former involvement in self-employed work. As for the occupational information, this is typically coded at the 2-digit level (ISCO-08), while industries are coded at the 1-digit level (NACE Rev.2) in EU-SILC.15 We aggregate the occupations at the 3-digit level (ISCO-08) in EU-LFS to the 2-digit level (ISCO-08) before we match both databases (see Table A3).
Measuring teleworking
Dingel and Neiman (2020) derive their teleworking measure from the responses to two O*NET surveys: “work context” and “generalized work activities”.16 From “work context” the following items were retained:17
-
•
How frequently does your current job require electronic mail? (Q4)
-
•
How often does your current job require you to work outdoors? (Q17)
-
•
How often is dealing with violent or physically aggressive people part of your current job? (Q14)
-
•
In your current job, how often do you wear common protective or safety equipment such as safety shoes, glasses, gloves, hearing protection, hard hats, or life jackets? (Q43)
-
•
How much time in your current job do you spend walking or running? (Q37)
-
•
How often does your current job require that you be exposed to minor burns, cuts, bites, or stings? (Q33)
-
•
How often does your current job require that you be exposed to diseases or infection? (Q29)
From “generalized work activities” the following items were considered:18
-
•
How important is Performing General Physical Activities to the performance of your current job? (Q16A)
-
•
How important is Handling and Moving Objects to the performance of your current job? (Q17A)
-
•
How important is Controlling Machines and Processes [not computers nor vehicles] to the performance of your current job? (Q18A)
-
•
How important is Operating Vehicles, Mechanized Devices, or Equipment to the performance of your current job? (Q20A)
-
•
How important is Performing for or Working Directly with the Public to the performance of your current job? (Q32A)
-
•
How important is Repairing and Maintaining Mechanical Equipment to the performance of your current job? (Q22A)
-
•
How important is Repairing and Maintaining Electronic Equipment to the performance of your current job? (Q23A)
-
•
How important is Inspecting Equipment, Structures, or Materials to the performance of your current job? (Q4A)
For each question, occupations are classified as “able to work from home” if answers are 1, 2 or 3, and as “cannot be performed at home” if answers are 4 or 5. Finally, occupations are classified as “able to telework” if they are categorised as “able to work from home” in the 15 questions.
A total of 968 occupations of the O*NET-Standard Occupation Classification (O*NET-SOC2010) were categorised as teleworkable or non-teleworkable in this way and then mapped to the corresponding US-SOC10 (at the 6-digit level).
Next, to obtain results for Europe, we use the ILO crosswalk to translate all US-SOC10 occupations into the EU-LFS occupations (ISCO-08 at the 3-digit level). This mapping between SOC10 and ISCO-08 is far from trivial because it is an unbalanced ‘many-to-many’ match, and correspondence needs to take into account relative weighting of related occupations. For this task, we use the Occupational Employment Statistics (OES) 2018 (which uses US-SOC 10 at the 6-digit level) and has the US employment weights for each occupation. Thus, we can map US-SOC10 occupations in OES (at the 6-digit level) to the ISCO-08 occupations (at the 3-digit level) in EU-LFS, a process which allocates US's employment across ISCOs in proportion to European employment shares. This mapping of 6-digit SOCs to 3-digit ISCOs (and the corresponding teleworking value for each occupation) is common to all European countries, but the posterior calculation of the weighted teleworking average for each 2-digit ISCO is country-specific, based on the labour weights of the different 3-digit occupations included in each 2-digit code. Finally, we impute the teleworking index based on EU-LFS at the 2-digit ISCO level to each occupation in EU-SILC at the 2-digit ISCO level. 19
Appendix B: The categorization of essential and closed occupations in Europe.
Given the levels of disaggregation by industry and occupation existing in the EU-LFS and EU-SILC databases (see a description in Tables A1-A3), our classification of occupations is mainly based on the Royal Decree 463/2020 (Boletin Oficial del Estado, 14th March, 2020) approved by the government of Spain on March 14th (2020). We have also considered the Royal Decree 10/2020 (Boletin Oficial del Estado, 29th March, 2020) approved by the government of Spain on March 29th (2020), and the Decree Law 23 (Gazzetta Ufficiale della Repubblica Italiana, 23rd February, 2020) approved by the government of Italy on February 23rd (2020). The values shown in Tables B1 and B2 correspond to the essential and closed occupations at the ISCO-08 2-digit level and NACE (Rev.2) 1-digit level. Based on these Tables, we calculate the values at the ISCO-08 1-digit level and NACE (Rev.2) 1-digit level (Tables B3 and B4 ), and the ISCO-08 2-digit level (Table B5 ) by averaging occupations and industries.
Table B1.
Categorization of essential occupations in Europe by Isco (2 digits) and Nace.
| Isco\Nace | A | B-E | F | G | H | I | J | K | L-N | O | P | Q | R-T |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 12 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 13 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 14 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 21 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 22 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 23 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 24 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 25 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 26 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 31 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 32 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 33 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 34 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 35 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 41 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 42 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 43 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 44 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 51 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 52 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 53 | 1 | 0.1 | 0 | 1 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 54 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 61 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 1 | 1 | 0 | 0 | 1 |
| 62 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 71 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 72 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 73 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 74 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 75 | 1 | 0.1 | 0 | 0 | 0 | 0.25 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 81 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 82 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 83 | 1 | 0.1 | 0 | 0 | 0.5 | 0.25 | 0.25 | 0.25 | 0 | 1 | 0 | 0.5 | 0 |
| 91 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 92 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 93 | 1 | 0.1 | 0 | 0 | 0.25 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 94 | 1 | 0.1 | 0 | 1 | 0.25 | 0.25 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 96 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
Table B2.
Categorization of closed occupations in Europe by Isco (2 digits) and Nace.
| Isco\Nace | A | B-E | F | G | H | I | J | K | L-N | O | P | Q | R-T |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 12 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 13 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 14 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 24 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 25 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 26 | 0 | 0.75 | 0.75 | 0.75 | 0.75 | 1 | 0.75 | 0.75 | 0.75 | 0 | 0.75 | 0 | 1 |
| 31 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 33 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 34 | 0 | 0.75 | 0.75 | 0.75 | 0.75 | 1 | 0.75 | 0.75 | 0.75 | 0 | 0.75 | 0 | 1 |
| 35 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 41 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 42 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 43 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 44 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 51 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 52 | 0 | 0.75 | 0.75 | 0.75 | 0.75 | 0 | 0 | 0 | 1 | 0 | 0.75 | 0 | 1 |
| 53 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 54 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 61 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 62 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 71 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 72 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 73 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 74 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 75 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 81 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 82 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 83 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 91 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 92 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 93 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 94 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 96 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Table B3.
Categorization of essential occupations in Europe by Isco (1 digit) and Nace.
| Isco\Nace | A | B-E | F | G | H | I | J | K | L-N | O | P | Q | R-T |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 2 | 1 | 0.1 | 0 | 0 | 0.3 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 3 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0.1 | 0 | 0 | 0.25 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 6 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 7 | 1 | 0.1 | 0 | 0 | 0 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0.25 | 0 |
| 8 | 1 | 0.1 | 0 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0.1 | 0 | 0 | 0.15 | 0 | 0.25 | 0.25 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0.1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
Table B4.
Categorization of closed occupations in Europe by Isco (1 digit) and Nace.
| Isco\Nace | A | B-E | F | G | H | I | J | K | L-N | O | P | Q | R-T |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0.5 | 0.5 | 1 | 0.5 | 1 | 0 | 0 | 0 | 0 | 0.5 | 0 | 1 |
| 6 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 7 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 9 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Table B5.
Categorization of essential and closed occupations in Europe by Isco (2 digits).
| Isco | Essential | Closed |
|---|---|---|
| 11 | 0.5 | 0 |
| 12 | 0.1 | 0 |
| 13 | 0.1 | 0 |
| 14 | 0 | 0.25 |
| 21 | 0 | 0 |
| 22 | 1 | 0 |
| 23 | 0 | 0 |
| 24 | 0.1 | 0 |
| 25 | 0.25 | 0 |
| 26 | 0 | 0.75 |
| 31 | 0 | 0 |
| 32 | 1 | 0 |
| 33 | 0 | 0 |
| 34 | 0 | 0.75 |
| 35 | 0.25 | 0 |
| 41 | 0.1 | 0 |
| 42 | 0 | 0 |
| 43 | 0.1 | 0 |
| 44 | 0.1 | 0 |
| 51 | 0 | 0.5 |
| 52 | 0 | 0.75 |
| 53 | 0.75 | 0 |
| 54 | 0.25 | 0 |
| 61 | 1 | 0 |
| 62 | 1 | 0 |
| 71 | 0 | 0 |
| 72 | 0 | 0 |
| 73 | 0 | 0 |
| 74 | 0.1 | 0 |
| 75 | 0.25 | 0 |
| 81 | 0 | 0 |
| 82 | 0 | 0 |
| 83 | 0 | 0 |
| 91 | 0.25 | 0 |
| 92 | 1 | 0 |
| 93 | 0.25 | 0 |
| 94 | 0.25 | 0 |
| 96 | 0.25 | 0 |
Note: see Table A2 for the explanation of the entries of this table.
Appendix C. Correlation between the changes in poverty and inequality and the LWA index under scenario (iv).
Appendix D. Poverty and wage inequality changes for alternative scenarios
Table D1.
Poverty changes in Europe (9 months of closure).
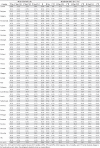 |
Table D2.
Wage inequality changes in Europe (9 months of closure).
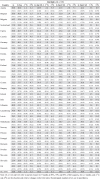 |
Table D3.
Between- and within-countries inequality in Europe (9 months of closure).
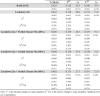 |
Appendix. Supplementary materials
References
- BBVA Research (2020): “Impacto de la COVID-19 sobre el consumo en España en tiempo real y alta definición”, Release 16th of July, 2020. Retrieved at: www.bbvaresearch.com/publicaciones/global-impacto-de-la-covid-19-en-consumo-en-tiempo-real-y-alta-definicion-16-de-julio/.
- Bluhm R., de Crombrugghe D., Szirmai A. Poverty accounting. Eur. Econ. Rev. 2018;104:237–255. [Google Scholar]
- Boletin Oficial del Estado (14th March, 2020): Royal decree 463/2020. Retrieved at: www.boe.es/diario_boe/txt.php?id=BOE-A-2020-3692.
- Boletin Oficial del Estado (29th March, 2020): Royal decree 10/2020. Retrieved at: www.boe.es/buscar/doc.php?id=BOE-A-2020-4166.
- Bourguignon F. Decomposable income inequality measures. Econometrica. 1979;47(4):901–920. [Google Scholar]
- Brunori P., Maitino M.L., Ravagli L., Sciclone N. Distant and unequal. Lockdown and Inequalities in Italy. 2020 , Mimeo, Italy. [Google Scholar]
- Chetty R., Friedman J.N., Hendren N., Stepner M. How did COVID-19 stabilization policies affect spending and employment? A new real-time economic tracker based on private sector data. NBER Work. Pap. No. 27431. 2020 www.therecovery.org Retrieved at: Data release of week ending July 12th. [Google Scholar]
- del Rio-Chanona R.M., Mealy P., Pichler A., Lafond F., Farmer D.F. Supply and demand shocks in the COVID-19 pandemic: An industry and occupation perspective. Covid Econ. 2020;6:65–104. [Google Scholar]
- Dingel J., Neiman B. How many jobs can be done at home? NBER Work. Pap. No. 26948. 2020 [Google Scholar]
- Eichhorn W., Funke H., Richter W.F. Tax progression and inequality of income distribution. J. Math. Econ. 1984;13:127–131. [Google Scholar]
- Essama-Nssah B., Lambert P.J. Measuring pro-poorness: a unifying approach with new results. Rev. Income Wealth. 2009;55:752–778. [Google Scholar]
- Foster J.E., Shneyerov A.A. Path independent inequality measures. J. Econ. Theory. 2000;91(2):199–222. [Google Scholar]
- Furceri D., Loungani P., Ostry J.D., Pizzuto P. Will Covid-19 affect inequality? Evidence from past pandemics. Covid Econ. 2020;12:138–157. doi: 10.1007/s10888-022-09540-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazzetta Ufficiale della Repubblica Italiana (23rd February, 2020): Decreto-legge 23 febbraio 2020, n. 6. Retrieve at: www.gazzettaufficiale.it/eli/id/2020/02/23/20G00020/sg.
- Goolsbee A., Syverson Ch. Fear, lockdown, and diversion: comparing drivers of pandemic economic decline 2020. NBER Work. Pap. No. 27432. 2020 doi: 10.1016/j.jpubeco.2020.104311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hicks M.J., Faulk D., Devaraj S. Center for Business and Economic Research. Ball State University; 2020. Occupational exposure to social distancing: a preliminary analysis using O*NET data. [Google Scholar]
- IMF, 2020. World economic outlook update. June 2020. Retrieved at: www.imf.org/en/Publications/WEO/Issues/2020/06/24/WEOUpdateJune2020.
- ILO, 2020. ILO Monitor 2nd edition: COVID-19 and the world of work. International Labour Organisation. April 2020. Retrieved at: https://www.ilo.org/wcmsp5/groups/public/---dgreports/---dcomm/documents/briefingnote/wcms_740877.pdf.
- Irlacher M., Koch M. Working from home, wages, and regional inequality in the light of Covid-19. CESifo Work. Pap. No. 8232. 2020 [Google Scholar]
- Kakwani N., Pernia N. What is pro-poor growth. Asian Dev. Rev. 2000;16(1):1–22. [Google Scholar]
- Kakwani N., Son H. Poverty equivalent growth rate. Rev. Income Wealth. 2008;54(4):643–655. [Google Scholar]
- Mongey S., Pilossoph L., Weinberg A. Which workers bear the burden of social distancing policies? NBER Work. Pap. No. 27085. 2020 doi: 10.1007/s10888-021-09487-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravallion M., Chen S. Measuring pro-poor growth. Econ. Lett. 2003;78:93–99. [Google Scholar]
- Prieto-Rodríguez J., Rodríguez J.G., Salas R. A study on the relationship between economic inequality and mobility. Econ. Lett. 2008;99(1):111–114. [Google Scholar]
- Ravallion M. Global inequality when unequal countries create unequal people. Eur. Econ. Rev. 2019;111:85–97. [Google Scholar]
- Shorrocks A.F. The class of additively decomposable inequality measures. Econometrica. 1980;48(3):613–625. [Google Scholar]
- Watts H.W. In: On Understanding Poverty. Moynihan D.P., editor. Basic Books; New York: 1968. An economic definition of poverty. [Google Scholar]
- Zheng B. An axiomatic characterization of the Watts index. Econ. Lett. 1993;42:81–86. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.