Abstract
Background and Objectives
Chloroquine/hydroxychloroquine has recently been the subject of intense debate regarding its potential antiviral activity against SARS-Cov-2, the etiologic agent of COVID-19. Some report possible curative effects; others do not. Therefore, the objective of this study was to simulate possible scenarios of response to hydroxychloroquine in COVID-19 patients using mathematical modeling.
Methods
To shed some light on this controversial topic, we simulated hydroxychloroquine-based interventions on virus/host cell dynamics using a basic system of previously published differential equations. Mathematical modeling was implemented using Python programming language v 3.7.
Results
According to mathematical modeling, hydroxychloroquine may have an impact on the amplitude of the viral load peak and viral clearance if the drug is administered early enough (i.e., when the virus is still confined within the pharyngeal cavity). The effects of chloroquine/hydroxychloroquine may be fully explained only when also considering the capacity of this drug to increase the death rate of SARS-CoV-2-infected cells, in this case by enhancing the cell-mediated immune response.
Conclusions
These considerations may not only be applied to chloroquine/hydroxychloroquine but may have more general implications for development of anti-COVID-19 combination therapies and prevention strategies through an increased death rate of the infected cells.
Electronic supplementary material
The online version of this article (10.1007/s13318-020-00640-6) contains supplementary material, which is available to authorized users.
Key Points
| Hydroxychloroquine might impact the amplitude of the viral load peak and might also affect viral clearance if the drug is administered early enough when the virus is still confined to the pharyngeal cavity |
| Hydroxychloroquine's effects against SARS-CoV-2 might be exerted more through its capacity to enhance cell-mediated immunity than through its direct antiviral effects |
| The effects of hydroxychloroquine on SARS-CoV-2 viral load may thus be missed in clinical trials if measurements are not done at the peak of viral replication and are evident only at dosages able to guarantee a certain plasma drug concentration, i.e., > 400 mg/day |
Introduction
Chloroquine is a quinoline molecule first synthesized by Italian-Austrian chemist Hans Andersag in Germany in 1934 [1]. It became popular for the treatment of malaria and antimalarial prophylaxis. Hydroxychloroquine is its hydroxy analog: originally synthesized as an antimalarial as well, it was found to be less toxic than its parent compound and soon found an application in the treatment of lupus erythematosus and rheumatoid arthritis because its toxicity profile allowed long-term administration [2]. Chloroquine and hydroxychloroquine are weak bases that become readily thesaurized in intracellular acidic organelles [3]. This property confers both antimalarial and antirheumatic effects to them, the former being due to inhibition of hemozoin polymerization in the Plasmodium falciparum food vacuole and the second being derived from inhibition of the endosomal processing of molecules such as transferrin, which requires an acidic environment. As proliferating peripheral blood mononuclear cells require iron for their optimal activation and proliferation, this property confers an immunomodulatory effect [4].
However, after many decades of clinical use of hydroxychloroquine, part of its pharmacokinetics is still unknown (e.g., the effective drug concentrations in tissues such as the lung are only deduced [5]). Because of this, some studies rely on the drug plasma concentrations [6]. Studies conducted in P. falciparum and human erythrocytes have shown that the unprotonated portion of chloroquine/hydroxychloroquine diffuses passively through the plasma membrane and enters the cytosol where it becomes protonated according to the Henderson-Hasselbalch law. Protonation impedes the drug from exiting through the plasma membrane and the drug becomes thesaurized within cells. In these, the drug is accumulated within acidic organelles through active transport by members of the ATP-binding cassette. In whole blood, the drug displays a concentration that is approximately fourfold higher than in plasma [7]. The endosomal accumulation constitutes the basis for chloroquine/hydroxychloroquine long duration of action, its long elimination time and large apparent volume of distribution [8, 9]. As shown in acute treatment of malaria, the achievement of the desired steady-state levels of the drug can be facilitated by administration of a loading dose [10, 11].
Chloroquine/hydroxychloroquine was later found to display broad-spectrum antiviral properties [3]. As many viruses require an internalization step to infect cells, the lysosomotropic properties of the drug(s) were found to inhibit a large number of viruses (reviewed in: [3]). In the context of HIV, which does not require an internalization step, chloroquine/hydroxychloroquine was considered because of its antiinflammatory properties [12], as the disease is characterized by malignant immune hyperactivation [13]. It was also found that chloroquine/hydroxychloroquine inhibits maturation of the HIV envelope glycoproteins by counteracting the acidic environment in the trans-Golgi network [12], an effect that was also exerted on other enveloped viruses [3]. Given these properties, chloroquine/hydroxychloroquine was proposed in 2003 for treatment of severe acute respiratory syndrome (SARS) [3].
In that period, another interesting aspect of inhibition of lysosomal acidification by chloroquine was shown. The drug induces endosomal escape of viral peptides into the cytoplasm, thus facilitating their processing through the proteosomal pathway and presentation through HLA class I [14]. This in turn enhances CD8+ T cell responses against the infected cells and their subsequent elimination.
Recently, due to its promising in vitro antiviral effects [16], chloroquine was then repurposed as a drug for the treatment of COVID-19. Hydroxychloroquine immediately followed as a potential therapeutic candidate [17]. As clinical trials for COVID-19 patients have so far produced mixed results, further study of the interaction of this drug with the virus/host dynamics in vivo is necessary to provide insight into the optimal timing of the administration, dosing and association with other interventions.
More light on how drugs intervene in the virus/host interplay could be shed by mathematical modeling taking into account clinical observations [18–21]. Such models have already been proved able to simulate the response to drugs in HIV/AIDS [22, 23].
In the present article, we use a mathematical model (derived from Ref. [19]) to simulate possible scenarios of response to hydroxychloroquine in COVID-19 patients. Differently from previously presented modeling simulations [18], this model shows that the drug may have a significant impact on virus/host dynamics. This different conclusion has been reached by considering an immune-modulating effect of the drug so far left unexplored in mathematical modeling, i.e., the increased death rate of the infected cells through cell-mediated immunity [14]. This result has implications for the future design of clinical trials for COVID-19 treatment and prevention.
Methods
A Mathematical Model for Viral Dynamics in the Target Cell Population
To simulate hydroxychloroquine-based interventions on virus/host cell dynamics, we used the basic system of differential equations (Eqs. 1a–1d) as published by Best et al. [19], applicable to infection by non-integrating RNA viruses. The system used by Best et al. [19] is as follows:
| 1a |
| 1b |
| 1c |
| 1d |
Equations 1a–1d: These are ordinary differential equations describing the viral dynamics in a model of the target cell population with an eclipse phase.
T represents the target cells, assumed to be 4 × 108 [24, 25] based on an assumption of 30 ml nasopharyngeal volume [20]. This volume maintains a cellular concentration of 1.33 × 107 cells/ml [18], which becomes infected with a constant parameter β, which changes depending on another parameter (1 − ε) where ε reflects the antiviral effectiveness of the drug. I1 represents the infected cells in the eclipse phase, i.e., those cells “incubating” viral replication but not yet productively infected. I2 represents the productively infected cells, which start the productivity phase after an average time 1/k, wherein the k values considered were 1/day in order to allow prediction of intervention timing on viral propagation. In this system, the release of virions (V) is controlled by a parameter p, which is assumed under baseline conditions to be 20,000/day. Virions (V) are later cleared with a constant parameter rate c, which was assumed to be 12/day in light of previous clinical data [15], while infected cells I2 are lost at a death rate δ, by default considered to be 0.55/day, according to Gonçalves et al. [18]. V, as stated above, reflects the viral population that was modeled by changing V0 at {11, 103, 106} copies/ml. The model neglects the proliferation and death rates of target cells with respect to the concise time scale of infection; instead, the model focuses on the viral effect on target cells. Finally, the β value represents the possibility of the encounter between the virus (V) and a target cell (T). The choice of the different β values is discussed in the figures when using different values of this parameter.
Calculation of Antiviral Efficacy
The antiviral effectiveness of the drug (ɛ) was herein simulated at (0, 33, 62, 70, 78%, adopted in the system as 0, 0.33, 0.62, 0.7, 0.78, assuming a 100% drug efficacy of 1 and 0% drug efficacy of 0), on the basis of clinical pharmacokinetic results [7, 18, 26] (Figs. 1, 2). The percentage values are the percent inhibition of virus replication in the presence of a given concentration of the drug, as specified in the Results section (see below). This percentage of inhibition was derived from our previous in vitro experiments, using a standard curve relating the drug concentration to the virus yields at the end of incubation of an infected cell culture with the drug and comparing the effects with the virus yield in control untreated cultures. Previously, Gonçalves et al. [18], using the plasma drug concentrations derived from patients treated with 400 mg of hydroxychloroquine/day, concluded that hydroxychloroquine had no sufficient effect on the viral load dynamics because the pharmacokinetic parameter that they used to conduct the simulations was the plasma drug concentration. We also considered the whole blood concentration from individuals treated with 400 mg/day of hydroxychloroquine (including the drug compartment entrapped in lysosomes) [7], as derived from the ratios provided in the same publication used by these authors to derive the plasma concentration [7]. When considering the whole blood concentrations, we implemented (Eq. 2) from the ɛ calculation provided by Gonçalves et al. [18] to calculate a drug efficacy of approximately 0.7, based on the concentration-response curves previously published by our group (Fig. 3), using cells infected with the canine coronavirus (CCoV) after pre-incubation with the hydroxychloroquine analog chloroquine [27]:
| 2 |
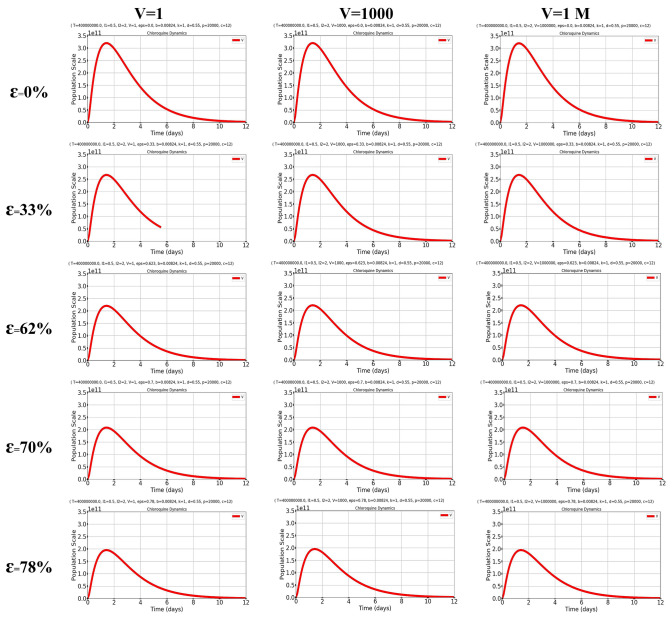
Fig. 1.
Simulation plots under k = 1/day, T = 4e8 (initial value [24]), = 1.65/day, p = 2e4 [46], β = 8.24 × 10e−3 [21] and V0 at {11, 103, 106} copies/ml (initial values) describing the dynamics of reduction in viral load under six drug efficacy (ɛ) conditions. Baseline conditions with ε = 0, ε = 33%, ε = 62.3%, ε = 70% and ε = 78%
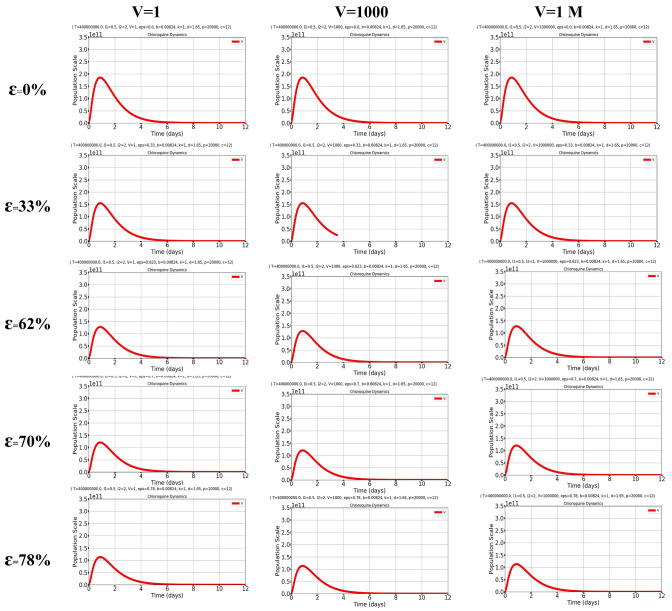
Fig. 2.
Simulation plots under k = 1/day, T = 4e8 (initial value [24]), = 1.65/day, p = 2e4 [46], β = 8.24 × 10e−3 [21] and V0 at initial {11, 103, 106} copies/ml describing the dynamics of reduction in viral load under six drug efficacy (ɛ) conditions. Baseline conditions with ε = 0, ε = 33%, ε = 62.3%, ε = 70% and ε = 78%. The results obtained should be compared with the first row of graphs in Fig. 1, simulating a condition in the absence of chloroquine/hydroxychloroquine. The first row of the present figure instead aims at simulating the effect of a drug or intervention able to increase the death of infected cells but having no antiviral effect per se
Fig. 3.
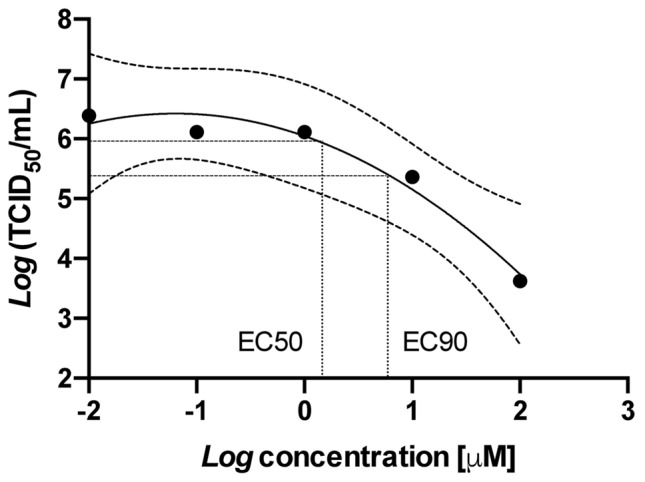
Effect of chloroquine on replication of canine coronavirus (CCoV) in canine fibrosarcoma A72 cells. Cells were preloaded with chloroquine for 1 h and infected with CCoV; the infectious titer (TCID50/ml) in supernatants was assessed in A72 cells. Data were analyzed by non-linear regression (95% confidence limits of the curve are shown). Adapted from [27]. TCID50 median tissue culture infectious dose, EC50 half maximal effective concentration, EC90 90% effective concentration
Equation 2 calculates the efficacy ɛ; Cx represents the molar concentration of the drug of interest.
Gautret et al. [6] recently published the trough serum concentrations of hydroxychloroquine obtained from patients with COVID-19 and treated with a higher dosage (i.e., 600 mg/day) of hydroxychloroquine. Unfortunately, no blood concentrations were reported by Gautret et al., but these could be proportionally derived from the standard curve in (Fig. 3) and the standard curves for conversion of serum to whole blood and serum to plasma provided in [26]. This calculation led to a prediction of drug efficacy using Eq. 2 from plasma and whole blood of 62 and 78%, respectively.
Adjusting the System for Modeling Efficacy of a Drug with a Double Mechanism of Action
The system of differential equations that we adopted was set up for drugs with a single mechanism of action, especially in the early phases of the infection. However, an aspect that needs attention is the double mechanism of the antiviral effects of hydroxychloroquine. As derived from studies on a huge number of viruses, lysosomal accumulation of hydroxychloroquine is highly likely to affect both the viral entry (simulated by Best et al. [19] and Gonçalves et al. [18]) and post-entry stages in cellular organelles such as viral budding and viral particle glycosylation [3, 16] (not considered in the aforementioned studies). According to the data of Wang et al. [16], the hydroxychloroquine analog chloroquine displayed approximately half of its antiviral activity when it was added after virus adsorption onto cells, confirming that part of its activity occurs at a post-entry level. As we also wanted to estimate the impact of hydroxychloroquine-induced impairment of viral production, we thus adjusted the system by optimizing (Eq. 1d) into (Eq. 3), as follows:
| 3 |
Equation 3: p-adjusted ordinary differential equation describing the viral dynamics in a model of target cell population with an eclipse phase.
Modeling the Death Rate of Infected Cells
The death rate value adopted in the present study was taken from Gonçalves et al. [18]. Among the immune-modulating effects of chloroquine/hydroxychloroquine is its capacity to induce antigen cross-presentation and increase the immune cytotoxic response [14, 15]. In this case, the effect of cell-mediated immune responses could be modeled with the system of differential equations adopted by increasing the death rate δ. Indeed, enhanced cytotoxic responses result in increased death of the infected cells. To model the effect of chloroquine/hydroxychloroquine on CD8+ T-cell-mediated killing of the infected cells, we increased the δ factor by approximately threefold (data derived from Accapezzato et al. [14]).
Computational Simulations
Mathematical modeling was implemented using Python programming language v 3.7 (http://www.python.org). The ODEINT function of the SciPy package was used for solving ordinary differential equations [28], numerical solutions were applied through NumPy package [29], and simulations were plotted within a 12-day time frame using Matplotlib package [30]. To adapt our data to the maximum number of cases and quantitative viral load assays, the viral load was kept dimensionless [31].
Results
In the absence of any treatment, the model [18] shows that there is an early peak in viral replication followed by a gradual and slow abatement of viral load accompanying consumption of target cells (Fig. 1, first row). Some of the parameters such as the initial viral inoculum (V), the viral production rate (p) and the rate of virus/cell encounter β did not alter the virus/host dynamics substantially (Fig. 1, Supplemental Figures S1, S2).
The parameters that most influenced the virus/host dynamics were the drug efficacy (ε; Figs. 1, 2), the infected cell death rate (δ; Figs. 1, 2) and viral clearance (c; data not shown). The first was the principal determinant of the viral load at peak, while the second two were the principal determinant of the timing to return to the initial viral inoculum. We focused our attention on ɛ and δ because they are the parameters influenced by chloroquine/hydroxychloroquine at an early stage, i.e., in a scenario mimicked by our simulations, in which the infection is still confined within the pharyngeal cavity.
Our simulations show that the initial viral load peak is inversely dependent on the drug efficacy ε, but that even the highest ε values do not influence the return to the initial viral inoculum (Fig. 1). We estimated drug efficacy based on both a more conservative approach (using ε values based on the plasma drug concentrations) and an explorative approach (using ε values based on the whole blood concentrations) mimicking administration of the two most widely used dosing schedules of hydroxychloroquine for treatment of COVID-19 [200 mg BID, second (plasma concentration) and third (whole blood concentration) row of Fig. 1; 200 mg three times a day, fourth (plasma) and fifth (whole blood) row of Fig. 1]. These data show that drug efficacy alone cannot explain the results of the clinical studies administering hydroxychloroquine at the higher dosages and in which the drug was shown to induce faster negativization of the assays for detection of the virus in pharyngeal swabs.
We then attempted to mimic an early immunologic effect of chloroquine/hydroxychloroquine, i.e., the increase in cell-mediated immunity increasing the death rate of the infected cells (δ). Based on biologic data (Accapezzato et al. [14]), we increased the δ parameter by threefold and found that the time of return to the initial viral inoculum was remarkably decreased (Fig. 2).
Interestingly, from the simulations above, it appeared that the plasma drug concentrations are sufficient for explaining the data of Gautret et al. [6] [fourth row of Fig. 2 (plasma concentration), fifth row of Fig. 2 (whole blood concentration)], in line with a recent report concluding that the unbound plasma concentration of the drug is an accurate marker of its in vivo activity [32]. The δ value could in fact compensate for the partial lack of direct antiviral activity. The study of Gautret et al. may serve as a credible validation of our in silico simulations, as day 6 of treatment was used as a turning point (Fig. 2), since, at that time point, a significantly higher proportion of COVID-19 patients receiving hydroxychloroquine displayed negative pharyngeal swabs compared to the patients who had not received it (Gautret et al. [6]). Interestingly, in our simulations, day 6 of hydroxychloroquine treatment with the dosage adopted by Gautret et al. was the day at which the viral load reverted to the level of the initial viral inoculum (Fig. 2). As the study of Gautret et al. [6] also included patients at an initial stage of the infection (i.e., presenting only pharyngeal symptoms), our simulations of hydroxychloroquine treatment when viral loads are still very low may account for nasopharyngeal swab negativization.
Finally, we further validated our in silico simulations against those of an independent study recently rendered available and being one of the first reports of early treatment with hydroxychloroquine in non-hospitalized COVID-19 patients [33]. In that report, Guerin et al. showed, in the group of patients treated with hydroxychloroquine and azithromycin, a time to recovery that was 0.71 fold that of patients treated with azithromycin alone. This time is comparable with that from our calculations of reversal to the original viral inoculum, which was 0.61-fold under our conditions simulating treatment with hydroxychloroquine (Figs. 1, 2).
Discussion
Our results agree in part with the simulations conducted by Arnold and Buckner [5], showing that the 600 mg/day regimen is likelier to have a significant impact on viral replication compared to a 400 mg/day dosage and with those of Garcia-Cremades et al. [34], showing that a dosage > 400 mg/day would be necessary to obtain viral suppression. The approach that we have followed is more conservative than that adopted by Arnold and Buckner [5], in that we also considered the plasma and whole-blood concentrations as a measure of prediction of tissue accumulation rather than the predicted accumulation in the lung. According to the model adopted by Arnold and Buckner [5], the drug lung concentrations are hundreds of times higher than those in plasma and are predicted to reach a concentration able to inhibit 100% of SARS-CoV-2 replication. We decided not to follow the lung distribution prediction in light of two orders of considerations. (1) Tissue accumulation of hydroxychloroquine may result in dishomogeneous accumulation in sub-compartments, being mainly driven by tissue macrophages [35], which are not a main target for the virus-induced tissue damage, and (2) according to the data previously published [27], 100% inhibition of coronavirus replication is not reachable experimentally using a quinoline antimalarial, not even at supra-physiologic concentrations. Our data however showed in the end that the drug plasma concentration is sufficient for estimating the in vivo effect of chloroquine/hydroxychloroquine if the early immunomodulatory effect of the drug is considered (see below).
This accumulating evidence shows that the virologic response to hydroxychloroquine in COVID-19 patients has a pharmacokinetic basis and that the higher drug dosage has the highest chances of being effective on the viral load peak, whether because of the plasma or the whole-blood concentration.
Our calculations can also explain the clinical data reported so far on COVID-19. A small trial in France suggested that hydroxychloroquine helps treat COVID-19 [6], and a small study from China [36] reported the opposite results. Both studies have their own limitations and very limited statistical power due to the fact that they were prepared during an emergency. The discrepancy of these results may reside, according to the results of the present study, in the dosage of hydroxychloroquine adopted, with the French study reporting positive results using 600 mg/day of hydroxychloroquine and the Chinese study being unable to show any efficacy following adoption of a lower dosage (400 mg/day). These considerations are corroborated by the results obtained in randomized clinical trials, reporting varying degrees of success using chloroquine and hydroxychloroquine at an equivalent dosage superior to that reported in the two aforementioned studies [38–40]. These considerations are also in line with a retrospective study, reporting positive effects of chloroquine at a high dosage (500 mg bid) [37].
As the safety margin of chloroquine/hydroxychloroquine is narrow [35], administration of higher dosages is unfortunately hampered by toxicity, as shown by Borba et al. [39], and pharmacokinetic modeling [34], although recent data show that the toxicity observed by Borba et al. could in fact be ascribed to the concomitant administration of azithromycin [41].
In the discussions so far undertaken on the effects of chloroquine/hydroxychloroquine on COVID-19, immune-mediated mechanisms have not been taken into account [3]. A late impact on immune hyperactivation, occurring in the advanced phases of the disease, cannot in this case be inferred, also because the present model is limited to an early phase of the disease in which the virus is still confined within the pharyngeal cavity. Modeling of late virologic and immune effects would go beyond the capacity of the system of differential equations adopted and involve a number of other as yet poorly known parameters, resulting in the risk of becoming extremely artificial. Confinement to the early events in any case represents a major limitation of the present study.
As anticipated above, an immune-mediated mechanism that we considered is the effect of chloroquine/hydroxychloroquine on antigen cross-presentation. Cross-presentation is a phenomenon in which a dendritic cell presents the antigen to CD8+ T-cells, improving their priming. Activation of CD8+ T-cells after priming through antigen recognition can induce the selective killing of the infected cells [14]. By increasing the death rate δ factor by only threefold, we could observe a further decrease in the peak amplitude and a shorter time to viral load exhaustion compared to conditions under normal death rates. If our simulations are correct, not only will strategies enhancing immunity be able to contribute to the decreased δ factor, but also drugs aimed at the direct killing of infected cells. Interestingly, one drug taken into consideration for COVID-19 treatment is auranofin [47], an agent able to modulate oxidative stress and favoring death of cells infected by a virus such as HIV-1 [48]. In line with this theory, auranofin has recently been proven to limit virus outgrowth in infected cell cultures [49]. Its capacity to kill coronavirus-infected cells will thus need to be tested.
Conclusions
To sum up, our simulations suggest that chloroquine/hydroxychloroquine might display some beneficial effects in vivo more through its capacity of enhancing cell-mediated immunity than through its direct antiviral effects, although the latter may undoubtedly play a role due to viral load curve flattening. One limitation of the present study is that we kept the drug concentration constant, without taking into account its accumulation. These simulations may however refer to steady-state conditions considering a good deal of COVID-19 patients’ time of exposure to the drug, as loading doses are foreseen in a number of clinical protocols to shorten the time to optimal drug accumulation [17, 42]. In this case, the simulations with a starting viral load (V) of 1 copy/ml are unlikely to occur in a clinical setting following a COVID-19 diagnosis, but might be a possible scenario of the virus/host dynamics during interventions of post-exposure prophylaxis. Hydroxychloroquine is currently also being investigated as a prophylactic agent [43]. In case chloroquine/hydroxychloroquine should prove ineffective in protecting from SARS-CoV-2 acquisition, it is plausible that it may mitigate disease severity by attenuating viral replication.
Finally, this research may lead to new promising directions. For example, given the great interest that this strategy has so far evoked in the context of COVID-19 [44, 45], and the aforementioned effects of chloroquine/hydroxychloroquine on viral antigen presentation, future vaccines against this disease should be considered in co-administration with chloroquine/hydroxychloroquine. Another promising future direction of this research could be the research on new drugs able to directly kill coronavirus-infected cells as a novel possible avenue to mitigate/shorten the clinical course of COVID-19.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Declarations
Funding
No funding source.
Conflict of interest
The authors declare that they have no competing interest.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
The authors have consent from their institutions.
Availability of data and material
Not applicable.
Code availability
Available at: https://colab.research.google.com/drive/1Qp2h8n_q89xQlxucyJ-62dy5P1TUAdB7.
References
- 1.Pötsch WR, Fischer A, Müller W. Lexikon bedeutender Chemiker. New Delhi: Anamika Publishers & Distributors; 1988. [Google Scholar]
- 2.Wallace DJ, Hahn B, editors. Dubois’ lupus erythematosus. Philadelphia: Lippincott Williams & Wilkins; 2007. [Google Scholar]
- 3.Savarino A, Boelaert JR, Cassone A, Majori G, Cauda R. Effects of chloroquine on viral infections: an old drug against today’s diseases? Lancet Infect Dis. 2003;3(11):722–727. doi: 10.1016/S1473-3099(03)00806-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fong KY, Wright DW. Hemozoin and antimalarial drug discovery. Future Med Chem. 2013;5(12):1437–1450. doi: 10.4155/fmc.13.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Arnold SLM, Buckner F. Hydroxychloroquine for treatment of SARS-CoV-2 infection? Improving our confidence in a model-based approach to dose selection. Clin Transl Sci. 2020;13(4):642–645. doi: 10.1111/cts.12797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gautret P, Lagier JC, Parola P, Meddeb L, Mailhe M, Doudier B, Courjon J, Giordanengo V, Vieira VE, Dupont HT, Honoré S. Hydroxychloroquine and azithromycin as a treatment of COVID-19: results of an open-label non-randomized clinical trial. Int J Antimicrob Agents. 2020;20:105949. doi: 10.1016/j.ijantimicag.2020.105949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Morita S, Takahashi T, Yoshida Y, Yokota N. Population pharmacokinetics of hydroxychloroquine in Japanese patients with cutaneous or systemic lupus erythematosus. Ther Drug Monit. 2016;38(2):259–267. doi: 10.1097/FTD.0000000000000261. [DOI] [PubMed] [Google Scholar]
- 8.Smit C, Peeters MYM, van den Anker JN, Knibbe CAJ. Chloroquine for SARS-CoV-2: implications of its unique pharmacokinetic and safety properties. Clin Pharmacokinet. 2020;59(6):659–669. doi: 10.1007/s40262-020-00891-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Oscanoa TJ, Romero-Ortuno R, Carvajal A, Savarino A. A pharmacological perspective of chloroquine in SARS-CoV-2 infection. Int J Antimicrob Agents. 2020;4:106078. doi: 10.1016/j.ijantimicag.2020.106078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pussard E, Lepers JP, Clavier F, et al. Efficacy of a loading dose of oral chloroquine in a 36-hour treatment schedule for uncomplicated plasmodium falciparum malaria. Antimicrob Agents Chemother. 1991;35(3):406–409. doi: 10.1128/aac.35.3.406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lim HS, Im JS, Cho JY, et al. Pharmacokinetics of hydroxychloroquine and its clinical implications in chemoprophylaxis against malaria caused by Plasmodium vivax. Antimicrob Agents Chemother. 2009;53(4):1468–1475. doi: 10.1128/AAC.00339-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Boelaert JR, Piette J, Sperber K. The potential place of chloroquine in the treatment of HIV-1-infected patients. J Clin Virol. 2001;20(3):137–140. doi: 10.1016/S1386-6532(00)00140-2. [DOI] [PubMed] [Google Scholar]
- 13.Savarino A, Bottarel F, Malavasi F, Dianzani U. Role of CD38 in HIV-1 infection: an epiphenomenon of T-cell activation or an active player in virus/host interactions? Aids. 2000;14(9):1079–1089. doi: 10.1097/00002030-200006160-00004. [DOI] [PubMed] [Google Scholar]
- 14.Accapezzato D, Visco V, Francavilla V, et al. Chloroquine enhances human CD8+ T cell responses against soluble antigens in vivo. J Exp Med. 2005;202(6):817–828. doi: 10.1084/jem.20051106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chang D, Mo G, Yuan X, et al. Time kinetics of viral clearance and resolution of symptoms in novel coronavirus infection. Am J Respir Crit Care Med. 2020;201(9):1150–1152. doi: 10.1164/rccm.202003-0524LE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang M, et al. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro. Cell Res. 2020 doi: 10.1038/s41422-020-0282-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yao X, Ye F, Zhang M, Cui C, Huang B, Niu P, Liu X, Zhao L, Dong E, Song C, Zhan S. In vitro antiviral activity and projection of optimized dosing design of hydroxychloroquine for the treatment of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) Clin Infect Dis. 2020 doi: 10.1093/cid/ciaa237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gonçalves A, Bertrand J, Ke R, Comets E, de Lamballerie X, Malvy D, Pizzorno A, Terrier O, Rosa Calatrava M, Mentré F, Smith P. Timing of antiviral treatment initiation is critical to reduce SARS-CoV-2 viral load. CPT Pharmacometr Syst Pharmacol. 2020 doi: 10.1002/psp4.12543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Best K, Guedj J, Madelain V, et al. Zika plasma viral dynamics in nonhuman primates provides insights into early infection and antiviral strategies. Proc Natl Acad Sci. 2017;114(33):8847–8852. doi: 10.1073/pnas.1704011114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li C, Xu J, Liu J, et al. The within-host viral kinetics of SARS-CoV-2. Math Biosci Eng. 2020;17:2853–2861. doi: 10.1101/2020.02.29.965418. [DOI] [PubMed] [Google Scholar]
- 21.Kim KS, Ejima K, Ito Y, et al. Modelling SARS-CoV-2 dynamics: implications for therapy. medRxiv. 2020 doi: 10.1101/2020.03.23.20040493. [DOI] [Google Scholar]
- 22.Rong L, Perelson AS. Modeling latently infected cell activation: viral and latent reservoir persistence, and viral blips in HIV-infected patients on potent therapy. PLoS Comput Biol. 2009;5(10):e1000533. doi: 10.1371/journal.pcbi.1000533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shytaj IL, Norelli S, Chirullo B, et al. A highly intensified ART regimen induces long-term viral suppression and restriction of the viral reservoir in a simian AIDS model. PLoS Pathog. 2012;8(6):e1002774. doi: 10.1371/journal.ppat.1002774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baccam P, Beauchemin C, Macken CA, Hayden FG, Perelson AS. Kinetics of influenza A virus infection in humans. J Virol. 2006;80(15):7590–7599. doi: 10.1128/JVI.01623-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Perelson AS, Rong L, Hayden FG. Combination antiviral therapy for influenza: predictions from modeling of human infections. J Infect Dis. 2012;205(11):1642–1645. doi: 10.1093/infdis/jis265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Carlsson H, Hjorton K, Abujrais S, Rönnblom L, Åkerfeldt T, Kultima K. Measurement of hydroxychloroquine in blood from SLE patients using LC-HRMS—evaluation of whole blood, plasma, and serum as sample matrices. Arthritis Res Ther. 2020;22:1–9. doi: 10.1186/s13075-020-02211-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Savarino A, Buonavoglia C, Norelli S, Trani LD, Cassone A. Potential therapies for coronaviruses. Expert Opin Ther Pat. 2006;16(9):1269–1288. doi: 10.1517/13543776.16.9.1269. [DOI] [Google Scholar]
- 28.Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J. van der Walt SJ. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods. 2020;17(3):261–272. doi: 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Walt SV, Colbert SC, Varoquaux G. The NumPy array: a structure for efficient numerical computation. Comput Sci Eng. 2011;13(2):22–30. doi: 10.1109/MCSE.2011.37. [DOI] [Google Scholar]
- 30.Hunter JD. Matplotlib: a 2D graphics environment. Comput Sci Eng. 2007;9(3):90–95. doi: 10.1109/MCSE.2007.55. [DOI] [Google Scholar]
- 31.Langtangen HP, Pedersen GK. Scaling of differential equations. Berlin: Springer Nature; 2016. [Google Scholar]
- 32.Fan J, Zhang X, Liu J, et al. Connecting hydroxychloroquine in vitro antiviral activity to in vivo concentration for prediction of antiviral effect: a critical step in treating COVID-19 patients. Clin Infect Dis. 2020 doi: 10.1093/cid/ciaa623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Guérin V, Lévy P, Thomas JL, Lardenois T, Lacrosse P, Sarrazin E, de Andreis NR, Wonner M. Azithromycin and hydroxychloroquine accelerate recovery of outpatients with mild/moderate COVID-19. Preprints. 2020. 10.20944/preprints202005.0486.v1.
- 34.Garcia-Cremades M, Solans BP, Hughes E, Ernest JP, Wallender E, Aweeka F, Luetkemeyer AF, Savic RM. Optimizing hydroxychloroquine dosing for patients with COVID-19: an integrative modeling approach for effective drug repurposing. Clin Pharmacol Ther. 2020 doi: 10.1002/cpt.1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Smit C, Peeters MY, van den Anker JN, Knibbe CA. Chloroquine for SARS-CoV-2: implications of its unique pharmacokinetic and safety properties. Clin Pharmacokinet. 2020;18:1. doi: 10.1007/s40262-020-00891-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chen J, Liu D, Liu L, et al. A pilot study of hydroxychloroquine in treatment of patients with common coronavirus disease-19 (COVID-19). J Zhejiang Univ (Med Sci). Published online March 6, 2020. 10.3785/j.issn.1008-9292.2020.03.03.
- 37.Huang M, Tang T, Pang P, Li M, Ma R, Lu J, Shu J, You Y, Chen B, Liang J, Hong Z. Treating COVID-19 with chloroquine. J Mol Cell Biol. 2020;12(4):322–325. doi: 10.1093/jmcb/mjaa014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gao J, Tian Z, Yang X. Breakthrough: chloroquine phosphate has shown apparent efficacy in treatment of COVID-19 associated pneumonia in clinical studies. Biosci Trends. 2020 doi: 10.5582/bst.2020.01047. [DOI] [PubMed] [Google Scholar]
- 39.Borba MGS, Almeida Val F, Sampaio VS, et al. Chloroquine diphosphate in two different dosages as adjunctive therapy of hospitalized patients with severe respiratory syndrome in the context of coronavirus (SARS-CoV-2) infection: preliminary safety results of a randomized, double-blinded, phase IIb clinical trial (CloroCovid-19 Study). medRxiv. April 2020. 10.1101/2020.04.07.20056424.
- 40.Zou L, Ruan F, Huang M, Liang L, Huang H, Hong Z, Yu J, Kang M, Song Y, Xia J, Guo Q. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N Engl J Med. 2020;382(12):1177–1179. doi: 10.1056/NEJMc2001737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sarayani A, Cicali B, Henriksen CH, Brown JD. Safety signals for QT prolongation or Torsades de Pointes associated with azithromycin with or without chloroquine or hydroxychloroquine. Res Soc Adm Pharm. 2020 doi: 10.1016/j.sapharm.2020.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Boulware D. Post-exposure prophylaxis/preemptive therapy for SARS-coronavirus-2 (COVID-19 PEP). Minneapolis: University of Minnesota. https://clinicaltrials.gov/ct2/show/NCT04308668. Accessed 27 Apr 2020.
- 43.Lee SH, Son H, Peck KR. Can post-exposure prophylaxis for COVID-19 be considered as one of outbreak response strategies in long-term care hospitals? Int J Antimicrob Agents. 2020;17:105988. doi: 10.1016/j.ijantimicag.2020.105988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pagliano P, Piazza O, De Caro F, Ascione T, Filippelli A. Is hydroxychloroquine a possible postexposure prophylaxis drug to limit the transmission to healthcare workers exposed to coronavirus disease 2019? Clin Infect Dis. 2020 doi: 10.1093/cid/ciaa320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Principi N, Esposito S. Chloroquine or hydroxychloroquine for prophylaxis of COVID-19. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30296-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yen YT, Liao F, Hsiao CH, Kao CL, Chen YC, Wu-Hsieh BA. Modeling the early events of severe acute respiratory syndrome coronavirus infection in vitro. J Virol. 2006;80(6):2684–2693. doi: 10.1128/JVI.80.6.2684-2693.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gil-Moles M, Basu U, Büssing R, Hoffmeister H, Türck S, Varchmin A, et al. Gold metallodrugs to fight the corona virus: inhibitory effects on the SpikeACE2 interaction and on PLpro protease activity by auranofin and gold organometallics. ChemRxiv. 2020. Preprint. 10.26434/chemrxiv.12488390.v1. [DOI] [PMC free article] [PubMed]
- 48.Shytaj IL, Chirullo B, Wagner W, Ferrari MG, Sgarbanti R, Della Corte A, LaBranche C, Lopalco L, Palamara AT, Montefiori D, Lewis MG. Investigational treatment suspension and enhanced cell-mediated immunity at rebound followed by drug-free remission of simian AIDS. Retrovirology. 2013;10(1):71. doi: 10.1186/1742-4690-10-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rothan HA, Stone S, Natekar J, Kumari P, Arora K, Kumar M. The FDA-approved gold drug Auranofin inhibits novel coronavirus (SARS-COV-2) replication and attenuates inflammation in human cells. Virology. 2020 doi: 10.1016/j.virol.2020.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.