Abstract
This paper examines the impacts of COVID-19 on the multifractality of gold and oil prices based on upward and downward trends. We apply the Asymmetric Multifractal Detrended Fluctuation Analysis (A-MF-DFA) approach to 15-min interval intraday data. The results show strong evidence of asymmetric multifractality that increases as the fractality scale increases. Moreover, multifractality is especially higher in the downside (upside) trend for Brent oil (gold), and this excess asymmetry has been more accentuated during the COVID-19 outbreak. Before the outbreak, the gold (oil) market was more inefficient during downward (upward) trends. During the COVID-19 outbreak period, we see that the results have changed. More precisely, we find that gold (oil) is more inefficient during upward (downward) trends. Gold and oil markets have been inefficient, particularly during the outbreak. The efficiency of gold and oil markets is sensitive to scales, market trends, and to the pandemic outbreak, highlighting the investor sentiment effect.
Keywords: Gold, Crude oil, High frequency, COVID-19, Hurst exponent, A-MF-DFA
1. Introduction
The COVID-19 outbreak has resulted in over 17.2 million confirmed cases and over 670,000 deaths worldwide. This malignant virus has caused severe damage not only to the global healthcare systems but also to the world economy. This pandemic has more negative repercussions than the global financial crisis (GFC) in 2008 or even the Severe Acute Respiratory Syndrome coronavirus 2 (SARS-COV-2). During the COVID-19 outbreak, oil prices experienced a spectacular fall in April 2020. The US crude futures fell to negative values, crashing from $18 a barrel to -$38, for the first time in history, as stockpiles overwhelmed storage facilities, which left oil investors reeling.1 On the other hand, gold prices have experienced a smaller decline with the outbreak of COVID-19, but this was followed by an upside trend starting in February 2020. Evidently, the global uncertainty tied to this COVID-19 outbreak has significantly perturbed the price dynamics of crude oil and gold. The behavioral finance theory documents that investment decisions in such uncertain periods are strongly affected by the investor sentiment. For example, Icheck and Marinč (2018) argue that the 2014–2016 Ebola outbreak events combined with intense media coverage influenced investors’ strategies significantly.
Commodity markets are vulnerable to not only the law of demand and supply, macroeconomic variables (exchange rates and inflation, etc.), and political events (Wang et al., 2011), but also to pandemic factors (Icheck and Marinč, 2018). The relationship between oil and gold can be explained through inflation channel. The general price level increases when the crude oil prices rise because oil is a principal input of several goods and services therefore the cost of production rises (Hunt, 2006; Hooker, 2002). When the inflation increases, the gold price up since gold is also a good. Thus, gold can serve as a protection instrument (or hedge asset) against inflation (Jaffe, 1989). Melvin and Sultan (1990) explain the linkages between gold and oil markets via the export revenue channel. Specifically, gold is an essential portion of the international reserve portfolio of several economies, including the oil-producer economies. The authors document that if some shock leads to expectations of official gold purchases, the expected future price of gold will rise. When oil price rises, oil exporters revenues from oil rise. A vast empirical literature has examined the relationship between oil and gold (Cashin et al., 1999; Lescaroux, 2009; Singhal et al., 2019; Soytas et al., 2009). Therefore, the market dynamics show important variations during this new pandemic that affect all the financial and commodity markets worldwide. Accordingly, in this paper, we aim to examine the asymmetric multifractality of both gold and oil prices using a high frequency dataset on contract for differences (CFDs) covering periods both pre- and during COVID-19 outbreak.
Analyzing the fractal features of non-stationary price series is generally a complex task. Therefore, the development of various methods (R/S analysis, detrended fluctuation analysis, detrended moving average method, wavelet based fluctuation analysis, wavelet transform modulus maxima, multifractal detrended cross-correlation analysis, multifractal detrended fluctuations analysis, and asymmetric multifractal detrended fluctuations analysis) to capture this phenomenon confirms their importance for market participants. Accordingly, the presence of multifractality contradicts the efficient market hypothesis and reveals the predictability of future prices, which is of utmost importance to investors, regulators, and policy makers.
The literature on the symmetric multifractality of commodity markets, in particular oil and gold, is extensive. Beckers (1984) examine the efficiency of the gold option markets and find evidence against market inefficiency. Ball et al. (1985) find price clustering in gold futures. Using dynamic factor analysis, Bertus and Stanhouse (2001) show rational speculative bubbles in gold futures market. Narayan et al. (2010) show that gold is used a protection asset against inflation and that oil can be used to forecast and predict gold prices, suggesting that both markets are inefficient.
Gu et al. (2010) studied the multifractality of both West Texas Intermediate (WTI) and Europe Brent oil markets and found that these markets become more efficient for the long term. In addition, the Iraq war had no effect on the time scale behavior of crude oil price returns. Moreover, the highest degree of multifractality in oil markets was observed during Iraq war. Using both multifractal detrended fluctuation analysis (MF-DFA) and multifractal singular spectrum analysis (MF-SSA) method, He and Cehn (2010) found that WTI and Brent oil show a multifractal behavior and that multifractality is affected by the non-linear dynamic correlations. Pal et al. (2014) use the multifractal detrended cross-correlation method to examine the cross-correlations between gold, oil, and foreign exchange rates. They find evidence of multifractal cross-correlation between these markets. Wang et al. (2010) examine the multifractality in Chinese crude oil futures and their correlations with WTI and Europe Brent crude oil. The authors find that the Chinese crude oil price returns exhibit significant multifractal features which are weaker relative to those of Brent but stronger than WTI oil. Furthermore, the risk of the Chinese crude oil futures market is less than both the WTI and Brent oil markets. Using the MF-DFA approach, Wang et al. (2011) find the multifractal nature of the gold market in smaller time scales, which is attributable to fat-tail distributions. Both fat-tail distribution and long-range correlations result in multifractality for a larger time scale. Using the same methodology, Mali and Mukhopadhyay (2014) examine the gold consumer price index (CPI) and the market trend in three emerging countries (China, India, and Turkey) and find significant multifractality, which is explained by the long-range correlations.
Using permutation entropy, permutation statistical complexity and Fisher Information Measure, Bariviera et al. (2019) examine the variability of informational efficiency of gold prices during economic distress period. The results exhibit strong persistence of volatility and the market inefficiency is sensitive to political and economic crises. Ntim et al. (2015) investigate the informational efficiency in its weak-from version of 28 gold markets using variance-ratios and martingale sequence difference hypotheses. The results show significant variabilities in the efficiency level. Moreover, they show that macro variable changes reduce the likelihood of rejecting the efficiency hypothesis. In addition, the emerging markets are more inefficient than the developed markets. Ghazani and Ebrahili (2019) test the adaptive market hypothesis (AMH) for Brent and West Texas Intermediate (WTI) oil market. Tabak and Cajueiro (2007) and Charles and Darne (2009) find evidence of time-varying efficiency. Charles et al. (2015a,b) find that the return predictability of precious metals is time varying and that the efficiency degree of gold and silver enhance over time. Baruník et al. (2012) shows that technical indicators, diffusion indices, and economically motivated restrictions in predictive regressions do not provide accurate predictability of gold excess returns. Lucey (2011), Baur et al. (2016), Peirdzioch et al. (2014) have also explored the predictability of gold prices. Charles et al., 2015a, Charles et al., 2015b examine the efficiency of main precious metals (gold, silver, and platinum) have become an important part of investment portfolios for individuals as well as for institutions. This paper examines the weak-form efficiency of precious metal markets, using the automatic portmanteau and variance ratio tests. It is found that return predictability of these markets has been changing over time, depending on the prevailing economic and political conditions. The return predictability of gold and silver markets has been showing downward trends, implying that the degree of the weak-form efficiency of these markets has been gradually improving. In particular, the gold market has been highly efficient recently, showing the highest degree of market efficiency among the three precious metal markets.
Motivated by the lack of studies on asymmetrical multifractality in commodity markets and considering the importance of the COVID-19 outbreak on global financial markets, we examine the impact of COVID-19 on asymmetric multifractality of gold and oil prices and contribute to the existing literature in various, novel ways. First, to the best of our knowledge, this is the first paper that examines the multifractality during downward and upward trends of crude oil and gold CFD prices. In fact, commodity prices have experienced phases of upside and downside trends during our sample period; thus, it is essential to distinguish these trends and their multifractality states.
Second, we analyze the asymmetric multifractality before and during the times of COVID-19 outbreak using 15-min data that covers the period from April 23, 2018 to April 24, 2020. We not only cover the COVID-19 phase but also cover it at an intraday high-frequency scale. Considering the fact that financial market trading is dominated by algorithmic and especially high-frequency traders, we believe that a high-frequency perspective is a must in this research. Eventually, our analysis provides a full picture on the price dynamics of two strategic commodity assets (gold and oil).
Third, oil and gold play an essential role, not only in financial markets but also in the real economy and policy design. For instance, crude oil is a vital and strategic resource for the economy. In addition, it is an important input for many goods and services, and the variations of oil prices can affect corporations’ cash flows, which affect the stability of financial markets. Gold is a store of value and is used for investment and hedging purposes. In fact, gold is a safe haven asset in financial markets (Baur and Lucey, 2010), energy markets (Reboredo, 2013), and during inflation growth (Aye et al., 2017) and is further used by many central banks as an asset in their reserves. Moreover, the demand for crude oil and gold has been increasing over the last two decades, particularly due to growing emerging market economies like China.
Investors reactions and anticipations change based on upward (positive returns) and downward (negative returns) trends. The asymmetric correlations are attributable to the asymmetric response to economic news announcements which influences the portfolio diversification and risk management (Ang and Chen, 2002; Bae et al., 2003; Charles et al., 2015; Longin and Solnik, 2001). Thus, the price behavior and investor risk appetite are different during upward and downward trends. This fact has been confirmed by the empirical literature that shows the importance of examining the asymmetries in the scaling behavior of time series (Alvarez-Ramirez et al., 2009). The overheated bull market with false hope (irrationality in long position) and the crisis-phase bearish market with excessive fears (irrationality in short position) may be the source of inefficiency (Lee et al., 2018). Therefore, testing the asymmetric market efficiency by dividing the commodity market according to the market trends in which the commodity asset price rises or falls is important for market development and the resource allocation (Lee et al., 2017). Alvarez-Ramirez and Rodriguez (2015) find significant difference in inefficiency during oil price downturns and upturns. Moreover, they demonstrate that negative price trends exhibit less persistence than positive price trends. Gu et al. (2010) use the cross-correlation analysis and the nonlinear Granger causality analysis to examine the evolving relationship between efficiency and multifractality of crude oil market. The authors find that the inefficiency and multifractality of the oil returns interact positively in a nonlinear mechanism, suggesting an inverse relationship between the degree of efficiency and the multifractality degree. Gallais-Hamonno et al. (2015) show that the efficiency is related to the type of assets rather than the market ’legal status.
Fourth, we utilize a novel method to perform our analysis. In particular, we use the asymmetric MF-DFA (A-MF-DFA) methodology developed by Cashin et al. (1999). Detrended fluctuations analysis (DFA) is able to identify only mono-fractal scaling properties (Kaufmann and Winters, 1989). A-MF-DFA is an extension of the symmetric MF-DFA approach developed by Kaufmann and Winters (1989). Despite its advantage relative to DFA, the MF-DFA examines the multifractality in price dynamics assuming that the effects of downside trends are identical to the upside trends on price dynamics. Thus, the MF-DFA assumes that asset prices behave symmetrically during upward and downward periods. However, the energy markets respond differently to bad news and good news, which have different effects on stock price returns and volatility. Thus, accounting for asymmetric upward and downward movements to optimize fund allocations and to predict future price returns is crucial for market participants. Since good and bad news have different effects on the extent of the movements of market returns and volatility, the A-MF-DFA is flexible to capture this asymmetry in the scaling behavior in a return series with upside and downside trends (Alvarez-Ramirez et al., 2009).
Finally, we apply the A-MF-DFA method to high frequency data to obtain accurate information on the asymmetric multifractality of crude oil and gold before and during the COVID-19 outbreak. Due to the timing of the outbreak, the COVID-19 phase does not allow us to perform a robust analysis from a daily data perspective due to having a small sample. However, our high-frequency observations provide us enough samples both pre- and during COVID-19 outbreak; therefore, we are able to obtain more precise results.
We notice that gold and oil prices exhibit asymmetric and leptokurtic behaviors, which are the main source of multifractality (Baruník et al., 2012; Green et al., 2014). The analysis of multifractality is fundamental for investors to identify the specific price patterns and predict the future prices, contradicting the efficiency hypothesis (Cajueiro and Tabak, 2004; Tabak and Cajueiro, 2007; Wang et al., 2010). The multifractality evolves over time and depends whether good or bad information is transmitted into the markets. Thus, disentangling upside multifractality and downside multifractality is crucial for portfolio management as the price responsiveness to bad/good news is asymmetric (Mensi et al., 2019). The A-MF-DFA investigates the asymmetries in the scaling behavior of time series. Specifically, it evaluates the multifractality in different correlations and can identify the asymmetry of scaling behavior in time series with uptrends and downtrends. Alvarez-Ramirez et al. (2009) find that the scaling behavior depends on the signal trend (whether it is positive or negative), indicating the presence of different scaling behaviors.
The results show that the multifractality is different during upward and downward trends for both commodities, and it increases with an increase in fractality scale. Moreover, the multifractality is especially higher in the downside (upside) trend for Brent oil (gold), and this excess asymmetry is more accentuated during the COVID-19 outbreak. Both gold and oil futures markets are more inefficient during this time. Before the outbreak, the gold market was more inefficient during downward trends, whereas oil was more inefficient during upward trends. During the COVID-19 outbreak period, gold (oil) is more inefficient during upward (downward) trends. It is worth noting that the inefficiency degree for both markets is higher during the outbreak compared to the pre-COVID-19 period. In summary, the efficiency of gold and oil markets is sensitive to scales, market trends, and to the outbreak, highlighting the investor sentiment effect. These results have implications for investors and policy makers.
The remainder of this study is organized as follows. Section 2 discusses the data. Section 3 explains the methodology. Section 4 reports and analyzes the empirical results. Finally, Section 5 concludes the paper.
2. Data
We consider the CFD prices for two essential commodities, Gold and Brent crude oil (Brent). We use the closing price of 15-min interval intraday data that covers the full two-year period from April 23, 2018 to April 24, 2020. The sample is divided further into two periods: (i) before COVID-19, from April 23, 2018 to November 30, 2019, and (ii) during COVID-19, from December 1, 2019 to April 24, 2020. Our breakpoint is December 1, 2019, when COVID-19 spread in Hubei Province and then spread to 212 countries where the United States and European Union alongside Iran are the most affected. The source of our data is Dukascopy Bank SA, a Swiss forex bank and an ECN broker with its headquarters in Geneva and branch offices in Hong Kong, Riga, Kiev, Moscow, Kuala Lumpur, Shanghai, Dubai, and Tokyo. The Bank provides a platform where investors can trade spot FX, metals, binary options, contract for differences (CFDs) on bonds, commodities, indexes, stocks, ETFs, and cryptocurrencies. Dukascopy Bank, which was founded in 2004, has a regulated capital of about CHF 40mn and provides trading services based on equal trading rights and a transparent pricing environment.
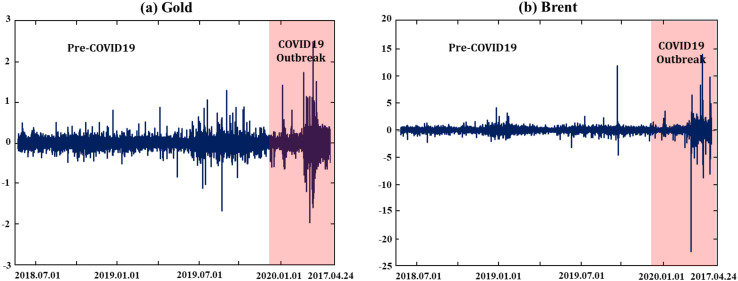
We calculate continuously compounded intraday returns by taking the difference in the logarithm percentage of two consecutive prices at 15-min intervals. Fig. 1 displays the dynamics of 15-min returns of (a) Gold and (b) Brent over the sample period. The graphical evidence shows a significant peak during the COVID-19 period in both markets, but it is more pronounced for Brent oil. More importantly, the volatility clustering is significant during the COVID-19 period compared to the pre-COVID-19 period. This result suggests that price dynamics and market volatility are different for the two sub-periods.
Fig. 1.
The dynamics of intraday returns of gold and Brent crude oil.
Table 1 presents the descriptive statistics of 15-min price returns of oil and gold for the whole period, pre-COVID-19 and during COVID-19 outbreak periods. The average return for the gold market is positive for the three periods, whereas it is negative for Brent crude oil. More interestingly, the average returns for gold are higher during the COVID-19 outbreak than pre-COVID-19 outbreak period. In addition, the loss in the oil market is high during the COVID-19 outbreak period than before the COVID-19 period. We note that the negative oil price returns for the pre-COVID period are explained by the great oil bust that started in mid-2014 and is accentuated by the new outbreak. We also notice that both oil and gold markets are more volatile during the COVID-19 outbreak period. In addition, the oil market is more volatile than the gold market for different market episodes. This result highlights the importance of this metal for diversification strategies. The skewness and kurtosis values are different from zero and three respectively, denying the Gaussian distribution for the different periods and indicating asymmetric and leptokurtic behaviors. The Jarque-Bera statistics test formally rejects the null hypothesis of Gaussian distributions. The unit root (Augmented Dickey-Fuller (ADF) and Phillips-Perron (PP)) and the stationary (Kwiatkowski-Phillips-Schmidt-Shin (KPSS)) test shows that the gold and oil price return series are stationary for the whole period, pre-COVID-19, and during the COVID-19 outbreak.
Table 1.
Descriptive statistics and unit root tests for intraday returns.
| Gold |
Brent |
|||||
|---|---|---|---|---|---|---|
| Whole period | Pre-COVID19 | COVID19 Outbreak | Whole period | Pre-COVID19 | COVID19 Outbreak | |
| Mean | 0.0005 | 0.0002 | 0.0017 | −0.0029 | −0.0005 | −0.0124 |
| Maximum | 2.6084 | 1.3623 | 2.6084 | 14.286 | 12.094 | 14.286 |
| Minimum | −2.0684 | −1.7639 | −2.0608 | −22.945 | −4.7336 | −22.945 |
| Std. Dev. | 0.0929 | 0.0718 | 0.1512 | 0.3576 | 0.2190 | 0.6725 |
| Skewness | 0.2405 | −0.0091 | 0.2693 | −4.0366 | 4.6895 | −3.6928 |
| Kurtosis | 57.541 | 34.041 | 34.728 | 566.70 | 300.38 | 215.47 |
| Jarque Bera | 5,854,950*** | 1,523,646*** | 389,400*** | 5.56e+08*** | 1.24e+08*** | 14,631,118*** |
| ADF | 224.60*** | −198.16*** | −101.03*** | −101.92*** | −184.25*** | −45.148*** |
| PP | 224.57*** | −198.13*** | −101.01*** | −204.69*** | −184.27*** | −90.791*** |
| KPSS | 0.3421 | 0.3339 | 0.0488 | 0.5233 | 0.0422 | 0.2453*** |
Notes: ADF and PP stand respectively for Augmented Dickey and Fuller and Philipps-Perron tests for unit root. KPSS refers to Kwiatkowski Philipps Schmidt Shin test for stationarity. *** indicates the rejection of null hypothesis at the 1% significance level.
3. Methodology
To explore the asymmetric multifractal scaling behavior, we divide the financial time series and its profile into nonoverlapping sub-time series of length that are selected from 5 to , based on the recommendations of Pierdzioch et al. (2014). Since may not be a multiple of , the length of the last segment may be shorter than . To consider the remainder of , we also divide by starting from the other end of . Thus, we obtain a sub-time series for . The sub-time series for can be obtained in the same manner. The sub-time series of is denoted by , where indicates the element of .
For and , we estimate the linear fit and , which represent the linear trends for the sub-time series. is used to determine the direction of the trend of via slope , while is used to detrend . We then determine the fluctuation functions as follows:
| (1) |
The directional -order average fluctuation functions are calculated by
| (2) |
| (3) |
where and denote the upward and downward -order average fluctuation functions, respectively. Assuming that for all , then .
From the fluctuation functions of Eqs. (1), (2), (3), we calculate the scaling or power-law relationship, which is defined as
| (4) |
where , , and denote the overall, upward, and downward scaling exponents respectively. The scaling behavior of the fluctuations in Eq. (4) is determined by analyzing the log-log plots of , , and versus for each value . , , and can be estimated by the ordinary least squares method based on the logarithmic form. Furthermore, the correlation in the time series is persistent or long memory when , whereas the correlation is anti-persistent when . If , the time series follows the random walk process. Similarly, if , the correlation in the time series is symmetric, whereas if , the correlation in the time series is asymmetric. The asymmetric scaling behavior indicates that the correlations in the time series are different with respect to positive and negative trends.
4. Empirical analysis results
4.1. Analysis of multifractality in gold and oil
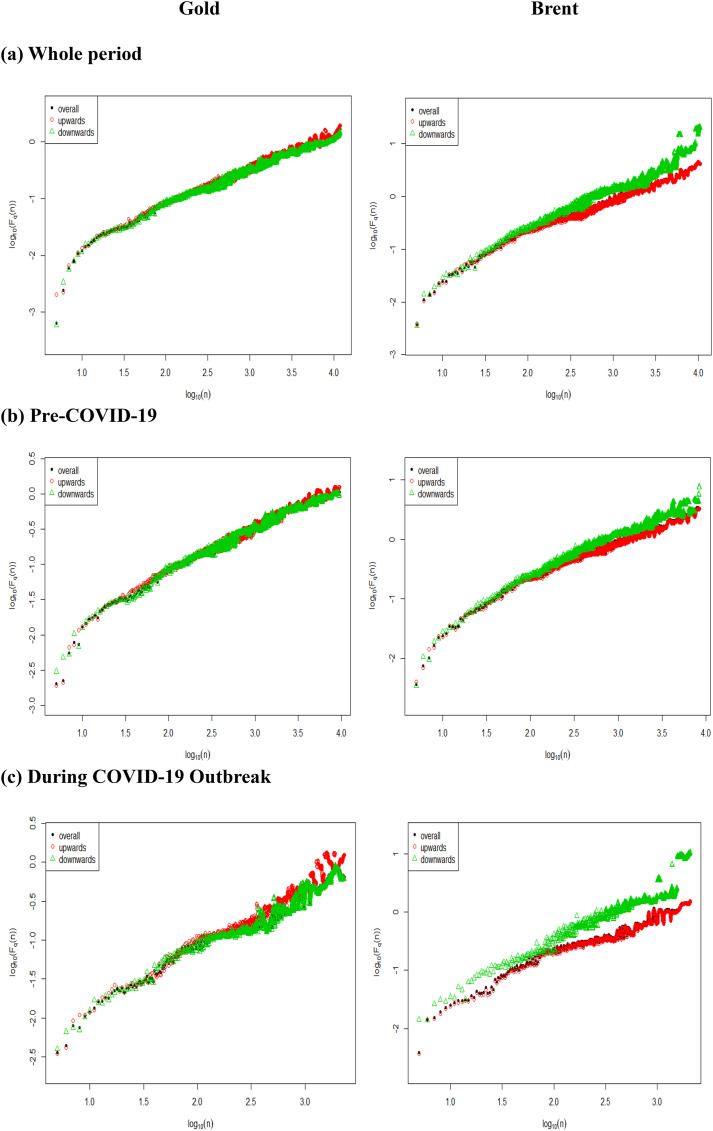
Fig. 2 depicts the trajectory of the A-MF-DFA functions versus the time scale of both gold and oil. We find that the multifractality is different during upward and downward trends. In addition, the multifractality increases with scale rises. We notice that the extent of downside multifractality is higher than upside multifractality for Brent oil, especially during the COVID-19 outbreak. For gold, the upside multifractality is higher than multifractality during the COVID-19 outbreak period. The results show evidence of an asymmetric multifractality feature for both markets especially during the pandemic outbreak period. This result is consistent with the findings of Telli and Chen (2020) where they found that gold demonstrates different regimes with different characteristics of multifractality. More interestingly, the asymmetric multifractality of Brent oil is more important than that of gold because the magnitude of the deviation from symmetry is clear for various scales. This difference is explained by the different characteristics of each market. In particular, the oil market is more uncertain, unstable, and volatile than the gold market.
Fig. 2.
Asymmetric MF-DFA functions F2(n) vs. the time scale (). Note: This figure represents the plot of 2(2()) vs. 2() for each intraday return series.
The excess asymmetry in multifractality ()is defined as follows:
| (5) |
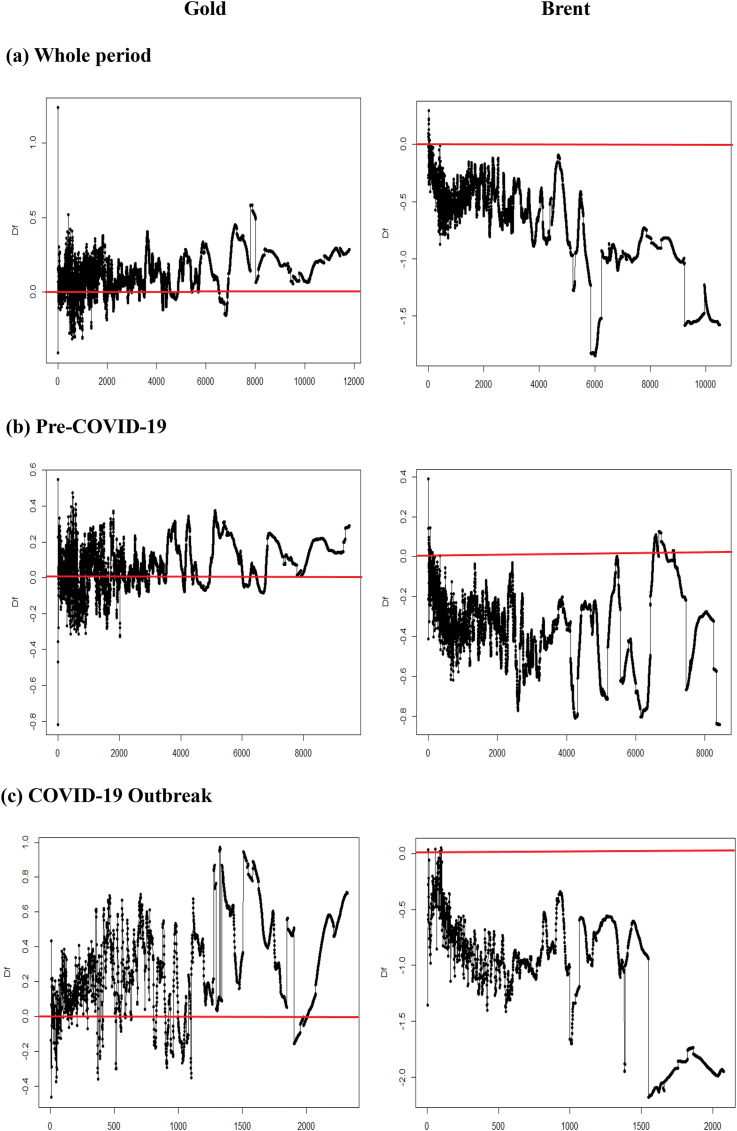
The evolving excess asymmetries in multifractality for gold and oil prices are displayed in Fig. 3 . The asymmetric behavior of the gold and oil prices is higher when the absolute value of excess multifractality is higher. If is zero, gold and oil exhibit symmetric multifractality, whereas if is different than zero, the commodity market experiences asymmetric multifractality that increases with the rise (in absolute value) of values. More importantly, the cross-correlation exponent is higher when the return series has a positive trend than when it has a negative trend when is positive, and vice versa. A close inspection of Fig. 4 reveals a significant excessive asymmetric multifractality for gold and oil. Moreover, the extent of excessive asymmetric multifractality is not the same between two markets and before or during the COVID-19 outbreak periods.
Fig. 3.
Excess asymmetry in multifractality for intraday returns. Note: The x-axis represents the time scale n, which varies from 5 to ⁄4 (where N is the number of observations in the time series). The y-axis represents the difference between 2(()) and 2(()).
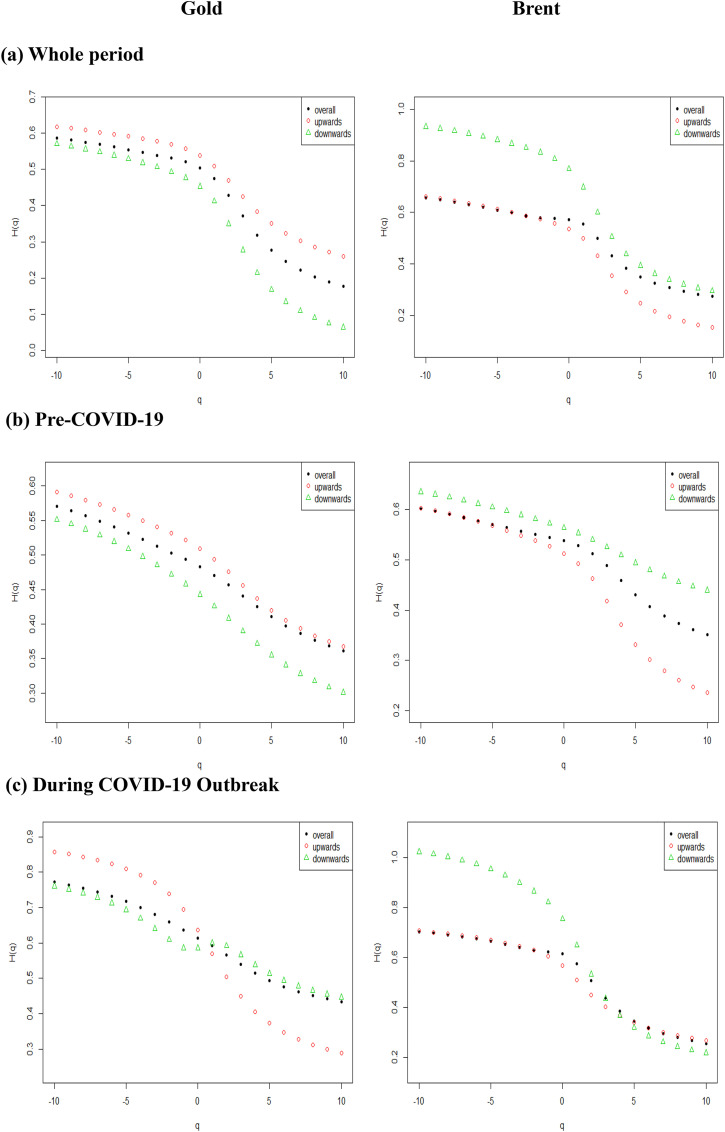
Fig. 4.
Plots of Hurst exponents for commodity markets. Note: This figure shows the trend of overall H(), upwards (), and downwards () versus (=-10, -9, …, 9, 10).
We find that for oil, the excess asymmetry in multifractality has negative values in most periods. This result shows that the multifractality is much stronger in downward price movements. In addition, the excess asymmetry in multifractality is more accentuated during the COVID-19 outbreak, as demonstrated by the coefficient in the y-axis. As for gold, the result exhibits stronger multifractality in upward price movements. Like oil, the excess multifractality is more apparent during the COVID-19 outbreak. These excess asymmetries in multifractality show that both gold and oil markets are inefficient, in particular during the COVID-19 outbreak.
Fig. 4 displays the Hurst exponent for gold and oil for overall , downward , and upward trends. As shown, the Hurst exponent values vary across scales, market trends, and before and during the COVID-19 outbreak. Looking at gold, we observe that the deviation of the upside Hurst exponent value from the downside Hurst exponent is larger for positive scales. In addition, along scales, the values of upside Hurst is larger than downside Hurst for the whole period and pre-COVID-19 period. During the COVID-19 outbreak period, we have two different results. Specifically, we observe that the upward Hurst exponent is higher than the downward Hurst exponent for negative scales, while the inverse case is observed for positive scales. These results are consistent with those of Charles et al., 2015a, Charles et al., 2015b who find dynamic return predictability of precious metals (gold, silver, and platinum). They also show that the return predictability of gold and silver shows a downside trend, indicating improve in efficiency level.
For Brent crude oil, we also find significant deviations of the Hurst exponent during upward and downward trends, over scales and pre- and during COVID-19. Like gold, the oil Hurst exponent shows a downside trend with a rising scale. For the whole period, the large deviation was observed for negative scales, where the Hurst exponent under the downward trend is superior to those under upward trends. The extent of deviation decreases for positive scales. By comparing the period before and during the outbreak, we show that the upward Hurst exponent is larger than the downward Hurst exponent pre-COVID-19 outbreak, particularly for positive scales. The deviation exists for negative scales but is less important than positive scales. However, the deviation under negative scales is more important during COVID-19 outbreak, whereas for positive scales, we find that the downward and upward Hurst exponent trends are similar. The graphical evidence also displays that both markets show high persistence for the lowest scale and during the COVID-19 period compared to the pre-COVID19 period. In summary, the efficiency of gold and oil markets is sensitive to scales, market trends, and to the outbreak, highlighting the investor sentiment effect.
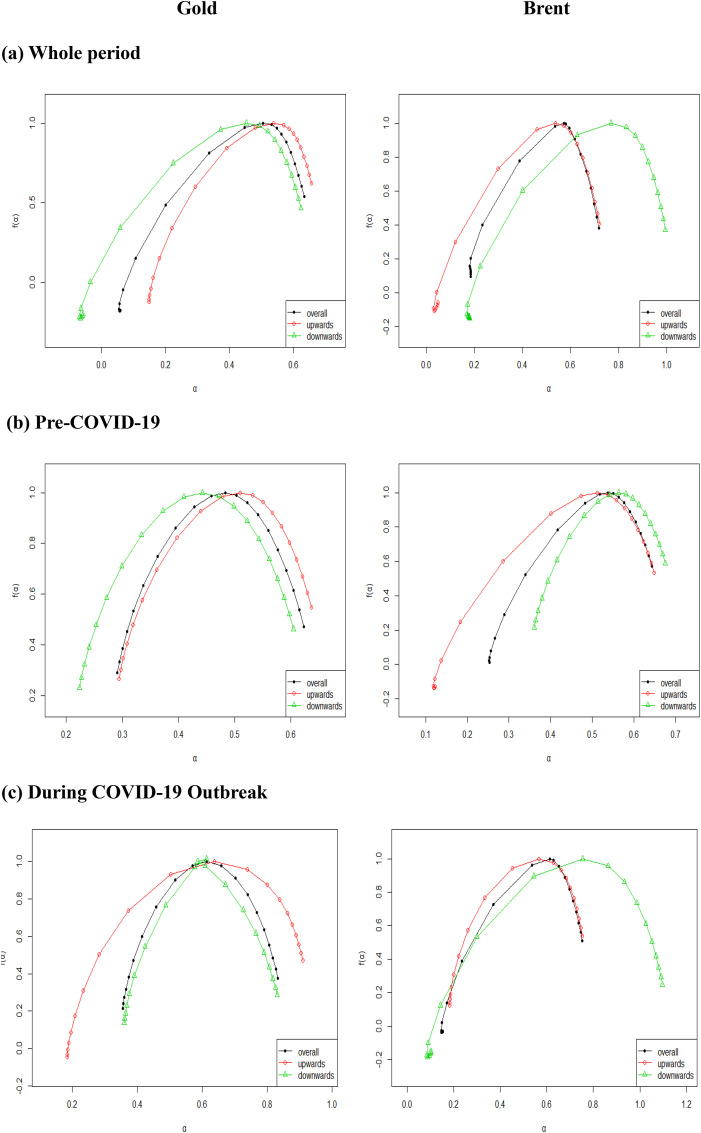
Fig. 5 displays the multifractal spectrum for overall, downward, and upward trends. The results reveal that the multifractality of gold has a very large width for the downward trend, which is also larger than those for the overall and upward trends. However, during the COVID-19 outbreak, we observe that the upward multifractal spectrum has a larger width than the downside and overall multifractal spectrum. In addition, oil has a larger width than gold for the different periods.
Fig. 5.
Asymmetric multifractal spectrum.
4.2. Analysis of dynamic efficiency in gold and oil
Following the method of Wang et al. (2009), we quantify the level of inefficiency by utilizing the market deficiency measure defined as follows:
| (6) |
It is worth noting that a commodity market is efficient if all fluctuations, including small and large , follow a random walk process. The value will therefore be zero for an efficient market and high for an inefficient market.
Table 2 summarizes the results of MDM for gold and oil assets for the whole period, pre-COVID-19, and during COVID-19 outbreak, as well as for different market trends to account for the asymmetric case. For the whole period, we find that the gold and oil markets are more inefficient during the downward trend than for both overall and upward trends. In addition, Brent oil is more inefficient than the gold market. Before the outbreak, the gold market was more inefficient during downward trends. This result is similar during the whole period despite inefficiency decreasing. The oil market is more inefficient during the upward trend. During the COVID-19 outbreak period, we see that the results are different from the pre-COVID-19 period. More precisely, we find that gold (oil) is more inefficient during upward (downward) trends. More importantly, both markets became more inefficient during the outbreak compared to the pre-COVID-19 period. Oil is more inefficient than gold for different sub-periods.
Table 2.
Measurement of market efficiency using MDM.
| Gold | Brent | |||||
|---|---|---|---|---|---|---|
| Overall | Upward | Downward | Overall | Upward | Downward | |
| Whole period | 0.2051 | 0.1788 | 0.2533 | 0.1913 | 0.2533 | 0.3182 |
| Pre-COVID19 | 0.1047 | 0.1122 | 0.1254 | 0.1248 | 0.1835 | 0.0979 |
| During COVID19 Outbreak | 0.1688 | 0.2844 | 0.1571 | 0.2231 | 0.2858 | 0.4019 |
Note: The bold values indicate the most inefficient market for each intrady return series.
We strengthen our analysis by robustness tests. First, we test the null hypothesis that the Hurst exponent under scale 2 equals 0.5, i.e., we test the random walk () against its alternative hypothesis (). Table 3 reports the estimation results of this test. The results reject the null hypothesis of parameter homogeneity across different market conditions for the overall and downward trend for gold, and for the downward trend for Brent crude oil.
Table 3.
-Test results of the null hypothesis for..
| Gold |
Brent |
|||||
|---|---|---|---|---|---|---|
| Overall | Upward | Downward | Overall | Upward | Downward | |
| Whole period | −2.1801** [0.041] | −0.7614 [0.455] | 3.2618*** [0.003] | −0.1190 [0.906] | −1.2242 [0.235] | 2.9448*** [0.008] |
| Pre-COVID19 | 1.8012 [0.086] | −0.5256 [0.605] | −3.5857*** [0.001] | 0.1866 [0.853] | −1.4873 [0.152] | 3.4613*** [0.003] |
| During COVID19 Outbreak | 4.0911*** [0.000] | 2.0123 [0.057] | 4.4541*** [0.000] | 0.5674 [0.576] | 0.3477 [0.731] | 2.2564** [0.035] |
Notes: The generalized Hurst exponent in the case of , i.e., , is identical to the standard Hurst exponent, which can be used to test the long-memory property of a time series. ** and *** denotes the rejection of the null hypotheses at the 5% and 1% significance levels.
Second, we apply the mean and variance equality test to check for the equality of the slopes for downward and upward trends. We carry out the Singhal et al. (2019) and Aye et al. (2017) mean equality tests of, and two variance equality tests of Levene (1960) and Brown and Forsythe (1974). The results are reported in Table 4 and show evidence of significant mean differences for the Hurst exponent for different trends and sub-periods. As for the results of variance equality tests, we do not reject the null hypothesis of variance equality during overall, upward, and downward trends and before and during outbreak periods.
Table 4.
Robustness tests for heterogeneity of slopes.
| Equality mean tests |
Equality variance tests |
||||
|---|---|---|---|---|---|
|
Satterthwaite-Welch |
Anova |
Bartlett |
Levene |
Brown-Forsythe |
|
| Gold | |||||
| Whole period | 516.56 [0.000] | 128.41 [0.000] | 0.2444 [0.885] | 0.0398 [0.961] | 0.0437 [0.957] |
| Pre-COVID19 | 133.77 [0.000] | 121.04 [0.000] | 1.1383 [0.888] | 0.4636 [0.761] | 0.4241 [0.789] |
| During COVID19 Outbreak |
91.080 [0.000] |
81.375 [0.000] |
0.7859 [0.852] |
0.6252 [0.608] |
0.3019 [0.823] |
| Brent | |||||
| Whole period | 139.14 [0.000] | 143.82 [0.000] | 2.1693 [0.538] | 1.0275 [0.405] | 0.7801 [0.521] |
| Pre-COVID19 | 392.61 [0.000] | 124.35 [0.000] | 5.5403 [0.236] | 1.6761 [0.204] | 1.5644 [0.231] |
| During COVID19 Outbreak | 150.72 [0.000] | 144.22 [0.000] | 4.0957 [0.393] | 1.5952 [0.223] | 1.1117 [0.385] |
Notes: This table presents the mean equality tests (Satterth-Welch and Anova statistics) and the variance equality tests (Bartlett, Levene, and Brown-Forsythe) for upward and downward Hurst exponents.
5. Conclusions
Wuhan, the sprawling capital of central China's Hubei province, is the area where COVID-19 began to spread. Along with causing death worldwide, this virus has paralyzed the worldwide economic cycle. Financial and commodity markets showed huge losses since the outbreak. Inevitably, the outbreak also created structural changes in the pricing dynamics for various markets, with an emphasis on commodity markets due to their interlinkages with the real economy. In this study, we focus on a particular aspect of these pricing dynamics, namely asymmetric multifractality and how it is affected by the COVID-19 outbreak.
By applying the asymmetric MF-DFA method on a high-frequency dataset of gold and crude oil futures, we reveal that the multifractality is different during upward and downward trends for both commodities, and it increases with an increase in fractality scale. Multifractality is especially higher in the downside (upside) trend for Brent oil (gold), and this excess asymmetry is more accentuated during the COVID-19 outbreak. This finding shows that both gold and oil markets are inefficient, in particular during the outbreak episode.
Interestingly, before the outbreak, the gold (oil) market was more inefficient during downward (upward) trends. During the COVID-19 outbreak period, we see that the results have changed. More precisely, we find that gold (oil) is more inefficient during upward (downward) trends. More importantly, both markets become more inefficient during the pandemic outbreak compared to the pre-COVID-19 period, showing us the negative impact of the pandemic on market efficiency for commodities.
Overall, we see that the efficiency of gold and oil markets is sensitive to scales, market trends, and to the outbreak, highlighting the investor sentiment effect. The findings of this study provide important implications.
First, both commodity prices display inefficient behavior during our sample period, which brings out the possibility to forecast future pricing behaviors in these markets based on past information. Therefore, investment and consumption decisions including crude oil and gold cannot be made under the assumption that prices for these assets behave as a geometric Brownian motion. This situation generates exploitable patterns in prices that makes these markets more speculative, especially during the COVID-19 outbreak. Therefore, regulation in these markets becomes more important and necessary during the pandemic compared to earlier periods.
Second, the inefficient behavior of crude oil and gold overrules the usage of classical methods to price financial derivatives since all these classical methods assume the geometric Brownian motion of the underlying asset. Accordingly, it is likely to see mispricing in commodity-related derivates, especially during the COVID-19 phase. This might likely trigger an underestimation of the risk exposed due to the gold- and oil-related derivatives. In case this happens at a global scale with big enough notional amounts, it is probable that the current financial crisis that we are in will continue and keep enlarging.
Third, we have found that the efficiency of gold and oil markets is sensitive to market trends and a comparison of pre- and during COVID-19 phases shows that this sensitivity changes characteristics. In particular, during the pandemic, gold (oil) has been more efficient during upward (downward) trends, whereas we have the opposite case in the pre-COVID phase. This switching behavior requires special attention when trading these commodities. Such sudden and severe changes in pricing characteristics show us that real-time monitoring by regulators is essential in these markets.
The dynamic inefficiency of oil and gold markets have significant implications for market participants interested by these commodity assets. In fact, the increasing uncertainty and fluctuations of crude oil prices are widely associated to the international economic states including among others inflation, interest rates, economic activity fiscal policy, and dollar exchange rates as well as the geopolitical events such political events, military tensions, serious climate changes, natural catastrophes. Such these uncertainties enhance the volatility of crude oil market, leading to quick oil price changes and as a result to an increase in their inefficiency levels (Areal et al., 2015; Ciner, 2001; Fan et al., 2008; Hammoudeh et al., 2010; Kaufmann and Winters, 1989; Rockerbie, 1999). During COVID-19 pandemic outbreak, the speed of information transmission and the existence of profit opportunities augment significantly in these strategic commodity markets. The inability of Organization of the Petroleum Exporting Countries (OPEC), due to their conflict with Russia, to reach a production quota agreement has enhanced the inefficiency of the crude oil market especially during the COVID-19 pandemic spread where the oil price reaches a negative value. The difference in the degree of efficiency between crude oil and futures is that commodity speculators operating on a purely financial logic turned to the gold market to enhance the performance of their portfolio which lead to a slight increase in gold futures during the COVID-19 pandemic.
Acknowledgements
The last author acknowledges the financial support by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2019S1A5A2A01035116).
Footnotes
References
- Alvarez-Ramirez J., Rodriguez E. Asymmetric long-term autocorrelations in crude oil markets. Physica A. 2015;424:330–341. [Google Scholar]
- Alvarez-Ramirez J., Rodriguez E., Echeverria J.C. A DFA approach for assessing asymmetric correlations. Physica A. 2009;388:2263–2270. [Google Scholar]
- Ang A., Chen J. Asymmetric correlations of equity portfolios. J. Financ. Econ. 2002;63:443–494. [Google Scholar]
- Areal N., Oliveira B., Sampaio R. When times get tough, gold is golden. Eur. J. Finance. 2015;21:507–526. [Google Scholar]
- Aye G.C., Carcel H., Gil-Alana L., Gupta R. Does gold act as a hedge against inflation in the UK? Evidence from a fractional cointegration approach over 1257 to 2016. Resour. Pol. 2017;54:53–57. [Google Scholar]
- Bae K.H., Karolyi G.A., Stulz R.M. A new approach to measuring financial market contagion. Rev. Financ. Stud. 2003;16:717–764. [Google Scholar]
- Ball C.A., Torous W.A., Tschoegl A.E. The degree of Price resolution: the case of the gold market. J. Futures Mark. 1985;5:29–43. [Google Scholar]
- Bariviera A., Font-Ferrer A., Sorrosal-Forradellas M., Rosso O. An information theory perspective on the informational efficiency of gold price. N. Am. J. Econ. Finance. 2019;50:101018. [Google Scholar]
- Baruník J., Aste T., Di Matteo T., Liu R. Understanding the source of multifractality in financial markets. Physica A. 2012;391:4234–4251. [Google Scholar]
- Baur D.G., Lucey B.M. Is Gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financ. Rev. 2010;45(2):217–229. [Google Scholar]
- Baur D.G., Beckmann J., Czudaj R. A melting pot – gold price forecasts under model and parameter uncertainty. Int. Rev. Financ. Anal. 2016;48:282–291. [Google Scholar]
- Bckers S. On the efficiency of the gold options market. J. Bank. Finance. 1984;8:459–470. [Google Scholar]
- Bertus M., Stanhouse B. Rational speculative bubbles in the gold futures market: an application of dynamic factor analysis. J. Futures Mark. 2001;21:79–108. [Google Scholar]
- Brown M.B., Forsythe A.B. Robust tests for the equality of variances. J. Am. Stat. Assoc. 1974;69:364–367. [Google Scholar]
- Cajueiro D.O., Tabak B.M. The Hurst exponent over time: testing the assertion that emerging markets are becoming more efficient. Physica A. 2004;336:521–537. [Google Scholar]
- Cashin P.A., McDermott C.J., Scott A.M. 99/169. International Monetary Fund; 1999. (The Myth of Comoving Commodity Prices. IMF Working Papers). [Google Scholar]
- Charles A., Darne O. The efficiency of the crude oil markets: evidence from variance ratio tests. Energy Pol. 2009;37(11):4267–4272. [Google Scholar]
- Charles A., Darne O., Ki J.H. Will precious metals shine? A market efficiency perspective. Int. Rev. Financ. Anal. 2015;41:284–291. [Google Scholar]
- Charles A., Darne O., Kim J. Int. Rev. Financ. Anal. 2015;41:284–291. [Google Scholar]
- Ciner C. On the long-run relationship between gold and silver: a note. Global Finance J. 2001;12:299–303. [Google Scholar]
- Fan Y., Liang Q., Wei Y. A generalized pattern matching approach for multi-step prediction of crude oil price. Energy Econ. 2008;30:889–904. [Google Scholar]
- Gallais-Hamonno, Van Hoang T.H., Oosterlinck J. Informational efficiency of the clandestine and official gold markets in Paris. Econ. Lett. 2015;126:28–30. [Google Scholar]
- Ghazani M.M., Ebrahimi S.B. Testing the adaptive market hypothesis as an evolutionary perspective on market efficiency: evidence from the crude oil prices. Finance Res. Lett. 2019;30:60–68. [Google Scholar]
- Green E., Hanan W., Heffernan D. The origins of multifractality in financial time series and the effect of extreme events. The European Physical Journal B. 2014;87:1–9. [Google Scholar]
- Gu R., Chen H., Wang Y. Multifractal analysis on international crude oil markets based on the multifractal detrended fluctuation analysis. Physica A. 2010;389:2805–2815. [Google Scholar]
- Hammoudeh S., Bhar R., Thompson M.A. Re-examining the dynamic causal oil-macroeconomy relationship. Int. Rev. Financ. Anal. 2010;19:298–305. [Google Scholar]
- He L., Chen S. Are crude oil markets multifractal? Evidence from MF-DFA and MF-SSA perspectives. Physica A. 2010;389:3218–3229. [Google Scholar]
- Hooker M.A. Are oil shocks inflationary? Asymmetric and nonlinear specifications versus changes in regime. J. Money Credit Bank. 2002;34:540–561. [Google Scholar]
- Hunt B. Oil price shocks and the US stagflation of the 1970s: some insights from GEM. Energy J. 2006;27:61–80. [Google Scholar]
- Ichev R., Marinč M. Stock prices and geographic proximity of information: evidence from the Ebola outbreak. Int. Rev. Financ. Anal. 2018;56:153–166. doi: 10.1016/j.irfa.2017.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe J.E. Gold and gold stocks as investments for institutional portfolios. Financ. Anal. J. 1989;45:53–59. [Google Scholar]
- Kaufmann T.D., Winters R.A. The price of gold: a simple model. Resour. Pol. 1989;15:309–313. [Google Scholar]
- Lee M., Song J.W., Park J.H., Chang W. Asymmetric multi-fractality in the US stock indices using index-based model of A-MFDFA. Chaos, Solit. Fractals. 2017;97:28–38. [Google Scholar]
- Lee M., Song J.W., Kim S., Chang W. Asymmetric market efficiency using the index-based asymmetric-MFDFA. Physica A. 2018;512:1278–1294. [Google Scholar]
- Lescaroux F. On the excess co-movement of commodity prices—a note about the role of fundamental factors in short-run dynamics. Energy Pol. 2009;37:3906–3913. [Google Scholar]
- Levene H. In: Contributions to Probability and Statistics. Olkin I., editor. Stanford Univ. Press; Palo Alto, CA: 1960. Robust testes for equality of variances; pp. 278–292. [Google Scholar]
- Longin F., Solnik B. Extreme correlation of international equity markets. J. Finance. 2001;56:649–676. [Google Scholar]
- Lucey B.M. What do academics think they know about gold? Alchemist. 2011;62:12–14. [Google Scholar]
- Mali P., Mukhopadhyay A. Multifractal characterization of gold market: a multifractal detrended fluctuation analysis. Physica A. 2014;413:361–372. [Google Scholar]
- Melvin M., Sultan J. South African political unrest, oil prices, and the time varying risk premium in the fold futures market. J. Futures Mark. 1990;10:103–111. [Google Scholar]
- Mensi M., Lee Y.-J., Al-Yahyaee K.H., Sensoy A., Yoon S.M. Intraday downward/upward multifractality and long memory in Bitcoin and Ethereum markets: an asymmetric multifractal detrended fluctuation analysis. Finance Res. Lett. 2019;31:19–25. [Google Scholar]
- Narayan P.K., Narayan S., Zheng X. Gold and oil futures markets: are markets efficient? Appl. Energy. 2010;87:3299–3303. [Google Scholar]
- Ntim C., English J., Nwchukwu J., Wang Y. On the efficiency of the global gold markets. Int. Rev. Financ. Anal. 2015;41:218–236. [Google Scholar]
- Pal M., Rao P.M., Manimaran P. Multifractal detrended cross-correlation analysis on gold, crude oil and foreign exchange rate time series. Physica A. 2014;416:452–460. [Google Scholar]
- Pierdzioch C., Risse M., Rohloff S. On the efficiency of the gold market: results of a real-time forecasting approach. Int. Rev. Financ. Anal. 2014;32:95–108. [Google Scholar]
- Reboredo J.C. Is gold a hedge or safe haven against oil price movements? Resour. Pol. 2013;38:130–137. [Google Scholar]
- Rockerbie D.W. Gold prices and gold production: evidence for South Africa. Resour. Pol. 1999;25:69–76. [Google Scholar]
- Singhal S., Choudhary S., Biswal P.C. Return and volatility linkages among International crude oil price, gold price, exchange rate and stock markets: evidence from Mexico. Resour. Pol. 2019;60:255–261. [Google Scholar]
- Soytas U., Sari R., Hammoudeh S., Hacihasanoglu E. World oil prices, precious metal prices and macroeconomy in Turkey. Energy Pol. 2009;37:5557–5566. [Google Scholar]
- Tabak B.M., Cajueiro D.O. Are the crude oil markets becoming weakly efficient over time? A test for time-varying long-range dependence in prices and volatility. Energy Econ. 2007;29:28–36. [Google Scholar]
- Telli Ş., Chen H. Multifractal behavior in return and volatility series of Bitcoin and gold in comparison. Chaos, Solit. Fractals. 2020;139:109994. [Google Scholar]
- Wang Y., Liu L., Gu R. Analysis of efficiency for Shenzhen stock market based on multifractal detrended fluctuation analysis. Int. Rev. Financ. Anal. 2009;18(5):271–276. [Google Scholar]
- Wang Y.-D., Liu L., Gu R.-B., Cao J.-J., Wang H.-Y. Analysis of market efficiency for the Shanghai stock market over time. Physica A. 2010;389:1635–1642. [Google Scholar]
- Wang Y., Wei Y., Wu C. Analysis of the efficiency and multifractality of gold markets based on multifractal detrended fluctuation analysis. Physica A. 2011;390:817–827. [Google Scholar]