Highlights
-
•
Modeling the epidemic trends for COVID-19 is essential to take effective containment measures.
-
•
We show that time is one of the most important weapons we have in the battle against the COVID-19.
-
•
To keep the social distance and to isolate asymptomatic individuals are efficient measures to flatten the epidemic curve.
-
•
Our results show that nonpharmacological strategies must be applied as soon as possible.
Keywords: Coronavirus, COVID-19, Power-law growth, SEIR Model, Containment measures
Abstract
The cumulative number of confirmed infected individuals by the new coronavirus outbreak until April 30th, 2020, is presented for the countries: Belgium, Brazil, United Kingdom (UK), and the United States of America (USA). After an initial period with a low incidence of newly infected people, a power-law growth of the number of confirmed cases is observed. For each country, a distinct growth exponent is obtained. For Belgium, UK, and USA, countries with a large number of infected people, after the power-law growth, a distinct behavior is obtained when approaching saturation. Brazil is still in the power-law regime. Such updates of the data and projections corroborate recent results regarding the power-law growth of the virus and their strong Distance Correlation between some countries around the world. Furthermore, we show that act in time is one of the most relevant non-pharmacological weapons that the health organizations have in the battle against the COVID-19, infectious disease caused by the most recently discovered coronavirus. We study how changing the social distance and the number of daily tests to identify infected asymptomatic individuals can interfere in the number of confirmed cases of COVID-19 when applied in three distinct days, namely April 16th (early), April 30th (current), and May 14th (late). Results show that containment actions are necessary to flatten the curves and should be applied as soon as possible.
1. Introduction
Since the first infection of the coronavirus in December 2019, observed in Wuhan (China), the virus has spread around the world very quickly and nowadays 215 countries, areas, or territories1 report confirmed cases of the infection. Innumerable scientists in distinct areas are using their knowledge in the battle against the still evolving COVID-19 outbreak around the globe. The daily analysis of data about the spreading of the virus and possible interpretations that allow us to track and control the virus are of most relevance. It is a timely appeal to find explanations and models which may allow us to understand the evolution of the viruses better, saving lives and avoiding economic and social catastrophes [2].
In the battle against the COVID-19 spreading, some models focus on the geographical spread of the virus [3], [4], while others remain restricted to a given area, or country, but analyze the local temporal development of the epidemic. In the context of diseases, in 1760, Daniel Bernoulli proposed a mathematical model of disease propagation and showed the efficiency of the preventive inoculation technique against smallpox [5]. This model included susceptible and immune individuals [6]. Later on, Kermack and McKendrick [7] came up with the Susceptible-Infected-Recovered (SIR) model. During the last years, other more sophisticated models have been proposed like the delayed SIR epidemic model [8], the Susceptible-Exposed-Infected-Recovered (SEIR) model [9], [10], [11] and its modified versions [12], [13], [14], [15], [16]. Both approaches, the geographical spread, and the local temporal evolution, are of most relevance. More recently, the use of heterogeneous effects in the SIR model [17] and the viral infections in the presence of latently infected cells [18] have been analyzed. While the present work focuses on non-pharmacological containment measures, in the battle against the COVID-19, studies about the use of ivermectin are in progress [19], a drug used in malaria spreading scenarios which allows the transition from the prevalence to the eradication of the disease [20].
It is well-known that the decisive quantity used to regulate the dynamical evolution of epidemics, in general, is the average reproductive number R 0, which gives the number of secondarily infected individuals generated by a primary infected individual. While for values R 0 < 1 the number of newly infected individuals decreases exponentially, for 1 < R 0 < ∞ it increases exponentially [21], [22]. Starting from the primordial exponential solution put up by Verhulst in 1838, the well known logistic model for the law of population growth [23], models were improved more and more in the last decades to better describe the nonlinear and complex comportments which occur in our environment. In fact, in many realistic systems, power-law functions are the law of growth (or decrease), as in the branching processes with a diverging reproductive number [21], in scale-free networks and small worlds [24], and in foraging in biological systems [25]. Indeed, recent investigations showed a power-law growth of the cumulative number of infected individuals by the new coronavirus [12], [13], [26], [27], which might be typical of small world networks [28] and possibly related to fractal kinetics and graph theory [29].
Recently, we have shown that power-law growth is observed in countries from four distinct continents [12] until March 27th, 2020. The considered countries were: Brazil, China, Germany, Italy, France, Japan, Spain, the Republic of Korea, and the United States of America (USA). One leading observation was that after an initial time with a low incidence of newly infected people, the growth of the cumulative number of confirmed cases for all studied countries followed a power-law. The Distance Correlation [30], [31], [32], [33] between these countries was found to be very strong and suggest a universal characteristic of the virus spreading. One of the goals of the present work is to update to April 30th, 2020 the time-series analysis for the COVID-19 growth for the countries Brazil and USA. We included Belgium and United Kingdom (UK) on this list and leave out the other countries which are reaching the saturation regime.
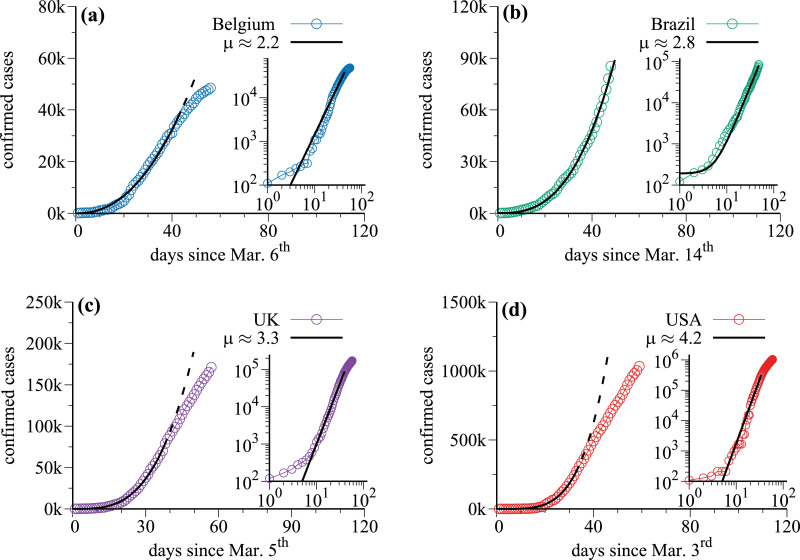
Fig. 1 displays the cumulative number of confirmed cases of COVID-19 (empty circles) as a function of time for four exemplary countries: Belgium [Fig. 1(a)], Brazil [Fig. 1(b)], UK [Fig. 1(c)], and USA [Fig 1(d)]. Data were collected from the situation reports published daily by the World Health Organization (WHO) [1]. We call to attention that the values in the vertical axis in Fig. 1 change for different countries. Initial data, regarding the days with less than 100 infected individuals, were discarded. The black-continuous curves represent the function ∝ tμ that fits the time series, and the exponent μ for each country is indicated in each panel. The insets display the same curves but in the log-log plot. Straight lines in the log-log plot indicate power-law growth. The only country for which the power-law growth still takes place is Brazil, as shown in Fig. 1(b). The reason is that it is still away from the saturation point. This is different for Belgium, UK, and USA, as can be seen in Fig. 1(a), (c), and (d), respectively. Dashed-black lines in these three panels are projections in case the power-law would have guided the growth.
Fig. 1.
The cumulative number of confirmed cases of COVID-19 (empty circles) as a function of time for (a) Belgium, (b) Brazil, (c) UK, and (d) USA, excluding days with less than 100 infected. The black-continuous curves represent the function ∝ tμ that fit the time-series, with exponent μ for each country. The insets display the same curves but in the log-log plot.
Besides the above updates, in this paper, we describe in detail the modified SEIR model which was used recently [12] to propose strategies to flatten the power-law curves. It is shown how to adjust the parameters of the model to real data. Furthermore, using the same model we discuss what would be the effect of early, current, and late non-pharmacological actions to flatten the curves of the four countries shown in Fig. 1. This clearly shows that each day lost by delaying non-pharmacological actions can cost many lives.
The paper is divided as follows. In Section 2, we present in detail the model used in this work. Section 3 discusses the effect of containment actions on the total number of confirmed infected cases applied in three distinct days and Section 4 summarizes our results.
2. The model
2.1. Equations, variables and parameters
In this section we describe in detail the model used to reproduce the realistic data of the WHO and to predict the effect of strategies used to flatten the power-law curves. The model that we used is the modified SEIR model described by the following six Ordinary Differential Equations (ODEs) [12]
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
In addition to these equations, we compute the cumulative number of confirmed cases C of COVID-19 from the following ODE:
| (7) |
Through this variable, the parameters (θ, κs) can be adjusted, as described later on. Table 1 brings together all variables and parameters of the model and their meaning. In the case of the variables, the initial conditions are also presented and in the case of the parameters, the predefined values obtained from preceding studies are also listed. The highlight lines in Table 1 call to attention to the variable C, which is the main quantity analyzed in this work, to the adjustable parameters θ and κs, and to the strategic parameter κa. After the adjustment, the parameters θ and κa will be varied to give rise to specific strategies. Worth to mention that where R 0 is the basic reproductive number without social distance actions, and γ is the interaction factor between individuals. This factor comprises the parameters of isolation and social interaction. Larger social distance implies smaller values of θ, which is equivalent to reduce R 0. The distinction between θ and R 0 allows us to identify the direct effects of the actions in the battle against the pandemic. Thus, the ideal situation would be to find θ < 1.
Table 1.
Variables and parameters (with their meaning) of the model with initial conditions and predefined values, respectively.
| Variable | Meaning | Initial condition |
|---|---|---|
| N | Country population. | Depends on the country |
| S | Individuals susceptible to infection. | |
| E | Exposed individuals, latent cases. | Adjusted from data |
| Is | Symptomatic infectious cases. | |
| Ia | Asymptomatic and mild infectious cases. | |
| Q | Isolated individuals. | |
| R | Recovered individuals. Became imune. | |
| C | Total of confirmed cases. | WHO data [1] |
| Parameter | Meaning | Class |
| Serial interval. | Predefined [34] | |
| Mean incubation period. | Predefined [16], [34] | |
| Infectious period. | Predefined [16] | |
| Ratio between infectiousness of Ia and Is. | Predefined | |
| Population ratio which remains asymptomatic. | Predefined [1] | |
| R0 the reproduction number, γ is the interaction factor. | Adjustable/Strategies | |
| κs | Isolation rate of symptomatic individuals. | Adjustable/Strategies |
| κa | Isolation rate of asymptomatic individuals. | Strategies |
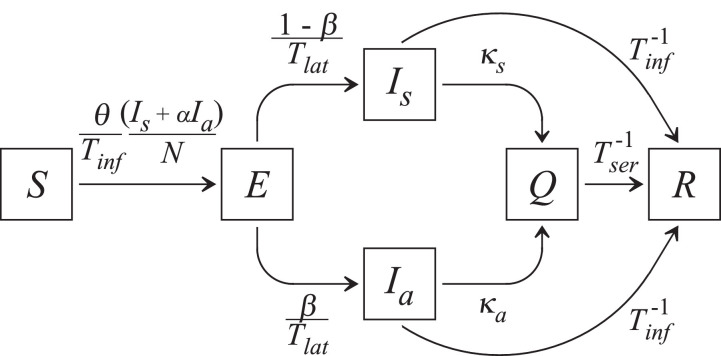
Fig. 2 is a schematic representation of the model, showing the variables and the connections between them through the parameters. Condensing the explanation of the schema, starting from the left, susceptible individuals S develop into exposed individuals E by a rate which, after a latent time Tlat, become symptomatic Is or asymptomatic Ia with the rate and β/Tlat, respectively. Applying daily tests in a rate κs (κa) to identify symptomatic (asymptomatic) infected individuals, they are immediately sent to quarantine Q, staying there for a time Tser before recovering (R). On the other hand, infected individuals who have not been tested are sent to the class R after the infection time Tinf. Since no vaccine has been developed until today, the model does not contain an immunization term. No rigid quarantine is taken into account. Furthermore, in Eq. (5), the factor Tser dividing Q represents a rate of exit from the quarantine (to the group R).
Fig. 2.
Schematic representation of the modified SEIR model, their variables, and the role of the parameters connecting the variables.
From the dynamical point of view, the model is non-chaotic. This allows us to discuss the asymptotic behavior of the relevant quantities. In fact, multigroup epidemiological models of SEIR type have been shown, in general, to be asymptotically stable [35], [36]. The fixed point is found by assuming zero for all time derivatives of the variables in the epidemiological model, furnishing
as well as the total number of confirmed cases goes to C*, where the stars denote the fixed point and S* and C* depend on initial conditions and parameters. For we have and for S* ≠ 0 we obtain . Since all variables and parameters from the model are positive, from Eq. (1) we realize that S(t) always decreases and that asymptotically
| (8) |
Furthermore, it is possible to rewrite Eq. (2) as
| (9) |
Thus, for sufficently small values of |dS/dt| close to S*, E(t) decreases exponentially and . With a similar analysis we conclude that in Eq. (6), and in Eq. (7). Thus, the dynamics always reaches the fixed point S* which is stable for all considered parameters.
2.2. Adjusting parameters to real data
It is known that for systems composed of differential equations with r unknown parameters, experiments with real data are needed to obtain all the information that is potentially available about the parameters [37]. Since in our case we have only two adjustable parameters (), we need at least 5 real data to adjust parameters correctly. This minimum value is automatically taken into account in all numerical simulations when adjusting the parameters.
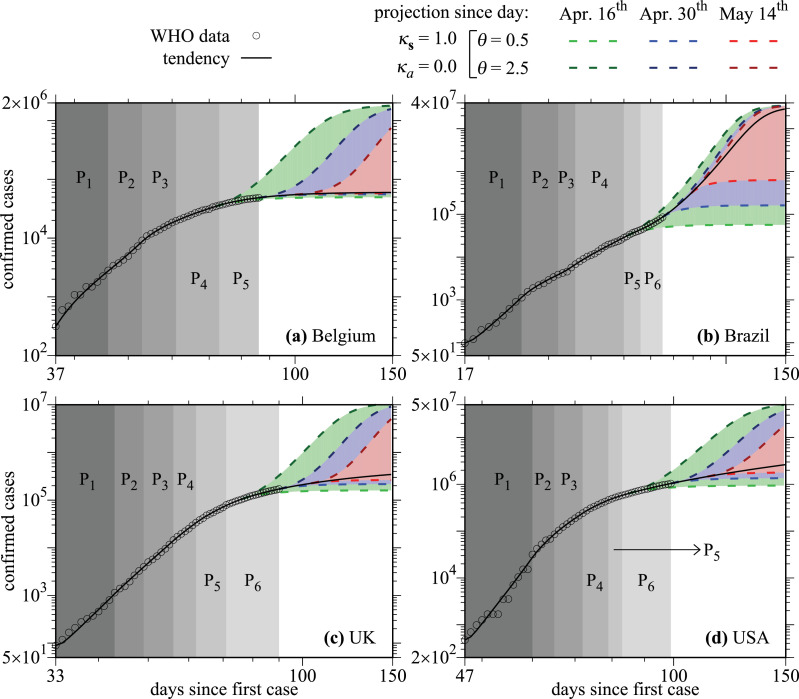
Empty circles in Fig. 3 are the real data for the cumulative number of confirmed cases of COVID-19 for the four countries analyzed. To find the best values for the pairs that fit the real data and the best time-series split in periods Pi, we performed simulations varying θ ∈ [0.5, 5.0] using a step equal to 0.1 and κs ∈ [0.0, 1.0] using a step equal to 0.05 and testing different combinations of periods Pi, always obeying the minimum amount of real data requested in each period. The goal of these simulations is to minimize the mean square error between the numerical results and real data. Thereon, we need five pairs of parameters in Fig. 3(a), namely P1, P2, P3, P4, and P5 for Belgium, and six pairs of parameters for the other countries, seen in Fig. 3(b)–(d). Details of the adjustable parameters are given in Table 2 . The initial condition E(t 0) for the variable E(t) is determined inside the first period P1 of the data considering the interval E(t 0) ∈ [C(t 0)/5, 10C(t 0)] using a step equal C(t 0)/5, where C(t 0) is the cumulative number of confirmed cases obtained from the WHO data for the first day in P1. We do not start the parameter adjustment from the first day of reported infections, but later on. The model produces better results in such cases.
Fig. 3.
The cumulative number of confirmed cases of COVID-19 in the countries: (a) Belgium, (b) Brazil, (c) UK, and (d) USA. Empty circles are the real data and the black-continuous curves are the results from the simulations. Colors are related to social distance actions applied in distinct days (discussed in the text).
Table 2.
Values of θeff and for each period obtained by adjusting the model to the real data.
| P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | θeff | θeff | θeff | θeff | θeff | θeff | ||||||
| Belgium | 2.50 | 1.00 | 2.60 | 0.00 | 1.00 | 0.00 | 1.20 | 0.80 | 0.70 | 0.40 | – | |
| Brazil | 4.40 | 0.20 | 1.50 | 0.20 | 2.70 | 0.00 | 1.70 | 0.50 | 1.40 | 1.00 | 2.10 | 0.45 |
| UK | 3.60 | 0.10 | 2.80 | 0.00 | 2.60 | 0.10 | 1.90 | 0.00 | 1.30 | 0.05 | 1.00 | 0.30 |
| USA | 4.60 | 0.05 | 2.60 | 1.00 | 2.00 | 0.40 | 1.30 | 0.75 | 0.90 | 1.00 | 1.10 | 0.15 |
After adjusting the parameters to the real data, the black-continuous curves in Fig. 3 display the results of integrating equations of the model. We observe that these curves nicely reproduce the data in all cases. When real data are not available anymore, the black-continuous curves represent projections of the cumulative number of infected individuals until the day 150, considering that the pair found in the last period will not be changed.
3. Containment measures: early, current and late actions
In this section, we discuss the effects of distinct strategies applied in different days on the total number of infected individuals. Essentially we discuss two strategies:
-
(i)
vary the degree of the social distance;
-
(ii)
for a constant value of the social distance, vary the number of daily tests that allow identifying and isolating the infected asymptomatic individuals.
3.1. The social distance effect
As mentioned before, Fig. 3 displays the real data (empty circles) and black-continuous curves, which were adjusted to fit the data. The results are shown for Belgium in Fig. 3(a), Brazil in Fig. 3(b), UK in Fig. 3(c), and USA in Fig. 3(d). During the integration of the ODEs of the model, it is possible to change the parameter θ, which represents the amount of social distance. Therefore, we changed this parameter from 0.5 to 2.5 using a step of 0.002 in three distinct dates, namely April 16th (green-dashed curves), April 30th (blue-dashed curves), and May 14th (red-dashed curves). Curves with dark colors are related to and light colors to . Worth mention that high values of θ mean low degrees of social distance, what can potentialize the epidemic spread. We see, in the case of Belgium, for example, that strong social distance strategies () can flatten the curves for the three distinct days. However, their efficiency in flattening the curves becomes less for later days (see blue and red light dashed curves). On the other hand, if social distance strategies are relaxed to in Belgium when compared to obtained for the last period P5 (see Table 2), the number of infected people increases very much. Furthermore, if you wait longer to relax the social distance, days April 30th (blue-dashed curves) or May 14th (red-dashed curves), for example, the total number of infected cases diminishes. Essentially the same behavior is observed for all the other countries analyzed. Please see Figs. 3(b)-3(d). In all these simulations the values and were kept fixed.
3.2. Testing asymptomatic individuals
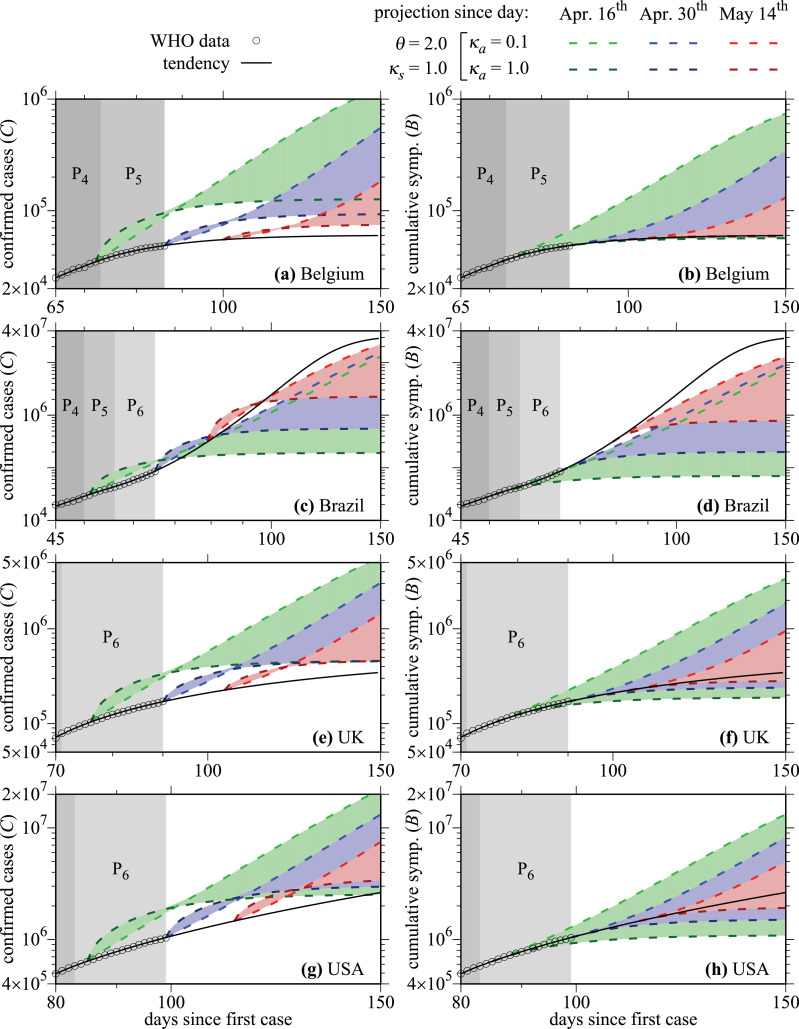
At next, we keep the social distance parameter constant at set and change the daily rate of identification of asymptomatic infected individuals. The choice for this strategy is that without tests it is impossible to recognize that asymptomatic individuals are infected. In the simulations, we varied κa from 0.1 to 1.0 using a step of 0.009. Results are presented in Fig. 4 for the same countries from Fig. 3. For better visualization, we start the plot at later times when compared to Fig. 3. Fig. 4(a), (c), (e), and (g) display the total cumulative number of confirmed infected cases and Fig. 4(b), (d), (f), and (h) show the cumulative number of only symptomatic infected individuals. Strategies are again applied in days April 16th (green-dashed curves), April 30th (blue-dashed curves), and May 14th (red-dashed curves). Curves with dark colors are related to and curves with light colors to . This constant can be interpreted as follows: for example, represents a daily rate of identification and isolation of 10% of all asymptomatic infected individuals. This represents a huge number of daily tests for countries like Brazil and USA, which have a large population.
Fig. 4.
The left column displays the total cumulative number of confirmed cases of COVID-19 for the same countries from Fig. 3, and the right column displays the cumulative number of symptomatic infected individuals for the same countries. Colors are related to the starting of the strategy of testing asymptomatic infected individuals in distinct days (discussed in the text).
To make it possible to compare the projection tendencies, for which and the scenarios shown in Fig. 4, we compute the cumulative number of symptomatic infectious cases (B). In this quantity, asymptomatic cases or those with mild symptoms are not considered. Similar to the C variable, B is an auxiliary variable of the model, obtained by integrating the ODE
| (10) |
Let us discuss results from Fig. 4 taking just one country: UK. In Fig. 4(e) we observe that the strategy of realizing tests on asymptomatic individuals increases the total number of confirmed cases instantly. For the largest value for example, the dark green curve increases very much on the day April 16th. For the light green curve barely changes in this day. However, after around 15 days, both curves cross each other, and the dark green curve asymptotically converges to a much smaller value than the light-green curve, which shows that the realization of a huge amount of daily tests to identify and isolate asymptomatic individuals is also an efficient strategy that could be applied to relax the social distance (increase the value of θ). Nevertheless, it is important to mention that, for countries with large populations, values κa ≈ 1.0 are not practical parameters. The same behavior can be observed when the tests are applied in days April 30th (blue-dashed curves) and May 14th (red-dashed curves). Essentially an analogous interpretation is valid for the other countries. One difference is observed in Brazil. In Fig. 4(c) we can see that all the dashed curves cross the black-continuous curve of the tendency, meaning that even the late actions were able to diminish the number of infected individuals. It occurs because of the constant value is lower than the obtained in the last period P6 for Brazil (see Table 2). This is not the case for the other countries since black-continuous curves had a smaller value of θeff at P6, or P5 for Belgium (see Table 2), when compared to used in Fig. 4.
At next, we discuss some projections for the cumulative number of symptomatic infected individuals, shown in Fig. 4(b) for Belgium, 4(d) for Brazil, 4(f) for UK, and 4(h) for USA. Now, we take the example of the USA. When increasing the value of θ from (see Table 2) to and setting on April 16th, the dark green curve tends to flatten the growth of the cumulative number of symptomatic infected cases. On the other hand, for the tendency is to increase such quantity when compared to the black-continuous curve. This projects bad news for the USA in case they relax the social distance (increase the value of θ) and apply a small number of tests to the identification of asymptomatic infected individuals. Similar behavior is observed for the other countries. The only difference is for Brazil, shown in Fig. 4(d), where the black-continuous curve is lying above the dashed curves once the value of θ used in these strategies is lower than the θeff obtained in P6 for Brazil. The projections tend to get worst as the application day of the strategy is delayed.
4. Conclusions
The cumulative number of confirmed cases of COVID-19 until April 30th, 2020, is demonstrated for four exemplary countries: Belgium, Brazil, UK, and USA, representing three distinct continents. After an initial period with a low incidence of newly infected people, a power-law growth of the number of confirmed cases is observed. For each country, we found a distinct growth exponent. USA leads the increasing rate, followed by UK, Brazil, and Belgium. For Belgium, UK, and USA, countries with a large number of infected individuals, the power-law growth gave place to a distinct behavior when approaching saturation. Brazil is still in the power-law regime. Such updates of the data and projections corroborate recent results regarding the power-law growth of the cumulative number of infected individuals by the new coronavirus and its strong correlation between different countries around the world [12].
Furthermore, we study a variation of the well known SEIR epidemic model [16], [38] for predictions using (or not) distinct government strategies applied on three distinct dates, namely April 16th (early action), April 30th (current action), and May 14th (late action). The main goal is to show that time is one of the most important weapons we have in the battle against the COVID-19. Recently, it has been shown that there is a short time window for which it is possible to avoid the spread of the epidemic [39]. In this work, the authors applied the Richards growth model to study the fatality curves of some countries. Their findings show that, in general, the efficiency of an intervention strategy decays quickly as the adoption time is delayed, corroborating that time is essential in containing an outbreak. In our case, in the three days mentioned above, we applied two strategies: (i) distinct degrees of social distance (vary θ), and (ii) distinct degrees of identification of asymptomatic individuals (vary κa). In the first strategy, we change the values of θ from 0.5 to 2.5, meaning strong and essentially no social distance containments, respectively. In the second strategy, we change κa from 0.1 to 1.0. This can be interpreted as identifying daily 10% of all asymptomatic individuals when . The ideal case is represented using when all asymptomatic infected people are identified each day. Results for all countries convince us that non-pharmacological strategies must be applied as soon as possible. These include social distance and a large number of testing and immediate isolation of asymptomatic infected individuals. Furthermore, time delays in applying such strategies lead to an irreversible catastrophic number of infected people.
Author contributions
E.L.B. contributed to the model implementation. R.M.S. and C.M. collected and analyzed the data, and M.W.B. mainly wrote the paper. All authors contributed to the discussion and analysis of the results and the final compilation of the work.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors thank CNPq (Brazil) for financial support (grant numbers 432029/2016-8, 304918/2017-2, 310792/2018-5 and 424803/2018-6), and they also acknowledge computational support from Prof. C. M. de Carvalho at LFTC-DFis-UFPR (Brazil). C. M. also thanks FAPESC (Brazilian agency) for financial support.
Footnotes
“Territories” include territories, areas, overseas dependencies and other jurisdictions of similar status [1].
References
- 1.W. H. Organization. Coronavirus disease (COVID-2019) situation reports. 2020. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/.
- 2.Puevo T.. Coronavirus: why you must act now. 2020. https://medium.com/@tomaspueyo/coronavirus-act-today-or-people-will-die-f4d3d9cd99c.
- 3.Blasius B.. Power-law distribution in the number of confirmed COVID-19 cases. 2020. arXiv:2004.00940v1. [DOI] [PMC free article] [PubMed]
- 4.Arenas A., et al. A mathematical model for the spatiotemporal epidemic spreading of COVID19. medRxiv2020. doi: 10.1101/2020.03.21.20040022. [DOI]
- 5.Bernoulli D. Essai d’une nouvelle analyse de la mortalite causee par la petite verole et des avantages de l’inoculation pour la prevenir. Mem Math Phys Acad Sci Paris. 1760:1–45. [Google Scholar]
- 6.Dietz K., Heesterbeek J. Daniel Bernoulli’s epidemiological model revisited. Math Biosci. 2002;180:1–21. doi: 10.1016/s0025-5564(02)00122-0. [DOI] [PubMed] [Google Scholar]
- 7.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc R Soc Lond A. 1927;115:700–721. [Google Scholar]
- 8.Hattaf K., Lashari A., Louartass Y., Yousfi N. A delayed SIR epidemic model with general incidence rate. Electron J Qual Theory Differ Equ. 2013;3:1–9. [Google Scholar]
- 9.Khalil K.M. Handbook on Decision Making. Springer-Verlag; Berlin: 2012. An agent-based modeling for pandemic influenza in Egypt; pp. 205–218. [Google Scholar]
- 10.Coburn B.J., Wagner B.G., Blower S. Modeling influenza epidemics and pandemics: insights into the future of swine flu (H1N1) BMC Med. 2009;7:30. doi: 10.1186/1741-7015-7-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lipsitch M. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(5627):1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Manchein C. Strong correlations between power-law growth of COVID-19 in four continents and the inefficiency of soft quarantine strategies. Chaos. 2020;30:041102. doi: 10.1063/5.0009454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Maier B.F., Brockmann D.. Effective containment explains sub-exponential growth in confirmed cases of recent COVID-19 outbreak in Mainland China. 2020. arXiv:2002.07572. [DOI] [PMC free article] [PubMed]
- 14.Long Y.S., et al. Quantitative assessment of the role of undocumented infection in the 2019 novel coronavirus (COVID-19) pandemic. 2020. ArXiv preprint arXiv:2003.12028.
- 15.Hethcote H., Zhien M., Shengbing L. Effects of quarantine in six endemic models for infectious diseases. Math Biosci. 2002;180:141–160. doi: 10.1016/s0025-5564(02)00111-6. [DOI] [PubMed] [Google Scholar]
- 16.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ellison G.. Implications of heterogeneous SIR models for analyses of COVID-19. 2020. doi: 10.3386/w27373. [DOI]
- 18.Hattaf K., Dutta H. Modeling the dynamics of viral infections in presence of latently infected cells. Chaos Soliton Fractals. 2020;136:109916. doi: 10.1016/j.chaos.2020.109916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schmith V., JZhou J., Lohmer L. The approved dose of Ivermectin alone is not the ideal dose for the treatment of COVID-19. Clin Pharmacol Ther. 2020 doi: 10.1002/cpt.1889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sequeira J., Louçã J., Mendes A., Lind P. Transition from endemic behavior to eradication of malaria due to combined drug therapies: an agent-model approach. J Theor Biol. 2020;484:110030. doi: 10.1016/j.jtbi.2019.110030. [DOI] [PubMed] [Google Scholar]
- 21.Vazquez A. Polynomial growth in branching processes with diverging reproductive number. Phys Rev Lett. 2006;96:038702. doi: 10.1103/PhysRevLett.96.038702. [DOI] [PubMed] [Google Scholar]
- 22.Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. [Google Scholar]
- 23.Bacaër N. A Short History of Mathematical Population Dynamics. Springer-Verlag; London: 2011. Verhulst and the logistic equation (1838) pp. 35–39. [Google Scholar]
- 24.Watts D.J. Princeton University Press; 2004. Small worlds: the dynamics of networks between order and randomness. [Google Scholar]
- 25.Viswanathan G.M., Luz M.G.E.d., Raposo E.P., Stanley H.E. Cambridge University Press; 2011. The physics of foraging: an introduction to random searches and biological encounters. [Google Scholar]
- 26.Singer H.. The COVID-19 pandemic: growth patterns, power law scaling, and saturation. 2020. arXiv:2004.03859v1. [DOI] [PubMed]
- 27.Marsland R., Mehta P.. Data-driven modeling reveals a universal dynamic underlying the COVID-19 pandemic under social distancing. medRxiv2020;. 10.1101/2020.04.21.20073890
- 28.Ray T.. Graph theory suggests COVID-19 might be a ‘small world’ after all. 2020. https://www.zdnet.com/article/graph-theory-suggests-covid-19-might-be-a-small-world-after-all/.
- 29.Ziff A., Ziff R.. Fractal kinetics of COVID-19 pandemic. 2020. doi: 10.1101/2020.02.16.20023820. [DOI]
- 30.Székely G.J., Rizzo M.L., Bakirov N.K. Measuring and testing dependence by correlation of distances. Ann Stat. 2007;35:2769–2794. [Google Scholar]
- 31.Székely G.J., Rizzo M.L. The distance correlation t-test of independence in high dimension. J Multivar Anal. 2013;117:193–213. [Google Scholar]
- 32.Mendes C.F.O., Beims M.W. Distance correlation detecting Lyapunov instabilities, noise-induced escape times and mixing. Phys A. 2018;512:721–730. [Google Scholar]
- 33.Mendes C.F.O., Silva R.M.d., Beims M.W. Decay of the distance autocorrelation and Lyapunov exponents. Phys Rev E. 2019;99:062206. doi: 10.1103/PhysRevE.99.062206. [DOI] [PubMed] [Google Scholar]
- 34.Li Q. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N Engl J Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ma Z., Zhou Y., Wu J. World Scientific Publishing Company; 2009. Modeling and Dynamics of Infectious Diseases (Series in Contemporary Applied Mathematics) [Google Scholar]
- 36.Hethcote H.W., Thieme H.R. Stability of the endemic equilibrium in epidemic models with subpopulations. Math Biosci. 1985;75:205–227. [Google Scholar]
- 37.Sontag E.D. For differential equations with r parameters, experiments are enough for identification. J Nonlinear Sci. 2002;12:553. [Google Scholar]
- 38.Li M.Y. Global dynamics of a SEIR model with varying total population size. Math Biosci. 1999;160:191–213. doi: 10.1016/s0025-5564(99)00030-9. [DOI] [PubMed] [Google Scholar]
- 39.Vasconcelos G.L. Modelling fatality curves of COVID-19 and the effectiveness of intervention strategies. PeerJ. 2020;8:e9421. doi: 10.7717/peerj.9421. [DOI] [PMC free article] [PubMed] [Google Scholar]