Summary
Understanding the impact that environmental exposure during different stages of pregnancy has on the risk of adverse birth outcomes is vital for protection of the fetus and for the development of mechanistic explanations of exposure–disease relationships. As a result, statistical models to estimate critical windows of susceptibility have been developed for several different reproductive outcomes and pollutants. However, these current methods fail to adequately address the primary objective of this line of research; how to statistically identify a critical window of susceptibility. In this article, we introduce critical window variable selection (CWVS), a hierarchical Bayesian framework that directly addresses this question while simultaneously providing improved estimation of the risk parameters. Through simulation, we show that CWVS outperforms existing competing techniques in the setting of highly temporally correlated exposures in terms of (i) correctly identifying critical windows and (ii) accurately estimating risk parameters. We apply all competing methods to a case/control analysis of pregnant women in North Carolina, 2005–2008, with respect to the development of very preterm birth and exposure to ambient ozone and particulate matter  2.5
2.5  m in aerodynamic diameter, and identify/estimate the critical windows of susceptibility. The newly developed method is implemented in the R package CWVS.
m in aerodynamic diameter, and identify/estimate the critical windows of susceptibility. The newly developed method is implemented in the R package CWVS.
Keywords: Bayesian variable selection, Gaussian process, Linear model of coregionalization
1. Introduction
Adverse birth outcomes have been linked to increases in neonatal morbidity and mortality, long-term health and developmental problems, and appreciable medical costs (McCormick, 1985; Butler and others, 2007). Recently, there has been considerable interest in examining associations between ambient air pollution exposure during pregnancy and the risks of adverse birth outcomes. Epidemiological work in this area has focused primarily on linking a pregnant woman’s exposure to a selected pollutant, averaged over different pregnancy periods, to various adverse birth outcomes in order to estimate general associations between exposure and risk (Vrijheid and others, 2011; Stieb and others, 2012). However, due to the temporal aggregation of the exposures over long periods, these studies were unable to investigate the impact of exposure timing on adverse birth outcome development in a more continuous manner across pregnancy.
In its set of strategic goals for 2012–2017, the National Institute of Environmental Health Sciences (NIEHS) included the identification of these more specific periods of vulnerability to environmental exposures, also known as “critical windows of susceptibility,” as part of its mission (NIEHS, 2012). Identification of critical windows can lead to an improved understanding of possible mechanisms of disease development and provide guidelines for protection of the fetus. As a result, a number of advanced statistical methods have recently been introduced and applied in the reproductive epidemiological setting.
Accounting for correlation in exposures and risk parameters across pregnancy has been handled in a variety of ways in these past studies. Much of the work has relied on a Gaussian process (GP) prior distribution with correlation structures to encourage borrowing of information between parameters across pregnancy periods, spatial location, multiple pollutants, multivariate outcomes, and outcome weeks (Warren and others, 2012, 2013; Chang and others, 2015; Warren and others, 2016). Warren and others (2012) extended this work to the Bayesian semiparametric setting while Wilson and others (2017) considered alternative smoothing techniques including the use of principal components and splines. Similarly defined distributed lag models (Schwartz, 2000) have been considered to estimate the impact of time-varying exposures using penalized splines (Zanobetti and others, 2000), Gaussian processes (Heaton and Peng, 2012), hierarchical modeling (Welty and others, 2009), and autoregressive priors (Fahrmeir and Knorr-Held, 1997).
These methods have successfully uncovered more informative associations between specific exposure timing and adverse health outcomes. However, none of the current methods are designed to directly address the primary question of interest; how to statistically define a critical window of susceptibility. Instead, the models most often focus on stabilized estimation (i.e., smoothness) of the risk parameters across time in order to identify general temporal trends in exposure risk. These methods define a critical window based on whether the calculated confidence/credible interval (CI/CrI) corresponding to a particular time period excludes (critical window) or includes (non-critical window) zero. It is currently unknown how well this definition performs at recovering the true critical window set. In addition, Warren and others (2012) showed that use of a Gaussian process may lead to over-smoothing during estimation of risk parameters, potentially complicating the identification of critical windows, and that a more flexible model may help to reduce this error. The impact that this potential over-smoothing has on risk parameter estimation and on identifying critical windows is also currently unknown.
In this work, we introduce critical window variable selection (CWVS) as a method for explicitly identifying the true critical windows of susceptibility and avoiding the over-smoothing inherit to many existing methods, allowing for improved estimation of risk parameters. CWVS is an innovative Bayesian variable selection method that introduces temporal smoothness during estimation of the risk parameters as well as in the variable selection process. This is accomplished via a flexible cross-covariance model based on the linear model of coregionalization (LMC) for the inclusion probabilities and risk parameters. Bayesian variable selection under collinearity of the predictors has been studied previously by Ghosh and Ghattas (2015) who recommended that under complex correlation structures, information regarding grouping patterns of covariates should be incorporated into the prior distribution. We take this approach when developing CWVS.
We investigate the properties and performance of CWVS in comparison to existing methods through simulation, and use CWVS to identify and estimate critical windows of susceptibility with respect to prenatal exposure to ambient ozone and particulate matter less than 2.5  m in aerodynamic diameter (PM
m in aerodynamic diameter (PM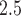 ), and very preterm birth (VPTB) in North Carolina (NC), 2005–2008. Both pollutants have been linked with adverse birth outcomes in past studies (Stieb and others, 2012). Preterm birth, a birth occurring before 37 completed gestational weeks, is one of the leading causes of mortality in children under 5 years of age and is often associated with significant developmental issues for survivors (Blencowe and others, 2012). Children born even earlier are at a far greater risk of morbidity and/or mortality. A number of epidemiological studies have investigated the association between prenatal exposure to ambient air pollution and preterm birth development but fewer have focused on children born well before 37 weeks as we do in this study (Landgren, 1996; Brauer and others, 2008; Wu and others, 2009).
), and very preterm birth (VPTB) in North Carolina (NC), 2005–2008. Both pollutants have been linked with adverse birth outcomes in past studies (Stieb and others, 2012). Preterm birth, a birth occurring before 37 completed gestational weeks, is one of the leading causes of mortality in children under 5 years of age and is often associated with significant developmental issues for survivors (Blencowe and others, 2012). Children born even earlier are at a far greater risk of morbidity and/or mortality. A number of epidemiological studies have investigated the association between prenatal exposure to ambient air pollution and preterm birth development but fewer have focused on children born well before 37 weeks as we do in this study (Landgren, 1996; Brauer and others, 2008; Wu and others, 2009).
2. Data
We analyze birth records data from NC in 2005–2008. The dataset includes all live births occurring across the entire state during the selected years. We limit the analyses to singleton births, without any documented congenital anomalies, and with a gestational age of at least 27 weeks (based on the clinical estimate of gestational age) (Chang and others, 2015). In addition, the mother must be between 15 and 50 years of age, inclusively. The primary study outcome, VPTB, is defined as a birth occurring before 32 completed weeks of gestation (Blencowe and others, 2012). Due to the low prevalence of VPTB in our study population (3672/454,058; 0.81%) and the computational complexities of working with large datasets within the Bayesian setting, we opt for a case/control analysis of the data by retaining each of the eligible VPTB cases in the data and randomly selecting four controls (children born at 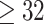 weeks) for each. This study was approved by the Institutional Review Board at the University of North Carolina at Chapel Hill.
weeks) for each. This study was approved by the Institutional Review Board at the University of North Carolina at Chapel Hill.
We utilize the Environmental Protection Agency (EPA) fused downscaler estimates (https://www.epa.gov/hesc/rsig-related-downloadable-data-files) to link pollution exposures with each of the women across the relevant calendar periods of pregnancy. The statistical model that produced these estimates has been previously described (Berrocal and others, 2010). Briefly, in its most general form, the model links observed pollution values from EPA monitoring sites with deterministic chemistry/meteorology model output from the Community Multiscale Air Quality Modeling System (CMAQ) through a spatially and temporally varying regression coefficients model. The full spatial and temporal coverage of the CMAQ output allows for prediction of air pollution concentrations in locations and on days without recorded measurements from a fixed-site monitor, while the varying coefficients allow the form of the bias in the CMAQ output (with respect to the monitoring data) to change across space and time. Daily ozone [8 h maximum; parts per billion (ppb)] and PM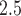 (24 h average; micrograms per cubic meter (
(24 h average; micrograms per cubic meter (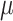 g/m
g/m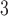 )) point estimates are provided at the year 2000 Census tract centroids for 2004–2008 (based on data downloaded in June–July, 2017). We link each woman’s residence at delivery (latitude/longitude) with the closest Census tract centroid (possibly outside of NC) to create estimated weekly average pollution exposures across the entire pregnancy. Figure S1 of the supplementary material available at Biostatistics online displays the full set of Census tract centroids in NC and relevant surrounding areas (4054 locations in total). Individuals with missing covariates were removed from the final analysis. Table S2 of the supplementary material available at Biostatistics online displays study population information by case/control status.
)) point estimates are provided at the year 2000 Census tract centroids for 2004–2008 (based on data downloaded in June–July, 2017). We link each woman’s residence at delivery (latitude/longitude) with the closest Census tract centroid (possibly outside of NC) to create estimated weekly average pollution exposures across the entire pregnancy. Figure S1 of the supplementary material available at Biostatistics online displays the full set of Census tract centroids in NC and relevant surrounding areas (4054 locations in total). Individuals with missing covariates were removed from the final analysis. Table S2 of the supplementary material available at Biostatistics online displays study population information by case/control status.
3. Critical window variable selection
We introduce CWVS, a general framework for modeling a binary outcome as a function of time-varying predictors with the goals of (i) identifying an important, and temporally proximal, subset of those predictors and (ii) making proper inference on the parameters corresponding to that subset. In the context of reproductive epidemiology, these informative predictors/parameters can be thought of as critical windows of susceptibility where higher levels of environmental exposures lead to increased risk of an adverse birth outcome.
We model the observed outcome as 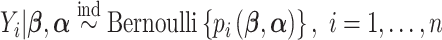 , where
, where 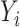 is the binary outcome associated with subject
is the binary outcome associated with subject 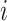 ;
; 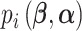 is the probability that subject
is the probability that subject 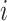 ’s response results in the adverse outcome and is a function of unknown parameters
’s response results in the adverse outcome and is a function of unknown parameters 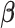 and
and 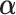 ; and
; and 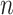 is the number of subjects. We model the probability that an outcome occurs as a function of subject-specific covariates, some of which are static across time and others that are time-varying and represent the main exposures of interest. We introduce a logistic regression framework such that
is the number of subjects. We model the probability that an outcome occurs as a function of subject-specific covariates, some of which are static across time and others that are time-varying and represent the main exposures of interest. We introduce a logistic regression framework such that
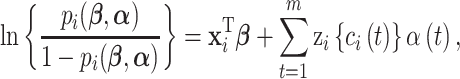 |
(3.1) |
where 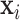 is the vector (length
is the vector (length 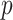 ) of static covariates/confounders specific to subject
) of static covariates/confounders specific to subject 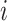 , including the intercept;
, including the intercept; 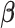 is the accompanying vector of unknown regression parameters;
is the accompanying vector of unknown regression parameters; 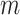 represents the number of exposure time periods that are considered;
represents the number of exposure time periods that are considered; 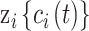 is the average exposure at subject
is the average exposure at subject 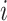 ’s spatial location occurring during time period
’s spatial location occurring during time period 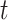 (e.g., week of pregnancy) that covers calendar interval
(e.g., week of pregnancy) that covers calendar interval 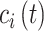 (e.g., 7 day calendar date range of pregnancy week
(e.g., 7 day calendar date range of pregnancy week 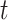 for subject
for subject 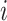 ); and
); and 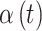 is the unknown regression parameter that describes the association between an exposure occurring during time period
is the unknown regression parameter that describes the association between an exposure occurring during time period 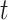 and the risk of outcome development.
and the risk of outcome development.
Our interest is in performing temporally smoothed variable selection in order to create a method for identifying a time period of great importance while maintaining the stability and smoothness of risk parameter estimation that results through use of commonly applied penalized regression techniques. In order to achieve both of these aims, we decompose 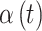 as
as 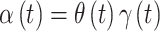 and introduce separate models for
and introduce separate models for 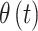 (effect magnitude component) and
(effect magnitude component) and 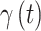 (variable selection component) that each account for correlation across time and potential cross-covariance.
(variable selection component) that each account for correlation across time and potential cross-covariance.
The real-valued parameter that describes the association between exposure during period 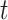 and occurrence of the binary outcome is denoted by
and occurrence of the binary outcome is denoted by 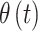 . We assume a priori that
. We assume a priori that 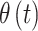 and
and 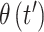 are potentially more similar when
are potentially more similar when 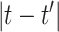 is small, and model this relationship using a GP with time series correlation structure. The binary random variable that describes the overall importance of exposure during period
is small, and model this relationship using a GP with time series correlation structure. The binary random variable that describes the overall importance of exposure during period 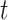 on development of the outcome and is denoted by
on development of the outcome and is denoted by 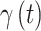 and is modeled such that
and is modeled such that 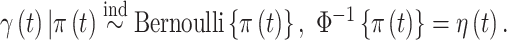 The probability that exposure period
The probability that exposure period 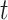 is included in the regression model is given as
is included in the regression model is given as 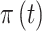 and is defined as a function of an underlying set of real-valued latent parameters,
and is defined as a function of an underlying set of real-valued latent parameters, 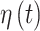 , through use of a probit link function (
, through use of a probit link function (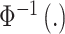 is the inverse cumulative distribution function of the standard normal distribution). Similar to
is the inverse cumulative distribution function of the standard normal distribution). Similar to 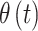 , we model the vector of
, we model the vector of 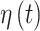 parameters using a separate GP with time series correlation structure under the assumption that important (and conversely unimportant) predictors are temporally clustered. This GP allows for temporal smoothness and stability in the identification of important time-varying predictors.
parameters using a separate GP with time series correlation structure under the assumption that important (and conversely unimportant) predictors are temporally clustered. This GP allows for temporal smoothness and stability in the identification of important time-varying predictors.
In order to flexibly model temporal correlation separately for the 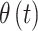 and
and 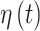 processes, as well as the cross-covariance between the two processes, we utilize the LMC (Wackernagel, 2013) such that
processes, as well as the cross-covariance between the two processes, we utilize the LMC (Wackernagel, 2013) such that
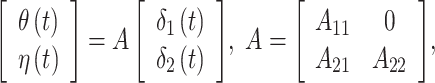 |
where 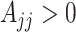 for
for 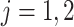 and
and 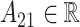 . This constructive definition leads to
. This constructive definition leads to
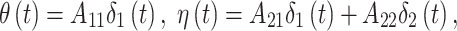 |
where we define 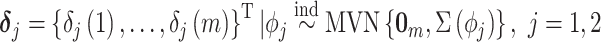 , where
, where 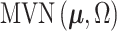 is the multivariate normal distribution with mean vector
is the multivariate normal distribution with mean vector 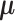 and variance/covariance matrix
and variance/covariance matrix 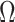 ;
; 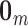 is a column vector of length
is a column vector of length 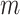 where each entry is equal to 0; and
where each entry is equal to 0; and 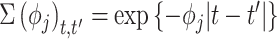 with
with 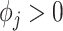 . We note that any general 1D isotropic correlation function can be used, and we select the exponential version to be consistent with existing critical window methods. Correlation between
. We note that any general 1D isotropic correlation function can be used, and we select the exponential version to be consistent with existing critical window methods. Correlation between 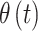 and
and 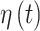 is induced by the shared latent
is induced by the shared latent 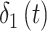 parameter.
parameter.
In order to complete the model specification, we assign prior distribution to each of the model parameters. We opt for weakly informative priors in order to place more emphasis on the data rather than our prior beliefs during posterior estimation. The vector of covariate/confounder regression parameters is modeled as 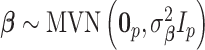 where
where 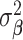 is fixed at a large value and
is fixed at a large value and 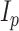 is the
is the 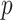 by
by 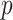 identity matrix. The LMC correlation parameters are specified as
identity matrix. The LMC correlation parameters are specified as 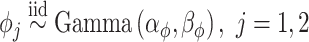 , where
, where 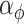 and
and 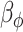 are fixed at small values; while the LMC variance/covariance parameters are modeled as
are fixed at small values; while the LMC variance/covariance parameters are modeled as 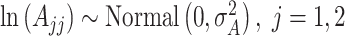 ; and
; and 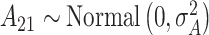 , where
, where 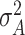 is fixed at a large value. Full details on the Markov chain Monte Carlo (MCMC) posterior sampling algorithm are given in Section S1 of the supplementary material available at Biostatistics online.
is fixed at a large value. Full details on the Markov chain Monte Carlo (MCMC) posterior sampling algorithm are given in Section S1 of the supplementary material available at Biostatistics online.
3.1. Induced covariance structure
Use of the LMC leads to a flexible variance–covariance structure for the set of latent parameters that define 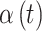 , the main risk parameters. Understanding the induced covariance structure is key in understanding how our model balances temporal smoothness in parameter estimation with abrupt changes in risk modeled through the variable selection components. The LMC allows for separate levels of temporal smoothness in parameter estimation for
, the main risk parameters. Understanding the induced covariance structure is key in understanding how our model balances temporal smoothness in parameter estimation with abrupt changes in risk modeled through the variable selection components. The LMC allows for separate levels of temporal smoothness in parameter estimation for 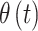 and
and 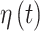 while simultaneously modeling of the cross-covariance between both sets of parameters.
while simultaneously modeling of the cross-covariance between both sets of parameters.
The covariance between two of the continuous components of 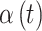 on exposure periods
on exposure periods 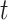 and
and 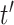 is given as
is given as 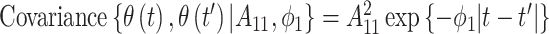 where
where 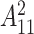 represents the variance of the process and
represents the variance of the process and 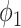 describes the level of temporal smoothness in the risk parameters. Smaller values of
describes the level of temporal smoothness in the risk parameters. Smaller values of 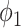 indicate more temporal similarity in parameter values across time. As
indicate more temporal similarity in parameter values across time. As 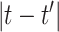 increases, the level of correlation between the parameters decreases.
increases, the level of correlation between the parameters decreases.
The covariance between two parameters that ultimately define the variable selection inclusion probabilities for 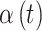 on exposure periods
on exposure periods 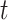 and
and 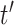 is given as
is given as 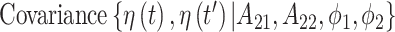
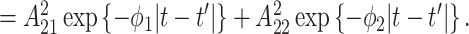 Compared to the previously defined covariance, this expression includes an additional term that is similar in structure. Allowing for separate smoothness parameters increases the flexibility of the model and allows for the possibility that the two processes differ greatly in terms of temporal smoothness. We note that if we define
Compared to the previously defined covariance, this expression includes an additional term that is similar in structure. Allowing for separate smoothness parameters increases the flexibility of the model and allows for the possibility that the two processes differ greatly in terms of temporal smoothness. We note that if we define 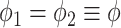 then the LMC collapses to a more commonly used separable cross-covariance framework. Finally, the cross-covariance between the two sets of parameters on exposure periods
then the LMC collapses to a more commonly used separable cross-covariance framework. Finally, the cross-covariance between the two sets of parameters on exposure periods 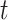 and
and 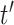 is defined as
is defined as  where
where 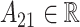 determines if the correlation is positive or negative.
determines if the correlation is positive or negative.
4. Simulation study
We design a simulation study to determine the most appropriate definition of a critical window using CWVS and to explore various properties of CWVS in comparison with existing approaches. Specifically, we are interested in each method’s ability to (i) correctly identify the true set of critical windows and (ii) to properly estimate the parameters associated with these critical windows with respect to mean squared error (MSE) and CrI coverage.
We begin by describing the process of generating a single simulated dataset for analysis in the study. Our main priority is to simulate data that closely resemble data from our area of application (see Section 5) so that the simulation study findings can provide relevant insights into the use of our model within that setting. The underlying data generating model is given as
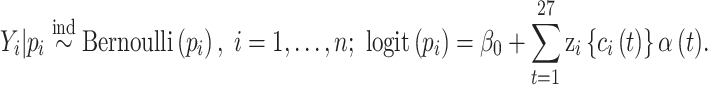 |
We choose the sample size of the simulated dataset to exactly match the NC VPTB analysis sample size (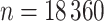 ) and similarly,
) and similarly, 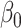 is set at
is set at  1.39 so that
1.39 so that 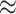 20% of the simulated responses result in the outcome. The pollution exposures for a particular woman in the dataset across the first 27 weeks (
20% of the simulated responses result in the outcome. The pollution exposures for a particular woman in the dataset across the first 27 weeks (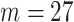 weeks, chosen to match the NC VPTB application) of pregnancy are randomly sampled without replacement directly from the full cohort of pregnant women ozone exposures in NC (
weeks, chosen to match the NC VPTB application) of pregnancy are randomly sampled without replacement directly from the full cohort of pregnant women ozone exposures in NC (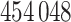 women in total) in order to obtain realistic exposure correlation and magnitudes across pregnancy. An entire time series of exposure connected to an actual individual is selected and assigned to a simulated person/response. Finally, we explore a number of different options for the pollution risk parameters,
women in total) in order to obtain realistic exposure correlation and magnitudes across pregnancy. An entire time series of exposure connected to an actual individual is selected and assigned to a simulated person/response. Finally, we explore a number of different options for the pollution risk parameters, 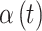 .
.
In each 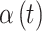 setting, we ensure that the magnitude of simulated risk is realistic by using results obtained from fitting CWVS to the NC VPTB dataset while focusing on ozone exposure. We define total exposure risk across pregnancy by summing over the posterior means of
setting, we ensure that the magnitude of simulated risk is realistic by using results obtained from fitting CWVS to the NC VPTB dataset while focusing on ozone exposure. We define total exposure risk across pregnancy by summing over the posterior means of 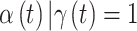 for all
for all 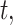 where the posterior marginal inclusion probability was at least 0.50 (i.e.,
where the posterior marginal inclusion probability was at least 0.50 (i.e., 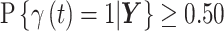 ). We refer to this summation as
). We refer to this summation as
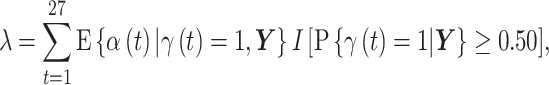 |
where 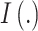 represents the indicator function, and note that
represents the indicator function, and note that 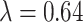 in the NC VPTB ozone application. Therefore, if we assume there is a short critical window only covering one pregnancy week, all of this risk would be placed in that particular week. More generally, if we assume a critical window set spanning
in the NC VPTB ozone application. Therefore, if we assume there is a short critical window only covering one pregnancy week, all of this risk would be placed in that particular week. More generally, if we assume a critical window set spanning 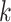 pregnancy weeks, the risk would be divided evenly across those
pregnancy weeks, the risk would be divided evenly across those 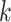 parameters such that
parameters such that 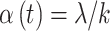 for all
for all 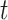 included in the critical window set. We formally define the critical window set by setting
included in the critical window set. We formally define the critical window set by setting 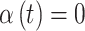 for the unimportant time periods. In total, we choose six settings for
for the unimportant time periods. In total, we choose six settings for 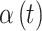 as shown in Table 1. Figure S2 of the supplementary material available at Biostatistics online displays each of the different settings on the odds ratio scale. “Early” and “Middle” refer to the location of the critical window within the duration of pregnancy. These settings allow us to explore how each method performs when the true critical window length varies and when the timing of importance shifts from the tail to the middle of pregnancy.
as shown in Table 1. Figure S2 of the supplementary material available at Biostatistics online displays each of the different settings on the odds ratio scale. “Early” and “Middle” refer to the location of the critical window within the duration of pregnancy. These settings allow us to explore how each method performs when the true critical window length varies and when the timing of importance shifts from the tail to the middle of pregnancy.
Table 1.
Simulation study data generating settings for 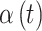 where
where 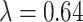
| Setting | Critical week(s) |
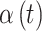 on critical week(s) on critical week(s) |
|---|---|---|
| Early 1 (E1) | 1 |
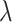
|
| Middle 1 (M1) | 14 |
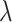
|
| Early 4 (E4) | 1–4 |
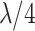
|
| Middle 4 (M4) | 13–16 |
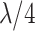
|
| Early 7 (E7) | 1–7 |
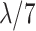
|
| Middle 7 (M7) | 11–17 |
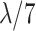
|
Once the exposures are selected for each simulated individual in the dataset and we have chosen the 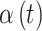 setting, we calculate the probability of the outcome for each individual and simulate the binary response variables using these probabilities. For each of the six different settings, we simulated 50 independent datasets (simulating different exposures each time).
setting, we calculate the probability of the outcome for each individual and simulate the binary response variables using these probabilities. For each of the six different settings, we simulated 50 independent datasets (simulating different exposures each time).
4.1. Defining a critical time period
We consider three different options for defining a critical time period using CWVS and investigate the most appropriate version. First, we explore the use of the median probability model (Barbieri and others, 2004), where we define the critical window set to include all time periods 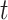 such that
such that 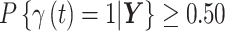 . Next, we focus attention on the continuous component of
. Next, we focus attention on the continuous component of 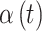 and define a time period
and define a time period 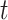 as critical if the 95% CrI of
as critical if the 95% CrI of 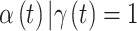 excludes zero (in either direction). Finally, we combine both ideas such that time period
excludes zero (in either direction). Finally, we combine both ideas such that time period 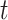 is in the critical window set if its marginal posterior inclusion probability is
is in the critical window set if its marginal posterior inclusion probability is 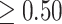 and the 95% CrI for
and the 95% CrI for 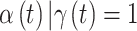 excludes zero.
excludes zero.
4.2. Competing methods
Along with fitting CWVS to the simulated data and identifying the most appropriate definition of a critical time period, we also explore a number of competing methods to determine the benefits of our newly developed framework. Each method uses the statistical model in (3.1), but differs in the prior distribution introduced for the 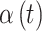 parameters.
parameters.
Gaussian process (GP): The original method used by Warren and others (2012) to identify and estimate critical windows of susceptibility, where
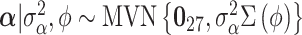 and
and 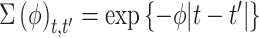 .
.Stochastic search variable selection (SSVS): A Bayesian variable selection technique originally introduced by George and McCulloch (1993), where
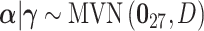 ;
; 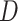 is a diagonal matrix with
is a diagonal matrix with 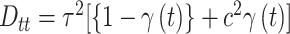 ; and
; and 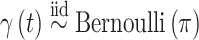 for
for 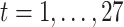 .
.- CWVS Separable: A simplified form of CWVS where we no longer include the LMC specification and instead model the joint process using a separable covariance matrix such that
where
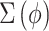 matches the matrix described in GP,
matches the matrix described in GP, 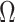 is an unstructured two-by-two cross-covariance matrix, and
is an unstructured two-by-two cross-covariance matrix, and 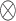 represents the Kronecker product.
represents the Kronecker product.
For each of the competing methods, we select weakly informative prior distributions to complete the model specifications. Across all models, 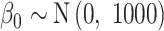 . For GP,
. For GP, 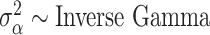
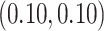 and
and 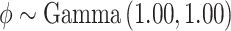 . In SSVS,
. In SSVS, 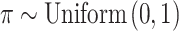 while
while 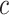 and
and 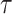 are selected based on guidance from George and McCulloch (1993) and output from GP fitted to each simulated dataset. Specifically,
are selected based on guidance from George and McCulloch (1993) and output from GP fitted to each simulated dataset. Specifically, 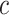 is fixed at
is fixed at 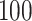 and
and 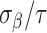 is fixed at 10, where
is fixed at 10, where 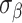 represents the median of the posterior standard deviations for the weekly effect estimates from GP. We then solve for
represents the median of the posterior standard deviations for the weekly effect estimates from GP. We then solve for 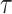 and note that this value changes across simulated datasets based on the results from GP. In CWVS Separable,
and note that this value changes across simulated datasets based on the results from GP. In CWVS Separable, 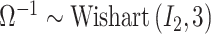 , allowing for marginally uniform prior correlations between the parameters (Gelman and others, 2014). For CWVS, we follow the priors specified in the NC VPTB analysis (see Section 5 for full details).
, allowing for marginally uniform prior correlations between the parameters (Gelman and others, 2014). For CWVS, we follow the priors specified in the NC VPTB analysis (see Section 5 for full details).
4.3. Results
Each of the competing methods were fit to each of the simulated datasets. All methods were run for 15 000 MCMC iterations, with the first 5000 discarded as a burn-in period. For CWVS, CWVS Separable, and SSVS, we explore the most appropriate definition of a critical time period based on each definition’s ability to correctly identify the true critical window set. GP does not include a variable selection component, so we define a critical time period as an individual 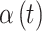 parameter whose 95% quantile-based CrI fails to include zero (in either direction) as is standard in previous work. We also calculate the posterior mean and 95% CrI for each
parameter whose 95% quantile-based CrI fails to include zero (in either direction) as is standard in previous work. We also calculate the posterior mean and 95% CrI for each 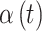 parameter from every model. For the variable selection methods, we only consider the posterior samples where
parameter from every model. For the variable selection methods, we only consider the posterior samples where 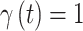 when calculating these quantities, resulting in inference for
when calculating these quantities, resulting in inference for 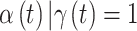 . Using the output from each fitted model, we estimate the average MSE for the true critical window set for a particular method and setting as
. Using the output from each fitted model, we estimate the average MSE for the true critical window set for a particular method and setting as 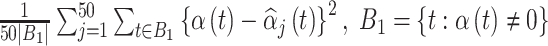 , where
, where 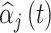 is the posterior mean estimated from simulated dataset
is the posterior mean estimated from simulated dataset 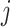 and time period
and time period 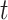 for a selected method and
for a selected method and 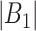 represents the number of time periods included in the true set of critical windows. We also evaluate two other definitions of
represents the number of time periods included in the true set of critical windows. We also evaluate two other definitions of 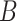 where
where 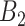 represents the set of time periods
represents the set of time periods 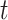 such that
such that 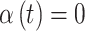 but
but 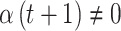 or
or 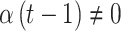 . This represents the time period(s) that immediately surround the true critical window set. We define
. This represents the time period(s) that immediately surround the true critical window set. We define 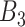 as the set of time periods that are not in
as the set of time periods that are not in 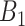 or
or 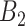 . These reflect the unimportant periods of pregnancy, far removed from the true critical window time periods. These three versions of
. These reflect the unimportant periods of pregnancy, far removed from the true critical window time periods. These three versions of 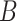 allow us to compare the performances of the methods across every possible option of risk estimation behavior during the pregnancy; significant periods, bordering significant periods, and more general non-significant periods. Next, we estimate the average empirical coverage of the 95% CrIs for the different forms of
allow us to compare the performances of the methods across every possible option of risk estimation behavior during the pregnancy; significant periods, bordering significant periods, and more general non-significant periods. Next, we estimate the average empirical coverage of the 95% CrIs for the different forms of 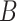 for a particular method such as
for a particular method such as 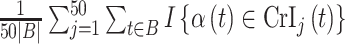 , where
, where 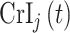 is the 95% CrI for
is the 95% CrI for 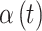 calculated from simulated dataset
calculated from simulated dataset 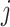 and time period
and time period 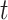 for a selected method. Finally, we calculate the proportion of times that each method correctly identifies the true critical window set exactly (no more or less periods identified) based on each method’s definition of a critical window such as
for a selected method. Finally, we calculate the proportion of times that each method correctly identifies the true critical window set exactly (no more or less periods identified) based on each method’s definition of a critical window such as 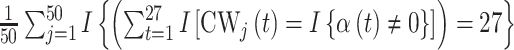 , where
, where 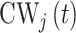 is the indicator for whether time period
is the indicator for whether time period 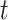 is identified as a critical window based on simulated dataset
is identified as a critical window based on simulated dataset 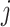 for a selected method. This metric is also used to determine the most appropriate definition of a critical time period among the competing definitions. As a sensitivity analysis, we also explore the ability of each method to correctly identify the true critical window set without penalty for classifying non-critical time periods as important.
for a selected method. This metric is also used to determine the most appropriate definition of a critical time period among the competing definitions. As a sensitivity analysis, we also explore the ability of each method to correctly identify the true critical window set without penalty for classifying non-critical time periods as important.
The results for determining the most appropriate critical window definition for each method are displayed in Table 2. For simulation settings E1 and M1, the CrI definition performs poorly across all variable selection methods. When comparing the median probability model with the combined definition, it is clear that the combined definition leads to more accurate identification of the true critical window set for CWVS, particularly for settings with more than one critical time period. SSVS and CWVS Separable are relatively robust to this choice. GP struggles to identify the true critical window set in comparison to CWVS for the majority of simulation settings. The ability of each method to correctly identify the true critical window set declines as the number of critical periods increases. This may be due to the decreasing risk magnitude at each critical period when the total number of non-zero time periods increases, resulting in reduced statistical power (see Table 1). For the sensitivity analysis results in Table S3 of the supplementary material available at Biostatistics online, the median probability model for CWVS more often identifies the critical window set across all simulation settings than the other definitions when there is no penalty for false positives. However, the results in Table 2 suggest that the median probability model often has very low specificity. GP and CWVS perform similarly when the combined definition is considered and no penalty is enforced. Based on these findings, from this point forward we use the combined definition of a critical time period when applying the variable selection techniques to simulated and real data.
Table 2.
Simulation study results to determine the most appropriate critical time period definition. The proportion of times that each definition correctly identifies the exact true set of critical time periods is presented across all simulation settings. Standard errors are presented in Table S4 of the supplementary material available at Biostatistics online. Median probability: 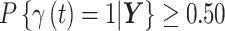 ; Credible interval: 95% credible interval of
; Credible interval: 95% credible interval of 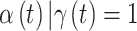 excludes zero
excludes zero
| Method | E1 | M1 | E4 | M4 | E7 | M7 |
|---|---|---|---|---|---|---|
| Median probability | ||||||
| SSVS | 0.98 | 1.00 | 0.30 | 0.14 | 0.00 | 0.00 |
| CWVS Sep. | 0.96 | 0.98 | 0.68 | 0.42 | 0.10 | 0.00 |
| CWVS LMC | 0.90 | 0.96 | 0.38 | 0.14 | 0.26 | 0.02 |
| Credible interval | ||||||
| SSVS | 0.50 | 0.30 | 0.36 | 0.30 | 0.00 | 0.00 |
| CWVS Sep. | 0.48 | 0.44 | 0.50 | 0.52 | 0.04 | 0.06 |
| CWVS LMC | 0.36 | 0.32 | 0.80 | 0.60 | 0.44 | 0.16 |
| Median probability and credible interval | ||||||
| SSVS | 0.98 | 1.00 | 0.30 | 0.14 | 0.00 | 0.00 |
| CWVS Sep. | 0.96 | 0.98 | 0.66 | 0.42 | 0.04 | 0.02 |
| CWVS LMC | 0.90 | 0.96 | 0.80 | 0.60 | 0.44 | 0.16 |
| GP | 0.40 | 0.38 | 0.62 | 0.58 | 0.34 | 0.20 |
The average MSE and empirical coverage results across all definitions of set 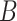 are displayed in Table 3. In Figures S3–S14 of the supplementary material available at Biostatistics online, we display boxplots of the posterior means and CrI lengths across the 50 simulated datasets for each method and simulation setting. With respect to average MSE, CWVS consistently performs well across the different simulation settings and set
are displayed in Table 3. In Figures S3–S14 of the supplementary material available at Biostatistics online, we display boxplots of the posterior means and CrI lengths across the 50 simulated datasets for each method and simulation setting. With respect to average MSE, CWVS consistently performs well across the different simulation settings and set 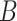 definitions while GP struggles when the number of critical periods is small. SSVS and CWVS Separable perform worse when the number of critical periods is large. In terms of average empirical coverage, CWVS more often performs near the advertised coverage of 95% than GP (as do the other variable selection methods), though in some settings the estimated coverage is below or above 95%. GP fails to consistently cover the true effect size for the
definitions while GP struggles when the number of critical periods is small. SSVS and CWVS Separable perform worse when the number of critical periods is large. In terms of average empirical coverage, CWVS more often performs near the advertised coverage of 95% than GP (as do the other variable selection methods), though in some settings the estimated coverage is below or above 95%. GP fails to consistently cover the true effect size for the 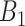 and
and 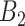 sets of weeks.
sets of weeks.
Table 3.
Average mean squared error (MSE) and empirical coverage simulation study results across all simulation settings and sets 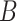 . Standard errors are presented in Table S5 of the supplementary material available at Biostatistics online
. Standard errors are presented in Table S5 of the supplementary material available at Biostatistics online
| Metric | Method | E1 | M1 | E4 | M4 | E7 | M7 |
|---|---|---|---|---|---|---|---|
Critical weeks (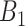 ) ) | |||||||
| MSE*1000 | GP | 12.57 | 16.76 | 1.23 | 2.72 | 0.68 | 0.78 |
| SSVS | 1.43 | 1.28 | 3.66 | 3.62 | 5.05 | 4.91 | |
| CWVS Sep. | 1.55 | 1.47 | 1.90 | 1.71 | 1.89 | 1.40 | |
| CWVS LMC | 1.79 | 2.23 | 1.17 | 1.92 | 0.76 | 0.68 | |
| Coverage | GP | 0.66 | 0.60 | 0.90 | 0.85 | 0.96 | 0.95 |
| SSVS | 0.92 | 1.00 | 0.93 | 0.94 | 0.90 | 0.91 | |
| CWVS Sep. | 0.90 | 1.00 | 0.96 | 0.99 | 0.97 | 0.99 | |
| CWVS LMC | 0.88 | 0.98 | 0.98 | 0.96 | 0.99 | 0.99 | |
Bordering critical weeks (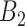 ) ) | |||||||
| MSE*1000 | GP | 8.34 | 3.67 | 2.78 | 2.75 | 1.25 | 1.53 |
| SSVS | 2.40 | 2.24 | 3.14 | 4.13 | 4.02 | 4.32 | |
| CWVS Sep. | 2.95 | 2.49 | 2.62 | 3.29 | 2.16 | 2.74 | |
| CWVS LMC | 2.96 | 2.51 | 2.21 | 2.48 | 1.31 | 1.67 | |
| Coverage | GP | 0.72 | 0.93 | 0.76 | 0.82 | 0.88 | 0.87 |
| SSVS | 0.96 | 0.97 | 0.96 | 0.91 | 0.94 | 0.92 | |
| CWVS Sep. | 0.92 | 0.95 | 0.96 | 0.94 | 0.90 | 0.88 | |
| CWVS LMC | 0.88 | 0.94 | 0.92 | 0.89 | 0.90 | 0.90 | |
Non-critical, non-bordering critical weeks (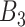 ) ) | |||||||
| MSE*1000 | GP | 2.25 | 2.71 | 0.55 | 0.61 | 0.45 | 0.50 |
| SSVS | 1.64 | 2.04 | 2.32 | 2.36 | 2.92 | 2.98 | |
| CWVS Sep. | 1.86 | 2.25 | 1.23 | 1.47 | 0.96 | 1.27 | |
| CWVS LMC | 1.68 | 2.13 | 0.69 | 0.77 | 0.51 | 0.68 | |
| Coverage | GP | 0.98 | 0.97 | 0.99 | 0.99 | 0.99 | 1.00 |
| SSVS | 0.97 | 0.96 | 0.96 | 0.96 | 0.95 | 0.95 | |
| CWVS Sep. | 0.98 | 0.96 | 0.98 | 0.98 | 0.99 | 0.98 | |
| CWVS LMC | 0.94 | 0.95 | 1.00 | 0.99 | 0.99 | 0.99 | |
These results suggest that GP may be over-smoothing when the length of the critical window is short, leading to difficulties in properly identifying and estimating significant risk parameters in the true critical window set and those bordering the true set. CWVS on the other hand has strong performance in all categories across all data generating settings due to the combination of GP smoothness and variable selection discreteness. In Section S2 of the supplementary material available at Biostatistics online, we present additional simulation studies to compare the performance of GP and CWVS when the true risk parameters are smoothly varying across pregnancy and their magnitudes are inflated. The results suggest similar performances of the methods when the risk parameter magnitudes are larger, regardless of their level of smoothness.
5. Very preterm birth in North Carolina, 2005–2008
We apply CWVS and each competing method from Section 4.2 to analyze critical windows of susceptibility for the VPTB outcome with respect to ozone (8 h maximum) and PM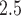 (24 h average) weekly average exposures across pregnancy. In (3.1), we select
(24 h average) weekly average exposures across pregnancy. In (3.1), we select 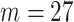 in order to only consider the impact of the first 27 weeks of pregnancy on VPTB risk. Extending past this point would lead to women giving birth and leaving the risk set, potentially biasing the results; an issue explored in depth by Chang and others (2015). Use of the case–control study design means that we are unable to estimate VPTB prevalence in the population. However, the estimated odds ratios are still appropriate measures of risk (Seaman and Richardson, 2004).
in order to only consider the impact of the first 27 weeks of pregnancy on VPTB risk. Extending past this point would lead to women giving birth and leaving the risk set, potentially biasing the results; an issue explored in depth by Chang and others (2015). Use of the case–control study design means that we are unable to estimate VPTB prevalence in the population. However, the estimated odds ratios are still appropriate measures of risk (Seaman and Richardson, 2004).
The covariates in the 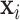 vector are available from the birth certificate and include maternal information: smoking status, diabetes status, age category ([15,25), [25–30), [30,35), [35,50]), race/ethnicity (White non-Hispanic, Black non-Hispanic, Hispanic, Other), education level (
vector are available from the birth certificate and include maternal information: smoking status, diabetes status, age category ([15,25), [25–30), [30,35), [35,50]), race/ethnicity (White non-Hispanic, Black non-Hispanic, Hispanic, Other), education level (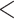 high school, high school, and
high school, high school, and 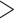 high school), and marital status (married, unmarried); spatiotemporal information: an indicator for year of delivery to capture long-term trends in VPTB risk, an indicator for month of delivery to capture seasonal variation in VPTB risk, and the latitude and longitude of maternal residence at delivery (and their interaction) to account for spatial variability in VPTB risk across the state; and miscellaneous information on each birth: the trimester that prenatal care began (first, second, or third) and sex of the child. See Table S2 of the supplementary material available at Biostatistics online for full information.
high school), and marital status (married, unmarried); spatiotemporal information: an indicator for year of delivery to capture long-term trends in VPTB risk, an indicator for month of delivery to capture seasonal variation in VPTB risk, and the latitude and longitude of maternal residence at delivery (and their interaction) to account for spatial variability in VPTB risk across the state; and miscellaneous information on each birth: the trimester that prenatal care began (first, second, or third) and sex of the child. See Table S2 of the supplementary material available at Biostatistics online for full information.
Continuous covariates were standardized to have a mean of 0 and standard deviation of 1 without loss of generality in order to stabilize model fitting. For the pollution data, we standardized exposure on each pregnancy week by subtracting off the median and dividing by the interquartile range (IQR), allowing for an IQR increase/decrease interpretation of the 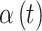 parameters. Figures S15 and S16 of the supplementary material available at Biostatistics online display the IQRs for each pollutant across each week of pregnancy in order to facilitate interpretation of the parameters. In general, the variability in IQRs across pregnancy week was low, with values ranging from 20.54–21.59 ppb and 5.52–5.74
parameters. Figures S15 and S16 of the supplementary material available at Biostatistics online display the IQRs for each pollutant across each week of pregnancy in order to facilitate interpretation of the parameters. In general, the variability in IQRs across pregnancy week was low, with values ranging from 20.54–21.59 ppb and 5.52–5.74 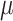 g/m
g/m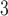 for ozone and PM
for ozone and PM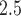 , respectively.
, respectively.
From Section 3, we select 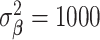 ,
, 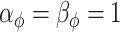 , and
, and 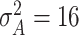 to complete the model specification. Each of the methods are fit for
to complete the model specification. Each of the methods are fit for 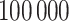 MCMC iterations, discarding the first
MCMC iterations, discarding the first 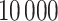 as a burn-in period. We thin the remaining 90 000 posterior samples resulting in
as a burn-in period. We thin the remaining 90 000 posterior samples resulting in 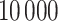 posterior samples with which to make inference. Convergence was assessed through visual inspection of individual parameter trace plots as well as calculation of the Geweke convergence diagnostic (Geweke and others, 1991). Neither tool suggested signs of non-convergence for any of the models. See Table S6 of the supplementary material available at Biostatistics online for more details on the Geweke results.
posterior samples with which to make inference. Convergence was assessed through visual inspection of individual parameter trace plots as well as calculation of the Geweke convergence diagnostic (Geweke and others, 1991). Neither tool suggested signs of non-convergence for any of the models. See Table S6 of the supplementary material available at Biostatistics online for more details on the Geweke results.
In order to compare the results with traditional epidemiological analyses, we also fit logistic regression models that included the same set of covariates/confounders as CWVS along with average first and second trimester exposures to each pollutant (fit separately to each pollutant for comparison purposes). For CWVS, we summarize the posterior distribution of 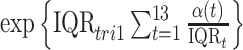 for each pollutant where
for each pollutant where 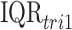 is the IQR of the first trimester average exposure and
is the IQR of the first trimester average exposure and 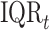 is the IQR of the exposure during week
is the IQR of the exposure during week 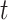 of pregnancy. This represents the impact of experiencing an
of pregnancy. This represents the impact of experiencing an 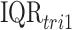 increase in first trimester average exposure under the assumption that this increase is spread evenly across the first 13 weeks of pregnancy. We similarly summarize the posterior distribution for the second trimester exposure as well (weeks 14–26). Results between the two models are expected to be comparable when viewed on the same exposure time scale.
increase in first trimester average exposure under the assumption that this increase is spread evenly across the first 13 weeks of pregnancy. We similarly summarize the posterior distribution for the second trimester exposure as well (weeks 14–26). Results between the two models are expected to be comparable when viewed on the same exposure time scale.
5.1. Results
Table S7 of the supplementary material available at Biostatistics online displays the covariate results ( ) from the CWVS model fit using the ozone exposure data. The results using the PM
) from the CWVS model fit using the ozone exposure data. The results using the PM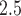 data were nearly identical and are not shown as a result. Maternal information including smoking during pregnancy, having less vs. greater than a high school education, having no previous live births, advanced age, being Black (non-Hispanic), and unmarried were found to be associated with increased risk of VPTB development. Having a male child and beginning prenatal care in the first trimester were also shown to be associated with elevated risk. The average correlation between weekly ozone exposures separated by 1 week is 0.79, dropping to 0.64 at 5 weeks, and 0.25 at 10 weeks. For PM
data were nearly identical and are not shown as a result. Maternal information including smoking during pregnancy, having less vs. greater than a high school education, having no previous live births, advanced age, being Black (non-Hispanic), and unmarried were found to be associated with increased risk of VPTB development. Having a male child and beginning prenatal care in the first trimester were also shown to be associated with elevated risk. The average correlation between weekly ozone exposures separated by 1 week is 0.79, dropping to 0.64 at 5 weeks, and 0.25 at 10 weeks. For PM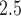 , the comparable correlations are 0.50, 0.36, and 0.11.
, the comparable correlations are 0.50, 0.36, and 0.11.
Figures 1 and 2 display the graphical output from each of the competing models fit to the ozone exposure dataset, while similar results are shown in Figures S17 and S18 of the supplementary material available at Biostatistics online for PM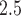 . In Figure 1 and Figure S17 of the supplementary material available at Biostatistics online, we present the posterior means and 95% CrIs of
. In Figure 1 and Figure S17 of the supplementary material available at Biostatistics online, we present the posterior means and 95% CrIs of 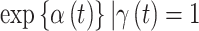 (odds ratio scale) for CWVS, CWVS Separable, and SSVS. For GP, we present the same posterior summaries for
(odds ratio scale) for CWVS, CWVS Separable, and SSVS. For GP, we present the same posterior summaries for 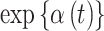 . Results shown as dashed lines indicate that the pregnancy week is included in the critical window set (as defined in Section 4.3 for each method). In Figure 2 and Figure S18 of the supplementary material available at Biostatistics online, we present the marginal posterior inclusion probabilities,
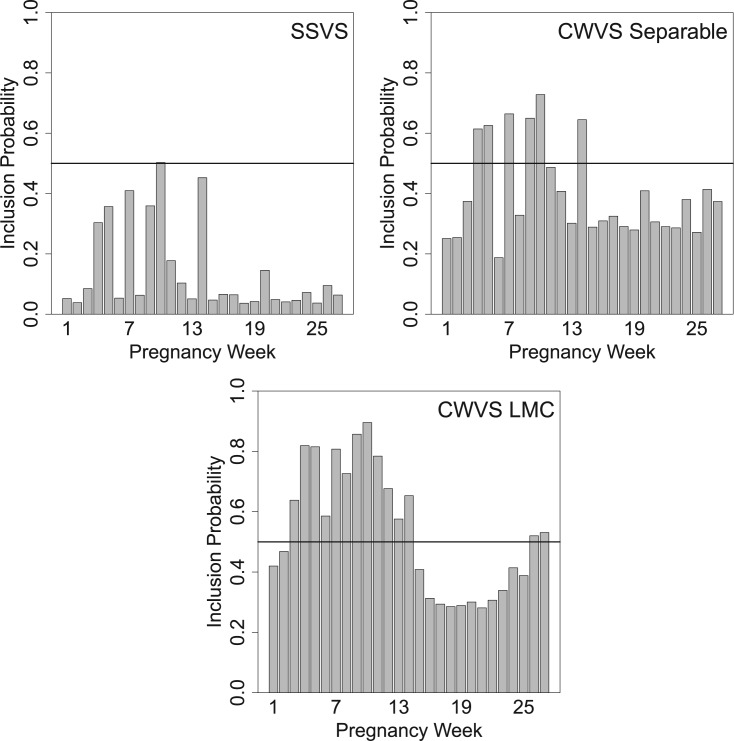
. Results shown as dashed lines indicate that the pregnancy week is included in the critical window set (as defined in Section 4.3 for each method). In Figure 2 and Figure S18 of the supplementary material available at Biostatistics online, we present the marginal posterior inclusion probabilities,  , for the models that include a variable selection component (CWVS, CWVS Separable, and SSVS).
, for the models that include a variable selection component (CWVS, CWVS Separable, and SSVS).
Fig. 1.
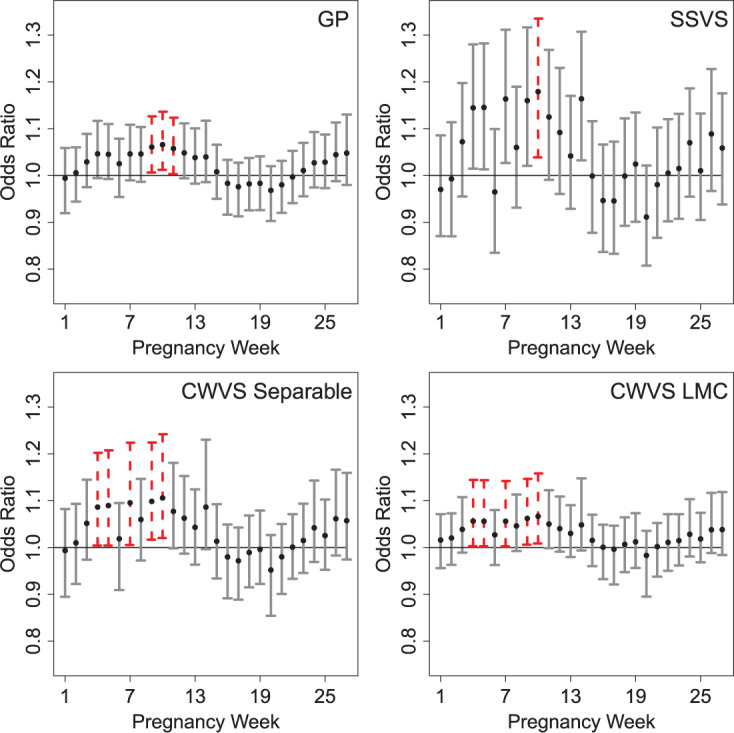
Posterior mean and 95% credible interval results from the very preterm birth and ozone (8 h maximum) exposure analysis in North Carolina, 2005–2008. Results based on an IQR increase in weekly exposure. Weeks identified as part of the critical window set are shown as dashed lines. These definitions depend partly on the posterior inclusion probabilities in Figure 2 for the variable selection methods.
Fig. 2.
Posterior inclusion probability results from the very preterm birth and ozone (8 h maximum) exposure analysis in North Carolina, 2005–2008.
For the ozone results in Figure 1, CWVS (and CWVS Separable) identifies pregnancy weeks 4, 5, 7, 9, 10 as a the critical window set. We also observe that while CWVS and CWVS Separable agree with respect to critical window identification, CWVS has shorter CrIs. SSVS has relatively long CrIs and produces less stable results as it ignores temporal correlation during parameter estimation. CWVS and GP result in CrIs of similar length though GP identifies fewer critical windows than CWVS. This is potentially due to the over-smoothing of GP as is evident when observing the parameter estimates from weeks 4–6. Weeks 4 and 5 are nearly significant, but due to the behavior of week 6, they are pulled towards the null in the GP results. However, CWVS does not penalize weeks 4 and 5 as harshly and identifies these weeks as relevant. A similar phenomenon may be occurring in the opposite direction during week 11 in both models. In Figure 2, the smoothness of the posterior inclusion probabilities across pregnancy due to the modeling of temporal correlation in the 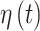 parameters is evident. Similar patterns are seen across the three variable selection methods, with a clearer indication of the important weeks shown using CWVS. The 95% CrI for
parameters is evident. Similar patterns are seen across the three variable selection methods, with a clearer indication of the important weeks shown using CWVS. The 95% CrI for 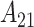 is positive and excludes zero, indicating cross-correlation between
is positive and excludes zero, indicating cross-correlation between 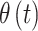 and
and 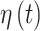 for CWVS.
for CWVS.
For the PM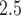 results in Figures S17 and S18 of the supplementary material available at Biostatistics online, CWVS (and CWVS Separable) suggest no critical windows of susceptibility while GP identifies two protective periods. The first 2 weeks of pregnancy have 95% CrIs that do not include zero but posterior inclusion probabilities below 0.50 for CWVS Separable. As a result, these 2 weeks are not identified as part of the critical window set. The smoothness in parameter estimation is once again evident for CWVS from these figures. The posterior distribution of
results in Figures S17 and S18 of the supplementary material available at Biostatistics online, CWVS (and CWVS Separable) suggest no critical windows of susceptibility while GP identifies two protective periods. The first 2 weeks of pregnancy have 95% CrIs that do not include zero but posterior inclusion probabilities below 0.50 for CWVS Separable. As a result, these 2 weeks are not identified as part of the critical window set. The smoothness in parameter estimation is once again evident for CWVS from these figures. The posterior distribution of 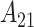 is centered around zero, suggesting no cross-correlation.
is centered around zero, suggesting no cross-correlation.
For the traditional epidemiological analysis, the odds of VPTB increased 47.47% for an IQR increase of 18.03 ppb in average first trimester ozone exposure (odds ratio 1.47; 95% CI 1.31, 1.66), while no statistically significant association was seen in the second trimester. CWVS estimated the comparable first trimester odds ratio as 1.43 (95% CrI 1.25, 1.63) with a similar null response in the second trimester. For PM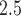 in the second trimester, the odds decreased 9.40% for an IQR increase of 3.70
in the second trimester, the odds decreased 9.40% for an IQR increase of 3.70 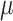 g/m
g/m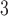 (odds ratio 0.91; 95% CI 0.84, 0.98) using the traditional model, while no statistically significant association was seen in the first trimester. CWVS estimated the comparable second trimester odds ratio as 0.94 (95% CrI: 0.87, 1.00), suggesting no impact of exposure, with a similar null result observed in the first trimester.
(odds ratio 0.91; 95% CI 0.84, 0.98) using the traditional model, while no statistically significant association was seen in the first trimester. CWVS estimated the comparable second trimester odds ratio as 0.94 (95% CrI: 0.87, 1.00), suggesting no impact of exposure, with a similar null result observed in the first trimester.
In the supplementary material available at Biostatistics online, we present a sensitivity analysis to the choice of prior distributions for the temporal smoothness parameters (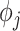 ) and an investigation into the need for spatial random effects in the modeling framework. We find that the primary results are generally robust to the choice of prior distribution for
) and an investigation into the need for spatial random effects in the modeling framework. We find that the primary results are generally robust to the choice of prior distribution for 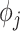 (see Figures S19 and S20 of the supplementary material available at Biostatistics online). By analyzing the Pearson residuals obtained from the traditional epidemiological models using a spatial semivariogram analysis, we conclude that there is no meaningful residual spatial correlation in either the ozone or PM
(see Figures S19 and S20 of the supplementary material available at Biostatistics online). By analyzing the Pearson residuals obtained from the traditional epidemiological models using a spatial semivariogram analysis, we conclude that there is no meaningful residual spatial correlation in either the ozone or PM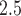 results (see Figures S21 and S22 of the supplementary material available at Biostatistics online).
results (see Figures S21 and S22 of the supplementary material available at Biostatistics online).
6. Discussion
Through simulation, we have shown that CWVS has the ability to more accurately identify critical windows of susceptibility and improve risk parameter estimation in a number of different data generating settings compared to existing methods. By incorporating a model for temporal correlation into the variable selection process, CWVS maintains smoothness in parameter estimation as well as the posterior inclusion probabilities. Use of the LMC allows for flexibility in the degree of smoothness for the different processes as well as a non-separable cross-covariance structure. Unlike SSVS, which struggles due to the high correlation between predictors that leads to high correlation between risk parameters, and GP, which can often over-smooth during parameter estimation, CWVS represents a balance between both modeling strategies. When using CWVS and other variable selection methods that account for adjustment uncertainty to estimate causal effects, it is important to consider a weighted average effect across probable models instead of relying on inference from a single selected model. The confounders/covariates in CWVS (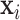 ) do not include a variable selection component. Therefore, all models being averaged across include the same set of confounders/covariates and this may help to stabilize estimation of the environmental exposure risk parameters that are typically smaller in magnitude. Please see Wang and others (2012) and Zigler and Dominici (2014) for further discussion.
) do not include a variable selection component. Therefore, all models being averaged across include the same set of confounders/covariates and this may help to stabilize estimation of the environmental exposure risk parameters that are typically smaller in magnitude. Please see Wang and others (2012) and Zigler and Dominici (2014) for further discussion.
When used to examine VPTB risk due to ambient air pollution exposure in NC, 2005–2008, CWVS identified a different critical window set than the standard GP model. However, both methods suggested that elevated exposure to ozone during selected weeks in the first trimester was associated with increased risk of VPTB. The identified critical window set from CWVS suggested the possibility of multiple critical periods (weeks 4, 5, 7, 9, 10). It is possible that the true critical window set also includes weeks 6 and 8 and that these weeks were omitted due different sources of error leading to exposure misclassification or due to power issues because of differing risk magnitudes across the weeks. However, the simulation study results suggest that CWVS has improved estimation and critical window set identification properties than the competing methods. For PM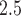 , CWVS suggested no relevant weeks of interest while GP identified a protective effect in the first 2 weeks of pregnancy. CWVS was also shown to produce results with shorter CrIs in comparison to CWVS Separable and SSVS. Standard logistic regression analyses that included the same set of covariates/confounders confirmed these findings.
, CWVS suggested no relevant weeks of interest while GP identified a protective effect in the first 2 weeks of pregnancy. CWVS was also shown to produce results with shorter CrIs in comparison to CWVS Separable and SSVS. Standard logistic regression analyses that included the same set of covariates/confounders confirmed these findings.
A strength of this work is use of the dataset of pollution exposure estimates from the EPA fused downscaler statistical model that has improved spatial/temporal coverage compared to observed monitoring data. However, use of the residence at delivery to link exposures results in exposure misclassification as some women move between date of conception and delivery date. A summary of recent work in this area suggests that 9–32% of pregnant women move at some point during pregnancy, while the distances actually traveled tend to be short; typically less than 10 kilometers (Bell and Belanger, 2012). Additionally, Warren and others (2017) found that critical window estimation was remarkably robust to exposure misclassification due to this movement in the population of pregnant women. Another limitation is the use of outdoor ambient air pollution concentration as a surrogate for individual exposure.
Future work in this area should focus on relaxing the linearity assumption often made in this framework. Exposure at a given time period is almost always assumed to be linearly associated with risk, with different prior structures specified for these regression parameters. However, non-linear dose–response relationships have been observed in previous studies and accounting for these non-linear associations may uncover previously unobserved information regarding exposure timing and risk. Extensions to the modeling of multiple pollutants will also be needed given the importance of understanding the impact of pollution mixtures on human health. Additionally, alternative smoothing and variable selection methods within the functional data analysis setting may be useful for identifying critical windows. Finally, future work and uses of CWVS should consider the level of correlation between the temporal predictors. Our simulation study results were based on weekly ozone exposures in NC that may be more or less correlated across time than alternative exposures and/or different averaging times (e.g., daily, monthly).
Supplementary Material
Acknowledgments
The authors thank the NC State Center for Health Statistics for providing the birth data. The views expressed do not necessarily represent the views/policies of the EPA.
Conflict of Interest: None declared.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org. The R package CWVS and worked example are available at https://github.com/warrenjl/CWVS.
Funding
National Institutes of Health (UL1 TR001863, KL2 TR001862, R01 NIEHS ES028346).
References
- Barbieri, M. M. and Berger, J. O. (2004). Optimal predictive model selection. The Annals of Statistics 32, 870–897. [Google Scholar]
- Behrman, R. E. and Butler, A. S. (2007). Preterm Birth: Causes, Consequences, and Prevention. National Washington, D.C.: Academies Press. [PubMed] [Google Scholar]
- Bell, M. L. and Belanger, K. (2012). Review of research on residential mobility during pregnancy: consequences for assessment of prenatal environmental exposures. Journal of Exposure Science and Environmental Epidemiology 22, 429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berrocal, V. J., Gelfand, A. E. and Holland, D. M. (2010). A spatio-temporal downscaler for output from numerical models. Journal of Agricultural, Biological, and Environmental Statistics 15, 176–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blencowe, H., Cousens, S., Oestergaard, M. Z., Chou, D., Moller, A.-B., Narwal, R., Adler, A., Garcia, C. V., Rohde, S., Say, L.. and others (2012). National, regional, and worldwide estimates of preterm birth rates in the year 2010 with time trends since 1990 for selected countries: a systematic analysis and implications. The Lancet 379, 2162–2172. [DOI] [PubMed] [Google Scholar]
- Brauer, M., Lencar, C., Tamburic, L., Koehoorn, M., Demers, P. and Karr, C. (2008). A cohort study of traffic-related air pollution impacts on birth outcomes. Environmental Health Perspectives 116, 680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, H. H., Warren, J. L., Darrow, L. A., Reich, B. J. and Waller, L. A. (2015). Assessment of critical exposure and outcome windows in time-to-event analysis with application to air pollution and preterm birth study. Biostatistics 16, 509–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahrmeir, L. and Knorr-Held, L. (1997). Dynamic discrete-time duration models: estimation via Markov chain Monte Carlo. Sociological Methodology 27, 417–452. [Google Scholar]
- Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A. and Rubin, D. B. (2014). Bayesian Data Analysis, Volume 2 Boca Raton, FL: CRC Press. [Google Scholar]
- George, E. I. and McCulloch, R. E. (1993). Variable selection via Gibbs sampling. Journal of the American Statistical Association 88, 881–889. [Google Scholar]
- Geweke, J. (1991). Evaluating the Accuracy of Sampling-based Approaches to the Calculation of Posterior Moments, Volume 196 Minneapolis, MN, USA: Federal Reserve Bank of Minneapolis, Research Department. [Google Scholar]
- Ghosh, J. and Ghattas, A. E. (2015). Bayesian variable selection under collinearity. The American Statistician 69, 165–173. [Google Scholar]
- Heaton, M. J. and Peng, R. D. (2012). Flexible distributed lag models using random functions with application to estimating mortality displacement from heat-related deaths. Journal of Agricultural, Biological, and Environmental Statistics 17, 313–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landgren, O. (1996). Environmental pollution and delivery outcome in southern Sweden: a study with central registries. Acta Paediatrica 85, 1361–1364. [DOI] [PubMed] [Google Scholar]
- McCormick, M. C. (1985). The contribution of low birth weight to infant mortality and childhood morbidity. New England Journal of Medicine 312, 82–90. [DOI] [PubMed] [Google Scholar]
- NIEHS. (2012). 2012–2017 Strategic Plan: Advancing Science, Improving Health: A Plan for Environmental Health Research. US Department of Health and Human Services. [Google Scholar]
- Schwartz, J. (2000). The distributed lag between air pollution and daily deaths. Epidemiology 11, 320–326. [DOI] [PubMed] [Google Scholar]
- Seaman, S. R. and Richardson, S. (2004). Equivalence of prospective and retrospective models in the Bayesian analysis of case-control studies. Biometrika 91, 15–25. [Google Scholar]
- Stieb, D. M., Chen, L., Eshoul, M. and Judek, S. (2012). Ambient air pollution, birth weight and preterm birth: a systematic review and meta-analysis. Environmental Research 117, 100–111. [DOI] [PubMed] [Google Scholar]
- Vrijheid, M., Martinez, D., Manzanares, S., Dadvand, P., Schembari, A., Rankin, J. and Nieuwenhuijsen, M. (2011). Ambient air pollution and risk of congenital anomalies: a systematic review and meta-analysis. Environmental Health Perspectives 119, 598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wackernagel, H. (2013). Multivariate Geostatistics: An Introduction with Applications. Berlin, Heidelberg: Springer Science & Business Media. [Google Scholar]
- Wang, C., Parmigiani, G. and Dominici, F. (2012). Bayesian effect estimation accounting for adjustment uncertainty. Biometrics 68, 661–671. [DOI] [PubMed] [Google Scholar]
- Warren, J., Fuentes, M., Herring, A. and Langlois, P. (2012a). Bayesian spatial–temporal model for cardiac congenital anomalies and ambient air pollution risk assessment. Environmetrics 23, 673–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren, J., Fuentes, M., Herring, A. and Langlois, P. (2012b). Spatial-temporal modeling of the association between air pollution exposure and preterm birth: identifying critical windows of exposure. Biometrics 68, 1157–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren, J. L., Fuentes, M., Herring, A. H. and Langlois, P. H. (2013). Air pollution metric analysis while determining susceptible periods of pregnancy for low birth weight. ISRN Obstetrics and Gynecology 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren, J. L., Son, J.-Y., Pereira, G., Leaderer, B. P. and Bell, M. L. (2017). Investigating the impact of maternal residential mobility on identifying critical windows of susceptibility to ambient air pollution during pregnancy. American Journal of Epidemiology. 187, 992–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Warren, J. L., Stingone, J. A., Herring, A. H., Luben, T.J., Fuentes, M., Aylsworth, A. S., Langlois, P. H., Botto, L. D., Correa, A. and Olshan, A. F. (2016). Bayesian multinomial probit modeling of daily windows of susceptibility for maternal PM
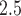 exposure and congenital heart defects. Statistics in Medicine 35, 2786–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
exposure and congenital heart defects. Statistics in Medicine 35, 2786–2801. [DOI] [PMC free article] [PubMed] [Google Scholar] - Welty, L. J., Peng, R. D., Zeger, S. L. and Dominici, F. (2009). Bayesian distributed lag models: estimating effects of particulate matter air pollution on daily mortality. Biometrics 65, 282–291. [DOI] [PubMed] [Google Scholar]
- Wilson, A., Chiu, Y.-H.M., Hsu, H.-H.L., Wright, R. O., Wright, R. J. and Coull, B. A. (2017). Bayesian distributed lag interaction models to identify perinatal windows of vulnerability in children’s health. Biostatistics 18, 537–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, J., Ren, C., Delfino, R. J., Chung, J., Wilhelm, M. and Ritz, B. (2009). Association between local traffic-generated air pollution and preeclampsia and preterm delivery in the South Coast Air Basin of California. Environmental Health Perspectives 117, 1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanobetti, A., Wand, M. P., Schwartz, J. and Ryan, L. M. (2000). Generalized additive distributed lag models: quantifying mortality displacement. Biostatistics 1, 279–292. [DOI] [PubMed] [Google Scholar]
- Zigler, C. M. and Dominici, F. (2014). Uncertainty in propensity score estimation: Bayesian methods for variable selection and model-averaged causal effects. Journal of the American Statistical Association 109, 95–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.