Double Dipping in Machine Learning: Problems and Solutions

Machine learning refers to an increasingly popular set of tools can that can be used to make predictions using complex data, such as using neuroimaging data to predict psychiatric outcomes. However, the complexity of machine learning techniques can sometimes obscure methodological problems that are clear in other contexts, such as double dipping (1). In this commentary we define double dipping, explain why it is a problem, and give five recommendations for detecting and avoiding double dipping.

The Problem of Double Dipping

Building valuable predictive models requires finding the right level of complexity to avoid overfitting or underfitting the data. A modeling procedure that closely matches every nuance of the data (i.e., overfitting) will have high accuracy for the original dataset to which it is applied but will fail to replicate in new datasets. In contrast, an overly general model (i.e., underfitting) may perform consistently across datasets yet provide low accuracy and thus low utility. Double dipping is a term for overfitting a model through both building and evaluating the model on the same data-set, yielding inappropriately high statistical significance and circular logic.

Making predictions with or without machine learning involves two steps. The first step is to determine which variables to use in predicting the outcome (i.e., feature selection). The second step is to assess how accurately a model predicts the outcome (i.e., model evaluation). Double dipping occurs when features are selected using the same criteria, and in the same sample, as model evaluation. In other words, if one first searches for predictor variables that relate to the outcome within a sample of subjects, and then builds a predictive model containing only those variables, the model will unavoidably demonstrate high accuracy in that sample. This accuracy may be based on chance relationships specific to the sample, and such a double-dipped model will therefore be highly biased, consistently overestimating how the model will perform outside the specific sample (2).

This is not a uniquely machine learning problem. If a clinician sees 20 patients and notices that all the women do well in treatment but none of the men do, it would not be surprising that a model based on patient gender will have excellent accuracy among those 20 patients. Similarly, no one will be surprised if other clinicians do not replicate this result when using this model with their patients. However, when a similar situation arises in the context of complex machine learning, this faulty reasoning can be harder to spot.

Double Dipping in Random Forests: An Example

One promising and widely used machine learning algorithm is random forest modeling (3), which protects against double dipping by building hundreds of decision “trees” to predict an outcome. Each tree is created using a different random subsample of predictor variables and a different random subsample of subjects. Crucially, each tree is evaluated using the subjects that were not included in its creation. In this way, the performance of the full “forest,” aggregated across all trees, is estimated without double dipping.

However, even random forest’s internal protection against double dipping cannot prevent all double-dipping issues. For example, double dipping will occur if one applies random forest modeling twice using the same subjects: first on the full set of variables to identify those that perform best and then on the subset of the best-performing variables to evaluate the performance of a more parsimonious model. This, in fact, was what we initially tried when applying random forest using clinical, demographic, neuropsychological, and magnetic resonance imaging variables to predict which youths would transition to moderate to heavy alcohol use (4). We use that dataset and procedure as an example to show how to detect and avoid double dipping in machine learning–based predictive models.

Recommendations to Detect and Avoid Double Dipping

Given that issues of double dipping can plague even the most well-intentioned researcher, it is important to implement checks to detect inadvertent double dipping (e.g., random data testing and permutation testing) and strategies to avoid double dipping (e.g., feature selection only, model evaluation only, and cross-validation). We describe each of these in detail using the example dataset and procedure described above.

Strategies to detect double dipping include random data testing and permutation testing. Running the analysis using completely random data (i.e., random data testing) is a quick way to detect whether an analytic procedure involves double dipping. A hallmark of double dipping is that a greater number of predictor variables yields greater accuracy, because double dipping capitalizes on chance associations, which is easier with a greater number of variables (Figure 1A).

Figure 1.

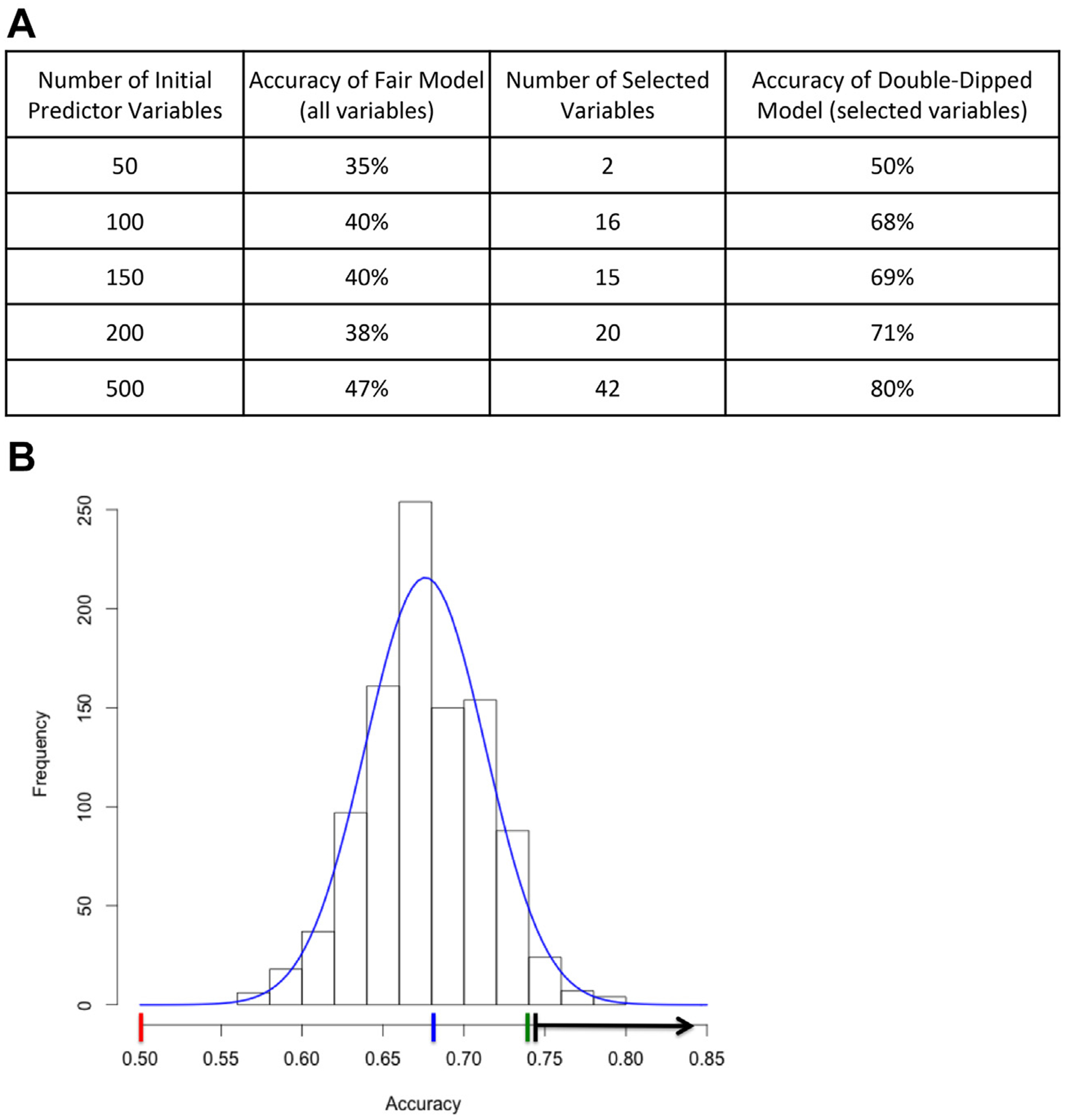
Strategies for detecting double dipping. (A) Results of random data test generated using a dataset of entirely random numbers representing a varying number of “predictor variables” (first column), and a random binary “outcome,” evenly distributed in 136 “subjects.” Because the data are random noise, model performance should be #50% and should not improve dramatically with an increasing number of random predictors, as in the fair model with all variables (second column). However, with a 2-step random forest procedure that includes double dipping to select a subset of variables (third column), the model based on fully random data shows high accuracy, especially with a large number of predictors (final column). (B) Results of a permutation test on a random forest analysis procedure that included double dipping. The red line indicates expected average accuracy of permuted outcome data if no double dipping were present (outcome base rate). The blue line indicates average accuracy of permuted data using double-dipped analysis procedure. The green line indicates observed accuracy in double-dipped analysis with real data. The black line indicates range of accuracy with 2-tailed p < .05.

A more computationally intensive test to detect double dipping is a permutation test, in which real data are used but the outcome variable is permuted (i.e., scrambled), resulting in an estimate of the null distribution of predictive accuracy based on one’s procedure and data structure. In our example, we used real data from 137 subjects and 203 clinical, demographic, neuropsychological, structural magnetic resonance imaging, and functional magnetic resonance imaging variables, permuted the outcome variable (here, the initiation of alcohol use in adolescence), and ran the double-dipped analysis procedure. We repeated this process 1000 times, repermuting the outcome and recording the accuracy each time (Figure 1B).

This permutation test can provide evidence either for or against double dipping. If there is no double dipping, the null distribution obtained through permutation testing should roughly match the base rate of the outcome in the sample. In this example, 50% of adolescents in our sample became moderate to heavy alcohol users (Figure 1B, red line). If there is double dipping, the null distribution obtained through permutation testing will not match the base rate (Figure 1B; compare blue and red lines). Permutation testing also has the benefit of providing a range of accuracy values that can be considered better than chance at p < .05 (Figure 1B, black arrow). This allows the accuracy estimates obtained on real, nonpermuted data (Figure 1B, green line) to be placed in context.

We suggest three strategies to avoid double dipping: feature selection only approaches, model evaluation only approaches, and cross-validation approaches.

Double dipping can be avoided by focusing exclusively on feature selection. In our example, we corrected our manuscript to focus entirely on the best variables selected by the random forest models (4). Random forest modeling is an extremely useful tool for feature selection because of its ability to identify complex interactions among variables. A thorough understanding of the variables and combinations of variables that most contribute to predicting an outcome allows future research to focus on evaluating predictive models grounded in this understanding.

When “feature selection only” approaches have already been conducted, or when there are strong theoretical grounds for feature selection, model evaluation only approaches may be appropriate. By selecting features based on either theory or previous research, models can be evaluated in a single sample. The preregistration of selected features and the analytic plan is particularly important for model evaluation approaches to ensure that models are not being altered based on the same data on which they are evaluated.

Cross-validation approaches are a powerful empirical approach to avoid double dipping (1). In cross-validation, the dataset is split into a training set that is exclusively used for feature selection and a held-out validation set that is exclusively used for model evaluation. This is often done iteratively (k-fold cross-validation), avoiding double dipping by splitting the sample into k subsamples and running the analysis k times, each time using k − 1 subsamples for feature selection and the final subsample to evaluate the resulting model. Although k-fold cross-validation generates multiple slightly different models rather than a single model, it provides a set of consensus predictors for future model building and evaluation and an unbiased cross-validated estimate of predictive accuracy (averaged across the k models). This procedure, however, requires sufficient power for a stable estimate of accuracy in only a fraction of the sample. One could decrease k to increase the proportion of the sample on which accuracy is estimated; however, this results in decreased proportion of the sample to identify consensus variables. Thus, with a greater k, the feature selection stabilizes, while the model accuracy estimates begin to vary widely. In contrast, with smaller k there is less consensus regarding the best-performing variables. Because of this, we recommend that k-fold cross-validation of random forest analysis be attempted only in samples of ≥200 subjects, with smaller samples focusing their power on feature selection.

The Bigger Picture

Overall, machine learning offers great potential to contribute significantly to the most difficult problems in psychiatry by leveraging complex datasets to predict disorder onset and recovery. However, enthusiasm for machine learning should be tempered by caution and consultation to ensure that models are methodologically sound and can generalize outside the data on which they were developed. Machine learning has the promise to generate clinically relevant predictive models, but this is useful only if models are valid, sensitive, specific, and generalizable, and yield actionable predictions that have real-world benefits.