Prefrontal cortex predicts state switches during reversal learning

Summary

Reinforcement learning allows organisms to predict future outcomes and to update their beliefs about value in the world. The dorsal-lateral prefrontal cortex (dlPFC) integrates information carried by reward circuits, which can be used to infer the current state of the world under uncertainty. Here, we explored the dlPFC computations related to updating current beliefs during stochastic reversal learning. We recorded the activity of populations up to 1000 neurons, simultaneously, in two male macaques, while they executed a two-armed bandit reversal learning task. Behavioral analyses using a Bayesian framework showed that animals inferred reversals and switched their choice preference rapidly, rather than slowly updating choice values, consistent with state inference. Furthermore, dlPFC neural populations accurately encoded choice preference switches. These results suggest that prefrontal neurons dynamically encode decisions associated with Bayesian subjective values, highlighting the role of the PFC in representing a belief about the current state of the world.

Introduction

The ability to learn from experience and adapt flexibly to environmental changes is critical for survival. Reversal Learning tasks have often been used to study behavioral flexibility (Butter, 1969; Costa et al., 2015; Dias et al., 1996; Farashahi et al., 2017; Groman et al., 2019; Iversen and Mishkin, 1970; Rudebeck et al., 2013; Schoenbaum et al., 2003). In these tasks, the associations between two choices and their reward outcomes are initially learned over a series of trials, and then reversed. For example, in a two-armed bandit reversal learning task, rewards are stochastically associated with two images. Choosing one image may lead to a reward more often (e.g. a circle-70%) than choosing the other image (e.g. a square-30%). After subjects have learned the initial association and consistently select the circle, the choice-outcome mapping is reversed at one trial, and the square becomes the more frequently rewarded option. One must switch from selecting the circle to selecting the square. The ability of animals to adapt their behavior after the reversal is used as a measure of behavioral flexibility.

Many behavioral strategies and neural systems may be used to learn and update choice-reward mappings on these tasks including working memory (Collins and Frank, 2012), model-free reinforcement learning (RL) (Sutton and Barto, 1998), adaptive model-free RL (Farashahi et al., 2017; Pearce and Hall, 1980) and model-based Bayesian strategies (Costa et al., 2015). In deterministic environments where choices consistently lead to the same outcome, working memory can be effective since the outcome on the last trial dictates the best choice in the current trial. However, to learn efficiently when outcomes are stochastic, information must be integrated over many trials, beyond the limits of working memory. Model-free RL, including Rescorla-Wagner (RW) and temporal-difference RL, can integrate outcomes over long periods of time (Averbeck, 2017; Averbeck and Costa, 2017) using the difference between predicted and received outcomes (i.e. reward prediction error-RPE) to incrementally update choice-outcome mappings (Rescorla and Wagner, 1972; Sutton, 1988). After a reversal, when the previously rewarded option is no longer rewarded, its value would gradually decrease over a series of trials.

In contrast to model-free RL algorithms, animals may use Bayesian or state inference strategies to infer reversals (Costa et al., 2015; Jang et al., 2015; Wilson et al., 2014). Bayesian models of reversal learning have knowledge of the structure of the task. They assume that one of the cues is initially more frequently rewarded and that there is a reversal in the choice-outcome mapping, after which the other cue is more frequently rewarded. The goal of the algorithm is to determine which cue is initially best, and then to detect the reversal. Inferring the reversal is equivalent to latent state inference (Schuck et al., 2016; Starkweather et al., 2017; Starkweather et al., 2018), and in reversal learning the current state indicates which cue is currently best (Wilson et al., 2014). Bayesian strategies can efficiently detect reversals, because they model correctly the switches in choice-outcome mappings that happen across single trials (Wilson et al., 2010). Model-free RL algorithms implicitly assume that values change incrementally across trials, an incorrect assumption for reversal learning, where values change abruptly.

Increasing evidence show that, with enough experience, animals can use Bayesian or state-inference strategies to solve reversal learning tasks (Costa et al., 2015; Gallistel et al., 2001; Hampton et al., 2006; Jang et al., 2015; Wilson et al., 2014). Furthermore, there is evidence that prefrontal cortex (PFC) regions may be important for representing, or inferring, current state in other tasks (Durstewitz et al., 2010; Sarafyazd and Jazayeri, 2019; Schuck et al., 2016; Starkweather et al., 2018). Here we examine neural population signals related to state switching processes in dorsal-lateral PFC, while monkeys performed a reversal learning task (Rothenhoefer et al., 2017). Neural population activity was recorded with 8 Utah arrays implanted bilaterally (4 in each hemisphere) in area 46 (Mitz et al., 2017). We found that monkeys adopted a Bayesian strategy to infer reversals. Furthermore, there was a clear signal in PFC indicating the trial in which the animals switched their choice preference following a reversal. High channel-count recording data (up to 1000 simultaneously recorded neurons) allowed us to infer behavioral state switches in single trials.

Results

Monkeys reverse their choices abruptly rather than gradually

We trained 2 macaques to perform a two-armed bandit reversal learning task (Fig. 1A, see Methods). The task is organized in blocks of 80 trials. On each trial, monkeys fixated centrally for a variable time (400-800ms), then two target images were simultaneously presented to the left and right of the fixation point, prompting them to choose one. Animals had to make a saccade towards the chosen target and hold for 500ms. Reward was delivered stochastically. One of the two options had a higher reward probability than the other (p=0.7 vs p=0.3) and the monkeys had to discover which option was the best by trial-and-error. The reward probability mapping in each block was defined in one of two possible ways: in What blocks, reward probabilities were associated to the images, independent of their location (left/right from the fixation point). Conversely, in Where blocks, either the left or right target had the high reward probability, independent of the specific image presented at that location. Block type was randomized and not cued, thus, monkeys had to discover if image or location determined reward delivery. Within each block, the reward mappings were switched across options at a random trial within a switch window (trials 30-50) dividing the block into two phases: a) the initial acquisition phase in which the animals learned the block type and the best option, and b) the reversal phase in which they had to switch their choice preference to maximize reward. The monkeys completed between 1840-1920 valid trials per session. We show results from 8 sessions, 4 per animal.

Figure 1.

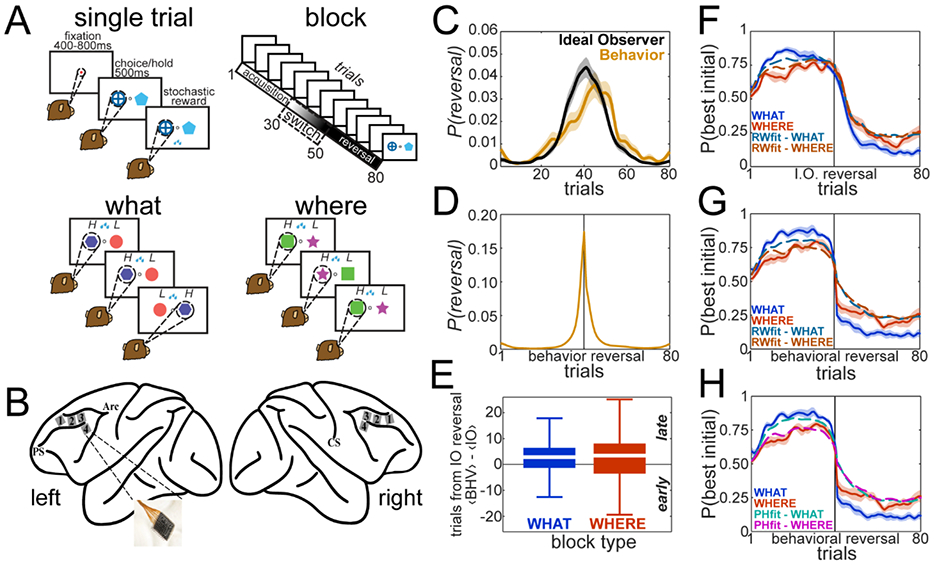
Task and Recording Sites. A. Schematic of the reversal learning task. On each trial, the animals were required to fixate centrally, and after a variable fixation time the fixation spot was toggled off and two targets were simultaneously presented to the left and right. Then, animals made a saccade to select a target, holding it for 500ms to successfully complete a trial. Reward was delivered stochastically with one option having a higher reward probability (p=0.7 vs p=0.3). On each block of 80 trials, reward probability mappings were defined in two ways defining two block types: in What blocks reward probabilities were associated to the images independent of where they were presented, whereas in Where blocks probabilities were associated to locations (left/right) independent of the image presented at that location. Animals explored the available options to find both the block type and the best option, acquiring a choice preference. Then, at a random trial within a switch window (trials 30-50) reward mappings were flipped across options according to block type, dividing the block into acquisition and reversal phases. Block type was held constant within a given block. B. Location of the 8 microelectrode arrays (96 electrodes, 10×10 arrangement) on the prefrontal cortex, surrounding the principal sulcus. C. Bayesian estimates of the posterior probability of a reversal in the choice-outcome mapping (Ideal Observer (IO) model, P(reversal∣M=IO)) and in the choice preference (Behavioral (BHV) model, P(reversal∣M=BHV)). These curves were generated by averaging trial-by-trial the posteriors across blocks. D. Bayesian estimate of the posterior probability of a reversal in choice preference aligned to the point estimate of the trial at which the reversal occurred. These curves were generated by calculating the expected value of P(reversal∣M=BHV) in each block, and then aligning P(reversal∣M=BHV) around that estimate before averaging across blocks. E. Boxplots of the difference between the point estimates for the reversal based on the posterior P(reversal∣M) distributions for the BHV and the IO models. Positive values indicate that the reversal in choice preference occurred after the reward mapping switched. F. Choice and Rescorla-Wagner model data aligned to the IO reversal estimate. Because the reversal trial varied across blocks, the choice and model data from each block were split into acquisition (i.e. trials < the IO reversal trial) and reversal (i.e. trials >= the IO reversal trial) phases. The data were then interpolated such that the acquisition and reversal phases both had 40 trials. Interpolated data was then averaged. Plots show the fraction of times the animals chose the option that initially had a higher reward probability, split by block type. Overlays are choice probability estimates from the Rescorla-Wagner model fit. G. Same as F, except acquisition and reversal phases were defined by the BHV reversal point. H. Same as G, except that overlays are Pearce-Hall model choice probabilities. F-H show means±SEM across sessions (n=8).

We first examined the behavioral data. Given the stochasticity of the reward delivery, estimates of the reversal trial may not match the programmed switch trial. To account for this, we fit two Bayesian change-point models. First, we fit a Bayesian Ideal Observer (IO) model to estimate the posterior probability distribution across trials that the reward mapping had reversed, p(reversal∣Model=IO). The p(reversal∣Model=IO) distribution was on average in agreement with the programmed reversal, peaking at the center of the switch window (Fig. 1C). Second, we fit a Bayesian model of the monkey choice behavior (BHV) to estimate the posterior probability distribution across trials that the animal switched its choice preference, p(reversal∣M=BHV), independently of when the actual reversal in the choice-outcome mapping occurred (Fig. 1C). From the IO and BHV model distributions we computed point estimates of the trial at which either the choice-outcome mapping or the animal’s choice preference reversed, by calculating the expected value of the corresponding p(reversal∣M). When we aligned the BHV reversal distributions to the estimated trial on which the behavioral reversal occurred, and then averaged, it could be seen that the BHV reversal distributions were narrow, focused around the reversal point (Fig. 1D). This suggests that reversals were well-defined. The broader distributions seen in Fig. 1C follow from averaging narrow distributions that peak on different trials.

Next, we aligned the choice data using the IO reversal point (Fig. 1F). At the beginning of the block, monkeys quickly inferred which option was optimal and chose it more often. After the reward probability mapping switched they reversed their choice behavior. With this alignment, the animals appeared to slowly change preference to the best post-reversal option. However, if we align the choices to the BHV reversal point, it is evident that monkeys changed their choice preferences abruptly (Fig. 1G). The apparent slow change when aligned to the IO reversal point (Fig. 1F) is due to averaging rapid changes that occur on different trials relative to the IO reversal. We compared the reversal point estimates between the BHV and the IO models. Typically, the animals reversed their choices a few trials after the IO (Fig. 1E), but in several blocks the animals reversed before the IO model, i.e. before the evidence would suggest that the reward mapping had switched. This is inconsistent with a gradual updating process, since it can only be explained if the animals have an expectation that a switch in the reward mapping will occur at some point.

We also fit Rescorla-Wagner (RW) reinforcement learning models to the choice behavior and overlaid the average choice probabilities from the model on the choice data. While RW models approximated the data well for the acquisition phase (Fig. 1F-H) and most of the reversal phase for the IO aligned data (Fig. 1F), the RL model reversed preference much more slowly than the animals. This could be seen when the data was aligned around the BHV reversal trial (Fig. 1G). The RW rule may be too restrictive, because learning might be enhanced around the reversal. To account for this, we fitted a Pearce-Hall (PH) model, that allows the learning rate to vary when reward prediction errors are larger. The PH model predictions were similar to those of the RW model (Fig. 1H). Both models failed to fit properly the observed behavior in the first few trials after the behavioral reversal point. Critically, the association parameter of the PH model showed only a small increase around the reversal point (Fig S1), which likely follows from the fact that animals reversed quickly after the contingencies switched (Fig. 1E). We compared the fit of the RW, PH and Bayesian models around the reversal point (trials 20-60). The Bayesian model predicted reversals better than the RW (mean log BF=97, SEM=32, t₇=3.25, p=0.014) and the PH (log BF=123, SEM=31.4, t₇=4.20, p=0.004) models across sessions. Thus, the Bayesian model accounted better for choice behavior after a reversal in the reward mapping. These findings are consistent with the animals using Bayesian state inference to reverse their choice behavior.

Neurons in the Prefrontal Cortex show activity associated with task parameters

We hypothesized that PFC neurons would display activity associated with the process of switching preferences after reversals in our task. To test this hypothesis, we recorded the extracellular activity of neural populations in the dlPFC (size range: 573-1023 neurons, median: 706.5) using 8 multielectrode arrays (Fig. 1B) while the monkeys performed the task. The recorded neurons were evenly distributed across left and right hemispheres (47.21 ± 5.32% / 52.79 ± 5.31%, mean±SD).

The task robustly engaged a large fraction of the recorded neurons. We observed a broad diversity of activity profiles, including differential responses to image and location chosen (e.g. Fig. 2A,B). Within this diversity, many units exhibited responses associated with the chosen option in both What and Where blocks. We ran ANOVAS on spike counts from a sliding window that was moved across trial execution (300ms width, 20ms step). The results revealed that image and location chosen drove the activity of a large fraction of neurons (Fig. 2C, ~62% and ~50%, respectively). Toward the end of the trial, there was a strong neural response associated with the outcome.

Figure 2.

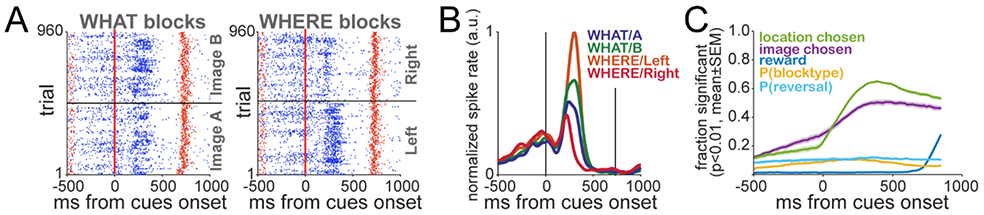
Neural responses. A. Raster plots of an example neuron during What and Where blocks. Each row of blue ticks represents the spikes during a trial. Red dots along each line represent trial start, cue onset, outcome time/end of trial. Because the image varies in each block, trials were sorted by preferred (Image B) and non-preferred (Image A) images in each block. B. Spike densities for the example unit during each option and block type combination. C. Activity associations to behavior found in the population of recorded single units. The plot shows the average fraction of neurons across sessions (mean±SEM) with significant main effects for the indicated factors from an ANOVA on spike counts from a sliding window (300ms width, 20ms step). The total number of neurons recorded is 6081.

We also examined associations between neural responses and Bayesian estimates related to learning in the task. Around 20% of the neurons had activity associated with the posterior probability of a reversal in the choice behavior - P(reversal∣M=BHV). An interesting feature is that activity was related to P(reversal∣M=BHV) even before the cue onset, suggesting that the neurons represent the choice to switch preferences throughout the trial, in agreement with previous observations (Asaad et al., 2000; Averbeck and Lee, 2007; Mushiake et al., 2006). We focus on this reversal related activity in detail below. From the BHV model, we also estimated if the animals were choosing consistently between images or locations, that is, the posterior probability of block type being What (P(blocktype=what)) or Where (P(blocktype=where)). Similar to the activity related to P(reversal), the association between neural activity and Bayesian estimates for block type existed from the beginning of the trial, and there is only a small increase in the fraction of neurons with a significant effect of this factor after cue onset (Fig. 2C), revealing Block Type inference processes in the PFC. We did not observe differences in behavior around reversal (Fig 1E-H) or in reversal decoding between block types (Fig 3D legend). Therefore, further reversal analyses included all blocks together independently of block type.

Figure 3.

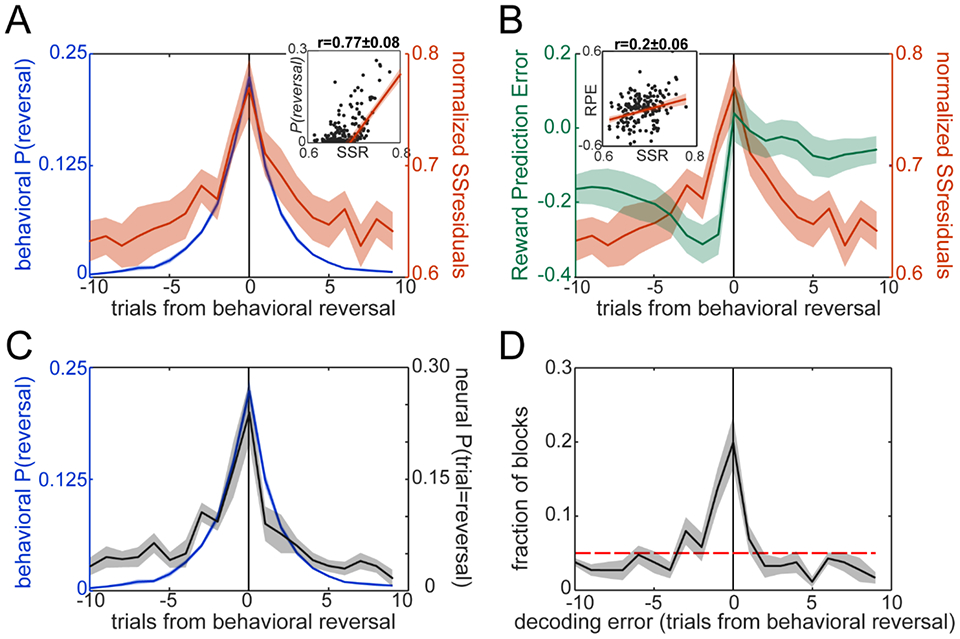
Decoding of Reversal from activity between 0-300ms after cue onset. A. Sum of Squared Residuals (SSResid) across neurons. The residual for each neuron in each trial was squared, then the squares were summed across neurons. The average Sum of Squares (red) on each trial within the switch window is shown overlaid on the Bayesian posterior P(reversal∣M=BHV) (blue). Inset shows the correlation between the two curves, the red line is the best linear fit. B. Reward Prediction Error (RPE) from a Rescorla-Wagner model. SSResid (red) is overlaid on the RPE around the trial of behavior reversal (green). Inset, same as in A. C. Neural posterior distribution, P(reversal∣Neural Response), from a Linear Discriminant Analysis (black) overlaid on P(reversal∣M=BHV) (blue). Note that the decoding algorithm generates a posterior over reversal trials for each block. This plot shows the average of those posteriors. D. Histogram of decoded trial of reversal. Within a window around the actual reversal in each block, we searched for the trial with the maximum posterior from the neural decoding model: trial = argmax_(trial) P(reversal=trial ∣ Neural Response) and used this trial as the predicted reversal. We labeled decoded reversals as decoding error, i.e. the number of trials from the Bayesian point estimate for the behavioral reversal. The red dashed line shows chance level. Note that the histogram of decoded trials (D) usually matches the average posterior (C) but not always. The 5^th and 95^th percentiles of the decoding errors were −9 and 7 trials relative to reversal, respectively. The distribution of decoding errors was not significantly different between What and Where blocks (KS test, D_94,96=0.072, p=0.96), hence they were pooled together. Plots show mean±SEM across sessions (n=8).

Neural activity predicts choice preference reversal.

Next, we examined the reversal-related neural activity in more detail. We fit a linear model (Fig. 2C) to the spike count data using all regressors except the Bayesian estimate of the posterior p(reversal∣M=BHV) (see Methods). We then extracted the residuals from this model and computed the Sum of Squared Residuals across all recorded neurons (SSresid) for each trial and time window within a trial. For the time window from 0-300ms after cue onset, the SSresid followed closely the posterior over reversals, p(reversal∣M=BHV), when examined trial-by-trial (Fig. 3A). Both p(reversal∣M=BHV) and SSresid peaked at the trial at which the choice preference reversal occurred. We also examined the reward prediction error (RPE) from the RW model, as they would be large around the time of the reversal. RPEs peaked before the behavioral reversal trial and was overall biased to the trials before reversal (Fig. 3B). This is consistent with the animals integrating the RPE to drive their switch, but suggests that the neural activity represents the switch itself, and not the RPE. Supporting this point, SSresid has a significantly higher correlation with p(reversal∣M=BHV) than with the RPE, when examined session-by-session (t₇=9.83, p<0.001; see Fig. 3A,B, insets).

Next, we used the residual neural activity to predict the reversal trial and compared this to the actual behavioral reversal trial. We first predicted the reversal trial in each block by finding the trial (within a window ±10 trials around reversal) with the highest SSresid. We found that the trial with the largest SSresid was useful to decode the reversal (Fig. S2). However, SSresid is an unsigned quantity, thus this approach is blind to activity patterns (i.e. both increases and decreases in single cell activity that may signal reversals) in the neural population. To take the population response pattern into account, we used the adjusted neural activity (e.g. the residual activity without squaring) to classify trials into reversal and non-reversal using Linear Discriminant Analysis (LDA). In each block, the LDA takes the adjusted activity of all the recorded neural population (predictors) and generates a posterior probability distribution that the reversal occurred on each trial, p(reversal∣Neural Response). We first examined the mean p(reversal∣Neural Response), and found that the neural posterior probability peaked at the behavioral reversal trial (Fig. 3C) and approximated p(reversal∣M=BHV) closely. Next, we decoded the single trial in each block on which the reversal occurred, using the neural activity. The decoded reversal trial in each block was the trial with the maximum posterior probability (MAP). By computing this MAP estimate for each block from p(reversal∣Neural Response), we were able to decode accurately the trial at which the choice preference reversed for most of the blocks (Fig. 3D). We repeated this analysis on raw spike counts rather than the adjusted activity (Fig. S3) and found a similar p(reversal∣Neural Response), however, the distribution of decoded reversal trials is less accurate than that obtained using the residual activity. This mismatch indicates that activity not related to reversal introduces noise in the decoding.

Reversal decoding uncertainty is related to uncertainty in behavior

We examined p(reversal∣M=BHV) separately for blocks that differed in the neural decoding error (i.e. the difference between the behavioral reversal and the decoded reversal) to assess whether p(reversal∣M=BHV) was related to decoding accuracy. When we plotted p(reversal∣M=BHV) as a function of the size of the decoding error (Fig. 4A), we found that larger decoding errors were associated with wider distributions of p(reversal∣M=BHV). Thus, when the animal failed to reverse abruptly, as evidenced by a broad distribution over trials, the decoding error was large (Fig. 4B). To characterize uncertainty in the behavioral posterior, we calculated the standard deviation of the p(reversal∣M=BHV) distribution. The standard deviation was correlated with the decoding error (Pearson R=0.224±0.07, mean±SEM across sessions). Because noisy posterior distributions tended to have more than one peak, we also calculated the entropy of the p(reversal∣M=BHV) distribution to measure of the concentration of the distribution. Entropy was also correlated with decoding error (Fig. 4C). In fact, t-tests revealed that the Pearson correlation coefficient was significantly different from zero (t₇=3.76, p=0.007), as well as the slope of the regression (t₇=3.82, p=0.006). Plus, an ANOVA that used block-by-block decoding error and entropy revealed a significant main effect of decoding error size on the entropy (F_1,188=22.81, p<0.0001).

Figure 4.

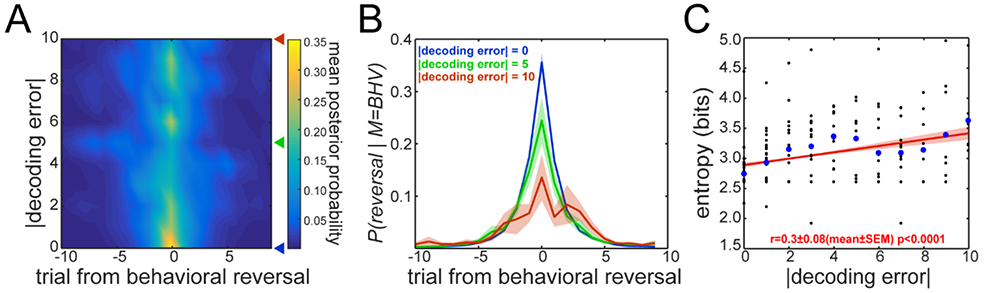
Decoding error and noise in behavior. A. Bayesian P(reversal∣M=BHV) distribution averaged across blocks as a function of absolute neural decoding error. Color code indicates probability. The triangle markers to the right of the plot mark decoding error values 0 (blue), 5 (green) and 10 (red). B. P(reversal∣M=BHV) distributions (mean±SEM, n=8 sessions) around the behavioral reversal point for three different decoding error values. C. Entropy of the P(reversal∣M=BHV) distributions as a function of decoding error. Black dots are entropy values for individual blocks and blue circles are the mean across blocks with the same absolute decoding error value. Mean regression line across sessions in red, shading is the SEM of the regression line.

The reversal signal develops at the time of the outcome on the pre-reversal trial

Up to this point we have focused on a time window from 0-300ms after cue onset. To examine the time-course of this signal, we decoded the reversal using spike counts from a sliding window (300ms width, 50ms steps, Fig. 5A). We were able to accurately decode the reversal trial from ~100ms after cue onset until ~400ms after cue onset, then the peak of the decoded reversal distribution shifted to −1, i.e. the trial previous to the behavioral switch (Fig. 5B). The timing of this shift matched the average time at which the reward was stochastically delivered (or not), suggesting that the neural signal related to reversals develops after the animal knows the outcome on the trial before it reverses its choices. To examine this, we decoded the reversal trial using neural data aligned to the expected time of the trial outcome. Results of decoding using data from a sliding window showed that after the outcome was revealed, the decoded reversals predict that the choice reversal will happen in the next trial (Fig. 5C,D). In fact, for a window from 0-300ms after trial outcome, the p(reversal∣Neural Response) distribution is shifted to the left, peaking 1 trial before the behavioral reversal (Fig. 5E). Thus, the intention to switch is represented as soon as the monkeys learn the outcome and continues into the switch trial.

Figure 5.

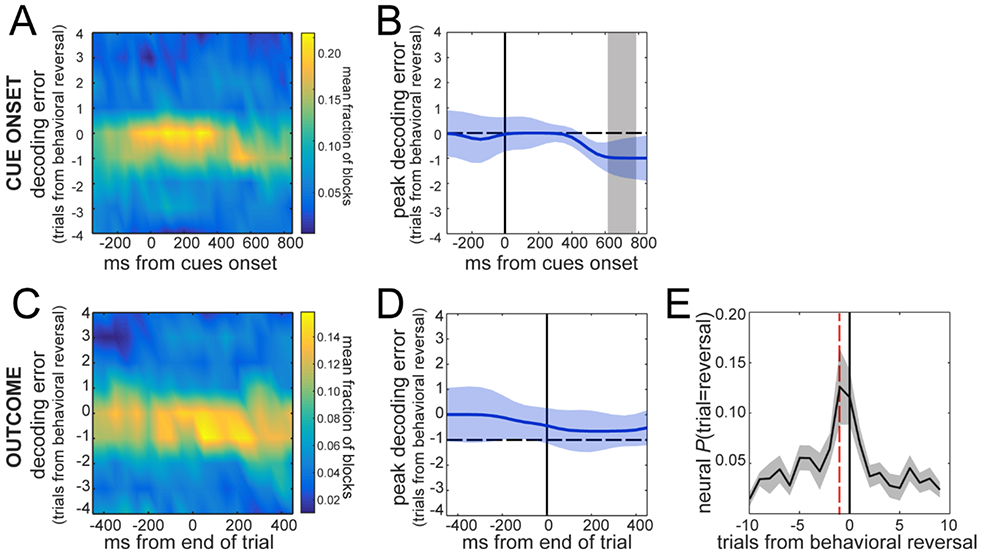
Decoding of Reversal across trial execution. A. Decoding error distributions for a sliding time window (300ms width, 50ms step) during trial time using data aligned to cue onset. Color code is fraction of blocks. B. Peak decoding error during trial execution. The gray shaded area depicts the time window at which the trials ended and the outcome (reward/no-reward) was known to the animals. C. Decoding error distributions for data aligned to cue onset. Color code is fraction of blocks. Spikes were aligned to the time of the trial outcome/end of trial. D. Peak decoding error during trial execution around outcome time. The dashed line marks decoding error = −1. E. Mean posterior probability P(trial=reversal∣Neural Response) distribution for a 300ms window starting at outcome time. Red dashed line shows trial −1 from behavioral reversal. Values in B, D and E are means±SEM across sessions (n=8).

Uncertainty at the beginning of a new block

Next, we asked if the observed signal could be interpreted as a general state uncertainty signal, rather than a signal for the reversal of choice behavior. On the first few trials of a new block, the SSresid is roughly as high as at the trial of reversal (Fig. 6A). When we repeated this using spike counts in a window 0-300ms from trial outcome (Fig. 6B), the SSresid decreased faster. This shows that there is a response at the beginning of a new block similar in magnitude to the response at the reversal point. Thus, this could be a general state inference signal, since a state (i.e. Block Type) has to be inferred at the beginning of the block, as well as at the reversal point.

Figure 6.

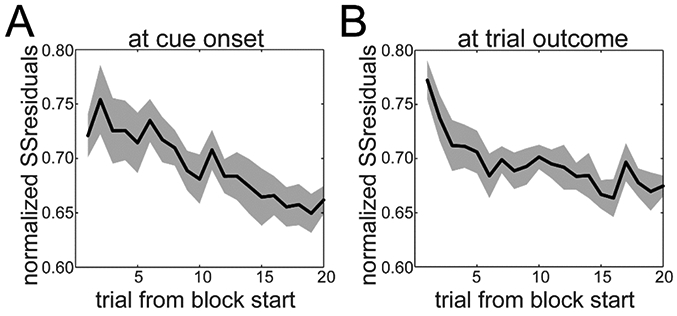
Sum of Squared Residuals (SSresid) during the first 20 trials in the block. A. SSresid for a window from 0-300ms after cue onset. B. SSresid for a window from 0-300ms after trial outcome. Means±SEM across sessions (n=8).

Following this, we examined whether the population code for state uncertainty at the beginning of the block is the same as the code at the time of reversal. Since SSresid is unsigned, it could be that the response patterns were different in these two epochs. For all units in our recorded population, we compared the mean residual activity during the first three trials of the block with the mean response of three trials centered at the behavioral reversal. We found a small negative correlation between the two response patterns which was significant, given the large number of neurons (r=−0.0474, p=0.044). When we squared the residuals, thus ignoring the direction of the response, the correlation turned out to be high and significant (r=0.6627, p<0.0001). Furthermore, by fitting a multiple linear regression model to the spike count data (see Methods) we found an association between population activity and the Bayesian BHV estimates for Block Type (Fig S4A,B). Thus the blocktype inference is also represented in the PFC. Note that the initial state of the network seems to be biased toward the Where block type (Fig S4B).

These results indicate that PFC neural populations carry a signal that may reflect uncertainty, during both acquisition and reversal. However, the activity pattern of the population differs between these two epochs of the block, suggesting that the state of the neural population changes throughout learning.

Network state evolves from a pre-reversal state to a final state within a block of trials.

We further analyzed the evolution of network activity during the execution of a block of trials, and how different the network state was between epochs of a block. Using spike counts from 0-500ms after cue onset, we performed a Principal Component Analysis (PCA) to compute neural trajectories across trials in a block. In an example session (Fig 7A), the network activity moved within the first 10 trials of the block from an initial state (Fig 7A, blue segment) to a more stable pre-reversal state restricted to a region of the PCA space. Then, around the reversal, the trajectory exited the pre-reversal region and moved toward a final region (orange shade), remaining in it during the last 20 trials of the block, far from the acquisition. We computed the Euclidean distance between the centroid of the final state (mean PC score during the last 20 trials) and each trial during the block. The maximum separation was between the first trial and the final state (Fig 7B), then it quickly decreased to a plateau that lasted for most of the acquisition phase, until the behavioral reversal, indicating that the population remained in the same state during the late acquisition phase. After the reversal, the distance quickly decreased as the neural activity moved toward its final state (Fig 7B, orange shading). Interestingly, neural trajectories computed separately for What and Where blocks start in a similar region of the PCA space and then diverge (Fig S4C,D) indicating that block type inference leads to different latent subspaces.

Figure 7.

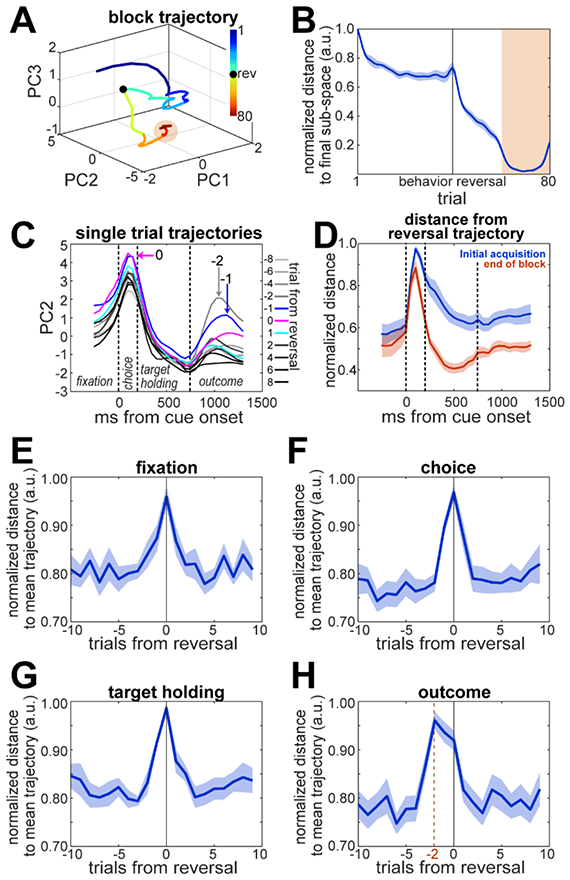
Neural state-space trajectories. A. Neural trajectory across trials for an example recording session. The curve represents the average trajectory for all blocks in the session. Color code is trial number within block. Orange shading illustrates the final state-space region where the neural activity lies, centered on the average of the last 20 trials in the block. B. Euclidean distance between the location for each trial in the PCA space and the centroid of the final state-space (means±SEM across sessions). C. Trial neural trajectories over the 2nd principal component for an example session. Each trace corresponds to a trial around the reversal (trials −10 to 9 from reversal, color coded), averaged over blocks. Dashed lines divide the different trial periods (see Fig 1A). Arrows and numbers point at the period of the trial on which the trajectory of the indicated trial (−2, −1 and 0) deviates the most from the average trajectory of all other trials. D. Distance from the average trajectory around the reversal (trials - 2 to 0 from reversal) to the average trajectory during the initial acquisition (first 5 trials in the block, blue) and to the average trajectory at the end of the block (last 10 trials in the block, red). Distances were normalized by the maximum observed value, thus ranging between 0 and 1. E-H. Distances between trajectories of each individual trial and the average of all other trials in different trial periods. Data are means±SEM across sessions (n=8).

Neural trajectories diverge around the behavioral reversal.

In Fig 7A there is a disturbance around the point of reversal. We asked if the single-trial neural trajectories around the reversal diverged from the trajectories of the other trials. We divided each trial into overlapping time bins (100ms width), evenly distributed within each trial period. Then, we used PCA to obtain single-trial neural trajectories. Fig 7C shows the evolution of the neural activity over the 2nd PC for trials around the reversal from an example recording session. In this example, PC2 shows interesting differences in the neural trajectories of different trials at different times within each trial: the neural trajectories of the reversal trial (trial 0) and the trial before the reversal (trial −1) diverge from the trajectories of other trials during the choice period. Furthermore, after the outcome the trajectories of the two trials before the reversal deviate from the average trajectory. To characterize these deviations, we computed the Euclidean distance between the neural trajectory around the reversal (average of trials −2 to 0 from reversal) and the average trajectory during the initial acquisition (first 5 trials in the block) or the end of the block (last 10 trials in the block) (Fig 7D). The distance between reversal and acquisition is generally larger than that between reversal and the end of the block, suggesting that the state of the network changes more dramatically during the acquisition phase, when value is assigned to each option. The distance between the trajectories in the reversal trials and the trajectories from the end of the block peak during the choice period, reflecting the change in the state of the network between phases. It then decreases during the target hold period and is smaller than the distance between reversal and acquisition trajectories. This suggests that target-holding activity may be related the valuation of the chosen option. To examine trials around the reversal more closely, we computed the distance between the trajectory for each trial around the reversal and the average trajectory of all other trials during each trial period (Fig 7E-H). The trajectory deviations peak at the trial of reversal during the fixation, choice, and target-holding periods, but after the outcome, the peak deviation switches to 2 trials before the behavioral reversal (Fig 7H). These results match our decoding analysis.

Using small populations decreases reversal decoding performance.

Finally, we investigated if we would obtain the same results using smaller populations. We repeated the decoding analysis using randomly selected populations of varying size from the total recorded population in each session (500 populations of each size). We computed the average posterior P(reversal∣Neural Response) distribution for each population size (Fig 8A). As the population size decreased, the posterior distribution became uniform and was less peaked around the reversal trial. We also computed the distributions of decoding errors for each population size (Fig 8B). Reversal decoding accuracy was dramatically lower for small populations (25 neurons) than for large populations (>500 neurons). In fact, the mean fraction of blocks for which the reversal was decoded accurately (i.e. decoding error=0) was 0.086, which is not significantly above chance level (0.05) for a given session of 24 blocks (binomial test, p=0.116).

Figure 8.

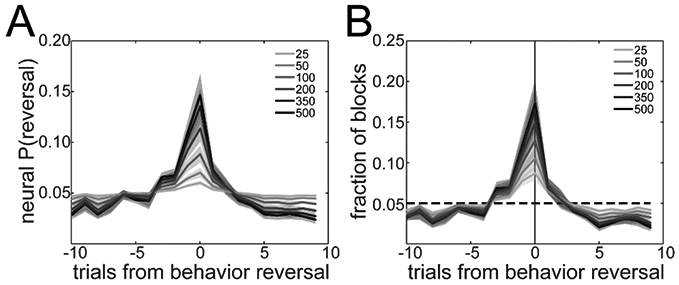
Effect of population size on decoding of reversal A. Distribution of the classification P(reversal∣Neural Response) over trials around the estimated reversal for different population sizes (grayscale coded). B. Histogram of decoded trial of reversal. The dashed line shows chance level. Data are means±SEM across sessions.

Discussion

Reversal learning tasks have long been used to study behavioral flexibility (Dias et al., 1996; Groman et al., 2019; Iversen and Mishkin, 1970; Jones and Mishkin, 1972). They were originally motivated by the finding that patients with dorsal-lateral PFC damage had perseverative deficits in the Wisconsin Card Sorting task (Milner, 1963). There are several approaches to studying reversal learning, with important differences between them. Originally, animals were studied while they learned that reversals occur (Butter, 1969; Iversen and Mishkin, 1970; Jang et al., 2015; Rudebeck et al., 2013). These tasks test learning to learn (Harlow, 1949; Neftci and Averbeck, 2019), which is the process of learning a model of the world (Jang et al., 2015). Before animals have acquired a model of the task, learning may be driven by general-purpose model-free mechanisms, similar to the RW model used here. Evidence suggests that ventral-lateral PFC in macaques (Murray and Rudebeck, 2018; Rudebeck et al., 2017b; Rudebeck et al., 2013) and neighboring OFC in rats (Stalnaker et al., 2007) and marmosets (Dias et al., 1996) play an important role in acquiring a model of the task.

Other work, including the presented here, has focused on over-trained animals that have acquired a Bayesian model of the task, which allows for more efficient inference and better decisions (Costa et al., 2016; Costa et al., 2015; Farashahi et al., 2017; Groman et al., 2019; Rothenhoefer et al., 2017). After the task is over-trained, animals are no longer learning the task structure. Rather, they are using the acquired model to carry out inference and make choices, integrating multiple behavioral and neural processes. The animals must infer the block type (i.e. What vs. Where), the best initial choice within the block, and then infer reversals. We have previously shown that the amygdala and ventral-striatum contribute to inferring the correct choice within a block (Costa et al., 2016; Rothenhoefer et al., 2017), with the ventral-striatum playing a specific role in learning the values of objects (Rothenhoefer et al., 2017). This is consistent with these subcortical structures mediating a model-free learning process, as has been suggested by previous work (Averbeck and Costa, 2017; Daw et al., 2006; Hampton et al., 2007; Lee et al., 2015; O'Doherty et al., 2004; Rudebeck et al., 2017a; Seo et al., 2012; Taswell et al., 2018). We have not found evidence that either the ventral-striatum or the amygdala drives reversals, although both structures are capable of representing complex reward values, e.g. the value of exploring novel options when mediating explore-exploit trade-offs (Costa et al., 2019). In addition, although we focused on inferring reversals, we show that two state inference processes are performed. At the beginning of each block animals have to infer the Block Type, which is equivalent to inferring a task from a known set (Collins and Frank, 2013). The finding of a bias toward the Where condition, along with previous findings (Rothenhoefer et al., 2017), lead us to hypothesize that the Where rule is used as a starting point.

We found that the animals rapidly switched their choice preference following reversals in this task, consistent with Bayesian state inference. Previous studies have suggested that regions of the PFC are important for state inference, including the orbitofrontal cortex (Schuck et al., 2016; Wilson et al., 2014), limbic PFC (Starkweather et al., 2018), anterior cingulate cortex (Durstewitz et al., 2010; Sarafyazd and Jazayeri, 2019) and the frontal-parietal network (Glascher et al., 2010). Similarly, neural activity coding ‘explore’ vs ‘exploit’ states has also been observed in the frontal eye fields (Ebitz et al., 2018) and anterior cingulate (Karlsson et al., 2012). The dorsal-lateral PFC also represents current choice strategies, which may reflect states (Genovesio et al., 2005). These studies have all found correlates of the current state. Our study shows that dorsal-lateral PFC also codes state switches, in the context of a task where detecting switches in choice-outcome mappings to switch behavior accordingly is optimal. In addition, we found that the signal arose in the trial before the monkey reversed its choice preference, after receiving feedback (usually negative) for its choice. The signal was also not consistent with the reward prediction error. Although there were large RPEs around the time of the switch, they peaked in the trial before the switch. Hence, the signal appears to code a state switch, further supported by our decoding analysis.

From a behavioral modeling point of view, the Bayesian model provides a formal description of the reversal process, whereas the RW model captures aspects of the update mechanism, and the reward prediction errors used by the RW and PH model have been closely linked to dopamine (Schultz and Romo, 1990; Steinberg et al., 2013). A wide space of models exists between the RW model, which has no information about the statistical structure of the task, and the Bayesian model, which has complete information about the structure of the task. Future work could examine, for example, models that incorporate knowledge of the acquisition and reversal phases, which have been used previously to study reversal behavior. In addition, more general reinforcement learning models based on sophisticated state spaces that incorporated information about the trial in the block could be developed. Such models could be used to learn that reversals happen in the middle of the block, therefore they would likely reverse choice preferences more rapidly.

There is extensive work on the neural systems underlying model-free RL learning (Frank et al., 2004; Houk et al., 1995). This work has focused on dopamine and its projections to the striatum (Lau and Glimcher, 2008; Lee et al., 2012; Lee et al., 2015; Pessiglione et al., 2006; Samejima et al., 2005), following the finding that dopamine codes RPEs (Kim et al., 2009; Montague et al., 1996; Schultz et al., 1997). However, many important learning processes, including the state inference studied here, are more complex than model-free RL. For example, complex behavior is often hierarchically organized, and hierarchical RL algorithms can learn more efficiently than non-hierarchical algorithms in these scenarios (Badre and Frank, 2012; Botvinick, 2008; Botvinick et al., 2009; Collins and Frank, 2013; Dayan and Hinton, 1993; Frank and Badre, 2012). Current theories suggest that complex learning mechanisms, including hierarchical RL and model-based learning (Abe et al., 2011; Daw et al., 2011; Doll et al., 2012), may be mediated by the PFC (Wang et al., 2018). However, much work still needs to be done to understand how these various behavioral mechanisms are implemented by cortical and subcortical structures, and how they are integrated, when tasks tap into more than one.

Conclusion

Learning to make optimal choices in diverse environments is mediated by a network of cortical and subcortical areas, including PFC, the amygdala, basal ganglia and thalamus (Lee et al., 2012; Neftci and Averbeck, 2019). Even simple learning tasks likely engage learning processes on multiple time-scales (Averbeck, 2017) from working and episodic memory (Collins and Frank, 2012; Gershman and Daw, 2017), to plasticity mediated by dopamine or spike-timing mechanisms that operate on longer time-scales (Averbeck and Costa, 2017; Frank, 2005). The reversal learning task we used is likely solved by both model-free mechanisms, perhaps mediated by sub-cortical structures including the striatum and amygdala (Costa et al., 2016; Costa et al., 2019) and Bayesian mechanisms, which may be mediated by cortical structures, as shown here. Future work analyzing the contributions of multiple cortical and subcortical nodes, and their interactions, is necessary to build a detailed understanding of how multiple learning processes are orchestrated to implement these behaviors.

STAR Methods.

LEAD CONTACT AND MATERIALS

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Ramon Bartolo (ramon.bartoloorozco@nih.gov).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experimental procedures were performed in accordance with the ILAR Guide for the Care and Use of Laboratory Animals and were approved by the Animal Care and Use Committee of the National Institute of Mental Health. Procedures adhered to applicable United States federal and local laws, regulations and standards, including the Animal Welfare Act (AWA 1990) and Regulations (PL89–544; USDA 1985) and Public Health Service (PHS) Policy (PHS2002). Two male monkeys (Macaca mulatta, W - 6.7kg, age 4.5yo, V - 7.3kg, age 5yo) were used as subjects in this study. All analyses were performed using custom made scripts for MATLAB (The Mathworks, Inc.). All behavioral parameters were controlled using the open source MonkeyLogic software (http://www.brown.edu/Research/monkeylogic/). Eye movements were monitored using the Arrington Viewpoint eye-tracking system (Arrington Research, Scottsdale, AZ).

METHOD DETAILS

Reversal Learning Task.

Monkeys were trained to perform a two-arm reversal learning task (Fig. 1A) while they were seated in front of a computer screen. The task was organized in blocks of 80 trials. On each trial, animals had to acquire and hold central fixation for a variable time (400-800ms). After fixation, two cues (squared images 2°×2° degrees of visual angle) were presented simultaneously to the left and right of the fixation dot (6° away from fixation) instructing the monkeys to make a choice. The monkeys reported their decision by making a saccade to the chosen option. After holding sight on their choice for 500ms reward was delivered stochastically with a few drops of juice.

On What blocks, high (p=0.7) or low (p=0.3) reward probabilities were randomly assigned to each image. On Where blocks, reward probabilities were randomly assigned to each location (left/right), independently of the image presented on that location. Two novel images were used on every new block and their locations (left/right of the central fixation) was randomized across trials. By trial-and-error, monkeys had to learn which factor (location or picture) was the relevant for reward and which one of the two available options was the high reward probability choice. On each individual block, the type (What or Where) was help constant, but the reward mappings were switched across options at a random trial (Reversal) within a window from trials 30-50, thus the monkeys had to reverse their choice behavior to maximize the received reward. Typically, monkeys performed 24 blocks on a given recording session (12 What + 12 Where, randomized) receiving a total daily amount of 175-225 mL of juice.

The images used as cues were normalized for luminance and spatial frequency using the SHINE toolbox for MATLAB (Willenbockel et al., 2010). All images were converted to grayscale and subjected to a 2-D FFT to control spatial frequency. To obtain a target amplitude spectrum, the amplitude at each spatial frequency was summed across the two image dimensions and then averaged across images. Next, all images were normalized to have this amplitude spectrum. Using luminance histogram matching, we normalized the luminance histogram of each color channel in each image to match the mean luminance histogram of the corresponding color channel across all images. Spatial frequency normalization always preceded the luminance histogram matching. We manually screened each image to verify its integrity. Images that were unrecognizable after normalization were discarded.

Data acquisition and preprocessing.

Microelectrode arrays (BlackRock Microsystems, Salt Lake City, USA) were surgically implanted over the prefrontal cortex (PFC), surrounding the principal sulcus (Fig. 1B). Four 96-electrode (10×10 layout) arrays were implanted on each hemisphere. Details of the surgery and implant design have been described previously (Mitz et al., 2017). Briefly, a single bone flap was temporarily removed from the skull to expose the PFC, then the dura mater was cut open in order to insert the electrode arrays into the cortical parenchyma. Finally, the dura mater was sutured, and the bone flap was placed back and attached to the skull with absorbable suture, thus protecting the brain and the implanted arrays. In parallel, a custom designed connector holder, 3D-printed using biocompatible material, was implanted onto the posterior portion of the skull.

Recordings were made using the Grapevine System (Ripple, Salt Lake City, USA). Two Neural Interface Processors (NIPs) made up the recording setup, one NIP (384 channels each) was connected to the 4 multielectrode arrays of one hemisphere. Synchronizing behavioral codes from Monkey Logic and eye tracking signals were split and sent to each NIP box. Raw extracellular signal was high-pass filtered (1kHz cutoff) and digitized (30kHz) to acquire single unit activity. Spikes were detected online and the waveforms (snippets) were stored using the Trellis package (Grapevine). Single units were manually sorted offline. We collected neural data in 8 recording sessions (4 sessions per animal).

QUANTIFICATION AND STATISTICAL ANALYSIS

Bayesian model of choice behavior.

We fit a Bayesian model to estimate probability distributions over several features of the animals’ behavior as well as ideal observer estimates over these features as described elsewhere (Costa et al., 2015; Rothenhoefer et al., 2017). We extracted probability distributions over the behavioral reversal point as well as the block type.

Briefly, to estimate the Bayesian model we fit a likelihood function given by:

$$f(x,y\mid r,h,b,p)={\prod }_{k=1}^{T}q(k)$$ (1)

Where r is the trial on which the reward mapping switched across options (r ϵ 0-81). The variable h encodes whether option 1 or option 2 is the high reward option at the start of the block (h ϵ 1, 2),b encodes the block type (b ϵ 1, 2 – What or Where) and p indexes the reward rate in the block (0.5 < p < 1.0). The variable k indexes trial number in the block and T is the current trial. The variable k indexes over the trials up to the current trial so, for example, if T = 10, then k = 1, 2, 3, … 10. The variable r ranges from 0 to 81 because we allow the model to assume that a reversal may not have happened within the block, and that the reversal occurred before the block started or after it ended. In either scenario where the model assumes the reversal occurs before or after the block, the posterior probability of reversal would be equally weighted for r equal to 0 and 81. The choice data are given by x and y, where elements of x are the rewards (x_i ϵ 0, 1) and elements of y are the choices (y_i ϵ 1, 2) in trial, i.

For the ideal observer model used to estimate the reversal trial and the “ideal” curve in the Bayesian analysis, we estimated the probability that a reversal happened at the current trial, T, based on the outcomes from the previous trials. Thus, the estimate is based on the information that the monkey had when it made its choice in the current trial. The following mappings from choices to outcomes gave us q(k). For estimates of What (i.e. b = 1), options 1 and 2 refer to the individual images and location is ignored; whereas for Where (i.e. b = 2), options 1 and 2 refer to the location (left/right) and the image is ignored. Let p be the reward probability of the high probability option. For k < r and h = 1 (namely, the current trial is prior to the reversal and option 1 has the high reward probability) choose 1 and get rewarded q(k) = p, choose 1 and receive no reward q(k) = 1 – p, choose 2 and get rewarded q(k) = 1 – p, choose 2 and have no reward q(k) = p. For k ≥ r these probabilities are flipped. For k < r and h = 2 the probabilities are complementary to the values where k < r and h = 1. To estimate reversal, all values were filled in up to the current trial, T.

For the animal’s choice behavior, the model is similar, except the inference is only over the animal’s choices independently of the outcomes of the choices. We assumed that the animal had a stable choice preference which switched at some point in the block from one option to the other. Given the choice preference, the animals chose the wrong stimulus (i.e. the stimulus inconsistent with their choice preference) at some lapse rate 1-p. Thus, for k < r and h = 1 choosing option 1: q(k) = p, choosing option 2: q(k) = 1 – p. For k ≥ r and h = 1, choosing option 1: q(k) = 1 — p, choosing option 2: q(k) = p. Correspondingly for k < r and h = 2, choosing option 2: q(k) = p, etc.

Using these mappings for q(k), we then calculated the likelihood as a function of r, h, b and p for each block of trials. The posterior is given by:

$$p(r,h,b,p\mid x,y)=\frac{f(x,y\mid r,h,b,p)p(r)p(h,b,p)}{p(x,y)}$$ (2)

For h, r, b, and p the priors were flat and independent. The normalization constant is given by p(x, y) = ∑_r,h,b,p f(x, y∣r, h, b, p) p(r) p(h, b, p) as we used a discrete approximation to p(p). With these priors, there is general agreement between the ideal observer estimate of the reversal point and the actual programmed reversal point (Fig. 1C).

We calculated the posterior over the reversal trial (denoted p(reversal∣M) in the results section) by marginalizing over h, b and p.

$$p(r\mid x,y)={\sum }_{h,b,p}p(r,h,b,p\mid x,y)$$ (3)

The posterior over block type could correspondingly be calculated by marginalizing over r, h and p.

Reinforcement Learning models of choice behavior.

We fit Rescorla-Wagner (RW) reinforcement learning models to the choice data for each block type. We fit models with separate learning rates and inverse temperatures for the two block types. In the mode, value updates were given by:

$$v_i(k+1)=v_i(k)+{\delta }_f\left(R-v_i(k)\right)$$ (4)

Where v_i is the value estimate for option i, R is the outcome for the choice for trial k, and δ_f is the outcome-dependent learning rate parameter, where f indexes whether the current choice was rewarded (R = 1) or not (R = 0), i.e. δ_pos, δ_neg. For each trial, δ_f is one of two fitted values used to scale prediction errors based on the type of reward feedback for the current choice. We then passed these value estimates through a logistic function to generate choice probability estimates:

$$d_1(k)=(1+e^{\beta \left(v_2(k)-v_1(k)\right)}{)}^{-1},d_2(k)=1-d_1(k)$$ (5)

The likelihood for these models is given by:

$$f\left(x,y\mid \beta ,{\delta }_{pos},{\delta }_{neg}\right)={\prod }_k[d_1(k)c_1(k)+d_2(k)c_2(k)]$$ (6)

Where c₁(k) had a value of 1 if option 1 was chosen on trial k and c₂(k) had a value of 1 if option 2 was chosen. Conversely, c₁(k) had a value of 0 if option 2 was chosen, and c₂(k) had a value of 0 if option 1 was chosen for trial k. We used standard function optimization methods to maximize the likelihood of the data given the parameters.

We also fit Pearce-Hall (PH; sometimes referred to as hybrid Pearce-Hall) reinforcement learning models to the data, to allow for more flexibility in the learning rates:

$$v_i(t+1)=v_i(t)+\kappa {\alpha }_t\left(R-v_i(t)\right)$$ (7)

where v_i is the value estimate for option i, R is the outcome for the choice for trial t, κ is the salience parameter and α_t is the associability parameter, which is updated on each trial by:

$$\alpha (t+1)=\eta \mid R-v_i(t)\mid +\alpha (t)\ast (1-\eta )$$ (8)

where η is the maximum associability. We then passed these value estimates through a logistic function to generate choice probability estimates (Eq. 5). The likelihood function was given by:

$$f(x,y\mid \beta ,\alpha ,\kappa ,\eta )={\prod }_k[d_1(k)c_1(k)+d_2(k)c_2(k)]$$ (9)

For both models we used standard function optimization methods to maximize the likelihood of the data given the parameters.

Comparison of models of reversal behavior

We predicted the behavior around the reversal trial (i.e. from trial 20-60) using the Bayesian model and RW and PH models. To compare the RW and PH models to the Bayesian model we marginalized over model parameters to estimate the marginal likelihood of each model:

$$p(x,y\mid \theta ,M=RWorPH)=\int f(x,y\mid \theta {)}_{k\in \{20\dots 60\}}p(\theta )d\theta .$$ (10)

For the RW model θ_RW = β, α_pos, α_neg and for the PH model θ_PH = β, κ, η. For the RW and PH models the likelihood is given by:

$$f(x,y\mid \theta {)}_{k\in \{20\dots 60\}}={\prod }_{k\in \{20\dots 60\}}[d_1(k)c_1(k)+d_2(k)c_2(k)].$$ (11)

The integral in equation 10 was approximated numerically. We used flat priors, consistent with the Bayesian model. Learning rates (i.e. α, κ, η) were assumed uniform on [0, 1] and betas were uniform on [1, 11]. We then directly sampled from f(x, y∣θ)_kϵ{20…60}p(θ) 500 times to estimate the integral.

For the Bayesian model we explicitly computed the marginal likelihood, which is also the normalization constant of the Bayesian model, p(x, y∣M = Bayes) as defined above. When then computed the pair-wise log Bayes Factors (BF), which are the posterior pair-wise log odds of the models:

$$logBF=ln\frac{p(x,y\mid M=Bayes)}{p(x,y\mid M=PHorRW)}.$$ (12)

In the results we report the mean BF as well as a t-stats across the BF calculated in each session. The Bayesian model was favored to both models (i.e. BF > 0) in 7/8 sessions.

Analysis of single unit responses.

ANOVAs were applied to the single neuron data to assess response association. The dependent variable was the spike count of the single neuron in a sliding window (300ms, 25ms steps), aligned to cue onset. The ANOVA included main effects for trial-in-block, block-in-day, chosen location, chosen image (nested in block-in-day) and reward. These were included as categorical factors. In the same model, the Bayesian estimates across trials for the posterior P(reversal∣M=BVH) and P(block type=What∣M=BHV) were included as continuous factors. The same model was applied to all time windows, even when the variable could not have been reflected in the neural data, for example reward outcome at the time of choice. This allowed us to see that we were only getting significance at the alpha level (i.e. 0.01) for these variables.

Decoding of behavioral reversal.

We computed the residual activity of each recorded single unit fitting a linear model to the trial by trial neural responses. The model included as regressors: trial-in-block (TIB), block-in-day (BID), trial by trial posterior probability for Block Type, image chosen (nested within BID), location chosen, and choice outcome (reward/no-reward). The response variable of the model was a vector of spike counts within a 300ms sliding window moving in 50ms steps. For each time window we computed the Sum of Squared Residuals (SSResid) across all the units recorded in each session as a measure of response strength.

Next, we decoded the trial of reversal using Linear Discriminant Analysis (LDA). We fitted an LDA model to the residual activity in the window that started at the time of cue onset using the function fitcdiscr in Matlab. To control for the imbalance between the number of observations ‘reversal’ trials (1 per block) vs. ‘non-reversal’ trials (19 per block) we fitted the LDA model using a flat prior. Then, we used this model to decode the trial of reversal in all time windows. We predicted the trial of reversal searching for the trial with the maximum posterior P(reversal∣Neural Response) within a 20 trial window centered at the point estimate for the behavioral reversal. The results are shown as decoding error, which was defined as the difference between the predicted trial of reversal and the behavioral reversal from the Bayesian model. For this procedure we performed 10-fold cross-validation.

Regression of posterior probabilities for Block Type on neural response patterns.

We analyzed the association between the neural activity and Block Type Bayesian estimates fitting a multiple linear regression model regularized with early stopping. We used spike counts from a window from 0-300 ms from cue onset as predictors, and the logit-transformed posterior P(Block Type=what ∣ BHV) as the dependent variable. To estimate the model parameters, we maximized the log-likelihood using a cross-validated early-stopping algorithm (Fukushima et al., 2014). We split the data into 3 subsets of randomly taken trials: 1) A training set (90% of the trials) was used to train the model, updating the parameters to improve the log-likelihood on each iteration, 2) a stopping subset (5% of the trials) used to stop the algorithm when the log-likelihood value calculated with this subset became smaller than the value in the previous iteration, and 3) a reporting subset (5% of the trials), from which spike counts were projected onto the parameter estimates. We performed 20-fold cross-validation. The model predictions were back converted using the inverse logit function to compute the predicted P(Block Type=what ∣ Neural Response).

Neural trajectories.

We analyzed the evolution of neural activity across trials using Principal Component Analysis (PCA). First, we generated a spike count matrix using a sliding window (100ms) that was moved at variable step size in order to have the same number of windows (31) for all trials, independently of variations in total trial duration due to unequal reaction times. We aligned the time windows to have a constant number of windows per trial period, namely: fixation (5 windows), choice (4 windows), target holding (11 windows) and post-outcome (11 windows) periods. These windows were evenly spaced within each period of a trial and had a ~50ms overlap with each other.

Next, to generate block neural trajectories, for each trial we averaged the spike rate of the first 8 time-windows after cue onset. Then we stacked the averaged spike rates from all trials in a given recording session and performed the PCA on this stacked matrix. The size of this matrix was given by the number of trials × number of blocks (rows) and the number of neurons (columns) in the recording session. For all calculations made using neural trajectories (Euclidean distances, principal angles) we used the n-principal components that explained 70% of the variance. Block trajectories were smoothed using a kernel weighted moving average (gaussian, σ=3 trials) and the reversal points were aligned across blocks in a session.

To compute single-trial neural trajectories, we took the neural activity from trials −10 to +9 from the reversal point. We stacked the spike counts from all time windows and all trials and performed the PCA on this matrix. The size of this matrix was given by the number of trials × number of blocks × number of time windows in each trial (rows) and the number of neurons (columns) in the recording session. To calculate the Euclidean distances, we considered a sub-space defined by the n-principal components that explained 70% of the variance, as it was done for block trajectories. The total distance between the trajectory of each individual trial and the average of all other trajectories was calculated as the sum of all the pairwise distances between corresponding time windows. The distance was then normalized within each block to have a maximum value of 1.

DATA AND SOFTWARE AVAILABILITY

Analysis-specific code and data are available upon request to the authors.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Rhesus macaque (Macaca mulatta)	NIMH/NIH	N/A
Software and Algorithms
MATLAB	The MathWorks.	SCR_001622