A Guide for Private Outlier Analysis

Abstract

The increasing societal demand for data privacy has led researchers to develop methods to preserve privacy in data analysis. However, outlier analysis, a fundamental data analytics task with critical applications in medicine, finance, and national security, has only been analyzed for a few specialized cases of data privacy. This work is the first to provide a general framework for private outlier analysis, which is a two-step process. First, we show how to identify the relevant problem-specifications and then provide a practical solution that formally meets these specifications.

1. Introduction

Outlier analysis is extremely useful in practice, but the demand of data privacy hinders such an analysis—creating an urgent need to solve the problem of private outlier analysis, which we tackle in this work.

We emphasize that “private outlier analysis” is an umbrella term for a class of data analytics problems where privacy is to be protected. An obvious reason for having different problems is the need for different outlier models (i.e. a description of what is an “outlier”). However, even when we fix an outlier model, yet there are many distinct “private outlier analysis” problems. This is due to subtle but crucial differences in what information we seek from an outlier query and what information we want to protect.

The key contribution of this work is to provide a set of evaluation criteria—which are supported by theoretical and empirical analysis—that suggest which exact privacy problem one can solve in a way that is feasible but also meaningful and practical. To this end, we provide a novel taxonomy of privacypreserving outlier analysis problems and its solutions.

Below we provide three examples of outlier queries that cover a wide range of outlier analyses of practical interest. Here, at an intuitive level, for any given database, we either wish to identify which records are potentially outliers, or find if there is an “outlying event” (an event is a notion that depends on many records).

Q₁: Is the following transaction potentially a fraudulent one? “transfer 1 million dollars to acc# 123-4567, Cayman Isl. Bank”

Q₂: Which of today’s transactions are potentially fraudulent?

Q₃: Is there an Ebola outbreak in the last two days?

We will discuss (in the following sections) what is a suitable privacy notion in each of these three cases by looking at their differences. Note that privacy cannot be considered in a vacuum and any private analytics task needs to take both privacy and accuracy into account. Thus, in this context, the notion of privacy and the notion of outlier query form the two fundamental constituents of the problem of private outlier analytics.

Let us now highlight the heart of the matter by comparing Q₁, Q₂, and Q₃. In the case of an Ebola outbreak, the notion of “Ebola” and “outbreak” are universally defined concepts, and further, an “Ebola outbreak” is a property of the entire database (a predicate over its records). This sets Q₃ apart from Q₁ and Q₂. Because Q₁ and Q₂ regard individual records, where we tag a transaction as “potentially fraudulent” relative to other records in the database. Furthermore, we note that the query Q₁ pertains to information that is not necessarily an entry in the database; Q₂ however pertains to information about the records that exist in the database. This seemingly unimportant issue not only plays a pivotal role in specifying the right privacy-outlier problem, but it serves as a crucial technical distinction when solving the problem.

1.1. Outliers: the 1st constituent of the problem

Here we present a general and intuitive notion of an outlier, introduce basic notation for outlier model representation, and discuss what is a typical setting in practice.

Outliers are the non-conforming patterns or events. The nature of the non-conforming pattern varies across applications, domains, and data types. Hence, no single outlier model appropriately characterizes outliers in all environments [1], [7]. The existing models for characterizing outliers solve a specific formulation of the problem [1], [7]. Examples of widely used outlier models include LOF (local outlier factor), (ρ, D)-outlier, and AVF (attribute value frequency) outlier, or extreme value analysis based outliers [1], [16].

To represent an outlier model, we use a predicate. The domain of the predicate is decided by the type of the outlier. We consider two fundamentally different types of outliers: (i) outlier is a record, e.g. Q₂ where transactions are the records; and (ii) outlier is an event, e.g. epidemic outbreak, where database records are the health records. For (i), we represent the given outlier model by a predicate, p, over the domain $\mathcal{X}\times \mathcal{D}$. Here $\mathcal{D}$ and $\mathcal{X}$ denote¹ the set of all databases and the set of all possible values of records respectively—and each database $x\in \mathcal{D}$ is a multiset of elements from $\mathcal{X}$. Now, p(i, x) = 1 if a record of value i is an outlier with respect to the database x, otherwise p(i, x) = 0. We emphasize that for the predicate, p, to be true, a record of value i need not present in x, namely, p(i, x) = 1 does not imply i ∈ x. Similarly, for (ii), one can define a predicate $\widehat{p}$ over the domain $E\times \mathcal{D}$ for a given outlier model, where E is the set of events under consideration.

Practical settings.

We consider that databases are (1) typically sparse and (2) contain a small number of outliers. By sparsity, we mean that the size (∣x∣) of the database x is much smaller than the size of $\mathcal{X}$, i.e. $\mid x\mid <<\mid \mathcal{X}\mid$. The empirical evidence supports this belief² [2]. The typical outlier models rely on these assumptions to characterize (define) outlyingness [1], [7].

1.2. Privacy: the 2nd constituent of the problem

We consider two primary notions of data privacy: process privacy and output privacy, two fundamentally different concepts. Process privacy is a security/cryptography concept where information is hidden. Output privacy however regards information that is “plainly” presented but in a “sanitized” form. Let us explain through the following example.

Consider two banks each owning a database of transactions of its customers. Suppose the banks would like to collaborate to find fraudulent transactions in their respective databases (since such a collaboration increases the accuracy [3], [4]). They use an algorithm A for this purpose, which is given as input both the databases and an agreed outlier model.

Process privacy requires that each party who is involved in computing an outlier query should get no information beyond its input and output and everything that can be inferred from them³. For the example above, if the computation of A is such that each bank only receives the fraudulent transactions in its respective database (and nothing else), then A provides process privacy. If a third party is available, who is fully trusted⁴ and has access to all the data, we call it trusted curator and, in this case, achieving process privacy is immediate. But if there is no trusted curator for a setting, we can utilize secure computation to simulate the trusted curator and achieve process privacy. For this, we can either use general-purpose compilers, such as Yao garbled circuit [21] and Goldreich-Micali-Wigderson [14], or build problem-specific secure protocols to meet the efficiency requirements. Furthermore, Trusted Platform Modules or Hardware Security Modules can also be utilized to offload some of the costs of secure multiparty computation to further improve the efficiency [8].

Output privacy demands that from the output of a query we cannot tell (statistically) if any specific person’s information is recorded in the database [10]. For our example, if the output of A for each bank is such that it does not leak information about any individual customer of the other bank, then A provides output privacy. Here is one way to formalize this notion. Consider all the databases and a way to define which of them are neighbors. Then, for any α > 1, a mechanism M (mechanism = type of query), with domain $\mathcal{D}$, preserves α-output privacy if for every two neighboring databases x and y and every set R ⊆ Range(M), Pr[M(x) ∈ R] ≤ α Pr[M(y) ∈ R].

This notion of privacy was formalized as differential privacy (DP) [10], [11], and is widely used today. In DP, any two databases that differ by exactly one record are considered neighbors. Thus, it ensures that the presence or the absence of any one record, i.e. an individual’s information, in the database has an insignificant effect on the output of a private mechanism.

An analyst prefers DP to preserve privacy in outlier analysis since DP is the gold standard for many data analytics tasks. But DP is the “wrong” choice for some important settings for outlier analysis that arise from the kind of query we ask, the type of outlier we analyze, and the outlier model we employ. Here “wrong” means a setting is unsuitable for DP, that is, the definition of privacy is too stringent to be useful in practice since it destroys utility.

What makes a setting unsuitable for DP? How to deal with such settings? We answer the first question in Section 2 and the second one in Section 3.

We note, however, the second question has been addressed for a few special cases of unsuitable settings. There are ways to get the best of both worlds: meaningful privacy guarantees and accurate outlier analysis. Such solution provide privacy guarantees that may be less strong compared to DP but, nevertheless, are good enough for all practical purposes. Basically, these solutions change the notion of privacy by relaxing DP—that, of course, leads to the question of whether this is always necessary. The answer is no and is explained in Section 3. These new notions, for the most part, loosen the constraints on the neighbors in DP. We refer to such privacy notions as Relaxed-DP. In the context of outlier analysis, examples of Relaxed-DP are: anomaly-restricted DP [5], protected DP [15], DP over relaxed sensitivity [6], and sensitive privacy [2]. Note that if the outlier model is data-dependent (i.e. a record is outlier only relative to the other records in the data) then only sensitive privacy effectively handles an unsuitable setting.

2. Outlier Queries and a Taxonomy

Here we present a novel taxonomy for outlier queries, which we conceptualize to isolate the suitable settings for DP from the unsuitable ones. Under this taxonomy, we formally characterize the privacy-utility trade-off of the class that is comprised of the unsuitable settings. The formal treatment, here, is necessary since our analysis is not confined to a specific outlier model or a specific outlier query.

We will first give the important notion of existence-independence that naturally separates the two settings, and hence, will be used to define the classes under our taxonomy. This notion helps characterize if an outlier query depends on the existence of any particular record(s) in the database—a property of the queries that is crucial to DP performing well in practice (as we will see shortly). To this end, let us first formalize what is an outlier query.

An outlier query is a function, f, over $\mathcal{D}$, whose output (directly or indirectly) gives some information about the outlier(s). We assume, for each outlier query, an outlier model is prefixed. For clarification, consider our example queries. The output of Q₁ is yes or no (to indicate if the record is an outlier). The output of Q₂ is a subset of records in the database, which are outliers. Next, consider an outlier query f that outputs the number of Ebola cases, a variant of the Q₃ used by CDC⁵ ; the output of f then can be used to check for an outbreak, an outlying event.

Now for a given outlier query, f, a database x satisfies the existence-independence constraint if for every record i such that i ∈ x, there exists a database y such that i ∉ y and f(x) = f(y) ; namely, the output for an input database, which has a record i, can be obtained for another database that does not have the record i. For instance, consider an outlier query, f, that outputs the number of outliers in the given database. Now, fix a database x. If for every i ∈ x, we have another database y that has the same number of outliers as in x (i.e. f(y) = f(x)) but it does not contain i, then x satisfies the existence-independence constraint. This holds for most of the typical settings in practice, wherein how many outliers a database contains is independent of the existence of any one particular record in the database. Note that we choose to formulate existence-independence as oppose to its inverse since it is intuitively easier to understand.

Below, we use the existence-independence constraint to define three classes of outlier queries and show how achieving DP in the unsuitable settings leads to poor accuracy in practice.

Existence-independent query.

An outlier query is existence-independent if all the databases in $\mathcal{D}$ satisfy the existence-independence constraint. Examples are: (i) How many outliers are in the given database? This is existence-independent as explained above. (ii) Q₃ is also existence-independent since the occurrence of Ebola outbreak is independent of any single individual contracting the disease.

We know that DP protects the existence of any record in the given database. The existence-independent queries, in a sense, are independent of this information, and hence for such queries, DP mechanisms can achieve both privacy and utility that is practically meaningful, e.g. [3], [4], [13], [19]. Many outlier queries of practical interest, however, are not existence-independent—a major reason for DP to result in poor utility. Such outlier queries are existence-dependent.

Existence-dependent query.

An outlier query is existence-dependent if it is not existence-independent, namely, there exists a database that violates the existence-independence constraint, e.g. Q₂, where a record that is not present in the database, cannot be in the output.

We note, however, many existence-dependent outlier queries of practical significance are such that there is not one but many databases (encountered in practice) that violate the existence-independence constraint. We call such queries typical (defined shortly). The examples are: (i) What are the outlier records in the database? and (ii) What are the top-k outlier records in the database?

We first clarify some notation and then define typical outlier queries. For any $x\in \mathcal{D}$ and $i\in \mathcal{X}$, x⁽⁺ⁱ⁾ gives the database that has exactly one record of value i and is otherwise identical to x. For any outlier query, f, and $i\in \mathcal{X}$, let R_f(i) = {f(y) : i ∉ y}. We say an existence-dependent outlier query, f, is typical if there exists a non-empty set $X_f\subseteq \mathcal{X}$ such that for every i ∈ X_f there are many databases x such that f(x⁽⁺ⁱ⁾) ∉ R_f(i) (i.e. x⁽⁺ⁱ⁾ violates the existence-independence constraint).

We call X_f the discriminative set. Note that for Q₂, the discriminative set is equal to $\mathcal{X}$. As for what constitutes many, it depends on the particular outlier model, its parameter values, the maximum size of the database, and the size of $\mathcal{X}$. In general, however, we assume it is at least linear in $\mid \mathcal{X}\mid$.

Next we show, via an upper bound on accuracy, how DP leads to poor accuracy for typical queries.

Why DP results in low utility for typical outlier queries?

We first present a high-level example to give an intuition of why DP does not seem to solve the right problem for the setting under consideration. Consider a database where the landscape of the database is such that in various places the removal or addition of a record changes the outlier status of one or more records. Addition or removal of a record is what defines a neighboring database, and thus for many common definitions of outliers any DP mechanism will irrevocably introduce excessive levels of noise, leading to poor utility.

The poor utility for typical queries is due to the lower bound on the error of any DP mechanism, which we give in Claim 1. Henceforth, we refer to a typical existence-dependent outlier query as typical query.

To state Claim 1, we need the following notion. For any typical query, f, M_f is a randomized mechanism with domain Domain(f) and range Range(f). For any database x and $i\in \mathcal{X}$, x⁽⁻ⁱ⁾ gives the database that has no record of value i and is otherwise identical to x.

Claim 1. Fix α > 0. For every typical query, f, α-DP mechanism, M_f, i ∈ X_f, and database x such that f(x⁽⁺ⁱ⁾) ∉ R_f(i),

$$\max \left\{\begin{array}{c}\text{Pr}[M_f(x^{(-i)})\in \text{Range}(f)\setminus R_f(i)],\hfill \\ \text{Pr}[M_f(x^{(+i)})\in R_f(i)]\hfill \end{array}\right\}\ge \frac{1}{1+\alpha }$$

Proof. Arbitrarily fix α > 1, and let ϵ(α) = 1/(1 + α). Arbitrarily fix a typical query f and an α-DP mechanism M_f. Let X_f be the discriminative set for f. Lastly, fix arbitrary i ∈ X_f and $x\in \mathcal{D}$ such that $f(x^{(+i)})\in R_f^{\prime }(i)=\text{Range}(f)\setminus R_f(i)$.

For x⁽⁺ⁱ⁾ and x⁽⁻ⁱ⁾ (neighboring databases under DP), if $\text{Pr}[M_f(x^{(-i)})\in R_f^{\prime }(i)]\le ϵ(\alpha )$ then $\text{Pr}[M_f(x^{(+i)})\in R_f^{\prime }(i)]\le \alpha ϵ(\alpha )$, which is due to the DP constraints. Since R_f(i) and $R_f^{\prime }(i)$ partition Range(f), it follows from the above that

$$\text{Pr}[M_f(x^{(+i)})\in R_i(f)]\ge 1-\alpha ϵ(\alpha )=ϵ(\alpha )$$

Similarly, Pr[M_f(x⁽⁺ⁱ⁾) ∈ R_f(i)] ≤ ϵ(α) implies $\text{Pr}[M_f(x^{(-i)})\in R_f^{\prime }(i)]\ge ϵ(\alpha )$. Since α, f, M_f, i ∈ X_f, and x were fixed arbitrarily, the claim follows from the above. ◻

We note that to achieve good privacy guarantees, α must be small, i.e., closer to 1. In this case, the error would be closer to 1/2; namely, the chance of getting the correct answer (e.g. M_f(x) = f(x)) is almost the same as deciding the answer by the toss of a fair coin.

What are the implications of Claim 1 in typical real-world settings? To understand this, consider Q₂. We know that for Q₂, $X_f=\mathcal{X}$. From Claim 1 we know that for any database x and any i such that p(i, x) = 1 (recall that p is the predicate that represents the outlier model),

1. if x = x⁽⁺ⁱ⁾, i ∉ M_f(x) with probability ≥ $\frac{1}{1+\alpha }$ or

2. if x = x⁽⁻ⁱ⁾, i ∈ M_f (x) with probability ≥ $\frac{1}{1+\alpha }$.

Now recall that real-world databases are such that: (1) many of the outliers are unique records in the database, i.e. for many i’s in f(x), i ∉ f(x⁽⁻ⁱ⁾); and (2) there are many possible records that are not present in the database and if we add any one of them to the database, it will be considered an outlier, i.e. there is a large set $I\subseteq \mathcal{X}$ such that for every i ∈ I, x_i = 0 and p(i, x⁽⁺ⁱ⁾) = 1. Thus due to (1), the antecedent of (a) holds for many outliers in x, and that of (b) holds for a large subset of $\mathcal{X}$ due to (2) (recall $\mid x\mid <<\mid \mathcal{X}\mid$)—see [2] for further empirical evidence. Hence, if we try to reduce the error in the case of (a) (where i ∈ f(x)), the error for (b) will increase (where i ∉ x and thus i ∉ f(x)) and vice versa. Therefore, achieving DP for Q₂ will result in little utility in practice.

3. A Manual for Private Outlier Analysis

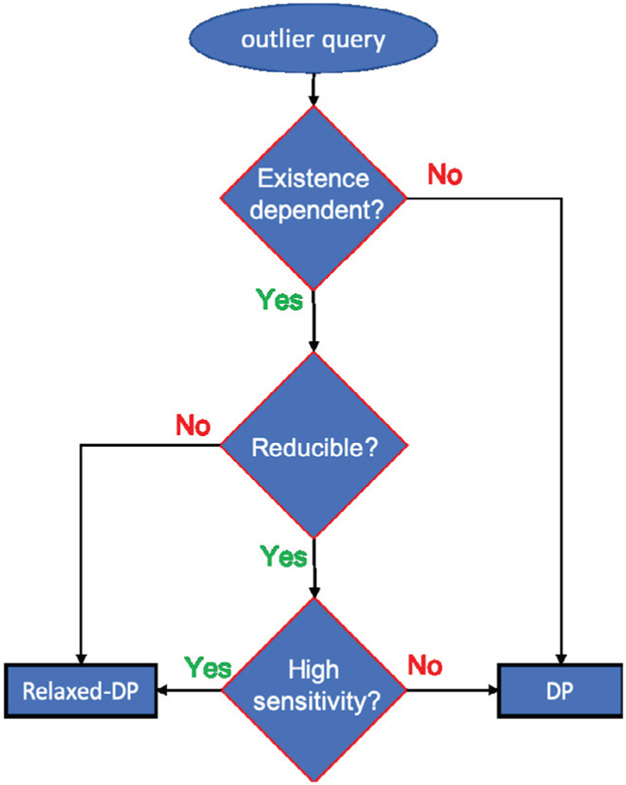
We now discuss how an analyst should analyze data for outliers to preserve both privacy and utility. Although this approach may seem rudimentary, it covers the most critical factors that an analyst must considered to achieve both privacy and accuracy, which is practically meaningful. We first provide an overview (also depicted in Figure 1), which is followed by the detailed account.

Fig. 1:

Overview of the approach.

Given an outlier query, an analyst should first check if the query is existence-independent. If it is, then DP is the appropriate choice. If the query, however, is existence-dependent, then the analyst should try to reduce the query to a set of existence-independent queries, and compute the original query via the new queries. The above reduction (defined shortly) must take into account the various utility and information leakage constraints (imposed by the application or the analyst). If there is no reduction that meets the constraints, an appropriate Relaxed-DP notion may be used. But if a reduction does meet the constraints, then the next step is to analyze the accuracy in relation to achieving DP. If the accuracy achievable under DP is not practically meaningful for the application, then a befitting Relaxed-DP notion may be used.

Reduction.

Let us say, after analyzing the given query, the analyst establishes that the query is an existence-dependent outlier (endo) query. The first step for the analyst is to analyze if the query can be computed via a set of new queries, where, for example, none of the new queries is existence-dependent. We call such a set of new queries a reduction (defined below). If the outlier query, however, is existence-independent, then the analyst should use DP. We will refer to an existence-independent outlier query as nendo-query.

Let us formalize the notion of reduction we consider here—later we will also give an example to explain it. Say n parties are to compute an endo-query, f, on the database x that may be distributed among the parties. For each party t, ${\mathcal{L}}_t(f)$ represents the information it receives through the computation. You may think of ${\mathcal{L}}_t(f)$ as the leakage similar to the one typically considered in secure computation [14], [21]. Let us call ${\mathcal{L}}_t(f)$ the leakage for party t, which contains the output (i.e. the part of f(x)) of the party t and any other information that the party receives about any other party’s input.

A reduction, ${\mathcal{T}}_f$, of an endo-query, f, is {(f_t,1, f_t,2, … , f_t,rt)}_t∈[n] with leakage ${\mathcal{L}}_t({\mathcal{T}}_f)$ (for each party t) such that for every t = 0, … , n:

• Each f_t,l is a nendo-query or a functionality that the party t can compute locally (i.e. without relying on any other party) given the outputs of f_t,1, f_t,2, … , f_t,l−1 and

• Each ${\mathcal{L}}_t({\mathcal{T}}_f)$ contains the output of the party t ( and it may also contain some other information).

There may be multiple possible reductions for an endo-query. But a reduction is acceptable if it satisfies the utility and information leakage constraints imposed by the analyst. The utility constraints may include a bound on error and computation and communication power etc. The error we consider here may be inherent to one of the reduced queries (see the example below) or due to the internal coin tosses of the algorithm that the analyst uses to compute a reduced query (randomness may be needed for efficiency) [8]. We remark that, at this stage, we do not consider the error due to achieving output privacy. As for the question, what constitutes information leakage? The answer is any information about any of the party’s input that cannot be revealed to the other parties.

Now given that an acceptable reduction is possible, the next step is to analyze the accuracy as it relates to achieving DP, the output privacy (discussed under the heading ‘Sensitivity’). If an acceptable reduction, however, is not possible, then an appropriate Relaxed-DP notion needs to be employed.

As an illustrative example of reduction, consider the following situation. Assume n parties and k = 20. Each party t has its own database x_t such that ∣x_t∣ ≥ k. Let x = ∪_t∈[n]x_t. Next consider AVF outlier model [16], p, that is known to all the parties (recall, p is a predicate). Let f be the outlier query that to each party outputs its records (in x_t) that are among the top-k outliers in x, i.e. k records with the smallest AVF score⁶. Clearly, f is an endo-query, and for x, ${\mathcal{L}}_t(f)=\{i\in f(x):i\in x_t\}$.

Example ${\mathcal{T}}_f$ from [3], [4].

Privacy constraint: for each party, besides its output, the leakage may contain the frequency of each attribute value, as per x, and nothing else. Each party t proceeds as follows. First, it collaboratively computes f_t,1, f_t,2, … , f_t,m on x, where f_t,l gives the frequency of each value of l-th attribute as per x, and m is the total number of attributes. Second, using the output of the above queries, it computes f_t,m+1 on x_t, which gives O_t = {i_t,1, … , i_t,k}, the top-k outliers in x_t. Lastly, for l = 1, … , k, it computes f_t,m+1+l(x) = p(i_t,l, x) (which if true, means i_t,l is among the top-k outliers in x).

All of the above queries are nendo-queries except for f_t,m+1, which can be computed locally given AVF’s. If p is such that for every $z\in \mathcal{D},y\subseteq z$, and i ∈ y, p(i, z) = 1 implies p(i, y) = 1, then $O_t={\mathcal{L}}_t(f)$ for every t. Many outlier models, e.g. (ρ, D) and AVF, satisfy this property. Thus, for our example, the accuracy remains the same. If the outlier model does not satisfy the above property, then we must confirm for the given setting if the reduction yields an accuracy that is acceptable for the application; otherwise a new reduction must be sought, or a Relaxed-DP notion may be used.

Sensitivity.

Given an acceptable reduction, the analyst should check if computing the query via the reduction gives the required accuracy under an appropriate DP guarantee, i.e. the value of α. Recall, there is a trade-off between the value of the α and the accuracy one can achieve: smaller the value of α, the lower the accuracy. We say an outlier query has high sensitivity if for typical values of α, the required accuracy is unachievable.

Here we briefly discuss some of the ways to improve accuracy under DP. If the range of a reduced query is real numbers (or integers), then one can calculate the global sensitivity⁷ and use Laplace mechanism⁸ [11], [12] to achieve DP. In the previous example, the AVFs can be computed via Laplace mechanism, while preserving reasonable accuracy. If the global sensitivity of the query is too high, and the Laplace mechanism cannot produce the required accuracy, one can opt for mechanisms that are based on a smooth bound on the local sensitivity [18]. For example, accuracy in reporting the number of outliers can be improved by using local sensitivity based mechanism [19]. One could also employ mechanisms optimized for a batch of queries [17]. The exponential mechanism [12] is another way to design DP mechanisms to meet the accuracy constraint. Note that the analyst needs to consider the sensitivity of each query in the reduction, and its overall effect on the accuracy.

In the case, all of the above (and other available) options fail to satisfy the constraints, then opting for a Relaxed-DP notion is an appropriate choice.

Relaxed-DP.

There are a few relaxations of DP that have been introduced to deal with the problem of private outlier analysis (as discussed in Section 1.2). Except for sensitive privacy, all of these relaxations are limited to a few specialized cases. Anomaly-restricted privacy [5] and protected differential privacy [15] assume the outlier model to be data-independent9. Additionally, the former assumes there is only one outlier in the database, and the latter is specific to networks. Relaxed sensitivity [6] is a relaxation of global sensitivity and is only relevant in the context of Laplace mechanism. It assumes that there is a boundary (which is independent of any database) separating outlier records from the non-outlier records. Thus, conceptually, it also deals with data-independent outlier models.

In many practical settings, outlier models are data-dependent. Such an outlier model characterizes outlyingness of a record relative to the other records in the database. To address the problem in this context, the notion of sensitive privacy [2] is the appropriate choice. Sensitive privacy generalizes some of the above notions of privacy (including DP) and is well-suited for existence-dependent outlier queries, especially, when the outlier model is data-dependent.

4. Conclusion

To date, work on private outlier analysis has been limited to specific problems, narrow in scope, and ad-hoc in nature. In this article, we develop a conceptually important categorization of the outlier queries, identify various features that impact the utility, and propose an approach to deal with the problematic category of existence-dependent outlier queries. This work provides a guide to facilitate the analyst in performing outlier analysis while preserving privacy. It is meant as a starting point to guide the decision process of choosing an appropriate privacy model that can provide sufficient utility for outlier analysis. In the future, we plan to use the proposed guiding principles to explicate solutions for different outlier queries under various models and settings.