A chemical interpretation of protein electron density maps in the worldwide protein data bank

Sen Yao; Hunter N B Moseley

doi:10.1371/journal.pone.0236894

. 2020 Aug 12;15(8):e0236894. doi: 10.1371/journal.pone.0236894

A chemical interpretation of protein electron density maps in the worldwide protein data bank

Sen Yao ^1,^2,³, Hunter N B Moseley ^1,^2,^3,^4,^5,^*

Editor: Oscar Millet⁶

PMCID: PMC7423092 PMID: 32785279

Abstract

High-quality three-dimensional structural data is of great value for the functional interpretation of biomacromolecules, especially proteins; however, structural quality varies greatly across the entries in the worldwide Protein Data Bank (wwPDB). Since 2008, the wwPDB has required the inclusion of structure factors with the deposition of x-ray crystallographic structures to support the independent evaluation of structures with respect to the underlying experimental data used to derive those structures. However, interpreting the discrepancies between the structural model and its underlying electron density data is difficult, since derived sigma-scaled electron density maps use arbitrary electron density units which are inconsistent between maps from different wwPDB entries. Therefore, we have developed a method that converts electron density values from sigma-scaled electron density maps into units of electrons. With this conversion, we have developed new methods that can evaluate specific regions of an x-ray crystallographic structure with respect to a physicochemical interpretation of its corresponding electron density map. We have systematically compared all deposited x-ray crystallographic protein models in the wwPDB with their underlying electron density maps, if available, and characterized the electron density in terms of expected numbers of electrons based on the structural model. The methods generated coherent evaluation metrics throughout all PDB entries with associated electron density data, which are consistent with visualization software that would normally be used for manual quality assessment. To our knowledge, this is the first attempt to derive units of electrons directly from electron density maps without the aid of the underlying structure factors. These new metrics are biochemically-informative and can be extremely useful for filtering out low-quality structural regions from inclusion into systematic analyses that span large numbers of PDB entries. Furthermore, these new metrics will improve the ability of non-crystallographers to evaluate regions of interest within PDB entries, since only the PDB structure and the associated electron density maps are needed. These new methods are available as a well-documented Python package on GitHub and the Python Package Index under a modified Clear BSD open source license.

Introduction

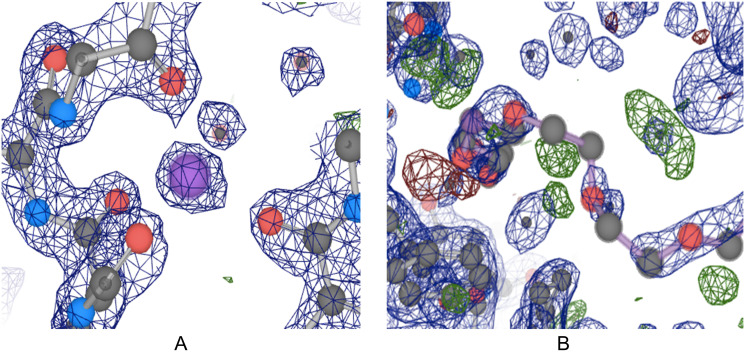
Proteins are active components in the biochemical implementation of biological processes, and understanding their structure is important for interpreting their biochemical functions. The Worldwide Protein Data Bank (wwPDB, www.wwpdb.org) [1] is the international organization that manages the Protein Data Bank (PDB, www.rcsb.org) [2], the central repository of biological macromolecules structures. Thousands of structures are deposited into the wwPDB every year, but their data quality can vary significantly from structure to structure, and even region to region within a structure. Low-quality data can cause problems for both a single macromolecule structure inspection and aggregated systematic analyses across hundreds or thousands of structural entries [3, 4]. Thus, the analysis and interpretation issues caused by the presence of low-quality structural data are pushing the structural biology community to pay more attention to the quality of deposited structural entries [5]. The wwPDB has initiated several efforts to improve the quality of entries being deposited, including launching a deposition, biocuration, and validation tool: OneDep [6]. Many data quality measures are now available for PDB structures, such as a resolution, B-factors, MolProbity clashscores [7], to name a few. However, low-quality regions can still exist even in structures with very good metrics of global structural quality, as shown in the overlay of structures with electron density maps in Fig 1. These low-quality regions arise from structural model and electron density mismatches that can be due to a variety of reasons including problems with regional protein mobility that can often lead to an apparent lack of electron density [8–10], data processing [11, 12], or model fitting [10, 13, 14]. These mismatches often occur around bound ligands where a lot of interesting biological activities happen, making the analysis of protein sequence-structure-function relationships more difficult. Therefore, the evaluation of structure quality, especially around regions of interest, is paramount before accurate structural inferences can be made.

Fig 1 — Both panels A and B are from the same structure, PDB ID: 3B1Q, and are centered around the ligands B.330 (A) and P.33 (B). Blue meshes represent the model electron density. Green and red meshes represent discrepancies between experimental data and the structure model. The structure has very good overall quality, as demonstrated by a resolution of 1.7 Å, an R-factor value of 0.176, and an R-free value of 0.207. The panel A shows a high-quality region in the structure where the experimental data and model match very well. And the panel B shows that there are still low-quality regions within the structure, as demonstrated by the green and red blobs around the coordinating ligand residue (“ligand” refers to the coordination chemistry definition of this word).

Driving improved evaluations of structure quality are newer deposition requirements like mandatory deposition of structure factors (x-ray structures) and constraints (NMR structures) starting from 2008 [15], NMR-assigned chemical shifts from 2010, and 3DEM volume maps from 2016 [7]. The inclusion of underlying experimental data used in structure determination enables researchers to better validate structural models, improving the inferences they can make from these structures. For x-ray crystallographic structures, electron density maps enable a direct comparison between the observed electron density Fo to calculated electron density Fc based on the structural model. The 2Fo-Fc map represents the electron densities surrounding well-determined atoms in the model across a three-dimensional (3D) space and the Fo-Fc map represents the electron density discrepancies between the observed and calculated electron density across a 3D space. For x-ray crystallographic PDB entries with deposited experimental data, sigma-scaled electron density maps are made available by the PDB in Europe (PDBe) [16]. Previously from about 1998 to 2018 [17], electron density maps were made available by the Uppsala Electron Density Server (Uppsala EDS), which was created and maintained outside of the PDB [18]. However, the PDBe uses newer methods to provides higher quality density maps, which prompted the retirement of the Uppsala EDS by 2018. Many electron density map viewers [19–22] exist for manually examining the quality of a model versus its electron density; however, this software and evaluation approach is not suitable for batch analysis of hundreds of structures. Also, these sigma-scaled electron density maps are in arbitrary units of electron density, with no direct physicochemical meaning. This normally does not affect the visualization of electron densities and is a by-product of creating maps with a summative intensity of zero (zero-sum) across the whole map, which is done primarily for visual simplification during modeling [23, 24]. But this zero-sum representation can be detrimental for understanding a model, especially a local region of a model, where the number of electrons represented by the density or density discrepancy would be useful for evaluation. While methods exist that can derive electron density maps on an absolute scale, these methods require a reanalysis of the underlying structure factors with software packages that are not designed for automated use across large numbers of structural entries [25, 26]. Due to these limitations, we have developed a new method that derives a conversion factor from the arbitrary electron density units of a given electron density map with corresponding PDB entry into the absolute value of electrons per angstroms cubed, without the need to reprocess and reanalyze the underlying structure factors. With this conversion factor, we have developed new evaluation methods that normalize electron density and electron density discrepancies into estimated quantities of electrons. These new electron discrepancy values can provide chemically-informative information for evaluating structural models or for filtering structure entry regions for inclusion into systematic analyses that span large numbers of PDB entries.

Methods

Calculating the electron density ratio for atoms, residues, and chains

A workflow of the analysis is shown in Fig 2. Structural data (in PDB format) was downloaded from wwPDB on Jul 3, 2018, and their electron density data (in CCP4 format), if available, was acquired from the PDBe website [16]. Structural data was processed using a self-developed parser and Biopython [27]. Electron density data was analyzed according to the CCP4 suite [28] format guidance. The electron density map is represented as a 3D array in the data, which corresponds to voxels in the real space. An electron density voxel with a density value greater than 1.5σ of all voxels is considered significant for 2Fo-Fc maps, and 3σ for Fo-Fc maps. For structures with electron density data available, symmetry operations were performed to include the surrounding environment for the modeled structure.

To calculate the total electron density around each atom, we initially used the radii from literature [29] and calculated the sum of all densities within the corresponding radius. The voxel center is used when calculating the distance from a density voxel to an atom. Different atoms (without hydrogens) from the 20 common amino acids are categorized into 13 atom types as shown in S1 Table. Electron density ratio (r_i) is defined as the total density of all associated voxels (ρ_m) divided by the number of electrons (Z_i) for a given atom i,

r_{i} = \frac{\sum ρ_{m}}{z_{i}}

(1)

As the unit for electron density is eÅ^-3, the electron density ratio thus has the unit as Å^-3. The total density is adjusted by a factor of the occupancy of the atom. Since hydrogen is normally not resolvable within electron density maps, their electrons were added to their bonded atom. A table of electron counts used for each atom is shown in S2 Table.

After all atom electron densities are calculated, they are aggregated into residue and chain densities where the residue cloud contains at least 4 atoms and the chain cloud contains at least 50 atoms. The overlapping density voxels between two or more atoms are only counted once through the aggregation. The total number of electrons is calculated by adding contributing atom’s electron numbers together. Residue (r_r) and chain (r_c) density ratios are then calculated accordingly.

Normalizing the electron density ratio by the number of voxels

To smooth the representation of continuous electron densities using discrete voxels, the electron density ratio is then normalized by the median volume (in number of voxels) of a given atom type. If we denote the original density ratio as r_i and the volume of a given atom i with atom type t as V_i, and the median volume of all atoms with atom type t as median(V_t), the normalized density ratio r_i-norm can be defined as follow:

r_{i - n o r m} = r_{i} * m e d i a n (V_{t}) / V_{i}

(2)

Correcting the unit electron density by the atom B-factor

As the actual value of the density ratio is highly specific to individual structures, we then define a more universal measure as the chain deviation fraction (f_i) for a given atom i as:

f_{i} = (r_{i - n o r m} - m e d i a n (r_{c})) / m e d i a n (r_{c})

(3)

The dispersion of electron density around an atom can be approximated using the B-factor of the given atom. The chain deviation fraction and logarithmic B-factor have a linear correlation both statistically and visually, and thus a slope (s_t) of chain deviation fraction over logarithmic B-factor can be calculated for each atom type and for every structure. If there are less than three points for a given atom type, the median slope over 1000 random structures is used. Then for each individual atom i with atom type t, its unit electron density can be corrected by its deviation from the median B-factor:

f_{i - c o r r e c t e d} = f_{i} + (l o g (b_{i}) - m e d i a n (l o g (b_{t}))) * s_{t}

(4)

r_{i - c o r r e c t e d} = f_{i - c o r r e c t e d} * m e d i a n (r_{c}) + m e d i a n (r_{c})

(5)

Optimization of radii

After the initial calculation, the median density ratios of different atom types were still quite different from each other. Thus, to achieve a more uniformly interpretable density ratio within a structure as well as across structures, an optimization of radii was performed. First, we tested the radius for each atom type on 100 random structures and obtained an initial estimation of the radii. The metric we used to optimize was the median of corrected chain deviation fraction (f_i-corrected) for a given atom type. Based on the results from the initial step, we then optimized one atom type at a time on 1000 randomly selected structures. For every iteration, the atom type that has the largest deviation from last round was optimized. Different radii were tested for the given atom type and the radius that has a median corrected chain deviation fraction closest to zero was picked out. At the end of each optimization, the set of B-factor slopes were updated as well. This process continued until the median chain deviation fraction for all atom types were smaller than 0.05. The final set of radii were then tested on another 1000 random structures and the whole PDB database for validation.

Adding an F₀₀₀ term

The average value of the 2mFo-DFc map (i.e. a Sigma-A weighted map) is practically zero for most of the structures in the PDB. Theoretically, an F₀₀₀ term should be added to get the proper number of electrons on an absolute scale. Unfortunately, not all structure factor programs provide the F₀₀₀ value. So as an estimation, we add up the numbers of electrons for all the atoms of a model in the unit cell, including symmetry structure units and modeled water molecules,

F_{000} = \sum n_{t} Z_{t}

(6)

Where n_t is number of atoms of element t in the asymmetric unit and Z_t is the number of electrons (atomic number) of element t. This estimated F₀₀₀ term is then divided by the unit cell volume V in Å³ and added to the density values of all the voxels.

Design, implementation, and distribution of the above methods

These new methods are implemented in a Python package, pdb-eda. It is written in major version 3 of the Python program language and is available on GitHub, https://github.com/MoseleyBioinformaticsLab/pdb_eda, and the Python Package Index (PyPI), https://pypi.org/project/pdb-eda/. There are three main parts of pdb-eda: the pdb parser, the ccp4 parser, and the electron density analysis. Starting from a PDB id, pdb-eda can either read a local pdb or ccp4 file or download it on the fly. Intermediate and final results of all three parts can be accessed via either importing as a library or using the command line interface. Many options are available for handling and processing the data with the details documented in the package guide and tutorial files. As part of the development process, new versions are updated on GitHub regularly. The version that is described and implemented for this paper has been frozen, tarballed, and published on FigShare (https://doi.org/10.6084/m9.figshare.7994294), along with all the result files and codes in generating all results, figures, and tables.

Results

We downloaded and used a total of 141,763 wwPDB entries, of which 106,321 structures have electron density maps available and suitable for the analysis in this study. The assumption of this study is based on a fundamental rule for electron density construction, that is the electron density is proportional to the number of electrons. However, after being deposited into the PDB, this information of absolute value of electrons is hard to derive and is inconsistent across structures. Different structures can vary a lot in terms of density ratios, due to the quality of the crystal or the choice of data processing software. Therefore, we need an internal measure to enable a consistent interpretation within and across structures. If we simply use the radii from the literature and do not apply any correction, the median of atom density ratio shows that the density ratios are inconsistent within a single structure for atoms, residues, and chains, as illustrated in Fig 3 Panels A-C as Sina plots, an enhanced jitter strip chart that visualizes the distribution of each dataset for better visual comparison [30]. The atom density ratios span over the largest range, while the chain density ratio has the smallest range. Therefore, we chose the chain deviation fraction as a reliable measure to optimize all atom types to the same level.

Fig 3 — PDB ID: 3UBK. The atom density ratios have the largest range, and chain density ratios have the smallest range, which can be used as internal standard to optimize the atom ratios to.

Volume and B-factor adjustment

An example of the volume distribution for a single structure is shown in Fig 4. Ideally, atoms of the same atom type should occupy the same volume. However in reality, different parts of a structure may be more or less ordered within the crystal than others. Also, during the reconstruction of the electron density data from complex structure factors, continuous electron density through space is represented as a point density value for every voxel. And the use of the point density to estimate the whole voxel depends on the smoothness of the density function. Moreover, based on the placement of the atom in relation to the voxel and the selection of grid length, the inclusion of a voxel is an all-or-none decision. Thus, we performed the volume normalization to minimize these effects.

B-factor measures the temperature-dependent atomic displacement in a crystal. As a result, it is inversely correlated with the total electron density within a distance of an atom, and thus the density ratio. After examining several different relationships between density ratio and B-factor, both statistically and visually, the chain deviation fraction versus logarithmic B-factor demonstrated the strongest linear correlation, and thus was used for the correction. This is not surprising due to the expected non-linear relationship of B-factors [10]. Fig 5 provides an example of this relationship.

The volume normalization correction helps to reduce the high variability of the density ratio while the B-factor correction improves the symmetry of each atom density ratio distribution. Fig 6 illustrates the distributions of atom density ratios before and after each step (Panels A-C). After both adjustments, the atom density ratio is coherent within each atom type, though it is still uneven between atom types (Panel C).

The final set of radii after optimization

Fig 6, Panel D illustrates the distributions of atom density ratios after radii optimization, where different atom types have much more similar median ratios. Moreover, the standard deviation of the overall distribution drops to 0.09, representing a 40% decrease in the calculated density ratio variability. This improvement percolates through to the residue and chain level, but is not as obvious (see Fig 3, Panels D-F). A comparison of initial and final set of radii is shown in Table 1. In general, most of the backbone atoms decrease in radius, while most of the optimized radii on the side chain are larger than those on the backbone. This is due to the lower order and higher flexibility of the side chain atoms, which practically requires a larger radius to capture the expected number of electrons.

Table 1. The atom radii before and after radii optimization.

Atom Type	Original Radius (Å)	Optimized Radius (Å)
C_single	0.77	0.84
C_single_bb	0.77	0.72
C_double	0.67	0.67
C_double_bb	0.67	0.61
C_intermediate	0.72	0.72
O_single	0.67	0.80
O_double	0.60	0.71
O_double_bb	0.60	0.77
O_intermediate	0.64	0.71
N_single	0.70	0.95
N_single_bb	0.70	0.70
N_intermediate	0.62	0.77
S_single	1.04	0.75

Open in a new tab

“_bb” identifies backbone atom types.

The radius of sulfur changes the most as compared to the other elements. This could be due to how most software construct electron density data from structure factor and associated phase via Fourier transforms. The electron density is approximated with a Gaussian distribution, and its variance is affected mainly by the B-factor. Thus, the final optimized radius is a combination of the actual radius of the atom, the displacement of an atom center, as well as the thermal motion of the atom (B-factor). Moreover, studying the behavior of sulfur atoms could be useful for other less common elements such as metal ions.

Overview of density ratio for the whole PDB database

The final set of radii was first tested on another 1000 random structures and all atom types held true to have no more than a 5% chain deviation fraction. It was then applied to all PDB structures that had usable electron density data, and the results are shown in Fig 7. For all atom types, the distributions center around 0, which indicates the set of optimized radii yields consistent measures of density ratios across structures. As shown in S1 Fig, for high-quality structures with a resolution smaller than 1.5Å, the chain deviation fraction illustrates tighter distributions with modes above 0, because of the narrower electron dispersion around atoms in the experimental data. As the resolution gets worse, this distribution tends to broaden for all atom types with the modes smaller than 0.

F₀₀₀ term and the absolute scale

Analysis of electron density on an absolute scale (i.e. in units of e/Å³) requires the value of F₀₀₀ and the unit cell volume. As the shape of the density matters more than the absolute scale in the structure modeling, most maps lack this F₀₀₀ term. Therefore, the mean value of the 2mFo-DFc map is practically zero across the whole PDB, as shown in Fig 8. To get the true electron density values, we would need to add an F₀₀₀ term to the set of Fourier coefficients going into the calculation of the map. However, as Fig 9 shows before and after adding the estimated F₀₀₀ term, it makes very little contribution to the overall absolute electron density values. This is probably due to missing the contribution from the bulk solvent, which is not easy to retrieve without extra data and software packages [25, 26]. Furthermore, the bulk solvent is estimated in different ways depending on resolution [31, 32]. Thus, an F₀₀₀ term as theoretically represented in textbooks and papers [33, 34] is not easy to calculate and likely depends on software parameters used in the creation of the map. Therefore, the chain median is used as a conversion factor to relate all electron density values back to the absolute scale.

Fig 8 — The histogram illustrates that most of the electron density maps in the PDB are effectively zero-meaned. A) 2Fo-Fc density map, B) Fo-Fc density map.

Fig 9 — Panel A shows the density ratios vs. inverse of voxel volume plot indicates that there is a consistent 1:3 ratio. Panel B is the histogram of the multiplication of the x and y axes values from Panel A. They both show that the density ratio is not affected much by adding an estimated F₀₀₀ term.

Evaluative use-case for the electron density conversion factor

One of the most important applications of this work is to estimate the difference density map in terms of electrons. The total difference in expected vs actual electron density can be represented in electron units by dividing the total electron densities by the conversion factor (the median of chain density ratios). As shown in Fig 10, the Fo-Fc map overlaying the 2Fo-Fc map and structure model show several positive (green) and negative (red) density blobs between the measured density from the experiment and the density explained by the given model. On panel A, most of the discrepancies are below six electrons, which can be reasonably interpreted as random background or water noise. Whereas on panel B, there are some difference density blobs worth about 16 and 29 electrons, which could imply actual missing atoms from the model. Moreover, the red missing electron density and the green extra density suggest that the side chain of A389 glutamine should be modeled at the green mesh position rather than the current position. In a similar manner, regions of interest that are common to many PDB entries can be automatically filtered based on electron deviation quality before systematic analysis.

Fig 10 — PDB id: 2P7Z, panel A highlighted residue: A.351, panel B highlighted residue: A.389. The blue lattice represents the significant density regions in the 2Fo-Fc map, while the green lattice represents the significant positive discrepant density blobs and the red lattice represents the significant negative discrepant density blobs, both from the Fo-Fc map.

Discussion

One of the biggest challenges in using electron density maps is that they are in arbitrary scale with no direct physicochemical meaning. This is partly because of missing the magnitude of the structure factor F₀₀₀, which is generally not needed or reported in structure factor files or electron density maps, as it does not affect standard modeling and visualization procedures. Therefore, to put everything back onto an absolute scale so that it is more meaningful for general scientists, this issue needs to be addressed. An approximation of the F₀₀₀ term can be derived from the structure model; however, it is still incomplete because of unknown solvent region compositions and potentially other factors, which are calculated in different ways depending on resolution. Also, the zero-mean conversion methods for creation of electron density maps appear to complicate a simple F₀₀₀ correction. This study thus derived new methods that use the median of chain density ratio as a conversion factor to allow the calculation of the missing or excessing electron densities in terms of absolute unit of electrons. These methods implemented in the pdb-eda package provide consistent measures across structures in the PDB with publicly available electron density maps. The pdb-eda methods for deriving a conversion of electron density into a quantity of electrons appear robust with respect to resolution and other PDB entry-specific issues like B-factors, but these methods are currently limited to PDB entries containing a significant peptide/protein component. However, the pdb-eda package contains the basic facilities necessary for deriving atomic radii for other polymeric and repetitive supermacromolecular structures. Also, S1 Fig illustrates a correlation between chain density ratios and resolution, which illuminates a clear path for improvement of atom radii based on resolution. These relationships between atomic radii, B-factors, and resolution with respect to observed electron density have been described previously [35]; however, Fig 5 and S1 Fig provide a useful visualization of these relationships. Also, S1 Fig implies that the current radii are likely optimized for the median resolution of x-ray crystallographic structures present in the wwPDB.

For the purpose of region-specific model evaluation, our pdb-eda package derives a conversion factor from arbitrary electron density per Å³ to electrons per Å³ based only on the provided 2Fo-Fc map and uses this conversion factor to convert electron density discrepancy from the provided Fo-Fc map into absolute units of electrons of discrepancy. At a specified number of standard deviations (sigma level), voxels with significant electron density discrepancies can be detected, absolutely summed, and converted into units of electrons of discrepancy to evaluate local regions [36]. A possibly sophisticated approach would be to use a region-specific estimate of noise [25, 37] to detect voxels with significant electron density discrepancies within a local region.

A complementary method called electron density support for individual atoms (EDIA) utilizes the 2Fo-Fc map to evaluate the electron density support for the location of individual atoms as well as groups of atoms within the electron density [38]. However, the values for EDIA do not have a direct physiochemical interpretation like electrons of discrepancy that our pdb-eda package derives from the Fo-Fc map. But between these two methods, both the Fo-Fc and the 2Fo-Fc maps can be directly used to evaluate the structural quality of a region of interest with respect to the experimental data. Moreover, pdb-eda electrons of discrepancy and EDIA metrics should be highly complementary since the first focuses on the evaluation of significant electron density discrepancies in the Fo-Fc map and EDIA focuses on the evaluation of less significant (below 1.2σ) electron density in the 2Fo-Fc map. Therefore, these new measures provide useful region-specific model evaluation and are suitable for systematic quality control analyses across large numbers of PDB structure entries, as demonstrated for bound metal ion regions [36].

Over time, the user-base of the wwPDB has shifted from mainly protein crystallographers to a broader community of biologists, computational biochemists, and bioinformaticians, which poses new challenges for how structural data is effectively utilized. While crystallographers are familiar with the concept that not all regions in a structure are of the same quality, this concept is relatively unfamiliar to the other scientists, who tend to focus on global metrics of structure quality like resolution, R-factor, and R-free. Moreover, the experimental details are rather overwhelming for non-crystallographers without extensive training. Thus, this study takes advantages of the recent addition of electron density maps to the PDBe, enabling general scientists to better utilize electron density information now available from the public repository. Our Python pdb-eda package provides easy-to-use methods for interpreting and evaluating structural data with a better physiochemical context. The primary goal of this package is to facilitate a shift in x-ray crystallographic structure evaluation from an entry-specific perspective to a region-specific perspective for the broader scientific community that utilizes the PDB.

Supporting information

S1 Table. Atom type mapping and the electron counts for the 20 common residues.

(DOCX)

Click here for additional data file.^{(13.9KB, docx)}

S2 Table. Atom-specific electron counts for the 20 common residues.

(DOCX)

Click here for additional data file.^{(13KB, docx)}

S1 Fig. Density plot of the median chain deviation fraction for all structures in the PDB of different resolutions.

(TIFF)

Click here for additional data file.^{(599.2KB, tiff)}

Acknowledgments

We would like to acknowledge helpful conversations with Dr. David Rodgers.

Data Availability

An older version of this manuscript is available on the bioRxiv preprint server: https://doi.org/10.1101/613109. Also the described software is available on GitHub (https://github.com/MoseleyBioinformaticsLab/pdb_eda) and the Python Package Index (https://pypi.org/project/pdb-eda/), the documentation is available on ReadTheDocs (https://pdb-eda.readthedocs.io/en/latest/), and all results are available on a FigShare repository (https://doi.org/10.6084/m9.figshare.7994294).

Funding Statement

HNBM received National Science Foundation (https://www.nsf.gov/) award 1419282. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1.Berman H, Henrick K, Nakamura H. Announcing the worldwide Protein Data Bank. Nat Struct Biol. 2003;10(12):980 Epub 2003/11/25. 10.1038/nsb1203-980 . [DOI] [PubMed] [Google Scholar]
2.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28(1):235–42. Epub 1999/12/11. 10.1093/nar/28.1.235 . [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Yao S, Flight RM, Rouchka EC, Moseley HN. A less-biased analysis of metalloproteins reveals novel zinc coordination geometries. Proteins. 2015;83(8):1470–87. Epub 2015/05/27. 10.1002/prot.24834 . [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Yao S, Flight RM, Rouchka EC, Moseley HN. Aberrant coordination geometries discovered in the most abundant metalloproteins. Proteins. 2017;85(5):885–907. Epub 2017/02/01. 10.1002/prot.25257 . [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Yao S, Flight RM, Rouchka EC, Moseley HN. Perspectives and expectations in structural bioinformatics of metalloproteins. Proteins. 2017;85(5):938–44. Epub 2017/02/09. 10.1002/prot.25263 . [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Young JY, Westbrook JD, Feng Z, Sala R, Peisach E, Oldfield TJ, et al. OneDep: Unified wwPDB System for Deposition, Biocuration, and Validation of Macromolecular Structures in the PDB Archive. Structure. 2017;25(3):536–45. Epub 2017/02/14. 10.1016/j.str.2017.01.004 . [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Gore S, Sanz Garcia E, Hendrickx PMS, Gutmanas A, Westbrook JD, Yang H, et al. Validation of Structures in the Protein Data Bank. Structure. 2017;25(12):1916–27. Epub 2017/11/28. 10.1016/j.str.2017.10.009 . [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Mitroshin I, Garber M, Gabdulkhakov A. Crystallographic analysis of archaeal ribosomal protein L11. Acta Crystallogr F Struct Biol Commun. 2015;71(Pt 8):1083–7. Epub 2015/08/08. 10.1107/S2053230X15011395 . [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Fraser JS, Jackson CJ. Mining electron density for functionally relevant protein polysterism in crystal structures. Cellular and molecular life sciences. 2011;68(11):1829–41. 10.1007/s00018-010-0611-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Shapovalov MV, Dunbrack RL Jr. Statistical and conformational analysis of the electron density of protein side chains. Proteins: Structure, Function, and Bioinformatics. 2007;66(2):279–303. [DOI] [PubMed] [Google Scholar]
11.Akey DL, Brown WC, Konwerski JR, Ogata CM, Smith JL. Use of massively multiple merged data for low-resolution S-SAD phasing and refinement of flavivirus NS1. Acta Crystallogr D Biol Crystallogr. 2014;70(Pt 10):2719–29. Epub 2014/10/08. 10.1107/S1399004714017556 . [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Karplus PA, Diederichs K. Assessing and maximizing data quality in macromolecular crystallography. Current opinion in structural biology. 2015;34:60–8. 10.1016/j.sbi.2015.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.van Beusekom B, Lutteke T, Joosten RP. Making glycoproteins a little bit sweeter with PDB-REDO. Acta Crystallogr F Struct Biol Commun. 2018;74(Pt 8):463–72. Epub 2018/08/08. 10.1107/S2053230X18004016 . [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Cowtan K. Fitting molecular fragments into electron density. Acta Crystallographica Section D: Biological Crystallography. 2008;64(1):83–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Dutta S, Burkhardt K, Young J, Swaminathan GJ, Matsuura T, Henrick K, et al. Data deposition and annotation at the worldwide protein data bank. Mol Biotechnol. 2009;42(1):1–13. Epub 2008/12/17. 10.1007/s12033-008-9127-7 . [DOI] [PubMed] [Google Scholar]
16.Gutmanas A, Alhroub Y, Battle GM, Berrisford JM, Bochet E, Conroy MJ, et al. PDBe: Protein Data Bank in Europe. Nucleic Acids Res. 2014;42(Database issue):D285–91. Epub 2013/11/30. 10.1093/nar/gkt1180 . [DOI] [PMC free article] [PubMed] [Google Scholar]
17.EMBL-EBI. http://www.ebi.ac.uk/pdbe/eds.
18.Kleywegt GJ, Harris MR, Zou JY, Taylor TC, Wahlby A, Jones TA. The Uppsala Electron-Density Server. Acta Crystallogr D Biol Crystallogr. 2004;60(Pt 12 Pt 1):2240–9. Epub 2004/12/02. 10.1107/S0907444904013253 . [DOI] [PubMed] [Google Scholar]
19.Sehnal D, Deshpande M, Varekova RS, Mir S, Berka K, Midlik A, et al. LiteMol suite: interactive web-based visualization of large-scale macromolecular structure data. Nat Methods. 2017;14(12):1121–2. Epub 2017/12/01. 10.1038/nmeth.4499 . [DOI] [PubMed] [Google Scholar]
20.DeLano WL. Pymol: An open-source molecular graphics tool. CCP4 Newsletter on protein crystallography. 2002;40(1):82–92. [Google Scholar]
21.Goddard TD, Huang CC, Ferrin TE. Visualizing density maps with UCSF Chimera. Journal of structural biology. 2007;157(1):281–7. 10.1016/j.jsb.2006.06.010 [DOI] [PubMed] [Google Scholar]
22.Emsley P, Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallographica Section D: Biological Crystallography. 2004;60(12):2126–32. [DOI] [PubMed] [Google Scholar]
23.Read RJ. Improved Fourier coefficients for maps using phases from partial structures with errors. Acta Crystallographica Section A: Foundations of Crystallography. 1986;42(3):140–9. [Google Scholar]
24.Schwarzenbach D, Abrahams S, Flack H, Gonschorek W, Hahn T, Huml K, et al. Statistical descriptors in crystallography: Report of the IUCr Subcommittee on Statistical Descriptors. Acta Crystallographica Section A: Foundations of Crystallography. 1989;45(1):63–75. [Google Scholar]
25.Lang PT, Holton JM, Fraser JS, Alber T. Protein structural ensembles are revealed by redefining X-ray electron density noise. Proceedings of the National Academy of Sciences. 2014;111(1):237–42. [DOI] [PMC free article] [PubMed]
26.Quillin ML, Wingfield PT, Matthews BW. Determination of solvent content in cavities in IL-1β using experimentally phased electron density. Proceedings of the National Academy of Sciences. 2006;103(52):19749–53. [DOI] [PMC free article] [PubMed]
27.Cock PJ, Antao T, Chang JT, Chapman BA, Cox CJ, Dalke A, et al. Biopython: freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics. 2009;25(11):1422–3. Epub 2009/03/24. 10.1093/bioinformatics/btp163 . [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Collaborative Computational Project N. The CCP4 suite: programs for protein crystallography. Acta Crystallogr D Biol Crystallogr. 1994;50(Pt 5):760–3. Epub 1994/09/01. 10.1107/S0907444994003112 . [DOI] [PubMed] [Google Scholar]
29.Heyrovska R. Atomic Structures of all the Twenty Essential Amino Acids and a Tripeptide, with Bond Lengths as Sums of Atomic Covalent Radii. arXiv preprint arXiv. 2008;0804(2488). [Google Scholar]
30.Sidiropoulos N, Sohi SH, Pedersen TL, Porse BT, Winther O, Rapin N, et al. SinaPlot: an enhanced chart for simple and truthful representation of single observations over multiple classes. Journal of Computational and Graphical Statistics. 2018;27(3):673–6. [Google Scholar]
31.Weichenberger CX, Afonine PV, Kantardjieff K, Rupp B. The solvent component of macromolecular crystals. Acta Crystallographica Section D: Biological Crystallography. 2015;71(5):1023–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Guo D, Blessing RH, Langs DA. Bulk-solvent correction in direct-methods phasing. Acta Crystallographica Section D: Biological Crystallography. 2000;56(4):451–7. [DOI] [PubMed] [Google Scholar]
33.Dorset DL. Filling the missing cone in protein electron crystallography. Microscopy research and technique. 1999;46(2):98–103. [DOI] [PubMed] [Google Scholar]
34.Wang B-C. Resolution of phase ambiguity in macromolecular crystallography. Methods in enzymology. 115: Elsevier; 1985. p. 90–112. [DOI] [PubMed] [Google Scholar]
35.Tickle IJ. Statistical quality indicators for electron-density maps. Acta Crystallographica Section D: Biological Crystallography. 2012;68(4):454–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Yao S, Moseley HNB. Finding High-Quality Metal Ion-Centric Regions Across the Worldwide Protein Data Bank. Molecules. 2019;24:3179 10.3390/molecules24173179. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Beckers M, Jakobi AJ, Sachse C. Thresholding of cryo-EM density maps by false discovery rate control. IUCrJ. 2019;6(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Meyder A, Nittinger E, Lange G, Klein R, Rarey M. Estimating electron density support for individual atoms and molecular fragments in X-ray structures. Journal of chemical information and modeling. 2017;57(10):2437–47. 10.1021/acs.jcim.7b00391 [DOI] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0236894.r001

Decision Letter 0

Oscar Millet

14 May 2020

PONE-D-20-10145

A chemical interpretation of protein electron density maps in the worldwide protein data bank

PLOS ONE

Dear Dr. Moseley,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

There are a significant numbers of concerns that have to be addressed in the manuscript before it can be accepted. In light of the number and magnitude of the issues raised by the reviewers, the paper will likely undergo a second round of review.

We would appreciate receiving your revised manuscript by Jun 28 2020 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

We look forward to receiving your revised manuscript.

Kind regards,

Oscar Millet

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Please include captions for your Supporting Information files at the end of your manuscript, and update any in-text citations to match accordingly. Please see our Supporting Information guidelines for more information: http://journals.plos.org/plosone/s/supporting-information.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

Reviewer #3: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: No

Reviewer #3: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: This is a clear manuscript that describes a process by which electron density maps from protein structures are renormalized to units of number of electrons - which has a direct physical interpretation. It is a valuable contribution to the field of protein science that is suitable for publication in its current format. This reviewer is someone who routinely uses the PDB to obtain region-specific information about proteins and we anticipate exploring the tools described in this article and assessing their suitability for determining the quality of local protein structure regions.

One page six at the bottom - the rho character is misprinted as a >.

I was a little concerned about subsuming the hydrogen electrons into the heavy atom as this would explain variations in the radii of atoms within a structure. It is unclear what would be lost by ignoring these electrons completely.

At the end, some use cases are presented which is helpful and the comment is made that a deviation of 6 electrons is negligible but a dozen or more could represent a problematic region of the structure. At what point is the deviation in number of electrons significant from a physical chemical perspective?

Reviewer #2: General comments

The authors state, very correctly, that there exists a need to be able to study electron density in an independent manner as the election density calculated from structure factors exists on a relative scale. The problem of relative density scales means that it is difficult for large numbers of PDBs to be evaluated collectively. It is also perhaps confusing for scientists, who are not particularly familiar with MX, biologists for example, and they might be drawn into making incorrect conclusions based on a spurious understanding of relative electron density maps. The authors propose, as a solution to these problems, a novel method that not only translates the arbitrary units of electron density into electrons per angstroms cubed, but also, normalises the density. Unlike previous methods, which require structure factors for the F000 calculation, this technique instead is based upon optimised atomic radii which have, in turn, been calculate from observations of the entire PDB.

As a much as I appreciate the goals this work I think this work would be made more powerful it if the authors could more properly highlight the benefits of this method in comparison to an F000 calculation. The authors highlight that there are two groups of people who would benefit from this work: less informed scientists who are viewing single structures, and bioinformaticians, viewing 1000s. I feel that this article could be improved by treating these two goals separately e.g. at a very specific level for a biologist interested in a single enzyme and a bioinformatician looking at 1000s of enzymes. The results could then properly demonstrate how this new method of analysing structures could be implemented and how it can improve the analysis of structures.

Another aspect which I think is slightly unclear/could be improved upon, is a direct comparison with the current method of putting electron density maps on the same scale i.e. from the F000 [Lang et al., (2014)] and by utilizing deposited structure factor data. The authors have not really made clear why this method cannot be automated and done on a larger scale. The authors have attempted to do an F000 calculation but then negated to include a bulk solvent estimation. Lang et al., (2014) does describe how to do this and it, therefore, seems strange that the authors have attempted to compare their method with the F000 calculation without attempting to take into account bulk solvent. This comparison should be made at both the specific (single structure electron density) and the 1000s structure level to really show that the authors’ method is an improvement. The authors’ method is independent of structure factor data and can, therefore, be used on the whole PDB, not just those PDBs which have been deposited since 2008. By my estimation, there should be some 47,569 structures - not inconsiderable - deposited before 2008 where an F000 calculation cannot be performed - the authors could highlight this advantage more fully.

There also seems to be a false premise in the way that the authors have calculated their normalised electron density radii. Part of the calculation appears to be based upon data derived from the PDB as a whole. However, as the authors say in the introduction, the radii deposited in the PDB are all on a relative scale and, therefore, difficult to compare even in the aggregate. Could the authors either confirm that my reading of the article is incorrect and that this has not been done, or if it has, explain that the results they derive are still accurate.

Finally, the referencing in the text is appears to be a bit poor in places. The authors have referenced papers which do not appear to support their conclusions and this distracts from the paper (specific comments are outlined under point 4 below). Please check that the references you have used to cite a particular point are correct.

Is the manuscript technically sound, and do the data support the conclusions? - Partly

As outlined in the general comments, in my opinion the paper could be greatly improved by a clear demonstration of the benefits of using this method in the results section. This could be done by first giving a real comparison with an F000 calculation at both the specific and general level, and then an example of how this method could be used in practice for a particular scientific question.

2. Has the statistical analysis been performed appropriately and rigorously? - No

No statistical analyses appear to have been performed. The authors offer very non-specific comments when comparing how sparse their data are (for example bottom of page 11, top of page 12) and these analyses would be greatly improved by calculating if changes in relative variability are statistically significant.

3. Have the authors made all data underlying the findings in their manuscript fully available? - Yes

I commend the authors for the clarity and ease of accessing their software.

4. Is the manuscript presented in an intelligible fashion and written in standard English? - Yes

Specific comments in text:

Suggest that x-ray should be written as X-ray.

Introduction

Page 3

Bottom-page - Suggestion to correct, “These low-quality regions arise from structural model and electron density mismatches can be due to a variety of reasons including problems with regional protein mobility (8), data processing (9), or model fitting (10).”

“These low-quality regions arise from structural model and electron density mismatches that can be due to a variety of reasons including problems with regional protein mobility (8), data processing (9), or model fitting (10).”

Same sentence - check references.

8 and 9 are very specific references and do not obviously support the authors’ statements.

Page 4

Top-page - Suggestion to correct, “Therefore, evaluation…”

“Therefore, the evaluation”

Figure 1. The image quality of panel is poor, suggestion to improve resolution of image used for publication. Furthermore, a suggestion to use ‘standard’ structure visualisation programs used by the structural biology community for example PyMOL or Chimera to parallel how structural biologists view and present structures.

Page 5

Mid-page - Many electron density map viewers (15, 16) - 16 does not reference an electron density map viewer. Perhaps add common visualisation tools and their references such at Coot, Pymol and Chimera.

Mid-page - Not clear what is meant by “electrons of density” - do the authors mean “electrons represented by the density”?

Mid-page - Suggestion to correct ”these methods require a reanalysis of the underlying structure factors with software packages that are not easily automated (19, 20).” Suggestion to remove, “that are not easily automated”

Methods

Page 6

Mid-page - Should this be 1.5 and 3 σ (sigma)?

Bottom-page - (>m) should this be ⍴m (rho m)?

Page 7

Top-page - "Since hydrogen is normally not resolvable within electron density maps, their electrons were added to their bonded atom." The authors show later that for high resolution their electron density model does not work as well as for low resolution structures. Can the authors comment on whether high resolution structures need their hydrogen electrons specifically modeled? Instead of being included with the electrons of their bonded atom?

Top-page-second paragraph - Suggestion to correct. “After all atom electron densities are calculated, they are aggregated into residue and chain densities where the residue cloud contains at least 4 atoms and the chain cloud contains at least 50 atoms. The overlapping density voxels between two or more atoms are only counted once through the aggregation. The total number of electrons are calculated by adding contributing atom’s electron numbers together. Residue (rr) and chain (rc) density ratios are then calculated accordingly.”

“After all the atom electron densities were calculated, they were aggregated into residue and chain densities where the residue cloud contains at least 4 atoms and the chain cloud contains at least 50 atoms. The overlapping density voxels between two or more atoms were only counted once through the aggregation. The total number of electrons were calculated by adding the contributing atom’s electron numbers together. Residue (rr) and chain (rc) density ratios are then calculated accordingly.

Bottom-page - Suggestion to correct - “…we then define a more universal measure…” to “…we then defined a more universal measure…

Page 8

Optimisation of radii - Suggestion to correct - “After the initial calculation, the median density ratios of different atom types were still quite different from each other. Thus, to achieve a more uniformly interpretable density ratio within a structure as well as across structures, an optimization of radii is performed. First, we tested the radius for each atom type on 100 random structures and obtained an initial estimation of the radii. The metric we used to optimize is the median of corrected chain deviation fraction (fi-corrected) for a given atom type. Based on the results from the initial step, we then optimize one atom type at a time on 1000 randomly selected structures. For every iteration, the atom type that has the largest deviation from last round is optimized. Different radii are tested for the given atom type and the radius that has a median corrected chain deviation fraction closest to zero is picked out. At the end of each optimization, the set of bfactor slopes are updated as well. This process goes on until the median chain deviation fraction for all atom types are smaller than 0.05. The final set of radii are then tested on another 1000 random structures and the whole PDB database for validation.”

“After the initial calculation, the median density ratios of different atom types were still quite different from each other. Thus, to achieve a more uniformly interpretable density ratio within a structure as well as across structures, an optimization of radii was performed. First, we tested the radius for each atom type on 100 random structures and obtained an initial estimation of the radii. The metric we used to optimize was the median of corrected chain deviation fraction (fi-corrected) for a given atom type. Based on the results from the initial step, we then optimize one atom type at a time on 1000 randomly selected structures. For every iteration, the atom type that had the largest deviation from last round, was optimized. Different radii were tested for the given atom type and the radius that had a median corrected chain deviation fraction closest to zero was picked out. At the end of each optimization, the set of bfactor slopes was updated as well. This process went on until the median chain deviation fraction for all atom types were smaller than 0.05. The final set of radii were then tested on another 1000 random structures and the whole PDB database for validation.”

Page 9

Can the authors comment on why their F000 calculation does not include a bulk solvent estimation?

Results

Fig. 3 - panels D-F have not been referenced in the text, suggestion to remove or to reference in the text.

Page 11

Fig. 5 - Suggestion to separate graphs further. At present the labels of the X axes overlap and make them challenging to read.

Page 11

Top-page - Please comment on whether the observed improvement is statistically significant.

Table. 1 - For clarity, suggestion to indicate which atom types are side and which are main chain using an additional column in the table.

Page 13

Mid-page - Suggestion to correct “The final set of radii was first tested on another 1000 random structures and all atom types hold true to have no more than a 5% chain deviation fraction. It was then applied to the all PDB structures that has usable electron density data…”

“The final set of radii was first tested on another 1000 random structures and all atom types held true to have no more than a 5% chain deviation fraction. It was then applied to the all PDB structures that had usable electron density data…”

Mid-page - Can the authors add a comment here about how they have identified that this model is better or worse for high-resolution data (perhaps with reference to the methods section).

Page 14

Mid-page - Suggestion to correct - “Thus, conversion is not as simple as adding an F000 term as often theoretically represented in textbooks (25, 26)” - Please note that ref 25 is not a textbook and ref 26 does not imply that the bulk solvent calculation is easy. Consider revising this sentence.

Page 15

Fig. 10 - From this figure it is not clear what benefit this annotation would give a non-crystallographer. I agree there is now an estimation of the electron density in terms of the number of electrons. But what does this mean for a biologist? Is it really a great improvement on sigma? For a non-crystallographer, and even many crystallographers, what difference is a number of electrons or a sigma contour level estimation of the density? A cut off in one or the other still feels like an arbitrary rule to live by. To rectify this, suggestion that this figure should demonstrate the value of method. It should perhaps also show the output from the software and indicate how a scientist would find the number of electrons associated with each blob and then why this image/representation would ease interpretation. Could the authors please include such a Figure as a demonstration of the value of this method.

Reviewer #3: Review of PLOS ONE ms PONE-D-20-10145 “A chemical interpretation of protein electron density maps in the worldwide protein data bank” by S.Yao & H.N.B.Moseley

The goal of this work is very commendable (to generate electron density on absolute level) and the solution is elaborated through a convoluted algorithm, which - although basically, I think, correct and well documented - is… unnecessary. In principle, the Authors arrive at the “arbitrary” => “absolute” scale factor by a tedious comparison of the experimental electron density map with its atomic model. Or in other words, they want to scale apples with oranges. But a much simpler solution exists: compare oranges with oranges. In the simpler approach one would first convert the atomic model to its Fourier Transform Fc(hkl), and then use a subset of those calculated structure factors corresponding exactly to the set of experimental Fo(hkl) data, to generate ρc(xyz), i.e. the calculated (Fc) electron density map. This map would be the target for scaling the experimental (observed) ρo(xyz) electron density map (Fo). The scaling would be of course linear: ρc(xyz) = a·ρo(xyz) + b, and would have to be fulfilled at all grid points on which the two maps have been calculated. Since this strictly linear problem is hugely overdetermined, only the most reliable grid points could be included, e.g. within 1 A of the atomic centers of the model, or indeed within the atomic radii used in the ms. The set of linear equations could be solved by the method of least squares, with the addition of a robust method to filter out outliers, e.g. if some fragments of the model are of poor quality. This way the best values of the a and b parameters are obtained. I have not tried this algorithm myself - it’s not my paper. But I am pretty sure it should work quite well. At least the Authors should try a simple method first, before proposing an algorithm that may be unduly complicated.

In conclusion, I cannot recommend acceptance of this paper in its present form. In addition to the doubts outlined above, there is one more misgiving. Assuming that we have electron density re-scaled to absolute units by one method or the other, the real question is : “So what?” The Authors should provide examples to clearly demonstrate what is possible with their maps that would not be possible with sigma-scaled 2Fo-Fc and Fo-Fc maps. Right now there is a lot of verbal promise but very little of concrete proof. BTW, the caption of Fig. 10 is amazingly unhelpful.

It may be irrelevant in view of my final recommendation (reject), but since I’ve read the paper very carefully, I’m also including my more specific comments and critical remarks, divided into “Substantive” and “Technical”.

Substantive problems

The convoluted algorithm includes a series of corrections, one after another. At some point the reader is lost as to the purpose of all those corrections. Perhaps it would be helpful to add a graph showing the distribution of the sample 1000 structures?

The Authors should calibrate their method with ultrahigh-resolution PDB crystal structures which provide accurate estimate of electron density levels in e/A3 because they have a large Ewald sphere of very accurate F(hkl) data and in addition allow reliable estimation of F(000) since the (nearly) complete atomic content of the unit cell is practically known. The recommended examples would be the PDB entries 3NIR (0.48 A, crambin, highest resolution but unsatisfactory refinement), 1EJG (0.54 A, crambin) (comparison of the two crambin structures would provide an interesting “internal standard”) and 2VB1 (0.65 A, lysozyme) for proteins, and 3P4J (0.55 A, Z-DNA) for nucleic acids.

I also note that, infrequent as they are, occasionally ultrahigh-resolution macromolecular structures are presented with the electron density maps expressed on the absolute scale (e.g. Addlagatta et al. (2001) Acta Cryst. D57: 649-663). Such maps could also be used to validate the scaling procedures proposed in this work.

p3, “These low-quality regions arise from structural model and electron density mismatches…”, actually, most often the low-quality regions arise because of absence of electron density.

p6, I am surprised that the Authors have completely overlooked the paper by Tickle (2012) Acta Cryst. D68: 454-467, which is the standard classical reference for sigma-contoured electron density maps and more. Also, there is a good discussion there about the radii of atoms that cover 95% of electron density, and about the influence of B-factors and resolution (see 5.6. The limiting radius of the atomic density; as well as Table 3 and Fig. 11 therein).

Fig. 2 caption; it is correct to include H atoms in the electronic inventory of their “carriers” if H atoms were not included in Fc calculations. However, as is very often the case, if H atoms were included in Fc, then this strategy is incorrect. Moreover, if the electron density of H atoms is added to the bound atom, then interpretation by a simple spherical volume around that atom will lead to systematic errors. In addition, the resolution of the electron density map is also important.

I don’t understand the idea of dividing the formula for F(000) in eq. (6) by V. Structure factors F (including F(000), of course), are expressed directly in electrons (e). Also, counting the electron contribution of the solvent molecules is necessary, but in most cases we miss a lot of water molecules (not included in the model). At low resolution, we cannot count the water molecules at all. What could be done, however, would be to estimate the number of water molecules from Matthews volume and specific density of water (1 g/cm3) and add their electrons to F(000).

I wonder, how much the re-scaled difference maps show-cased on p15 and Fig. 10 would differ from normal mFo-DFc and 2mFo-DFc maps. I think such a comparison should be illustrated.

The method should be extended (in the future?) to explicitly apply to nucleic acids as well. Nucleic acids constitute an important segment of PDB structures.

To be of general applicability, a method like this should produce electron density maps in mtz or other ccp4/coot/pymol-readable format, so that they could be easily loaded and displayed for visualization.

Technical remarks

p3, “activities happens”, singl./pl. problem.

p6 and elsewhere, the Greek letter sigma (and other symbols) is misprinted as a funny character.

I couldn’t find anywhere in the ms the key information about the density of the grid over which the electron density is calculated and analyzed.

Fig. 2 caption, “20 common amino acid”, singl./pl. problem.

Correct the grammar in Fig. 2 (“by atom the b-factor”).

p7, “total number of electrons are”, singl./pl. problem.

On p8, the term “chain deviation fraction” is suddenly changed to “chain fraction” (without definition).

p8 and elsewhere, “on 100 random structures”, change to “of…”.

p10, “Fig. 3. Sina plots of density ratio for atoms, residues, and chains”, perhaps it would be helpful to add a short description a sina plots, for example as in https://ggforce.data-imaginist.com/reference/geom_sina.html: “Sina plot is an enhanced jitter strip chart, where the width of the jitter is controlled by the density distribution of the data within each class.”.

Fig. 3, frankly, I don’t see much difference between the top and bottom panels… Moreover, it seems to me that the x axis of panels C and F shows residues, not chain IDs; I am confused…

The “optimized” atomic radii are usually >= the “original” radii. An outstanding exception in Table 1 is S. Any reason why?

p13, last sentence before new section, don’t begin sentence with “And…”.

p13, explain “distribution modes”.

p13, “It was then applied to the all PDB structures that has usable electron density data”, several grammatical errors in this sentence.

Fig. 8 caption talks about 2mFo-DFc maps, but panels A/B are supposed to correspond to 2Fo Fc/Fo Fc maps.

Something wrong with the first sentence of Fig. 9 caption.

p14, “with a local region.”, perhaps “within a local region.”.

p15, difference electron density of “16 and 29 e” sounds like serious overshooting. Should be metal or halide ions, or at least S.

Fig. S1, the axes need proper labels and units. The values of the ticks on the x axes are squeezed too much and unreadable. The plots, with the current caption, are not very useful.

Tables S1 and S2 with the inventory of bonds and atoms in standard amino acid residues are banal and could be omitted.

Please note that the proper symbol to be used for Atomic Displacement Parameter (temperature factor) is B-factor.

I am glad to note that the GITHUB documentation and examples seem to work well. I note that GITHUB reports version 1.0.1. and PythonPackageIndex version 1.1.0. There are also some shortcomings and bugs. For example, the command:

python3 -m pdb_eda single 3han 3han.all.csv --all --out-format=csv

instead of human-readable printouts, returns a printout of rather useless python objects.

Execution of:

python3 -m pdb_eda single 3han 3han.all.csv --all --out-format=csv

generates an error message:

AttributeError: 'int' object has no attribute 'aggregateCloud'

which is not very helpful.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: Yes: John H. Beale

Reviewer #3: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files to be viewed.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org. Please note that Supporting Information files do not need this step.

Attachment

Submitted filename: PLOS-1-20-10145.pdf

Click here for additional data file.^{(565KB, pdf)}

PLoS One. 2020 Aug 12;15(8):e0236894. doi: 10.1371/journal.pone.0236894.r002

Author response to Decision Letter 0

27 Jun 2020

Reviewer #1:

This is a clear manuscript that describes a process by which electron density maps from protein structures are renormalized to units of number of electrons - which has a direct physical interpretation. It is a valuable contribution to the field of protein science that is suitable for publication in its current format. This reviewer is someone who routinely uses the PDB to obtain region-specific information about proteins and we anticipate exploring the tools described in this article and assessing their suitability for determining the quality of local protein structure regions.

Response:

We thank the reviewer for recognizing the value of our research presented here. We are trying to provide tools that make it easier to evaluate structural regions without needing to work with structure factor files and x-ray crystallography software that requires a lot of expertise to use properly.

Issue 1:

One page six at the bottom - the rho character is misprinted as a >.

Response:

Fixed.

Issue 2:

Response:

The hydrogen electron is part of the electron density and cannot be ignored. Exactly how to represent the electron cloud around the heavy atom and the hydrogen could be an issue if the resolution of a given structure was really high (probably below 0.5 angstroms). But pragmatically, macromolecular x-ray crystallographic structures are not high enough resolution to make a difference.

Issue 3:

Response:

We do not know how much of a deviation is problematic. It will depend on how the region is being used and to what level of interpretation. We are actively exploring how quantified regional deviations affect molecular docking of ligands, but have just started this collaborative work.

Reviewer #2:

Response:

We thank the reviewer for recognizing the importance of the problem we are trying to address in this research.

Issue 1:

Response:

If it was practical to calculate an F000 for thousands of PDB entries, we would have done this and more importantly, there would not be a need for the methods and software that we have developed. Therefore, we presented alternative ways to evaluate and validate the method. While these approaches do not represent a classical analytical cross-validation with another method, they do represent a statistical validation that demonstrates mostly unimodal distributions that highlight the level of uncertainty in the data. Please understand that there are different approaches to validation. The one we have presented is statistically rigorous and compelling. The corresponding author, Hunter Moseley, has degrees in Chemistry, Biochemistry, Mathematics, and Computer Science. He currently teaches statistics to biomedical graduate students and authored the statistics for biologists introduction in Bioinformatics: A Practical Guide to the Analysis of Genes and Proteins 4th Edition, editors: Andreas D. Baxevanis, Gary D. Bader, and David S. Wishart, John Wiley & Sons: New Jersey (2020). We understand that there is often confusion between analytical and statistical approaches, but rigorous evaluation is possible with both types of approaches. We often use both types of approaches to validate our methods and research, when both can be utilized.

Issue 2:

Response:

We have not automated analysis of structure factors, because we focused on the Fo-Fc maps. If you can identify a method that automates use of structure factors to derive F000, we are very willing to do a direct comparison. But ultimately, our goal was to analyze the Fo-Fc and 2Fo-Fc maps for regional analysis. Therefore, our development efforts were focused there. We went through the old CCP4 codebase to determine the ccp4 file formats and implemented libraries to fully parse these files. To produce the quality of the codebase we have implemented takes a significant amount of effort. We are not just developing methodology, but implementing it in high-quality code bases following best software development practices. This is in contrast to the vast majority of scientific software that is developed and published.

Also, our method cannot be used on the whole wwPDB. There are many entries that do not have Fo-Fc electron density maps made available by PDB in Europe. So, no we cannot claim that our methods work on all x-ray crystallographic structures deposited in the wwPDB.

Issue 3:

Response:

Actually, we started with radii published in the literature:

“To calculate the total electron density around each atom, we initially used the radii from literature (23) and calculated the sum of all densities within the corresponding radius.”

Then we optimized these radii utilizing a set of 1000 randomly selected PDB entries, then tested against another set of 1000 randomly selected PDB entries, and ultimately validated them against all usable wwPDB entries.

Issue 4:

Response:

Thanks for the important feedback. We have updated and improved the references.

Issue 5:

Is the manuscript technically sound, and do the data support the conclusions? - Partly

Response:

We understand the reviewer’s desire for an analytical cross-validation comparison with another way to calculate the results, but that was not practical in this instance and is actually a major reason for the development of this approach.

Our other publication where we apply our methods to a systematic analysis of all metal-bound ions across the wwPDB should demonstrate a practical application of our methods: Sen Yao and Hunter N.B. Moseley. "Finding high-quality metal ion-centric regions across the worldwide Protein Data Bank" Molecules 24, 3179 (2019).

Issue 6:

2. Has the statistical analysis been performed appropriately and rigorously? - No

Response:

We used a visualization approach to demonstrate statistical rigor. Figure 5 shows a clear correlation between log B-factors and chain deviation fraction. More importantly, Figure 6 shows the improvement in the density ratio distributions derived for each atom type. This includes a reduction in variation, but more importantly, the improvement in the consistency of these unimodal distributions across atom types. We could have quantified this improvement by calculating the overlap across the distributions with each refinement, but honestly the visualization is just so compelling. In our opinion, a well-done visualization of the distributions so that they can be easily compared (i.e. the reason for the Sina plots in Figure 6), allows for much better interpretation. However, we recognize the utility in providing a quantitation on the improvement in the density ratio distributions. Therefore, we have added this in terms of a standard deviation for each refinement illustrated in Figure 6. In the main text, we highlight this improvement in standard deviation as follows:

“Moreover, the standard deviation of the overall distribution drops to 0.09, representing a 40% decrease in the calculated density ratio variability.”

Issue 7:

3. Have the authors made all data underlying the findings in their manuscript fully available? - Yes

I commend the authors for the clarity and ease of accessing their software.

Response:

Thank you. We put a lot of effort into making our software accessible and usable.

Issue 8:

4. Is the manuscript presented in an intelligible fashion and written in standard English? - Yes

Response:

Thank you. This manuscript has gone through many rounds of revision.

Issue 9:

Specific comments in text:

Suggest that x-ray should be written as X-ray.

Response:

We do not think this is appropriate. The word “x-ray” is not a proper noun.

Issue 10:

Introduction

Page 3

Response:

Thanks! Fixed:

“These low-quality regions arise from structural model and electron density mismatches that can be due to a variety of reasons including problems with regional protein mobility that can often lead to an apparent lack of electron density [8-10], data processing [11, 12], or model fitting [10, 13, 14].”

Issue 11:

Same sentence - check references.

8 and 9 are very specific references and do not obviously support the authors’ statements.

Response:

These references are specific, but are meant as examples of each issue. We have added additional references that include reviews that highlight these issues.

Issue 12:

Page 4

Top-page - Suggestion to correct, “Therefore, evaluation…”

“Therefore, the evaluation”

Response:

Fixed.

Issue 13:

Response:

We have improved the resolution of the image.

Issue 13:

Page 5

Response:

Thank you for catching reference 16. This was accidentally added at some point in the revision process. We have added references for Coot, Pymol, and Chimera:

“Many electron density map viewers [19-22] exist for manually examining the quality of a model versus its electron density; however, this software and evaluation approach is not suitable for batch analysis of hundreds of structures.”

Issue 14:

Mid-page - Not clear what is meant by “electrons of density” - do the authors mean “electrons represented by the density”?

Response:

This is exactly what we meant and have modified the text accordingly:

“But this zero-sum representation can be detrimental for understanding a model, especially a local region of a model, where the number of electrons represented by the density or density discrepancy would be useful for evaluation.”

Issue 15:

Response:

This point emphasizes a major advantage that our software provides. But we understand why the reviewer may take offense to the statement, which can be interpreted to mean something else. Therefore, we have reworded it as follow:

“While methods exist that can derive electron density maps on an absolute scale, these methods require a reanalysis of the underlying structure factors with software packages that are not designed for automated use across large numbers of structural entries (19, 20).”

Issue 16:

Methods

Page 6

Mid-page - Should this be 1.5 and 3 σ (sigma)?

Response:

Thanks for catching this. Looks like some of our Greek symbols got converted to weird symbols going back and forth between Windows and Mac versions of Word. Fixed.

Issue 17:

Bottom-page - (>m) should this be ⍴m (rho m)?

Response:

Same Mac-Windows conversion issue. Fixed.

Issue 18:

Page 7

Response:

Figure S1 shows the opposite of what the reviewer interpreted. Our method works a bit better for high resolution structures than low resolution structures. Simply compare the >3 angstroms distribution to the <=1.5 angstroms distribution across the atom types. So no, we do not need to specifically model hydrogen electrons. We expect the resolution would need to be below 0.5 angstroms before this becomes a factor. Because we see a correlation between resolution and the median chain deviation fraction for some atom types, we see a path to a future refinement of the method. Also, we think the current radii are optimized for the median resolution of x-ray crystallographic structures in the wwPDB. We have added a statement to make this point:

“This figure also implies that the current radii are likely optimized for the median resolution of x-ray crystallographic structures present in the wwPDB.”

Issue 19:

Response:

Respectfully, we disagree. We believe that the present verb tense is the correct verb tense to use here. We had used a past verb tense two sentences previous, because it referred to a decision on how to represent the hydrogen electrons.

Issue 20:

Bottom-page - Suggestion to correct - “…we then define a more universal measure…” to “…we then defined a more universal measure…

Response:

Again, we respectfully disagree. We are using a present verb tense in describing the calculations. If this was a specific calculation performed, we would have used the past tense.

Issue 21:

Page 8

Response:

We agree completely with the verb tense change. Here is the revised section:

“After the initial calculation, the median density ratios of different atom types were still quite different from each other. Thus, to achieve a more uniformly interpretable density ratio within a structure as well as across structures, an optimization of radii was performed. First, we tested the radius for each atom type on 100 random structures and obtained an initial estimation of the radii. The metric we used to optimize was the median of corrected chain deviation fraction (fi-corrected) for a given atom type. Based on the results from the initial step, we then optimized one atom type at a time on 1000 randomly selected structures. For every iteration, the atom type that has the largest deviation from last round was optimized. Different radii were tested for the given atom type and the radius that has a median corrected chain deviation fraction closest to zero was picked out. At the end of each optimization, the set of B-factor slopes were updated as well. This process continued until the median chain deviation fraction for all atom types were smaller than 0.05. The final set of radii were then tested on another 1000 random structures and the whole PDB database for validation.”

Issue 22:

Page 9

Can the authors comment on why their F000 calculation does not include a bulk solvent estimation?

Response:

We think it is because we tried to derive this from the 2mFo-DFc map instead of the structure factors themselves, but honestly we are not sure. We tried a lot of variations and none of them worked.

Issue 23:

Results

Fig. 3 - panels D-F have not been referenced in the text, suggestion to remove or to reference in the text.

Response:

We added the following sentence:

“This improvement percolates through to the residue and chain level, but is not as obvious (see Fig 3, Panels D-F).”

Issue 24:

Page 11

Fig. 5 - Suggestion to separate graphs further. At present the labels of the X axes overlap and make them challenging to read.

Response:

We have fixed this.

Issue 25:

Page 11

Top-page - Please comment on whether the observed improvement is statistically significant.

Response:

We are assuming that the reviewer is referring to the improvements visualized in Figure 6. But, statistical significance generally refers to null hypothesis testing. There is no null hypothesis being testing here. We can quantify the improvement and have done so in terms of a standard deviation of the density ratio values across all atom types at each stage of refinement. So we can quantify the improvement, but whether this is enough to affect statistical significance is context specific and depends on the specific dataset being analyzed. In the main text, we highlight this improvement as follows:

“Moreover, the standard deviation of the overall distribution drops to 0.09, representing a 40% decrease in the calculated density ratio variability.”

Issue 26:

Table. 1 - For clarity, suggestion to indicate which atom types are side and which are main chain using an additional column in the table.

Response:

Backbone atoms are indicated by “_bb”. We have added a footnote to the table to make this clear.

Issue 27:

Page 13

Response:

Thanks. We made this change:

“The final set of radii was first tested on another 1000 random structures and all atom types held true to have no more than a 5% chain deviation fraction. It was then applied to all PDB structures that had usable electron density data, and the results are shown in Fig 7.”

Issue 28:

Mid-page - Can the authors add a comment here about how they have identified that this model is better or worse for high-resolution data (perhaps with reference to the methods section).

Response:

In Figure S1, simply compare the >3 angstroms distribution to the <=1.5 angstroms distribution across the atom types. Our method works a bit better for high resolution structures than low resolution structures. More importantly, we think the current radii are optimized for the median resolution of x-ray crystallographic structures in the wwPDB. We have added a statement to make this point:

“This figure also implies that the current radii are likely optimized for the median resolution of x-ray crystallographic structures present in the wwPDB.”

Issue 29:

Page 14

Response:

The way the reviewer interpreted this sentence was not our intended meaning. We have reworded the sentence as follows:

“Thus, an F000 term as theoretically represented in textbooks and papers (25, 26) is not easy to calculate and likely depends on software parameters used in the creation of the map.“

Issue 30:

Page 15

Response:

We are trying to improve the chemical interpretation of the deviation. Biological interpretation is another step after the chemical or biochemical interpretation. We demonstrate the utility of our method and software in the following paper: Sen Yao and Hunter N.B. Moseley. "Finding high-quality metal ion-centric regions across the worldwide Protein Data Bank" Molecules 24, 3179 (2019).

Reviewer #3:

Review of PLOS ONE ms PONE-D-20-10145 “A chemical interpretation of protein electron density maps in the worldwide protein data bank” by S.Yao & H.N.B.Moseley

Response:

We do not argue that working with structure factors could allow one to derive a conversion factor with a simpler approach. We are demonstrating a method to do this from the Fo-Fc maps that is implemented is a relatively easy to use software package. Complicated or not, we strove to demonstrate that it works.

Honestly, the third reviewer is a crystallographer and not the target audience for our software. Any well-trained crystallographer is going to expertly use their favorite raw data analysis software to derive and evaluate new macromolecular structures. But we want to enable the non-crystallographer users of the PDB to be able to make better choices in the PDB entries that they use and not just base it on the resolution, R-factor, and R-free of the entry. Also, we are trying to provide easy-to-use software that can be applied to large numbers of PDB entries so that systemic analyses can be performed using easy to obtain processed x-ray crystallographic data (Fo-Fc and 2Fo-Fc maps) provided by the PDB in Europe REST interface.

Issue 1:

Response:

To reject a manuscript presenting a method that the reviewer concludes does work is not following the PLOS One review criteria that says to review on the grounds of if the presented research is sound and done correctly. If we have presented a method that works and is scientifically sound, then rejecting because the reviewer does not see a personal use of the research is not a valid reason to reject for this journal.

Furthermore, we have demonstrated an application of this methodology to the systematic characterization of metal-binding sites across the wwPDB: Sen Yao and Hunter N.B. Moseley. "Finding high-quality metal ion-centric regions across the worldwide Protein Data Bank" Molecules 24, 3179 (2019). We are looking at applying this method as a way to improve molecular docking of ligands, but that work has just started.

We apologize that we may have developed a software package that the reviewer does not personally find useful to their research. But in all fairness, we were not developing our software package for crystallographers.

Issue 1:

Substantive problems

Response:

Figure 6 and Figure 3 Panels D-F show the improvement provided with each refinement. By the final refinement, each atom type density ratio distribution are much more consistent. We have now quantified this improvement in terms of a shrinking standard deviation directly indicated in Figure 6. In the main text, we highlight this improvement as follows:

“Moreover, the standard deviation of the overall distribution drops to 0.09, representing a 40% decrease in the calculated density ratio variability.”

Issue 2:

Response:

As Figure S1 shows, calibrating to the ultrahigh-resolution alone will produce worse results for the majority of the wwPDB entries which consist of lower resolution entries. In fact, the final radii appear optimized to the median wwPDB resolution:

“This figure also implies that the current radii are likely optimized for the median resolution of x-ray crystallographic structures present in the wwPDB.”

Issue 3:

p3, “These low-quality regions arise from structural model and electron density mismatches…”, actually, most often the low-quality regions arise because of absence of electron density.

Response:

The lack of electron density is one implied outcome of regional protein mobility; however, based on the reviewer’s comments we have made this point explicit:

“These low-quality regions arise from structural model and electron density mismatches that can be due to a variety of reasons including problems with regional protein mobility that can often lead to an apparent lack of electron density [8-10], data processing [11, 12], or model fitting [10, 13, 14].”

Issue 4:

Response:

We thank the reviewer for highlighting this important reference to add! We know this paper, but had not recognized the its significance with respect to the relationships between atomic radii, B-factor, and resolution. We have added it in the following context in the Discussion section:

“These relationships between atomic radii, B-factors, and resolution with respect to observed electron density have been described previously [32]; however, Figures 5 and S1 provide a useful visualization of these relationships.”

Issue 5:

Response:

We immensely thank the reviewer for this bit of information!! In the future, we can optimize two sets of radii based on hydrogen electrons included or not. We should be able to reliably predict if the Fc is calculated with or without the hydrogens. But this would be in a future improvement of the methodology. Given that all of the electron density maps we analyzed are generated by the PDB in Europe, we would assume that they are consistently generated with either Fc calculations including or excluding hydrogen electrons. Based on this consistency, the radii will be optimized to compensate for either situation.

Issue 6:

Response:

Again, we thank the reviewer for their comments! We tried many permutations of calculating F000 based on the representations we had seen in different sources. Based on this information, we may try additional approaches in the future. However, given that there are different methods for deriving F000 for structures of different resolutions, our approach does provide one general approach for deriving a conversion factor that is somewhat resolution agnostic. We have made this point indirectly in the manuscript:

“Furthermore, the bulk solvent is estimated in different ways depending on resolution [31, 32].”

Issue 6:

I wonder, how much the re-scaled difference maps show-cased on p15 and Fig. 10 would differ from normal mFo-DFc and 2mFo-DFc maps. I think such a comparison should be illustrated.

Response:

We did not rescale the maps. We just labeled the discrepant density blobs in terms of eletrons of discrepancy. However, we did add the following to the Fgure 10 legend:

“The blue lattice represents the significant density regions in the 2Fo-Fc map, while the green lattice represents the significant positive discrepant density blobs and the red lattice represents the significant negative discrepant density blobs, both from the Fo-Fc map.”

Issue 7:

The method should be extended (in the future?) to explicitly apply to nucleic acids as well. Nucleic acids constitute an important segment of PDB structures.

Response:

This is our future plan and the software is capable of generating the radii for other biomacromolecules.

Issue 8:

Response:

The pdb-eda software analyzes electron density maps, it does not generate them. In particular, it is designed to download and analyze the electron density maps provided by the PDB in Europe REST interface.

Issue 9:

Technical remarks

p3, “activities happens”, singl./pl. problem.

Response:

Thanks! Fixed.

Issue 10:

p6 and elsewhere, the Greek letter sigma (and other symbols) is misprinted as a funny character.

Response:

Thanks for catching this. Looks like some of our Greek symbols got converted to weird symbols going back and forth between Windows and Mac versions of Word. Fixed.

Issue 10:

I couldn’t find anywhere in the ms the key information about the density of the grid over which the electron density is calculated and analyzed.

Response:

This manuscript is about deriving the electron density conversion factor. We have another publication where we apply methods that sum up absolute electron density discrepancy in a given region of a wwPDB entry: Sen Yao and Hunter N.B. Moseley. "Finding high-quality metal ion-centric regions across the worldwide Protein Data Bank" Molecules 24, 3179 (2019).

Issue 11:

Fig. 2 caption, “20 common amino acid”, singl./pl. problem.

Response:

Thanks again! Fixed.

Issue 12:

Correct the grammar in Fig. 2 (“by atom the b-factor”).

Response:

We fixed this as follows: “Adjust electron density ratios using atom-specific B-factor correction”

Issue 13:

p7, “total number of electrons are”, singl./pl. problem.

Response:

Thanks! Fixed.

Issue 14:

On p8, the term “chain deviation fraction” is suddenly changed to “chain fraction” (without definition).

Response:

Nice catch. Fixed.

Issue 15:

p8 and elsewhere, “on 100 random structures”, change to “of…”.

Response:

Respectfully, we believe this grammar is correct.

Issue 16:

Response:

We described them as follows, which includes a reference:

“If we simply use the radii from the literature and do not apply any correction, the median of atom density ratio shows that the density ratios are inconsistent within a single structure for atoms, residues, and chains, as illustrated in Fig 3 Panels A-C as Sina plots, an enhanced jitter strip chart that visualizes the distribution of each dataset for better visual comparison [30]”

Issue 16:

Fig. 3, frankly, I don’t see much difference between the top and bottom panels… Moreover, it seems to me that the x axis of panels C and F shows residues, not chain IDs; I am confused…

Response:

There is quite a bit of difference at the residue level (comparing panels A and D) before and after radii optimization. There is less difference at the residue and chain level, but these are included to highlight how stable the density ratio is at the chain level versus the residue and atom level. We highlight these points in the main text:

Issue 17:

The “optimized” atomic radii are usually >= the “original” radii. An outstanding exception in Table 1 is S. Any reason why?

Response:

We suspect that there is some old assumption made a long time ago that is either baked into most x-ray crystallographic software or into the original sulfur radius estimation. What it is exactly, we do not know, but we would wager that it is some assumption about sulfur behaving like another element when in reality it does not. However, we are not willing to make this type of statement in this manuscript. We have already highlighted this point about the sulfur as follows:

“The radius of sulfur changes the most as compared to the other elements. This could be due to how most software construct electron density data from structure factor and associated phase via Fourier transforms. The electron density is approximated with a Gaussian distribution, and its variance is affected mainly by the B-factor. Thus, the final optimized radius is a combination of the actual radius of the atom, the displacement of an atom center, as well as the thermal motion of the atom (B-factor).”

Issue 18:

p13, last sentence before new section, don’t begin sentence with “And…”.

Response:

Technically, this is not considered bad writing form anymore, but that is a matter of perspective. However, we went ahead and changed it to:

“Moreover, studying the behavior of sulfur atoms could be useful for other less common elements such as metal ions.”

Issue 19:

p13, explain “distribution modes”.

Response:

The phrase is “tighter distributions with modes above 0”. For a unimodal distribution, the distribution has one mode. In this phrase, we are talking about the mode of each chain deviation fraction distribution associated with each atom type for high-resolution structures (< 1.5 angstroms). All of these distributions have a mode above zero as illustrated in Figure S1.

Issue 20:

p13, “It was then applied to the all PDB structures that has usable electron density data”, several grammatical errors in this sentence.

Response:

Thanks! All grammatical errors are fixed as follows:

“It was then applied to all PDB structures that had usable electron density data, and the results are shown in Fig 7.”

Issue 21:

Fig. 8 caption talks about 2mFo-DFc maps, but panels A/B are supposed to correspond to 2Fo Fc/Fo Fc maps.

Response:

Our mistake. We have change the Figure 8 title to: “Histogram of the mean value of electron density maps provided by PDBe.”

Issue 22:

Something wrong with the first sentence of Fig. 9 caption.

Response:

We change the Figure 9 title to: “The absolute scale of the density ratio for all structures in the PDB.”

Issue 23:

p14, “with a local region.”, perhaps “within a local region.”.

Response:

Thanks. Fixed.

Issue 24:

p15, difference electron density of “16 and 29 e” sounds like serious overshooting. Should be metal or halide ions, or at least S.

Response:

Our point exactly. The number of electrons of discrepancy can inform the likely issue in the structural model.

Issue 25:

Fig. S1, the axes need proper labels and units. The values of the ticks on the x axes are squeezed too much and unreadable. The plots, with the current caption, are not very useful.

Response:

We have fixed the overlap in the values. However, the x-axis deals with a fraction that is unitless.

Issue 26:

Tables S1 and S2 with the inventory of bonds and atoms in standard amino acid residues are banal and could be omitted.

Response:

This is supplementary material. It does not matter if it is banal. We try to always error on the side of completeness with supplemental material.

Issue 27:

Please note that the proper symbol to be used for Atomic Displacement Parameter (temperature factor) is B-factor.

Response:

We have fix this across the manuscript.

Issue 28:

python3 -m pdb_eda single 3han 3han.all.csv --all --out-format=csv

instead of human-readable printouts, returns a printout of rather useless python objects.

Execution of:

python3 -m pdb_eda single 3han 3han.all.csv --all --out-format=csv

generates an error message:

AttributeError: 'int' object has no attribute 'aggregateCloud'

which is not very helpful.

Response:

We do try very hard to develop well-documented scientific codebases. We also beg to differ about Python objects being useless, but we will work on developing more human-readable printouts in future releases. Also, we have limited control over the quality of the error messages that the Python interpreter generates.

Attachment

Submitted filename: response_to_reviewer_comments_v3.docx

Click here for additional data file.^{(45.4KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0236894.r003

Decision Letter 1

Oscar Millet

7 Jul 2020

PONE-D-20-10145R1

A chemical interpretation of protein electron density maps in the worldwide protein data bank

PLOS ONE

Dear Dr. Moseley,

Specifically, there are a few technical issues pointed out by the reviewer that need to be addressed.

Please submit your revised manuscript by Aug 21 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Oscar Millet

Academic Editor

PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #3: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #3: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #3: N/A

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #3: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #3: Yes

**********

6. Review Comments to the Author

Reviewer #3: (No Response)

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #3: No

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2020 Aug 12;15(8):e0236894. doi: 10.1371/journal.pone.0236894.r004

Author response to Decision Letter 1

9 Jul 2020

Reviewer 3:

In view of the rebuttal, in particular emphasising that the audience of this paper are not professional crystallographers but less trained consumers of the PDB, as well as highlighting that the application of the proposed method and software lies in PDB-wide analyses, I reluctantly tend to agree that this manuscript could be accepted after additional minor revision. I am also amused by the correct unmasking of Referee 3 (i.e. myself) as a (well trained, I supposed) crystallographer! However, I have the impression that in many cases the Authors have glossed over the highlighted problems too easily, sometimes actually evading to address the issue at hand directly.

Response:

We thank the reviewer for seeing the utility of our software for the general consumer of the PDB. We were not trying to gloss over issues raised by the reviewers, but there were quite a few issues raised by all three reviewers, some issues with more merit than others. The revisions and response document take real effort to generate.

Issue 1:

One such remark is “my” Issue 6 (first instance with this issue number, as the Authors’ numbering of issues has errors), in which I pointed out that F(000) (as any other structure factor) is expressed in electrons. Therefore, the division of formula (6) by unit cell volume (V) is incorrect.

Response:

We misunderstood the point being made here the first time, because we were focused on how to use F(000) for correction. Thank you for raising it again! We would not want this kind of definition error in the published literature. We have made the following revisions:

“Unfortunately, not all structure factor programs provide the F000 value. So as an estimation, we add up the numbers of electrons for all the atoms of a model in the unit cell, including symmetry structure units and modeled water molecules,

F000 = ∑n_t Z_t (6)

Where nt is number of atoms of element t in the asymmetric unit and Zt is the number of electrons (atomic number) of element t. This estimated F000 term is then divided by the unit cell volume V in Å3 and added to the density values of all the voxels.

”

Issue 2:

Also, I think that the Authors are too quick to dismiss bug reports and to defer action to the future. Reports like the one below are useless for untrained users and can be certainly handled in a better way by error-handling routines included in the software package.

>> python3 -m pdb_eda single 6xyz 6xyz.atom.csv --atom --out-format=csv

>> AttributeError: 'int' object has no attribute 'aggregateCloud'

Response:

It is not that we are dismissing a bug report. We handle all issues posted on our GitHub repositories. Please look at https://github.com/MoseleyBioinformaticsLab to see where we address issues raised by users (for example, https://github.com/MoseleyBioinformaticsLab/GOcats/issues). However, we cannot anticipate all possible errors raised by the Python interpreter and provide a meaningful response to the user. All we can reasonably do is fix bugs and return more meaningful error messages for the bugs or edge cases that we find ourselves or are pointed out to us by others. Towards this end, we have verified the error and concluded that it is due to a flaw in the command line interface where object creation was not correctly tested for success. We have created an issue on our GitHub pdb-eda repository based on what the reviewer has provided and our testing of the error: https://github.com/MoseleyBioinformaticsLab/pdb_eda/issues/1 . We expect to have this issue fixed when we roll out a larger set of updates to the codebase in the next 2-4 weeks. Please be patient with us.

Attachment

Submitted filename: response_to_reviewer_comments_revision1_v1.docx

Click here for additional data file.^{(15KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0236894.r005

Decision Letter 2

Oscar Millet

16 Jul 2020

A chemical interpretation of protein electron density maps in the worldwide protein data bank

PONE-D-20-10145R2

Dear Dr. Moseley,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Oscar Millet

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

PLoS One. doi: 10.1371/journal.pone.0236894.r006

Acceptance letter

Oscar Millet

20 Jul 2020

PONE-D-20-10145R2

A chemical interpretation of protein electron density maps in the worldwide protein data bank

Dear Dr. Moseley:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Oscar Millet

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Table. Atom type mapping and the electron counts for the 20 common residues.

(DOCX)

Click here for additional data file.^{(13.9KB, docx)}

S2 Table. Atom-specific electron counts for the 20 common residues.

(DOCX)

Click here for additional data file.^{(13KB, docx)}

S1 Fig. Density plot of the median chain deviation fraction for all structures in the PDB of different resolutions.

(TIFF)

Click here for additional data file.^{(599.2KB, tiff)}

Attachment

Submitted filename: PLOS-1-20-10145.pdf

Click here for additional data file.^{(565KB, pdf)}

Attachment

Submitted filename: response_to_reviewer_comments_v3.docx

Click here for additional data file.^{(45.4KB, docx)}

Attachment

Submitted filename: response_to_reviewer_comments_revision1_v1.docx

Click here for additional data file.^{(15KB, docx)}

Data Availability Statement

[pone.0236894.ref001] 1.Berman H, Henrick K, Nakamura H. Announcing the worldwide Protein Data Bank. Nat Struct Biol. 2003;10(12):980 Epub 2003/11/25. 10.1038/nsb1203-980 . [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref002] 2.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28(1):235–42. Epub 1999/12/11. 10.1093/nar/28.1.235 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref003] 3.Yao S, Flight RM, Rouchka EC, Moseley HN. A less-biased analysis of metalloproteins reveals novel zinc coordination geometries. Proteins. 2015;83(8):1470–87. Epub 2015/05/27. 10.1002/prot.24834 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref004] 4.Yao S, Flight RM, Rouchka EC, Moseley HN. Aberrant coordination geometries discovered in the most abundant metalloproteins. Proteins. 2017;85(5):885–907. Epub 2017/02/01. 10.1002/prot.25257 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref005] 5.Yao S, Flight RM, Rouchka EC, Moseley HN. Perspectives and expectations in structural bioinformatics of metalloproteins. Proteins. 2017;85(5):938–44. Epub 2017/02/09. 10.1002/prot.25263 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref006] 6.Young JY, Westbrook JD, Feng Z, Sala R, Peisach E, Oldfield TJ, et al. OneDep: Unified wwPDB System for Deposition, Biocuration, and Validation of Macromolecular Structures in the PDB Archive. Structure. 2017;25(3):536–45. Epub 2017/02/14. 10.1016/j.str.2017.01.004 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref007] 7.Gore S, Sanz Garcia E, Hendrickx PMS, Gutmanas A, Westbrook JD, Yang H, et al. Validation of Structures in the Protein Data Bank. Structure. 2017;25(12):1916–27. Epub 2017/11/28. 10.1016/j.str.2017.10.009 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref008] 8.Mitroshin I, Garber M, Gabdulkhakov A. Crystallographic analysis of archaeal ribosomal protein L11. Acta Crystallogr F Struct Biol Commun. 2015;71(Pt 8):1083–7. Epub 2015/08/08. 10.1107/S2053230X15011395 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref009] 9.Fraser JS, Jackson CJ. Mining electron density for functionally relevant protein polysterism in crystal structures. Cellular and molecular life sciences. 2011;68(11):1829–41. 10.1007/s00018-010-0611-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref010] 10.Shapovalov MV, Dunbrack RL Jr. Statistical and conformational analysis of the electron density of protein side chains. Proteins: Structure, Function, and Bioinformatics. 2007;66(2):279–303. [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref011] 11.Akey DL, Brown WC, Konwerski JR, Ogata CM, Smith JL. Use of massively multiple merged data for low-resolution S-SAD phasing and refinement of flavivirus NS1. Acta Crystallogr D Biol Crystallogr. 2014;70(Pt 10):2719–29. Epub 2014/10/08. 10.1107/S1399004714017556 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref012] 12.Karplus PA, Diederichs K. Assessing and maximizing data quality in macromolecular crystallography. Current opinion in structural biology. 2015;34:60–8. 10.1016/j.sbi.2015.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref013] 13.van Beusekom B, Lutteke T, Joosten RP. Making glycoproteins a little bit sweeter with PDB-REDO. Acta Crystallogr F Struct Biol Commun. 2018;74(Pt 8):463–72. Epub 2018/08/08. 10.1107/S2053230X18004016 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref014] 14.Cowtan K. Fitting molecular fragments into electron density. Acta Crystallographica Section D: Biological Crystallography. 2008;64(1):83–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref015] 15.Dutta S, Burkhardt K, Young J, Swaminathan GJ, Matsuura T, Henrick K, et al. Data deposition and annotation at the worldwide protein data bank. Mol Biotechnol. 2009;42(1):1–13. Epub 2008/12/17. 10.1007/s12033-008-9127-7 . [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref016] 16.Gutmanas A, Alhroub Y, Battle GM, Berrisford JM, Bochet E, Conroy MJ, et al. PDBe: Protein Data Bank in Europe. Nucleic Acids Res. 2014;42(Database issue):D285–91. Epub 2013/11/30. 10.1093/nar/gkt1180 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref017] 17.EMBL-EBI. http://www.ebi.ac.uk/pdbe/eds.

[pone.0236894.ref018] 18.Kleywegt GJ, Harris MR, Zou JY, Taylor TC, Wahlby A, Jones TA. The Uppsala Electron-Density Server. Acta Crystallogr D Biol Crystallogr. 2004;60(Pt 12 Pt 1):2240–9. Epub 2004/12/02. 10.1107/S0907444904013253 . [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref019] 19.Sehnal D, Deshpande M, Varekova RS, Mir S, Berka K, Midlik A, et al. LiteMol suite: interactive web-based visualization of large-scale macromolecular structure data. Nat Methods. 2017;14(12):1121–2. Epub 2017/12/01. 10.1038/nmeth.4499 . [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref020] 20.DeLano WL. Pymol: An open-source molecular graphics tool. CCP4 Newsletter on protein crystallography. 2002;40(1):82–92. [Google Scholar]

[pone.0236894.ref021] 21.Goddard TD, Huang CC, Ferrin TE. Visualizing density maps with UCSF Chimera. Journal of structural biology. 2007;157(1):281–7. 10.1016/j.jsb.2006.06.010 [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref022] 22.Emsley P, Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallographica Section D: Biological Crystallography. 2004;60(12):2126–32. [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref023] 23.Read RJ. Improved Fourier coefficients for maps using phases from partial structures with errors. Acta Crystallographica Section A: Foundations of Crystallography. 1986;42(3):140–9. [Google Scholar]

[pone.0236894.ref024] 24.Schwarzenbach D, Abrahams S, Flack H, Gonschorek W, Hahn T, Huml K, et al. Statistical descriptors in crystallography: Report of the IUCr Subcommittee on Statistical Descriptors. Acta Crystallographica Section A: Foundations of Crystallography. 1989;45(1):63–75. [Google Scholar]

[pone.0236894.ref025] 25.Lang PT, Holton JM, Fraser JS, Alber T. Protein structural ensembles are revealed by redefining X-ray electron density noise. Proceedings of the National Academy of Sciences. 2014;111(1):237–42. [DOI] [PMC free article] [PubMed]

[pone.0236894.ref026] 26.Quillin ML, Wingfield PT, Matthews BW. Determination of solvent content in cavities in IL-1β using experimentally phased electron density. Proceedings of the National Academy of Sciences. 2006;103(52):19749–53. [DOI] [PMC free article] [PubMed]

[pone.0236894.ref027] 27.Cock PJ, Antao T, Chang JT, Chapman BA, Cox CJ, Dalke A, et al. Biopython: freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics. 2009;25(11):1422–3. Epub 2009/03/24. 10.1093/bioinformatics/btp163 . [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref028] 28.Collaborative Computational Project N. The CCP4 suite: programs for protein crystallography. Acta Crystallogr D Biol Crystallogr. 1994;50(Pt 5):760–3. Epub 1994/09/01. 10.1107/S0907444994003112 . [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref029] 29.Heyrovska R. Atomic Structures of all the Twenty Essential Amino Acids and a Tripeptide, with Bond Lengths as Sums of Atomic Covalent Radii. arXiv preprint arXiv. 2008;0804(2488). [Google Scholar]

[pone.0236894.ref030] 30.Sidiropoulos N, Sohi SH, Pedersen TL, Porse BT, Winther O, Rapin N, et al. SinaPlot: an enhanced chart for simple and truthful representation of single observations over multiple classes. Journal of Computational and Graphical Statistics. 2018;27(3):673–6. [Google Scholar]

[pone.0236894.ref031] 31.Weichenberger CX, Afonine PV, Kantardjieff K, Rupp B. The solvent component of macromolecular crystals. Acta Crystallographica Section D: Biological Crystallography. 2015;71(5):1023–38. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref032] 32.Guo D, Blessing RH, Langs DA. Bulk-solvent correction in direct-methods phasing. Acta Crystallographica Section D: Biological Crystallography. 2000;56(4):451–7. [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref033] 33.Dorset DL. Filling the missing cone in protein electron crystallography. Microscopy research and technique. 1999;46(2):98–103. [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref034] 34.Wang B-C. Resolution of phase ambiguity in macromolecular crystallography. Methods in enzymology. 115: Elsevier; 1985. p. 90–112. [DOI] [PubMed] [Google Scholar]

[pone.0236894.ref035] 35.Tickle IJ. Statistical quality indicators for electron-density maps. Acta Crystallographica Section D: Biological Crystallography. 2012;68(4):454–67. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref036] 36.Yao S, Moseley HNB. Finding High-Quality Metal Ion-Centric Regions Across the Worldwide Protein Data Bank. Molecules. 2019;24:3179 10.3390/molecules24173179. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref037] 37.Beckers M, Jakobi AJ, Sachse C. Thresholding of cryo-EM density maps by false discovery rate control. IUCrJ. 2019;6(1). [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0236894.ref038] 38.Meyder A, Nittinger E, Lange G, Klein R, Rarey M. Estimating electron density support for individual atoms and molecular fragments in X-ray structures. Journal of chemical information and modeling. 2017;57(10):2437–47. 10.1021/acs.jcim.7b00391 [DOI] [PubMed] [Google Scholar]

PERMALINK

A chemical interpretation of protein electron density maps in the worldwide protein data bank

Sen Yao

Hunter N B Moseley

Roles

Abstract

Introduction

Fig 1. Model and difference electron density maps.

Methods

Calculating the electron density ratio for atoms, residues, and chains

Fig 2. Workflow of the electron density analysis.

Normalizing the electron density ratio by the number of voxels

Correcting the unit electron density by the atom B-factor

Optimization of radii

Adding an F000 term

Design, implementation, and distribution of the above methods

Results

Fig 3. Sina plots of density ratio for atoms, residues, and chains, before (Panels A-C) and after (Panels D-F) radii optimization.

Volume and B-factor adjustment

Fig 4. Sina plot for the volumes of each atom type.

Fig 5. Correlation between chain deviation fractions and logarithm B-factors for each atom type.

Fig 6. Atom density ratios at each major step of improvement.

The final set of radii after optimization

Table 1. The atom radii before and after radii optimization.

Overview of density ratio for the whole PDB database

Fig 7. Histogram of the median chain deviation fraction for all structures in the PDB.

F000 term and the absolute scale

Fig 8. Histogram of the mean value of electron density maps provided by PDBe.

Fig 9. The absolute scale of the density ratio for all structures in the PDB.

Evaluative use-case for the electron density conversion factor

Fig 10. Evaluative use-case for the electron density conversion factor.

Discussion

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Oscar Millet

Roles

Author response to Decision Letter 0

Decision Letter 1

Oscar Millet

Roles

Author response to Decision Letter 1

Decision Letter 2

Oscar Millet

Roles

Acceptance letter

Oscar Millet

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Adding an F₀₀₀ term

F₀₀₀ term and the absolute scale