Predictive Modeling for Metabolomics Data

Abstract

In recent years, mass spectrometry (MS) based metabolomics has been extensively applied to characterize biochemical mechanisms, and study physiological processes and phenotypic changes associated with disease. Metabolomics has also been important for identifying biomarkers of interest suitable for clinical diagnosis. For the purpose of predictive modeling, in this chapter, we will review various supervised learning algorithms such as random forest (RF), support vector machine (SVM), and partial least squares-discriminant analysis (PLS-DA). In addition, we will also review feature selection methods for identifying the best combination of metabolites for an accurate predictive model. We conclude with best practices for reproducibility by including internal and external replication, reporting metrics to assess performance and providing guidelines to avoid overfitting and dealing with imbalanced classes. An analysis of an example data will illustrate the use of different machine learning methods and performance metrics.

1. Introduction

In the past twenty years, there has been a dramatic increase in the development and use of high-throughput technologies for measuring various types of biological activity. Common examples include transcriptomics (the measurement of gene expression) and proteomics (the measurement of protein levels). The focus of this chapter is on metabolomics, which involves the measurement of small compounds, referred to here as metabolites, on a high-throughput basis. As products of activity at the protein level, metabolites represent an intermediate level between regulatory processes such as methylation and transcription, and the full spectrum of physiological and disease states. One appealing feature of metabolites is their ability to be used as clinical biomarkers, and for this reason, metabolomics have been extensively applied for finding biomarkers and studying physiological processes and phenotypic changes associated with disease [1–4].

Metabolomics experiments fall into two categories: targeted and untargeted. Targeted metabolomics experiments measure ions from known biochemically annotated metabolites. By contrast, untargeted metabolomics experiments measure all possible ions within a pre-defined mass range and as a result may also include ions that do not map to known metabolites [5–8]. The main objective of metabolomics is to quantify and characterize the whole spectrum of metabolites. There are a variety of platforms by which metabolomics can be measured. Examples include Gas Chromatography Mass Spectrometry (GC-MS) and Liquid Chromatography Mass Spectrometry (LC-MS) [9–11]. At a high level, these platforms input a sample, fragment it into ions and separate them using physical properties in order to generate spectra for the sample. The fragmented ion spectra are then selected based on their physical properties, e.g. the retention time and the mass/charge ratio. In many instances, these properties can be used to map the ions to known metabolites.

Metabolomics data pose a variety of analytical challenges [12,13], and thus carefully constructed analytical pipelines need to be developed in order to preprocess and normalize the data. Once the data are normalized, one can proceed with various downstream analytical tasks, such as differential expression analysis, clustering, classification, network discovery and visualization. In this chapter, we focus on the particular task of classification, which also goes by the name of prediction, supervised learning and biomarker discovery. We give an overview on some of the most commonly used methods for classification, along with an illustrative example using a dataset from our group. The structure of this chapter is as follows. In Section 2.1., we provide a short review of missing values and techniques for missing value imputation in metabolomics data. We then briefly describe the most commonly used supervised learning methods (Random Forest, Support Vector Machine and Partial Least Square- Discriminant Analysis) in the rest of the method section. In Section 3, we lay out a framework on fitting prediction models and their practical issues. This is followed by an illustrative example of data analysis and performance evaluation, and the chapter ends with a short discussion in Section 5. In this chapter, we interchangeably use the term supervised learning, predictive modelling and machine learning.

2. Methods

2.1. Missing Values

Supervised learning methods require complete data, however untargeted metabolomic data is prone to missing values, where the data matrix contains zeros in one or more entries. Some studies have reported 20% – 30% missing values in datasets generated using untargeted MS [14,15]. It is difficult to deduce whether a missing value is a genuine absence of a feature, a feature below the lower limit of detection of the machine, or the failure of the algorithms’ employed to identify real signals from the background. In practice, statisticians have defined three types of mechanisms that lead to missing values: missing at random (MAR), missing not at random (MNAR) and missing completely at random (MCAR) [16–18]. MCAR means that the missingness mechanism is completely random and depends neither on the observed data nor on the missing data. Scientifically plausible reasons that are compatible with missing completely at random include random errors or stochastic fluctuations of peak detection during the acquisition process of the raw data (incomplete derivations of signals). MAR means that the probability of a variable being missing is fully accounted for by other observed variables. Missing not at random (MNAR) means that the missingness mechanism depends on the unobserved values. If analysts believe MNAR to hold, there are unfortunately no ways to assess this assumption using observed data. A practical strategy is to collect as much covariate information as possible in order to make the MAR assumption plausible with the observed data.

There have been several attempts in the literature to deal with missing values for metabolomics data. For example, fillPeaks [19] in the XCMS software package has many missing value imputation tools available. A practical rule of thumb is to impute missing values by a small value or zero. This is problematic in that this leads to distortions of the distribution of missing variables and can cause the standard deviations to be underestimated [20]. Finally, Zhan et al. developed kernel-based approaches which explicitly modelled the missingness into a differential expression analysis. [21]. Other imputation strategies include imputing missing values by zero, half of the minimum value or by the mean or median of observed values. More advanced methods use, random forest (RF) [22,20], singular value decomposition (SVD) [23,24] and k-nearest neighbors (kNN) [25]. The choice of these methods can influence the data analyses and inferences [26,14,22]. It is therefore extremely crucial to select the most suitable method for tackling missing values before moving forward with prediction. Recent work has compared performance of various missing value imputation methods [27,14,25,28] on MS metabolomics data [20].

2.2. Classification Methods: An early look

It is important to note that what we now call supervised learning dates back to over 80 years ago, when Sir R. A. Fisher introduced the use of linear discriminant analysis (LDA) [29]. This was a generative model in which the features conditional on class label were modelled as a multivariate normal distribution with a mean vector that depended on group, and a common covariance matrix. This was generalized to quadratic discriminant analysis, in which the covariance matrix also depends on the group. Linear discriminant analysis possessed two desirable properties:

1. Since the multivariate normal distribution is fully specified by the mean vector and covariance matrix, it is relatively simple to compute.

2. The classification rule from LDA is linear in the predictors and thus simple to interpret.

While this methodology is well established, there are two challenges with modern metabolomics data that make the utility of LDA less effective. First, in most situations, the number of metabolites being measured is greater than the sample size, which means that the covariance matrix will not be directly estimable from the observed data. Second, there is an increasing recognition that the linear classification rule might be too restrictive and that analysts should consider other nonlinear classifiers. This will motivate the classification tools we describe in Sections 2.3 – 2.5.

A second technique that dates back to the 1950s and has been used extensively in machine learning is Naïve Bayes [30]. In this framework, we assume the features are conditionally independent given the group label and model the likelihood ratio of the feature given the group label. Based on the product of these likelihood ratios, we are able to assign a new observation to a predicted group. The term “Naïve” comes from the fact that we assume that the features are statistically independent when in fact, we know that they are not. That being said, Naïve Bayes has been shown to be an effective tool in classification problems [31], and it can handle the situation when the number of metabolites measured is greater than the sample size.

2.3. Decision Tree

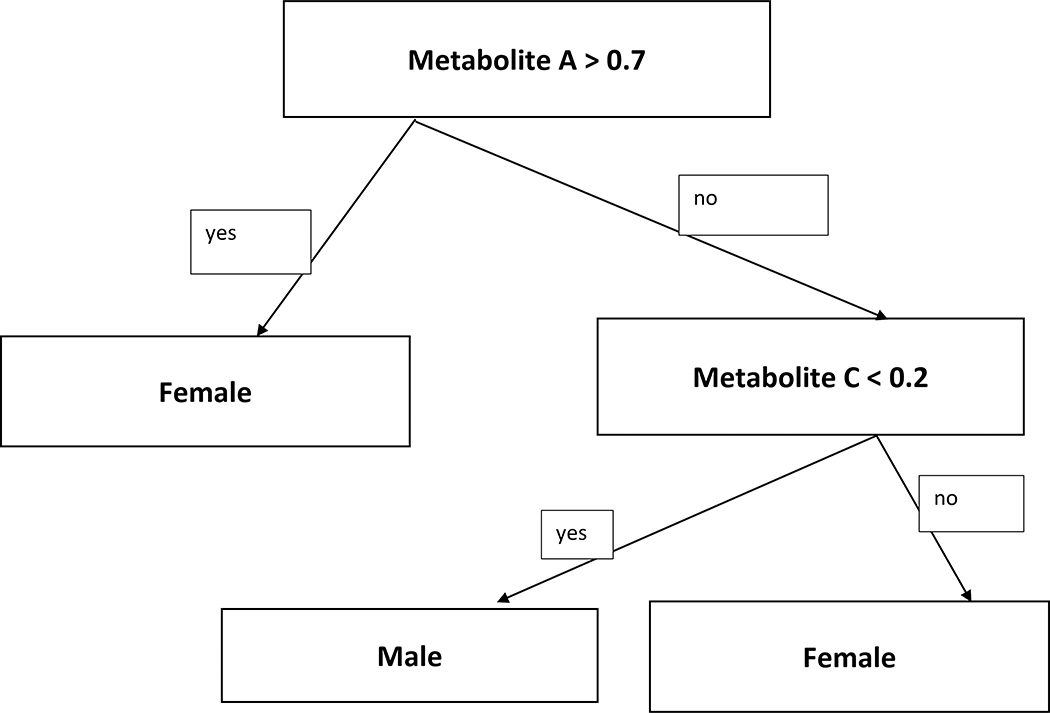
A Decision Tree (DT) is a supervised machine learning model, that outputs a hierarchical structure to classify subjects [32]. It is a non-linear classifier which is mainly used for classifying non-linearly separable data. The objective of a decision tree is to develop a model that predicts the value of a response variable based on several predictor variables. Figure 1 shows an example of a hypothetical DT, which divides the data into two categories based on two input variables. DT used in data mining can be classified into two groups:

Figure 1:

A simple decision tree that splits the data into two gender groups based on two metabolites.

• Classification tree: The predicted outcome is a categorical variable, representing two or more classes to which the observation belongs.

• Regression tree: The predicted value is a continuous variable.

DT is also known as Classification and Regression Trees (CART), which was first introduced in the machine learning literature [33]. The main difference between classification and regression trees is the criteria on which the split-point decision is made.

2.4. Random Forest

A Random Forest (RF) is an extremely reliable classifier and robust to over-fitting. It constructs an ensemble of DTs, which means an aggregation of tree-structured predictors [34]. In RF, each tree is independently constructed using a bootstrap sample of the original data (the “bagged” sample”). This training data is used to build the classification model. The data that was not sampled using the bootstrap is referred to as the out-of-bag sample. Since these data were not used in model building, they can be used as a test data set, which can be used to evaluate classification accuracy in an unbiased manner, by calculating the “out-of-bag error” [35]. A measure of the variable importance of classification is also computed by considering the difference between the results from the original and randomly permuted versions of the data set. Cross-validation is not needed since RF is estimated from the bootstrap samples.

RF has become popular as a biomarker detection tool in various metabolomics studies [36–38]. RF has the strength to deal with missing and data [39,34] and over-fitting issues [40,41]. In addition, it can also tackle high-dimensional data sets without feature elimination as a requirement [42].

2.5. Support Vector Machines

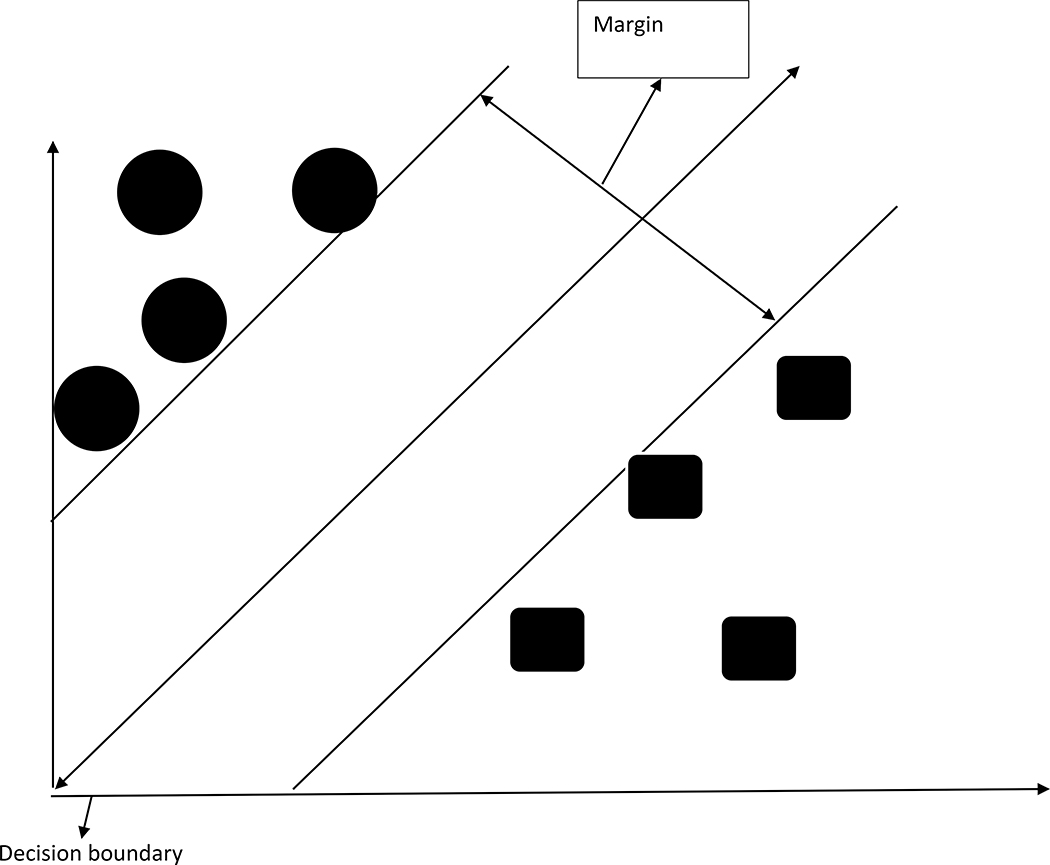
Support Vector Machines (SVM) have been previously used in the analysis of several omics studies, particularly gene expression data [43–45]. A simple figure of an SVM is shown in Figure 2. The main characteristics that define the concept of SVMs are: a) the criteria they use to categorize non-linear relationships b) the set of training sets that are necessary to optimize the linear classifier; c) the use of kernel machines to transform the variable into a higher order non-linear space where linear separability holds; d) utility in terms of performance and efficiency for high dimensional data sets.

Figure 2:

A simple graphical representation of SVM.

A major drawback of SVM is its restrictions to binary classification problems. For example, it can only discriminate between two classes where the data points are categorized by two classes in n-dimensional space, where n corresponds to the number of metabolites in our context. A hyperplane is constructed that separates the data points from the two classes. The hyperplane coefficients are determined based on the variable (metabolite) importance for discriminating between two classes.

SVM can yield a hyperplane of p-1 dimension in p dimensional space. The main purpose of SVM is to optimize the largest margin. In practice, a separation often does not exist as the data points cannot always be linearly separated. In such non-linear cases, a kernel substitution is adopted to map the data to a higher order dimension. The maximum-margin hyperplane was the original algorithm developed as a linear classifier [46]. An extension to create nonlinear classifiers was proposed by applying the kernel trick to maximum-margin hyperplanes [47]. The advantage of using the kernel trick is that it can substitute the linear kernel with other robust kernels, such as the Gaussian kernel [48]. Also in the family of non-linear supervised learners are deep neural networks (DNN), which construct a non-linear function from input variables to outcome variables using a combination of convolution filters and hidden layers [49].

2.7. PLS-DA

PLS-DA is a supervised technique widely used in metabolomics studies [50–53]. It is mainly constructed on the rotation of metabolite abundances in order to maximize the covariance between the independent variables (metabolite abundances) and the corresponding response variable (classes) in high-dimension by finding a linear subspace of the predictors [54]. PLS-DA is an extension of classical PLS regression which was implemented for solving linear equations and estimating parameters of interest. PLS-DA method has been extensively used in various metabolomics studies for disease classification and bio- marker detection [55–57,51]. Furthermore, PLS-DA can also be used for classification [58], dimension reduction, feature selection techniques [53] and variable selection [59] by ranking the loading vectors in decreasing order.

Orthogonal PLS (OPLS)-DA was developed as an improvement to PLS-DA in order to discriminate two or more classes of metabolites using multivariate data [60,61]. The main advantage of OPLS-DA over PLS-DA is that a single component is used as a predictor where the other components constitute the orthogonal contrasts for analysis of variance, which are independent linear comparisons between the classes of a component.

Multilevel PLS-DA is another classification technique that can be used to classify multivariate data from cross-over designed studies [62]. For example, each subject in a controlled experimentation set-up undergo treatment in a random order [63]. Multilevel PLS-DA can be thought as a multivariate extension of the paired t-test [62].

3. Practical issues in Fitting Prediction models

3.1. Feature Selection

Feature Selection (FS) is an important step in successful data mining procedures [64], such as SVMs [65], [66] and Naïve Bayes [67]. Although FS techniques can be incorporated to enhance performance and reduce computational efficiency, FS is not a necessary criterion for some supervised algorithms, such as SVM due to its reliance on regularization, which is the process of adding information to prevent over-fitting in order to enhance the predictive accuracy and interpretability of the supervised learning model. The purpose of feature selection is similar to model selection [68], which tries to find a compromise between high predictive accuracy and a model with few predictors. The insignificant input features in a supervised model may lead to overfitting. Hence, it is reasonable to ignore those input features with negligible or no effect on the output. For example, in the example later in this chapter, the objective is to infer the relationship between gender and their corresponding metabolite features. However, if the sample identifier or any other redundant column is included as one of the input features, it may cause over-fitting. FS is generally used as a pre-processing tool, in order to reduce the dimension of a data set by only selecting subsets of features (metabolites), on which a supervised learning is employed. Some well-known extensions of these FS techniques are Recursive Feature Elimination, L1 norm SVM [69] and Sequential Minimal Optimization (SMO) [70].

One of the most commonly used measure in FS is the Variable Importance Score (VIS), which evaluates features using a model-based approach [71] by ranking the features according to their relevance in a classification problem [72]. The main advantage of using VIS is that incorporates the correlation structure between the predictors (metabolite features) into the importance calculation.

3.2. Cross-validation

The classification performance of supervised learners is crucial to determine their predictive power and accuracy. Generally, the validation procedures are implemented by assuming the model on a training set and then testing it on an independent set (validation data set). However, in practical situations, due to the relatively small number of samples and unavailability of an unbiased independent validation data set, cross-validation (CV) can be applied by splitting a data set into training and test sets. Using k-fold cross validation [37], the training data set is split into k subsets (folds) of almost equal size, i.e., where k-1 training sets consist of x% of the data and the remaining (100-x)% data is contained in the kth test data set. Ideally, x% far exceeds (100-x)%, and x is usually chosen as 90, 80 or 70. Leave-One-Out-CV is a special case of CV, where k is equal to the total number of data points.

3.3. Metrics for Evaluation

There are several potential metrics by which one can evaluate a risk prediction model. The most common metric that is used in practice is the classification accuracy, meaning the proportion of predictions from the model that are correct based on the gold standard label. An alternative classification metric is given by the receiver operating characteristic (ROC) curve. Assume that we have two groups, disease and control and that higher values of the model correspond to a greater probability of having disease. We will let the model output be Y and group label be D, where D = 0 means control and D = 1 means diseased. One can define the false positive rate based on a cutoff c by FP(c) = P(Y > c| D = 0). Similarly, the true positive rate is TP(c) = P(Y > c| D = 1). The true and false positive rates can then be summarized by the receiver operating characteristic (ROC) curve, which is a graphical presentation of TP(c),FP(c) for all possible cutoff values of c. The ROC curve shows the tradeoff between increasing true positive and false positive rates. Then, the area under the ROC curve (AUC) can be measured for the curve and is a summary based on how well the model can distinguish between two diagnostic groups (diseased/control). Other commonly used metrics are defined in terms of TP(c) and FP(c) as below:

Sensitivity (SENS): SENS=TP(c)

Specificity (SPEC): SPEC=1-FP(c)

Precision (PREC): TP(c)/(TP(c)+FP(c)

Recall (REC): REC=SENS=TP(c)

False Discovery Rate (FDR): FP(c)/(TP(c)+FP(c)

Cut-off value c: The predicted classes are conventionally computed based on the cut-off c (=50%) for the probabilities. However, the cutoff (threshold) value can be tuned to control the FDR depending on the problem setting in order to attain maximum predictive accuracy.

Calibration is another property that has been espoused for risk prediction models. Well-calibrated models are those in which the predicted risk matches the observed risk for individuals. The manner in which this is typically assessed is by comparing the risk predictions from the model to some nonparametric (i.e., non model-based) estimate; the closer the predictions are, the better calibrated the model is. Calibration has been advocated in the risk prediction [73]. As a matter of course, nonparametric estimates of risk models require binning of covariates or categorization of predicted values in order to deal with the inherent sparsity that exists with using continuous covariates. One method of performing calibration, in the binary outcome setting, is to use the Hosmer-Lemeshow goodness of fit statistic [74]; smaller values of the statistic correspond with better calibrated models.

In the calibration setting, what is important is understanding the distribution of the predicted probabilities, or equivalently, the risk scores, from the fitted model. Calibration of the model then is equivalent to modelling the distribution of risk scores; a useful quantity for accomplishing this is the predictiveness curve [75].

3.3. Imbalanced Classes

In numerous data sets, there are unequal numbers of cases in each class. In this instance, the classifier is biased towards better performance of the larger (or majority) class, compared to the smaller (or minority) class. Often, the research question is much more focused on performance of discriminating the minority class from the majority class. But the size of the minority class may be limited by the difficulty, expense or time of obtaining the rarer type of sample. This unequal distribution between classes of a data set is referred to as the imbalanced class problem [76].

In such cases, the main interest lies in the correct classification of the “minority class” [77]. Classes with fewer samples or no sample have a low prior probability and low error cost [78]. The relation between the distribution of samples in the training set and costs of misclassification can be controlled by setting a prior probability at each class.

Several methods have been discussed for tackling imbalanced data [79,80], and two techniques which have been extensively applied in the last decade are resampling and cost sensitive learning. In resampling, the approach is to either over-sample the minority class or under-sample the majority class. For example, the minority class can be over-sampled by producing duplicates [81] or under sampling (removing samples) of the majority class [82,83]. One major drawback of under sampling is that the majority class may lose some information, if a large part of majority class in a small training set is not considered. In cost sensitive learning, the approach is to assign a cost misclassification of the minority class and minimize the overall cost function [84,85]. Both the resampling and cost sensitive learning approaches are considered to be more effective in terms of predictive accuracy than by using equal class prior constraints [86].

3.4. TRIPOD guidelines

A recent scientific initiative has focused on developing more reproducible approaches to the building, evaluation and validation of prediction models. A document resulting from this effort that helps in this goal is the TRIPOD (Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis) statement, which provides recommendations for fair reporting of studies developing, validating, or updating a prediction model. It consists of a 22-item checklist detailing vital information that must be incorporated in a prediction model study report [87]. For our example analysis below, we provide supporting information to illustrate how our analysis satisfies the 22-item TRIPOD checklist (Supporting Table 1).

4. Illustrative Example

4.1. Data

For the predictive comparison of classifiers, we obtained a LC-MS metabolomics dataset from https://www.metabolomicsworkbench.org (Project ID: PR00038). The data were generated from subjects enrolled in the Genetic Epidemiology of Chronic Obstructive Pulmonary Disease Gene study (COPDGene) [88,89]. Plasma from 131 subjects was collected from the COPDGene study cohort and analyzed using untargeted LC-MS (C18+ and HILIC+) metabolomics. The lipid fraction of the human plasma collected from current and former smokers was analyzed using Time of Flight (ToF) liquid chromatograph (LC) (Agilent 6210 Series) and a Quadrupole ToF mass spectrometer (Agilent 6520) which yielded combined data on 2999 metabolite features. Data were annotated, normalized and pre-processed using the methods described in [88,89].

COPD is an extremely heterogeneous disease comprising multiple phenotypes. The 131 subjects were either current or former smokers with various chronic obstructive pulmonary disease (COPD) phenotypes including airflow obstruction, radiologic emphysema, and exacerbations. Within this set there were 56 males and 75 females. For additional information about the cohort, sample collection and data storage data generation, see [88].

4.2. Training and Test Sets

We split the data (131 samples) into 70% (93 samples) training and 30% (38 samples) test (evaluation) data. For the training data, we use 5 fold CV, where we split the training data (93 training samples) into 5 different subsets (or 5 folds). We used the first four folds to train the data and left the last (fifth) fold as holdout-test dataset. We then performed the algorithms against each of the folds and then compute (average over 5 folds) the metrics for training dataset. The test dataset (n=38 samples) is used to provide an unbiased evaluation of the best model fit on the training dataset. The test dataset can be regarded as an external dataset which basically provides the gold standard used to evaluate the models, using ROC curves and other metrics for evaluation. For model validation, we predicted the performance of the test data using the trained models for all the 3 classifiers.

4.3. Feature Ranking and Variable Importance

In this section, we implement different predictive models using metabolite abundances as the predictor variables and Gender (Male/Female) as the response based on the training dataset. We then computed the Variable Importance Score, which is a measure of feature relevance to gender for each metabolite (see Section 3.1). These scores are non-parametric in nature, and range between 0 and 100. They are subsequently used to rank all the features to the classification of our response variable, i.e., Gender. Metabolites with high values are considered to more relevant features in classification problem.

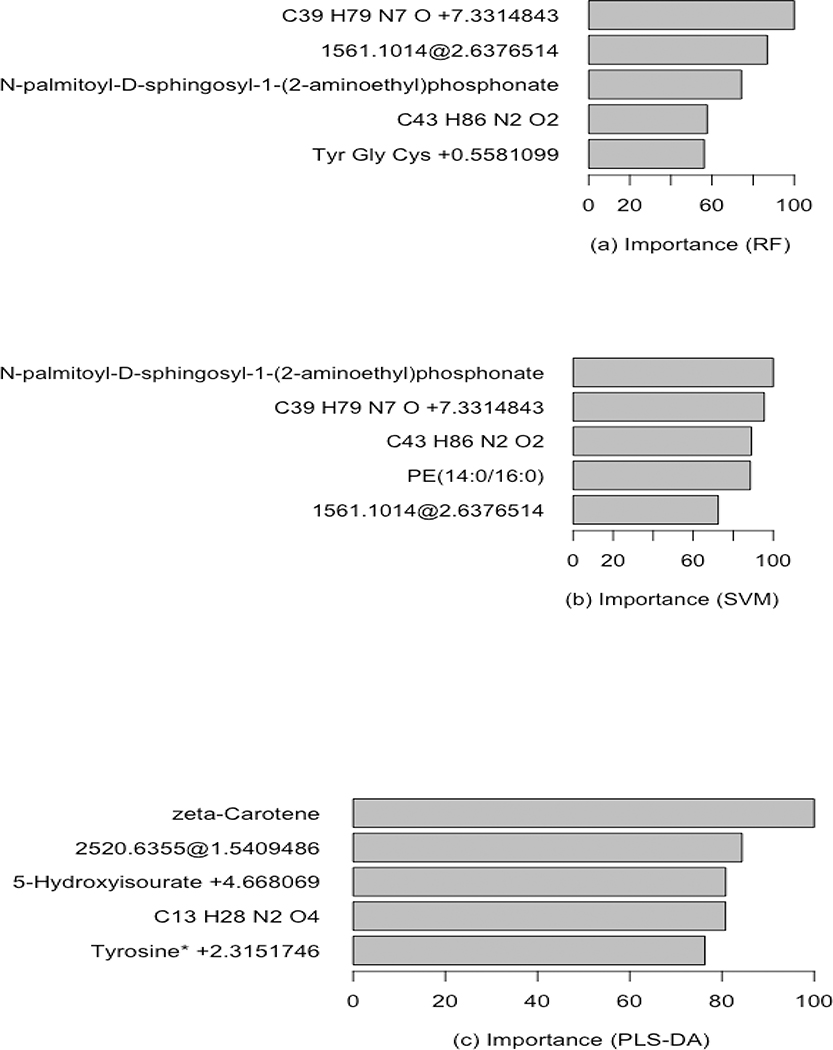
In the dataset, the top 5 metabolites are detected as feature metabolites out of 2999 metabolites in the training set with 5 fold Cross Validation for 3 different classifiers (Figures 3(a)–(c)). Among them, C39 H79 N7 O +7.3314843,N-palmitoyl-D-sphingosyl-1-(2-aminoethyl)phosphonate and C43 H86 N2 O2 are considered to be significant metabolite features based on RF and SVM classifiers. However, zeta-Carotene, unannotated metabolite (mass: 2520.6355 and retention time:1.5409486), 5-Hydroxyisourate +4.668069, C13 H28 N2 O4 and Tyrosine* +2.3151746 are identified as good predictors based on PLS-DA.

Fig 3:

Metabolite relevant feature ranking barplots (top 5 metabolites) using Variable Important Scores ranging from 0–100. (a) Random Forest, (b) Support Vector Machine (SVM) and (c) Partial Least Square- Discriminant Analysis (PLS-DA) for the training dataset.

4.4. Model Validation

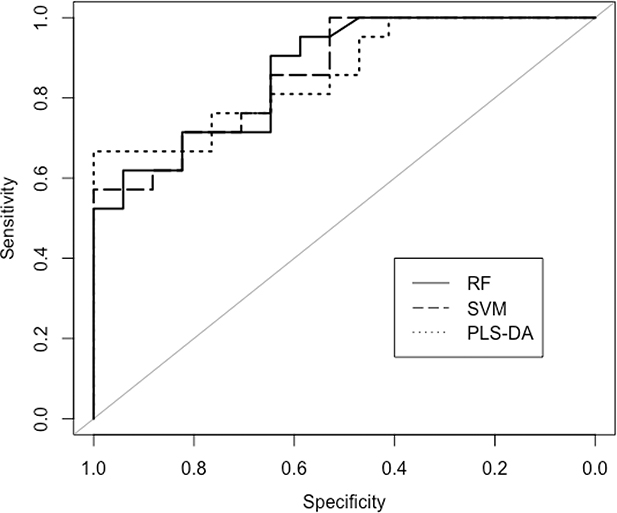
In this section, we evaluated the performance of all the 3 classifiers based on the 30% test data 38 test samples) using the trained models. Here, we present ROC curves for all the predictive models of the testing data used to compute the diagnostic potential of a classifier in this clinical metabolomics application. From the ROC curves, the three methods perform similarly (Fig. 4). Table 1 shows the performance metrics of the testing data evaluated for all the classifiers. In this testing dataset, we use AUC as our metric to choose the best performing classifier. Based on this metric RF has a small advantage over the other methods (0.87 versus 0.86), but with other metrics the other methods have a small advantage. In addition, we also computed the Variable Importance Score on the test dataset. The top 5 metabolites for all the 3 classifiers using the test dataset were exactly the same selected using the training dataset with 5 fold CV in the previous section.

Figure 4:

ROC curves of the testing dataset obtained from 3 classification algorithms (RF, SVM and PLS-DA).

Table 1:

Metrics (Area Under Curve (AUC), Sensitivity (SENS), Specificity (SPEC), Precision (PREC), Recall (REC)) to evaluate the performance of classification on testing dataset.

Metrics/Methods	AUC	SENS	SPEC	PREC	REC
RF	0.87	0.71	0.64	0.71	0.71
SVM	0.86	0.76	0.71	0.76	0.76
PLS-DA	0.86	0.81	0.65	0.74	0.81

5. Discussion

Biomarker detection in the field of metabolomics is popular both in the context of prognostic studies. In this chapter, we discussed the most commonly used supervised learning algorithms, feature selection methods and performance metrics, used in the downstream analyses of metabolomics studies. In addition, we also reported predictive accuracy of three classifiers on an example human plasma LC/MS test dataset to predict gender. Even though there were advantages of one method compared to the other depending on the metric, our results cannot be held as a comprehensive comparison of these methods, since different classifiers perform differently depending on the datasets. We encourage investigators to explore a variety of methods. For more detailed discussions of biomarker detection and predictive accuracy, see [90–93]. Finally, we present a table with selected open source tools that implement supervised learning algorithms (Table 2).

Table 2:

Selected open source (R/Bioconductor/Web-based) tools for supervised learning algorithms.

Method	Source	Reference
PLS-DA	Bioconductor (ropls)	[1]
PLS-DA, RF and SVM	Bioconductor (biosigner)	[2]
SVM, RF	Bioconductor (MLSeq)	[3]
RF, SVM, PLS-DA	Metaboanalyst http://www.metaboanalyst.ca/	[4]
PCA, PLS-DA, RF	Bioconductor (statTarget)	[5]
Feature selection, Metric evaluation	Bioconductor (OmicsMarker)	[6]
Sparse PLS-DA	Bioconductor (mixOmics)	[7]
Feature selection, Metric evaluation	CRAN (lilikoi)	[8]
Probabilistic Principal Component Analysis	CRAN (MetabolAnalyze)	[9]
Kernel-based Metabolite Differential Analysis	CRAN (KMDA)	[10]
PLS-DA, OPLS-DA	CRAN (muma)	[11]
RF	CRAN (RFmarkerDetector)	[12]
RF, SVM, PLS-DA	CRAN (caret)	[13]

References

^1.Thévenot, E.A.: ropls: PCA, PLS (-DA) and OPLS (-DA) for multivariate analysis and feature selection of omics data. (2016).

^2.Rinaudo, P., Boudah, S., Junot, C., Thévenot, E.A.: Biosigner: a new method for the discovery of significant molecular signatures from omics data. Frontiers in molecular biosciences 3, 26 (2016).

^3.Zararsiz, G., Goksuluk, D., Korkmaz, S., Eldem, V., Duru, I.P., Unver, T., Ozturk, A., Zararsiz, M.G., klaR, M., biocViews Sequencing, R.: Package ‘MLSeq’. (2014).

^4.Xia, J., Psychogios, N., Young, N., Wishart, D.S.: MetaboAnalyst: a web server for metabolomic data analysis and interpretation. Nucleic acids research 37(suppl_2), W652-W660 (2009).

^5.Luan, H., Ji, F., Chen, Y., Cai, Z.: statTarget: A streamlined tool for signal drift correction and interpretations of quantitative mass spectrometry-based omics data. Analytica chimica acta 1036, 66–72 (2018).

^6.Determan Jr, C.E., Determan Jr, M.C.E.: Package ‘OmicsMarkeR’. (2015).

^7.Rohart, F., Gautier, B., Singh, A., Le Cao, K.-A.: mixOmics: An R package for ‘omics feature selection and multiple data integration. PLoS computational biology 13(11), e1005752 (2017).

^8.Al-Akwaa, F.M., Yunits, B., Huang, S., Alhajaji, H., Garmire, L.X.: Lilikoi: an R package for personalized pathway-based classification modeling using metabolomics data. GigaScience 7(12), giy136 (2018).

^9.Gift, N., Gormley, I.C., Brennan, L., Gormley, M.C.: Package ‘MetabolAnalyze’. (2010).

^10.Zhan, X., Patterson, A.D., Ghosh, D.: Kernel approaches for differential expression analysis of mass spectrometry-based metabolomics data. BMC bioinformatics 16(1), 77 (2015).

^11.Gaude, E., Chignola, F., Spiliotopoulos, D., Spitaleri, A., Ghitti, M., Garcìa-Manteiga, J.M., Mari, S., Musco, G.: muma, An R package for metabolomics univariate and multivariate statistical analysis. Current Metabolomics 1(2), 180–189 (2013).

^12.Palla, P.: Information management and multivariate analysis techniques for metabolomics data. Universita’degli Studi di Cagliari (2015)

^13.Kuhn, M.: Building predictive models in R using the caret package. Journal of statistical software 28(5), 1–26 (2008).