The bee Tetragonula builds its comb like a crystal

Abstract

Stingless bees of the genus Tetragonula construct a brood comb with a spiral or a target pattern architecture in three dimensions. Crystals possess these same patterns on the molecular scale. Here, we show that the same excitable-medium dynamics governs both crystal nucleation and growth and comb construction in Tetragonula, so that a minimal coupled-map lattice model based on crystal growth explains how these bees produce the structures seen in their bee combs.

1. Introduction

The geometry of the bee comb has for centuries astonished those who have examined it [1,2]. Many studies have concentrated on understanding how honeybees make almost perfectly hexagonal cells [3–6]. But beyond its hexagonal packing of neighbouring cells, the overall structure of the bee comb is equally interesting. An example is the Southeast Asian and Australian stingless bee Tetragonula [7–12]. In Tetragonula nests, we find a variety of brood comb structures in three dimensions (figure 1) that can be classified into (a) target (i.e. bullseye-shaped) patterns, (b) spirals, (c) double spirals and (d) more disordered terraces. In a totally different field of science, crystals also grow in three-dimensional patterns with spirals and target patterns [13,14]. Here we show that a minimal model, a coupled-map lattice excitable medium, explains both crystal nucleation and growth and the architecture of Tetragonula brood combs. This is an example of how the applicability of the same dynamics across different fields of science leads to similar patterns in very diverse systems, and of how complex structures can emerge from simple behavioural rules.

Figure 1.

Combs of two species of the stingless bee Tetragonula showing structures of (a) target patterns (Tetragonula carbonaria), (b) spirals (Tetragonula carbonaria), (c) double spirals (Tetragonula carbonaria) and (d) more disordered terraces (Tetragonula hockingsi). Images courtesy of (a) Elke Haege; (b–d) Tim Heard.

Various species of the Southeast Asian and Australian stingless bee Tetragonula construct brood combs with three-dimensional, open structures consisting of terraces built one on top of another [8,10–12] (figure 1). Worker bees add new cells to the edges of each terrace, each of which is then filled with an egg and closed before repeating the process. The resulting morphology is similar to what we see in crystal growth, where crystals grow in terraces of atoms or molecules one on top of another [13,14]. New so-called growth units (i.e. atoms, molecules, ions, etc.) attach to the crystal at the edges of terraces, called steps and kinks. This dynamics was explored by Burton et al. [13], who proposed a dynamical model to explain how crystals should grow layer by layer through the addition of material at kinks: growth sites at the edges of a spiral or target pattern. Likewise, although bees are free to move across and between the terraces—the levels are open so that the bees can get between them (figure 2a) like a multi-storey car park—bees are found concentrated at the terraces in these three-dimensional structures (figure 2b).

Figure 2.

(a) The open structure is like a multi-storey car park or, in this case of a spiral ramp, like the Guggenheim museum in New York (T. carbonaria). (b) Worker bees are observed to spend time clustered at the growing edges of terraces (T. carbonaria). Images courtesy of Tim Heard.

Spiral and target patterns are found across nature from chemical oscillators to the heart, and from cellular slime moulds to the brain [14]. Common to these varied systems is that they are excitable media: they all have a threshold in some parameter, below which the system returns quickly to its resting state, but above which it undertakes a large excursion before doing so, and then has a refractory period during which the system is unresponsive to further perturbations. Some of us developed a model of Burton–Cabrera–Frank dynamics as an excitable system, and showed that it could be applied both to crystal growth [15] and to liquid crystals growing layer by layer as they do in the formation of the mother-of-pearl produced by molluscs [16]. In the present work, we show that a version of this coupled-map lattice excitable medium model explains how the complex structures seen in Tetragonula combs emerge from simple behavioural rules.

2. Model

In both crystals and bee combs, growth occurs in a layered manner, each layer growing by addition of individual units. This is a discrete process, so we apply a discrete model in which a surface is divided into cells. In order to avoid anisotropic effects in the growth process, we randomize the grid [17]. We use a hexagonal grid of cells to reproduce the cellular growth process in the comb—that is to say, bees choose to tile the plane with a hexagonal, rather than a square or triangular, array—although it is not necessary to use a hexagonal grid of cells in order to produce the patterns observed: the physics is not determined by the grid chosen, and a square lattice gives similar results. We comment below on how this choice of array might come about in bees. We define a neighbourhood radius, R, so that the neighbours k of the cell i are all elements within this radius

$$|r_i-r_k|<R.$$ 2.1

Each cell has an associated height, h_i(t), with initial value h_i(0) = 0. Height is a continuous variable, so that different patterns will arise, although the time t advances in discrete iterations, making the model a coupled-map lattice. In both systems, new cells may be added as a new island on a flat surface (nucleation) or by adding new materials at a growth front (growth), so in our model we impose a nucleation condition and a growth condition. The condition for nucleation is that the cell in question must be on a flat surface, meaning that the height difference with its neighbouring cells must be smaller than a certain margin, ΔH_N,

$$\sum _k|h_k(t)-h_i(t)|<\mathrm{\Delta }{H}_N.$$ 2.2

If this condition is met, the height of the cell is increased by 1 plus or minus a small random factor α, 0 ≤ α ≤ α_max,

$$h_i(t+1)=h_i(t)+1+\alpha .$$ 2.3

The condition for growth of a new cell in the comb is that the cell must be at the edge of a growth front, meaning it has at least one neighbour with a height difference larger than a certain threshold, ΔH_G,

$$h_k(t)-h_i(t)>\mathrm{\Delta }{H}_G.$$ 2.4

When growth takes place, the height of the cell is increased by the mean height difference with its higher neighbours,

$$h_i(t+1)=h_i(t)+\sum _k\frac{h_k(t)-h_i(t)}{n}+\alpha ,$$ 2.5

where k is the coordinate for each higher neighbour and n is the total number of higher neighbours, which depends on R. This growth algorithm is performed simultaneously for all cells and the process is iterated in time t.

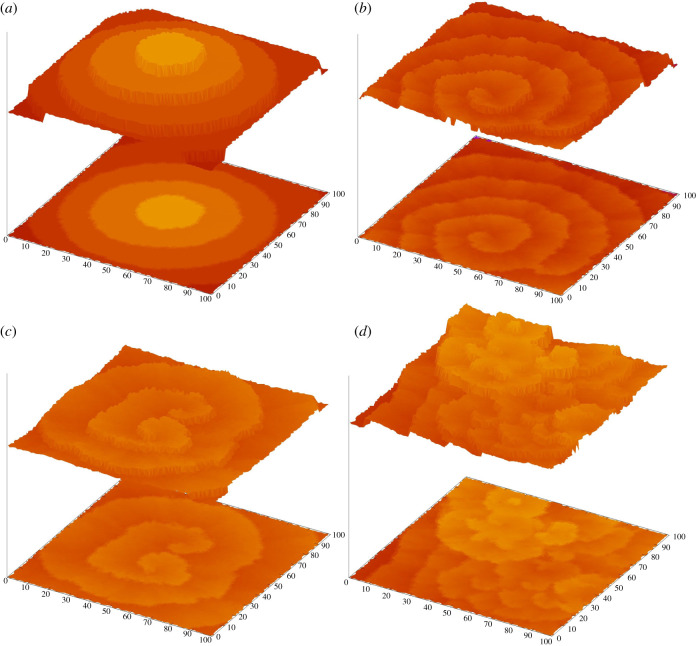
The model has four parameters that can be adjusted to generate all the different patterns observed in stingless bee combs (figure 3 and table 1): (i) α is the amount of randomization applied to every growth unit. It is necessary for the emergence of defects and spiral patterns. In a growing crystal, it is related to the amount of impurities, while in a bee comb it is related to the ability of the bees to produce a flat surface. (ii) ΔH_N defines how flat a surface needs to be for it to nucleate a new growth front. This influences the frequency of nucleations which lead to target patterns. In crystallization, it is related with the supersaturation of the precipitating material, while in a bee comb it is probably related to the availability of worker bees. (iii) ΔH_G is responsible for the appearance of screw dislocations which lead to spiral patterns. Both in crystals and in bee combs there can be several causes for this kind of defect, such as the heterogeneity of the growth units or the presence of impurities. (iv) R will influence the separation between terraces on the growing surface because nucleation cannot happen in cells that are closer than R to a growth front. In crystals, this is viewed as the amount of surface diffusion, as growth units tend to be added at steps or kinks. In the bee comb this is associated with the space that bees require to work; bigger bees construct bigger cells [18].

Figure 3.

Our growth model produces versions of the structures seen in figure 1: (a) target patterns for α_max = 0.01; R = 5, (b) spirals for α_max = 0.09; R = 3, (c) double spirals for α_max = 0.11; R = 4, (d) disordered terraces for α_max = 0.15; R = 2. For all cases ΔH_N = 0.5 and ΔH_G = 0.5. In each case, the bottom layer is the projection of the top.

Table 1.

The parameters in the model and their meanings in crystal growth and in bee comb construction.

parameter	description	responsible for	physical meaning in crystal growth	physical meaning in bee comb construction
α	stochastic term	size of defects	impurities/heterogeneity	how flat the bees can make a layer
R	radius of the cell neighbourhood	terrace separation	surface diffusion	order of size of a bee
ΔHN	surface height margin between neighbours considered to be flat enough to nucleate	frequency of nucleations, i.e. target patterns	supersaturation	availability of worker bees
ΔHG	surface height threshold between neighbours considered to be the base of a step	amount of spiral patterns	impurities/heterogeneity of growth units	how similar the bees can make growth units

During a time step, nucleation has a probability of 1 to occur at all the cells where the condition (2.2) is satisfied. In previous work with a numerical model of this type, we had a nucleation probability, a small number, typically 10⁻³, so that nucleation would be a rare event [15,16]. In the present case, we have removed this parameter, with the objective to have a more elegant model; to eliminate as much complexity as possible while still being able to reproduce all the patterns observed. With this simplified model, if we start with a perfectly flat surface h(t = 0) = 0, every cell in the map would nucleate. However, after the first time iteration of the model, the surface is no longer perfectly flat because of the addition of the random parameter α, as shown in equation (2.3). So, after the first iteration, the number of nucleations that appear is small and can be controlled with α.

In the case both of the crystal and of the bee comb, the model puts growth and nucleation on an equal footing. We have attempted to codify a few simple rules, which make no fundamental distinction between nucleation and growth, because at the level of the atom in the crystal or the bee in the comb that distinction is artificial. There has of course to be a way to move mathematically from the discrete to the continuum level above it. At the continuum level concepts like diffusion can be defined. But both bee combs and crystals are built by discrete steps, and this model is to explain the growth process at that low level of the individual growth unit in a crystal and the individual bee building a comb.

The time step in the model is by definition the time of the addition of one cell. This addition may in fact involve more than one bee and more than one mandibleful of wax. Our time discretization is then whatever is suitable for the building process—i.e. to keep the growth surface reasonably smooth—just like a numerical discretization. The time step in crystal growth would naturally be the moments at which new growth units become incorporated, and likewise in the bees the moments at which a new cell is added are the natural time scale.

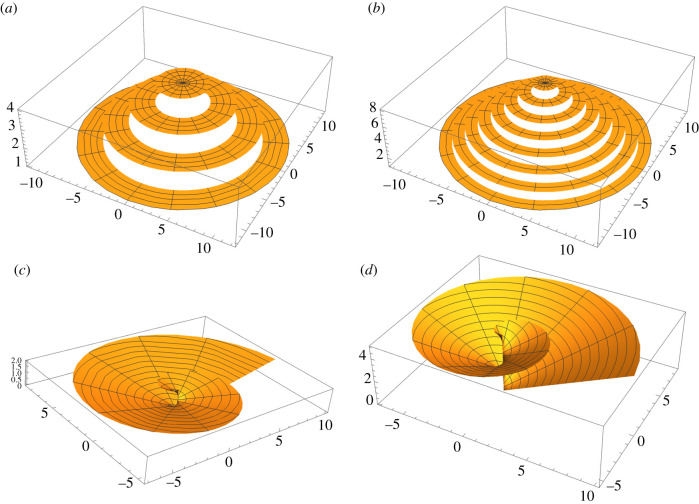
In the limit of continuous smooth growth, for which α is taken to be constant and a unit of growth is infinitesimal, we can obtain analytical solutions for the target and spiral patterns. Growth occurs at a constant rate. For a target pattern, the first nucleation occurs at t = 0 and the growth front moves radially according to dr/dt = 1. Subsequent nucleations occur at t_k = kR, where k is the number of the nucleation. The number of nucleations that occur within time t is M = Integer(t/t_k). So the surface of the comb at time t is described by

$$\begin{array}{rl}& h(r,\theta ,t)=\sum _{k=0}^{M}H[t-t_k-r]=\sum _{k=0}^{M}H[t-kR-r],\\ & 0<\theta <2\pi ,\end{array}$$ 2.6

where H denotes the Heaviside step function. Since growth occurs in the horizontal direction, α has been taken to be zero. Two examples of analytical target patterns are shown in figure 4a,b. Spirals develop as a result of only one initial nucleation, corresponding to R → ∞, so that the growth pattern depends only on α. Growth occurs in the radial, azimuthal and vertical directions at rates dr/dt = 1, dθ/dt = 1 and dh/dt = α. The growth in the radial direction takes place between the time of birth of a new radial layer $t_{\theta }$ and the time of growth of the comb t, while the growth in the azimuthal direction occurs over time $t_{\theta }$. The height h grows over the full time $t_{\theta }+r$. So the surface of the comb is described by

$$\begin{array}{rl}& x=r\cos t_{\theta }\\ & y=r\sin t_{\theta }\\ \text{and}& h=\alpha (t_{\theta }+r)0<r<t-t_{\theta },\hspace{0.17em}0<t_{\theta }<t.\end{array}$$ 2.7

These equations represent a helicoidal surface with decreasing radius from bottom to top and tilt α in both the radial and azimuthal directions, as exemplified in figure 4c,d.

Figure 4.

Analytical solutions in the cases of targets (equation (2.6)) and spirals (equation (2.7)); (a) target with R = 3, (b) target with R = 1.5, (c) spiral with α = 0.2, (d) spiral with α = 0.5.

3. Discussion

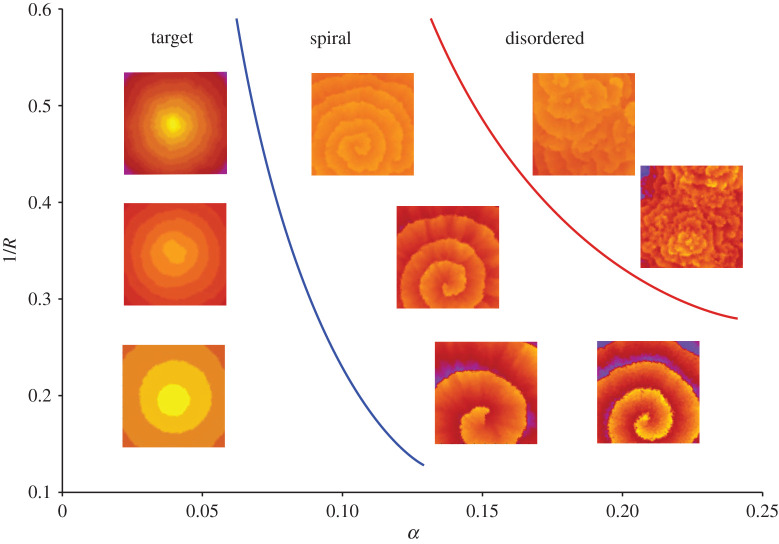
These two limiting behaviours described by equations (2.6) and (2.7) help us understand the role of the parameters R and α in the more complex comb structures. R represents the distance between nucleations while α determines the slope of the growth. Figure 5 shows a regime diagram which maps the different structures. We can conclude that a range of complex bee-comb structures arises from only two directives in stingless bee behaviour during construction of a comb: the tilt as neighbouring cells are added and the distance between nucleations.

Figure 5.

Regime diagram of 1/R versus α. By increasing the randomizing factor α, the regime changes from flat terraces (target patterns) to steep terraces (spiral patterns) and eventually disordered terraces at higher values of α. The radius R influences the separation between terraces.

Further interesting and experimentally testable points follow. The surface area for work grows with time. So either more bees must join in the construction or the growth rate per unit area slows down with time. The two cases are distinguishable by growth rate. Which of the two occurs depends on whether growth is limited by available area for growth or by availability of growth units. In the general case of crystal growth under conditions of saturation it is available area that limits growth and growth units are normally in excess. Also, in the case of stingless bees, more bees will join in building as the structure gets bigger. This is so for as long as there is never a shortage of worker bees available for this task.

A key concept in the field of swarm intelligence and social insects is stigmergy [19], a social mechanism of indirect coordination in which individuals communicate with one another by modifying their local environment. Simulations of the architecture of wasp nests with these ideas showed results similar to those seen in nature [20]; honeybees clearly do utilize stigmergy [6]. This is not to say that their behaviour is not flexible. There should be, and is, scope for both adaptability to local circumstances and error recovery in bee behaviour [21]. Bees clearly possess cognitive capabilities [22,23]—recall the waggle dance of the honeybee [24–26]—but that does not mean that their architecture need be the result of a master plan.

Our model shows the minimal complexity necessary—the minimal amount of information a bee needs—to be able to construct such a structure. It has been considered that bees might be using some overall plan set down (for example) by diffusing chemicals. But this model demonstrates that they do not need such an overall plan if they have the small set of behavioural rules to follow. Thus bee behaviour is determined by something: pressure measurements, chemical measurements or dimension/flatness measurements. Bees sense something in their environment, make some sort of computations and then do something. But what is fundamentally different between one view and the other is that in one case only local information is available; in the other view global information is available, albeit sampled locally. Our model thus shows that stingless bee comb construction, like crystal construction, can be the result of self-organization [27].

Consider an aspect of comb building that we mentioned at the beginning: bees construct the comb with a hexagonal lattice. How can this come about? A way to approach the matter is to see the same problem from a grocer’s point of view: when making a display of oranges, the first orange can be placed anywhere and the second anywhere alongside the first. It is when the third and subsequent oranges are to be placed that a choice must be made. If the third orange is placed as compactly as possible, touching both the previous oranges, and subsequent ones in the same fashion, then a hexagonal packing of oranges is formed. If, on the other hand, the third orange is placed in a looser configuration touching only one previous orange, then a square packing will be the result. So bees can make a hexagonal array simply by following a local rule always to construct a new cell as compactly as possible, touching two others when there are at least two cells.

The overall pattern emerges as a result of the repeated application of strictly local rules. As examples of such local rules in social insects, honeybees seem to use their body parts for measuring distances when building the comb [6,28,29]. Further towards understanding the minimal information bees need for construction, we may note that each cell is constructed from the bottom up and that stingless bees have been seen to use a vertical displacement between cells to construct the spiral pattern [10]. This corresponds to the tilt α in our model. Such construction can be performed using only discrete decisions at each moment, which correspond to the decisions bees make about what to do next and where to do it. These rules taken together lead to the system being describable as an excitable medium, characteristic of a large class of systems in physics, chemistry and biology. It is notable that other instances of bees showing behaviour compatible with an excitable description are to be found, such as spiral waves in ‘shimmering’ honeybees repelling hornet attacks [30].

We focus on the genus Tetragonula in this work, since that genus produces all these patterns. One can certainly have parallel evolution of these structures. Other genera show similar patterns too [12], and they should be describable by our model. By concentrating on one genus we know that we are looking at a genetically related set of species—a clade. In fact, in Tetragonula, many species are distinguished precisely by their comb patterns [8]. It is then possible to hypothesize that, during the radiation of the genus Tetragonula, the genetic changes through evolution have led to the parameters affecting our model shifting in different directions in different species, so that they produce different patterns of comb building.

Of course, both crystal growth and bee combs are subject to fundamental laws that govern everything in the Universe, including thermodynamics. But there is plenty of room within the laws of thermodynamics for different phenomena to emerge, which is why the universe can be the complex place that it is. Crystal growth and bee comb construction are two systems operating within very different spheres of science. So what leads to the similar structures? This is the beauty of the applicability of mathematics to nature. It turns out, so often, that similar laws and similar principles govern the formation of very different systems in different areas of science, and thus are describable by the same mathematics. And this is one of those cases. Both crystal growth and this bee comb construction are describable within the mathematical framework of excitable media. Crystals, slime moulds, the brain, the heart, chemical oscillators, forest fires and many other systems can function as excitable media. And, in this instance, bees making their combs too. So what the mathematics tells us is that the processes that drive atoms or molecules to aggregate as a crystal have the same mathematical structure as the processes that drive bees when making their bee comb, so that they both possess the same spiral and target patterns. There is a beautiful mathematical equivalence between how molecules build a crystal and how bees build a bee comb.

The beehive has long been used as a metaphor for a self-organized society: Mandeville argued in The Fable of the Bees (1714) that local behaviour for private gain might result in global behaviour for the public good [31]. Our purpose has been to show that, just like a molecule that makes up a crystal, the individual bee need only take account of local information in order for the colony to be able to construct a complex structure, so that the bee builds its comb like a crystal.

Data accessibility

We provide videos and code as electronic supplementary material.

Authors' contributions

All the authors have contributed to the research and writing of this work.

Competing interests

We declare we have no competing interest.

Funding

J.H.E.C. and C.I.S.D. acknowledge the financial support of the Spanish MINCINN FIS2016-77692-C2-2-P and A.G.C., CGL2017-85118-P.