Variation in the strength of allometry drives rates of evolution in primate brain shape

Abstract

Large brains are a defining feature of primates, as is a clear allometric trend between body mass and brain size. However, important questions on the macroevolution of brain shape in primates remain unanswered. Here we address two: (i), does the relationship between the brain size and its shape follow allometric trends and (ii), is this relationship consistent over evolutionary time? We employ three-dimensional geometric morphometrics and phylogenetic comparative methods to answer these questions, based on a large sample representing 151 species and most primate families. We found two distinct trends regarding the relationship between brain shape and brain size. Hominoidea and Cercopithecinae showed significant evolutionary allometry, whereas no allometric trends were discernible for Strepsirrhini, Colobinae or Platyrrhini. Furthermore, we found that in the taxa characterized by significant allometry, brain shape evolution accelerated, whereas for taxa in which such allometry was absent, the evolution of brain shape decelerated. We conclude that although primates in general are typically described as large-brained, strong allometric effects on brain shape are largely confined to the order's representatives that display more complex behavioural repertoires.

1. Introduction

Body size exerts pervasive effects on animal morphology and behaviour [1]. Macroevolutionary trends in body size are thus expected to play a major role in the evolution of morphological structures, influencing the tempo and mode of phenotypic change [2,3].

Among primate clades, some have followed no clear pattern regarding body size over time, but others have consistently increased in size (Cope's rule) [4]. By contrast, the evolution of a large brain, in both absolute and relative terms, has been a consistent trend [5–7], culminating in the emergence of large-brained apes and humans. Progressive encephalization has had profound physiological, ecological and social consequences [8], linked to diet [9], home range size and activity period [10], mating system [11], life-history traits [12,13], dexterity [14] and sociality [15].

In addition to brain size, a diversity of ecological and behavioural characteristics has also been attributed to changes in the shape, position and orientation of individual brain structures [16,17]. Several studies have suggested that brain reorganization in primates follows a mosaic pattern [18–20], with separate cortical areas responding differently to different selective pressures [21,22]. It has been argued that this has produced a greater diversity in brain shape than would be predicted on the basis of absolute or relative brain sizes alone [16,19,22]. For example, previous investigations have linked the evolution of a more globular brain to behavioural modernity in humans [23,24] and provided insights into the ecological factors driving behavioural adaptations in New World monkeys [16,25].

However, although it is clear that body mass influences brain size, whether the relationship between brain size and brain shape themselves is characterized by allometry is not known. Yet, allometric scaling may occur at different evolutionary rates [22] and previous studies have highlighted how brain size can evolve at different rates in different primate lineages [7,22,26].

Here, we ask whether the relationship between primate brain size and brain shape is characterized by allometry, and whether any such relationship may reflect shared macroevolutionary trends in primate brain shape. Identifying the brain components associated with major shifts in rates of morphological evolution will contribute to the understanding of how primates and humans evolved their varied and complex behavioural repertoires.

To answer these questions, we apply the most broad-ranging, data-rich three-dimensional (3D) geometric morphometrics study of primate brains conducted to date (figure 1a, electronic supplementary material, table S1 and S2). Our study is based on 386 skull endocasts (including both males and females for each species where available) representing 151 primate species. These taxa represent all families excepting Tarsidae and Daubentoniidae (Strepsirrhini: 31; Platyrrhini: 42; Colobinae: 24; Cercopithecinae: 35; Hominoidea: 19). Our sample further includes four fossil species: Homo heidelbergensis Kabwe 1, Australopithecus africanus Sts5, Antillothrix bernensis PN:09:01, Archaeolemur sp. DPC9104) reconstructed from CT scans (see electronic supplementary material, table S1, for details on sampling. Full data are available from the Dryad digital Repository: https://doi.org/10.5061/dryad.crjdfn320 [27].

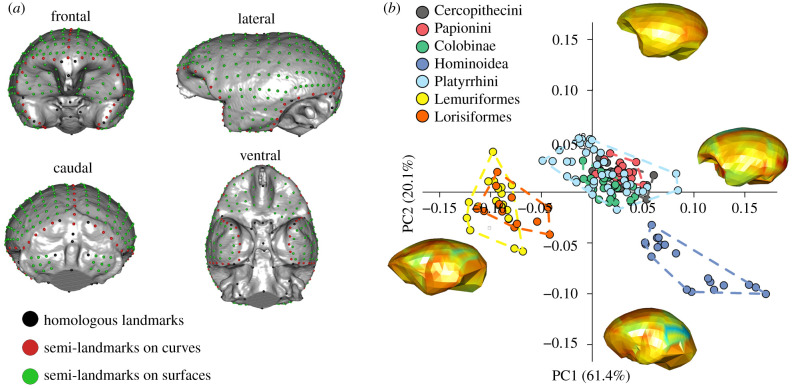
Figure 1.

Brain shape variation in Primates. (a) Landmarks and semi-landmarks used to record brain (endocast) shape variability. (b) Scatterplot of PC1/PC2 scores of brain endocast shape variables in Primates. The warped meshes refer to positive and negative extremes of the axes. Mesh colours indicate the magnitude of shape changes associated with each axis, from low deformation (cool colours) to high deformation (warm colours). (Online version in colour.)

We assessed allometric relationships between brain size and brain shape in a phylogenetically explicit context and investigated whether size has a global (affecting brain shape as a whole) or a localized (to specific cortical areas) effect on brain shape reorganization using the novel ‘shape integration' concept proposed by Bookstein ([28]; electronic supplementary material, Supplementary methods). We further used a novel comparative method based on phylogenetic ridge regression to determine the presence of shifts in the evolutionary rates across primate history in a phylogenetic context [29] marking brain shape discontinuity across the primate tree.

2. Results

(a). Shape analysis

To explore the endocranial variation of primates we performed a principal component analysis (PCA) on Procrustes shape variables (figure 1a to visualize the landmark and semi-landmark configuration). This technique allows the ordination of the specimens along major axes of variation (principal components) and the visualization of the associated shape changes (figure 1b).

The first two PCA vectors of brain shape account for 61.4% and 20.1% of the total shape variation, respectively (figure 1b). Along these axes the main primate clades follow a size gradient, with hominoids and strepsirrhines occupying extremes of the morphospace (figure 1b).

Along PC1 (61.4% of the total variation), there is a clear distinction between the Strepsirrhini (negative values), the Platyrrhini and Cercopithecoidea (distributed close to the consensus shape) and the Hominoidea (positive values).

The endocast displays a generally flat and elongated configuration at negative values with a marked reduction in the neocortical areas. The frontal area projects anteriorly, but does not show any bulging, the parietal areas are low and depressed, the temporal region is large and laterally expanded relative to the fronto-parietal region, and the stem is postero-caudally oriented. At positive PC1 values, the endocast is globular in shape, the frontal area becomes rounded and expanded ventrally and the parietal areas bulge to acquire a round shape. The temporal areas are smaller relative to the fronto-parietal region, and the occipital area becomes rounder and more caudally pronounced. Along the PC2 (20.1% of the total variation), the Hominoidea (negative values) separate from Platyrrhini and Cercopithecoidea (positive to slightly negative values), whereas Strepsirrhini largely overlap with Platyrrhini and Cercopithecoidea (from positive to near consensus values) and only partially overlap with Hominoidea (at negative values). At positive values, the endocast shows a more slender and elongated morphology. The frontal area is anteriorly more distinct and reduced overall. The temporal regions are wide and ventrally directed, the occipital areas are moderately rounded with a great reduction of the cerebellar region and the stem is more posteriorly flexed. At negative PC2 values, the endocast displays a more globular configuration, the frontal areas are greatly expanded in ventral and frontal directions, the parietal shows conspicuous bulging and these areas appear globular in shape. The cerebellum is markedly expanded and the stem is positioned more ventrally. To account for shared ancestry, we performed a phylogenetic generalized least squares (PGLS) regression, which indicated that there are significant brain shape differences between primate clades (r² = 0.07, p-value = 0.001).

(b). Multivariate allometry

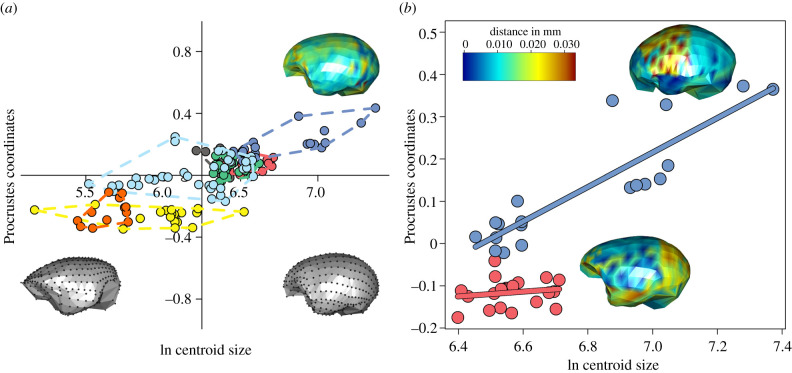
The allometric relationship between brain size (the logarithm of centroid size, lnCS, a measure of brain volume) and shape shows that the main allometric effect visible in primate endocasts is the change from a flat and antero-posteriorly elongated brain in small species, to a more globular, rounded, fronto-parietally expanded brain in large species (figure 2a). The PGLS regression between shape variables and the lnCS is highly significant (r² = 0.17, p-value = 0.01). Yet, phylogenetic MANCOVA (multivariate analysis of covariance) indicates that allometric slopes differ among clades (p-value = 0.001). Per-clade PGLS regressions revealed that significant allometric effects are entirely restricted to Hominoidea and Cercopithecinae (table 1), although their allometric trajectories diverge from one another (difference at small size = 0.09, difference at large size = 0.21; p-value = 0.008, figure 2b). In hominoids, allometry affects brain shape as a whole, although the consequence of brain size change is more pronounced in the fronto-parietal region which expands with brain size, culminating in the globular brain shape of hominids. Relative to the latter, in Cercopithecinae the main allometric effects are evident in the expanded, ventrally projected temporal region and in the round and caudally projected occipital region (figure 2b).

Figure 2.

Multivarite evolutionary allometry. (a) Scatterplot of the multivariate regression between brain endocast shape variables and the logarithm of endocast size (lnCS). Warped meshes refer to brain shape at the lnCS extremes. The heat map represents the magnitude of shape changes associated with maximum lnCS. (b) The plot represents the diverging allometric trajectories for Hominoidea (blue, upper line) and Papionini (red, lower line). The heat maps representing the brain shape deformation for each group at its respective maximum size are superimposed on the plot. (Online version in colour.)

Table 1.

Allometric shape regressions per clade. The separate per clade multivariate regression models tested in the present work. Significant results are italicized. Phylogenetic generalized least square regression results are indicated under the heading ‘PGLS'.

clade	linear model		PGLS
	r2	p-value	r2	p-value
Cercopithecinae	0.16	0.001	0.094	0.017
Colobinae	0.03	0.55	0.034	0.449
Hominoidea	0.37	0.001	0.19	0.012
Platyrrhini	0.13	0.001	0.021	0.559
Lemuriformes	0.19	0.001	0.11	0.055
Lorisiformes	0.14	0.001	0.17	0.076

(c). Bookstein ‘integration' test

Bookstein's integration test allows evaluation of the degree to which spatial scale the brain size is impacting brain shape. In Hominoidea and Cercopithecinae, the impact is great (Bookstein ‘integrated' pattern, see electronic supplementary material , table S3). Unlike Hominoidea and Cercopithecinae, in Platyrrhini and Colobinae, allometry drives no discernible effect (Bookstein's ‘self-similarity' pattern, see Material and methods). In Strepsirrhini (Lemuriformes and Lorisiformes), brain size influences brain shape only at the local scale, hence showing a ‘dis-integrated' pattern (electronic supplementary material, table S3).

(d). Rates and trajectories of morphological evolution

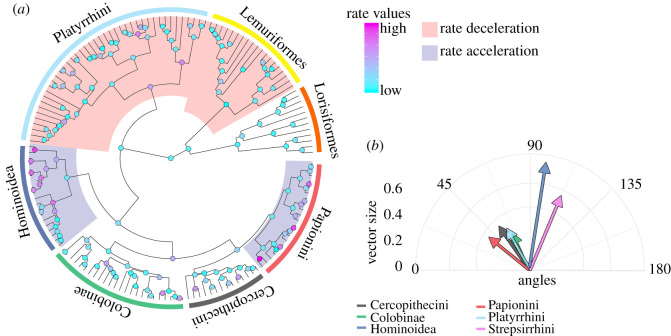
When investigating the rates of morphological evolution using the RRphylo approach (a strategy based on phylogenetic ridge regression designed to incorporate fossil taxa in the analyses), we found contrasting results depending on whether allometry was present or not. In fact, using a two-tailed permutation test of rates across the tree, we found instances of phenotypic rate acceleration in the clades showing strong allometric effects, Hominoidea (p-value = 0.99) and Papionini (within Cercopithecinae; p-value = 1.00) and two significant occurrences of rate deceleration in clades which did not show allometry: Strepsirrhini (p-value = 0.003) and Platyrrhini (p-value = 0.001), (figure 3a, electronic supplementary material, figures S1, S2). These results are not a consequence of the tree topology we adopted, remaining stable after accounting for phylogenetic uncertainty by randomly swapping tree branches and node ages to account for phylogenetic uncertainty (Hominoidea: p-value = 0.98; Papionini: p-value = 0.99; Strepsirrhini: p-value = 0.01; Platyrrhini: p-value = 0.001). The evolutionary rates represent the actual magnitudes of shape change per time unit. However, they do not provide any information about the direction of such change. The vectors of regression coefficients, as produced by means of phylogenetic ridge regression [29], possess specific magnitudes and directions, which can be compared to each other in terms of the angles they form in reference to a common vector [30,31] (figure 3b). Given the presence of rate shifts in brain shape evolution in all the major primate clades, we took the tree root as a common reference to measure the angles of the vectors describing the shape changes and compared them between the clades in a pairwise fashion (figure 3a and b; table 2). Due to the presence of possible biases when estimating ancestral states, this approach provides biologically meaningful results under the assumption that the root phenotypic estimate is a good representation of the ancestral mean shape, which is expected under non-directional evolution [6,31]. We found that the shape change trajectories of Hominoidea and Strepsirrhini were different to those of the other primate clades, in terms of both direction (angle) and magnitude. However, hominoids showed greater shape change than any other clade. Papionini differ from Platyrrhini and Cercopithecini in the direction, but not in the magnitude of shape change (table 2; figure 3b).

Figure 3.

Rates and trajectories of brain shape evolution. (a) Distribution of evolutionary rate shifts on the Primates tree. The red shades represent clades showing evolutionary rate slowdowns (Strepsirrhini, p = 0.01; Platyrrhini, p = 0.021). The blue shades represent clades showing evolutionary rate acceleration (Hominoidea, p = 0.01; Papionini, p = 0.001). (b) Direction and magnitude of shape changes of Primate clades. The angles are calculated in reference to the brain shape at the tree root and reported in two dimensions, taking the mean angle to represent each clade. (Online version in colour.)

Table 2.

Summary statistics of pairwise comparisons of shape change trajectory angles and magnitudes. Upper triangle: p-values refer to trajectory angles; lower triangle: p-values refer to trajectory magnitudes. Angles = the mean angle to the root shape for all species within individual clades. Magnitude = the mean vector size per clade. Significant results are italicized.

clade	Cercopithecini	Papionini	Colobinae	Hominoidea	Platyrrhini	Strepsirrhini
Cercopithecini		0.001	0.001	0.001	0.299	0.001
Papionini	0.712		0.064	0.001	0.001	0.001
Colobinae	0.001	0.001		0.001	0.002	0.001
Hominoidea	0.001	0.001	0.001		0.001	0.001
Platyrrhini	0.310	0.322	0.021	0.001		0.001
Strepsirrhini	0.001	0.001	0.001	0.005	0.001
Angles	56.15°	46.4°	62.3°	102.68°	61.7°	112.34°
Magnitudes	0.33	0.32	0.23	0.75	0.28	0.55

3. Discussion

Our results demonstrate that the trajectories and rates of brain shape evolution in different primate clades were strongly influenced by the presence or absence of allometry between brain size and shape. Different primate clades occupy distinct regions of morphospace along a brain size gradient (figure 1a), with the small-brained strepsirrhines and the large-brained hominoids at opposite extremes (figure 1b). This trend was particularly evident along the first PC axis. Species characterized by larger brain size tend to have more rounded aspect of the frontal region, more flexed cranial base, caudally projected occipital areas and overall taller endocasts. However, unlike the relationship between brain size and body size, this pattern does not fit a common allometric relationship. When phylogenetic effects are considered, only hominoids and cercopithecines show significant allometry.

In both of these two Old World anthropoid clades, brain shape variation is highly ‘integrated’ with size (table 1, electronic supplementary material, table S3). However, although brain size exerts a powerful influence on brain shape in both Hominoidea and Papionini, the two are characterized by very divergent allometric trajectories across different brain regions. Shape change is amplified anteriorly in hominoids, but laterally and posteriorly in cercopithecoids (figure 2b). The highly developed temporal lobes in this latter taxon are associated with increased visual acuity and geographic, individual and object recognition [32], whereas fronto-parietal reorganization in hominoids is associated with the emergence of increased cognitive capacities, tool use and language [33–36].

Clearly functional specialization can be acquired through changes in brain shape and proportions [22]. Our results suggest that evolutionary changes in allometric parameters may have triggered the adaptive expansion and reorganization of the fronto-parietal areas in hominoids, and of the temporal areas in papionin monkeys. Moreover, changes in the brain shapes of Hominoidea and Papionini occurred at comparatively faster evolutionary rates than those of other primate taxa. Similar results have been found in the investigation of face and basicranium by Neaux et al. [37], where positive evolutionary rate shifts were identified for these clades, suggesting correlated evolution between external brain shape and the encasing cranial elements. These clades display broadly different locomotion patterns (terrestrial quadrupedalism in Papionini and suspension, knuckle-walking and bipedalism in hominoids), and this asymmetric pattern of brain shape reorganization may reflect different selective pressures on these two Old World lineages.

Although both Strepsirrhini and Platyrrhini (New World monkeys) display a great range of body sizes, their brain shape was not affected by allometric change (table 1). We found that platyrrhines show a self-similar allometric pattern (i.e. brain shape does not change consistently with brain size) and slow phenotypic evolutionary rates. Similarly, weak allometric effects have been identified regarding platyrrhine brains [16,38]. Further studies have demonstrated an adaptive radiation for this clade characterized by rapid early morphological differentiation and a subsequent decreasing trend [3,37,39], suggesting that size may exert a stabilizing effect on their brain shape diversity [28]. Aristide et al. [16] posited that ecological convergence on shared adaptive optima across the platyrrhine tree can be responsible for this pattern, indicating that they depart significantly from Old World monkeys and apes in this regard.

Strepsirrhines display markedly reduced rates of evolution and a weak allometric effect. As has been found in studies on the cranium and mandible [39,40], the eco-morphological differentiation that occurred in Strepsirrhini was not impacted by size changes. Our result is further confirmed by the inclusion of the fossil taxon Archaeolemur, which, despite its larger brain size, did not show any significant shift in its brain shape. However, unlike platyrrhines, strepsirrhines show a ‘dis-integrated' pattern (electronic supplementary material, table S3), indicating that changes in brain size impact brain shape only at the local scale. This suggests that strepsirrhine brains evolved in accordance with the mosaic model of evolution, hinting at moderately higher brain shape flexibility in this clade when compared to platyrrhines. The ‘dis-integrated' pattern can be related to the relatively large number of eco-morphological differentiation events that occurred during strepsirrhine evolutionary history and potentially to the emergence in some cases of complex behaviours such as tool use [40–43].

In conclusion, our study demonstrates that the evolution of brain shape in primates cannot be explained by any single, simple evolutionary model. The presence of allometry significantly impacted evolutionary rates and triggered the diversification of brain shape in hominoids and papionins along two distinct trajectories (electronic supplementary material, figures S3 and S4). We propose that faster rates of evolution driven by the presence of allometry may help to explain how Hominoidea and Papionini evolved more versatile and complex range of behaviours (such as multi-level social interactions), possibly reflecting a shift in their ecological and positional behaviour [42–44]. By contrast, strepsirrhines and platyrrhines both exhibit slowdowns in the rate of brain shape evolution (electronic supplementary material , figures S3 and S5) and, in New World monkeys, reduced magnitudes of shape change, consistent with the conservative ecological habits of platyrrhines. In strepsirrhines, brain shape shows no allometry and a ‘dis-integrated' pattern of shape variation possibly related to the higher eco-morphological diversity of this clade. Eventually, in platyrrhines neither mosaicism nor allometry are present, in compliance with the predictions of the adaptive radiation model and with the observation that New World monkeys possess less diverse lifestyles, lack terrestrial species and converge towards common adaptive peaks [16,39,41].

4. Methods

(a). Geometric morphometric shape and size analysis

The form of an object can be decomposed into two components: shape and size, the first bearing information about the spatial organization, the latter dealing with dimension. Geometric morphometrics is the statistical study of the form based on Cartesian landmarks coordinates. This strategy allows separating the shape of an object form its dimension, which can be subjected to further statistical analysis.

To investigate the shape and size of the primate brain we assembled a sample including 386 endocasts from 151 primate species (extant: 147; extinct: 4). On each endocast (figure 1a), we digitized 40 anatomical landmarks, 76 semi-landmarks (placed equidistantly along curves) and 406 semi-landmarks placed on surfaces using IDAV Landmark software (electronic supplementary material, table S1). We manually digitized the homologous landmarks on each specimen, then performed PCA to identify the individual closest to the consensus shape (Piliocolobus badius USNM 481795). We manually digitized the semi-landmarks on curves and surfaces on the consensus specimen endocast and used it as the template individual. Once all the semi-landmarks were automatically placed (see electronic supplementary material, Supplementary Methods for details on the process), we imported the landmark coordinates into R version 3.5.2 for further analyses. We performed generalized Procrustes analysis [45] (GPA) on all landmarks, implemented in the procSym() function from the R package ‘Morpho' [46] to rotate, translate and scale landmark configurations to unit centroid size (CS), i.e. the square root of squared differences between landmark coordinates and centroid coordinates [47]. To visualize the multivariate ordination of the aligned Procrustes coordinates, we performed a regular non-phylogenetic PCA. We classified the species using similar taxonomic groups to those defined by Fleagle et al. [48] and Neaux et al. [49] in their analyses of primate cranial shape diversity: Hominoidea (Hylobathidae and Hominidae), Cercopithecinae (Papionini and Cercopithcini), Colobinae, Platyrrhini (Cebidae, Atelidae and Pithecidae), Lemuriformes and Lorisiformes. The significance of the observed shape changes between the major primates clades was evaluated by performing a Procrustes ANOVA on aligned Procrustes coordinates (shape) using the function procD.lm() from the R package ‘geomorph' [50]. Multivariate regressions between aligned Procrustes coordinates and the logarithm of centroid size (brain size measure, lnCS) were applied to determine the presence of evolutionary allometry in the endocasts. To test for differences in slopes among the different primate clades, we ran a permutational multivariate analysis of covariance, using aligned Procrustes coordinates as dependent variables, lnCS as an independent variable and the groups as factors. To visualize shape changes in the ordination plots, we used the method described in [51], which consisted of visualizing local, infinitesimal variation within a deformation grid using the Jacobian (J) of the thin plate spline (TPS) interpolation function. J captures very localized information as localized variation in the non-affine component of the deformation using derivatives of the used interpolation function (TPS in our case). In two-dimensional J is a 2 × 2 matrix that can be evaluated at any point within a body. The logarithm of its determinant represents the change in the area in the region about the interpolation point. Values less than 0 indicate that, with respect to the source (here the sample consensus), the target (here the PC's extremes) experiences a reduction in the local area, while values greater than 0 indicate an enlargement [52].

(b). Global integration and the scaling of shape variation

Bookstein [28] recently proposed a new method to evaluate the degree of morphological integration of an anatomical structure (see electronic supplementary material, Supplementary Methods for further details). This approach is based on a similitude with how time series are investigated in modern palaeobiology where ‘directional trends' and ‘stasis' are extremes of a distribution. The null hypothesis separating these two models is the ‘random walks' or the lack of interpretable changes at any given temporal scale.

Accordingly, what can be applied to investigate timescales can be applied to investigate variation over different spatial scales. This method tests the null hypothesis of ‘self-similarity’ (e.g. the absence of any interpretable shape change across different spatial scales) in a sample of shapes and it is based on a linear regression of log partial warps variance against their proper log bending energy (i.e. the log of eigenvalues of the bending energy matrix computed on the consensus). Partial warps describe the net local deformations, whereas the bending energy quantifies the displacement of a given shape change. Here, a regression slope less than −1 indicates ‘integration’ whereas a slope greater than −1 indicates ‘dis-integration'. If the regression slope is exactly −1, data can be considered ‘self-similar' (electronic supplementary material, Supplementary Methods). In this context, ‘integration' implies a major contribution from large-scale variation (global patterns), whereas ‘dis-integration’ can be interpreted as major contribution from small-scale variation on the endocast shape. To understand the effect of size on the scaling of shape variation in primate endocasts, we followed previously published protocols [53]. First, we performed separate per clade multivariate regressions between shape and size, then we extracted the predicted landmark variation from the regressions that proved to be significant. Finally, we applied the ‘global integration’ procedure to our set of predicted shapes to determine the patterns of correlation between shape and size in the different clades.

(c). Phylogeny and comparative methods

The phylogenetic tree used in our analyses is a time-calibrated tree based on a Bayesian estimate obtained from the 10kTrees Project v3 [54] for the 147 extant species in our dataset (electronic supplementary material, Supplementary Methods). A maximum clade credibility tree of the extant species in the analysis was constructed from a set of 1000 molecular trees using the function MaxCredTree() from the R package ‘phangorn' [55]. Finally, the four fossil species included in our dataset were manually added to the tree. The final phylogenetic hypothesis is available in electronic supplementary material, Supplementary methods.

The significance of the observed shape changes between primate clades was evaluated by performing a Procrustes ANOVA in a phylogenetic framework on aligned Procrustes coordinates using the function procD.pgls() included in the R package ‘geomorph' [50]. To analyse the relationships between size and shape, we tested the differences between the evolutionary allometric trajectories of the primate clades performing a phylogenetic MANCOVA using Procrustes coordinates as dependent variables, lnCS as an independent variable, and the clades as a factor. The test was performed using the function procD.pgls() in the package ‘geomorph'. Finally, we compared the direction of the allometric slopes found to be significantly different using the ‘allometric convergence test' [52].

(d). RRphylo

We applied a recently developed phylogenetic comparative method named RRphylo [29] to compute phenotypic evolutionary rates for each branch of the phylogeny. The RRphylo method is based on phylogenetic ridge regression (a strategy providing better parameter estimation) to estimate values at nodes and to compute rates along individual branches. Once individual rates are assigned, a function can locate clades displaying average evolutionary rates that are significantly higher or lower than the average for the rest of the tree. The significance of the located shifts is then assessed by means of randomization.

In RRphylo, the phenotypic change along a node-to-tip phyletic path is computed as Δy = β₁l₁ + β₂l₂ + …. β_nl_n, where l_i and β_i represent the branch length and the regression coefficients, respectively, for each of the n branches intervening along the path. As regression slopes, the β coefficients represent the actual rates of phenotypic transformation along each branch. The vector of β is estimated simultaneously for all branches in the tree and independently for each variable by applying a normalization factor λ which avoids fitting extreme β values and prevents multicollinearity.

After computing the rates for the tree branches, we applied the function search.shift() [29] to identify clades showing significant shifts in the rate of phenotypic evolution. search.shift() uses the phylogenetic tree and the branch-wise rates of phenotypic evolution (derived by the RRphylo() function) to locate clades with average evolutionary rates that are significantly higher or lower than the rest of the tree. Significance is assessed by means of randomization. We identified the trajectories and the magnitudes of shape change by applying the RRphylo function evo.dir() [31]. Dealing with multivariate data, each species has its own phenotypic vector defined by each variable. By applying RRphylo() on such multivariate phenotypic data, a vector of rates (as many as the variable) is derived for each species and node in the tree. The magnitude of the rate vector is computed as the root sum squared of the vector. Direction is defined in reference to another vector by computing the angle θ between them. Given two rate vectors A and B, the angle between them is calculated as [30]

$$\theta =\text{arccos}\frac{A\hspace{0.17em}\bullet \hspace{0.17em}B\hspace{0.17em}}{|A||B|}.$$

Thus, the trajectory of phenotypic change between a node and a daughter tip can be computed as the trigonometric addition of successive rate vectors aligned along a node-to-tip path. This addition produces a resultant vector having its own magnitude and direction in respect to the node.

Data accessibility

The datasets used in the current study are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.crjdfn320 [27].

Authors' contribution

The study was conceived by G.S., J.L., S.W., K.A. and P.R. with contributions from all the other authors. D.R.M., S.L., A.P., J.L. and K.A. processed the endocasts. S.L. and G.S. digitized the landmarks. G.S., P.R., A.P., C.S., S.C., M.M. and A.M. analysed the data. G.S., P.R. and S.W. wrote the manuscript with contributions from all the other authors.

Competing interests

The authors declare no competing interests.

Funding

This research was funded by an ARC Discovery Grant to S.W. (DP140102659).