Abstract
Logistic models have been widely used for modelling the ongoing COVID-19 pandemic. This study used the data for Kuwait to assess the adequacy of the two most commonly used logistic models (Verhulst and Richards models) for describing the dynamics COVID-19. Specifically, the study assessed the predictive performance of these two models and the practical identifiability of their parameters. Two model calibration approaches were adopted. In the first approach, all the data was used to fit the models as per the heuristic model fitting method. In the second approach, only the first half of the data was used for calibrating the models, while the other half was left for validating the models. Analysis of the obtained calibration and validation results have indicated that parameters of the two models cannot be identified with high certainty from COVID-19 data. Further, the models shown to have structural problems as they could not predict reasonably the validation data. Therefore, they should not be used for long-term predictions of COVID-19. Suggestion have been made for improving the performances of the models.
Keywords: Infectious disease modeling, Logistic growth models, Parameter identification, Model performance, COVID-19 in Kuwait
1. Introduction
Epidemiology is a science concerned with the distribution patterns and causes of diseases. Disease and sickness have tormented humanity since the beginning of life on earth. Mankind history has seen many epidemics characterized by high mortality and morbidity [Zappa et al., 2009]. However, the scale of these diseases has increased since the advent of globalization. As new opportunities for human interactions have become more common due to the rise in global trade; expansion of civilization; and more chances for contacts with population across the globe, globalization has somehow helped in the proliferation of epidemics.
The scientific efforts made during the mid-20th century have reduced the spread of epidemics in the world. This was mainly a result of the advances in medical services; improvements in health care and the urban environment; and availability of vaccines and antibiotics [Zappa et al., 2009]. However, the widespread of outbreaks have again returned to the world in the 21st century. A probable consequence of: pollution; overpopulation; and poverty, present in several places on earth. Recently, the world has gone through an intermittent communicable disease outbreak that led to unprecedented epidemics, which have significantly impacted the humanity claiming many innocent lives and costing billions of dollars. Epidemics such as: the sever-acute-respiratory syndrome (SARS), middle-eastern-respiratory syndrome (MERS) and of course the current coronavirus that has been classified as a pandemic (COVID-19). While the spread of latest COVID-19 continues to increase throughout the world without a vaccine emerging soon, supressing the transmission of the virus following conventional methods - such as lockdown, quarantine, social distancing, wearing masks, washing and disinfecting hands - appear to be the advisable strategies for the time being. Unfortunately, these prolonged measures have negatively impacted the global economy.
Mathematical models are important tools used by epidemiologists to have insight into the temporal and spatial distribution patterns of the spread of diseases (Caccavo, 2020). They can be utilized to help governments and health authorities to decide what control measures to be implemented and how to allocate appropriately the often limited health resources. In times of epidemics which has no known treatment, like COVID-19, mathematical modeling is the only way to predict the spread of the disease and to decide and access the effectiveness of the intervention measures to be imposed.
The main types of mathematical models that have been used to describe the dynamics of COVID-19 are the compartmental and logistic growth models. Compartmental models generally assume that the community is closed, which is often unrealistic assumption. Further, compartmental models attempt to model the complex interactions between the different compartment (e.g. susceptible, the infected, and the recovered persons), which have different dynamics. Examples of compartmental models are the susceptible-infected-recovered (SIR) model, the susceptible-infected-recovered-death (SIRD) model, the susceptible-exposed-infected-recovered (SEIR) model, and the quarantined-susceptible-exposed-infected-recovered (QSEIR) model (Batista, 2020; Liu 2020; Ma, 2020; Roda 2020).
In contrast, the logistic growth models are simpler as they describe only the change in the cumulative number of infected persons. The two logistic models used widely for modeling COVID-19 are Verhulst and Richards models. In 1838, Verhulst proposed the differential equation shown below (Eqn. (1)) originally for the modeling population dynamics (Batista, 2020).
| (1) |
where C is the accumulated number of cases, r is the infection rate, and K is the final epidemic size.
Solution of Eqn. (1) is:
| (2) |
To improve the fit to actual data, Richards added in1959 the scaling parameters ‘a’ to Verhulst’s model as shown in Eqn. (3) (Hiseh, 2009; Roosa et al., 2020).
| (3) |
The solution of Eqn. (3) is:
| (4) |
The main aim of this study was to assess the adequacy of Verhulst’s and Richards’ models for describing the dynamics of COVID-19 data. Specifically, the study examined the identifiability of the parameters and evaluated the prediction reliability of the two models.
2. Methodology
Daily COVID-19 data for Kuwait was obtained from the Worldometer website [Worldometer, 2020]. Then the data was fitted to Verhulst and Richards models, using MATALB least square function and adopting two different calibration approaches. In the first approach, the commonly used heuristic model fitting approach was followed, in which all the data were used in model fitting. In the second approach, the models were calibrated with only the first half of the data, while the second half of the data was left for validating the models.
For both calibration approaches, the uncertainties in the estimates of the parameters were evaluated based on the standard deviations obtained from the covariance matrix () calculated from the Jacobi matrix as follows (Abusam et al., 2000, Abusam et al., 2001):
| (5) |
where X is the locally available Jacobi matrix:
| (6) |
and the residual variance is:
| (7) |
Finally, reliability of the prediction of the two models were evaluated from model validation results.
3. Results and discussion
3.1. Heuristic fitting and proper model calibration
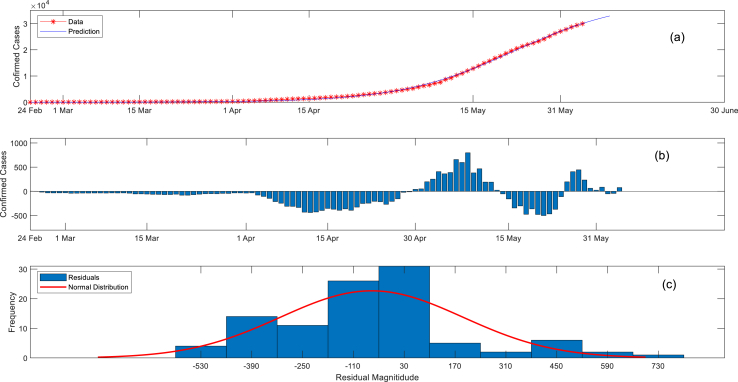
Results of using all data to fit Verhulst’s Model are presented in Fig. 1a. As shown in this figure, the data appears to fit the model well. Despite that, Fig. 1b - which presents the profile of the model misfit (residuals) - shows that the fit was good only for the first five weeks of the epidemic (24 February to 3 March). After that, the magnitude of model misfit increased significantly as the epidemic approached the peak. If the assumption that the model satisfactorily describes the dynamics of COVID-19 is valid, the residuals will be approximately following a normal distribution pattern. To check that, the residuals were fitted to a standard normal distribution as depicted in Fig. 1c. From this figure, it is clear that the residuals are not normally distributed as they are highly skewed to the right. Assuming the data is accurate, this indicates existence of a systematic error that became evident as the epidemic approaches the peak.
Fig. 1.
Results of heuristic fitting of Verhulst’s model.
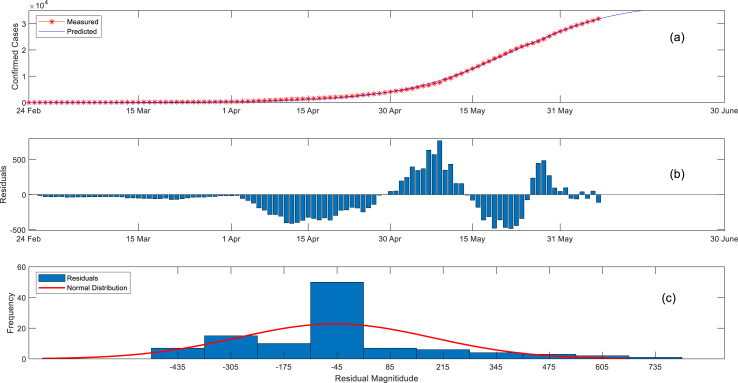
Results of fitting Richards’ model with all data are presented in Fig. 2a. Similar to the results obtained from fitting Verhulst’s model (Fig. 1a), the data seems to fit the model well at the beginning of the epidemic. However, the increased magnitude of residuals as the epidemic approached the peak (Fig. 2b) and the apparently skewed distribution of the residuals to the right (Fig. 2c) indicate that Richards’ model has also failed to accurately describe the dynamics as the epidemic as it approached the peak, probably is due to a systematic error in the model on assumption that the data is correct.
Fig. 2.
Results of heuristic fitting of Richards’ Model.
3.2. Parameters identification
Table 1 presents the estimated values for the parameters of Verhulst’s model (K, r, and A) together with the standard deviation of each. Notice that the standard deviations were calculated from the covariance matrix according to eqn. (7). As evident from Table 1, all the values estimated for the parameters are less than twice the corresponding standard deviations. This shows that the estimation errors are significantly high for all the parameters. Thus, it can be concluded that all model parameters cannot be reliably identified from the epidemic data. This indicates that the model needs re-parameterization. Parameter identifiability problems affect significantly performances of models. Roda et al. (2020) has attributed the variations in the results of logistic models to the existence of unidentifiable parameters.
Table 1.
Estimated values for the parameters of Verhulst’s model.
| Size of Data | K | r | A |
|---|---|---|---|
| All the data | 3.9e+4 ± 1.5e+5 | 0.10 ± 0.30 | 5.2e+3 ± 1.1e+5 |
| Half of the data | 9.1e+3 ± 1.2e+6 | 0.10 ± 0.50 | 1.0e+3 ± 1.2e+5 |
Re-parameterization means re-defining and re-selection of the parameters of the model. It can be achieved by setting some of the parameters to zero or combining two or more of them to form a new parameter (Keesman, 2002). Re-parameterization process usually results in alternative structures for the model that need to be analyzed further to select the appropriate model structure.
Table 2 presents the estimated values and the calculated standard deviations for the parameters of Richards’ model. Similar to the results obtained for Verhulst’s model, Table 2 indicates that all parameters of Richards’ model cannot be identified reliably from COVID-19 data. Therefore, it also needs re-parameterization as suggested for Verhulst’s model.
Table 2.
Estimated values for the parameters of Richards’ model.
| Size of Data | K | r | tm | a |
|---|---|---|---|---|
| All the data | 5.4e+4 ± 3.4e+6 | 0.04 ± 5.6 | 9.7e+1 ± 4.0e+1 | 1.1e+0 ± 7.5e+1 |
| Half of the data | 1.3e+5 ± 8.3e+9 | 0.1 ± 1300 | 9.9e-1 ± 6.7e+5 | 1.1e0 ± 1.4e+4 |
3.3. Reliability of models’ predictions
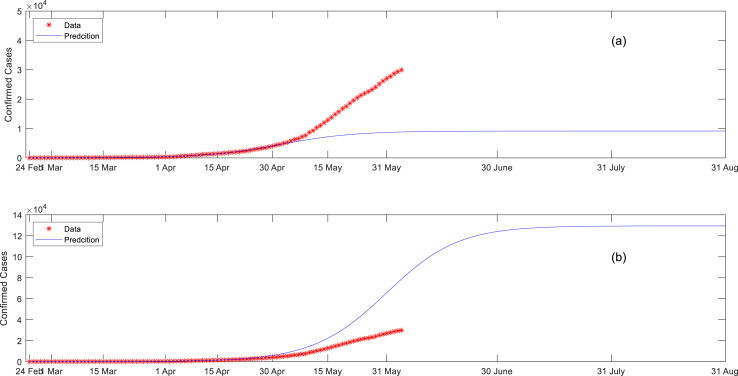
When trained with sufficient amount of data, a model that adequately describes the dynamics of a system, should be able to predict reasonably the validation data. Fig. 3 compares the validation results of Verhulst and Richards models after calibrating them with the first half of the data. This figure shows that both models could not reasonably predict the actual data. It also shows that predictions of Verhulst’s model underestimated the actual (validation) data, while those of Richards’ model overestimated them. Therefore, predictions of these two models are unreliable and should accessed with great care. Caccavo (2020) suggested not to use such models for long-term forecasts, as their parameters have no physical meaning. Arino and Portet (2020) were more precise and advised not to use the models for more than 30-days predictions. As shown below, however, the prediction ability of these models varies depending on the epidemic stage.
Fig. 3.
Validation results of the properly calibrated models: (a) Verhulst’s model (b) Richards’ model.
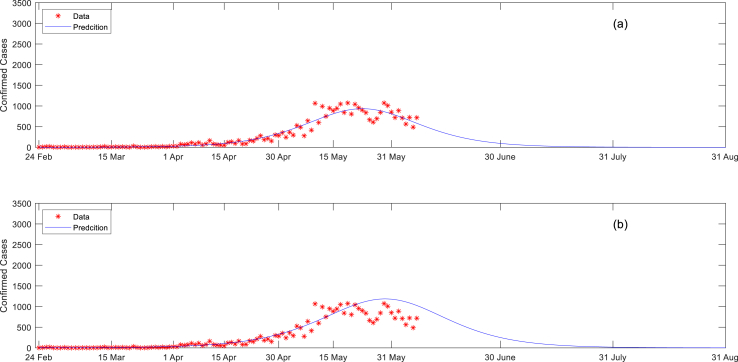
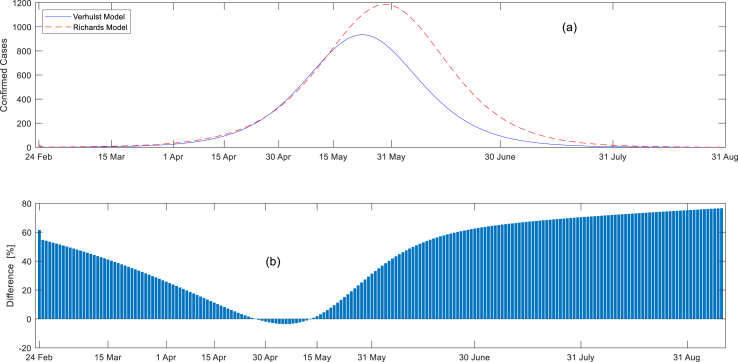
Fig. 4 compare predictions of the two models calibrated with all available data. From this figure it seems that there is no big difference between the predictions of the two models. As shown in Fig. 5, the two models behave differently depending on the stage of epidemic particularly while approaching the peak point. As can be seen from Fig. 5a, predications of Richards’ model are apparently higher than the predictions of Verhulst’s model predications as the epidemic passes the peak. However, Fig. 5b shows that predications of Richards’ model are also higher before the peak. Actually, the difference in predictions is more than 55% (average 35%) and decreases to almost 0% near the peak. But after the peak the difference increases rapidly to more than 75% (average 65%). This mathematical relationship between the predictions of the two models is important for understanding and reconciling the results of the two models.
Fig. 4.
Comparison of models’ performances when all data were used in model fitting: (a) Verhulst’s model (b) Richards’ model.
Fig. 5.
Relative Difference of the prediction of Richards’ model compared to Verhulst’s model: (a) Profile of predictions, (b) Difference between the two predictions.
3.4. Suggestion for improving models’ performances
Results presented and discussed above indicated that the two models suffer from structural problems and they require re-parameterization. The parameters of the models should be re-defined and re-selected. Since they cannot be identified reliably from the data, some of the existing parameters can be removed (put to zero value) or combined to form a new parameter. For example, the size of the final epidemic, K, should be removed. Actually K is an output of the model rather than a parameter. Three hundred years ago when the model was initially proposed, it was probably difficult to accurately calculate the final size of the epidemic (K). However, today with the advances in computational technologies, it is no longer a big issue. Further, the main structural problem of the model can be solved through the introduction of new term(s) to model the impact of control measures and interventions to be taken, while limiting the parameter “r” to only describe the infection spread rate.
4. Conclusions
This study assessed the adequacy of Verhulst’s and Richards’ models to describe the dynamics of the on-going COVID-19.
These two logistic models were found to fit reasonably the COVIT -19 data for Kuwait. However, analyses of parameters’ identifiability and models’ performance have indicated the followings:
-
•
Parameters of Verhulst’s and Richards’ models cannot be identified reliably from COVID-19 data.
-
•
Both of the models do not predict accurately the actual data as the epidemic approaches the peak point.
-
•
On average, predictions of Richards’ model are higher than that of Verhulst’s model by of 35%, before the peak, and of 65%, after the peak.
-
•
Both Verhulst’s and Richards’ suffer from structural problems, and therefore, they should not be used for long-term predictions of COVID-19.
The study has also suggested some methods for improving the performances of the two models.
Declaration of competing interest
Hereby we declare there is no any conflict of interest with anybody regarding the work presented in this paper.
Handling editor: Dr. J Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
References
- Abusam A., Keesman K.J., Van Straten G. Oxygen transfer rate estimation in oxidation ditches from clean water measurements. Water Research. 2001;35(8):2058–2064. doi: 10.1016/s0043-1354(00)00451-6. [DOI] [PubMed] [Google Scholar]
- Abusam A., Keesman K.J., Van Straten G., Spanjers H., Meinema K. Parameter estimation procedure for complex non-linear systems: Calibration of ASM No.1 for N-removal in a full-scale oxidation ditch. Water Science and Technology. 2000;43(7):357–365. [PubMed] [Google Scholar]
- Arino J., Portet S. A simple model for COVID-19. Infect. Dis. Model. 2020;5:309–315. doi: 10.1016/j.idm.2020.04.002. https://www.sciencedirect.com/science/article/pii/S2468042720300129 Available at: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batista M. Estimation of the final size of the COVID-19 Epidemic. 2020. https://www.researchgate.net/publication/339355847_Estimation_of_the_final_size_of_the_COVID-19_epidemic Available at:
- Caccavo D. Chinese and Italian COVID-19 outbreaks can be correctly described by modified SIRD model. 2020. https://www.researchgate.net/publication/340078430_Chinese_and_Italian_COVID-19_outbreaks_can_be_correctly_described_by_a_modified_SIRD_model Available at:
- Hiseh Y.H. Richards model: A simple procedure for real-time prediction of outbreaks severity. 2009. https://www.researchgate.net/publication/228982186_Richards_Model_A_Simple_Procedure_for_Real-time_Prediction_of_Outbreak_Severity Available at:
- Keesman K. Stare and parameter estimation in biotechnical batch reactors. Control Engineering Practice. 2002;10(2):219–225. [Google Scholar]
- Liu X., Hewings G., Wang S., Qin M., Xiang X., Zheng S., Li X. Modelling the situation of COVID-19 and effects of different containment strategies in China with dynamic differential equations and parameters estimation. 2020. https://www.researchgate.net/publication/340879118_Modeling_the_situation_of_COVID-19_and_effects_of_different_containment_strategies_in_China_with_dynamic_differential_equations_and_parameters_estimation_Preprint Available at:
- Ma J. Estimating epidemic exponential growth rate and basic reproduction number. Infect. Dis. Model. 2020;5:129–141. doi: 10.1016/j.idm.2019.12.009. https://www.researchgate.net/publication/338454727_Estimating_Epidemic_Exponential_Growth_Rate_And_Basic_Reproduction_Number Available at: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roda W.C., Varughese M.B., Han D., Li M.Y. Why it is difficult to predict accurately the COVID-19 epidemic? Infect. Dis. Model. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. https://www.researchgate.net/publication/339850601_Why_Is_It_Difficult_to_Accurately_Predict_the_COVID-19_Epidemic Available at: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M., Yan P., Chowell G. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang, China: February 13–23, 2020. Journal of Clinical Medicine. 2020;9(9):1–9. doi: 10.3390/jcm9020596. https://www.researchgate.net/publication/339443428_Short-term_Forecasts_of_the_COVID-19_Epidemic_in_Guangdong_and_Zhejiang_China_February_13-23_2020 596. Available at: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worldometer COVID-19 coronavirus outbreak. World meters, 2020. 2020. https://www.worldometers.info/coronavirus/#countries Available at:
- Zappa A., Amendola A., Romano L., Zanetti A. Emerging and re-emerging viruses in the era of globalization. Blood Transfusion. 2009;7:167–171. doi: 10.2450/2009.0076-08. [DOI] [PMC free article] [PubMed] [Google Scholar]