Artificial Intelligence for MR Image Reconstruction: An Overview for Clinicians

Abstract

Artificial intelligence (AI) shows tremendous promise in the field of medical imaging with recent breakthroughs applying deep learning models for data acquisition, classification problems, segmentation, image synthesis and image reconstruction. With an eye towards clinical applications, we summarize the active field of deep learning-based MR image reconstruction. We will review the basic concepts of how deep learning algorithms aid in the transformation of raw k-space data to image data and specifically examine accelerated imaging and artifact suppression. Recent efforts in these areas show that deep learning-based algorithms can match and, in some cases, eclipse conventional reconstruction methods in terms of image quality and computational efficiency across a host of clinical imaging applications including musculoskeletal, abdominal, cardiac, and brain imaging. This article is an introductory overview aimed at clinical radiologists with no experience in deep learning-based MR image reconstruction and should enable them to understand the basic concepts and current clinical applications of this rapidly growing area of research across multiple organ systems.

INTRODUCTION

The use of artificial intelligence (AI) in medical imaging is not new. In fact, machine learning, a subset of AI, has been used for computer aided diagnosis and detection (CAD) in radiology for decades (1-3). Recent advances in computer vision – specifically convolutional neural networks (CNNs) of deep learning – are now leading to exciting breakthroughs across diverse areas of medical imaging including disease classification, anatomic segmentation, image synthesis as well as image reconstruction (4-6).

The process of transforming MRI data measured in the Fourier domain (k space) to the image domain (MR image reconstruction) lies at the very heart of how MRI works and has been a rich area of research since the advent of MRI: varying k-space trajectory, parallel imaging, compressed sensing, et al. Recent applications of deep learning-based tools to aid in reconstruction problems are poised to further revolutionize this area (7).

For this review, we performed PubMed searches for varying combinations of the following keywords: “deep learning”, “convolutional neural network”, “MRI”, “reconstruction”, “k space”, which yielded in aggregate 139 articles. Works pertaining to image reconstruction from k space to image space were selected, which is described in more detail in a later section of this review. The intention of this article is not to be exhaustive or overly technical but to feature cutting-edge, illustrative, and representative examples for the clinical reader hoping to understand the general concepts and clinical applications in this area of rapidly growing research.

Here we review with a clinical audience in mind the application of these deep learning-based approaches to the unique problems of MR image reconstruction. First, we review the basics of a convolutional neural network. Then, we summarize the range of clinical applications of convolutional neural networks to sparse sampling in static and dynamic imaging across multiple organ systems. Reducing artifacts such as motion and ghosting are then considered, followed by applications in PET/MR. This review concludes with a discussion of the challenges and limitations of these approaches as well as a map for future research directions.

CONVOLUTIONAL NEURAL NETWORKS

Current deep learning-based image reconstruction uses supervised learning techniques with convolutional neural networks (CNN) (8-13). Supervised learning refers to techniques where a machine learning model learns to map an input to an output by training on a large set of given input and output pairs (training data) (14). CNNs are deep learning models that are designed to handle data arranged in arrays such as that encountered in imaging data. CNNs are made up of layers of learnable convolutional kernels; the elements of each kernel are trainable weights that extract features from the previous layer. CNNs used for image reconstruction are typically encoder-decoder style network architectures so that the output yields an image: the encoder portion of the network learns a compressed representation of the input data, and the decoder portion of the network reconstructs an output image from the compressed representation. For applications in MR image reconstruction, the models currently being used are high capacity, multilayer CNNs; training data consist of under-sampled, corrupted or otherwise non-optimal k space data as inputs and corresponding target images reconstructed using current standard algorithms as outputs.

A full review of how CNNs work is beyond the scope of this review and we refer the reader to a few recent resources on the topic (14-17). We include here an example using natural images (not MRI data) in order to illustrate the main components of the general form of encoder-decoder CNN network architecture, currently popular in MR image reconstruction deep learning methods (Figure 1). In this example, a CNN is developed to colorize an image. The model learns realistic colors for various parts of the image by training on many input (black and white image) / target output (color version of the same image) pairs that it is provided. Each time an input image is fed into the network, the network’s output is compared to the target output by calculating a measure of error based on the difference between network and target outputs; such an error measure can be defined variously and is called a loss function. In one of its most basic forms, comparing one image to another, a pixel-wise measure of mean squared error (MSE) can be used as a loss function. As the model is exposed to more examples, the weights in the model are continuously updated in an effort to minimize the loss function. This is achieved with a gradient descent optimization algorithm and backpropagation (18). If there are enough training data that broadly represent the range of potential inputs, the accuracy of the model improves iteratively to a point where we hope it will perform well on unseen data.

Figure 1.

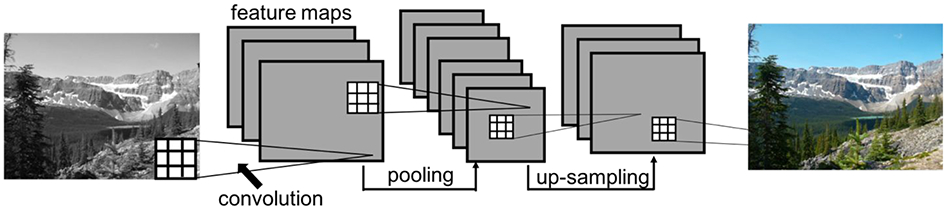
Example of a convolutional neural network (CNN) to predict image colors. The CNN takes the input image and estimates the red, green, blue components of the image, based on learned features extracted from the image by the convolution kernels. The square grids represent convolution kernels, which are made up of trainable weights. Each voxel in a feature map is the result of a convolution operation applied to the previous layer (illustrated by the connecting lines). An image processing CNN typically will have an encoder-decoder style architecture, which contains pooling layers followed by upsampling layers. In this didactic example, the network has 4 convolutional layers as well as a pooling layer (encoding) and an up-sampling layer (decoding). The CNN ultimately learns to synthesize a color image from a black and white image given many training pairs.

MR IMAGE RECONSTRUCTION

Current deep learning-based solutions in MRI for problems of artifact reduction, motion correction, and denoising generally fall into two categories: deep learning-based image reconstruction and deep learning-based image post-processing. Deep learning-based image reconstruction methods, which form the focus of this review, use multi-coil complex (magnitude and phase) raw data. On the other hand, there are also a significant number of efforts using deep learning-based image post-processing methods on coil-combined magnitude images. Post-processing, as defined here, is performed to enhance the image quality of an already reconstructed image. The two general approaches are both currently being explored to address similar problems in MRI (9,19-23) and ultimately may be complementary. The two approaches have different strengths: image reconstruction methods have the potential to tap an inherently richer corps of information that include phase and coil sensitivity data whereas post-processing methods take advantage of the simplicity of the inputs as well as a larger potential pool of training data and potentially less dependence on acquisition parameters and hardware. Thus, it is important to note that the two general approaches differ and are not interchangeable (Figure 2). The works included here relate to deep learning methods that tackle improving MR image reconstruction quality.

Figure 2.

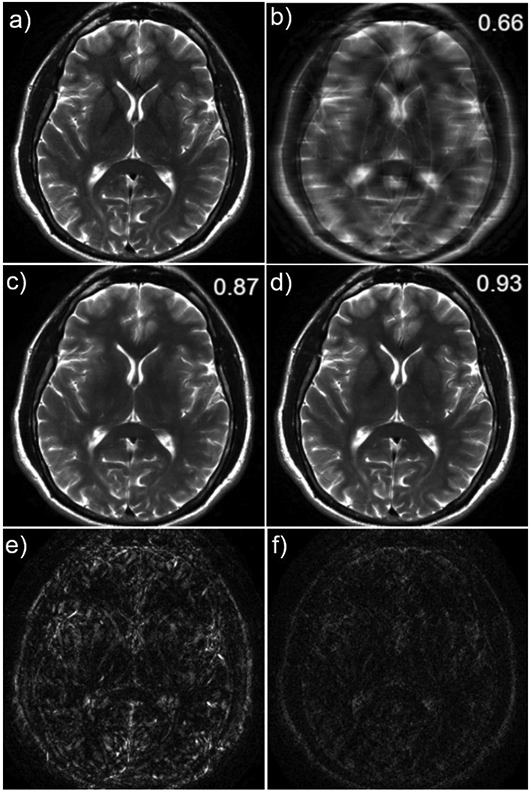
Example illustrating the difference between image post-processing and image reconstruction of a 4X accelerated T2-weighted brain image. These results were obtained using a convolutional neural network for image reconstruction (4) and a modified version of this network not utilizing the raw data for image post-processing. The fully-sampled reference is shown in (a), and the zero-filled reconstruction in (b). The image post-processing result is shown in (c) and the reconstruction result is shown in (d). The absolute errors are shown in (e) and (f). The displayed values are structural similarity index (SSIM) (60) – a measure of similarity between the network output and the target, in this case the fully-sampled image (a). SSIM values range from 0 to 1, where 1 indicates perfect agreement. In this example of generating high-quality images from under-sampled data, the result obtained from the image reconstruction tool utilizes information from the raw data and outperforms the post-processing tool. The reconstruction has fewer residual artifacts and less blurring with better preservation of important structures such as the globus pallidus. It has not been established in the literature whether image reconstruction will always outperform image post-processing, or vice versa, in other applications.

DEEP LEARNING IN SPARSE SAMPLING

MRI is an inherently slow imaging modality, limited traditionally by Nyquist sampling requirements. The problems of long acquisition times include: increased vulnerability to artifacts arising from motion, decreased patient comfort and ability to tolerate imaging, increased fixed costs associated with individual imaging studies resulting in an overall reduction in access to imaging at a population level. However, with conventional reconstruction procedures, sub-Nyquist sampling results in aliasing. Thus, it is no surprise that from the very advent of MRI, accelerating image data acquisition has been an active area of research.

A major development in accelerated acquisition is Parallel Imaging (PI) (24-26). With PI techniques, the sensitivities of multiple receive coils provide additional information for the reconstruction, allowing for successful reconstruction from sparser sampling. In brief, two common PI methods are generalized auto-calibrating partial parallel acquisition (GRAPPA), which is applied in k space as an interpolation procedure (24), and sensitivity encoding (SENSE), which is applied in image space using explicitly calculated coil sensitivity maps (25). Utilizing prior information in the form of regularization to solve an under-sampled reconstruction is a very common method of reconstruction, one simple example being partial Fourier. A particularly successful method for accelerating MR image data that uses a sparsity prior and incoherent sampling is compressed sensing (CS) (27). CS reconstruction is an extension of traditional iterative reconstruction methods, which estimate images from under-sampled data by enforcing data consistency and utilizing prior information in the form of a regularizer. Utilizing prior information in the reconstruction provides a constraint on the optimization and ultimately results in a better solution to the ill-posed reconstruction problem. Examples of this prior information are the assumptions that medical images are compressible (i.e. sparse in some spatial transform domain) and piece-wise constant.

Unfortunately, the reconstruction problems that PI and CS methods are designed to solve are themselves time-consuming. This is due in part to the fact that PI and CS approaches treat every examination and reconstruction task as a new, independent optimization problem. While reconstruction can be done off-line, ultimately clinical scenarios require speed for the reconstruction of individual scans. Deep learning methods are useful because they perform the optimization over many training images prior to solving the reconstruction for any particular given image. They can take advantage of common features of anatomy as well as the structure of undersampling artifacts that are present across the training images. With deep learning reconstruction, the optimization process is effectively then decoupled from the time-sensitive image reconstruction process for each individual study. Thus, for a new scan, unlike CS reconstructions which each require lengthy computation time, deep learning-based models can complete the reconstruction in seconds. It is for these reasons that several groups are now investigating the use of deep learning-based approaches to achieve accelerated, high-quality MRI reconstruction. Several techniques use deep learning to learn more effective regularization terms (prior information), and the approaches are derived from the concepts of GRAPPA, SENSE and CS. Like parallel imaging, deep learning techniques for reconstruction of sparsely sampled data can be applied both in k space or in image space.

Static Imaging

The variational network (VN) (28), the Model-based deep learning architecture (MoDL) (29), and deep density priors (DDP) (30) are all deep learning-based extensions of traditional iterative reconstructions. Traditional iterative reconstruction techniques, including CS, exploit prior information to compensate for missing k-space data; this information is applied in the form of a regularization term. Deep learning provides a method of learning this regularization term from a large amount of existing image data. Deep learning methods solve the image reconstruction problem from the undersampled k space by utilizing the additional spatial encoding offered by multiple receive coils, enforcing consistency with acquired data, and applying a trained CNN as the regularization term. The CNN is trained with fully-sampled and corresponding retrospectively undersampled data as training pairs. The VN, MoDL, and DDP methods have been successfully used to accelerate MR image reconstructions. Specifically, MoDL and DDP have been applied in brain imaging (29,30) and the VN in both MSK and abdominal imaging (10,28). In the following sections, we review some of the clinical applications and clinical uses of deep learning-based models for MR image reconstruction.

Brain Imaging

In neuroimaging, accelerated imaging can be especially useful in patients with altered mental status whose motion may compromise image quality or in longer imaging protocols with multiple sequences that can each increase total scan time. Aggarwal et al proposed a model-based approach for image reconstruction using deep learning called MoDL (Model-based deep learning architecture) (29) in the brain and showed superior performance of this algorithm in terms of peak signal to noise ratio when compared to CS across a wide range of acceleration factors (from 2 to 20).

Instead of using paired datasets of undersampled and fully sampled images, Tezcan et al proposed an alternative approach using unsupervised deep learning (30) and applied the method to a publicly available dataset of T1-weighted images of the brain, multi-coil complex images from healthy volunteers, and images with white matter lesions with resultant visually high-quality reconstructions and low root mean square error (RMSE) values that were superior to existing deep learning methods. Importantly, on images with white matter lesions, the method was able to faithfully reconstruct the lesions. In addition to not requiring paired datasets of undersampled and fully sampled images, another advantage of this method was less sensitivity to acquisition specifications such as sampling parameters, coil settings, and k-space trajectories.

Musculoskeletal Imaging

In musculoskeletal MR imaging, patients with pain or limited range of motion can have difficulty maintaining optimal imaging position. At the same time, however, musculoskeletal imaging is extremely demanding in terms of resolution, sharpness, and image quality. Accelerated acquisitions have the potential to minimize the need for repeat sequences and patient recalls for poor image quality. In Hammernik et al, a VN was applied to a clinical knee MRI imaging protocol (28). Testing various acceleration factors and sampling patterns using both retrospectively and prospectively undersampled MRI data, they showed VN reconstructions to outperform combined parallel imaging and compressed sensing (PI-CS) based on quantitative error measures like structural similarity index (SSIM) as well as in a clinical reader study. SSIM is a measure of similarity between the network output and the target image obtained from the coil-sensitivity combined fully sampled reconstruction, where values range from 0 to 1 and where 1 indicates perfect agreement. VN results for four-fold acceleration of a clinical knee and ankle protocol are shown in Figure 3.

Figure 3.

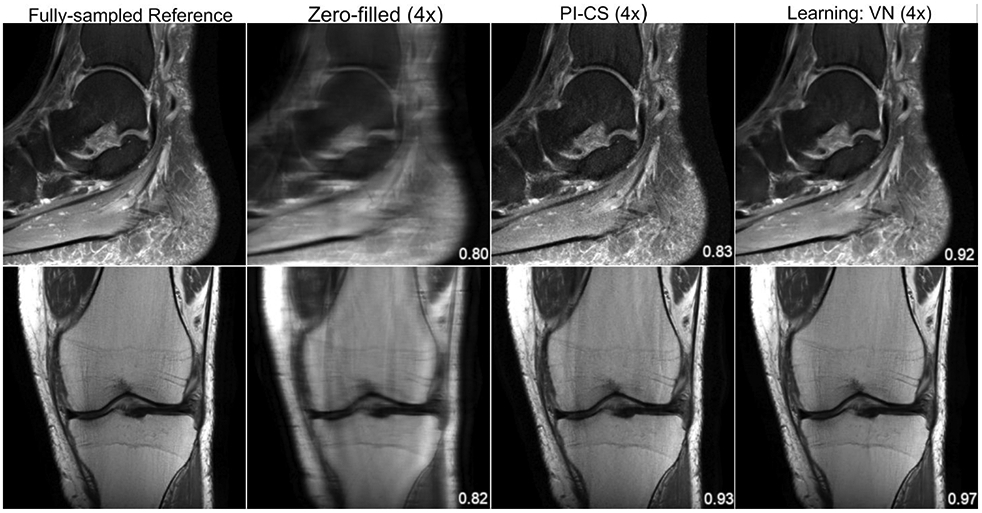
From left to right: A single slice of the reference, zero-filled, PI-CS and VN reconstructions of a sagittal, proton-density weighted, fat-suppressed ankle image (top) and a coronal proton-density weighted knee image (bottom). The displayed structural similarity index (SSIM) was calculated for the presented slice. The VN reconstruction has less noise amplification and residual artifact than the PI-CS reconstruction. The sequence parameters were as follows: ankle – sagittal fat-saturated proton-density (PD-FS): TR = 2800 ms, TE = 30 ms, turbo factor (TF) = 5, matrix size = 384 x 384, in-plane resolution 0.42 x 0.42 mm², slice thickness = 3.0 mm; knee – coronal PD: TR = 2750 ms, TE = 32 ms, TF = 4, matrix size = 320 x 320, in-plane resolution = 0.44 x 0.44 mm², slice thickness = 3.0 mm.

Abdominal Imaging

Acquisition acceleration has always been imperative in abdominal MRI due to the challenges of cardiac and respiratory motion and the limitations of patient breath-holds. Chen et al used a VN approach to accelerate the reconstruction of variable-density single-shot fast spin-echo (SSFSE) sequences to improve overall image quality and increase perceived signal-to-noise ratio and sharpness, compared to conventional PI-CS reconstruction (10). More recent work by the same group explored accelerated reconstruction of wave-encoded SSFSE imaging. While wave-encoded SSFSE improves image sharpness and reduces scan time compared to conventional SSFSE, this comes at the cost of the increased computation time necessary for self-calibration and reconstruction. Chen et al showed that a deep learning-based pipeline of trained self-calibration and reconstruction neural networks could decrease computation time and perceived noise for clinical abdominal non-Cartesian wave-encoded SSFSE imaging while maintaining image contrast and sharpness when compared to conventional self-calibration and PI-CS reconstruction (31).

Cardiac Imaging

Cardiac MR imaging, specifically coronary MR angiography (MRA), provides its own challenges, with motion inherent to the organ of interest as well as the requirement of extremely high spatial resolution. Therefore, evaluation of coronary artery luminal stenosis has traditionally required long, gated acquisitions. Fuin et al used a VN undersampled reconstruction approach to obtain free-breathing motion-compensated whole-heart 3D coronary artery MRA images (32), demonstrating improved image quality when compared to zero-filled and CS reconstructions (Figure 4). Using the VN approach, the authors were able to obtain high-resolution images (1.2 mm³ isotropic resolution) with substantially shorter scan times (acquisition time of ~2-4 minutes) and rapid computational speed (reconstruction time of ~20 seconds) compared with wavelet-based CS (average reconstruction time of 5 minutes).

Figure 4.

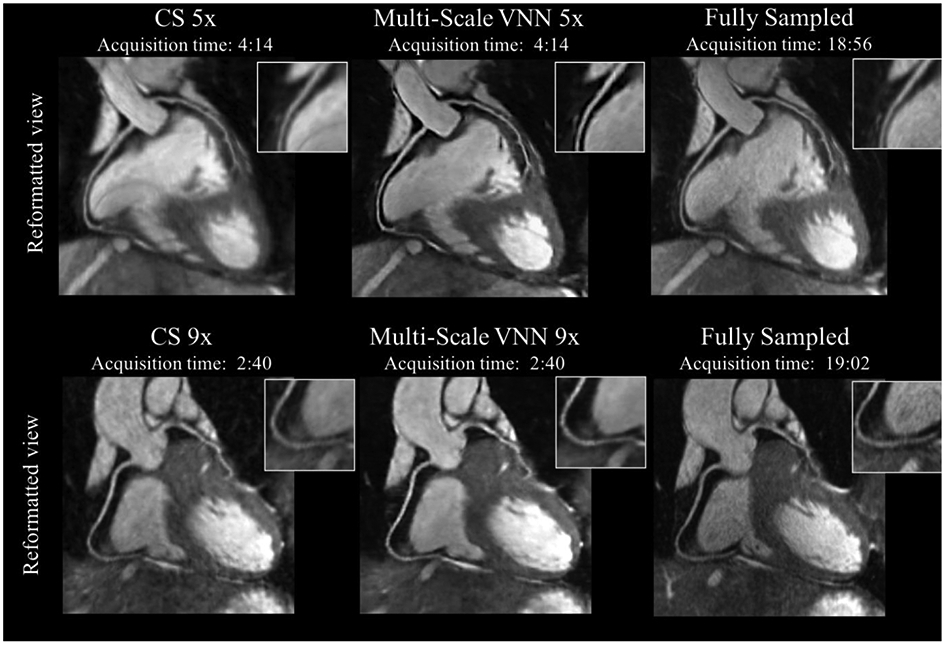
Coronary MR angiography (CMRA) images reformatted along the left anterior descending and right coronary arteries for two representative healthy subjects. Acquisitions were performed with isotropic resolution 1.2 mm³ and 100% respiratory scan efficiency (no respiratory gating). Prospective undersampled acquisitions with acceleration factors 5x (first row) and 9x (second row) are shown. Images were reconstructed using a Wavelet-based compressed-sensing reconstruction (CS) and a Multi-Scale variational neural network (MS-VNN) reconstruction framework. Corresponding (consecutively acquired) fully-sampled acquisitions are shown in the last column for comparison. MS-VNN provides higher image quality than CS for both acceleration factors, achieving similar image quality to the fully-sampled reference. The reconstruction of a whole 3D CMRA volume took ~14s with MS-VNN. In comparison, the reconstruction for Wavelet-based CS was 5 minutes on average. Figure courtesy of Claudia Prieto.

Robust Artificial-Neural-Networks for k-space Interpolation (RAKI)

Similar to parallel imaging methods that can be applied in both image space (SENSE) and k space (GRAPPA), deep learning techniques for image reconstruction can also be applied in both domains. The methods described previously apply CNNs in image space; it is also possible for deep learning techniques to be applied in k space. A technique called robust artificial-neural-networks for k-space interpolation (RAKI) (33) – a deep learning extension of GRAPPA – uses the fully sampled center of k space and interpolation to estimate unsampled k space lines. However, RAKI uses CNNs – trained from the fully sampled k-space center – as the interpolation function. Akcakaya et al demonstrated that RAKI outperforms traditional GRAPPA reconstruction for cardiac and brain imaging, particularly at high accelerations (rates of 5-6) (33). Example results using RAKI in simultaneous multi-slice (SMS) echo planar images (EPI) of the brain are shown in Figure 5. A unique aspect of this method is that it is scan-specific; the CNN is trained from the center k space lines of the same scan therefore obviating the requirement of large training sets.

Figure 5.

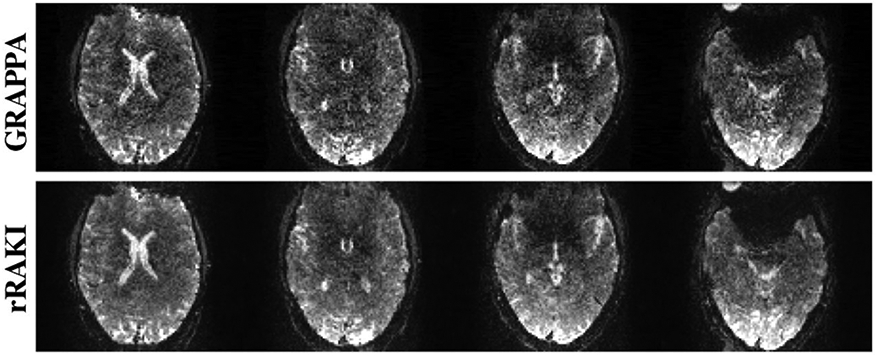
GRAPPA (top) and RAKI (bottom) reconstruction of simultaneous multi-slice (SMS) echo planar images (EPI) of the brain. SMS imaging acquires multiple slices at the same time (16 in this example) and is traditionally reconstructed with GRAPPA. RAKI reconstruction of SMS-EPI brain images outperforms GRAPPA reconstruction with decreased noise (61). Figure courtesy of Mehmet Akcakaya.

Generative Adversarial Networks (GANs)

A major challenge in deep learning is how best to define the loss function. In image reconstruction problems, minimizing a pixel-wise loss metric such as MSE does not always result in clinically useful or optimally realistic-appearing images; for example, images can achieve low overall MSE but also be diagnostically useless if they have high accuracy everywhere except in small but anatomically critical regions. Using deep learning reconstruction methods tried thus far, resulting images often appear over-smoothed, rendering such images easily distinguishable from those reconstructed conventionally (Figure 6). It is not yet clear whether and how such differences may impact diagnosis; however, in practice, this may lead to lower radiologist confidence in terms of clinical interpretation and could hinder adoption of these techniques to clinical practice.

Figure 6.

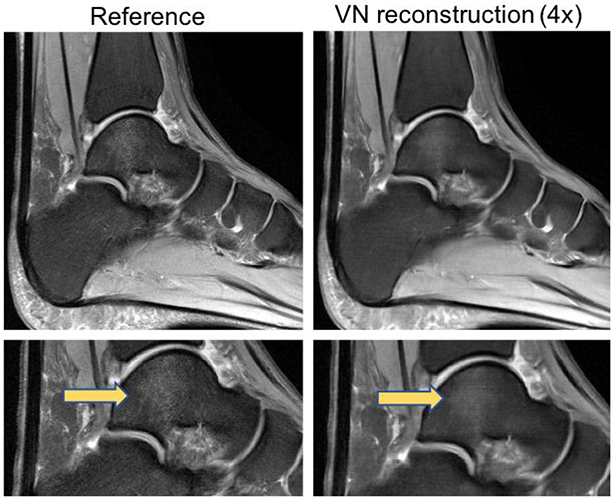
Example of oversmoothing from deep learning reconstruction. Sagittal fat-saturated proton-density weighted images of the ankle of the fully sampled reference (left column) and the VN reconstruction (right column) demonstrate the oversmoothed appearance that can occur with these deep learning reconstruction methods, rendering such images easily distinguishable from those reconstructed conventionally. Note the loss of detail of the normal trabecular architecture that is present generally across the entire image and the decreased conspicuity of the focal talar dome bone marrow edema (arrows) on the VN reconstructed image (bottom right). The bottom images are cropped and magnified from corresponding images in the top row.

As a result, some groups have explored the use of generative adversarial networks (GANs) (13,34,35), which incorporate a learned loss function. A GAN consists of two interacting networks: a generator and a discriminator, where the generator is an image reconstruction network like those previously discussed and the discriminator is a classifier network trained to distinguish between output from the generator and a true target image. The error in the discriminator (termed the adversarial loss), becomes an additional loss term in the optimization problem, which then enforces the generation of images that most closely mimic the appearance of standard images. The generator and discriminator are trained simultaneously, where the objective of the generator is to at once minimize the pixel-wise loss metric while maximizing the adversarial loss and the objective of the discriminator is to distinguish between generator output images and target images and minimize the adversarial loss. This concept is illustrated in Figure 7.

Figure 7.

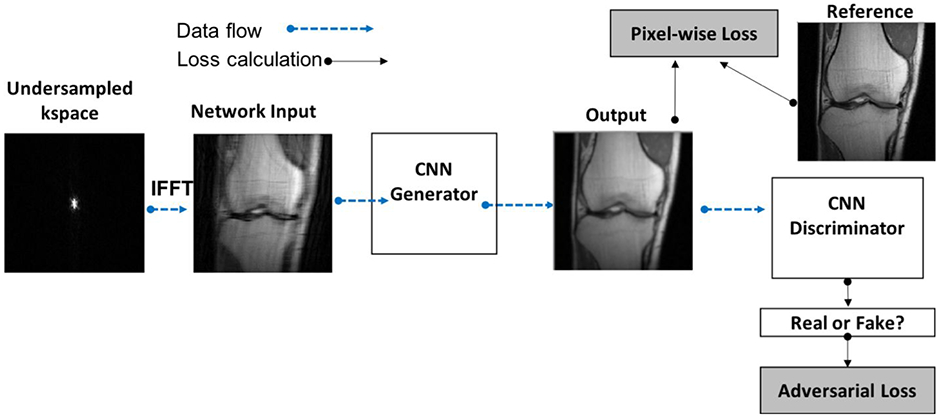
Flow chart illustrating a generative adversarial network (GAN). Every GAN is made up of two CNNs, a generator and a discriminator. Incorporating the adversarial loss forces the generator to produce images that are indistinguishable from target images. The methods described in Mardani et al, Quan et al and Yang et al all have this general architecture; the main difference between methods lies in how data consistency is enforced.

Automap

Automap (36) is a technique that learns the entire reconstruction procedure for undersampled data and makes no assumptions regarding physical reconstruction models. While both VN and automap have k-space input and image output, automap additionally learns the Fourier transform and coil combination – the complete mapping – whereas VN does not. The automap technique was applied to several complex and traditionally time-consuming reconstruction tasks including non-Cartesian and undersampled Cartesian reconstruction in brain images. The authors reported comparable or superior image quality compared with conventional methods though using far shorter computation time. Due to the global nature of the Fourier transform, the technique requires a fully connected layer before the CNN. A fully connected layer connects each element of the input k space to each element of the first network layer and substantially increases total number of model parameters. This puts some limitations on matrix size of images that can be reasonably processed. Additionally, there are overall limitations to flexibility of the network, as the network is trained for specific k-space locations.

Dynamic Imaging

Deep learning-based reconstruction approaches to sparsely sampled k space have also been applied to dynamic MRI, specifically cardiac imaging. The temporal component of dynamic imaging lends itself well to deep learning reconstruction applications. Schlemper et al developed a deep cascade of CNNs to reconstruct dynamic sequences of 2D cardiac MR from undersampled data, showing that their proposed method outperformed existing state-of-the-art 2D CS approaches in terms of both reconstruction error and reconstruction speed (37). When reconstructing individual frames from the dynamic sequence, the authors demonstrated that CNNs can learn spatio-temporal correlation by combining convolution and data sharing approaches, outperforming current methods in image quality with up to an impressive 11-fold undersampling.

Data sharing approaches allow for aggressive undersampling through the exploitation of spatio-temporal redundancies present in dynamic imaging. For example, the image content in pixels outside of the heart remain very stable from image to image across time. And even for a pixel that falls within the moving heart, the signal at any given moment is informed by the preceding and following signal in that particular pixel location. Thus samples from adjacent frames in a dynamic sequence can be used to fill missing k-space samples in the current frame. In subsequent work by the same group, Qin et al proposed a convolutional recurrent neural network (RNN) to reconstruct high-quality cardiac MR images from highly undersampled (6, 9, and 11-fold undersampled) k-space data. This approach embeds the structure of traditional iterative algorithms while leveraging the RNN’s ability to learn spatio-temporal dependencies across time sequences in order to achieve superior reconstruction accuracy and speed compared to 3D CNN and conventional CS-based methods (38).

REDUCING ARTIFACTS

Motion Correction

Recently, deep learning reconstruction techniques have been explored for motion correction of MR images (39,40). The methods presented in Oksuz et al and Haskell et al are both model-based reconstructions that enforce consistency with the acquired data. In Oksuz et al, motion correction was performed in cine SSFP cardiac magnetic resonance images (39). They developed an artifact detection network that identifies motion-corrupted k-space lines, for example due to triggering errors or arrhythmias. The corrupted lines are removed and zero-filled with the problem then transforming to an undersampled reconstruction task, where the recurrent CNN described in Qin et al (38) is then used for the reconstruction task. Haskell et al introduced network accelerated motion estimation and reduction (NAMER), a model-based reconstruction that jointly performs motion estimation and solves for the motion-corrected image (40). Motion correction was performed on 2D T2-weighted rapid acquisition with refocused echoes (RARE) images of the brain. Example results are shown in Figure 8.

Figure 8.

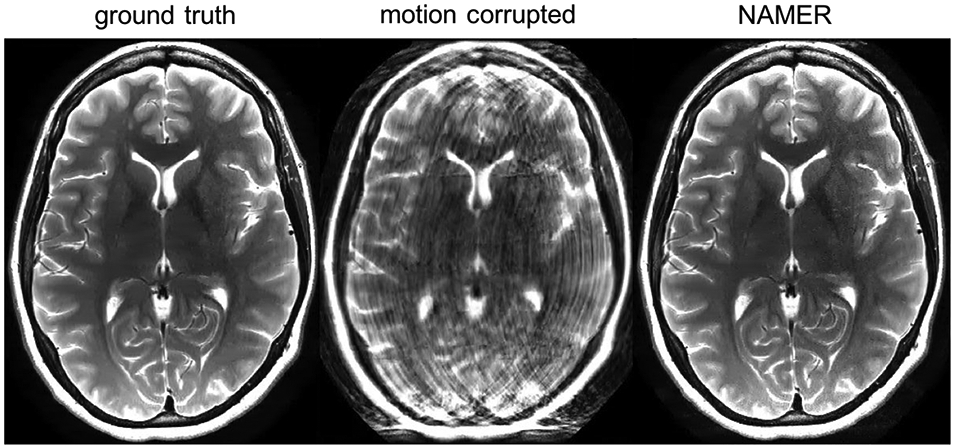
NAMER motion correction of a 2D T2-weighted brain image. Figure courtesy of Melissa Haskell.

Eddy Current Correction

Echo planar imaging (EPI) is a commonly applied MR sequence; it offers high temporal resolution and is useful in brain imaging for diffusion-weighted imaging and functional MRI. A single shot EPI sequence works by using a single RF pulse with an alternating readout gradient to acquire all of k space by changing direction with each echo in odd and even lines. A consequence of the rapidly changing gradient, however, is the induction of eddy currents within the coils and magnet housing. These eddy currents create local fields that distort B₀ and cause phase mismatch between the odd and even echoes, leading to ghost artifact.

EPI ghost artifacts are traditionally corrected by acquiring an additional reference or calibration scan, resulting in longer overall scan time. Conventional correction methods also produce suboptimal results related to difficulties accounting for nonlinear and time-varying field inhomogeneity, especially at high field strength. Based on concepts derived from recent work that reframes ghost correction as a k-space interpolation problem, Lee et al designed a k-space deep learning approach to correct the phase mismatch without a reference scan in both accelerated and non-accelerated EPI acquisitions (41). Reconstruction of in vivo brain imaging data at 3T and 7T using their proposed method outperformed existing methods in image quality defined as ghost-to-signal ratio with rapid computation time (Figure 9).

Figure 9.

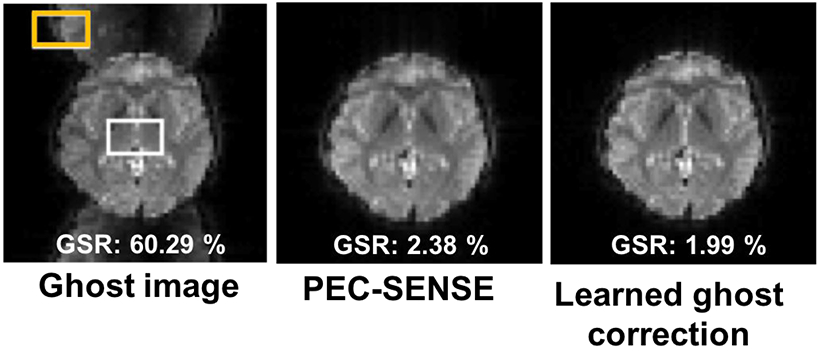
Ghost correction results of 3T GRE-EPI in vivo data demonstrating improved image quality defined as ghost-to-signal ratio (GSR), when comparing the learned ghost correction and phase error correction with sensitivity encoding (PEC-SENSE), a conventional method of ghost artifact correction. The lower the GSR value, the better the image quality. Example ROIs for ghost and signal values are depicted by the orange and white rectangles, respectively. Figure courtesy of Jong Ye.

PET/MR ATTENUATION CORRECTION

In PET (positron emission tomography), an accurate attenuation map is required for correction of both photon attenuation as well as photon scattering, and this attenuation map is typically derived from CT. Though there are advantages to soft tissue delineation using PET/MR, one major challenge of PET/MR hybrid imaging is achieving accurate attenuation correction without a concurrent CT. For example, on MRI, bone and air demonstrate near identical signal characteristics though they differ obviously in attenuation characteristics, leading to problematic, suboptimal PET reconstructions and systemic errors in PET standard uptake values (SUV). Some MR imaging advances such as short- or zero-echo-time imaging, in which bone carries signal, show promise as a potential solution (42-46), but overall, accuracy of attenuation correction remains a factor contributing to limited translation of PET/MR to clinical practice.

Several authors have shown that deep learning models can be used to synthesize “pseudoCT” from MR images for the purpose of attenuation correction (47,48). Essentially, the solution to the PET attenuation-correction problem in PET/MR is a deep learning image synthesis step. In pelvic PET/MRI, Leynes et al trained a deep network to transform zero-echo-time and Dixon MR images into pseudoCT images and found that the resultant images were “natural-looking”, quantitatively accurate, and led to reduced error in attenuation correction when compared to standard methods (43). In the brain, Liu et al developed a deep learning approach to generate a pseudoCT from 3D volumetric T1-weighted MR images with decreased PET reconstruction error when compared to existing MR-based attenuation correction approaches (49). Even more recently, the same group of authors and others, have explored whether any sort of anatomic imaging is necessary (CT or MR) for attenuation correction, demonstrating the feasibility of training a network from non-attenuation corrected PET imaging alone to synthesize pseudoCT images (50,51).

CHALLENGES AND LIMITATIONS

Training Requirements and Dataset Availability

Despite considerable advances and the promise that deep learning methods hold for MR image reconstruction, significant challenges remain. Training high model capacity CNNs for image reconstruction, depending on the task at hand, may require large amounts of diverse training data. Without a sufficient training set, as with any machine learning algorithm, these networks could overfit training data and not perform well on unseen data. For some applications such as undersampling and denoising reconstructions, synthetic data can be relatively easy to generate though this may not be the case in other situations, for example in cases where realistic artifacts are difficult to predict.

Availability of datasets in medical imaging can be limited due to privacy and ethical concerns and in the specific context of MR image reconstruction problems, currently there are very few publicly available databases containing multi-channel raw k space data. Access has thus far been somewhat limited to those at major academic medical centers, hindering progress in the field. Collaboration with the greater machine learning community would be useful. Recent initiatives such as the fastMRI dataset (https://fastmri.med.nyu.edu/) and mridata.org have started to address this need, but more data sharing is required to adequately train and compare new models.

Unique Nature of MRI and Medical Data

Thus far, there are only a small number of published studies using deep learning methods on k space data for MR image reconstruction. Despite recent major advances in computer vision and image processing using natural images, the techniques often are not easily applied to k space. Furthermore, the scale of training examples of natural images that are available are on the order of millions for deep learning computer vision problems (14,52) and dwarfs the number of training examples of medical images available. Another major difference between medical image reconstruction and image restoration in computer vision problems is how quality is best defined. For medical imaging problems, the best quality metric may ultimately be task-based (diagnosis) rather than generic performance metrics such as peak SNR or SSIM.

Generalizability and Interpretability

Major questions remain as to how specific trained models must be. It is not yet known whether a single model can be trained for a variety of MR exam types or whether separate models are required for different sampling trajectories, acceleration factors, coils and coil configurations, field strengths, pulse sequences, or anatomical regions. In clinical practice, scan parameters are tailored for body part imaged, for individual patient characteristics (e.g., body habitus, pediatric), as well as clinical indication (e.g., headache protocol differs from brain tumor follow-up); however, it is not clear how differences in scan parameters might affect a model’s performance. In addition, failure modes of these models may be unpredictable; for example, while it has been shown that deep learning reconstructions can perform well with changes in image contrast between training and test data, they can be vulnerable to systematic deviations in SNR (11).

Systematic differences in data distributions between institutions, imaging sites, and scanners may prohibit direct translation of trained models across the board. There are limited reports on how well deep learning-based reconstruction techniques transfer between sites and scanners. An additional limitation, is the difficulty in interpreting trained models. Trained CNNs are complicated, interconnected and high dimensional representations with predictions based on features that are often too abstract to really understand. This leads to some concern that deep learning-based image reconstruction methods could behave in unexpected ways under new or unusual scenarios such as might occur in the case of rare pathologies or anatomical abnormalities. The challenge of obtaining large, diverse and well-curated training datasets remains. Estimates of network uncertainty might be helpful in assessing validity of the image produced. Therefore, continued and extensive validation of deep learning models and a thorough understanding of their generalizability and their limitations will be necessary in order to incorporate such schemes into clinical practice.

FUTURE PERSPECTIVES

The challenges and limitations outlined in the previous section at once sketch out the opportunities for future research. The key next steps are: continued sharing of image and raw k space datasets to expand access and allow for model comparisons, defining the best clinically relevant loss functions and/or quality metrics by which to judge a model’s performance, examining perturbations in model performance relating to acquisition parameters, and validating high-performing models in new scenarios to determine generalizability. In addition, how reconstruction approaches from k space may dovetail with deep learning efforts in image post-processing in the image domain will surely prove powerful.

Convenient or not, noise removal is often an unintended consequence of most of the deep learning image reconstruction techniques described previously. With an objective to minimize pixel-wise error metrics such as MSE, there is incentive for the network to generate a denoised version of the target image. Denoising in MR is a potential task that could be tackled with deep learning reconstruction approaches. Kobler et al have taken advantage of this characteristic of deep learning-based reconstruction methods to specifically tackle denoising in CT (53). We have also found this to be a promising approach in MR in an experimental model (Figure 10), which could be explored in future research.

Figure 10.

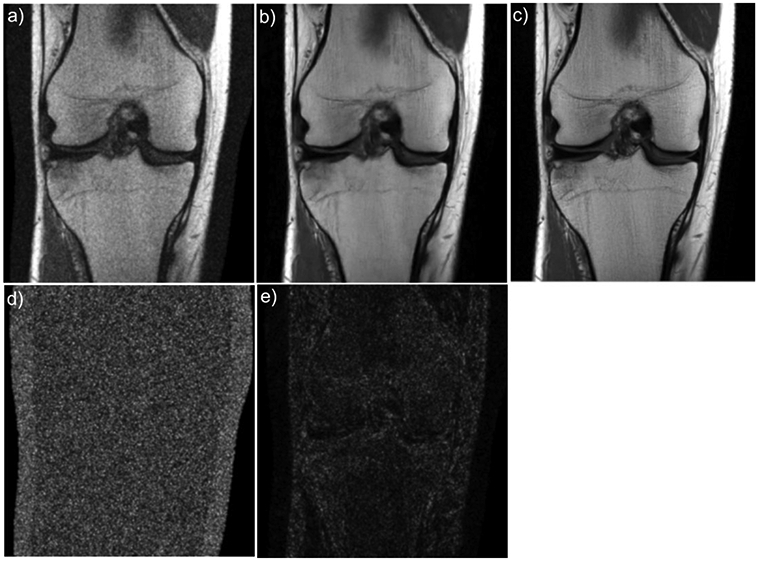
Example VN image denoising result. In these experiments Gaussian noise was added to coronal proton density weighted knee images and the noisy/clean image pairs were used to train the VN. The network was trained using the Adam optimizer with a learning rate of 1x10-3 and a batch size of 1 for 20 epochs. A coronal proton-density weighted image of the knee with added noise (a), the network output (b), and the target image (c). The absolute value of the difference between the target and noisy images and between the target and network output are shown in (d) and (e), respectively.

Super-resolution is the process of recovering or estimating a high-resolution image from a low-resolution image (54). In medical imaging, it can improve image resolution without requiring changes in imaging hardware or scan protocols. Present literature on super-resolution CNNs in medical imaging use post-processing methodologies in organ systems and modalities that require high levels of fine detail such as chest radiography (55), mammography (56), and musculoskeletal MRI (57,58). Translation of current deep learning MR reconstruction approaches to super-resolution is a promising technique that merits further investigation. Super-resolution in MRI has similarities to sparse sampling discussed previously; however, instead of uniform undersampling of the entire k-space volume, the sampled region would include only the low-resolution center lines of k space. Figure 11 shows the difference between the two approaches in the context of k-space sampling, and a simple experiment comparing super-resolution reconstruction and traditional accelerated reconstruction with uniform undersampling is shown in Figure 12. Typical accelerated reconstruction techniques with uniform density undersampling can be thought of as interpolating missing image information whereas super-resolution would be extrapolating this information, which may be more challenging.

Figure 11.

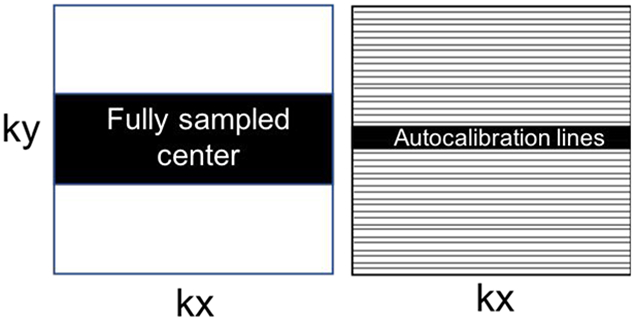
Illustration of k-space sampling patterns for super-resolution (left) and sparse sampling (right). The black regions and lines represent acquired k space lines. The white regions are zero-filled.

Figure 12.

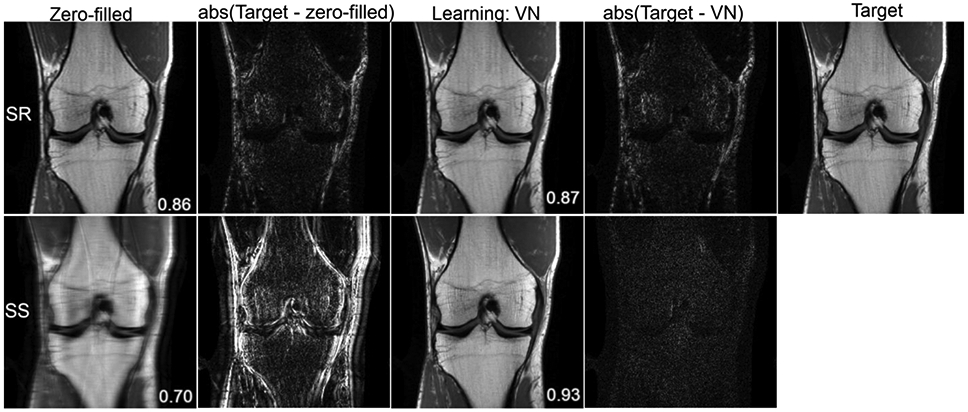
Reconstruction results of a 3x accelerated coronal proton-density weighted knee image for super resolution (SR) and sparse sampling (SS). The displayed structural similarity index (SSIM) values and difference images are provided for the presented slice. The variational network, implemented in Pytorch, was trained on 20 proton density weighted coronal knee images with the two sampling patterns illustrated in Figure 11. The network was trained using the Adam optimizer with a learning rate of 1x10-3 and a batch size of 1 for 30 epochs. One of the undersampling patterns is consistent with an acceleration factor of 4, where 24 center lines were acquired along with every 4th line outside the center region. The other undersampling pattern had the same number of acquired lines, restricted entirely to the center of k space. An alternative to regularly spaced undersampling is non-uniform undersampling, typically used with compressed sensing applications. Previous work has shown that uniform and non-uniform undersampling perform comparably for deep learning reconstructions (28,54).

Hybrid techniques may ultimately be powerful in deep learning reconstruction approaches. One advantage of neural networks is the ability to stack algorithms together. There may also be potential synergy that could be achieved between deep learning-based image reconstruction methods and deep learning-based image post-processing methods, between MR image reconstruction methods and CT image reconstruction methods, and projection or adaptation of one modality to a different modality domain. For example, Han et al exploited similarities between sparse-view CT and accelerated radial MR to remove artifacts from undersampled radial MR images (59). Based on the ability to convert radial k space data into sinogram data corresponding to the CT domain, the authors essentially employed transfer learning to augment a small radial MR dataset with pre-training on a large CT dataset and thereby adapted a network trained in the CT domain for the task of radial MR image restoration.

CONCLUSION

In summary, we have provided a basic overview of the clinical applications for state-of-the-art deep-learning-based MR image reconstruction methods. Deep-learning-based image reconstruction shows considerable promise to accelerate both static and dynamic MR imaging and to address imaging artifacts including aliasing, motion, and ghosting. Current models are applicable across a variety of clinical MR imaging applications from neuroimaging to abdominal, cardiac, musculoskeletal, and hybrid PET/MR imaging, each posing its own unique challenges and may require customization of solutions. Deep learning models for MR image reconstruction have the potential to shift the paradigm in terms of breadth of MR applications if substantial decreases in acquisition time and improvements in image quality can be realized.