Genetic growth potential, rather than phenotypic size, predicts migration phenotype in Atlantic salmon

Abstract

Knowledge of the relative importance of genetic versus environmental determinants of major developmental transitions is pertinent to understanding phenotypic evolution. In salmonid fishes, a major developmental transition enables a risky seaward migration that provides access to feed resources. In Atlantic salmon, initiation of the migrant phenotype, and thus age of migrants, is presumably controlled via thresholds of a quantitative liability, approximated by body size expressed long before the migration. However, how well size approximates liability, both genetically and environmentally, remains uncertain. We studied 32 Atlantic salmon families in two temperatures and feeding regimes (fully fed, temporarily restricted) to completion of migration status at age 1 year. We detected a lower migrant probability in the cold (0.42) than the warm environment (0.76), but no effects of male maturation status or feed restriction. By contrast, body length in late summer predicted migrant probability and its control reduced migrant probability heritability by 50–70%. Furthermore, migrant probability and length showed high heritabilities and between-environment genetic correlations, and were phenotypically highly correlated with stronger genetic than environmental contributions. Altogether, quantitative estimates for the genetic and environmental effects predicting the migrant phenotype indicate, for a given temperature, a larger importance of genetic than environmental size effects.

1. Introduction

Environmental versus genetic determinants of developmental transitions between life stages are a major topic in ecological and evolutionary studies [1–3]. Generally, both the environment and genes are assumed to underlie the expression of plastic developmental phenotypes [3], but the relative contribution of each often remains unknown [4,5]. However, knowledge of environmental versus genetic contributions underlying life-stage transitions is pivotal to making accurate ecological or evolutionary predictions under environmental change, such as global warming [5,6]. A major life-stage transition in many species is associated with feeding or reproduction migrations, whereby the migrant phenotype, as opposed to the resident phenotype (defined as individuals not migrating during a particular season [7]), may express in only part of the population, or vary with age [8,9]. Even though such partial migration, or variation of migrant age, is assumed to have considerable ecological and evolutionary consequences [8–10], evidence for major underlying genetic effects is scarce or controversial [11–13]. Nonetheless, selection and crossing experiments in birds and fishes indicate a heritable genetic basis [8,14], but for fishes, underlying mechanisms remain elusive (reviewed in [14]). To disentangle environmental from genetic components of binary traits, including migration phenotypes, the threshold model may be appropriate [10,15]. The threshold model assumes that the expression of categorical phenotypes underlies a (usually unobserved) continuous liability [16–18]. Only if the liability, influenced by both environmental and genetic effects, exceeds one (or several) threshold(s) during a sensitive period is the developmental transition towards the alternative phenotype(s) initiated.

In many fish species the age of the developmental transition towards the migratory phenotype also shows considerable variation. In salmonid species, such as salmon, trout, charr and whitefish, the age when the freshwater-hatched fish migrate to the sea (or larger water bodies, such as lakes) varies considerably, encompassing one to eight years in Atlantic salmon (reviewed by [19]). Importantly, within a population, older migrants are usually larger than younger migrants, whereby body size increases salinity tolerance and predator avoidance ability [4,19,20]. As a result of the latter, size at seaward migration, both within and across migrant ages, often covaries with migration survival [4,21–23].

Whether an Atlantic salmon of a given age undergoes the required developmental transition to become a migrant (smolt) in the following spring has long been suggested to be determined by body length in the previous summer or autumn (reviewed in [19]). Therefore, and because the liability remains unknown, body length is often used as an a priori liability proxy, and many previous indirect estimates for genetic migration phenotype variation stem from investigations on such proxies (reviewed in [24]). However, the liability proxy trait variation as relevant to initiating the developmental transition is expressed well in advance of the actual migration [25], as is suspected for many other developmental transitions [26]. Such a time lag poses logistical challenges not only for organisms after they have adopted a developmental transition, but also for researchers studying a dynamic liability proxy. It is thus unsurprising that—despite considerable knowledge on the physiological changes and underlying mechanisms during the transition [27]—exact mechanism initiating the transition from the resident towards the migrant phenotype remain unknown.

Even though body size may be a useful proxy determining whether the migrant phenotype is initiated, it may provide an inappropriate liability proxy in many cases. Specifically, initiation of the migrant phenotype triggers additional growth differences between prospective migrants and residents (which may migrate at older age in Atlantic salmon) that increase their size differences, thereby blurring cause and effect. During the transition, prospective migrants express accelerated growth relative to residents, which results in size bimodality and culminates in migrants being larger than residents at the time of migration, both among and within families [25,28–32]. Similar confounding between causes for and effects of the transition towards the migrant phenotype apply to inferences about body condition. Probably owing to these methodological challenges, past inferences about effects on migration phenotypes were often based on size records from any time between presumed growth acceleration and the time of migration (reviewed in [24]), and thus statistical associations between size and migrant probability are inconsistent across studies.

Here, we overcome a number of the abovementioned limitations and use Atlantic salmon as a model to investigate environmental and genetic determinants for the probability to exhibit the migrant phenotype in the second spring (hereafter called migrant probability; MIG), focussing on body size at the end of the first summer as a liability proxy. Specifically, we combined longitudinal common-garden experimentation in two water temperatures and two feeding regimes with quantitative genetic methodology. We followed development of 663 individuals from 32 pedigreed Atlantic salmon half-sib families until their second spring, when we assessed migration phenotypes (figure 1). We used uni- and bivariate models to test for environmental effects of water temperature, feeding regime, body condition and male maturation on MIG. Further, we tested within and between two environments with a 2°C seasonal temperature difference, whether body length covaried with MIG and partitioned this covariance into environmental and genetic components. Our results support a long-suspected strong genetic joint governance of body size in late summer with migration phenotype in spring, which we demonstrate to be extremely stable between two temperature environments. These results widen our understanding of genetic and environmental importance in developmental transitions, as well as their thermal stability, thereby providing quantitative primers for future modelling relying on environmental versus genetic relationships among life-history traits across environmental temperatures (e.g. [33]).

Figure 1.

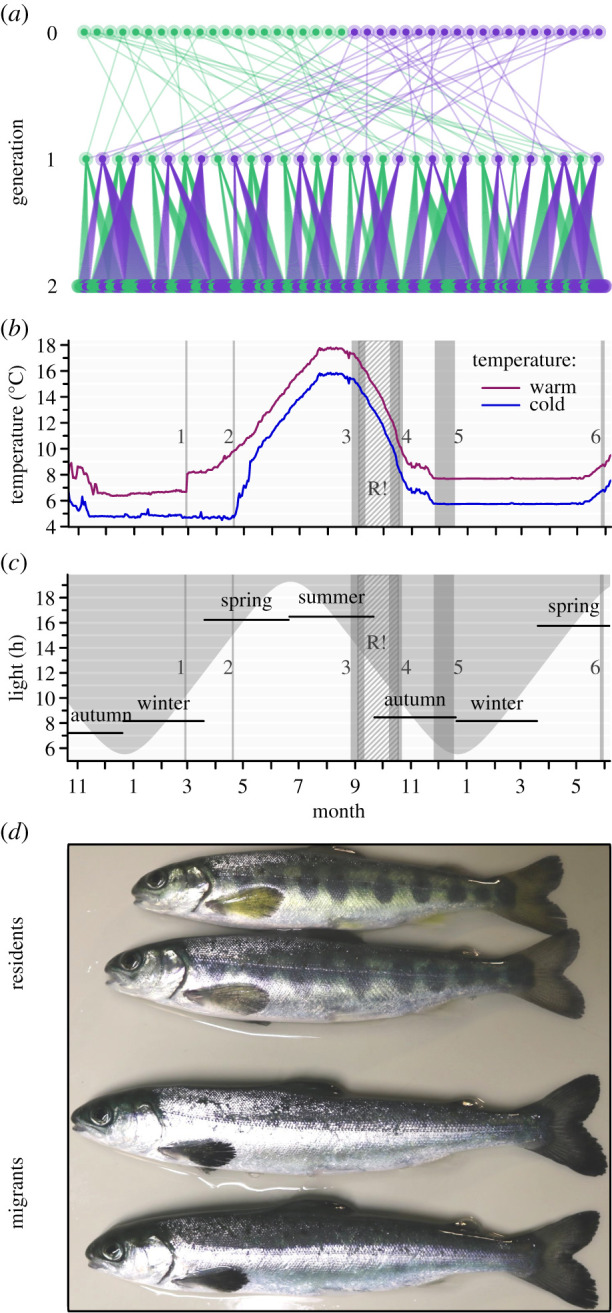
Pedigree (a) depicting relatedness among experimental individuals (generation 2) and the 2 × 2 partial factorial breeding design of parents (generation 1) with females in green (appearing on the left in generation 0) and males in purple. Seasonal water temperature (b) and light-regime curve (c) with experimental timeline and data collection time points indicated (1 & 2: first feeding in warm and cold environments, respectively; 3: determination of length and mass, followed by the feed-restriction period indicated by the grey hatched rectangle marked with R!; 4: determination of length and mass after the feed restriction period; 5: determination of maturation status; 6: determination of migration phenotype). Picture of typical phenotypes of residents and migrants in spring (d). (Online version in colour.)

2. Material and methods

(a). Experimental population and settings, and data collection points and routines

In October 2017, we created 32 half-sib families (generation 2) by crossing 32 parents (generation 1) in eight 2 × 2 factorials of unrelated individuals (figure 1a). The parents originated from a broodstock (generation 0) that was hatchery raised, maintained by the Natural Resources Institute Finland, Taivalkoski, Finland, but whose individuals successfully completed a sea migration (Oulu River; described in [34]). We created and reared the experimental cohort commonly in a newly established laboratory with two similar water recirculation systems at the University of Helsinki, Finland, controlled for water temperature, oxygen, dissolved nitrate components and light. We incubated eggs and larvae in vertical incubators with two replicates per family and temperature environment. At first feeding, we pooled same-temperature family replicates and randomized an equal number of individuals from each family (3–7) to each of eight similar 250 l tank replicates per temperature environment (i.e. all families in all tanks). The fish were part of other studies, of which one required lethal sampling [35], reducing fish numbers continuously. After sampling and natural mortality, 663 individuals yielded data for migration status in May 2019 (393 in cold and 270 in the warm environment, respectively). Water temperature in egg incubators and tanks was controlled to follow a seasonal cycle, approximating a 2°C difference referred to hereafter as ‘warm' and ‘cold' temperature treatments (warm, range: 6.3–17.7°C; cold, range: 4.1–16.0°C; figure 1b). Tank illumination, using fluorescence lights (4000 K, 35 W; 500 Lux at the surface) and controlled by a digital astronomical time switch (without dimming), followed the natural cycle at 61.054° (latitude) and 25.042° (longitude) (figure 1c).

Fish were fed a commercial salmon diet ad libitum with particle sizes meeting fish-size compositions at all times (start dates: figure 1b). In August 2018 (warm) and September 2018 (cold), we anaesthetized individuals (using methanesulfonate), inserted passive integrated transponder tags (into the body cavity; 12 mm) to enable re-identification, and fin clipped individuals to allow for genotyping. After fasting fish for 24 h, we measured fork length (±1 mm) between August and September 2018—around the time of day lengths suspected to characterize the sensitive period when migration status initiation is determined (figure 1c; 15–12 h) [30]. These measurements were followed by a feed-restriction treatment period (either ad libitum feeding for 7 days per week, or ad libitum feeding for 2 days per week with no feeding for two or three days between feedings) that was crossed with the temperature treatment for a five-week period per tank (September–October 2018; figure 1b,c). We again fasted and re-measured fish after the feed-restriction treatment in October. We determined maturation status in December 2018 (during the natural spawning period), when we categorized males as mature when observing milt during gently pressing the abdomen (females rarely mature at this age). We determined migration status in May 2019 (during the population-specifc period of highest migration success; [34]; figure 1b), when we categorized individuals as first-year migrants when showing darkened fin edges, lack of colour patches (parr marks) and enhanced body silvering (figure 1d). We categorized individuals as residents when not displaying signs of the migrant phenotype at this time. It should be noted that many Atlantic salmon remaining resident at 1 year of age may become migrants in later years [4], and therefore the resident category also includes potential later year (older) migrants. However, it is also possible that residents, especially males, can reproduce without migrating [4,36].

(b). Pedigree construction

We determined genotypes of parents and experimental individuals using a multiplex-PCR for 177 single nucleotide polymorphisms (SNPs) of an established panel [37], and by sequencing using an Ion Torrent (984 broodstock individuals from which we drew parental individuals) or Illumina platform (MiSeq or Next-Seq) (parental individuals, experimental individuals). Using unlinked, polymorphic SNPs, we reconstructed grandparents of the experimental individuals (with 131 usable SNPs) under maximum likelihood [38], which we combined with knowledge about the crossing scheme used to create the parental generation, and assigned the experimental individuals to their 32 parents (with 141 usable SNPs) with a likelihood approach [39], resulting in a three-generation pedigree (figure 1a). On this pedigree, we based the inverse relationship matrix (A⁻¹) used to infer additive genetic variance via animal model analyses [40] described below.

(c). Statistical analyses

To test model terms and estimate means and (co)variance components for MIG and LEN, we used uni- and bivariate generalized animal models with probit link function for MIG, corresponding to animal threshold models [41]. The models were fitted with the R package MCMCglmm [42] using Bayesian Markov chain Monte Carlo simulations, which appear an appropriate method for animal models on categorical data [41,43]. Initially, we fitted a univariate linear model:

$$\begin{array}{rl}& y=\mu +\text{Feed}+\text{Temp}+\text{Feed: Temp}+\text{Mat}+\text{Feed: Mat}+\text{Dam}\\ & +\text{Animal}+\text{Tank}+\text{Residual},\end{array}$$

where y is the liability for migrant probability, μ a model constant, Feed the fixed feed-restriction environment effect (full, restricted), Temp the fixed temperature restriction environment effect (cold, warm), Mat the fixed male maturation effect (0, 1), Feed:Mat the fixed interaction effect of the feed restriction with the maturation effect (restricted to the warm environment), Dam the random dam effects (n = 32), Animal the random additive genetic effects (736 entries in A⁻¹), Tank the random tank effects (n = 16) and Residual the random residual effects (n = 663). We also extended a reduced version of the univariate model (see results) by including body length in late summer as a continuous covariate (‘length', a predictor; log-transformed, mean centred and variance scaled), which we interacted with the temperature treatment. We also extended the reduced univariate models to test whether MIG differed among genotypes of a locus (vgll3) that has been shown to have a strong effect on male maturation probability in this experimental population [35], but we did not detect vgll3 effects, either when controlling or not controlling for phenotypic length in late summer (electronic supplementary material, table S1). We estimated all variances conditional on temperature environments with 2 × 2 covariance matrices between environments for dam (D) and animal (G) effects and diagonal covariance matrices for tank (C) and residual (R) effects. We fitted bivariate models by extending the reduced model (without the length covariate) with body length in late summer as a second response (‘LEN', ‘length' as a response). For the bivariate model, we additionally allowed for between-trait covariances.

We ran univariate and bivariate models for 1 500 000 and 6 000 000 iterations, respectively, and sampled every 100 iterations. For each model, we ran four chains and determined (i) whether the MCMC sampling had converged as indicated by a scale reduction factor around 1 per chain [44], (ii) the required number of samples to discard (burnin) until consistently reaching a scale reduction factor less than 1.1 across chains [44], (iii) required thinning to have autocorrelations at lag 2 < 0.1 per chain, and confirmed whether MCMC resulted in sufficient mixing using visual examination of trace plots per chain. These criteria resulted in subsequently combined posteriors across chains with sample sizes between 8000 and 22 000. We conducted a prior sensitivity analysis as reported in the electronic supplementary material (electronic supplementary material, figures S2–S4). We tested feed-restriction treatment effects on growth rate by a general animal model and predicted the sexual maturation rate using a generalized animal model (electronic supplementary material, table S2, figure S1 and table S3, respectively).

(d). Derived parameters

We calculated heritability as the proportion of additive genetic variance (V_A) to the total phenotypic variance (V_P). Under the threshold model interpretation of generalized model estimates that include common environmental variance (V_C), residual variance fixed to 1 (V_R) and a variance of 1 for the probit link function [45], this results for MIG in

$$h^2=\frac{V_A}{V_P}=\frac{V_A}{V_A+V_C+V_R+1}.$$

We estimated correlations at the phenotypic (R_P), residual environmental (R_E) and genetic levels (R_G) as in [46], but additionally accounted for common environmental effects on R_P. To translate liability estimates to the proportional scale, we used either the ‘predict.MCMCglmm' function of the MCMCglmm R package or (for heritabilities) the ‘QGmvparams' function of the QGglmm R package [45]. We present mean estimates with credible intervals (95% highest posterior density estimates of model posteriors).

3. Results

(a). Migrant probability is not affected by a temporary feed restriction, male maturation or maternal effects

Using a univariate generalized animal model and not controlling for phenotypic body length, we detected that MIG was higher in the 2°C warmer environment (table 1). However, although the feed restriction reduced the specific growth rate by about 50% (electronic supplementary material, table S2, figure S1), MIG was not affected by this restriction (table 1). MIG was also not affected by male sexual maturation, which occurred only in males in the warm environment at a rate of 0.19 (95% CI: 0.08–0.33; electronic supplementary material, table S3), nor by any interaction term (table 1). We also did not detect any maternal (dam) or common environmental (tank) effect variance on MIG (table 1). We therefore removed dam, but not tank effects, from models because the latter constitute the experimental replicates for the temperature environments.

Table 1.

Model mean posterior estimates (on the liability scale), lower and upper 95% credible intervals, and number of effective samples (N_eff) for the initial univariate generalized animal model on migration phenotype binaries of 663 Atlantic salmon individuals from 32 half-sib families. Variances were modelled as either diagonal (tanks, residuals) or unstructured (dams, animals) covariance matrices for the two temperature environments. Residual variance was fixed to 1 in each environment, resulting in scaling of all components relative to the residual variance. Effects or variances different from zero (i.e. credible interval not including zero) are in italics.

term	mean	lower	upper	Neff
mean effects
model intercept	−0.467	−1.325	0.423	15 392
temperature (cold–warm)	1.942	0.988	2.920	13 242
feed (full–restricted)	−0.010	−0.687	0.677	14 000
maturation (immature–mature)	1.147	−0.892	3.161	14 669
feed:temperature	−0.514	−1.607	0.537	14 000
feed:maturation	−1.130	−3.536	1.151	14 000
variance effects
tank cold	0.127	0.000	0.455	13 432
tank warm	0.166	0.000	0.608	14 000
dam cold	0.182	0.000	0.691	13 359
dam cold,warm	0.046	−0.139	0.319	13 601
dam warm	0.188	0.000	0.694	14 000
animal cold	2.677	0.641	4.766	14 000
animal cold,warm	1.709	0.496	3.145	13 430
animal warm	1.709	0.319	3.322	14 000

(b). Migrant probability, but not its heritability, differs between temperature environments

After removing model effects not different from zero, we estimated an average MIG of 0.41 (0.27–0.55) in the cold and 0.76 (0.63–0.87) in the warm environment (probit scale contrast: 1.68, 0.95–2.36). We also estimated relatively high heritabilities (h²) for MIG liability ($h_{\mathrm{Cold}}^2=0.53$, 0.33–0.72; $h_{\mathrm{Warm}}^2=0.43$, 0.22–0.64), that were not different between temperature environments (thereby rejecting evidence for one component of genotype-by-environment interactions; $h_{\mathrm{Cold}}^2-h_{\mathrm{Warm}}^2=0.10$, −0.17–0.36). We further estimated a high between-environment genetic correlation (${\text{R}}_{{\mathrm{G}}_{\mathrm{Cold},\mathrm{Warm}}}$) with the upper 95% credible interval being very close to unity (${\text{R}}_{{\mathrm{G}}_{\mathrm{Cold},\mathrm{Warm}}}=0.84$, 0.62–0.99), indicating that genotype re-ranking for MIG was negligible between the temperature environments (thereby rejected another aspect of genotype-by-environment interactions). Thus, despite strong temperature effects on average MIG, environmental temperature appeared to have negligible effects on the relationship between genotype and phenotype.

(c). Migrant probability and body size in late summer show high correlations

To test whether phenotypic body length in late summer contributes to MIG liability, we expanded the reduced univariate model by adding phenotypic body length as a temperature-specific continuous predictor (length). We expected that if length contributes to (or even constitutes) the liability, it would positively covary with MIG. Furthermore, we expected that if genetic effects contribute positively to this covariance, the explicit modelling of this covariance as slope would reduce MIG heritability. Length was indeed a strong phenotypic predictor of MIG (figure 2). Controlled for length, temperature effects on MIG became dependent on the size at which the contrast was made because the slope between MIG and length was estimated as steeper in the warm than the cold environment (liability scale contrast: −1.18, −1.85 to –0.49; figure 2). Estimated at the overall geometric mean length, MIG was higher in the cold than the warm environment (liability scale contrast: −1.18, −1.8 to –0.47).

Figure 2.

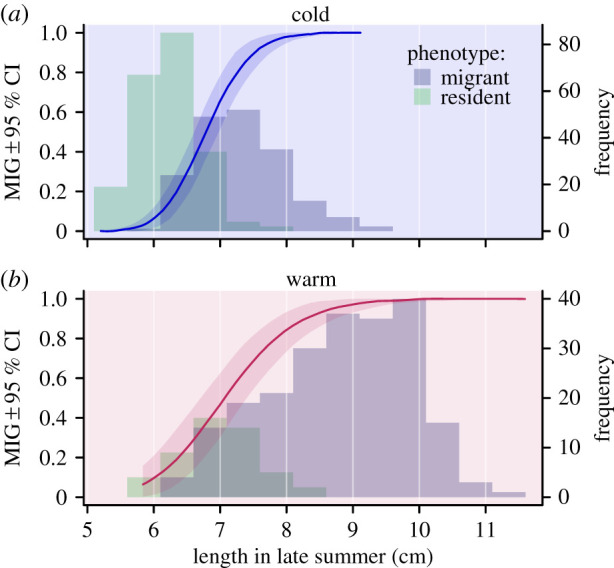
Body length distributions of prospective migrants and residents in late summer and corresponding back-transformed regression slope estimates for migrant probability (MIG) versus body length in late summer with 95% credible bands in the cold (a) and warm environments (b). (Online version in colour.)

Controlling for length also reduced heritability similarly in both environments (i.e. the heritability difference between environments was similar regardless of whether length was controlled for; figure 3). Heritability became non-significant in the warm but not the cold environment ($h_{\mathrm{Cold}}^2=0.26$ 0.11–0.42; $h_{\mathrm{Warm}}^2=0.12$, 0.00–0.28; figure 3a,b), and controlling for length also reduced the between-environment genetic correlation (figure 3c). Thus, phenotypic length in late summer explained a considerable share of MIG heritability (a phenotype expressed eight months later) in both temperature environments (52% and 71%, respectively).

Figure 3.

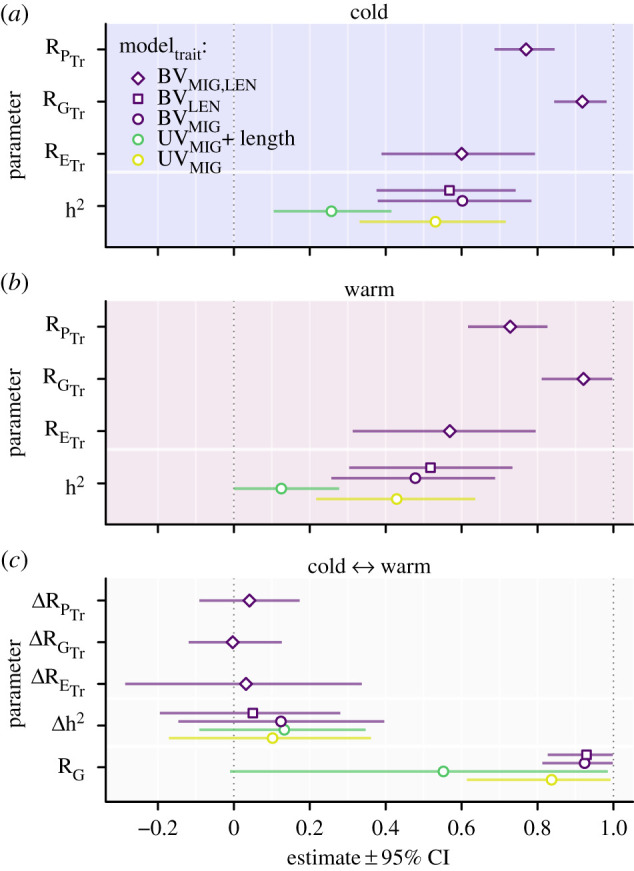
Estimates for heritability (h²), and correlations at the phenotypic (R_P), environmental (R_E) and genetic (R_G) levels within (a,b) and between temperature environments (c) and environmental contrasts of parameters (c). Estimates are based on univariate models (UV) for the migrant probability (MIG; response), either with or without a covariate for body length in late summer (length; predictor), or based on a bivariate model (BV) for MIG and body length in late summer (LEN; response), which allowed for correlation estimates between both traits (subscript Tr in axis labels). (Online version in colour.)

Having established that MIG covaried with phenotypic length, we quantified the phenotypic covariance and the relative contributions of environmental and genetic effects by fitting a bivariate model for MIG and body length in late summer as a second modelled response (LEN). Bivariate model estimates for average MIG in each temperature met those by the univariate model not controlling for phenotypic length (MIG_Cold = 0.42, 0.28–0.57; MIG_Warm = 0.76, 0.63–0.88). Estimates for average LEN in each temperature indicated strong temperature effects, whereby average LEN was 1.3 (1.1–1.5) phenotypic standard deviations (equating to 25%, 20–30%) larger in the warm than the cold environment. Back-transformed average LEN was 8.2 cm (7.8–8.7) in the warm and 6.6 cm (6.3–6.9) in the cold environment. For LEN, we estimated, unlikely for MIG, common environmental (tank) effects in the cold, but not the warm, environment that accounted for 9% of the phenotypic variance (c²; electronic supplementary material, figure S2).

Bivariate model estimates for MIG heritability were somewhat higher than by the univariate model (MIG; $h_{\mathrm{Cold}}^2=0.60$, 0.38–0.78, $h_{\mathrm{Warm}}^2=0.48$, 0.26–0.69; figure 3; electronic supplementary material, figure S2) and we estimated also high LEN heritabilities, which were surprisingly similar to the MIG heritabilities (LEN; $h_{\mathrm{Cold}}^2=0.57$, 0.38–0.74; $h_{\mathrm{Warm}}^2=0.52$, 0.30–0.73; figure 3a,b). Using alternative prior specifications for the variances of MIG, heritabilities for both traits were estimated somewhat lower but their difference remained similar (electronic supplementary material, figure S3). The between-temperature genetic correlations (${\text{R}}_{{\mathrm{G}}_{\mathrm{Cold},\mathrm{Warm}}}$) were also high and very similar for both MIG and LEN and their credible intervals were very close to unity (all ${\text{R}}_{{\mathrm{G}}_{\mathrm{Cold},\mathrm{Warm}}}=0.92$; figure 3a,b). These remarkably similar genetic correlations estimates differed only marginally with alternative prior specifications for the genetic covariances (electronic supplementary material, figure S4). Translated to the probability scale, we found MIG heritabilities to be lower and less similar between environments than on the liability scale (MIG; $h_{\mathrm{Cold}}^2=0.37$, 0.23–0.49; $h_{\mathrm{Warm}}^2=0.26$, 0.13–0.38), but the 95% credible interval of the contrast on the probability scale also encompassed zero (MIG; $h_{\mathrm{Cold}}^2-h_{\mathrm{Warm}}^2=0.12$, −0.06–0.28). Thus, heritability and between-temperature genetic correlation estimates were similar for MIG (on the liability scale) and the liability proxy trait LEN.

As expected from univariate modelling, we detected high positive phenotypic correlations (R_P) between MIG and LEN in both environments (${\text{R}}_{{\mathrm{P}}_{\mathrm{Cold}}}=0.77$, 0.69–0.85; ${\text{R}}_{{\mathrm{P}}_{\mathrm{Warm}}}=0.73$, 0.62–0.83; figure 3a,b). The phenotypic correlations within temperature environments underlaid both genetic and environmental correlations, whereby the former exceeded the latter; the between-trait genetic correlation (R_G) was with 0.92 consistently high in both environments and thereby equal to the between-temperature genetic correlation estimates for each trait. Between-trait environmental (residual) correlation estimates (R_E), for both temperature environments were somewhat lower (${\text{R}}_{{\mathrm{E}}_{\mathrm{Cold}}}=0.60$, 0.39–0.79; ${\text{R}}_{{\mathrm{E}}_{\mathrm{Warm}}}=0.57$, 0.31–0.79; figure 3a,b), and even lower when using alternative prior specifications for the residual covariances (electronic supplementary material, figure S4). Relative contributions (weights) to the phenotypic correlation were either stronger or equal for genetic than environmental effects, whereby weights equate to the relative importance of the genetic and non-genetic components, respectively [46]. Specifically, the weights for genetic effects were 0.58 in the cold and 0.50 in the warm environment. As detected for MIG in the univariate model, no difference between temperatures was detected for variance parameters of either MIG or LEN (figure 3). Thus, correlation estimates between MIG and LEN were higher at the genetic than environmental level and both traits showed similar heritability and high correlation estimates across environmental temperatures, even though average expression of each trait differed considerably between temperature environments.

4. Discussion

The basis for variation in the developmental switches that result in categorical phenotypes remains a major research topic in several fields, including biology and medicine. The control of such categorical phenotypic variation may occur via (one or many) thresholds for the quantitative expression of a, usually unknown, liability that underlies environmental and genetic effects [16–18]. In this study, we investigated the developmental switch that determines whether Atlantic salmon express the migration phenotype associated with either a sea migration at one year of age (migrant) or with remaining in freshwater for longer (resident), and tested for association with its presumed liability proxy, body size in late summer. We estimated relatively high heritabilities for both migrant probability liability and its liability proxy trait, and high environmental, genetic and phenotypic correlations between the two traits in two seasonal temperature environments. Furthermore, we estimated high between-environment genetic correlations for each trait. We, however, failed to detect male maturation, maternal and feed-restriction effects on migration phenotypes. Altogether, the results widen our understanding of environmental and genetic importance in the developmental transition towards age-specific migration phenotypes, as well as their strong thermal stability, and have implications for ecological and evolutionary subjects and future studies, which we elaborate on below.

(a). Absence of male maturation and maternal effects on migration probability

Our results strengthen previous findings, under both wild and culture conditions, that sexual maturation of males in autumn is not inhibiting the migrant phenotype expression the following spring [36,47–49]. Thus, the view that maturation and smoltification are conflicting processes [50], and which is also under debate for the congeneric brown trout [15], may not hold generally in Atlantic salmon. We also rejected the hypothesis that maternal effects affect migration phenotypes (such as suggested in [15]), agreeing with previous results in rainbow trout [51].

(b). The relationship between migrant probability and body length

Our results on Atlantic salmon strongly support a long-suspected, but often questioned, joint governance of body size in late summer and migration phenotype expression the following spring [9,24]. We demonstrate that, for a given temperature environment, this joint governance is stronger for genetic than environmental effects, and that the genetic effects were extremely stable between two temperature environments (figure 3). The results, thereby, provide quantitative primers for future modelling relying on environmental versus genetic relationships among life-history traits across environmental temperatures [e.g. 4,26,33]. Given that the tested temperature difference of 2°C aligns with global warming scenarios [52], modelling may encompass evolution under current global warming. Specifically, the combined high between-trait and between-environment genetic correlation estimates suggest strong coevolution of migration phenotypes and body size across temperature environments, which may, depending on ecological settings [9], be an advantage or a constraint.

We estimated high and similar heritability estimates for migrant probability and body size and high genetic correlations, but only moderate environmental (residual) correlations (figure 3). Thus, the association between traits appeared stronger for the genetic than the realized phenotypic values, which suggests that genetic growth potential is also a proxy for migrant probability and not only size during a sensitive period. An explanation could be that unknown genetically determined key components, such as growth hormone levels or its receptor densities, may commonly control body size and migrant probability but need not correlate tightly with phenotypic size during the sensitive period. Identifying such components may explain how a scaling of the genetic growth potential occurs relative to actual body size, which varies environmentally (such as by our temperature environments). Answers to this question may require more detailed genetic mapping and in-depth investigations on the actual biological mechanism involved.

Given the time lag between the presumed sensitive period (in late summer) and expression of the migration phenotype (the following spring), there may be time to catch up on missed growth opportunities after the sensitive period. Thus, if we assume that a liability threshold ensures viable migrant sizes, phenotypic size in late summer may be a poorer predictor of migrant size in spring than genetic growth potential. In support of this, individuals initially falling within the lower group of a bimodal distribution in late summer or autumn, assumed to represent prospective residents, may still grow rapidly during winter and become migrants the following spring, both in captivity and in the wild [47,53,54]. As an alternative, the sensitive period may last longer than suspected. In that case, individuals with a high genetic potential for, but low realized, growth until late summer may still realize their genetic potential thereafter, thereby reaching a phenotypic size threshold later and initiate the transition later. Given that a growth spurt occurs in prospective migrants between late summer and winter as a consequence of the developmental transition [25,55], it may be difficult to differentiate between ‘normal' and ‘spurt' growth to test between competing hypotheses. Nonetheless, the lack of effects on migration phenotypes by the feed restriction, applied after the presumed period, argues against the presence of an extended sensitive period (see below). Regardless of the sensitive period duration, our results suggest that individuals with relatively small body size in late summer may still become migrants if they possess a high genetic growth potential.

The presence of a higher genetic than environmental correlation between migrant probability and body size (figure 3) has several implications. For example, investigations on the physiological mechanisms of the developmental transition rely on body size based migration phenotype prediction for lethally sampling prospective migrants and residents prior to expression of the migration phenotype. Our results suggest that body size based phenotype prediction may lead to conservative results because small migrants may get incorrectly assigned resident status. Such wrong assignments may blur differences of studied variables between true prospective migrants and residents. Another implication pertains to identifying the genetic basis for migration phenotypes via locus associations such as genome-wide association, or gene transcription studies, which may easily be confounded with identifying the highly polygenic basis for growth because of the high genetic between-trait correlation. To identify genes underlying also, or solely, the migration phenotype, a bivariate approach including size during the sensitive period may be advantageous. Investigations on associations based on transcription levels during the sensitive period may also be promising, but pose logistical challenges due to the abovementioned phenotype prediction required for lethal sampling.

There are several inferential limitations to our estimates. Genetic parameter estimates often pertain to specific populations and conditions, but knowledge about their magnitudes may still provide useful information [56,57]. Our estimates within and between temperature environments may then be useful for future short-term predictions in response to selection under changing environmental conditions [58]. However, it is important to remember that heritabilities on the liability scale (and also heritabilities for liability proxy traits) do not relate linearly to the probability scale across many factors, including the—environmentally governed—overall probability [18]. This effect was here exemplified by disparate heritability differences between temperature environments on the liability (more similar) versus the proportional (less similar) scale. As discussed by de Villemereuil et al. [45], predicting the responses to selection for migration phenotypes may follow standard assumptions if based on liability scale heritability, but less so on proportional scale heritability.

Pertaining to correlation estimates, Cheverud [59] proposed that many genetic, but not phenotypic, correlations estimates may be inflated, especially under sample size limitations and when heritabilities are low [59,60]. In comparison to studies assessed by Cheverud [59], our effective sample sizes—the product of number of families and geometric mean heritability—are at the lower end where Cheverud [59] suspected upwards bias. However, Bayesian heritability estimates for length matched those by REML that should yield reliable estimates [43], and which supports the presence of moderate to high heritabilities. For migrant probability estimates, we rely on comparisons with previous estimates. To our knowledge, the only study in Atlantic salmon estimated a small heritability on the proportional scale (0.16 ± 0.05) at a lower migrant rate (0.18) than in the present study [55]. In that study, migrants were defined as exceeding a particular size threshold in spring [55], altogether making a comparison difficult. In other salmonids, similarly high estimates for migrant probability liability as presented here exist, such as 0.61 in cultured rainbow trout [51] and 0.52–0.56 in wild brook charr [61]. Thus, migrant probability liability in salmonids may exhibit high heritabilities, which lends some support to the correlation estimates. Furthermore, previous genetic correlations estimates in rainbow trout between body length at age 12 and 15 months and migrant probability one year later, under much larger sample sizes, also were relatively high and exceeded the phenotypic correlation [51]. Thus, the detected stronger genetic than environmental relationship may not, at least entirely, be a statistical artefact.

(c). Temperature effects on migration phenotypes: liability versus threshold variation

Threshold model interpretations affect biological inferences, including inferences about the here-detected temperature difference. Using the threshold model (or its variants), it is generally not possible to discern variation for thresholds from liability [41,62]. This statistical uncertainty extents to general definitions. As a hypothetical example, it may be unclear whether circulating hormones and their receptors should be regarded as contributing commonly to liability variation, or the latter to threshold variation (as suggested in [24]). Here, we did not adopt either view when interpreting our results, but discuss all possibilities.

A possible interpretation for the detected temperature difference for average migrant probability (not controlled for length) could be that temperature affects body length positively. This more rapid growth in the warm environment would then increase migrant probability because more individuals exceed a size threshold during a sensitive period. Assuming equal thresholds between temperatures, this idea leads to the expectation that controlling for size results in equal migrant rates. However, length-controlled migrant probability was higher in the cold environment (figure 2). This result could then be interpreted as the presence of a lower size threshold in the cold environment, supported by the high genetic correlations between environments as predicted in [62]. Nonetheless, because the exact sensitive period remains unknown, the length measured at a presumed sensitive period may be different than the length expressed at the actual sensitive period. This bias between approximated and actual liability proxy length may be larger in the warm than the cold environment simply because growth proceeds more rapidly in the warm environment. Thus, subtle methodological bias can create statistically different migrant rates at a standardized length that mimic the presence of different environmental (or in other cases: population) thresholds.

To not confound liability proxy bias with differences for environmental (or population) thresholds, it would be necessary to base inferences on the true liability, or, when information is lacking, on the liability proxy but as expressed at the true sensitive period. This leads to the question how close we got to the true period. The developmental transition is inducible by shortening day length from 24 to 12 h for 6 weeks [63] and may occur when day length is shortened to between 15 and 12 h [30]. For our experimental setting, a six-week period after day lengths got shorter, or day lengths between 15 and 12 h, occurred shortly before, or at the beginning of, the size recording period at the end of the summer and the middle of the feed restriction, respectively (figure 1c). Because the feed restriction reduced specific growth rates by about 50% but not migrant probability, it appears likely that the sensitive period preceded the feed restriction, as similarly inferred for amago salmon [64]. Future experiments destined to identify the sensitive period—a required prior for sound investigations on the physiological or genetic mechanisms determining the developmental transition—may thus be worthwhile if covering the entire summer.

Ethics

Animal experimentation followed European Union Directive 2010/63/EU under license ESAVI-2778–2018 by the Animal Experiment Board in Finland (ELLA).

Data accessibility

Underlying data and R-scripts are available on the Dryad Digital Repository: https://doi.org/10.5061/dryad.9w0vt4bbw [65].

Authors' contributions

P.V.D. and C.R.P. conceived the study; C.R.P. and J.E. contributed materials; C.R.P. coordinated genotyping; P.V.D. and N.P. performed experiments and recorded data; P.V.D. analysed data and wrote the manuscript. All authors critically revised the article and contributed to its final version.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Academy of Finland (project numbers 284941, 286334, 314254 and 314255), the European Research Council under the European Articles Union's Horizon 2020 research and innovation program (grant no. 742312), and the University of Helsinki.