A reinforcement-learning model of active avoidance behavior: Differences between Sprague Dawley and Wistar-Kyoto rats

Abstract

Avoidance behavior is a typically adaptive response performed by an organism to avert harmful situations. Individuals differ remarkably in their tendency to acquire and perform new avoidance behaviors, as seen in anxiety disorders where avoidance becomes pervasive and inappropriate. In rodent models of avoidance, the inbred Wistar-Kyoto (WKY) rat demonstrates increased learning and expression of avoidance compared to the outbred Sprague Dawley (SD) rat. However, underlying mechanisms that contribute to these differences are unclear. Computational modeling techniques can help identify factors that may not be easily decipherable from behavioral data alone. Here, we utilize a reinforcement learning (RL) model approach to better understand strain differences in avoidance behavior. An actor-critic model, with separate learning rates for action selection (in the actor) and state evaluation (in the critic), was applied to individual data of avoidance acquisition from a large cohort of WKY and SD rats. Latent parameters were extracted, such as learning rate and subjective reinforcement value of foot shock, that were then compared across groups. The RL model was able to accurately represent WKY and SD avoidance behavior, demonstrating that the model could simulate individual performance. The model determined that the perceived negative value of foot shock was significantly higher in WKY than SD rats, whereas learning rate in the actor was lower in WKY than SD rats. These findings demonstrate the utility of computational modeling in identifying underlying processes that could promote strain differences in behavioral performance.

1. INTRODUCTION

Avoidance behavior is a response intended to prevent negative experiences, thoughts, or situations. Avoidance is key in self-preservation, as it prevents potentially life-threatening events from occurring. As such, these behaviors can be vital to survival, and can also influence how an individual functions throughout daily life.

Differences in threat response may exist between different populations [1–3]. Although typically adaptive, avoidance can become pathological if it persists out of proportion to the threat, or fails to extinguish when the threat is no longer present. For instance, pathological avoidance behavior is present in all anxiety disorders and in post-traumatic stress disorder (PTSD) [4]. Interestingly, avoidance correlates with anxiety disorder severity [5,6], suggesting the individual differences in avoidance responding may directly contribute to anxiety. Understanding avoidance behavior may be key in identifying those individuals who are vulnerable to develop anxiety disorders, and could allow early interventions to prevent anxiety disorders.

Just as humans show individual and group differences in avoidance behavior, animals also show individual differences and strain differences. For example, our laboratory has investigated avoidance using the outbred Sprague-Dawley rat as well as the inbred Wistar-Kyoto (WKY) rat. The WKY rat shows a variety of behaviorally inhibited behaviors, including increased social avoidance [7] and decreased exploration in a novel environment such as the open field and elevated plus maze [8,9]. Interestingly, the WKY rat also demonstrates enhanced acquisition of avoidance and impaired extinction of avoidance responding, when contrasted with the SD rat [10–12]. Compared to SD rats, WKY rats are more motivated to actively escape and avoid foot shock [13,14], and the enhanced motivation for negative reinforcement may be a key process underlying these differences in avoidance behavior between strains.

Since avoidance is, by its nature, an acquired behavior, the onset of avoidance can be examined as a learning process. Avoidance has been posited as a learned reaction to environmental stimuli perceived to be threatening [15,16], where the avoidance behavior is reinforced by the perception of relief [17–19]. Because the reinforcement for avoidance is the absence of an expected aversive event, avoidance learning is more complicated than simple stimulus-response associations and has attracted a long theoretical history, exemplified by two-factor theory [20,21] and opponent-process theory [22]. Moreover, successful avoidance is associated with dopamine release in the mesolimbic system, part of the incentive-motivation-reward circuitry [23,24], and further implicating the reinforcement value of preventing an expected aversive event.

Computational models, such as reinforcement learning (RL) models, are useful in providing insights into behavior that are difficult or impossible to obtain with an experimental approach. RL models attempt to fit a simple mathematical learning rule onto individual subject data by discovering a set of parameters (such as learning rate, tendency to explore vs. exploit, and subjective value of a reward or punisher) that allow the model to most closely reproduce that individual’s trial-by-trial performance. These RL models have been successfully applied to trial-by-trial data from humans on simple associative learning tasks, and have shown systematic differences in average parameter values obtained from various neurological and psychiatric patient groups [17,25–27], thus identifying potential mechanisms that could be driving group differences in behavior. For example, RL modeling of data from a probabilistic categorization task indicated that Veterans with severe self-reported PTSD symptoms tended to value ambiguous or neutral outcomes more negatively than peers with few to no PTSD symptoms [28], suggesting that differences in outcome evaluation may contribute to PTSD symptoms. Similarly, RL modeling of the same probabilistic categorization task in patients with opioid addiction indicated a heightened tendency to change response strategies after an unexpected rule violation (i.e., “lose-shift”), compared to never-addicted controls [29], implying a tendency to overvalue short-term gains over strategies to maximize long-term reward. Interestingly, RL models have been linked to similar learning theories as avoidance behavior [20,22], and the training algorithms used in RL models use a concept of prediction error (mismatch between actual vs. expected reward or punishment) that has been shown to correlate with dopaminergic responses to reinforcement [30–32].

However, the RL model approach has not been widely applied to animal data. This is partly because animal studies generally have small sample sizes, which decreases the statistical reliability of RL model-fitting techniques. Those studies for which RL models have been applied typically examined a group of “healthy” outbred rats on simple forced-choice tests, often examining behavior when manipulating the probability of rewards [33–36]. To date, there has been a dearth of studies applying RL model techniques beyond simple, discrete-trial forced-choice learning paradigms. Recent work by Langdon et al. [37] considered a rodent version of a gambling task, and found that learning from punishment corresponded with the degree of risk preference in individual rats. Zhukovsky et al. [38] screened rats for anxiety prior to cocaine self-administration; RL modeling suggested that rats with high, but not low cocaine escalation failed to exploit previous reward learning and showed increased perseveration. Thus, using the RL model in animal models of psychopathology may shine new light on the pathophysiology of neurological and psychological disease.

In our previous work [39], we applied an RL model to simulate group data from a previously-published study showing differences between rat strains in learning active avoidance. The model successfully reproduced acquisition curves and also demonstrated “warm-up,” a feature demonstrated by SD but not WKY rats that may be important in the development of nonpathological avoidance. Importantly, the model suggested differences between strains in latent variables including learning rate and explore/exploit bias. In this prior study, the RL model was qualitatively fit to group data from each rat strain, and therefore, the focus was to describe how different model parameters could contribute to observed behavioral differences. In the current study, we apply an RL model to trial-by-trial data from individual animals with the goal to uncover individual differences in latent variables that could produce the observed group-level differences in behavior.

In the present study, we take advantage of a recently-published large dataset (n=40 per strain) on an active avoidance task in outbred Sprague-Dawley (SD) rats and in inbred behaviorally-inhibited WKY rats [40]. We use the RL model, as previously employed to fit human individual data, but apply it to individual rat trial-by-trial data to extract estimated parameters for each individual rat. Then the extracted parameters are evaluated to determine whether they differ between strains, suggesting qualitative differences in how the two strains approach the avoidance task.

2. METHODS

2.1. Empirical Data

Animal behavioral data were collected using a lever press escape-avoidance task, where the animal learned to lever press in order to avert an aversive event (foot shock). The full experimental methods and behavioral data have been previously published [40].

To review briefly, 40 Sprague-Dawley (SD) and 40 Wistar-Kyoto (WKY) rats were given 12 acquisition sessions; each composed of 25 trials. Each trial began with a danger signal (tone, maximum 72-s duration) that could be followed by a shock period (maximum 72-s duration) during which mild (1.0mA, 0.5s) foot shocks were delivered at a rate of 1 per 3.5s. A lever press during the danger signal and prior to foot shock was scored as an avoidance response, terminated the danger signal, and initiated a 180-s intertrial interval (ITI) during which a safety signal (flashing light) was presented. An avoidance response resulted in omission of the foot shock for that trial. If no avoidance response was made within 72-s from the start of the danger signal, foot shock commenced. A lever press during the shock period was scored as an escape response, terminated the shock period, and initiated an ITI. All sessions started with a 60-s habituation period (no tone, light, or shock). Lever presses during the ITI were scored as inter-trial responses (ITRs) and lever presses during the habituation period were scored as anticipatory responses. Three sessions occurred each week with a minimum of 48-h between sessions. Figure 1A illustrates example events at the start of an acquisition session. Figures 1B–D summarize group and individual-level data from the experiment, in terms of percent avoidance responses across sessions.

Figure 1.

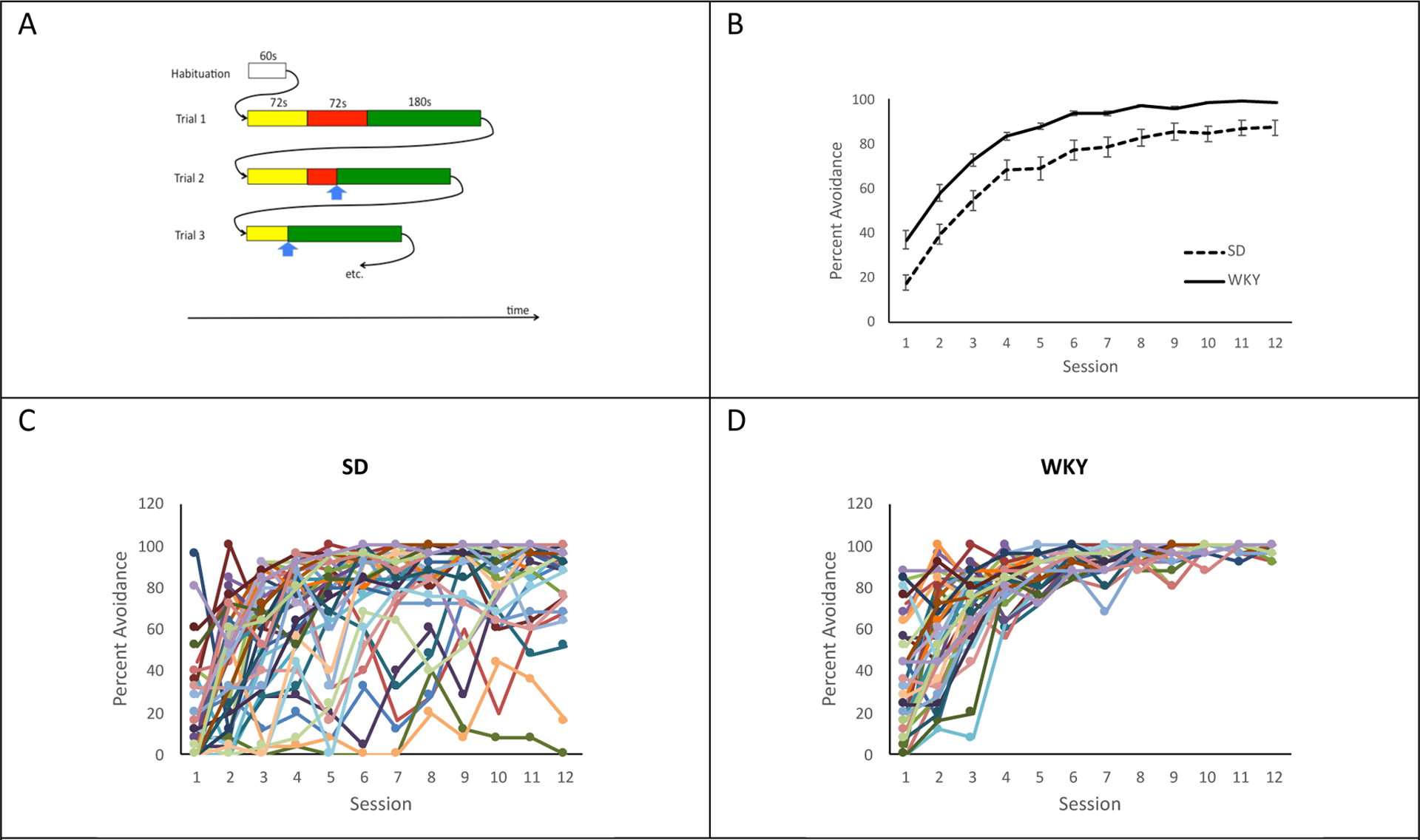
Empirical data from the avoidance task. (A) Schematic of acquisition session. Each session begins with a 60s habituation period, during which no experimental stimuli are presented. Each trial consists of a danger signal (yellow bars, maximum 72s), shock period (maximum 72 s) during which shock and danger signal are present (red bars, only present if an avoidance response is not made, i.e., Trials 1 and 2, but not 3), and 180s ITI period during which safety signal is present (green bars). If the rat makes a lever press (blue arrow) during the shock period, it terminates the shock and danger signal and initiates the ITI (escape response, see Trial 2). If the rat lever presses during the danger period (initial 72 s of the trial), it terminates the danger signal, causes omission of the shock period, and initiates the ITI (avoidance response, see Trial 3). Overall session time (in sec) depends on whether/when the animal emits escape and avoidance responses. (B) Both rat strains showed acquisition of the avoidance response across training sessions, with a main effect of faster learning in the WKY than SD rats. (C) The group data in (B) mask considerable individual variation among the SD rats; individual rats’ acquisition curves vary, showing some animals acquired quickly to near 100% performance, while others seldom emitted avoidance responses even after 12 training sessions. Note that (after the first session) animals typically emitted escape responses on those trials where they did not make avoidance responses. (D) The data from individual WKY animals also show individual variation, with some WKY rats showing robust acquisition even in the first training session, and most exhibiting reliable avoidance responding after 5 or 6 sessions. Errors bars in (B) indicate ±1 SEM.

2.2. Data Recoding

During the experiment, the onset and termination of danger signals, shocks, safety signals, and lever press responses were recorded during each session. For computational modeling, session data were discretized into a series of 12-s “timesteps.” At each timestep, three binary variables recorded whether the danger signal, safety signal, and shock were present (1) during any part of that timestep or absent (0). At each timestep, the animal’s response was scored as 1 if at least one lever press occurred during that timestep, or 0 if no lever presses occurred. Finally, two variables coded whether the animal was in the experimental chamber (1=yes, 0=no) or in the home cage (1=yes, 0=no).

Although each rat experienced 12 acquisition sessions each including 25 trials, the exact duration of each trial (and therefore, number of timesteps) was variable, depending on how often the animal terminated a trial via an escape or avoidance response. Total in-chamber time averaged 5670 timesteps (i.e. about 18.9h) for the SD rats (std. dev. 376; range 5230–6922 timesteps) and 5386 timesteps (i.e. about 18.0h) for the WKY rats (std. dev. 156; range 5135–5846 timesteps); the fact that WKY rats spent significantly less time in the experimental chamber than SD rats (Wilcoxon rank sum test with continuity correction, W=1247, p<.001) is consistent with their higher rate of avoidance responding (since an avoidance response immediately terminates the trial).

Since sessions lasted about 1.5h on average (i.e. about 450 timesteps) and occurred on alternate days, with animals returning to the home cage between sessions, an additional 46.5h (13,950 timesteps) were inserted between sessions to simulate home cage time. In pilot work (not shown), results did not change appreciably if the duration of simulated home cage time was reduced to as few as 500 timesteps between sessions; accordingly, “overnight” home cage periods were simulated as 500 timesteps (i.e., 100 min simulated time), to decrease computer processing time per simulated rat. For each timestep of simulated “overnight” period, the danger, safety, shock, lever press, and chamber variables were all set to 0 but home cage was set to 1.

2.3. RL Model

A reinforcement learning (RL) model was applied to each rat’s timestep-by-timestep behavior. The RL model was adapted from the actor-critic model [41–43] as used to simulate rat lever-press avoidance learning by Myers et al. [39], and schematized in Figure 2. Code was programmed in C using the XCode (version 5) programming environment (Apple, Inc., Cupertino CA).

Figure 2.

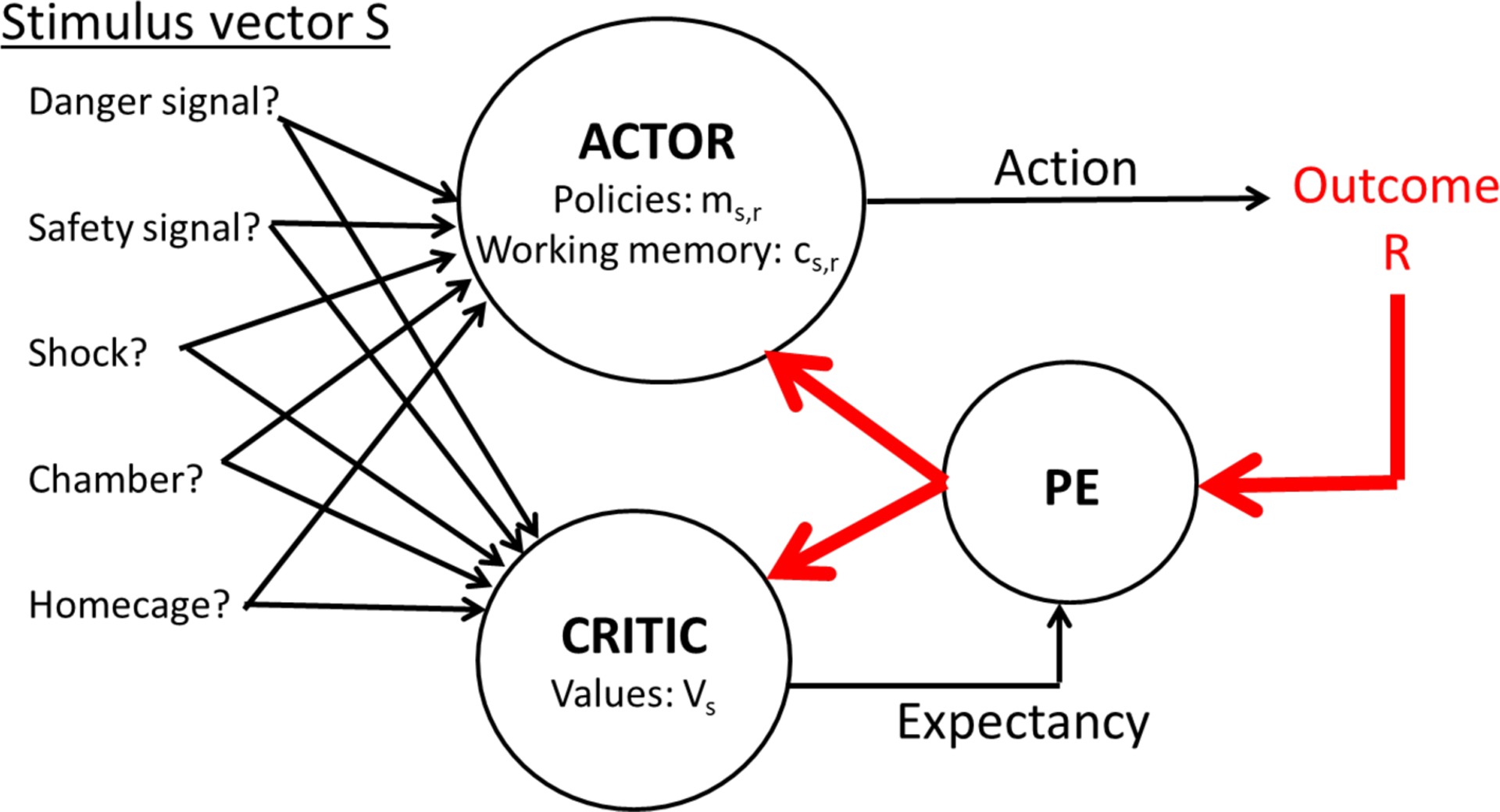
Schematic of the actor-critic model. At each timestep t, input vector S specifies the presence (1) or absence (0) of each of a set of stimuli (danger signal, safety signal, and shock) and contextual cues (experimental chamber or home cage). The actor module learns a set of policies m_s,r specifying how strongly each stimulus s should promote response r. Based on these policy values, the actor selects an action (lever press or another behavior), which may evoke an external outcome R, such as shock. Meanwhile, the critic module learns a set of values V_s indicating the expected outcome when each stimulus s is present. Prediction error (PE) is then computed as the difference between the actual outcome at timestep t and the outcome that was predicted based on available evidence at time t-1. PE is then used to update the policies and values, reducing the likelihood of repeating actions that were followed by punishing outcomes (e.g., shock), and increasing the likelihood of repeating actions that were followed by rewarding outcomes (e.g. omission of an anticipated shock). The actor also maintains a working memory trace c_s,r that decays with time since r was selected given stimulus s.

2.3.1. Action Selection in the Actor Module

At each timestep t, a stimulus vector S was presented representing the experimental stimuli experienced by the rat at that timestep (in this case, a set of 5 binary values coding presence or absence of danger signal, safety signal, shock, and whether the animal was in the experimental chamber or in the home cage). Given S at timestep t, the actor module selected one action to execute in response. The probability of selecting lever press response, from among all possible responses r, was calculated using a softmax function [44]:

$$\mathrm{Pr}\left(press\right)=e^{f\left(press,S\right)}/\left[e^{f\left(press.S\right)}+e^{f\left(other,S\right)}\right]\text{\hspace{0.17em}where\hspace{0.17em}}f\left(r,s\right)={\sum }_s\left(m_{r,s}{S}_s+P{c}_{r,s}{S}_s\right)/\beta$$ Eq.1

For simplicity, possible responses were limited to lever pressing (press), or other, which included all other possible behaviors available to the rat (e.g. grooming, rearing, exploring, or sleeping); the lever press response was defined as unavailable when the rat was in the home cage (which has no lever). For the five input stimuli s, S_s=1 if that stimulus was present and S_s=0 if not. The m-values were policies that represent tendency to select a particular action r in the presence of stimulus s; m-values were initialized to 0.01 (indicating a small chance of spontaneously emitting each possible behavior at the start of training). ϐ was an “exploration” parameter governing the tendency to choose the response with the highest expectancy value (ϐ near 0; “exploitation” of prior knowledge) or choose a response at random (ϐ near 1; “exploration” of new responses). P was a “perseveration” parameter that encoded the tendency to repeat (P>0) or avoid (P<0) prior actions, regardless of reinforcement. These prior actions were stored in a working memory trace, where c_r,s held a record of the last response r when stimulus s was present. The c-values were initialized to 0, and updated after each timestep as c_r,s ←1 for the current r and s; for all other stimulus-response pairs, the working memory trace decayed as c_r,s ← 0.95*c_r,s.

Regardless of m-values calculated at the current timestep, the action selected by the model at timestep t was constrained to be the rat’s actual behavior at timestep t (i.e. r=press if response=1 in the datafile, else r=other).

After an action was executed at time t, reinforcement R was presented to the model at time t+1; the value of R was calculated based on whether the animal did or did not experience shock during timestep t+1. Following Myers, Smith et al. [39], R could take one of three values: if at least one shock was present, R=R_shock (presumably a large negative value); otherwise, R=0 unless the action selected at time t was lever press, in which case R=R_press (a small negative value indicating the “cost” of emitting a lever press in terms of energy expenditure as well as the missed opportunity to engage in other behaviors). In our prior paper [39], the relative difference (ratio) between R_shock and R_press appeared more important than the absolute values of each, so R_shock was allowed to vary as a free parameter, while the value of R_press was held fixed at −0.2.

2.3.2. State Evaluation in the Critic Module

The critic module maintained a vector of expectancy values V_s encoding expected contribution from each stimulus s to the expected outcome; the total expectancy E(t) was the sum of these weights, for all stimuli s that were present at timestep t:

$$E\left(t\right)=\sum _s{V}_s{S}_s$$ Eq.2

All V_s were initialized to 0.0, and so E(0)=0.

Prediction error PE, which was the difference between the actual and expected outcomes, was computed using a variation on the temporal difference rule (see [45]), adapted for avoidance learning paradigms (following [46,47]):

$$PE=R+{\gamma }^{*}E\left(t\right)+E\left(t-1\right)$$ Eq.3

Here, γ was a discount factor implementing temporal discounting (see [45]). In effect, smaller γ (near 0) means that immediate rewards and punishments were more important than outcomes expected sometime in the future; larger γ (near 1) would be appropriate for situations where there may be many steps (many sequential individual behaviors) required to reach a goal.

PE was then used to update the policies and values, increasing the likelihood that the model would repeat actions that previously resulted in positive outcomes (or expectation of positive outcomes), and reducing the likelihood that the model would repeat actions that previously resulted in punishing outcomes (or expectation of punishing outcomes). In the critic, for all stimuli s that were present at the prior timestep:

$$V_s\leftarrow V_s+\alpha PE$$ Eq. 4

Here, α was the learning rate in the critic, which was a free parameter. The V-values were clipped at ±10, to prevent weights growing out of bounds. In the actor, for response r chosen by the rat at the prior timestep, and each stimulus s that was present:

$$m_{r,s}\leftarrow \epsilon \left(PE-m_{r,s}\right)$$ Eqn. 5

Here, ε was the learning rate in the actor. In our prior paper [39], the value of ε was held fixed at 0.005.

In summary, the basic model reported here (termed Model A) contained five free parameters: learning rate α, exploration parameter ϐ, shock magnitude R_shock, perseveration parameter P, and discount factor γ. For each rat, each of these parameters was assessed across a range of values, as shown in Table 1; the range and stepsize for each parameter were established based on preliminary simulations (data not shown) to establish ranges within which model behavior was stable and which appeared to produce reasonably good fit for all rats simulated. In addition, we explored whether there was additional explanatory power to be gained by adding additional free parameters ε or R_press, as described further below.

Table 1.

Summary of parameters in the actor-critic model, with range (minimum and maximum absolute value) and stepsize explored for the “basic” model, Model A (with 5 free parameters), and two alternate models: Model B (which also allowed R_press to vary), and Model C (which also allowed ε to vary).

Parameter	Function	Model A (5 free parameters)	Model B (allow Rpress to vary)	Model C (allow ε to vary)
α	Learning rate in the critic (Eqn. 4)	Range [0..0.01] by 0.001	Same as A	Same as A
β	Exploration parameter (Eqn. 1)	Range (0..1] by 0.1	Same as A	Same as A
P	Perseveration parameter (Eqn. 1)	Range [−0.05..+0.50] by 0.05	Same as A	Same as A
γ	PE discount factor (Eqn. 3)	Range [0..1] by 0.1	Same as A	Same as A
Rshock	Reinforcement value of shock (Eqn. 3)	Range [−10..+1] by 1.0	Same as A	Same as A
Rpress	Reinforcement value of lever press (Eqn. 3)	Fixed at −0.2, as in [39]	Range [−2..+0.2] by 0.2	Same as A
ε	Learning rate in the actor (Eqn. 5)	Fixed at +0.005, as in [39]	Same as A	Range 0..0.01 by 0.001

2.4. Model Fitting

For each possible combination of parameter values, model fit was assessed by computing negative log likelihood estimates (negLLE) to estimate the a priori probability of the data, given that particular combination of free parameter values:

$$negLLE=-\sum _t\text{1n}\left(match\left(r,t\right)\right)$$ Eq. 6

Here, match(r,t) was the probability of the model selecting the same response r as the rat did at time t; i.e., if the rat made at least one lever press, then match(r,t)=Prob(press), else match(r,t)=1-Prob(press). Overnight timesteps were excluded from this calculation, as the rat’s behavior was not monitored in the home cage. Thus, negLLE was computed over the in-chamber timesteps, which (as noted above) ranged from 5146–6933 timesteps depending on the time an individual rat had spent in the chamber.

Estimated parameters for each rat were defined as the configuration of parameter values (α, ϐ, R_shock, P, and γ for Model A) that together resulted in the smallest negLLE (closest to 0) for that rat’s data. As a lower estimate, a model implementing random action selection (Pr(press)=0.5 for all timesteps) applied to a rat dataset containing 6000 in-chamber trials would produce negLLE=4158; as an upper bound, a perfect model (i.e., Pr(press)=1 for those timesteps where the rat made a lever press and Pr(press)=0 for all remaining timesteps) would produce negLLE=0.

2.5. Model Comparisons

In addition to the “default” model (Model A), with five free parameters as shown in Table 1, we also considered whether additional free parameters could improve model fit. Specifically, we also examined Model B in which R_press, the “opportunity cost” of lever press, was allowed to vary (in a range from −2 to +0.2, by stepsize 0.2), and Model C in which ε, the learning rate in the critic was allowed to vary (in a range from 0.0 to 0.01 by stepsize 0.001).

By definition, these two larger models (with 6 free parameters each) fit the data at least as well as the smaller Model A (with 5 free parameters), since the optimal parameter values identified in Model A could also be instantiated in the larger models. However, in evaluating models, it is ideal to obtain the best, most parsimonious explanation of the data: i.e., closest simulation of animals’ behavior with fewest free parameters (k).

In assessing model fit while taking model complexity into account, we used the Bayesian information criterion (BIC), defined as BIC=k*ln(n)+2*negLLE, where n is the number of observations (here, number of timesteps) and negLLE is the negative log likelihood (smaller numbers indicate better fit of the model to the data); low values of BIC indicate a better, more parsimonious fit [48]. Previous work has suggested criterion that a 10-point decrease in BIC indicates a significantly better model fit [49]; if the more complex model does not result in significantly reduced BIC, then the simpler model is to be preferred.

2.6. Group Comparisons

Next, for the “best” model identified above, we compared whether the estimated parameters and model fit metrics derived for individual rats differed as a function of strain, using mixed-design ANOVA (with Greenhouse-Geisser correction for data that failed assumption of sphericity) followed by univariate post-hoc tests with Bonferroni correction for multiple comparisons; we also used Pearson correlation to examine relationships between estimated parameter values and behavioral performance (percent avoidance responses).

As a confirmation that the model was actually learning the task in a principled way, we recorded m-values (weights in the actor module) and V-values (state values in the critic model) at the end of acquisition session 12 under the estimated parameters for each rat. Because each stimulus is associated with two m-values (one providing a weight in favor of the press response and one providing a weight in favor of the other response option), we calculated a difference score between the m-weight from each stimulus to the press response minus the m-weight from that stimulus to the other response; d-score>0 indicates a bias for the actor module to select a press response, while d-score<0 indicates a bias not to press. There is only a single V-value for each stimulus, with positive values indicating expectation of positive outcomes by the critic module, and negative values indicating expectation of negative outcomes.

2.7. Behavioral Recovery Studies

Finally, as a check on the validity of estimated parameters, we conducted behavioral recovery studies. We used the estimated parameters for each rat to build a simulated rat, which was then trained on the same behavioral protocol as the animals, i.e. 12 sessions of 25 acquisition trials. Now, however, the model was allowed to select and express its own behaviors, and execution of a lever press response terminated the trial (as in Figure 1A). For each trial, we recorded whether the model executed an escape, avoidance, or no response, identical to the animal protocol. Each simulated rat was run 100 times, with the model weights re-initialized at the start of each run, and the average avoidance responses per session were computed.

We then used the data from the individually-simulated rats to compare avoidance performance across sessions as a function of strain in the same way as it was previously done for the real animals [40] using mixed ANOVA (within-subjects factor of session, between-subjects factor of strain).

2.8. Statistical Analysis

Statistical analyses were carried out using R version 3.6.3 [50]; for mixed-design ANOVA (type III SS), the ez package for R [51] and the aRnova plug-in for R Commander were used [52]. Where data did not meet tests for equality of variance (Levene’s test p≥0.05) or normality (Shapiro-Wilk test p≥0.05), non-parametric tests were used. Criterion for significance was set at 0.05 (two-tailed); where noted, Bonferroni correction was used to adjust alpha to protect against inflated risk of Type I error under multiple comparisons.

3. RESULTS

3.1. Summary of Behavioral Data

As shown in Figure 1B, the existing behavioral data indicated that both rat strains increased avoidance responding across the 12 training sessions; there was also a main effect of strain, where WKY animals showed higher percentage of trials with an avoidance response than SD animals (Mann-Whitney U=308, p<.001). On average, WKY animals made significantly more total lever presses over the course of an experiment than SD animals (SD mean 671.0, std. dev. 166.5; WKY mean 757.0, std. dev. 129.7; Welch’s t(75.6)=2.68, p=.009) and experienced significantly fewer shocks (SD mean 449.1, std. dev. 345.7; WKY mean 258.3, std. dev. 288.9; t(78)=2.58, p=.012). This is consistent with numerous prior datasets showing facilitated acquisition in the WKY rat compared to SD rat [10–12]. However (and also consistent with prior datasets), within each strain, there was considerable individual variation, as shown by the acquisition curves for individual SD (Figure 1C) and WKY (Figure 1D) rats, with more variability in SD than in WKY.

3.2. Model Comparisons

Figure 3 shows results for each of the three models examined, including the default model with 5 free parameters (Model A, k=5), Model B which allowed R_press to vary (k=6) along with the 5 free parameters of Model A, and Model C which allowed ε to vary (k=6) along with the 5 free parameters of Model A. Figures 3A,B show that estimated parameters did not vary widely across the models, indicating some stability of optimal parameter values. The one minor exception was in Model B, where R_press was allowed to vary; here, mean values of R_press were somewhat more strongly negative than the value of −0.2 used in the other models, and mean values of R_shock were correspondingly also more strongly negative than other models. Figure 3C shows model-fitting values (negLLE) for each model. By definition, model fit was as least as good in the larger models than in the smaller model. Specifically, mean BIC was 4107 in Model A, 4103 in Model B, and 4090 in Model C.

Figure 3.

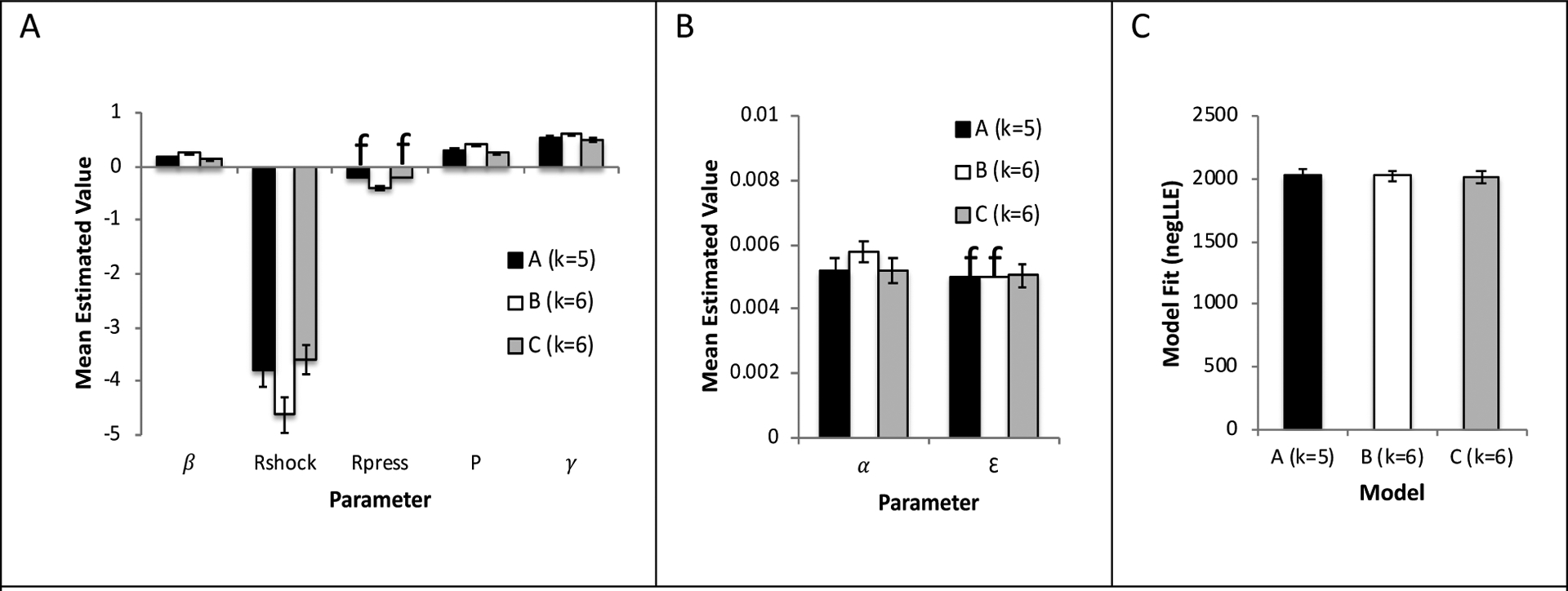
Comparison of three models - the “default” Model A with 5 free parameters α, β, R_shock, P, and γ; Model B which includes the same five free parameters as well as R_press (6 free parameters); and Model C which includes the five free parameters plus ε (6 free parameters). (A,B) Mean best-fit parameter values obtained under each model are also similar, although Model B (which allows R_press to vary) has somewhat more negative values of both R_press and R_shock, compared to the other models. (C) The models are similar in terms of ability to fit the empirical data (negative log-likelihood estimate, negLLE), with Model C providing numerically best fit (lowest negLLE). Results reported in Figures 4–7 are based on the best-fitting Model C. Y-axes are in arbitrary units; f in (A,B) indicates parameter values that are fixed in a model. Error bars indicate ±1 SEM for free parameters.

Using the criterion of at least a 10-point decrease in BIC as indicating a significant change [49], allowing R_press to vary did not significantly improve model fit (only a 4-point improvement in Model B relative to Model A), but allowing ε to vary did improve model fit (17-point improvement in Model C relative to Model A). Accordingly, the analyses that follow are based on results obtained with Model C.

3.3. Group Comparisons

3.3.1. Between-Strain Differences in Estimated Parameters

Figure 4 shows mean parameter values for the SD and WKY groups under Model C (with k=6, including ε as a free parameter). Since the data failed Mauchly’s test of sphericity (W<.001; p<.001), Greenhouse-Geisser correction was used to adjust degrees of freedom (epsilon=0.21). Mixed ANOVA, with six within-subject factors representing the six parameters and one between-subject factor of strain, indicated main effects of parameter (F(1.05, 81.9)=213.4, p<.001) and strain (F(1,78)=16.1, p<.001), as well as an interaction between strain and parameter (F(1.05, 81.9)=18.50, p<.001).

Figure 4.

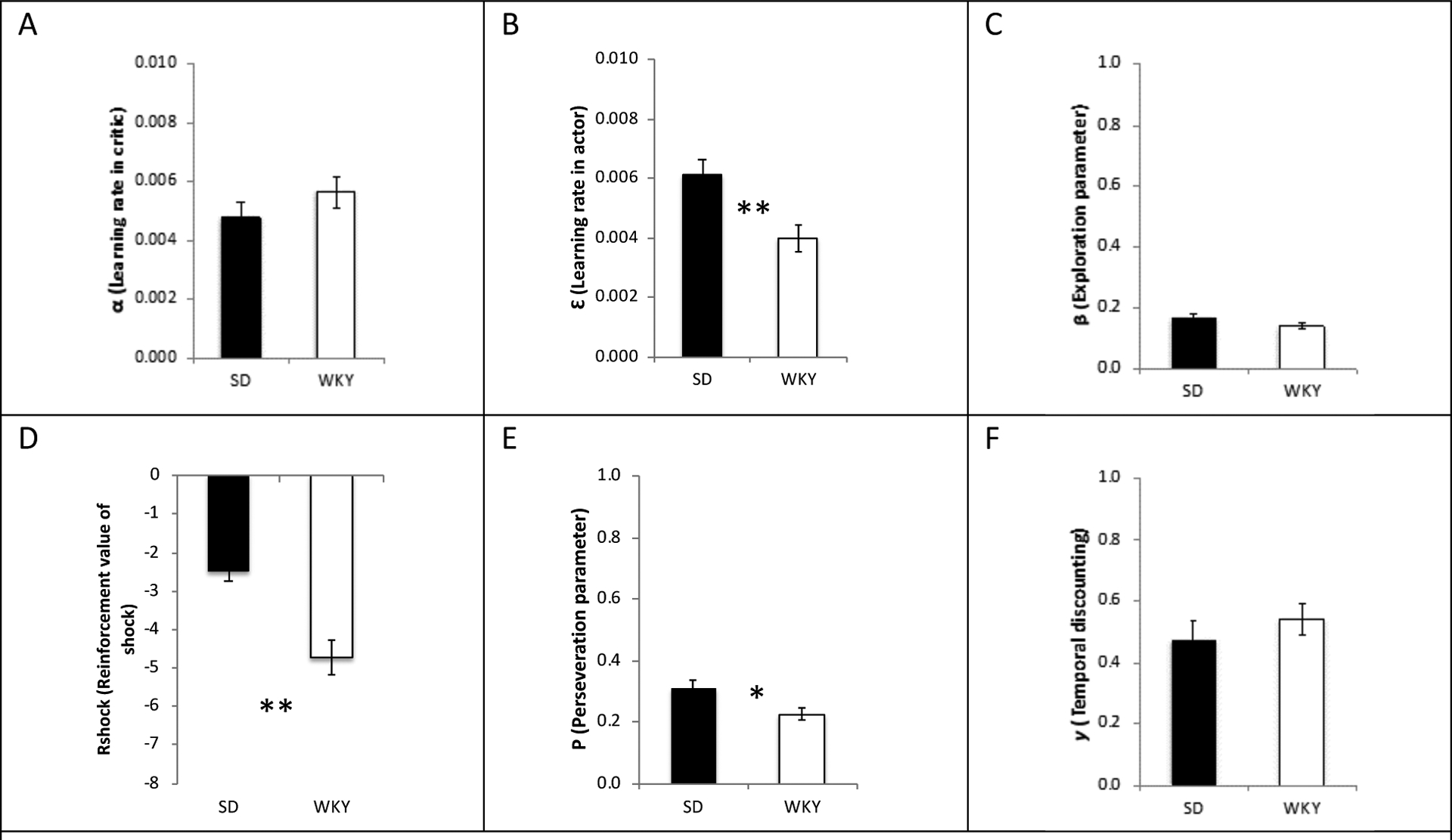
Mean best-fit parameter values for the SD and WKY groups. WKY rats had more negative values of R_shock (subjective value of the shock as a punisher) and lower values of ε (learning rate in the actor), compared to SD rats (both p<.002); the strain differences in P (perseveration) also approached corrected significance (p=.01), indicating less perseveration in the WKY. Error bars indicate ±1 SEM. Double asterisks indicate significance at p<.0083; single asterisk indicates .0083<p<.05.

To examine between-strain differences on individual parameters, we conducted post-hoc tests on each parameter (alpha corrected to 0.05/6=0.0083). The data were non-normal (Shapiro-Wilk test, p<0.025 for every parameter in both strains), so non-parametric tests (Wilcoxon rank sum) were used. These revealed significant strain differences in ε (W=1128, p<.002) and R_shock (W=1208, p<.001); strain differences in P approached corrected significance (W=1066, p=.01). No other strain differences approached significance (α: W=676, p=0.23; ϐ: W=940, p=0.13; γ: W=758, p=.68).

Overall, Model C succeeded in fitting the individual animal data better for SD rats than WKY rats, reflected in lower negLLE (SD: mean 1917.4, SD 457.4; WKY: mean 2121.5, 310.6) and also BIC (SD: mean 3886.6, SD 914.7; WKY: mean 4294.6, SD 621.1; Wilcoxon rank sum test W=551, p=.016).

3.3.2. Relationship Between Estimated Parameters and Behavior

Next, we explored the relationship between estimated parameters and animal behavior, scored as total percent avoidance (Figure 5) Considering the full set of 80 animals, there were strong negative correlations between avoidance behavior and estimated values of ε (Spearman’s r_s = −.32, p = .004), ϐ (r_s = −.44 , p < .001), R_shock (r_s = −.70, p < .001), and P (r_s = −.61, p = .001), while there were weak positive correlations between avoidance behavior and α (r_s = .11, p = .35) and γ (r_s = .16 , p = .16). Figure 5 shows two SD rats with very poor learning (% Avoidance < 25%); results were similar when these two points were excluded.

Figure 5.

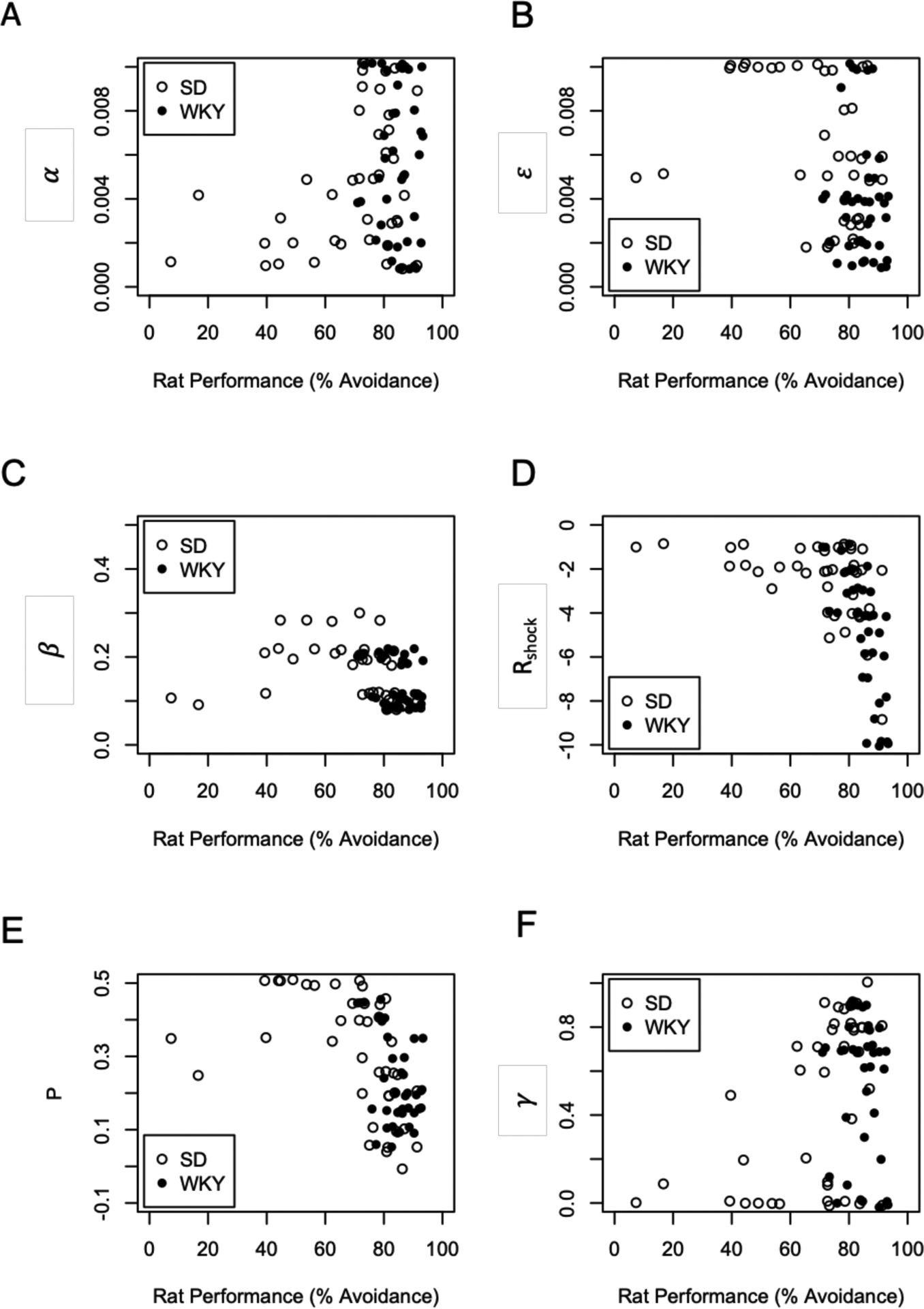
Relationship between behavior (percent avoidance responses across the acquisition training) and estimated parameter values. Across all 80 animals, rats showing more avoidance tended to have smaller values of ε (learning rate in the actor, p=.004), smaller values of ϐ (less exploration, p<.001), larger (more negative) values of R_shock (subjective value of shock, p<.001), and smaller values of P (less perseveration, p<.001). Results are similar if the two SD animals with poor performance (<25% avoidance) are excluded. These scatterplots include jitter to avoid overlapping points.

The negative correlations of ϐ, R_shock, and P with behavior would be as expected: lower tendency to explore, more strongly negative valuation of shock, and decreased perseveration, would all be expected to promote learning and expression of avoidance responses; the negative correlation of ε with performance may appear paradoxical, as higher learning rates would typically be associated with better learning, but in this case lower values of ε may protect the model from instability, producing incremental weight change in the actor rather than overwriting prior learning with large weight changes when an unexpected outcome is experienced.

Because there was considerably more variability in performance among the SD than WKY rats, we also performed correlation testing for each strain separately (alpha adjusted to .05/6=.0083); the general pattern of negative correlations of behavior with ε, ϐ, R_shock, and P remained in each strain separately, (Table 2), although correlations were generally weaker in the WKY rats (probably partly reflecting the fact that there was less variability in performance among inbred WKY rats); an exception is the relationship between behavior and R_shock, which was stronger in WKY than SD.

Table 2.

Spearman correlation r_s (and two-tailed p-value) for correlations between rat performance (% avoidance, averaged across the 12 acquisition sessions) and estimated values of each parameter, for SD and WKY strains.

	α	ε	β	Rshock	P	γ
SD (n=40)	+.24 (p=.130)	−.33 (p=.041*)	−.46 (p=.003**)	−.41 (p=.010*)	−.69 (p<.001**)	+.48 (p=.002**)
WKY (n=40)	−.07 (p=.680)	−.10 (p=.540)	−.27 (p=.095)	−.76 (p<.001**)	−.25 (p=.120)	−.21 (p=.190)

^*p<.05;

^**p<.0083.

Additionally, we analyzed the correlation between shocks and shock valuation (R_shock). There was a strong positive correlation between total number of shocks experienced and estimated value of R_shock (i.e., more strongly negative value of R_shock associated with fewer shocks experienced) (r=0.58, p<.001); this relationship remained even after controlling for the effect of strain (partial r=0.54, p<.001). For each animal, we calculated a total “shock cost,” defined as the absolute value of the animal’s estimated value of R_shock times the number of shocks that animal experienced [53]; there were no strain differences in this total “shock cost” (SD mean 835.5 std. dev. 509.6; WKY mean 784.1, std. dev. 572.2; Welch’s t(77)=0.42, p=0.67).

3.3.3. M and V Values at the End of Training

Finally, as a confirmation that the model had learned the task in a principled way under these estimated parameters, Figure 6A shows d-scores (m weights in the actor module, shown as difference between bias to press vs. not press) at the end of the final acquisition session. Positive d-scores indicates the probability of performing a lever press, whereas negative d-scores indicate the probability of withholding from lever pressing. As expected, d-scores are positive for danger and shock signals, and negative for the safety signal; d-scores are near zero for the two contexts, in the absence of these signals.

Figure 6.

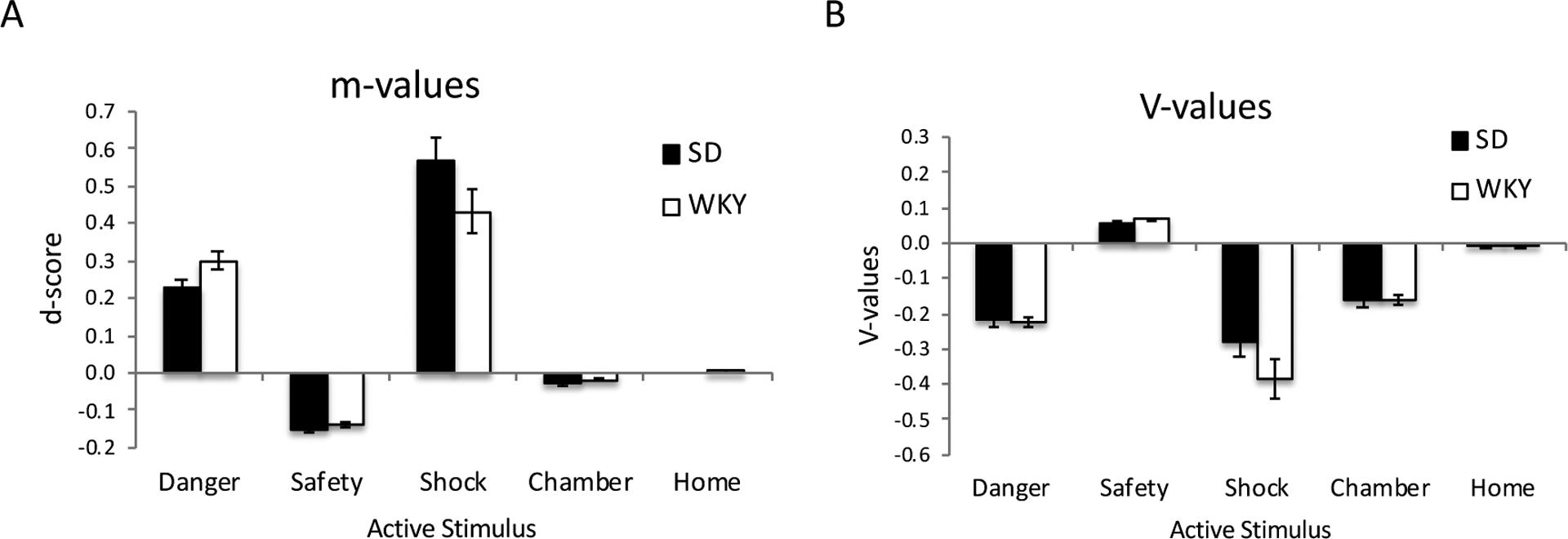
(A) Mean weights in the actor module (“m-values”) at the end of acquisition session 12, shown as a d-score (weight from each stimulus to “press” response minus the weight from that stimulus to “other” responses). The d-scores were positive for danger and shock signals, indicating a bias for the actor to select “press” when danger or shock is present; negative for safety, indicating a bias to select “other” when safety is present; and near zero for the contextual stimuli. (B) Mean weights in the critic module (“V-values”) at the end of acquisition session 12. As expected, weights were strongly negative for the danger signal, the shock, and the experimental chamber context (where danger and shock were experienced), positive for the safety signal, and near zero for the home cage (where danger, safety, and shock were never experienced). Y-axes are in arbitrary units; errors bars indicate ±1 SEM.

To examine possible strain differences in relative weighting of actions for the different stimuli, mixed ANOVA was performed on d-scores with within-subject factors of signal/context inputs (5 levels) and between-subjects factor of strain. Since Mauchly’s test indicated violation of the assumption of sphericity (W=0.001, p<.001), Greenhouse-Geisser correction was used (epsilon=.32) to adjust degrees of freedom. The ANOVA revealed significant within-subject effects of signal (F(1.3,88.8)=166.66, p<.001) and a signal x strain interaction (F(1.3,88.8)=3.74, p=.045), with no main effect of strain (F(1,78)=0.13, p=.717). Post-hoc tests (Welch’s t-test, alpha adjusted to .05/5=.001) revealed that strain differences in d-score for the Danger and Safety signals approached corrected significance, with WKY having stronger positive d-scores for Danger than SD (t(73.8)=2.25, p=.028) while SD had stronger negative d-scores for Safety than WKY (t(77.9)=2.08, .041); strain differences in d-scores for Shock, Chamber, and Home did not approach significance (all t<2, all p>.100). Results are similar if the two “non-learner” SD animals (identified in Figure 5) are excluded from analysis.

In the critic module, expectancy weights (V-values) appeared similar across strains (Figure 6B). Overall, state values were negative for the danger signal, shock, and the experimental chamber (where danger was experienced); V-values were positive for the safety signal, and near zero for the home cage (where danger, safety, and shock were never experienced). Again, Mauchly’s test indicated violations of the assumption of sphericity (W=.001, p<.001), so Greenhouse-Geisser correction was used (epsilon=.29) to adjust degrees of freedom. As expected, there was a significant effect of signal (F(1.2,90.5)=89.83, p<.001), but no main effect of strain or signal x strain interaction (both p>.100), indicating no reliable differences in V-values across strains.

3.4. Behavioral Recovery

As a measure of both reliability and predictive value of the RL model, behavioral recovery simulations were performed for both strains (Figure 7). Each curve in Figures 7B,C represents the performance of one simulated rat, averaged across 100 simulation runs using the estimated parameters for that rat. Within each strain, qualitative patterns are similar to the avoidance behavior observed in the individual animals (compare Figures 1C,D), with faster learning among WKY simulations and more variability among SD simulations.

Figure 7.

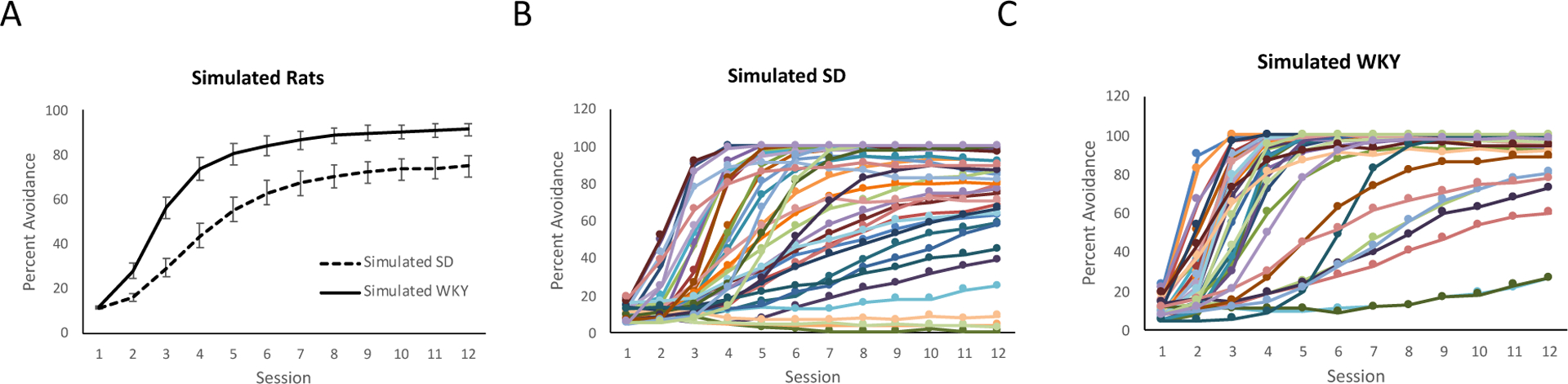
Results of behavioral recovery simulations. (A) Group performance, averaged across the simulated rats in each strain, using the best-fit parameters estimated for each rat. (B) Individual learning curves for the 40 simulated SD rats; each curve shows average percent avoidance responses for one simulated rat, averaged over 100 simulation runs per rat. (C) Individual learning curves for the 40 simulated WKY rats. All results are averaged over 100 simulation runs per rat. Errors bars in (A) indicate ±1 SEM.

Similarly, when the results from simulated rats are averaged for each strain (Figure 7A), the curves are qualitatively analogous to the grouped behavioral data (see Figure 1B). Mixed-design ANOVA was used to quantitively compare simulated strains; since Mauchly’s test indicated violations of the assumption of sphericity (W<.001, p<.001), Greenhouse-Geisser correction was used (epsilon=.21) to adjust degrees of freedom. As expected, there was a significant effect of session (F(2.3,180.2)=225.87, p<.001) as well as a main effect of strain (F(1,78)=12.85, p<.001) and a session x strain interaction (F(2.3,180.2)=5.29, p=.004), indicating faster learning in the WKY simulations than in the SD simulations, consistent with the empirical data.

4. DISCUSSION

Avoidance behavior is critical for an organism to interact with and ultimately survive within its environment. Acquisition and expression of avoidance may differ between individuals or populations, as in the increased and persistent avoidance observed in patients with anxiety and anxiety-related disorders such as PTSD. Thus, understanding the learning properties that may contribute to acquiring avoidance behavior would be useful. Animal models have been utilized to help understand avoidance behaviors, yet these behavioral models are limited by the costs in time and animals to parametrically explore all of the critical variables. In this regard, computational models are extremely useful, but reinforcement learning models have not yet been widely applied to animal behaviors, as animal studies tend to have low subject numbers. Thus, the current manuscript attempts to describe animal avoidance behavior by applying an RL model to a relatively large sample size of behaviorally inhibited WKY rats and outbred SD rats.

Using the performance of individual rats on an active avoidance task, the current study showed that an RL model was able to extract latent parameters to describe underlying learning processes. After estimating parameters for each animal, simulations incorporating these parameters were able to recapitulate both quantitative strain differences observed in the rats, as well as qualitative patterns of individual learning curves. This extends the findings of our previous work showing the ability of RL models to simulate both WKY and SD strains in this active avoidance task [39]. However, whereas the prior work used top-down assumptions to construct “SD-like” and “WKY-like” models, the current work shows that strain differences in behavior can emerge from a bottom-up, data-driven approach that does not embed pre-existing assumptions about the two strains. This data-driven approach allowed us to examine what parameters might differ across strains after the model had been fit individually to each animal in both strains.

Comparing across strains, the R_shock parameter significantly differed, with WKY rats tending to have larger (more strongly negative) values. One interpretation of the increased R_shock in WKY rats may be an enhanced motivation to escape or avoid foot shock, which would presumably result in faster and greater acquisition of avoidance as observed in WKY rats compared to SD rats [13,14]. Although the R_shock parameter in the model cannot differentiate between physical or psychological pain, we previously demonstrated that pain threshold using vocalization and flinch were similar between SD and WKY rats [14], suggesting that strain difference in R_shock may be more associated with psychological valuation of shock. This is supported further by the negative correlation between R_shock and number of shocks experienced. Further, this is congruent with the risk/loss aversion literature [54–57], as increased avoidance behavior coincides with a more negative evaluation of punishment.

Additionally, the estimated learning rate in the actor (ε) parameter was significantly slower in WKY than SD rats. This was an unexpected finding, as we did not assume any strain differences in ε in our previous modeling study [39]. The idea that WKY are slower to modify response rules to prevent footshock may appear paradoxical given their quicker acquisition of avoidance behavior. However, as noted above, lower values of ε may protect the model from instability, producing incremental weight change in the actor rather than overwriting prior learning with large weight changes when an unexpected outcome is experienced. Slower learning rate in the actor would also be expected to lead to slower extinction, as observed in WKY behavior [12,40,58]. The current bottom-up modeling approach thus identified an additional feature that may distinguish avoidance learning between SD and WKY strains, one that is not obvious from examination of behavioral data alone.

Strain differences in estimated values for the perseveration parameter (P) also approached corrected significance, with SD rats showing higher values of P than WKY rats (Figure 4C). In the context of the RL model, the tendency to perseverate reflects a bias to continue repeating recent actions, regardless of reinforcement. In the current paradigm, one result of a high value of P would be that a rat which has recently emitted a lever press response would be likely to repeat that action, while one which has not recently emitted a lever press response would be less likely to spontaneously emit such a response. For example, in the escape/avoidance paradigm, sessions are separated by overnight time in the homecage, where no lever is available (and lever press responses cannot occur). Animals with high value of P might be less likely to spontaneously switch to emitting lever press responses when returned to the experimental chamber at the start of the next session. Consistent with this interpretation, our lab has previously demonstrated that SD rats display “warm-up”, a decreased rate of lever pressing behavior at the beginning of an avoidance session, compared to WKY who often emit lever presses on the very first trial of a session [10]. Indeed, our prior modeling paper showed that variations in P could help explain warm-up and several related phenomena in rats [39].

In addition to strain differences in P, our prior paper also suggested reduced values of the exploration parameter ϐ in WKY rats [39]. In the current bottom-up approach, SD and WKY rats did not differ in ϐ, although the values of ϐ were numerically lower in WKY than SD (Figure 4C). We also found no significant strain differences in temporal discounting of expected future outcomes (γ). In their own right, the lack of significant difference between strains for each these parameters indicates decreased support for alternative explanations of avoidance behavior. WKY rats have demonstrated a decreased exploratory tendency in open field and elevated T-maze [9,59], data which have been used to define WKY as an behaviorally inhibited strain. Although WKY show decreased exploratory behaviors, it does not appear to directly contribute to the differences in active avoidance acquisition between SD and WKY rats. Likewise a tendency to overvalue immediate/recent reward has been proposed to be involved in anxiety-like behaviors [60,61], as well as in comorbid disorders such as depression [62] and substance abuse [63], which are disorders that seem to share similar behavioral and neurobiological mechanisms as anxiety [64,65]. Again, this overvaluing of immediate reward did not appear to contribute to the increased avoidance seen in the WKY strain.

Despite strain differences in the estimated learning rate in the actor (ε), no significant difference was found between strains in estimated values of learning rate in the critic (α), indicating WKY and SD rats learn state valuations at a similar rate. Interestingly, the dorsal striatum is often considered the biological correlate of the actor, whereas the critic is usually associated with the mesolimbic dopamine system [66–68]. Our lab has found that WKY and SD rats have differences in synaptic plasticity (long-term potentiation) in memory and valuation circuits [69,70], which seems parallel to the idea of reduced learning rate in the actor, and provides a potential linkage to neural mechanisms that could contribute to the behavioral differences seen between these strains.

While the current findings do not rule out the possible contributions of critic learning rate, delay discounting, or explore/exploit tendencies in behaviorally inhibited WKY animals, the contribution of the RL model is to suggest that these factors are not necessary to explain the observed behavior, and that a more parsimonious description of the results would focus on strain differences in the motivational value of punishers and in learning action-selection rules. This in turn could suggest future empirical experiments to examine brain substrates of reward and punishment to see if important strain differences exist.

In addition to examining estimated parameter values, we also examined the weights learned in the actor model, examined as d-values for making the “press” response to each of the stimuli. Our prior empirical work indicated that SD and WKY rats used danger and safety signals differently after acquisition of avoidance [14]. Specifically, WKY rats were more likely than SD rats to lever press in the presence of danger signals, whereas SD rats were more likely than WKY rats to withhold lever pressing in the presence of safety signals. Based on these previous results, it was expected that learned m-values for “lever press” in the presence of the danger signal would be stronger in simulated WKY rats compared to SD rats. Likewise, m-values opposing (inhibiting) “lever press” in the presence of the safety signal were expected to be stronger for simulated SD rats than WKY rats. Our results are in partial agreement with these findings, as results from the model showed strain differences in the expected directions, although falling short of significance. Similarly, no strain differences were seen in the critic as marked by learned V-values. This could indicate a subtlety of the animal data which is not well-captured by the model, but it could also reflect the fact that learned stimulus-response patterns at the end of acquisition do not differ greatly across strains, i.e., the important strain differences may emerge during learning, rather than in a well-learned behavior. At this point, further behavioral studies are indicated to better understand the ways in which signals control behavior in SD and WKY rats, but RL models could be useful by allowing researchers to search a large space of possible experimental manipulations relatively quickly and cheaply, without cost of animal life, to determine which specific future experiments may be most likely to generate robust between-group differences.

Another interesting point emerging from the model concerns the within-subject relationships between estimated parameters and behavioral performance (Figure 5; Table 2). Among SD rats, the relationship between γ and performance was significant. Among WKY rats, the correlation between R_shock and performance was much stronger than the comparison in SD rats, while that between γ and performance was significant in SD but not WKY. While negative results must be interpreted with caution due to reduced power after subdividing the data, this pattern nevertheless suggests an interesting difference between strains. At least in “control” SD rats, avoidance behavior increased with decreasing γ. A lower valuation of γ is associated with the tendency to prefer immediate rewards and discount future rewards. This falls in line with recent studies linking temporal discounting with the brain substrates that mediate avoidance learning [71,72]. The lack of correlation observed in WKY for γ - as well as β and P - may simply reflect their uniformly high level of performance. Despite this, both SD and WKY rat performance correlated with R_shock. This appears to fit with existing data in that reinforcement valuation plays a critical role in how individuals attain high rates of avoidance [13,73–75].

An alternative explanation for our data is that SD rats may be intentionally delaying an avoidance response in order to delay subsequent trials, thus postponing future punishment. This approach has been previously described as “sloth” behavior [76]. However, as noted above, γ, a measure of delay discounting, did not differ significantly between strains but was, if anything, numerically lower in SD (Figure 4F). Indeed, recent studies from our laboratory showed that removing the immediacy of danger signal termination upon lever pressing increased avoidance latency and decreased total avoidance responding regardless of strain, thus resulting in increased immediate punishment [77]. Thus, the current data support the idea that psychological valuation of shock is a primary driving factor behind avoidance behavior.

The current study, however, is not without limitations. First and most important, the current study (like any latent parameter analysis method) is correlative and cannot establish causation. That is, it can detect patterns in the dataset, and propose mechanistic variables (such as R_shock) that could produce these patterns, but it cannot definitively prove that the hypothesized mechanisms are driving behavior. Rather, the model suggests plausible mechanisms that are sufficient to explain the observed behavior. These results must be validated in additional datasets, and tested with empirical studies in which the mechanisms can be explicitly manipulated to examine their effects on behavior. Another limitation of the current study was its focus on empirical data obtained from male rats. Female SD and WKY rats have shown different tendencies in avoidance learning [11,78]. Thus, future work should investigate avoidance behavior in female rats using the RL model.

Although RL modeling has proven useful in understanding reinforcement learning, the model may not encompass all aspects of reinforcement learning. RL modeling alone fails to represent neurobiological mechanisms that may account for the behavior. On the other hand, previous studies have shown RL models to correlate with dopaminergic activity in striatum during reward [30–32]. Further, the RL model does not consider how learning may be modulated by emotional or neurochemical states. Thus, important factors that distinguish WKY and SD rat learning may still be veiled despite the use of RL modeling. Nevertheless, the current study does suggest that strain differences in the motivational value of aversive stimuli can adequately explain observed differences in avoidance behavior.

5. Conclusions

In conclusion, the RL model successfully described WKY and SD rat behaviors in the acquisition of an active avoidance task. The RL model identified latent parameters that influenced avoidance acquisition in both SD and WKY rats. Further, the model simulated the performance of individual rats. The valuation of punishers (or aversive stimuli and events) appears to play a significant role in how behaviorally inhibited and non-inhibited animals acquired avoidance behavior. Overall, motivational processes seem to be the underlying factor leading to individual differences in this avoidance task. This work opens the door to expand the use of RL modeling of animal behaviors in avoidance as well as other animal behavioral tasks.

ABBREVIATIONS:

WKY

Wistar Kyoto

SD

Sprague Dawley

RL

Reinforcement Learning