Abstract
Hv1 is a voltage-gated proton channel whose main function is to facilitate extrusion of protons from the cell. The development of effective channel blockers for Hv1 can lead to new therapeutics for the treatment of maladies related to Hv1 dysfunction. Although the mechanism of proton permeation in Hv1 remains to be elucidated, a series of small molecules have been discovered to inhibit Hv1. Here, we computed relative binding free energies of a prototypical Hv1 blocker on a model of human Hv1 in an open state. We used alchemical free energy perturbation techniques based on atomistic molecular dynamics simulations. The results support our proposed open state model and shed light on the preferred tautomeric state of the channel blocker. This work lays the groundwork for future studies on adapting the blocker molecule for more effective inhibition of Hv1.
Subject terms: Cancer, Ion channels, Ion channels, Biophysical chemistry, Thermodynamics, Computational chemistry, Molecular dynamics, Statistical mechanics
Introduction
The flux of ions across the cell membrane is regulated by a variety of ion channels. Hv1 is a voltage-dependent ion channel whose main function is to conduct protons through the cell membrane. Like voltage-dependent metal ion channels, the activation of Hv1 is regulated by voltage-sensing domains (VSDs), which are transmembrane modular units that detect changes in the membrane potential. However, in contrast to voltage-dependent metal ion channels, Hv1 lacks a separate pore domain as the VSD is sufficient for proton permeation in addition to mediating channel gating1–3. The action of Hv1 contributes to physiological processes such as the production of reactive oxygen species, the bioluminescence of dinoflagellates, and the maturation of human sperm4–6. Hv1 expression was found to be selectively enhanced in metastatic relative to non-metastatic breast tissue and inhibition of Hv1 was shown to reduce cancer metastasis and tumor development7–9. More generally, the development of inhibitors to block the Hv1 channel may also lead to therapeutic benefit for other Hv1-related maladies, including allergies10,11 or exacerbated brain damage in ischemic stroke12.
The full structure of human Hv1 has not yet been experimentally determined. Human Hv1 is a homodimer, but each monomer has its own pore and can function independently13,14. We recently developed an atomistic model of the human Hv1 VSD open state using molecular dynamics (MD) simulations on the microsecond timescale in a hydrated lipid bilayer under an applied membrane potential15. As discussed in Geragotelis et al.15, there exist other proposed structures for the human Hv1 open state16–20, which differ in the way they were generated or the templates they were based upon. These other structures were either modeled from crystallographic structures of voltage-gated ion channels which do not contain a native permeation pathway through the VSD16–18,20, or they have alternative VSD conformations from restraints applied during MD simulations19. Our structure was modeled starting from the crystal structure of a chimeric construct based on mouse Hv1 in a putative closed state21 from which we generated closed and open state configurations exclusively of the applied membrane potential. The elicited conformational changes were consistent with the mechanism of activation proposed for metal ion channel VSDs22–24. Further investigation of our open state model with respect to small molecule inhibitor binding would contribute to its validation and refinement and pave the way to designing more effective channel blockers.
Effective inhibition of Hv1 can be achieved by ligands that bind the extracellular side of the channel, including Zn1,2,25; small peptide toxins such as Hanatoxin, C6, and AGAP/W38F26–28; or by ligands that bind the cytoplasmic side, such as guanidine derivatives29,30. We focus on a representative guanidine derivative, 2-guanidinobenzimidazole (2GBI), to understand how it binds to the channel. Compounds targeting the VSD often have multiple targets31,32. However, the open state VSD in Hv1 is more hydrated compared to non-conducting VSDs and offers enough space for 2GBI to bind at a location that, in other VSDs, is occupied by S4 arginines33–36. We propose that this feature could be exploited for the development of Hv1-specific drugs. 2GBI and related compounds can produce maximal inhibition of human Hv1 of > 90% and can block Hv1 both at the plasma membrane and in intracellular compartments. The binding of 2GBI to Hv1 is described as a “foot in the door” mechanism of block, by which binding of the ligand prevents channel closure and slows down channel deactivation23. There is currently no known experimental structure of 2GBI in complex with Hv1, and the details of 2GBI binding are not completely known; however, mutagenesis experiments29 suggest several key residues that play a role, including the selectivity filter D11237 as well as F150 and R211 lining the central constriction region16.
The structure of 2GBI (Fig. 1, top) was rationalized by the fact that Hv1 is inhibited by the guanidinium ion13 which is structurally similar to the voltage-sensing arginine residues in the S4 helix38. 2GBI is a more effective inhibitor for Hv1 than guanidinium with the addition of its benzimidazole moiety. Despite that fact, replacement of one nitrogen atom on the five-membered ring by an oxygen atom resulted in less effective inhibition than even guanidinium23. Details of the binding site aside, this raises the question of the structure and charge distribution of 2GBI in relation to its tautomeric forms39.
Figure 1.
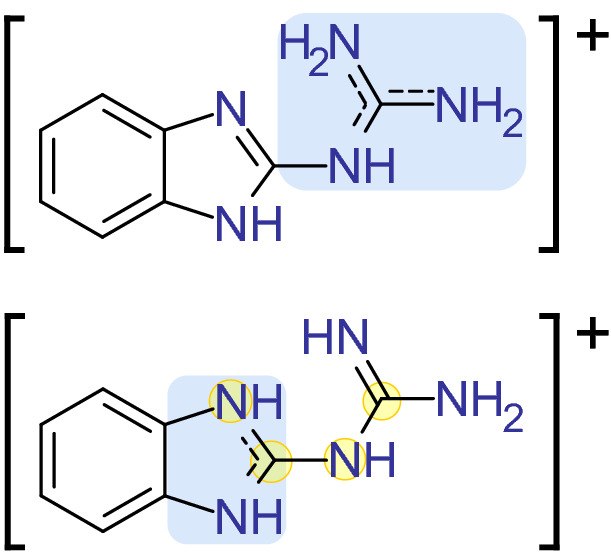
Two tautomers of 2GBI are investigated in Hv1 binding: “gbi1” (top) and “gbi2” (bottom). Blue regions have higher positive charge density. Yellow circles mark atoms of the dihedral angle selected for the dihedral scan in this work.
In this work, we studied the binding of 2GBI to our open state human Hv1 model15 using alchemical free energy perturbation with atomistic molecular dynamics simulations. We considered a series of six protein mutations previously shown to alter 2GBI apparent binding affinity, and we computed relative binding free energies of these mutations compared to wild type Hv1 for two tautomeric forms of the inhibitor. This work reveals structural characteristics of 2GBI binding, emphasizes the prevalence of gbi2 in binding Hv1, and may inform future efforts to optimize small molecule blockers of Hv1.
Methods
Ligand parameterization with CGenFF
Our study examines two tautomers of the positively charged 2GBI, depicted in Fig. 1. Both of these structures contain a guanidine-like moiety but have different centers of excess charge, located in either the guanidine region (gbi1) or in the central imidazole moiety (gbi2). The force field for each tautomer was developed using the CHARMM General Force Field (CGenFF)15,40,41. We generated reference structures from gas phase quantum mechanical (QM) geometry optimizations using the Psi4 software package42. We employed the MP2/6-31G* method43–47 to stay consistent with CGenFF development41. The generated gbi2 force field was modified to achieve better agreement regarding the geometry-optimized structures between the force field and QM results. The force field modification details and final parameters for both ligands can be found in the supplementary information (“Ligand parameterization for 2GBI”).
Docking calculations and pose refinement with molecular dynamics simulations
We docked each tautomer of 2GBI into Hv1 with AutoDock Vina version 1.1.248. Twenty protein configurations were selected from a ~ 33 μs simulation15, and we removed the membrane and all water molecules during docking. While the presence or absence of water molecules may influence results from docking49,50, specific water molecules involved in binding 2GBI are as of yet unknown. Thus, our aim in docking was just to generate an initial set of binding poses to be further refined in MD simulations, which allow waters to rearrange as they prefer. The ligand dihedral angle, defined by the four atoms marked in Fig. 1 (bottom), was held fixed in a planar conformation to prevent high-energy initial structures resulting from strained non-planar conformations (see Supplementary Information Figs. S1, S4).
The resulting poses were filtered by a “reverse clustering” technique. We used the Clustering plugin51 in VMD52 to cluster all poses by root mean square deviation (RMSD) with a 3.0 Å cutoff. We retained poses that were distinct from each other by more than this threshold. This process yielded a diverse set of starting poses ensuring good coverage of the multiple possible binding modes in the binding site, allowing minor differences between similar poses to be explored by our subsequent MD simulations. Each binding pose was placed back into its hydrated protein-membrane configuration, and we removed water molecules overlapping within 2 Å of the ligand, otherwise retaining original hydration of the pore.
We then ran short (5 ns) MD simulations for all distinct poses of each 2GBI tautomer using the NAMD software package, version 2.1153. Prior to dynamics, 5000 minimization steps were performed using the conjugate gradient algorithm. Backbone alpha carbon atoms were fixed during minimization using harmonic position restraints with a force constant of 1 kcal/mol/Å. The restraints were gradually turned off over 400 ps. Dynamics were then run with a 2 fs time step in the isothermal-isobaric ensemble at a temperature of 300 K and a pressure of 1 bar. The Langevin thermostat was applied with a damping constant of 5 ps, and the Langevin piston method was applied with an oscillation period of 200 fs and a damping time of 100 fs. Periodic boundary conditions were applied in all dimensions, with the z-axis normal to the membrane bilayer. The SHAKE algorithm was used to restrain all bonds involving hydrogen atoms to their equilibrium values. Long-range electrostatic interactions were applied with the Particle Mesh Ewald (PME) algorithm; short-range Lennard-Jones and Coulombic interactions were calculated using a cutoff of 12 Å and a switching function applied beyond 10 Å. Bonded interactions and short-range forces were calculated every 2 fs, and long-range forces were calculated every 4 fs. An electric field was applied using a field vector of 0.14 kcal/(mol Å e) in the z direction, corresponding to a depolarizing membrane potential of +150 mV.
The final poses selected for free energy calculations were chosen based on the stability of the ligand in the binding position as well as evaluation of the hypothesized placement of 2GBI from experimental double-mutant cycle analyses29. Our evaluation criteria for pose analysis is outlined in the supplementary information (“Pose selection and refinement with MD”). The poses were equilibrated for at least 20 ns before initiating free energy calculations. We verified that the pore retained hydration in each of the docked configurations during the equilibration simulations (see Supplementary Information Fig. S6).
Configurations from our MD simulations for pose refinement and subsequent free energy calculations were all rendered using VMD version 1.9.352.
Alchemical free energy calculations
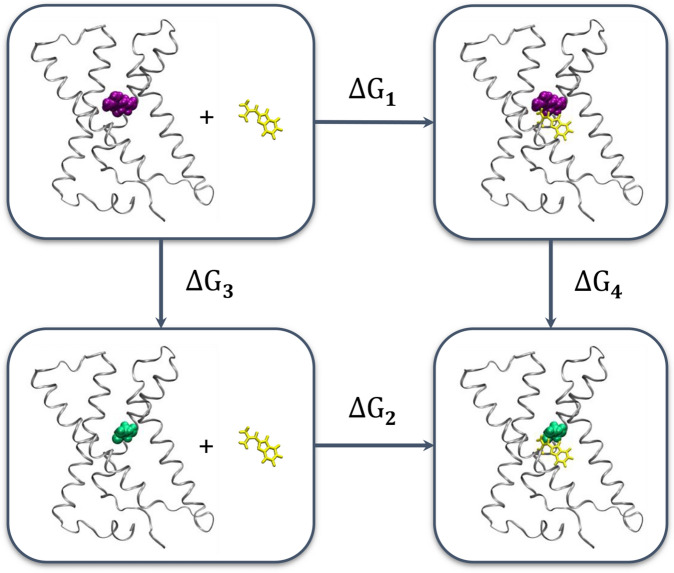
We applied the thermodynamic cycle approach as depicted in Fig. 2 to calculate the change in the binding free energy of 2GBI from wild type Hv1 to the following protein mutations: D112E, V178A, S181A, V109A, R208K, and R211S. The first and last single letter codes denote the starting and final amino acids, respectively. The relative binding free energy in this cycle is calculated as the difference in the free energies of mutation from the holo state to the apo state, i.e., . The computed values were evaluated alongside the relative binding energies from experimental mutagenesis studies29, which correspond to processes and of the thermodynamic cycle; i.e., .
Figure 2.
Thermodynamic cycle used to compute relative binding free energies. The initial side chain from wild type Hv1 is shown in purple vdW spheres, and the final side chain after alchemical mutation of Hv1 is shown in green vdW spheres. The 2GBI ligand is drawn in yellow licorice. The membrane and water molecules are not shown for clarity. The relative binding free energy from experiment is calculated from , which is thermodynamically equivalent to the alchemically computed relative binding free energy of .
Processes and of the thermodynamic cycle represent the alchemical transformations conducted computationally. The initial and final states for each of and are connected through a series of non-physical intermediate states (“ windows”) that comprise the alchemical transformation. This transformation is controlled by a parameter , starting from a value of zero at the initial state (i.e., wild-type protein residue) and reaching a value of one at the final state (i.e., mutant protein residue).
The alchemical transformation is subdivided into 40 equivalently spaced windows, such that the first window ranges from to and the final window ranges from to . With simple linear modification of interactions, “end point catastrophes” may result when () or (), during which incoming atoms may appear where other particles already exist54. We avoid this by applying a soft-core potential on perturbed atoms to gradually scale their short-range nonbonded interactions with the rest of the system55.
Each alchemical transformation was conducted in both the forward and reverse directions (e.g., aspartate mutated to glutamate as well as glutamate mutated to aspartate) to facilitate convergence and sampling of overlapping phase space of the end states. While the free energy difference between two states can be determined by the Zwanzig relationship56, this method is often slow to converge and results in poor phase space overlap57,58. The Bennett acceptance ratio (BAR)59 minimizes the statistical variance between two ensembles with overlapping configurational space and yields the optimal averaging of the forward and reverse simulations. We used BAR to combine the data from both directions to estimate the final free energies for each of and . The reported uncertainties of the relative binding free energies are the root sum square values of the and standard errors from BAR.
A dual-topology paradigm was applied throughout the alchemical transformation in which both the initial and final states were simultaneously present but non-interacting. Only nonbonded interactions for perturbed (incoming or outgoing) atoms contributed to the cumulative free energy. Van der Waals interactions were scaled as a function of across the full range from zero to one. Electrostatic interactions of the annihilating atoms were linearly decoupled over the first half of the transformation ( to ), after which electrostatic interactions were linearly coupled for the incoming atoms.
We computed the relative binding free energies using alchemical free energy perturbation with atomistic molecular dynamics simulations in NAMD53. Each window started from the same initial hybrid structure and comprised 1,000 minimization steps, 1 ns of equilibration, and 4 ns of production. The MD simulation settings were maintained as described earlier. For each protein mutation, we simulated a total of 400 ns, consisting of 5 ns in each of the 40 windows for the forward and reverse directions. The data from each window was subsampled to extract uncorrelated, effectively independent samples using the pyMBAR Python package60. For all apo/holo states, ligand tautomers, and protein mutations represented in this study, including mutation S211R (see “Results and discussion” section), the total simulation time is 8.4 μs.
We modified our standard setup for free energy calculations for mutations R208K and R211S. In these two cases, we additionally applied flat-bottom distance restraints to prevent hypermobility of the arginine and lysine residues. During normal MD simulations, these positively charged side chains are involved in salt bridge interactions with nearby acidic residues. Residue 208 is in proximity to D119, D123, and E192, and residue 211 is in proximity to D112 and D185. However, these salt bridges are not able to be maintained during the alchemical transformations because of the decoupled nonbonded interactions in the dual-topology hybrid molecule. In other words, considering the case of R208K when arginine is mutated to lysine, arginine is fully interacting and present at the start, when . In the final stage when , arginine is now non-interacting with the system and therefore does not form its usual contacts. The non-interacting, flexible side chains end up sampling an artificially broadened area of phase space. This improperly skews the phase space overlap between the forward and reverse calculations and adversely affects the free energy estimate (see “Results and discussion” section). To avoid this issue and improve convergence of the calculations, we added additional distance restraints on the flexible mutating residues for R208K and R211S. The flat-bottom restraints were applied from the terminal nitrogen atom in arginine or the terminal carbon of lysine to surrounding protein residues that were not involved in the alchemical transformation. The reference distances were chosen to be large enough such that the restraint energies were zero when applied to the initial or final structure yet restrictive enough to prevent excessive side chain mobility during the free energy calculations (see supplementary information: “Flat-bottom restraints for mutations involving Arg or Lys residues”). The force constants on the restraint walls were set to 10 kcal/mol/Å.
Because some of our free energy calculations involved changes in formal charge, it was necessary to take particular care in these cases. Specifically, following the free energy simulations, we accounted for the energetic contribution arising from the change in net charge in the R211S mutation. To do this, we applied analytical corrections for the electrostatic finite-size effects as described by Rocklin et al.61. That being said, these corrections were found to have almost no impact on the final relative binding free energies as we show in the "Results and discussion" section.
Results and discussion
We employed docking calculations, atomistic molecular dynamics simulations, and alchemical free energy calculations to examine the binding of 2GBI to human Hv1 (Fig. 3). We computed relative binding free energies for a series of six protein mutations compared to wild type Hv1. Each set of binding free energy calculations was conducted for two tautomers of 2GBI, gbi1 and gbi2, which vary in their centers of excess charge (Fig. 1). Our results show general qualitative agreement with experimental mutagenesis data and suggests that one tautomer may be more relevant than the other in the protein-bound configuration. We also discuss some limitations when carrying out alchemical transformations of flexible protein side chains.
Figure 3.
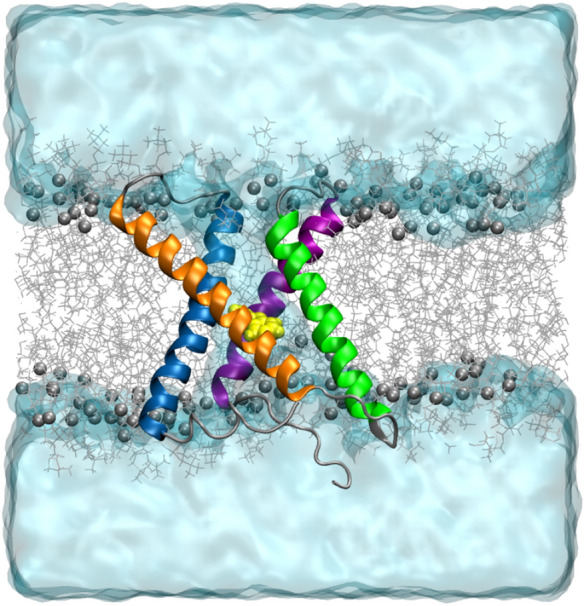
Configuration snapshot of 2GBI (gbi1) bound to Hv1, rendered in VMD52. The four alpha helical segments of Hv1 are colored as follows: S1 in blue, S2 in orange, S3 in green, and S4 in purple. 2GBI is shown in yellow with the VDW representation. Waters are drawn in slabs of light blue, and lipids are depicted as gray sticks with their carbonyl carbons shown as vdW spheres. The extracellular region is on top.
Positioning of 2GBI tautomers within the Hv1 open state
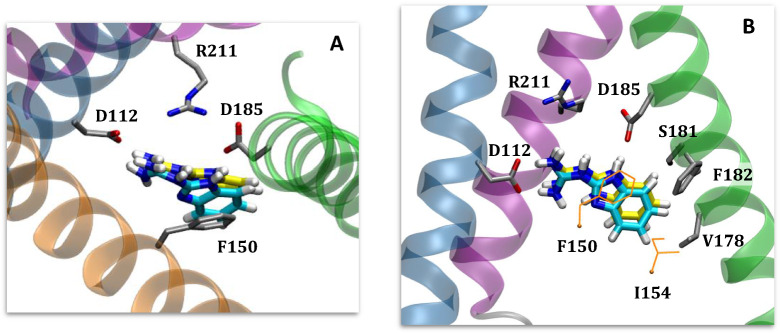
From the docking calculations, we employed a “reverse clustering” approach to identify 2GBI binding poses (see Methods). That is to say, because the binding mode is unknown and given that docking does not predict definitive binding modes, we aimed to sample a variety of potential poses of 2GBI within the expected binding region in order to find the most reasonable binding mode. The resulting poses from docking calculations were assessed using the predicted interactions between 2GBI and Hv1 from experimental mutagenesis data29. Hong et al. proposed a model of binding involving residues D112, F150, S181, and R211. For both gbi1 and gbi2, we selected binding poses where 2GBI was in close enough proximity to interact with these residues. Based on these poses, we note likely contacts with two additional residues, D185 and F182.
Following refinement in MD simulations, we selected a binding pose (Fig. 4) with the following features: interactions of the guanidine region with the charged residues D112 and R211; hydrogen bond donation from one of the imidazole NH groups to acidic residue D185; and proximity of the hydrophobic residues F150, I154, and F182 to the benzimidazole moiety. While D112 and R211 are believed to interact in the open state conformation of Hv162, the presence of 2GBI as a channel blocker in the proposed binding site necessarily interrupts this salt bridge formation. We chose the same binding pose for gbi1 and gbi2.
Figure 4.
2GBI docked into the open state model of human Hv1, rendered in VMD52. The binding pose is consistent with experimental mutagenesis data. Segments are colored in the same manner as in Fig. 3. The ligand is colored cyan for gbi1 and yellow for gbi2. (A) Top-down view from the extracellular end of the channel of bound 2GBI. Loops are hidden for viewing clarity. (B) Lateral view of Hv1 (extracellular side on top) with S2 hidden for clarity. The two residues F150 and I154 are part of S2.
Our pose is distinct from that proposed in recent work by Gianti et al.19 who performed induced fit docking of 2GBI (our gbi1 structure). They obtained a binding pose in which 2GBI is roughly in the same region of Hv1 but angled differently such that the benzo moiety of 2GBI is closer to S1 than to S3. The location of the guanidine group in our pose pointing to R211 is more consistent with experimental work29. Differences in binding configuration may be in part due to differences in our open state models15.
Chamberlin et al. also described a binding site for 2GBI, using the ligand model we refer to as gbi1, docked into a model of Ciona intestinalis Hv1, which itself was based on the crystal structure for the open state chimeric channel Kv1.2-2.118,63. Their ligand position is similar to our results in that the 2GBI benzo moiety is adjacent to F150; however, their binding pose has the guanidine moiety of 2GBI pointing towards the intracellular end of the channel in contact with E153, D174, and E171. While the salt bridge patterns are similar between both protein models, the Chamberlin et al. protein structure has S2 in a relatively higher position (towards extracellular side) than the other segments. Protein models notwithstanding, this intracellular-pointing ligand orientation would preclude any interactions with S181 or R211 as proposed by Hong et al.29 (see Supplementary Information Fig. S7). Neither of Gianti’s or Chamberlin’s studies considered alternate tautomers or binding free energy calculations.
Calculation of relative binding free energies
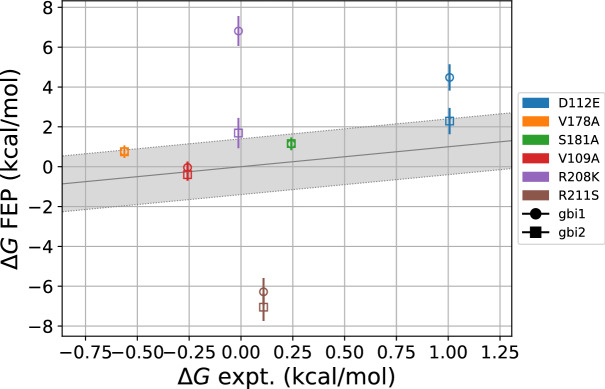
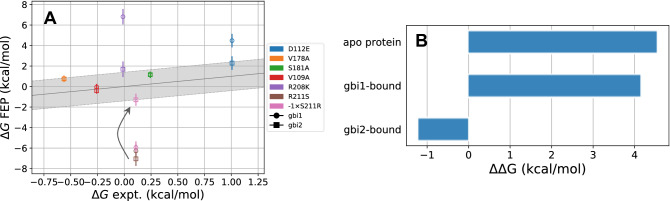
We calculated the relative binding free energies for two tautomers of 2GBI binding to wild type and mutant Hv1 using our open state model. The relative binding free energies were computed using molecular dynamics simulations with alchemical free energy perturbation. We considered six Hv1 mutations, previously reported by Hong et al. using electrophysiological and site-directed mutagenesis experiments29. Compared to 2GBI binding to wild type Hv1, these mutations comprise the effects of unfavorable binding (D112E, S181A), favorable binding (V178A, V109A), and relatively no change in the binding free energy (within ~0.1 kcal/mol: R208K, R211S). These values are plotted in Fig. 5 and listed in Table 1. Overall, with the exception of R211S, the calculated values are in good qualitative agreement with the experimental mutagenesis data which contributes to the validity of our open state Hv1 model. Between the two 2GBI tautomers, the results for gbi2 are more consistent with experiment. The mean absolute error (MAE) for gbi2 is 2.1 kcal/mol, compared to gbi1 with an MAE of 3.2 kcal/mol, which suggests that gbi2 may be the more prevalent species. Without consideration of R211S (discussed later), the MAE improves to 1.1 kcal/mol for gbi2 and 2.5 kcal/mol for gbi1.
Figure 5.
Relative binding free energies for the two 2GBI tautomers and six protein mutations considered. The error bars represent the root sum square values of standard errors from the Bennett acceptance ratio for the apo and holo states. The shaded region represents ±1.4 kcal/mol from the experimental value, representing a 10-fold change in the equilibrium constant. Alternate tautomers use different symbols. The markers for V178A (orange) and S181A (green) overlap for gbi1 and gbi2. Computed relative binding free energies are in qualitative agreement with experimental data, especially for gbi2.
Table 1.
Binding free energies of 2GBI (gbi1 and gbi2) to Hv1, for mutant Hv1 compared to wild type Hv1. The uncertainties represent the root sum square values of standard errors from the Bennett acceptance ratio for the apo and holo states. The data presented here is also plotted in Fig. 5.
| mutation | expt | gbi1 | gbi2 |
|---|---|---|---|
| D112E | |||
| V178A | |||
| S181A | |||
| V109A | |||
| R208K | |||
| R211S |
Protein mutations which involve charged side chains (D112E, R208K, and R211S) are more challenging for which to compute binding free energies compared to mutations having neutral residue end states. D112E involves charge movement by the addition of a methylene group, R208K changes the charge density of the cationic region64, and R211S changes the charge of the system from neutral to −1 e. There are greater disparities in the relative binding free energies of gbi1 and gbi2 for these three mutations, with gbi2 values generally closer to experiment.
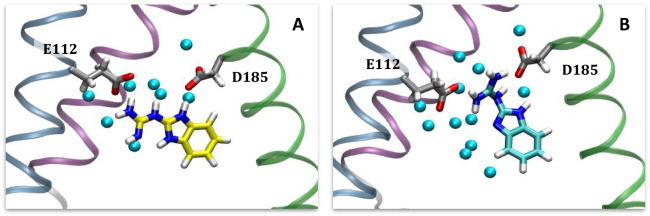
Compared to WT, the reported experimental value for the D112E mutation leads to a change in binding free energy of + kcal/mol. In our simulations, this mutation induced a shift in the gbi1 ligand orientation after ~5 ns as gbi1 rotates to prevent crowding of the glutamate residue and to maximize interactions of its guanidine moiety (Fig. 6). Lengthening of the side chain of residue 112 appears to encroach on the binding site and affect the native hydrogen bonding interactions between the positively-charged 2GBI and the nearby acidic side chains of residues 112 and 185 (see Supplementary Information Fig. S8). This crowding may explain the unfavorable binding represented by the relative binding free energy.
Figure 6.
2GBI bound to the human Hv1 D112E mutant in the (A) gbi2 and (B) gbi1 systems, rendered in VMD52. The ligand and surrounding residues are displayed in licorice representation, and the oxygen atoms of waters within 3 Å of the ligand are shown as light blue spheres. Concerning hydrogen bonding interactions between 2GBI and the neighboring acidic residues E112 and D185, the tautomer gbi1 does not contain a protonated imidazole region as in gbi2 (see Fig. 1). It seems for this reason that gbi2 maintains its original binding pose after mutation, while gbi1 reorients in order to maximize the interactions of its more positively charged guanidine moiety with both E112 and D185.
Of the mutations considered here, the V178A mutation is most favorable for binding 2GBI, with an experimental relative binding free energy of kcal/mol compared to wild type. In contrast, our predicted value was between 0.7 and 0.8 kcal/mol for both tautomers, indicating binding becomes less favorable. We wondered if the experimental value reflected additional protein rearrangements not captured in the timescale of our MD simulations. To explore this further, we focused on a nearby aromatic residue, F182, in proximity to both V178 and the benzo moiety of 2GBI. This residue has been found to play a role in 2GBI binding via -stacking interactions65. We hypothesized that F182 may reorient itself, occupying some of the space from the mutation of valine to alanine, in order to better interact with the bound ligand. We evaluated the energetic contribution of this putative conformational change by computing the potential of mean force for rotating the F182 dihedral angle. Our results did not support this theory but rather suggested an energetic cost of around 8 kcal/mol for the F182 aromatic ring being in a parallel configuration with the 2GBI aromatic moiety (see Supplementary Information “Potential of mean force calculation for F182 rotation after V178A mutation”).
Hysteresis in free energy calculations involving “floppy” residues
One way that we evaluate convergence in our free energy calculations is by analyzing the histogram overlap of work values from the forward and reverse processes66. We observe that mutations involving flexible and charged side chains, such as arginine and lysine, are more prone to have poor overlap, signifying inadequate sampling of overlapping regions of phase space during the alchemical transformations. This presumably arises from the scaling of nonbonded interactions. Towards the start of the transformation ( close to 0), the incoming atoms are mostly decoupled from, or not interacting with, the rest of the system. Similarly, at states where is close to 1 near the end of the alchemical transformation, the outgoing atoms are decoupled from the rest of the system. The decoupled nonbonded interactions may “free” the flexible, charged side chains to adopt various nonphysical conformations.
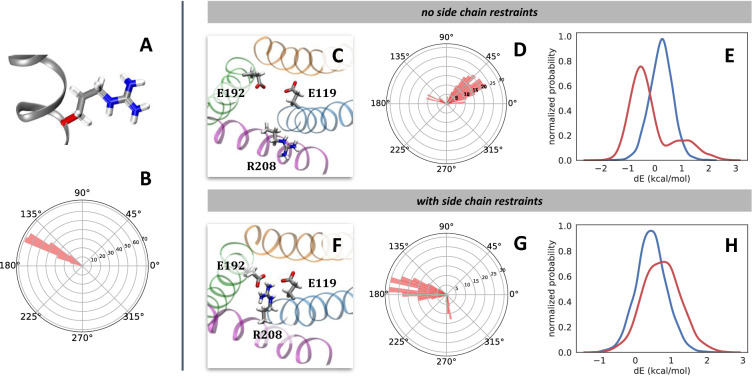
We illustrate this hysteresis in context of the R208K Hv1 mutation, focusing on the arginine residue. In wild type Hv1, the measure of the R208 dihedral angle (Fig. 7A) averaged around 154 in equilibrium simulations (histogrammed in Fig. 7B), and R208 is in close proximity to the acidic side chains E119 and E192. However, during free energy calculations with the scaled nonbonded interactions, the side chain pivots such that R208 is artifactually outside the channel (Fig. 7C), and the dihedral angle values are inconsistent with the range expected from wild type Hv1 simulations (Fig. 7D). The lack of fully coupled van der Waals and electrostatic interactions of the floppy, charged residue with the rest of the system interrupts native ionic interactions and leads to unnatural wandering of the side chain in simulations of these artificial intermediate states. The sampled unphysical configurations were directly correlated with poor overlap between the forward and reverse transformations, evidenced here by bimodal histograms of the work values from the forward and reverse transformations (Fig. 7E). Similar observations were made for the lysine dihedral angle.
Figure 7.
Correlation of the mutating arginine dihedral angle to the work overlap in the R208K transformation. Without side chain restraints, takes unexpected values, causing the side chain to point outside the Hv1 channel and leading to poor overlap of forward and reverse work values. (A) The central bond of the arginine dihedral angle is drawn in red. (B) Histogram in polar coordinates of dihedral angle values belonging to R208 during a normal, fully-interacting MD simulation. (C) View of the channel from the extracellular side. The incoming K208 residue is not shown for clarity. (D) Polar histogram of dihedral angle values belonging to R208 during alchemical free energy calculation of R208K. The angle values are plotted from the window. (E) Overlap of forward (blue) and reverse (red) work values for the window in the R208K mutation of the apo protein. Both R208 and K208 partially interact with the system as per the alchemical potential. (F–H) Analogous to (C–E), respectively, but with the addition of flat-bottom distance restraints.
We reduced this hysteresis by imposing a series of flat-bottom distance restraints with nearby interacting acidic residues (see Methods and supplementary information: “Flat-bottom restraints for mutations involving Arg or Lys residues”). This yielded fewer abnormal side chain configurations (Fig. 7F–G) and better overlap of the forward and reverse work (Fig. 7H).
Further exploration on R211S
The computed binding free energies of R211S are least consistent with experimental results. Our results were predicted to be overly favorable by −6.3 kcal/mol for gbi1 and −7.1 kcal/mol for gbi2 (the experimental reference value is 0.1 kcal/mol). We considered whether a potential contribution may have been the change in total charge of the system. The mutation from a positively charged arginine to a neutral serine changes the system’s net charge from neutral to −1 e. Our simulations employed the particle-mesh Ewald (PME) method for treatment of long-range electrostatics in the periodic system. However, PME enforces neutrality by introducing a uniform neutralizing background charge. Therefore, with the non-neutral end state, the calculated free energy not only has the expected contribution of turning off the arginine charge but also undesired contribution for turning on the neutralizing background charge. We corrected for the electrostatic finite-size effects by applying an analytical correction based on the Poisson–Boltzmann continuum electrostatics model in CHARMM (version c40b1)61,67. The corrections to the binding free energy were not trivial when considered individually (apo = −3.1042 kcal/mol, gbi1 = −3.1030 kcal/mol, gbi2 = −3.1019 kcal/mol). However, they become negligible when considering relative binding free energies. As a result, we believe that the change in net charge is not the primary reason for poor agreement of the experimental and computed R211S relative binding free energies.
We investigated the possibility of unconverged conformational sampling as a cause for the R211S outlying behavior. We performed the same transformation in the opposite direction, i.e., preparing the system with S211 and perturbing to R211. The S211 structures for the apo, gbi1-bound, and gbi2-bound states came from the end of the respective R211S transformations. Each configuration was equilibrated for 5 ns before the S211R free energy calculations. We maintained the same schedule and simulation parameters as described earlier.
We consider the negative value of S211R in order to adequately compare the free energy change in the same direction, and we subsequently refer to this mutation as . The free energies for R211S and should be the same ideally, as free energy is a state function which is independent of the path or direction taken between two states. The computed binding free energies for gbi1 and gbi2 are −5.9 kcal/mol and −1.3 kcal/mol respectively (Fig. 8A, brown vs. pink). In this plot, gbi1 seems to be more consistent between R211S and . However, the plotted values are relative binding free energies where the apo value is subtracted from each of the gbi1 and gbi2 values (see the thermodynamic cycle in Fig. 2). Here, the of apo and the of gbi1 increase by about 4 kcal/mol between R211S and , but the for gbi2 only changes by about 1 kcal/mol between R211S and (Fig. 8B).
Figure 8.
Calculated relative binding free energies for the mutation of residue 211 between the arginine and serine end states reveal discrepancies based on the starting structure. (A) Computed relative binding free energies, analogous to Fig. 5, with the addition of the S211R mutation. The pink markers show the negative of the S211R values to compare on the same scale as R211S. The R211S relative binding free energies ideally should be the same as those for S211R. The error bars represent the root sum square values of standard errors from the Bennett acceptance ratio for the apo and holo states. (B) Bar plot showing the change in the computed (apo protein) or (holo protein) of individual processes of the thermodynamic cycle (Fig. 2) for the R211S/S211R mutation. The apo protein value represents , and the analogous expression is applied to the values of gbi1 and gbi2. These values should be zero since free energy is a state function which is independent of the path taken.
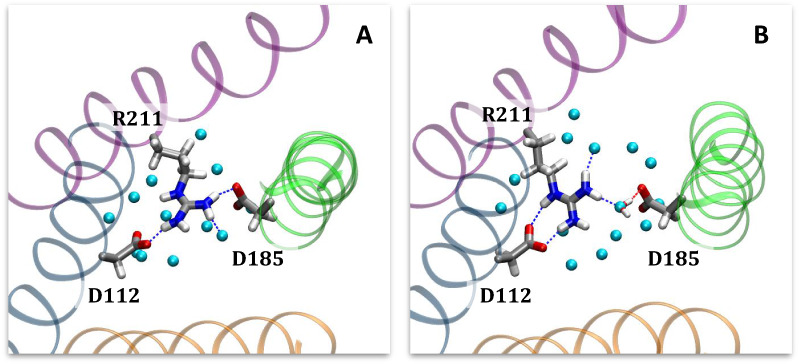
We posit that this discrepancy may arise from differences in R211 interactions with other protein residues as well as differences in hydration patterns in the local region. In simulations of wild type Hv1, R211 is a hydrogen bond donor to two aspartate residues, D112 and D185 (Fig. 9A). These interactions are disrupted when the arginine is mutated to serine, and there is a slight influx of waters to the mutation site to stabilize D185. The S211R mutation reintroduces arginine, but R211 does not reform native contacts with D185, now surrounded by the water molecules (Fig. 9B). This may occur if the system is slower to dispel waters from the pore than it is to allow waters inside, especially near the buried region of the mutated residue (Fig. 10). Hence the underlying end states of R211 are not the same for the R211S and S211R mutations, potentially due to insufficient rearrangement of the surrounding solvent network. In other words, non-overlapping ensembles are being sampled in the R211S and S211R transformations, precluding reasonable comparison of these calculations with experimental mutagenesis results. Thus, our results for this transformation are reported here, but the apparent agreement between and for gbi2 and the mutation (Fig. 8A) cannot be used meaningfully to assess the validity of our structural model due to the difficulties with this particular calculation.
Figure 9.
View from the extracellular side of the apo channel showing representative interaction networks around R211 (A) before and (B) after simulating a null transformation of R211 to Ser and back to Arg. Oxygen atoms of waters within 2 Å of the R211, D112, and D185 are colored as light blue spheres. The interaction differences between (A) and (B) reveal potential sampling barriers in what ought to be equivalent systems. Figures rendered using VMD52.
Figure 10.
Average number of water molecules within 3 Å of the mutating residue (Arg or Ser 211), D112, and D185. The error bars represent standard deviations. Hydration patterns are not always consistent in the vicinity of R211 during the R211S and S211R mutations. For example, in the apo state, the number of water molecules near D185 increases (left subplot, right group, blue orange bars). When mutating the system with S211 back to R211, the number of water molecules decrease near D112 instead of near D185 (left subplot, middle group, orange green bars). It might be expected that the blue bars (wild type protein with R211) and the green bars (twice mutated protein also with R211) should be the same in all three systems. Between the two R211 states of before and after mutation, both the apo and gbi1 systems differ by 1–2 water molecules in the specified vicinity of D112 and D185, whereas gbi2 is more consistent in hydration around the two acidic residues.
Conclusions
In this study, we employed free energy calculations with atomistic molecular dynamics simulations to characterize the binding of 2GBI to Hv1 as a foundational step to optimize small molecule blockers of Hv1. Our molecular insights of the binding mechanism of 2GBI to Hv1 agree with double-mutant cycle experiments, helping to validate our structural model for the channel and the bound state.
The mutations that were most computationally challenging were those involving charged side chains: D112E, R208K, and R211S. The R211S calculation might be further examined using enhanced sampling methods such as REST268–70, with the inclusion of protein side chains and water molecules in the vicinity of R211.
Results from alchemical free energy calculations show that both the gbi1 and gbi2 tautomers are comparable in most relative binding free energies calculated. The gbi1 structure is limited in its extent of forming protein-ligand contacts without the protonated imidazole region. We reason that gbi2, the tautomer with excess charge in the imidazole region, is likely the primary state to bind Hv1. We hope to investigate the extent to which free energy calculations may be used to design new compounds based on the 2GBI scaffold, particularly with an imidazole-based pharmacophore with substitutions at the 2-position that stabilize ring protonation, for more effective binding to Hv1 for potential therapeutic benefit.
Supplementary Information
Acknowledgements
The authors appreciate helpful discussions from Christopher Bayly on the tautomeric state of 2GBI and from Wei Jiang on water molecules in the binding site. The authors are grateful for computing support from Nathan Crawford and the UCI GreenPlanet cluster, supported in part by NSF Grant CHE-0840513. V.T.L. and N.M.L. acknowledge funding from the National Science Foundation Graduate Research Fellowship Program. The authors appreciate financial support from the National Institutes of Health (Grant GM108889 to D.L.M., and GM098973 to F.T.).
Author contributions
V.T.L. conducted the research, prepared the figures, and wrote the manuscript. A.D.G. and N.M.L. contributed to setup of the system and molecular simulations. J.A.F. contributed to analysis of the results. F.T. provided insight on results and research directions. D.L.M. and D.J.T. jointly supervised the work. All authors reviewed the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
David L. Mobley, Email: dmobley@mobleylab.org
Douglas J. Tobias, Email: dtobias@uci.edu
Supplementary information
is available for this paper at 10.1038/s41598-020-70369-4.
References
- 1.Sasaki M, Takagi M, Okamura Y. A voltage sensor-domain protein is a voltage-gated proton channel. Science. 2006;312:589. doi: 10.1126/science.1122352. [DOI] [PubMed] [Google Scholar]
- 2.Ramsey IS, Moran MM, Chong JA, Clapham DE. A voltage-gated proton-selective channel lacking the pore domain. Nature. 2006;440:1213–1216. doi: 10.1038/nature04700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ramsey IS, et al. An aqueous H+ permeation pathway in the voltage-gated proton channel Hv1. Nat. Struct. Mol. Biol. 2010;17:869–875. doi: 10.1038/nsmb.1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.El Chemaly A, et al. VSOP/Hv1 proton channels sustain calcium entry, neutrophil migration, and superoxide production by limiting cell depolarization and acidification. J. Exp. Med. 2010;207:129–139. doi: 10.1084/jem.20091837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rodriguez JD, et al. Identification of a vacuolar proton channel that triggers the bioluminescent flash in dinoflagellates. PLoS ONE. 2017;12:e0171594. doi: 10.1371/journal.pone.0171594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lishko PV, Kirichok Y. The role of Hv1 and CatSper channels in sperm activation. J. Physiol. 2010;588:4667–4672. doi: 10.1113/jphysiol.2010.194142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang Y, et al. Specific expression of the human voltage-gated proton channel Hv1 in highly metastatic breast cancer cells, promotes tumor progression and metastasis. Biochem. Biophys. Res. Commun. 2011;412:353–359. doi: 10.1016/j.bbrc.2011.07.102. [DOI] [PubMed] [Google Scholar]
- 8.Hondares E, et al. Enhanced activation of an amino-terminally truncated isoform of the voltage-gated proton channel HVCN1 enriched in malignant B cells. Proc. Natl. Acad. Sci. 2014;111:18078–18083. doi: 10.1073/pnas.1411390111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang Y, Li SJ, Wu X, Che Y, Li Q. Clinicopathological and biological significance of human voltage-gated proton channel Hv1 protein overexpression in breast cancer. J. Biol. Chem. 2012;287:13877–13888. doi: 10.1074/jbc.M112.345280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Seredenina T, Demaurex N, Krause K-H. Voltage-Gated Proton Channels as Novel Drug Targets: From NADPH Oxidase Regulation to Sperm Biology. Antioxid. Redox Signal. 2014;23:490–513. doi: 10.1089/ars.2013.5806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhu X, Mose E, Zimmermann N. Proton channel HVCN1 is required for effector functions of mouse eosinophils. BMC Immunol. 2013;14:24. doi: 10.1186/1471-2172-14-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu L-J, et al. The voltage-gated proton channel Hv1 enhances brain damage from ischemic stroke. Nat. Neurosci. 2012;15:565–573. doi: 10.1038/nn.3059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tombola F, Ulbrich MH, Isacoff EY. The voltage-gated proton channel Hv1 has two pores, each controlled by one voltage sensor. Neuron. 2008;58:546–556. doi: 10.1016/j.neuron.2008.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Koch HP, et al. Multimeric nature of voltage-gated proton channels. Proc. Natl. Acad. Sci. U.S.A. 2008;105:9111. doi: 10.1073/pnas.0801553105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Geragotelis AD, et al. Voltage-dependent structural models of the human Hv1 proton channel from long-timescale molecular dynamics simulations. Proc. Natl. Acad. Sci. 2020 doi: 10.1073/pnas.1920943117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wood ML, et al. Water wires in atomistic models of the Hv1 proton channel. Biochim. et Biophys. Acta (BBA) Biomembr. 1818;286–293:2012. doi: 10.1016/j.bbamem.2011.07.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kulleperuma K, et al. Construction and validation of a homology model of the human voltage-gated proton channel hHV1. J. Gen. Physiol. 2013;141:445–465. doi: 10.1085/jgp.201210856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chamberlin A, et al. Hydrophobic plug functions as a gate in voltage-gated proton channels. Proc. Natl. Acad. Sci. U.S.A. 2014;111:E273. doi: 10.1073/pnas.1318018111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gianti E, Delemotte L, Klein ML, Carnevale V. On the role of water density fluctuations in the inhibition of a proton channel. PNAS. 2016;113:E8359–E8368. doi: 10.1073/pnas.1609964114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Randolph AL, Mokrab Y, Bennett AL, Sansom MS, Ramsey IS. Proton currents constrain structural models of voltage sensor activation. eLife. 2016;5:e18017. doi: 10.7554/eLife.18017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Takeshita K, et al. X-ray crystal structure of voltage-gated proton channel. Nat. Struct. Mol. Biol. 2014;21:352–357. doi: 10.1038/nsmb.2783. [DOI] [PubMed] [Google Scholar]
- 22.Kalia J, Swartz KJ. common principles of voltage-dependent gating for Hv and Kv channels. Neuron. 2013;77:214–216. doi: 10.1016/j.neuron.2013.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hong L, Pathak MM, Kim IH, Ta D, Tombola F. Voltage-sensing domain of voltage-gated proton channel Hv1 shares mechanism of block with pore domains. Neuron. 2013;77:274–287. doi: 10.1016/j.neuron.2012.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qiu F, Rebolledo S, Gonzalez C, Larsson HP. Subunit interactions during cooperative opening of voltage-gated proton channels. Neuron. 2013;77:288–298. doi: 10.1016/j.neuron.2012.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cherny VV, DeCoursey TE. Ph-dependent inhibition of voltage-gated H+ currents in rat alveolar epithelial cells by Zn2+ and other divalent cations. J. Gen. Physiol. 1999;114:819–838. doi: 10.1085/jgp.114.6.819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Alabi AA, Bahamonde MI, Jung HJ, Kim JI, Swartz KJ. Portability of paddle motif function and pharmacology in voltage sensors. Nature. 2007;450:370–375. doi: 10.1038/nature06266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhao R, et al. Role of human Hv1 channels in sperm capacitation and white blood cell respiratory burst established by a designed peptide inhibitor. PNAS. 2018;115:E11847–E11856. doi: 10.1073/pnas.1816189115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tang D, et al. Scorpion toxin inhibits the voltage-gated proton channel using a Zn2+-like long-range conformational coupling mechanism. Br. J. Pharmacol. 2020;177:2351–2364. doi: 10.1111/bph.14984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hong L, Kim IH, Tombola F. Molecular determinants of Hv1 proton channel inhibition by guanidine derivatives. Proc. Natl. Acad. Sci. U.S.A. 2014;111:9971. doi: 10.1073/pnas.1324012111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rennhack A, Grahn E, Kaupp UB, Berger TK. Photocontrol of the Hv1 proton channel. ACS Chem. Biol. 2017;12:2952–2957. doi: 10.1021/acschembio.7b00523. [DOI] [PubMed] [Google Scholar]
- 31.Guo J, et al. Structure driven design of novel human ether-a-go-go-related-gene channel (hERG1) activators. PLoS ONE. 2014;9:e105553. doi: 10.1371/journal.pone.0105553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Carterall, W. A. Molecular mechanisms of gating and drug block of sodium channels. in Sodium Channels and Neuronal Hyperexcitability, 206–225, 10.1002/0470846682.ch14 (Wiley, 2008). _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/0470846682.ch14. [PubMed]
- 33.Krepkiy D, et al. Structure and hydration of membranes embedded with voltage-sensing domains. Nature. 2009;462:473–479. doi: 10.1038/nature08542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tronin AY, et al. Direct evidence of conformational changes associated with voltage gating in a voltage sensor protein by time-resolved x-ray/neutron interferometry. Langmuir. 2014;30:4784–4796. doi: 10.1021/la500560w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Freites JA, Tobias DJ, White SH. A voltage-sensor water pore. Biophys. J. 2006;91:L90–L92. doi: 10.1529/biophysj.106.096065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wood ML, Freites JA, Tombola F, Tobias DJ. Atomistic modeling of ion conduction through the voltage-sensing domain of the shaker k+ ion channel. J. Phys. Chem. B. 2017;121:3804–3812. doi: 10.1021/acs.jpcb.6b12639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Musset B, et al. Aspartate 112 is the selectivity filter of the human voltage-gated proton channel. Nature. 2011;480:273–277. doi: 10.1038/nature10557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gonzalez C, Rebolledo S, Perez ME, Larsson HP. Molecular mechanism of voltage sensing in voltage-gated proton channels. J. Gen. Physiol. 2013;141:275–285. doi: 10.1085/jgp.201210857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hernández-García RM, Barba-Behrens N, Salcedo R, Höjer G. Theoretical study of 2-guanidinobenzimidazole. HF, MP2 and DFT calculations. J. Mol. Struct. THEOCHEM. 2003;637:55–72. doi: 10.1016/S0166-1280(03)00370-1. [DOI] [Google Scholar]
- 40.Vanommeslaeghe K, MacKerell AD. Automation of the CHARMM general force field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012;52:3144–3154. doi: 10.1021/ci300363c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Vanommeslaeghe K, Raman EP, MacKerell AD. Automation of the CHARMM general force field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. J. Chem. Inf. Model. 2012;52:3155–3168. doi: 10.1021/ci3003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Parrish RM, et al. Psi4 1.1: An open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J. Chem. Theory Comput. 2017;13:3185–3197. doi: 10.1021/acs.jctc.7b00174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Head-Gordon M, Pople JA, Frisch MJ. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1988;153:503–506. doi: 10.1016/0009-2614(88)85250-3. [DOI] [Google Scholar]
- 44.Weigend F, Häser M, Patzelt H, Ahlrichs R. RI-MP2: Optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998;294:143–152. doi: 10.1016/S0009-2614(98)00862-8. [DOI] [Google Scholar]
- 45.Frisch MJ, Head-Gordon M, Pople JA. A direct MP2 gradient method. Chem. Phys. Lett. 1990;166:275–280. doi: 10.1016/0009-2614(90)80029-D. [DOI] [Google Scholar]
- 46.Frisch MJ, Head-Gordon M, Pople JA. Semi-direct algorithms for the MP2 energy and gradient. Chem. Phys. Lett. 1990;166:281–289. doi: 10.1016/0009-2614(90)80030-H. [DOI] [Google Scholar]
- 47.Rassolov VA, Pople JA, Ratner MA, Windus TL. 6–31G* basis set for atoms K through Zn. J. Chem. Phys. 1998;109:1223–1229. doi: 10.1063/1.476673. [DOI] [Google Scholar]
- 48.Trott O, Olson AJ. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010;31:455–461. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wong SE, Lightstone FC. Accounting for water molecules in drug design. Expert Opin. Drug Discov. 2011;6:65–74. doi: 10.1517/17460441.2011.534452. [DOI] [PubMed] [Google Scholar]
- 50.Roberts BC, Mancera RL. Ligand-protein docking with water molecules. J. Chem. Inf. Model. 2008;48:397–408. doi: 10.1021/ci700285e. [DOI] [PubMed] [Google Scholar]
- 51.Gracia, L. VMD clustering plugin. https://github.com/luisico/clustering (2018).
- 52.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 53.Phillips JC, et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Beutler TC, Mark AE, van Schaik RC, Gerber PR, van Gunsteren WF. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett. 1994;222:529–539. doi: 10.1016/0009-2614(94)00397-1. [DOI] [Google Scholar]
- 55.Zacharias M, Straatsma TP, McCammon JA. Separation-shifted scaling, a new scaling method for Lennard-Jones interactions in thermodynamic integration. J. Chem. Phys. 1994;100:9025–9031. doi: 10.1063/1.466707. [DOI] [Google Scholar]
- 56.Zwanzig RW. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954;22:1420–1426. doi: 10.1063/1.1740409. [DOI] [Google Scholar]
- 57.Shirts MR, Pande VS. Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J. Chem. Phys. 2005;122:144107. doi: 10.1063/1.1873592. [DOI] [PubMed] [Google Scholar]
- 58.Lu N, Singh JK, Kofke DA. Appropriate methods to combine forward and reverse free-energy perturbation averages. J. Chem. Phys. 2003;118:2977–2984. doi: 10.1063/1.1537241. [DOI] [Google Scholar]
- 59.Bennett CH. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976;22:245–268. doi: 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
- 60.Shirts MR, Chodera JD. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rocklin GJ, Mobley DL, Dill KA, Hünenberger PH. Calculating the binding free energies of charged species based on explicit-solvent simulations employing lattice-sum methods: An accurate correction scheme for electrostatic finite-size effects. J. Chem. Phys. 2013;139:184103. doi: 10.1063/1.4826261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Berger TK, Isacoff EY. The pore of the voltage-gated proton channel. Neuron. 2011;72:991–1000. doi: 10.1016/j.neuron.2011.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Long SB, Tao X, Campbell EB, MacKinnon R. Atomic structure of a voltage-dependent K+ channel in a lipid membrane-like environment. Nature. 2007;450:376–382. doi: 10.1038/nature06265. [DOI] [PubMed] [Google Scholar]
- 64.Armstrong CT, Mason PE, Anderson JLR, Dempsey CE. Arginine side chain interactions and the role of arginine as a gating charge carrier in voltage sensitive ion channels. Sci. Rep. 2016;6:1–10. doi: 10.1038/srep21759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zhao C, Hong L, Galpin JD, Ahern CA, Tombola F. Exploiting -stacking interactions to improve inhibition of the Hv1 channel by aromatic guanidine derivatives. Biophys. J. 2018;114:374a. doi: 10.1016/j.bpj.2017.11.2073. [DOI] [Google Scholar]
- 66.Pohorille A, Jarzynski C, Chipot C. Good practices in free-energy calculations. J. Phys. Chem. B. 2010;114:10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- 67.Brooks BR, et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jiang W, Thirman J, Jo S, Roux B. Reduced free energy perturbation/hamiltonian replica exchange molecular dynamics method with unbiased alchemical thermodynamic axis. J. Phys. Chem. B. 2018;122:9435–9442. doi: 10.1021/acs.jpcb.8b03277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Jo S, Jiang W. A generic implementation of replica exchange with solute tempering (REST2) algorithm in NAMD for complex biophysical simulations. Comput. Phys. Commun. 2015;197:304–311. doi: 10.1016/j.cpc.2015.08.030. [DOI] [Google Scholar]
- 70.Wang L, Friesner RA, Berne BJ. Replica exchange with solute scaling: A (REST2) J. Phys. Chem. B. 2011;115:9431–9438. doi: 10.1021/jp204407d. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.