Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Jul 28;5(31):19371–19376. doi: 10.1021/acsomega.0c01059

Ab Initio Evaluation of Complexation Energies for Cyclodextrin-Drug Inclusion Complexes

Kenji Oqmhula †, Kenta Hongo ‡,§,∥, Ryo Maezono ⊥,*, Tom Ichibha ⊥
PMCID: PMC7424588  PMID: 32803030

Abstract

graphic file with name ao0c01059_0006.jpg

We investigated the reliability of ab initio methods to predict the binding energies of molecular encapsulation complexes. Vast possibilities for the docking conformations were screened down to a couple of geometries using a semiempirical docking simulation. For the candidates, we applied density functional theory (DFT) with several exchange–correlation (XC) functionals to evaluate the binding energy. We carefully selected and compared the functionals to elucidate the role of the characteristic factors in achieving the XC effects. It is clarified that the improper combination in XC with D3 dispersion force correction leads to overbinding. For achieving a proper combination, the exchange interaction over the longer range to avoid the overbinding was found to be important.

Introduction

Biopharmaceuticals, which are manufactured, extracted, and semisynthesized from biological sources, have high potencies at low doses and unique medical properties in general1,2 compared to conventional chemical pharmaceuticals. However, biopharmaceuticals often have poor physical and/or chemical stabilities, which cause various issues; for example, they cannot be stored stably for long periods or administered orally. To address such problems, one of the most promising solutions is molecular encapsulation, wherein1,2 the biopharmaceutical molecule (guest) is combined with a carrier molecule (host) for physical and chemical stabilization. This approach also enables control of the absorption location and timing.3

These properties heavily depend on the binding strength between the guest and host molecules. Therefore, reliably predicting the binding energy based on simulations could significantly accelerate the development of the molecular encapsulation technique. Although the most promising simulation tool for this purpose is density functional theory (DFT), it remains difficult to describe molecular encapsulation complexes using exchange–correlation (XC) functionals because the binding arises from various noncovalent forces: hydrogen bonding, dispersion forces, hydrophobic interactions, and so on.4 Several unique ideas to describe these noncovalent interactions have been suggested thus far. One promising approach is long-range correction,5,6 which increases the proportion of exact exchange in long-range interactions and improves the description of van der Waals forces.7 Another approach is to use Minnesota functionals, whose parameters are trained for both covalent and noncovalent systems unlike B3LYP.8 Although this significantly enhances the reliability of the simulations for noncovalent systems, these functionals have an apparent defect in that they cannot reproduce the asymptotic decrease in van der Waals forces.9 The most popular way to describe the damping is Grimme’s dispersion force corrections (D3),10 which employ an empirical function akin to the Lennard–Jones potential.11

In this paper, we examine the reliability of the functionals listed in Table 1 for evaluating the binding energy between cyclodextrins (CDs) (host) and plumbagin (guest). CDs are some of the most important host molecules for molecular encapsulation due to their various advantages (see the System section). However, no studies have yet explored which functionals can reliably describe the encapsulation process by CDs. Thus, we compared the predictions obtained by each XC functional with those obtained by the diffusion Monte Carlo (DMC) method12,13 to evaluate their performances.

Table 1. List of Tested XC Functionalsa.

plain D3 CAM CAM + D3
B3LYP B3LYP-D3 CAM-B3LYP CAM-B3LYP-D3
M06L M06L-D3    
Open in a new tab
a

We examined the reliability of the commonly used functionals B3LYP and M06L and their relatives with D314 and/or CAM15 corrections to predict the binding energies between plumbagin and CDs.

The paper is organized as follows. In the System section, we introduce our target systems, CDs and plumbagin. In the Methods section, we explain how we obtained the binding geometries used in the docking analysis, as well as the details of our DFT and DMC calculations. In the Results and Discussion section, we present and discuss our results, and finally, we summarize the study in the Conclusions section.

System

Plumbagin is an organic molecule containing two benzene rings.16 This molecule is known to have medical efficacy against prostate cancer,17,18 but the difficulty of its storage hinders its practical use: 63.8% of plumbagin is lost in one month under atmospheric conditions due to oxidation and degradation.19 To address this, molecular encapsulation by CDs could be the most promising solution.19

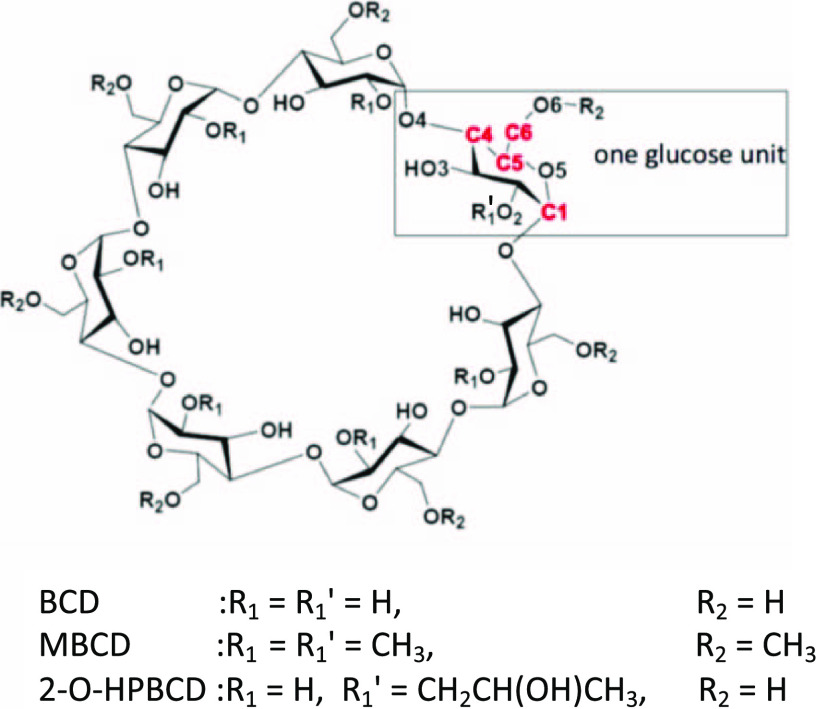
CDs are circular molecules consisting of glucose units, as shown in Figure 1. They are commonly used as a carrier for various pharmaceuticals because of the various benefits, as explained below in addition to their chemical stabilities.3 The cavity sizes of CDs can be adjusted by changing the number of glucose units, n (≥6), so that a given guest molecule can be appropriately accommodated. When n is 6, 7, or 8, the CD is called α-, β-, or γ-CD, respectively. Because of encapsulation by CD, the plumbagin exhibits improved solubility or dissolution, which aids in drug adsorption. The drug release rate/timing can be controlled by replacing the functional groups. The suitable ring size for plumbagin is β-CD (BCD).16 We calculated the binding energies between plumbagin and several representative CDs: BCD, methyl-BCD (MBCD), and 2-O-HPBCD.

Figure 1.

Figure 1

Open in a new tab

Molecular structure of BCDs, where the ring consists of seven glucose units. There are various BCDs with different functional groups; we selected BCD, MBCD, and 2-O-HPBCD, as shown. Here, for 2-O-HPBCD, only one R1 is CH2CH(OH)CH3 and the remaining R1 are all hydrogen atoms.

Methods

We obtained the binding structures between plumbagin and BCDs using docking analysis with the Lamarckian algorithm implemented in AutoDock 4.2.6.20,21 This approach is often used to predict the ligand arrangements of protein systems. A set of genes represents the ligand arrangements, and they are updated to obtain energetically stable structures. Here, each of the genes represents the translations, orientations, and conformations of the ligands. We regarded plumbagin as the “ligand” of BCDs to perform the docking analysis.

The molecular structures of plumbagin and BCDs were taken from their entries (PVVAQS01, BCDEXD03, BOYFOK04, and KOYYUS) in the Cambridge Structural Database.22 We optimized the structures using CAM-B3LYP-D3 prior to the docking analysis. In the analysis, the translation of plumbagin was discretized on a 50 × 38 × 24 grid with a spacing of 0.375 Å. We updated ∼150 genes for 100 iterations and selected only one gene at the end of each iteration to “survive” to the next. The energy corresponding to each gene was calculated by an empirical force field, whose electrostatic interaction was calculated based on the Gasteiger charges.23 The other input parameters were set to the default values in Autodock 4.2.6.

We used Gaussian09/1624,25 for DFT calculations. We performed all-electron calculations with 6-31++G(d,p) Gaussian basis sets, since the 6-31G family of basis sets is often used for analyzing host–guest docking systems similar to ours.4,26−29 We corrected the basis set superposition error (BSSE) with the counterpoise method.30 The eight functionals listed in Table 1 were used to calculate the barrier energies, where the geometries of the isolated plumbagin and BCD molecules and their complexes were optimized for each functional.

For the analysis (Results and Disccusion section), we used DMC12 to obtain reliable reference values. The calculations were performed using QMCPACK implementation31 for the geometries optimized by DFT with the M06L functional. The orbital functions used in the Slater determinant were generated by the DFT method with the M06L functional implemented in GAMESS.32,33 The core potential in the hydrogen atoms was described by Annaberdiyev’s effective core potential,34 and the core potential and electrons in carbon and oxygen atoms were described by Bennett’s.35 We described the Kohn–Sham orbitals with the augmented cc-pVDZ Gaussian basis sets.36 The Jastrow factor consists of one-, two-, and three-body terms amounting to 212 variational parameters in total. The parameters were optimized by a numerical scheme to minimize the hybridization of energy and variance with a ratio of 7:3 at the variational Monte Carlo level.12,13 We estimated the time-step bias by linear extrapolation of the energies obtained at two time steps, dt = 0.020 and 0.005 a.u.–1. We set the target population of walkers to be 4000. Practically, this target population size is large enough to suppress any population control error.

Results and Discussion

We found that the structures obtained by the docking analysis could be classified into two types of conformations, as shown in Figure 2. In type I (II), the hydroxyl phenolic (methyl quinone) group of plumbagin is located around the narrow side of the cavity in BCDs. We calculated the binding energies for both types of conformations.

Figure 2.

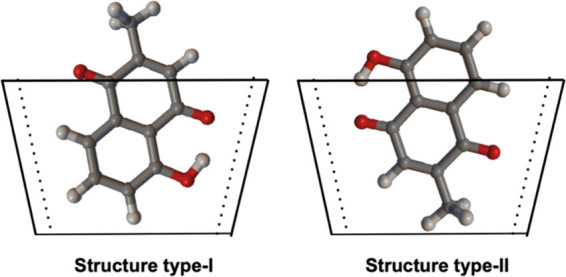
Figure 2

Open in a new tab

Two types of stable conformations found by the docking analysis. In type I (II), the hydroxyl phenolic (methyl quinone) group of plumbagin is located around the narrow side of the cavity in BCDs.

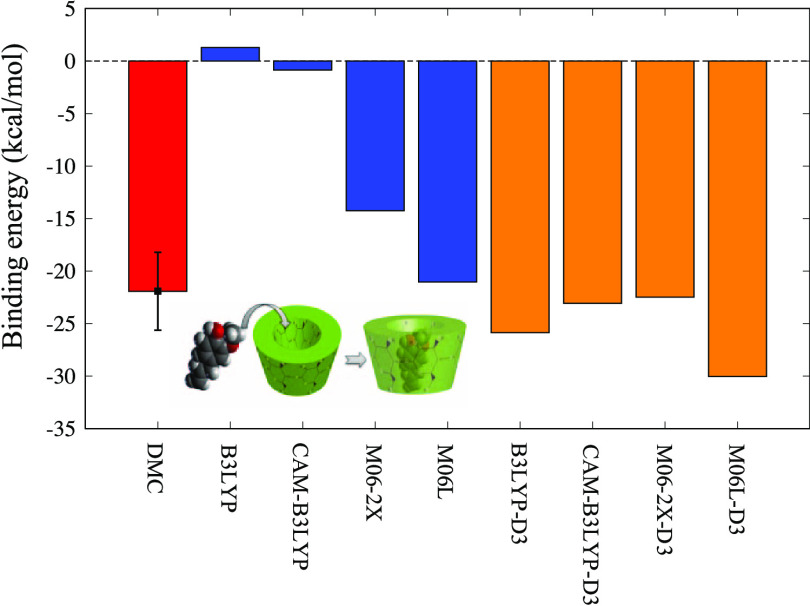
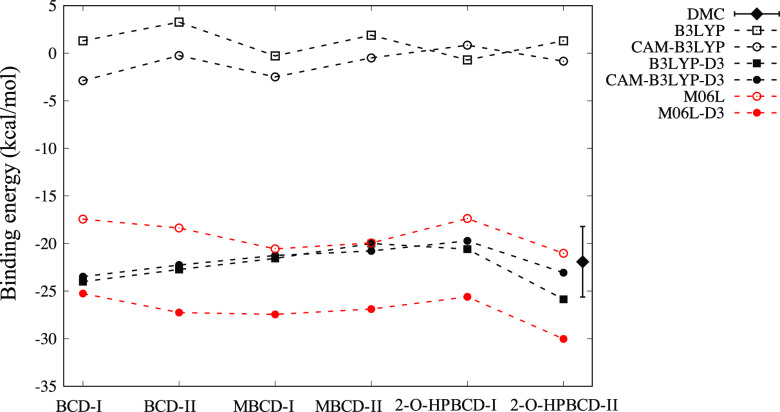
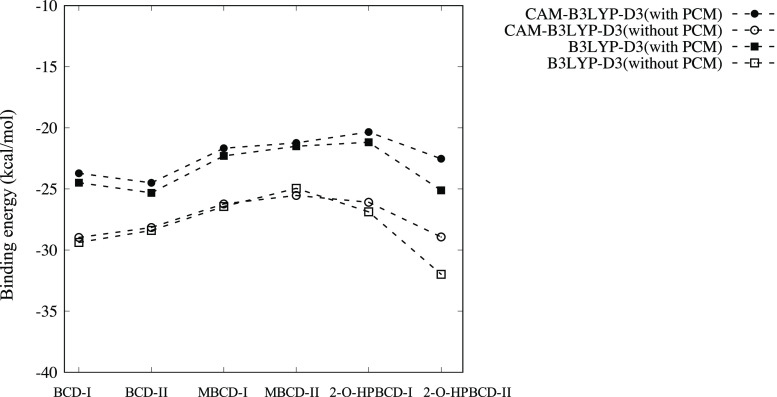
Figure 3 shows the binding energies evaluated by several methods. By comparing the results obtained with the functionals without D3 corrections, (CAM-)B3LYP and M06L, it is clear that M06L reproduces the stabilization induced by docking, whereas (CAM-)B3LYP does not. The primary reason for this is the fact that the internal parameters of (CAM-)B3LYP are trained only for covalent systems.37 Similar results have also been reported for various types of noncovalent systems.37−43 Compared to all other applied functionals, M06L-D3 alone predicts a significantly higher binding energy. This is due to the lack of exact exchange in long-range interactions. This claim is supported by a previous ab initio study demonstrating that an insufficient proportion of exact exchange in long-range interactions leads to overbinding in the case of the argon dimer.44 Deeper binding by M06L even without D3 being closer to other XC with D3 could then be attributed simply to the accidental error cancellation between the overbinding due to the lack of exact exchange and underbinding due to the lack of dispersion force correction.

Figure 3.

Figure 3

Open in a new tab

Comparison of binding energies predicted by DMC and DFT with the selected functionals. Closed and open symbols with the same shape correspond to the XC functional with and without D3 correction. DMC was applied only to 2-O-HPBCD-II, since the DMC calculation cost is high. The difference between type I and type II is the location of the hydroxyl phenolic group on plumbagin. The conformational details are illustrated in Figure 2.

By admitting the overbinding by M06L-D3, we could support both B3LYP-D3 and CAM-B3LYP-D3 as the appropriate choice of XC functionals reproducing the host–guest interactions, thus giving the predictions between M06L and M06L-D3. Surprisingly, both B3LYP-D3 and CAM-B3LYP-D3 give almost the same quantitative prediction except 2-O-HPBCD-II. To analyze the difference (with and without CAM), we concentrated on the case of 2-O-HPBCD-II and performed DMC estimation as the reference. As seen in Figure 3, we found that B3LYP-D3 overestimates the binding energy compared to CAM-B3LYP-D3. The CAM correction takes into account the long-range exchange interaction, introducing more components than that in B3LYP-D3 at long distance. Consequently, the CAM correction made B3LYP-D3 closer to DMC by improving the B3LYP-D3 overbinding caused by the lack of long-range exchange.

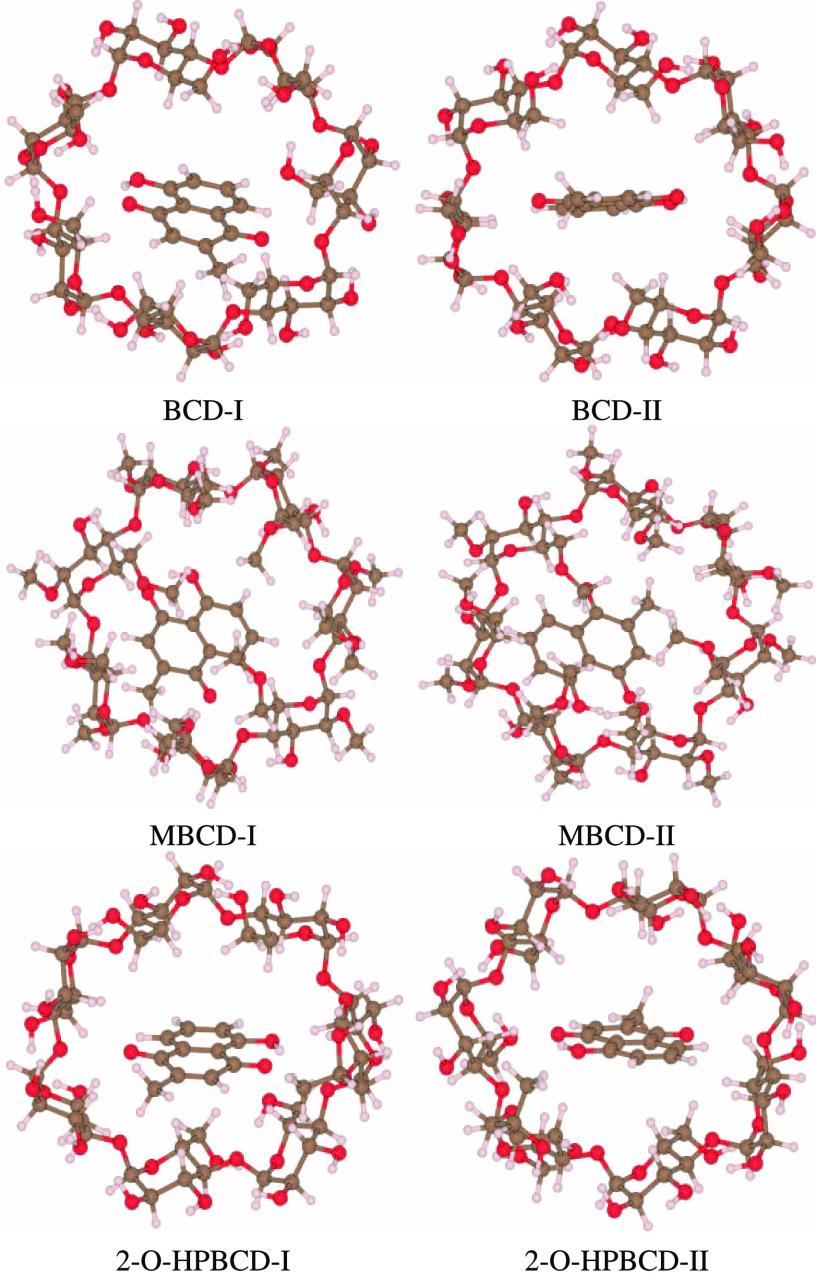
Figure 2 also provides the predictions whether type I or II is stabilized for each host (BCD, MBCD, and 2-O-HPBCD). Except for BCD, the predictions are not affected by the choice of XC (we exclude B3LYP from the consideration because it is apparently an inappropriate choice and can be used just for reference). The BCD results indicate that the presence or absence of D3 correction does not affect the prediction; however, the prediction is conflicting between M06L- and B3LYP-based XCs. This conflict occurs only in BCD, which can be resolved by the optimized structure, serving as a clue, as shown in Figure 4. Only in the case of BCD, the orientation of the guest molecules (normal direction of planar molecules) is significantly different for types I and II. The type I structure of BCD is stabilized by the CH/π interaction between π-electrons of the benzene ring and hydrogen atoms of the host molecule. The significant difference therefore implies that the prediction of type I or II would be conflicting only for BCD when the compared XCs have different capabilities to capture the interaction.

Figure 4.

Figure 4

Open in a new tab

Docking structures appear in Figure 3. The structures are optimized by CAM-B3LYP-D3. The normal orientations of the planer plumbagin inside the capsule are almost the same for types I and II except BCD.

For realistic applications, the behavior of the system in an aqueous solution would be of interest rather than that in vacuum, as we evaluated. However, for the ab initio approach, it is impractical to completely consider the solvent effects from the feasibility viewpoint and computational costs. It is, therefore, practical to consider45−49 such predictions made in vacuum as a rough estimation to provide a trend that is expected to be unchanged qualitatively even in a solution. In such cases, it is important to consider the extent of expectation that would be justified. We can briefly estimate how much the estimated energies change in the solution environments using the polarizable continuum model (PCM) with the integral equation formalism variant (IEFPCM).50 Estimated binding energies with and without PCM are compared in Figure 5. As observed, the estimation gets less stabilized when the solution effects are considered by PCM. Note that the numerical results without PCM differ from each other in Figures 5 and 3 because of the lack of BSSE corrections in Figure 5 (PCM implementation in Gaussian09 excludes BSSE; hence, the comparison in Figure 5 should be made without BSSE). The stabilization is consistent with other preceding reports using PCM.45−49 Except for BCD, the trend over the conformations is qualitatively unchanged, for which the binding energies could roughly be corrected by a common scaling factor. A previous study on a host–guest system using β-cyclodextrin51 reported that their predictions using IEFPCM corrections could reproduce the most stable conformation that is experimentally observed in solution, thus supporting the present predictions. It is, however, pointed out that the performance of the IEFPCM correction depends on the polarity of the solvent species.52 The comparison between the brief treatment (IEFPCM) and a serious treatment (water molecules explicitly handled) shows that the agreement is negatively affected when the polarity of the solvent molecule decreases. A good agreement is reported for polarity with a relative dielectric constant εr of ∼46.7, which is lower than that of water (εr = 78.4 at 298.15 K); hence, the present case exists in the safer range for IEFPCM to be justified.

Figure 5.

Figure 5

Open in a new tab

Comparison of binding energies predicted by DFT with and without the water solvent effect modeled with IEFPCM. Close and open symbols with the same shape correspond to the XC with and without PCM, respectively.

For BCD, the relative stability between types I and II is predicted to be reversed when IEFPCM is introduced. The exceptional structures for BCD, as explained in Figure 3, might be relevant to the reason, namely, the sensitivity of IEFPCM to capture the CH/π interaction which is in sharp contrast between types I and II. In this sense, one should reserve vacuum predictions applied further to the practical estimations when the target system includes the CH/π interaction as a dominating binding.

Conclusions

We evaluated the reliability of several exchange-correlation functionals for predicting the binding energies between CDs (BCD, MBCD, and 2-O-HPBCD) and plumbagin. By comparing the functionals without D3 correction, we found that the Minnesota functionals qualitatively reproduce the binding-induced stabilization, whereas the (CAM-)B3LYP functionals do not. This could be because the parametrization in the latter functionals is optimized only for covalent systems. Among the functionals examined, B3LYP-D3, CAM-B3LYP-D3, and M06L yield binding energies in a quantitatively reasonable range and achieve consistent results. However, by analyzing M06L further with/without D3 correction, we found that the coincidence of M06L prediction with other XC is accidental because of the error cancellation between the overbinding from the lack of long-range exchange interactions and the underbinding from the lack of dispersion correction. We also considered to what extent the predictions made under vacuum could be justified to estimate the binding trend in realistic environments with a solvent. A brief treatment of the commonly observed solvent effect is applied to confirm that the trends are not considerably affected, except the case with CH/π interactions that are possibly dominating.

Acknowledgments

This research used the resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract No. DE-AC02-06CH11357, and the Research Center for Advanced Computing Infrastructure (RCACI) at JAIST. We thank Dr. Anouar Benali for letting us use the former calculation resources. T.I. is grateful for financial support from a Grant-in-Aid for JSPS Research Fellow (18J12653). K.H. is grateful for financial support from KAKENHI grants (17K17762 and 19K05029), Grant-in-Aid for Scientific Research on Innovative Areas (16H06439 and 19H05169), PRESTO (JPMJPR16NA), and the Materials research by Information Integration Initiative (MI2I) project of the Support Program for Starting Up Innovation Hub from Japan Science and Technology Agency (JST). R.M. is grateful for financial support from MEXT-KAKENHI (17H05478 and 16KK0097), Toyota Motor Corporation, I-O DATA Foundation, and the Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049). R.M. and K.H. are also grateful for financial support from MEXT-FLAGSHIP2020 (hp170269 and hp170220).

Author Present Address

# Physical Sciences Directorate, Oak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, Tennessee 37830, United States.

The authors declare no competing financial interest.

References

  1. Mitragotri S.; Burke P. A.; Langer R. Overcoming the challenges in administering biopharmaceuticals: formulation and delivery strategies. Nat. Rev. 2014, 13, 655. 10.1038/nrd4363. [DOI] [PMC free article] [PubMed] [Google Scholar]; Review Article.
  2. George M.; Abraham T. E. Polyionic hydrocolloids for the intestinal delivery of protein drugs: Alginate and chitosan - a review. J. Controlled Release 2006, 114, 1–14. 10.1016/j.jconrel.2006.04.017. [DOI] [PubMed] [Google Scholar]
  3. Vyas A.; Saraf S.; Saraf S. Cyclodextrin based novel drug delivery systems. J. Inclusion Phenom. Macrocyclic Chem. 2008, 62, 23–42. 10.1007/s10847-008-9456-y. [DOI] [Google Scholar]
  4. Ye R.; Nie X.; Zhou Y.; Wong C. F.; Gong X.; Jiang W.; Tang W.; Wang Y. A.; Heine T.; Zhou B. Exploring host guest complexation mechanisms by a molecular dynamics/quantum mechanics/continuum solvent model approach. Chem. Phys. Lett. 2016, 648, 170–177. 10.1016/j.cplett.2016.02.006. [DOI] [Google Scholar]
  5. Iikura H.; Tsuneda T.; Yanai T.; Hirao K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540–3544. 10.1063/1.1383587. [DOI] [Google Scholar]
  6. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  7. Tsuneda T.Fundamentals of Density Functional Theory; Kodansha, 2012; pp 160–163. [Google Scholar]
  8. Zhao Y.; Truhlar D. G. Density Functionals for Noncovalent Interaction Energies of Biological Importance. J. Chem. Theory Comput. 2007, 3, 289–300. 10.1021/ct6002719. [DOI] [PubMed] [Google Scholar]; PMID: 26627172
  9. Hongo K.; Maezono R. A Computational Scheme To Evaluate Hamaker Constants of Molecules with Practical Size and Anisotropy. J. Chem. Theory Comput. 2017, 13, 5217–5230. 10.1021/acs.jctc.6b01159. [DOI] [PubMed] [Google Scholar]; PMID: 28981266
  10. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  11. Grimme S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 211–228. 10.1002/wcms.30. [DOI] [Google Scholar]
  12. Foulkes W. M. C.; Mitas L.; Needs R. J.; Rajagopal G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33–83. 10.1103/RevModPhys.73.33. [DOI] [Google Scholar]
  13. Maezono R. Optimization of Many-Body Wave Function. J. Comput. Theor. Nanosci. 2009, 6, 2474–2482. 10.1166/jctn.2009.1308. [DOI] [Google Scholar]
  14. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  15. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  16. Oommen E.; Shenoy B. D.; Udupa N.; Kamath R.; Devi P. U. Antitumour Efficacy of Cyclodextrin-complexed and Niosome-encapsulated Plumbagin in Mice Bearing Melanoma B16F1. Pharm. Pharmacol. Commun. 1999, 5, 281–285. 10.1211/146080899128734857. [DOI] [Google Scholar]
  17. Aziz M. H.; Dreckschmidt N. E.; Verma A. K. Plumbagin, a Medicinal Plant–Derived Naphthoquinone, Is a Novel Inhibitor of the Growth and Invasion of Hormone-Refractory Prostate Cancer. Cancer Res. 2008, 68, 9024–9032. 10.1158/0008-5472.CAN-08-2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Abedinpour P.; Baron V. T.; Chrastina A.; Rondeau G.; Pelayo J.; Welsh J.; Borgström P. Plumbagin improves the efficacy of androgen deprivation therapy in prostate cancer: A pre-clinical study. Prostate 2017, 77, 1550–1562. 10.1002/pros.23428. [DOI] [PubMed] [Google Scholar]
  19. Suthanurak M.; Sakpakdeejaroen I.; Rattarom R.; Itharat A. Formulation and stability test of Benjakul extract tablets: a preliminary study. Thai J. Pharmacol. 2010, 32, 160–164. [Google Scholar]
  20. Morris G. M.; Goodsell D. S.; Halliday R. S.; Huey R.; Hart W. E.; Belew R. K.; Olson A. J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998, 19, 1639–1662. . [DOI] [Google Scholar]
  21. Srihakulung O.; Maezono R.; Toochinda P.; Kongprawechnon W.; Intarapanich A.; Lawtrakul L. Host-Guest Interactions of Plumbagin with β-Cyclodextrin, Dimethyl-β-Cyclodextrin and Hydroxypropyl-β-Cyclodextrin: Semi-Empirical Quantum Mechanical PM6 and PM7 Methods. Sci. Pharm. 2018, 86, 20 10.3390/scipharm86020020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Groom C. R.; Bruno I. J.; Lightfoot M. P.; Ward S. C. The Cambridge Structural Database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72, 171–179. 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Gasteiger J.; Marsili M. A new model for calculating atomic charges in molecules. Tetrahedron Lett. 1978, 19, 3181–3184. 10.1016/S0040-4039(01)94977-9. [DOI] [Google Scholar]
  24. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09, Revision E.01; Gaussian Inc.: Wallingford, CT, 2009. [Google Scholar]
  25. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.. et al. Gaussian 16, Revision B.01; Gaussian Inc.: Wallingford, CT, 2016. [Google Scholar]
  26. Bachrach S. M. DFT Study of the ExBox Aromatic Hydrocarbon Host Guest Complex. J. Phys. Chem. A 2013, 117, 8484–8491. 10.1021/jp406823t. [DOI] [PubMed] [Google Scholar]; PMID: 23927562.
  27. Bachrach S. M.; Andrews A. E. All-Carbon, Neutral Analogue of ExBox4+: A DFT Study of Polycyclic Aromatic Hydrocarbon Binding. J. Phys. Chem. A 2014, 118, 6104–6111. 10.1021/jp504408u. [DOI] [PubMed] [Google Scholar]; PMID: 25029611.
  28. Bouhadiba A.; Belhocine Y.; Rahim M.; Djilani I.; Nouar L.; Khatmi D. E. Host-guest interaction between tyrosine and β-cyclodextrin: Molecular modeling and nuclear studies. J. Mol. Liq. 2017, 233, 358–363. 10.1016/j.molliq.2017.03.029. [DOI] [Google Scholar]
  29. Deka B. C.; Bhattacharyya P. K. DFT study on host-guest interaction in chitosan amino acid complexes. Comput. Theor. Chem. 2017, 1110, 40–49. 10.1016/j.comptc.2017.03.036. [DOI] [Google Scholar]
  30. Simon Sl.; Duran M.; Dannenberg J. J. How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers. J. Chem. Phys. 1996, 105, 11024–11031. 10.1063/1.472902. [DOI] [Google Scholar]
  31. Kim J.; Baczewski A.; Beaudet T.; Benali A.; Bennett M.; Berrill M.; Blunt N.; Casula M.; Ceperley D.; Chiesa S.; et al. QMCPACK: An open source ab initio Quantum Monte Carlo package for the electronic structure of atoms, molecules, and solids. J. Phys.: Condens. Matter 2018, 30, 195901 10.1088/1361-648X/aab9c3. [DOI] [PubMed] [Google Scholar]
  32. Gordon M. S.; Schmidt M. W. In Theory and Applications of Computational Chemistry; Dykstra C. E.; Frenking G.; Kim K. S.; Scuseria G. E., Eds.; Elsevier: Amsterdam, 2005; pp 1167–1189. [Google Scholar]
  33. Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Nguyen K. A.; Su S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
  34. Annaberdiyev A.; Wang G.; Melton C. A.; Chandler Bennett M.; Shulenburger L.; Mitas L. A new generation of effective core potentials from correlated calculations: 3d transition metal series. J. Chem. Phys. 2018, 149, 134108 10.1063/1.5040472. [DOI] [PubMed] [Google Scholar]
  35. Bennett M. C.; Melton C. A.; Annaberdiyev A.; Wang G.; Shulenburger L.; Mitas L. A new generation of effective core potentials for correlated calculations. J. Chem. Phys. 2017, 147, 224106 10.1063/1.4995643. [DOI] [PubMed] [Google Scholar]
  36. Kendall R. A.; Dunning T. H.; Harrison R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. 10.1063/1.462569. [DOI] [Google Scholar]
  37. Marom N.; Tkatchenko A.; Rossi M.; Gobre V. V.; Hod O.; Scheffler M.; Kronik L. Dispersion Interactions with Density-Functional Theory: Benchmarking Semiempirical and Interatomic Pairwise Corrected Density Functionals. J. Chem. Theory Comput. 2011, 7, 3944–3951. 10.1021/ct2005616. [DOI] [PubMed] [Google Scholar]; PMID: 26598340.
  38. Hongo K.; Watson M. A.; Sánchez-Carrera R. S.; Iitaka T.; Aspuru-Guzik A. Failure of Conventional Density Functionals for the Prediction of Molecular Crystal Polymorphism: A Quantum Monte Carlo Study. J. Phys. Chem. Lett. 2010, 1, 1789–1794. 10.1021/jz100418p. [DOI] [Google Scholar]
  39. Watson M. A.; Hongo K.; Iitaka T.; Aspuru-Guzik A.. Advances in Quantum Monte Carlo, Chapter 9, pp 101–117..
  40. Hongo K.; Cuong N. T.; Maezono R. The importance of electron correlation on stacking interaction of adenine-thymine base-pair step in B-DNA: A quantum Monte Carlo study. J. Chem. Theory Comput. 2013, 9, 1081–1086. 10.1021/ct301065f. [DOI] [PubMed] [Google Scholar]
  41. Hongo K.; Watson M. A.; Iitaka T.; Aspuru-Guzik A.; Maezono R. Diffusion Monte Carlo Study of Para-Diiodobenzene Polymorphism Revisited. J. Chem. Theory Comput. 2015, 11, 907–917. 10.1021/ct500401p. [DOI] [PubMed] [Google Scholar]; PMID: 26579744.
  42. Hongo K.; Maezono R.. Recent Progress in Quantum Monte Carlo, Chapter 9, pp 127−143.
  43. Qin K. S.; Ichibha T.; Hongo K.; Maezono R. Inconsistencies in ab initio evaluations of non-additive contributions of DNA stacking energies. Chem. Phys. 2020, 529, 110554 10.1016/j.chemphys.2019.110554. [DOI] [Google Scholar]
  44. Kamiya M.; Tsuneda T.; Hirao K. A density functional study of van der Waals interactions. J. Chem. Phys. 2002, 117, 6010–6015. 10.1063/1.1501132. [DOI] [Google Scholar]
  45. de Sousa S. M. R.; Guimarães L.; Ferrari J. L.; Almeida W. B. D.; Nascimento C. S. A DFT investigation on the host/guest inclusion process of prilocaine into β-cyclodextrin. Chem. Phys. Lett. 2016, 652, 123–129. 10.1016/j.cplett.2016.04.053. [DOI] [Google Scholar]
  46. Costa M. A.; Anconi C. P.; Santos H. F. D.; Almeida W. B. D.; Nascimento C. S. Inclusion process of tetracycline in β and γ-cyclodextrins: A theoretical investigation. Chem. Phys. Lett. 2015, 626, 80–84. 10.1016/j.cplett.2015.03.016. [DOI] [Google Scholar]
  47. Abranches P. A. S.; Varejão E. V. V.; da Silva C. M.; de Fátima; Magalhães T. F. F.; da Silva D. L.; de Resende-Stoianoff M. A.; Reis S.; Nascimento C. S.; de Almeida W. B.; et al. Complexes of fluconazole with sodium p-sulfonatocalix[n]arenes: characterization, solubility and antifungal activity. RSC Adv. 2015, 5, 44317–44325. 10.1039/C5RA05423K. [DOI] [Google Scholar]
  48. Lopes J. F.; Nascimento C. S.; Anconi C. P.; Santos H. F.; Almeida W. B. Inclusion complex thermodynamics: The β-cyclodextrin and sertraline complex example. J. Mol. Graphics Modell. 2015, 62, 11–17. 10.1016/j.jmgm.2015.08.008. [DOI] [PubMed] [Google Scholar]
  49. de Assis J. V.; Teixeira M. G.; Soares C. G.; Lopes J. F.; Carvalho G. S.; Lourenço M. C.; de Almeida M. V.; de Almeida W. B.; Fernandes S. A. Experimental and theoretical NMR determination of isoniazid and sodium p-sulfonatocalix[n]arenes inclusion complexes. Eur. J. Pharm. Sci. 2012, 47, 539–548. 10.1016/j.ejps.2012.07.015. [DOI] [PubMed] [Google Scholar]
  50. Cancès E.; Mennucci B.; Tomasi J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. 10.1063/1.474659. [DOI] [Google Scholar]
  51. Maia P. P.; de Sousa S. M. R.; De Almeida W. B.; Guimarães L.; Nascimento C. S. Computational investigation on the host-guest inclusion process of norfloxacin into β-cyclodextrin. J. Mol. Model. 2016, 22, 220. 10.1007/s00894-016-3098-6. [DOI] [PubMed] [Google Scholar]
  52. Schönbeck C.; Li H.; Han B.-H.; Laursen B. W. Solvent Effects and Driving Forces in Pillararene Inclusion Complexes. J. Phys. Chem. B 2015, 119, 6711–6720. 10.1021/acs.jpcb.5b02515. [DOI] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES