An integrative approach for fine-mapping chromatin interactions

Abstract

Motivation

Chromatin interactions play an important role in genome architecture and gene regulation. The Hi-C assay generates such interactions maps genome-wide, but at relatively low resolutions (e.g. 5-25 kb), which is substantially coarser than the resolution of transcription factor binding sites or open chromatin sites that are potential sources of such interactions.

Results

To predict the sources of Hi-C-identified interactions at a high resolution (e.g. 100 bp), we developed a computational method that integrates data from DNase-seq and ChIP-seq of TFs and histone marks. Our method, χ-CNN, uses this data to first train a convolutional neural network (CNN) to discriminate between called Hi-C interactions and non-interactions. χ-CNN then predicts the high-resolution source of each Hi-C interaction using a feature attribution method. We show these predictions recover original Hi-C peaks after extending them to be coarser. We also show χ-CNN predictions enrich for evolutionarily conserved bases, eQTLs and CTCF motifs, supporting their biological significance. χ-CNN provides an approach for analyzing important aspects of genome architecture and gene regulation at a higher resolution than previously possible.

Availability and implementation

χ-CNN software is available on GitHub (https://github.com/ernstlab/X-CNN).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Genome-wide maps of chromatin contacts are important for understanding genome architecture and gene regulation (Mumbach et al., 2016; Rao et al., 2014). These contact maps also have implications to understanding the mechanism of disease-associated genetic variation (Lupiáñez et al., 2015; Won et al., 2016). Hi-C is an assay widely used for producing such genome-wide maps (Lieberman-Aiden et al., 2009). These maps are often represented with an N × N contact matrix, where N is the length of the genome divided by the chosen resolution. Within this matrix, sub-regions can be annotated as ‘peaks’ if the number of contacts within the sub-region is significantly higher than expected (Ay et al., 2014; Rao et al., 2014). These peaks correspond to chromatin ‘loops’, where two loci are significantly closer to each other than expected by chance. Peaks enrich for promoters, enhancers and cohesin-bound regions, which are often mediated by CTCF (Rao et al., 2014).

However, the resolution at which these peaks can be identified from Hi-C data is substantially coarser than transcription factor (TF) binding or open chromatin sites, which can be considered potential sources of these interactions. The deepest human Hi-C sequencing experiment to date was performed on the GM12878 lymphoblastoid cell line with 3.6 billion reads generated (Rao et al., 2014) and led to a contact matrix at a 1 kb resolution. However, interaction peaks were only reported at 5 or 10 kb resolution. Other cell types from the same study had peaks called at up to 25 kb resolution, substantially coarser than the 100-200 bp resolution of TF binding and open chromatin sites. There are two major challenges with directly increasing resolution of Hi-C. First, Hi-C is limited by the distribution of restriction sites (Naumova et al., 2012). Second, to increase resolution by a factor of k, one would need to increase the sequencing depth by k².

We propose an alternative approach to obtain fine-resolution information in chromatin interaction peaks. Our approach is based on computationally integrating high-resolution data from DNase-seq and ChIP-seq of histone marks and TFs (Park, 2009; Song and Crawford, 2010). This is motivated by the observation that signal from such experiments shows specific patterns within interaction peaks such as pairs of CTCF sites or enhancer-promoter pairs (Rao et al., 2014). Our approach takes chromatin interaction peaks at coarse resolution (e.g. 25 kb) along with DNase-seq and ChIP-seq data to predict the source of each interaction at a fine resolution (e.g. 100 bp). The approach is based on combining a convolutional neural network (CNN) trained to predict interactions with a feature attribution method to fine-map the interactions to their sources.

Limitations in Hi-C resolution have previously been recognized, and have inspired development of novel computational methods. For example, a transfer learning method was developed that learns from a high-resolution Hi-C map in one cell type to enhance the resolution of a Hi-C map in another cell type (Zhang et al., 2018b), but it was not shown to be effective at resolutions finer than 10 kb. Other strategies have been proposed to enhance the resolution of contact maps genome-wide directly from Hi-C data (Cameron et al., 2018; Carron et al., 2019), but they are inherently limited to achieving at best restriction fragment length resolution, which depends on the restriction enzyme used and locally on the position of restriction sites. Other methods have been proposed that incorporate TF binding and epigenomic data to predict Hi-C data directly (Farré et al., 2018; Zhang et al., 2018a). However, these methods are designed to make predictions at the resolution of the Hi-C data used for training, and not individual TF binding sites or open chromatin. By applying a feature attribution method, χ-CNN makes predictions within interacting regions, but at the finer resolution of DNase-seq and ChIP-seq data (∼100 bp).

Other methods have aimed to solve related, but different, problems. Some methods have focused on using epigenetic data to predict specific aspects of chromatin structure genome-wide. For example, one method predicted the boundaries of topologically associated domains (Huang et al., 2015). Other work aimed to predict promoter-enhancer interactions from epigenetic data, TF binding or sequence data (Cao et al., 2017; Roy et al., 2015; Whalen et al., 2016), though the performance claims of some of these method in some cases has recently been challenged (Xi and Beer, 2018). These methods differ from our proposed method in that their goal is to predict enhancer-promoter interactions, while we consider any type of Hi-C detected interaction, and our goal is to fine-map coarse, but detected, interactions.

In this article, we first present our computational method, chromatin interaction CNN (χ-CNN, χ for the Greek letter Chi), to identify the likely sources of Hi-C identified interactions at high resolution. χ-CNN leverages readily available high-resolution information in complementary data, specifically DNase-seq and ChIP-seq. We applied χ-CNN to data from two cell types, and present a series of analyses providing quantitative evidence of the effectiveness of the approach. We also biologically characterize the fine-mapped positions. We expect χ-CNN to be useful in the study of chromatin interactions.

2 Materials and methods

Our method, χ-CNN, uses a CNN (Krizhevsky et al., 2012) together with a feature attribution scoring method to fine-map called chromatin interactions. χ-CNN first learns to discern called interactions from non-interactions using data from DNase-seq and ChIP-seq of histone marks and TF binding. It then performs fine-mapping by using integrated gradients (Sundararajan et al., 2017), a feature attribution method, to identify the pair of sub-loci that contribute most to the prediction of each interaction.

2.1 Training data

In χ-CNN, each positive data point corresponds to an intra-chromosomal chromatin interaction peak. We applied χ-CNN to peaks called from two Hi-C datasets: one from the lymphoblastoid cell line GM12878, and the other from the leukemia cell line K562. We focused on these cell types because they also had data from DNase-seq and ChIP-seq of many histone marks and TFs publicly available. For both of these cell types, we applied χ-CNN to chromatin interaction peaks called by HiCCUPS at up to three different resolutions: 5, 10 and 25 kb (Rao et al., 2014). For each peak, HiCCUPs chooses the finest resolution that surpasses a significance threshold. It called 9448 peaks in GM12878 across the 5 and 10 kb resolutions and 6057 peaks in K562 across all three resolutions at a false discovery rate (FDR) of 0.1.

Each negative data point corresponds to a sample from a distance-matched, random genomic background. To form this background, χ-CNN first computes the distribution of distances between interacting pairs observed in the positive training data, and then chooses random pairs of regions in the genome that match that distribution. We chose to use as many non-interacting pairs as observed interacting pairs, but we verified that the exact ratio did not significantly affect fine-mapping performance (Supplementary Fig. S1). We note that since our objective is fine-mapping, and not predicting Hi-C interactions, the ratio does not need to match the genome-wide ratio. We expected that when comparing interacting peaks to this negative background, χ-CNN would learn which epigenetic and TF features differentiate peak regions from non-peak regions while controlling for distance-based effects.

2.2 Feature representation

Each side of an interaction, whether a positive or negative data point, is represented by a matrix. Each matrix is of size F × B, where F is the number of features, and the number of bins B = W/R, where W is the width of the peak region and R is the binning resolution. For each cell type, we used a set of previously uniformly processed DNase-seq and ChIP-seq data tracks from the ENCODE consortium (data available at http://ftp.ebi.ac.uk/pub/databases/ensembl/encode/integration_data_jan2011/byDataType/signal/jan2011/bigwig/), where each track corresponds to one feature (ENCODE Consortium, 2012). This resulted in 100 features for GM12878 and 148 features for K562 (Supplementary Table S1). We later show that χ-CNN is also effective with subsets of these features. We used W = 25 kb for both GM12878 and K562 because this was the largest size peak called in these cell types, and it allowed for direct comparison of results (Rao et al., 2014). We use R = 100 bp resolution for the binning resolution, yielding B = 25 kb/100 bp = 250 bins across each region.

Each DNase-seq and ChIP-seq track represents a normalized signal coverage (Hoffman et al., 2013). For each track, we first averaged the values within each bin. We then added 1 to each value and then performed a log₂-transformation to make the training more robust to extreme outliers. Finally, because only the relative orientation of the regions is relevant and not the specific strand they are on, we also took each matrix on the 5′ to 3′ strand (the ‘right’ interacting region) and reversed it to go from 3′ to 5′ before adding it to the dataset, effectively doubling the size of the dataset.

2.3 Neural network architecture

χ-CNN uses a CNN (Fig. 1). CNNs are often used in image recognition applications (Krizhevsky et al., 2012) for their translational invariance and flexibility in learning complex data. The CNN that χ-CNN uses is composed of a compressing encoding layer, followed by a convolutional layer, then a global max-pooling layer. Data from the global max-pooling layer is then passed to a dense layer and, finally, a logistic regression layer, which calculates a probability of the region being part of an interaction. χ-CNN uses a ReLu non-linear transformation, defined as ReLu(x) = max(0, x), effectively setting negative values to 0, after the encoding, convolution and dense layers.

Fig. 1.

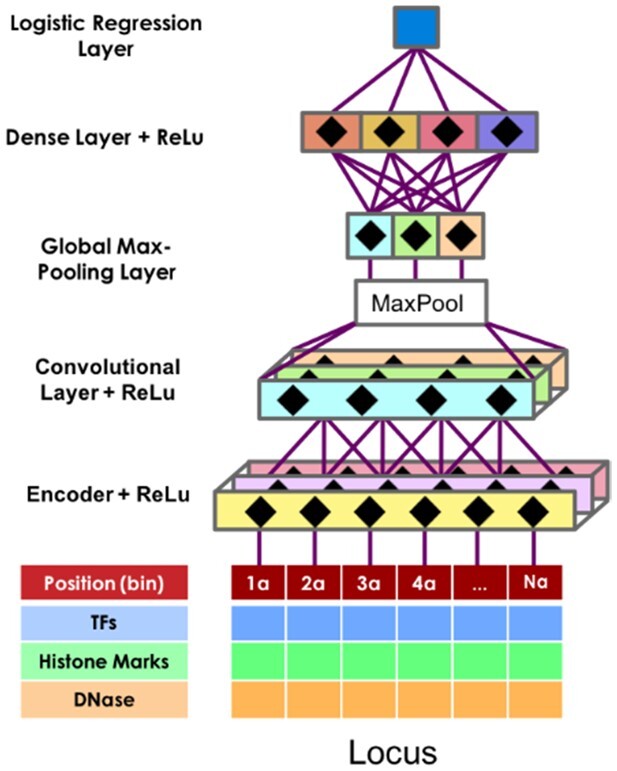
The structure of the CNN in χ-CNN. A data matrix from an interacting locus is passed through an encoding layer, convolutional layer, global max-pooling layer, a dense layer and finally, a logistic regression layer. The encoder, convolutional and dense layers use a ReLu activation function

Encoder: The encoder projects a high-dimensional space (F × B) to a lower one (K_Enc × B), where K_Enc  < F is the number of encoder kernels. Encoders make neural networks easier to optimize and more difficult to overfit, and have a similar objective to other dimensionality reduction approaches such as principal component analysis, except that they are further tuned after initialization. Here, χ-CNN initializes the encoder by pre-training an autoencoder (an encoder-decoder pair) (Ballard, 1987) on interacting regions in the training data, then transfers the learned encoder weights to the final CNN. The autoencoder has a width of 1 bin, meaning that it is applied to each position independently, and only has one hidden layer to keep the number of parameters low and prevent overfitting.

Convolutional layer: Following the encoder, the convolutional layer slides a matrix of K_Enc × C values across the entire matrix of size K_Enc × B for each of the K_Conv kernels. At each of the D = B − C + 1 sub-matrices of size K_Enc × C in the region, it calculates the element-wise product of the data with each of K_Conv kernels, followed by summation. This produces a matrix of K_Conv × D values. Intuitively, the convolution layer is used to find local spatial patterns of signal in the DNase-seq and ChIP-seq data, such as co-binding of several TFs or a promoter followed by an actively transcribed region. Importantly, it does not make any assumptions about the specific positions of patterns in a region, a useful characteristic for our application, as the interaction source is expected to be in different positions for different interactions.

Global max-pooling layer: The global max-pooling layer takes as input the K_Conv × D matrix output by the convolutional layer, and then outputs the maximum value for each of the K_Conv rows.

Dense layer: The output of the global max-pooling layer is then passed to the dense layer. Each of the K_Dense kernels in the dense layer has access to every value from the global max-pooling layer. It multiplies these values by learned weights, sums them, adds a bias term and outputs a vector of size K_Dense. This layer finds which signal profiles tend to co-occur within the same interacting region.

Logistic regression layer: The final layer is the logistic regression layer, which takes the K_Dense values output from the dense layer, multiplies them by learned weights and passes their sum with a learned bias term through the logistic function. The logistic layer returns a probability between 0 and 1, corresponding to the model’s confidence that a sample is positive.

Training and hyperparameter search: We implemented χ-CNN using Keras 2.2.4, a Python neural network library built on top of TensorFlow (Abadi et al., 2016). The autoencoder is pre-trained to optimize a mean-squared logarithmic error loss function, which is appropriate for continuous data. For binary classification, the whole CNN uses a binary cross-entropy loss function. Both use stochastic gradient descent using the ADADELTA optimizer (Zeiler, 2012). Chromosomes 8 and 9 are withheld for validation after each epoch of training, and chromosome 1 for final testing evaluation. We performed a random search to select a combination of hyperparameters (Bergstra and Bengio, 2012). Specifically, we searched for the width of the convolutional filter (C), the number of kernels for the autoencoder (K_Enc), convolutional layer (K_Conv) and dense layer (K_Dense), the type and strength of regularization for all trained parameters and the dropout magnitude (Srivastava et al., 2014) (Supplementary Table S2). For each dataset, we tried 60 random combinations of hyperparameters, as it yields at least a 95% probability of the performance being within the top 5% of hyperparameter choices. The probability of a model trained with a random combination of hyperparameters not being in the top 5% of all combinations is 0.95. For n combinations of hyperparameters, the probability of none of them being in the top 5% of all combinations is (0.95)ⁿ, which is less than 0.05 for n ≥ 59. We chose the hyperparameter combination that achieved the best area under the receiver operator characteristic (AUROC) on validation data, and we report the test data AUROC and area under the precision-recall curve (AUPRC) for chromosome 1 (Supplementary Table S2). We note that different applications of χ-CNN can lead to the selection of different hyperparameter combinations.

Finally, after selecting the optimal hyperparameter combination, χ-CNN is retrained using all peaks except those on chromosomes 8 and 9, which are used as a stopping condition for training. This model is used for fine-mapping and all subsequent analyses.

2.4 Fine-mapping

After training the CNN, χ-CNN fine-maps peaks using a feature attribution method to score each position within the peak region. Feature attribution methods were developed to help explain why a machine learning model made a specific prediction. For example, in the context of image recognition, it can be used to determine which pixels of an image contributed the most to the image’s classification; if an image is predicted to contain a cat, it would be expected to highly score areas around the whiskers and ears, but ignore irrelevant background.

χ-CNN uses a feature attribution method called integrated gradients (Sundararajan et al., 2017) to apply the same methodology to its predictions, wherein ‘pixels’ correspond to bins in the input matrices. We chose to use integrated gradients because of its simplicity in assumptions and implementation. As in the original application of integrated gradients, to determine the importance of a pixel with multiple individual features (RGB values), χ-CNN determines the total importance for a bin by summing the importance of all features at that bin (Fig. 2).

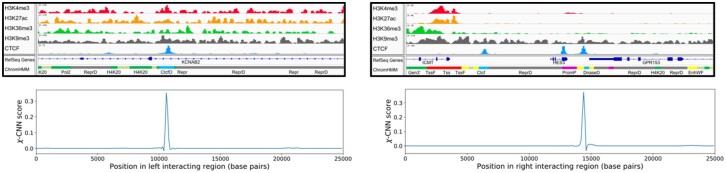
Fig. 2.

An example of a fine-mapped peak. The left and right sides correspond to the two sides of an interaction. The top images show tracks for H3K4me3, H3K27ac, H3K36me3, H3K9me3 and CTCF. The bottom images show χ-CNN’s fine-mapping score for each position in the region (in kilobases). There is a sharp peak on the left corresponding to a CTCF peak, and in the right region, χ-CNN assigns the highest importance score to one of three CTCF peaks

The feature importance scores that integrated gradients assigns are roughly equal to the output probability difference when setting that feature to a baseline of 0 (which corresponds to no signal) (Sundararajan et al., 2017). A score of s > 0 at some bin means that setting the data in that bin to 0 would decrease the calculated probability of the two regions interacting by approximately s. Conversely, if s is negative, setting the data in the bin to 0 would increase the probability of interaction by s. For each side of an interaction, we took the position with the highest overall score as the ‘fine-mapped’ peak, and used these positions for all subsequent analyses and validation.

3 Results

3.1 χ-CNN is highly predictive of interactions

Before fine-mapping called interactions, we first established that the CNN of χ-CNN is effective at discriminating between positive and negative interacting regions. We note that this is a necessary, though not sufficient, condition for fine-mapping called interactions. We conducted the evaluations on a withheld test set of interactions on chromosome 1, which was not used for training the CNN or selecting hyperparameters. The CNN achieved a high AUROC curve for predicting interactions in GM12878 and K562, 0.94 for both. We also evaluated the AUPRCs (Davis and Goadrich, 2006), and obtained value of 0.92 for both GM12878 and K562 (Supplementary Table S2). We note that the AUPRC depends on the ratio between positive and negative samples, and since we are considering balanced data it is expected to be higher here than if predicting genome-wide. We emphasize, however, that our goal is not to predict interactions genome-wide, but rather to fine-map called interactions.

3.2 χ-CNN fine-mapping predictions are reproducible

Having established that χ-CNN could effectively discriminate positive from negative interactions, we next sought to establish that χ-CNN’s fine-mapping method is reproducible. For each cell type, we took the corresponding set of HiCCUPs peaks calls and split by chromosome into two non-overlapping sets of approximately equal size; one set was composed of interactions on odd chromosomes, and the other on even chromosomes and chromosome X. We did not create a third withheld set because the typical application of χ-CNN is training and fine-mapping on the same set of peaks. We trained two separate models, one on each split set. We then fine-mapped all the interactions and calculated the fine-mapping concordance by calculating Euclidean distance on a 2D grid between the fine-mapped peaks (Supplementary Fig. S2). We found that 87% and 84% of interactions fine-mapped within 100 bp in any direction for GM12878 and K562, respectively, as compared to an expected 0.01% by chance, and this concordance further increased at more relaxed distance thresholds. We note that each of the datasets in this analysis was roughly half the size of the full dataset, and thus the results should be considered a lower bound of expected reproducibility.

3.3 χ-CNN fine-mapped predictions recover original Hi-C peaks after extension

Having established χ-CNN fine-mapping predictions are reproducible, we next sought evidence that they are also accurate. As we do not have Hi-C interaction peak calls available at the resolution of χ-CNN predictions, we instead evaluated how well χ-CNN predictions can identify the original called peaks when provided those peaks after extending their boundaries.

For each peak narrower than 25 kb (i.e. 5 or 10 kb), we extended the boundaries of each side of an interaction uniformly in both directions to produce a 25 kb peak. Together with peaks originally called at 25 kb, we extracted DNase-seq and ChIP-seq data from these 25 kb regions and applied χ-CNN. We then evaluated how often the fine-mapping fell in the center 5 kb region.

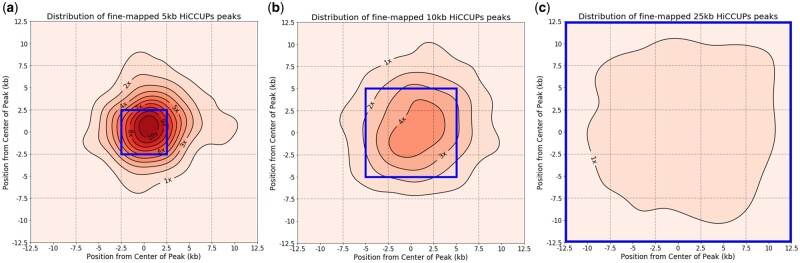
We found that for 5 kb HiCCUPs peaks in K562 extended to 25 kb, χ-CNN fine-mapping predictions were, as expected, frequently found in the center 5 kb region (33% of peaks, 8.3-fold enrichment compared to random guessing, P-value < 0.001, binomial test) (Fig. 3a). Similarly, fine-mapping predictions of 10 kb HiCCUPS peaks in K562 extended to 25 kb had a strong enrichment in the center 5 kb (4.2-fold enrichment, P-value < 0.001) (Fig. 3b). Fine-mapping predictions for peaks that were originally called at 25 kb had a much smaller enrichment in the center cell (1.6-fold enrichment, P-value < 0.001) (Fig. 3c). This smaller enrichment was expected, since the true peak source is more likely to fall anywhere within the 25 kb region than for peaks called at a finer resolution. We also applied the same evaluations to GM12878 and found that it performed better with 9.2- and 4.5-fold enrichments for 5 kb and 10 kb peaks, respectively. These results show that χ-CNN strongly enriches for recovering finer resolution peaks after extending the peaks to be 25 kb (Supplementary Table S3 and Fig. S3).

Fig. 3.

Distribution of fine-mapping predictions for different size HiCCUPs peaks. Kernel density estimation (KDE) plots showing the distribution of χ-CNN’s fine-mapping predictions within K562 peaks after extending the original peak equally in both directions to form a 25 kb peak. To generate plots, we used the ‘jointplot’ function with the KDE option in Python’s Seaborn package. (a) For 5 kb interaction peaks extended to 25 kb, fine-mapped positions are strongly concentrated around the original 5 kb peak (center blue box). Enrichment in center 5 kb bin is 8.3-fold compared to random guessing. (b) For 10 kb peaks extended to 25 kb, fine-mapped positions are concentrated in the original 10 kb peak (center blue box). Enrichment in center 5 kb bin is 4.2-fold. (c) Fine-mapped positions are not concentrated in any specific region in interactions called at 25 kb. Enrichment in center 5 kb bin is 1.6-fold. The positive direction on the axes points toward the exterior of the interactions. The mode of the 5 kb peak plot is shifted toward the positive direction, meaning that fine-mapped peaks are most likely to be approximately 1 kb further out than the center of the originally called peak. Similar plots for GM12878 can be found in Supplementary Figure S3. (Color version of this figure is available at Bioinformatics online.)

We also applied χ-CNN to 5 kb peaks after extending unevenly, specifically extending the original 5 kb peak by 20 kb on one side and holding the other side fixed. We found that χ-CNN performed similarly in peak recovery as when extending uniformly (8.2- versus 8.3-fold enrichment in K562 and 9.2-fold for both in GM12878).

When extending evenly, a large percentage of χ-CNN fine-mapping predictions for extended 5 kb peaks did not map to the center bin, but to one of the four directly adjacent bins (39%, 2.4-fold enrichment, P-value < 0.001 for both cell types). Many of these off-center predictions could be expected to be the true source, as the original HiCCUPS predictions are based on noisy Hi-C data, which can lack the resolution to differentiate between interaction sources near the boundary of two 5 kb cells.

Next, for both cell types, we analyzed how well χ-CNN predictions overlapped high-ranked 5 kb resolution Hi-C signal. We normalized this signal using the KR normalization vectors as in Rao et al. (2014). For this, we took all 5 kb HiCCUPs peaks and looked at a 25 kb grid centered on the peak. We found a median rank for χ-CNN predictions of 5 and 7 out of the 25 5 kb squares for GM12878 and K562, respectively, compared to a median rank of 13 for random genomic interactions used for training (Supplementary Fig. S4). When we split the HiCCUPs speaks into halves based on the total number of normalized Hi-C reads falling into this peak, we observed the same median values for both halves as the combined set, suggesting χ-CNN would still be applicable to less confident peaks.

We also directly looked at 1 kb resolution Hi-C signal at χ-CNN fine-mapped positions in GM12878, as this was the finest resolution signal available. We found that on average, normalized Hi-C signal was the highest at the fine-mapped position, and as the distance from the fine-mapped position increased, Hi-C signal decreased (Supplementary Fig. S5).

3.4 χ-CNN better recovers original Hi-C peak after extension than baseline approaches

We compared the performance of χ-CNN at recovering the original 5 and 10 kb Hi-C peaks to several baselines (Supplementary Table S3). The first set of baselines consisted of considering each DNase-seq and ChIP-seq track separately and fine-mapping to the position with the highest signal. This included 100 tracks for GM12878 and 148 tracks for K562. In cases where there were multiple features corresponding to the same histone mark, TF or DNase-seq, we also created a baseline prediction by averaging the signals across those features, and we used this for the reported enrichments. We note that the best performing of these baselines only provides an upper bound on expected fine-mapping performance when selecting a single track or feature average, as in practice there is no guarantee the selection made would be optimal for fine-mapping.

We found that several TFs, notably CTCF and the cohesin marks RAD21 and SMC3, had high enrichment for recovering the original 5 and 10 kb HiCCUPs peaks (Supplementary Table S3), consistent with their previously reported high enrichment in interactions (Rao et al., 2014), but were all less than χ-CNN’s predictions. Combining counts from both 5 and 10 kb peaks, χ-CNN outperformed all other tracks (P-value < 0.05, two-proportions z-test). DNase-seq and ChIP-seq tracks besides CTCF, RAD21, SMC3 and ZNF143 had lower performances, at most 6.4 and 5.2 in GM12878 and K562, respectively, as compared to the 8.9- and 8.2-fold enrichments for χ-CNN (Fig. 4).

Fig. 4.

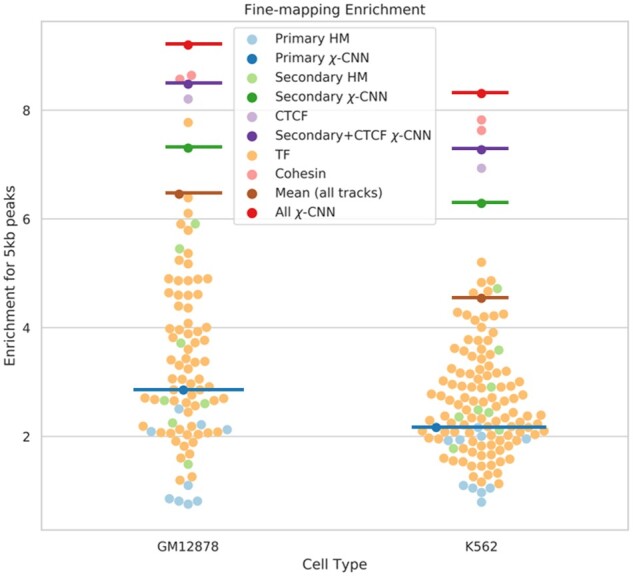
The 5 kb peak fine-mapping performance for χ-CNN and baseline methods. Fine-mapping performance using individual features is marked with points, and methods integrating multiple features are emphasized with horizontal bars. Light blue points and the dark blue bar correspond to ‘primary’ histone marks and χ-CNN trained on these marks, respectively. Similarly, light green points and the dark green bar correspond to ‘secondary’ marks. CTCF, in lavender, performs well, but χ-CNN trained on ‘secondary’ marks and CTCF performs better. Cohesion sub-units, in pink, are the best performing single marks; however, χ-CNN trained on all features, in red, shows greater enrichment than any individual mark. All other TFs, in orange, perform similarly to histone marks. Finally, a baseline method of averaging all features is marked with a brown bar. (Color version of this figure is available at Bioinformatics online.)

Another baseline we evaluated was predicting based on averaging all DNase-seq and ChIP-seq signal tracks and then taking the position with highest average signal. For the 5 kb evaluation, this had a fold enrichment of 6.5 and 4.5 in GM12878 and K562, respectively, which was significantly less than χ-CNN’s enrichments (P-value < 0.001) (Fig. 4).

Finally, we compared our fine-mapping predictions to a logistic regression model trained to distinguish between interacting regions and random ones. We trained the logistic regression model using the same DNase and ChIP-seq data as features and the same interacting and random regions as for training χ-CNN. However, we had to train it with data at the same resolution as fine-mapped positions. Therefore, we generated our positive and negative training data by taking each 100 bp bin in each interacting region and each random region, respectively. We trained the logistic regression model with default parameters using the Python package scikit-learn. To fine-map, we took each 100 bp position in each peak and returned the position that yielded the highest probability. For the 5 kb evaluation, the logistic regression model achieved 8.2- and 6.7-fold enrichments for GM12878 and K562, respectively. These were also significantly lower than χ-CNN’s enrichments (P-value < 0.001, two-proportions z-test).

3.5 χ-CNN outperforms baseline approaches in recovering relevant external annotations

We next analyzed the enrichment of χ-CNN’s fine-mapping predictions and baseline approaches for several external annotations. The external annotations considered are defined at or near base pair resolution and are suggestive of functionally relevant positions. Specifically, we considered: (i) evolutionarily conserved bases, as this is a relatively unbiased annotation of likely functionally relevant positions. We used GERP++ elements to define these (Davydov et al., 2010); (ii) expression of quantitative trait loci (eQTL) variants, as they provide evidence a position may affect expression of genes at distal loci, and transcriptional regulation has been shown to be associated with chromatin contacts (Won et al., 2016). The eQTL annotations were obtained from GTEx (The GTEx Consortium, 2017). We used EBV-transformed lymphocytes and whole blood, as these cell types are closely related to GM12878 and K562, respectively; (iii) CTCF motifs annotations (Kheradpour and Kellis, 2014), as their importance in loop interactions has previously been established (Rao et al., 2014; Sanborn et al., 2015). We expected that more accurate fine-mapping predictions would show overall greater enrichment for these annotations.

For each of the three external annotations, we calculated the average overlap of bases between the annotation and χ-CNN’s 100 bp fine-mapped predictions. We then calculated the enrichment of these overlaps relative to randomly guessing within peak regions and separately relative to the entire genome. We compared these enrichments to enrichments from (i) predictions from the logistic regression baseline, and (ii) directly using the GM12878 1 kb Hi-C data signal, the finest resolution Hi-C data available for humans (Rao et al., 2014). We performed this final comparison only in GM12878, as 1 kb resolution data is not available for K562.

To make a fine-mapping prediction directly from Hi-C signal, we took the number of normalized reads in each 1 kb by 1 kb Hi-C contact matrix cell for the corresponding peak as in Section 3.3. We found that χ-CNN outperformed the baseline methods in all comparisons (Supplementary Table S4). Surprisingly, directly using the 1 kb Hi-C data did not provide any additional predictive power in recovering GERP++ elements, eQTLs, or CTCF motifs over randomly guessing within the peak region. This suggests that 1 kb Hi-C signal does not have additional information for their recovery beyond the 5-25 kb interaction peak, and highlights the value of integrating epigenomic or TF-binding data to make finer resolution predictions.

3.6 Fine-mapped positions show distinct chromatin state enrichments

To gain insight into the type of locations that are predicted to be the source of interactions, we analyzed χ-CNN’s predictions relative to a 25-state ChromHMM model from the ENCODE integrative analysis (Ernst and Kellis, 2012, 2013; Hoffman et al., 2013). For each interaction, we took the highest-scoring 100 bp sub-region on each side and found the corresponding pair of ChromHMM annotations. We counted the number of fine-mapped sites found for each ChromHMM state. We normalized this to find a frequency of each state and compared it to randomly guessing in interacting regions to compute the fold enrichment, and then took the log₂ of this value (Supplementary Fig. S6). The most enriched state was ‘CtcfO’, a state associated with CTCF binding in open chromatin regions, with fold enrichments of 44 and 35 in GM12878 and K562, respectively.

Besides the ‘CtcfO’ state, we also found notable enrichment for states associated with transcription start sites (‘Tss’, 5-fold enrichment for both GM12878 and K562), poised promoters (‘PromP’, 8- and 9-fold enrichments), enhancers (‘Enh’, 4-fold enrichment for both), weak enhancers (‘EnhW’, 4-fold enrichment for both), CTCF binding without open chromatin (‘Ctcf’, 4- and 3-fold enrichments) and the artifact state (‘Art’, 10- and 6-fold enrichments). We saw similar states preferentially enriched when computing relative to a whole genome background (Supplementary Fig. S6).

3.7 χ-CNN is effective using a limited set of features

In applying χ-CNN to GM12878 and K562, we used more input features than are typically available in most cell types. To estimate the expected performance of χ-CNN for cell types with more limited data, we evaluated its performance using subsets of features. Our basic feature set is composed of ChIP-seq data for ‘primary’ histone marks: H3K27me3, H3K36me3, H3K4me1, H3K4me3, H3K9me3, and H3K27ac, which are available for 98 cell and tissue types from Roadmap Epigenomics. We then extended this ‘primary’ feature set with a ‘secondary’ set by adding the histone marks H3K4me2, H3K9ac, H4K20me1, H3K79me2, and H2A.Z, in addition to DNase-seq. We chose this set as these features were all deeply mapped by either the ENCODE or Roadmap Epigenomics projects, and they are available as imputed data for 127 reference epigenomes (Ernst and Kellis, 2015). As CTCF is also available for many cell types, we also tried adding CTCF to the secondary set. Finally, we compared results from these three sets to results achieved by using all data.

We first evaluated the performance of the CNN at discriminating between positive and negative interactions using subsets of features. We found that when using only primary marks, the performance was reasonably high (AUROCs of 0.78 and 0.81 for GM12878 and K562, respectively). The performance increased substantially by adding the secondary set of features, (AUROCs of 0.91 for both) and a smaller improvement when further adding CTCF (AUROCs of 0.94 and 0.92), close to the performance using all the marks (AUROCs of 0.94 for both cell types).

We then evaluated the performance in peak recovery after extending 5 kb HiCCUPs peaks to 25 kb using the same subsets of marks. Using only primary marks yielded a fold enrichment in the center 5 kb window of 2.9 and 2.2 for GM12878 and K562; adding the secondary set had a larger enrichment of 7.3 and 6.3; adding CTCF to this set yielded 8.5 and 7.1 enrichment, whereas using all marks had the largest enrichment at 9.2 and 8.3 (Fig. 4).

3.8 χ-CNN fine-mapping reveals CTCF-associated and non-CTCF-associated interactions

We investigated how χ-CNN predictions relate to CTCF binding. To investigate this, we first downloaded peak calls for ChIP-seq data of CTCF (data available at http://ftp.ebi.ac.uk/pub/databases/ensembl/encode/integration_data_jan2011/byDataType/peaks/jan2011/spp/optimal/) and took the intersection of peak calls from different laboratories following the procedure of Rao et al. (2014). We compared CTCF peaks with HiCCUPs peaks, and found that most interacting regions overlapped at least one CTCF peak (72.0% for GM12878 and 83.3% for K562), largely consistent with previous findings. This is lower than the 86% and 88.1% previously reported, which was found by extending HiCCUPs peaks to 15 kb before finding CTCF peak overlap (Rao et al., 2014). When extending HiCCUPs peaks to 25 kb as in this application, the number rises to 95.3% and 95.2% for GM12878 and K562, respectively.

We observed that 34% and 44% of regions involved in an interaction contained multiple CTCF peaks in GM12878 in K562, respectively. We investigated whether χ-CNN can better identify original 5 kb interacting peaks after extending the peak to 25 kb, relative to two baselines: (i) choosing the CTCF peak with the highest signal and (ii) choosing a CTCF peak at random. We evaluated fine-mapping on a one-dimensional axis instead of a two-dimensional grid as described previously (Fig. 3), as we were only evaluating individual sides of interactions that had multiple CTCF peaks. We found based on a one-dimensional axis, that using χ-CNN with all marks had 2.8- and 2.7-fold enrichments in recovering the original 5 kb peaks for GM12878 and K562, respectively. This was significantly greater than the enrichments from choosing the peak with the highest CTCF signal, 2.5 and 2.3 for GM12878 and K562, respectively and from randomly guessing a CTCF peak, 2.0 enrichment for both cell types (P-value < 0.001, two-proportions z-test for all comparisons). These conclusions also held when comparing to SMC3. χ-CNN had enrichments of 2.8 and 2.7 for GM12878 and K562, choosing the SMC3 peak with the highest signal had enrichments of 2.6 and 2.5 and randomly guessing an SMC3 peak achieved enrichments of 2.1 and 2.0 (P-value < 0.001, two-proportions z-test, all comparisons).

We then separated all of χ-CNN's fine-mapping predictions into two sets: ‘CTCF-associated’, those that overlapped the union of all CTCF peaks (92.6% and 94.1% for GM12878 and K562, respectively) and the remaining ‘non-CTCF-associated’ that did not overlap any CTCF peaks. We chose to look at the union of CTCF peaks to get a more confident set of peaks that did not overlap CTCF. Of the non-CTCF-associated interactions, 36.5% in GM12878 and 14.0% in K562 had a CTCF peak not at the fine-mapped position, but elsewhere in the broader interacting region, also supporting that χ-CNN does not simply predict based on CTCF.

Finally, we compared chromatin state enrichments between CTCF-associated and non-CTCF-associated interactions. We found that CTCF-associated interactions were mostly frequently mapped to the ‘CtcfO’ state (45- and 37-fold enrichments for GM12878 and K562). In GM12878, non-CTCF-associated interactions were most likely to map to the ‘Tss’ and ‘Enh’ states (14- and 15-fold). In K562, they showed large enrichments for the ‘Tss’, ‘Enh’ and ‘Ctcf’ states (8-, 5-, and 5-fold) (Supplementary Fig. S6). We also saw substantial enrichments for the ‘FaireW’ and ‘Art’ states, associated with weak signal from the FAIRE open chromatin assay and artifacts, respectively, but these accounted for only 12.8% of interactions compared to 21.3% for the ‘Tss’ and ‘Enh’ states combined, suggesting a substantial contribution from promoters and enhancers among the non-CTCF-associated interactions. We saw similar state enrichment patterns for SMC3 (Supplementary Fig. S6).

3.9 Limited interaction specificity found with shuffled background

The distance-matched, random genomic background allows χ-CNN to learn signatures of locations involved in interactions in general, but not necessarily pairwise signatures for pairs of interacting loci. To learn pairwise signal, we modified our CNN into a Siamese CNN (χ-SCNN, Supplementary Fig. S7) (Bromley et al., 1994). Instead of taking one data matrix at a time, an SCNN takes two matrices—one for each side of an interaction. These matrices are passed through identical subnetworks until the max pooling layers, after which the information from the two subnetworks are integrated at the dense and logistic layers. We compared performance of χ-CNN to χ-SCNN and found that χ-CNN performed better in fine-mapping than χ-SCNN (Supplementary Tables S3 and S4).

We investigated whether epigenetic and TF data could inform which pairs of regions interact given all interacting regions. To do this, we modified the negative training dataset to control for per-locus signal of all input tracks. Specifically, we generated a negative training dataset where instead of randomly sampling two random genomic loci, we shuffled interactions. In other words, each region that was part of an interaction was now paired with a region from a different interaction. We followed the same procedure for hyperparameter search, training and testing as with the genomic background. We found that models trained on Hi-C peaks in GM12878 and K562 achieved AUROCs of 0.64 and 0.70, respectively. This suggests there is some detectable pairwise epigenetic and TF-binding signal predictive of interactions, but because of the relatively low separability of true and shuffled interactions, we were unable to robustly characterize this pairwise signal.

4 Discussion

We developed χ-CNN, a method for fine-mapping coarse Hi-C interactions to their sources by leveraging high-resolution DNase-seq and ChIP-seq data. The method applies an CNN to learn epigenomic signatures of interactions. We then analyzed each interaction using a feature attribution method, integrated gradients, to identify the positions that are most informative to the prediction of the interaction, and thus can be inferred to be the ‘fine-mapped’ peak.

We applied χ-CNN to data from two cell types and demonstrated that it effectively identifies original Hi-C peaks after extending them. We demonstrated that χ-CNN has higher enrichment than using the signal of any single mark alone or the average of all them. We showed that χ-CNN predictions have greater enrichment for evolutionarily conserved bases, eQTLs and CTCF motifs than several baseline comparisons, which suggests greater functional relevance of χ-CNN predictions. The fine-mapped loci also strongly enrich for primarily CTCF-associated chromatin states, which is expected based on existing knowledge (Rao et al., 2014; Sanborn et al., 2015), and also highlighted enhancer and promoter states associated with non-CTCF-associated interactions. We note that because the 100 bp resolution of our predictions exceeded that at which current technology could directly map long-range interactions at a large scale, we resorted to more indirect evaluations.

Our framework can be applied with alternative background models to detect potentially subtler, but still potentially biologically relevant signal. Specifically, we developed a Siamese CNN to integrate signal between two interacting regions, and investigated an alternative ‘shuffled’ background, which was a way to identify if there was pairwise epigenetic signal that differentiated interactions from each other, as opposed to identifying signals associated with interactions in general. However, when training against this shuffled background, we saw limited predictive power, suggesting limited pairwise signal, consistent with previous observations in predicting enhancer-promoter interactions (Xi and Beer, 2018).

We demonstrated that χ-CNN is effective when used with data from DNase-seq and ChIP-seq for a set 11 histone marks that have been experimentally mapped in many cell and tissues types and also have accurate imputations available (Ernst and Kellis, 2015; Roadmap Epigenomics Consortium et al., 2015). One potential direction for further improvements to χ-CNN is to have the fine-mapping step determine the most likely pair of regions instead of fine-mapping the two sides independently. While we focused on Hi-C here, an avenue for future investigation would be to apply and evaluate χ-CNN on other types of interaction data such as promoter-capture Hi-C or HiChIP data (Mifsud et al., 2015; Mumbach et al., 2016). We expect χ-CNN predictions to serve as a resource to better understand chromatin interactions and non-coding variants relevant to disease.

Funding

This work was supported by U.S. National Institute of Health [grants T32HG002536 (A.J.), R01ES024995, U01HG007912 and DP1DA044371 (J.E.)], and National Science Foundation (NSF) CAREER award 1254200 (J.E.) and an Alfred P. Sloan Fellowship (J.E.).

Conflict of Interest: none declared.