Abstract
Motivation
The elucidation of all inter-protein interactions would significantly enhance our knowledge of cellular processes at a molecular level. Given the enormity of the problem, the expenses and limitations of experimental methods, it is imperative that this problem is tackled computationally. In silico predictions of protein interactions entail sampling different conformations of the purported complex and then scoring these to assess for interaction viability. In this study, we have devised a new scheme for scoring protein–protein interactions.
Results
Our method, PIZSA (Protein Interaction Z-Score Assessment), is a binary classification scheme for identification of native protein quaternary assemblies (binders/nonbinders) based on statistical potentials. The scoring scheme incorporates residue–residue contact preference on the interface with per residue-pair atomic contributions and accounts for clashes. PIZSA can accurately discriminate between native and non-native structural conformations from protein docking experiments and outperform other contact-based potential scoring functions. The method has been extensively benchmarked and is among the top 6 methods, outperforming 31 other statistical, physics based and machine learning scoring schemes. The PIZSA potentials can also distinguish crystallization artifacts from biological interactions.
Availability and implementation
PIZSA is implemented as a web server at http://cospi.iiserpune.ac.in/pizsa and can be downloaded as a standalone package from http://cospi.iiserpune.ac.in/pizsa/Download/Download.html.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Proteins, often referred to as ‘biology's workforce’, rarely act in isolation. More than 80% of all proteins in a cell interact with one another and with other biomolecules to bring about cellular functions such as mediating signal transduction, translating energy to physical motion, immunological response, enzymatic reactions and a host of other cellular processes (Berggård et al., 2007). Proteins function in a crowded cellular environment, diffusing randomly and colliding with one another. Only a small fraction of these collisions results in biologically meaningful associations. Disrupting or interfering with these associations or complexes could lead to disease conditions such as cancer or neurodegenerative conditions in humans (Kuzmanov and Emili, 2013; Ryan and Matthews, 2005). Unsurprisingly, identification and characterization of protein–protein interactions (PPIs) is a fundamental problem in biology that is a necessary step for a complete understanding of the full repertoire of cellular pathways (Stelzl et al., 2005; Vazquez et al., 2003; Zhang et al., 2012).
A variety of experimental methods, based on either biophysical, biochemical or genetic principles have been developed to detect PPIs (see Zhou et al., 2016 for a comprehensive review). These methods, however, are expensive, labor-intensive, and often have additional limitations. Hence, there is considerable interest toward the development of computational approaches to predict and analyze PPIs (Aloy and Russell, 2006). The computational predictions usually have to surmount two challenges—sampling and scoring. While different computational approaches are utilized in constructing plausible models (sampling) of interacting proteins (see Soni and Madhusudhan, 2017 for a review of methods), a crucial aspect of these predictions is to correctly recognize (scoring) the native (or near-native) interaction from among the models sampled. Ideally, the scoring scheme would rank-order the predicted conformations to match what is or should be experimentally observed. Scoring schemes are usually based on free energy calculations incorporating different atomic interactions (Lyskov and Gray, 2008; Pierce and Weng, 2007) or on statistical methods (also referred to as statistical potentials) that extract information from known protein interactions (Huang and Zou, 2008; Liu and Vakser, 2011; Rykunov and Fiser, 2010). Some scoring scheme even combine these two methods (Zimmermann et al., 2012). In addition to this, there are machine learning techniques to score/evaluate possible interactions conformations (Bordner and Gorin, 2007).
The premise of the statistical potentials is that the ratio of an observation (of interaction) to its expectation is indicative of interaction strength. The higher the ratio, the greater is the binding energy. The key to these computations is in making a precise estimate of the expectation value. The initial methods were simple and attempted to convert the observed/expected ratios into free energies (Sippl, 1995; Tanaka and Scheraga, 1976). These potentials got increasingly more nuanced with the inclusion of additional considerations, such as solvent effects and Lennard-Jones potentials (Miyazawa and Jernigan, 1996; Tovchigrechko and Vakser, 2006).
In this study, we have devised a new statistical potential. Here, we derive amino acid interaction preference matrices from 3D protein structures in the Protein Data Bank (PDB) (Berman et al., 2000). We use these preference matrices to propose a new scoring function for the binary classification of protein assembly stability as well as for rank-ordering different docking poses for a given protein complex. We refer to the binary classification algorithm as PIZSA for Protein Interaction Z-Score Assessment. Our potential function explicitly includes local geometry and interface propensities while also incorporating the strength of individual residue pair interactions and accounting for clashes. The expected probability function in our formulation also accounts for the relative abundance of different amino acid residues leading to a more appropriate reference state. We compare our scoring function to the CIPS (Nadalin and Carbone, 2018) potential in their abilities to discriminate between native and near-native protein complex structures from the Dockground Decoy Set (Kundrotas et al., 2018), CAPRI Score_set (Lensink and Wodak, 2014) and report an improvement in discriminatory performance. In this study, we have also tested the ability of PIZSA in detecting near-native structures and compared its performance in comparison with several other methods. Our potential could also be used to discriminate between biologically meaningful interfaces from crystal artifacts with true- and false positive rates (TPR and FPR) of 69% and 18%, respectively. In this, PIZSA’s ability of identifying crystal artifacts is comparable to that of the de facto standard PISA (Krissinel and Henrick, 2007).
2 Materials and methods
2.1 Datasets used for construction of statistical potentials
2.1.1. Construction of residue pairing preference matrices
Protein–protein interface residue pairing preference matrices were constructed from the 3D structural data of dimeric protein complexes retrieved from the PDB (Berman et al., 2000). A set of dimeric proteins was retrieved from PDBe PISA web server (Krissinel and Henrick, 2007; Velankar et al., 2016). The dataset was culled using the PISCES (Wang and Dunbrack Jr, 2003) web server to eliminate redundancy and retain structures with a maximum sequence identity of 40%, a minimum resolution of 3Å and a maximum R-factor of 0.3. Complexes with unknown amino acids at the interface were eliminated. After culling, the dataset reduced from 40 073 to a set of 4913 dimeric complexes (Supplementary S1). In our dataset, 81% (3987) and 19% (926) of the complexes are homo- and heterodimers, respectively. This closely matches the fraction of homodimeric (80%) and heterodimeric (20%) protein complexes in the PISA database (Velankar et al., 2016).
2.1.2. Binary classification
Protein associations are classified as native crystallographic interface or docking decoys by calculating Z-scores. The background distribution for the calculation of Z-scores was estimated using 1000 decoy structures of 351 native protein complexes from the Dockground Docking Decoy Set 2 (Kundrotas et al., 2018). This set of precalculated scores is used as the background for all Z-score calculations. The classification performance was tested on Dockground Docking Decoy Set 1 (Kundrotas et al., 2018), comprising 61 native complexes with 100 decoys for each native complex. The two Dockground Docking Decoy Sets share 17 targets but the decoys have been constructed from different unbound X-ray structures in different docking experiments.
2.1.3. Ranking native and near-native complexes
The ability to rank native complexes amongst the best scoring interactions was benchmarked using the CAPRI Score_set (Lensink and Wodak, 2014) and both the Dockground Docking Decoy Sets. The CAPRI Score_set consists of 13 dimeric and 2 trimeric target complexes. Only 322 of 351 targets in Dockground Docking Decoy Set 2 were used for benchmarking as 26 targets had decoys with noncanonical atom names and 3 targets had decoys that we were unable to score using CIPS (Supplementary S2). It should be noted that using the Dockground Docking Decoy Set 2 for calculating the background scores does not affect the rank-ordering on the same set as it is independent of the background and proportional to the normalized raw score (Equation 9).
Our ability to rank near-native complexes was evaluated on the Dockground Docking Decoy Set 1, ZDock Protein-Protein Docking Benchmark 4 (Hwang et al., 2010) and decoy sets created from Protein-Protein Docking Benchmark 5 (Vreven et al., 2015) targets using various docking tools. Models for Protein-Protein Docking Benchmark 5 were constructed with SwarmDock (Torchala et al., 2013), pyDock (Cheng et al., 2007), ZDock (Pierce et al., 2014) and HADDOCK (Dominguez et al., 2003). Two hundred models per target were generated for constructing the ZDock Protein-Protein Docking Benchmark 4 decoy set using the ZDock 3.0.2, 6 degree sampling set. Docking software-specific decoy sets for Protein-Protein Docking Benchmark 5 targets were acquired from SBGrid Data Bank (Geng et al., 2020). Near-natives from the Dockground Docking Decoy Set 1 and ZDock Protein-Protein Docking Benchmark 4 were identified as models with ligand RMSD <5Å. Decoys from CAPRI Score_set and the docking software-specific sets of Protein-Protein Docking Benchmark 5 targets were identified as near-native decoys if they were of acceptable- or higher-quality (medium/high) models as classified by the CAPRI criteria. These decoys were preclustered, as reported in Geng et al. (2020), and the top two best scoring models from the top five clusters were selected for evaluation. In case of the Dockground Docking Decoy Set 1 and ZDock Protein-Protein Docking Benchmark 4, top 10 best scoring models were chosen for evaluation. The docking software-specific decoy sets from SBGrid Data Bank contain ∼125–500 decoys with an average of 378 decoys per case (Geng et al., 2020).
2.1.4. Identification of crystal artifacts
We tested the ability of our potentials to distinguish between biologically meaningful interactions and crystal packing artifacts on two datasets (Bahadur et al., 2004; Duarte et al., 2012). The ‘Duarte’ dataset (Duarte et al., 2012), consisting of 81 biological interactions (DCbio) and 82 crystal contacts (DCxtal) was used to optimize the classification threshold. Classification performance was tested on 88 crystal contact structures from the ‘Bahadur’ dataset (Bahadur et al., 2004) (Supplementary S3).
2.2 Construction of the composite scoring functions
2.2.1. Scoring function
Scoring matrices were constructed from the ratio of observed probabilities of interface residue pairs to their expected probabilities of occurrence at the interface. Two residues from different protein chains are identified as an interface residue pair if one or more atoms from one residue is within a threshold distance from atoms of the other residue. The score for a residue pair ij is calculated as:
| (1) |
where (Equation 3) is the atomic propensity of interface residue pair ij with k number of atoms. ab is any interface residue pair and c is the number of atoms involved in any interface residue pair interaction. x and y are different instances of residue pairs ij and ab, respectively. and are the average atomic propensities of interface residues i and j, respectively. fi and fj are the frequencies of interface residues i and j, respectively. All frequencies are observed counts of occurrence. γij is the abundance normalization term for residue pair ij. N is the total number of interfaces and int is any interface. The abundance normalization term γij is calculated as:
| (2) |
where ni and nj are the total number of residues in the monomeric subunits of residues i and j, respectively. The uniform probability of occurrence for any residue is 0.05 (1/20).
The atomic propensity, of an interface residue pair ij with k number of atoms within a threshold distance is calculated as:
| (3) |
where is the frequency of residue pair ij with k number of atoms. fk is the frequency of any residue pair with k number of atoms and c is any number of atoms observed in interactions.
Three different scoring matrices were constructed using only main chain atoms, side chain atoms or main chain/side chain atoms exclusive from each residue partner. Favorable interface residue pairs have positive scores whereas unfavorable interface residue pairs have negative scores. Variants of the scoring matrices were constructed at distance thresholds of 4, 6 and 8Å.
2.2.2. Scoring protein–protein complexes
A raw score (Scomplex) is assigned to a protein complex by summing up the individual weighted residue pair scores over the interface. Each residue pair receives a score () that is a linear combination of the main chain (), side chain () and main chain/side chain () interaction score. Each component of the residue pair score is weighted with a clash penalty as:
| (4) |
| (5) |
| (6) |
where is the unweighted score from any of the three scoring matrices. Favorable residue pair interactions have positive whereas unfavorable residue pair interactions have negative . δij is the clash penalty for residue pair ij and has values between 0 and 1. Since can be either positive or negative, we multiply or divide by δij, respectively, such that the scaling factor always penalizes the score when interactions have steric clashes (). and are the weighted main chain, side chain, main chain/side chain and all atom interaction scores, respectively. is the raw score of the protein complex.
Clash penalty δij is a measure of the severity of atomic clashes in a residue pair interaction. It ranges from 0 for severe clashes to 1 for no clashes and is calculated as:
| (7) |
where,
| (8) |
where x is the maximum overlap fraction between interacting atoms that varies from 0 to 1 and is set to 0 when there is no overlap. is the sum of the van der Waals radii of interacting atom pairs and is the Euclidean distance between the interacting atom pairs. Atom pairs that have hydrogen bond donor and acceptor atoms are identified. Such hydrogen bonded atom pairs have an additional tolerance of 0.4Å. The sigmoidal function used as the clash penalty has been optimized to penalize 20% of the highest overlap fractions observed in the training set such that least number of native complexes are predicted as unstable associations (Supplementary S4).
2.3 Binary classification for the stability of protein complexes
The residue preference matrices constructed above were employed to classify protein complexes as native crystallographic interface or docking decoys. To account for the effect of interface size, raw scores for each complex were further normalized by the number of interacting residue pairs (Equation 9). Z-score is a measure of how likely a protein complex is to form a native association in contrast to interactions from random docking poses. A protein complex is predicted to be a native crystallographic interface if the Z-score is greater than a threshold. The Z-score of protein complexes is calculated as:
| (9) |
| (10) |
where is the normalized raw score for a protein complex. is the number of interacting residue pairs observed in the protein complex. and are the average and standard deviation of normalized raw scores precalculated from background decoys (Dockground Docking Decoy Set 2).
The background distribution for the calculation of Z-scores was estimated using 1000 decoy structures of 336 native protein complexes from the Dockground Docking Decoy Set 2 (Kundrotas et al., 2018). Receiver operator characteristic (ROC) curves were constructed to estimate the observed FPR and TPR at different Z-score thresholds and different distance thresholds. ROCs were then integrated to calculate the area under the curve and identify the operating points. Z-scores with operating points closest to (0, 1) in the ROC curves were chosen as optimal binary classification thresholds to maximize the TPR and minimize the FPR. Classification performance was tested on Dockground Docking Decoy Set 1 and evaluated in terms of accuracy, balanced accuracy and a modified Matthews correlation coefficient (MCC) (Equation 11). Scoring PPIs with PIZSA took 1.13 s per model on average on a single core of a 2.60 GHz Intel® CoreTM i7-3720QM CPU.
| (11) |
where TPR is true-positive rate, FPR is false-positive rate, TNR is true-negative rate and FNR is false-negative rate.
2.4 Binding mode selection
The ability of our potential to select the proper binding mode when multiple alternative binding interfaces are present has been illustrated with a case study. The antigen-binding fragment of camelid antibodies are composed of a single, heavy chain antibody VH domain (VHH). Structures of three different dromedary VHH domains bound to porcine pancreatic α-amylase (PPA) at nonoverlapping orthogonal sites have been deposited in the PDB (Desmyter et al., 2002). 3D structures of non-native binding modes were constructed with homology modeling using MODELLER v9.15 (Davis et al., 2006; Šali and Blundell, 1993) (Supplementary S5). Structures of camelid VHH domains AMB7, AMD9 and AMD10 bound to PPA (PDB codes: 1KXT, 1KXV and 1KZQ, respectively) were evaluated for each VHH–PPA complex using the PIZSA potential.
2.5 Identification of crystallization artifacts
We used the fraction of interactions with optimal atomic propensities () as a measure to distinguish biological interactions from crystallization artifacts (Equation 12).
| (12) |
where is the number of interactions with and is the total number of interactions at the interface. The classification performance was optimized on the ‘Duarte’ dataset. ROC curves with different cutoffs were assessed to identify the classification operating point. Classification accuracy was tested on the ‘Bahadur’ dataset and compared with that of PISA.
3 Results
3.1 Construction of the statistical potential matrices
Amino acid pairing propensities capture the likelihood that amino acids i and j interact across a protein–protein interface. We constructed such propensity matrices defined for different atomic interaction categories (main chain–main chain, side chain–side chain and main chain–side chain) at three different distance thresholds (4, 6 and 8Å) (Supplementary S6). The number of favorable amino acid pairs at the interface, at distance thresholds of 4 and 6Å, was highest for the side chain–side chain mode of interaction followed by main chain–side chain and main chain–main chain interaction. For example, at 4Å, 50% (105 out of 210) of the side chain–side chain, 13.8% (55 out of 400) of the main chain–side chain and 1% (2 out of 210) of the main chain–main chain amino acid pairs were favorable. However, at 8Å, main chain–main chain interactions (86.2%, 181 out of 210) have the most prevalent number of favorable amino acid pairs followed by side chain–side chain (74.8%, 157 out of 210) and main chain–side chain interactions (58.8%, 235 out of 400). The number of favorable amino acid pairs increases with an increase in distance cutoff. For example, with an increase in distance cutoff from 4 to 6Å and 8Å the number of favorable side chain–side chain pairs increases from 50% to 68.6% and 74.8%; main chain–side chain increases from 13.8% to 46% and 58.8%; main chain–main chain increases from 1% to 39.5% and 86.2%, respectively. At distance cutoffs of 4 and 6Å, side chain–side chain mode of interaction contributed the most, as most interactions on the interface were side chain mediated. For example, at 4Å distance cutoff 59% of the interactions were of the side chain–side chain type whereas the main chain–side chain and main chain–main chain account for 33% and 8% of the interactions, respectively.
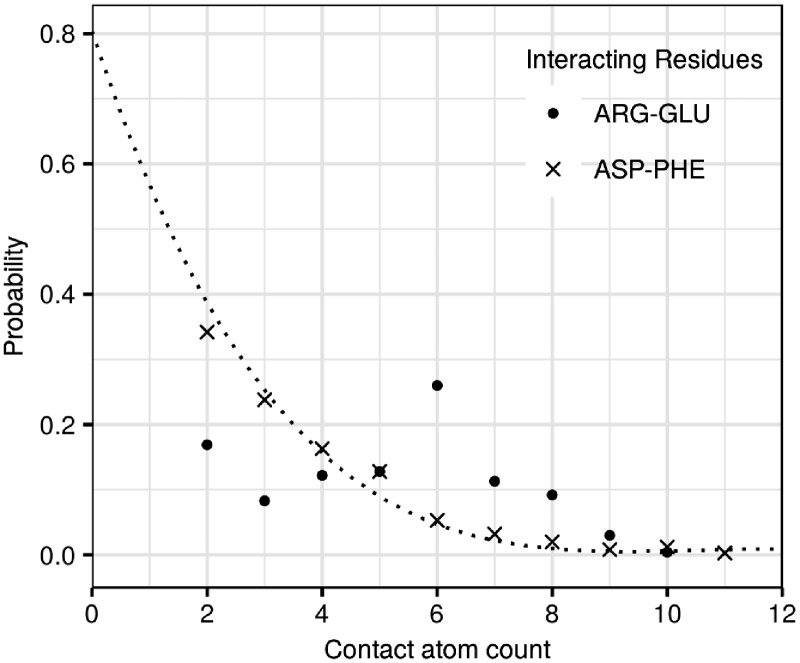
Since the residue pairing preferences across different modes of interaction were not identical, we identified the contribution from all different modes separately. Furthermore, we estimated the distribution of the number of atomic contacts shared by each residue–residue interaction on the interface and found that many residue pairs have a strong tendency to interact with a preferred number of atomic contacts. Our propensity scores account for this optimal number of atomic contacts (, Equation 3). The atomic propensities () are an observed by expected ratio of the probability that an interaction between residues i and j is mediated by k number of atomic contacts. The expected probability that any residue pair interacts through k number of atoms declines exponentially with increasing number of atoms. The observed probability distribution fits the expected probability distribution closely for some residue pairs but for other residue pairs the observed probabilities are much higher than their expected probabilities for a certain number of interacting atoms. For example, the observed and expected probability distributions match closely for the ASP–PHE residue pairs whereas ARG–GLU pairs tend to have 6–8 atomic contacts (6 being the highest) at 4Å distance cutoff and side chain–side chain mode of interaction. Interactions with atomic propensities above 1 (observed probabilities higher than the expected) indicate favorable number of atomic contacts whereas those below 1 (observed probabilities lower than the expected) indicate suboptimal number of atomic contacts (Fig. 1, Supplementary S7). ARG–GLU amino acid pairs have higher observed probabilities for 6–8 atomic interactions as compared to what is expected (Fig. 1). Also, ARG–GLU pairs with 2–4 atomic interactions are suboptimal as indicated by the lower observed probability when compared to the expected (Fig. 1).
Fig. 1.
The observed (closed circle, multiplication sign) and expected (dotted line) probability distribution profile of the number of atoms mediating residue pair interactions in ARG–GLU and ASP–PHE
The amino acid pairing preferences exhibited by the PIZSA scoring matrices are qualitatively similar across the three distance thresholds and suggest that: (i) oppositely charged residues have a strong tendency to pair across the interface with a large overlap of atomic contacts, (ii) residues with aromatic rings (HIS, TRP, TYR and PHE) have favorable interactions with most amino acids indicating they play a crucial role on interfaces, (iii) interactions among hydrophobic residues were less favorable at 4Å but more favorable at 6 and 8Å, especially for the side chain–side chain potentials. The side chain–side chain propensity matrices show the highest degree of specificity, followed by the main chain–side chain matrices and then the main chain–main chain matrices across the three distance thresholds. Top three highest scoring residue pairs in the main chain–main chain and main chain–side chain matrices were HIS–HIS, TRP–TRP and CYS–CYS in no particular order. In the side chain–side chain matrices, the top three scoring amino acid pairs included CYS–CYS, ASN–ASN and HIS–TYR at 4Å, GLN–GLN, HIS–TYR and HIS–HIS at 6Å and HIS–TYR, HIS–HIS and MET–MET at 8Å. Side chain matrices accounted for many high scoring residue pairs with diverse interaction types. For example, electrostatically interacting residue pairs such as ARG–GLU, hydrogen bonding interactions such as ASN–ASN, π–π stacking, such as TRP–TYR, cation–π interactions, such as HIS–ARG and hydrophobic interactions, such as ILE–PHE. ALA and VAL, had the least number of favorable interactions in all cases. Smaller amino acids, such as SER, THR, PRO, had less favorable interactions except in case of their main chain–main chain interactions at 8Å whereas larger amino acids, such as GLU, ILE, LEU and LYS, had less favorable main chain–main chain interactions. Interestingly, THR favorably interacts with ARG, ASN, ASP, GLN and HIS at 4Å, whereas the closely related SER favorably interacts only with ASN, ASP and HIS. CYS–CYS interactions were less favorable in side chain–side chain matrices at 6 and 8Å, whereas they were amongst the highest scoring interactions in all other matrices. Side chain–side chain interactions of large aliphatic amino acids LEU and ILE were favorable at 6 and 8Å. Interestingly, ARG–ARG interactions were favorable in side chain–side chain matrices at all distance thresholds.
3.2 Binary classification of protein complexes
Our scoring matrices describe individual residue pairing preferences on the interface. On an interface containing several interacting residue pairs, we use pair preference values from our scoring matrices in the form of a Z-score to identify native protein–protein associations and discriminate them from interactions arising from random docking poses. Optimum Z-score thresholds for classification of protein complexes as native crystallographic interfaces or docking decoys were obtained by analyzing ROC curves (Supplementary S8). The area under the ROC curves was 0.98, 0.92 and 0.87 for distance thresholds of 4, 6 and 8Å, respectively. Optimal Z-score thresholds for distance cutoffs of 4, 6 and 8Å are 1.72, 0.92 and 0.76, respectively. The TPR and FPR at optimal Z-score thresholds are 94.6% and 4.7% for 4Å, 88.6% and 18.1% for 6Å, 83.1% and 23.4% for 8Å, respectively. For all further analyses we used 4Å as the distance cutoff as it had the highest TPR and lowest FPRs of classification.
We tested the classification accuracy of PIZSA on the Dockground Docking Decoy Set 1, which comprises of 61 protein complexes with 100 decoy conformation for every native conformation. As this testing set is skewed with respect to the ratio of positives to negatives (1:100), we evaluated the performance by estimating the accuracy, balanced accuracy and a modified MCC as described in Section 2. PIZSA was able to correctly predict 58 out of 61 natives as native crystallographic interfaces with an accuracy of 0.80, a balanced accuracy of 0.87 and an MCC of 0.75 (Supplementary S9).
3.3 Identification of native/near-native protein complexes and comparison with CIPS potentials
Recently, a new amino acid pairwise interaction potential, CIPS (Nadalin and Carbone, 2018), was proposed to rank-order different docking configurations. It takes into account a contact-based measure that weighs residue pairing frequencies by the number of atomic contacts shared between the residue pair. When compared to three previously published residue preference matrices (Glaser et al., 2001; Mezei, 2015; Pons et al., 2011), CIPS was found to be better at discriminating high-quality structural models from decoys than others.
In this article, we compare ourselves with CIPS as they have been shown to outperform three other statistical potentials in rank-ordering PPI complexes. Our method differs from that of CIPS in five essential ways: (i) we have constructed three mutually exclusive amino acids preference matrices that categorize interactions according to the type of atoms involved in an interaction; (ii) we do not make use of explicit solvent accessibility calculation and the amino acids preferences are solely based on the distribution of residues and their interacting atoms in Euclidean space; (iii) we account for atomic propensities similar to CIPS’ contact propensity but with a completely different reference state; (iv) we have introduced a penalty for steric clashes that scales scores according to the severity of the clash; and lastly (v) we have introduced a measure that classifies a protein–protein complex as a native crystallographic interface or docking decoy. We also compare ourselves with recently published scoring functions GraphRank and iScore that have been reported to perform as good as or even better than current state-of-the-art methods (Geng et al., 2020). Both GraphRank and iScore are graph kernel-based scoring functions that use evolutionary information with additional energetic terms in the case of iScore (Geng et al., 2020). We evaluate our performance in docking software-specific decoy sets as well as the CAPRI Score_set that has been constructed from decoys generated using various different docking methods.
3.3.1. Performance on docking software-specific decoy sets
Protein docking experiments aim to predict biologically meaningful interactions. This is usually achieved with the help of a scoring function that utilizes features of interfaces such that native/near-native complexes score optimally. One class of such scoring functions, employed by both PIZSA and CIPS, make use of amino acid contact propensities derived from known structures of protein complexes. Previously, CIPS had compared the performance of their scoring scheme to other scoring schemes (Glaser et al., 2001; Mezei, 2015; Pons et al., 2011) on the Dockground Docking Decoy Sets and CAPRI decoy sets. Here, we compare the performance of PIZSA to CIPS on docking software-specific decoy sets such as the Dockground Docking Decoy Set and the ZDock Protein-Protein Docking Benchmark 4.0. We further evaluate our performance on decoys generated from targets of the Protein-Protein Docking Benchmark 5.0 using various docking software. We compare our performance with that of CIPS, GraphRank, iScore and the scoring functions of respective docking software used for generating decoys (Geng et al., 2020).
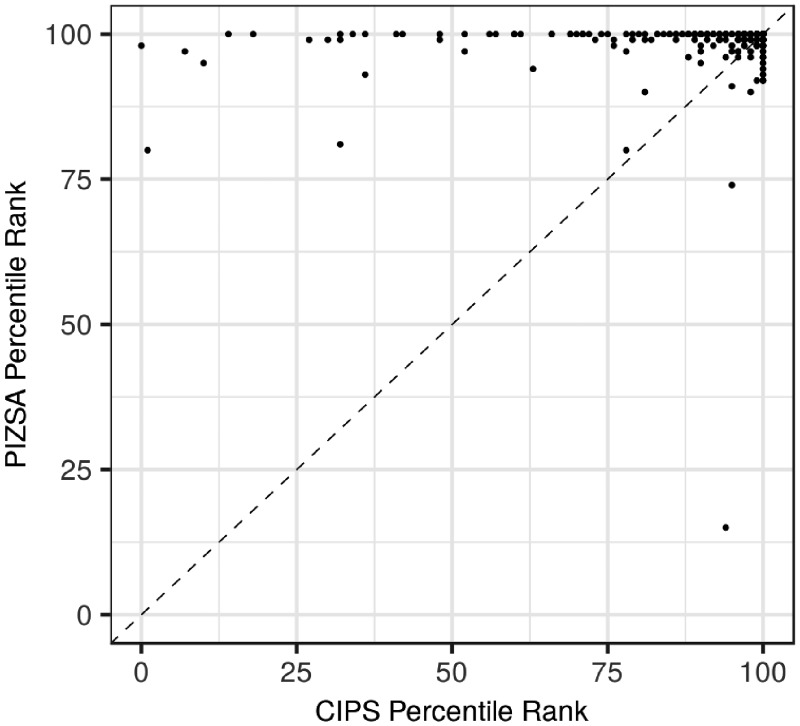
The ability of PIZSA pair potentials to discriminate the native structural conformation was compared with CIPS potentials on two testing sets comprising of 61 and 322 native structures with 100 decoy structures each from the Dockground Docking Decoy Sets 1 and 2, respectively (Supplementary S10). PIZSA ranked the target complexes, from the Dockground Docking Decoy Set 1, as the best (Rank 1), or in top 3, 5 or 10 ranks for 51 (84%), 54 (89%), 56 (92%) and 57 (93%) protein complexes, respectively. The corresponding performance for CIPS was 34 (56%), 46 (75%), 47 (77%) and 50 (82%) protein complexes, respectively. Furthermore, for individual complexes, PIZSA ranked 25 structures better than CIPS, 30 structures equal to that of CIPS and 6 structures worse than CIPS. For 3 of 6 targets where CIPS ranks were better, PIZSA scored the native complex (1HXY: 7, 1OPH: 2, 3FAP: 4) not more than 3 ranks below CIPS’ rank (1HXY: 6, 1OPH: 1, 3FAP: 1). On the Dockground Docking Decoy Set 2, PIZSA ranked the target complexes as the best (rank 1), in top 3, 5 and 10 ranks for 216 (67%), 298 (93%), 307 (95%) and 317 (98%) protein complexes, respectively. The corresponding performance for CIPS was 107 (33%), 170 (53%), 203 (63%) and 237 (74%) protein complexes, respectively (Fig. 2). Furthermore, PIZSA ranked 196 structures better than CIPS, 81 structures equal to CIPS and 45 structures worse than CIPS. For 43 of 45 targets where CIPS ranks were better, PIZSA scored the native complex not more than 8 ranks below CIPS’ rank. In 25 of 43 cases there was a difference of a single rank assigned by CIPS and PIZSA.
Fig. 2.
The percentile ranks assigned by PIZSA and CIPS to target complexes from the Dockground Docking Decoy Set. Points above/below the diagonal indicate cases where PIZSA assigned a better/worse rank than CIPS
PIZSA’s ability to identify near-native decoys was evaluated as per the CAPRI assessment protocol in terms of the number of targets that have at least a single near-native structure predicted in top 10 models (Lensink et al., 2017). Near-native structures were defined as models with ligand RMSD <5Å or according to the CAPRI criteria as acceptable-, medium- or high-quality models wherever applicable. The Dockground Docking Decoy Set 1 has 6600 models of 61 targets, with every target having at least a single near-native model and 505 near-natives in total. PIZSA was able to identify near-natives in the top 10 models for 47 of 61 targets whereas CIPS identified 49 (Supplementary S17).
The ZDock Protein-Protein Benchmark 4 has 176 unique targets categorized as easy (123), medium (29) and difficult (24) docking models. Ninety-nine of 176 targets had at least a single near-native model. PIZSA identified near-natives in its top 10 predictions in 48 cases whereas CIPS identified 41 (Supplementary S18). PIZSA and CIPS identified near-natives from 10 and 8 medium/difficult targets, respectively (Table 1). Of the 48 hits identified by PIZSA, 16 were classified as enzyme inhibitor/substrate complexes, 7 as antigen–antibody complexes and 25 as other types of complexes. We also compared PIZSA’s ability to identify near-native models from decoy sets generated using SwarmDock, pyDock, ZDock and HADDOCK using targets from Protein-Protein Docking Benchmark 5 (Geng et al., 2020). Our method was compared with CIPS, GraphRank, iScore and the scoring function of the respective docking method used for creating the decoy set (Table 2, Supplementary S19). As mentioned earlier, the performance is evaluated according to the CAPRI criteria as the number of targets that have at least a single near-native structure (acceptable- or higher-quality models) in the top 10 predicted models. PIZSA outperforms CIPS in 2 of 4 decoy sets by identifying near-natives for 1 and 2 more targets in the SwarmDock and pyDock decoy sets, respectively. Although both PIZSA and CIPS perform equally on the HADDOCK decoy set, PIZSA identifies medium-quality models in two targets (3K75, 3PC8; Supplementary S19) whereas CIPS identifies only in one (3PC8; Supplementary S19). PIZSA and GraphRank outperform each other in a single decoy set (SwarmDock and pyDock, respectively). iScore identifies more targets with near-natives, as compared to PIZSA, in two decoy sets (pyDock and ZDock) and identifies the same number of targets with near-natives in the others (SwarmDock and HADDOCK). GraphRank and iScore also identify a greater number of medium-/high-quality models in cases where they perform equally with PIZSA. The two machine learning algorithms GraphRank and iScore perform better than the statistical potentials, CIPS and PIZSA on this benchmark. However, PIZSA identifies more near-natives or better quality near-natives in comparison to a similar method CIPS for most cases.
Table 1.
Comparison of PIZSA and CIPS on ZDock Protein-Protein Docking Benchmark 4
| PIZSA | CIPS | Total | |
|---|---|---|---|
| Easy | 38 | 33 | 78 |
| Medium | 7 | 6 | 16 |
| Difficult | 3 | 2 | 5 |
| All | 48 | 41 | 99 |
Table 2.
Comparison of PIZSA, CIPS, GraphRank, iScore and scoring functions from respective docking methods on software-specific Protein-Protein Docking Benchmark 5 decoys
| Method | PIZSA | CIPS | GraphRanka | iScorea | Self |
|---|---|---|---|---|---|
| SwarmDock (18) | 10/1***/3** | 9/1***/2** | 7/1***/6** | 10/2***/6** | 9/1***/5** |
| pyDock (14) | 3/2** | 1/1** | 5/3** | 6/3** | 6/1** |
| ZDock (10) | 4/2** | 5/2** | 4/3** | 6/5** | 3/2** |
| HADDOCK (9) | 3/2** | 3/1** | 3/2***/2** | 3/2***/2** | 3/2***/3** |
Note: Summary of the number of targets with near-natives in 10 selected models. The total number of targets from each docking method is indicated in parentheses. Self indicates docking method’s respective scoring function. High- and medium-quality models are indicated by *** and **, respectively.
Performance of methods directly adapted from Geng et al. (2020).
3.3.2. Performance on the CAPRI Score_set
The consolidated benchmark set made available from the CAPRI experiments (CAPRI Score_set) serves as another independent decoy set to benchmark the rank-ordering abilities of scoring functions. The benchmark set contains roughly 19 000 predicted complexes for 15 published CAPRI targets, of which 13 are dimeric complexes and 2 are trimeric complexes (Lensink and Wodak, 2014). Once again we compared our performance in rank-ordering the native complexes with that of CIPS. The percentile ranks for the 15 targets assigned by PIZSA and CIPS are reported in Table 3. PIZSA assigns better ranks than CIPS for 10 out of 15 targets with 7 native targets ranked in the top 10 percentile and all the native targets ranked in the top 22 percentile. CIPS in comparison assigns top 10 percentile ranks to 4 target structures.
Table 3.
Rank-ordering of the native complexes for targets in the CAPRI Score_set
| Target | PDB ID | Number of decoys | PIZSA ranka | CIPS rankb |
|---|---|---|---|---|
| T29 | 2VDU | 2016 | 78.87 | 93.33 |
| T30 | 2REX | 1119 | 96.69 | 96.13 |
| T32 | 3BX1 | 599 | 99.67 | 45.74 |
| T35 | 2W5F | 499 | 100.00 | 23.25 |
| T36 | 2W5F | 309 | 100.00 | 3.24 |
| T37 | 2W83 | 1495 | 99.93 | 76.86 |
| T38 | 3FM8 | 888 | 96.62 | 80.47 |
| T39 | 3FM8 | 1386 | 98.27 | 82.14 |
| T40 | 3E8L | 2144 | 84.79 | 61.42 |
| T41 | 2WPT | 1180 | 80.76 | 28.83 |
| T46 | 3Q87 | 1640 | 81.89 | 85.17 |
| T47 | 3U43 | 1051 | 85.44 | 96.48 |
| T50 | 3R2X | 1448 | 81.35 | 89.94 |
| T53 | 4JW2 | 1400 | 85.00 | 94.71 |
| T54 | 4JW3 | 1398 | 82.98 | 48.79 |
and
% decoys that score worse than the native.
The CAPRI Score_set classifies protein complex decoys into high-, medium- and acceptable-quality models by filtering through a set of criteria, such as the fraction of native and non-native contacts, number of clashes, ligand/receptor/interface RMSD, misorientation angle and residual displacement (Lensink and Wodak, 2014). We used this set of models to test PIZSA’s ability to identify ‘near-native’ complexes. PIZSA was able to identify 188 near-native complexes within the top 100 scoring decoys from either of the target sets whereas CIPS identified 149 complexes. Although both PIZSA and CIPS identified similar number (13 and 14, respectively) of near-natives in the top 10 ranking decoys, PIZSA was able to identify all three classes of near-natives (4 high, 6 medium and 3 acceptable), whereas CIPS did not identify any high-quality models in the top 10 ranked decoys (0 high, 5 medium and 9 acceptable). Furthermore, PIZSA ranks 6 (1.3%) and 152 (32.6%) high-quality models, 12 (1.7%) and 246 (34.2%) medium-quality models, 4 (0.6%) and 301 (42.3%) acceptable-quality models in the top 1% and 25% of decoys, respectively. CIPS ranks 0 and 152 (32.6%) high-quality models, 10 (1.4%) and 293 (40.7%) medium-quality models, 18 (2.5%) and 238 (33.5%) acceptable-quality models in the top 1% and 25% of decoys, respectively (Supplementary S11). Furthermore, we tested our ability to identify near-native models from the CAPRI Score_set by following the CAPRI assessment criteria of submitting 10 predictions per target. Scoring performance is evaluated as the number of targets with one or more acceptable- or higher-quality models in the selected predictions. A summary of our performance in comparison to CIPS, GraphRank and iScore is reported in Table 4. PIZSA outperforms CIPS by identifying a greater number of near-natives in four targets (T40, T41, T47 and T53). PIZSA identifies more number of near-natives in four targets in comparison to GraphRank (T29, T37, T40 and T50) whereas GraphRank performs better than PIZSA on four other targets (T32, T41, T46 and T53). iScore identifies a greater number of near-natives in six targets (T32, T41, T46, T47, T50 and T53) as compared to PIZSA which performs better on two targets (T29 and T40). PIZSA identifies the most number of medium- or higher-quality models (21, 15 medium and 6 high) followed by iScore (20, 13 medium and 7 high), CIPS (16, 14 medium and 2 high) and GraphRank (14, 9 medium and 5 high). The performance of 37 groups/methods assessed on the CAPRI Score_set has been previously reported (Geng et al., 2020). PIZSA ranks in the sixth position in comparison to the other groups/methods including CIPS (Supplementary S20). The CAPRI Score_set used to evaluate the performance of GraphRank and iScore had been prefiltered to remove clashing models. PIZSA inherently penalizes atomic clashes as a result of which the performance remains unchanged even without filtering the dataset.
Table 4.
Comparison of PIZSA, CIPS, GraphRank and iScore on the CAPRI Score_set
| Target | PIZSA | CIPS | GraphRanka | iScorea | CAPRI besta |
|---|---|---|---|---|---|
| T29 | 5/3** | 5/2** | 4 | 4 | 9/5** |
| T30 | 0 | 0 | 0 | 0 | 0 |
| T32 | 0 | 0 | 4/1** | 4/1** | 2 |
| T35 | 0 | 0 | 0 | 0 | 1 |
| T37 | 4/1***/1** | 4/1***/3** | 2/1** | 4/2** | 6/1*** |
| T39 | 0 | 0 | 0 | 0 | 0 |
| T40 | 8/2***/5** | 6/4** | 4/3** | 4/1*** | 10/10*** |
| T41 | 5 | 4/1** | 8 | 10/2** | 10/2*** |
| T46 | 0 | 0 | 3 | 4 | 4 |
| T47 | 8/3***/5** | 7/1***/6** | 8/5***/3** | 10/6***/4** | 10/10*** |
| T50 | 2/1** | 2/1** | 0 | 4/3** | 7/6** |
| T53 | 1 | 0 | 5/1** | 5/1** | 8/3** |
| T54 | 0 | 0 | 0 | 0 | 0 |
| Total | 7/3***/5** | 6/2***/6** | 8/1***/4** | 9/2***/5** | 10/4***/3** |
Note: Summary of the number of acceptable-, medium- (**) or high-quality (***) model identified by different scoring methods on various CAPRI targets. CAPRI best indicates the best result for each target obtained by any of the CAPRI participants.
Performance of methods directly adapted from Geng et al. (2020).
We also tested PIZSA’s ability to identify near-native complexes as native crystallographic associations. PIZSA classified near-native complexes as native associations with an accuracy of 0.62. On one hand, 66% of high-quality models, 57% of medium-quality models and 64% of acceptable-quality models were classified as native associations. On the other hand, 38% of the non-near-native decoys were classified as native associations.
3.4 Binding mode selection
We have already demonstrated PIZSA’s ability to identify the native binding mode as one of the best scoring interactions in the Dockground and CAPRI decoy sets. In this section, we illustrate PIZSA’s ability to identify the correct binding mode with an example of three homologous VHH domains (AMB7, AMD9 and AMD10) interacting with PPA (Desmyter et al., 2002). The VHH domains bind to orthogonal sites on the PPA despite sharing a high structural similarity with Cα RMSD ranging from 0.61 to 0.84Å. We built models for each of the VHH domains interacting with their non-native epitopes on PPA (Davis et al., 2006) and scored them with PIZSA along with their native complexes (Table 2). The native binding modes were successfully identified as the highest scoring interfaces amongst the models. It should be noted that none of the six non-native binding modes is scored as viable binders. We also scored all complexes with the CIPS potential. CIPS was able to identify only one out of three native complexes as the highest scoring interactions (Supplementary S12).
3.5 Identification of crystallization artifacts
Distinguishing whether structures of protein assemblies solved by X-ray crystallography are biologically meaningful or simply artifacts of the crystallization process is an important problem in PPI studies. Although crystallographic interfaces have smaller surface areas than biologically relevant structures, this is not frequently the case and significant overlap in interface areas has been observed. We trained PIZSA to distinguish between crystallization artifacts and biologically relevant interactions based on the fraction of interactions that have an optimal atomic propensity () (Table 5).
Table 5.
Z-scores of VHH–PPA complexes
| AMB7 mode | AMD9 mode | AMD10 mode | |
|---|---|---|---|
| AMB7 | 2.33 | 0.91 | 1.47 |
| AMD9 | 1.17 | 2.43 | −0.47 |
| AMB10 | 1.04 | 1.33 | 2.82 |
Note: Scores for highest scoring complexes (also native complexes) are in bold.
The optimal threshold for classification was identified using ROC curves constructed from the ‘Duarte’ dataset (Duarte et al., 2012). The area under the ROC curves was 0.79, 0.66 and 0.60 at 4, 6 and 8Å, respectively (Supplementary S13a). Optimal thresholds at 4, 6 and 8Å were 0.575, 0.510 and 0.489, respectively. The TPR and FPR of classification were 69% and 18% for 4Å, 64% and 32% for 6Å, 51% and 35% for 8Å. Interfaces in the DCbio and DCxtal datasets with scores greater than the threshold were classified as true and false positives, respectively. Interfaces in the DCbio and DCxtal datasets with scores less than or equal to the threshold were classified as false and true negatives, respectively. PIZSA achieved the highest classification performance at 4Å with an accuracy of 0.75, balanced accuracy of 0.75 and MCC of 0.51 (Supplementary S13b). We tested PIZSA’s ability to identify crystallization artifacts on the ‘Bahadur’ dataset and compared our performance with that of PISA. Of the 88 crystal interfaces, PIZSA predicts 54 as crystallization artifacts whereas PISA predicts 61. There are 10 common crystal interfaces that are predicted as biological interactions by both the methods (Supplementary S13c and d).
4 Discussion
We constructed statistical potentials to assess the stability of protein quaternary assemblies based on amino acid preferences extracted from a large dataset of experimentally deduced protein–protein interfaces. Defining amino acid preferences for different categories of atomic interactions (main chain–main chain, main chain–side chain and side chain–side chain) and at different distance thresholds helped dissect the specific modes through which residues interact across protein interfaces. These residue pairing preferences were further refined by incorporating the relative abundance of amino acid residues in proteins. We observe that residue pairings across the interface tend to occur with a preferred number of shared atomic contacts and incorporate this as an atomic propensity parameter in our scoring function. The inclusion of this parameter also enables us to capture the specificity in atomic interactions between different residue types across the protein–protein interface. We also include a clash penalty to correct for steric clashes in protein structures that can lead to spurious contacts and confound the signal from residue preferences. Our scoring function is able to discriminate native assemblies from docking decoys with an accuracy of 0.80, a balanced accuracy of 0.87 and an MCC of 0.75 on the Dockground Docking Decoy Set 1.
The construction of amino acid preference matrices also enables us to identify crucial residues involved in protein binding. Residues containing aromatic rings (TYR, TRP, PHE and HIS) are assigned favorable scores for their interactions with most residues suggesting their versatility in mediating residue pair interactions across the interface. These amino acid residues are characterized by the presence of a π–electron cloud above and below the aromatic ring that can interact with other aromatic and nonaromatic residues imparting stability (Ma and Dougherty, 1997; Makwana and Mahalakshmi, 2015). We find that interactions between hydrophobic residues were deemed less favorable at shorter distance thresholds but as more favorable at larger distance thresholds, especially for side chain–side chain interactions of large aliphatic amino acids such as LEU and ILE, an observation that has previously been reported (Bahar and Jernigan, 1997). Electrostatic interactions between oppositely charged residues also had favorable interaction scores and have been found to play an important role in determining specificity in protein interfaces (Sheinerman et al., 2000). These interactions were also frequently found to have high atomic propensities for a specific number of interacting atoms. These patterns are supported by previous observations that the formation of salt bridges between oppositely charged amino acids exhibit well-defined geometric preferences (Donald et al., 2011). For interactions between similarly charged residues, we find that interactions between positively charged residues are more favorable compared to interactions between negatively charged residues which were predominantly unfavorable. Among the positively charged residues, we confirm observations from previous studies that ARG–ARG pairs are more favorable than LYS–LYS pairs (Glaser et al., 2001; Nadalin and Carbone, 2018). Arginine along with tryptophan and tyrosine exhibit strong favorable interactions with most other amino acid types. This could be due to arginine’s capability to form multiple types of favorable interactions, similar to the aromatic residues. In addition to the capability to form H-bonds and salt bridges via its positively charged guanidinium motif, the electron delocalization of its guanidinium π–system gives it a pseudo-aromatic character (Crowley and Golovin, 2005). The presence of three methylene carbon atoms in its side chain also enables arginine to participate in hydrophobic interactions. Small polar amino acids THR and SER share common favorable interacting partners. THR interacts favorably with ARG, ASN, ASP, GLN and HIS, whereas SER interacts favorably with a subset containing ASN, ASP and HIS. The higher number of favorable interactions by THR could be attributed to the presence of an extra methyl group that additionally interacts with two or more methylene groups of ARG and GLN. THR’s favorable interactions with MET, PHE, TYR and TRP further emphasize the role of its methyl group in mediating such interactions.
The qualitative patterns of amino acid preferences across interfaces extracted with PIZSA potentials differ slightly than those described previously (Glaser et al., 2001; Keskin et al., 1998; Nadalin and Carbone, 2018). However, these patterns are in close agreement with amino acid preferences found in protein interaction hot-spots (Bogan and Thorn, 1998) and hence better represent the specificity in interactions between types of interactions across protein–protein complexes. It was observed that diagonal elements in the scoring matrices had favorable interactions on an average 4% more often than off-diagonal elements (Supplementary S14). This can be speculated to have arisen from our training dataset consisting 81% homodimers that tend to have symmetric interactions (André et al., 2008). The 12 favorable diagonal elements observed in the side chain–side chain matrix constructed at 4Å distance threshold can possibly be explained by various interactions, such as disulfide bridges (CYS pairs), side chain hydrogen bonding (ASN/GLN pairs), aromatic stacking (HIS/TYR/PHE/TRP pairs), hydrophobic exclusion (ILE/VAL/MET/PRO pairs) and methylene group interaction (ARG pairs).
Using the Dockground Docking Decoy Sets and the CAPRI Score_set, we report a significant improvement for the effective rank-ordering of native conformations over the recently published CIPS potentials, which reported better performance compared to three other propensity matrices and two atomic potentials (Nadalin and Carbone, 2018). The inclusion of a clash penalty term in the scoring function of PIZSA results in a better discriminatory performance (Supplementary S15). Furthermore, a distance threshold of 4Å performs better than 6 and 8Å (Supplementary S16). Most residue–residue interactions at the interface are mediated by side chains. The matrices at a cutoff of 4Å give the best description of such specific interactions. These specificities diminish at higher cutoff distances. We also report better performance as compared to CIPS in identifying near-native complexes among the top scoring decoys in most cases. Our method further classifies the near-native complexes as native associations with an accuracy of 0.62. We have also tested the efficacy of our method in detecting near-native structures from the CAPRI Score_set. For this we have used the CAPRI categorization of near-natives being of high, moderate and acceptable accuracy. In comparison to 36 other methods, PIZSA is better than 31 of the methods and identifies 2 lesser number of targets with acceptable- or higher-quality models in comparison to the best performer. However, the ranking of PIZSA would be better if an unfiltered dataset were to be used. PIZSA is capable of considering decoys with clashes and such structures do not have to be eliminated as it was done in the case of the comparison mentioned above. Although PIZSA ranks sixth in identifying targets with acceptable- or higher-quality models, PIZSA is one of the top two methods to identify the highest number of medium- or higher-quality models in comparison to other methods. We also attempted to compare the PIZSA Z-score and CIPS score with DockQ scores (Basu and Wallner, 2016), a quality measure of docking models, but were unable to detect any reliable correlation (Supplementary S21).
We have compared PIZSA to various other classes of scoring functions that not only include statistical potentials but also scoring functions employing physics-based energy terms, machine learning algorithms and hybrid methods. Physics-based scoring functions such as HADDOCK (Dominguez et al., 2003), pyDock (Cheng et al., 2007), SwarmDock (Moal and Bates, 2010) and ZDock (Pierce and Weng, 2007) use a linear combination of various energy terms that often have functions to estimate the electrostatic energy, van der Waals energy, bound surface area and desolvation energy. GraphRank and iScore make use of a Support Vector Machine classifier to identify near-native models of PPIs. iScore makes use of a hybrid methodology by combining its machine learning approach with intermolecular energetic terms (Geng et al., 2020). Conceptually PIZSA is akin to CIPS (Nadalin and Carbone, 2018), more than any of the aforementioned methods, as both are statistical potentials but the two methods differ in the formulation of their scoring functions. PIZSA uses three different scoring matrices for the three different modes of interactions whereas no such distinction is made by CIPS. Both PIZSA and CIPS have analogous metrics to weight the absolute frequencies of interface residue pairs. CIPS uses a function based on the average number of contacts made by interface residues whereas PIZSA uses atomic propensities that account for probabilities of residue pairs interacting with a certain number of atoms. PIZSA also differs from CIPS by incorporating a function to penalize atomic clashes at the interface. Docking methods often generate models with atomic clashes that can lead to spurious interactions with unnaturally high number of native contacts (Geng et al., 2020; Lensink and Wodak, 2010). Such models with clashes are often removed from testing datasets as was the case with the SBGrid dataset (Geng et al., 2020). The clash penalty is an important feature of our scoring function as it preempts the need to filter out models with clashes. Both iScore and GraphRank do not work on antibody complexes in their current form (Geng et al., 2020) whereas PIZSA successfully identifies such complexes from the ZDock Docking Benchmark 4.0. Fourteen of 25 antibody complex targets in the ZDock decoy set had at least a single near-native model. PIZSA was able to identify near-natives in its top 10 predictions for 7 such targets. Interestingly, PIZSA was also able to identify the near-native model for the one and only target that was classified as being a difficult case (2HMI) from the set of 14. Another unique feature of our method is its ability to discriminate between biologically relevant interactions from crystallization artifacts. Our method was able to correctly identify 54 out of 88 crystal artifacts, which is 7 less than the state-of-the-art method PISA.
The ability of PIZSA potentials to distinguish between favorable and unfavorable binding modes is exemplified on a case study of VHH domains in complex with PPA. The three VHH domains have distinct binding modes for complexation with PPA and PIZSA potentials were able to select the native binding modes for all three VHH domains. In addition to effective rank-ordering of near-native structures and the binary classification of protein assemblies, testing on two distinct datasets, PIZSA potentials were also successful in distinguishing between biologically meaningful complexes and crystallization artifacts. We believe that crystal contacts represent cases where we have 3D structures of noninteracting interfaces and identification of such cases is a crucial test for any protein complex assessment method. We have two different metrics for identification of biologically meaningful interactions from crystal contacts and near-natives from docking decoys since these represent two different problems. On one hand, we require our scoring metric to be coarse grained to avoid near-natives with suboptimal packing from being undetected. On the other hand, we require another scoring metric that is fine tuned to be sensitive to packing at the interface for distinguishing biological interactions from crystal contacts. We have therefore used two different scoring metrics with and without atomic propensity () as a weight that are used for the identification of crystal contacts and near-natives, respectively. Our performance in distinguishing biological interactions from crystal contacts is comparable to the state-of-the-art method PISA. We attempted to identify if there exists a pattern between incorrectly identified crystal contacts and the bound surface area or the size of interacting partners. We did not find an appreciable correlation between the bound surface area or the size of interacting partners with (Pearson’s correlation coefficient of −0.13 and −0.14, respectively).
We demonstrate that knowledge-based potentials based on known PPIs capture crucial information about protein binding and can be successfully applied to identify biologically meaningful protein complexes in protein docking experiments, PPI predictions and also in distinguishing complexes formed as artifacts of the protein crystallization process. Such potentials could also aid in the design of noncanonical protein complex.
Supplementary Material
Acknowledgements
We would like to thank members of the COSPI lab at IISER Pune for valuable discussions and insights.
Funding
A.S.D. was supported by a DST-INSPIRE fellowship. M.S.M. was funded by a Wellcome Trust-DBT India alliance senior fellowship.
Conflict of Interest: none declared.
References
- Aloy P., Russell R.B. (2006) Structural systems biology: modelling protein interactions. Nat. Rev. Mol. Cell Biol., 7, 188–197. [DOI] [PubMed] [Google Scholar]
- André I. et al. (2008) Emergence of symmetry in homooligomeric biological assemblies. Proc. Natl. Acad. Sci. USA, 105, 16148–16152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahadur R.P. et al. (2004) A dissection of specific and non-specific protein–protein interfaces. J. Mol. Biol., 336, 943–955. [DOI] [PubMed] [Google Scholar]
- Bahar I., Jernigan R.L. (1997) Inter-residue potentials in globular proteins and the dominance of highly specific hydrophilic interactions at close separation. J. Mol. Biol., 266, 195–214. [DOI] [PubMed] [Google Scholar]
- Basu S., Wallner B. (2016) DockQ: a quality measure for protein–protein docking models. PLoS One, 11, e0161879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berggård T. et al. (2007) Methods for the detection and analysis of protein–protein interactions. Proteomics, 7, 2833–2842. [DOI] [PubMed] [Google Scholar]
- Berman H.M. et al. (2000) The Protein Data Bank. Nucleic Acids Res., 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogan A.A., Thorn K.S. (1998) Anatomy of hot spots in protein interfaces. J. Mol. Biol., 280, 1–9. [DOI] [PubMed] [Google Scholar]
- Bordner A.J., Gorin A.A. (2007) Protein docking using surface matching and supervised machine learning. Proteins, 68, 488–502. [DOI] [PubMed] [Google Scholar]
- Cheng T.M.-K. et al. (2007) pyDock: electrostatics and desolvation for effective scoring of rigid-body protein–protein docking. Proteins, 68, 503–515. [DOI] [PubMed] [Google Scholar]
- Crowley P.B., Golovin A. (2005) Cation–π interactions in protein–protein interfaces. Proteins, 59, 231–239. [DOI] [PubMed] [Google Scholar]
- Davis F.P. et al. (2006) Protein complex compositions predicted by structural similarity. Nucleic Acids Res., 34, 2943–2952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmyter A. et al. (2002) Three camelid VHH domains in complex with porcine pancreatic α-amylase inhibition and versatility of binding topology. J. Biol. Chem., 277, 23645–23650. [DOI] [PubMed] [Google Scholar]
- Dominguez C. et al. (2003) HADDOCK: a protein–protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc., 125, 1731–1737. [DOI] [PubMed] [Google Scholar]
- Donald J.E. et al. (2011) Salt bridges: geometrically specific, designable interactions. Proteins, 79, 898–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duarte J.M. et al. (2012) Protein interface classification by evolutionary analysis. BMC Bioinformatics, 13, 334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng C. et al. (2020) iScore: a novel graph kernel-based function for scoring protein–protein docking models. Bioinformatics, 36, 112–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaser F. et al. (2001) Residue frequencies and pairing preferences at protein–protein interfaces. Proteins, 43, 89–102. [PubMed] [Google Scholar]
- Huang S.-Y., Zou X. (2008) An iterative knowledge-based scoring function for protein–protein recognition. Proteins, 72, 557–579. [DOI] [PubMed] [Google Scholar]
- Hwang H. et al. (2010) Protein–protein docking benchmark version 4.0. Proteins, 78, 3111–3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keskin O. et al. (1998) Empirical solvent-mediated potentials hold for both intra-molecular and inter-molecular inter-residue interactions. Protein Sci., 7, 2578–2586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krissinel E., Henrick K. (2007) Inference of macromolecular assemblies from crystalline state. J. Mol. Biol., 372, 774–797. [DOI] [PubMed] [Google Scholar]
- Kundrotas P.J. et al. (2018) Dockground: a comprehensive data resource for modeling of protein complexes. Protein Sci., 27, 172–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmanov U., Emili A. (2013) Protein–protein interaction networks: probing disease mechanisms using model systems. Genome Med., 5, 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lensink M.F., Wodak S.J. (2010) Docking and scoring protein interactions: CAPRI 2009. Proteins, 78, 3073–3084. [DOI] [PubMed] [Google Scholar]
- Lensink M.F., Wodak S.J. (2014) Score_set: a CAPRI benchmark for scoring protein complexes. Proteins, 82, 3163–3169. [DOI] [PubMed] [Google Scholar]
- Lensink M.F. et al. (2017) Modeling protein–protein and protein–peptide complexes: Capri 6th edition. Proteins, 85, 359–377. [DOI] [PubMed] [Google Scholar]
- Liu S., Vakser I.A. (2011) DECK: distance and environment-dependent, coarse-grained, knowledge-based potentials for protein–protein docking. BMC Bioinformatics, 12, 280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyskov S., Gray J.J. (2008) The RosettaDock server for local protein–protein docking. Nucleic Acids Res., 36, W233–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J.C., Dougherty D.A. (1997) The cation–π interaction. Chem. Rev., 97, 1303–1324. [DOI] [PubMed] [Google Scholar]
- Makwana K.M., Mahalakshmi R. (2015) Implications of aromatic–aromatic interactions: from protein structures to peptide models. Protein Sci., 24, 1920–1933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mezei M. (2015) Statistical properties of protein–protein interfaces. Algorithms, 8, 92–99. [Google Scholar]
- Miyazawa S., Jernigan R.L. (1996) Residue–residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol., 256, 623–644. [DOI] [PubMed] [Google Scholar]
- Moal I.H., Bates P.A. (2010) SwarmDock and the use of normal modes in protein–protein docking. Int. J. Mol. Sci., 11, 3623–3648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadalin F., Carbone A. (2018) Protein–protein interaction specificity is captured by contact preferences and interface composition. Bioinformatics, 34, 459–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce B., Weng Z. (2007) ZRANK: reranking protein docking predictions with an optimized energy function. Proteins, 67, 1078–1086. [DOI] [PubMed] [Google Scholar]
- Pierce B.G. et al. (2014) ZDock server: interactive docking prediction of protein–protein complexes and symmetric multimers. Bioinformatics, 30, 1771–1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pons C. et al. (2011) Scoring by intermolecular pairwise propensities of exposed residues (SIPPER): a new efficient potential for protein–protein docking. J. Chem. Inf. Model., 51, 370–377. [DOI] [PubMed] [Google Scholar]
- Ryan D.P., Matthews J.M. (2005) Protein–protein interactions in human disease. Curr. Opin. Struct. Biol., 15, 441–446. [DOI] [PubMed] [Google Scholar]
- Rykunov D., Fiser A. (2010) New statistical potential for quality assessment of protein models and a survey of energy functions. BMC Bioinformatics, 11, 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Šali A., Blundell T.L. (1993) Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol., 234, 779–815. [DOI] [PubMed] [Google Scholar]
- Sheinerman F.B. et al. (2000) Electrostatic aspects of protein–protein interactions. Curr. Opin. Struct. Biol., 10, 153–159. [DOI] [PubMed] [Google Scholar]
- Sippl M.J. (1995) Knowledge-based potentials for proteins. Curr. Opin. Struct. Biol., 5, 229–235. [DOI] [PubMed] [Google Scholar]
- Soni N., Madhusudhan M.S. (2017) Computational modeling of protein assemblies. Curr. Opin. Struct. Biol., 44, 179–189. [DOI] [PubMed] [Google Scholar]
- Stelzl U. et al. (2005) A human protein–protein interaction network: a resource for annotating the proteome. Cell, 122, 957–968. [DOI] [PubMed] [Google Scholar]
- Tanaka S., Scheraga H.A. (1976) Medium-and long-range interaction parameters between amino acids for predicting three-dimensional structures of proteins. Macromolecules, 9, 945–950. [DOI] [PubMed] [Google Scholar]
- Torchala M. et al. (2013) SwarmDock: a server for flexible protein–protein docking. Bioinformatics, 29, 807–809. [DOI] [PubMed] [Google Scholar]
- Tovchigrechko A., Vakser I.A. (2006) GRAMM-X public web server for protein–protein docking. Nucleic Acids Res., 34, W310–W314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez A. et al. (2003) Global protein function prediction from protein–protein interaction networks. Nat. Biotechnol., 21, 697–700. [DOI] [PubMed] [Google Scholar]
- Velankar S. et al. (2016) PDBe: improved accessibility of macromolecular structure data from PDB and EMDB. Nucleic Acids Res., 44, D385–D395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vreven T. et al. (2015) Updates to the integrated protein–protein interaction benchmarks: docking benchmark version 5 and affinity benchmark version 2. J. Mol. Biol., 427, 3031–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G., Dunbrack R.L. Jr (2003) PISCES: a protein sequence culling server. Bioinformatics, 19, 1589–1591. [DOI] [PubMed] [Google Scholar]
- Zhang Q.C. et al. (2012) Structure-based prediction of protein–protein interactions on a genome-wide scale. Nature, 490, 556–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M., Li. et al. (2016) Current experimental methods for characterizing protein–protein interactions. ChemMedChem, 11, 738–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann M.T. et al. (2012) Combining statistical potentials with dynamics-based entropies improves selection from protein decoys and docking poses. J. Phys. Chem. B, 116, 6725–6731. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.