Collagen fiber interweaving is central to sclera stiffness

Abstract

The mechanical properties of the microstructural components of sclera are central to eye physiology and pathology. Because these parameters are extremely difficult to measure directly, they are often estimated using inverse-modeling matching deformations of macroscopic samples measured experimentally. Although studies of sclera microstructure show collagen fiber interweaving, current models do not account for this interweaving or the resulting fiber-fiber interactions, which might affect parameter estimates. Our goal was to test the hypothesis that constitutive parameters estimated using inverse modeling differ if models account for fiber interweaving and interactions. We developed models with non-interweaving or interweaving fibers over a wide range of volume fractions (36-91%). For each model, we estimated fiber stiffness using inverse modeling matching biaxial experimental data of human sclera. We found that interweaving increased the estimated fiber stiffness. When the collagen volume fraction was 64% or less, the stiffness of interweaving fibers was about 1.25 times that of non-interweaving fibers. For higher volume fractions, the ratio increased substantially, reaching 1.88 for a collagen volume fraction of 91%. Simulating a model (interweaving/non-interweaving) using the fiber stiffness estimated from the other model produced substantially different behavior, far from that observed experimentally. These results show that estimating microstructural component mechanical properties is highly sensitive to the assumed interwoven/non-interwoven architecture. Moreover, the results suggest that interweaving plays an important role in determining the structural stiffness of sclera, and potentially of other soft tissues in which the collagen fibers interweave.

Graphical Abastract

1. Introduction

The mechanical properties of sclera play a central role on many aspects of eye physiology and pathology. [1, 2] Accordingly, there have been many studies aimed at characterizing the macroscale sclera mechanical properties, using a diversity of experimental mechanical tests, including inflation and biaxial tensile testing. [3–10] Recognizing that the macroscale behavior arises from the microscale, there is also great interest in understanding the architecture and mechanical properties of the microstructural components of sclera, such as collagen fibers and bundles. Whilst several techniques have been developed to characterize the microarchitecture of sclera, such as small-angle light scattering, small-angle X-ray scattering, second-harmonic generation, and polarized light microscopy, [1] it remains extremely difficult to measure directly the mechanical properties of the microstructural components of sclera. Hence, these parameters are often estimated using inverse-modeling matching deformations of macroscopic samples measured experimentally [6, 10–13] The quality of the estimates obtained from the inverse models is strongly dependent on the physiologic accuracy of the assumed microstructure of the model. Based on lessons from studies of other soft tissues, several models of sclera have been developed to account for the collagen preferred orientation and degree of alignment, or anisotropy. [10, 12, 14–19] Recent models incorporate detailed properties, such as collagen fiber crimp and stretch-induced recruitment. [20–22]

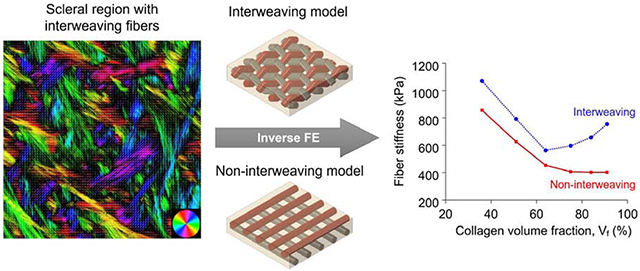
Analysis of sclera imaged using polarized light microscopy, [23–25] and other techniques, [1, 26–29] show that the collagen fibers are often interwoven (Figure 1). Actually, the interweaving architecture of collagen fibers is also observed in other connective tissues, such as cornea, [30] adventitia, [31] heart valves, [32] and articular cartilage. [33] Although it seems reasonable to expect that interweaving will affect the tissue mechanics, to the best of our knowledge, there have been no numerical models of sclera that account for this interweaving, or the resulting fiber-fiber interactions. We hypothesized that a model of sclera with interweaving fibers that interact with one another will have a distinct mechanical behavior from a model in which the fibers are not interweaving and do not interact.

Figure 1.

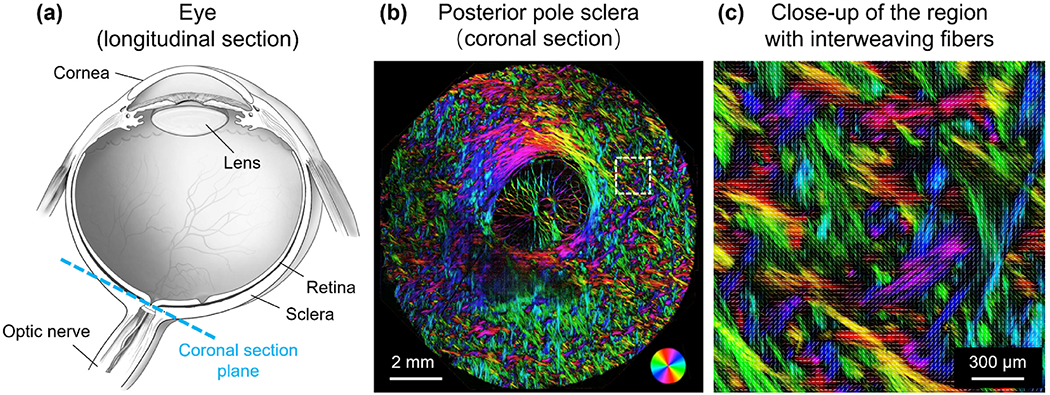
(a) Schematic of an eye sectioned longitudinally. (b) Polarized light microscopy image of a coronal section of the posterior pole sclera in a sheep eye. Colors indicate local fiber orientation, whereas intensity is proportional to collagen fiber density. (c) Close-up of a region in the sclera exhibiting interweaving fibers.

Our long-term goal is to understand the role of fiber interweaving on scleral biomechanics. Specifically, in this study we aimed to determine if there are differences in the constitutive model parameters estimated using inverse-modeling between models that account for fiber interweaving and interactions and models that do not. Because our initial interest is to establish first if there are any effects of interweaving, we considered simplified, regular fiber architectures. These simplifications and equi-biaxial loading meant that we could model the fiber-fiber interactions in an also simplified way without need to model slippage, which is highly complex. In addition, the simple geometries meant that the models could be readily parameterized. We took advantage of this to study how the role of interweaving might depend on collagen volume fraction. We set aside for later the use of more complex architectures, parameters and fiber interactions.

2. Methods

We developed two sets of finite element (FE) models representing interweaving and non-interweaving collagen fibers embedded in a matrix. We anticipated that the undulations and number of fiber-fiber interactions in an interweaving model would increase with the number of fibers in a model. To understand how this might affect the results, each set of interweaving/non-interweaving models consisted of several models with varying number of fibers and collagen volume fractions. For each model, the fiber stiffness was estimated using an inverse modeling approach in which the predictions from the models were matched with an experimental stress-strain curve obtained from the biaxial extension test of a macroscopic sample of human sclera. [9] We then compared the stiffness between interweaving and non-interweaving fiber models over a wide range of collagen volume fractions.

2.1. Finite element modeling

Model geometry.

The models consisted of fibers embedded in a matrix with dimensions of 1000 μm × 1000 μm × 200 μm (Figure 2). Two types of fiber architecture were considered: non-interweaving and interweaving. Non-interweaving fibers were straight in two layers by orientation. Interweaving fibers were undulated in a zigzag manner such that they alternated going above and below crossing fibers, akin to a plain weave. All fibers had a uniform diameter of 100 μm. The interweaving and non-interweaving fibers had the same end-to-end length of 1000 μm. The number of fibers was the same in the x and y directions, N × N, with N = (2, 3, 4, 5, 6, 7), with the fibers distributed uniformly.

Figure 2.

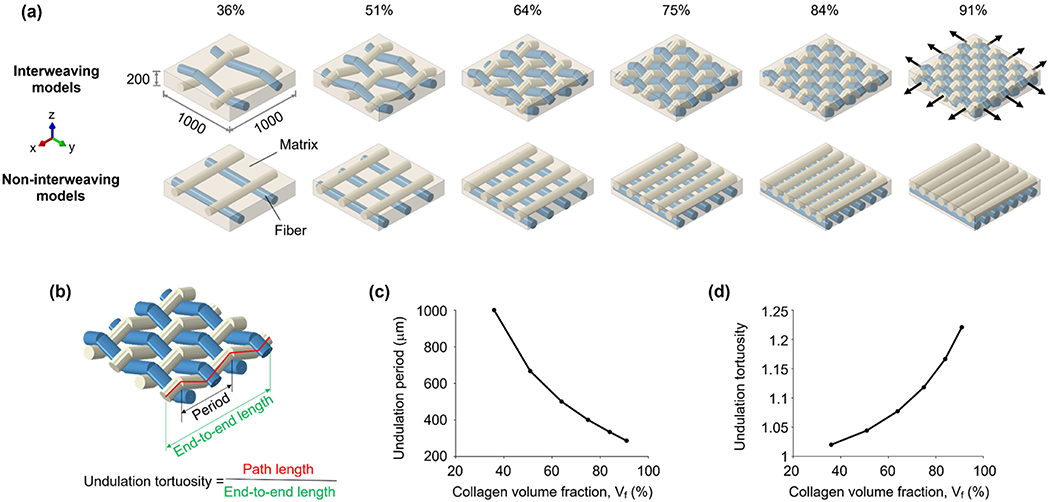
(a) Models of interweaving and non-interweaving architectures with collagen volume fractions ranging from 36% to 91%. For all models, the matrix surrounding the fibers had the same dimensions (1000 μm by 1000 μm by 200 μm). Fibers within the matrix were arranged in the x (white) and y (blue) directions. The number of fibers was the same in both directions. In the non-interweaving models, the fibers were straight, and there were no interactions between the fibers. In the interweaving models, the fibers were undulated in a zigzag manner, and we considered the interactions between them. For the mechanical simulation, we assigned an equi-biaxial stretch of 2.18% in the x-y plane as displacements at the edge of the fiber-matrix assembly (black arrows). Note that the fibers are continuous. However, because of software limitations, they appear as if they have a “gap” on the exterior side of a curve. (b) Fiber period and tortuosity were measured for all the interweaving models. As collagen volume fraction increased, (c) the period decreased, and (d) the tortuosity period increased, both smoothly and nonlinearly. For the non-interweaving models, since all fibers were straight, the tortuosities were all equal to 1.00 and the periods are ill-defined.

The collagen volume fraction was calculated based on the ratio of projection areas between the collagen and matrix in the x-y plane. There are two reasons. First, this method is consistent with some studies in which collagen density is evaluated based on either projections or 2D “flat” images or histology. [1, 34, 35] Second, it allows for a fairer comparison between models with interweaving and non-interweaving architectures: when we create a model with the interweaving architecture, we only change the architecture of collagen fibers, and keep the general geometric parameters (i.e., number of fibers, fiber diameter, matrix dimension) the same as those of the non-interweaving architecture. Therefore, the projected collagen volume fractions of both architectures are the same. For the cases considered in this study, the interweaving and non-interweaving models had collagen volume fractions of 36%, 51%, 64%, 75%, 84%, and 91%, within the range reported in the literature (18-93%). [36–39] For a comparison between the collagen volume fractions computed from projected views and a three-dimensional calculation, please see Supplementary Table 1. In the rest of this work, unless specified, the collagen volume fraction is referred to as the projected volume fraction.

Mechanical properties.

The fibers were modeled as a hyperelastic Mooney-Rivlin material with the form: [40]

$$W=C_{10}(I_1-3)+C_{01}(I_2-3)+\frac{1}{2}K{(J-1)}^2$$ (1)

where W is the strain energy density, C₁₀ and C₀₁ are material constants defining the stiffness of the material and will be determined by inverse fitting (see more details below), I₁ and I₂ are the first and second invariants of the right Cauchy-Green deformation tension (non-directional measures of material deformation), K is the bulk modulus which defines the compressibility of the material and J is the determinant of the deformation gradient. The fiber stiffness (i.e., shear modulus) was calculated as 2(C₁₀ + C₀₁). [41] The matrix was modeled as a neo-Hookean material with a shear modulus of 200 kPa. [13]

Discretization (meshing).

The fibers were meshed with hybrid linear truss elements (T3D2H). The matrix was meshed with linear eight-noded, hybrid hexahedral elements (C3D8H).

Interactions.

Fiber interactions only had to be considered in models with the interweaving architecture. Considering a simplified geometry of evenly distributed fibers under equi-biaxial loading, there would be no sliding between fibers. Thus, fiber-fiber interactions could be approximated by the gap contact element. [42] When the two fibers are separated, the gap contact element does not carry any forces, but when in contact, it behaves as a rigid body preventing fiber inter-penetration.

Boundary conditions.

We applied an equi-biaxial stretch of 2.18% in the x-y plane as displacement boundary conditions to the fiber-matrix assembly. This is consistent with the applied stretch in the experiment. [9]

Sensitivity analysis.

To better understand the role of interweaving, we re-calculated the stress-strain curves of each model using the material properties from the other architecture, and quantified the deviation relative to the experimental data:

$$\%\text{deviation}=\frac{\sum \Vert {\sigma }_{\text{switch}}-{\sigma }_{\exp }\Vert }{\sum \Vert {\sigma }_{\exp }\Vert }$$ (2)

where σ_switch denotes the stress values predicted by models with switching material properties, and σ_exp denotes the experimental stresses. This allowed us to directly compare the role of architecture (interwoven vs. non-interwoven) with fibers of the same mechanical properties. We also get insight into the impact that the different material properties have on a given model. This was repeated for the whole range of collagen volume fractions.

A note on terminology.

The architecture and hierarchical organization of sclera collagen is complex with important variations through the globe. [24, 43, 44] Microscopy images of sclera show bundles or lamellae composed of hundreds or thousands of fibers, fibrils, micro-fibrils, etc. [1, 25, 44, 45] It was not our intent in this work to do a detailed analysis or interpretation of scleral collagen architecture. For simplicity, we have used the term “fiber”, but we recognize that it may not be ideal. An important consideration is that the scale of the undulations of interweaving is different from that of the collagen fiber waviness referred to as crimp by us, [21, 43, 46, 47] and others [11, 20]. Collagen fiber crimp waviness has amplitudes on the order of a few μm, and periods typically under 20 μm. [21, 43, 46, 47] Although the interweaving undulations are not yet well-characterized, images such as those in Figure 1 suggest that they could be on the order of 100-300 μm. From a mechanical perspective, the undulations of crimp affect directly the biomechanical behavior of a fiber under load, with the crimp “disappearing” as the fiber is loaded or stretched. [21] The interactions between interwoven fibers mean that these undulations do not “disappear” under load, and are limited by the interlocking.

2.2. Extraction of fiber stiffness

The fiber model parameters (C₁₀ and C₀₁) were identified using an inverse FE method by matching an experimental stress-strain curve obtained from the biaxial extension testing of human sclera. [9] We used a differential evolution optimization algorithm, [48]. The differential evolution algorithm sought to identify the two model parameters that yielded the closest match between the FE-simulated and the experimentally-measured equivalent stress of the fiber-matrix assembly under equi-biaxial stretch. The equivalent stress was calculated by the total force along x direction divided by the cross-sectional area of the fiber-matrix assembly. We confirmed that the forces along x and y were identical. Numerically, the stresses of the FE model were fit to their experimental values at 21 sampled strains by minimizing the following cost function:

$$F={\sum _{n=1}^N\left({\sigma }_{num,n}-{\sigma }_{\exp ,n}\right)}^2$$ (3)

where σ_num,n and σ_exp,n denote the numerical and experimental stresses, respectively, at the nth sampled strain. N = 21 was the number of sampled strains during the loading phase.

The following initial ranges were used with the differential evolution algorithm for the considered model parameters: − 2 GPa < C₁₀ < 2 GPa, − 2 GPa < C₀₁ < 2 GPa, with a restriction that C₁₀ + C₀₁ > 0. The inverse FE procedure was terminated when 1) the maximum number of the optimization iterations was larger than 100, 2) the tolerance on the cost function value was smaller than 1e-9, and 3) the tolerance on the parameter variation was smaller than 1e-9.

2.3. Software

All finite element modeling was done in Abaqus 2020X (Dassault Systemes Simulia Corp., Providence, RI, USA). Model pre and post-processing and inverse-modeling fits were done using custom code and the GIBBON toolbox [49] for Matlab v2020 (MathWorks, Natick, MA, USA).

3. Results

All interweaving and non-interweaving models fit the experimental stress-strain data very closely (Table 1). As an example, Figure 3 shows the results of the inverse fitting process of the interweaving and non-interweaving models with a collagen volume fraction of 91%. The constitutive model parameters are summarized in Table 2.

Table 1.

R-squared values of the inverse fits of the experimental stress-strain data at various collagen volume fractions.

Collagen volume fraction	Interweaving	Non-interweaving
36%	0.9912	0.9913
51%	0.9917	0.9916
64%	0.9922	0.9919
75%	0.9925	0.9921
84%	0.9927	0.9922
91%	0.9929	0.9923

Figure 3.

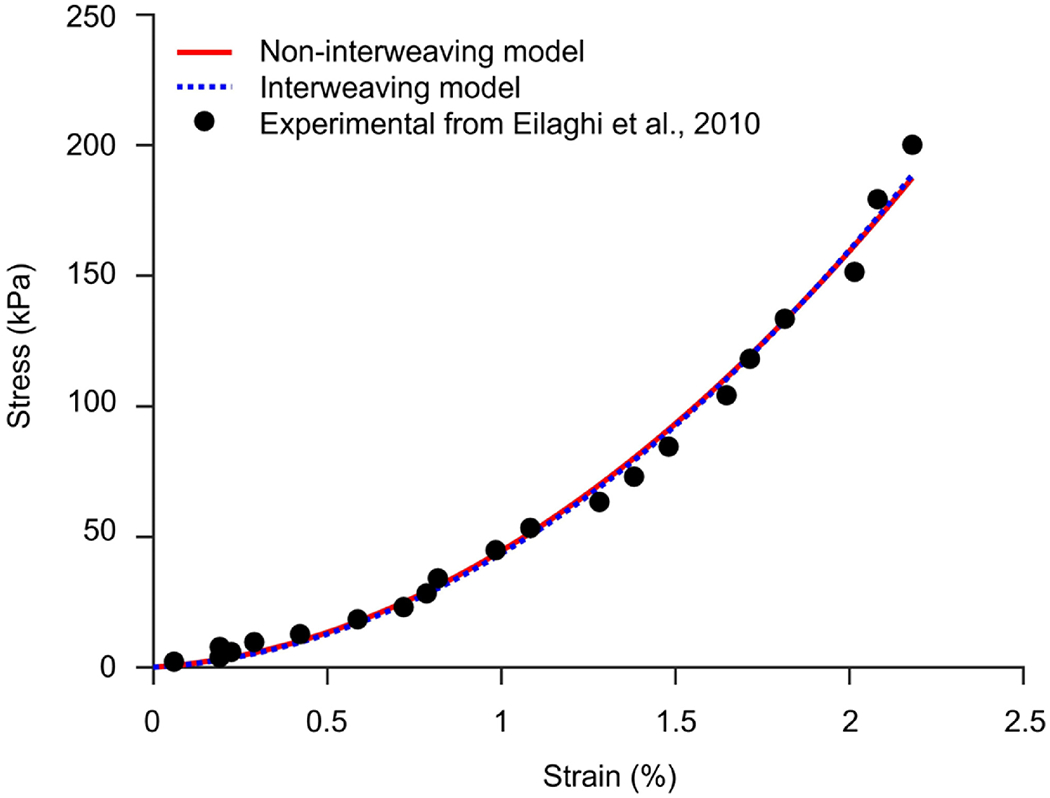
Example fits of the interweaving and non-interweaving models to data taken from the biaxial extension testing on the human sclera. [9] The case shown is the one with a collagen volume fraction of 91%. Both the interweaving and non-interweaving models fit the experimental stress-strain data very well.

Table 2.

Hyperelastic parameters for fibers in interweaving and non-interweaving models, respectively, obtained from the inverse fitting process. All values in kPa.

Collagen volume fraction	Interweaving			Non-interweaving
	C10	C01	2(C10+C01)	C10	C01	2(C10+C01)
36%	798,608	−798,073	535	729,838	−729,410	428
51%	602,392	−601,996	396	492,300	−491,987	313
64%	540,892	−540,611	281	375,273	−375,048	226
75%	522,863	−522,565	298	303,481	−303,278	203
84%	545,605	−545,277	328	254,811	−254,610	201
91%	589,996	−589,619	377	220,008	−219,808	200

The stiffness of the interweaving and non-interweaving fibers calculated by inverse fitting at all collagen volume fractions is shown in Figure 4a. The stiffness of the interweaving fibers was consistently larger than that of the non-interweaving fibers. The same observation was obtained when we re-plotted Figure 4a using the full 3D collagen volume fractions for all models (Supplementary Figure 1).The fiber stiffness ratio, computed by dividing the stiffness of the interweaving fibers by that of the non-interweaving fibers of the same collagen volume fraction, is shown in Figure 4b.

Figure 4.

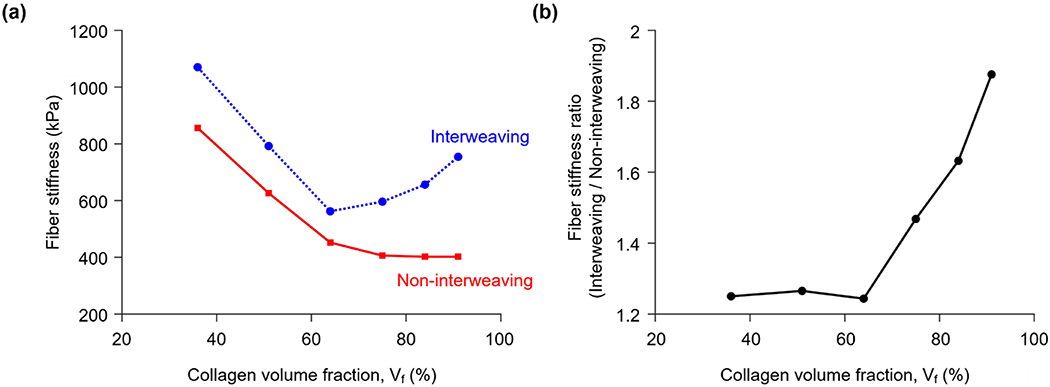
(a) The stiffness of the interweaving and non-interweaving fibers calculated by inverse fitting for several collagen volume fractions. For non-interweaving fibers the stiffness decreased monotonically as collagen volume fraction increased. Interweaving fibers had a minimum stiffness of around 570 kPa at 64% volume fraction. Importantly, the stiffness of the interweaving fibers was larger than that of the non-interweaving fibers at all volume fractions. (b) The ratio of interweaving to non-interweaving fiber stiffness, which we name the fiber stiffness ratio, was fairly constant around 1.25 when the collagen volume fraction was 64% or less. For higher volume fractions, the fiber stiffness ratio increases quickly, reaching 1.88 for a volume fraction of 91%.

Figure 5 illustrates the effects of changing model architecture without changing the mechanical properties on the model with a volume fraction of 91%. Removing the interweaving shifted the curve up, making the model stiffer. Conversely, adding interweaving shifts the curve down, making the model more compliant. Since the fiber properties were constant in each test, these represent changes in the structural stiffness due to the interweaving alone.

Figure 5.

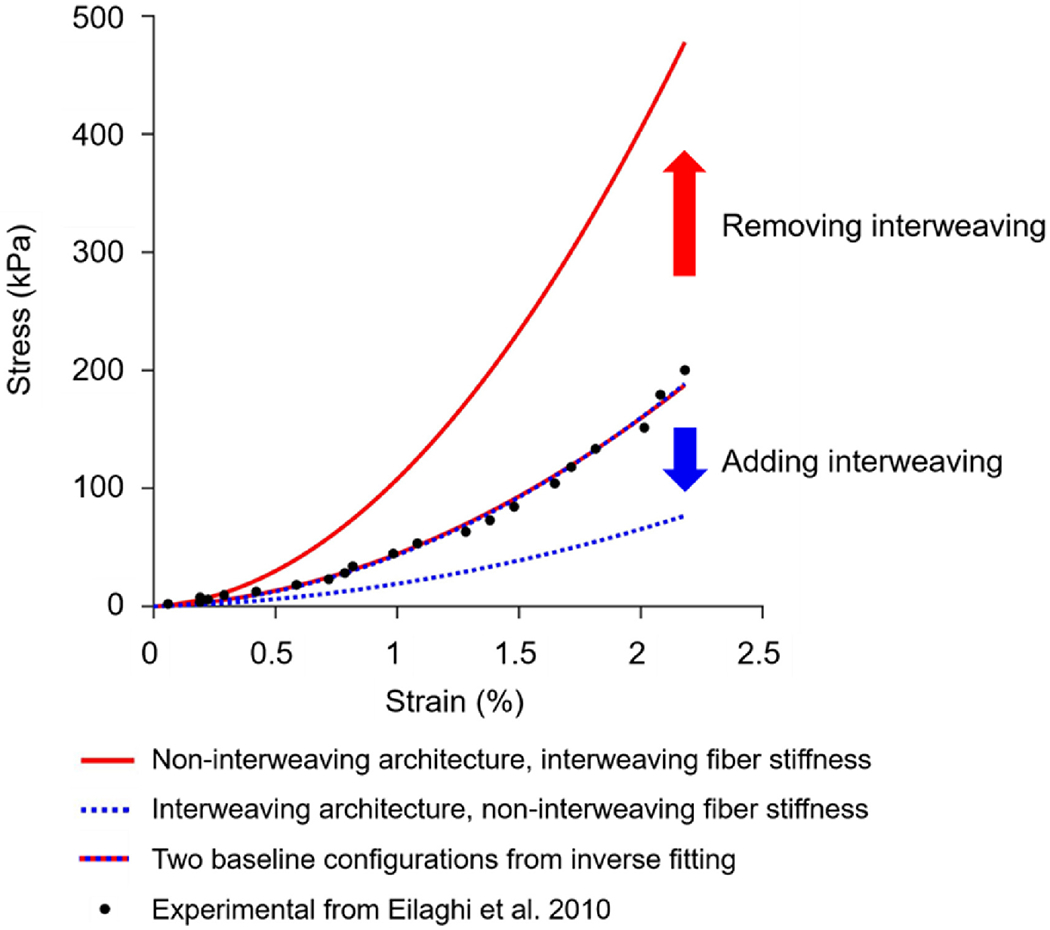
Effects on the stress-strain curve of changing model architecture, without changing the mechanical properties, on the model with a volume fraction of 91%. The two baseline configurations were those obtained through the inverse fitting process. These were obtained for an interwoven model with interweaving fiber mechanical properties, and for a non-interwoven model with non-interweaving fiber mechanical properties. The two curves agree well with the experimental data, R-squares of 0.9929 and 0.9923, and are almost indistinguishable. Removing the interweaving shifted the curve up, making the model stiffer. Conversely, adding interweaving shifts the curve down, making the model more compliant.

Figure 6 shows the result of the same analysis for several volume fractions. The spread of the curves indicates the strength of the effects of architecture or of fiber stiffness. For low volume fractions all curves are similar and close to the experimental data. In these cases, interweaving has almost no effect, the parameters estimated are very similar and it makes no difference whether model architecture is interwoven or not. For higher volume fractions, however, as interweaving becomes more pronounced, there were substantial differences between the curves. This indicates that the model architecture has a large influence on the model mechanics, or similarly that the parameters estimated will depend strongly on the architecture.

Figure 6.

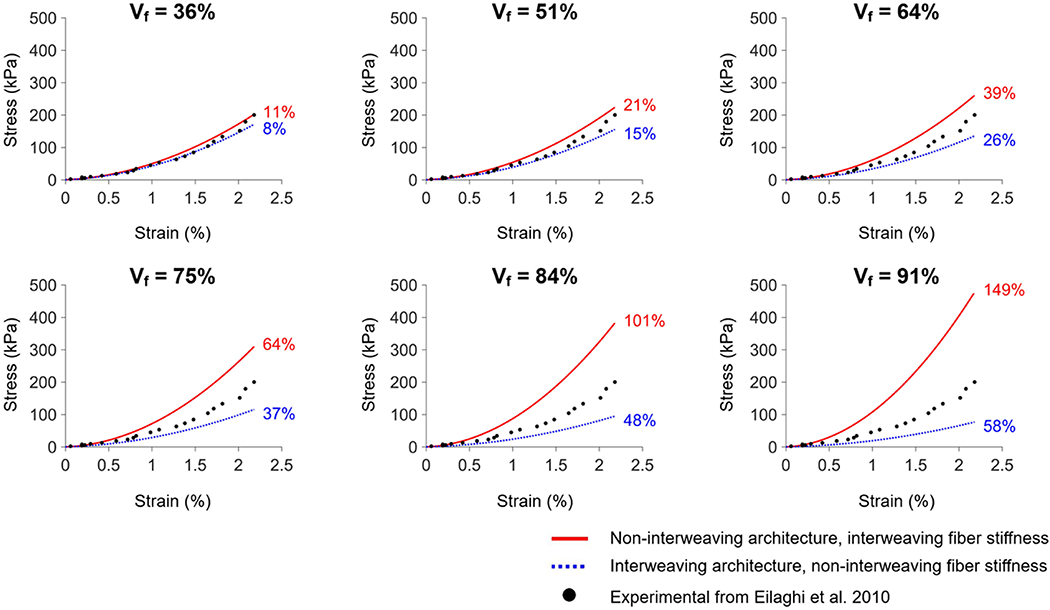
Evaluating the impact of the differences in parameters, akin to that of Figure 5, but for various collagen volume fractions. Non-interweaving model simulated with parameters from interweaving model and vice versa. The numbers next to the curves indicate the % deviation relative to the experimental data (see Methods section for the definition). Removing the interweaving of the interwoven model, or adding interweaving to the non-interwoven model results in changes in the stiffness curves. The effects were minimal for low volume fractions, but increased substantially at large volume fractions. Readers may find it useful to refer to Figure 2 for the model geometries. V_f: collagen volume fraction.

4. Discussion

Our long-term goal is to understand the role of fiber interweaving on scleral biomechanics. In this study we aimed to determine if there are differences in fiber mechanical properties estimated using inverse FE methods between models with interweaving and non-interweaving fibers. Two main findings arise from this work. First, there were indeed differences in the parameters; specifically, the fiber stiffness estimated from interweaving models was 25-89% higher than that from non-interweaving models. Second, the differences in the estimated fiber stiffness due to interweaving were more pronounced at higher collagen volume fractions (3.56 times larger at a collagen volume fraction of 91% than at 36%). Below we discuss the main findings and expand on the motivation for the study and rationale for our study strategy.

Although it seems to be well accepted that the collagen fibers of sclera are interwoven, [23–25, 34, 50] this aspect of the architecture has not been considered in studies of scleral biomechanics. Interweaving plays a crucial role in the mechanics of many human-made materials, such as textiles and composites. [51–56] We reasoned that if this is also the case in scleral tissues, it could have important implications for our understanding of how fiber microarchitecture contributes to determine macroscale biomechanics, of sclera and potentially of other soft tissues with interwoven fibers. [30–33] To the best of our knowledge, there are no constitutive model formulations for sclera, or more broadly soft tissue, that explicitly incorporate fiber interweaving and the resulting fiber-fiber interactions. This may be because it remains unproven whether interweaving actually has any meaningful effect on tissue mechanics. Our aim was, therefore, to gauge the order of magnitude of a potential effect of an interweaving architecture relative to a non-interweaving one. In other words, we want to determine whether the effects of interweaving are a small fraction of the results, and thus arguably safe to continue ignoring, or a large fraction and thus important and should not be neglected. Towards this goal, we believe that the argument can be made that a model with a simplified geometry is appropriate. Considering a simplified geometry of evenly distributed fibers under equi-biaxial loading meant that there would be no sliding between fibers. Thus, fiber-fiber interactions could be approximated by avoiding interpenetration. Simulating fiber-fiber sliding is extremely complicated and would require parameters that are not yet characterized (i.e., friction coefficient between). Simplified models were convenient because they allow for a fair comparison between models with interweaving and non-interweaving architectures, and provide an ideal setup to assess the role of collagen volume fraction and, in the future, of other parameters. We acknowledge that the models used in this work are highly simplified, and we advise caution before using the models or parameters from this work beyond what they were developed for. Future work using more realistic models is necessary before the predictions from the simple models are accepted as a general rule. Still, we posit that the models in this work, simplified as they are, provide an important first glimpse into the potential role of interweaving in scleral biomechanics and are therefore useful as a transition to more advanced models.

We found that, to match experimental data from macroscopic samples, the fibers of models with interweaving had to be stiffer than the fibers of models without interweaving. This indicates that the interwoven architecture is, as a structure, “weaker”, “more compliant” or “less stiff” than a non-interwoven architecture. This effect was clear when we simulated models with a given stiffness and added/removed the interweaving (Figure 5). Removing interweaving produced a structurally stiffer model and adding interweaving did the opposite. A potential explanation could be that the fibers of the interweaving architecture are undulated, whereas those from the non-interweaving models are straight. Straight fibers aligned with the load carry the forces more efficiently, and are shorter, and thus, the overall model is stiffer. Higher collagen volume fractions implied more wavy fibers, which further increases model compliance. This is consistent with the observation that increased collagen volume fraction also led to increases in the differences due to interweaving. It is important to recall that the undulations associated with interweaving are different from those of crimp, [21, 43, 46, 47] as discussed in more detail elsewhere in this manuscript. Note that the main conclusions of this work would not change if we had used the 3D full collagen volume fractions instead of the projected collagen fractions (Supplementary Figure 1).

It is unclear yet how the influence of interweaving on tissue mechanics ranks compared with the influences of parameters that are traditionally considered, such as fiber density, orientation, and the degree of anisotropy or fiber concentration, [10, 12, 14, 15, 19, 57, 58] or more recently developed ones, such as fiber crimp and stretch-induced recruitment. [20–22] Our results suggest that, two tissue samples with identical collagen fibers, collagen fiber density, orientation distribution and anisotropy will exhibit substantially different macroscopic mechanical behavior, depending on whether the fibers are interwoven or not. This would be the case for techniques such as small-angle light scattering or small-angle X-ray scattering that measure the collagen fibers in 2D from outside the globe and provide no information on interweaving. [1, 57] In a more practical perspective, our results show that inverse modeling to estimate collagen fiber microstructural properties will lead to incorrect parameters whether by ignoring interweaving when the fibers are interwoven, or by assuming interweaving if the fibers are not. The magnitude of the error will depend on the interweaving, which itself potentially depends on other parameters, such as collagen volume fraction. Thus, our results indicate that it is essential to develop methods to characterize fiber interweaving so that it can be incorporated into the models before these can be expected to accurately relate micro and macroscopic behavior.

We should point out that the finding that interweaving affects the macroscale mechanical behavior of the sclera under equi-biaxial loading does not mean that this is its only or primary effect. It is entirely possible that interweaving has larger effects on other aspects of scleral biomechanics, such as bending stiffness, or the resistance to failure. Boubriak et al., for example, suggested that interweaving may affect scleral swelling. [59]

It is important to point out that there are several limitations in this study. First, as mentioned above, the models had simplified geometries. The cross-sectional shape and area of the fibers were assumed constant, and the fibers were arranged in two perpendicular directions. Collagen fibers in scleral tissues have variable orientations and cross-sectional shapes and areas. [23–25, 50] The fibers in our models had regular undulations, whereas actual tissue fibers have irregular undulations. Also, we did not consider fiber undulations at other scales, such as crimp, that have important contributions to fiber mechanics. The role of crimp will thus be encoded in the constitutive model parameters. Future work would benefit from using constitutive models with parameters that can be more easily interpreted.

The models had a maximum collagen volume fraction of 91%. The spaces between the fibers in tissues are filled by other components, including other forms of collagen, cells, vessels, etc. [37, 38] Future models might benefit from incorporating these other components, or from other undulation patterns to better represent the collagen architecture and its relationship with other tissue components.

The fiber-matrix interactions were not considered, as is common in biomechanical models of the eye. [11, 20, 30] It is difficult to predict exactly the effects of adding fiber-matrix interactions on top of those of interweaving. If the interactions store distortion energy, their presence could make the tissue stiffer. [60] It is also possible that non-fibrous components, such as GAG chains, may affect sliding, acting as lubricants, directly or through tissue hydration, in which case their presence could make the tissue more compliant. [61, 62] Lubrication could be particularly important for interweaving cases with increased direct fiber-fiber interactions. Fiber-matrix interactions may also depend on the magnitude of lateral fiber displacement (perpendicular to the local fiber axis), which could differ between interweaving and non-interweaving architectures, and likely also with loading. Interweaving may also be a mechanism to limit fiber or lamellae slippage directly from the collagen architecture.

The fibers were modeled as a hyperelastic Mooney-Rivlin material. Although this is an approximation, agreement with the experiment was excellent (R² > 0.99). Current work is ongoing to incorporate microstructural information of collagen fibers into the constitutive model, such as crimp. [21, 43, 46, 47] Also note that in the inverse modeling process, we only fit the mechanical properties of the fibers, keeping those of the matrix constant at values from the literature. [13] We did this for the sake of simplicity. An inverse modeling process that can optimize both matrix and fiber properties may have more than one solution. More advanced inverse modeling techniques that sort out this issue may be necessary to properly account for the effects of age and interweaving given the evidence that some of the age-related changes in sclera properties are due to changes in matrix properties. [63] Although experiments have shown age-related increases in macro-scale sclera stiffness, [17, 63–65] and decreases in the micro-scale collagen fiber undulations, or crimp, [43] there is no evidence of age-related changes in interweaving.

We simulated equi-biaxial stretch to best approximate the conditions in the experiments from Eilaghi and colleagues from which we obtained the stress-strain data. [9] This condition is a fairly common assumption in studies on sclera biomechanics when the intent is to simulate the tension in the sclera induced by intraocular pressure. [15, 57, 66] It remains to be determined whether the role of fiber interweaving identified in this study extends to other loading conditions or not.

An interesting advantage of the explicit fiber modeling used in this work is that it did not require us to assume that the scleral microstructure undergoes affine deformations. Although this is a fairly common assumption of numerical models of the posterior sclera, [10, 13, 15, 67] it is possible that collagen fibrils may undergo non-affine deformations on the micron scale, particularly when loaded in the cross-fiber direction. [68–71]

Despite the simplifications and limitations of the models, we argue that they are useful as a first approximation to explore the potential for interweaving effects in scleral biomechanics. Our results support the notion that interweaving plays an important role in determining the macroscopic biomechanical behavior of scleral tissues. The results indicate that a better characterization of interweaving, and of the role of interweaving effects, are necessary and potentially central to understand the biomechanics of sclera, and of other soft tissues with interwoven fibers.

Statement of Significance:

The collagen fibers of sclera are interwoven, but numerical models do not account for this interweaving or the resulting fiber-fiber interactions. To determine if interweaving matters, we examined the differences in the constitutive model parameters estimated using inverse modeling between models with interweaving and non-interweaving fibers. We found that the estimated stiffness of the interweaving fibers was up to 1.88 times that of non-interweaving fibers, and that the estimate increased with collagen volume fraction. Our results suggest that fiber interweaving is a fundamental characteristic of connective tissues, additional to anisotropy, density and orientation. Better characterization of interweaving, and of its mechanical effects is likely central to understanding microstructure and biomechanics of sclera and other soft tissues.