Extensions of Multiple-Group Item Response Theory Alignment: Application to Psychiatric Phenotypes in an International Genomics Consortium

Abstract

Large-scale studies spanning diverse project sites, populations, languages, and measurements are increasingly important to relate psychological to biological variables. National and international consortia already are collecting and executing mega-analyses on aggregated data from individuals, with different measures on each person. In this research, we show that Asparouhov and Muthén’s alignment method can be adapted to align data from disparate item sets and response formats. We argue that with these adaptations, the alignment method is well suited for combining data across multiple sites even when they use different measurement instruments. The approach is illustrated using data from the Whole Genome Sequencing in Psychiatric Disorders consortium and a real-data-based simulation is used to verify accurate parameter recovery. Factor alignment appears to increase precision of measurement and validity of scores with respect to external criteria. The resulting parameter estimates may further inform development of more effective and efficient methods to assess the same constructs in prospectively designed studies.

Introduction

Large-scale measurement data are now being collected globally for many reasons, including to study genetic associations, to gain insights from electronic medical records, and to harvest health information from mobile device use. The analysis of aggregated data from multiple studies, or meta-analysis, is now being supplanted by aggregation of data at the individual level across multiple studies, a practice sometimes referred to as mega-analysis (McArdle, Prescott, Hamagami, & Horn, 1998). Mega-analyses that span multiple projects or instruments require a multistep procedure to ensure comparability of measurements across samples. First, researchers must identify a set of data elements or items that putatively harmonize by identifying items that appear to assess essentially the same thing (with face validity). Second, investigators need to determine if the data elements used comparable response scales and transform items to have comparable response scales if needed. Third, the researcher must ensure that the items used across the studies have similar measurement properties; differences in the measurement properties of items, if found, must be incorporated into the measurement model. This process is referred to in the psychometric literature as an assessment of measurement invariance (Vandenberg & Lance, 2000).

Historically, measurement invariance testing has relied on a series of model modifications in which constraints on item measurement parameters are imposed or freed, depending on the search strategy, based on the results of statistical tests of those constraints (Leite, Huang, & Marcoulides, 2008; Vandenberg & Lance, 2000). As the number of groups increases, the number of statistical tests required for measurement invariance analysis becomes prohibitively large, rendering traditional measurement invariance methods impractical for large numbers of groups. For example, with 10 groups there would be 45 possible pairwise comparisons per item, and a 10-item test administered to those 10 groups would require up to 450 statistical tests to assess measurement invariance for each item parameter. Furthermore, when item sets are not identical across groups (i.e., some harmonized items are shared across one or more samples, but not all items are shared across all samples) and response formats differ across groups (e.g., an item is scored as absent [0] or present [1] in one scale, but as absent [0], mild [1], moderate [2], or severe [3] in another), specialized software and estimation techniques are required to estimate the multiple-group measurement model at each step of the search; in particular, the large amount of missing data that result from nonidentical item sets makes often-used methods of estimation (e.g., maximum likelihood) very difficult (see McArdle, Grimm, Hamagami, Bowles, & Meredith, 2009). Thus, there is a growing need for integrative measurement techniques that can flexibly accommodate large numbers of groups and nonidentical item sets and response formats.

To elaborate further, it is often the case in measurement mega-analysis (e.g., Gu & Guttman, 2017; Kaplan & McCarty, 2013; Marcoulides & Grimm, 2017; McArdle et al., 2009) that many, or even all, items intended to measure the same construct have highly similar, but not identical, content and response formats across instruments and/or samples. For example, the following questions about the core symptom of “depressed mood” are asked in slightly different ways in two of the instruments used in our study, the DI-PAD (Diagnostic Interview for Psychotic and Affective Disorders) and the SCID (Structured Clinical Interview for the Diagnostic and Statistical Manual of Mental Disorders [DSM]):

DI-PAD: “Have you ever been sad, down, depressed, or blue most of the day, nearly every day, for at least one week?” Rated 0 (Not present) or 1 (present)

SCID: “In the last month . . . has there been a period of time when you were feeling depressed or down most of the day nearly every day? How long did it last? (As long as 2 weeks?)” Rated 1 (Absent), 2 (Subthreshold), or 3 (Threshold)

For such items, it is sensible to assume that the same latent factor (here, depressive symptomatology) underlies item responses for both items (configural invariance; Vandenberg & Lance, 2000) and that the two items harmonize, which here means that they measure the severity of the same symptom (depressed mood).

In such applications, even after harmonizing items across instruments, there are likely to remain many items which are unique to a single or small number of samples and/or very few items with measurements from all samples, resulting in a large amount of missing data which need to be accounted for. For instance, one instrument may focus on the physical symptoms of depression (e.g., decreased appetite, impaired sleep, psychomotor dysfunction), while another may focus on the psychological symptoms of depression (e.g., anhedonia, irritability), resulting in nonidentical item sets. In this case, the two instruments would have some items in common (e.g., depressed mood) but responses to items that are not in both instruments would be missing in the samples in which those items were not administered. Furthermore, differences in item wording (e.g., the inclusion of “blue” in the DI-PAD) and small but meaningful content differences (e.g., depressed mood for 1 versus 2 weeks) will lead to items that differ in their relationship to the construct of interest (depression); in other words, it is not reasonable to expect that items have perfect measurement invariance (specifically, metric or scalar invariance; Vandenberg & Lance, 2000) across studies, and this lack of invariance must be accounted for in the modeling approach. Last, it is desirable to maximize the information gained from each participant’s responses by preserving the original response scales, rather than, for example, collapsing all items to a dichotomous measurement scale.

We believe that, with several modifications, the alignment approach introduced by Asparouhov and Muthén (2014; see also Marsh et al., 2017; Muthén & Asparouhov, 2018) can achieve these goals. The main purpose of this report is to describe and evaluate an application of this method to a large data set that presented multiple challenges for traditional linking or measurement invariance studies, including the study of different clinical and healthy samples assessed using different instruments.

Our motivating example for these modifications to alignment comes from analysis of psychiatric symptom ratings from the Whole Genome Sequencing in Psychiatric Disorders Consortium (WGSPD; Sanders et al., 2017). In this project, different clinical diagnostic instruments, including the SCID (First, 2014), Comprehensive Assessment of Symptoms and History (CASH; Andreasen, Flaum, & Arndt, 1992), Diagnostic Interview for Genetic Studies (DIGS; Nurnberger et al., 1994), Mini-International Neuropsychiatric Interview (MINI; Sheehan et al., 1998), Diagnostic Interview for Psychotic and Affective Disorders (DI-PAD; Perlman et al., 2016), were used to assess symptoms relevant to diagnostic criteria in 12 samples, many of which were further subdivided into distinct clinical subgroups (e.g., Controls, Major Depressive Disorder, Bipolar I Disorder, Schizoaffective Disorder, Schizophrenia). The assessments comprised a total of 6,560 items across a variety of clinical domains (e.g., depression, mania, positive, negative, and disorganized psychotic symptoms).

The resulting data set could not be analyzed using traditional approaches to multigroup data given the diversity of instruments and confounds of site with both diagnostic group and instrument used, the absence of any predefined “linking” items, and the lack of participants examined with multiple instruments. Despite these major challenges, we sought to produce factor scores on clinical domains using as much data as possible, so that the resulting scores could be used in genetic analyses as “dimensional phenotypes” to complement the categorical diagnoses. To do so, we modified the alignment method (Asparouhov & Muthén, 2014) to accommodate nonidentical item sets and nonidentical response formats. Our work represents an attempt to improve phenotype definition by creating scores that putatively identify variation on a shared measurement scale.

In the following sections, we first discuss existing approaches to multiple-group item response theory and prior work in item response theory mega-analysis. Next, we review the alignment method for the graded response model before introducing two modifications which allow for the application of alignment across instruments with differing response formats and item sets. We then apply the modified alignment method to data from the WGSPD Consortium. This application has three primary goals: demonstrating the utility of the alignment method for explaining cross-study differences in measurement models, using a real-data-based simulation study to examine parameter recovery under the unique design conditions in WGSPD, and comparing the external validity of scores generated from alignment to those based on the configural model. We conclude with recommendations about future methodological directions in item-level mega-analysis and for instrument development that may facilitate and increase the power and efficiency of mega-analyses in future multisite studies.

Multiple-Group Item Response Theory and Mega-Analytic Measurement

In order to compare Muthén’s alignment method with conventional methods for multiple-group factor analysis, we will utilize the framework of Vandenberg and Lance (2000; see also, Widaman & Reise, 1997), who synthesized the somewhat chaotic measurement invariance literature into a unified modeling framework. In this framework, multiple-group factor analysis is a multistep process assessing the equivalence of factor model parameters across groups. These steps usually take a particular order and invariance needs to be obtained at each step for subsequent tests to be meaningful (Vandenberg & Lance, 2000). First, configural invariance is tested to determine if different groups have the same factor structure, regardless of the specific parameter estimates obtained. Assuming configural invariance has been obtained, the next test is of metric invariance, which holds if the factor loadings for like items are invariant across groups, followed by tests of scalar invariance, which holds if the measurement intercepts for like items are invariant across groups, and invariant uniquenesses, which holds if the item uniquenesses for like items are invariant across groups. Assuming a multiple-group data set passes all four tests, the measurements can be considered statistically invariant and the measurement models can be used to test for group differences in mean, variance, and/or covariance of the latent variable(s) measured.

If any of these tests of measurement invariance fail to hold, researchers have the opportunity to settle for partial measurement invariance, in which the aforementioned invariances hold for some subset of items, possibly across some subset of groups, but not for all items or all groups. Establishing partial measurement invariance across two groups often requires a large number of statistical tests, for example, tests of equal factor loadings across groups for a subset of items to establish partial metric invariance, and the number of possible tests scales exponentially with the number of items. The number of required tests also scales exponentially with the number of groups, and thus, when there are many items and groups, conventional approaches quickly become infeasible. In brief, although the measurement invariance approach described above has been applied fruitfully in the literature (e.g., Ang et al., 2007; Antonakis, Avolio, & Sivasubramaniam, 2003; Lee et al., 2016; Schwartz & Rubel, 2005), a critical limitation is its lack of scalability, or ability to accommodate large numbers of groups and/or items. Although distributed search procedures have been proposed to address this problem (e.g., Leite et al., 2008), such approaches can be computationally expensive, in effect exchanging one deficiency in scalability for another.

In contrast to typical multiple-group measurement applications, recent mega-analyses of item-level measurement data generally ignored the measurement invariance problem because of its computational intractibility. These analyses have primarily been conducted in the context of longitudinal growth modeling, wherein differences in item content across form versions and overlapping content among similar scales yield complex data structures similar to those in the current study. One mega-analytic approach has been to jointly model all available data in a single item response theory (IRT) model using a Rasch or one-parameter logistic (1PL) model in which all items at all time points have the same discrimination and each item is equally difficult, conditional on the latent trait value, at all time points (e.g., Marcoulides & Grimm, 2017; McArdle et al., 2009). Others have adopted the statistical matching approach (D’Orazio, Di Zio, & Scanu, 2006), creating a synthetic completed data set using Bayesian methods, resampling, and/or IRT modeling (e.g., Gu & Gutman, 2017; Kaplan & McCarty, 2013) which can then be used in subsequent analyses. These statistical matching techniques also generally assume that the measurement parameters for items are identical across groups or measurement occasions to computationally simplify the imputation procedure. Other work in the psychiatry literature (e.g., Ruderfer et al., 2014) has approached mega-analysis in this context by conducting separate factor analyses in each unique sample, generating sample-specific factor scores, and then using those scores together in a second analytical step without first determining if the derived factors satisfy assumptions of measurement invariance, and leaving unclear if the scores reflect similar scales across the different samples and instruments.

Differences in item wording across instruments in the current context (e.g., depression across 1 vs. 2 weeks), preclude the use of either of the first two approaches unless the measurement invariance restrictions are removed. However, removing those restrictions would result in the lengthy and error-prone measurement model specification search described above, and removing all constraints would yield an unidentified model unless factor means and variances were instead constrained to be equal across groups, an untenable assumption given the differences in populations from which the groups were sampled. In addition, as the size of the amalgamated data set grows, the computational resources needed to implement the statistical matching approach (e.g., latent-variable matching; Markov Chain Monte Carlo) become prohibitive.

The alignment method attempts to sidestep these issues by assuming approximate scalar and metric invariance, that is, that factor loadings and measurement intercepts are approximately equal across groups but are not constrained to be exactly equal. By requiring approximate measurement invariance, the alignment method can accommodate small differences between items across groups if these differences are not systematically in one direction (i.e., higher/lower average factor loadings or measurement intercepts), and thus, has an additional advantage over conventional measurement invariance testing procedures in not requiring the specification of a priori invariant anchor items or requiring a search procedure. Instead, it is assumed that the group of items which are entered into the alignment complexity function is approximately measurement invariant; thus, the assumption of exact invariance in a single item or set of items is exchanged for the assumption of approximate invariance across the set of aligned items.

In the alignment method, the assumption of approximate measurement invariance is used to identify the factor hyperparameters (i.e., the factor means and variances), enabling their estimation. This is done in a two-stage procedure which is described below in detail. In brief, alignment begins by assuming that configural invariance has been met, and the first step of alignment is to estimate the configural model within each group. In the configural model, the mean and variance of the latent factor are constrained to 0 and 1, respectively, in order to identify the model. Next, the configural model parameters are transformed to minimize measurement invariance, taking advantage of the assumption of approximate measurement invariance and yielding estimates of the factor hyperparameters. Because alignment is a two-step process, it is highly scalable, as it requires neither the (sometimes complex) step of estimating a multiple-group item response theory model, nor the iterative, risky procedure of post hoc model modification to identify a partially invariant measurement model, nor the costly imputation of all missing item responses involved in the statistical matching approach.

Motivating Example: Whole Genome Sequencing in Psychiatric Disorders

In the WGSPD Consortium, many of the 12 component studies used a different clinical diagnostic instrument to assess psychiatric symptoms in their respective samples. All symptom ratings were designed to assess DSM criteria. Prior to our work on applying the alignment method, an extensive matching process was used to identify the specific items across instruments that putatively measure the same psychiatric symptoms, notwithstanding subtle differences in wording. Due to differences in the instruments used (e.g., SCID vs. CASH) and different versions of some instruments (e.g., SCID-I vs. SCID-IV), each pair of instruments shares only a subset of items with each other instrument, and instruments often contain items that are unique to that instrument. One possible solution to this mismatch is to consider only items that exist in all samples. Unfortunately, this would have restricted the number of available items drastically, rendering mega-analysis of little use. For instance, only two symptom ratings for disorganized psychosis putatively harmonized across all studies, although most instruments contained from six to nine items measuring disorganization, and the two items that did putatively harmonize (aggressive and agitated behavior, and derailment) were not those considered most important for diagnosis. Because factor scores from these analyses were to be used in subsequent genetic analyses, for which high power is of utmost importance, we sought to maximize the information available for each clinical dimension by using all available items, rather than only those items that were consistent across studies.

Furthermore, instruments often differed in their response formats. For many instruments (e.g., CASH, MINI), symptoms were judged as present or absent, but for others (e.g., SCID, DI-PAD), polytomous response formats were used, often differing in the meaning of response categories. For the instruments with polytomous response formats, the first category always indicated the absence of the symptom, while the remaining categories indicated that the symptom was present; however, for some (e.g., SCID), the categories indicating the presence of a symptom differed in the severity of the symptom, while in others (e.g., DI-PAD), these categories differed in the duration of the symptom.

These issues motivated modifications to the alignment method, permitting its application in this rich and unique database, and demonstrating its simplicity and scalability as applied to data structures that otherwise presented an extremely complex multiple-group measurement problem. In the next two sections, we explain the alignment method for polytomous item response data before introducing two modifications that enable item-level mega-analysis of the clinical phenotype data in WGSPD.

Item Response Theory Alignment and Extensions for Mega-Analysis: Muthén’s Alignment Method for Polytomous Item Response Data

Muthén and Asparouhov (2014) extended the alignment method to dichotomous items using IRT (Embretson & Reise, 2013). Recently, alignment for polytomous items has been implemented in Mplus Version 7.3, and a recent simulation study showed that the method generally performs well under small and moderate amounts of measurement noninvariance (Flake & McCoach, 2018). In this section, we briefly review the alignment method for polytomous items.

Consider a data set X consisting of N polytomous item response vectors ${\mathbf{x}}_{\mathit{i}}$, i = 1, . . ., N, each of length P, and each of the P items has Q ordered response categories labeled 0, . . ., $k_Q$. One parameterization of the graded response model for polytomous items (Samejima, 1968) is

$$\begin{array}{c}P(x_i=k_q|\eta )=P(x_i\ge k_q|\eta )-P(x_i\ge k_q+1|\eta )\hfill \end{array},$$ (1)

where $P(x\ge k_q|\mu )$ is the probability of responding in category $k_q$ or in a higher category and is given by

$$\begin{array}{c}P(x_i\ge k_q|\eta )=\frac{1}{1+\exp (-(a_p\eta +d_{\mathrm{pq}}))}\hfill \end{array}.$$ (2)

Here, a_p is called the discrimination parameter and $d_{\mathrm{pq}}$ is the item intercept for category boundary $k_q$ for item p, p = 1, . . ., P. The graded response model can be conceptualized as a series of models for each category boundary, all sharing a common discrimination parameter but with (Q− 1) unique, ordered intercept parameters.

Next consider that instead of a single sample, there exist G samples of responses to the same set of items. Consistent with Asparouhov and Muthén (2014), we will assume a unidimensional measurement model in which each variable loads on a single factor, and that the structure of this model holds across a set of groups g = 1, 2, . . ., n_g (configural invariance; Vandenberg & Lance, 2000). Then Equation (2) can be written as

$$\begin{array}{c}P(x_{\mathrm{ig}}\ge k_{\mathrm{qg}}|\eta )=\frac{1}{1+\exp (-(a_{\mathrm{pg}}\eta +d_{\mathrm{pqg}}))}\hfill \end{array}.$$ (3)

As written above, the multiple-group item response theory model is not identified, and constraints must be imposed to enable parameter estimation. A common identification constraint involves fixing the mean of the latent variable η to zero and its variance to one within each group, and the resulting model is referred to as the configural model.

In multiple-group item response theory, it is usually not assumed that the means and variances of the latent variable(s) are equal in all groups; indeed, this is considered one of the strongest forms of measurement invariance in the literature (Vandenberg & Lance, 2000). However, estimating the configural model in each group separately yields models with equal factor means and variances in all groups, and thus, appears to eliminate group differences from the model. The core principle underlying Muthén’s alignment method is that these group differences do not disappear entirely when the configural model is estimated separately in each group; rather, assuming no test bias, group differences manifest as differences in item discrimination parameters across groups, which reflect group differences in latent variances, and as differences in item intercepts across groups, which reflect group differences in latent means.

In alignment, the group differences on the latent variable are recovered by reversing this transformation, identifying the latent means and variances that yield transformed models with the most similar measurement parameters as possible across groups. In other words, the differences in item parameters when the latent distribution is held fixed are used to inform on group differences in the latent distribution itself. The key to understanding this process is the fact that a set of item parameters for the configural model can be transformed to any other metric, defined according to the mean and variance of the latent variable, yielding an equivalent model. Let ${\mathrm{a}}_{\mathrm{pg},0}$, p = 1, . . ., P denote the estimates of the item discrimination parameters in the configural model for group g, and $d_{\mathrm{pg},0}$, p = 1, . . ., P denote the estimates of the item intercept parameters in the configural model for group g, wherein the metric of the latent variable is set for identification purposes to have a mean of 0 and variance of 1. The equations to transform IRT parameters to a new latent variable metric with mean α_g and variance ψ_g are given by

$$\begin{array}{c}{a}_{p{g}_1,1}=\frac{a_{p{g}_1,0}}{\sqrt{{\psi }_{\mathrm{pg}}}}\hfill \end{array},$$ (4)

$$\begin{array}{c}{d}_{\mathrm{pq}{g}_1,1}=d_{\mathrm{pq}{g}_1,0}-a_{p{g}_1,1}*{\alpha }_g\hfill \end{array},$$ (5)

where the (,1) in the subscripts of the item parameters indicates transformed item parameters to the metric defined by α_g and ψ_g.

Muthén’s alignment method searches this space of equivalent models to identify the model with the most measurement invariance, quantified by a complexity function. Alignment for the graded response model proceeds as follows. First, the configural model, which fixes latent means to 0 and latent variances to 1, is estimated in each group, yielding estimates of $a_p$ and $d_{\mathrm{pq}}$, q = 1, . . ., Q_p− 1. Next, alignment proceeds by minimizing the graded response model (GRM) complexity function:

$$\begin{array}{c}{F}_{\mathrm{GRM}}=\sum _p\sum _{g_1<g_2}{w}_{g_1,g_2}f(a_{p{g}_1,1}-a_{p{g}_2,1})+\sum _p\sum _{g_1<g_2}\sum _q{w}_{g_1,g_2}f(d_{\mathrm{pq}{g}_1,1}-d_{\mathrm{pq}{g}_2,1})\hfill \end{array}.$$ (6)

Once factor means and variances are estimated through alignment, Equations 4 and 5 are used to compute the parameter estimates that minimize measurement noninvariance across groups, and the resulting parameters can be used to produce factor scores which are comparable across groups.

The extension of the alignment method from factor analysis to item response theory relies on the equivalence of the categorical factor analysis model and the item response theory model (see, Kamata & Bauer, 2008; Takane & de Leeuw, 1987). This equivalence allows the IRT parameters to be converted to equivalent factor analysis parameters, and alignment is performed on the factor analysis metric. The aligned factor analysis parameters can then be transformed to equivalent IRT parameters for reporting and scoring purposes.

Extensions of Alignment for Mega-Analysis

To accommodate the complexities of the WGSPD data, the alignment complexity function (Equation 6) was modified to allow for missing items across studies, essentially optimizing over the available item parameters, and all but the first threshold value was excluded from the alignment complexity function to account for differing response formats across studies. Although these modifications were developed to solve the specific mega-analytic measurement problems presented in WGSPD, we believe that these modifications will be useful to many integrative data analysis projects with similar mismatches in instruments and populations across studies.

To account for these differences, the instruments in WGSPD were aligned by modifying the GRM complexity function to exclude missing item pairs, that is, the complexity function was calculated for each pair of items that was administered in each pair of instruments. Instead of summing over all P items, the complexity function sums over all items p such that $p\in I_1$ and $p\in I_2$, where $I_g$ is the set of items administered to group g.

In this application, it would not be sensible or feasible to align the models using all item intercepts because the item intercepts differ in number and meaning across instruments. However, all instruments shared a common “anchor category” corresponding to the absence of the symptom. The item intercept parameter corresponding to the boundary between the absence of a symptom ($k_q=0)$ and the presence of that symptom ($k_q>0$) was present in all samples and had a common interpretation. Therefore, to align the models in WGSPD, only the first item intercept $d_0$ was included in the alignment complexity function. An alternative approach would have been to collapse all response categories indicating the presence of a symptom into a single category in instruments with polytomous rating formats; however, this would have reduced power, as each category boundary yields additional information on an individual’s relative standing on the latent trait (Samejima, 1968, 1997; Vispoel & Kim, 2014). Thus, in the interest of maximizing power for genetic analyses, we chose to include all response options in our analyses, but to align the models using only the first item intercept parameter.

With these modifications, the final alignment complexity function is given by

$$F_{\mathrm{GRM}}^{*}=\sum _{g_1<g_2}\sum _{p\in I_1,p\in I_2}{w}_{g_1,g_2}f(a_{p{g}_1,1}-a_{p{g}_2,1})+\sum _{g_1<g_2}\sum _{p\in I_1,p\in I_2}{w}_{g_1,g_2}f(d_{p0g_1,1}-d_{p0g_2,1}).$$

As described above, measurement noninvariance is only minimized for items that appear in each pair of instruments, and only the first measurement intercept is considered.

In the WGSPD analyses, described below, this modified alignment method was implemented using custom functions built in R (R Core Team, 2019). Item response models were estimated using the mirt package (Chalmers, 2012).

Plausible Value Imputation

When item response theory is used to estimate scores for individuals, such estimates may be MAP, EAP, ML, or other estimates, each with their own sets of strengths and weaknesses (Embretson & Reise, 2013; Reise & Revicki, 2014, pp. 309, 310). All such point estimates of latent trait level are inherently incomplete in that they are single-number summaries of the posterior distribution of the latent trait given the observed item responses; specifically, these point estimates do not represent measurement error. When using factor scores in regression analyses, these issues can lead to bias in the resulting regression coefficients (but, see Warm, 1989) and negatively biased standard error estimates for those regression coefficients as a result of treating posterior distributions as point estimates (Mislevy, Beatom, Kaplan, & Sheehan, 1992; Wu, 2005). Even when point estimates are augmented by estimates of the standard error of each measurement, the use of such standard errors assumes that the posterior distribution is normal, an assumption which will generally not be met in practice.

In contrast, plausible value imputation allows researchers to directly incorporate the posterior distributions of the latent trait estimates into analysis (Beatom & Gonzales, 1995; Mislevy, 1991). This involves a three-step process which is identical to that used to accommodate for missing values using multiple imputation (Rubin, 1976; see also Enders, 2010). In the first step, instead of estimating a single factor score for each participant, the analyst draws multiple plausible values from the posterior distribution of the latent variable given each individual’s observed item scores; each of the resulting imputations of the factor score consists of one such plausible value per participant. Next, these imputations are treated as complete data in estimating the statistics of interest, such as mean levels of the latent variable in subgroups or regression coefficients predicting the latent variable from external correlates. These estimates will differ across imputations, with this difference reflecting the variability in the estimates due to measurement error; note that this between-imputation variability is not accounted for if factor scores are treated as point estimates and used directly in subsequent analyses. In the final step, the statistical analysis results (means, variances, regression coefficients, etc.) are combined into pooled point estimates and unbiased estimates of sampling variability (e.g., standard errors) which properly account for between-imputation variability.

An important statistic in evaluating results derived from multiple imputation, whether using plausible values or otherwise, is the fraction of missing information (FMI), given by

$$\mathrm{FMI}=\frac{(1+1/m)v_B}{v_W+(1+1/m)v_B},$$

where v_B is between-imputation variability, estimated as the variance in estimates across imputations, and v_W is within-imputation variability, estimated as the averaged square standard error of the estimates across imputations, and m is the number of plausible values drawn for each observation. The fraction of missing information quantifies the proportion of sampling variability in the estimates (e.g., means, variances, regression coefficients) which is due to measurement error; values of FMI close to 1 indicate that most of the variability in these estimates is due to measurement error, while values of FMI close to 0 indicate that measurement error contributes little to estimation precision.

As a final statistical note, plausible value imputation yields estimates of means which are biased toward the prior used in their estimation, which here was an identical N(0, 1) prior for all cases regardless of age, sex, or diagnosis. Thus, all estimated means and correlations are biased toward 0, yielding smaller estimates of group differences than may truly exist in the samples (Mislevy, 1991; Wu, 2005). This bias can be removed by including these variables as covariates during estimation; however, this would not be appropriate in the current context, because CFA models which include covariates cannot be estimated with the alignment method (Asparouhov & Muthén, 2014), and extending alignment to accommodate group differences is outside the scope of this work.

Alignment of Psychiatric Symptoms in WGSPD

The overarching goal of the WGSPD Consortium (Sanders et al., 2017; Senthil, Dutka, Bingaman, & Lehner, 2017) is to aggregate data on psychiatric phenotypes in large groups of people with diagnosed psychiatric syndromes, healthy comparison groups, and their relatives, and to relate these phenotypes to genetic variation observed in whole genome sequence data derived from these individuals. A challenge for the WGSPD was that the participating projects were launched independently, and phenotyping was therefore done in different sites and countries by different investigators with different instruments across the participating studies. The overall scope of the WGSPD projects is shown in Table 1.

Table 1.

Overview of Projects, Instruments, and Sample Characteristics Comprising the Whole Genome Sequencing in Psychiatric Disorders (WGSPD) Consortium.

Project	Instrument	N	Females, n (%)	Age M±SD
Project 1: Whole Genome Sequencing for Schizophrenia and Bipolar Disorder in the GPC (Boehnke, McCarroll, Pato)
Los Angeles, New York City
SCZ	DI-PAD, GPC screener	7,758	2,361 (30.4%)	44.0 ±12.7
SA	DI-PAD, GPC screener	2,551	1,110 (43.5%)	43.8 ± 11.5
BP	DI-PAD, GPC screener	3,798	2,025 (53.3%)	42.8 ± 12.8
BP-I	DI-PAD, GPC screener	3,696	1,966 (53.2%)	42.8±12.8
BP-II	DI-PAD, GPC screener	102	59 (57.8%)	41.4±13.8
DEP	DI-PAD and/or GPC screener	812	476 (58.6%)	40.4 ± 14.7
OTHER (no diagnosis of BP, psychosis or DEP)	GPC screener	12,335	6,925 (56.1%)a	39.2 ± 15.2a
Project 3: Genomic strategies to identify high-impact psychiatric risk variants (Freimer, Palotie, Geschwind)
Dutch BP
SCZ	SCID, CASH	1	0 (0%)	33.0
SA	SCID, CASH	1	1 (100%)	36.0
BP	SCID, CASH	1,412	809 (57.3%)	49.3 ± 12.4
BP-I	SCID, CASH	1,384	789 (57.0%)	49.2±12.4
BP-II	SCID, CASH	26	20 (76.9%)	52.2±15.4
BP-NOS	SCID, CASH	2	0 (0%)	67.5±9.2
DEP	SCID, CASH, MINI	134	101 (75.4%)	51.7 ± 14.9
OTHER	SCID, CASH, MINI	103	56 (54.4%)	51.0 ± 15.9
CON	MINI	556	317 (57.0%)	53.6 ± 16.0
Dutch SCZ
SCZ	CASH	600	122 (20.3%)	27.7 ± 7.1a
SA	CASH	99	33 (33.3%)	27.8 ± 6.9
BP	CASH	16	6 (37.5%)	27.5 ± 7.7
BP-I	CASH	16	6 (37.5%)	27.5±7.7
DEP	CASH	1	1 (100%)	29.0
OTHER	CASH	101	23 (22.8%)	28.0 ± 8.0
Finland Schizophrenia Family Study
SCZ	SCID	246	85 (34.6%)	45.8 ± 9.3
SA	SCID	60	28 (46.7%)	44.9 ± 7.1
BP	SCID	22	13 (59.1%)	47.9 ±10.0
BP-I	SCID	17	10 (58.8%)	47.5±8.3
BP subtype unclear	SCID	5	3 (60%)	49.2±15.7
DEP	SCID	41	27 (65.9%)	50.2 ± 12.9
OTHER	SCID	55	26 (47.3%)	49.6 ± 11.6
CON	SCID	412	223 (54.1%)	53.1 ± 13.6
Psychosis in Finland
SCZ	SCID	39	22 (56.4%)	54.2 ± 12.0
SA	SCID	14	12 (85.7%)	49.6 ± 10.2
BP	SCID	20	8 (40.0%)	49.0 ± 13.0
BP-I	SCID	14	7 (50.0%)	50.6±14.6
BP-II	SCID	3	1 (33.3%)	41.3±1.5
BP-NOS	SCID	3	0 (0%)	49.0±11.4
DEP	SCID	159	89 (56.0%)	54.5 ± 12.2
OTHER	SCID	153	63 (41.2%)	52.9 ± 13.4
CON	SCID	157	96 (61.1%)	55.9 ± 15.0
Colombia/LA
BP	DIGS, MINI	87	54 (62.1%)	50.7 ± 15.2
BP-I	DIGS, MINI	87	54 (62.1%)	50.7±15.2
DEP	DIGS, MINI	35	26 (74.3%)	45.1 ± 16.8
OTHER	DIGS, MINI	172	89 (52.0%)a	40.4 ± 14.4
CON	DIGS, MINI	62	35 (56.5%)	65.1 ± 16.4
Costa Rica/LA
SZA	DIGS, MINI	4	2 (50.0%)	36.8 ± 14.2
BP	DIGS, MINI	65	37 (56.9%)	45.4 ± 15.0
BP-I	DIGS, MINI	53	28 (52.8%)	46.8±14.8
BP-II	DIGS, MINI	12	9 (75.0%)	39.5±15.0
DEP	DIGS, MINI	46	30 (65.2%)	45.4 ± 15.9
OTHER	DIGS, MINI	161	87 (54.4%)a	44.5 ± 14.2
CON	DIGS, MINI	69	31 (44.9%)	58.3 ± 16.4
Project 4: Pedigree-Based Whole Genome Sequencing of Affective and Psychotic Disorders (Glahn, Blangero, Gur)
Pennsylvania/EA
SCZ	DIGS	66	21 (31.8%)	44.7 ± 10.3
SA	DIGS	12	10 (83.3%)	44.5 ±18.9
BP	DIGS	7	3 (42.9%)	48.6 ± 13.3
BP-I	DIGS	2	1 (50%)	64.5±12.0
BP-II	DIGS	3	2 (66.7%)	41.0±9.8
BP-NOS	DIGS	2	0 (0%)	44.0±1.4
DEP	DIGS	129	89 (69.0%)	42.3 ± 14.5
OTHER	DIGS	176	60 (34.1%)	48.0 ±17.7
CON	DIGS	237	139 (58.6%)	47.0 ± 18.8
Texas/LA
SCZ	MINI	8	0 (0%)	45.3 ± 13.2
SA	MINI	15	10 (66.7%)	43.1 ± 15.6
BP	MINI	30	18 (60.0%)	36.1 ± 9.3
BP-I	MINI	16	9 (56.3%)	37.9±9.9
BP-II	MINI	14	9 (64.3%)	34.1±8.5
DEP	MINI	585	422 (72.1%)	43.1 ± 14.7
OTHER	MINI	549	204 (37.2%)	40.9 ± 15.4
CON	MINI	717	496 (69.2%)	42.3 ±16.9

Note. SCID = Structured Clinical Interview for the Diagnostic and Statistical Manual of Mental Disorders (DSM); CASH = Comprehensive Assessment of Symptoms and History; DIGS = Diagnostic Interview for Genetic Studies; MINI = Mini-International Neuropsychiatric Interview; Di-PAD = Diagnostic Interview for Psychotic and Affective Disorders; SCZ = schizophrenia; SA = schizoaffective disorder; BP = bipolar disorder; BP-I = bipolar disorder type I; BP-II = bipolar disorder type II; BP-NOS = bipolar disorder not otherwise specified; DEP = any depressive disorder. SCZ includes individuals with a diagnosis of schizophrenia and schizophreniform disorder, CON includes individuals with no diagnosis, OTHER includes individuals with a diagnosis other than SCZ, SA, BP, DEP, or with diagnosis unknown.

^aMissing data Project 1: Sex (n = 1); Age (n = 3), Missing data Project 3, Colombia: Sex (n = 1); Age (n = 2), Costa Rica: Sex (n = 1); Age (n = 3).

Data were aggregated across the major diagnostic instruments used in the WGSPD studies; the analyses presented here aimed to include all usable data from studies of adults with schizophrenia (SCZ), schizoaffective disorder (SA), bipolar disorder (BD), and depression (DEP), along with data from healthy comparison groups included in these studies (see Table 1). We did not include data from studies of autism spectrum disorders (Project 2) because the phenotypes measured in those studies have little overlap with those obtained in the studies of adult SCZ, SA, BD, and DEP samples. We aggregated item-level data from six different diagnostic instruments (DIPAD, SCID, CASH, DIGS, OPCRIT, and MINI) across 12 different studies in six different countries, representing ratings on a total of 38,551 individuals (see Table 1).

WGSPD Sites and Participants

The sites at which data were collected are described elsewhere (Sanders et al., 2017; Senthil et al., 2017). Project 1 is a case-control study principally targeting patients with SCZ, SA, and BD in two different regions: Los Angeles, where a large number of individuals with Hispanic/Latino ancestry were ascertained; and New York, where a large number of individuals with African American ancestry were ascertained. Project 3 consisted of case-control studies of SCZ, SA, and BD individuals, relatives and controls in Finland and the Netherlands, family and twin studies of BD in Finland, and family studies with BD from Costa Rica and Colombia. Project 4 consisted of family studies of SCZ, SA, BD, and DEP in Texas and Pennsylvania. The specific inclusion/exclusion criteria varied across studies, as detailed in Supplemental Material A. In general, patients were included based on satisfaction of diagnostic criteria using either the DSM-III-R, DSM-IV, or ICD diagnostic systems, which share most criteria for the diagnosis of these psychiatric disorders. The projects included mostly adults in the age range 18 to 80 years inclusive. Patients with other neurological diseases that might also be associated with idiopathic psychiatric syndromes were typically excluded. The family-based studies involved more complex ascertainment designs, with some (e.g., Finnish studies) involving national registry reviews, while others involved recruitment of family members in specific regions (e.g., Colombia, Costa Rica, Philadelphia, Texas).

Variables

A first step in harmonization was the construction of a master instrument comparison file (ICF) which identifies items that putatively match in content across different instruments. This involved examining 6,560 individual rating variables which we represented in a series of tables organized by overall diagnostic construct (Mood Disorder; Psychotic Disorder, Substance Use Disorder, Anxiety Disorder, Eating Disorder). Within each of these groups of ratings, we further identified three different kinds of ratings: Screeners, or items whose responses determine whether subsequent items will be administered; Symptoms, which are the specific symptoms of the disorder; and Specifiers, or ratings that qualify other symptom ratings or disorder characteristics, for example by indicating their duration or context. Supplemental Material B (available online) provides descriptions of all putatively harmonized items, along with the IRT parameters for both the prealigned and the postaligned data.

For each set of putatively matching variables, we created a master variable description (see Supplemental Material B). For example, in the Mood Disorders domain, the variable “Dysphoria ≥2 weeks” is found on the SCID-IV, SCID-I, MINI, and GPC screener; because there are different versions of the SCID-IV, SCID-I, and MINI across sites, languages and substudies, our data set includes 20 different rating variables which putatively measure this single symptom. Our first steps in variable comparison involved trained individuals fluent in the relevant languages determining which individual items would be treated as comparable (or approximately so) across studies.

Assumptions of Alignment in WGSPD

Table 1 shows the instrument(s) used in each study. Use of alignment given this extreme variation in methods requires a strong assumption of approximate measurement invariance. Specifically, we assume that, in all instruments containing a given set of symptom measurements, those symptoms have approximately the same probability of being detected in an individual with a given phenotype score. Because all symptom ratings came from similar diagnostic systems (i.e., DSM/ICD) we believe this assumption is likely satisfied in the aggregate, but this assumption may be violated to some degree for any given symptom and/or instrument combination, and due to the near-complete confounding of study site and instrument, it is not possible to conclusively assess this assumption in the data presented here. Such an assessment could be made by conducting a test-linking study in which all instruments were administered to the same sample (Dorans, Pommerich, & Holland, 2007; Kolen & Brennan, 2014).

Validation Approach and Hypotheses

We predicted that clinical diagnostic groups would differ in their average levels of symptomatology in each domain; specifically, we predicted that bipolar and schizoaffective individuals would have higher levels of mania and depression than those with other diagnoses or no diagnosis and that individuals with schizophrenia or schizoaffective disorder would have higher levels of psychotic symptoms (delusions, hallucinations) than those with other diagnoses or no diagnosis. These predictions reflect the diagnostic criteria and should be supported; the question for our validation study here was whether the aligned data would show more robust differences than prealigned scores, consistent with the hypothesis that the aligned scores are more reliable and valid. Predictions based on age and sex are less robust, but overall the literature suggests that women may have less severe psychotic symptoms, but more severe depressive symptoms. We also expected there to be age effects, primarily based on the differences in typical age of onset of the relevant samples (e.g., individuals with primary diagnoses of schizophrenia or schizoaffective disorder were expected to be younger than those with primary diagnoses of depression or bipolar disorder).

Method

Data Preparation

All instruments possess a branching structure typical of diagnostic instruments, such that if individuals do not satisfy certain symptom criteria (Screener symptoms), certain other symptoms or sets of symptoms will not be measured. This missing data structure results in incomplete two-way contingency tables between screener and screened items, leading to difficulties in estimating the necessary IRT models. To account for this structure, we used logical imputation (e.g., Kaufman, 1988) such that if a given screening criterion was not satisfied, all screened items were “filled in” with a rating corresponding to the absence of that symptom. When responses to screened symptom measurements were present despite not passing the screening criterion (most likely due to rater error; Brodey et al., 2016), the original responses were left intact and were not replaced by imputed responses. After imputation, each imputed variable was cross-tabulated with that same variable prior to imputation and examined as a quality control procedure.

After imputing missing values, we combined symptom ratings for identical symptoms across all time periods episodes, and/or instruments (for samples that were measured multiple times on different instruments) to establish a lifetime symptom presence and severity rating. This was done by taking the most severe symptom rating for each symptom across all time periods episodes assessed in each instrument, and/or instruments. We note briefly that some instruments, for example SCID and DIGS, assess symptoms according to specific episodes, while other instruments, for example, the MINI screener and OPCRIT items, directly assessed lifetime symptomatology, and thus, these measurements may not be exactly comparable if symptoms were experienced in time periods and/or episodes not assessed by the former class of instruments.

Factor Specification

As an extension of confirmatory factor analysis, alignment requires that a factor structure be specified in advanced of model estimation. In addition, each item is assumed to load on a single factor, requiring a fully independent cluster structure to be specified prior to alignment. We therefore chose an a priori factor structure based on commonly used DSM distinctions between psychiatric syndromes. The WGSPD data contained items measuring 15 distinguishable domains: depression, mania, hypomania, dysthymia, delusions, hallucinations, disorganized psychosis, negative psychotic symptoms, catatonia, disengagement, phobias, generalized anxiety disorder, panic disorder, obsessive–compulsive disorder, and posttraumatic stress disorder. Due to challenges with data sufficiency (too few items, too few responses per item), sparsity (domain measured in only one or two samples), or poor fit, we did not attempt alignment in 10 domains (catatonia, hypomania, dysthymia, disengagement, obsessive–compulsive disorder, phobias, panic disorder, PTSD, GAD, and negative symptoms). These domain exclusion steps left five domains: depression, mania, delusions, hallucinations, and disorganization (see Supplemental Material B).

Simulation Study

The modifications to the alignment method outlined in the “Method” section may differ in performance across contexts. Much like the alignment method itself, these modifications require a sufficient sample size in each study to estimate item parameters well. In addition, the performance of the alignment method with nonidentical item sets may vary by item, where items which are only represented in a small number of low-n groups may be estimated poorly, whereas items which are well represented across most groups will be estimated well. Rather than perform an exhaustive simulation study with a variety of test conditions, we opted to perform a small simulation study using the estimated parameters, sample sizes, item sets, and item properties based on the WGSPD data in order to examine how this modified alignment method performs within this specific context. Because a flexible tool like this modified alignment method can be used in a wide variety of contexts, we recommend that researchers interested in the method conduct a similar post hoc simulation study using the properties of their own data.

The median item parameters used for scoring each psychiatric domain in WGSPD (item slope parameters and first item threshold parameter) were treated as the corresponding true population item parameters for the simulation. These item parameters were used to construct population models corresponding to each trait-sample combination in the WGSPD data. To reproduce the item overlap patterns in WGSPD, the model for each trait in each sample consisted only of the items administered measuring that trait in that sample for which item parameters were estimated in the WGSPD analysis. This allowed us to examine in simulation the performance of the alignment method when items overlap, but are not identical, across studies.

To simulate the alignment of only the first threshold parameter used in the analysis above, items with more than two item categories in the WGSPD data were given additional threshold parameters in the population models in the simulation study, such that the items in the simulation study would have the same number of item categories as the corresponding items in WGSPD. To construct these additional threshold parameters, the median item intercept parameters were transformed into threshold parameters using the equations in Kamata and Bauer (2008, p. 140). From these threshold parameters, additional threshold parameters were added based on quantiles of a standard univariate normal distribution such that the corresponding item response probabilities would match those observed in the WGSPD data as closely as possible. These threshold parameters were then transformed into item intercept parameters for the simulation models, resulting in polytomous simulated items with similar response frequencies to those observed in the WGSPD data.

From these population models, we simulated item response data with sample sizes in each simulated sample equal to the sample sizes in the corresponding WGSPD sample. The underlying trait distributions for each simulated sample were univariate normal distributions with mean and variance equal to the estimated mean and variance from the alignment analyses in the WGSPD data. Such simulation resulted in a set of simulated samples, each with identical sample size, underlying trait distribution (as estimated by alignment) and item content (set of included items, numbers of response categories) to the corresponding WGSPD data set.

After simulating a set of data sets, we analyzed it using a simplified version of the mega-analysis performed on the WGSPD data. First, items with insufficient item responses were dropped from analysis and item response categories were collapsed as in the WGSPD analyses. Next, unidimensional item response models were fit to each simulated data set. Models that did not converge after 1,000 cycles of the expectation-maximization (EM) algorithm were dropped from subsequent analysis. Models that had too few degrees of freedom to obtain unique parameter estimates were also dropped; this occurred when too many variables were dropped from analysis due to insufficient item responses. The item discrimination parameters and first item intercept parameters for each item were extracted from all remaining models and were used to perform alignment as described above. After alignment, the median aligned item parameters across studies were recorded. The above process of simulation, data cleaning, estimation, and alignment was repeated 250 times.

Validation Using Plausible Value Imputation

Once the alignment models were estimated and the simulation study conducted, we examined the relationships between estimated factor scores on the five domains and three external correlates: age, sex, and diagnosis. To accurately account for differences in measurement precision across individuals, instruments, and studies, we employed plausible value imputation (Mislevy, 1991) to represent the uncertainty in estimates of the latent variables.

Results

Model Specification and Parameter Estimation

Several specific models from the five domains exhibited poor model fit and were excluded from alignment: two of the depression models (schizoaffective subsamples of Project 1, standardized root mean square residual [SRMSR] = .106; controls and family members in the Project 3 Dutch bipolar study, SRMSR = .154), and one of the mania models (schizophrenia subsample of Project 1; SRMSR = .115; see Table 1). Table 2 contains a summary of the analysis pipeline for these five domains, indicating how many participants were included, how many variables were included, and which domains were used in the alignment procedure.

Table 2.

Model Estimation, Alignment, and Scoring Statistics.

Data set	Data file n	Data file p	Data file domains	Domains with sufficient data	pE	nE	nS	Domains included in alignment	Domains excluded from alignment
CASH—Dutch Schizophrenia Unrelated Probands	855	47	DEP, MAN, DEL, HAL, ORG	DEP, MAN, DEL, HAL, ORG	43	817	810	DEP, MAN, DEL, HAL, ORG
DIGS & MINI Colombia/Costa Rica	704	54	DEP, MAN, DEL, HAL, ORG	DEP, MAN	23	701	701	DEP, MAN
DIGS Pennsylvania	669	55	DEP, MAN, DEL, HAL, ORG	DEP	13	628	628	DEP
GPC Screener & DI-PAD Pato—Bipolar	3694	51	DEP, MAN, DEL, HAL, ORG	DEP, MAN, DEL, HAL, ORG	49	3693	3688	DEP, MAN, DEL, HAL, ORG
GPC Screener & DI-PAD Pato—Control	12550	51	DEP, MAN, DEL, HAL, ORG	DEP	4	12498	12498	DEP
GPC Screener & DI-PAD Pato—Other Patients	876	51	DEP, MAN, DEL, HAL, ORG	DEP, MAN	27	801	801	DEP, MAN
GPC Screener & DI-PAD Pato—Schizophrenia	7791	51	DEP, MAN, DEL, HAL, ORG	DEP, MAN, DEL, HAL, ORG	51	7713	7710	DEP, DEL, HAL, ORG	MAN
GPC Screener & DI-PAD Pato—Schizoaffective	2551	51	DEP, MAN, DEL, HAL, ORG	DEP, MAN, DEL, HAL, ORG	51	2551	2551	MAN, DEL, HAL, ORG	DEP
MINI Dutch Controls & Family	1687	11	DEP, MAN, DEL, HAL	DEP	4	847	847		DEP
MINI Texas	1904	25	DEP, MAN, DEL, HAL, ORG	DEP	9	1904	1904	DEP
SCID & CASH Dutch Bipolar	1391	55	DEP, MAN, DEL, HAL, ORG	DEP, MAN, DEL, HAL, ORG	43	1360	1352	DEP, MAN, DEL, HAL, ORG
SCID Finnish Bipolar Family	140	29	DEP, MAN, DEL, HAL, ORG
SCID Finnish Bipolar Twin	64	23	DEP, MAN, DEL, HAL, ORG
SCID Finnish Controls	46	42	DEP, MAN, DEL, HAL, ORG
SCID Psychosis in Finland	544	42	DEP, MAN, DEL, HAL, ORG	DEP	11	542	542	DEP
SCID Finnish Schizophrenia	887	29	DEP, MAN, DEL, HAL, ORG	DEP, MAN, DEL, HAL	26	858	147	DEP, MAN, DEL, HAL

Note. SCID = Structured Clinical Interview for the Diagnostic and Statistical Manual of Mental Disorders (DSM); CASH = Comprehensive Assessment of Symptoms and History; DIGS = Diagnostic Interview for Genetic Studies; MINI = Mini-International Neuropsychiatric Interview; Di-PAD = Diagnostic Interview for Psychotic and Affective Disorders = n = Number of cases with any imputed symptom data; p = number of symptoms; p_E = number of symptoms used during estimation; n_E = number of cases used during estimation; n_S = number of scored cases; p_S = number of symptoms used for scoring. Symptoms with sufficient data (p_E) are defined as those with at least 50 symptomatic and at least 50 asymptomatic individuals in the imputed data, and only these symptoms were used for estimation. Data sets with at least four symptoms with sufficient data were included in estimation. All cases with ratings for symptoms with sufficient data (n_E; imputed data) are used for estimation. After estimation, models with standardized root mean square residual (SRMSR) < .1 were included in alignment. Data sets containing symptoms with estimated parameters from alignment (p_S) were used for scoring. Only cases with ratings for those symptoms were scored (n_S; nonimputed data).

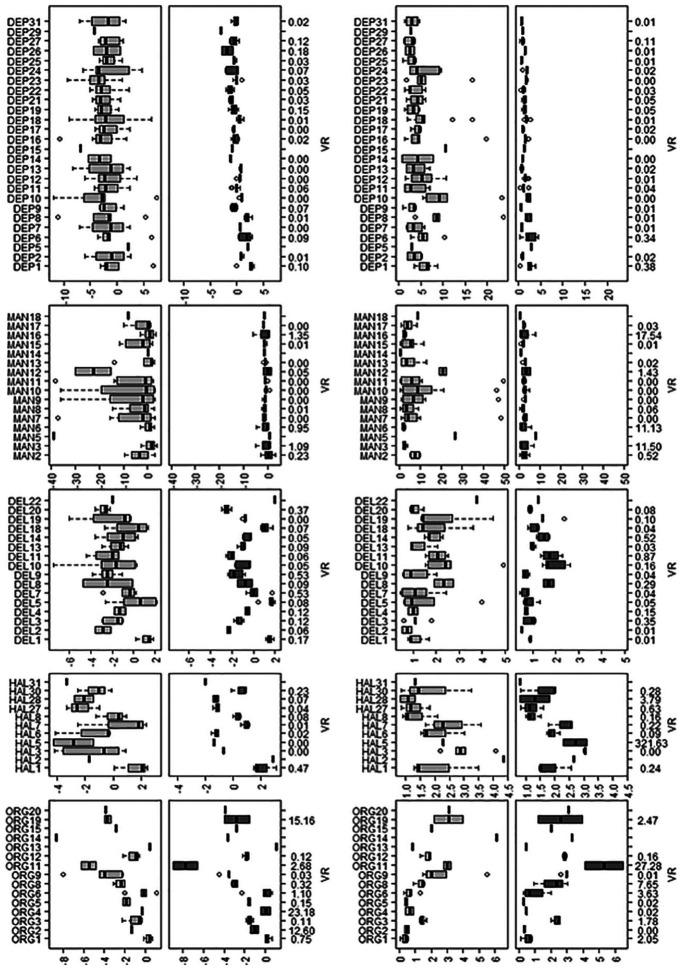
Parameter estimates (intercepts and slopes) for items in these the five domains are presented graphically in Figure 1 (for further details, also see Supplemental Material B, Tables SB1a-SB5b). Figure 1 also shows the variance ratio statistic VR for each item parameter; VR was calculated by dividing the variance in parameter estimates for each item parameter after alignment by the same quantity calculated before alignment. Values less than one indicate that parameters varied less after alignment than before alignment, with values close to 0 indicating that nearly all of the variance between item parameters in the configural model is explainable by group differences in latent trait distribution. In these data, VR was below 0.1 for most item parameters and below 1 for nearly all item parameters, indicating that a large majority of group differences in item parameters can be explained by group differences in the mean and/or variance of the latent trait.

Figure 1.

Distributions of parameter estimates in the configural and aligned models.

Note. First column: Intercept parameters in the configural model. Second column: Intercept parameters in the aligned model. Third column: Slope parameters in the configural model. Fourth column: Slope parameters in the aligned model. VR = variance ratio, calculated as the ratio of postalignment parameter variance to prealignment parameter variance.

Following alignment, two sets of factor scores were estimated to visually inspect the shift in distributions of factor scores due to alignment. The first set of factor scores (prealignment) was estimated using the estimated configural model parameters in each sample. The second set of factor scores (postalignment) was estimated using the transformed item parameters resulting from alignment. All factor scores were estimated using the EAP estimator.

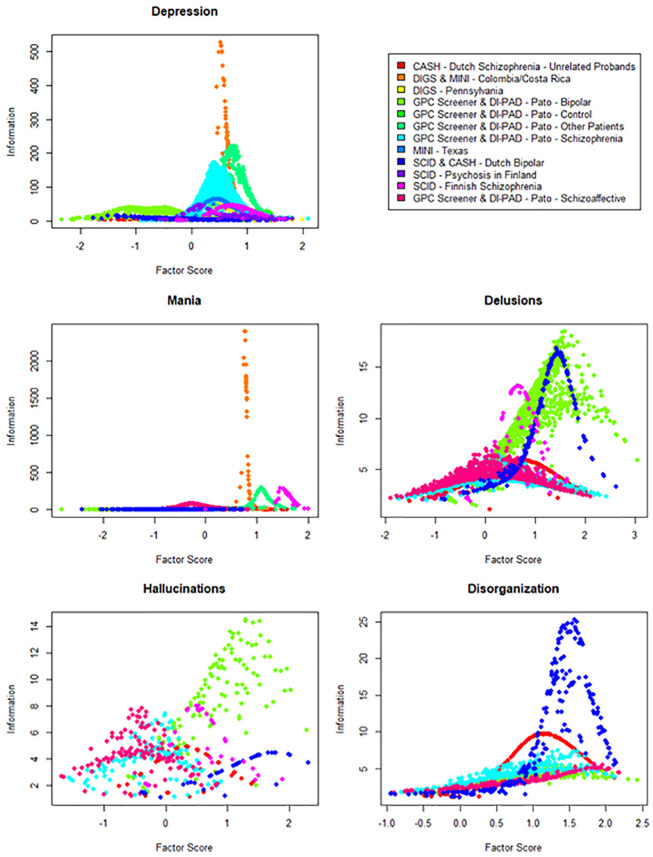
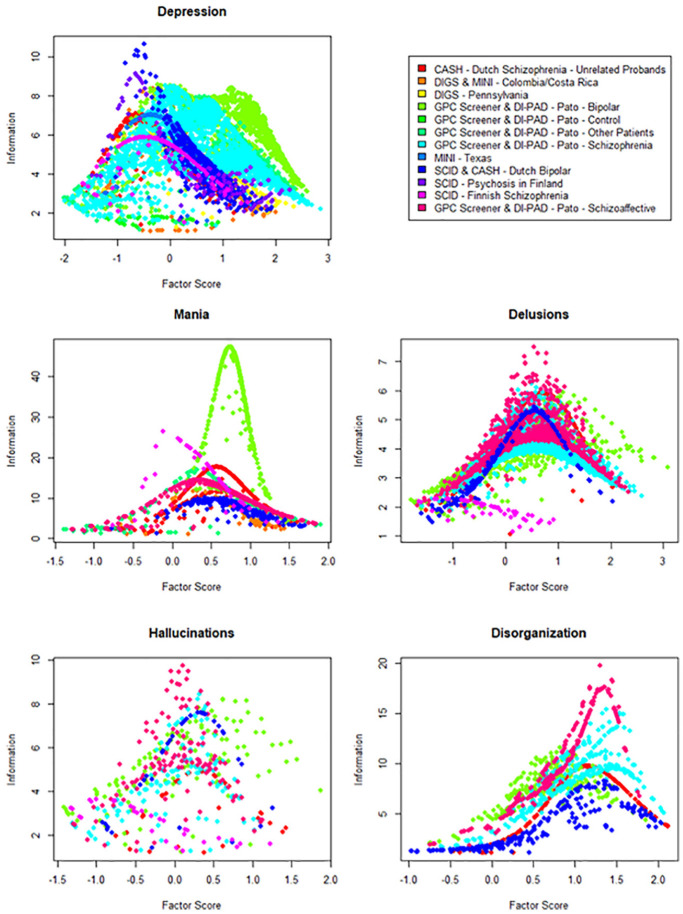
Figures 2 and 3 contain scatterplots of prealignment (Figure 2) and postalignment (Figure 3) factor score estimates in each domain, with factor scores estimated on the x-axis and estimated factor score information on the y-axis. In these scatterplots, the maximum information value for each factor score estimate can be treated, roughly speaking, as an empirical test information function for each sample. This comparison between the distributions of prealignment and postalignment test information functions across samples provides a visual illustration of the alignment procedure. When group differences in factor mean and variance are not accounted for (prealignment), each item is calibrated relative to the specific sample, and thus the item slope and intercept parameters are only interpretable relative to the sample in which those parameters were estimated. As such, the test information function is scaled and shifted according to the mean and variance of the estimation sample, yielding test information functions which vary widely across samples, as can be seen in Figures 2. In contrast, after alignment these parameters can be interpreted relative to the reference sample (first column in Supplemental Tables SB1a-SB5b), yielding test information functions in which the scaling and shifting produced by estimating the configural model have been reversed and the test functions coincide based on the overlapping subsets of harmonized items (Figure 3).

Figure 2.

Panel plot of factor score and information estimates for prealignment models.

Note. SCID = Structured Clinical Interview for the Diagnostic and Statistical Manual of Mental Disorder (DSM); CASH = Comprehensive Assessment of Symptoms and History; DIGS = Diagnostic Interview for Genetic Studies; MINI = Mini-International Neuropsychiatric Interview; Di-PAD = Diagnostic Interview for Psychotic and Affective Disorders. Top-left: Depression scores. Top-right: Legend. Center-left: Mania scores. Center-right: Delusions scores. Bottom-left: Hallucinations scores. Bottom-right: Disorganization scores. For factor score estimation, a prior of N(0, 1) was used.

Figure 3.

Panel plot of factor score and information estimates for postalignment models.

Note. SCID = Structured Clinical Interview for the Diagnostic and Statistical Manual of Mental Disorder (DSM); CASH = Comprehensive Assessment of Symptoms and History; DIGS = Diagnostic Interview for Genetic Studies; MINI = Mini-International Neuropsychiatric Interview; Di-PAD = Diagnostic Interview for Psychotic and Affective Disorders. Top-left: Depression scores. Top-right: Legend. Center-left: Mania scores. Center-right: Delusions scores. Bottom-left: Hallucinations scores. Bottom-right: Disorganization scores. For factor score estimation, a prior of N(0, 1) was used.

Simulation Results

Results of the simulation study are shown in Figure 4, which contains distributions of simulated parameter estimates for the five domains. All parameter estimates (item intercepts, item slopes) were within one empirical standard error of the population values for the simulation study, verifying that the alignment method is able to accurately recover the median item parameters across groups. For most symptoms, sampling distributions are very small and centered around the population values. Some symptoms, such as “Elevated, expansive, or irritable mood lasting ≥1 week” had much higher sampling distributions than others; this reflects the fact that these symptoms were only measured in a small number of studies (here, only the Finnish Schizophrenia family study).

Figure 4.

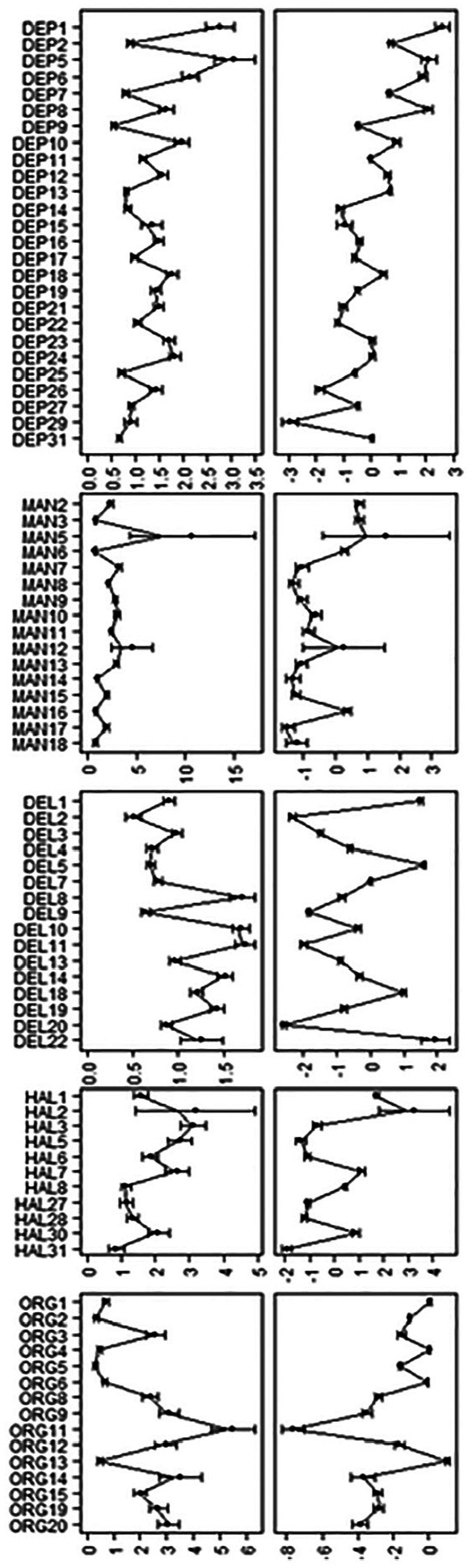
Parameter estimates from simulation study.

Note. Left column: Slope parameter. Right column: Intercept parameter. The center of the intervals indicates the mean item parameter across replications, and the width of the interval is 2 times the empirical standard error of the mean item parameter. The jagged line indicates the observed parameter estimates in the Whole Genome Sequencing in Psychiatric Disorders (WGSPD) data.

Validation Results

To compare the ability of pre- and postalignment measurement models to detect the hypothesized effects of diagnostic group, age and sex, we generated 100 imputations of plausible values for each symptom domain for all individuals whose data were used in estimation of the corresponding symptom domains (n_E in Table 2). From these plausible values, we estimated mean latent trait levels for the five domains of interest (depression, mania, delusions, hallucinations, disorganization) across levels of diagnosis and sex. Diagnostic groups were assigned following primary diagnosis: bipolar disorder, schizophrenia, schizoaffective disorder, depressive disorder, no diagnosis, or “other or unknown” which includes both cases without any of the other diagnoses and cases for which a diagnosis was not recorded or could not be identified based on available data. In addition to age and sex, we estimated the correlations between age and each of the latent traits measured.

Table 3 contains sample sizes, means, standard deviations, standard errors, and fraction of missing information statistics by diagnosis and sex for the five domains in the prealignment and postalignment models. Table 4 contains correlations of each domain’s plausible values with age in the prealignment and postalignment models.

Table 3.

Plausible Value Statistics for Five Domains of Interest by Diagnostic Group.

Domain	Score set	Statistic	BD	SA	SCZ	DEP	CON	OTH	Male	Female
Depression		n	5,423	207	8,754	1,809	1,660	13,708	16,242	15,322
	Prealignment	MEAN	0.12	0.69	0.04	1.33	−0.46	−0.13	−0.02	0.10
		SD	0.98	0.96	0.98	0.63	0.78	0.91	0.99	0.99
		SE	0.01	0.07	0.01	0.02	0.02	0.01	0.01	0.01
		FMI	.16	.18	.13	.21	.38	.44	.25	.31
	Postalignment	MEAN	1.34	0.50	−0.12	0.91	−1.16	−1.06	−0.32	−0.21
		SD	1.22	1.11	1.65	0.87	0.81	0.94	1.51	1.53
		SE	0.02	0.09	0.02	0.03	0.02	0.01	0.01	0.01
		FMI	.13	.19	.13	.34	.37	.35	.13	.16
Mania		n	5,365	2,701	695	190	141	995	5,127	4,957
	Prealignment	MEAN	0.09	0.09	−0.03	−0.23	−0.35	−0.23	0.04	0.04
		SD	1.02	1.00	0.99	0.86	0.83	0.91	1.01	0.99
		SE	0.02	0.02	0.04	0.08	0.09	0.04	0.02	0.02
		FMI	.28	.15	.20	.36	.38	.33	.20	.23
	Postalignment	MEAN	1.28	0.78	−0.17	−0.83	−0.55	−0.74	0.75	0.81
		SD	0.57	1.26	0.97	0.96	1.00	1.06	1.14	1.14
		SE	0.01	0.03	0.04	0.09	0.12	0.04	0.02	0.02
		FMI	.34	.14	.23	.40	.50	.36	.15	.19
Delusions		n	5,112	2,713	8,594	43	418	167	1,0242	6,803
	Prealignment	MEAN	0.05	0.03	0.04	−0.33	−0.64	−0.23	0.04	−0.01
		SD	0.97	0.99	1.00	0.81	0.69	0.94	0.99	0.98
		SE	0.02	0.02	0.01	0.15	0.05	0.08	0.01	0.01
		FMI	.24	.21	.23	.35	.53	.24	.22	.23
	Postalignment	MEAN	−0.80	0.28	0.18	−1.37	−1.66	−0.64	−0.06	−0.30
		SD	1.02	0.99	1.01	0.86	0.70	1.02	1.11	1.14
		SE	0.02	0.02	0.01	0.16	0.05	0.09	0.01	0.02
		FMI	.26	.22	.22	.35	.54	.28	.20	.21
Hallucinations		n	5,104	2,713	8,592	43	418	166	1,0235	6,799
	Prealignment	MEAN	0.02	0.03	0.05	−0.08	−0.60	−0.09	0.02	0.01
		SD	1.00	0.98	0.98	0.86	0.72	0.98	0.99	0.99
		SE	0.02	0.02	0.01	0.16	0.05	0.09	0.01	0.01
		FMI	.24	.23	.25	.34	.50	.29	.26	.28
	Postalignment	MEAN	−0.68	0.36	0.25	−0.95	−1.40	−0.40	0.02	−0.18
		SD	0.94	0.93	0.96	0.88	0.64	0.98	1.05	1.07
		SE	0.02	0.02	0.01	0.16	0.04	0.09	0.01	0.01
		FMI	.25	.29	.24	.31	.49	.26	.22	.19
Disorganization		n	5,081	2,651	8,344	1		108	9,793	6,393
	Prealignment	MEAN	0.00	0.00	0.00	−0.70		−0.16	0.02	−0.03
		SD	1.00	1.00	1.00			0.94	1.00	1.00
		SE	0.02	0.02	0.01			0.11	0.01	0.01
		FMI	.29	.29	.30			.32	.30	.25
	Postalignment	MEAN	−0.25	0.20	0.21	−0.73		−0.16	0.11	−0.01
		SD	0.90	0.82	0.94			0.93	0.93	0.93
		SE	0.02	0.02	0.01			0.11	0.01	0.01
		FMI	.33	.28	.29			.35	.27	.28

Note. n = Sample size; MEAN = imputed mean; SD = imputed standard deviation; SE = pooled standard error; FMI = fraction of missing information; BIP = bipolar I; SZA = schizoaffective disorder; SCZ = schizophrenia; DEP = major depression; CON = no diagnosis; OTH = other diagnosis or undiagnosed.

Table 4.

Plausible Value Correlations of Each Domain With Age in the Prealignment (Pre-) and Postalignment (Post-) Models.

Domain	Type	n	r	SE	FMI
Depression	Pre-	31,556	−.001	0.006	.232
	Post-	31,556	.048	0.006	.180
Mania	Pre-	10,079	−.038	0.012	.253
	Post-	10,079	−.024	0.011	.163
Delusions	Pre-	17,044	−.046	0.009	.235
	Post-	17,044	−.073	0.009	.228
Hallucinations	Pre-	17,033	−.015	0.009	.270
	Post-	17,033	−.041	0.009	.192
Disorganization	Pre-	16,185	−.007	0.009	.254
	Post-	16,185	−.013	0.009	.261

Note. n = sample size; r = imputed Pearson correlation coefficient; SE = pooled standard error; FMI = fraction of missing information.

Statistics obtained using prealignment models, in general, were less robust than the effects observed using the aligned data. Gender differences and correlations of scores with age are also small when prealignment models are used, and sometimes in directions opposite theoretical expectations. This is not unexpected, as the configural model can be used to scale people within each sample but cannot be used to do so across samples. One notable exception is that individuals with depressive disorders score higher on depression than controls; this is because no sample consists of only individuals with depressive disorders, and therefore individuals with these disorders tend to score higher on depression than others within those samples, leading to high factor score estimates when the configural model is used.

In contrast, when postalignment models are used for validation analyses, expected group differences are large and robust. In these models, individuals with mood disorders (bipolar, schizoaffective, depression) score higher on mood symptom domains than controls and individuals with psychotic disorders (schizophrenic, schizoaffective) score higher on psychosis symptom domains than controls. The effects of gender are in line with predictions, specifically men showed more severe delusions, while women showed more severe depressive symptoms. Age was indeed positively associated with depressive and bipolar symptoms, and negatively correlated with both delusions and hallucinations.

The estimated fraction of missing information (FMI) varied by domain and analysis and was generally lowest for analyses based on postalignment models. The minimum FMI (.11) was obtained for the mean depression level for schizophrenic individuals in the postalignment results, while the highest FMI (.49) was obtained for the mean disorganization level in depressed individuals in the extended alignment results, illustrating the range of FMI values observed.

Discussion

There is a growing need for measurement models that can be applied to mega-analyses as recent revolutions in genomics, informatics, and ubiquitous sensing technologies have created opportunities to aggregate individual participant data on an unprecedented scale. These models need to be flexible enough to accommodate cross-study differences in data structure that may arise from variation across environments, participants, and measurement methods. The usual tools for assessing and correcting for measurement invariance are cumbersome and may be ineffective. In this study, we defined and applied a method for conducting multiple-group item response modeling while accommodating two types of difference in data structure, item set and response category structure, modifying the existing alignment method (Muthén & Asparouhov, 2014). We applied the new method to a highly complex and sparse data structure consisting of psychiatric phenotype measures in the WGSPD Consortium, finding that much of the variance in parameter estimates across samples could be explained by group differences in the mean and variance of the latent variables. Parameter recovery for the modified version of the alignment method was validated using a simulation study based on the real-data results from WGSPD.

We also found that models resulting from the alignment procedure (postalignment) yielded estimates of diagnostic group differences, sex differences, and correlations with age that were more consistent with prior literature and expectations based on our understanding of how the samples were ascertained, compared with simply aggregating scores from the configural model estimated within each data set (prealignment scores), demonstrating the increased validity afforded by the new method. The latter approach, aggregating results from the configural model estimated separately within each sample, has previously been used to scale individuals on psychiatric symptom dimensions, and so far, has reflected the state of the art in psychiatric genetics research (Ruderfer et al., 2014). As the prealignment results demonstrate, this approach may misestimate between-group differences, and fail to fully measure between-sample variations that may be important for subsequent analyses. The advantages of alignment can be observed best by comparing effect sizes for key measures across these methods. For example, the effect size (which can be estimated simply by inspecting the differences between the mean values for each domain, given these scores have SD of approximately 1) for the group difference between the depressed group and the other/no diagnosis group was 1.49 in the prealigned data but 2.02 in the aligned data. The difference was even more striking for the difference in the bipolar disorder group, where prealignment scores yielded an effect size of only 0.29, while after alignment the difference was 2.36. These differences in the magnitude of effect would be expected to have a substantive impact on validity in other contexts, for example, in detecting genetic associations. Despite the limitations of the current approach, discussed below, we were able to generate more robust group differences between major clinical subgroups by accounting for cross-study differences in modeling approach (postalignment). Researchers interested in generating phenotype scores for use in subsequent analyses (e.g., genetic analysis) may benefit from explicitly accounting for group differences in their measurement models, rather than using the configural model, and thus, implicitly assuming invariance in the distribution of the latent variables across groups.

To assess the loss of precision resulting from the missing latent trait values, we calculated the (FMI) for all estimates based on plausible values. These FMI values are of critical importance to secondary data analysts interested in using these models for analyses such as genome-wide association studies (GWAS) because they inform the researcher about the loss of power that results from having measurements that are less than perfectly reliable. Sample size requirements for such analyses need to be adjusted to account for this missing information.

In this study, as in much of the multiple-group factor analysis literature, we were forced to make an assumption about the invariance of measurement parameters (item slopes and intercepts) and structural parameters (factor means and variances) across groups. In using the alignment method, we assumed that the entire set of measurement parameters was approximately invariant, that is, it was assumed that most parameters were very similar in magnitude across groups, but no strict equality constraints were placed on parameter estimates across groups, and alignment allows for some parameters to exhibit differential item functioning (DIF). Without knowing the true values of the latent variable in all groups, it is not possible to conclusively test this assumption of approximate measurement invariance. Instead, we calculated the ratio of the variance in parameter estimates across groups before and after alignment (VR), using this value as an estimate of how much of the group difference in model parameters in the configural model (i.e., assuming equal factor mean and variance across all groups) can be explained by group differences in factor means and variances, estimated through alignment. Most VR values were close to 0, indicating that the alignment method did well in explaining systematic group differences in IRT model parameters. The high degree to which alignment was able to explain group differences in item parameters is consistent with the assumption of approximate measurement invariance.

The measurement models used within each sample were incomplete in that they did not account for potential residual relationships between items after controlling for the latent variable (Cai, Yang, & Hansen, 2011; Gibbons et al., 2007; Marsh, 1989) and they did not account for the varying and often complicated sampling methods used in the component studies listed in Table 1 (Adams, Wilson, & Wu, 1997; Fragoso, de Andrade, & Soler, 2014; Pastor, 2003). In order to do so, the alignment method would need to be validated, both theoretically and empirically, in these contexts. The effectiveness of parameter recovery and the stability of the resulting models is contingent upon the structure of the data in each mega-analysis (sampling methods, item content, item overlap). When these structures are not determined by the data analyst, as in consortium-type studies where data were collected prior to the development of a cross-study analysis plan, we recommend validating extensions of the alignment method using a real-data-based simulation study similar to the one employed here.

Modeling issues aside, the largest limitation of this work is the severe sparsity of the data matrices analyzed within each sample. By using logical imputation to reduce this sparsity for estimation, we were able to estimate IRT models within each sample, and these exhibited reasonable fit to the data and yielded parameter estimates which, after alignment, were within reasonable ranges. Without having observed the item responses which were imputed logically, we have no way of knowing whether the resulting models were affected by this imputation; however, without it we could not have performed this estimation at all. In order to accurately represent the amount of information in the observed data, we used nonimputed data for scoring and validity analyses, resulting in very little information for large portions of the sample (Figures 2 and 3) and high fractions of missing information for estimated sample statistics (Tables 3 and 4).

The problems posed by sparsity of measurement in these data resulted from the fact that the consortium was assembled after the individual studies were already underway. The analysis strategy developed here aimed to maximize the information yield given the available data. This research illustrates the challenges involved in post hoc cross-study item-level IRT analyses given only partially overlapping item sets, different category structures, and high percentages of missing data, and it is hoped that some of the approaches taken here may be useful to others. These results further suggest design features that might facilitate multisite mega-analyses. Ideally, the field could develop stronger consensus on shared instrumentation and scoring methods that could be used across studies (Curran & Hussong, 2009; Hofer & Piccinin, 2009), but it is recognized that different investigators have unique interests and loyalties to existing instruments with which they have long and deep experience. An alternative is to develop a “Rosetta Stone” strategy, whereby certain core items are selected as common data elements, that can be shared across studies, while still permitting diverse additional questions to be asked. This research contributes to that goal by providing item-level analysis results that span many clinical instruments. These results can be used to design or improve upon instruments currently used to measure psychopathology constructs. Future measurement tools could be developed that would be more efficient, informative, well standardized, and compatible with existing measures. The results presented here already provide item parameter estimates for several of the most widely assessed domains in psychopathology research. These estimates may provide a useful starting point for future multisite international efforts by identifying those items most likely to be useful across sites and diagnostic groups, and particularly, in determining how many items are necessary to provide desired levels of precision in estimating the levels of each construct. The results may further inform efforts to develop evidence-based screening tools, to avoid the risks of “logical imputation” that may fail to adequately define construct levels because informative questions were never asked.

Past research on cross-study item-level measurement has historically been limited to cases in which the same instrument was administered to all participants in all included studies (e.g., Hussong et al., 2007; Hussong, Huang, Curran, Chassin, & Zucker, 2010), although recent work has attempted to account for nonidentical item sets (e.g., Gu & Gutman, 2017; Kaplan & McCarty, 2013; Marcoulides & Grimm, 2017; McArdle et al., 2009). In designs with identical item sets across groups or time points, a multiple-group item response theory model can accommodate differences in item properties and sample characteristics into a single estimated model which spans both studies. Using concepts from the test-linking literature, other studies have performed cross-study measurement when at least some participants were given all the instruments used; see Curran & Hussong (2009) for an example of this work. In the educational assessment literature, it has become increasingly common to administer a subset of items from a larger item pool to each participant (e.g., in balanced incomplete block designs; Beatom & Gonzales, 1995; Van der Linden, Veldkamp, & Carlson, 2004); such designs can be accommodated straightforwardly by most IRT estimators which are robust to the resulting missing data structures. Such approaches would be an appealing alternative to the current approach for multisite research; specifically, if a set of “common data elements” comprising a core group of “linking” items could be agreed upon. Such an item set could even be based on the parameter estimates provided by our study or those by others. This could be complemented by administration of diverse additional item content, enabling different investigators to pursue additional hypotheses while facilitating mega-analyses. Of course, the practicality of this approach may be limited as the number of core items may already exceed the pragmatics of large-scale studies.

Ultimately, we view this work as proof-of-concept for an inclusive measurement modeling strategy that incorporates as much data as possible from highly disparate samples and study designs into a single harmonized measurement model. The beauty of extending alignment as demonstrated here resides in the simplicity of the statistical procedures. Each model is estimated only within its own sample, avoiding the complications involved in identifying a well-fitting measurement model that spans a large number of disparate groups in the face of daunting amounts of missing data. Ideally, such procedures would be unnecessary; in an ideal study, everyone would be measured with one instrument and one could simply conduct a multiple-group item factor analysis or, if the number of groups is large, the alignment method as it currently exists in the literature. For post hoc consortium-style mega-analyses such as these, the approach of modifying the alignment method to account for cross-study differences may offer a valuable tool that enables scalable model-based measurement in this complex and challenging context.