Tree-based Machine Learning Methods for Survey Research

Abstract

Predictive modeling methods from the field of machine learning have become a popular tool across various disciplines for exploring and analyzing diverse data. These methods often do not require specific prior knowledge about the functional form of the relationship under study and are able to adapt to complex non-linear and non-additive interrelations between the outcome and its predictors while focusing specifically on prediction performance. This modeling perspective is beginning to be adopted by survey researchers in order to adjust or improve various aspects of data collection and/or survey management. To facilitate this strand of research, this paper (1) provides an introduction to prominent tree-based machine learning methods, (2) reviews and discusses previous and (potential) prospective applications of tree-based supervised learning in survey research, and (3) exemplifies the usage of these techniques in the context of modeling and predicting nonresponse in panel surveys.

1. Introduction

Investigating and explaining error sources in surveys often involves applying some form of (parametric) regression method in the research process. In many situations, such models are used to achieve an overarching goal, such as estimating contact and response propensities (e.g. Schonlau et al. 2009, Bethlehem et al. 2011), constructing weights (Brick 2013), or implementing targeted designs (e.g. Peytchev et al. 2010, Calderwood et al. 2012). These tasks require that the underlying model represents a proper approximation of the true function f(x) (e.g. the relations between nonresponse and all relevant covariates predicting nonresponse). In the context of parametric regression, this implies careful model specification. However, prior knowledge about the correct functional form might not always be available, or estimating the potentially complex function in a parametric framework might be computationally infeasible (e.g. perfect separation in a logit model).

Concurrently, advances in the field of machine learning created an array of flexible modeling techniques that often do not require prior knowledge about the functional form of the relationship and are able to adapt to complex non-linear and non-additive interrelations between outcome and covariates. These methods therefore represent interesting alternatives to parametric regression and may be used to substitute any given regression model when a more flexible representation of the relationship is needed (Berk 2006).

In a survey context, various sources of errors may be thought of as constituting prediction problems which can be used to develop targeted interventions based on learned experience (i.e. prediction models). Examples include predicting unit nonresponse in cross-sectional studies or panel surveys or predicting break-offs and straightlining in a web survey context. Machine learning techniques facilitate to tackle such research problems due to their inherent focus on prediction performance. The prediction setting requires to build models that generalize well to new data, a task that is handled in supervised learning by introducing some regularization to model flexibility (e.g. by controlling the depth of a decision tree). We will come back to this when describing the methods.

The methodology and potential of machine learning has been discussed in the context of economics (Varian 2014, Mullainathan and Spiess 2017), psychology (Strobl et al. 2009), political science (Jones and Linder 2015, Hainmueller and Hazlett 2014), within social science (Ghani and Schierholz 2017, Kopf et al. 2013), and survey research (Buskirk et al. 2018).

The present study extends the introductory work of Buskirk et al. (2018) by focusing on the usage of tree-based methods as both exploratory modeling and prediction tools in a panel data setting. Tree-based methods represent an important branch of supervised learning that offers a variety of flexible methods which build on a common framework. In this context, we discuss tree building algorithms such as Classification And Regression Trees (CART), Conditional Inference Trees (CTREE), and model-based recursive partitioning (MOB) and ensemble methods such as random forests, boosting and Bayesian additive regression trees (BART). CTREE, MOB and BART represent relatively recent approaches that have rarely been considered in a survey context (see Klausch 2017, Kern 2017), but have valuable characteristics for the types of questions asked by survey methodologists.

Supervised learning is particularly beneficial for large data analysis, such as in the context of panel data. From a modeling perspective, the wealth of information that accumulates over time and involves different types of observations (e.g. individuals, households, regions, interviewers) intensifies specification issues when an accurate representation of f(x), e.g. for deriving longitudinal weights, is sought. Furthermore, longitudinal data collection naturally connects with the idea of adaptive designs (Groves and Heeringa 2006, Lynn 2017), e.g. by learning about dropout patterns from previous waves in order to derive interventions for new waves of the panel.

Following this argument, the present study illustrates the usage of machine learning for modeling and predicting unit nonresponse in the German Socio-Economic Panel study (GSOEP). GSOEP consists of a diverse pool of data from different subsamples, collected using different modes over time and also involves information from various sources. We show that feeding this information to flexible modeling techniques allows researchers to gather insights that would likely be overlooked by traditional regression modeling. Furthermore, preliminary findings indicate that tree-based ensemble methods such as random forests and boosting markedly outperform logistic regression when focusing on nonresponse prediction. Variable importance and partial dependence plots are used to investigate this result.

This paper is structured as follows: Section 2 introduces and compares and contrasts the various supervised learning methods. Section 3 reviews applications of machine learning methods in survey research, and discusses some potential additional applications. The application of these methods to panel nonresponse follows in section 4. We close with a discussion and outlook in section 5.

2. Supervised Learning Methods

In this paper we focus on techniques from the field of supervised learning, which aim to build prediction models for some outcome of interest, given a set of predictor variables (features). The relationship between outcome and features is learned with training data (predictors and outcome available), such that the derived model can be applied to predict the outcome for new, previously unseen observations (test data). This task requires to find a model that is flexible enough to closely approximate the true function between the outcome and its predictors while also being robust to (changes in) the particular training set being used (bias-variance trade-off; Hastie et al. 2009). Against this background, the machine learning pipeline often involves finding the optimal model setup for a given method (model tuning) and/or selecting the best model among different learning methods, both with respect to expected performance in new data. Within a given training set, out-of-sample prediction performance can e.g. be estimated by cross-validation, which (repeatedly) uses different training data pieces for model building and evaluation (for an overview, see Ghani and Schierholz 2017, Kuhn and Johnson 2013).

While a wide range of supervised learning methods can be used in the prediction setting, tree-based approaches might be particularly useful in a (longitudinal) survey research context: Tree-based methods offer a variety of flexible tools that are (a) able to handle diverse data without the need of extensive pre-processing and for which (b) fast computational implementations are often available. Using trees furthermore precludes the necessity to pre-select predictor variables from a set of potential features since the informative variables can be detected by the tree building algorithm. Tree-based methods, however, differ in terms of the prediction performance they may achieve and the effort that is typically needed for model tuning, as outlined in the following sections.

2.1.1. CART and CTREE

While decision trees can be grown in different ways (see Loh 2014), we begin with focusing on one prominent algorithm – Classification And Regression Trees (CART; Breiman et al. 1984), and on one more recent tree building approach – Conditional Inference Trees (CTREE; Hothorn et al. 2006) – to outline the main ideas of tree-based learning.¹ In the CART context, the predictive model is built by partitioning the predictor space (the set of values of all predictors) into a set of regions or nodes, which are sought to be homogeneous with respect to the outcome. In order to find these regions, given training data (x_i, y_i) for i = 1, 2, . . . , n observations with x_i being a vector of j = 1, 2, . . . , p predictors and y_i representing the outcome, the tree growing process starts with all observations (representing the root node) and searches for the variable j and cut point c, i.e. the best split, which lead to the two most homogeneous subregions. More specific, a split s is sought which leads to the largest decrease in node impurity I when splitting a node τ into two child nodes τ_L and τ_R. For continuous outcomes (regression trees), the splitting criterion

$$\Delta I_{SS}(s,\tau )=I_{SS}(\tau )-I_{SS}\left({\tau }_L\right)-I_{SS}\left({\tau }_R\right)$$ (1)

simply boils down to investigating decreases in residual sums of squares, since in this case node impurity can be defined by summing over the squared deviations from the mean in a given node

$$I_{SS}(\tau )=\sum _{i\in \tau }{\left(y_i-{\overline{y}}_{\tau }\right)}^2.$$ (2)

Thus, the splitting objective (argmax_s ΔI_SS(s, τ)) seeks to find regions with low within but high between variance over all potential split points.

For categorical outcomes (classification trees), node impurity can be measured with e.g. the Gini index in order to determine the heterogeneity of a group with respect to their composition of class labels. For a categorical outcome with classes k = 1, 2, . . . , K, this measure is given by

$$I_{Gini}(\tau )=\sum _{k=1}^K{\widehat{p}}_{k_{\tau }}\left(1-{\widehat{p}}_{k_{\tau }}\right)$$ (3)

with ${\widehat{p}}_{k_{\tau }}$ being the proportion of observations from class k in node τ. On this basis, the reduction in overall impurity due to a split can be assessed by

$$\Delta I_{Gini}(s,\tau )=I_{Gini}(\tau )-p\left({\tau }_L\right)I_{Gini}\left({\tau }_L\right)-p\left({\tau }_R\right)I_{Gini}\left({\tau }_R\right).$$ (4)

Here, p(τ_L) and p(τ_R) represent the probability of falling into the left and right nodes, respectively. As with continuous outcomes, the variable and cut point which lead to the most homogeneous subregions – and thereby to the largest reduction in overall impurity – are chosen for splitting.

Equipped with a way to determine the best split, the CART algorithm takes a recursive approach to growing a tree (see Algorithm 1). Once the first split is found, the resulting subregions are themselves considered for splitting, i.e. the splitting process is repeated given the results of the previous step. This leads to a top-down tree structure with a potentially large number of fine-grained regions as terminal nodes. Since very large trees can overfit the training data, stopping criteria such as a minimum number of cases per node are introduced in order to limit tree size. In addition, cost-complexity pruning can be used with which the best subtree can be found by cutting back tree branches. Subtree performance is hereby typically estimated via cross-validation while treating tree complexity as a tuning parameter.

While finding an optimal CART tree for prediction involves iterative pruning procedures, Hothorn et al. (2006) proposed a tree growing framework which utilizes statistical tests to determine the best tree size (Conditional Inference Trees; CTREE). In this context, the global null hypothesis of independence between the outcome and any of the predictor variables is tested as a first step via permutation tests. The result of this test is then used to determine whether any (further) splitting should be performed, i.e. the associated p-value is used as a stopping criterion. Given a positive test decision, the predictor variable with the strongest association with the outcome (smallest p-value of the partial null hypotheses tests) is selected and a variant of the permutation test statistic is used to determine the best split point in the next step. As this procedure separates the variable selection and split point decision, CTREE overcomes a major limitation of CART, which is a selection bias towards predictors with many potential split points.

After the – CART or CTREE – partitioning process, a decision tree can be considered to consist of a set of m = 1, 2, . . . , M terminal nodes which can be used for predicting the outcome for new data. For this task, a constant γ_m is used for each new observation which falls into τ_m, such that a tree $\mathcal{T}$ with parameters Θ = {τ_m, γ_m} can be expressed as

$$\mathcal{T}(x;\mathrm{\Theta })=\sum _{m=1}^M{\gamma }_{m}I\left(x\in {\tau }_m\right).$$ (5)

For regression trees, γ_m simply represents the mean of the outcome variable for all training observations in τ_m. With categorical outcomes, the majority class in τ_m is used for prediction.

The prediction surface of decision trees as outlined here has a block-wise structure with regions or boxes of constant predictions for different sections of the predictor space. As a result of the recursive partitioning process, this structure can approximate complex interactions and non-linearities, which may be detected with a simple visual representation of the tree result (for modest tree sizes). Decision trees can therefore be used as a data-driven tool for exploring distinct subgroups that can be defined by complex constellations of the predictor set. In the survey context, such groups might represent observations that have a high risk of dropping out of a panel study (see section 4.2).

Algorithm 1:

Tree growing process

2.1.2. Model-based Recursive Partitioning

The tree-building concept of splitting the data into smaller and more homogeneous pieces can also be utilized in a different setting. While decision trees such as CART or CTREE consist of a set of nodes with constant values for prediction, model-based recursive partitioning (MOB) combines parametric regression with the tree idea (Zeileis et al. 2008). In general, this approach first fits a parametric regression model with all available observations (root node) and then passes this model to a partitioning algorithm that considers whether a single model is suitable for all observations and – if this is not the case – subsequently fits distinct models for different subgroups via recursive partitioning to account for heterogeneous effects across these groups.

In order to grow models on a tree, a set of partitioning variables z_i has to be selected to provide potential split points for partitioning e.g. a pre-specified generalized linear model (whereas some overlap with x_i is allowed). The decision on whether to estimate distinct models for different sections of the data is based on generalized M-fluctuation tests (Zeileis and Hornik 2007), which are used to detect parameter instabilities in the current model given the partitioning variables. More precisely, consider an objective function Ψ (e.g. error sum of squares) and a vector of parameter estimates

$$\widehat{\theta }=\underset{\theta }{\mathrm{argmin}}\sum _{i=1}^n\mathrm{\Psi }\left(y_i,x_i,\theta \right).$$ (6)

The parameter instability tests are based on the individual contributions to the partial derivatives of the objective function

$$\psi \left(y_i,x_i,\theta \right)=\frac{\partial \mathrm{\Psi }\left(y_i,x_i,\theta \right)}{\partial \theta }$$ (7)

evaluated at the current estimates, i.e. ${\widehat{\psi }}_i=\psi \left(y_i,x_i,\widehat{\theta }\right)$. Potential instabilities are detected by ordering these contributions (e.g.${\widehat{\psi }}_i=x_i\left(y_i-x_i^{\prime }\widehat{\theta }\right)$ for OLS) according to a given partitioning variable, whereas systematic deviations from their mean zero would indicate a structural change in the inspected relationship. The instability test evaluates the strength of the change and eventually rejects the null hypothesis of a constant effect of a given covariate in the case of considerable deviations.

If parameter instabilities are detected, the associated partitioning variable is used to split the current model into two locally optimal submodels. This involves searching for the best subgroup partition over the range of potential cutpoints of the selected partitioning variable. Having parametric models in the left (τ_L) and right (τ_R) daughter nodes, optimality for the cutpoint decision can be defined by comparing the sum of the segmented objective function

$$\sum _{i\in {\tau }_L}\mathrm{\Psi }\left(y_i,x_i,{\widehat{\theta }}^{(L)}\right)+\sum _{i\in {\tau }_R}\mathrm{\Psi }\left(y_i,x_i,{\widehat{\theta }}^{(R)}\right)$$ (8)

over all potential cutpoints of the partitioning variable.

After the initial model in the root node has been tested for parameter instabilities and eventually split into two submodels by searching for the cutpoint that minimizes (8), the coefficients of the resulting models in both tree nodes might be subject to further instabilities. Therefore, M-fluctuation tests can be carried out for both models, respectively, in order to determine whether a tree with two nodes is sufficient. Model-based recursive partitioning therefore adapts the repeated splitting approach of decision trees and continues the partitioning process within each node (see Algorithm 2). As with decision trees, stopping criteria have to be defined in order to control tree complexity. A natural criterion is to stop splitting when no significant parameter instabilities are found in a given node, although additional rules can be defined as well (e.g. requiring a minimum number of cases per node).²

In a prediction setting, MOB can be used to predict the outcome of interest with a set of local regression models or to predict node membership, i.e. identifying which model is appropriate for a new observation. In a survey research context, the latter usage could be useful to e.g. identify observations for which a particularly strong effect of a certain survey management variable in a nonresponse model is expected. An additional feature of MOB is that the partitioning process can also be informative from a model specification perspective (Kopf et al. 2013). Since the split decision is based on parameter instabilities, a model-based tree with at least one split suggests that the initial model in the root node is not adequate for the entire sample. MOB therefore allows to find interactions in the data that can be used to identify subgroups that are distinct in terms of the specified relationships. In a sense, this could be viewed as exploratory modeling based on a theory-guided initial guess.

Algorithm 2:

Recursive partitioning with GLMs

2.2. Random Forests

The aforementioned methods have in common that their splitting process results in a single tree. Given a research objective which focuses on prediction performance, this might not be a desirable property. Besides approximating the relationship between features and outcome with a (non-smooth) step function, decision trees are vulnerable to small changes in the training data given the hierarchical nature of the tree growing process (i.e., a change in one split point affects the remaining splits down the tree). As a result, decision trees are often thought of as being instable high-variance procedures that, built on a given training data set, typically do not generalize well to new test data. This limitation is addressed by ensemble methods.

Random forests (Breiman 2001) represent a prominent ensemble approach that builds on the CART algorithm for growing individual trees.³ Instead of building only one decision tree for prediction, the guiding idea is to combine many trees into a robust ensemble. In order to grow multiple trees, random forests utilize the bagging approach (Breiman 1996) by drawing a large number of bootstrap samples from the training data, i.e. generating samples of the same size as the training data by sampling with replacement. The sampled data is then handed over to a CART-like algorithm in order to grow a decision tree on each bootstrap sample, respectively. Since these bootstrap samples contain different portions of the original data, the corresponding trees are likely to differ across samples and therefore form an ensemble of distinct trees.

However, in addition to bagging, random forests introduce an extra trick when growing the individual decision trees. The tree growing algorithm is restricted to consider only a random sample of features at each split point when growing trees for a forest (see Algorithm 3). Building a random forest therefore involves randomization with respect to the rows (bootstrapping) and columns (sampling features) of the training data. Since bootstrapping induces trees that all draw from the same training data, this approach helps to decorrelate the individual trees such that – in comparison with pure bagging – a more diverse ensemble is formed. An interesting feature of this approach is that utilizing multiple trees precludes the necessity to penalize tree complexity. Therefore, trees in a random forest are grown deep. While the number of trees of the forest is typically set to a sufficiently large number (e.g. 500), the best subset size m of the p predictors depends strongly on the specific problem such that a range of try-out values should be considered (starting from p/3 (regression) and $\sqrt{p}$ (classification)).

After growing a random forest, the ensemble of trees can be used for prediction. With continuous outcomes, this amounts to recording the predictions of each individual (regression) tree ${\mathcal{T}}_b$ for a new observation and then taking the average over all B trees:

$${\widehat{f}}_B(x)=\frac{1}{B}\sum _{b=1}^B{\mathcal{T}}_b(x).$$ (9)

For categorical outcomes, the predicted class ${\widehat{C}}_b(x)$ of each classification tree of the forest is recorded and the most commonly occurring class over all trees is chosen:

$${\widehat{C}}_B(x)=\text{majority vote}{\left\{{\widehat{C}}_b(x)\right\}}_1^B.$$ (10)

Averaging (or voting) helps in counterbalancing the instability of single decision trees, which is further facilitated by growing decorrelated trees to effectively decrease variance. As a result, random forests typically achieve a considerable boost in prediction performance in comparison with CART.

Combining predictions from an ensemble of diverse trees also leads to a smoother prediction surface in comparison with the block-wise structure of a single tree. As this structure is picked up solely from the data, i.e. not specified in advance, random forest results can be useful for exploring relationships and identifying non-linear and/or non-additive patterns in the context of a powerful ensemble, e.g. through graphical techniques (besides using them in a prediction setting; see section 4.2). A related usage would be to directly compare the performances of a random forest and a parametric model, whereas large differences might point to model misspecification in the latter case (Berk 2006).

Algorithm 3:

Grow a Random Forest

2.3. Boosting

While in random forests each tree is grown separately, i.e. independent of the other trees, boosting represents a family of ensemble methods that focuses on sequential learning. In this context, decision trees are – again – most commonly used as building blocks to form an ensemble, whereas the individual trees are now built in sequence such that each tree depends on the results of its predecessor. Here we consider a prominent framework for boosting; Gradient Boosting Machines (GBM, Friedman et al. 2000, Friedman 2001).

GBM seek to find a sequence of trees where each component provides an improvement to the previous tree. At a given iteration t in this process, the goal is to find the tree parameters Θ_t = {τ_mt, γ_mt}, the nodes with associated constants of the new tree, that reduce the (e.g. quadratic) loss as much as possible, given the previous tree f_t−1(x_i):

$${\widehat{\mathrm{\Theta }}}_t=\underset{{\mathrm{\Theta }}_t}{\mathrm{argmin}}\sum _{i=1}^n\mathrm{\Psi }\left(y_i,f_{t-1}\left(x_i\right)+\mathcal{T}\left(x_i;{\mathrm{\Theta }}_t\right)\right).$$ (11)

One way to think about this problem is that the ultimate goal of the new tree is to improve the predicted values that the previous tree got wrong. Stated differently, the new tree should focus on “difficult” observations. In GBM, difficulty is represented by pseudo-residuals, which take on different forms depending on the type of the outcome variable and the chosen loss function. The GBM solution to (11) is to grow a regression tree using the pseudo-residuals of the previous tree as the outcome:

$${\tilde{\mathrm{\Theta }}}_t=\underset{\mathrm{\Theta }}{\mathrm{argmin}}\sum _{i=1}^n{\left(-g_{it}-\mathcal{T}\left(x_i;\mathrm{\Theta }\right)\right)}^2.$$ (12)

Here, denoting pseudo-residuals as −g_it refers to the relation of GBM to optimization via gradient descent, as fitting a regression tree to pseudo-residuals aligns with moving into the direction of the negative gradient. With continuous outcomes and squared error loss, −g_it = y_i − f_t−1(x_i), i.e. the usual regression residual. For binary outcomes the difference between the observed class and the predicted probability (based on the logit transformation) is used, i.e. $-g_i=y_i-\widehat{p}\left(x_i\right)$.

Equipped with a way to optimize results of a given tree, the GBM approach starts with a simple model for all training observations, e.g. for regression f₀(x) = $\overline{y}$. Given this initial model, pseudo-residuals are computed and handed over to the tree growing algorithm. In contrast to random forests only small trees are grown, i.e. boosting uses a number of “weak learners” as building blocks that are sequentially combined into a powerful ensemble. Individual tree size is controlled by the number of splits (interaction depth), which is a tuning parameter in the GBM context. The initial f₀(x) is then updated by adding the predictions from the first tree, whereas these predictions are typically shrunken towards zero which eventually allows to fit a large number of trees at a slow learning rate to improve flexibility. The new combined model is used to compute new pseudo-residuals in the next iteration (see Algorithm 4). As there is no clear stopping rule for the resulting loop, the number of iterations is a tuning parameter which should be tuned in accordance with the shrinkage rate (higher shrinkage needs more trees).

After a potentially large number of iterations, the final prediction model consists of a sequence of trees (including f₀(x)),

$${\widehat{f}}_T(x)=\sum _{t=1}^T\mathcal{T}\left(x;{\mathrm{\Theta }}_t\right).$$ (13)

Besides slowing down the learning rate by shrinkage, additional optimizations have been introduced in the context of boosting. This includes e.g. drawing random samples of the training data (without replacement) while growing trees, which has been shown to improve prediction performance while also decreasing computational costs. This approach – termed stochastic gradient boosting – thereby introduces yet another tuning parameter, the subsample size to be drawn in each iteration (Friedman 2002). Other boosting variants borrow the random forest trick and consider random subsampling of features at each split point when growing trees. This idea is – along with other tweaks – picked up by extreme gradient boosting (XGBoost), a scalable boosting implementation that allows efficient parallelization (Chen and Guestrin 2016).

As it was the case for random forests, boosting provides a data-driven approach to building a prediction ensemble that typically outperforms single decision trees. However, boosting often requires considerable tuning given the number of hyperparameters involved. Potential applications in survey research are therefore predominantly related to pure prediction problems that e.g. might arise in the context of developing adaptive designs.

Algorithm 4:

Gradient Boosting for regression

2.4. Bayesian Additive Regression Trees (BART)

Random forest and boosting can be seen as two different approaches to fit and linearly combine trees. A recent addition to this group of ensemble learning techniques are Bayesian additive regression trees, BART (Chipman et al. 2010). The technique aims at approximating the functional relationship between outcomes and predictors by a sum-of-trees model in which each tree only explains a small variation of the outcome. In doing so, BART shares similarities with Boosting. However, contrary to the aforementioned techniques that focus on optimizing predictive performance by minimizing an objective function, BART proceeds differently by imposing a probability model, which entails priors for different elements of each tree in the ensemble and a data likelihood. This procedure is used for two goals. First, priors are chosen in such a way that individual trees are kept small in terms of depth and pertain moderate predictions in the tree leaves relative to the overall sample mean. Such ‘regularized trees’ only explain small shares of the overall outcome variance, resulting essentially in ‘weak learners’ similar to gradient Boosting. Secondly, due to its Bayesian nonparametric methodology BART allows for posterior inference on the final predictions by considering, for example, their posterior (credible) intervals. It is this inference feature that sets BART apart from boosting and random forests, besides having shown comparable or better predictive performance.

The BART model (Chipman et al. 2010) consisting of T additive trees is given by

$$y_i=\sum _{t=1}^{T}g\left(x_i;{\mathcal{T}}_t,{ℳ}_t\right)+{ϵ}_i,{ϵ}_i~\mathcal{N}\left(0,{\sigma }^2\right)$$ (14)

with g the function returning the tree’s leave node mean corresponding to x_i with tree structure ${\mathcal{T}}_t$ and parameters ${ℳ}_t$. It can be seen that the conditional likelihood of y is normal. ${\mathcal{T}}_t$contains the interior node decision rules as well as the leave nodes. The parameter vector ${ℳ}_t$ = {μ₁, μ₂, ..., μ_M } contains the leave node means, where g returns exactly the μ_it ∈ ${ℳ}_t$ corresponding to x_i.

Assuming prior independence of trees and leave nodes, the probability model assigns priors to the tree structure $p\left({\mathcal{T}}_t\right)$, the tree leave means given the tree structure p(μ_t|${\mathcal{T}}_t$), and the variance p(σ²). As noted the primary role of the choice of priors is regularizing the individual trees. The first way in which this is achieved is assigning a prior probability of α(1 + d)^−β to the event that a node at depth d is not the leave node. A default recommended by Chipman et al. is α = 0.95, β = 2 putting most probability mass on trees of depth d = 2, i.e. very small trees. Prior $p\left({\mu }_t\mid {\mathcal{T}}_t\right)$ is specified normal $\mathcal{N}$ (0, σ_σ) with ${\sigma }_{\sigma }=0.5/k\sqrt{T}$. This choice effectively shrinks all leave nodes towards zero, the overall sample mean after centering y at 0. In doing so, nodes with extreme values receive low prior probability, effectively avoiding overfitting by regularization akin to the gradient boosting shrinkage parameter. Chipman et al. recommend k = 2 as a default which assigns 95 % prior probability to the event that E(Y |x) is in the interval (y_min, y_max) denoting the sample minimum and maximum respectively. The prior on σ, finally, is determined by first fitting an OLS regression of y on x obtaining residual standard deviation $\widehat{\sigma }$. The goal is then to choose an inverse chi-square prior distribution ${\sigma }^2~\nu /\lambda {\chi }_{\nu }^2$ such that P $(\sigma <\widehat{\sigma })$ = q. This prior formulates the (plausible) expectation that the BART residual variance will be smaller than the variance from a simple OLS model. Chipman et al. suggest to choose q = 0.75, 0.90, 0.99. The exact form of the inverse Chi-square distribution is given by degrees of freedom ν suggested between 3 and 10.

The exact choice of prior parameters can impact the posterior distribution. It is therefore warranted to cross-validate all prior parameters within plausible ranges. For suggested ranges see Chipman et al. (2010). Another model parameter which is candidate for cross-validation is the number of trees T typically chosen in the range of 50 to 200. Chipman et al. report lager values for T will lead to improvements in fit until some point after which fit slowly decreases again due to over-fitting.

The actual model fitting algorithm is implemented as part of a MCMC (Markov Chain Monte Carlo) algorithm called backfitting. It owes its name to the fact that upon each sequence of draws in a Gibbs sampler the residuals

$$R_t:=y-\sum _{k\ne t}g\left(x_i;{\mathcal{T}}_k,{ℳ}_k\right)$$ (15)

are conditioned on in a draw of tree structure ${\mathcal{T}}_t\mid R_t,\sigma$. A mathematically complex procedure is used here to make small changes to trees that improve fit. Conditional on ${\mathcal{T}}_t$ a draw from ${ℳ}_t\mid {\mathcal{T}}_t,R_t,\sigma$ of leave node means is taken from a normal distribution. A schematic overview on the MCMC sampler is given in Algorithm 5 and for details we refer to Chipman et al. (2010) and Kapelner and Bleich (2016).

A particularity emerges for binary responses Y. In this case, the probit model is assumed which says for continuous latent variable Z that Y = 1 if Z > 0 and Y = 0 if Z ≤ 0 while implying ${ϵ}_i~\mathcal{N}(0,1)$ for $z_i\mid x_i$ such that a prior for σ² is not needed. The MCMC Algorithm 5 is altered by adding a data augmentation step imputing unobserved values of Z.

Algorithm 5:

Bayesian Additive Regression Trees

3. Machine Learning in Survey Research

Machine learning applications in survey research often exploit the flexibility of trees or ensembles in order to tackle research problems that usually involve specifying parametric regression models. In addition, these tools are also beginning to be used as pure prediction methods in another branch of research which thereby offers promising directions for developing responsive or adaptive designs.

The most prominent (“traditional”) application of supervised learning methods in survey research is their usage in the context of modeling and correcting for unit nonresponse. This is particularly the case for (single) classification trees, where various tree building algorithms have been used for constructing nonresponse weights (for an overview, see Toth and Phipps 2014). Decision trees are considered as an alternative to logistic regression that can be used to derive weights in the presence of considerable interactions among the nonresponse predictors. In this context, response propensities are estimated based on the proportions of respondents in the terminal nodes of a given tree. Various studies consider decision tree methods, such as CHAID (CHi-squared Automatic Interaction Detector; Kass 1980), as a flexible approach for detecting subgroups with homogeneous response propensities and – ultimately – for constructing nonresponse weights (e.g. Rizzo et al. 1996, Lynn 2006, Judkins et al. 2005, Roth et al. 2006). As a side effect of using trees, the resulting terminal nodes can directly be used as adjustment cells, bypassing the problem of highly variable weights that might result from logistic regression (Toth and Phipps 2014). A related application of trees is the usage of CART for bias analysis by utilizing the tree structure from a nonresponse model in order to investigate whether the derived interactions are also associated with (a proxy of) the outcome of interest (Phipps and Toth 2012).

More recent studies investigate the usage of conditional inference trees or tree-based ensemble methods such as random forests and conditional random forests for estimating response propensities. Random forests are considered to robustly handle sparse data with many factors and relatively few observations per category and are therefore expected to provide better response propensities in situations where parametric regression would run into problems (Buskirk and Kolenikov 2015). Not surprisingly, simulations indicate that tree-based methods outperform logistic regression when comparing true with predicted response propensities, given a non-additive functional form of the nonresponse model (Lohr et al. 2015). It was also shown that particularly CTREEs’ weights performed well in terms of mitigating bias for a substantive variable across different simulated nonresponse mechanisms. In terms of reproducing true response propensities, the simulation results of Buskirk and Kolenikov (2015) also favored random forest over logistic regression, given a complex underlying nonresponse model. However, when focusing on the performance of the derived weights, their results indicated that random forests are best combined with response propensity weighting, whereas propensity stratification weights based on random forests yielded higher bias and variance than corresponding weights from logistic regression. In a similar context, random forests were considered as an exploratory tool to study whether a tree ensemble and a multilevel logistic regression identify the same top predictors from a pool of features when modeling nonresponse (Iachan et al. 2015). Furthermore, Wengrzik et al. (2016) use boosting for estimating response propensity scores and study whether reluctant respondents with low response propensities are more prone to motivated misreporting. Mercer (2018) utilizes BART to employ propensity score weighting and doubly-robust estimation in order to correct for selection bias in non-probability surveys.

Supervised learning methods have also been considered as imputation tools. When dealing with item nonresponse, Borgoni and Berrington (2013) argue that complex missing patterns in surveys may require flexible methods that can handle a large number of predictor variables computationally efficient and propose a sequential tree procedure for multivariate imputation under the assumption of missing at random. Tree-based imputation has also been introduced to replace observed values of sensitive variables in the context of generating synthetic data with lower disclosure risks (Caiola and Reiter 2010). As in missing value imputation, this task requires careful model specification when parametric methods are used which may be bypassed by plugging in nonparametric models in the imputation process. In a simulation study, particularly CART has been shown to efficiently balance analytical validity and disclosure risks (Drechsler and Reiter 2011).

Another field of survey research where the usage of supervised learning methods as an alternative to parametric modeling has been proposed is model-assisted estimation of population parameters (Breidt and Opsomer 2017, McConville et al. 2017). In this context, the idea of supplementing survey estimators with auxiliary information that is known for the population in order to improve efficiency requires relating the auxiliary variables to the outcome of interest. The functional form of such models might not be known in advance, especially since (administrative) auxiliary data often includes categorical variables with many categories, which may give rise to a number of interactions. Considering regression trees in the model-assisted estimation framework, McConville and Toth (2017) demonstrate that such an approach can improve efficiency over both the linear regression and the Horvitz-Thompson estimator.

Besides using machine learning tools as flexible substitutes for regression, their origin in the context of predictive modeling opens up new research questions by switching the focus onto prediction. Whereas various research objectives in survey research can be formulated as prediction problems, the most straight-forward application is predicting nonresponse. Focusing on tree-based methods, Buskirk (2018) predict response status based on a simulated non-additive response model in a cross-sectional setting and demonstrate that a classification tree and random forest outperform a logistic regression model, with random forest yielding the best performance on most measures. In a longitudinal setting, Earp et al. (2014) train a tree ensemble for predicting nonresponse using census data and response status from multiple years of an establishment survey. Applying the model to a new survey year indicated a weak but significant relationship between the tree ensemble propensity score and actual nonresponse. An important feature in the context of repeated surveys is that the prediction model can be applied prior to data collection, which was utilized by Earp et al. (2012) to tailor the data collection process given nonresponse predictions. It was shown that specific treatments were effective in increasing response rates among establishments which were originally least likely to respond and most likely to bias estimates when not responding.

Recent work extends the prediction perspective to other contexts. In web surveys, break-offs before completion of the questionnaire raise concerns of break-off bias and increased variance due to a lower number of complete observations. However, prediction models might be employed to target interventions that aim to prevent early break-offs, while drawing on the wealth of response-level paradata that is typically available for web surveys (Mittereder and West 2018, Eck et al. 2015). Optimizing data collection can also motivate predicting other sources of errors such as straightlining (Eck and Soh 2017), reporting errors (McCarthy and Earp 2009) or, more generally, the quality of survey questions (Saris et al. 2011).

Instead of focusing on errors as the prediction objective, supervised learning can also be used to assist in the data collection process in order to improve data quality and efficiency directly. This approach has been considered for error-prone tasks such as occupation coding, for which Schierholz et al. (2018) present an automated technique that suggests candidate job categories based on initial verbal descriptions of the respondents during the interview. In a similar spirit, Arunachalam et al. (2015) predict potential next activities given reported previous activities in a time diary to provide live suggestions in a time use survey. More generally, Schonlau and Couper (2016) utilize supervised learning to automate coding of easy-to categorize text answers from open-ended questions.

Inspired by the ideas in responsive (Groves and Heeringa 2006) and adaptive (Schouten et al. 2017) survey design, several surveys are exploring the use of prediction models for this purpose. A good example is the annual Agricultural Resource Management Survey (ARMS), where targeted data collection procedures were developed based on input from field staff and tested in an adaptive design (McCarthy et al. 2017) or the work done in the Center for Adaptive Design at the U.S. Census Bureau (see for example Coffey and Reist 2013).

4. Empirical Example - Panel Nonresponse

To give a practical example for the potential of utilizing machine learning techniques in a panel survey context we use one of the most widely used panel studies in Germany – the German Socio-Economic Panel (GSOEP; Wagner et al. 2007). GSOEP is an annual longitudinal survey of the German population that started in 1984 and includes a wide range of topics from the field of economics, sociology, psychology and political science. The first panel wave included two subsamples (A: Households in West Germany, B: Immigrants), which were complemented by additional samples in later waves to account for population dynamics (C: Households in East Germany, D: Immigrants II, M: Immigrants III), ensure sufficient coverage of specific subpopulations (G: High income households, L: Families, single parents), or enlarge overall sample sizes (E, F, H, I, J, K: refreshment samples). Given its household concept and academic organization, GSOEPs’ architecture is similar to household panels in other countries (see CNEF) and can therefore be thought of as representing an important type of longitudinal survey.

Since GSOEP provides data that is used to study a wide range of research questions across various disciplines, maintaining a high quality panel over time is a critical aspect to enable valid inference. However, as it is also the case for other panel studies (see Watson and Wooden 2009), GSOEP struggles with decreasing samples sizes due to drop-outs over time. As an example, roughly 25% of the original sample dropped out during the first four years (1984 to 1988) due to survey-related attrition. Attrition rates for newer refreshment samples are markedly higher (sample H: about 42.5% from 2006 to 2010; sample J: about 45% from 2011 to 2015; Kroh et al. 2017). In order to correct for biases that might arise from systematic drop-outs, GSOEP provides longitudinal weights which draw on predicted probabilities from logistic regressions that model response status in a given wave (Goebel et al. 2008).

For the purpose of the analysis below, we use GSOEP data from wave 2013 to model response status in 2014 using tree-based methods (SOEP 2016). More precisely, the analysis sample consists of GSOEP members that were interviewed in 2013, excluding cases that mailed in their questionnaire (n = 31, 360).⁴ On this basis, the outcome variable distinguishes between a re-interview in 2014 and a temporal or final refusal in that year (see Table 1a). The latter category combines the original response codes “Unwilling Then”, “No Time, Desire”, “Other Unclear Case”, “Final Refusal”, and “Not Usable”. Non-contacts in 2014 were treated as missing.⁵

Table 1:

Description of Variables

(a) Outcome

Variable	Scale/Categories	Year
Refusal 2014	interview/temp. or final refusal	2014

(b) Features

Variable	Scale/Categories	Year
Age	16–99	2013
Education (years)	7–18	2013
Gender	male/female	2013
Migration background	no/direct/indirect	2013
Employment status	full-time/part-time/in training/marginal employed/not employed	2013
Household income†	0–70000 (180–70000)	2013
Household income: Missing	missing/non missing	2013
Home	owner/renter	2013
Household type	1-pers./couple without ch./single parent/couple w. ch. ≤ 16/couple w. ch. > 16 couple w. ch. ≤ & > 16/other	2013
Marital status	married, together/married, separate unmarried/divorced/widowed	2013
Household size	1–13	2013
Subjective health	1–5	2013
Subjective well-being	0–10	2013
Region	East/West Germany	2013
Area	rural/urban	2013
House	farm/1–2 fam. house/apt. 3–8 unit/apt. 9+ unit	2013
SOEP years	0–29	1984–2013
Interviewer contacts	1–3/4–6/7+	2013
Mode	oral/written/mixed/CAPI	2013
Refusal in household	no refusal/refusal	2013
Contact information	no contact/mail or phone/mail & phone	2013
Response 2012	new household/interview/nonresponse	2012
Item missing ratio	0–0.556	2013
Interviewer: Gender	male/female	2013
Interviewer: Age	23–91	2013
Interviewer: Experience (years)	1–30	2013
Interviewer: Response rate	0.333–1	2013
Interviewer:$\varnothing$ Interview length	5–120	2013
SOEP sample	A–D/E–F/H–K/L/M	1984–2013
Inverse staying probability	0–5.27	2013

^†Missings have been imputed (used in Logit, MOB) or set to zero (used in CTREE, RF, XGBoost, BART).

The following analyses draws on two sets of predictor variables (see Table 1b). The first set includes respondent-related variables such as socio-demographics, household income and income nonresponse, as well as some contextual characteristics (East/West Germany, rural/urban, house type). The second set of predictors includes interview-related variables, such as the number of contact attempts, survey mode, ratio of item nonresponse and interviewer characteristics in 2013. Information from previous waves is added implicitly by considering subsample membership and GSOEP experience (number of GSOEP years), and explicitly by including response status in 2012. Furthermore, the inverse staying probability (based on estimated contact and response probabilities; provided by GSOEP) is treated as an additional feature, assuming that a low estimated staying probability in 2013 is associated with an increased risk of nonresponse in the next wave.

We use machine learning methods with respect to two objectives: First, we use model-based recursive partitioning and conditional inference trees as data-driven approaches to explore the relationship between the outlined features and panel nonresponse. Second, we use a wider set of supervised learning methods (CTREE, MOB, random forests (RF), XGBoost, BART) to study nonresponse from a prediction perspective. To facilitate both objectives, we split the sample into a training (80%) and a test set (20%), based on random sampling within the categories of the outcome variable (stratified random splitting). In the following, the training set is used to both exemplify the usage of recursive partitioning in the context of modeling panel nonresponse and to build the machine learning models for prediction. The analysis is implemented in R (R Core Team 2017) using the partykit (Hothorn and Zeileis 2015), randomForest (Liaw and Wiener 2002), xgboost (Chen et al. 2018), bartMachine (Kapelner and Bleich 2016) and caret (Kuhn 2017) packages.

4.1. Modeling Panel Nonresponse

For an illustration of the insights that can be gained when modeling panel nonresponse from a data-driven perspective, model-based recursive partitioning provides a suitable tool due to its “hybrid” approach to data analysis. In this example, a logit model of response status in 2014 is considered which includes only respondent-related variables as predictors (set 1 in Table 1b) and interview-related variables as potential partitioning variables (set 2 in Table 1b). This setup allows to study whether e.g. the effects of socio-demographic variables on panel nonresponse depend on survey-operational characteristics.

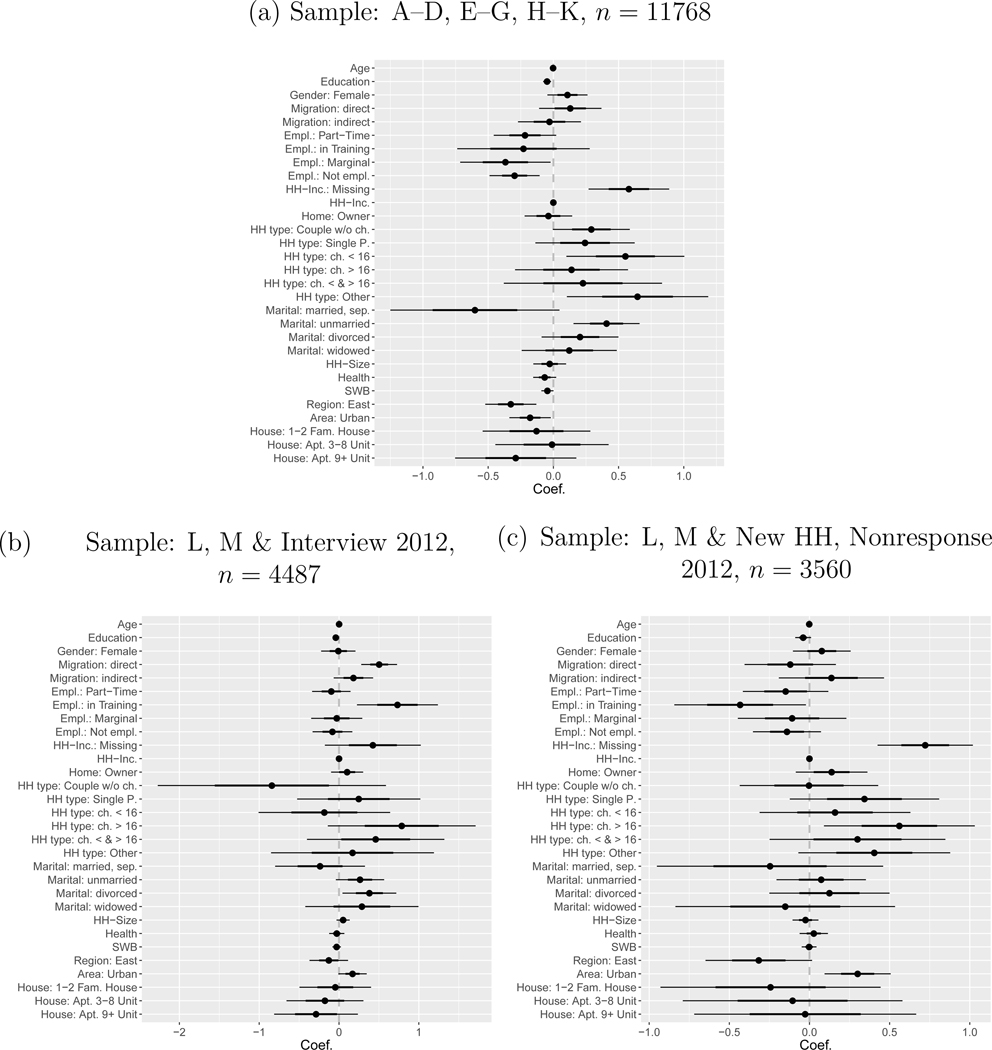
The MOB results are illustrated in Figure 1.⁶ The final tree encompasses three terminal nodes, i.e. three distinct logit models, suggesting that a single model as specified in the root node is not sufficient given the data at hand. Starting with the initial model, parameter instability tests identified varying effects of the predictor variables across GSOEP subsamples, leading to the first split that partitions the data into observations that belong to older (A–D, E–G, H–K) and newer (L and M) samples. Whereas the first group already represents a terminal node (Figure 1a), the second subgroup was subject to further splitting, given parameter instabilities induced by response status in the previous wave (2012). As sample M was introduced in 2013, the second terminal node is essentially formed by individuals of GSOEP sample L who were interviewed in 2012 (Figure 1b), whereas the third node predominantly represents individuals from sample M who were not interviewed in 2012 since they were not GSOEP members yet (as well as individuals from sample L who were not interviewed due to nonresponse; Figure 1c). In this context, it is worth noting that sample L and M are not only the most recent GSOEP samples, but also represent specific populations (L: low income and large families, single parents, M: immigrants, second-generation migrants). While this might induce estimating distinct models also from a substantive perspective, it is important to keep in mind that the three node solution obtained here is solely the result of applying automated recursive partitioning with a set of potential splitting variables.

Figure 1:

Coefficient Plots of Terminal Node Models of MOB Tree (y = Refusal in GSOEP Wave 2014)

Across the three terminal nodes, distinct effect patterns emerge. As an example, in node one being marginally or non-employed is associated with a lower probability of refusing to participate in 2014, whereas in node two and three only the status “in training” is predictive of nonresponse, with opposing effect directions in both nodes. Furthermore, household income nonresponse in 2013 is a strong predictor of unit nonresponse in 2014 particularly for individuals in node one and three, whereas node two is the only node where a substantial positive effect of having a direct migration background can be observed. Differences between groups also become evident with respect to contextual variables, with lower refusal probabilities of individuals living in an urban environment in node one and an opposing effect in node three.

While model-based recursive partitioning is a powerful approach to find subgroups given a prespecified parametric model, following interactions through nodes of a model-based tree in order to identify observations that are at high risk of non-participation in a given wave can become cumbersome. In addition, in an exploratory setting one might not know which variables are predictors that establish the model and which features should be considered as partitioning variables.

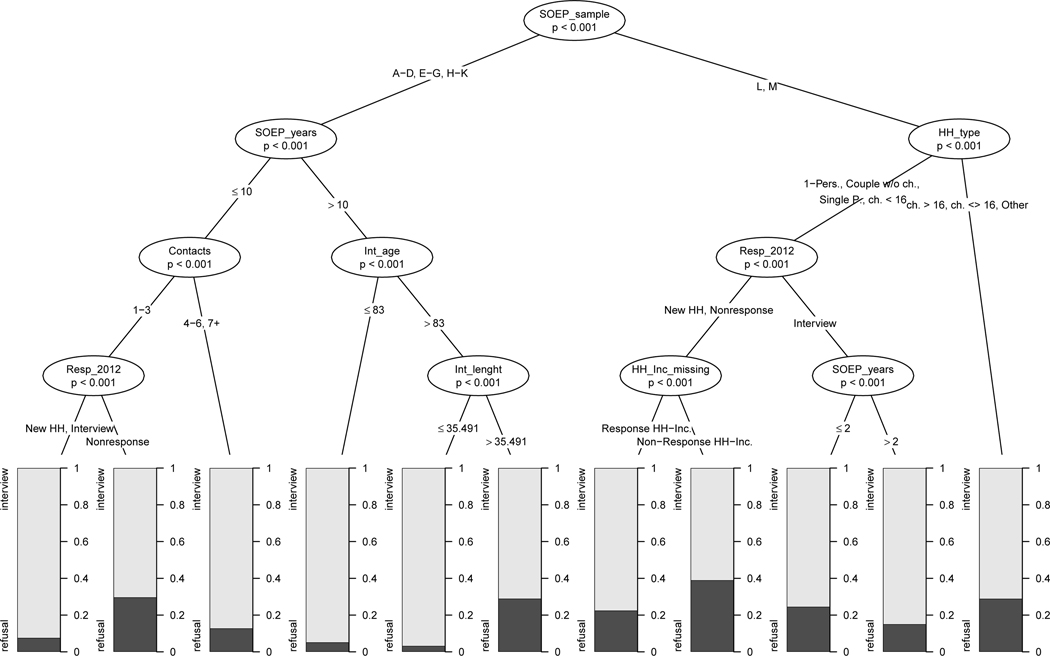
As an alternative approach, Figure 2 presents a small conditional inference tree where both respondent- and interview-related characteristics were considered as potential splitting variables for predicting refusal in 2014.⁷ Starting at the root node, CTREE reproduces the first split of the MOB result, i.e. partitions the data into two branches based on GSOEP sample membership. Within these branches, different combinations of respondent- and interview-related variables lead to markedly diverging risks of non-participation. It can be seen that, somewhat similar to the MOB result, household income nonresponse is particularly predictive of refusal for observations in sample L and M that did not respond in 2012 and are members of certain household types (1-person household, couple without children, single parents, couple with children under 16 years, node 8). On the other hand, individuals from sample A to K that have been GSOEP members for at least 10 years show a relatively high risk of non-participation in 2014 if they were interviewed by an older interviewer in 2013 which exhibits long average interview lengths (node 6). The CTREE approach can therefore be used to identify risky combinations of respondent- and interview-characteristics, again solely based on a data-driven partitioning process. As with MOB, finer-grained regions can be found by adjusting the tree building parameters.

Figure 2:

Conditional Inference Tree (y = Refusal in GSOEP Wave 2014)

4.2. Predicting Panel Nonresponse

Besides using recursive partitioning with models or constant leaves as terminal nodes in an exploratory setting, tree-based methods are particularly suitable for prediction. Building on the previous example, the following analysis considers a set of machine learning methods for predicting refusal in wave 2014, including single tree approaches (CTREE, MOB) and ensemble methods (RF, XGBoost, BART). A single (main effects only) logistic regression is used as a reference model. For each method, the modeling process includes the following steps:

1. Tune hyperparameters within the training set using stratified 10-fold cross-validation

2. Re-train model with best hyperparameter setup on full training data

3. Evaluate performance of the final model in the test set

Stratification in step 1 refers to random sampling within the categories of the outcome variable to preserve the class distribution across splits. The tuning process is governed by searching over a grid of hyperparameter settings for each method. After cross-validation, the respective best model (i.e. tuning parameter setup for each method) is chosen by evaluating which tuning parameter constellation maximizes the cross-validated AUC-ROC. This setup is then used to train the final model on the full training data (step 2) which is subsequently applied and evaluated with multiple metrics in the test set (step 3), respectively.

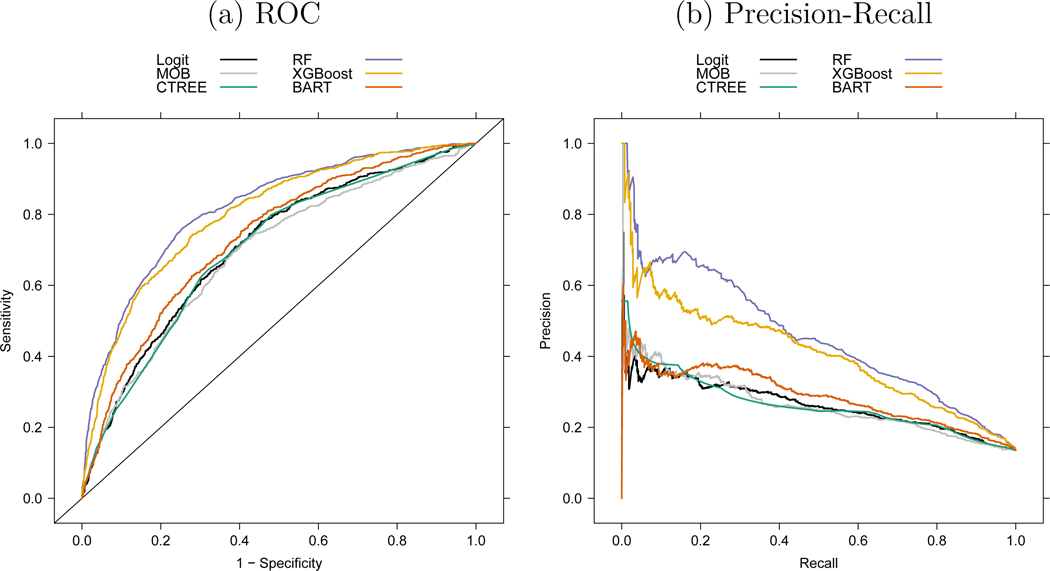
Starting with the overall test set performance (step 3), Figure 3 displays the receiver operating characteristic (ROC) and precision-recall (PR) curves which plot sensitivity (proportion of all nonrespondents that are correctly classified) versus one minus specificity (proportion of all respondents that are correctly classified; Figure 3a) and precision (proportion of correctly classified nonrespondents among all predicted nonrespondents) versus recall (same as sensitivity; Figure 3b) over the range of applicable classification thresholds given the predicted probabilities of the final prediction models. The corresponding AUC-ROC and AUC-PR measures (areas under the ROC, PR curves) are listed in Table 2a. It can be seen that simply estimating a logistic regression model with the training set and using this model for predicting refusal in the test set leads to fair performance with an AUC-ROC of 0.707. Similar, or slightly lower, discrimination can be obtained when applying MOB and CTREE as prediction methods, suggesting that for the problem at hand not much can be gained from using a set of logistic regressions or constant leaves in terms of test set prediction performance. However, it becomes evident that random forest (RF) and boosting (XGBoost) markedly outperform the former methods by achieving AUC-ROC values at and above 0.8. While – at first sight – this might demonstrate the effectiveness of ensembles over single models or trees, applying BART in the current context shows (somewhat surprisingly) only a modest improvement over logistic regression, MOB and CTREE. However, it should be noted that for intermediate thresholds Figure 3b suggests BART predictions to be more precise in comparison with single trees, although still on a considerably lower level than the results from random forest and boosting.

Figure 3:

Performance Curves in Test Set (y = Refusal in GSOEP Wave 2014)

Table 2:

Performance Metrics in Test Set (y = Refusal in GSOEP Wave 2014)

(a) AUCs

	Logit	MOB	CTREE	RF	XGBoost	BART
AUC-ROC	0.707	0.691	0.702	0.818	0.800	0.733
AUC-PR	0.263	0.264	0.265	0.458	0.408	0.288

(b) Performance at Optimal Threshold

	Accuracy	Sens.	Spec.	Prec.	F1	Kappa
Logit	0.799	0.371	0.865	0.301	0.333	0.216
MOB	0.816	0.314	0.894	0.316	0.315	0.209
CTREE	0.809	0.284	0.891	0.289	0.287	0.176
RF	0.836	0.559	0.879	0.419	0.479	0.384
XGBoost	0.828	0.556	0.871	0.402	0.467	0.367
BART	0.818	0.377	0.887	0.342	0.359	0.253

(c) Performance at Restrictive Threshold

	Accuracy	Sens.	Spec.	Prec.	F1	Kappa
Logit	0.826	0.272	0.913	0.328	0.297	0.199
MOB	0.835	0.244	0.928	0.345	0.286	0.196
CTREE	0.824	0.251	0.913	0.311	0.278	0.179
RF	0.850	0.490	0.907	0.451	0.470	0.383
XGBoost	0.856	0.421	0.924	0.464	0.442	0.359
BART	0.832	0.322	0.912	0.364	0.342	0.246

In a real-world application, the prediction models would most likely be used to predict class membership, i.e. interview or refusal, at a specific probability threshold in order to implement measures that keep likely nonrespondents from non-participation. Performance metrics for class predictions at two different sets of thresholds are displayed in Table 2b and 2c. In both cases, the optimization criterion aims at finding thresholds that are closest to the top-left point of the ROC graph, while putting a stronger weight on specificity by setting the prevalence (of refusal) to 0.1. For computing the second set of thresholds, a higher relative cost of a false positive classification is considered as an additional condition, resulting in more restrictive, i.e. higher, cutoff values.⁸ Using the first (“optimal”) threshold criterion, a similar ranking as with AUC-ROC occurs, with random forest and boosting markedly outperforming logistic regression, MOB and CTREE (Table 2b). Both methods are able to find more than 50% nonrespondents out of all true nonrespondents (sensitivity), while correctly predicting participation for about 87% of all true participants (specificity). However, in an application that allocates survey resources based on a prediction model one might not only be interested in the ability of a classifier to find nonrespondents, but also in the precision of the classifiers’ predictions. With the second, more restrictive threshold criterion, 46% (280/603) of the individuals that are predicted by XGBoost as being nonrespondents are truly nonrespondents (precision), at the expense of a somewhat lower sensitivity (Table 2c). With a precision of about 33% (181/552), using a logit model results in a lower number of true nonrespondents that would be targeted if predictions would be used to inform the data collection process. Given the rather basic set of predictor variables, the performance of random forests and boosting therefore points to a promising potential for building an effective prediction model for panel nonresponse using machine learning methods.

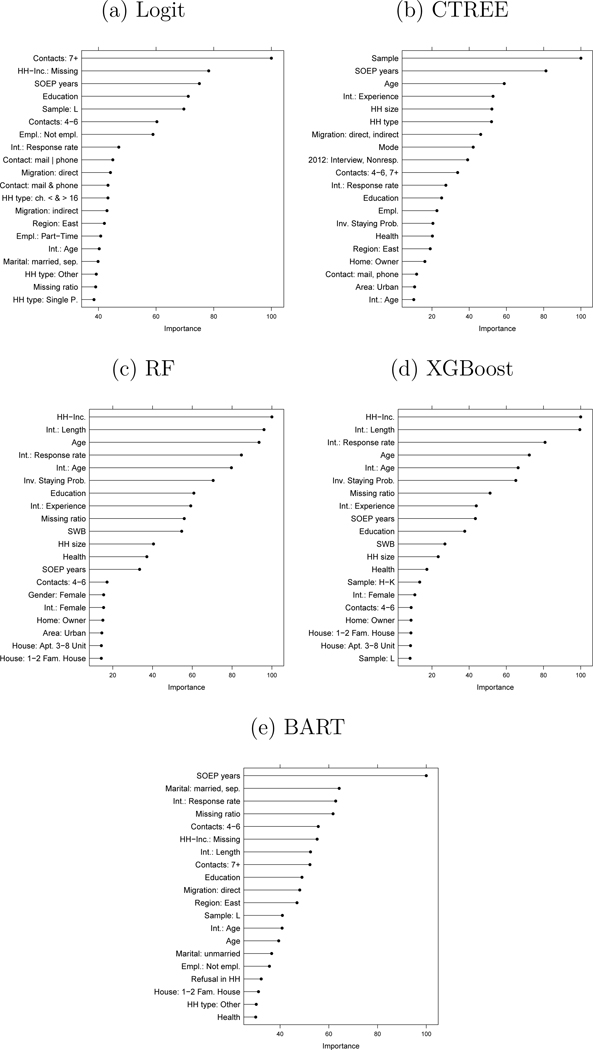
The trained models can also be used to gather insights about the predictive structure that was learned from the training data. Figure 4 presents variable importance plots for the logit, CTREE, RF, XGBoost and BART model.⁹ While in the logit case, t−values are often used as measures for variable importance, importance’s with tree-based methods can, for example, be obtained by summarizing the decrease in impurity that is induced by the splits of a given variable. For comparison purposes, the importance scores in Figure 4 are scaled to have a maximum value of 100. It can be seen that the predictor variables are utilized quite differently across prediction methods, with markedly different importance profiles when e.g. comparing the two best performing ensemble models (RF, XGBoost) with logistic regression. As the former methods are able to learn complex relationships from the data, this result might indicate that variables such as age or average interview length per interviewer exhibit non-linear and/or non-additive effects that have not been picked up by the logit model.¹⁰

Figure 4:

Top-20 Variable Importance (y = Refusal in GSOEP Wave 2014)

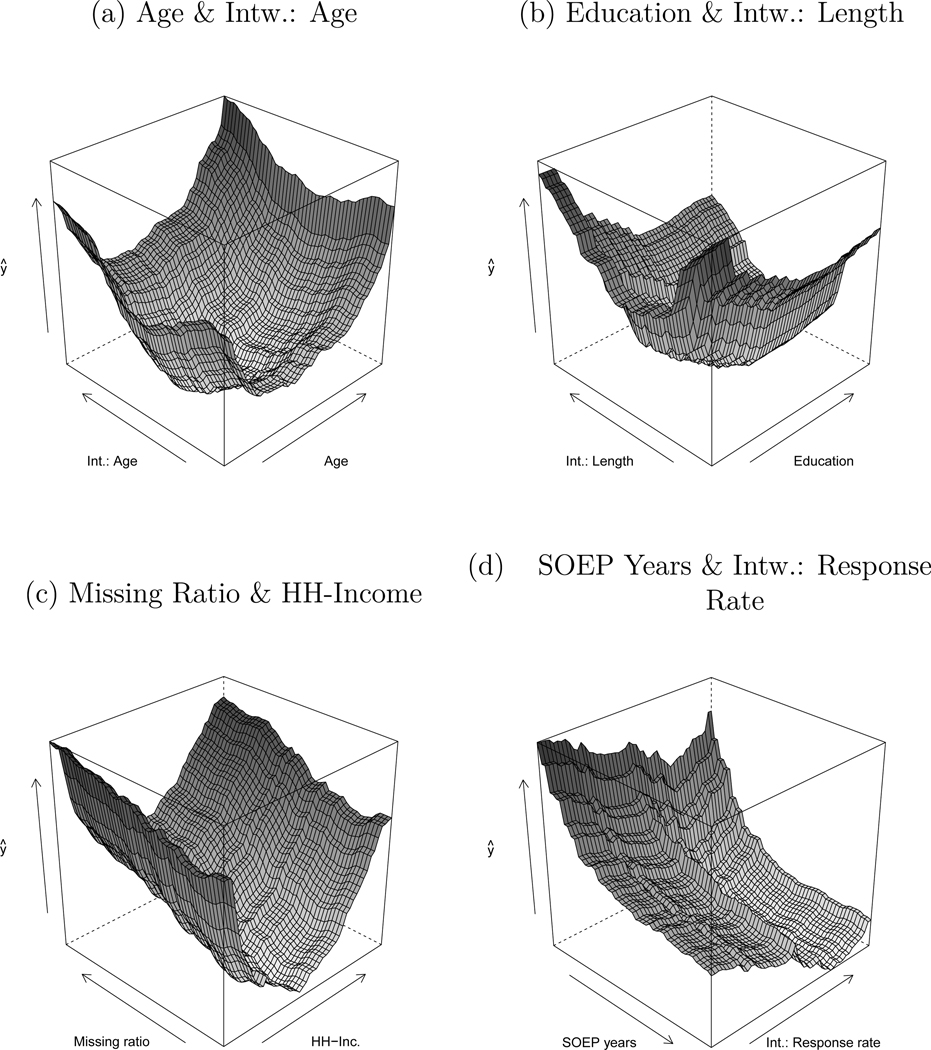
To get an idea of the predictive structure that drives the predictions of the random forest model, Figure 5 displays partial dependence plots for a selected set of features based on the random forest result (Greenwell 2017). These figures plot the predicted probabilities of refusal over a range of fixed values of the predictors of interest, while averaging over the effects of the remaining variables. It becomes clear that strong non-linear relationships occur in the data that have been incorporated in the random forest model. As an example, the lowest predicted probabilities of refusal occur for combinations of medium respondent and interviewer age, whereas nonresponse risks increase when moving to more extreme combinations (Figure 5a). Nonlinearities also become evident with respect to the aforementioned variables household income and average interview length, indicating higher predicted probabilities of refusal on either end of the distributions (Figure 5b, 5c). Finally, Figure 5d nicely demonstrates that nonresponse risks are highest in the beginning of GSOEP participation and level off after the first years.

Figure 5:

Partial Dependence Plots Based on Random Forest Result (y = Refusal in GSOEP Wave 2014)

5. Discussion

The machine learning approach to data analysis offers a wide range of methods which are beginning to be utilized by survey researchers in a variety of contexts. These applications suggest that supervised learning can not only be thought of as offering flexible substitutes for parametric regression, but also as providing powerful prediction methods that can be used to target interventions, which naturally aligns with the idea of adaptive designs. Against this background, this paper focused on tree-based learning methods, which are able to adapt to complex relationships while at the same time being effective in terms of computational costs and pre-processing effort needed. We argued that these methods can be particularly useful in a panel survey setting, e.g. for building a nonresponse model with a diverse set of features which might involve complex interactions.

Using supervised learning for modeling nonresponse in the German Socio-Economic Panel study (GSOEP) exemplified that different (groups of) tree-based methods offer distinct advantages that can be utilized in different contexts. First, model-based recursive partitioning has been considered as a data-driven tool for finding an optimal set of subgroups when effect heterogeneity in a pre-specified regression model is suspected. In the present application, MOB showed that newer GSOEP subsamples induce distinct effect patterns and should therefore be modeled separately. The CTREE approach has then been used for identifying combinations of respondent-and interview-related features that are associated with high drop-out risks, indicating that for new GSOEP subsamples and certain household types household income nonresponse is particularly predictive of unit nonresponse in the next wave.

Finally, tree-based ensemble methods have been shown to be effective when studying nonresponse from a prediction perspective, with random forests and boosting markedly outperforming logistic regression and single trees in the GSOEP example. Class predictions based on these two ensemble methods resulted in considerably higher precision scores, such that – given a specific classification threshold – a higher number of true nonrespondents were identified that could potentially be targeted in an adaptive design. Inspecting random forests’ partial dependence plots suggested that the ensembles’ performance might be driven by non-linear relationships of some nonresponse predictors, which have not been included adequately in the (main effects only) logistic regression model. However, even though random forest and boosting showed better prediction performance, it is important to note that these methods still might have been underutilized in the present application, given the rather basic set of predictor variables considered. This is particularly the case with respect to the longitudinal aspect, since the prediction models predominantly used information from only one pair of GSOEP waves.

Building on the latter argument, further research is needed to investigate how to best utilize supervised learning methods with longitudinal survey data. In the context of predicting nonresponse in the next wave given a number of previous waves in a panel study, longitudinal information can (and should) be introduced in the model building, tuning and evaluation process. This could be achieved by combining wave-specific tree-based models into a higher-level ensemble or by building pooled models with features that introduce longitudinal information (via aggregation). Concerning model tuning and evaluation with multiple waves, the train and test splits should account for the temporal structure of the data, e.g. by iterating through pairs of panel waves such that the train and test sets move in time (temporal cross-validation). In summary, this problem set can be understood as constituting one example where techniques and practices of the machine learning field have to be combined and/or adjusted such that they fit the needs of a specific application in survey research.