Routes to global glaciation

Abstract

Theory and observation suggest that Earth and Earth-like planets can undergo runaway low-latitude glaciation when changes in solar heating or in the carbon cycle exceed a critical threshold. Here, we use a simple dynamical-system representation of the ice–albedo feedback and the carbonate–silicate cycle to show that glaciation is also triggered when solar heating changes faster than a critical rate. Such ‘rate-induced glaciations’ remain accessible far from the outer edge of the habitable zone, because the warm climate state retains long-term stability. In contrast, glaciations induced by changes in the carbon cycle require the warm climate state to become unstable, constraining the kinds of perturbations that could have caused global glaciation in Earth’s past. We show that glaciations can occur when Earth’s climate transitions between two warm stable states; this property of the Earth system could help explain why major events in the development of life have been accompanied by glaciations.

1. Introduction

Palaeoclimate evidence suggests that the Earth has undergone several episodes of low-latitude glaciation in the geologic past [1–5], most prominently towards the end of the Neoproterozoic Era (1000–542 Ma). The possibility that some or all of these glaciations were global in extent has given rise to the concept of the ‘snowball Earth’. Runaway glaciation, and the persistence of the resulting climate state, is possible because of the ice–albedo feedback [5–10]. On Earth, global glaciation would likely be transient because weathering is vastly reduced in the glaciated state; thus, atmospheric CO₂ accumulates in the atmosphere, and the resultant greenhouse warming eventually melts the ice [1]. Far enough from its host star, however, an Earth-like planet will remain glaciated regardless of CO₂ concentration. This marks the outer edge of the classical ‘habitable zone’ [11,12].

Although there remains debate about the specific triggers of the low-latitude glaciations in Earth’s geologic past [5], there is a general understanding that glaciation is initiated when changes in radiative fluxes [6–10] or in CO₂ fluxes [13,14] exceed a critical threshold. In this paper, we propose an additional possibility: glaciation is initiated when changes in radiative fluxes exceed a critical rate. We first demonstrate how this phenomenon arises in a simple dynamical-system model of the ice–albedo feedback and the carbonate–silicate cycle, finding that it is a consequence of the vast timescale contrast between radiative equilibration and CO₂ equilibration. Because the warm climate state does not lose long-term stability during such a rate-induced glaciation, we further find that Earth-like planets remain susceptible to transient glaciation far from the outer edge of the habitable zone. Finally, we apply this to the glaciations of the geologic past. We show how the properties of the different ‘routes to glaciation’ constrain potential trigger mechanisms for the Neoproterozoic snowball events, and suggest that the observed co-occurrence of glaciations with periods of major biogeochemical transition in the geologic past becomes less perplexing in light of rate-induced glaciation.

2. Dynamical system

The interplay of the ice–albedo feedback and the carbonate–silicate cycle has been studied across a range of model complexities [13–17]. Seeking to elucidate the qualitative dynamics of the system, we follow [14,16] in constructing a two-component dynamical system which tracks changes in mean surface temperature, T, and atmospheric pCO₂, P. Outgoing longwave radiation is linearized around a stable warm state [14]. However, in contrast to [14], we consider albedo to be a smoothly varying function of temperature, to mimic the effects of partial ice coverage. The resulting dynamical system is

$$C\dot{T}=\frac{S}{4}(1-\alpha (T))-\frac{S_0}{4}(1-{\alpha }_0)-a(T-T_0)+b\log \left(\frac{P}{P_0}\right)$$ 2.1

and

$$\dot{P}=V-W(T)\hspace{0.17em}{\text{e}}^{k(T-T_0)}{\left(\frac{P}{P_0}\right)}^{\beta }.$$ 2.2

Here, C is the planetary heat capacity, S is the stellar flux and α(T) is planetary albedo. S₀, α₀, T₀, P₀ are the stellar flux, albedo, temperature and pressure of the stable warm state, respectively. V is the rate of volcanic outgassing. The parameters a and b reflect the slope of outgoing longwave radiation with respect to T and log P. k is a rate constant for the dependence of weathering on temperature, and β is the exponent which parametrizes the dependence of weathering rates on CO₂ concentration. The weathering formulation largely follows previous work [14,18,19]; however, the temperature dependence due to precipitation rates is neglected because it makes no qualitative difference in the behaviour of the system [14]. Finally, we use W(T) to represent the decrease of weathering with decreasing temperature due to increased planetary ice coverage. Its value at T₀ and P₀ is denoted as W₀. We discuss the values of the various parameters, the functional forms of α(T) and W(T), and the sensitivity of our results to these choices in the electronic supplementary material.

The dynamical system (equations (2.1) and (2.2)) exhibits a range of possible steady states, or fixed points. These include both a stable warm climate state and a stable glaciated climate state. Consistent with previous work [13–17], it also exhibits the possibility of a limit cycle in which the system oscillates between warm and glaciated states. A regime diagram in terms of the parameters V (volcanic outgassing) and S (stellar flux) is shown in figure 1; further details are in the electronic supplementary material. Here, it suffices to note that the stable warm regime is adjacent to the limit cycle regime in parameter space; perturbations to carbon fluxes (i.e. V) and/or radiative fluxes (i.e. S) can act to move the system between these regimes.

Figure 1.

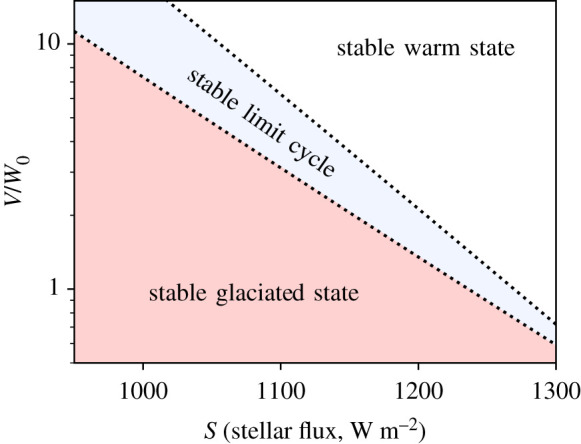
The climate states associated with particular values of volcanic outgassing and stellar flux. Volcanic outgassing V has been normalized by the weathering rate at (T₀, P₀), denoted as W₀. The system exhibits the possibility of stable warm and stable glaciated states. Consistent with previous work [13–17], it also exhibits the possibility of a limit cycle, in which the system oscillates between warm and glaciated states. (Online version in colour.)

The system operates on two distinct timescales. Radiative adjustment of T occurs much faster than the geologic adjustment of P through the carbonate–silicate cycle. Thus, the dynamics can be well understood by considering the nullclines (the two curves where $\dot{T}=0$ and where $\dot{P}=0$). Figure 2 demonstrates this for modern Earth parameters, where the model exhibits a uniquely stable warm state. Because T equilibrates much faster than P, the slow dynamics of the system occur essentially exclusively on the $\dot{T}=0$ nullcline; we refer to this as the critical manifold [20,21]. Once the system arrives on the high-temperature branch of the critical manifold, it slowly relaxes towards the stable warm climate state. If the system lands on the low-temperature branch of the critical manifold, CO₂ slowly builds up over millions of years and eventually triggers a jump to the high-temperature branch of the critical manifold, with subsequent relaxation to the stable warm climate state.

Figure 2.

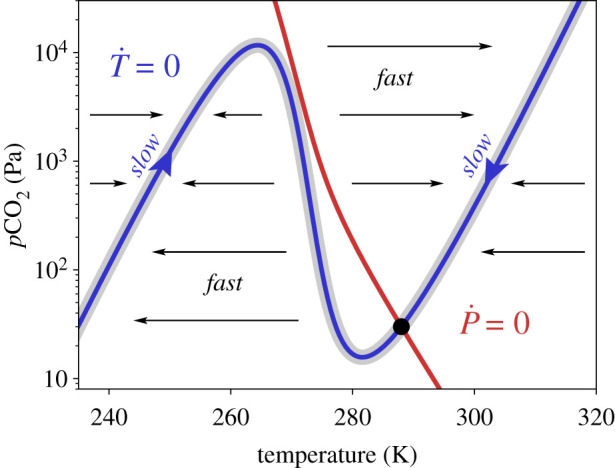
The dynamical system operates on two distinct timescales. Here, we plot the curves of $\dot{T}=0$ and $\dot{P}=0$ (nullclines) of the dynamical system for modern Earth parameters (S = 1365 W m⁻², V/W₀ = 1). Because the radiative adjustment of temperature occurs much faster than the geologic adjustment of CO₂, the system spends most of its time near the $\dot{T}=0$ nullcline (the critical manifold), greatly simplifying the dynamics. Once the system arrives on the high-temperature branch of the critical manifold, it slowly relaxes towards the stable warm climate state. If the system lands on the low-temperature branch of the critical manifold, CO₂ slowly builds up over millions of years and eventually triggers a jump to the high-temperature branch of the critical manifold, with subsequent relaxation to the stable warm climate state. (Online version in colour.)

3. Rate-induced glaciation

It is well recognized that, starting from a stable warm climate state, glaciation can be initiated if parameter changes cause the climate state to lose stability [5,9,14], i.e. if the system passes through a bifurcation. More generally, climate ‘tipping points’, where small changes in a parameter result in much larger responses, are often thought to involve passage through bifurcations [22]. However, this need not be the case. Elements of Earth’s climate system may ‘tip’ even while the steady state remains uniquely stable [21–23].

Our model also exhibits such behaviour: transient multi-million-year glaciations can occur while the stable warm climate state remains uniquely stable. Figure 3 demonstrates how and why. On the fast radiative timescale, the system relaxes to the critical manifold $\dot{T}=0$. The critical manifold has a local minimum near the stable fixed point: we refer to this as a fold. Some trajectories are able to reach the critical manifold before it folds, and can thus return to the stable state in a short amount of time. Other trajectories pass beneath the fold, heading for the cold branch of the critical manifold. Once the system reaches this branch, it is in a glaciated state, and must wait millions of years for CO₂ concentrations sufficient to trigger deglaciation. The critical threshold which separates these two cases is given by the class of trajectories which follow the unstable branch of the critical manifold (the left branch in figure 3): these are known in dynamical systems theory as ‘canard’ trajectories [24].

Figure 3.

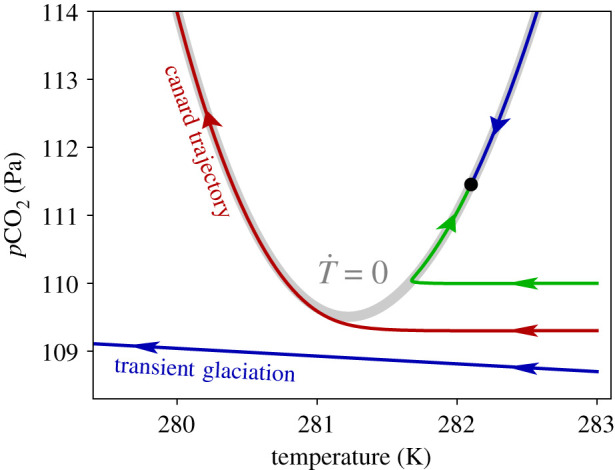
Transient glaciations can occur even though the warm state remains uniquely stable. Here, S = 1280 W m⁻² and V/W₀ = 1. The critical manifold $\dot{T}=0$ is folded (has a local minimum) near the fixed point; the right-hand side branch is stable and the left-hand side branch is unstable (see figure 2). The upper trajectory (green) is able to reach the stable part of the critical manifold (i.e. before the fold), relaxing quickly back to the fixed point. The lowest trajectory (blue) is unable to intersect the stable part of the manifold and passes beneath the fold, heading towards the cold branch of the critical manifold (see figure 2). A transient, million-year glaciation results. There is a special kind of trajectory that separates these two cases: it is known in dynamical systems theory as a ‘canard’ [24]. (Online version in colour.)

Understanding which parameter changes can initiate these transient glaciations is straightforward. Figure 3 shows the response of the system to different initial conditions, but it can equally be interpreted as the evolution of a prior steady state in response to an instantaneous movement of the $\dot{T}=0$ nullcline in different directions. In this view, the lowest trajectory (blue) represents a case where the $\dot{T}=0$ nullcline has moved to higher pCO₂ values, such that the system state finds itself beyond the threshold canard trajectory: now, transient glaciation results. The upper trajectory (green), on the other hand, represents a case where the $\dot{T}=0$ nullcline has moved to lower pCO₂ values: now, the system state remains above the canard trajectory and safely relaxes back to the stable warm climate state. Therefore, a perturbation to any of the parameters in equations (2.1) or (2.2) will initiate transient glaciation starting from a steady state if and only if it moves the fold in the $\dot{T}=0$ nullcline (i.e. its local minimum in figure 3) to high enough pCO₂ values such that the system state crosses the threshold canard trajectory. However, the only parameters that can change the shape of the $\dot{T}=0$ nullcline are those present in equation (2.1), i.e. those that govern the radiative balance of the planet. Notably, this excludes changes in CO₂ fluxes.

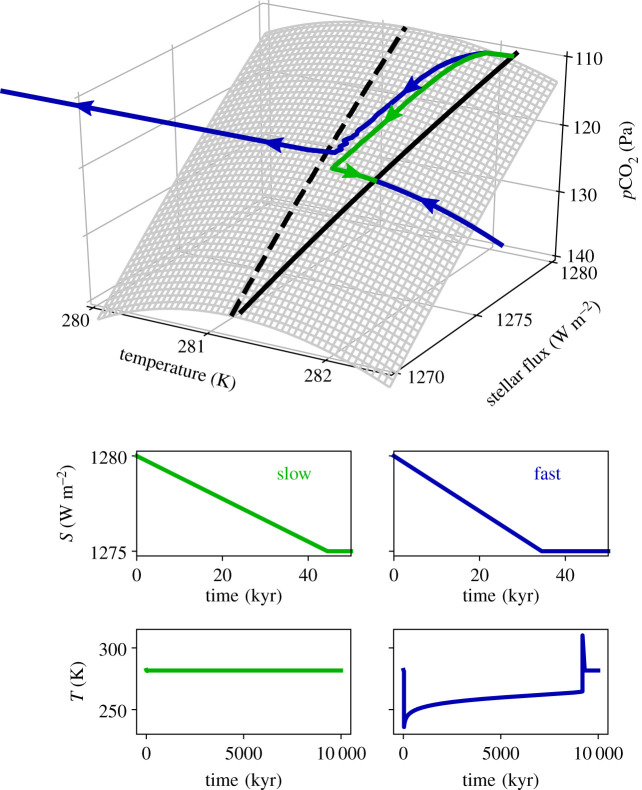
It is not only an instantaneous movement of the $\dot{T}=0$ nullcline which can trigger glaciations starting from the stable warm climate state; all that matters is that the change occurs fast enough for the system state to pass beyond the threshold canard trajectory in figure 3. Hence, we call this kind of glaciation ‘rate-induced’. In figure 4, we demonstrate rate-induced glaciation for decreases in stellar flux S. Having let the system equilibrate to the stable warm climate state at S = 1280 W m⁻², we decrease S linearly to 1275 W m⁻² over two different time periods. As S decreases, the fold in the $\dot{T}=0$ nullcline and the fixed point move to higher pCO₂ values; to better depict this change, we add S to our plot as a third dimension alongside the phase space of temperature (T) and pCO₂ (P). We also reverse the P axis to make the dynamics easier to visualize. Now, the warm stable climate state and the position of the fold become curves on a three-dimensional critical manifold $\dot{T}=0$. If the stellar flux decrease occurs slowly, the system state does not cross the fold curve and settles to the warm stable state. If the stellar flux decrease occurs more quickly, the system state moves beyond the fold, and transient multi-million-year glaciation results. There exists a critical rate of change of S: exceeding it triggers transient glaciation.

Figure 4.

Demonstration of rate-induced glaciation in our model. In both cases, stellar flux S is decreased linearly from 1280 to 1275 W m⁻², but in the slow case this occurs over 60 kyr and in the fast case this occurs over 40 kyr. Changes in S alter the location of the fixed point, as well as that of the $\dot{T}=0$ nullcline and its fold (local minimum); this is illustrated in the top graph by including S as a third dimension. Now, the warm stable climate state (black, solid) and the fold (black, dashed) become curves on the three-dimensional critical manifold $\dot{T}=0$ (grey). The pCO₂ axis (P) is reversed to better illustrate the dynamics. In the slow case, the trajectory does not pass beyond the fold and is able to quickly relax back to the fixed point once ramping stops. In the faster case, the trajectory passes beyond the fold curve, and transient ‘rate-induced glaciation’ ensues. It takes millions of years for the system to return to the unique stable warm climate state. The fluctuations that occur near the fold crossing are numerical. (Online version in colour.)

The critical rate of change to initiate a transient glaciation further depends on the timescale of the perturbation, τ. At timescales far below that of the geologic adjustment of CO₂, the critical rate of stellar flux change to induce glaciation scales like τ⁻¹ (electronic supplementary material). This implies the existence of an effective ‘critical amount’ of change at these short timescales [23]. The characterization of the glaciation as rate-induced still applies, however; the key criterion is that the initiating perturbation does not cause the warm climate state to lose stability [22]. The critical instantaneous change ΔS required to trigger a permanent transition to the snowball state in models that neglect the carbonate–silicate cycle [5–10] is likely similar to the effective critical amount ΔS that results from the rate-induced glaciation mechanism presented here.

Our identification and description of the phenomenon of rate-induced glaciation appear new, but we note that the concept should not come as a surprise. Adjustment of atmospheric CO₂ over time due to the carbonate–silicate cycle is often viewed as part of the solution to the Faint Young Sun problem [25]. On the other hand, it has been proposed that rapid, relatively small transient changes in effective stellar flux have triggered past low-latitude glaciations [26]. For both of these hypotheses to be plausible, there must be an implicit understanding that rates of change matter. The work presented in this paper makes this understanding explicit.

4. Routes to glaciation

These results indicate that there are two fundamentally different dynamical routes to glaciation: they are illustrated schematically in figure 5. To explore conceptually the effects of a diverse array of perturbations affecting radiative fluxes or carbon cycle fluxes starting from a stable warm climate state, we introduce the coordinates of generalized volcanic outgassing V_g and generalized stellar flux S_g. These are chosen because any perturbation to carbon cycle fluxes or radiative fluxes can be straightforwardly mapped onto the (V_g, S_g) space. For example, an anomalous increase in weathering is functionally equivalent to a decrease in V_g, while an anomalous increase in planetary albedo is equivalent to a decrease in S_g. The behaviour of the model in terms of the real parameters V, S is shown in the regime plot in figure 1. The following discussion considers the ‘real-world’ implications of that mathematical view.

Figure 5.

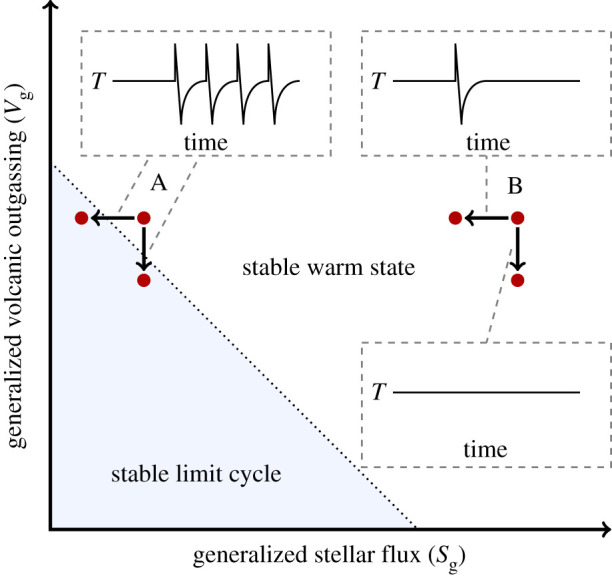
Schematic illustrating the two dynamical routes to glaciation. The parameter space of generalized volcanic outgassing V_g and generalized stellar flux S_g follows the regime plot in figure 1. Changes in carbon cycle fluxes and radiative fluxes can be straightforwardly mapped into this space; for example, an increase in weathering corresponds to a decrease in V_g and an increase in albedo corresponds to a decrease in S_g. Route A is a crossing of the limit cycle boundary due to decreases in V_g and/or S_g. Route B is a transient rate-induced glaciation triggered by sufficiently fast decreases in S_g; this is accessible anywhere in the parameter space. A decrease in V_g which does not cross the limit cycle boundary does not lead to glaciation. (Online version in colour.)

The first route to glaciation (route A in figure 5) involves the stable warm climate state losing stability (i.e. it bifurcates). In our model, decreases in V_g and S_g can accomplish this by pushing the system into the neighbouring limit cycle regime. The climate state will begin oscillating between warm and cold states unless future parameter changes move the system out of the stable limit cycle regime. The timescale on which the initiating perturbation occurs does not matter. The second route to glaciation (route B in figure 5) is through a decrease in S_g that exceeds the critical rate. Here, the stable warm climate state does not lose stability; instead, a single transient glaciation occurs, and the stable warm climate state is eventually recovered. Because the stability boundary does not need to be crossed, route B is accessible in a vastly larger region of parameter space than route A. As figure 5 indicates, a decrease in V_g cannot trigger rate-induced glaciation. This is because it does not affect the shape of the $\dot{T}=0$ nullcline, as discussed previously.

In previous models of glaciation, decreases in atmospheric CO₂ and in effective stellar flux have been considered as dynamically equivalent [4,5]. Our model indicates that this is no longer true once the carbonate–silicate cycle is included. Here, decreases in CO₂ occur because of decreases in V_g, which can only initiate glaciation via passage through the bifurcation (route A). Decreases in S_g, on the other hand, can also trigger rate-induced glaciation (route B). However, changes in radiative fluxes from other greenhouse gases are appropriately mapped onto changes in S_g; thus, they can trigger rate-induced glaciation. The expected correspondence between CO₂ and other greenhouse gases disappears because of the strong negative feedback on CO₂ from the carbonate–silicate cycle.

5. Glaciation far from the outer edge of the habitable zone

The outer edge of the ‘habitable zone’ (OHZ) is classically defined as the stellar flux value beyond which an Earth-like planet can no longer maintain surface liquid water at any atmospheric CO₂ concentration [11,12]. However, the discovery that Earth-like planets may experience limit cycles between temperate and glaciated states within the classical habitable zone suggest the existence of an ‘effective’ OHZ, beyond which the warm climate state loses long-term stability [13,14,17]. In our model, this effective OHZ is the boundary of the limit cycle regime (see figure 5). The previous result (rate-induced glaciation) can therefore also be phrased as follows: changes in radiative fluxes can initiate glaciation via the rate-induced route without moving the system state beyond the effective OHZ; changes in CO₂ fluxes cannot.

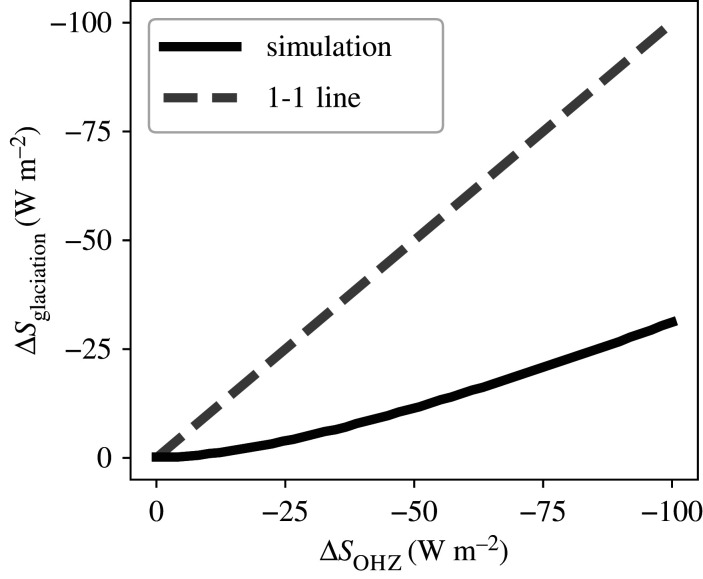
In figure 6, we compare the critical instantaneous stellar flux change to induce glaciation in our model, denoted ΔS_glaciation, with the stellar flux change needed to cross the effective outer edge of the habitable zone, ΔS_OHZ. As we see, ΔS_glaciation is always significantly smaller than ΔS_OHZ. This demonstrates that Earth-like planets can remain surprisingly susceptible to glaciation even if they are far from the OHZ.

Figure 6.

Susceptibility to glaciation far from the outer edge of the habitable zone. Here, we plot the critical instantaneous change in stellar flux required to trigger a glaciation in our model (ΔS_glaciation) versus the change in stellar flux needed to cross the effective outer edge of the habitable zone (ΔS_OHZ). Here, V/W₀ = 1. We see that ΔS_glaciation is significantly smaller than ΔS_OHZ; thus, Earth-like planets can be in stable warm climate states far from the OHZ while remaining quite susceptible to glaciation.

6. Glaciation in Earth’s geologic past

The palaeoclimate record suggests that the Earth has experienced multiple transient low-latitude glaciations in its geologic past. These include the Makganyene glaciation in the Palaeoproterozoic, at ca 2.2 Ga [2], and the Sturtian and Marinoan glaciations in the Neoproterozoic, at ca 717 and 649 Ma, respectively [3,4]. A third group of younger Neoproterozoic glacial deposits in the Ediacaran Period has been referred to as the Gaskiers glaciation; however, it has not been established that all of these deposits were synchronous, and the evidence for low-latitude glaciation at this time is weak [27]. In any case, there remains extensive debate about what initiated these glaciations, and why the Neoproterozoic glaciations occurred so ‘close’ together in time [5]. Proposed mechanisms include decreased CO₂ degassing rates [28] as well as increased weathering due to a host of reasons: a concentration of landmass in the tropics [29], the breakup of the supercontinent Rodinia [3,30], emplacement of highly weatherable continental flood basalts [31,32], or biological innovations [33,34]. Another class of potential triggers includes changes in radiative fluxes, such as volcanic aerosol forcing [26], a sudden collapse of a methane greenhouse [29,35–37], or an increase in cloud condensation nuclei due to the expansion of eukaryotic algae [38].

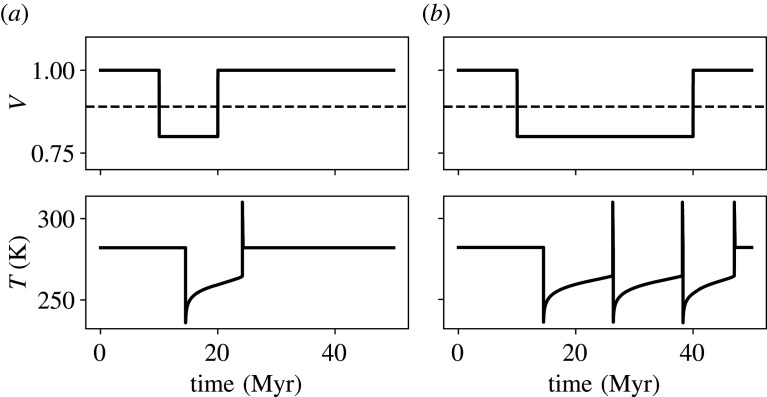
The identification and understanding of the two dynamical routes to glaciation (figure 5) constrains the kinds of perturbations that could have initiated past low-latitude glaciations. Perturbations to carbon fluxes (specifically, decreases in V_g) can only initiate glaciation by causing the warm climate state to lose stability (route A). In our model, this results in a permanent limit cycle; this is likely inconsistent with the observational record. An apparent periodicity of the Sturtian, Marinoan and Gaskiers glaciations in the geochemical record led Mills et al. [15] to suggest that they represented three iterations of a limit cycle; however, this theory is challenged by the revised dating of the Sturtian termination [39]. The only way that a perturbation to carbon fluxes can produce a single transient glaciation event is if the perturbation is ‘reversed’ before a single period of the limit cycle has elapsed. In terms of figure 5, envision a scenario where glaciation is triggered by a decrease in V_g that moves the system into the limit cycle region. Once the first deglaciation occurs, a second glaciation can only be prevented if V_g has returned back to a value which permits a stable warm state (figure 7). Therefore, if these past glaciations were indeed individual transient events triggered by decreases in V_g, such as from increased weathering, conditions in the post-glacial hothouse must have returned V_g to a higher value, preventing a second glaciation.

Figure 7.

Forcing the model with step decreases of V (volcanic outgassing) that persist for different time periods. S = 1280 W m⁻². The dashed line indicates the position of the limit cycle bifurcation. Recall that anomalous increases in weathering are functionally equivalent to decreases in V. Since changes in carbon fluxes can only initiate glaciation via passage into the limit cycle regime (figure 5), the only perturbation that can create a single transient glaciation event is one that decays before one period of the limit cycle has elapsed (a). Otherwise, multiple iterations of the limit cycle result: after a short-lived post-deglaciation hothouse, glaciation ensues again (b).

This reasoning suggests that the low-latitude palaeogeography of the Neoproterozoic, which was much longer-lasting than the Neoproterozoic glaciation events, is unlikely to have been a proximal trigger. In contrast, increases in weathering from continental flood basalts or biological innovations are inherently reversed by the glaciation to some extent, making them attractive candidates for meeting this V_g reversal constraint. Glaciation would strip the continents of their newly acquired blanket of basalt [32], decreasing post-glacial weatherability. For increases in weathering due to biological innovations, the evolutionary pathway of the organisms responsible would likely be strongly modified by the glaciation. Glaciation would have other complicating effects, however; for example, scouring of the long-lived continental regolith by the Sturtian glaciation should have increased weatherability [40], while deglaciation could in general increase volcanic outgassing rates [41]. Rigorous quantification of the relative importance of all of these processes would provide further insight.

Perturbations to radiative fluxes, on the other hand, are most likely to initiate glaciation in the rate-induced manner (route B in figure 5). The critical rate of change to trigger glaciation is a function of the timescale (electronic supplementary material). Potential triggers include volcanic aerosol forcing [26], a sudden collapse of a methane greenhouse [29,35–37], and biological innovations [38]. Aerosol forcing is especially attractive for the Sturtian glaciation because the emplacement of the Franklin Large Igneous Province essentially coincides with the onset of glaciation [42]. In our model, a one-way decrease in effective stellar flux S is sufficient to initiate glaciation, no specific boundary needs to be crossed, and relatively small perturbations can trigger glaciation in a relatively large region of parameter space (figure 6). These comparatively weak constraints suggest that mechanisms that change radiative fluxes make promising proximal triggers for glaciation; perhaps more so than those that change carbon fluxes.

Regardless of the specific mechanisms responsible, our model also offers a framework for analysing the susceptibility to glaciation. Closer to the boundary where the warm state loses stability, it becomes easier for perturbations to induce glaciation (via both routes). Thus, long-term changes probably acted to move the Earth’s climate close to the limit cycle boundary in the late Neoproterozoic. Furthermore, the rate-induced dynamics discussed in this paper suggest that transient low-latitude glaciation may occur quite generally when Earth-like planets transition too quickly from one stable state to another. Both the Palaeoproterozoic and Neoproterozoic glaciations occurred during periods of oxygenation and major biological innovation [5,43]. These likely represented transitions between different stable states [44,45] and were additionally accompanied by dramatic recurring fluctuations [32,45]. Therefore, given the mechanism of rate-induced glaciation, the coincidence of these transitions with multiple low-latitude transient glaciations in the geologic past may simply reflect a fundamental characteristic of the Earth system: sufficiently fast transitions between different warm stable states can induce transient glaciation along the way.

7. Discussion

In this work, we have used a simple dynamical-system representation of the ice–albedo feedback and the carbonate–silicate cycle; many important features of the real climate system were necessarily neglected or simplified. However, we expect that none of these omissions will affect our qualitative conclusions. The general behaviour of the ice–albedo feedback is consistent across simple models to highly resolved three-dimensional general circulation models [9,10]. There remains debate about how best to approximate the ocean’s heat capacity in a simple model [46]; we discuss this in the electronic supplementary material. Volcanic outgassing and weathering are much more complex processes than their simplified representation in the model indicates; the temperature and pCO₂ dependencies employed here ultimately derive from the widely used model of [18], which may have substantial deficiencies [47]. We have further neglected the effects of seafloor weathering [48,49]. Nevertheless, we expect that our qualitative results are robust to changes in weathering formulation: we discuss this in the electronic supplementary material. Finally, we have only represented outgoing longwave radiation and the effects of spatial resolution in a highly simplified manner. However, recent modelling work which integrates both of these complexities [13,17] displays qualitatively the same two-timescale system, the same limit cycles, and the same kind of transition from a stable warm state to a limit cycle as our model does. Therefore, we expect that the dynamics elucidated in this paper should remain robust across more complex models: this represents an avenue for further research.

In our model, the warm stable state bifurcates to a limit cycle everywhere in the parameter range of interest (figure 1). However, when the potential for the CO₂ greenhouse to reach a maximum at high partial pressures is included, for some parameter choices, the warm stable state bifurcates directly to a cold stable state [13]. In this case, the first route to glaciation (route A) involves passage to the cold stable state. Because this makes no difference to the rate-induced route, this does not affect our conclusions regarding susceptibility to glaciation. Because a permanent snowball is also inconsistent with the Neoproterozoic record, this has no effect on our V_g reversal constraint for carbon flux perturbations: any perturbation which induces transition to a cold, permanently stable state still needs to be reversed before the system can return to the warm stable state.

8. Conclusion

It is well understood that glaciation can be initiated on Earth-like planets when changes in radiative fluxes [6–10] or in CO₂ fluxes [13,14] exceed a critical threshold. Here, we have demonstrated and explained an additional possibility: glaciation is initiated when changes in radiative fluxes exceed a critical rate. This is a consequence of the timescale contrast between radiative equilibration and equilibration of atmospheric CO₂ by the carbonate–silicate cycle. During a rate-induced glaciation, the warm stable climate state does not lose stability; this motivates our identification of the two dynamically different routes to glaciation (figure 5). Dynamical correspondences with more complex models [13,17], as well as the simplicity of the mechanism, lend confidence in the robustness of our results.

Rate-induced glaciation is accessible in a much larger region of parameter space than its alternative; thus, planets far from the outer edge of the habitable zone remain susceptible to global glaciation (figure 6). Changes in carbon fluxes can only trigger glaciation through causing the warm state to lose stability; therefore, a carbon flux perturbation can only initiate a single transient glaciation if it pushes the system beyond the instability boundary (figure 5) but is ‘reversed’ before a second glaciation can occur. In contrast, radiative flux perturbations can initiate transient glaciations quite far from the instability boundary (figure 6) and without such a reversal constraint. Because rate-induced glaciation can be initiated via one-way movement between two long-term stable states, the co-occurrence of transient glaciations with periods of major biogeochemical transition in Earth’s geologic past could reflect a fundamental characteristic of the Earth system rather than a mere coincidence. Intriguingly, transient catastrophic climate disruptions may be a general feature of Earth-like planets that move between different stable states too quickly.

Data accessibility

Code to generate all of the plots in this paper is available as electronic supplementary material.

Authors' contributions

C.W.A. and D.H.R. designed research, C.W.A. conducted research, and C.W.A. and D.H.R. wrote the paper.

Competing interests

We declare that we have no competing interests.

Funding

This work was supported by the Lorenz Center.