Simulation of Excitation by Sunlight in Mixed Quantum-Classical Dynamics

Abstract

This paper proposes a method to simulate nonadiabatic dynamics initiated by thermal light, including solar radiation, in the frame of mixed quantum-classical (MQC) methods, like surface hopping. The method is based on the Chenu–Brumer approach, which treats the thermal radiation as an ensemble of coherent pulses. It is composed of three steps: (1) sampling initial conditions from a broad blackbody spectrum, (2) dynamics propagation using conventional methods, and (3) ensemble averaging considering the field and realization time of the pulses. The application of MQC dynamics with pulse ensembles (MQC-PE) to a model system of nucleic acid photophysics showed the emergence of a steady excited-state population. In another test case, modeling retinal photophysics, MQC-PE predicted that although the photoisomerization occurs within 200 fs, it may take tens of microseconds of continuous solar irradiation to photoactivate a single retinal. Such emergent long timescales may impact our understanding of biological and technological phenomena occurring under solar radiation.

1. Introduction

Nonadiabatic mixed quantum-classical (NA-MQC) dynamics encompass some of the most popular methods to simulate nonadiabatic molecular time evolution after a photoexcitation.¹⁻³ In these methods, the nuclear motion follows classical equations, while electrons are treated quantum-mechanically. The equations of motion are complemented by nonadiabatic algorithms, allowing the coupling of different electronic states. The advantage of such methods is that they allow the retention of full dimensionality and do not require precomputed or parametrized potential energy surfaces.

NA-MQC simulations are usually set to be compared to experimental data from time-resolved spectroscopy, where the molecular systems are excited by coherent ultrashort sub-100-fs pulses, pumping the molecular systems into specific bands.⁴ Despite several developments aiming at dealing with the initial laser field acting on the molecule,⁵⁻¹² most simulations just assume instantaneous pulses, with the molecule starting its dynamics in one or few excited states of a single absorption band. (For a recent discussion on this issue, including the proposition of a new approach to sample continuum-wave (CW) fields, see ref¹³).

To the best of my knowledge, one aspect that has not been discussed in the context of NA-MQC dynamics is how to simulate excitation by thermal radiation, most specifically sunlight. Brumer and co-workers have pioneered in the studies of theoretical photochemistry induced by thermal light, using different methodologies.¹⁴⁻¹⁷ In addition to the expected broadening of the spectral excitation range, they have shown that thermal light should kill all time-dependent coherences commonly observed in the results of ultrafast spectroscopy.^17,18 Moreover, the continuous field slowly populates the excited states, giving rise to long time constants sometimes exceeding milliseconds, even when the underlying photophysics are within the picosecond regime.¹⁴ Therefore, mastering the methodologies to simulate the molecular response to thermal light may profoundly impact the way we investigate many different fields, including photosynthesis, vision, solar-induced mutagenesis and carcinogenesis, photovoltaic devices, and environmental and atmospheric photochemistry to name a few.

How should we translate such a broadband, incoherent, continuous radiation acting on a molecule into NA-MQC trajectories? Should each trajectory be created in a coherent superposition of excitations covering the spectral radiation? Should the excitation be treated incoherently, with each trajectory created in a different state of the spectrum? Should the trajectories be necessarily propagated with the molecule interacting with a stationary electric field?

In this paper, I address these questions by adapting the transform-limited-pulse representation of thermal light proposed by Chenu and Brumer.¹⁵ This approach is particularly well-suited to be used in NA-MQC dynamics because the incoherent radiation is treated as an ensemble of coherent pulses, providing a natural bridge for methods like surface hopping.

Assuming the validity of the first-order perturbation theory of radiation-matter interaction in a stationary field of a black body at temperature T, Chenu and Brumer¹⁵ have shown that the thermal light can be described as an ensemble average of realizations of coherent pulses. Each field realization is a pulse given as

1

where t_s is an arbitrary timescale constant, A is an attenuation factor discussed later, and γ marks the time of each realization of the pulse. In the case of sunlight, with a temperature T = 5778 K,¹⁹ the pulse described by eq 1 has about 5 fs duration and a peak amplitude of 1 kV/m, as shown in Figure 1.

Figure 1.

Pulse shape for the field realization at γ = 0 (T = 5778 K). The shape for the other field realizations is the same but displaced in time. t_s = 1 fs.

In practical terms, in the Chenu–Brumer approach, the thermal excitation happens over an ensemble of molecules, each of them excited by a different realization of E^(γ)(t). Thus, γ can be interpreted as a counting index of the ensemble. It must be emphasized that the excitation process must always be described by an average over the ensemble, while a single realization does not bear any physical meaning in itself.

Such an ensemble of short coherent pulses has a familiar ring for users of NA-MQC methods. These methods are naturally tailored to work with ensembles, in the form of either independent or coupled trajectories.²⁰⁻²² The results from surface hopping,²² in particular, also only make sense as an average over the ensemble. Moreover, the ultrashort pulse of each realization at high temperatures plays favorably for the validity of the instantaneous approximation.

Therefore, it seems natural to identify each pulse realization to a different trajectory in the NA-MQC simulations, using them to define a set of initial conditions to start dynamics. There is a catch, however: a coherent pulse as short as 5 fs must cover a broad spectral band, and as such, it poses a challenge of how to define the initial electronic states. I show below that there are different ways of dealing with this issue, depending on the NA-MQC method adopted. After having defined the broadband initial conditions for dynamics, we can run the simulations in conventional ways, thanks to the decoupling between the nuclear motion and the short pulses. Finally, the results of the dynamics must be averaged accounting for the effect of the weak pulse on the electronic density and the fact that each pulse occurs at a different time. I call all this three-step procedure NA-MQC dynamics with pulse ensembles (MQC-PE). Before discussing it, however, we should first review some key points of the Chenu–Brumer approach.

2. The Chenu–Brumer Approach for Thermal Light

Each pulse realization (eq 1) excites the molecule into an electronic wavepacket given by

2

where α′ counts over the N_α electronic excited states of the molecule. For a specific state α, with the wavefunction |α⟩, the energy is ε_α, and transition dipole moment norm is μ_αg. K and C_α are

3

and

4

where ω_αg = (ε_α – ε_g)/ℏ,

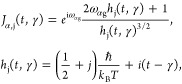5

and F(x) is the Dawson function

6

The definition of K in eq 3 differs from that in the original paper by a factor 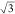. This factor stems from the missing sum over of three cartesian coordinates of the electric field of the thermal light in eq 7 of ref¹⁵ (see the Supporting Information, note SI-1).

From a practical point of view, the infinite sum in eq 4 is replaced by a finite sum over the first N terms, C_α ≈ C_α^(N). As shown in Figure SI-1, only few terms are needed to reach convergence.

After the pulse is over, the coefficients tend to become a constant value (Figure SI-2), which is a function of the excitation energy ε_αg = ω_αg/ℏ of state α (Figure SI-3). A significant feature at high temperature is that |C_α( ∞ , γ)|²does not depend on γ for values larger than few femtoseconds (Figure 2), as it becomes proportional to the spectral radiance of the black body

7

Figure 2.

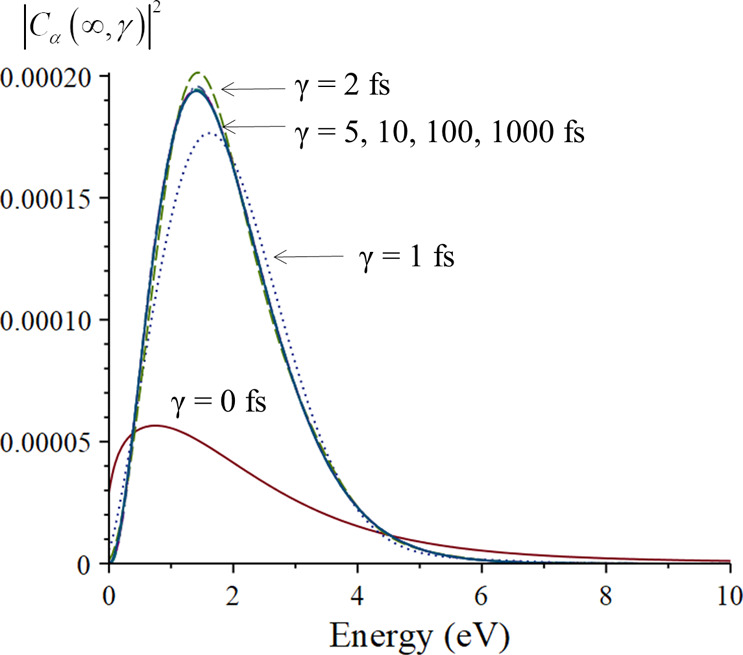
|C_α^(N)( ∞ , γ)|²as a function of the energy of state α, plotted for different values of γ. Values computed for t = γ + 10,000 fs and N = 4. The blackbody spectral radiance at T = 5778 K is the solid line underlying the curves for large γ values. It has been normalized by maximum of the curve for γ = 5 fs.

For a single realization γ, the population in state α at time t is given by

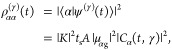8

and the coherence between excited states α and β is

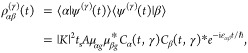9

where ε_αβ = ε_α – ε_β is the energy gap between the states. |C_α(t, γ)|² and C_α(t, γ)C_β(t, γ)* are shown in Figure SI-4. Note that the density matrix elements ρ_αβ^(γ)(t) are given per unit of area. Note also that summing the population over α does not amount to unity. To recover the full population, the ground state must be added as well.

After the field is over, the population of state α is

10

For computational convenience, in the last equation, the transition dipole moment was rewritten in terms of the oscillator strength f_αg using²³

11

Equation 10 shows that the probability of exciting state α is proportional to the product of a molecular factor f_αg/ω_αg and a field factor |C_α( ∞ , γ)|² accounting for the spectral distribution. At T = 5778 K, |C_α( ∞ , γ)|² modulates the probabilities, enhancing molecular transitions in the red-to-blue region (1.5 to 2.5 eV). For γ values near zero, the modulation is broader, from infrared to violet (see Figure 2).

Any quantity derived from the Chenu–Brumer approach must be analyzed in terms of an ensemble average, which for the density matrix elements is given as

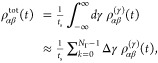12

where Δγ is the time interval between consecutive field realizations, and N_Γ is the total number of realizations. In the ensemble average, t_s cancels out (it also appears within ρ_αβ^(γ)(t)), and because of this, it does not impact the averaged results. However, quantities relative to each field realization are still dependent on t_s, and it is desirable to attribute a reasonable value to it. Given the definition of the ensemble average in the Chenu–Brumer approach, t_s could be given as the time interval between consecutive field realizations Δγ times the number of realizations N_Γ. Such a definition is, however, inconvenient, as N_Γ is arbitrary. In the numerical simulations discussed below, I adopted t_s = Δγ.

In this work, I followed the original formulation by Chenu and Brumer, adopting uniform ensembles of field realizations. Nevertheless, there is no unique representation of the incoherent light in terms of an ensemble. In principle, other ensembles could be used, as long as they satisfy the constraint that the ensemble average is equal to the first-order correlation function of the incoherent field (Eq SI-1).

The original derivation of the Chenu–Brumer approach is strictly valid near the surface of the black body generating the thermal light (equivalent to A = 1 in all previous equations). To simulate sunlight reaching our planet, we should consider that the orbital distance attenuates the emitted power. Thus, if the Sun’s radius is R_S and the Earth–Sun distance is D, the attenuation factor is

13

With such an attenuation factor and t_s = 1 fs, the electric field pulse in eq 1 has a peak intensity of , slightly above the mean annual solar irradiance at the top of the atmosphere, 1361 W/m².²⁴ The factor A should be further reduced by about 25% to match the solar irradiance at Earth’s surface, about 1000 W/m². Nevertheless, an accurate description of the solar radiation at the surface should also consider the spectral deviation from the blackbody profile caused by diverse atmospheric factors.²⁵

3. NA-MQC Dynamics with Pulse Ensembles (MQC-PE)

To simulate the thermal light in MQC-PE, we should (1) create an ensemble of initial conditions for trajectories, each one corresponding to a single field realization, (2) run the dynamics for each trajectory, and (3) do a statistical analysis of the ensemble. The first step should consider the broad-spectrum excitation. The second step is nonadiabatic dynamics as usual. The third step should consider that each realization happens at a different time and that the excitation probability depends on the field. Let us discuss in more detail each of these steps.

In Ehrenfest dynamics² and fewest switches surface hopping,²² nonadiabatic information is computed from the χ_α(t) coefficients of the time-dependent wavefunction

14

In the simulations, χ_α(0) is usually assumed to be unity at the initially occupied state and null in the others. Comparing this equation to eq 2, we could alternatively assign the coefficients of each state to the Chenu–Brumer coefficient for each trajectory.

If the NA-MQC method includes electric-field propagation,⁵⁻¹² the wavefunction can be initialized with

15

and the field in eq 1 should be included in the Hamiltonian. In this equation, s is the area of the molecule exposed to the radiation.

On the other hand, if the NA-MQC method does not include electric field propagation (as usually it is the case), we may use the Chenu–Brumer coefficients after the field is over to initialize the electronic wavefunction:

16

Such prescription may work well for Ehrenfest dynamics in which the trajectory is propagated in the weighted mean of the potential energy surfaces of the electronic states. It can also be used to initialize the wavefunction coefficients in fewest switches surface hopping. Nevertheless, in this case, the use of eq 16 is not fully consistent, as the classical equations for the nuclei would still be initialized in a single state. Either way, eq 16 creates an initially coherent wavefunction for each trajectory (we may call it a coherent initial condition or CIC).

Another possibility for using the Chenu–Brumer approach for simulating thermal light excitation in MQC dynamics without electric-field propagation is just to sample a number of trajectories starting in each state proportional to P_α^(γ), which is defined in terms of the population (eq 10) as

17

Such prescription should also be valid beyond the fewest switches approach, for surface hopping variants that do not explicitly propagate the electronic coefficients, like the Zhu–Nakamura method.²⁶ Different from the CIC approach, using P_α^(γ) to sample the initial states creates an entirely incoherent ensemble of initial conditions (IIC).

Both the coherent and the incoherent approaches for initial conditions for dynamics without field propagation assume that the pulse is instantaneous, in the sense that there is no nuclear motion during the field application. This is a reasonable hypothesis in the case of sunlight, with pulses shorter than 5 fs (see Figure 1), as the fastest motions in ordinary molecules are X-H stretching modes, with periods of about 10 fs. Nevertheless, cold blackbody sources may be completely out of the scope of the method. To give an extreme example, the microwave background produced at 2.7 K has pulses lasting 5 ps,¹⁵ therefore, intermixing with the molecular dynamics.

After generating the initial conditions, the dynamics simulations are not different from the usual. An instantaneous pulse initiates the molecular excitation, and we propagate the state evolution afterward. This process is repeated for an ensemble of N_Γ trajectories.

Any quantity computed as a function of time for each trajectory must be analyzed in the ensemble average. For dynamics initiated with incoherent initial conditions, making use of eq 12, the ensemble average of a quantity Q^(γ)(t)is

18

where α is the initial state, and Q^(kΔγ) means that the initial time for the corresponding trajectory should be shifted to t₀ = kΔγ. Here, Q^tot(t) is given per unit of area. It should be multiplied by s to get it per molecule.

Note that when using IIC, the population ρ_αα plays a double role in the model. First, it defines the spectral region that should be excited. This is done during the initial condition generation. Nevertheless, because the excited state populations do not sum to unity, we do not directly use ρ_αα but employ the re-normalized quantity P_α^(γ) (eq 17). This re-normalization kills the field information, which is contained in the small transfer rate between the ground and the excited states; thus, ρ_αα should be once more considered when the ensemble average is computed through eq 18.

If dynamics are initiated with coherent initial conditions, we can take the wavefunction coefficients in eqs 15 or 16 to compute the population that should be used in the ensemble average.

Finally, note that the average in eq 18 should not correct any over-coherence present in Q^(kΔγ). Therefore, decoherence corrections²⁷ should still be applied during trajectory propagation.

4. Test Cases

Let us first discuss the broadening of the excitation spectrum. Figure 3-top shows the absorption cross-section of 9H-adenine as a function of the excitation energy. It was computed as a simple Gaussian convolution²⁸ of vertical excitation energies and oscillator strengths for 40 adiabatic states. These states were calculated in the gas phase with the resolution-of-identity algebraic diagrammatic construction to second order^29,30 (RI-ADC(2)) using the aug-cc-pVDZ basis set.³¹ The convolution was done assuming 0.3 eV bandwidth and 0.1 eV shift for all transitions. Figure 3-top also shows the probability P_α^(γ) (eq 17) calculated at γ = 0 and 3 fs. The probability distributions for γ larger than 3 fs are virtually identical to the 3-fs curve.

Figure 3.

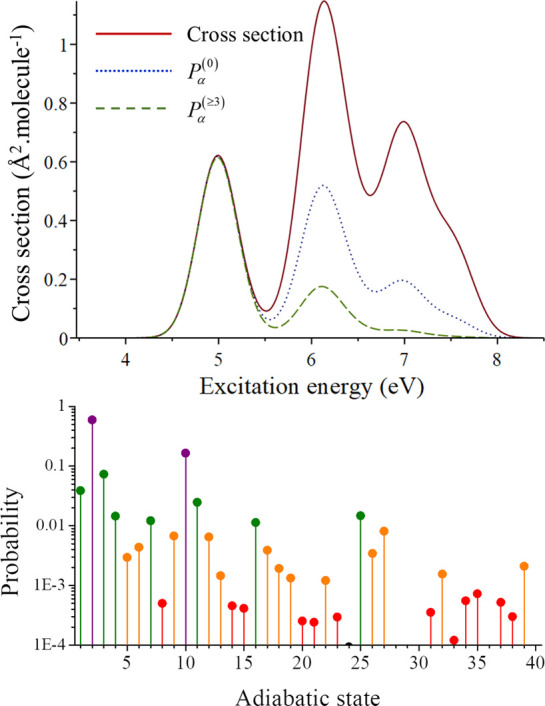
Top: absorption cross-section and excitation probabilities as a function of the excitation energy (eq 17) for adenine. The probability curves were normalized by the maximum of the first cross-section band. Bottom: Excitation probability (P_α⁽³⁾) of each adiabatic state S_α. Numerical values for energies, oscillator strengths, and probabilities are given in Table SI-1. The bar colors indicate the oscillator strength intensity, increasing from red to violet.

From the molecular properties only, without considering the solar radiation, the cross-section shows three strong bands at 5.0, 6.5, and 7.5 eV. Nevertheless, when the solar radiation is considered, excitation in the high-energy bands is screened out. For the first field realization at γ = 0, the probability of exciting the strongest band at 6.5 eV is reduced to approximately the same as to excite the first band. For the following field realizations, this probability becomes even smaller, although it is still sizable. For a large number of field realizations, it is statistically safe to neglect the odd behavior of P_α⁽⁰⁾ and take P_α(dashed curve in Figure 3-top) to sample the initial state for all starting trajectories. For instance, taking the minimum of the ground-state geometry, the probability P_α⁽³⁾ associated with each of the 40 adiabatic states α is plotted in Figure 3-bottom. Following this distribution, for a set of 100 trajectories, we should start 59 in state S₂, 16 in state S₁₀, 7 in state S₃, 4 in S₁, 3 in S₁₁, and so on.

If the initial conditions are formed by an ensemble of geometries spanning the phase space (via a Wigner distribution, for instance³²), the initial state for a specific geometry should be assigned byP_α⁽³⁾ computed for that geometry. In this example of adenine, it would imply that most of the trajectories would start in the states forming the first band, a considerable number of trajectories would begin in the states forming the second band, and few trajectories would start in the states forming the third band. Such a distribution of initial states is strikingly distinct from what we do when simulating monochromatic radiation in which a single state is initially populated usually within a narrow excitation energy window.³³

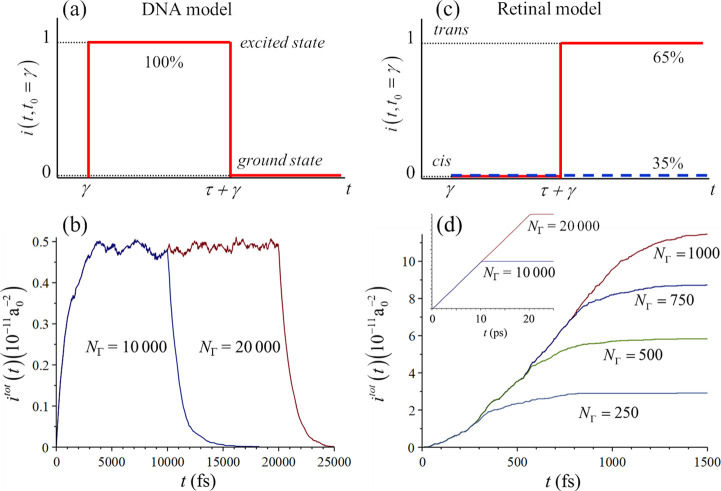
To illustrate the role of the ensemble average, I will discuss two analytical models emulating some typical nonadiabatic MCQ dynamics results (Figure 4). I start with a model for DNA photophysics.³⁴ Let us assume that each nucleotide can be initially photoexcited with any energy within a Gaussian absorption band centered at 4.77 eV and with a standard deviation of 0.3 eV.³⁴ The band has oscillator strength 1. (Note that I am neglecting the excitation into the high energy bands.) After an instantaneous excitation, the nucleotide is supposed to return to the ground state with 1 ps lifetime (Figure 4a).³⁵ (I am also neglecting long-lived excitation processes.³⁶) Suppose we have run nonadiabatic dynamics, say with surface hopping, and we are monitoring the current molecular state. We define the function i(t) that has the value 0 when the molecule is in the ground state and 1 when it is in the excited state. Considering that each trajectory starts at a different time γ, the excited-state population of a single trajectory as a function of the time can be modeled as

19

where H(t) is the Heaviside function, and t_r is the internal conversion time sampled from an exponential distribution with the 1 ps time constant.

Figure 4.

Analytical models emulating results from MQC trajectories. (a) DNA model (eq 19). Trajectories are excited at the time γ and return to the ground state at τ + γ. Each trajectory starts at a different γ. (b) Function i^tot(t) (eq 20) representing the excited-state population of nucleotides as a function of time for different values of N_Γ. (c) Retinal model with two types of trajectories starting at the time γ (eq 21). The solid curve illustrates a trajectory that isomerizes at time τ + γ. The dashed curve represents a trajectory that does not isomerize. 65% of trajectories are of the first type. (d) i^tot(t) for the population of the trans photoisomer for different values of N_Γ. The inset shows i^tot(t) for N_Γ = 10 and 20 thousand. In both models, τ is sampled from a statistical distribution.

Using eq 18, the ensemble-averaged excited-state population (per unit of area) is

20

This quantity is plotted in Figure 4b for N_Γ equal to 10,000 and 20,000 trajectories, each trajectory corresponding to one field realization. Δγ is 1 fs and, as discussed, t_s = Δγ. The figure shows that the ensemble-averaged excited-state population increases as a function of time nearly independent of N_Γ. Initially, there is a fast, transient rise triggered by the field starting at time 0. At 3 ps, the population reaches a stationary regime and remains constant, while each excitation is compensated by a return to the ground state. After the illumination window is closed at ΔγN_Γ, the excited-state population quickly drops. The mean value of the excited-state population in the stationary region is i_mean^tot = 0.5 × 10^–11 a₀^–2 (or 1.8 × 10^–11 Å^–2).

To get a feeling of the impact of this population, consider that a human skin cell has N_nuc = 6.4 × 10⁹ nucleotides.³⁷ If the nucleobase area exposed to the radiation is s = 17 Ų (see Figure SI-5), it means that under continuous solar irradiation, there are always about N_nuci_mean^tots = 2 excited nucleotides in the cell.

As a second example, consider the cis-trans photoisomerization of retinal.³⁸ In this case, the molecule is supposed to be initially in the cis isomer, and only one excited state is considered, with an excitation energy of 2.1 eV and oscillator strength of 1. After an instantaneous excitation, the molecule may isomerize into trans following an exponential distribution within the 200 fs time constant and 0.65 quantum yield, like it does in bovine rhodopsin.³⁸ Once more, suppose we have run surface hopping, we are monitoring the molecular isomer at each time step of each trajectory. We define the function i(t) that becomes 0 when the molecule is in the original conformation (cis) or 1 if a new isomer (trans) is formed (Figure 4c). To compute the ensemble average, we should consider that each trajectory starts at a different time γ. Under these conditions, the isomeric form at time t for a single trajectory can be modeled as

21

where t_r is the isomerization time sampled from an exponential distribution with the 200 fs time constant, and r_y is a random number sampled from a Bernoulli distribution with probability 0.65. By construction, 35% of trajectories will be at i(t) = 0 at all times.

The function i^tot(t) can be computed in the same way as in eq 20. Figure 4d shows that the ensemble-averaged trans population increases as a function of time. In the first 200 fs, there is a transient due to the first field realization at time 0. After this, the population increases at a constant rate, which is approximately independent of N_Γ. Finally, after the illumination window is closed at ΔγN_Γ, the population starts to saturate at different levels depending on N_Γ. In principle, while the light is shining and the cis population is not depleted, the trans population should continue to raise with a constant rate. Fitting the region of linear rise of i^tot(t) with a linear function gives a rate of k_trans = 4.3 × 10²² s^–1 m^–2 for the trans isomer formation. Taking the cis-retinal area as s = 56 Ų (Figure SI-5), the rate per molecule is k_s = k_transs = 2.4 × 10⁴ s^–1. This means that it takes 42 μs of continuous solar irradiation to isomerize the molecule. The k_s rate calculated under other illumination conditions is given in Table 1.

Table 1. Cis-trans Isomerization Rate per Molecule under Different Illumination Conditions^a.

condition	T (K)	A (RS2/D2)	ks (s–1)
extra-terrestrial	5778	1	2.4 × 104
ground level	5778	0.75	1.8 × 104
scotopic vision	4100	3.06 × 10–11	1.2 × 10–7 (MQC-PE)
			1.9 × 10–7 (Redfield theory14)

^aComputed with MQC-PE with the analytical model emulating retinal MQC trajectories (eq 21) and s = 56 Ų unless stated otherwise.

Considering that a cone cell has about N_ret = 7.8 × 10⁷ retinal molecules,³⁹ how long should the cell be irradiated before the isomerization starts? The probability per cone cell that r or more of these molecules will be in the trans conformation at time t follows the binomial distribution¹⁴

22

where k_ste^–k_st is the Poisson probability of isomerization of a single molecule at time t. Therefore, under continuous solar irradiation, it takes about 0.5 ps to isomerize one or more molecules and 6 ps to isomerize more than 10 molecules.

Hoki and Brumer¹⁴ studied retinal isomerization under incoherent light excitation using the Redfield theory applied to a one-dimensional model coupled to a bath. They showed that under conditions of scotopic vision (T = 4100 K and maximum luminance 0.06 cd.m²), the cis-trans isomerization rate is 1.9 × 10^–7 s^–1 (Table 1), corresponding to about 1.3 ms of continuous irradiation to isomerize one or more molecules in a rod cell containing 4 × 10⁹ retinal molecules. With MQC-PE (see note SI-2), the isomerization rate under the same condition is 1.2 × 10^–7 s^–1, and it takes 1.9 ms to isomerize one or more molecules in a rod cell. The excellent agreement between these two completely distinct approaches is a good indication of the validity of the MQC-PE method.

We have seen that N_Γ should be chosen to set an illumination window ΔγN_Γ that spans the ensemble averaged properties beyond the transient region and includes the steady regime (constant population in the DNA model or constant rate in the retinal model). The information from the steady region can be used to estimate properties in timescales much longer than those from the ultrafast dynamics. Thus, the value of N_Γ will change case to case. In both examples discussed here, I showed results for up to N_Γ = 20,000 trajectories (or field realizations). This is a large number viable only for analytical models. If our goal in MQC-PE is to run realistic situations, where trajectories are computed with on-the-fly electronic structure calculations, the affordable number of trajectories is one hundred times smaller, about 200. This means that each trajectory must be repeated many times (but with different γ) in the evaluation of the ensemble average. We should, however, ensure that the number of trajectories actually simulated is statistically representative of all mechanistic and nonadiabatic effects occurring in the system, with acceptable accuracy.

I have shown in the examples the emergence of long timescales out of the treatment of the MQC-PE dynamics results. Some of them are astonishing, like the 96 days of continuous irradiation needed to isomerize a single retinal molecule under scotopic vision conditions. Nevertheless, these long timescales only reflect the information contained in the ultrafast dynamics. Thus, the total time the trajectories must run must be large enough to include all relevant photophysical and photochemical effects that are expected to take place in the molecular system.

5. Conclusions

Thermal light emitted by a black body like the Sun is remarkedly distinct from laser sources used in many spectroscopic techniques.¹⁶ If we aim at unveiling the details of photoprocesses like those at the molecular basis of photosynthesis, vision, or photovoltaics, we may have to take a step toward simulations of incoherent light sources. My goal in this paper was to propose a methodology to simulate the excitation by thermal light in multidimensional mixed quantum-classical dynamics.

Working in the frame of the Chenu–Brumer approach, which models incoherent light by an ensemble of coherent pulses, I proposed the MQC-PE method consisting of three steps:

• 1)sample the initial state for the MQC trajectories from a broadband spectral distribution of the black body (eq 17);
• 2)run dynamics in the conventional way (using surface hopping, for instance);
• 3)displace the initial time of each trajectory to correspond to a distinct field realization and average the results of the dynamics weighting them by the excited-state density induced by the pulse (eq 18).

A test case showed that the first step requires starting dynamics from many different states in different absorption bands. Taking adenine as an example, I showed that the two most initially populated states are S₂ and S₁₀, which are 1.1 eV apart.

Exciting with thermal light does not change the nature of the dynamics in its main aspects. An ultrafast photoprocess like the ultrafast internal conversion of a nucleobase will still take place within 1 ps. Nevertheless, the continuous irradiation by a weak field causes a slow transfer to the excited states. When this slow transfer is considered in the average of many ultrafast processes, we see time constants emerging in much longer scales. Using a simple model for nucleic acid photodynamics, MQC-PE showed that continuous sunlight irradiation leads to a steady population of two excited nucleotides in a skin cell. With a simple model for retinal photoisomerization, the method showed that it takes 40 μs of continuous irradiation to isomerize a retinal molecule in a photoreceptor cell. This time jumps to few milliseconds under conditions of scotopic vision, in excellent agreement with previous predictions from the Redfield theory.

Although the dynamics step is based on conventional methodologies, reaching statistical significance in MQC-PE may be harder than usual. Both test cases I discussed here required about 10,000 trajectories to deliver converged rates. This implies that when only a small number of trajectories is affordable, each trajectory must be repeated many times with different starting times in the calculation of the ensemble average.

MQC-PE should work well for simulating radiation from hot, broadband black bodies. In such cases, each pulse realization in the Chenu–Brumer approach is short enough to allow us to decouple the electric field dynamics from the molecular dynamics. Cold sources, however, may have too long pulses and require coupled field-nuclear dynamics.

Despite these shortcomings, the MQC-PE provides a straightforward way to simulate excitation by sunlight and other hot thermal light sources in mixed quantum-classical methods with and without field propagation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00501.

• Note about the definition of K in eq 3; figures with a characterization of C_α^(N)(t, γ), |C_α(t, γ)|², |C_α^(N)(t, γ)C_β(t, γ)*|², and C_α^(N)(t, γ)C_β(t, γ)*; excitation energies, oscillator strengths, and excitation probabilities for adenine; estimates of the molecular area of adenine and the cis-retinal protonated Schiff base; information about the attenuation factor under conditions of scotopic vision (PDF)

The author declares no competing financial interest.