Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jul 31;142(32):13709–13717. doi: 10.1021/jacs.0c02635

Caught in the Act: Mechanistic Insight into Supramolecular Polymerization-Driven Self-Replication from Real-Time Visualization

Sourav Maity †, Jim Ottelé ‡, Guillermo Monreal Santiago ‡, Pim W J M Frederix §, Peter Kroon §, Omer Markovitch ‡,∥, Marc C A Stuart ‡, Siewert J Marrink §,*, Sijbren Otto ‡,*, Wouter H Roos †,*
PMCID: PMC7426903  PMID: 32786814

Abstract

graphic file with name ja0c02635_0005.jpg

Self-assembly features prominently in fields ranging from materials science to biophysical chemistry. Assembly pathways, often passing through transient intermediates, can control the outcome of assembly processes. Yet, the mechanisms of self-assembly remain largely obscure due to a lack of experimental tools for probing these pathways at the molecular level. Here, the self-assembly of self-replicators into fibers is visualized in real-time by high-speed atomic force microscopy (HS-AFM). Fiber growth requires the conversion of precursor molecules into six-membered macrocycles, which constitute the fibers. HS-AFM experiments, supported by molecular dynamics simulations, revealed that aggregates of precursor molecules accumulate at the sides of the fibers, which then diffuse to the fiber ends where growth takes place. This mechanism of precursor reservoir formation, followed by one-dimensional diffusion, which guides the precursor molecules to the sites of growth, reduces the entropic penalty associated with colocalizing precursors and growth sites and constitutes a new mechanism for supramolecular polymerization.

Introduction

The focus of research on supramolecular self-assembly is broadening from exclusively thermodynamically controlled structures to out-of-equilibrium systems.1−5 While for the former the final structure is not influenced by the route it takes, the outcome of out-of-equilibrium self-assembly is dictated by the assembly pathway,6−8 which spurs efforts to unravel assembly mechanisms. Insight is needed into how labile nanoscale assemblies change with time, for which only a few techniques are available. Current methods for real-time visualization of such systems use confocal laser scanning microscopy9 or stochastic optical reconstruction microscopy.10 These methods provide for resolutions down to 80 and 20 nm, respectively, and require the use of fluorescent probes. Recent advances in the field of atomic force microscopy (AFM) have enabled the studying of dynamic processes of (bio)molecular systems using high-speed AFM (HS-AFM)11 at even smaller length scales, including the configurational dynamics of proteinaceous structures,12−14 the assembly of amyloid-like fibrils,15,16 and the movement of synthetic molecular transporters17 with unprecedented spatiotemporal resolution.

By employing HS-AFM, we have now been able to elucidate the molecular mechanism of the recently discovered systems of self-assembly-driven self-replication.18 A prominent feature of such systems is that, under mechanical agitation (shaking, stirring), the assembly processes take place in a mixture of interconverting molecules leading to the autocatalytic sequestration of the assembling molecules and causing their exponential self-replication.18,19 The spontaneous emergence of self-replicators out of such systems appears general, has been observed for different compound classes,20−22 and is relevant in the context of the origin and the de novo synthesis of life.23,24

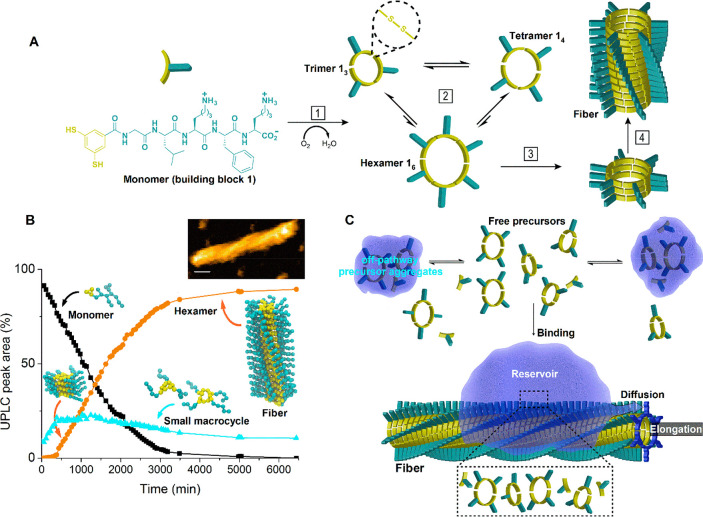
We focused our mechanistic investigation on self-assembling replicators that are formed from the monomeric building block 1, which features two thiols that are readily oxidized to form disulfide bonds, and initially produces a mixture of differently sized macrocycles that interconvert through thiol–disulfide exchange25 (Figure 1A). When investigated under mechanical agitation (stirring), subsequent to a lag phase in which trimers and tetramers (13 and 14) are the dominant products, a self-replicator (cyclic hexamer 16) emerged, following a nucleation–growth mechanism, during which 13 and 14 are converted into 16 (Figure 1B). To obtain the molecular details of the supramolecular polymerization-driven replication process, we used HS-AFM, supported by chemical analysis and molecular dynamics (MD) simulations. The results (presented below) revealed an unexpected assembly/replication mechanism summarized in Figure 1C. Monomer 1 jointly with the small macrocycles 13 and 14 (together termed the “precursors”) form small off-pathway aggregates in solution that are in equilibrium with the nonassembled precursors. Importantly, the free precursors can also bind and accumulate as aggregates onto the fiber surface, to form a reservoir from where they diffuse toward the end of the fiber, which results in fiber elongation. This new mechanism of reservoir formation followed by one-dimensional diffusion is essential for efficient fiber growth as it directs the precursors to the fiber ends that are present at very low concentration.

Figure 1.

Figure 1

Open in a new tab

The fiber self-assembly pathway. (A) Fiber formation from building block 1. Upon oxidation (1) the monomer forms a mixture of macrocycles that can interchange building blocks with one another through disulfide exchange reactions (2). Following slow nucleation (3), 16 can elongate by the stacking of additional hexamer macrocycles (4). (B) Representative kinetic analysis of relative molecular concentrations over time, performed using ultra-performance-liquid-chromatography (UPLC) under stirred conditions. Concentration of monomer (1) (■) diminishes by reaction with oxygen to form small, soluble macrocycles (cyan ▲). After an initial lag phase (roughly 500 min), the concentration of hexamer (16) (orange ●) increases as fibers are formed. Insets show the coarse-grained models of monomer, trimer (13), tetramer (14), and stacks of hexamers (fibers), and a high-resolution AFM image of a single fiber on a lipid bilayer (top right, scale bar 10 nm). Amino acid side chains are not shown in the coarse-grained models. (C) Model representation of the self-assembly pathway summarizing the main findings of the present work (see main text).

Results and Discussion

Capturing the Assembly Pathway of a Self-Replicator at the Single Particle Level

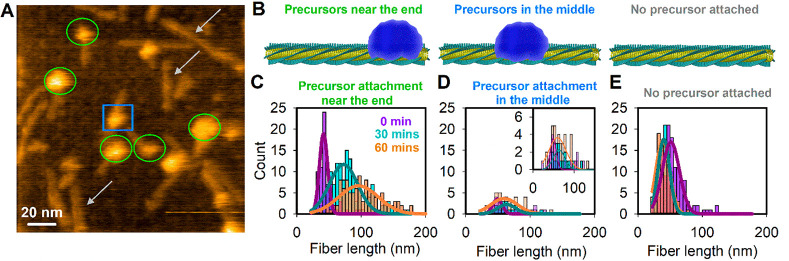
We monitored fiber growth by HS-AFM. Fibers were absorbed onto a mica surface covered with a slightly negatively charged lipid bilayer to ensure binding while still allowing for fiber growth (see Methods). Upon addition of a solution containing precursors, we observed aggregates of these precursors attached to the sides of the fibers (Figure 2A). We distinguished between instances where (i) precursors are attached near the end of the fiber, (ii) precursors were attached near the middle of the fiber, and (iii) no precursor was attached (Figure 2A,B). Analyzing AFM images revealed that precursor attachment near the end occurs at a higher frequency than attachment close to the middle (Figure S1). Interestingly, the majority of the fibers with precursors attached near their ends were growing substantially over time (Figure 2C, see supplementary note for a statistical analysis), while the fibers without bound precursor, or those where the precursors stayed attached near the middle, showed limited or no growth during the same time interval (Figure 2D,E). These observations suggest that both the formation of aggregates of precursors and their proximity to the fiber end are necessary conditions for extension of the fiber.

Figure 2.

Figure 2

Open in a new tab

Precursor attachment near the fiber end is essential for successful growth. (A) Example of an AFM image of fibers grown on a membrane surface in the presence of precursors. Three different fiber–precursor interactions are indicated as green circles (precursors attached near the end of the fiber), a blue square (precursors attached in the middle of the fiber), and gray arrows (fibers without any precursor attached). (B) Schematic representation of these three fiber–precursor arrangements. (C) Histogram of the length of fibers having precursors attached near the end and imaged at three different times in the presence of a 2.31 mM precursor solution. An increase in fiber length can be observed going from 0 min (in purple, N = 70), to 30 min (in cyan, N = 139), and 60 min (in orange, N = 108). (D) Same as (C) but for the fibers having precursors attached in the middle of the fibers. No significant growth was observed after 60 min. N = 20, 17, and 39 for imaging after 0, 30, and 60 min, respectively. Inset shows the same data enlarged. (E) Same as (C) but for fibers having no precursor attached on the fiber. No significant growth was observed after 60 min. N = 120, 77, and 90 for imaging after 0, 30, and 60 min, respectively.

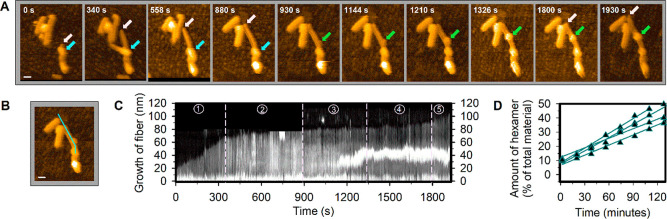
Next, we performed dynamic studies using HS-AFM imaging at 0.5 frame/s, to focus on the fibers that have precursors bound near their end (Figure S2A–F). As can be seen in Figure S2A–F and Video S1, these fibers grow at an average rate of ∼5 nm/min (N = 40), which corresponds to the attachment of ∼11 units of 16 per minute. Note that, as the fibers grow, the relative volume of the attached precursors shrinks (Figure S2D,E). On the other hand, for a fiber with precursors attached in the middle, both the length and the relative volume of attached precursors remain unchanged over time (Figure S2G–I and Video S2). These observations of decrease in precursor volume, only on a growing fiber, suggest that the aggregates serve as a reservoir supplying material for fiber extension. Further dynamic studies confirm this hypothesis by capturing the complete process of fiber self-assembly. Video S3 and Figure 3A show a growing fiber for which five stages were identified. These distinct states are clearly visible when a kymograph is made from a line section over the fiber for the full period of the recording (Figure 3B and C). An initial growth phase from 0 to 340 s at ∼8.5 nm/min (phase 1) is followed by a slower growth of ∼2 nm/min as the reservoir becomes more distant from the growing fiber end (phase 2 [until ∼880 s]). Later, a stagnant phase is observed when the reservoir is presumably too far away from the growing end of the fiber (phase 3 [until ∼1330 s]). New precursor accumulation from solution takes place in between ∼930–1330 s along with diffusion along the fiber. Next, slow growth occurs from ∼1330–1800 s (phase 4), while a new reservoir is gradually forming on the fiber. From ∼1800 s on, the fiber grows rapidly again at ∼8 nm/min, while the reservoir starts depleting (phase 5). Interestingly, while the gradually emerging precursor aggregates show an early stage diffusivity toward the fiber end (phase 3 in Figure 3C and Video S3), the aggregate eventually stabilizes on the fiber surface (phase 5 in Figure 3C) and participates in the growth process. This observation is consistent with what is shown in Video S1, where the already formed precursor aggregate does not move while the fiber still grows. These observations lead us to speculate that the precursor attachment followed by accumulation into aggregates occurs randomly, while the rate of diffusion of aggregates reduces with increasing aggregate mass. This would also explain the low probability of finding the precursors attached near the middle of the fiber (Figure 2). Precursors may initially have attached anywhere along the fiber, but both individual molecules as well as precursor aggregates seem to be prone to diffuse along the fiber toward its end. The small fraction of fibers that were observed to contain the precursors roughly in the middle (Figure 2A,D and Figure S1) is likely the result of inefficient diffusion due to a surface attachment-induced blockage. For the growing fibers, typically a clear asymmetry in growth was observed as only one direction of the fiber elongated. At the used frame rate of 0.5 frame/s and an image size of 300 × 300 pixels, the pixel to pixel acquisition time is 22 μs/pixel, which seems to allow for capturing the presence of precursors on top of the fiber without smearing their position out. When a movie of a growing fiber is analyzed using image segmentation by masking the height of the fiber (∼3.5 nm) and anything above this height is monitored over time, the dynamics on top of the fiber surface can be observed (Figure S3 and Video S4). Following this dynamics indicates that the diffusion dominates in the direction of fiber growth, as visualized in Figure S3.

Figure 3.

Figure 3

Open in a new tab

Precursor accumulation, diffusion, and fiber growth as observed in real-time. (A) Snapshots of AFM images of fibers growing on a membrane surface at different times. The cyan arrows indicate the first active precursor aggregate’s position, the pink arrows indicate the growth site of the fiber, and the green arrows indicate the second precursor aggregate’s accumulation and position. (B) Representative image of the growing fiber from panel A showing the line (in cyan) selected to construct the time-resolved intensity kymograph in panel C. Scale bars in (A) and (B) are 20 nm. (C) Kymograph along the line section in (B) over 1930 s. Dashed lines mark the different stages of growth as described in the text. The immobile fiber that is encountered by the growing fiber in phase 2 was removed from the kymograph for clarity. (D) Fiber elongation rate determination by UPLC. Shortened fibers were used as a seed in the presence of preoxidized precursors to measure the elongation speed in solution. The results are consistent with the values obtained from AFM experiments.

Elongation of the Fibers Scrutinized in Bulk Solution

We also monitored the rate of fiber elongation without any mechanical agitation, and in bulk solution containing 2.31 mM of precursors and 4.3% (in terms of building block 1) of 16 replicator by UPLC analysis, to reveal a growth rate of ∼4 nm per minute per fiber end, or ∼8 units of 16 per minute (Figure 3D), consistent with the AFM results obtained from the fibers attached and grown on a membrane surface (Figure S2F). When we repeated the same experiment using a 15-fold less concentrated precursor solution, we found that the growth rate decreased only by a factor of ∼3 (Figure S4). A systematic investigation revealed that the growth rate levels off at high precursor concentrations (Figure S5). This behavior cannot be explained by saturation of the fibers with precursors, because AFM analysis shows a significant number of fibers that are devoid of precursors in the same concentration range. Instead, these results suggest the existence of an off-pathway assembled state of the precursors that does not contribute directly to the growth of the fibers.

To investigate the nature of this off-pathway state, we studied the precursor solutions by cryo-transmission electron microscopy, by dynamic light scattering, and by analyzing the fluorescence of a solvatochromic probe. The resulting data confirm that the precursors form aggregates in solution (Figure S6). These aggregates are present already from very low concentrations of precursors (critical aggregation concentration of 23 ± 5 μM in building block 1), and because we do not observe them directly attaching to the fibers by AFM (fiber-bound aggregates appear to grow gradually), we infer that they do not contribute to fiber growth. However, they do have an active role by releasing free precursors into the solution, which replenishes those that participated in fiber growth.

To prove that the postulated fiber growth mechanism is also occurring for fibers free in solution and to rule out surface artifacts, we allowed fibers to grow in bulk solution, while periodically taking samples and imaging these using AFM. The resulting data (Figures 4A and S7) reveal a distribution of precursor attachment to fibers similar to that observed in the on-surface experiments. For the first 10 min, the precursors stay attached while the fiber length increases. Interestingly, after 25–35 min, the precursors appear to have migrated to the ends of the fibers, while the fibers had continued to grow. After 60 min, the aggregates have almost disappeared from the fibers and presumably also from the solution, while the fibers have grown to their full extent. The spreading of the aggregates with time is accompanied by a reduction in their height (Figure S7). From the change of fiber length over time (Figure S7), a growth rate of around ∼5 nm/min (N > 20 for each interval) was obtained, in good agreement with our previous estimation from Figure S2F (fiber grown on a membrane surface) and Figure 3D (estimated in bulk by UPLC from fibers grown free in solution). A summary of estimated growth rates from different experimental approaches can be found in Table S1 and supplementary discussion 1. Also, as observed in Figure 4A (and Figure S7), in the course of the first 35 min, the precursors have spread out from the reservoir and moved toward the fiber ends. This suggests that the rate of diffusion of the precursors along the fiber may be significantly faster than the rate of growth, which causes precursors to accumulate near the fiber ends rather than being inserted into the fiber. It also suggests that the diffusion along the fibers occurs unobstructed in solution, while surface artifacts inhibit efficient diffusion when the precursors are attached in the middle (Figures 2A,D and S1). However, the observed rates of fiber growth in both conditions are similar to each other (Table S1). These observations suggest that the diffusivity of the precursors along the fiber is not the growth-limiting factor in this assembly mechanism. To support this hypothesis, we have compared the rate of volume gained by the fiber itself during an elongation to the rate of volume loss by the corresponding precursor aggregate (Figure S8 and Video S5). It can be observed that the precursors diffuse out of the aggregate faster than the growth of the fiber occurs, which fits with our other observations.

Figure 4.

Figure 4

Open in a new tab

Diffusion of precursors along the fiber toward the end. (A) Representative AFM images of fibers immobilized at different times on a surface after growth free in solution. Scale bar 50 nm. The green insets show the cross-section side view of the fiber along the dotted green line in the corresponding figures. The arrows indicate the position of the precursor aggregates. (B) Simulated coarse-grained (CG) fiber structure (16 hexamers, 8 nm) with one molecule of trimer showing the diffusion at different times over a 500 ns simulation. Different colors (from red to blue) indicate the position of the trimer at different times (from 0 to 500 ns). The fiber is represented as a gray surface. (C–E) CG MD simulation of fiber (outlined in black) and single trimer molecules over time. Relative density of trimer added to a preassembled fiber is averaged over 400 simulations at the start of the simulation (0 ns), after 60 ns, and after 500 ns, respectively. The color bar representing the density plots in (C)–(E) is normalized from 0 to 1.

Mechanistic Insights into Precursor Diffusion and Fiber Elongation from MD Simulations and Mass-Kinetic Models

Further support for the postulated assembly and replication mechanism comes from MD simulations. Recent improvements in soft- and hardware, force fields, and enhanced sampling techniques have created new possibilities for the study of complex assembly processes.26−30 Specifically, we employed MD simulations to confirm the hypothesis of the diffusion of precursors along the fiber. A short fiber composed of 16 16 macrocycles was simulated as previously,30 and a single 13 macrocycle was added at a random location in the surrounding explicit solvent at a distance of >2 nm from the stack. The macrocycle was allowed to diffuse and bind to the fiber. Repeated atomistic simulations (N = 200, Video S6) show that binding is typically rapid (<20 ns), but exhibits no preference for any specific location along the fiber axis, except for a tendency to bind to the hydrophobic core of the fiber (Figure 4B). As time progressed, diffusion of 13 occurred along the fiber toward the fiber ends, in agreement with the experimental observations. To probe this process over longer time scales, using larger fibers and with better statistics, a coarse-grained (CG) model for the self-replicating macrocycles was developed using the Martini force field.31 This model correctly reproduces the binding free energy of hexamer macrocycles to the fiber ends, the chiral pitch observed using cryo-TEM and AFM (Figures 1A, S9, and S10), and other structural parameters (Figure S11). CG binding simulations, performed in the same way as for the atomistic simulations, confirmed the diffusion of the macrocycles along the fibers in the course of 500 ns (N = 400) after binding to the fiber (Figure 4C–E and Video S7). The indications that precursor diffusion follows the chiral pitch of the fiber could upon strong fiber attachment to the surface lead to precursor blockage by the surface as shown by the data of Figure 2D.

Finally, mass-action kinetic models of the assembly and replication processes were constructed (supplementary discussion 2). In the simplest model, the fibers grow directly from nonassembled 16 that is sequestered from bulk solution, where it is a minor constituent of the dynamic macrocycle mixture. The more elaborate model includes a role of the fibers in converting precursors into 16, which thus captures the role of the fibers in assimilating the precursors and directing them to the fiber ends. Attempts to fit the experimental kinetic data using the two models only yielded an acceptable fit for the more elaborate model, which provided further support for the validity of the postulated mechanism, as shown in Figure 1B.

Conclusion

We have been able to directly visualize molecular self-replication in real-time with unprecedented resolution and obtained detailed and unexpected insights into the mechanism of the self-assembly-driven self-replication process. HS-AFM revealed a mechanism of supramolecular polymerization, where accumulation of precursor reservoirs occurs along the sides of the existing assemblies. While this mechanism bears some resemblance to the previously proposed secondary nucleation model for amyloids,32 it is distinctly different from this model, as this new aggregate does not itself elongate, but instead promotes growth of the fiber after diffusion of the precursors from the reservoirs toward the fiber end. Results from atomistic and CG MD simulations provide support for molecular diffusion along the fiber as an important step in fiber growth. This diffusion of precursors reduces their search for a growing fiber end from a 3D to 1D problem, which lowers the entropic barrier of supramolecular polymerization. HS-AFM imaging of surfaces can be performed at a frequency of 10 frames per second.11 However, height fluctuations of a single line can be studied 100 times faster,33 which thereby allows for single-millisecond temporal resolution. Next, for studies of man-made systems, the presented HS-AFM approach can likely also shed light on the mechanism in which secondary nucleation and elongation occurs for amyloid fibrils, as the exact mechanism of this process remains unclear.34 To summarize, our results not only establish a new self-assembly mechanism that might well extend to other biological/synthetic systems, but also establish HS-AFM as a powerful tool to unravel self-assembly processes.

Methods

Fiber Formation

A stock solution of 16 was prepared by adding building block 1 [(3,5-dimercaptobenzoyl)glycyl-l-leucyl-l-lysyl-l-phenylalanyl-l-lysine)] to a 1 mL HPLC vial (12 × 32 mm) containing a Teflon-coated magnetic stirring bar (5 × 2 mm, VWR). The building block was dissolved in borate buffer prepared from 25 mM B2O3 and adjusted to a pH of 8.1 to a final concentration of 1.54 mM and was kept at elevated temperatures while mechanical agitation was applied (1200 rpm, 45 °C). The sample was subjected to periodic UPLC analysis and kept at the conditions described above until the sample contained >90% 16. The 16 fibers were then stored at room temperature while stirring and could be used up to 8 weeks after preparation without observing any significant changes in sample composition.

Seed Preparation by Mechanical Shearing

From the 16 stock solution, a 150 μL aliquot was placed in a Couette cell (Rcup = 20.25 mm, Rbob = 20 mm, average radius (R) = 20.125 mm). The sample was subjected to mechanical shearing by rapid rotation of the inner cylinder. The rotational frequency used was 4000 rpm for 30 min, corresponding to a shear rate (γ) of 33 702 s–1. The resulting seeds were stored at room temperature and used within 2 days of preparation.

Fiber End Estimation

The average fiber length of the sheared seeds was analyzed using transmission electron microscopy. Using ImageJ software, we measured the length of 994 sheared seeds, which resulted in an average length of 34.8 ± 15.2 nm. The average height of a single 16 macrocycle30 is 0.485 nm; therefore, we find an average of 71.8 ± 31.3 macrocycles in a sheared seed fiber.

Precursor Solution Preparation

A stock solution of a mixture of 1, 13, and 14 was prepared by adding building block 1 to a HPLC vial (12 × 32 mm) and transferring it to a glovebox. Building block 1 then was oxidized using sodium perborate (0.80–0.85 equiv) in borate buffer to obtain final concentrations of 1.54 and 2.31 mM. The resulting mixture was analyzed by UPLC and could be used up to 3 days if no mechanical agitation was supplied.

Ultra-Performance-Liquid-Chromatography (UPLC) Elongation Experiments

Low Concentration

In a 1 mL HPLC vial was diluted 85 μL of an oxidized precursor solution (92–94% oxidation, 1.54 mM in building block in 50 mM borate buffer, pH 8.12) with 900 μL of UPLC grade H2O. Sheared seeds were added (15 μL) and the mixture was thoroughly mixed, which resulted in a final concentration of 0.154 mM in building block (precursors). This mixture was kept without any mechanical agitation at a constant temperature of 25 °C, and the composition of the sample was monitored by UPLC every 18 min for >800 min. The elongation experiment was repeated four times.

High Concentration

A glass insert was placed in a 1 mL HPLC vial. Of an oxidized precursor solution (88% oxidation, 2.31 mM in building block in 50 mM borate buffer, pH 8.12), 95 μL was added to the inset. Two minutes before the UPLC injection, 5 μL of sheared seeds (2.0 mM in building block) was added and the sample was mixed thoroughly, which resulted in a final concentration of 2.29 mM. The mixture was kept without any mechanical agitation at a constant temperature of 25 °C, during which the library composition was monitored by UPLC every 18 min for 128 min. The elongation experiment was repeated four times.

Elongation Experiments Monitored by Fluorescence

Samples containing sheared 16 seeds (60 μM in building block), thioflavin T (500 μM), and increasing concentrations of precursors (0–2.3 mM in building block, 86% oxidation) were prepared in a 96-well plate using borate buffer as a solvent. The samples were shaken (orbital shaking for 30 s) at a controlled temperature of 25 °C, and the fluorescence of thioflavin T (λexc = 440 nm, λem = 500 nm) was measured every 5 min using a Synergy|H1 microplate reader (BioTek, U.S.). Simultaneously, samples containing thioflavin T (500 μM) and increasing concentrations of 16 seeds or precursors were monitored in the same way. These samples were used as calibration to correlate the fluorescence signal with concentrations of both precursors and 16, and to monitor the photobleaching of thioflavin T (which remained always lower than 5% of the initial signal). The fluorescence intensity at every time point was converted to the concentration of 16 after subtracting the signal coming from precursors, and the initial growth rate was calculated by linear regression of the first five points of each sample. This experiment was repeated three times.

Surface Preparation for AFM Studies

To immobilize the fibers on the surface and to provide at the same time freedom for the fiber to grow, we have used a lipid bilayer deposited on top of freshly cleaved mica. The lipid bilayer was formed by absorption of large unilamellar vesicles (LUVs) onto a freshly cleaved mica surface. LUVs were prepared using a lipid mixture composed of 60% dioleoyl-phosphatidylcholine (DOPC) and 40% dioleoyl-phosphatidyl-serine (DOPS) (mol:mol) from Avanti Polar. The lipid mixture containing 1 mg/mL of total lipids was mixed in 200 μL of chloroform in a small glass vial. Next, chloroform was evaporated using argon gas while the vial was slowly rotated to produce a lipid film on the glass wall. The film was kept in a vacuum desiccator for 30–45 min. After the lipid film was dried, 200 μL of a buffer composed of 10 mM HEPES, pH 7.4, 100 mM NaCl, and 50 mM sucrose was added and vortexed for 30 s. The mixture was freeze–thawed three times using liquid nitrogen. The LUVs were stored at −20 °C for further use within 1 month. For deposition on a mica surface, we have used 0.2 mg/mL concentration of the stock preparation (diluted in the same buffer) and incubated on top of freshly cleaved mica (HS-AFM sample holder) for 15–30 min. The surface was then cleaned 3–5 times with 50 mM borate buffer, pH 8.1.

HS-AFM Experiments

All of the AFM studies were done using HS-AFM (RIBM, Japan) in amplitude modulation tapping mode in liquid.17,35−37 Short cantilevers (USC-F1.2-k0.15, NanoWorld, Switzerland) with a spring constant of 0.15 N/m, resonance frequency around 0.6 MHz, and a quality factor of ∼2 in buffer were used. The cantilever free amplitude was set to 1 nm, and the set-point amplitude for the cantilever oscillation was set around 0.9 nm. Images were taken at 0.2–0.5 frame/s depending on the size of the image. A mica surface of diameter 1.5 mm glued on top of a 5 mm high glass rod was used as the AFM sample stage. The glass rod was then attached to the scanner Z-piezo using a small amount of wax. After formation of the lipid bilayer (as mentioned above), the short preassembled fibers (seeds) were incubated for 30 s and then cleaned with borate buffer. The scanner head was then put upside down into a small liquid chamber containing the cantilever and filled with 120 μL of the recording solution. All on-surface growth experiments were performed in the presence of 2.31 mM precursor in 50 mM borate buffer, pH 8.12. The HS-AFM works as a sample scanning system, and a minimum imaging force (<100 pN) was applied throughout all experiments.

All AFM measurements were done in solution, and we performed AFM imaging experiments on fibers that were grown on a membrane surface and on fibers that were grown free in solution (in a glass bottle) and later deposited on a mica surface to image the fiber. For long-term (> ∼10 min) characterization of the growth process, small seeds were immobilized on a lipid surface, and the chamber was filled with 2.31 mM precursor solution. AFM images were taken at different time points. Because of mechanical drift, imaging the exact place after several minutes was not possible; therefore, we have estimated the elongation by measuring the length of at least 10 fibers on the surface for each point in time. For dynamic studies, we used a similar approach, but after localizing a seed with precursors attached near its end, we zoomed in and imaged it continuously at typically 0.5 frames/s. Because of the low growth rate, mechanical drift during imaging, and the small piezo limit (900 nm × 900 nm), we were only able to follow a fiber for typically ∼10 min. Finally, we also performed AFM experiments on fibers that were not grown on a surface, but free in solution. To do this, we incubated the seeds and the precursors at a 5%:95% molar ratio in a sealed glass bottle. For every predecided time, we then took a small amount of the mixture, which we added onto a freshly cleaved mica surface and left to incubate for 30 s. Next, the surface was rinsed with borate buffer, and the AFM imaging was done immediately afterward in borate buffer.

AFM Data Analysis

For AFM data analysis, we have used Igor-pro software with built-in script from RIBM (Japan) and ImageJ software with additional home-written plugins. The HS-AFM images/movies were only processed minimally, through tilt correction, drift correction, and brightness correction. The kymographs were obtained from the cross-section at a fixed scale (marked for each image) over the entire movie. It represents the height distribution (in terms of intensity) along the line cross section as a function of time. For all different experimental conditions, we obtained and reported the results from several days of experiments. Rounding of growth rates and other values was performed on final numbers. Statistical tests on the relevant AFM data sets are reported in the supplementary notes (Tables S2 and S3).

Cryo-Transmission Electron Microscopy

An aliquot (3 μL) of solutions containing 16, precursors, or both (4 mM, prepared in borate buffer) was deposited on holey carbon-coated grids (3.5/1 Quantifoil Micro Tools, Jena, Germany) that were previously glow-discharged for 15 s. After the excess liquid was blotted for 4 s, the grids were vitrified in liquid ethane using a Vitrobot (FEI, Eindhoven, The Netherlands) and transferred to a FEI Tecnai T20 electron microscope equipped with a Gatan model 626 cryo-stage operating at 200 keV. Micrographs were recorded under low-dose conditions with a slow-scan CCD camera.

Dynamic Light Scattering

Dynamic light scattering measurements were performed on a NanoBrook 90Plus PALS Particle Size Analyzer (Brookhaven, NY), using a 659 nm laser at a 90° detection angle. Samples were prepared in borate buffer and filtered through a 0.2 μm pore size filter. The refractive index used for the particles was 1.5, but no significant differences were observed when changing it from 1.4 to 1.6. A set of 10 repeats were recorded for each sample.

Fluorescent Probe Measurements

A borate buffer solution containing Nile Red (15 μM) was titrated with a concentrated solution of precursors (4 mM in building block, 85% oxidized). After each addition of precursors, the sample was homogenized by immersing it in an ultrasound bath for 1 min, and its fluorescence spectra were recorded using a JASCO FP6200 fluorimeter (λexc = 553 nm). The titration was repeated three times, and we measured in each of them the point when the fluorescence band started blue-shifting and increasing in intensity.38

Atomistic Molecular Dynamics Simulations

Atomistic simulations were performed using the GROMOS 54a8 united atom force field,39,40 as described in detail in ref (30). A fully equilibrated fiber of 12 stacked hexameric macrocycles was created by simulating the fiber in water for 50 ns while using harmonic distance restraints between neighboring Cα atoms (force constant 1000 kJ/nm2, equilibrium distance 0.48 nm) and further simulation for 50 ns without these restraints. 200 binding simulations were performed using the following procedure: A single macrocycle configuration was randomly extracted from a separate 50 ns simulation of a single macrocycle in excess aqueous solvent. The selected macrocycle was then inserted in the simulation box containing the equilibrated fiber, in a randomized rotation at a distance of approximately 3.5 nm away from the surface of the fiber. The system was solvated, neutralized using chloride ions, and energy-minimized for 5000 steepest descent steps. The single macrocycle was allowed to diffuse and/or bind to the fiber during a 60.2 ns simulation with 2.0 fs time-steps while the fiber was maintained at its original position along the z-axis by means of roto-translational center of mass motion removal (software extension developed in-house41). No restraints were applied to keep the structure stable during production runs. 0.2 ns of simulation time was discarded as the equilibration period after which the density of all macrocycle atoms was averaged in blocks of 2.5 ns/25 frames to generate time-dependent density plots. Atomistic simulations were run using GROMACS 4.6.7.42 Explicit aromatic or polar hydrogens were converted to virtual sites, and all bonds were constrained in production runs using the LINCS algorithm,43 except for the SPC water,44 which was constrained using the efficient SETTLE algorithm.45 Center-of-mass motion was removed every 100 time-steps. The production runs were performed in the NPT ensemble with the velocity-rescaling thermostat46 (τT = 1.0 ps, separate coupling for solute and water+ions) and the Berendsen barostat47 (τp = 1.5 ps) while the temperature was kept at 298 K and the pressure at 1.0 bar, respectively. A Barker–Watts reaction field (εRF = 62) was used to treat electrostatic interactions with Coulomb and van der Waals forces cut off at 1.4 nm.

Coarse-Grained Molecular Dynamics Simulations

CG molecular dynamics simulations were performed using the Martini force field v. 2.2.48,49 Parameters for the dithiobenzene group were derived from the atomistic simulations by matching bond, angle, dihedral, and nonbonded distributions. Previous work has demonstrated a random coil secondary peptide structure for macrocycles in solution, while fibers exhibit high β-sheet content.30 As such, separate parameters were used for the peptide parts of the macrocycles in the fiber and in solution. In the fiber, the parameters were taken as β-sheet parameters with extended dihedrals from the standard Martini protein parameters,31 while for the single macrocycle the coil parameters were used.

A fiber of 16 stacked hexamer macrocycles was constructed. The structure was solvated in a box of 10.8 × 11.7 × 14.5 nm, and counterions (96 Na+, 192 Cl–; 261 mM) were added. 10% of the water beads were replaced with Martini “anti-freeze” particles to avoid possible freezing of the water in the confined geometry of the simulation box. The system was equilibrated for 85 ns with 0.52 nm distance restraints with a force constant of 100 kJ/nm2 between backbone beads of neighboring peptides. Afterward, the fiber was simulated for 1 μs without distance restraints. Separately, a single trimeric macrocycle was solvated in a box of 6.4 × 5.1 × 5.8 nm, together with counterions (3 Na+, 6 Cl–; 79 mM) and 10% “anti-freeze” particles. The system was equilibrated for 75 ns, before a 1 μs production simulation.

Four hundred binding simulations were performed. They were set up by taking a random frame from the 1 μs fiber simulation and a random frame from the 1 μs macrocycle simulation. The macrocycle was inserted in the box of the fiber at a random place in the XY plane at the middle for the fiber at 2–2.5 nm from the fiber surface. The original solvent was removed, the resulting structure was resolvated, and counterions were added (99 Na+, 198 Cl–; 269 mM) together with 10% “anti-freeze” particles. The system was equilibrated for 5 ns with 100 kJ/nm2 position restraints on the backbone beads of both the fiber and the macrocycle. The system was then simulated for 500 ns without restraints. To generate time-dependent density plots, the density of all macrocycle atoms was averaged in blocks of 2.5 ns/25 frames.

Coarse-grained simulations were performed using GROMACS versions 5.1 and 2018 (ref (48)). In all cases, the fiber was maintained at its original orientation and position along the z-axis by means of roto-translational center of mass motion removal as for the atomistic simulations. A time step of 10 fs was used. The production runs were performed in the NPT ensemble with the velocity-rescaling thermostat45 (τT = 1.0 ps) and the Parrinello–Rahman barostat50 (τp = 36 ps) keeping the temperature at 298 K and the pressure at 1.0 bar, respectively. Other simulation parameters used are described by De Jong et al.51

Acknowledgments

This work was supported by an MSCA Individual fellowship (INTERACT 751404) to S.M., an NWO Vidi grant to W.H.R., and a STW Perspectief grant “Cancer-ID” (project 14192) to W.H.R. We are grateful for support from the ERC, Netherlands Organization for Scientific Research (Veni, 722.015.005), and the Dutch Ministry of Education, Culture and Science (gravitation program 024.001.035). O.M. is funded through the NWA StartImpuls. We thank the Center for Information Technology of the University of Groningen for their support and for providing access to the Peregrine high performance computing cluster.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c02635.

  • Figures S1–S11, Table S1, supplementary discussion 1, supplementary note on statistical analysis, Tables S2 and S3, and supplementary discussion 2 on mass-action kinetic modeling (includes Figures S12–S18 and Tables S4–S6) (PDF)

  • Video S1: Growth of a fiber captured by HS-AFM (AVI)

  • Video S2: No observable growth of fiber with precursors attached in the middle as captured by HS-AFM (AVI)

  • Video S3: Growth of a fiber, accumulation, and diffusion of precursor aggregate captured by HS-AFM (AVI)

  • Video S4: Precursor diffusivity on a fiber surface captured by HS-AFM (AVI)

  • Video S5: Growth of a fiber captured by HS-AFM at an extended time (AVI)

  • Video S6: GROMOS all-atom simulation results of the diffusion of a precursor on a fiber (AVI)

  • Video S7: Martini coarse-grained simulation results of the diffusion of a precursor on a fiber (AVI)

The authors declare no competing financial interest.

Supplementary Material

ja0c02635_si_001.pdf (3.3MB, pdf)
ja0c02635_si_002.avi (585.8KB, avi)
ja0c02635_si_003.avi (2.6MB, avi)
ja0c02635_si_004.avi (5.2MB, avi)
ja0c02635_si_005.avi (5.7MB, avi)
ja0c02635_si_006.avi (602.6KB, avi)
ja0c02635_si_007.avi (1.2MB, avi)
ja0c02635_si_008.avi (3.8MB, avi)

References

  1. Aida T.; Meijer E. W.; Stupp S. I. Functional supramolecular polymers. Science 2012, 335, 813–817. 10.1126/science.1205962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Zhang S. Emerging biological materials through molecular self-assembly. Biotechnol. Adv. 2002, 20, 321–339. 10.1016/S0734-9750(02)00026-5. [DOI] [PubMed] [Google Scholar]
  3. Grzelczak M.; Vermant J.; Furst E. M.; Liz-Marzán L. M. Directed self-assembly of nanoparticles. ACS Nano 2010, 4, 3591–3605. 10.1021/nn100869j. [DOI] [PubMed] [Google Scholar]
  4. Mattia E.; Otto S. Supramolecular systems chemistry. Nat. Nanotechnol. 2015, 10, 111–119. 10.1038/nnano.2014.337. [DOI] [PubMed] [Google Scholar]
  5. Van Esch J. H.; Klajn R.; Otto S. Chemical systems out of equilibrium. Chem. Soc. Rev. 2017, 46, 5474–5475. 10.1039/C7CS90088K. [DOI] [PubMed] [Google Scholar]
  6. Kumar M.; Ing N. L.; Narang V.; Wijerathne N. K.; Hochbaum A. I.; Ulijn R. V. Amino-acid-encoded biocatalytic self-assembly enables the formation of transient conducting nanostructures. Nat. Chem. 2018, 10, 696–703. 10.1038/s41557-018-0047-2. [DOI] [PubMed] [Google Scholar]
  7. Ter Huurne G. M.; De Windt L. N. J.; Liu Y.; Meijer E. W.; Voets I. K.; Palmans A. R. A. Improving the folding of supramolecular copolymers by controlling the assembly pathway complexity. Macromolecules 2017, 50, 8562–8569. 10.1021/acs.macromol.7b01769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fukui T.; Kawai S.; Fujinuma S.; Matsushita Y.; Yasuda T.; Sakurai T.; Seki S.; Takeuchi M.; Sugiyasu K. Control over differentiation of a metastable supramolecular assembly in one and two dimensions. Nat. Chem. 2017, 9, 493–499. 10.1038/nchem.2684. [DOI] [PubMed] [Google Scholar]
  9. Onogi S.; Shigemitsu H.; Yoshii T.; Tanida T.; Ikeda M.; Kubota R.; Hamachi I. In situ real-time imaging of self-sorted supramolecular nanofibres. Nat. Chem. 2016, 8, 743–752. 10.1038/nchem.2526. [DOI] [PubMed] [Google Scholar]
  10. Da Silva R. M. P.; Van Der Zwaag D.; Albertazzi L.; Lee S. S.; Meijer E. W.; Stupp S. I. Super-resolution microscopy reveals structural diversity in molecular exchange among peptide amphiphile nanofibres. Nat. Commun. 2016, 7, 11561. 10.1038/ncomms11561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ando T.; Uchihashi T.; Scheuring S. Filming biomolecular processes by high-speed atomic force microscopy. Chem. Rev. 2014, 114, 3120–3188. 10.1021/cr4003837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kodera N.; Daisuke Y.; Ryoki I.; Ando T. Video imaging of walking myosin V by high-speed atomic force microscopy. Nature 2010, 486, 72–76. 10.1038/nature09450. [DOI] [PubMed] [Google Scholar]
  13. Colom A.; Redondo-Morata L.; Chiaruttini N.; Roux A.; Scheuring S. Dynamic remodeling of the dynamin helix during membrane constriction. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 5449–5454. 10.1073/pnas.1619578114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Maity S.; Caillat C.; Miguet N.; Sulbaran G.; Effantin G.; Schoehn G.; Roos W. H.; Weissenhorn W. VPS4 triggers constriction and cleavage of ESCRT-III helical filaments. Sci. Adv. 2019, 5, eaau7198 10.1126/sciadv.aau7198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fukui T.; Uchihashi T.; Sasaki N.; Watanabe H.; Takeuchi M.; Sugiyasu K. Direct observation and manipulation of supramolecular polymerization by high-speed atomic force microscopy. Angew. Chem., Int. Ed. 2018, 57, 15465–15470. 10.1002/anie.201809165. [DOI] [PubMed] [Google Scholar]
  16. Milhiet P. E.; Yamamoto D.; Berthoumieu O.; Dosset P.; le Grimellec C.; Verdier J. M.; Marchal S.; Ando T. Deciphering the structure, growth and assembly of amyloid-like fibrils using high-speed atomic force microscopy. PLoS One 2010, 5, e13240 10.1371/journal.pone.0013240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Katsuda Y.; Wickham S. F. J.; Bath J.; Hidaka K.; Sugiyama H.; Turberfield A. J.; Endo M. Direct observation of stepwise movement of a synthetic molecular transporter. Nat. Nanotechnol. 2011, 6, 166–169. 10.1038/nnano.2010.284. [DOI] [PubMed] [Google Scholar]
  18. Carnall J. M. A.; Waudby C. A.; Belenguer A. M.; Stuart M. C. A.; Peyralans J. J.-P.; Otto S. Mechanosensitive self-replication. Science 2010, 327, 1502–1507. 10.1126/science.1182767. [DOI] [PubMed] [Google Scholar]
  19. Colomb-Delsuc M.; Mattia E.; Sadownik J. W.; Otto S. Exponential self-replication enabled through a fibre elongation/breakage mechanism. Nat. Commun. 2015, 6, 7427. 10.1038/ncomms8427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Rubinov B.; Wagner N.; Rapaport H.; Ashkenasy G. Self-replicating amphiphilic β-sheet peptides. Angew. Chem., Int. Ed. 2009, 48, 6683–6686. 10.1002/anie.200902790. [DOI] [PubMed] [Google Scholar]
  21. Nowak P.; Colomb-Delsuc M.; Otto S.; Li J. Template-Triggered Emergence of a Self-Replicator from a Dynamic Combinatorial Library. J. Am. Chem. Soc. 2015, 137, 10965–10969. 10.1021/jacs.5b04380. [DOI] [PubMed] [Google Scholar]
  22. Komáromy D.; Tezcan M.; Schaeffer G.; Marić I.; Otto S. Effector-triggered self-replication in coupled subsystems. Angew. Chem., Int. Ed. 2017, 56, 14658–14662. 10.1002/anie.201707191. [DOI] [PubMed] [Google Scholar]
  23. Ruiz-Mirazo K.; Briones C.; De La Escosura A. Prebiotic systems chemistry: New perspectives for the origins of life. Chem. Rev. 2014, 114, 285–366. 10.1021/cr2004844. [DOI] [PubMed] [Google Scholar]
  24. Lancet D.; Zidovetzki R.; Markovitch O. Systems protobiology: Origin of life in lipid catalytic networks. J. R. Soc., Interface 2018, 15, 20180159. 10.1098/rsif.2018.0159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Otto S.; Furlan R. L. E.; Sanders J. K. M. Dynamic combinatorial libraries of macrocyclic disulfides in water. J. Am. Chem. Soc. 2000, 122, 12063–12064. 10.1021/ja005507o. [DOI] [Google Scholar]
  26. Frederix P. W. J. M.; Patmanidis I.; Marrink S. J. Molecular simulations of self-assembling bio-inspired supramolecular systems and their connection to experiments. Chem. Soc. Rev. 2018, 47, 3470–3489. 10.1039/C8CS00040A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Bochicchio D.; Pavan G. M. Molecular modelling of supramolecular polymers. Adv. Phys. X 2018, 3, 1436408. 10.1080/23746149.2018.1436408. [DOI] [Google Scholar]
  28. Bochicchio D.; Salvalaglio M.; Pavan G. M. Into the dynamics of a supramolecular polymer at submolecular resolution. Nat. Commun. 2017, 8, 147. 10.1038/s41467-017-00189-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Brotzakis Z. F.; Gehre M.; Voets I. K.; Bolhuis P. G. Stability and growth mechanism of self-assembling putative antifreeze cyclic peptides. Phys. Chem. Chem. Phys. 2017, 19, 19032–19042. 10.1039/C7CP02465G. [DOI] [PubMed] [Google Scholar]
  30. Frederix P. W. J. M.; Idé J.; Altay Y.; Schaeffer G.; Surin M.; Beljonne D.; Bondarenko A. S.; Jansen T. L. C.; Otto S.; Marrink S. J. Structural and spectroscopic properties of assemblies of self-replicating peptide macrocycles. ACS Nano 2017, 11, 7858–7868. 10.1021/acsnano.7b02211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. De Jong D. H.; Singh G.; Bennett W. F. D.; Arnarez C.; Wassenaar T. A.; Schäfer L. V.; Periole X.; Tieleman D. P.; Marrink S. J. Improved parameters for the martini coarse-grained protein force field. J. Chem. Theory Comput. 2013, 9, 687–697. 10.1021/ct300646g. [DOI] [PubMed] [Google Scholar]
  32. Törnquist M.; Michaels T. C. T.; Sanagavarapu K.; Yang X.; Meisl G.; Cohen S. I. A.; Knowles T. P. J.; Linse S. Secondary nucleation in amyloid formation. Chem. Commun. 2018, 54, 8667–8684. 10.1039/C8CC02204F. [DOI] [PubMed] [Google Scholar]
  33. Heath G. R.; Scheuring S. High-speed AFM height spectroscopy reveals μs-dynamics of unlabeled biomolecules. Nat. Commun. 2018, 9, 4983. 10.1038/s41467-018-07512-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Scheidt T.; Łapińska U.; Kumita J. R.; Whiten D. R.; Klenerman D.; Wilson M. R.; Cohen S. I. A.; Linse S.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J.; Arosio P. Secondary nucleation and elongation occur at different sites on Alzheimer’s amyloid-b aggregates. Sci. Adv. 2019, 5, eaau3112 10.1126/sciadv.aau3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Uchihashi T.; Kodera N.; Ando T. Guide to video recording of structure dynamics and dynamic processes of proteins by high-speed atomic force microscopy. Nat. Protoc. 2012, 7, 1193–1206. 10.1038/nprot.2012.047. [DOI] [PubMed] [Google Scholar]
  36. Ando T.; Kodera N.; Naito Y.; Kinoshita T.; Furuta K.; Toyoshima Y. Y. A High-speed Atomic Force Microscope for Studying Biological Macromolecules in Action. ChemPhysChem 2003, 4, 1196–1202. 10.1002/cphc.200300795. [DOI] [PubMed] [Google Scholar]
  37. Bertin A.; de Franceschi N.; de la Mora E.; Maity S.; Alqabandi M.; Miguet N.; di Cicco A.; Roos W. H.; Mangenot S.; Weissenhorn W.; Bassereau P. Human ESCRT-III polymers assemble on positively curved membranes and induce helical membrane tube formation. Nat. Commun. 2020, 11, 2663. 10.1038/s41467-020-16368-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Stuart M. C. A.; Van De Pas J. C.; Engberts J. B. F. N. The use of Nile Red to monitor the aggregation behavior in ternary surfactant-water-organic solvent systems. J. Phys. Org. Chem. 2005, 18, 929–934. 10.1002/poc.919. [DOI] [Google Scholar]
  39. Reif M. M.; Hünenberger P. H.; Oostenbrink C. New interaction parameters for charged amino acid side chains in the GROMOS force field. J. Chem. Theory Comput. 2012, 8, 3705–3723. 10.1021/ct300156h. [DOI] [PubMed] [Google Scholar]
  40. Reif M. M.; Winger M.; Oostenbrink C. Testing of the GROMOS force-field parameter set 54A8: Structural properties of electrolyte solutions, lipid bilayers, and proteins. J. Chem. Theory Comput. 2013, 9, 1247–1264. 10.1021/ct300874c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. GROMACS RTC code at https://github.com/Tsjerk/gromacs/tree/rtc.
  42. Hess B.; Kutzner C.; Van Der Spoel D.; Lindahl E. GRGMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  43. Hess B. P-LINCS: A parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 2008, 4, 116–122. 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
  44. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J.. Interaction models for water in relation to protein hydration. In Intermolecular Forces; Pullman B., Ed.; Springer: Dordrecht, 1981; Vol. 14, pp 331–342. [Google Scholar]
  45. Miyamoto S.; Kollman P. A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
  46. Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  47. Berendsen H. J. C.; Postma J. P. M.; Van Gunsteren W. F.; Dinola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  48. Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; De Vries A. H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
  49. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindah E. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1 2015, 2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  50. Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  51. De Jong D. H.; Baoukina S.; Ingólfsson H. I.; Marrink S. J. Martini straight: Boosting performance using a shorter cutoff and GPUs. Comput. Phys. Commun. 2016, 199, 1–7. 10.1016/j.cpc.2015.09.014. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja0c02635_si_001.pdf (3.3MB, pdf)
ja0c02635_si_002.avi (585.8KB, avi)
ja0c02635_si_003.avi (2.6MB, avi)
ja0c02635_si_004.avi (5.2MB, avi)
ja0c02635_si_005.avi (5.7MB, avi)
ja0c02635_si_006.avi (602.6KB, avi)
ja0c02635_si_007.avi (1.2MB, avi)
ja0c02635_si_008.avi (3.8MB, avi)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES