Data-driven modeling of COVID-19—Lessons learned

Abstract

Understanding the outbreak dynamics of COVID-19 through the lens of mathematical models is an elusive but significant goal. Within only half a year, the COVID-19 pandemic has resulted in more than 19 million reported cases across 188 countries with more than 700,000 deaths worldwide. Unlike any other disease in history, COVID-19 has generated an unprecedented volume of data, well documented, continuously updated, and broadly available to the general public. Yet, the precise role of mathematical modeling in providing quantitative insight into the COVID-19 pandemic remains a topic of ongoing debate. Here we discuss the lessons learned from six month of modeling COVID-19. We highlight the early success of classical models for infectious diseases and show why these models fail to predict the current outbreak dynamics of COVID-19. We illustrate how data-driven modeling can integrate classical epidemiology modeling and machine learning to infer critical disease parameters—in real time—from reported case data to make informed predictions and guide political decision making. We critically discuss questions that these models can and cannot answer and showcase controversial decisions around the early outbreak dynamics, outbreak control, and exit strategies. We anticipate that this summary will stimulate discussion within the modeling community and help provide guidelines for robust mathematical models to understand and manage the COVID-19 pandemic. EML webinar speakers, videos, and overviews are updated at https://imechanica.org/node/24098.

“The most astonishing thing about the pandemic was the complete mystery which surrounded it” [The Lessons of the Pandemic, G.A. Soper, 1919].

Motivation

Would you take a measles vaccine to protect yourself against COVID-19? Most likely not. Why then, should we trust models that were initially designed for the measles to predict the dynamics of COVID-19?

In the early stages of the COVID-19 pandemic, under an enormous pressure to deliver results, the obvious solution seemed to be to recycle existing infectious disease models [1] and adapt them to simulate the outbreak dynamics of COVID-19 [2]. In retrospect, this was an obvious mistake. Many elements of the current pandemic—although similar at first sight—are inherently different from infectious diseases early in the early 20th century [3]: We now have a longer life expectancy, we are more globally connected, and we travel more; but we also have better access to hygiene, to health care, and to massive amounts of data about the disease.

During the early onset of the outbreak, all eyes were on mathematical modeling with the general expectation that COVID-19 models could precisely predict the trajectory of the pandemic [4]. Mathematical modeling rapidly became front and center to understanding the exponential increase of infections, the shortage of ventilators, and the limited capacity of hospital beds—too rapidly as we now know. Bold and catastrophic predictions not only initiated a massive press coverage, but also a broad anxiety in the general population. However, within only a few weeks, the vastly different predictions and conflicting conclusions began to create the impression that all mathematical models are in generally unreliable and inherently wrong [5]. While the failure of COVID-19 modeling—often by an order of magnitude or more—was devastating for policymakers and public health practitioners, initial mistakes are not new to the modeling community where an iterative cycle of prediction, failure, and redesign is common standard and best practice [6]. However, the successful use of mathematical models implies to set the expectations right [7]. Understanding what models can and cannot predict is critical to the Art of Modeling.

Two classes of models have been proposed to understand the outbreak dynamics of COVID-19, statistic and mechanistic models [5]. Purely statistic models use machine learning or regression to analyze massive amounts of data and project the number of infections into the future [8]. Since purely statistic models do not include any disease specific information, their forecasts are reliable only within a short time window. Nonetheless, statistical modeling can be useful, for example, to understand how to allocate resources or make rapid short-term recommendations. Mechanistic models simulate the outbreak through interacting disease mechanisms by using local nonlinear population dynamics and global mixing of populations [9]. These models can include disease specific information and potentially make long-term predictions about the outcome of a pandemic. Mechanistic modeling can be useful to explore how the pandemic would change under various assumptions and political interventions. When selecting between statistic and mechanistic models, it is critical to know upfront which questions the model should address [7].

Two interacting features determine the outbreak dynamics of the COVID-19 pandemic: the local epidemiology of the disease and the global mobility of affected individuals [10]. For coronavirus diseases, the local epidemiology is defined by an exponential growth of the outbreak, where the number of new cases depends exponentially on the growth rate [2]. From an outbreak dynamics perspective, this implies that the outbreak behaves like a chaotic system for which even small inaccuracies in the prediction can trigger large changes in the number of cases. From an outbreak control perspective, small changes in intervention can alter the current growth rate and convert the dynamics from exponential growth to exponential decay or vice versa [7]. To understand the vulnerability of the model to these small changes, especially in view of the varying reporting practices of the COVID-19 case data, sensitivity analysis and quantifying uncertainty have become critical elements of robust predictive modeling [11], [12]. A promising technology that integrates statistic and mechanistic approaches and can inherently quantify model uncertainties is data-driven modeling. Throughout the past months, several research groups have started to integrate classical epidemiology models and machine learning to infer critical disease parameters from reported case data and make informed predictions about outbreak dynamics and outbreak control [11], [13], [14], [15], [16], [17]. In the reminder of this work, we share the lessons we have learned throughout this process, from the early beginning of the COVID-19 pandemic until the current concerns and challenges in an attempt to safely reopen from lockdown.

Modeling the early outbreak dynamics

Lesson 1. COVID-19 is spreads exponentially if uncontrolled

During the early stages of the COVID-19 outbreak, the world stood in awe to see the number of new infections climbing explosively [18]. This rapid increase created a lot of anxiety within both the general population and political decision makers. It seemed natural to turn to mathematical models to understand the rapid spreading of COVID-19 and estimate its consequences [4]. In fact, the first mathematical models for infectious diseases date back to a smallpox model in the middle of the 18th century [19]. Since the 1920s, compartment models have advanced to the method of choice to simulate the epidemiology of infectious diseases [3]. One of the simplest compartment models is the SEIR model. It represents the timeline of a disease through four compartments, the susceptible, exposed, infectious, and recovered populations [9]. The temporal evolution of these compartments is governed by four ordinary differential equations parameterized in terms of the three transition rates between them.

$$\begin{array}{c}\hfill \dot{S}=-\beta SI\hfill \\ \hfill \dot{E}=+\beta SI-\alpha E\hfill \\ \hfill \dot{I}=+\alpha E-\gamma I\hfill \\ \hfill \dot{R}=+\gamma I\hfill \end{array}$$

With only three parameters, $\alpha$, $\beta$, and $\gamma$, the classical SEIR model has been successfully used to model previous epidemic outbreaks. The parameters $\alpha$ and $\gamma$ characterize the transition from the exposed to the infectious state and from the infectious to the recovered state. In fact, they are the inverses of the latent period $A=1∕\alpha$, the time during which an individual is exposed but not yet infectious, and the infectious period $C=1∕\gamma$, the time during which an individual can infect others [9]. As such, they are disease specific parameters independent of region, state, or country. For COVID-19, in the example of Fig. 1, the latent and infectious periods are on the order of $A=2.5$ days and $C=6.5$

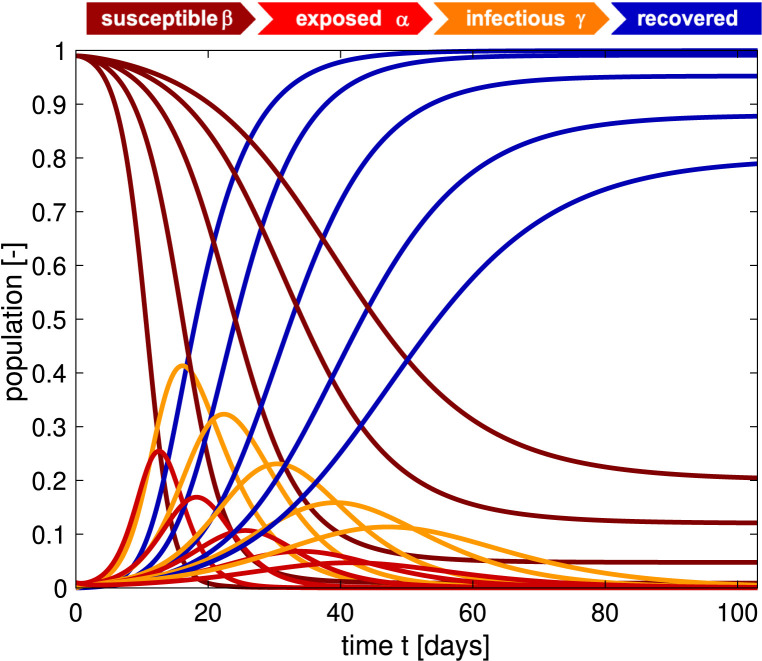
Fig. 1.

Outbreak dynamics of COVID-19 for varying basic reproduction numbers $R_0$. Decreasing the basic reproduction number, from left to right, decreases the exposed and infectious populations, red and orange curves. The susceptible and recovered populations, brown and blue curves, converge to larger and smaller endemic equilibrium values, and converges is slower. The steepest curves correspond to the smallest contact period $B$$=$ 0.8 days and largest basic reproduction number $R_0$$=$ 8.0 with the maximum infectious population of $I_{max}$$=$ 0.412 after 15 days. Latent period $A$$=$ 2.5 days, infectious period $C$$=$ 6.5 days, initial exposed fraction $E_0$$=$ 0.01, and contact period $B$$=$ 3.3, 2.7, 2.0, 1.4, 0.8 days, resulting in basic reproduction number $R_0=C∕B$$=$ 2.0, 2.4, 3.2, 4.8, 8.0 . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

days [10]. The defining feature of the SEIR model is its nonlinear feedback loop that defines transition from the susceptible to the exposed state. The model typically assumes that this transition scales with the susceptible population $S$, the infectious population $I$, and the contact $\beta$, the inverse of the contact period $B=1∕\beta$, between the two. Fig. 1 illustrates the dynamics of the susceptible, exposed, infectious, and recovered populations, for varying contact periods of $B=3.3$, 2.7, 2.0, 1.4, 0.8 days. During the early stages of the COVID-19 pandemic, many research groups have successfully applied the SEIR model to simulate the early period of free exponential growth and estimated the ratio between the infectious period and the contact period to $C∕B=4.8$ $-$8.0, associated with the two left-most sets of curves [20]. Fig. 1 suggests that, for this range of parameters, the outbreak would have peeked after only two weeks, with 30%–40% of the population infected, and it would have been over after less than two months. Obviously, this is not what happened [18]. How could a model, that had successfully simulated the measles and chickenpox fail so dramatically in predicting the timeline of COVID-19, despite its initial promise in modeling the early outbreak?

Lesson 2. COVID-19 is as contagious as previous coronaviruses

An important question to ask, especially during the early stages of the outbreak, is: How contagious is the new coronavirus? This closely relates to the question How does it compare to other coronaviruses or, even more broadly, to other infectious diseases? A powerful quantitative concept to characterize the contagiousness and transmissibility of the new coronavirus is the basic reproduction number $R_0$ [21]. This number explains—in simple terms—how many new infections are caused by a single one infectious individual in an otherwise completely susceptible population [22]. Since the beginning of the new coronavirus pandemic in December 2020, no other number has been discussed more controversially than the reproduction number of COVID-19 [20]. However, it is difficult—if not impossible—to measure $R_0$ directly. Most basic reproduction numbers of COVID-19 we see in the public media today are estimates of mathematical models that depend critically on the choice of the model, the initial conditions, and numerous other modeling assumptions [23]. For our SEIR model, the basic reproduction number is simply the product of the contact rate $\beta$ and the infectious period C, or the ratio between the infectious period $C$ and the contact period $B$,

$$R_0=\beta C=C∕B.$$

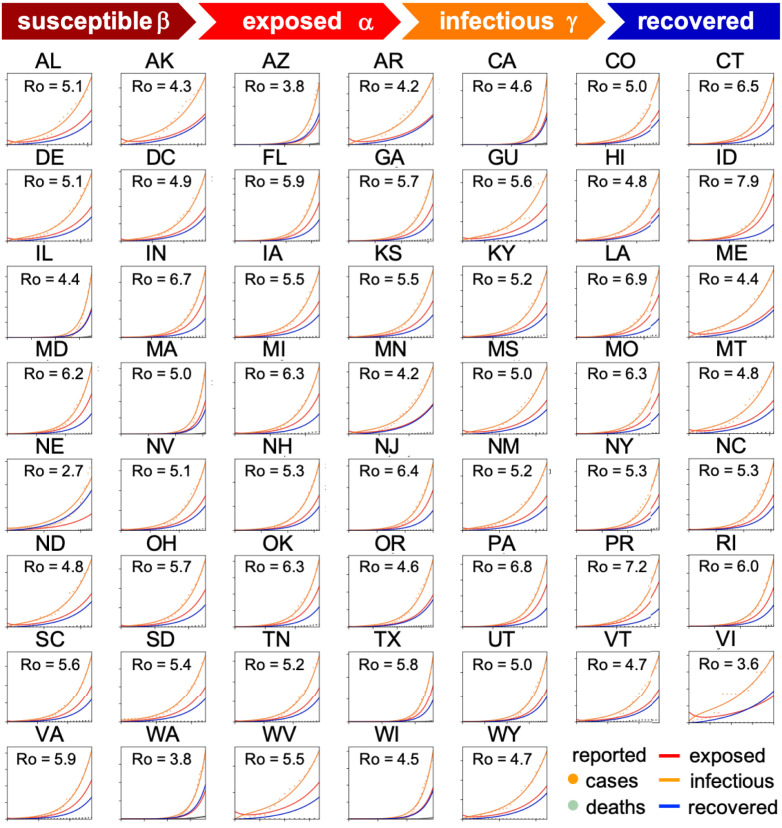
Fig. 2 shows how we can use reported case data to infer the contact period $B$ and with it the basic reproduction number $R_0=C∕B$ across all United States during the early stages of exponential growth [15]. The resulting mean basic reproduction number of 5.30 ± 0.95 for the United States is slightly higher than the mean basic reproduction number of 4.22 ± 1.69 for Europe [10]. Both values agree well with the reported value of 5.7 for the Wuhan outbreak [24] and with a recent review that suggests values from 4.1 to 6.5 from SEIR modeling [20]. Compared to traditional infectious diseases, these basic reproduction numbers are lower than the numbers of 18 for measles, 9 for chickenpox, 7 for mumps, and 7 for rubella, but on the order of 5 for poliomyelitis [1]. Compared to the SARS coronavirus with a range from 2 to 5 [20], our values for SARS-CoV-2 in Fig. 2 are on the higher end, and suggest that the new coronavirus would spread more rapidly than SARS [25]. Knowing the basic reproduction number of COVID-19 is critical to estimate the conditions for herd immunity and predict the success of vaccination strategies. However, from Fig. 1 we would conclude that, for this range of basic reproduction numbers, from $R_0=2.0$ to 8.0, 80%–100% of the population would have been infected with the virus within only three months. How useful is the concept of the basic reproduction number if fails do accurately reproduce the timeline of COVID-19, even in the first few weeks of the outbreak?

Fig. 2.

Early outbreak dynamics of COVID-19 in the United States. Reported infectious populations and simulated exposed, infectious, and recovered populations. Simulations are based on a state-specific identification of the contact period $B$ B to define the basic reproduction number $R_0=C∕B$. The mean basic reproduction number was $R_0$$=$ 5.30 $\pm$ 0.95 [15].

Lesson 3: Without vaccination, COVID-19 will be with us for a long time

The million-dollar question—literally—is: How long will the COVID-19 pandemic last? From other infectious diseases including the measles, chickenpox, mumps, polio, rubella, pertussis, and smallpox we know that epidemic outbreaks tend to come to an end before the entire population has been infected [1]. For this class of diseases, the basic reproduction number is larger than one, $R_0$ $>$ 1.0, and an infected individual will initially infect more than one other individual. Fig. 1 shows that, under these conditions, the infectious population first increases, then reaches a peak, and decreases toward zero [3]. As more and more individuals transition from the susceptible through the exposed and infectious states into the recovered state, the susceptible population decreases. Once a large enough fraction of a population has become immune—either through recovery from the infection or through vaccination—this group provides a protection for the susceptible population. The epidemic dies out as the rate of daily new cases, $\beta SI$, decreases [22]. As such, the classical SEIR model is self-regulating: It naturally converges to an endemic equilibrium, at which either the susceptible group $S$, or the infectious group $I$, or both have become small enough to prevent new infections. In epidemiology, this indirect protection is called herd immunity [26]. The concept of herd immunity implies that the converged susceptible population at endemic equilibrium is always larger than zero, $S_{\infty }$ $>$ 0, and its value depends on the basic reproduction number $R_0$. In a homogeneous, well-mixed population, herd immunity occurs once a fraction of $[1-1∕R_0]$ of the population has become immune, either through the disease itself or through vaccination. During the very early stages of the outbreak, political decision makers were actively focusing on answering the question: When we reach herd immunity? For the mean basic reproduction numbers of $R_0=4.22$ and $R_0=5.30$ we found for Europe and the United States in Fig. 1, the herd immunity threshold would lie between 76% and 81%. This value is lower than 94% for the measles, 89% for chickenpox with, 86% for mumps and rubella, and on the order of 80% for polio, but significantly higher than the values of 16% to 27% for the seasonal flu [1]. Even the countries with the highest prevalence, Chile with 1.75%, the United States with 1.22%, Brazil with 1.02%, and Sweden with 0.77% [18] do not come close to these values today. Against all initial enthusiasm for reaching herd immunity by the fall, we have now come to realize that we will likely not pass the immunity level threshold any time soon by infection alone. In the near future, vaccination remains the only viable strategy to achieve herd immunity. The basic reproduction number of COVID-19 suggests that at least three fourth of the population, more than 5 billion people worldwide, would have to be vaccinated to achieve herd immunity against COVID-19. While this sounds like a gigantic undertaking, massive vaccination campaigns have successfully controlled deadly contagious diseases such as polio, diphtheria, and rubella and even successfully eradicated smallpox in 1980 [1]. However, until a COVID-19 vaccine is developed and approved, it is crucial to slow the spread of the COVID-19 virus and protect individuals at increased risk of severe illness, including older adults and people of any age with underlying health conditions [27].

Modeling outbreak control

Lesson 4. We can flatten the curve

During the early stages of exponential growth, with new case numbers doubling within two or three days, the most urgent question amongst health care providers and political decision makers began to ask was: Can we reduce the reproduction number $R$? For the broad population, this question became famously and illustratively rephrased as: Can we flatten the curve? For the modeling community, this quest for a lower reproduction number all of a sudden meant that the traditional SEIR epidemiology models were no longer suitable to model changes in disease dynamics. While traditional models with static parameters were well-suited to model the outbreak dynamics of unconstrained, freely evolving infectious diseases with fixed basic reproduction numbers in the early 20th century [9], they fail capture how behavioral changes and political interventions can modulate the reproduction number to manage the COVID-19 pandemic in the 21st century [10]. In fact, static reproduction numbers are probably the single most common cause of model failure in COVID-19 modeling. To simulate a flattening, or rather early bending of the case curve, early modeling approaches adopted an ad hoc strategy that explicitly reduced the total population $N$ to a potentially affected population $N^{\ast }=\eta N$. This strategy introduces a scaling coefficient $\eta =N^{\ast }∕N$, essentially a mere fitting parameter, to indirectly quantify the level of confinement [28]. Averaged over 30 Chinese provinces, the level of confinement was $\eta =5.19$ 10⁻⁵ $\pm$ 2.23 10⁻⁴ [15] and averaged over the 27 countries of the European Union, it was $\eta =7.67$ 10⁻² $\pm$ 2.61 10⁻¹ [14] suggesting that the effect of COVID-19 was successfully confined to only a very small fraction of the total population. More mechanistic approaches are based on introducing a time-varying effective reproduction number $R\left(t\right)$ and on learning it dynamically from the reported case data. For example, we can infer discrete time points at which the contact rates vary [29] or used sliding windows over the amount of novel reported infections [30]. Strikingly, in many countries, the reported COVID-19 cases data follow a similar characteristic S-shaped pattern in response to political interventions. We can approximate this behavior with an effective reproduction number of hyperbolic tangent type [10],

$$R\left(t\right)=R_0-\frac{1}{2}[1+tanh(\left[t-t^{\ast }\right]∕T)][R_0-R_{\mathrm{t}}].$$

This ansatz has four physically meaningful parameters that provide valuable information about the responsiveness of the reproduction number to political action: the basic reproduction number $R_0$ at the beginning of the outbreak, the reduced reproduction number $R_t$ under political interventions, the adaptation time $t^{\ast }$, and the transition time $T$. We can infer these parameters from the reported case data using Bayesian inference with Markov-Chain Monte-Carlo [10]. This allows us to model an S-shaped case curve that plateaus long before a large fraction of the population has been affected by the disease. Another alternative that allows even more flexibility and does not require $R\left(t\right)$ to be monotonic is a Gaussian random walk function [12]. This free form approach naturally captures the effects of public health interventions, however, in a daily varying, rather unpredictable way. The random walk approach is a flexible method to analyze case data retrospectively, but since it does not allow for a closed functional form, it is not very useful to make informed predictions. Taken together, from the failure of traditional static SEIR models, we have learned that we need to introduce dynamic time-varying model parameters if we want to correctly model behavioral and political changes and reproduce the reported case numbers. This naturally introduces a lot of freedom, a large number of unknowns, and a high level of uncertainty. However, in stark contrast to epidemic outbreaks in the early 20th century, we now have well-documented case data and the appropriate tools to address this challenge [6]. The massive amount of COVID-19 case data, all freely available on public data bases [18], has induced a clear paradigm shift from traditional mathematical epidemiology [9] towards data-driven physics-based modeling of infectious disease. These new techniques naturally learn the most probable model parameters—in real time—from the time evolution of continuously updated case data, allow us to make projections into the future, and quantify the uncertainty on the estimated predictions.

Lesson 5. Constraining mobility is a drastic but effective mitigation strategy

Reducing mobility is a controversial but highly effective measure to manage a global pandemic [31]. On March 17, 2020, for the first time in history, the European Union closed all its external borders to reduce the spreading of COVID-19 [32]. In the following two weeks, the local governments augmented the European regulations with local lockdowns and national travel restrictions. These measures had a dramatic effect on the mobility within the European Union: Within five days, the average passenger air travel in Europe was cut in half, and within two weeks, it was reduced to 5%–10% [33]. These drastic actions have triggered ongoing debates about the effectiveness of different outbreak strategies and the appropriate level of constraints [34]. A simple way to probe the effect of mobility is to model the spreading of COVID-19 through a mobility network of passenger air travel. For the European Union, we can represent this network as a weighted graph $G$ in which the $N=27$ nodes represent the individual countries and the weighted $E$ edges represent the travel frequency between them. We can estimate the travel frequency within the graph using passenger air travel statistics before and during the outbreak [33]. We record this information in the adjacency matrix $A_{IJ}$ that represents the travel frequency between two countries $I$ and $J$, and in the degree matrix, $D_{II}=\text{diag}{\sum }_{J=1,J\ne 1}^N{A}_{IJ}$, that represents the number of incoming and outgoing passengers for each country $I$. The difference between the degree matrix $D_{IJ}$ and the adjacency matrix $A_{IJ}$ defines the weighted graph Laplacian $L_{IJ}=D_{IJ}-A_{IJ}$. We can then discretize the SEIR model on the weighted graph $G$ and introduce the susceptible, exposed, infectious, and recovered populations $S_I$, $E_I$, $I_I$, and $R_I$ as global unknowns at the nodes of the graph $G$ [14]. This results in a set of equations with $4N$ unknowns.

$$\begin{array}{c}\hfill \dot{S_I}=-\sum _{J=1}^N{L}_{IJ}{S}_J-\beta S_I{I}_I\hfill \\ \hfill \dot{E_I}=-\sum _{J=1}^N{L}_{IJ}{E}_J+\beta S_I{I}_I-\alpha E_I\hfill \\ \hfill \dot{I_I}=-\sum _{J=1}^N{L}_{IJ}{I}_J+\alpha E_I-\gamma I_I\hfill \\ \hfill \dot{R_I}=-\sum _{J=1}^N{L}_{IJ}{R}_I+\gamma I_I\hfill \end{array}$$

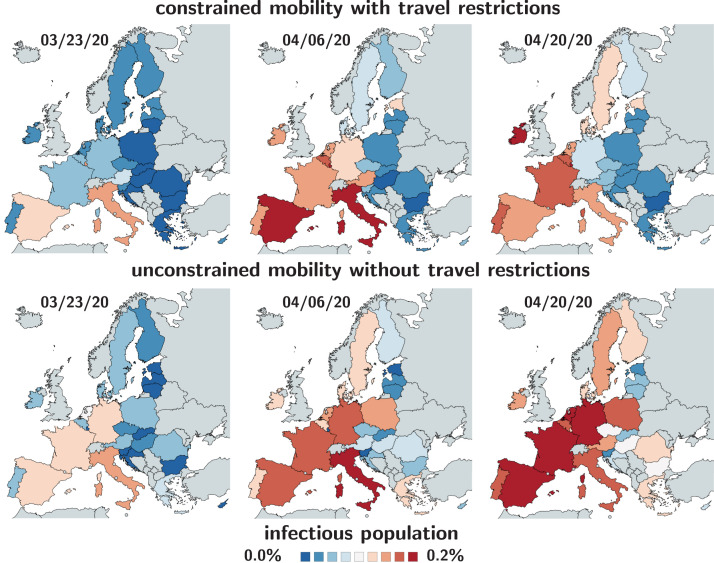
Fig. 3 highlights the effect of constrained mobility in managing the COVID-19 outbreak across Europe. The top row shows the simulated outbreak under constrained mobility with the imposed travel restrictions and border control in place, the bottom row shows the outbreak under unconstrained mobility without travel restrictions. During the early stages of the pandemic, the predicted outbreak pattern in the bottom row agrees well with the outbreak pattern in the top row. During the later stages, the side-by-side comparison shows a faster spreading of the outbreak under unconstrained mobility with a massive, immediate outbreak in Central Europe and a faster spreading to the eastern and northern countries. Although air travel is certainly not the only determinant of the outbreak dynamics, Fig. 3 suggests that mobility is a strong contributor to the global spreading of COVID-19 and supports the decision of the European Union and its local governments to implement rigorous travel restrictions to delay the outbreak of the pandemic [35].

Fig. 3.

Early outbreak control of COVID-19 in Europe. Infectious population for constrained mobility with travel restrictions versus unconstrained mobility without travel restrictions. Simulations are based on country-specific basic reproduction numbers without and with mobility. The mean basic reproduction number was 4.62 $\pm$ 1.32 [14].

Lesson 6. Reproduction is correlated to mobility with a time delay of two weeks

The drastic political measures, travel restrictions, and boarder control during the early stages of the pandemic have stimulated a wave of criticism [34]. While it was initially entirely unclear to which extent they would succeed in reducing the number of new infections [36], we now know that reducing mobility can effectively flatten the curve. In addition to global air mobility, several studies have proposed to explore correlations between outbreak control and driving, walking, and transit mobility from cell phone data [37]. A important question in outbreak control is: What is the time delay between intervention and effect?

Fig. 4 summarizes the mobility data from the relative volume of location requests per country, scaled by the baseline volume before the outbreak of the pandemic [35]. To smoothen the weekday–weekend fluctuations in outbreak and mobility data, we have applied a moving averaging window of seven days. In addition, Fig. 4 shows the hyperbolic tangent approximation of the effective reproduction number $R\left(t\right)$ inferred from combining the SEIR model with the reported case data in all 27 countries. Interestingly, the drop in global passenger air travel and in local driving, walking, and transit mobility follows a similar hyperbolic tangent type form. For each country, we can extract the time delay $\Delta$t between the reduction of air traffic, driving, walking, and transit mobility and the inflection point of the reproduction number curve. This time delay is an important socio-economical metric for the response time to political interventions. The population weighted mean time delay across the European Union is $\Delta t=17.24$ $\pm$ 2.00 days. The country-specific time delay varies hugely across Europe with the fastest response of 0.75 days in the Netherlands, followed by Germany with 3.25 days, Belgium with 4.00 days, and Italy with 5.00 days. These fast response times naturally also reflect early decisions on the national level. For example, Fig. 4 clearly showcases the special role of Sweden, where the government focusses efforts on encouraging the right behavior and creating social norms rather than mandatory restrictions: The time delay of 23.75 days is above the European Union average of 17.24 days, and Sweden is one of the few countries where the effective reproduction number has not notably decreased below one. Taken together, from correlating reproduction and mobility, we have learned that, especially during the early stages of an outbreak, controlling mobility can play a critical role in reducing the spread of the pandemic [35]. The time delay between mobility control and reduced reproduction is particularly important to plan exit strategies and estimate risks associated with gradually or radically relaxing local lockdowns and global travel restrictions.

Fig. 4.

Correlation between reduction in mobility and effective reproduction number of COVID-19 outbreak in Europe. Purple, blue, gray, and black dots represent reduction in air traffic, driving, walking, and transit mobility; red curves show effective reproduction number R(t) with 95% confidence interval. The time delay $\Delta$t denotes the delay between reduction in mobility and effective reproduction number. The mean time delay was 17.24 $\pm$ 2.00 days [10] . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Lesson 7. Most COVID-19 cases are asymptomatic and remain unreported

In the early stages of the COVID-19 pandemic, doctors, researchers, and political decision makers have mainly focused on symptomatic individuals that came for testing and required urgent medical attention. In the more advanced stages, the interest has shifted towards mildly symptomatic and asymptomatic individuals who, by definition, are difficult to trace and likely to retain normal social and travel patterns [38]. As of today, more than 50 studies have reported an asymptomatic population, 23 of them with a sample size of 500 and more [39]. The reported trends are strikingly consistent: A much larger number of individuals display antibody prevalence than we would expect from the reported symptomatic case numbers. In fact, the median undercount across all studies suggests that only one in twenty COVID-19 cases has been noticed and reported [12].

While there is a pressing need to better understand the prevalence of asymptomatic transmission, it is also becoming increasingly clear that it will likely take a long time until we can, with full confidence, deliver reliable measurements of this asymptomatic group. In the meantime, mathematical modeling can provide valuable insight into the tentative outbreak dynamics and outbreak control of COVID-19 for varying asymptomatic scenarios. We can model the effects of asymptomatic transmission by extending the classical SEIR model into and SEIIR model with five compartments, the susceptible, exposed, symptomatic infections, asymptomatic infections, and recovered groups [12].

$$\begin{array}{c}\hfill \dot{S}=-S[{\beta }_{\mathrm{s}}{I}_{\mathrm{s}}+{\beta }_{\mathrm{a}}{I}_{\mathrm{a}}]\hfill \\ \hfill \dot{E}=+S\left[{\beta }_{\mathrm{s}}{I}_{\mathrm{s}}+{\beta }_{\mathrm{a}}{I}_{\mathrm{a}}\right]-\alpha E\hfill \\ \hfill \dot{I_{\mathrm{s}}}=+{\nu }_{\mathrm{s}}\alpha E-{\gamma }_{\mathrm{s}}{I}_{\mathrm{s}}\hfill \\ \hfill \dot{I_{\mathrm{a}}}=+{\nu }_{\mathrm{a}}\alpha E-{\gamma }_{\mathrm{a}}{I}_{\mathrm{a}}\hfill \\ \hfill \dot{R}=+{\gamma }_{\mathrm{s}}{I}_{\mathrm{s}}+{\gamma }_{\mathrm{a}}{I}_{\mathrm{a}}\hfill \end{array}$$

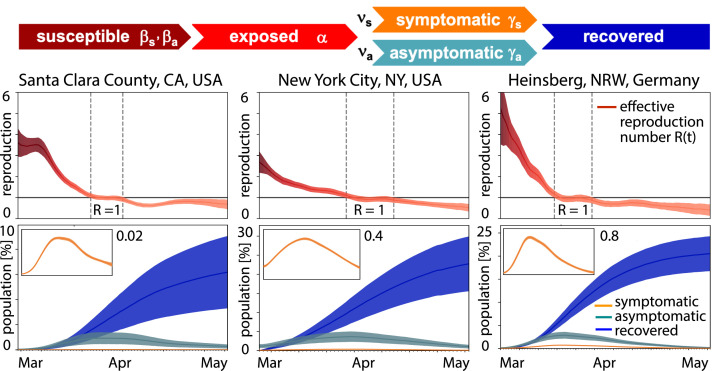
Here $I_{\mathrm{s}}$ and $I_{\mathrm{a}}$ denote the symptomatic and asymptomatic groups, which are fractions ${\nu }_{\mathrm{s}}$ and ${\nu }_{\mathrm{a}}$ of the total infectious group $I$. We postulate that both groups have the same latency rate $\alpha$, but they can have their own contact rates ${\beta }_{\mathrm{s}}$ and ${\beta }_{\mathrm{a}}$ and infectious rates ${\gamma }_{\mathrm{s}}$ and ${\gamma }_{\mathrm{a}}$. Fig. 5 illustrates the resulting model and a representative analysis for three locations where antibody seroprevalence was reported, Santa Clara County with ${\nu }_{\mathrm{s}}=1$.77% [40], New York City with ${\nu }_{\mathrm{s}}=5$.76% [41], and Heinsberg with ${\nu }_{\mathrm{s}}=20$.00% [42]. The model combines the SEIIR model and Bayesian inference to learn the time-varying effective reproduction number $R\left(t\right)$ from the reported case data and predicts the symptomatic, asymptomatic, and recovered populations with 95% credible intervals [12]. Strikingly, despite notable differences in seroprevalence, the effective reproduction numbers $R\left(t\right)$ and the infectious and recovered populations $I_{\mathrm{s}}$, $I_{\mathrm{a}}$, and $R$ in Fig. 5 follow similar trends: The effective reproduction number $R\left(t\right)$ drops rapidly to values below one within a window of about three weeks after the lockdown date, the infectious curves peak, and the recovered curve begins to plateau. Including asymptomatic transmission in the model also allows us to back-calculate the undercount from comparing mortality rates and death counts [13]. Knowing the exact dimension of the asymptomatic population is critical to truly estimate the severity of the outbreak, e.g., hospitalization or mortality rates [27], and to reliably predict the success of surveillance and control strategies, e.g., contact tracing or vaccination [43]. Precise knowledge about the asymptomatic population can significantly change our understanding and management of the COVID-19 pandemic: A large asymptomatic population will bring us closer to herd immunity, but will also make isolation, containment, and tracing of individual cases more challenging. Instead, managing community transmission through increasing population awareness, promoting physical distancing, encouraging behavioral changes and massive testing would become more relevant.

Fig. 5.

Outbreak dynamics of COVID-19 in Santa Clara County, New York City, and Heinsberg. Dynamic effective reproduction number R(t) and symptomatic, asymptomatic, and recovered populations at three different locations where antibody prevalence studies were performed. The model learns the time-varying effective reproduction number R(t) to predict the symptomatic, asymptomatic, and recovered populations with 95% credible intervals [12].

Lesson 8. There are massive amounts of data, but they do not always align well with the models

Within only six months, the COVID-19 pandemic has probably generated more data than any disease in history. New symptomatic cases, recovered cases, and deaths are well documented and publicly shared on numerous websites and reports [18]. Intuitively, we would think that this presents endless opportunities for modeling [6]. However, unfortunately, not all the available data align well with the input needed for epidemiology modeling. For example, one question we still cannot address is: When exactly did the outbreak start? To accurately model, monitor, and manage the dynamics of COVID-19, it is critical to know precisely when the outbreak first started in a particular region, state, or country. This issue is closely related to selecting appropriate initial conditions for the susceptible, exposed, infectious, and recovered populations $S_0$, $E_0$, $I_0$, and $R_0$. For example, the first reported COVID-19 death in the United States was reported in Santa Clara County, California. Although this happened as early as February 6, the case remained unnoticed until April 22 [44]. This unexpected finding suggests that the new coronavirus had been circulating in the Bay Area as early as January. Machine learning allows us to combine our SEIIR model with data from antibody prevalence studies [40] and reported case numbers [45], and trace the initial outbreak date back to January 20, 2020 [12]. This early outbreak estimate supports the common intuition that COVID-19 is often present in a population long before the first official case is reported. Knowing the initial outbreak date is critical to trace the origin of the disease, estimate the impact of community spreading, and design successful mitigation strategies.

Modeling exit strategies

Lesson 9. Selective reopening can be more effective than voluntary quarantine

A popular strategy to prevent a local outbreak during the COVID-19 pandemic is to restrict incoming travel and locally reduce the case numbers to a manageable dimension. Once a region has successfully contained the disease, the obvious question becomes: When is it save to reopen? There is a legitimate fear that easing off travel restrictions, even slightly, could trigger a new outbreak and accelerate the spread to an unmanageable degree. As we are trying to identify exit strategies from local lockdowns and global travel restrictions, political decision makers are turning to mathematical models for quantitative insight and scientific guidance [46].

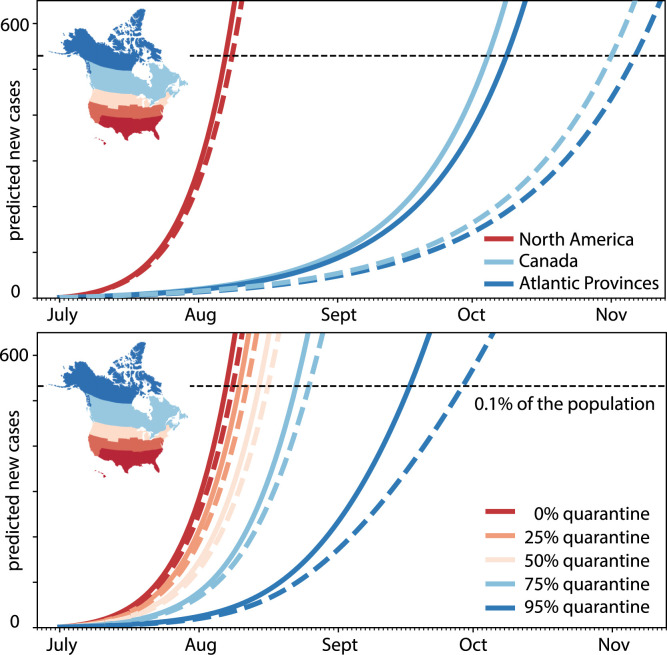
Global network mobility models, combined with local epidemiology models, can provide valuable insight into different reopening scenarios. Fig. 6 illustrates the effect of different exit strategies for the example of Newfoundland and Labrador, a Canadian province that has enjoyed no new cases since late April, 2020 [47]. This analysis combines a network epidemiology model with machine learning to infer parameters and predict the COVID-19 dynamics upon partial and full airport reopening, under perfect and imperfect quarantine conditions. To accurately mimic the incoming susceptible, exposed, infectious, and recovered fractions of travelers at the day of reopening, the model learns the populations of the SEIR model with individual dynamic effective reproduction numbers $R\left(t\right)$ for all territories, provinces, and states of North America from the reported case data and weights them with the average daily air travel prior to the outbreak [48]. An interesting metric is the estimated number of incoming exposed and infectious travelers upon full reopening, $\Delta E=0$.203/day and $\Delta I=0$.329/day. This implies that every five days and every three days, an exposed and an infectious traveler would enter the province of Newfoundland and Labrador. In other words, every other day, a new COVID-19 case would enter the Newfoundland and Labrador via air travel [46]. Since the exposed and early infectious individuals are still pre-symptomatic, it is impossible to identify and isolate them without strict quarantine requirements [49]. This raises the question: What is the best exit strategy? Is it safer to selectively reopen the province, to only the Atlantic Provinces, to Canada, or to all of North America, or, alternatively, rely on a sufficiently large fraction of the incoming travelers to comply with recommended quarantine requirements? Fig. 6 shows that—especially for smaller provinces or states like Newfoundland—tight border control is often easier and more effective than quarantine. Partial reopening, for example within local travel bubbles, is an effective compromise and a reasonable intermediate step towards complete reopening. While relaxing travel restrictions is possible, it would require strict quarantine conditions. Voluntary quarantine, even at an overall rate of 95%, is not enough to entirely prevent a new outbreak. Without comprehensive test-trace-isolate strategies [27], combined with a mandatory quarantine of 100% of COVID-19 positive individuals, reopening can always seed a new exponential outbreak. This concrete example shows that data-driven modeling can provide valuable quantitative insight into the efficacy of travel restrictions to inform political decision making in the controversy of reopening.

Fig. 6.

Outbreak dynamics of COVID-19 in Newfoundland and the effects of restricted travel and quarantine. Reopening forecast for 150-day period with incoming travelers from the Atlantic Provinces, Canada, and all of North America with no quarantine requirements, top, and from all of North America quarantining from 0% to 95%, bottom. Predictions are based on a local SEIR model using the mean effective reproduction number of $R$$=$ 1.35 for all of North America, solid lines, and $R$$=$ 1.16 for Canada, dashed lines, on the day of opening. The black horizontal line marks 0.1% of the population of Newfoundland and Labrador [46].

Lesson 10. Testing is critical for safe reopening

Several unexpected trends in the timeline of COVID-19 have recently raised the question: To which extent does testing manipulate the data? During the early stages of the pandemic, clearly, only severely symptomatic cases were tested and identified. After gaining a better understanding of the pathophysiology of COVID-19, we now know about the disproportionally high prevalence of asymptomatic transmission. In fact, the estimated undercount during the early stages of the pandemic was on the order of ten or more, meaning that only one in ten infections was detected and reported [39]. As testing is becoming more available and more common, we expect to detect a larger fraction of asymptomatic individuals and see the undercount decrease. From a data science standpoint, the question becomes: How can we best correct for under- and over-testing? A simple idea would be to interpret the reported deaths as ground truth, introduce a testing bias, and calibrate the models with respect to the total death count [5]. This approach critically depends on a region’s current stage within the outbreak and its definition of death, which can vary significantly by country. For example, some countries report death of COVID-19 while others report death with COVID-19. This could explain, at least in part, why some countries like the France, the United Kingdom, and Belgium report death rates of 16.7% 15.3%, and 14.9%, while others like Denmark, Germany, and Austria report 4.6%, 4.5% and 3.5% [18]. It is now widely recognized that broad testing will not only be important to advance our understanding of the data, but also be a mandatory step for safe reopening. Testing will help us to identify high-risk groups in the population based on age, gender, blood group, and underlying medial conditions. As test-trace-isolate is likely to become the new normal, mathematical models can help us estimate and understand how much and how often we need to test.

Asking the right question

Throughout the past six months, we have made impressive progress towards understanding the COVID-19 pandemic through data-driven modeling. We now know that the classical epidemiology models that have served us well during the early 20th century are a useful starting point to design models for infectious diseases in the 21st century [2]. However, since the word is a lot more connected than a hundred years ago [50], local behavior and global mobility play an equally important role in modeling the outbreak dynamics and outbreak control of COVID-19 today. Against our initial fear of seeing the number of infectious explode beyond control, we now know that we can actually modulate the disease dynamics through behavioral changes and political measures [Linka, 2020a]. Not only have we learned how rapidly the disease curve would grow in the absence of interventions; we also know how long it takes for political measures to effectively bend the curve. In fact, our current COVID-19 models are much better than their public reputation [5]. They can predict, interpret, and explain the effects with parameters and numbers [51].

But we had to learn to set expectations right and to be very specific about asking the right questions [7]. We have learned that generic questions like What will the disease trajectory look like? are virtually impossible to answer, especially when projected several weeks or months into the future. Instead, specific questions like What is the effect of changing this? are much easier to answer and can be equally insightful for political decision making. And, as a useful by-product, we can even quantify uncertainties and provide confidence intervals on our response.

Six months into the pandemic, there are many more open questions than answers, and we will likely not be able to solve all of them before the disease decays. One of the most pressing questions to complete our understanding of the outbreak dynamics is What is the true size of the affected population?, which we can reword into the easier-to-answer questions How would knowing the rate of asymptomatic transmission change our understanding of the disease? or How would this knowledge change with unlimited testing?. Another important questions that will drive our priorities upon reopening is How homogeneous is the spread?, which we could rephrase more quantitatively as What are the most vulnerable populations? or What are scientific metrics to identify superspreading events?, or even more specifically, How would our knowledge change if children were more asymptomatic and less infectious than adults?. Moving into the fall, we will likely want to know Will there be a second wave?, but rather we should ask How do increased mobility during the summer and seasonality during the fall impact the reproduction number?. Instead of asking the million-dollar question Can we prevent a resurge? we should ask, What is the limit reproduction number beyond which we can no longer manage the disease through test-isolate-trace strategies?. These are all questions which data-driven modeling can confidently help to address.

As modelers, it is our ethic responsibility to educate the public to ask the right questions and to communicate the limitations of our answers. One of the most frequent questions the general population is asking today is When will there be a vaccine? As modeling community, we should rephrase this question and ask If we are willing to wait 18 months to find the right vaccines for COVID-19, why do not we allow ourselves at least half of this same time to design the right models?

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.