Globe-hopping

Abstract

We consider versions of the grasshopper problem (Goulko & Kent 2017 Proc. R. Soc. A 473, 20170494) on the circle and the sphere, which are relevant to Bell inequalities. For a circle of circumference 2π, we show that for unconstrained lawns of any length and arbitrary jump lengths, the supremum of the probability for the grasshopper’s jump to stay on the lawn is one. For antipodal lawns, which by definition contain precisely one of each pair of opposite points and have length π, we show this is true except when the jump length ϕ is of the form π(p/q) with p, q coprime and p odd. For these jump lengths, we show the optimal probability is 1 − 1/q and construct optimal lawns. For a pair of antipodal lawns, we show that the optimal probability of jumping from one onto the other is 1 − 1/q for p, q coprime, p odd and q even, and one in all other cases. For an antipodal lawn on the sphere, it is known (Kent & Pitalúa-García 2014 Phys. Rev. A 90, 062124) that if ϕ = π/q, where $q\in \mathbb{N}$, then the optimal retention probability of 1 − 1/q for the grasshopper’s jump is provided by a hemispherical lawn. We show that in all other cases where 0 < ϕ < π/2, hemispherical lawns are not optimal, disproving the hemispherical colouring maximality hypotheses (Kent & Pitalúa-García 2014 Phys. Rev. A 90, 062124). We discuss the implications for Bell experiments and related cryptographic tests.

1. Introduction

The grasshopper problem was first introduced in [1], which analysed Bell inequalities for the case where two parties carry out spin measurements about randomly chosen axes and obtain the spin correlations for pairs of axes separated by angle ϕ. It was noted [1] that tighter bounds could be obtained by a version of the following problem on the Bloch sphere. Half the area of a sphere is covered by a lawn, with the property that exactly one of every pair of antipodal points belongs to the lawn. A grasshopper lands at a random point on the lawn and then jumps in a random direction through a spherical angle ϕ. What lawn shape maximizes the probability that the grasshopper remains on the lawn after jumping, and what is this maximum probability (as a function of ϕ)?

Goulko & Kent [2] studied the planar version of the grasshopper problem, giving a combination of analytic and numerical results, and also discussed several interesting variants. As these discussions illustrate, the grasshopper problem is an appealing problem in geometric combinatorics which is of intrinsic interest, independent of its original motivations.

In this paper, we consider versions of the grasshopper problem on the circle and the sphere. One can similarly motivate this work as an exploration of geometric combinatorics in simple manifolds with non-trivial topologies. Although the circle defines the simplest non-trivial version of the problem, its solution still has some interesting features. Results for antipodal lawns on the circle also imply some optimality results for antipodal lawns on the sphere, since a spherical antipodal lawn defines a circular one for every great circle. The spherical version of the grasshopper problem has some features in common with the planar version, but the non-trivial topology and compactness mean that planar results do not always have direct parallels, and one would not expect all regimes of the planar ‘phase diagrams’ of [2] to have qualitatively similar parallels in the spherical case.

Another strong motivation is to develop further the analysis of Bell inequalities initiated in [1], which considered the average anticorrelations attainable by local hidden variable models for random pairs of measurement axes separated by a given fixed angle. Both the circle and the sphere are relevant here, since the circle parametrizes the simplest class of projective polarization measurements commonly used in Bell experiments on photons, while the sphere parametrizes all possible projective polarization measurements, or more generally all possible projective measurements on any physical system defining a qubit. We show that, perhaps surprisingly, local hidden variable models can produce perfect anticorrelations for random pairs of axes separated by angle ϕ on the circle, unless ϕ = π(p/q) with p odd, q even and (p, q) = 1, i.e. p and q are coprime. This means that any imprecision in the axis separation, however slight, allows classical simulation of quantum correlations. For the sphere, our results show that hemispherical lawns are not optimal unless ϕ = π(p/q), where p is odd and (p, q) = 1. This means that local hidden variable models can achieve stronger anticorrelations than previously realized for generic ϕ. We discuss these results and their implications further below.

2. The grasshopper on a circle

We first consider what seems to be the simplest non-trivial version of the problem, in which the grasshopper is constrained to jump through a known fixed angle around a circle of circumference 2π. This also allows us to study the significance of an antipodal condition, by considering lawns of length π that contain precisely one of every pair of antipodes.

Then, we consider the case in which there are two potentially independent (maybe overlapping) antipodal lawns, in which the grasshopper starts at a random point on one. As before, it jumps through a known fixed angle in a random direction. In this case, the question is how to configure the lawns to maximize the probability that it lands on the second.

Pitalúa-García [3] previously discussed the grasshopper on the circle, with two antipodal lawns, and noted the optimality of the lawn S_π,q for the case of rational jumps with even numerator (see below).

These versions of the problem are physically motivated as follows. A great circle on the Bloch sphere defines linear polarization measurements, which are easily implemented and commonly used in Bell and other cryptographic tests. ‘Classical’ hidden variable models for these measurement outcomes are defined by antipodal colourings of the circle. A simple hidden variable model for the quantum singlet state, in which the outcomes of the same measurements on both subsystems are perfectly anticorrelated, is defined by a single antipodal colouring. The most general model, in which measurement outcomes may be independent, is defined by a pair of antipodal colourings. The retention probabilities define the anticorrelations predicted by these models, which can be compared to those predicted by quantum theory via Bell inequalities. As we discuss below, our results have interesting implications for testing and simulating quantum entanglement.

(a). Statement of the problem

General lawns: Following [2], the most general version of the grasshopper problem on the circle allows lawns of variable density, defined by a measurable probability density function f on the circle ${\mathbb{S}}^1$ satisfying f (θ) ∈ [0, 1] for all θ ∈ [0, 2π) and

$${\int }_{{\mathbb{S}}^1}\text{d}\theta f(\theta )=L.$$ 2.1

Here, L is the lawn length. We take the circle to have length 2π, so the non-trivial cases have 0 < L < 2π.

It will suffice for most of our discussion to consider indicator functions f with f (θ) ∈ {0, 1}. We represent such lawns by measurable subsets S ⊂ [0, 2π), where S = {θ : f (θ) = 1} has measure μ(S) = L.

The functional $p_f(\varphi )$ is defined by

$$p_f(\varphi )=\frac{1}{2L}{\int }_{{\mathbb{S}}^1}\text{d}\theta [f(\theta )f(\theta \mathbf{+}\varphi )+f(\theta )f(\theta \mathbf{-}\varphi )].$$ 2.2

Here and below all angles are taken modulo 2π. We refer to the expression in equation (2.2) as the retention probability: it defines the probability that a grasshopper starting at a randomly chosen point on the lawn remains on the lawn after jumping through angle ϕ in a random direction.

The grasshopper problem is then to answer the following. What is the supremum of p_f(ϕ) over all such functions f, for each value of ϕ ∈ [0, 2π)? Which f, if any, attain the supremum? Or if none, which sequences approach the supremum value?

We will show below that the supremum value is 1 for all ϕ ∈ [0, 2π).

Antipodal lawns: For the case L = π, we also consider these questions restricted to antipodal lawns, for which f (θ) ∈ {0, 1} and $f(\theta +\pi )=\overline{f(\theta )}=1-f(\theta )$ for all θ.

We will show below that the supremum value is 1 for all ϕ ∈ [0, 2π) except ϕ of the form π(p/q) where p and q are coprime and p is odd, when it is 1 − 1/q.

Two independent antipodal lawns: We can extend the grasshopper problem to the case of two lawns given by antipodal measurable subsets S^A, S^B of the circle, defined by suitable indicator functions f^A, f^B : [0, 2π) → {0, 1}, where S^X = {θ: f^X (θ) = 1}. Here, the relevant functional for jump ϕ is defined by

$$p_{f^A,f^B}(\varphi )=\frac{1}{2L}{\int }_{{\mathbb{S}}^1}\text{d}\theta [f^A(\theta )f^B(\theta \mathbf{+}\varphi )+f^A(\theta )f^B(\theta -\varphi )].$$

As we explain below, this is the version of the problem relevant to analysing general local hidden variable models for bipartite quantum states, where the measurements chosen on the two subsystems are independent and each parametrized by the circle. We will show below that the supremum value is 1 for all ϕ ∈ [0, 2π) except ϕ of the form π(p/q), where p and q are coprime with p odd and q even, when it is 1 − 1/q.

This illustrates that the two-lawn version of the problem is a non-trivial extension of the one-lawn version, even in the case of the circle. In particular, for jump values of the form π(p/q) with p and q coprime and both odd, the optimal one-lawn jump probability is strictly less than 1, while the optimal two-lawn jump probability is 1.

One-directional grasshopper: A natural and apparently simpler version of the grasshopper problem in one dimension is given by assuming that the grasshopper always jumps in the same direction. For a grasshopper on the real line [2], this restriction makes no essential difference: the supremum probability is still 1 for any jump length and the same limiting construction works for the one-directional and standard bidirectional case.

Similarly, one can assume that the grasshopper on the circle only jumps clockwise (or anticlockwise). For one lawn, our results and constructions for the bidirectional case carry over straightforwardly to this case, so we will not discuss it separately. With two lawns, the construction S^A = [0, L), S^B = [ϕ, L + ϕ) obviously gives retention probability 1 for clockwise jump ϕ.

For L = π, this construction defines antipodal lawns. The one-directional grasshopper problem on the circle thus turns out to be of no independent interest, and we will not discuss it further.

(b). Solution for general lawns

Lemma 2.1 (Rational case). —

The optimal retention probability is 1 for a lawn of length L with jump ϕ = (p/q) 2π, where the highest common factor (p, q) = 1.

Proof. —

Define the lawn S_L,q to be

$$S_{L,q}=\bigcup _{j=0}^{q-1}[2\pi \frac{j}{q},2\pi \frac{j}{q}+\frac{L}{q})$$ 2.3

An example of such a lawn is depicted in the left panel of figure 1. Clearly, S_L,q has length L and retention probability 1. ▪

Figure 1.

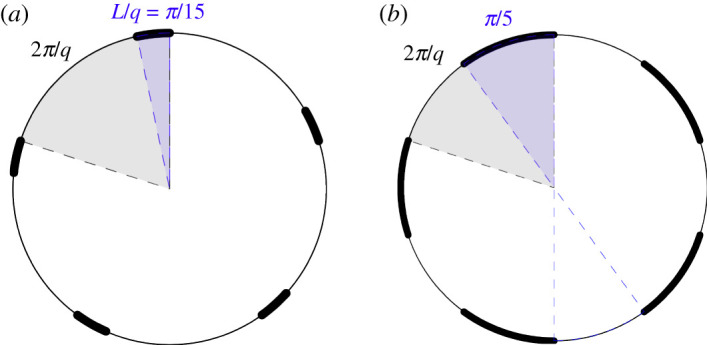
Sketch of an optimal general lawn S_L,q with L = π/3, for a rational jump ϕ = (p/q)2π with p = 2 and q = 5 (a) and of an optimal antipodal lawn S_π,q for a rational jump ϕ = π(p/q) with even numerator p = 2 and q = 5 (b). (Online version in colour.)

This solves the problem for rational jumps.

Lemma 2.2 (Irrational case). —

The supremum retention probability is 1 for a lawn of length L when the jump ϕ is an irrational multiple of 2π.

Proof. —

Define the lawn $S_{ϵ,\varphi }^k$ to be

$$S_{ϵ,\varphi }^k=\bigcup _{j=0}^{k-1}[j\varphi ,j\varphi +ϵ),$$ 2.4

where (following the usual definition of set union) any overlapping intervals are counted only once. Let K be the largest value of k such that $S_{ϵ,\varphi }^k$ has length smaller than L. Weyl’s equidistribution theorem [4] guarantees that such a K exists for any ϵ in the range L > ϵ > 0. Now define the lawn S_L,ϵ,ϕ by

$$S_{L,ϵ,\varphi }=S_{ϵ,\varphi }^K\cup [K\varphi ,K\varphi +\delta ),$$ 2.5

where δ ∈ (0, ϵ] is the smallest value in that range such that S_L,ϵ,ϕ has length L. Unless the grasshopper starts in the first interval and jumps anticlockwise, or the last interval and jumps clockwise, it remains on the lawn, which thus has retention probability ≥1 − ϵ. A sequence with ϵ → 0 gives us the supremum value of 1. ▪

Thus, we obtain the following theorem.

Theorem 2.3. —

For unconstrained lawns of length L the supremum retention probability is 1. The supremum is attained for rational jumps ϕ = (p/q)2π.

(c). Solution for antipodal lawns

Lemma 2.4 (Rational case, even numerator). —

The optimal retention probability is 1 for an antipodal lawn with jump ϕ = π(p/q), where (p, q) = 1 and p is even.

Proof. —

An antipodal lawn has length π. Since (p, q) = 1 and p is even, q is odd. From equation (2.3), we have

$$S_{\pi ,q}=\bigcup _{j=0}^{q-1}[2j\pi \frac{1}{q},(2j+1)\pi \frac{1}{q}).$$ 2.6

Clearly, S_π,q has length π, is antipodal, and has retention probability 1. ▪

An example for such a lawn in depicted in the right panel of figure 1.

Now consider a lawn of length π with jump ϕ = π(p/q), where (p, q) = 1 and p is odd. We take q ≥ 2 here; we consider the special case of q = 1 (which for p odd implies a jump through angle π) separately below.

Lemma 2.5 (Rational case, odd numerator). —

The optimal retention probability is (1 − 1/q) for an antipodal lawn with jump ϕ = π(p/q), where (p, q) = 1, p is odd and q ≥ 2.

Proof. —

First, consider lawns defined by indicator functions f with f (θ) ∈ {0, 1}. Consider any starting point θ and the set of points {θ_k = θ + k (π(p/q)) : 0 ≤ k ≤ (2q − 1)}. These points are all distinct, and the points θ_k, θ_k+q are antipodal, where the sum is taken modulo 2q. Hence any antipodal lawn will contain precisely q of these 2q points. A sequence of q jumps in either direction takes a point on the lawn to the antipodal point, which must be off the lawn. Thus, whichever q points are on the lawn, a clockwise jump from at least one of them takes the grasshopper off the lawn, and similarly for anticlockwise jumps. Because this is true for all such sets of lawn points, the probability of leaving the lawn is at least 1/q, i.e. the retention probability is at most 1 − 1/q.

For a general indicator function, consider again the discrete set of points D_θ,p/q = {θ_k = θ + k(π(p/q)):0 ≤ k ≤ (2q − 1)}, and suppose f(θ_k) = p_k, with p_k + p_k+q = 1 and 0 ≤ p_k ≤ 1. Suppose the grasshopper first lands at a point in D_θ,p/q. It then jumps to another point in D_θ,p/q. In what follows, we take all probabilities conditioned on the first landing being in D_θ,p/q.

Let p_k be the probability of first landing at θ_k, so we have p_k + p_k+q = 1 since the lawn is antipodal. The retention probability is

$$\begin{array}{rl}\frac{1}{2q}\sum _{k=0}^{2q-1}{p}_k(p_{k-1}+p_{k+1})& =\frac{1}{q}\sum _{k=0}^{2q-1}{p}_k{p}_{k+1}=\frac{1}{q}\sum _{k=0}^{q-1}(p_k{p}_{k+1}+p_{k+q}{p}_{k+q+1})\\ & =\frac{1}{q}(p_{q-1}(1-p_0)+(1-p_{q-1})p_0+\sum _{k=0}^{q-2}(p_k{p}_{k+1}+(1-p_k)(1-p_{k+1}))).\end{array}$$

The retention probability as a function of p₀,  …,  p_q−1 is linear in each variable, therefore its maximum value is attained for some choice of the extreme values 0 or 1 for each variable. This consideration returns us to the case with indicator functions previously discussed.

In the case p = 1, the semi-circular lawn

$$S_{\text{semi}}=[0,\pi ),$$ 2.7

which has retention probability 1 − 1/q, is thus optimal.

For general odd p, the lawn

$$S_{\pi ,p,q}=\bigcup _{j=0}^{q-1}[j\pi \frac{p}{q},j\pi \frac{p}{q}+\frac{\pi }{q})$$ 2.8

is antipodal and has retention probability 1 − 1/q, and is thus optimal. ▪

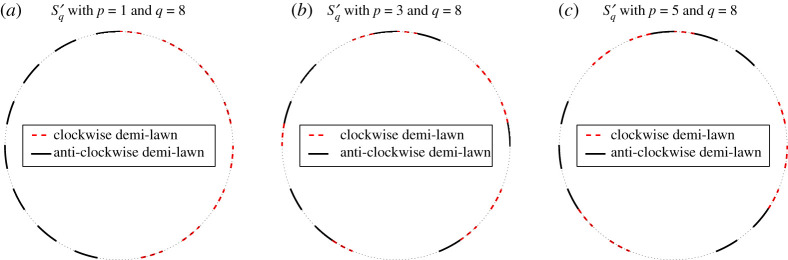
There are also other optimal lawns that are not rotated versions of these. For general p, we can construct a lawn with the maximal retention probability as follows:

$$S_q^{\prime }=\bigcup _{j=0}^{q-1}[\pi \frac{jp}{q},\pi \frac{jp}{q}+\frac{\pi }{2q})\cup \bigcup _{j=0}^{q-1}[-\pi \frac{jp}{q}-\frac{\pi }{2q},-\pi \frac{jp}{q}).$$ 2.9

Here, the two unions define disjoint ‘demi-lawns’ of length π/2. Several examples are plotted in figure 2.

Figure 2.

Sketch of an optimal antipodal lawn S′_q for a rational jump ϕ = π(p/q) with odd numerator p = 1 (a), p = 3 (b), p = 5 (c), and (in all panels) q = 8. The two demi-lawns are marked by different line styles (black solid lines and red dashed lines). (Online version in colour.)

The special case of a jump through angle π takes any point to its antipodal point. In the case when the indicator function is restricted to f(θ) ∈ {0, 1}, all antipodal lawns have probability 0. However, a higher probability can be attained for general indicator functions.

Lemma 2.6 (Jump through angle π). —

The optimal retention probability is 1/2 for an antipodal lawn with jump ϕ = π.¹

Proof. —

Since antipodal points have lawn density p and (1 − p) for some p ∈ [0, 1], the optimal density for each pair is given by p = 1/2, which maximizes p(1 − p). The optimal lawn in this case thus has uniform density 1/2 and the retention probability is 1/2. ▪

Lemma 2.7 (Irrational case). —

The supremum retention probability is 1 for antipodal lawns with jump angle ϕ = πx, when x is irrational.

Proof. —

By Hurwitz’s theorem [5], there are infinitely many rationals p/q such that

$$|x-\frac{p}{q}|\le \frac{1}{\sqrt{5}{q}^2}.$$ 2.10

We could apply this result directly, considering separately the possibilities that p is odd or even. A slightly shorter argument follows from an extension of Hurwitz’s theorem due to Uchiyama [6], elaborated by Elsner [7]. This implies that for any irrational x there are infinitely many rationals p/q with p even and q odd such that

$$|x-\frac{p}{q}|\le \frac{1}{q^2}.$$ 2.11

Let p/q be a rational approximation to x of this type. For jump x, the lawn S_π,q has leaving probability

$$q|x-\frac{p}{q}|\le \frac{1}{q}.$$ 2.12

By considering an infinite sequence of approximations with increasing q, we can make this arbitrarily small. Hence the supremum retention probability is 1. ▪

Combining the lemmas for antipodal lawns, we obtain the following theorem.

Theorem 2.8. —

For antipodal lawns with general indicator functions, the supremum retention probability is 1, except for jumps of the form ϕ = π(p/q), where (p, q) = 1 and p is odd. In the latter case, it is 1/2 for q = 1 and 1 − 1/q otherwise.

(d). Two antipodal lawns

We now consider the case of two lawns, S^A and S^B, where the grasshopper starts on one and we are interested in optimizing the probability that it lands on the other. In versions of the problem where the supremum probability is 1 for a single lawn, we can obviously obtain this supremum by taking S^A = S^B. The only case that remains of interest is thus two antipodal (thus length π) lawns with jump ϕ = π(p/q), where (p, q) = 1 and p is odd.

Lemma 2.9. —

The optimal retention probability for two antipodal lawns is (1 − 1/q) when the jump ϕ = π(p/q), where (p, q) = 1, p is odd and q is even.

Proof. —

We have that 2ϕ = π(p/q′), 2q′ = q and (p, q′) = 1. Again, we first consider the case in which the lawn densities take only values 0 or 1. Any such lawn is defined by the set S = {θ : f (θ) = 1} . Define the complementary lawn

$$\overline{S}=[0,2\pi )\setminus S.$$

If S is antipodal, then so is $\overline{S}$, since $\overline{S}$ is the set of points antipodal to points in S.

Consider any starting point θ and the sets of points

$$\begin{array}{rl}{A}_{\theta }& =\{{\theta }_k^A=\theta +k\left(\pi \frac{p}{q^{\prime }}\right):0\le k\le (2q^{\prime }-1)\},\\ B_{\theta }& =\{{\theta }_k^B=\theta +(k+\frac{1}{2})\left(\pi \frac{p}{q^{\prime }}\right):0\le k\le (2q^{\prime }-1)\}.\end{array}$$

These points are all distinct. The points ${\theta }_k^A,{\theta }_{k+q^{\prime }}^A$ are antipodal, as are the points ${\theta }_k^B,{\theta }_{k+q^{\prime }}^B$, where the subscript sums are taken modulo 2q′. Hence the antipodal lawns S^A, S^B contain precisely q′ of the 2q′ points A_θ, B_θ, respectively. Starting at a point on S^A, a sequence of 2q′ jumps clockwise through ϕ reaches the antipodal point, which must be off the lawn. Thus, at least one of these jumps links a point on S^A to a point off S^B or a point on S^B to a point off S^A. In the first case, there is at least one clockwise jump from a point in $A_{\theta }\cap S^A$ to $B_{\theta }\cap \overline{S^B}$. In the second case, there is at least one clockwise jump from $B_{\theta }\cap S^B$ to $A_{\theta }\cap \overline{S^A}$. As the lawns are antipodal, this implies at least one anticlockwise jump from $A_{\theta }\cap S^A$ to $B_{\theta }\cap \overline{S^B}$. Thus, whichever q′ points lie in $A_{\theta }\cap S^A$, there is at least one jump from one of them in one direction that takes the grasshopper to $\overline{S^B}$. Because this is true for all such sets of lawn points, the probability of leaving the lawn is at least 1/2q′, i.e. the retention probability is at most 1 − 1/2q′ = 1 − 1/q.

For the general case with unrestricted density functions, we can argue as before. If lawn A has a point θ such that f_A (θ) = 1 − f_A (θ + π) = p, where 0 < p < 1, then at least one of the choices p = 0 and p = 1 does not decrease the retention probability. The same argument holds for lawn B. We can thus restrict without loss of generality to lawns with density 0 or 1 everywhere.

In the case p = 1, where ϕ = π(1/2q′) = π(1/q), we can attain this retention probability by taking S^A = S^B = [0, π) (i.e. identical semicircular lawns). A jump from S^A clockwise remains on S^A unless it begins in the segment [π(1 − 1/q), π); similarly an anticlockwise jump remains on S^A unless it begins in the segment [0, π(1/q)).

For general p odd, we can construct a lawn with the same retention probability by taking S_A = S_B = S′_q, where S′_q is the antipodal lawn defined above, which has leaving probability 1/q. ▪

Lemma 2.10. —

The optimal retention probability for two antipodal lawns is 1 when the jump ϕ = π(p/q), where (p, q) = 1, p is odd and q is odd.

Proof. —

We have ϕ = π(p/q). Define the lawns

$$S_A=S_{\pi ,q}=\bigcup _{j=0}^{q-1}[\pi \frac{2j}{q},\pi \frac{2j+1}{q})\text{and}{S}_B=\overline{S_A}=\bigcup _{j=0}^{q-1}[\pi \frac{2j+1}{q},\pi \frac{2j+2}{q}).$$

These lawns are antipodal, and the jump probability from S_A to S_B for a jump of angle ϕ is 1, so this lawn configuration is optimal. ▪

Combining the lemmas for a pair of antipodal lawns, we obtain the following theorem.

Theorem 2.11. —

For antipodal lawns the supremum retention probability is 1, except for jumps of the form ϕ = π(p/q), where (p, q) = 1, p is odd and q is even. In the latter case, it is 1 − 1/q.

3. The grasshopper on a sphere

(a). Statement of the problem

We now consider the spherical (one-lawn, antipodal) version of the problem. The lawn is now a subset L of the sphere, ${\mathbb{S}}^2$, in three-dimensional space, that is antipodal: every point x of the sphere belongs to L if and only if the opposite point does not belong to L. As before, the grasshopper starts at a point chosen uniformly at random in the lawn, and jumps a fixed distance ϕ in a direction chosen uniformly at random. The goal is to pick the shape of L that maximizes the probability of a successful jump, i.e. the probability of staying on the lawn. Put differently, the goal is to maximize the integral

$${\int }_{{\mathbb{S}}^2}f(x)\hspace{0.17em}\text{d}s{\int }_{C_{\varphi }(x)}f(y)\hspace{0.17em}\text{d}\omega ,$$ 3.1

where the point x corresponds to the surface element ds on the sphere ${\mathbb{S}}^2$, the point y is taken from the circle C_ϕ(x) of radius ϕ around the point x, the angle ω ∈ [0, 2π) is the corresponding position on the circle, and the function $f:{\mathbb{S}}^2\to \{0,1\}$ is defined by f(x) = 1 if and only if x ∈ L.

Theorems 3.1 and 3.11 show that the retention probability, which is proportional to (3.1), is maximized by the hemispherical lawn if and only if ϕ = π/q, with q > 1 integer.

(b). Corollaries of results on the circle

Theorem 3.1. —

The optimal retention probability is (1 − 1/q) for an antipodal lawn on the sphere with jump π/q, where q ≥ 2 is a positive integer.

Proof. —

For a single antipodal lawn on the circle, with jump π/q for positive integer q, we have shown that the optimal retention probability is 1 − 1/q and is attained by a semi-circular lawn.

Now consider an antipodal lawn on the sphere with the same jump π/q. Any starting point on the lawn and any jump direction together define a great circle. The start point is equally likely to be in any arc of a given length on the circle. Hence our argument for the upper bound 1 − 1/q for antipodal lawns on the circle also applies to antipodal lawns on the sphere. ▪

Since a hemispherical lawn attains this bound, we see that hemispherical lawns are optimal for jumps π/q, where q ≥ 2 is a positive integer. We show below that hemispherical lawns are not optimal for any other jump values.

For a pair of antipodal lawns on the circle, with jump π/q for even positive integer q, we have shown that the optimal retention probability is 1 − 1/q and is attained by a pair of identical semicircular lawns. Again, our arguments extend to a pair of antipodal lawns on the sphere: the optimal retention probability is 1 − 1/q and is attained by a pair of identical hemispherical lawns. This result was proved in theorem 1 of [1].

(c). Construction of lawns with greater retention probability than the hemisphere for ϕ ≠ π/q

We now consider jumps ϕ ≠ π/q and show that hemispherical lawns are not optimal in these cases, by constructing lawns that have higher retention probability. Each of the lawns we construct will be a hemisphere with a ‘cogged’ boundary akin to the construction in [2]. The number, size and layout of the cogs varies according to the size ϕ of the grasshopper’s jump. We consider three cases according as ϕ/π is irrational, rational with even numerator, or rational with the odd numerator. These cases are resolved in lemmas 3.9, 3.8 and 3.10, respectively.

Lemma 3.8 will deal with the simplest case: ϕ = pπ/q where p and q are coprime and p is even. This construction is illustrated in figure 3(a) for ϕ = 6π/13. Starting from any point on the equator, take the set of q points visited by a sequence of q consecutive jumps of size ϕ travelling round and round the equator p/2 times before returning to the starting point. Take a second sequence with an antipodal starting point and continuing with the sequence of points antipodal to the first sequence. Note that these 2q points are distinct and separated from each other by a distance of at least π/q. The points are spaced evenly, distance π/q apart, round the equator. Draw circles of sufficiently small radius r = r(ϕ) around these 2q points such that there are no overlaps between them. Our lawn consists of the southern hemisphere with these circles added for the first sequence and removed for the second sequence. In other words, we modify the hemisphere to fill semi-circular caps above the equator and remove semi-circular cups below the equator, creating our cogged hemisphere.

Figure 3.

Construction of modified lawns for rational ϕ = pπ/q and p even, with p = 6 and q = 13 (a, lemma 3.8) and for irrational ϕ/π with ϕ = 1.2 (b, lemma 3.9). The caps and cups around the equator are shown as black and white dots, respectively.

For comparison, figure 3(b) looks ahead to the corresponding construction when ϕ/π is irrational. This case will be considered in lemma 3.9.

Our construction ensures that a jump of length ϕ cannot connect any point in a cap to any point in a cup, or vice versa. For lemma 3.8, most of our analysis involves estimating the probability of a jump between caps or between cups. For lemmas 3.9 and 3.10, we also need to consider jumps from caps or cups to the whole hemisphere S; we describe the modified constructions in the proofs of these lemmas. Lemma 3.10 requires the further complication of having caps and cups of varying sizes.

(d). Preliminaries

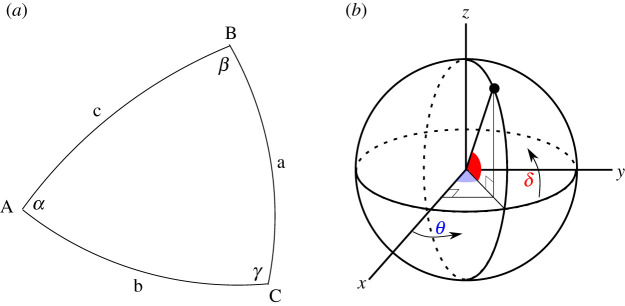
We recall some basic formulae in spherical geometry. Using the notation in figure 4, where a, b, c are (greatcircle) lengths and α, β, γ are angles, we have the sine rule:

$$\frac{\sin a}{\sin \alpha }=\frac{\sin b}{\sin \beta }=\frac{\sin c}{\sin \gamma },$$ 3.2

the cosine rule:

$$\cos a=\cos b\cos c+\sin b\sin c\cdot \cos \alpha ,$$ 3.3

and, in particular,

$$\text{if }\alpha =\frac{\pi }{2}\text{ then }\cos a=\cos b\cos c.$$ 3.4

The next formula follows easily:

$$\text{if }\alpha =\frac{\pi }{2}\text{ then }\tan a\cos \beta =\tan c.$$ 3.5

Figure 4.

Spherical triangle (a) and spherical coordinates (b). (Online version in colour.)

For points on the sphere, it is convenient to use pairs of angles (θ, δ) based on (longitude, latitude), where θ is the azimuthal angle and δ is the elevation or copolar angle, see figure 4. We take the radius of the sphere to be unity, so a typical point on the surface with spherical coordinates (θ, δ) has Cartesian coordinates (x, y, z) = (sinθcosδ, cosθcosδ, sinδ), where the z-axis passes through the poles.

For B and C points on the sphere, the dot-product of their Cartesian coordinates gives their angular distance. In figure 4,

$$B\cdot C=\cos a.$$ 3.6

We recall the notation for the cosecant function: $\csc a=1/\sin a$.

In §3h, we make use of the following trigonometric identities and corollaries.

Proposition 3.2. —

For all integers q ≥ 2,

$$\sum _{j=0}^{q-1}\cos \left(\frac{2j\pi }{q}\right)=\sum _{j=0}^{q-1}\cos \left(\frac{(2j+1)\pi }{q}\right)=0.$$

Proof. —

In each case, the summands are the real parts of a set of complex numbers regularly spaced around the origin in the Argand diagram. The sets are {e^2j iπ/q | 0 ≤ j < q} and {e^{(2j+1) iπ/q} | 0 ≤ j < q}. These symmetric sets and therefore their sums are each invariant under rotation by 2π/q about the origin. Hence each sum is zero. ▪

Corollary 3.3. —

• (i)$\sum _{j=0}^{q-1}2\sin \frac{j\pi }{q}\sin \frac{(j+1)\pi }{q}=q\cos \frac{\pi }{q}$;
• (ii)$\sum _{j=0}^{q}2{\sin }^2\frac{j\pi }{q}=q$.

Proof. —

For (i), from proposition 3.2

$$\begin{array}{rl}& \sum _{j=0}^{q-1}2\sin \frac{j\pi }{q}\sin \frac{(j+1)\pi }{q}=\sum _{j=0}^{q-1}(\cos (\frac{j\pi }{q}-\frac{(j+1)\pi }{q})-\cos (\frac{j\pi }{q}+\frac{(j+1)\pi }{q}))\\ & =\sum _{j=0}^{q-1}\cos \frac{\pi }{q}-\sum _{j=0}^{q-1}\cos \frac{(2j+1)\pi }{q}=q\cos \frac{\pi }{q}-0.\end{array}$$

For (ii), again from proposition 3.2.

$$\begin{array}{rl}\sum _{j=0}^{q-1}2{\sin }^2\frac{j\pi }{q}& =\sum _{j=0}^{q-1}(1-\cos \frac{2j\pi }{q})=q.\end{array}$$

 ▪

Finally, in the analysis of our construction, the following proposition will be useful.

Proposition 3.4. —

Let y and z satisfy y ≥ 0, y + z ≥ 0, and z = O(r^{2 d}) for some d > 0 as r → 0. Then

$$\sqrt{y+z}=\sqrt{y}+O(r^d).$$

Proof. —

Assume, without loss of generality, that z ≥ 0; then

$${(\sqrt{y+z}-\sqrt{y})}^2\le (\sqrt{y+z}-\sqrt{y})(\sqrt{y+z}+\sqrt{y})=z,$$

and therefore $\sqrt{y+z}-\sqrt{y}\le \sqrt{z}=O(r^d)$. ▪

(e). Analysis of the construction

In our constructions for any fixed jump distance ϕ, we will take the cap and cup radius r to be sufficiently small. We can assume that r is much smaller than ϕ and formally we will take r → 0.

For each of our lemmas, we need to analyse the difference between jumps on a hemisphere and jumps on our lawn L. Denote by A, U and S, the caps, the cups and the southern hemisphere, respectively. Note that L consists of S with A added and U taken away. The set of successful jumps from L to L can be classified as jumps from S to S plus jumps from A to S and vice versa, plus jumps from A to A, but minus jumps to or from U. These latter are jumps from U to $S\setminus U$ and vice versa since our construction ensures that no jump is possible between A and U. We account for jumps involving U as jumps U to S plus jumps S to U minus jumps U to U, since these last were counted twice. In symbols, we may express this as

$$\stackrel{\curvearrowright }{LL}=\stackrel{\curvearrowright }{SS}+\stackrel{\curvearrowright }{AS}+\stackrel{\curvearrowright }{SA}+\stackrel{\curvearrowright }{AA}-(\stackrel{\curvearrowright }{US}+\stackrel{\curvearrowright }{SU}-\stackrel{\curvearrowright }{UU}).$$ 3.7

For subsets X, Y of the spherical surface, we denote by $\stackrel{\curvearrowright }{XY}$ the probability that the grasshopper starts at a point in X and ends up at a point in Y. For a sequence of caps corresponding to distance ϕ and a corresponding antipodal sequence, we define the following quantities: $\stackrel{\curvearrowright }{aa}$ is the probability of a jump from one particular cap to another particular cap distance ϕ from the first, $\stackrel{\curvearrowright }{uu}$ for the corresponding probability for cups, $\stackrel{\curvearrowright }{aS}$ for the jump probability between one cap and S, $\stackrel{\curvearrowright }{uS}$ for the corresponding probability for a cup, $\stackrel{\curvearrowright }{SS}$ for the probability of a jump from S to S, and finally $\stackrel{\curvearrowright }{aN}$ for a jump from a cap to the northern hemisphere. We define $\stackrel{\curvearrowright }{Sa}$ and $\stackrel{\curvearrowright }{Su}$ similarly. For lemmas 3.8 and 3.9, each cap and cup is the same size. Later, for lemma 3.10, this will not be the case and we will revise our notation accordingly.

It is easy to show that, for all X, Y,

$$\stackrel{\curvearrowright }{XY}=\stackrel{\curvearrowright }{YX}.$$ 3.8

By symmetry, we find that

$$\stackrel{\curvearrowright }{aa}=\stackrel{\curvearrowright }{uu}\text{and}\stackrel{\curvearrowright }{uS}=\stackrel{\curvearrowright }{aN}.$$ 3.9

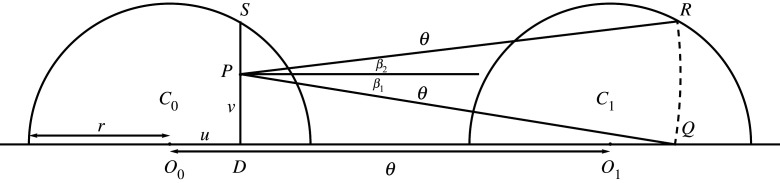
In figure 5, we show two successive caps C₀, C₁ of radius r, whose centres O₀, O₁ are at angular distance ϕ from each other, and a sample point P in C₀. For jumps from P towards C₁, β₁ and β₂ are the angles between the latitude through P and the direction of jumps to the equator at Q and to the circumference of C₁ at R, respectively. We see that β₁ ≥ 0 always, but it is possible that β₂ < 0, for example, if P is close enough to the point S in figure 5.

Figure 5.

Jump geometry.

Proposition 3.5. —

The circle of possible jump destinations from P intersects the upper semicircle of radius r centred at O₁ exactly once, so R is well-defined.

Proof. —

We first note that the point Q always lies within the diameter of C₁. Let x be the longitude of Q relative to O₁, so DQ = x + ϕ − u. By equation (3.4) applied to the right-angled spherical triangle ΔPQD, x is the solution to

$$f(x):=\cos v\cos (x+\varphi -u)-\cos \varphi =0.$$

Since f(x) is a decreasing function of x and f(u) = cos vcosϕ − cosϕ ≤ 0, showing that f( − r) ≥ 0 will establish that −r ≤ x ≤ u, and so Q lies within the diameter of C₁.

Since v ≤ SD and cos ucos SD = cos r by equation (3.4),

$$\begin{array}{rl}\cos u\hspace{0.17em}f(-r)& =\cos u\cos v\cos (-r+\varphi -u)-\cos u\cos \varphi \\ & \ge \cos r\cos (-r+\varphi -u)-\cos u\cos \varphi .\end{array}$$

The right-hand side of this equation is an increasing function of u and takes the value cos rcosϕ − cos ( − r)cosϕ = 0 at u = −r. Since u ≥ −r, we have f( − r) ≥ 0 as desired.

We use without proof the geometrically obvious fact that the jump circle around P intersects the equator exactly once to the right of P. This is true as long as ϕ is fixed and r → 0. Combined with the argument above, this fact implies that the jump circle intersects the circumference of C₁, as well as the circumference of the mirror image of C₁ below the equator.

It remains to see why the intersection point with the upper semicircle (the circumference of C₁) is unique. Notice that each of the two curves, the jump circle and the upper semicircle, lies in a single plane, and these two planes are different. Therefore, each possible location for the point R belongs to the line of intersection of these planes. This line passes through at most two points of the circle around O₁. We already know that the jump circle intersects not only the circumference of C₁ but also its mirror image; therefore, there is exactly one intersection point with the circumference itself. ▪

We see that

$$\begin{array}{rl}\stackrel{\curvearrowright }{aa}& ={\int }_C({\beta }_1+{\beta }_2)\hspace{0.17em}\text{d}s,\hspace{0.17em}\stackrel{\curvearrowright }{aS}={\int }_C(\pi -2{\beta }_1)\hspace{0.17em}\text{d}s,\hspace{0.17em}\stackrel{\curvearrowright }{aN}={\int }_C(\pi +2{\beta }_1)\hspace{0.17em}\text{d}s,\text{ and so }\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}=4{\int }_C{\beta }_1\hspace{0.17em}\text{d}s,\end{array}$$

where ds is a surface element of a cap C.

To prepare estimates for these integrals, we first find probabilities for a sample point P in a cap. In the following proposition, we use the notation given by figure 5, i.e. u and v are the azimuth and elevation (longitude and latitude) of P relative to the centre of C₀ and r is the radius of the cogs.

In the next proposition and everywhere below, the constants in our O( · ) notation depend on ϕ, but not on q, and we let r → 0.

Proposition 3.6. —

For 0 < ϕ < π/2,

$$\begin{array}{rl}& \text{(i)}\hspace{0.17em}{\beta }_1=v\cot \varphi +O(r^3),\\ & \text{(ii)}\hspace{0.17em}{\beta }_1+{\beta }_2=\sqrt{r^2-u^2}\csc \varphi +O(r^{3/2}).\end{array}$$

Proof. —

Let us first prove that β₁ and β₂ are both O(r). Observe that u, v are O(r). Notice that π/2 − β₁ is an angle in the right-angled spherical triangle PDQ. Hence by equation (3.5), sinβ₁ = O(r)/tanϕ = O(r), and so β₁ = O(r). Next, by the sine rule (3.2) for ΔPRQ, we have sin RQ/sin (β₁ + β₂) = sinϕ/sin ∠PRQ, and so sin (β₁ + β₂) = O(r), since the points R and Q are both inside a circle of radius r. Therefore, β₁ + β₂ = O(r) and β₂ = O(r).

We now prove parts (i) and (ii) of the proposition. We take the vertex O₁ in figure 5 as the point with spherical coordinates (0, 0). Then P has spherical coordinates ( − ϕ + u, v) and Cartesian coordinates ( − sin (ϕ − u)cos v, cos (ϕ − u)cos v, sin v). Let Q be the point with spherical coordinates (q, 0) on the equator inside C₁ at distance ϕ from P. From equation (3.5), we derive

$$\sin {\beta }_1=\cos \angle \mathrm{\#}QPD=\tan v\cot \varphi =v\cot \varphi +O(r^3),$$

which implies part (i) of the proposition.

Let R be the point with spherical coordinates (θ, δ) on the circumference of C₁ at distance ϕ from P. Then

$$\begin{array}{rl}P\cdot R& =\cos \varphi ,\end{array}$$ 3.10

$$\begin{array}{rl}\cos r& =\cos \theta \cos \delta ,\end{array}$$ 3.11

from equations (3.6) and (3.4).

We observe that u, v, θ, δ, q = O(r); note that for q this is by proposition 3.5. Equation (3.11) gives

$$r^2={\delta }^2+{\theta }^2+O(r^4),$$

and we will now focus on equation (3.10). We have

$$\begin{array}{rl}P& =(-\sin (\varphi -u)\cos v,\cos (\varphi -u)\cos v,\sin v);\\ Q& =(\sin q,\cos q,0);\\ R& =(\sin \theta \cos \delta ,\cos \theta \cos \delta ,\sin \delta ).\end{array}$$

Equation (3.10) thus becomes

$$\begin{array}{rl}P\cdot R& =\cos \varphi =-\sin (\varphi -u)\cos v\sin \theta \cos \delta +\cos (\varphi -u)\cos v\cos \theta \cos \delta +\sin v\sin \delta \\ & =-\sin (\varphi -u)\theta +\cos (\varphi -u)+O(r^2).\end{array}$$

So

$$\cos \varphi =-\theta \sin \varphi +\theta \cos \varphi \sin u+\cos \varphi +u\sin \varphi +O(r^2)=(u-\theta )\sin \varphi +\cos \varphi +O(r^2),$$

giving θ = u + O(r²). By our choice of Q,

$$\begin{array}{rl}P\cdot Q& =\cos \varphi =-\sin (\varphi -u)\cos v\sin q+\cos (\varphi -u)\cos v\cos q\\ & =-q(\sin \varphi \cos u-\cos \varphi \sin u)+O(r^3)+\cos \varphi +u\sin \varphi +O(r^2)\\ & =(u-q)\sin \varphi +\cos \varphi +O(r^2),\end{array}$$

and so q = u + O(r²) and q − θ = O(r²). From ΔPQR, we have

$$\cos ({\beta }_1+{\beta }_2){\sin }^2\varphi +{\cos }^2\varphi =\cos QR=Q\cdot R=\sin q\sin \theta \cos \delta +\cos q\cos \theta \cos \delta .$$

Subtracting each side from 1 and multiplying by 2 gives

$$\begin{array}{rl}{({\beta }_1+{\beta }_2)}^2{\sin }^2\varphi & =-2q\theta +q^2+{\theta }^2+{\delta }^2+O(r^4)={(q-\theta )}^2+{\delta }^2+O(r^4)\\ & ={\delta }^2+O(r^4)=r^2-{\theta }^2+O(r^4)=r^2-u^2+O(r^3).\end{array}$$

Applying proposition 3.4, we obtain

$$({\beta }_1+{\beta }_2)\sin \varphi =\sqrt{r^2-u^2}+O(r^{3/2}),$$

which establishes part (ii). ▪

We can now compare the probabilities $\stackrel{\curvearrowright }{aa}$ and $\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}$.

Proposition 3.7. —

For 0 < ϕ < π/2,

$$\frac{\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}}{2\stackrel{\curvearrowright }{aa}}=\cos \varphi +O\left(\sqrt{r}\right).$$ 3.12

Proof. —

To make comparison easier, it is convenient to combine the contributions from a pair of points. For any point P, we define its mate P′. When P has coordinates (u, v) relative to the centre of C₀, P′ has coordinates (u, v′) = (u, SD − v), where cos SDcos u = cos r (see figure 5 and equation (3.4)). If β₁′ and β₂′ are the angles corresponding to P′, then

$${\beta }_1^{\prime }=(SD-v)\cot \varphi +O(r^3)\text{and}{\beta }_1^{\prime }+{\beta }_2^{\prime }={\beta }_1+{\beta }_2+O(r^{3/2}),$$

from proposition 3.6. The equation cos SDcos u = cos r implies

$$1-{\cos }^{2}SD=\frac{1}{{\cos }^{2}u}\cdot ({\cos }^{2}u-{\cos }^{2}r)=r^2-u^2+O(r^4).$$

By proposition 3.4 with d = 2, we see that

$$\sin SD=\sqrt{r^2-u^2}+O(r^2)\text{and}SD=\sqrt{r^2-u^2}+O(r^2).$$

For any integrand β,

$${\int }_C\beta \hspace{0.17em}\text{d}s={\iint }_{C^{\prime }}\beta \cos v\hspace{0.17em}\text{d}u\hspace{0.17em}\text{d}v,$$

since the area of an element ds is cos v du dv, and where

$$C^{\prime }=\{(u,v)\mid \cos u\cos v\ge \cos r,-r\le u\le r\text{ and }0\le v\le r\}.$$

Note, however, that cos v = 1 − O(r²).

When we combine the integral for a sample point P with the integral for its mate P′, we obtain

$$\begin{array}{rl}2\stackrel{\curvearrowright }{aa}& ={\int }_C({\beta }_1+{\beta }_2)\hspace{0.17em}\text{d}s+{\int }_C({\beta }_1^{\prime }+{\beta }_2^{\prime })\hspace{0.17em}\text{d}s={\iint }_{C^{\prime }}({\beta }_1+{\beta }_2)\cos v+({\beta }_1^{\prime }+{\beta }_2^{\prime })\cos v^{\prime }\hspace{0.17em}\text{d}u\hspace{0.17em}\text{d}v\\ & ={\iint }_{C^{\prime }}(2\sqrt{r^2-u^2}\cdot \csc \varphi +O(r^{3/2}))\text{d}u\hspace{0.17em}\text{d}v.\end{array}$$

Similarly,

$$\begin{array}{rl}\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}& ={\int }_{C}2{\beta }_1\hspace{0.17em}\text{d}s+{\int }_{C}2{\beta }_1^{\prime }\hspace{0.17em}\text{d}s={\iint }_{C^{\prime }}2{\beta }_1\cos v+2{\beta }_1^{\prime }\cos v^{\prime }\hspace{0.17em}\text{d}u\hspace{0.17em}\text{d}v\\ & ={\iint }_{C^{\prime }}(2\sqrt{r^2-u^2}\cdot \cot \varphi +O(r^3))\text{d}u\hspace{0.17em}\text{d}v.\end{array}$$

As it is easy to check that $W={\iint }_{C^{\prime }}\sqrt{r^2-u^2}\hspace{0.17em}\text{d}u\hspace{0.17em}\text{d}v=\mathrm{\Theta }(r^3)$, meaning that W = O(r³) and r³ = O(W), we conclude that

$$\begin{array}{rl}\frac{\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}}{2\stackrel{\curvearrowright }{aa}}& =\frac{2W\cdot \cot \varphi +O(r^5)}{2W\cdot \csc \varphi +O(r^{7/2})}=\cos \varphi +O(r^{1/2}).\end{array}$$

 ▪

(f). Rational jump, even numerator

We have already introduced the case ϕ = pπ/q with p/q irreducible and p even: see figure 3(a).

Lemma 3.8. —

For a jump of size ϕ = pπ/q with p/q irreducible, p even and 0 < ϕ < π/2, there is an antipodal lawn L with a greater probability of a successful jump than the hemispherical lawn.

Proof. —

The q caps are regularly spaced at intervals π/q around the equator alternating with their q antipodal cups. A jump from a cap cannot get to a cup and can reach one other cap in each direction, while a jump from a cup cannot get to a cap and can reach one other cup in each direction. The caps (and similarly the cups) also correspond a cyclic sequence of q jumps of size pπ/q circling the equator p/2 times.

We summarize the total probabilities shown in equation (3.7) contributing to $\stackrel{\curvearrowright }{LL}$ in table 1.

Using equations (3.7), (3.8) and (3.9), we have

$$\begin{array}{rl}\stackrel{\curvearrowright }{LL}-\stackrel{\curvearrowright }{SS}& =\stackrel{\curvearrowright }{AS}+\stackrel{\curvearrowright }{SA}+\stackrel{\curvearrowright }{AA}-\stackrel{\curvearrowright }{US}-\stackrel{\curvearrowright }{SU}+\stackrel{\curvearrowright }{UU}=2q\cdot \stackrel{\curvearrowright }{aS}+2q\cdot \stackrel{\curvearrowright }{aa}-2q\cdot \stackrel{\curvearrowright }{uS}+2q\cdot \stackrel{\curvearrowright }{uu}\\ & =4q\cdot \stackrel{\curvearrowright }{aa}-2q\cdot (\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS})=4q\cdot \stackrel{\curvearrowright }{aa}(1-\frac{\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}}{2\stackrel{\curvearrowright }{aa}})=4q\cdot \stackrel{\curvearrowright }{aa}(1-(\cos \varphi +O(\sqrt{r}))),\end{array}$$

by proposition 3.7. Since cosϕ < 1, if the cap radius r is chosen sufficiently small then $\stackrel{\curvearrowright }{LL}>\stackrel{\curvearrowright }{SS}$. ▪

Table 1.

Classification of jumps for lemma 3.8.

	A	U	S
A	$2q\cdot \stackrel{\curvearrowright }{aa}$	0	$q\cdot \stackrel{\curvearrowright }{aS}$
U	0	$2q\cdot \stackrel{\curvearrowright }{uu}$	$q\cdot \stackrel{\curvearrowright }{uS}$
S	$q\cdot \stackrel{\curvearrowright }{Sa}$	$q\cdot \stackrel{\curvearrowright }{Su}$	$\stackrel{\curvearrowright }{SS}$

(g). Irrational jumps

The lawn we construct for irrational ϕ/π is similar to that in the previous section but with a significant difference. This is previewed in figure 3(b).

Lemma 3.9. —

For a jump of size ϕ where ϕ/π is irrational and 0 < ϕ < π/2, there is an antipodal lawn L with greater probability of a successful jump than the hemispherical lawn.

Proof. —

Beginning at an arbitrary point on the equator, we make a sequence of n caps of radius r corresponding to n − 1 jumps of size around the equator. Cups are placed at the antipodal positions. The value of n will be chosen later, but whatever the value of n, the irrationality of ϕ/π ensures that the centres of the caps and cups are all distinct. The value of r is chosen small enough that there is no overlap among the caps and cups, and, further, a jump from a cap cannot get to a cup and a jump from a cup cannot get to a cap. The difference from the previous case is that now the forward jump from the nth cap in the sequence and the backward jump from the first cap may not reach a cap, and similarly for the cups. This difference is shown in table 2.

We now find that the total probabilities yield

$$\begin{array}{rl}\stackrel{\curvearrowright }{LL}-\stackrel{\curvearrowright }{SS}& =4(n-1)\cdot \stackrel{\curvearrowright }{aa}-2n\cdot (\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS})=4(n-1)\cdot \stackrel{\curvearrowright }{aa}(1-(\frac{n}{n-1}\cos \varphi +O(\sqrt{r}))),\end{array}$$

by proposition 3.7 as before. Since cosϕ < 1, we may choose n > 1/(1 − cosϕ) and r sufficiently small so that $\stackrel{\curvearrowright }{LL}>\stackrel{\curvearrowright }{SS}$. ▪

Table 2.

Classification of jumps for lemma 3.9.

	A	U	S
A	$2(n-1)\cdot \stackrel{\curvearrowright }{aa}$	0	$n\cdot \stackrel{\curvearrowright }{aS}$
U	0	$2(n-1)\cdot \stackrel{\curvearrowright }{uu}$	$n\cdot \stackrel{\curvearrowright }{uS}$
S	$n\cdot \stackrel{\curvearrowright }{Sa}$	$n\cdot \stackrel{\curvearrowright }{Su}$	$\stackrel{\curvearrowright }{SS}$

(h). Rational jumps, odd numerator

This final case for our main result (ϕ = pπ/q with p/q irreducible, p > 1 and p odd) is more complicated than the previous cases. After q jumps round the equator, we have reached a point making an angle pπ with the initial point. Since p is odd, this is the point antipodal to the initial point.

Lemma 3.10. —

For a jump of size ϕ = pπ/q with p/q irreducible, 1 < p < q/2 and p odd, there is an antipodal lawn L with greater probability of a successful jump than the hemispherical lawn.

Proof. —

Consider the set of 2q points around the equator at angles j · pπ/q from some initial point, for 0 ≤ j < 2q. We will put caps at the points corresponding to 0 < j < q and cups at points corresponding to q < j < 2q. The positions for j = 0 and j = q have neither. (The arrangement is similar to the lawn in the proof of lemma 3.9, except in the present case we cannot take n, the number of caps, to be arbitrarily large. We are restricted to n ≤ q − 1, and we may have (q − 1)/(q − 2) · cos (pπ/q) ≥ 1 for large q.)

To achieve the required inequality we need to modify the shapes of the caps and cups. Recall that the standard caps and cups are bounded by semicircles of angular radius r. For 0 ≤ s ≤ 1, we define a cap a_s to be just like a standard cap except that its upper boundary is the usual semicircle but with its height (latitude) reduced by a factor s: that is, it is the set of all points (θ, sδ) such that (θ, δ) belongs to the original cap a. Note that its width (major axis) remains as 2r. The analysis of jump probabilities is almost the same as in §3e with just obvious changes. Suppose we are considering jumps from a cap a_s to a cap a_t. Proposition 3.5 works just as before. The results in proposition 3.6 hold with the modified equations:

$$\begin{array}{rl}& \text{(i')}\hspace{0.17em}{\beta }_1=sv\cot \varphi +O(r^3),\\ & \text{(ii')}\hspace{0.17em}{\beta }_1+{\beta }_2=t\sqrt{r^2-u^2}\csc \varphi +O(r^{3/2}).\end{array}$$

For the integrals in the proof of proposition 3.7, we now derive

$$\begin{array}{rl}2\stackrel{\curvearrowright }{a_s{a}_t}& ={\iint }_{C_r^{\prime }}(2t\sqrt{r^2-u^2}\cdot \csc \varphi +O(r^{3/2}))\hspace{0.17em}\text{d}u\hspace{0.17em}\text{d}v,\text{and}\\ \stackrel{\curvearrowright }{a_{s}N}-\stackrel{\curvearrowright }{a_{s}S}& ={\iint }_{C_r^{\prime }}(2s\sqrt{r^2-u^2}\cdot \cot \varphi +O(r^3))\hspace{0.17em}\text{d}u\hspace{0.17em}\text{d}v,\end{array}$$

where

$$C_r^{\prime }=\{(u,v)\mid \cos u\cos (v/s)\ge \cos r,-r\le u\le r\text{ and }0\le v\le sr\}$$

denotes a cap a_s. Then

$$\stackrel{\curvearrowright }{a_s{a}_t}=st\cdot \stackrel{\curvearrowright }{aa}+O(r^{7/2})\text{ and }\stackrel{\curvearrowright }{a_{s}N}-\stackrel{\curvearrowright }{a_{s}S}=s^2(\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS})+O(r^5).$$ 3.13

With preparations complete, we now define our lawn L. We put modified caps centred at the points round the equator with angles jϕ = j pπ/q for 0 ≤ j ≤ q. The cap corresponding to j has contraction s where s = sin (jπ/q). We place modified cups at points with angles jϕ for q ≤ j ≤ 2q to give an antipodal lawn. Note that for j = 0, q and 2q, the contraction ratio is 0, since sin 0 = sinπ = sin 2π = 0. So there is no contradiction and these two positions effectively have no cap or cup.

With our defined sequence of caps, from equation (3.13) and corollary 3.3, we see that

$$\begin{array}{rl}\stackrel{\curvearrowright }{AA}& =\sum _{j=0}^{q-1}2\sin \frac{j\pi }{q}\sin \frac{(j+1)\pi }{q}\cdot \stackrel{\curvearrowright }{aa}+O(r^{7/2})=q\cos \frac{\pi }{q}\cdot \stackrel{\curvearrowright }{aa}+O(r^{7/2})\end{array}$$

and

$$\begin{array}{rl}2(\stackrel{\curvearrowright }{AN}-\stackrel{\curvearrowright }{AS})& =\sum _{j=0}^{q}2{\sin }^2\frac{j\pi }{q}\cdot (\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS})+O(r^5)=q\cdot (\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS})+O(r^5).\end{array}$$

Now,

$$\begin{array}{rl}\stackrel{\curvearrowright }{LL}-\stackrel{\curvearrowright }{SS}& =2\stackrel{\curvearrowright }{AA}-2(\stackrel{\curvearrowright }{AN}-\stackrel{\curvearrowright }{AS})=q\cos \frac{\pi }{q}\cdot 2\stackrel{\curvearrowright }{aa}-q(\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS})+O(r^{7/2})\\ & =2q\cdot \stackrel{\curvearrowright }{aa}(\cos \frac{\pi }{q}-\frac{\stackrel{\curvearrowright }{aN}-\stackrel{\curvearrowright }{aS}}{2\stackrel{\curvearrowright }{aa}}+O(r^{1/2}))\text{ since }\stackrel{\curvearrowright }{aa}=\mathrm{\Theta }(r^3)\\ & =2q\cdot \stackrel{\curvearrowright }{aa}\cdot (\cos \frac{\pi }{q}-\cos \varphi +O(r^{1/2}))>0\end{array}$$

for sufficiently small r, since cosϕ = cos (pπ/q) < cos (π/q) for 1 < p < q/2. ▪

(i). Summary

Taken together, theorem 3.1 and lemmas 3.8, 3.9 and 3.10 give our principal result.

Theorem 3.11. —

For jumps of size ϕ with 0 < ϕ < π/2, the hemispherical lawn gives the greatest probability of a successful jump if and only if ϕ = π/q for some integer q > 1.

4. Discussion

In quantum physics, we can represent projective measurements on a qubit (for example, the polarization state of a photon) by an ordered pair of antipodal points on the Bloch sphere, where the first point represents the projector corresponding to the outcome obtained and the second point the orthogonal projector, which defines the other possible outcome. The circle represents a subset of these measurements; linear polarization measurements are a natural choice in the photon case.

One of the motivations of [1,2] was to work towards a more general class of Bell inequalities, by identifying the maximum average anticorrelation obtainable from local hidden variable models for pairs of measurements chosen randomly subject to the constraint that they are separated by a fixed angle on the Bloch sphere. This gives a Bell inequality whenever the quantum anticorrelation for the singlet (or any other given state) is larger. One can also ask whether this type of ‘grasshopper’ Bell inequality can be obtained for measurements restricted to a circle on the Bloch sphere. The ease of linear polarization measurements, and the desirability of distinguishing entangled quantum states from separable states (or classical systems designed to try to mimic quantum states) as efficiently as possible, make this a potentially practically significant question.

As noted in [2], it is simple to find a general analytic solution for the grasshopper problem on the real line for any jump distance. In contrast, solutions to the planar version exhibit quite complex behaviour, and analytic solutions are not presently known. Intuitively, this appears to reflect the fact that the problem simplifies when the jump (which is effectively one dimensional) takes place in the space of the same dimension. Our results on the circle support this intuition, but nonetheless have non-trivial features arising from the circle’s topology. In particular, they distinguish between a measure zero set of jumps that are rational multiples of π of a particular form, for which the upper bound on lawn retention probabilities is below 1, and the remainder, for which the supremum retention probabilities are 1.

(a). Results on the circle

The results for antipodal lawns are particularly interesting. For a single antipodal lawn, they sharply distinguish between the case where the jump is a rational multiple of π with an odd numerator and other jump values. In particular, they show that, even for the single lawn grasshopper problem, informal arguments based on continuous dependence on the jump value can fail. For a pair of antipodal lawns, they similarly sharply distinguish the case of jump π(p/q) with p odd and q even from other values.

An antipodal lawn on the circle then represents a simple local hidden variable model for photon polarization measurements. For two photons, the most general model uses two different antipodal lawns, which are not necessarily related. We can motivate the simpler model given by a single antipodal lawn as a specific type of local hidden variable model that attempts to reproduce the correlations of a singlet photon state, modelling one photon (A) by a lawn L and the other (B) by the ‘opposite’ lawn $\overline{L}$. This model implies that if the same linear polarization measurement is made on both A and B, then different results will always be obtained, reproducing the perfect anticorrelation for identical measurements exhibited by the singlet.

In either case, Bell’s theorem [8] shows that no local hidden variable model can reproduce all the quantum correlations of the singlet. Bell’s theorem applies even if we restrict to linear polarization measurements, as can be seen from Bell inequalities such as the CHSH [9] and Braunstein & Caves [10] inequalities. These give quantitative bounds on sums of local hidden variable correlations, which are violated by the (experimentally verified) predictions of quantum theory for the singlet.

Our results show that ‘grasshopper’ Bell inequalities corresponding to jumps on the circle, based on the correlations attainable by linear photon polarization measurements about randomly chosen axes separated by a given fixed angle, do exist. However, they do so only in the case where the measurements correspond to Bloch sphere axes separated by π(p/q) with p odd and q even. In these cases, the grasshopper Bell inequalities (which demonstrate a non-trivial bound on the optimal lawn) follow from the CHSH and Braunstein–Caves inequalities.

The CHSH and Braunstein–Caves inequalities apply to measurements chosen randomly from fixed finite sets. They are robust against measurement errors. This is because the inequalities apply to any sets containing the right number of measurements, whether or not the measurements are separated by the optimal angles. Quantum correlations violate the inequalities maximally when the optimal angles are chosen, but also violate the inequalities if there are small imprecisions in specifying the measurements.

It is important to stress that our generalized Bell inequalities corresponding to jumps on the circle are not robust in the same sense. If two parties aim to carry out measurements on the relevant circle that are randomly chosen subject to the constraint that they are separated by angle π(p/q) (for p odd and q even), but only approximate this separation, they cannot be guaranteed that their measurement results are inconsistent with a local hidden variable model. Indeed, an adversary who knows the precise value of the separation x ≠ π(p/q) could substitute a pair of classical devices for their quantum systems and achieve a stronger anticorrelation than quantum theory predicts. This is true no matter how closely x approximates π(p/q), so long as x is not itself a rational multiple of π. Knowing a significantly better rational approximation to x than p/q will also often suffice.

In other words, the grasshopper Bell inequalities corresponding to measurements defined by a Bloch great circle display a finite precision loophole somewhat analogous to that arising for Kochen–Specker inequalities [11–14]. They are mathematical results that cannot directly be tested experimentally, without further assumptions, since in practice no experiment can specify the separation between measurement axes with the infinite precision required.²

That said, it is questionable how exploitable this finite precision loophole would be in practice. One might imagine a test of the Bell inequalities in which pairs of measurement angles of the form (ϕ_A, ϕ_B) with |ϕ_B − ϕ_A | = ϕ are randomly generated in advance, and securely distributed to spacelike separated sites A and B, where dials on the measurement devices are set to measure angles ϕ_A and ϕ_B, respectively. The devices might have small and consistent errors, so that settings ϕ_A, ϕ_B produce measurements about the axes of angles ϕ_A + δ_A, ϕ_B + δ_B, respectively. The separations are thus actually ϕ ± (δ_B − δ_A), when ϕ_B − ϕ_A = ±ϕ. It is plausible that in this scenario the adversary (unlike the experimenter) might know the values of δ_A and δ_B very precisely, perhaps for example because the adversary supplied the experimental equipment, and plausible also that ϕ ± (δ_B − δ_A) may be irrational. If, for some reason, the experiment is restricted to one sign choice (a one-directional grasshopper jump, say clockwise), then the adversary could indeed exploit the loophole, since all jumps are through the same angle ϕ + (δ_B − δ_A), known to the adversary but not the experimenter.

Alternatively, if, for some reason, the adversary learns in advance which runs of the experiment involve clockwise jumps and which involve counterclockwise (perhaps because the experimenter unwisely carries out the first set in the morning and the second in the afternoon, for example), she can exploit her knowledge of the jump values in each run. However, without such restriction or advance knowledge, the adversary’s advantage is less clear. Finer analysis is needed to resolve this.

In any case, the finite precision loophole on the circle does not imply that ‘grasshopper’ Bell inequalities obtainable on the Bloch sphere are similarly unrobust. Although the results for the circle are relevant to the spherical case, one should not expect a close similarity. The two dimensionality of the sphere makes a crucial difference, and non-zero separations between local hidden variable and quantum anticorrelations are already known for a continuous range of jump angles on the Bloch sphere [1]. Indeed, as we discuss below, our results imply not only that there are new grasshopper Bell inequalities on the sphere, but also that for generic jumps these do not follow from known inequalities, unlike those on the circle.

Our results do, however, emphasize the need to specify carefully the class of measurements in any analysis, and the potential dangers in naively assuming that it is safe to impose even apparently natural and inconsequential restrictions on that class.

Finally, we note that the circle is a natural setting for exploring intuitions about generalizations of the grasshopper problem such as those mentioned in [2]. For example, the ‘ant problem’ [2], in which the ant attempts to walk along the path that a grasshopper would have jumped, but dies if it ever leaves the lawn, is trivially solved on the circle. This is because, for the ant, a connected lawn can never be inferior to a disconnected lawn of the same length and is superior unless the retention probability is zero. The optimal solutions are thus continuous arcs of length L; in the case of antipodal lawns they are semicircles of length π. Ant-optimal lawns are thus not generally grasshopper-optimal. However, if we restrict to antipodal lawns, there is a discrete set of jump angles for which ant-optimal lawns are also grasshopper-optimal.

It would be interesting to explore the ‘grasshopper in a breeze’ [2] on the circle, where (if we take the breeze to have constant angular momentum) it translates to requiring that the grasshopper jumps equiprobably through fixed angle ϕ₊ clockwise or fixed angle ϕ₋ anticlockwise, where ϕ₊ ≠ ϕ₋. It would also be interesting to explore versions [2] of the problem in which the jump angle is drawn from a probability distribution (which may be symmetric about zero or, as in the breeze example, may be asymmetric).

(b). Results on the sphere

The grasshopper problem was originally motivated [1] as a problem on the Bloch sphere, where antipodal lawns represent hidden variable models for projective measurements, and this remains the most interesting setting for fundamental physics applications. Although the versions of the problem considered previously on the plane [2] and the versions on the circle considered above are independently interesting, a major motivation for studying them has been to develop intuitions for the problem on the sphere, in order ultimately to resolve the questions about Bell inequalities raised in [1].

Our results represent significant progress in this direction. In particular, they refute the weak hemispherical colouring maximality hypothesis set out in [1] and so also the strong hemispherical colouring maximality hypothesis set out in the same paper.³ Theorem 3.11 shows that there are local hidden variable models for entangled two qubit systems that achieve stronger anticorrelations than the simple models defined by two hemispherical colourings for random pairs of measurement axes separated by fixed angle ϕ, for almost all angles ϕ. This is intriguing, given that such models nonetheless cannot [1] achieve anticorrelations as strong as those predicted by quantum theory, at least for 0 < ϕ < π/3.

Theorem 3.11 thus shows that there are previously undiscovered types of Bell inequality, separating the predictions of local hidden variable theories and quantum theory, that are based solely on the strength of these anticorrelations. To identify tight versions of these Bell inequalities, one would need to identify the supremum of the retention probabilities for pairs of antipodal lawns, as a function of ϕ. Numerical investigations (van Breugel B 2019, personal communication and Piovesan C 2019, personal communication), adapting the methods of [2], indicate that the optimal shapes for generic jumps up to ≈0.44π resemble a cogwheel-type configuration, similar to those found in the planar case, and give estimates of this supremum function. We expect the computational difficulty of the spherical problem to be similar to the planar case, since the surface of the sphere is also two-dimensional. The only significant novel features arise from the curvature of the sphere, but accurate discrete approximations can be employed. We expect that carefully cross-checked and tested numerical results for the spherical problem will appear in due course. Analytic results and proofs would of course be even more satisfying. We hope our results will motivate further work in these directions.

While our results apply directly only to Bell inequalities associated with projective measurements on qubits, they strongly suggest that similar types of Bell inequalities are likely to arise for other types of measurements and for higher dimensional Hilbert spaces. This looks a fruitful direction to explore for extending our mathematical understanding of quantum Bell non-locality.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed to all parts of the work reported in this paper and to writing the manuscript.

Competing interests

We declare we have no competing interests.

Funding

The research of D.C. and M.P. is supported by the Centre for Discrete Mathematics and its Applications (DIMAP). A.K. was supported by UK Quantum Communications Hub(grants nos EP/M013472/1 and EP/T001011/1) and by an FQXi grant. A.K. and O.G. were supported by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation.