Contributions of modern network science to the cognitive sciences: revisiting research spirals of representation and process

Abstract

Modelling the structure of cognitive systems is a central goal of the cognitive sciences—a goal that has greatly benefitted from the application of network science approaches. This paper provides an overview of how network science has been applied to the cognitive sciences, with a specific focus on the two research ‘spirals’ of cognitive sciences related to the representation and processes of the human mind. For each spiral, we first review classic papers in the psychological sciences that have drawn on graph-theoretic ideas or frameworks before the advent of modern network science approaches. We then discuss how current research in these areas has been shaped by modern network science, which provides the mathematical framework and methodological tools for psychologists to (i) represent cognitive network structure and (ii) investigate and model the psychological processes that occur in these cognitive networks. Finally, we briefly comment on the future of, and the challenges facing, cognitive network science.

1. Introduction

‘Spirals of science’ [1] refers to the continued exploration of research questions over generations, where each new generation of researchers benefits from the knowledge of those who came before. The shape of a spiral depicts how science grows, develops and evolves over time. The resources and knowledge available at a given point in time constrain how much movement up the spiral is possible, which may lead to either periods of small, incremental steps or instances of explosive momentum. This paper explores the ‘research spirals’ of cognitive science related to the representation and processes of the human mind and how the application of network science and graph-theoretic approaches, particularly after the publication of seminal papers from Watts & Strogatz [2], Barabasi & Albert [3] and Page et al. [4], has contributed to the upward movement of research spirals in the cognitive sciences.

The field of experimental psychology, which seeks to understand human behaviour, has its early roots in the behaviourist tradition [5–8]. Early behaviourists did not find it necessary to examine the internal properties of the human mind in order to understand and explain behaviour, because they viewed observable behaviours as by-products of reinforcement and punishment schedules in response to external environmental stimuli. Indeed, one of the earliest metaphors of the mind is the notion of a ‘black box’, where input goes in (i.e. stimuli in the environment) and output emerges (i.e. behaviour), and it is often assumed that it is impossible to completely know what is occurring in the black box. Stated differently, behaviourists generally view the processes of the mind as unobservable and unmeasurable.

The cognitive revolution emerged largely in response to the behaviourist perspective and has matured into the interdisciplinary field of cognitive science today, which focuses on understanding how humans think (i.e. the processes of the ‘black box’) through analyses of cognitive representations and structures as well as the computational procedures that operate on those representations [9]. Some of the early work challenging behaviourist principles by focusing on studying the internal properties and structure of the mind includes George Miller's research on short-term memory [10], John McCarthy, Marvin Minsky, Allen Newell, and Herbert Simon's research on artificial intelligence [11–13], and Noam Chomsky's research on universal grammar [14,15]. Among others, these researchers provided a foundation for new metaphors of the human mind. For example, one prominent metaphor is that the mind is a computer, an information-processing machine. This metaphor captures computationalism approaches to cognition, where information can be represented symbolically and processes of the mind can be described in terms of algorithms that operated on these symbols. Such an approach relied heavily on implementations of cognitive models in computer programs.

Another metaphor describes the ‘black box’ of the mind as the brain. This metaphor captures connectionist approaches to cognition, where researchers view the mind as systems of highly interconnected units of information. One way to compare computationalism and connectionism is through the following (albeit oversimplified) analogy: computationalism is to ‘software’ as connectionism is to ‘hardware’. Computationalism focuses on identifying idealized algorithms that achieve human-like performance in a computer, whereas connectionism focuses on the structure of the mind [16]. Indeed, one of the main draws of the connectionist approach is its potential to connect the mind and brain, since both have apparently compatible architectures (i.e. massively interconnected simple units which mimic the connectivity structure among neurons in the brain), although implementation is less straightforward than the similarities in structure might suggest. Regardless, a massive body of work on artificial neural networks, beginning with McCullock & Pitts [17], has proven fruitful in understanding many aspects of human cognition, such as intelligence and language. For example, today artificial neural networks are a prominent feature of many everyday technologies, ranging from voice recognition systems to search engines.

An important point to note is that metaphors of the mind shape the theoretical and methodological approaches adopted to investigate properties of the mind. Each perspective influences a researcher's decisions on how cognitive representations are defined and how cognitive processes are computationally implemented [18]. In this review, we show that network science has been and will continue to be a fruitful theoretical and methodological framework that advances our understanding of human cognition. Cognitive science and network science have surprisingly compatible and complementary aims: cognitive science aims to understand mental representations and processes [9], and network science provides the means to understand the structure of complex systems and the influence of that structure on processes [19]. Early cognitive models tended to be descriptive and qualitative in nature. Furthermore, such quantitative models tended to be small ‘toy’ models that do not reflect the large-scale and massively complex nature of human cognitive systems. In this paper, we argue that, when used in combination with exponentially increasing computational power and the availability of big data, network science provides a powerful mathematical framework for modelling the structure and processes of the mind, propelling cognitive scientists up the research spirals.

The remainder of this paper delves into two research spirals of cognitive science, one of representation and one of process, and explores how network science has been, and is currently being used, to further our understanding of these fundamental aspects of cognitive science. The first spiral specifically addresses issues related to defining cognitive representations, with a particular focus on conceptual and lexical representations. For example, without a clear understanding of how words and concepts are represented in the mind, our ability to understand language processes is hampered. The second spiral specifically addresses issues related to the dynamical processes that occur on cognitive representations (e.g. retrieving a word from the mental lexicon), and the dynamics of how cognitive representations themselves change over time (e.g. language acquisition and development). We discuss the beginnings of these research spirals, how network science has helped cognitive scientists progress up the spirals, and speculate on where these research spirals are headed.

2. Spiral of representation: defining cognitive representations

A literature review of psychology papers published in the 1970s (which coincides with the burgeoning of connectionism) that mentioned the term ‘graph theory’ revealed that a number of prominent psychologists have previously highlighted the potential of graph theory for representing cognitive structure. For instance, Estes [20] explicitly suggested that graph theory could provide a natural way of representing hierarchical relationships and organization of concepts in memory and language, particularly given the growing empirical evidence in cognitive psychology showing that behavioural responses in semantic categorization tasks reflect non-random memory structures [21,22]. Similarly, Feather [23] provided examples of graph formalizations of cognitive models examining the effects of communication between a receiver and a communicator, the ability to recall controversial arguments, and the attribution of responsibility for success or failure of a task to demonstrate the breadth of which graph-theoretic approaches could be used to quantify cognitive structures.

Before proceeding further, we would like to emphasize how network science and the use of graph-based networks differs from connectionism and the use of artificial neural networks in their approaches to modelling cognition, while acknowledging that both approaches have contributed much to research in the cognitive sciences. Both approaches use network architectures (i.e. collections of connected nodes) but for different theoretical purposes, which is reflected in part from their historical origins. The primary aim of network science is to use graph-based networks to model the structure of dyadic relationships between entities (e.g. semantic similarity) and mathematically quantify the influence of that structure on processes (e.g. word retrieval). On the other hand, connectionism primarily aims to model a process (e.g. learning), which is implemented as incremental modifications of a network-like structure (e.g. edge weights) to fine-tune the output and performance of the model. Each approach has advantages and limitations for modelling human cognition, and there are emerging lines of research that use the modern tools of network science to study the structure of neural networks (e.g. [24–29]). Our paper aims to highlight how modern network science can help advance our understanding of cognition, rather than to directly compare the network science and connectionism approaches. Indeed, there is already a large body of work that describes in detail the various ways that neural networks have been used to study human cognition (which we do not attempt to summarize here); for example, the reader may refer to Nadeau [30] for a review of the application of parallel distributed processing models to understand human cognition. However, much less has been said about how modern tools of network science have advanced, and continue to advance, our understanding of human cognition, which is our focus here. Another related issue to note is that the cognitive and language networks we describe below are conceptually quite similar to knowledge graphs commonly analysed in the domains of computer science [31] and learning and educational analytics [32]. In these areas, nodes represent cognitive units as well, although these knowledge graphs focus on summarizing large amounts of information for efficient search and retrieval processes in a database, which could potentially be analogous to human search and retrieval [33]. We briefly note that, while the focus here is on cognitive networks that represent the contents of the human mind, there is much room for these disciplines to interact in productive ways and we hope that this review could serve as a bridge to these communities. Hence, for the remainder of this paper, we focus on graph-based, cognitive networks of the human mind, and point out similarities and differences with neural networks as appropriate.

As indicated above, one of the prevailing notions of network science is that ‘structure always affects function’ [19]. Thus, in order to accurately study cognitive processes, we must ensure that an appropriate cognitive representation is first defined. Defining cognitive representations is not easy. The researcher faces many decisions that need to be made regarding which parameters to model (or not), which will have significant influence on the cognitive processes that can and cannot be tested within the model and how one might interpret the outputs of that model. For example, network science (in contrast to neural networks) has a ‘simplified’ representational structure since it focuses on pairwise similarities between entities, thus limiting what constitutes an edge in the network, which ultimately impacts what effect the representational structure has on the cognitive process to be modelled. In this section, we specifically focus on the structure of the mental lexicon, the place in long-term memory where lexical and conceptual representations are stored, although we note that many of the issues discussed below are relevant to the modelling of other aspects of human cognition.

(a). Origins of the spiral: approaches to representing the mental lexicon

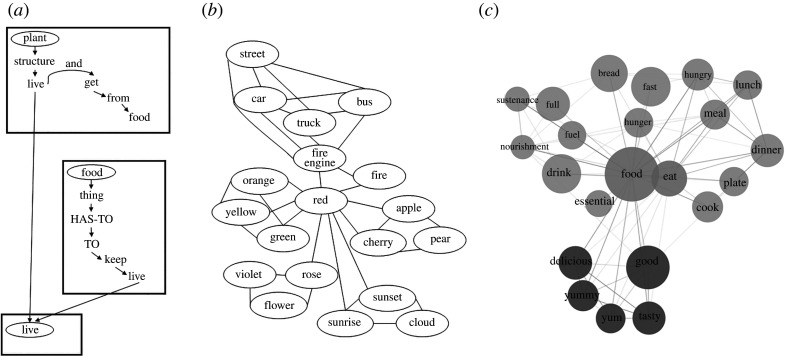
Given that language is central to being human, it is not surprising that cognitive scientists have had a long-standing interest in understanding how language is represented in the mind; specifically, how the lexical form and semantic information associated with words are stored in the mental lexicon (i.e. the mental dictionary or repository of lexical knowledge). It is notable that early models of the mental lexicon were essentially network representations (including neural network models), and many current, cognitive models of the mental lexicon can be recast as networks, even if they were not explicitly modelled as a network graph. Figure 1 depicts examples of classic and more modern semantic memory models, which illustrate the timeless ubiquity of the network metaphor as representing semantic memory. Quillian [34] constructed the first network model of semantic memory using dictionary entries (figure 1a). In a nutshell, Quillian's model contained type and token nodes embedded in planes that were connected via associative links. A plane represented a piece of semantic space that captured a specific entry in a dictionary. Each plane contained a type node (i.e. the word for that dictionary entry) and token nodes (i.e. other words composing that dictionary entry). Associative links connected type nodes to token nodes within each plane, and connected token nodes in one plane to their corresponding type nodes in other planes. Therefore, type nodes are similar to ‘concepts’ in semantic memory and token nodes correspond to lexical ‘words’.

Figure 1.

Depictions of semantic memory structure. (a) Adapted from Quillian [34]. (b) Adapted from Collins & Loftus [35]. (c) Obtained from https://smallworldofwords.org/en/project/visualize.

Following Quillian's [34] model of semantic memory, other models were developed by Anderson & Bower [36], Norman & Rumelhart [37], Schank [38] and Smith et al. [39], all of which have been substantially influenced by computer science and network models of language. However, the most influential model is an updated version of Quillian's [34] model by Collins & Loftus [35], as evident from citation metrics. The Collins & Loftus [35] paper has been cited 10 251 times, with the next highly cited model being that of Smith et al. [39] with 1826 citations (October 2019 from Google Scholar). Collins & Loftus [35] simplified Quillian's [34] model by removing planes of information for each individual concept and represented similarity between concepts via weighted edges (figure 1b). Furthermore, they proposed separate network structures to differentiate between conceptual and lexical representations, resulting in a semantic network of concepts and a lexical network of words. In the semantic network, nodes represented concepts and edges connected nodes based on shared properties. The more shared properties (e.g. visual features or associations) between a pair of concepts, the greater the weight of the link between their corresponding nodes, which is depicted as having shorter link length in the visualization of their model. In the lexical network, nodes represented the names of concepts (i.e. words) and edges connected nodes based on shared phonemic (and orthographic) similarity. Again, greater similarity between a pair of words was taken into account via edge weights/link lengths. Additionally, name nodes in the lexical network were connected to one or more concept nodes in the semantic network, maintaining the type/token node distinction in Quillian's [34] model. Critically, it should be noted that these early models of semantic memory were primarily descriptive accounts. Although Collins & Loftus [35] described the weighting of edges and provided a network visualization, they did not explicitly quantify the structure of the semantic and lexical networks.

In the late 1980s and 1990s, there was an emergence of alternative ways of quantifying semantic similarity, including the use of latent semantic analysis (LSA; also called distributional semantics; [40]) to extract the statistical structure of natural language and through an analysis of lexical databases such as WordNet [41]. In contrast to Quillian's [34] model, which quantified concept similarity through dictionary entries, WordNet resembles a thesaurus that connects words with similar meanings (i.e. synonyms) and shared categorical and hierarchical relations. For example, FURNITURE would be linked to more specific items, like BED, which in turn are linked to even more specific items, like BUNKBED or KING (size). On the other hand, LSA constructs a semantic space model based on word co-occurrences in text corpora. A pair of words that co-occur closely in a sentence (e.g. in the sentence ‘We have a dog and cat’, there is one intervening word between cat and dog) would be deemed more similar than a pair of words that co-occur distantly in a sentence (e.g. in the sentence ‘The man was chased by the dog’, there are four intervening words between man and dog). These papers highlight that, apart from shared properties or features, other aspects of semantic similarity, namely categorical dependency and text co-occurrence, are also important ingredients to consider when investigating the structure of semantic memory.

Given the rich body of work on models of semantic memory, it is intriguing that many of these models contain network-like features (e.g. associative or hierarchical links between related concepts). We speculate that this may be the case because networks are intuitive structures that provide a natural framework for representing relational information between entities (i.e. semantic or form-based similarity). Although cognitive scientists clearly recognize the importance of representation in understanding human cognition, the lack of computational power and mathematical sophistication back then has limited the ability to capture the large-scale structure of cognitive representations. Fortunately, seminal papers by Watts & Strogatz [2] and Barabasi & Albert [3], for example, have brought a new vigour to cognitive scientists interested in quantifying the structure of cognitive representations and the influence of that structure on cognitive processes.

(b). The state of the current spiral: the mental lexicon as a network

The previous section highlighted several types of semantic memory models, some of which employ explicit network representations and most of which have network-like features. Although network architectures, including neural network models, have been employed for decades in cognitive science research, modern network science has provided researchers with a much greater ability to formally quantify those structures and the influence of those structures on processes. For example, researchers can make use of free association responses, where a person provides the responses that first come to mind when given a particular cue word (e.g. the cue DOG often leads to the response CAT), to quantify the large-scale and complex nature of the mental lexicon [42], a subset of which is depicted in figure 1c). Such a network would contain tens of thousands of words that are related in myriad ways, through shared properties, meaning and phonology, representing structure at multiple levels of analysis, from the local structure of individual nodes to macro-level topological features of the network itself. This issue of scale is important, as a true model of the mental lexicon should reflect the vocabulary of an average human (e.g. the average 20-year-old knows approx. 42 000 words, which increases with age; [43]).

A pivotal paper by Steyvers & Tenenbaum [44] was the first to quantitatively analyse the structure of network models of semantic memory. Specifically, Steyvers & Tenenbaum [44] analysed three types of semantic networks (constructed from free association norms, thesaurus-based data and the WordNet database) and found that all three networks had small-world structure, which has been shown to be influential in the dynamical processes of networks [2,45–47]. Networks with small-world structure are characterized as having relatively short average path lengths (i.e. distantly connected nodes are reachable by passing through a small number of steps) and high average clustering coefficients (i.e. the neighbours of a node tend to also be connected to each other), as compared with a random network with the same number of nodes and edges. Despite the different ways of defining semantic relations among concepts, ranging from human-generated data (i.e. free association) to clearly defined linguistic criteria (i.e. thesaurus and synset relations), small-worldness was a prominent structural feature of semantic memory, suggesting that this is a universal feature of language that may have particular implications for enhancing the efficiency of cognitive processes that operate within the network.

At around the same time, there was an emerging line of work focused on modelling phonological word-form representations as a network [48]. In this network, words were connected if they share all but one phoneme (e.g. cat would be connected to _at, mat, and cap). An analysis of the form-similarity networks of English words, as well as those constructed from languages from different language families, revealed that these networks also displayed small-world structure [48,49], similar to the semantic networks analysed by Steyvers & Tenenbaum [44]. Given that words must be accessed rapidly while minimizing error in order for effective communication to occur, and that small-world structure facilitates efficient searching through the mental lexicon network, it is perhaps not too surprising to find small-world structure in language networks across different languages.

Another feature of language network is their resilience to perturbations to the network. Steyvers & Tenenbaum [44] found that all three semantic networks had power-law degree distributions, an important network feature for network resilience. A degree distribution captures the probability distribution of nodes with a certain number of immediate connections (i.e. degree) in the network. A power-law degree occurs when most nodes have low degree and few nodes have high degree (i.e. hubs). As work by Albert et al. [50] has indicated, networks with power-law degree distributions are robust to random node removal, but not degree-targeted node removal (i.e. removal of highest degree nodes first). On the other hand, Arbesman et al. [49] found that phonological networks did not have a power-law degree distribution, but a truncated exponential degree distribution reflecting an upper limit to the maximum degree of words in memory, and exhibited assortative mixing by degree (i.e. high-degree nodes tended to connect to other high-degree nodes; low-degree nodes tended to connect to other low-degree nodes). These features make phonological networks robust to both random and degree-targeted node removal. Consideration of resiliency in language networks might be particularly important for understanding how language systems might break down, particularly among clinical populations such as individuals with Alzheimer's disease (e.g. [51]).

This early work is further complemented with the rise of megastudies (i.e. the collection of massive datasets of behavioural and lexical norms) in psycholinguistic research (for a review, see [52]), making it possible to consider the various ways in which two words could be related and to build network models that more closely approximate the size of an average person's vocabulary (i.e. larger and more complex language networks). For example, the Small World of Words project [42] provides free association norms gathered from over 88 000 participants who generated responses to over 12 000 English cue words, with a total of 3.6 million word association responses. This massive amount of data allows researchers to construct more complex models of the mental lexicon, in contrast to small-scale ‘toy’ models that are common in the psycholinguistic and cognitive science literatures. One example of such a ‘toy’ model is the interactive activation model [53,54] used to account for word retrieval and language production processes in typical adults and individuals with aphasia (e.g. [55–59]). In this model the semantic and phonological connections of only six words were used to represent the idealized mental lexicon (see [55, table 2, p. 808]). Although this network model has had a profound impact on our understanding of word retrieval, one of its drawbacks is its inability to consider the relationships that are known to exist between specific words, without which such a model is unable to inform how the intricate relationships among a much larger set of words influences language processes.

Although language network models allow for the consideration of structural influence on lexical processes, current data-driven approaches to defining language networks have paid less attention to the motivations underlying specific parameter decisions made during the construction of the network model; specifically, how are nodes and edges defined in this particular network. This is a critical issue relevant to all analyses of graph-based networks [60]. In the case of language networks, it is likely that certain representations are better suited for some language processes than others and diligent testing of network model parameters is required to determine the most appropriate network representation given the researcher's specific agenda. Parameter decisions regarding what nodes and edges in any given network are representing should not be arbitrary. Parameter decisions should reflect what is already known through existing theories and the empirical evidence base of language structure and process. For example, while there exist many different semantic network representations (where edges represent free association, shared features or co-occurrences), less work has been done to directly compare how different network structures differentially influence language processes (cf. [44,61]). To further our understanding of structure of the mental lexicon, the remainder of this section discusses the parameter decisions that researchers should consider when developing a language network, and tackles issues related to (i) what the nodes and edges in such networks represent and (ii) the comparison of single-layered versus multi-layered approaches.

(i). Defining nodes and edges in a language network

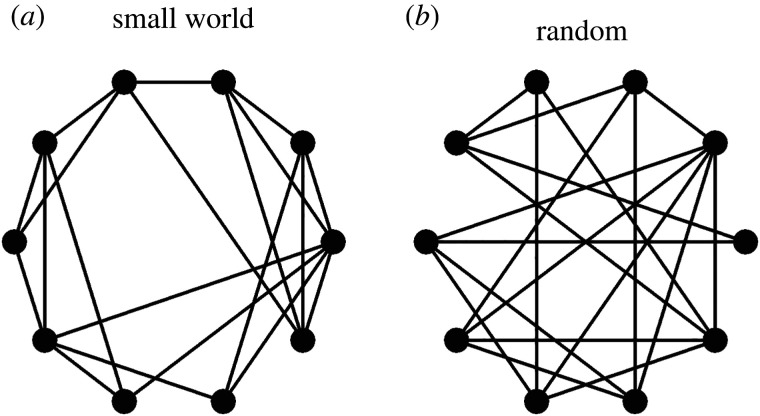
Defining the nodes and edges of a network is the most fundamental step in network analysis. These decisions can dramatically influence the resulting network structure and, in turn, the implementation of processes on the network, which have important implications for models or theories based on those networks. Consider a simple example where two networks have the same number of nodes and edges, but deciding where these edges should be placed was implemented differently for each network (figure 2). In the case where edges are placed with a clear theoretical justification, this could result in a small-world network (figure 2a), whereas in the case where edges are placed randomly, this would result in a random network (figure 2b). Without doubt, the purposefully designed network that is well motivated by theory will have a much more meaningful structure than the same-sized network with randomly placed edges (see also Butts [60], who demonstrated with several real-world network examples how changing the definition of nodes and edges will impact the topological features of the network).

Figure 2.

A small-world network (a) and a random network (b). Adapted from Watts & Strogatz [2]. Both networks have the same number of nodes (n = 10) and edges (on average each node has four edges) but have clearly different network topologies.

Most network models of the mental lexicon represent words as nodes, but vary greatly with respect to what the edges represent. Thus, defining the edges is one of the first critical decisions that needs to be made during language network modelling. The type of edge and other edge-related parameters (i.e. weight and directionality) should reflect the specific aspect of language that the researcher is interested in studying, which will in turn determine how useful the network is in modelling certain language processes [60,62]. To date, a significant body of research has focused on semantic network structures, where edges are defined using a variety of methods to quantify semantic similarity or relations between words. Edges in a semantic network could represent free association (e.g. [42,63,64]), shared features [65,66], word co-occurrences in text corpora [67] and hierarchical relations denoted in thesauri or dictionaries [41]. Others have constructed phonological and orthographic networks [48,68,69], where edges are defined using straightforward edit distance rules (i.e. the number of phoneme or letter changes required to transform one word to another word).

In addition to defining the edges in the network, there are two edge-related parameter decisions to make, specifically whether edges should be weighted and/or have directionality. For some network representations, such decisions may be particularly critical. Consider the case of free association networks constructed using participant-generated data where a person produces the first word that comes to mind in response to a cue word. In this type of network, a cue word might lead to a particular response, but potentially not the other way around. For instance, the cue DOG is likely to elicit the response BONE, but BONE when presented as a cue is less likely to elicit DOG as a response. In other words, free association data contain asymmetric relations between words, which might warrant the inclusion of edge directionalities during network construction (i.e. directed edges rather than undirected edges). Furthermore, some cue--response pairs may be more frequently generated than others (e.g. DOG--CAT is a more frequently occurring cue--response pair than DOG--BONE). Thus, the strength of the relationship between pairs of words should also be accounted for through edge weighting (i.e. weighted edges rather than unweighted edges).

Although such parameter decisions are theoretically important, it remains an open question as to the extent to which changing these parameters influences the interpretation and analysis of language processes that operate on the network structure. For example, Butts [60] presented an example of the neural network of Caenorhabditis elegans, where changing the edge weight of connections between neurons led to different neural network topologies, which could impact how one might interpret or analyse the processes that function within the given network structure. Relevant to language networks, previous work directly comparing the structure of different types of semantic networks provides one path forward in exploring the impact of choosing particular edge-related parameters. For example, Steyvers & Tenenbaum [44] found that the overall topology of three types of semantic networks (i.e. free association, feature and co-occurrence) were not different and Kenett et al. [70] indicated that, since weighting did not significantly impact the network distance between word pairs, they opted for the simpler, unweighted semantic network representation in their analyses. However, different semantic network types have also been shown to capture different aspects of language processes. In Steyvers & Tenenbaum [44], the free association network better captured language growth processes than the feature and co-occurrence networks. De Deyne et al. [71] also found that a free association network better represented the structure of one's internal mental lexicon, whereas a text co-occurrence network provided a better representation of the structure of natural language in the environment. These distinctions between network types, although all arguably reflecting semantic memory, are important for the types of questions cognitive scientists are interested in studying. For instance, De Deyne et al. [71] argue that a free association network may be more appropriate for modelling processes related to word retrieval and cognitive search, but a co-occurrence network may be more appropriate for investigating how structure in the natural language predicts word learning.

Similar kinds of network structure comparison and analysis of structural influence on language processes are also necessary for other aspects of the mental lexicon and word--word similarity relations, such as phonological similarity relations. Indeed, the phonological network commonly studied in the psycholinguistic literature follows the precedent set by Vitevitch [48], who placed edges between words that differ by only one phoneme. A question that remains to be answered is whether individuals indeed consider pairs of words that differ by a single phoneme as phonologically similar and pairs of words that differ by more than a single phoneme as phonologically dissimilar, thus motivating the use of unweighted edges. It may instead be the case that individuals are sensitive to gradients of phonological similarity as phonological distance between words increases, motivating the weighting of edges based on number of shared phonemes; for example, DOG--LOG, which differs by one phoneme, would have a higher edge weight than DOG--LOT, which differs by two. Individuals may also be sensitive to alternative aspects of phonological similarity that are less commonly considered, such as shared syllables and morphology. Taken together, there remains a significant need for a better understanding of how different parameter decisions (e.g. edge weighting and directionality) impact network topology and dynamics.

(ii). Multi-layered network representations

To date, most network representations of the mental lexicon have focused on representing one single aspect of language at a time (e.g. either semantic or phonological relationships). However, words can be related to each other in myriad ways. To fully capture the multi-relational nature of words, a network model of the mental lexicon might be best modelled as a multiplex network representation (a specific kind of multi-layered network representation) where various similarity relations among words are represented simultaneously (e.g. both semantic and phonological relationships). Recall that such a network representation was first described over 40 years ago by Collins & Loftus [35], and can now be implemented quantitatively as a multiplex network [72,73].

As the name implies, a multi-layered network is one in which there are multiple ‘layers’ of information. Each layer is itself a network with a set of defined nodes and edges (i.e. intra-layer edges), with nodes connected across layers by inter-layer edges. In a multiplex network, nodes are defined identically across layers, where each layer reflects a different edge definition (figure 3). For example, in a multiplex language network, nodes represent words in all layers of the network and edges connect words in each layer based on a specific aspect of similarity. Stella and colleagues (e.g. [74–76]) defined a multiplex language network with three semantic layers, where the edges in each layer represented free association, synonym relations and taxonomic dependencies, and one phonological layer, where edges represented phonological similarity relations based on a difference of one phoneme. Another recent multiplex language network analysed by Siew & Vitevitch [77] focused on phonological--orthographic relationships between words, with one phonological layer representing phonological similarities among words and one orthographic layer representing orthographic similarities among words.

Figure 3.

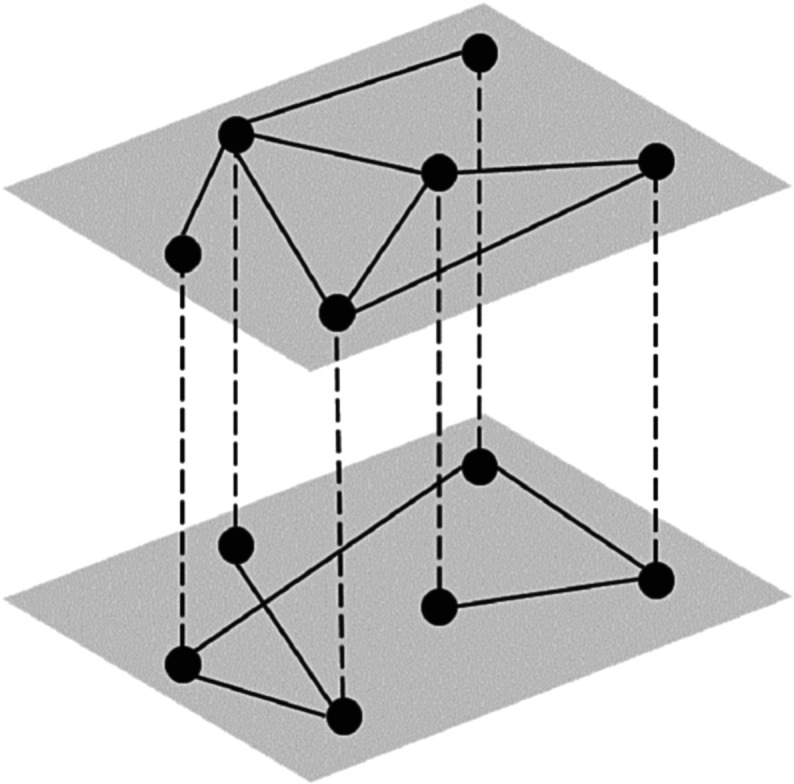
A multiplex network. There are two layers in this multiplex network. Nodes are identical across layers and are connected via inter-layer edges (dashed lines); they are connected differently within each layer (solid lines).

There are many reasons why multiplex network representations of the mental lexicon are theoretically relevant. At the most fundamental level, such an approach readily captures the fact that there are many ways in which words can be related to each other (e.g. semantically, phonologically and orthographically). Furthermore, psycholinguistic research provides compelling evidence that semantic and phonological systems interact during language processes (e.g. [54,59,78]), as well as phonological and orthographic systems [77,79,80], suggesting that these language systems are not discrete entities. Thus, having a cognitive representation that includes multiple word--word similarity relations is necessary.

Although the continual development of the mathematics and theories of multi-layered networks and increasing computational power has provided powerful tools to represent and analyse multiplex networks, caution is warranted as the mathematical complexity of such networks increases exponentially with each network layer added to the representation. This warrants careful consideration when making parameter decisions related to which (and how many) layers should be modelled in the network. A related critical question regarding the multiplex network representation of the mental lexicon is whether such a complex network representation is necessary for understanding human language representation and use. Specifically, what is the theoretical and predictive gain when existing cognitive ‘toy’ models are scaled up to a massively complex multiplex network representation?

(c). Progressing up the future spiral: connecting the mind and the brain

An important limitation in the study of cognitive networks is that these networks can be ‘noisy’ because of measurement error involved in the estimation of network edges. For example, the construction of popular cognitive networks often relies on behavioural data, such as free association data where a participant produces the first word that comes to mind in response to a cue word. Noise in this type of data can arise as a result of several factors, including the inability to capture weakly connected portions of the mental lexicon, limited sampling of the lexicon, which depends on the set of cue words presented to participants during data collection, and the difficulty in accounting for variability in responses across individuals and across time points within the same individual. Although some of these issues can be mitigated, cognitive networks are ultimately abstractions, akin to hypothesized theoretical constructs that are built on observable, measurable characteristics of psychological phenomena. Although there is inherent noise and measurement error in all types of networks [60,81], most of these networks model real, physical, tangible and measurable nodes and edges (e.g. the Internet, ecosystems, DNA, social groups, brain networks); it is important to emphasize that this is perhaps less true in the case of cognitive networks that attempt to capture the abstract structure of a person's mental lexicon.

Given that an ultimate goal of the research spiral on cognitive representation is to define and quantify the influence of internal, cognitive representations, we wish to propose one way forward that could potentially address this inherent limitation in defining cognitive network representations. Specifically, we suggest that, for continued progress to be made in the cognitive sciences, it is necessary to develop theoretical frameworks (akin to the connectionist approach) that connect the mind and the brain, in order to make abstract cognitive representations more tangible through implicit measures of brain activity in conjunction with explicit measures of behaviour. This is not a novel suggestion, but one that requires thoughtful, interdisciplinary collaboration between cognitive science and neuroscience [82,83]. As first suggested by Vitevitch [84], network science may serve as a ‘common language’ between the fields of cognitive science and neuroscience—a ‘lingua franca’ of sorts that can explicitly connect mind and brain. Relevant to the present discussion is Poeppel & Embick's [83] discussion of two major problems in connecting linguistic and neuroscience research: the granularity problem and the ontological incommensurability problem. The granularity problem is the notion that linguistic and neuroscience research focus on different granularities of language; for instance, linguists tend to focus on fine-grained distinctions in language processing, such as how listeners discriminate two phonemes, whereas neuroscientists tend to focus on broader conceptual distinctions, such as where speech perception is localized in the brain. The ontological incommensurability problem is the notion that fundamental units of linguistic theory are not easily matched to fundamental biological units. For example, it is not straightforward or obvious as to how specific phoneme discriminations could be linked to brain regions or patterns of neural activity. While connectionist models have certainly made strides in understanding how language, at a broad scale, may be represented and processed in the brain (e.g. [85]), we propose that network science could offer a promising framework to connect neural activity to more fine-grained cognitive representations of language [84]; specifically, network science could provide a framework for connecting networks of brain regions/activity (or other neurological units) to networks of words (or other linguistic units).

To illustrate this, we briefly review recent work that has begun connecting language networks with brain networks, e.g. a body of research has used network-like models of semantic memory to understand neuroimaging data (for a review, see [86,87]). For example, Huth et al. [88] used a WordNet model (a network structure that captures hierarchical dependencies in semantic knowledge) in combination with functional magnetic resonance imaging (fMRI) data to predict similarity between concepts. Participants viewed movies while their brain activity was measured using fMRI. As new concepts emerged, new patterns of neural activation also emerged, which were mapped onto a semantic network representation derived from WordNet data. For example, when the concept TALK was recognized, a neural pattern of activation emerged that shared a similar pattern to the neural patterns of activation of related concepts, such as SHOUT and READ; furthermore, TALK, SHOUT and READ are also closely connected concepts in the semantic network. This allowed for the identification of different dimensions of concept similarity through implicit neural activation, rather than relying on explicit behavioural output (e.g. a similarity judgement task). For example, one of the contrastive dimensions identified was related to ‘energy’ status and animacy, such that there was a distinction between high-energy objects (e.g. vehicles) and low-energy objects (e.g. sky) [88], analogous to research in developmental psychology that showed that children are able to acquire the ability to distinguish between animate–inanimate concepts over the course of conceptual development, further raising the question of whether cognitive language models are structured in similar ways to neural models [89].

The lingua franca that network science could proffer to connect mind and brain is via the framework of multi-layered networks [84,90–92], which could potentially address the two problems highlighted by Poeppel & Embick [83]. Recall that a multi-layered network does not require nodes to be identical across layers. Thus, one (or more) layer could reflect neural activity (e.g. patterns of neural activity connected via weighted edges based on similarity in activation patterns), with one (or more) layer reflecting linguistic units (e.g. concepts connected via weighted edges based on free association or corpus data). While the granularity mismatch problem cannot be completely eliminated, specifying the separate network layers in this way could allow for the joint consideration of different levels of analysis, from the fine-grained (e.g. specific linguistic units) to the broad (e.g. brain regions). More careful consideration will be needed to address the ontological incommensurability problem. In the multi-layered network, the inter-layer edges that connect nodes across the (linguistic and neural) layers could provide the ‘connective tissue’ that bridges the different fundamental units of each domain, although work will be needed in order to carefully define such inter-layer edges. The work by Huth and colleagues [88,89] suggests that it is possible to connect patterns of neural activity to linguistic concepts. While there remain challenges in resolving Poeppel & Embick's [83] two problems, we are hopeful that continuing efforts within and between the fields of network neuroscience and cognitive network science will prove fruitful [84,90–92].

(d). Summary

This section focused on the cognitive science research spiral of how cognitive structure, specifically the mental lexicon, is represented. Several early models of semantic memory drew on core concepts of graph theory and network science, albeit in mostly descriptive terms. With the rise of modern network science, there has been a new wave of applying network science to rigorously model the mental lexicon in more quantitative terms. This new wave of research is readdressing key theoretical issues in this research spiral, including defining basic properties of the network (i.e. nodes and edges) and consideration of more complex structures (e.g. a multiplex lexical network), which are also relevant to the representation of other cognitive systems. Finally, we discussed a key limitation in cognitive representation, namely the inherently abstract nature of cognitive representations and the reliance on behavioural data in the construction of cognitive networks, and suggest that these limitations could be overcome by adopting network science frameworks to explicitly connect the structure of the mind and the brain.

3. Spiral of process: dynamic cognitive representations

After the cognitive revolution of the 1950s, a central question that has driven research in the cognitive sciences revolves around the mechanisms and processes that operate in the ‘black box’ of the human mind. The previous section established that, in order to understand human behaviour and cognitive processes, it is important to pay close attention to how various aspects of the cognitive structure are formalized (i.e. how are nodes and edges defined in the cognitive network), and demonstrated how modern network science approaches provide us with a powerful mathematical language to do so. In this section, we focus on the question of what the cognitive ‘process’ is doing with respect to the network structure. Specifically, we consider the different kinds of network dynamics that could occur in the context of cognitive network representations.

Dynamics that occur with respect to a network structure can be broadly categorized as operating on either shorter or longer time horizons: processes on a shorter time scale may be assumed to operate on a (relatively) static network structure (e.g. a single processing episode during lexical retrieval), whereas processes on a longer time scale have the capacity to change the structure of the network itself (i.e. accumulative changes on the network structure that can be measured over longer time frames). Although network dynamics can be broadly categorized as occurring in either the short or long term, it is important to acknowledge that such a dichotomy is more spurious than it is apparent—for instance, one could view cognitive and language development as the accumulation of an individual's entire history of real-time psychological processes [93].

In this section we will see that cognitive scientists have had a long-standing interest in studying cognitive processes with a close consideration of how these processes interact with the underlying cognitive network representation (original spiral). Modern-day psychologists have made substantial advances in understanding these processes operationalized as network dynamics on and of the network representation (current spiral). Finally, we envision that explicit implementations of growth or process models on a cognitive network representation will be crucial for continued synergy between the cognitive and network sciences (future spiral).

(a). Origins of the spiral: what do cognitive network representations tell us about psychological processes?

Prior to the publication of the seminal papers [2–4] that heralded the advent of modern network science, mathematical and cognitive psychologists in the 1970s and 1980s saw the potential of using techniques from graph theory to represent a wide range of cognitive structures. However, as Feather [23] pointed out, despite the commonly accepted view that cognitive systems (which he broadly defined as the cognitive structures that a person possesses in order to make sense of the world) have some form of organization and structure, little attention had been directed towards understanding how this structure may have emerged and the organizing principles underlying the development of those cognitive systems. Psychologists saw limitations in graph-theoretic approaches. Simply representing cognitive structure is insufficient for cognitive science because of at least two reasons: (i) it does not directly connect to the cognitive processes of retrieval, learning and inference that cognitive and language scientists care intimately about, and (ii) it was not immediately clear (back then) how the development of, or changes in, cognitive structure could be captured in graph-theoretic terms.

Efforts to address these limitations were being made prior to modern network science, particularly in the area of problem solving and learning. For instance, Greeno [94] presented a detailed, formal mathematical treatment of how conceptual knowledge could be represented as a network and how that might be applied to understand how students solve mathematical problems. Greeno [94] further emphasized the need to describe structured knowledge in a way that reflected more than just simple associations, through the use of methods that truly capture the ‘relational nature of knowledge’. Similar efforts have been taken by Shavelson [95,96], an educational psychologist who used graph theory to examine and measure changes in cognitive structure over the course of physics instruction.

Despite the potential of applying network science methods to quantify cognitive structures, the application of graph-theoretic methods in the cognitive sciences does not appear to be widely adopted. One reason may lie in the ‘tendency for separation of structure and function in models for organization in psychology’ [20, p. 273]. The main argument here is that simply quantifying memory and cognitive structure as a graph is in itself not sufficient for helping psychologists understand processes of acquisition, retention and retrieval of information. This argument has been echoed by Johnson-Laird et al. [62], who argued that a mere theory of meaning representation (i.e. as a semantic network) is not sufficient for understanding how people process semantics and word meanings that are contextually bound and continually re-constructed from processes that operate on the semantic network, as well as Greeno [94], who pointed out that a key weakness in the application of graph theory was that the network itself does not ultimately represent the kinds of processes seen in problem solving. In the context of problem solving, more is needed to advance our understanding of the processes that operate on the network representation; for example, how are new relationships between concepts ‘discovered’ or learned by the student, and how does a learner navigate the knowledge space in order to uncover solutions to problems?

Ultimately, the application of network science to the cognitive sciences has to rise to the challenge of ‘produc[ing] theories that include assumptions as to how elements of hierarchical memory structures are laid down and how the structures are transformed as a function of experience’ [20, p. 274]. To put it another way, the cognitive scientist needs to not only represent cognitive structure, but also consider the dynamics of and on that structure—how to integrate processing or learning assumptions into the network representation so that cognitive scientists can build models that consider how cognitive processes of retrieval and learning operate on the network representation, and how processes and experience transform the structure itself.

(b). The state of the current spiral: how can we use network science to understand cognitive network dynamics?

Present-day research in the area of cognitive network science has made several advances in understanding both the short-term process dynamics that occur on the cognitive network structure and the growth and the long-term developmental dynamics that modulate and change the network structure itself. In this section, we review recent literature demonstrating how the implementation of network dynamics on a network structure can bring together function and structure in cognitive models and lead to new insights into diverse domains ranging from lexical retrieval to creativity. The first sub-section focuses on the cognitive processes that occur on the network representation and the second sub-section focuses on changes of the network representation itself, including long-term change over the course of cognitive development and short-term change during moments of creative insight.

(i). Dynamics on the network: how do psychological processes operate on cognitive structures?

This section focuses on cognitive processes that operate in real time over very short time frames, such as lexical retrieval, priming processes, discrimination and cognitive search. In the examples discussed below it is generally assumed that the structure of the cognitive network is more or less static or stable across each processing episode.

Spreading activation and random walks

The notion of spreading activation has a long history in theories of cognitive psychology and is frequently implemented in models of priming, memory and lexical retrieval. Spreading activation refers to the idea that the activation of one concept in memory can subsequently activate other related concepts in memory [35,97]. Inherent in this description of spreading activation is the assumption that it is a process that operates on some kind of cognitive structure—specifically, activation can be viewed as a cognitive resource that can be spread across a network-like structure of connected cognitive entities. Hence, the application of network science to the quantification of cognitive structure naturally provides the structural backdrop for cognitive scientists to examine spreading activation processes in a cognitive structure; for instance, semantic memory, which is assumed to have a network representation that consists of connected, related concepts.

Spreading activation is conceptually equivalent to the process of random walks on networks where a ‘random walker’ is released from a given node in the network and its movement through the network is constrained by the network structure [98–100]. Random walks on a network provide an indication of how information flows within a network, and can be used to identify higher order structural regularities in a network [100]. Random walk models implemented on various types of complex networks have increased our understanding of how misinformation or innovations propagate in a social system [101,102], and the spread of epidemics in ecological systems [103]. The generality of such processes suggests that these methods can be readily applied to study human behaviour as well.

Indeed, there has been much work within the cognitive sciences that has applied random walk models to account for performance on the category fluency task, where participants list as many category members as possible in a restricted amount of time (e.g. name as many ANIMALS as possible in 30 s; [104]), and how humans search for and retrieve information in cognitive search tasks [33]. For instance, implementing random walks on a network of free associations provides reasonable fits to empirical fluency data [105], and conversely random walk models can be used to infer the structure of the underlying semantic network from people's fluency responses [106]. Others have implemented dynamic processes that closely resemble the original description of spreading activation within a network representation in order to provide converging computational support for verbal accounts of semantic priming (when implemented on a semantic network; [107]) and of clustering coefficient effects in lexical retrieval (when implemented on a phonological language network; [108]). For instance, semantic priming effects can be implemented as a spreading activation process on a semantic network [70,107], and network similarity effects with respect to lexical access and memory recall in the phonological network that could not be accounted for by standard psycholinguistic models (e.g. [109,110]) could in fact be accounted for by a simple process of activation spreading in a complex language structure [107,108].

Finally, it is important to note that, when a process such as spreading activation or random walks is implemented in a non-random complex network structure, the behaviour of that system is likely to be nonlinear—meaning that it is not always possible to accurately predict the outputs of that system unless computational simulations are explicitly conducted on the network model [111]. Hence, considering how process models of spreading activation and random walks are implemented in a network representation enables cognitive scientists to be explicit about their modelling and processing assumptions. Verbal theories can be computationally tested, refined and further developed to inform the psychological mechanisms underlying lexical retrieval, semantic priming, cognitive search and semantic processing.

(ii). Dynamics of the network: how do psychological processes change cognitive structures?

This section focuses on cognitive processes that, leave measurable structural traces (i.e. addition and/or deletion of nodes and/or edges) on the network representation. Current research in cognitive network science has shown that networks present natural models of capturing both long-term and short-term structural changes in cognitive structures. We first highlight research showing how cognitive networks can undergo gradual changes that reflect the accumulative experience of language development and ageing, followed by research demonstrating how cognitive networks can undergo sudden changes that reflect moments of insight in the case of creative problem solving.

Gradual, accumulative changes to network structure

The lexicon over the lifespan. Disentangling the influence of environmental and cognitive factors on age-related changes in processing is a key debate in the cognitive ageing literature [112]. Recent reviews advocate that researchers should seriously consider the possibility that apparent deficits in memory performance of older adults may in fact be more strongly attributed to the accumulation of and exposure to more knowledge over their lifespan, rather than to mere declines in cognitive abilities [113–116].

We suggest that network models of the mental lexicon provide researchers in the field of cognitive ageing with a natural and elegant way of capturing the accumulative effects of such linguistic experiences over time. For instance, Dubossarsky et al. [117] analysed large-scale free association data from a cross-sectional sample using network analysis. Their results indicate that the semantic networks of older adults are less connected (i.e. lower average degree), less well-organized (i.e. lower average clustering coefficient) and less efficient (i.e. lower average shortest path length) than the semantic networks of younger adults. This is a theoretically important finding because previous studies comparing older adults' performance on associative learning and memory tasks with those of younger adults do not typically consider if structural differences in the semantic networks of younger and older adults may be partly responsible for differences in performance [114,118]. Furthermore, recent work has shown how considering the fact that older adults accumulate a lifetime of learning and exposure to diverse experiences could provide an alternative explanation for the increased costs of learning new pairs of associates (rather than invoking the conventional explanation of cognitive decline; [113]).

The structure of language networks also undergoes rapid changes over the course of early language acquisition and vocabulary development. A growing number of papers have capitalized on the tools of network science to investigate developing language networks in early life through the application of generative network growth models (e.g. preferential attachment) to examine the development of language networks [61,76,119–123]. One prominent generative network growth model is preferential attachment, where new nodes are more likely to attach to existing nodes that already have many connections, leading to a network with a power-law degree distribution [3]. Such generative network growth models have been adapted to fit the context of language acquisition. As compared with a random acquisition model where new words are randomly added to the language network, language networks that prioritize the acquisition of words that have many semantic connections (i.e. high degree) in the learning environment that learners are exposed to are more probable given the empirical data [61]. This network growth model is known as preferential acquisition in the literature [61], and indicates that language acquisition processes in young children are sensitive to the structure of the language environment that they are exposed to (i.e. preferential acquisition), rather than to the internal structure of the children's existing vocabulary (i.e. preferential attachment)—although this appears to be limited to network growth where edges in the network represent free associations between words. Collectively, the literature indicates that different network growth models are responsible for the development of different types of language networks where edges can represent various types of relationships between words, including free associations, shared features, co-occurrence and phonological similarity, painting a complex picture of how language acquisition is driven by a constellation of learning processes that prioritize the learning of different types of relationships among words [120].

Learning and the development of conceptual knowledge. Conceptual knowledge is difficult to define, but it is broadly agreed that such knowledge, particularly that of experts, should reflect a complex, hierarchical structure of connected concepts (i.e. more than simple associations between ideas). Although much progress has been made in the cognitive science of learning literature in identifying effective cognitive strategies to enhance learning (see [124], for a review), one limitation is the conspicuous lack of methods and techniques that quantify the complex, relational structure of knowledge. Within the psychological sciences, knowledge representations of experts and novices are not commonly quantified or mathematized, even though it is a commonly held notion that, compared novices, experts have more detailed, well-organized knowledge representations that allow for efficient retrieval of information (e.g. [125,126]).

As a concrete example, consider the studies that investigate retrieval-based learning [127,128]. A typical experimental protocol in such studies is to provide students with a text passage to study, with one group of students having more opportunities to restudy the material (i.e. restudy condition) and another group of students being repeatedly tested on their knowledge of the material (i.e. retrieval condition). The key finding from comparing the performance of both groups of students on a final test session is that retrieving knowledge (in a test) actually strengthens that knowledge more than simply restudying it. However, one critique of this body of research is that the way that knowledge is typically operationalized and measured is rather simplistic—relying on counts of correctly answered ‘informational units’ as a proxy for measuring the amount of ‘content’ that students have retained [129]. Such an experimental design is limited in its ability to examine how learners represent, acquire and ultimately retrieve a hierarchical, complex, network-like organization of concepts. An alternative approach is to harness the mathematical framework of network analysis to help quantify knowledge structures as networks that allow learning scientists to move towards a deeper understanding of the processes that support learning and acquisition of expertise in a given domain.

It might be worthwhile for cognitive and learning scientists to pay attention to a small but burgeoning literature that uses network science approaches to quantify the knowledge structures of pre-service teachers [130] and students [131]. These studies analysed the concept maps produced by teachers-in-training and high school students as networks to identify central, important concepts in their conceptual structure [132], detect meso-level structures that reflect thematic communities in a domain [133] and compare the overall network structure of experts against that of novices [134]. Recent work by Siew [135] showed that the overall network structure of concept maps is a significant predictor of quiz scores and could serve as one indicator of successful learning and retention of content. Lydon-Staley and colleagues [136] showed that the different search strategies that people adopted while navigating Wikipedia resulted in different knowledge networks (i.e. Wikipedia pages that were connected based on the sequence in which they were being navigated). Briefly, people driven by uncertainty reduction try to ‘fill gaps’ in their knowledge, resulting in networks with higher levels of clustering, whereas people driven by curiosity tend to explore the knowledge space more, resulting in looser, sparser networks with higher average shortest path length. Together, these studies have important implications for learning in educational settings. Research conducted by Koponen and colleagues demonstrates that it is possible to measure and quantify the internal knowledge structure of people and that this structure varies across levels of expertise, suggesting that network science methods could be useful in tracking development of domain expertise, whereas other research suggests that the network structure of knowledge could have implications for learning and retrieval processes [135] and that analysing knowledge as a network could help us understand individual variability in the processes that give rise to observed structural differences in knowledge networks [136].

Sudden, rapid changes to network structure

Creative insight and problem solving. The ‘Aha!’ moment when you suddenly find a solution to a problem is very visceral, but elusive and notoriously difficult to quantify. Here we discuss recent papers in the modern network science era that rely on the network science framework to provide theoretical and methodological grounding for investigating and quantifying that moment of creative insight. Schilling [137] suggested that, in the search for a non-straightforward solution to a given problem, local associations are first exhausted before moving on to distant associations in other areas of the network (analogous to cognitive foraging in a semantic space as demonstrated by Jones et al. [138]). This movement between clusters (i.e. moving from a space of obvious solutions to a space with less obvious solutions) within the network could be operationalized as a key psychological mechanism underlying the emergence of creative insight. A relevant paper demonstrating this empirically is that by Durso et al. [139], who presented puzzles for people to solve. These puzzles were in the form of a short story with a ‘missing piece’ that, when discovered, completed the narrative in a way that the story would suddenly make perfect sense. A network analysis of relatedness judgements between pairs of concepts relevant to the puzzle showed that solvers' and non-solvers' knowledge network structure differed such that the average shortest path length is smaller in the solver's networks. The implication is that, when a solution is found, the structure of the network changes dramatically to reflect the insight generated by finding the ‘solution’ to the story, which occurred when an association between unexpected concepts that were initially far apart in the network was found.

We suggest that the application of network science methods to the domain of creative insight and problem solving can enhance research by shifting the overwhelming emphasis on the process of problem solving to a perspective that considers how the structure of cognitive representation interacts with the process of problem solving. Extant computational models of problem solving tend to focus on the implementation of rather complicated processes (e.g. the interactivity between, and integration of, explicit and implicit processes), but have simple cognitive architectures that do not enable such models to fully consider the overall structure of the problem--solution space (e.g. [140]). However, some recent work is pushing forward the idea that some of the complexity in the processes of creative problem solving could be ‘offset’ by accounting for the complex structure of the internal cognitive representation of the problem-solver. For instance, measurable short-term structural changes in an associative network might reflect either the problem solver's attempts at finding a solution or discovery of the solution [141,142], or the ability of (more creative) individuals to flexibly adapt their semantic networks [143,144].

(c). Progressing up the future spiral: how can the innate incompatibility of network science and cognitive science approaches be resolved?

In this section, we consider the future of research on network dynamics in cognitive network science. Recall that our brief historical literature review of the cognitive sciences prior to the era of modern network science highlighted how some psychologists were (rightfully!) sceptical of the ability of network science approaches to further our understanding of cognitive and lexical processes. The underlying issue is that there appears to be an innate incompatibility of using mathematical approaches from network science to address fundamental questions about psychological and cognitive processes.

Leont'ev & Dzhafarov ([145]; as cited in [20, p. 280]) wrote that ‘psychology and mathematical instruments are still not compatible enough with one another to allow mathematization to assume a central place in the development of psychological knowledge’ and that ‘continual interaction that would… lead to a restructuring of psychological theories into forms more amenable to the proposed mathematical instruments… [and] revision of existing mathematical methods into forms more amenable to mathematized conceptual systems.’ Such concerns regarding how two very different fields of research could interface, or even be unified, in productive ways are echoed more recently in Poeppel & Embick's [83] discussion of the difficulties involved in interfacing between neuroscience and linguistics research. As previously discussed in §2c, the ‘ontological incommensurability problem’ is the problem where fundamental elements of linguistic theory (e.g. phonological segments or words) cannot be readily matched to the fundamental biological units that are central in neuroscience research (e.g. neuron clusters). When applied to the present context, it is the problem that fundamental elements of psychological theory and process (e.g. notions of activation or competition) cannot be directly matched to aspects or components of the network representation as identified by mathematical graph theory (e.g. nodes and edges). In other words, it is not immediately clear how or what aspects of the network representation could provide a useful account of psychological processes and computations that psychologists are most interested in.

This is a legitimate concern because, in order for continued progress up this spiral, it is important that the areas of network science and cognitive science continue to engage in productive cross-fertilization and interaction, despite this apparent theoretical mismatch of mathematical and psychological units and components. Indeed, our goals in writing this review are to introduce a wide array of cognitive science topics to network scientists, highlight the contributions of network science approaches to this field, and hopefully encourage network scientists to collaborate and engage with cognitive scientists to address outstanding theoretical and methodological questions in these research areas.

Poeppel & Embick [83] argue that one possible solution to the problem of ontological incommensurability in neuroscience and linguistics research is to establish plausible linking hypotheses across the two disciplines via the development of computational models that focus on primitive biological and linguistic operations. For instance, the operation of linearization is central in syntactic theory and required in phonological sequencing and motor planning of speech, making it plausible that linearization operations are implemented in a similar fashion in certain specialized brain regions. Here we suggest that a reasonable linking hypothesis for cognitive science and network science is the implementation of dynamic process or growth models on a network that represents cognitive structure. Within such an approach both the ‘process model’ and the ‘network structure’ represent hypothesis spaces that could then be thoroughly and rigorously explored and tested via computational and mathematical approaches. As a concrete example, consider the empirical finding by Chan & Vitevitch [109], who showed that the structure of words in the phonological language network affected how words were processed in psycholinguistic tasks. Specifically, they reported a processing advantage for words with low clustering coefficients (whose immediate neighbours tended not be connected to each other) over words with high clustering coefficients (whose immediate neighbours tended to be connected to each other). On its own, the fact that a structural measure of the network (clustering coefficient) was associated with behaviour (processing speeds in lexical tasks) does not do much to inform psycholinguistic models of word retrieval. However, when a linking hypothesis with respect to how activation flow among connected lexical units is constrained by the structure of the mental lexicon is proposed and computational simulations are conducted in conjunction to validate this hypothesis [107,108], the inherent mismatch of mathematical, network representations and psychological and behaviour phenomena can be greatly reduced. The outputs of nonlinear interactions between the ‘process model’ and the ‘network structure’ should be continually evaluated against empirical, behavioural data to disentangle process from structure and further inform the development of network models of cognition.

(d). Summary

In the pre-modern network science era, some psychologists saw the potential of using graph theory to represent a wide range of cognitive structures, but others were more sceptical of graph-theoretic approaches because network representations of cognitive structures on their own do not easily connect to cognitive processes of retrieval, learning and inference. Recent research has adopted modern network science approaches to study topics related to lexical retrieval, vocabulary development, cognitive ageing, learning, creativity and problem solving. Together this body of research has demonstrated that conceptual linkage between structure and process can be established via a network science framework that focuses on the dynamics that operate on the network (i.e. spreading activation and random walks) and the dynamics of the network representation itself (i.e. network growth, development and change). To make continued progress up the spiral, we highlight the need to be cognizant of potential problems of interfacing between two disciplines with very different theoretical motivations and conceptualizations, and suggest that the implementation of network dynamics (i.e. growth or process models) on a network representation serves as a plausible conceptual and quantifiable linkage between network science and the cognitive sciences.

4. Concluding remarks

To recapitulate, this paper provided a comprehensive review of the two research spirals of cognitive science, representation and process, through the lens of network science. As seen from the studies discussed, the application of modern network science has been crucial in enhancing our understanding of such fundamental aspects of cognitive science. The first section focused on the research spiral of how cognitive structure, specifically the mental lexicon, can be represented and quantified using networks. The rise of modern network science, along with the availability of more data and computational power, has given rise to a new wave of research that applies network science methods to quantitatively model the mental lexicon and semantic memory. The second section focused on the research spiral of the dynamics on and of cognitive structures. The fast growing body of research adopting modern network science approaches to study a diverse array of topics in the cognitive sciences, ranging from lexical retrieval, vocabulary development, cognitive ageing, learning and creativity to problem solving, clearly demonstrates how the interaction between structure and process can be investigated via a network science framework that focuses on the dynamics that operate on the network (i.e. spreading activation and random walks) and the dynamics of the network representation itself (i.e. network growth, development and change). Looking ahead, in order to make continued progress up the research spirals, we suggest that, given the inherently abstract nature of cognitive representations, researchers applying network science to the field of cognitive science need to recognize the limitations of relying on behavioural data in the construction of cognitive network representations and to also recognize the inherently dynamic structure of networks and the dynamic processes that occur within networks. Furthermore, we call to action greater exploration into the possibility of using the network science framework to explicitly connect the structure and processes of the mind and the brain. Indeed, network science itself could serve as the necessary theoretical and conceptual linkage between human cognition and the human brain.

Data accessibility

This article has no additional data.

Authors' contributions

N.C. and C.S.Q.S. contributed to the conceptualization of this manuscript. N.C. and C.S.Q.S. drafted and revised this manuscript and gave approval for the final version of this manuscript. N.C. and C.S.Q.S. agree to be accountable for all aspects of this work.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Institute on Deafness and Other Communication Disorders of the National Institutes of Health under award no. F32DC017174. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.