pK_a Calculations with the Polarizable Drude Force Field and Poisson-Boltzmann Solvation Model

Abstract

Electronic polarization effects have been suggested to play an important role in proton binding to titratable residues in proteins. In this work, we describe a new computational method for pK_a calculations, using Monte Carlo (MC) simulations to sample protein protonation states with the Drude polarizable force field and Poisson-Boltzmann (PB) continuum electrostatic solvent model. While the most populated protonation states at the selected pH, corresponding to residues that are half-protonated at that pH, are sampled using the exact relative free energies computed with Drude particles optimized in the field of the PB implicit solvation model, we introduce an approximation for the protein polarization of low-populated protonation states to reduce the computational cost. The highly populated protonation states used to compute the polarization and pK_a's are then iteratively improved until convergence. It is shown that for lysozyme, when considering 9 of the 18 titratable residues, the new method converged within two iterations with computed pK_a's differing only by 0.02 pH units from pK_a's estimated with the exact approach. Application of the method to predict pK_a’s of 94 titratable sidechains in 8 proteins shows the Drude-PB model to produce physically more correct results as compared to the additive CHARMM36 (C36) force field (FF). With a dielectric constant of two assigned to the protein interior the Root Mean Square (RMS) deviation between computed and experimental pK_a's is 2.07 and 3.19 pH units with the Drude and C36 models, respectively, and the RMS deviation using the Drude-PB model is relatively insensitive to the choice of the internal dielectric constant in contrast to the additive C36 model. At the higher internal dielectric constant of 20, pK_a's computed with the additive C36 model converge to the results obtained with the Drude polarizable force field, indicating the need to artificially overestimate electrostatic screening in a nonphysical way with the additive FF. In addition, inclusion of both syn and anti orientations of the proton in the neutral state of acidic groups is shown to yield improved agreement with experiment. The present work, which is the first example of the use of a polarizable model for the prediction of pK_a’s in proteins, shows that the use of a polarizable model represents a more physically correct model for the treatment of electrostatic contributions to pK_a shifts in proteins.

INTRODUCTION

Titratable sites are abundant in proteins¹ and play an essential role in the structure, function and stability.² Thus, it is essential to reliably predict proton dissociation constants, pK_a's, and to understand factors that modulate them.³ A large multitude of methods to predict proton binding affinities in proteins have been developed over the last decades.⁴ However, the accurate prediction of pK_a's of protein titratable sites is still a major challenge and an active area of research.^4b Accurate pK_a prediction faces several challenges including the need to consider protein conformational changes associated with the changes in protonation states, solvent contributions and interactions between titratable sites, which depend on each particular configuration of bound protons. Also contributing is the complex electronic response of the heterogeneous protein/solvent environment to changes in protonation states.⁵

A number of pK_a prediction methods rely on continuum dielectric models to describe the solvent degrees of freedom.^{2a, 6} In these methods, frequently the protein in solution is treated using the continuum dielectric approximation based on the Poisson or Poisson-Boltzmann (PB) model⁷ or generalized Born (GB) model in the context of an additive force field, with the GB model having the advantage of being more computationally efficient.⁸ Bashford and Karplus were first to develop and apply the PB model using detailed 3D structural information for pK_a calculations and taking into account interactions between titratable sites as defined by a particular arrangement of bound protons.⁹

The number of possible protonation states of the protein grows exponentially with the number of titratable sites. The exact calculation of all accessible protonation states is not feasible for proteins containing a large number of titratable residues and different approximations have been introduced to overcome this challenge.^{7b, 9-10} The early method of Tanford & Roxby introduced an approximation in the energy function which effectively reduces an ensemble of protonation micro-states to one.^10b In this method a titratable residue interacts with protonated and deprotonated forms of all other residues weighted based on their pK_a's and the targeted pH value. However, it was shown that this approximation is inaccurate for strongly interacting sites.^{10b, 10c} Later methods include different site-reduction methods^{9-10, 10c} and hybrid methods.¹¹ With site-reduction methods, most of configurations of bound protons are eliminated, for example based on precalculated occupancies or distances between titratable sites.^10a Arguably, a more precise method is to perform Monte-Carlo (MC) simulations since, in principle, all protonation states can be sampled.^7b With additional approximations, MC methods can be used together with a limited protein flexibility, for example, allowing for discrete side-chain conformational sampling with a rigid protein backbone.^{7c, 8a}

For computational efficiency, all these methods normally rely on the ability to decompose the free energy of the protein in a particular protonation state into energy contributions that depend only on the protonation states of individual residues or pairs of residues.^10c This is possible as the field or potential determined by the Poisson equation is additive.^6a The energy components can be precomputed and stored for subsequent free energy calculations performed during sampling of protonation states. However, with polarizable force fields the free energy cannot be represented in the pair-wise form, since the electronic state of the protein and, therefore, the free energy is defined by the protonation state of all titratable sites. To overcome this an effective approximation is needed to implement a polarizable model, such as the Drude-PB model, in constant-pH Monte Carlo simulations.

In this work, we present a new computational method to resolve the need to explicitly treat the polarization of a protein during pK_a calculations. While the calculation of pK_a’s for small molecules with a polarizable force field has been performed previously,¹² the present study represents their first application towards the estimation of pK_a’s in proteins. The approach is based on our previous study where we implemented and parametrized an implicit PB solvent model in conjunction with the Drude force field; similar work has been done with the AMOEBA polarizable force field.¹³ In the new method, the most populated protonation states at the target pH, as defined by those residues that titrate in the region of the target pH, are sampled using the relative free energies that include a self-consistent field (SCF) calculation of the Drude particles in the field of the PB implicit solvation model. The states used to compute the electronic polarization and pK_a's are iteratively improved until convergence. In addition, to facilitate the calculations, the interactions between titrating groups are calculated for a single electronic structure for each ionization state of each residue, with that approximation explicitly validated. The model was tested to predict the pK_a’s of 94 titratable sidechains in 8 proteins for which experimental pK_a's are available.

METHODS

Classical electrostatic pK_a calculations with additive force fields

The classical theory of pK_a calculations of a titratable residue group in the protein environment using the pK_a of the model compound in solvent is based on the thermodynamic cycle shown in Figure 1.

Figure 1.

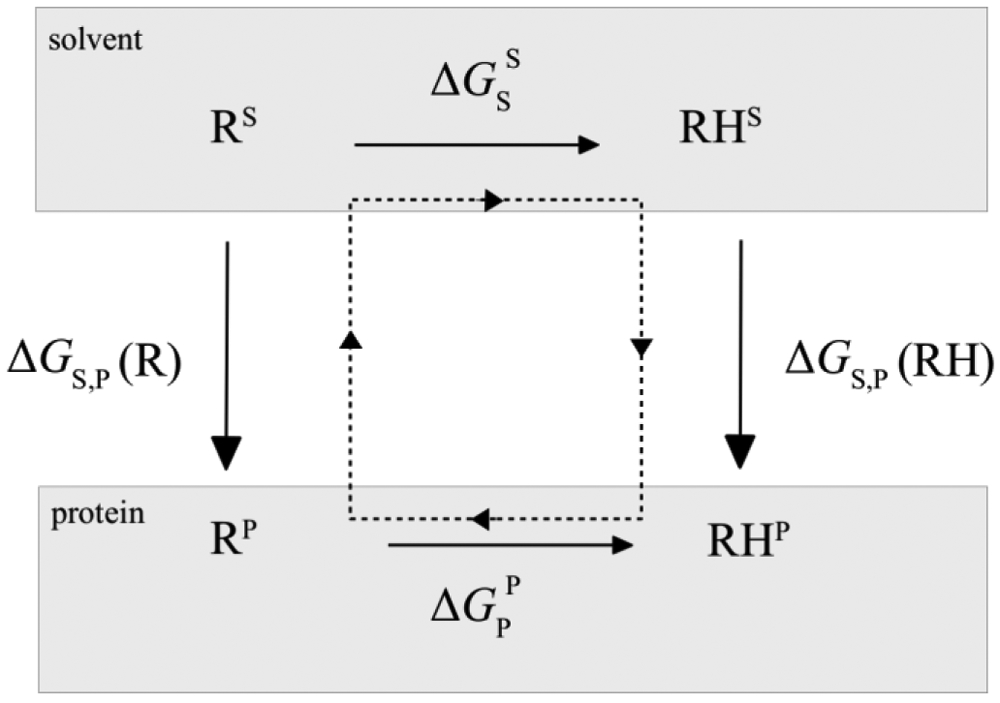
Thermodynamic cycle for proton binding. RH and R represent protonated and deprotonated forms of the residue, respectively, in the solvent environment as a model compound (upper) or in the protein environment (lower). The superscripts are used to highlight that the polarization of residue R/RH is different in the protein and solvent. With the additive force fields these polarizations are the same.

It is assumed that the proton binding affinity difference of a titratable residue in the protein and a model compound in solvent is only due to the electrostatic interactions. For a protein containing one titratable residue:

$$\mathrm{p}{K}_{\mathrm{a}}^{\text{protein}}=\mathrm{p}{K}_{\mathrm{a}}^{\text{model}}+\Delta \Delta G∕\text{ln}(10)∕RT,$$ [Eq 1]

where $\mathrm{p}{K}_{\mathrm{a}}^{\text{model}}$ is the pK_a of a model compound in solvent; R is the gas constant; T the temperature and ΔΔG is a double difference of the electrostatic free energy associated with the residue being in the protein environment. It is further assumed that the electrostatic field is governed by the macroscopic Poisson (or Poisson-Boltzmann) equation:

$$\nabla \epsilon (\overline{r})\nabla \phi (\overline{r})=-4\pi \rho (\overline{r}),$$ [Eq 2]

where φ is the electrostatic potential, ρ is the charge density and ε is the dielectric constant. This equation can be numerically solved, for example on a cubic lattice by finite difference methods, to give the charging free energy, W, of a set of protein atomic charges:

$$W=\frac{1}{2}{\sum }_i{Q}_i^P\phi ({\overline{r}}_i),$$ [Eq 3]

where the summation is done over the protein atomic charges, $Q_i^P$;$\phi ({\overline{r}}_i)$ is the electrostatic potential that satisfies Equation 2 and computed at the position ${\overline{r}}_i$ of the atomic charge $Q_i^P$.

For a macromolecule containing more than one titratable site, the protonation state of a residue, μ, is affected by the charge state of all other titratable residues. In this case, the fraction of molecules, θ_μ, protonated at site μ at a particular pH value is given by the Boltzmann average of all microstates where this residue is protonated:

$$\langle {\theta }_{\mu }\rangle =({\sum }_{\{\overline{x}\}}{x}_{i,\mu }\text{exp}(-\Delta G({\overline{x}}_{ı},\text{pH})∕RT))∕({\sum }_{\{\overline{x}\}}\text{exp}(-\Delta G({\overline{x}}_{ı},\text{pH})∕RT)),$$ [Eq 4]

where the summation is done over all possible protonation microstates $\{\overline{x}\}$; ${\overline{x}}_{ı}$ is a vector that defines protonation microstate i; x_i,μ is a μ-th element of the vector ${\overline{x}}_{ı}$ and is 1 or 0 if residue μ is protonated or deprotonated, respectively, in the microstate i; $\Delta G({\overline{x}}_{ı},\text{pH})$ is the relative free energy of protonation of microstate ${\overline{x}}_{ı}$, and within the context of additive force fields can be expressed as follows:

$$\Delta G({\overline{x}}_{ı},\text{pH})=E({\overline{x}}_{ı},\text{pH})+{\sum }_{\mu }(\Delta G_{\text{Born},\mu }(x_{i,\mu })+\Delta G_{\text{back},\mu }(x_{i,\mu }))+\frac{1}{2}{\sum }_{\mu \ne v}{W}_{\mu v}(x_{i,\mu },x_{i,v}),$$ [Eq 5]

where ΔG_Born,μ is the relative Born energy of a titratable residue located in the protein environment and related to its desolvation electrostatic free energy; ΔG_back,μ is due to interactions with the background charges on non-titratable residues; W_μν(x_i,μ, x_i,ν) is electrostatic interaction energy between two titratable residues μ and ν being in protonation states x_i,μ and x_i,ν respectively. $E({\overline{x}}_{ı},\text{pH})$ is a contribution from solvent pH and reference model compounds:

$$E({\overline{x}}_{ı},\text{pH})={\sum }_{\mu }E(x_{i,\mu },\text{pH})={\sum }_{\mu }\left(x_{i,\mu }RT\text{ln}(10)(\text{pH}-{\text{pK}}_{a,\mu }^{\text{model}})-\langle E_{\mu }^{\text{model}}(x_{i,\mu })\rangle \right),$$ [Eq 6]

where $\langle E_{\mu }^{\text{model}}(x_{i,\mu })\rangle$ is the average electrostatic free energy of the reference model compound for residue μ being in protonation form x_i,μ in solvent computed using the same force field model. For the convention, in summations we will use letters from the Latin alphabet to designate protein particles (atoms, Drudes, lone-pairs) and protein microstates, while Greek letters to denote residues in the protein. The ⟨θ_μ⟩ are evaluated at a discrete number of pH values to obtain a titration curve for site μ. pK_a,μ of a titratable residue μ in the protein is then defined as the pH value where the titratable residue is half-protonated.

In practice calculations of titration curves directly using Equation 4 are limited to macromolecules containing only a few titratable residues since it requires sampling of a large number of protonation microstates that grows exponentially (2^N) with the number of titratable residues. To solve this problem MC simulations are performed to sample only relevant protonation states, while high-energy states that do not contribute significantly in Equation 4 are not visited. To perform MC simulations, energies appearing in Equation 5 must be precomputed and stored in the first step. Relative free energy of the protein in a particular protonation state is then recovered from the energy matrices as a simple sum of energy terms in the MC simulations.

The Poisson-Boltzmann method for pK_a calculations with a polarizable force field and multiple titratable sites

In the case of polarizable force fields, ΔG_Born,μ, ΔG_back,μ and W_μν in Equation 5 depend on the electronic state, or polarization, of all protein atoms. In particular, with the Drude force field ΔG_Born,μ, ΔG_back,μ and W_μν are functions of the position of the Drudes on all atoms including titratable residues. In turn, the positions of all Drudes, including on protein backbone atoms, depend on the protonation states of all residues. In the case of polarizable force fields the relative free energy $\Delta G(\overline{x},\text{pH})$ contains additional contributions. In the context of the additive force field, these contributions do not depend on the protein protonation state $\overline{x}$, and thus do not contribute in Equation 5. These energy terms include (i) a contribution from interactions between background charges with background charges, since polarization of background atoms depends on the protonation state; (ii) the Born energy of background atoms, which now depends on the polarization affected by the protonation state of all residues; and (iii) the polarization work needed to polarize titratable and non-titratable groups of atoms from the polarization in solvent to the polarization in a protein. We will use $G_{\text{BB}}(\overline{x})$ to denote the sum of the first two terms (i) and (ii), and the term (iii) will be included in $G_{\text{BB}}(\overline{x})$, $G_{\text{Born},\mu }(\overline{x})$, and $G_{\text{back},\mu }(\overline{x})$. The term (iii) is computed within the Drude force field as the bond energy contributed by the atomic core-Drude particle bonds (i.e. self-polarization energy term or polarization work), which is different due to the different polarization in solvent and protein as well as being coupled to the protein protonation state. Thus, the total relative free energy of a microstate within the Drude polarizable force field is calculated using the following formula:

$$\Delta G(\overline{x},\text{pH})=E(\overline{x},\text{pH})+\Delta G_{\text{BB}}(\overline{x})+{\sum }_{\mu }(\Delta G_{\text{Born},\mu }(x_{\mu },\overline{x})+\Delta G_{\text{back},\mu }(x_{\mu },\overline{x}))+\frac{1}{2}{\sum }_{\mu \ne \nu }{W}_{\mu \nu }(x_{\mu },x_{\nu },\overline{x}),$$ [Eq 7]

where $\overline{x}$ is, as above, a vector with element x_μ defining the protonation state of residue μ; and the argument $\overline{x}$ in functions $G_{\text{Born},\mu }(x_{\mu },\overline{x})$, $G_{\text{back},\mu }(x_{\mu },\overline{x})$ and $W_{\mu \nu }(x_{\mu },x_{\nu },\overline{x})$ is repeated to emphasize that in contrast to Equation 5, these terms depend on the protonation state of all residues including titratable residues μ and ν.

In contrast to additive force fields, $G(\overline{x},\text{pH})$ given by Equation 7 is not a residue-pairwise function. This means that the free energy of all protein protonation microstates cannot readily be recovered in MC simulations. Accordingly, in what follows, we present an approximate MC method suitable for the polarizable Drude force field in the context of a constant pH formalism. We first note that to define pK_a,1/2 of a titratable residue only the point on the titration curve where pH = pK_a,1/2 needs to be identified. Thus, the approach just needs to reproduce exactly the free energies of microstates highly populated at pH ~ pK_a,1/2 that contribute significantly in Equation 4. In the method presented later in this section, free energies of the most populated states for the protonated and deprotonated forms of a residue are computed exactly using minimization of the position of the Drudes particles (i.e. performing the polarization SCF calculation) in the field of the implicit solvent. Thus, polarization effects for the most populated microstates are taken into account exactly, while free energies of less populated microstates perturbed by the polarization response to the change of the protonation state are computed less accurately during the MC simulation. To calculate $\Delta G_{\text{BB}}(\overline{x})$, $\Delta G_{\text{Born},\mu }(x_{\mu },\overline{x})$, $\Delta G_{\text{back},\mu }(x_{\mu },\overline{x})$ and $W_{\mu \nu }(x_{\mu },x_{\nu },\overline{x})$ in Equation 7 the position of all Drude particles should be defined. In the method, the highly populated protonation states at pH = pK_a,μ are used to calculate these energies for the protonated and deprotonated forms of residue μ.

pK_a calculations with the Drude force field and Poisson-Boltzmann model

In this section the calculation protocol of the new method is given. A flow chart of the computational protocol is presented in Scheme 1. Protonation states for all residues are predefined in the initial calculation of energy terms appearing in Equation 7, with titratable residues assigned neutral protonation states. These predefined states will be refined iteratively in subsequent steps. The method starts with molecular mechanics (MM) and Poisson-Boltzmann calculations of free energies needed to perform MC simulations:

Scheme 1.

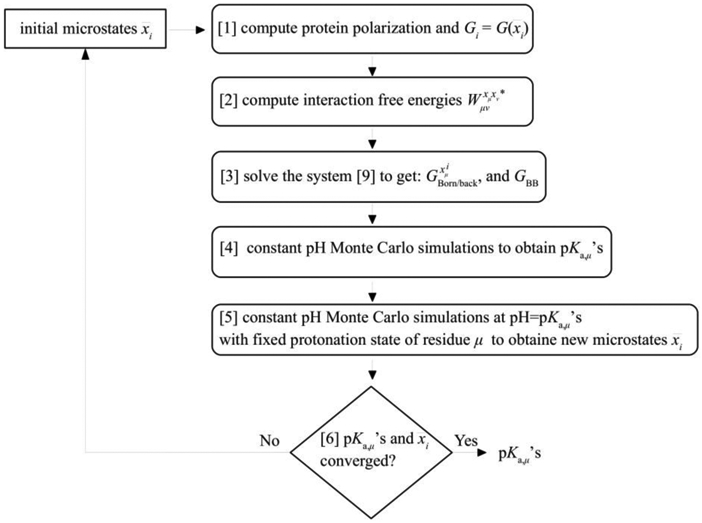
Flow Chart of the computations performed with the Drude-PB method. Steps 1-5 are repeated until pK_a,μ and microstates converge. Initial microstates are updated using the computed microstates at the end of the previous iteration.

Step 1.

Calculate protein free energies for both ionization states of all titratable residue with the remaining titratable residues assigned neutral protonation states. For each protonation state of titratable residue μ, neutral protonation states are used for all other titratable residues giving the vector defining the protonation microstate ${\overline{x}}_i$. These protonation microstates ${\overline{x}}_i$ are used to optimize the Drude particles. The free energies of the protein in each of these protonation microstates is calculated as $G_i=G({\overline{x}}_i)$, based on the system MM energy and the PB implicit solvation energy, with these energies including the polarization energy following the Drude SCF calculation.

Step 2.

Interaction free energies between titratable residues, which include MM electrostatic interactions and the solvent contribution, are calculated. This involves individually calculating the electrostatic potential for each titratable residue μ, by zeroing the charges on all atoms in the protein (including lone pairs and Drude particles) except those on the residue μ. The positions of Drude particles optimized in step 1 and corresponding to selected protein protonation microstates for residues μ and ν are used, so no optimization of Drude particles is needed at this step. To avoid the problem of artificial contributions arising when interaction energies are computed between neighboring residues due to 1,2 and 1,3 dipole-dipole interactions included in the Drude model, the contribution to the interaction energy from solvent is computed using the PB model and combined with the MM energy to obtain the total interaction free energy between residues. The PB equation is solved to obtain the electrostatic potential φ_Rμ (ε_ext = ε_w, ε_int = ε_p), due to the charges of residue μ being in the protonation state x_μ. Calculations are repeated using the protein dielectric constant for the protein exterior to obtain the electrostatic potential φ_Rμ(ε_ext = ε_p, ε_int = ε_p). The electrostatic potential is used to calculate the electrostatic interaction $W_{\mu \nu }^{x_{\mu },x_{\nu }\ast }$ between the titratable residues μ and ν being in protonation state x_μ and x_ν, respectively, according to $W_{\mu \nu }^{x_{\mu },x_{\nu }\ast }=1∕2{\sum }_{ij}{q}_i{q}_j∕{\epsilon }_p∕r_{ij}+{\sum }_j{q}_j({\phi }_{R{\mu }_j}({\epsilon }_{ext}={\epsilon }_w,{\epsilon }_{int}={\epsilon }_p)\text{-}{\phi }_{R{\mu }_j}({\epsilon }_{ext}={\epsilon }_p,{\epsilon }_{int}={\epsilon }_p))$, where q_i and q_j are charges of residues μ and ν, respectively. Note that in principle $W_{\mu \nu }^{x_{\mu },x_{\nu }\ast }\ne W_{\nu \mu }^{x_{\nu },x_{\mu }\ast }$, and these interaction energies are different from those appearing in Equation 7 since the polarization used for residues μ and ν corresponds to different protein protonation microstates. We use an asterisk to distinguish these energies from the interaction energies in Equation 7.

Step 3.

For each free energy, G_i computed in step 1 it is possible to write Equation 7 as follows:

$$G_i=G_{\text{BB}}({\overline{x}}_i)+{\sum }_{\mu }\left(\Delta G_{\text{Born},\mu }(x_{i,\mu },{\overline{x}}_i)+\Delta G_{\text{back},\mu }(x_{i,\mu },{\overline{x}}_i)\right)+\frac{1}{2}{\sum }_{\mu \ne \nu }{W}_{\mu \nu }(x_{i,\mu },x_{i,\nu },{\overline{x}}_i),$$ [Eq 8]

The latter expression does not form a closed system of linear equations relative to the terms $\Delta G_{\text{Born}∕\text{back}\mu }(x_{i,\mu },{\overline{x}}_i)=\Delta G_{\text{Born}\mu }(x_{i,\mu },{\overline{x}}_i)+\Delta G_{\text{back},\mu }(x_{i,\mu },{\overline{x}}_i)$, since the latter terms are different for different protonation microstates ${\overline{x}}_i$. To recover G_i later in MC simulations, instead of using Equation 8 we introduce a system of linear equations:

$$\begin{gathered} \sum _{\mu }{G}_{\text{Born/back},\mu }^{x_{\mu }^1}+G_{\text{BB}}=G_1-\frac{1}{2}\sum _{\mu \ne \nu }{W}_{\mu \nu }^{x_{\mu }^1,x_{\nu }^1\ast } \\ \sum _{\mu }{G}_{\text{Born/back},\mu }^{x_{\mu }^2}+G_{\text{BB}}=G_2-\frac{1}{2}\sum _{\mu \ne \nu }{W}_{\mu \nu }^{x_{\mu }^2,x_{\nu }^2\ast } \end{gathered}$$ [Eq 9]

where G_BB is again due to interactions between background atoms with themselves, but invariant relative to the protonation state of titratable residues; $W_{\mu \nu }^{x_{\mu }^1,x_{\nu }^1\ast }$ is the interaction energy between residues μ and ν computed in step 2; $G_{\text{Born/back},\mu }^{x_{\mu }^i}$ and G_BB can be regarded as unknowns that satisfy the system of equations. The right hand expressions in the system are calculated in steps 1 and 2. The system of linear equations can be resolved to find all $G_{\text{Born/back},\mu }^{x_{\mu }^i}$ and G_BB.

We note that $G_{\text{Born/back},\mu }^{x_{\mu }^i}$ are not calculated directly in step 1 as was performed in the original constant-pH MC method. This is due to the need to calculate free energies from step 1 in the MC simulations as required to identify the most likely protonation microstates for each titratable residue as a function of pH when residues titrate (at pH = pK_a,μ) rather than $G_{\text{Born/back},\mu }^{x_{\mu }^i}$ energies. In other words, G₁, G₂ … G_n are used in MC simulations to sample probabilities of protonated and deprotonated states and, thus are required to calculate the titration curves. It should be emphasized that in MC simulations with the Drude force field it is prohibitively expensive to calculate the free energies of all protein microstates in contrast to the calculations with additive force fields; instead, we recover free energies of the most important states using the above method.

It may happen that the most likely protein microstates are identical for protonation states of different residues at the pH where they are half-protonated. In this case, equations for the protonation states of these residues are identical in the system of equations 9 and the system is not complete as required to define $G_{\text{Born/back},\mu }^{x_{\mu }^i}$ and G_BB. To complete the system we introduce additional equations in the free energy G_l computed with zero charges on all titratable residues except residue μ. The additional equation added to the system of equations 9 is: $G_{\text{Born/back},\mu }^{x_{\mu }^1}+G_{\text{BB}}=G_l$.

Step 4.

Perform MC simulations. During the MC simulations at the pH corresponding to the pK_a,ϑ of residue θ, the free energy of microstates is computed according to:

$$G(\overline{x})=G_{\text{BB}}+{\sum }_{\mu }{G}_{\text{Born/back},\mu }^{x_{\mu }}+\frac{1}{2}{\sum }_{\mu \ne \nu }{W}_{\mu \nu }^{x_{\mu },x_{\nu }\ast }$$ [Eq 10]

In Equation 10, $W_{\mu \nu }^{x_{\mu },x_{\nu }\ast }$ are the same energies used in the system of equations 9 and $G_{\text{Born/back},\mu }^{x_{\mu }}$ and G_BB are the solutions. For the most populated microstate ${\overline{x}}_i$, selected in Step 1, this equation should give exactly G_i. Thus, this approximation allows the free energies to be recovered in the MC simulations computed with the correct polarization (e.g. SCF Drudes). It should be noted that G_BB is a constant for all microstates and thus, cancels out when relative free energies of microstates are computed in the MC simulations. The dependence of $G_{\text{BB}}(\overline{x})$ on the protonation state does not appear in Equation 10 explicitly. However, for the most populated states it is included in $G_{\text{Born/back},\mu }^{x_{\mu }}$, as they are solutions of the system of equations 9.

MC simulations are performed in the range of pH values between −10 to 30 with a step of 0.5 pH unit to obtain a titration curve for each titratable residue. The contribution $E(\overline{x},\text{pH})$ computed by Equation 6 is added to Equation 10 to obtain relative free energies of protein microstates. During the MC simulations one randomly selected titratable residue protonation state is changed with acceptance or rejection of that change based on the Metropolis criteria. In 50% of the MC steps a second residue is allowed to change its protonation state. In the present study, 100,000 MC steps were performed for each titratable residue in the system (eg. with 20 titratable residues 2·10⁶ MC steps are performed). To test the convergence of MC simulations the number of MC steps was doubled, but the change in relative populations of protonated and deprotonated forms was less than 10⁻³ observed for residues in eight proteins. Finally, using the titration curves the set of pK_a,μ values of all titratable residues can be defined based on the pH at which they are half-protonated.

Step 5.

MC simulations for each titratable residue μ and each of its protonation state x_μ are repeated at pH = pK_a,μ determined in the previous step. In contrast to the MC simulations in step 4, the targeted titratable residue μ is fixed in the protonation state x_μ to find the most likely protonation states for all other titratable residues. Note that the most likely protonation states may be different for the protonated and deprotonated forms of the same residue μ. The same number of MC steps was performed as in step 4.

Step 6.

Steps 1-5 are repeated with the most likely states of each titratable residue obtained from step 5. These iterations are required since initially in step 1 the most likely protonation states are not known but rather estimated based the neutral protonation state. Iterations over steps 1-5 are performed until the calculated pK_a,μ of all the titratable residues and the states computed in step 5 converge. Overall, the protocol has two types of self-consistent iterations: (i) in step 1 the position of the Drudes and the PB solvent polarization are fully optimized and (ii) globally, steps 1-6 are repeated to converge the individual titratable residue pK_a,μ values.

To summarize, using this method the polarization effects are included without any approximation in free energies for the most populated protonation microstates of a protein when residues titrate (at pH = pK_a,μ). Within this method, it is achieved at an additional computational cost to perform multiple iterations. It should be noted that polarization of less populated states is still incorrectly treated, since a surrogate of $G_{\text{Born/back},\mu }^{x_{\mu }}$ and $W_{\mu \nu }^{x_{\mu },x_{\nu }\ast }$ corresponding to protonation states that differ from that of the less populated states is used. The latter error is expected to be small, since those microstates make small contributions to the titration curves at pH equal pK_a,μ. Notice, that in principle, one could consider exact free energies for a limited number of less occupied microstates in Equation 4, however, in this work we limit to one state per protonation and rotameric state of a residue.

Proton binding sites and protein structure relaxation

In the present study, only titratable protons are allowed to change their positions to preserve the dielectric boundary. Otherwise, the PB equation would need to be solved for each W_μν element, which is prohibitively expensive. It should be noted that different approximations have been proposed with the sacrifice of the exact protein boundary to allow limited flexibility of sidechains^{8a, 14}, which will be explored in future studies with the Drude force field.

In the case of the acidic aspartate and glutamate residues, we consider five protonation states: one ionized negative state and four neutral states with the proton on either oxygen and in the syn and anti orientations. Two rotamers were included for neutral tyrosine that differ by the orientation of the hydroxyl group, and three rotamers for the neutral lysine, distinguished by the dissociation of amino protons. Histidines had two possible neutral tautomers: protonated on Nε (pK_a of the model compound 7.0) and Nδ (pK_a of the model compound 6.5). In the implementation, the neutral tautomers of histidines are simply treated as "rotamers" with a different contribution to the pH dependent term due to the pK_a difference of the Nε and Nδ sites. The total number of rotamers for neutral and ionized forms for titratable residues was chosen to be identical to avoid the problem of artificial biasing in MC simulations of protonation forms having a larger number of rotamers.

Reference state

Following the thermodynamic cycle shown in Figure 1, to calculate the protonation free energy in the protein the free energy of the model compound in solution, called the reference free energy, is subtracted. This free energy is estimated using the same force field model, which is needed for the cancelation of artefacts due to the employment of the empirical force field model. The force field term of the reference free energy is estimated as the free energy of the model compound in solution averaged over all possible compound conformations. In this work, we neglect the contribution from the bonded terms not associated with the Drude particles, since a single conformation for the protein calculations is used. Thus, the reference free energy of a model compound with a titratable residue x in solvent is:

$$G_x^{\text{ref}}=E_{\text{elec}}+E_{\text{bond}}^{\text{Drude}}+G_{\text{solv}}^{\text{PB}},$$ [Eq 11]

where E_elec is the intramolecular electrostatic energy computed with the same dielectric constant ε_p, which is used to calculate the solvation free energy $G_{\text{solv}}^{\text{PB}}=G_{\epsilon ext=80}^{\text{PB}}-G_{\epsilon ext={\epsilon }_p}^{\text{PB}}$. The same dielectric constant is also used for the protein calculations. $E_{\text{bond}}^{\text{Drude}}$ is the bond energy from the atomic core-Drude particle bonds (i.e. self-polarization energy term or polarization work).¹⁵ N-acetyl-x-N-methylamide with the corresponding titratable residue x was used as the model compound in solution. In this compound, charges involved in all 1-4 electrostatic interactions, including Drudes are identical to those charges in the protein system, leading to the cancelation of artefacts arising from the employment of the force field. To obtain pK_a 's in the protein, the computed pK_a shifts due to the protein environment were added to $\mathrm{p}{K}_{\mathrm{a}}^{\text{model}}$'s given in Table S2. The experimental pK_a shifts were computed as the difference between the pK_a in the protein environment and the pK_a of the corresponding model compound.

To obtain average free energies in solvent we performed molecular dynamics (MD) simulations of the N-acetyl-x-N-methylamides immersed in a cubic solvent box. The minimum distance between the compound atoms and the edge of the system was 12 Å. Periodic boundary conditions were assumed. All long range electrostatic interactions were computed efficiently by the particle mesh Ewald method¹⁶ using a real space cutoff of 12 Å. The Lennard-Jones term was evaluated out to 12 Å with a force switch smoothing function from 10 to 12 Å. MD simulations were performed at a constant temperature of 298 K and pressure of 1 ATM after 20 ps of thermalization. During MD simulations the center of mass of the model compound atoms was weakly harmonically restrained to the origin of the system with a force constant of 1.0 kcal·mol⁻¹·Å⁻². For the model compounds the CHARMM36 (C36)¹⁷ and Drude¹⁸ protein force fields were used along with the CHARMM TIP3P¹⁹ and SWM4-NDP²⁰ model for water for the additive and polarizable calculations, respectively. Simulations were done with the NAMD program.²¹ 50 nanoseconds of MD were performed at constant temperature and pressure for the compound containing each titratable residues. To calculate PB free energies, structures from the MD simulations were saved every 100 ps. The final PB free energies were averaged over these structures. The convergence was confirmed by dividing the data into five blocks corresponding to 10 ns MD simulations and computing the standard deviation, which was lower than 0.1 kcal·mol⁻¹ in all cases.

For the protonated form of the carboxylic acids, Asp and Glu, the syn and anti positions of the OH proton were simulated separately. The reference energy of the protonated form of Asp and Glu was Boltzmann-averaged over the free energies of the two forms.

Internal dielectric constant

As demonstrated and discussed in the work of Warshel et al, the dielectric constant ascribed to the protein medium is meant to represent physical contributions that are not considered explicitly.²² In the early model of Tanford and Roxby a protein was treated as a medium with a dielectric constant ε_int = 4 and solvent with a dielectric constant of 80, the experimental value. The protein dielectric constant of 4 is larger than the electronic polarizability estimate of 2, presumably to take into account the contribution due to the fluctuations of protein polar groups about their equilibrium positions.^{9, 23} In the model of Tanford and Roxby, the uniform continuum medium representing the interior of the protein, itself treated as a fixed object, was meant to implicitly incorporate the effects of the atomic fluctuations. This model is clearly an approximation. Obviously, the choice of the dielectric constant ascribed to the protein interior depends on the physical effects that are treated explicitly in the model.^{10a, 24} In this work, we do not treat fluctuations of protein atoms explicitly, which justifies the use of a higher dielectric constant for the protein interior (ε_int > 1). However, since reorganizations in the protein electronic structure are treated explicitly in the polarizable model, the protein dielectric constant is expected to be smaller than in the model with the additive force field. This conjecture will be verified with practical examples below. Following our previous work, the ionic strength was set to 0 M.¹⁵

Poisson-Boltzmann free energy calculations with the Drude Force field

The Poisson-Boltzmann free energy with the Drude force field is calculated in accord with our previous work.¹⁵ In brief, we need to calculate the electrostatic free energy, G_{εext=εw,εint=εp} of a solute with an internal dielectric constant of ε_p immersed in a dielectric medium with a high dielectric constant of ε_w. The free energies computed using the potential obtained by numerically solving the Poisson-Boltzmann equation and Equation 3 contain the artificial contributions of the grid as well as from electrostatic interactions between 1-2 and 1-3 bonded atoms. These contributions in the PB model should be removed by subtraction. To correct the electrostatic component of the free energy we modify G_{εext=εw,εint=εp} by the free energy computed with a uniform dielectric constant of ε_p:

$$G_{{\epsilon }_{ext}={\epsilon }_w,{\epsilon }_{int}={\epsilon }_p}=G_{{\epsilon }_{ext}={\epsilon }_w,{\epsilon }_{int}={\epsilon }_p}-G_{{\epsilon }_{ext}={\epsilon }_p,{\epsilon }_{int}={\epsilon }_p}+G_{{\epsilon }_{ext}={\epsilon }_p,{\epsilon }_{int}={\epsilon }_p},$$ [Eq 12]

where G_{εext=εp,εint=εp} is the contribution from the solute-solute interactions in a uniform dielectric medium with a dielectric constant of ε_p and is computed using $G_{{\epsilon }_{ext}={\epsilon }_p,{\epsilon }_{int}={\epsilon }_p}=\frac{1}{2}{\sum }_{i\ne j}\frac{q_i{q}_j}{{\epsilon }_p{r}_{ij}}$. The first two terms are computed using the Poisson-Boltzmann equation using the same set of parameters including those that define the grid, except the external dielectric constant. In this case, the artificial contributions cancel out, since the internal dielectric constant in both calculations is the same. In these calculations the state with the uniform dielectric constant, ε_p, is used as a reference state. To obtain the total free energy of a solute, the electrostatic component given by Equation 12 should be supplemented by self-polarization work, which is computed within the Drude force field as the bond energy contributed by the atomic core-Drude particle bonds.

An additional complication with a polarizable force field is that the interaction energy W_μν(x_i,μ,x_i,ν) in Equation 7 includes the electronic energy of the entire system that includes the self-polarization energy and the 1-2, 1-3 contributions from Drude particles. These terms disallow the calculation of W_μν(x_i,μ,x_i,ν) for two neighboring residues using only the Poisson-Boltzmann model. This is not the case for additive force fields where charges on the backbone atoms are normally fixed to the same values in the protonated and deprotonated forms, and thus these contributions cancel out for neighboring residues when the protonation free energy is computed. Thus, for the Drude force field the combination of the MM energy and PB solvation free energy are used to calculate the interaction energy, W_μν(x_i,μ,x_i,ν), as described above.

We use the solvation radii that were optimized in our previous work to reproduce experimental solvation free energies of a set of small molecules.¹⁵ The solvation radii were defined for all atom types except the deprotonated hydroxyl oxygen in tyrosine. The missing solvation radius of the O⁻ oxygen was optimized to reproduce the experimental absolute solvation free energy of the deprotonated tyrosine as described in the Supplementary Information.

PB free energy calculations were performed with the PBEQ module²⁵ implemented in the CHARMM program.²⁶ To include polarization effects explicitly the positions of Drude particles were optimized with the nuclear positions constrained in each protein microstate in step 1 using 50 steps of the Steepest Descent minimizer. Previously we showed that 20 steps of optimization was adequate for the minimization convergence for a set of protein complexes.¹⁵ As previously, dummy atoms were added to fill internal cavities not accessible by water molecules with a low dielectric medium.¹⁵ The protein PB energies were computed using the focusing method with a coarse grid of 0.8 Å resolution and fine grid with 0.4 Å resolution. The ion concentration was set to zero; we continue to call this method PB for the sake of simplicity, but use the finite-difference Poisson equation with no electrolyte present in the continuum solvent. The program to perform Monte-Carlo simulation for pK_a calculations was written in C++. The system of linear equation 9 was solved using the Eigen library for linear algebra.²⁷

Protein data set for pK_a calculations

The data set includes 94 titratable residues from eight proteins (Table S1, Supporting information). Protein structures were retrieved from the Protein Data Bank (PDB) and used for the position of heavy atoms in all calculations. Hydrogens were built using CHARMM,²⁶ and optimized with a uniform dielectric constant of 4 and titratable residues set to the standard protonation states at pH 6.5 (carboxylic acids deprotonated; lysines and tyrosines protonated; histidines doubly protonated). In this work we consider Asp, Glu, His, Lys, and Tyr as titratable, while Arg residues were present only in the protonated form. The protein data set did not contain any titratable cysteines. The N- and C-termini were not considered as titratable and were fixed in the standard protonation state, i.e. the terminal amino group is protonated and terminal carboxylate group is deprotonated. Thus, the data set included 31 aspartic acids, 30 glutamic acids, 10 tyrosines, 17 lysines and 6 histidines. Most of the experimental pK_a values used in this study were compiled by Georgescu et al.¹⁴ The experimental pK_a's for the SNase variant Δ+PHS were taken from Castaneda et al.³

RESULTS

Polarization effect on interaction free energies between titratable residues

We first examine the effect of polarization due to protonation of protein titratable sites on interaction free energies, $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ to test the approximation that these terms do not change significantly in the polarizable force field. Within classical additive force fields $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ are independent of protonation states of all residues except the protonation state x_μ and x_ν of the corresponding pair of residues μ and ν. With polarizable force fields, in principle $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ depends on the protonation state of all protein titratable sites: $W_{\mu \nu }^{x_{\mu },x_{\nu }}=W_{\mu \nu }^{x_{\mu },x_{\nu }}(\overline{x})$. To estimate the magnitude of this dependence we computed $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ for different pairs μ and ν in the eight proteins from the data set and random protein protonation states as follows. Random protonation states for each of the proteins were generated with the number of the generated random protonation states proportional to the number of titratable residues. The positions of the Drude particles were then fully optimized for each of these protonation states using the PB implicit solvent model for the complete protein structures. For these calculations, the dielectric constant of two was used for the protein interior. The interaction free energies, $W_{\mu \nu }^{x_{\mu },x_{\nu }}$, were then calculated yielding around 20 values for each $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ interaction energy when all the randomly generated models were considered. These interaction free energies for a pair of residues are different due to the protonation states of other residues through induced polarization. Table 1 gives statistics of computed interactions. The average absolute difference in the interaction free energy over all pairs of titratable residues is just 5·10⁻⁴ kcal·mol⁻¹ for the protein 1a2p, and values of a similar magnitude were found for the other proteins in the data set. The maximum absolute difference in $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ due to the protein protonation state is less than or equal to 0.15 kcal·mol⁻¹ for all protein except SNase variant Δ+PHS (PDB reference code 3bdc) and ribonuclease A (PDB reference code 3rn3). In SNase the large effect on the interaction is observed for the pair Tyr91-Glu75. This is explained by the fact that these residues directly interact with other titratable residues: Tyr91 makes a hydrogen bond with Asp77, and Glu 75 interacts with Tyr93 and His121. Deprotonation of these residues has a strong effect on the polarization of Tyr91 or Glu75 due to strong and unfavorable electrostatic interactions. In fact, we expect this effect to be smaller if the protein flexibility is taken into account and these pairs are allowed to rearrange upon titration. The maximum variation in $W_{\mu \nu }^{x_{\mu },x_{\nu }}$ in SNase excluding this pair is less than 0.1 kcal·mol⁻¹. Overall, we find that the effect of the induced polarization on interactions between ionizable residues due to the protein protonation state to be negligible for the eight proteins in the data set thereby allowing this term to be calculated based on a single protonation state of the system.

Table 1.

Absolute difference in the interaction free energies due to randomly-generated variations in the protein protonation state. Calculations used the protein dielectric constant of two and the Drude force field. Energies are given in kcal·mol⁻¹.

Protein	Abs. difference
	Max	Average
1a2p	0.15	0.0005
1pga	0.06	0.0006
1ppf	0.02	0.0004
2lzt	0.02	0.0001
2trx	0.05	0.0003
3bdc	0.34	0.0009
3rn3	0.24	0.0003
4pti	0.01	0.0001

Contribution of the polarization on background atoms induced by titration

Next the polarization effect of background atoms due to changes in protonation state of titratable residues on computed pK_a's was examined. This polarization contributes directly to interactions between titratable residues and background atoms, i.e. to the term $G_{\text{Born/back},\mu }^{x_{\mu }}$, as well as changes the interactions of background atoms with themselves $G_{\text{BB}}(\overline{x})$. To test if $G_{\text{BB}}(\overline{x})$ can significantly influence the population of the protonated versus deprotonated forms of a titratable residue we computed $G_{\text{BB}}(\overline{x})$ with different protonation states of the protein as follows. First, the most likely protein protonation state $\overline{x}$ was computed at the pH where a titratable residue is half protonated with a protein dielectric constant of 4. $G_{\text{BB}}(\overline{x})$ were then computed for all residues from the data set and all possible protonation states with the correct polarization, i.e. the polarization computed in the first step presented in the Methods section. The results are given in Table 2. As can be seen $G_{\text{BB}}(\overline{x})$ depends on the protonation state of titratable residues only moderately. For all studied proteins, the average values of $G_{\text{BB}}(\overline{x})$ are close to those obtained through solution of the system of equations 9. For example, for lysozyme (PDB 1a2p), the standard deviation of $G_{\text{BB}}(\overline{x})$ due to residue protonation states is just 0.3 kcal·mol⁻¹. Further analysis demonstrated that the largest variations in $G_{\text{BB}}(\overline{x})$ are associated with either interactions with arginines treated as background non-titratable atoms in the present work or very unfavorable interactions with the background atoms, explained by the fact that no explicit relaxation is taken into account. Thus, the results in Table 2 indicate that the polarization of the background charges induced by titration can be neglected in the calculation of $G_{\text{BB}}(\overline{x})$ for pK_a calculations thereby avoiding recalculation of this term for all protonation states.

Table 2.

Average contribution of background charges, $G_{\text{BB}}(\overline{x})$, to the calculated total free energy (kcal·mol⁻¹).

protein	Aexact GBB	BGBBsol
1a2p	−467.3 (0.3)	−467.3
1pga	−29.6 (0.2)	−29.5
1ppf	−156.8 (0.1)	−156.7
2lzt	−1092.6 (0.3)	−1092.5
2trx	−117.8 (0.2)	−117.8
3bdc	−443.3 (0.3)	−443.3
3rn3	−524.1 (0.9)	−524.2
4pti	−465.1 (0.1)	−465.2

^AThe average value of the exact $G_{\text{BB}}(\overline{x})$ computed for the most populated protonation states for each titratable residue in the proteins; standard deviations are given in parenthesis

^B$G_{\text{BB}}(\overline{x})$ obtained as a solution to the system of equations 9.

pK_a calculation with the Drude-PB model

Comparison to the exact solution

Initially, the method for pK_a calculations with the Drude model was tested on a simple system with fewer titration sites, for which the direct application of Equation 4 is still feasible. Lysozyme (PDB reference code 2LZT) was chosen as a test protein. To allow the application of Equation 4 only aspartates and glutamates were considered in the calculations as titratable and all other titratable residues were fixed in the standard protonation state at physiological pH, i.e. lysines and tyrosines protonated. Only one syn orientation for the proton in the protonated form was considered. With 7 aspartic and 2 glutamic acids, it gives 512=2⁹ possible protonation states. The structures corresponding to all possible protonation states were generated, and Drude particles were fully optimized in the field of the PB implicit solvation model in each of the structures. The internal dielectric constant of two was used. The total free energies were used to compute an average number of bound protons using Equation 4. pK_a's were estimated as the pH where residues were half-protonated on average. pK_a's were also calculated using the new method.

For the lysozyme system the new method converged within two self-consistent iterations as computed pK_a's were invariant with more iterations. The results indicate that the computed pK_a's with the new method and two iterations are practically identical to those estimated with the exact form of Equation 4. The RMS deviation between pK_a's computed with the two methods is just 0.02 pH units. pK_a's computed with one iteration of the new method differ more from the ones computed with the exact statistical approach, by 0.07 pH units.

pK_a calculations were performed with the protein dielectric constant of 4 and the Drude-PB model for all 8 proteins. The self-consistent iterations were repeated four times. The results for the pK_a calculations versus the experimental values as well as subsequent iterations as a function of the number of iterations are given in Table 3. The RMS deviation between pK_a's computed after the second iteration relative to those after the first iteration is 0.15 pH units, and reduces to 0.10 and 0.08 pH units after the third and the fourth iterations, respectively. However, that RMS deviation between computed and experimental pK_a’s only changes insignificantly from 1.94 to 1.93 pH units after the second iteration and stays practically the same after the third and fourth iterations. The linear correlation between computed and experimental pK_a's, R, does not improve. However, the computed pK_a's slightly change as a function of the number of iterations. Importantly, the difference between the first and subsequent iterations is that the polarization is inconsistent in the first round of pK_a calculations, but it is improved in the subsequent iterations. Though we find only a moderate change due to the consistent treatment of the polarization, it may be attributed, at least in part, to the lack of the protein flexibility in this work. In the following sections, all results of pK_a calculations with the Drude-PB model will be presented using two iterations, since the computed pK_a's change less than 0.1 pH units with more iterations and the exact pK_a's were reached within two iterations for the reduced lysozyme system.

Table 3.

Convergence of the pK_a calculation method with the Drude-PB model. Calculations were done using the protein dielectric constant of 4.

Iteration	aRMSD	bRMSD	bcorrelation	bmax ∣error∣
1	-	1.94	0.71	5.53
2	0.15	1.93	0.70	5.64
3	0.10	1.93	0.70	5.64
4	0.08	1.93	0.70	5.64

^aRMS deviation between pK_a's computed in this step and in the previous step

^brelative to the experimental pK_a's

Comparison of the polariable Drude and additive C36 force fields.

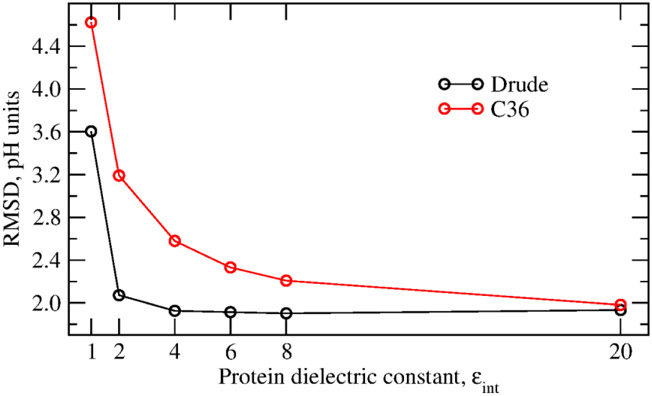
To test the dependence of the result on the internal dielectric constant, pK_a calculations were performed with ε_p in the range between 1 and 20 with the Drude and C36 force fields. For the calculations with the Drude force field, the resulting pK_a’s were taken after the second self-consistent iteration. For the calculations with C36, only one iteration is required as electronic polarization is included implicitly. The results are summarized in Table 4. The computed and experimental pK_a shifts are given in Table S3, and absolute pK_a's are given in Table S4 in the Supplementary Information. Figure 2 shows the dependence of the RMS deviation against the internal dielectric constant. The correlation is best with both models at the internal dielectric constant of two. However, in contrast to the results obtained with the C36 force field, with the Drude model the RMS deviation is characterized by a shallow minimum at ε in the range of 4-8. With the additive force field, the RMS deviation is improving monotonically in the tested range of ε. Overall, the Drude model demonstrates a better agreement with the experimental pK_a's than the C36 model at low values of the dielectric constant. The RMS deviation between the experimental pK_a's and pK_a's computed using the protein dielectric of two is 2.07 and 3.19 units with the Drude and C36 force fields, respectively. With the protein dielectric constant of four, the RMS deviation is 1.93 and 2.58 units with the Drude and C36 force field, respectively. With the Drude-PB model, the RMS deviation between the experimental pK_a's and pK_a's computed with the protein dielectric constant of 20 is 1.93, which is very close to the result of 1.93 and 2.07 units computed with the protein dielectric constant of four and two, respectively. In contrast to the results with the additive C36 model, the RMS deviation computed with the Drude-PB model is substantially less sensitive to the choice of the internal dielectric constant. However, with the Drude model, the RMS deviation sharply increases with an internal protein dielectric constant ε_p =1, and the linear correlation decreases to 0.46. A Drude-PB model with ε_p = 1 accounts only for the induced polarization, leaving out all contributions from structural fluctuations. The poor performance suggests that such a model does not represent the protein interior as sufficiently polarizable. Interestingly, the RMS deviation for the Drude model with ε_p = 1 is very similar to the RMS deviation for the additive force field with ε_p ≈ 1.7, a value that corresponds roughly to the expected dielectric constant associated with electronic induced polarization.

Table 4.

Performance of the methods for pK_a calculations against experimental pK_a‘s. RMS deviation and linear correlation coefficient between computed and experimental pK_a shifts from the model compound reference values are given.

Protein dielectric, εp	RMSD		Correlation		ASlope
	Drude	C36	Drude	C36	Drude	C36
1	3.57	4.62	0.46	0.71	1.8	3.6
2	2.07	3.19	0.71	0.74	1.7	2.6
4	1.93	2.58	0.70	0.73	1.5	2.0
6	1.91	2.33	0.67	0.71	1.4	1.7
8	1.90	2.21	0.64	0.68	1.3	1.5
20	1.93	1.98	0.53	0.57	1.0	1.1

^AThe slope of the liner fit to the computed and experimental pK_a shifts.

Figure 2.

RMS deviation between experimental and computed pK_a’s. pK_a’s with the Drude force field were calculated using two iterations to determine the most probable protonation microstates.

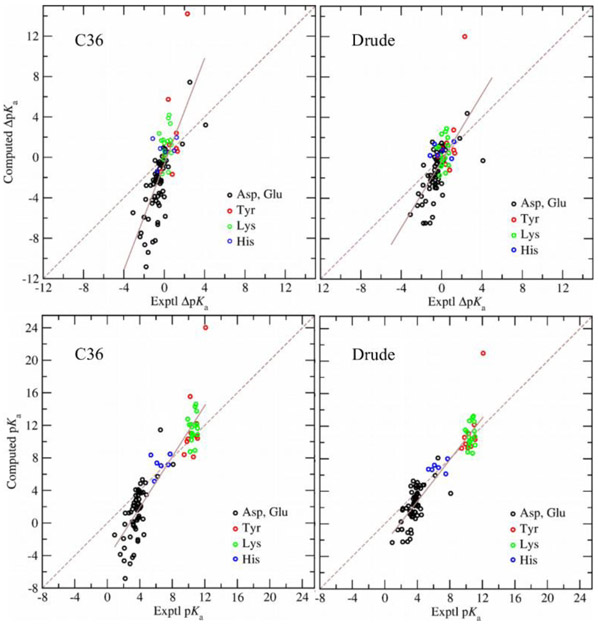
Figure 3 gives the comparison between experimental and predicted pK_a shifts with the protein dielectric constant of two and the Drude and C36 models. As may be seen, with both Drude and C36 models computed pK_a shifts are both systematically underestimated and overestimated relative to the experimental values, so that a linear fit has a constant positive slope. This slope is also given in Table 2 as a function of the protein dielectric constant. However, the pK_a computed with the Drude model are systematically less over and underestimated in comparison with the results obtained with the C36 model. The slope with the internal dielectric constant of two is 1.7 and 2.6 with the Drude and C36 models, respectively. The slope is decreasing with the higher protein dielectric constant and with ε_int = 20 it is practically 1.0 with both models. Figure 3 also contains comparison of the absolute computed and experimental pK_a values. The correlation coefficients for the absolute pK_a’s were 0.93 and 0.91 for the Drude and C36 force fields, respectively. These values are higher than those for the pK_a shifts reported in Table 4 due to the wider range of absolute pK_a’s associated with the different classes of residues.

Figure 3.

Experimental vs computed pK_a shifts and absolute pK_a's. Left panels: (upper) pK_a shifts and (lower) absolute pK_a's computed with the C36 force field; right panels: (upper) pK_a shifts and (lower) pK_a's computed with the Drude force field after iteration 2. In both calculations, the protein dielectric constant of two was used. The solid line shows the linear fit to the data; the dashed line shows the perfect match between computed and experimental pK_a shifts or pK_a's.

Table 5 gives the comparison between pK_a shifts computed with the Drude and C36 models. With the low internal dielectric constant of two, the RMS deviation between pK_a shifts of the titratable residues in the eight proteins computed with the two methods is 1.78 units and decreases with the higher dielectric constant values. With ε_int = 20, the pK_a shifts computed by the two methods are very close with the RMS deviation of just 0.34 units. The linear correlation between pK_a shifts computed by the two methods is 0.92 and 0.99 with ε_int = 2 and ε_int = 20, respectively. This further demonstrates that at the high internal dielectric constant pK_a's computed with the C36 model converge to those obtained with the polarizable Drude model. This result may be understood by the fact that with the high dielectric constant, electrostatic interactions are screened strongly, and thus polarization contributions due to those interactions are expected to be smaller. In other words, with the high internal dielectric constant, protein polarization is close to that observed in individual residues in solvent, so the difference in polarization observed in solvent and in the protein plays a smaller role in pK_a calculations in accordance with the thermodynamic cycle in Figure 1.

Table 5.

Comparison between pK_a shifts computed using the Drude and additive C36 models. RMS deviation and linear correlation coefficient between pK_a shifts computed with the Drude and C36 model are given. pK_a shifts computed with the Drude model were taken after two iterations in the method.

Protein dielectric constant, εp	RMSD	Correlation
2	1.78	0.92
4	0.93	0.97
6	0.68	0.98
8	0.58	0.98
20	0.34	0.99

The agreement between experimental and computed pK_a shifts for different residue types is given in Table 6. pK_a's were computed using the C36 and Drude force fields and the dielectric constant of 2. For all residue types, the RMS deviation with the Drude force field is better than with the additive force field. The RMS deviation is 3.23 units for tyrosines with the Drude force field, which is higher than the RMS deviation obtained for the other types. A similar result was obtained with the C36 force field. This may be due to the need for larger conformational rearrangements of the protein to occur upon changes in the protonation state of tyrosines, since they are larger than other residues and are frequently buried in the protein. The poorer correlations for His and Lys with both force fields may indicate the need for larger conformation changes of those sidechains upon changes in protonation. Further studies are required to address these issues.

Table 6.

Performance of the methods for pK_a calculations against experimental pK_a‘s for different types of residues. RMS deviation and correlation coefficient between computed and experimental pK_a shifts.

Residue	N sites	RMSD		Correlation
		Drude	C36	Drude	C36
Asp	31	2.10	3.40	0.66	0.78
Glu	30	2.01	3.40	0.65	0.64
His	6	1.18	1.41	0.18	0.27
Tyr	10	3.23	4.25	0.73	0.69
Lys	17	1.38	1.88	0.19	0.23

Proton orientation in the protonated form of carboxylic acids

The majority of constant pH studies to date have limited treatment of the orientation of the proton in neutral carboxylic acids to the syn form,²⁸ omitting consideration of the anti orientation, which is known to be accessible in condensed phase environments.²⁹ To investigate if this approximation may be limiting the accuracy of the pK_a estimates of acidic residues we undertook calculations of the carboxylic acid pK_a with and without consideration of the anti proton orientation in the protonated form of carboxylic acids. Calculations with the dielectric constant of two and only with the syn orientation of proton were performed and compared with the results of calculations considering both syn and anti positions of protons. The results were obtained using the Drude-PB model and after the second iteration. Results are summarized in Table 7. The average population of the anti protonated form for all aspartates and glutamates in the protein data set at a very low pH of 0, where practically all carboxylic acids are protonated, is 27.6%; for aspartic acids, this population is 34.0% and 19.5% for glutamic acids. Accordingly, inclusion of the anti orientation leads to a large improvement in the predicted pK_a's relative to the experimental values. For aspartates the RMS deviation is improved from 2.87 units considering only the syn orientations to 2.10 units when allowing both syn and anti rotamers. A similar improvement is observed for glutamates. In barnase (PDB reference code 1a2p), the large improvement with the anti orientation was found for residue Asp101. Both oxygens of Asp101 participate in hydrogen bond interactions with the backbone and sidechain of Thr105 and the sidechain of Thr99. These hydrogen bond interactions make energetically unfavorable the placement of proton in the syn orientation in the protonated form Asp101. Thus, the calculated pK_a shift of Asp101 is −6.7 pK_a units if only the syn orientations are considered, and −3.8 pK_a units if both syn and anti orientations are included. The latter value agrees better with the experimental value of −2.0 pK_a units for Asp101. However, as Asp101 as well as other acid moieties may change their orientation upon protonation. The improvement in the pK_a prediction needs to be addressed in future studies with methods that allow for conformational changes to occur upon changes in protonation state.

Table 7.

RMS deviation and correlation between computed and experimental pK_a’s. Calculations were performed using the syn and anti rotamers or only the syn rotamers for the proton in the protonated form of carboxylic acids. The Drude-PB model was used with the protein dielectric constant of two.

Residue	N sites	RMSD		Correlation
		syn/anti	only syn	syn/anti	only syn
Asp	31	2.10	2.87	0.65	0.68
Glu	30	2.01	2.82	0.65	0.63
All	94	2.07	2.60	0.67	0.69

Comparison to other methods

Assuming the null hypothesis,³⁰ i.e. that all residues have their solution pK_a in the protein environment, the RMS deviation with the experimental pK_a's is 1.16 pH units, lower than the RMS deviation obtained with the C36 or Drude force field. This implies that increasing electrostatic screening, in principle would improve the RMS deviation, since absolute pK_a shifts become smaller.

We first compare to the results of the H++ server, which uses a single-conformation version of the MEAD program for pK_a calculations.³¹ The server only provides pK_a's for the range between 0 and 12 pH units. Thus, the comparison will be limited to pK_a's within this range (70 values total). In principle, H++ relies on the same method that we used for the calculations with the additive C36 force field, but uses the AMBER force field and van der Waals radii defined by Bondi.³² With the internal dielectric constant of 4 and implicit salt concentration of 0, the RMS deviation between the experimental and computed pK_a's using the H++ server is 1.55 pH units, and the linear correlation coefficient is 0.65. The RMS deviation for the same 70 pK_a values computed using ε_int = 4 and the C36 force field and the radii specifically optimized previously for PB calculations³³ is 2.08 pH units and the linear correlation coefficient is 0.59. However, the Bondi radii are significantly smaller than the Born radii derived by Nina et al³³ that were optimized targeting explicit solvent molecular dynamics simulations with an internal dielectric constant of 1. For example, the radius of the OH oxygen of tyrosine is 1.85 Å and 1.5 Å in the Nina et al³³ and Bondi sets, respectively. The radius of Nδ and Nε of the protonated form of histidine is 2.3 Å and 1.55 Å in Nina et al and Bondi sets respectively. With the C36 force field and Bondi radii and ε_int = 4 and the molecular surface as the dielectric boundary (the water probe radius of 1.4 Å), the RMS deviation with the experimental pK_a's is 1.06 with a linear correlation of 0.70. However, with the Bondi radii, the absolute solvation energies of small molecules are significantly overestimated. The RMS deviation between computed and experimental absolute solvation free energies for the set of small molecules that was used in our previous study¹⁵ to optimize the Drude PB radii is 4.1 kcal·mol⁻¹, while with the optimized set of radii from Nina et al³³ the RMS deviation is 2.5 kcal·mol⁻¹. In the continuum dielectric model, the induced charges in the solvent continuum dielectric medium are located within an infinitesimal layer at the boundary of the solute volume. In contrast, the solvent charge density in an atomic model is distributed over a microscopic region of space of finite dimension.³³ Thus, the PB model with the van der Waals radii and dielectric constant of one significantly overestimates solvation energies. The radii that were optimized specifically to reproduce results of molecular dynamics free energy simulations are significantly larger than the Bondi (van der Waals) radii. Similar to using the higher internal dielectric constant, using smaller atomic radii significantly increases solvent screening leading to smaller absolute pK_a shifts and, thus giving a lower RMS deviation.

The reported pK_a's computed with the MCCE2 method^7c were used to compare with the results of the current work. MCCE2 introduces the conformational relaxation and uses the Poisson-Boltzmann model for electrostatic calculations, which involves approximations to the protein-solvent boundary, and uses the PARSE charges and radii.³⁴ The PARSE charges and radii were optimized to reproduce experimental solvation energies, but with the dielectric constant of two. Thus, like van der Waals radii, the PARSE radii are significantly smaller than the radii optimized with the internal dielectric constant of 1. For example, the radius of the OH oxygen of tyrosine is 1.85 Å and 1.5 Å in Nina et al³³ and PARSE sets, respectively. The radius of Nδ and Nε of the protonated form of histidine is 2.3 Å and 1.5 Å in Nina et al³³ and PARSE sets, respectively. The RMS deviation computed for the MCCE2 results obtained with ε_int = 4 that do not include the SNase variant Δ+PHS protein and Tyr53 in Lysozyme is 0.75 pH units with the linear correlation of 0.78. With the C36 force field and Bondi radii and ε_int = 4 using the same titratable residue sets the RMS deviation is 1.42 pH units and the linear correlation is 0.73. With the Nina et al radii the RMS deviation is 2.36 pH units and the linear correlation is 0.68. Overall, this demonstrates that the PB model strongly depends on the atomic Born radii, which is entirely expected.^{33, 35}

Conclusion

In this study, a new method to estimate pK_a of titratable residues is presented that uses the polarizable Drude-PB model and constant-pH Monte Carlo simulations. The main challenge in using the polarizable Drude-PB model, as well as any other polarizable PB force field, is due to the dependence of the energy terms on the electronic polarization of the entire system, which in turn depends on the protonation state of all protein residues. As this represents a large computational increase in the calculation of energy matrices used in the constant-pH simulations an additional approximation is required to make the calculation feasible, which we propose and implement in the present work. In this approximation, only the polarization of the highly populated protein protonation microstates (ie. when the pH is equivalent to the pK_a of the residue associated with those microstates) are treated explicitly using the corresponding protein protonation state in conjunction with optimization of the Drude particles as required to model the polarization response. The method necessitates self-consistent calculations of the most populated microstates and residue pK_a's, since the pK_a's are needed to define the most populated microstates and vice versa. A numerical test with a small protein, lysozyme, shows that the pK_a's computed with the new method differ by only 0.02 pH units from the ones estimated with the exact statistical approach, demonstrating that polarization effects are correctly included in the MC simulations.

The present method with the Drude-PB model considerably increases the computational cost relative to the calculations with the C36 additive force field. The extra cost is arising, first due to the need to compute the solute polarization, i.e. optimize the position of Drude particles for each protonation state of all residues. To optimize the position of the Drude particles, the solvent reaction field due to the PB implicit solvent model in the current implementation is allowed to fully relax after each minimization step to calculate solvent forces. In the previous work, we demonstrated that the optimization of the Drude particles converges within 50 minimization steps. Second, additional cost is due to the need to calculate the most populated microstates and pK_a's iteratively. The self-consistent approach converged within two iterations with pK_a’s computed after iteration 3 differing less than 0.1 pK_a units from pK_a’s after iteration 2. Thus, the SCF protocol of the pK_a calculation scheme increases the overall cost by two times. Overall, the method for pK_a calculations using the constant-pH simulations with the Drude force field takes an average of two orders of magnitude more CPU time than the standard protocol for the pK_a calculation with an additive force field and the PB solvation model. For example, the pK_a calculation for 3bdc, the protein with the largest number of titratable residues (44 residues) consumes approximately 2 CPU Hrs. with the additive force field versus 95 CPU Hrs. for the Drude force fields on an Intel Xeon E5-2630 type processor.

A significant improvement for the predicted pK_a's was observed with the Drude-PB model compared to results based on the additive force field C36 at low dielectric constants. Using the Drude-PB model with an internal protein dielectric constant of 2, the RMS deviation from the experimental pK_a's is 2.07 pK_a units. In contrast, the C36 additive force field yields a RMS deviation of 3.19 pK_a units with a dielectric constant of 2, and a RMSD of 2.58 pK_a units with a dielectric constant of 4. The RMS is still higher than with the Drude-PB model with a dielectric of 2. Notably, the results with the Drude force field are less sensitive to the choice of internal dielectric constant, with a higher protein dielectric constant of 4 and the Drude-PB model the RMS deviation is 1.93 pK_a units, close to 2.07 pK_a units obtained with ε_int = 2. We also observe that the pK_a's computed with the high internal dielectric constant of 20 are very similar for the two force fields with an RMS deviation of just 0.36 units and the linear correlation of 0.99. These results indicate that a model accounting explicitly for the induced polarization represents a physically more correct model that decreases the empirical requirement to ascribe an excessively high dielectric constant to the protein interior. Given the heterogeneity of the protein interior, it is likely that simply assigning a high dielectric constant to the protein interior cannot accurately substitute for an explicit treatment of polarization during protonation/deprotonation events.

An interesting observation was the better agreement with experimental pK_a’s when the anti protonated from of carboxylic acids was explicitly considered. This is due to a relatively high contribution from the anti protonated form of carboxylic acids of ~28% at a very low pH. However, the contribution of the anti orientation of the proton is expected to be impacted by the ability of the side chains as well as surrounding protein to relax upon protonation. This effect, as well as the impact of conformational flexibility on pK_a calculations using the polarizable model will be addressed in future studies.

The current implementation of the method for pK_a calculations with the Drude-PB models bears several limitations. Only polarization of one protonation microstate for each possible protonation state of all residues is computed exactly, while for minor microstates a surrogate of the energy components that include the residue interaction free energies and self-energies, corresponding to different pH’s is used. In principle, one can consider additional protonation microstates in energy matrix calculations, and use those energies in the MC simulations. However, the main limitation of the presented method is the lack of conformational relaxation and fluctuations, which is required to preserve a fixed protein dielectric boundary in the Poisson-Boltzmann calculations. Various approximations have been introduced in previous studies to circumvent this prescription.^{7c, 8a, 36} We will explore the presented Drude-PB method in combination with existing approximations to treat protein conformational changes in future studies.