Bayesian Network Marker Selection via the Thresholded Graph Laplacian Gaussian Prior

Abstract

Selecting informative nodes over large-scale networks becomes increasingly important in many research areas. Most existing methods focus on the local network structure and incur heavy computational costs for the large-scale problem. In this work, we propose a novel prior model for Bayesian network marker selection in the generalized linear model (GLM) framework: the Thresholded Graph Laplacian Gaussian (TGLG) prior, which adopts the graph Laplacian matrix to characterize the conditional dependence between neighboring markers accounting for the global network structure. Under mild conditions, we show the proposed model enjoys the posterior consistency with a diverging number of edges and nodes in the network. We also develop a Metropolis-adjusted Langevin algorithm (MALA) for efficient posterior computation, which is scalable to large-scale networks. We illustrate the superiorities of the proposed method compared with existing alternatives via extensive simulation studies and an analysis of the breast cancer gene expression dataset in the Cancer Genome Atlas (TCGA).

1. Introduction

In biomedical research, complex biological systems are often modeled or represented as biological networks (Kitano, 2002). High-throughput technology such as next generation sequencing (Schuster, 2007), mass spectrometry (Aebersold and Mann, 2003) and medical imaging (Doi, 2007) has generated massive datasets related to those biological networks. For example, in omics studies, a biological network may represent the interactions or dependences among a large set of genes/proteins/metabolites; and the expression data are a number of observations at each node of the network (Barabási et al., 2011). In neuroimaging studies, a biological network may refer to the functional connectivity among many brain regions or voxels; and the neural activity can be measured at each node of the network. In many biomedical studies, one important research question is given a known network, to select informative nodes from tens of thousands of candidate nodes that are strongly associated with the disease risk or other clinical outcomes (Greicius et al., 2003). We refer to these informative nodes as network markers (Kim et al., 2012; Peng et al., 2014; Yuan et al., 2017) and the selection procedure as network marker selection. One promising solution is to perform network marker selection under regression framework where the response variable is the clinical outcome and predictors are nodes in the network. The classical variable selection (George and McCulloch, 1993; Fan and Li, 2001) in the regression model can be considered as a special case of the network marker selection, where the variable refers to the nodes in a network without edges.

For variable selection in regression models, many regularization methods have been proposed with various penalty terms, including the least absolute shrinkage and selection operator or the L₁ penalty (Tibshirani, 1996; Zou, 2006, LASSO), elastic-net or the L₁ plus L₂ penalty (Zou and Hastie, 2005), the Smoothly Clipped Absolute Deviation penalty (Fan and Li, 2001, SCAD), the minimax concave penalty (Zhang, 2010, MCP) and so on. Several network constrained regularization regression approaches have been developed to improve selection accuracy and increase prediction power. One pioneering work is the graph-constrained estimation (Li and Li, 2008, Grace), which adopts the normalized graph Laplacian matrix to incorporate the network dependent structure between connected nodes. As an extension of Grace, the adaptive Grace (Li and Li, 2010, aGrace) makes constraints on the absolute values of weighted coefficients between connected nodes. Alternatively, an L_γ norm group penalty (Pan et al., 2010) and a fused LASSO type penalty (Luo et al., 2012) have been proposed to penalize the difference of absolute values of coefficients between neighboring nodes. Instead of imposing constraints on coefficients between neighboring nodes, an L₀ loss to penalize their selection indicators (Kim et al., 2013) has been proposed, leading to a non-convex optimization problem for parameter estimation, which can be solved by approximating the non-continuous L₀ loss using the truncated lasso penalty (TLP).

In addition to frequentist approaches, Bayesian variable selection methods have received much attention recently with many successful applications. The Bayesian methods are natural to incorporate the prior knowledge and make posterior inference on uncertainty of variable selection. A variety of prior models have been studied, such as the spike and slab prior (George and McCulloch, 1993), the LASSO prior (Park and Casella, 2008), the Horseshoe prior (Polson and Scott, 2012), the non-local prior (Johnson and Rossell, 2012), the Dirichlet Laplace prior (Bhattacharya et al., 2015) and more. To incorporate the known network information, Stingo et al. (2011) employed a Markov random field to capture network dependence and jointly select pathways and genes; and Chekouo et al. (2016) adopted a similar approach for imaging genetics analysis. Zhou and Zheng (2013) proposed rGrace, a Bayesian random graph-constrained model to combine network information with empirical evidence for pathway analysis. A partial least squares (PLS) g-prior was developed in Peng et al. (2013) to incorporate prior knowledge on gene-gene interactions or functional relationship for identifying genes and pathways. Chang et al. (2016) proposed a Bayesian shrinkage prior which smoothed shrinkage parameters of connected nodes to a similar degree for structural variable selection.

The Ising model is another commonly used Bayesian structural variable selection method. It has been used as a prior model for latent selection indicators that lay on an undirected graph characterizing the local network structure. They are especially successful for variable selection over the grid network motivated by some applications, for example, the motif finding problem (Li and Zhang, 2010) and the imaging data analysis (Goldsmith et al., 2014; Li et al., 2015). However, it is very challenging for fully Bayesian inference on the Ising model over the large-scale network due to at least two reasons: 1) The posterior inference can be quite sensitive to the hyperparameter specifications in the Ising priors based on empirical Bayes estimates or subjective prior elicitation in some applications. However, fully Bayesian inference on those parameters is difficult due to the intractable normalizing constant in the model. 2) Most posterior computation algorithms, such as the single-site Gibbs sampler and the Swendsen-Wang algorithm, incur heavy computational costs for updating the massive binary indicators over large-scale networks with complex structures. It worth noting that, different from using the known network structure for variable selection, Dobra (2009); Kundu et al. (2015); Liu et al. (2014) and Peterson et al. (2016) also proposed Bayesian structured variable selection without using a known network structure.

To address limitations of existing methods, we propose a new prior model: the thresholded graph Laplacian Gaussian (TGLG) prior, to perform network marker selection over the large-scale network by thresholding a latent continuous variable attached to each node. To model the selection dependence over the network, all the latent variables are assumed to follow a multivariate Gaussian distribution with mean zero and covariance matrix constructed by a normalized graph Laplacian matrix. The effect size of each node is modeled through an independent Gaussian distribution.

Threshold priors have been proposed for Bayesian modeling of sparsity in various applications. Motivated by the analysis of financial time series data, Nakajima and West (2013a) and Nakajima and West (2013b) proposed a latent threshold approach to imposing dynamic sparsity in the simultaneous autoregressive models (SAR). Nakajima et al. (2017) further extended this type of models for the analysis of Electroencephalography (EEG) data. To analyze neuroimaging data, Shi and Kang (2015) proposed a hard-thresholded Gaussian process prior for image-on-scalar regression; and Kang et al. (2018) introduced a soft-thresholded Gaussian process for scalar-on-image regression. To construct the directed graphs in genomics applications, Ni et al. (2017) adopted a hard threshold Gaussian prior in a structural equation model. However, all the existing threshold prior models do not incorporate the useful network structural information, and thus are not directly applicable to the network marker selection problem of our primary interest.

In this work, we propose to build the threshold priors using the graph Laplacian matrix, which has been used to capture the structure dependence between neighboring nodes (Li and Li, 2008; Zhe et al., 2013; Li and Li, 2010). Most of those frequentist methods directly specify the graph Laplacian matrix from the existing biological network. Liu et al. (2014) has proposed a Bayesian regularization graph Laplacian (BRGL) approach which utilizes the graph Laplacian matrix to specify a priori precision matrix of regression coefficients. However, BRGL is fundamentally different from our method in that it is one type of continuous shrinkage priors for regression coefficients which have quite different prior supports compared with our TGLG priors. BRGL were developed only for linear regression and its computational cost can be extremely heavy for large-scale networks. In addition, there is lack of theoretical justifications for BRGL when the large-scale network has a diverging number of edges and nodes.

Our method is a compelling Bayesian approach to variable selection with a known network structure. The TGLG prior has at least four markable features: 1) Fully Bayesian inference for large-scale networks is feasible in that the TGLG prior does not involve any intractable normalizing constants. 2) Posterior computation can be more efficient, since the TGLG-based inference avoids updating the latent binary selection indicators and instead updates the latent continuous variables, to which many existing approximation techniques can be potentially applied. 3) The graph Laplacian matrix (Chung, 1997; Li and Li, 2008; Zhe et al., 2013) based prior can incorporate the topological structure of the network which has been adopted in genomics. 4) The TGLG prior enjoys the large support for Bayesian network marker selection over large-scale networks, leading to posterior consistency of model inference with a diverging number of nodes and edges under the generalized linear model (GLM) framework.

The remainder of the manuscript is organized as follows. In Section 2, we introduce the TGLG prior and propose our model for network marker selection under the GLM framework. In Section 3, we study the theoretical properties for the TGLG prior and show the posterior consistency of model inference. In Section 4, we discuss the hyper prior specifications and the efficient posterior computation algorithm. We illustrate the performance of our approach via simulation studies and an application on the breast cancer gene expression dataset from The Cancer Genome Atlas (TCGA) in Section 5. We conclude our paper with a brief discussion on the future work in Section 6.

2. The Model

Suppose the observed dataset includes a network with p_n nodes, one response variable and q confounding variables. For each node, we have n observations. For observation i, i = 1, … , n, let y_i be the response variable, x_i = (x_i1, ⋯ , x_ipn)^T be the vector of nodes and z_i = (z_i1, ⋯ , z_iq)^T be the vector of confounding variables. Denote by $D_n=\{{\mathbf{z}}_i,{\mathbf{x}}_i,y_i{\}}_{i=1}^n$ the dataset. We write the number of nodes as p_n to emphasize on the diverging number of nodes in our asymptotical theory. Drop subscript i to have generic notation for a response variable y, a vector of nodes x and a vector of confounders z. Generalized linear model (GLM) is a flexible regression model to relate a response variable to a vector of nodes and confounding variables. The GLM density function for (y, x, z) with one natural parameter is:

$$f^{\ast }(y,h^{\ast })=\text{exp}\{a(h^{\ast })y+b(h^{\ast })+c(y)\},$$ (1)

where h* = z^T ω* + x^T β* is the linear parameter in the model, ω* and β* are true coefficients that generate data, a(h) and b(h) are continuous differentiable functions. The true mean function is

$${\mu }^{\ast }=\mathrm{E}(y\mid \mathbf{z},\mathbf{x})=-b^{\prime }(h^{\ast })∕a^{\prime }(h^{\ast })\equiv g^{-1}({\mathbf{z}}^{\mathrm{T}}{\omega }^{\ast }+{\mathbf{x}}^{\mathrm{T}}{\beta }^{\ast }),$$

where g⁻¹(·) is an inverse link function, which can be chosen according to the specific type of the response variable. For example, one can choose the identity link for the continuous response and the logit link for the binary response.

In (1), coefficient vector ω is a nuisance parameter to adjust for the confounder effects, for which we assign a Gaussian prior with mean zero and independent covariance, i.e. ω ~ N(0, ${\sigma }_{\omega }^2{\mathbf{I}}_q$) for ${\sigma }_{\omega }^2>0$. Here I_d represents an identity matrix of dimension d for any d > 0. Coefficient vector β represents the effects of nodes on the response variable. Here we perform network marker selection by imposing sparsity on β. To achieve this goal, we develop a new prior model for β: the thresholded graph Laplacian Gaussian (TGLG) prior. Suppose the observed network can be represented by a graph G, with each vertex corresponding to one node in the network. Let j ~ k indicate there exists an edge between vertices j and k in G. Let d_j represent the degree of vertex j, i.e., the number of nodes that are connected to vertex j in G. Denote by L = (L_jk) a p_n × p_n normalized graph Laplacian matrix, i.e. L_jk = 1 if j = k and d_j ≠ 0, $L_{jk}=-1∕\sqrt{d_j{d}_k}$ if j ~ k, and L_jk = 0 otherwise. For any d > 0, denote by 0_d an all zero vector of dimension d. For any λ, ε, ${\sigma }_{\alpha }^2$, ${\sigma }_{\gamma }^2>0$, we consider an element-wise decomposition of β for the prior specifications:

$$\beta =\alpha \circ {\mathbf{t}}_{\lambda }(\gamma ),\gamma \sim \mathrm{N}\{0_{p_n},{\sigma }_{\gamma }^2(\mathbf{L}+\epsilon {\mathbf{I}}_{p_n}{)}^{-1}\},\alpha \sim \mathrm{N}(0_{p_n},{\sigma }_{\alpha }^2{\mathbf{I}}_{p_n}).$$ (2)

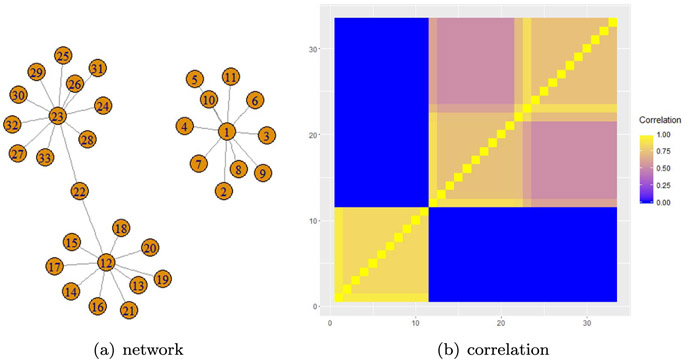
Here α = (α₁, … , α_pn)^T represents the effect size of nodes. The operator ”ο” is the element-wise product. The vector thresholding function is t_λ (γ) = {I(∣γ₁∣ > λ), … , I(∣γ_pn∣ > λ)}^T, where $I(\mathcal{A})$ is the event indicator with $I(\mathcal{A})$ = 1 if $\mathcal{A}$ occurs and $I(\mathcal{A})=0$ otherwise. The latent continuous vector γ = (γ₁, … γ_pn)^T controls the sparsity over graph G. We refer to (2) as the TGLG prior for β, denoted as β ~ TGLG (λ, ε, ${\sigma }_{\gamma }^2$, ${\sigma }_{\alpha }^2$). The TGLG prior implies that for any two nodes j and k, γ_j and γ_k are conditionally dependent given others if and only if j ~ k over the graph G. In this case, their absolute values are more likely to be smaller or larger than a threshold value λ together. This further implies that nodes j and k are more likely to be selected as network marker or not selected together if j ~ k. Figure 1 shows an example of a graph and the corresponding correlation matrix of γ for ε = 10⁻², where the γ’s of connected vertices are highly correlated.

Figure 1:

An example of the graph and the corresponding correlation matrix of γ that was constructed from the inverse graph Laplacian matrix.

There are four hyperparameters in the TGLG prior model. The threshold λ controls a priori the sparsity. When λ → 0, all the nodes tend to be selected. When λ → ∞, none of them will be selected. The parameter ε determines the impact of the network on the sparsity. When ε → ∞, γ’s of connected vertices tend to be independent while they tend to be perfectly correlated when ε → 0. The two variance parameters ${\sigma }_{\gamma }^2$ and ${\sigma }_{\alpha }^2$ control the prior variability of the latent vectors γ and α respectively. Note that ${\sigma }_{\gamma }^2$ and λ are not completely identifiable, but for some specifications they can affect much the sparsity of β_j’s in prior specifications. For example, when 3σ_γ is much smaller than λ, the prior probability of zero β_j can be close to one. On the other hand, for any positive σ_γ, when λ close to zero, β_j is nonzero with a high prior probability.

Now we discuss how to specify the hyperparameters. For variance terms ${\sigma }_{\gamma }^2$ and ${\sigma }_{\alpha }^2$, we use the conjugate prior model by assigning the Inverse-Gamma distribution IG(a_γ, b_γ) and IG(a_α, b_α) respectively. We fix ${\sigma }_{\omega }^2$ as a large value. We assign the uniform prior to the threshold parameter λ, i.e. λ ~ Unif(0, λ_u) with upper bound λ_u > 0. We choose a wide range by set λ_u = 10 in the rest of manuscript. For parameter ε, we can either assign an log-normal prior (logε ~ N (μ_ε, ${\sigma }_{\epsilon }^2$)) or set as a fixed small value.

3. Theoretical Properties

In this section, we examine the theoretical properties of TGLG prior based network marker selection under the GLM framework. In particular, we establish the posterior consistency with a diverging number of nodes in the large-scale networks.

Let ξ ⊂ {1, 2, ⋯ , p_n} denote the set of selected node indices, i.e. I(∣γ_j∣ > λ) = 1, if j ∈ ξ, I(∣γ_j∣ > λ) = 0, otherwise. The number of nodes in ξ is denoted as ∣ξ∣. For a model ξ = (i₁, ⋯ , i_∣ξ∣), denote by β_ξ = (β_i1, ⋯ , β_i∣ξ∣)^T the coefficient of interest, respectively. Let π(ξ, dβ_ξ, dω) represent the joint prior probability measure for model ξ, parameters β_ξ and confounding coefficients ω. Their joint posterior probability measure conditional on dataset D_n is:

$$\pi (\xi ,d{\beta }_{\xi },d\omega \mid D_n)=\frac{{\prod }_{i=1}^{n}f(y_i,h_i)\pi (\xi ,d{\beta }_{\xi },d\omega )}{{\sum }_{{\xi }^{\prime }}{\int }_{{\beta }_{{\xi }^{\prime }}}{\prod }_{i=1}^{n}f(y_i,h_i)\pi ({\xi }^{\prime },d{\beta }_{{\xi }^{\prime }},d\omega )},$$

where f(y_i, h_i) = exp{a(h_i)y_i + b(h_i) + c(y_i)} is the density function of y_i given x_i and z_i based on GLM with $h_i={\mathbf{z}}_i^{\mathrm{T}}\omega +{\mathbf{x}}_i^{\mathrm{T}}\beta$. We examine asymptotic properties of the posterior distribution of the density function f regarding to the Hellinger distance (Jiang, 2007; Song and Liang, 2015) under some regularity conditions. The Hellinger distance d(f₁, f₂) between two density functions f₁(x, y) and f₂(x, y) is defined as

$$d(f_1,f_2)={\left[\int \int {\left\{f_1^{1∕2}(x,y)-f_2^{1∕2}(x,y)\right\}}^{2}dxdy\right]}^{1∕2}.$$

We list all the regularity conditions in the Appendix. We show that the TGLG prior and the proposed model enjoy the following properties:

Theorem 1 (Large Support for Network Marker Selection). Assume a sequence ϵ_n ∈ (0, 1] with $n{ϵ}_n^2\to \infty$ and a sequence of nonempty models ξ_n. Assume conditions (C1)–(C3) and (C7) hold. Given ${\sigma }_{\alpha }^2$ and ${\sigma }_{\gamma }^2$, for any sufficiently small η > 0, there exists N_η such that for all n > N_η, we have

$$\pi (\xi ={\xi }_n)\ge e^{-n{ϵ}_n^2∕128}and$$ (3)

$$\pi ({\beta }_{\xi }\in B({\xi }_n,\eta )\mid \xi ={\xi }_n)\ge e^{-n{ϵ}_n^2∕128}withB({\xi }_n,\eta )=\{{\beta }_j^{\ast }\pm \eta {ϵ}_n^2∕\mid {\xi }_n\mid {\}}_{j\in {\xi }_n}.$$ (4)

There exists C_n > 0, such that for all sufficiently large n and for any j ∈ ξ_n:

$$\pi (\mid {\beta }_j\mid >C_n\mid {\xi }_n)\le e^{-n{ϵ}_n^2∕4}.$$ (5)

This theorem shows that the TGLG prior has a large support for the network marker selection. Particularly, (3) states that the TGLG prior can select the true network marker with a positive prior probability bounded away from zero, (4) ensures that the prior probability of the coefficients falling within an arbitrarily small neighborhood of the true coefficients with probability bounded away from zero, and (5) indicates a sufficiently small tail probability of the TGLG prior.

Theorem 2 (Posterior Consistency for Network Marker Selection). For the GLM with bounded covariates, i.e. ∣x_j∣ ≤ M for all j = 1, ⋯ , p_n and ∣z_k∣ ≤ M for all k = 1, ⋯ , q, suppose the true node regression coefficients satisfy

$$\underset{n\to \infty }{\text{lim}}\sum _{j=1}^{p_n}\mid {\beta }_j^{\ast }\mid <\infty .$$

Let ϵ_n ∈ (0, 1] be a sequence such that $n{ϵ}_n^2\to \infty$. Assume conditions (C1)–(C7) hold. Then we have the following results:

1. Posterior consistency:

   $$\underset{n\to \infty }{\text{lim}}\mathrm{P}\{\pi [d(f,f^{\ast })\le {ϵ}_n\mid D_n]\ge 1-2e^{-n{ϵ}_n^2∕64}\}=1,$$ (6)

   where f is the density function sampled from the posterior distribution and f* is the true density function.

2. For all sufficiently large n:

$$\mathrm{P}\{\pi [d(f,f^{\ast })>{ϵ}_n\mid D_n]\ge 2e^{-n{ϵ}_n^2∕64}\}\le 2e^{-n{ϵ}_n^2∕64}.$$ (7)

1. For all sufficiently large n:

$$\mathrm{E}\{\pi [d(f,f^{\ast })>{ϵ}_n\mid D_n]\}\le 4e^{-n{ϵ}_n^2∕32}.$$ (8)

Probability measure P and expectation E are both with respect to data D_n that are generated from the true density f*.

This theorem establishes the posterior consistency of network marker selection. In particular, (6) implies that the posterior distribution of density f concentrates on an arbitrarily small neighborhood of the true density f* under the Hellinger distance with a large probability. This probability converges to one as sample size n → ∞. (7) provides the convergence rate of the posterior distribution indicating how fast the tail probability approaches to zero. (8) indicates the average convergence rate of the posterior distribution of density f concentrating on the arbitrarily small neighborhood of the true density f*.

Please refer to the Supplementary File 1 (Cai et al., 2018a) for proofs of Theorems 1 and 2.

4. Posterior Computation

Our primary goal is to make posterior inference on regression coefficients for network markers, i.e. β. According to the model specification, the sparsity of β_j is determined by the sparsity of α_j and whether ∣γ_j∣ is less than λ or not, i.e. I(β_j = 0) = I(α_j = 0)I(∣γ_j∣ ≤ λ). Since α_j has a non-sparse normal prior, the posterior inclusion probability of node j is just equal to the posterior probability of ∣γ_j∣ being greater than λ; and given β_j ≠ 0, the effect-size can be estimated by E(β_j∥γ_j∣ > λ, D_n). All other parameters in the model can be estimated by its posterior expectations.

To simulate the joint posterior distribution for all parameters, we adopt an efficient Metropolis-adjusted Langevin algorithm (MALA) (Roberts and Rosenthal, 1998) for posterior computation. We introduce a smooth approximation for the thresholding function:

$$I(\mid {\gamma }_j\mid >\lambda )\simeq \frac{1}{2}\left\{1+\frac{2}{\pi }\text{arctan}\left(\frac{{\gamma }_j^2-{\lambda }^2}{{\epsilon }_0}\right)\right\}\text{for}{\epsilon }_0\to 0,$$

leading to the analytically tractable first derivative:

$$\frac{\partial {\beta }_j}{\partial {\gamma }_j}={\alpha }_j\frac{2{\gamma }_j∕{\epsilon }_0}{\pi (1+({\gamma }_j^2-{\lambda }^2{)}^2∕{\epsilon }_0^2)}.$$

We choose ε₀ = 10⁻⁸ in the simulation studies and real data application in this article.

Denote by f(y_i ∣ ω, α, γ, λ) the likelihood function for all the parameters of interest for observation i. Let φ(x ∣ μ, Σ) denote the density function of a multivariate normal distribution with mean μ and covariance matrix Σ and φ₊(x ∣ μ, μ_l, μ_u, τ²) denote the density of a truncated normal distribution N₊(μ, μ_l, μ_u, τ²) density with mean μ, variance τ² and interval [μ_l, μ_u]. Let $V_{\omega }={\sigma }_{\omega }^2{I}_q$ be the variance of the prior distribution for ω. Let Λ_γ = (L + εI_pn)⁻¹. To update λ, it is natural to use the random walk with a normal distribution as the proposal distribution. As we have a uniform prior specifications for λ, we use the truncated normal distribution to improve the sample efficiency, since the candidate sample falls in the same range in the prior specifications. Our choices are λ_l = 0 and λ_l = 10. The proposal variances ${\tau }_{\gamma }^2$, ${\tau }_{\alpha }^2$, ${\tau }_{\omega }^2$ and are all adaptively chosen by tuning acceptance rates to 30% for random walk and 50% for MALA in simulation studies and 15% for random walk and 30% for MALA in real data analysis. Our choice of the acceptance rate takes into account the general theoretical results on the optimal scaling of random walk (Roberts et al., 1997) and MALA (Roberts and Rosenthal, 1998; Roberts et al., 2001). However, the log-likelihood of our model involves both smooth and discontinuous functions, which do not satisfy the regularity conditions of the general theoretical results. Thus, we have made slight changes in the theoretical optimal acceptance rates according to our numerical experiments. See Algorithm 1 for the details of our posterior updates.

Algorithm 1 Posterior updates within each iteration.

$$\begin{gathered} \begin{array}{cc}\hfill & \mathrm{Input}:\text{the parameters from the last iteration}\hfill \\ \hfill & \mathrm{Output}:\text{the updated parameters for the next iteration}\hfill \\ \hfill & \\ 1:\text{Draw}{\omega }^{\ast }\sim \mathrm{N}(\omega ,{\tau }_{\omega }^2{I}_q).\text{Update}\omega ={\omega }^{\ast }\text{with probability}\hfill \\ \hfill & \text{min}\left\{1,\frac{\varphi ({\omega }^{\ast }\mid 0,V_{\omega }){\prod }_{i}f(y_i\mid {\omega }^{\ast },•)}{\varphi (\omega \mid 0,V_{\omega }){\prod }_{i}f(y_i\mid \omega ,•)}\right\}.\hfill \\ \hfill & \\ 2:\text{Draw}{\gamma }^{\ast }\sim \mathrm{N}\{\mu (\gamma ),{\tau }_{\gamma }^2{I}_p\},\text{where}\mu (\gamma )=\gamma +\frac{{\tau }_{\gamma }^2}{2}(\frac{\partial \log f}{\partial \gamma }-\frac{1}{2}{\sigma }_{\gamma }^2{\Lambda }_{\gamma }\gamma )\text{with}\frac{\partial \log f}{\partial {\gamma }_j}=\hfill \\ \hfill & \\ {\sum }_{i=1}^n(a^{\prime }({\mathbf{z}}_i^{\mathrm{T}}\omega +{\mathbf{x}}_i^{\mathrm{T}}\beta )+b^{\prime }({\mathbf{z}}_i^{\mathrm{T}}\omega +{\mathbf{x}}_i^{\mathrm{T}}\beta ))x_{ij}\frac{\partial {\beta }_j}{\partial {\gamma }_j}.\text{Update}\gamma ={\gamma }^{\ast }\text{with probability}\hfill \\ \hfill & \text{min}\left\{1,\frac{\varphi (\gamma \mid \mu ({\gamma }^{\ast }),{\tau }_{\gamma }^2{I}_p)\varphi ({\gamma }^{\ast }\mid 0,{\sigma }_{\gamma }^2{\Lambda }_{\gamma }){\prod }_{i}f(y_i\mid {\gamma }^{\ast },•)}{\varphi ({\gamma }^{\ast }\mid \mu (\gamma ),{\tau }_{\gamma }^2{I}_p)\varphi (\gamma \mid 0,{\sigma }_{\gamma }^2{\Lambda }_{\gamma }){\prod }_{i}f(y_i\mid \gamma ,•)}\right\}.\hfill \\ \hfill & \\ 3:\text{Update}\xi =\{j:\mid {\gamma }_j\mid >\lambda \}.\hfill \\ \hfill & \\ 4:\text{For}j\notin \xi ,\text{draw}{\alpha }_j\sim \mathrm{N}(0,{\sigma }_{\alpha }^2).\text{Draw}{\alpha }_{\xi }^{\ast }\sim \mathrm{N}\{\mu ({\alpha }_{\xi }),{\tau }_{\alpha }^2{I}_{\mid \xi \mid }\},\text{where}\mu ({\alpha }_{\xi })=\hfill \\ \hfill & \\ {\alpha }_{\xi }+\frac{{\tau }_{\alpha }^2}{2}(\frac{\partial \log f}{\partial {\alpha }_{\xi }}-\frac{1}{2}{\Sigma }_{\xi }{\alpha }_{\xi })\text{with}\frac{\partial \log f}{\partial {\alpha }_j}={\sum }_{i=1}^n(a^{\prime }({\mathbf{z}}_i^{\mathrm{T}}\omega +{\mathbf{x}}_i^{\mathrm{T}}\beta )+b^{\prime }({\mathbf{z}}_i^{\mathrm{T}}\omega +{\mathbf{x}}_i^{\mathrm{T}}\beta ))x_{ij}\hfill \\ \hfill & \\ \text{for}j\in \xi \text{and}{\Sigma }_{\xi }={\sigma }_{\alpha }^2{I}_{\mid \xi \mid }.\text{Update}{\alpha }_{\xi }={\alpha }_{\xi }^{\ast }\text{with probability}\hfill \\ \hfill & \\ \text{min}\left\{1,\frac{\varphi ({\alpha }_{\xi }\mid \mu ({\alpha }_{\xi }^{\ast }),{\tau }_{\alpha }^2{I}_{\mid \xi \mid })\varphi ({\alpha }_{\xi }^{\ast }\mid 0,{\Sigma }_{\xi }){\prod }_{i}f(y_i\mid {\alpha }_{\xi }^{\ast },•)}{\varphi ({\alpha }_{\xi }^{\ast }\mid \mu ({\alpha }_{\xi }),{\tau }_{\alpha }^2{I}_{\mid \xi \mid })\varphi ({\alpha }_{\xi }\mid 0,{\Sigma }_{\xi }){\prod }_{i}f(y_i\mid {\alpha }_{\xi },•)}\right\}.\hfill \\ \hfill & \\ 5:\text{Draw}{\sigma }_{\gamma }^2\sim \text{IG}({\tilde{a}}_{\gamma },{\tilde{b}}_{\gamma })\text{where}{\tilde{a}}_{\gamma }=a_{\gamma }+\frac{p}{2}\text{and}{\tilde{b}}_{\gamma }=b_{\gamma }+\frac{{\gamma }^{\mathrm{T}}{\Lambda }_{\gamma }^{-1}\gamma }{2}.\hfill \\ \hfill & \\ 6:\text{Draw}{\sigma }_{\alpha }^2\sim \text{IG}({\tilde{a}}_{\alpha },{\tilde{b}}_{\alpha })\text{where}{\tilde{a}}_{\alpha }=a_{\alpha }+\frac{p}{2}\text{and}{\tilde{b}}_{\alpha }=b_{\alpha }+\frac{{\sum }_j{\alpha }_j^2}{2}.\hfill \\ \hfill & \\ 7:(\text{Optional})\text{Draw}{\epsilon }^{\ast }\sim N(\epsilon ,{\tau }_{\epsilon }^2).\text{Update}\epsilon ={\epsilon }^{\ast }\text{with probability}\hfill \\ \hfill & \\ \text{min}\left\{1,\frac{\mid \mathbf{L}+{\epsilon }^{\ast }{\mathbf{I}}_{p_n}{\mid }^{\frac{1}{2}}\epsilon \text{exp}\{-{\epsilon }^{\ast }{\gamma }^T\gamma ∕(2{\sigma }_{\gamma }^2)-(\log {\epsilon }^{\ast }-{\mu }_{\epsilon }{)}^2∕(2{\sigma }_{\epsilon }^2)\}}{\mid \mathbf{L}+\epsilon {\mathbf{I}}_{p_n}{\mid }^{\frac{1}{2}}{\epsilon }^{\ast }\text{exp}\{-\epsilon {\gamma }^T\gamma ∕(2{\sigma }_{\gamma }^2)-(\log \epsilon -{\mu }_{\epsilon }{)}^2∕(2{\sigma }_{\epsilon }^2)\}}\right\}.\hfill \\ \hfill & \\ 8:(\text{Optional})\text{Draw}{\lambda }^{\ast }\sim N_{+}(\lambda ,{\lambda }_l,{\lambda }_u,{\tau }_{\lambda }^2).\text{Update}\lambda ={\lambda }^{\ast }\text{with probability}\hfill \\ \hfill & \\ \text{min}\left\{1,\frac{{\varphi }_{+}(\lambda \mid {\lambda }^{\ast },{\lambda }_l,{\lambda }_u,{\tau }_{\lambda }^2){\prod }_{i}f(y_i\mid {\lambda }^{\ast },•)}{{\varphi }_{+}({\lambda }^{\ast }\mid \lambda ,{\lambda }_{\lambda },{\lambda }_u,{\tau }_{\lambda }^2){\prod }_{i}f(y_i\mid \lambda ,•)}\right\}.\hfill \end{array} \end{gathered}$$

Denote by $\{{\gamma }^{(i)},{\alpha }^{(i)},{\lambda }^{(i)}{\}}_{i=1}^N$ the MCMC samples obtained after burn-in. We estimate the posterior inclusion probability for node j(j = 1, ⋯ , p_n) by

$$\widehat{\text{Pr}}({\beta }_j\ne 0\mid D_n)=\frac{1}{N}\sum _{i=1}^{N}I\{\mid {\gamma }_j^{(i)}\mid >{\lambda }^{(i)}\}.$$

According to Barbieri et al. (2004), we select the informative nodes with at least 50% inclusion probability, denote by $\widehat{M}=\{j:\widehat{\text{Pr}}({\beta }_j\ne 0\mid D_n)>0.5\}$ the indices of all the informative nodes. To estimate regression coefficients of informative nodes, we choose the estimated conditional expectation of β_j given β_j ≠ 0 by

$$\widehat{\mathrm{E}}\{{\beta }_j\mid {\beta }_j\ne 0,D_n\}=\frac{{\sum }_{i=1}^N{\alpha }_j^{(i)}I(\mid {\gamma }_j^{(i)}\mid >{\lambda }^{(i)})}{{\sum }_{i=1}^{N}I\{\mid {\gamma }_j^{(i)}\mid >{\lambda }^{(i)}\}},\text{for}j\in \widehat{M}.$$

5. Numerical Studies

We conduct simulation studies to evaluate performance of the proposed methods compared with existing methods for different scenarios.

5.1. Small Simple Networks

Following settings in Li and Li (2008), Zhe et al. (2013) and Kim et al. (2013), we simulate small simple gene networks consisting of multiple subnetworks, where each subnetwork contains one transcription factor (TF) gene and 10 target genes that are connected to the TF gene; and two of the subnetworks are set as the true network markers. We consider two types of true network markers. In Type 1 network marker, TF and all 10 target genes are informative nodes; see Figure 2(a). In Type 2 network marker, TF and half of target genes are informative nodes; see Figure 2(b). For each informative node, the magnitude of the effect size, β, is simulated from Unif(1, 3) and its sign is randomly assigned as positive or negative.

Figure 2:

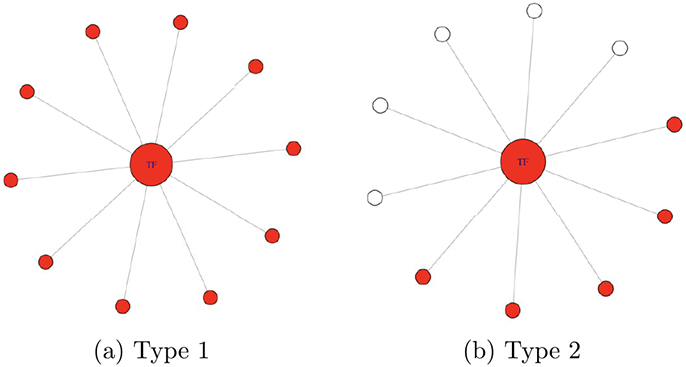
Two types network markers in the simulated small simple networks, where true informative nodes are marked in red. In Type 1 network marker, TF and all target genes are informative nodes. In Type 2 network marker, TF and half of target genes are informative nodes.

In each subnetwork, the covariate variables for 11 nodes, i.e., the expression levels of the TF gene and 10 target gene, are jointly generated from a 11-dimensional multivariate normal distribution with zero mean and unit variance, where the correlation between the TF gene and each target gene is 0.5; and the correlation between any two different target genes is 0.25. We assume the covariate variables are independent across different subnetworks.

To generate the response variable given the true network markers, we consider binary and continuous cases, where the continuous response variable is generated from linear regression, i.e. y ~ N(Xβ, ${\sum }_i{\beta }_i^2∕3$); and the binary response is generated from logistic regression, i.e. Pr(y = 1) = 1/{1 + exp(−Xβ)}.

We consider two scenarios for the number of subnetworks: 3 and 10; the corresponding numbers of nodes, p = 33 and p = 110 respectively. For the network with Type 1 markers, the number of informative nodes is 22; For the network with Type 2 markers, the number of informative nodes is 12. We generate 50 datasets for each scenario. For linear regression, each dataset contains 100 training samples and 100 test samples; for logistic regression, each dataset contains 200 training samples and 200 test samples.

We compare the proposed TGLG approach with the following existing methods: Lasso (Tibshirani, 1996), Elastic-net (Zou and Hastie, 2005), Grace (Li and Li, 2008), aGrace (Li and Li, 2010), L_∞ and aL_∞ (Luo et al., 2012), TTLP and LTLP (Kim et al., 2013), BRGL (Liu et al., 2014) and Ising model (Goldsmith et al., 2014; Li et al., 2015). For the hyper priors in the TGLG approach, we assign weakly informative priors: ${\sigma }_{\gamma }^2$ ~ IG(0.01, 0.01), ${\sigma }_{\alpha }^2$ ~ IG(0.01, 0.01). For all the regularized approaches, we adopt three-fold cross validations to choose tuning parameters. For the Ising prior model, we specify the priors as

$$p(\gamma )=\zeta (a,b)\text{exp}\left[a\sum _i{\gamma }_i+\sum _i\left\{\sum _{j\in N_i}bI({\gamma }_i={\gamma }_j)\right\}\right]$$

and β_i∣γ_i = 1 ~ N(0, ${\sigma }_{\beta }^2$), where N_i denotes the neighbor nodes set of node i. For hyper prior specifications in Ising model, we fix a = −2 and choose b from 2, 5, 7 and 10 based on model performance. We implement a single-site Gibbs sampler for Ising model. For BRGL by Liu et al. (2014), the network markers are selected when the posterior probability $\mathrm{P}(\mid {\beta }_j\mid >\sqrt{\text{Var}({\beta }_j)}\mid D_n)$ exceeds 0.5.

To evaluate posterior sensitivity to the prior specification of γ in TGLG, we consider three cases. 1) TGLG-I: assign a network-independent prior for γ, i.e., γ ~ N{0_p, ${\sigma }_{\gamma }^2{I}_p$); 2) TGLG-F: fix ε = 10⁻⁵ and 3) TGLG-L: assign a log-normal prior to ε, i.e., log ε ~ N(−5, 9).

For all the Bayesian methods, we run 30,000 MCMC iterations with the first 20,000 as burn-in. We also check the MCMC convergences by running five chains and computing the Gelman-Rubin diagnostics. For all the Bayesian methods, the estimated 95% CI of the potential scaled reduction factors for the deviance is [1.0, 1.0], indicating the convergence of the MCMC algorithm. To compare the performance of different methods, we compute true positives, false positives and the area under the curve (AUC) for true network markers recovery, prediction mean squared error (PMSE) for linear regression and classification error (CE) for logistic regression regarding to outcome. We report the mean and standard error over 50 datasets for each metric we choose to compare in the result table.

Table 1 summarizes the results for linear regression under different settings. In most cases, TGLG approaches with incorporating network structure achieve a smaller PMSE, smaller number of false positives with a comparable amount of true positives compared with other methods. For the Ising model, we only report the results in the case of b = 7 since it has an overall best performance among all choices of b values. In fact, the performance of the Ising model varies greatly for different choices of values for b and it may perform very bad with an inappropriate value of b. Table 3 shows the mean computation time over 50 datasets for Ising model and TGLG. It shows that our method is much more computationally efficient than the Ising model, especially for the large-scale networks.

Table 1:

Simulation results for linear regression. PMSE: prediction mean squared error. TP: true positives, FP: false positives; number of informative nodes in Type 1 network is 22; number of informative nodes in Type 2 network is 12.

Method	PMSE	TP	FP	AUC	PMSE	TP	FP	AUC
	Type 1 p = 33				Type 1 p = 110
Lasso	52.3(1.6)	20.6(0.2)	7.3(0.3)	0.778(0.006)	71.6(1.9)	17.2(0.3)	19.6(1.2)	0.792(0.005)
Elastic-net	50.9(1.4)	21.8(0.1)	10.4(0.2)	0.788(0.004)	73.7(1.8)	19.6(0.3)	46.6(2.9)	0.811(0.004)
Grace	56.8(1.5)	21.6(0.1)	10.1(0.2)	0.864(0.007)	87.5(2.0)	17.9(0.4)	37.5(2.5)	0.897(0.004)
aGrace	53.7(1.5)	22.0(0.0)	10.7(0.1)	0.875(0.007)	76.4(2.1)	20.6(0.3)	65.9(3.6)	0.899(0.005)
L∞	51.4(1.5)	21.8(0.1)	8.9(0.4)	0.970(0.006)	66.5(1.7)	21.5(0.2)	22.7(1.5)	0.973(0.005)
aL∞	54.2(1.3)	21.8(0.1)	8.2(0.6)	0.669(0.034)	63.5(1.5)	21.5(0.2)	19.6(1.4)	0.946(0.010)
TTLP	54.3(1.6)	21.9(0.0)	10.1(0.4)	0.834(0.019)	72.6(2.0)	20.9(0.4)	44.2(4.6)	0.920(0.004)
LTLP	51.3(1.2)	22.0(0.0)	8.8(0.6)	0.933(0.005)	67.1(1.7)	21.5(0.2)	57.6(2.7)	0.897(0.009)
BRGL	51.0(1.3)	19.5(0.2)	4.1(0.3)	0.883(0.008)	79.7(1.8)	17.9(0.2)	22.1(0.9)	0.867(0.006)
Ising(b=7)	54.9(3.0)	19.7(0.7)	2.9(0.7)	0.925(0.017)	94.9(5.9)	15.1(0.9)	33.9(2.4)	0.786(0.023)
TGLG-I	50.1(1.3)	21.9(0.1)	10.7(0.2)	0.863(0.010)	81.4(2.1)	14.8(0.5)	22.6(2.6)	0.779(0.009)
TGLG-F	45.2(1.2)	22.0(0.0)	2.2(0.6)	0.912(0.032)	63.9(2.8)	19.7(0.4)	17.8(2.9)	0.899(0.016)
TGLG-L	46.0(1.3)	21.9(0.1)	1.7(0.5)	0.968(0.016)	74.1(2.4)	17.1(0.5)	19.3(2.7)	0.847(0.013)
	Type 2 p =33				Type 2 p = 110
Lasso	23.1(0.6)	11.7(0.1)	11.8(0.6)	0.830(0.006)	30.6(0.8)	9.5(0.2)	19.1(1.1)	0.826(0.007)
Elastic-net	23.4(0.6)	11.8(0.1)	15.4(0.6)	0.802(0.006)	31.4(0.9)	10.6(0.2)	34.0(2.1)	0.818(0.006)
Grace	25.8(0.6)	11.4(0.1)	14.7(0.6)	0.813(0.005)	35.2(0.8)	9.1(0.2)	25.8(1.9)	0.855(0.005)
aGrace	25.9(0.7)	12.0(0.0)	20.3(0.3)	0.868(0.006)	32.8(0.8)	11.6(0.1)	73.0(3.5)	0.895(0.007)
L∞	23.8(0.6)	11.9(0.1)	17.2(0.6)	0.812(0.005)	30.3(0.7)	11.3(0.2)	28.9(1.9)	0.928(0.005)
aL∞	26.1(0.7)	11.9(0.1)	16.9(0.6)	0.643(0.018)	30.6(0.6)	11.3(0.2)	27.1(1.7)	0.893(0.009)
TTLP	25.9(0.8)	12.0(0.0)	20.0(0.5)	0.801(0.008)	32.2(0.8)	11.6(0.2)	64.3(5.2)	0.923(0.004)
LTLP	24.7(0.7)	12.0(0.0)	20.4(0.4)	0.825(0.008)	30.6(0.7)	11.7(0.2)	75.1(3.6)	0.864(0.006)
BRGL	23.7(0.6)	11.4(0.1)	7.3(0.4)	0.938(0.007)	37.7(0.9)	9.9(0.1)	23.8(1.1)	0.876(0.008)
Ising(b=7)	27.8(1.5)	9.9(0.5)	11.6(0.8)	0.855(0.024)	45.8(2.6)	7.6(0.6)	44.5(2.0)	0.709(0.032)
TGLG-I	23.7(0.6)	10.8(0.2)	8.0(0.9)	0.918(0.006)	33.9(0.9)	7.2(0.3)	7.6(1.5)	0.829(0.011)
TGLG-F	22.8(0.6)	11.4(0.1)	10.2(0.7)	0.901(0.015)	28.7(1.1)	10.5(0.3)	14.2(2.1)	0.922(0.012)
TGLG-L	22.3(0.6)	11.6(0.1)	8.9(0.6)	0.930(0.008)	28.8(0.9)	8.8(0.3)	6.4(1.1)	0.908(0.011)

Table 3:

Average computing time with standard error in seconds for Ising model and TGLG based network marker selection. All the computations run on a desktop computer with 3.40 GHz i7 CPU and 16 GB memory.

		Linear regression		Logistic regression
		Ising	TGLG	Ising	TGLG
p = 33	Type 1	140.1(0.5)	21.5(0.2)	230.1(7.6)	26.7(0.3)
	Type 2	140.1(0.5)	21.0(0.3)	229.9(7.6)	26.4(0.2)
p = 110	Type 1	1191.4(7.1)	31.7(0.2)	1210.1(10.1)	37.7(1.0)
	Type 2	1153.4(8.5)	30.6(0.1)	1203.6(8.4)	36.5(0.9)

As for the three cases of adopting TGLG approaches, TGLG-L has the best overall performance regarding to the PMSE and false positives. TGLG-F tends to have a larger false positive than TGLG-L and TGLG-I, since selection variables for connected nodes are highly dependent when fixed ε = 10⁻⁵. However, TGLG-F still has a smaller PMSE than TGLG-I. Compared with TGLG-I, TGLG-L has smaller false positives and PMSE in most cases. These facts show that incorporating network structure can improve model prediction performance of TGLG in linear regression.

Table 2 summarizes the results for the logistic regression under different simulation settings. Here the TGLG is only compared with Lasso, Elastic-net and the Ising model. For Type 1 network, the Ising model has a smaller number of false positives than all three TGLG approaches. However, the Ising model has a larger prediction error and a smaller number of true positives. In all other scenarios, TGLG outperforms the Ising model. Table 3 demonstrates the TGLG approach is much more computational efficient than the Ising model in Logistic regression. In addition, TGLG-F and TGLG-L have a smaller number of false positives and classification error than TGLG-I in most cases, which indicates that including network structure could improve model performance in logistic regression.

Table 2:

Simulation results for logistic regression with sample size 200. CE: classification error (number of incorrect classification); TP: true positive; FP: false positive; number of Type 1 true network markers: 22; number of Type 2 true network markers: 12.

Method	CE	TP	FP	AUC	CE	TP	FP	AUC
	Type 1 p = 33				Type 1 p = 110
Lasso	20.8(0.7)	21.2(0.1)	6.9(0.4)	0.811(0.004)	30.8(1.1)	19.1(0.4)	25.1(1.7)	0.836(0.004)
Elastic-net	21.0(0.8)	21.4(0.1)	8.4(0.4)	0.818(0.004)	32.6(0.8)	19.9(0.2)	29.4(2.1)	0.848(0.003)
Ising(b=5)	39.2(3.0)	15.2(1.2)	0.0(0.0)	0.937(0.011)	47.6(4.1)	13.5(1.1)	10.2(2.9)	0.826(0.031)
TGLG-I	19.2(0.6)	21.9(0.1)	10.0(0.2)	0.877(0.011)	30.5(0.9)	17.1(0.3)	16.0(1.4)	0.851(0.008)
TGLG-F	19.4(0.7)	21.8(0.1)	8.0(0.5)	0.858(0.021)	30.8(1.1)	17.6(0.4)	13.0(1.1)	0.870(0.007)
TGLG-L	18.7(0.7)	21.8(0.1)	7.5(0.5)	0.875(0.018)	30.4(1.0)	17.3(0.3)	13.4(1.1)	0.858(0.008)
	Type 2 p = 33				Type 2 p = 110
Lasso	25.2(0.9)	11.7(0.1)	10.1(0.7)	0.856(0.004)	32.7(1.0)	10.6(0.2)	22.7(2.2)	0.872(0.004)
Elastic-net	26.1(0.8)	11.9(0.0)	13.2(0.7)	0.796(0.004)	36.6(1.2)	10.5(0.3)	25.9(2.5)	0.849(0.004)
Ising(b=5)	27.4(1.4)	9.5(0.4)	7.2(0.4)	0.899(0.016)	37.7(2.8)	7.4(0.5)	9.0(1.7)	0.820(0.025)
TGLG-I	22.6(0.8)	11.4(0.1)	4.8(0.6)	0.961(0.007)	29.4(1.2)	9.7(0.3)	6.9(0.9)	0.897(0.0012)
TGLG-F	23.2(0.8)	11.5(0.1)	6.3(0.6)	0.941(0.010)	29.3(1.0)	9.9(0.3)	6.7(0.6)	0.903(0.010)
TGLG-L	22.1(0.8)	11.6(0.1)	5.8(0.7)	0.959(0.005)	28.6(1.0)	10.1(0.2)	6.2(0.8)	0.921(0.009)

5.2. Large Scale-Free Networks

We perform simulation studies on large scale-free networks, which are commonly used network models for gene networks. We simulate scale-free network (Barabási and Albert, 1999) with 1,000 nodes using R function barabasi.game in package igraph. In the simulated scale-free network, we set the true network markers by selecting 10 nodes out of 1,000 as the true informative nodes according to two criteria: 1) all the true informative nodes form a connected component (Hopcroft and Tarjan, 1973) in the network; 2) all the true informative nodes are disconnected, in which case the TGLG model assumption does not hold. For each informative node, the magnitude of the effect size is simulated from Unif(1, 3) and its sign is randomly assigned as positive or negative. Covariates X are generated from a multivariate normal distribution X ~ N(0, 0.3^D), where D is the shortest path distance matrix between nodes in the generated scale-free network. Response variable Y is generated using Y ~ N(Xβ, $\sum {\beta }_i^2∕3$) for linear regression and Pr(Y = 1) = 1/{1 + exp(−Xβ)} for logistic regression. According to the above procedure, we simulate 50 datasets with sample size 200.

We apply the aforementioned all three TGLG methods (TGLG-I, TGLG-F, TGLG-L) to each dataset compared with Lasso and Elastic-net. In addition, to evaluate the robustness of network structure mis-specifications, for each simulated scale-free network, we randomly select 20% of nodes and permute their labels; and then we apply TGLG-L with this mis-specified network. We refer to this approach as TGLG-M.

Table 4 reports the same performance evaluation metrics as Table 1 and Table 2. When the informative nodes form a connected component in the network, overall TGLG-L achieve the best performance regarding to PMSE or CE, and false positives. When the informative nodes are all disconnected, TGLG-L still has the best performance in linear regression, but is slightly worse than TGLG-I in logistic regression. This fact indicates that TGLG approaches is not sensitive to our model assumption regarding the true network markers. In both cases, TGLG-M performs worse than TGLG-L with correctly specified networks, but still better than Lasso and Elastic-net. This implies that the useful network information can improve the performance of TGLG, while TGLG-L is robust the network misspecification.

Table 4:

Simulation results for scale-free network. The number of true informative nodes is 10. Sample size is 200 and the number of nodes is 1,000.

Method	PMSE	TP	FP	AUC	CE	TP	FP	AUC
	Linear regression				Logistic regression
	True informative nodes form a connected component
Lasso	21.7(0.6)	9.5(0.1)	54.4(3.8)	0.936(0.004)	43.3(1.6)	8.4(0.2)	29.6(3.4)	0.771(0.028)
Elastic-net	23.2(0.7)	9.6(0.1)	69.0(3.9)	0.931(0.004)	57.9(2.4)	7.7(0.2)	22.4(3.2)	0.928(0.006)
TGLG-I	21.7(0.8)	9.1(0.1)	13.5(1.9)	0.950(0.007)	37.2(1.3)	7.7(0.2)	8.9(0.9)	0.892(0.011)
TGLG-F	21.8(0.9)	9.3(0.1)	14.6(1.5)	0.968(0.006)	35.2(1.3)	8.0(0.2)	7.8(0.9)	0.902(0.011)
TGLG-L	20.7(0.7)	9.1(0.1)	10.1(1.5)	0.957(0.006)	35.4(1.4)	7.9(0.3)	8.3(1.0)	0.893(0.011)
TGLG-M	21.2(0.8)	9.1(0.1)	11.3(1.5)	0.952(0.007)	37.1(1.3)	7.8(0.2)	9.3(1.1)	0.892(0.012)
	True informative nodes are all disconnected
Lasso	20.8(0.6)	9.8(0.1)	55.0(3.7)	0.940(0.003)	43.4(1.2)	8.9(0.2)	26.8(3.0)	0.824(0.028)
Elastic-net	22.2(0.7)	9.8(0.1)	68.6(3.9)	0.941(0.003)	55.7(1.9)	8.4(0.2)	27.3(4.0)	0.939(0.003)
TGLG-I	21.4(0.9)	9.4(0.1)	13.4(2.0)	0.974(0.006)	35.4(1.3)	8.6(0.2)	7.9(0.8)	0.931(0.009)
TGLG-F	21.7(0.8)	9.4(0.1)	16.7(1.9)	0.971(0.006)	35.5(1.4)	8.4(0.2)	7.8(0.9)	0.922(0.010)
TGLG-L	20.6(0.8)	9.6(0.1)	11.6(2.1)	0.980(0.004)	36.9(1.5)	8.5(0.2)	9.4(1.1)	0.925(0.009)
TGLG-M	21.3(0.9)	9.4(0.1)	11.4(1.7)	0.969(0.005)	35.3(1.2)	8.5(0.2)	8.4(0.9)	0.928(0.008)

5.3. Application to Breast Cancer Data from the Cancer Genome Atlas

In the real data application, we use the High-quality INTeractomes (HINT) database for the biological network (Das and Yu, 2012). We apply our method to the TCGA breast cancer (BRCA) RNA-seq gene expression dataset with 762 subjects and 10,792 genes in the network. The response variable we consider here is ER status – whether the cancer cells grow in response to the estrogen. The ER status is a molecular characteristic of the cancer which has important implications in prognosis. The purpose here is not focused on prediction. Rather we intend to find genes and functional modules that are associated with ER status, through which biological mechanisms differentiating the two subgroups of cancer can be further elucidated.

We code ER-positive as 1 and ER-negative as 0. We remove subjects with unknown ER status. In total, there are 707 subjects with 544 ER-positive and 163 ER-negative. We remove 348 gene nodes with low count number, which leaves us with 10,444 nodes. To apply our methods, we first standardize the gene nodes and then apply a logistic regression model for network marker selection. For prior settings, we use ${\sigma }_{\gamma }^2$ ~ IG(0.01, 0.01), ${\sigma }_{\alpha }^2$ ~ IG(0.01, 0.01) and ${\sigma }_{\omega }^2$ = 50. We fix λ at different grid values and choose λ = 0.004 by maximizing the likelihood values. The MCMC algorithms run 100,000 iterations with first 90,000 as burn-in and thin by 10. To perform the Gelman Rubin diagnostics, we run three chains with different initial values randomly drawn from priors and the upper bound of the 95% CI of the potential reduction scale factor for the model deviance is around 1.1, showing an acceptable MCMC convergence in terms of model fitting.

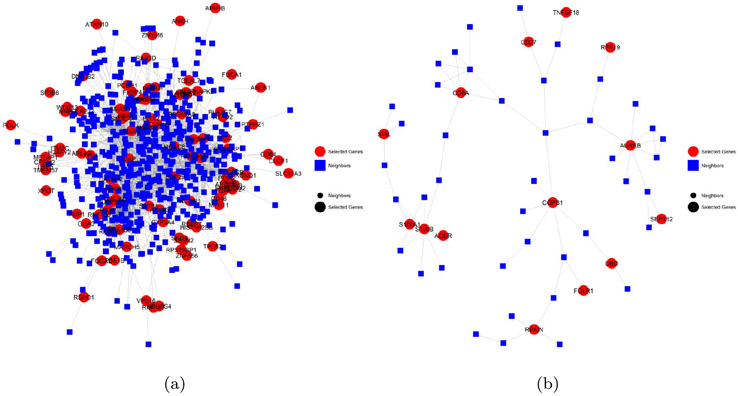
A total of 470 genes are selected as networks marker by our approach. To facilitate data interpretation, we conduct the community detection on the network containing the selected network markers and their one-step neighbors (Clauset et al., 2004). There is a total of eight modules that contain 10 or more selected genes. The plot of the modules, together with their over-represented biological process as identified using the ‘GOstats’ package (Falcon and Gentleman, 2007), are listed in Supplementary File 2 (Cai et al., 2018b).

Figure 3 shows two example network modules. The first example (Figure 3(a)) contains 95 selected gene network markers, including 14 that are connected with other network markers. The top 5 biological processes associated with these 95 genes are listed in Table 5. The most significant biological process that is over-represented by the selected genes in this module is regulation of cellular response to stress (p=0.00016), with 14 of the selected genes involved in this biological process. Besides the general connection between stress response and breast cancer, ER status has some specific interplay with various stress response processes. For example, breast cancer cells up-regulate hypoxia-inducible factors, which cause higher risk of metastasis (Gilkes and Semenza, 2013). Hypoxia inducible factors can influence the expression of estrogen receptor (Wolff et al., 2017). In addition, estrogen changes the DNA damage response by regulating proteins including ATM, ATR, CHK1, BRCA1, and p53 (Caldon, 2014). Thus it is expected that DNA damage response is closely related to ER status.

Figure 3:

Two example modules of selected genes.

Table 5:

Selected Goterm results for the two selected modules shown in Figure 3. The upper part is the Goterm results for Figure 3(a) and the lower part is the Goterm results for Figure 3(b).

GOBPID	Pvalue	Term
GO:0080135	0.0001618	regulation of cellular response to stress
GO:0044070	0.000381	regulation of anion transport
GO:0060969	0.0004409	negative regulation of gene silencing
GO:0055013	0.000757	cardiac muscle cell development
GO:0030888	0.0009629	regulation of B cell proliferation
GOBPID	Pvalue	Term
GO:0030097	0.00006398	hemopoiesis
GO:1902533	0.0003036	positive regulation of intracellular signal transduction
GO:0002250	0.0004063	adaptive immune response
GO:0032467	0.0004452	positive regulation of cytokinesis
GO:0070229	0.0005767	negative regulation of lymphocyte apoptotic process

Five other genes in this module are involved in the pathway of regulation of anion transport, which include the famous mTOR gene, which is implicated in multiple cancers (Le Rhun et al., 2017). The PI3K/AKT/mTOR pathway is an anticancer target in ER+ breast cancer (Ciruelos Gil, 2014). The other four genes, ABCB1 (Jin and Song, 2017), SNCA (Li et al., 2018), IRS2 (Yin et al., 2017) and NCOR1 (Lopez et al., 2016) are all involved in some other types of cancer.

In ER- breast cancer cells, the lack of ER signaling triggers the epigenetic silencing of downstream targets (Leu et al., 2004), which explains the significance of the biological process ”negative regulation of gene silencing”. Many genes in the ”cardiac muscle cell development” processes are also part of the growth factor receptor pathway, which has a close interplay with estrogen signaling (Osborne et al., 2005). Four of the genes fall into the process ” regulation of B cell proliferation”. Among them, AHR has been identified as a potential tumor suppressor (Formosa et al., 2017). ERα is recruited in AhR signaling (Matthews and Gustafsson, 2006). IRS2 responds to interleukin 4 treatment, and its polymorphism is associated with colorectal cancer risk (Yin et al., 2017). CLCF1 signal transduction was found to play a critical role in the growth of malignant plasma cells (Burger et al., 2003). It appears that these genes are found due to their functionality in signal transduction, rather than specific functions in B cell proliferation.

The second example is a much smaller module including 14 selected genes. Six of the 14 genes are involved in both hemopoiesis and immune system development (Table 5). They are all signal transducers. Among them, AGER is a member of the immunoglobulin superfamily of cell surface receptors, which also acts as a tumor suppressor (Wu et al., 2018). CD27 is a tumor necrosis factor (TNF) receptor. Treatment with the estrogen E2 modulates the expression of CD27 in the bone marrow and spleen cells (Stubelius et al., 2014). TNFSF18 is a cytokine that belongs to the tumor necrosis factor (TNF) ligand family. Although its relation with estrogen and breast cancer is unclear, its receptor GITR shows increased expression in tumor-positive lymph nodes from advanced breast cancer patients (Krausz et al., 2012), and is targeted by some anti-cancer immunotherapy (Schaer et al., 2012). UBD is a ubiquitin-like protein, which promotes tumor proliferation by stabilizing the translation elongation factor eEF1A1 (Liu et al., 2016).

Interestingly, three of the other top biological processes are also immune processes. In normal immune cells, estrogen receptors regulate innate immune signaling pathways (Kovats, 2015). In addition, some of the selected genes in these pathways have been found to associate with cancer. Examples include AURKB, which belongs to the family of serine/threonine kinases, and contributes to chemo-resistance and poor prognosis in breast cancer (Zhang et al., 2015), and SVIL, which mediates the suppression of p53 protein and enhances cell survival (Fang and Luna, 2013).

Overall, genes selected by TGLG are easy to interpret. Many known links exist between these genes and ER status, or breast cancer in general. Still many of the selected genes are not reported so far to be linked to ER status or breast cancer. Our results indicate they may play important roles.

6. Discussion

In summary, we propose a new prior model: TGLG prior for Bayesian network marker selection over large-scale networks. We show the proposed prior model enjoys large prior support for network marker selection over large-scale networks, leading to the posterior consistency. We also develop an efficient Metropolis-adjusted Langevin algorithm (MALA) for posterior computation. The simulation studies show that our method performs better than existing regularized regression approaches with regard to the selection and prediction accuracy. Also, the analysis of TCGA breast cancer data indicates that our method can provide biologically meaningful results.

This paper leads to some obvious future work. First, we can apply the TGLG prior for network marker selection under other modeling framework such as the survival model and the generalized mixed effects model. Second, the current posterior computation can be further improved by utilizing the parallel computing techniques within each iteration of the MCMC algorithm, for updating the massive latent variables simultaneously. Third, another promising direction is to use the integrated nested laplace approximations (INLA) for Bayesian approximating computation taking advantages of the TGLG prior involving high-dimensional Gaussian latent variables.