Large Dzyaloshinskii-Moriya interaction induced by chemisorbed oxygen on a ferromagnet surface

Observation of large Dzyaloshinskii-Moriya interaction and switching of skyrmion’s winding number induced by chemisorbed oxygen.

Abstract

The Dzyaloshinskii-Moriya interaction (DMI) is an antisymmetric exchange interaction that stabilizes chiral spin textures. It is induced by inversion symmetry breaking in noncentrosymmetric lattices or at interfaces. Recently, interfacial DMI has been found in magnetic layers adjacent to transition metals due to the spin-orbit coupling and at interfaces with graphene due to the Rashba effect. We report direct observation of strong DMI induced by chemisorption of oxygen on a ferromagnetic layer at room temperature. The sign of this DMI and its unexpectedly large magnitude—despite the low atomic number of oxygen—are derived by examining the oxygen coverage–dependent evolution of magnetic chirality. We find that DMI at the oxygen/ferromagnet interface is comparable to those at ferromagnet/transition metal interfaces; it has enabled direct tailoring of skyrmion’s winding number at room temperature via oxygen chemisorption. This result extends the understanding of the DMI, opening up opportunities for the chemisorption-related design of spin-orbitronic devices.

INTRODUCTION

The Dzyaloshinskii-Moriya interaction (DMI) is a spin-spin interaction that has finite values only in systems lacking inversion symmetry. Dzyaloshinskii proposed that the combination of low symmetry and spin-orbit coupling gives rise to an antisymmetric exchange interaction (1), and Moriya introduced how to calculate the antisymmetric exchange interaction for localized magnetic systems in a microscopic model (2). This picture was later used to successfully explain helical spin order and skyrmion lattices in the B20-type transition metal silicides and germanides lacking inversion symmetry (3, 4). In addition, Fert and Levy (5) proposed a DMI mechanism that involves magnetic and nonmagnetic sites in spin glasses, which was extended to thin film surfaces and interfaces where inversion symmetry breaks along the surface normal direction (6).

This DMI mechanism is now invoked to explain the stability of preferred chirality in a large variety of systems featuring noncollinear spin textures, such as spin spirals (7), skyrmions (8–10), or chiral domain walls (DWs) (11–13). Its energy term, −D_ij ∙ (S_i × S_j), indicates that the sign of the DMI vector D_ij determines the chirality of spin textures, i.e., being right- or left-handed, and the interplay between the magnitude of DMI and other magnetic interactions influences the lateral size of spin textures (10). Intense experimental and theoretical efforts have been made to explore the material dependence of the interfacial DMI and to exploit the flexibility of interface choices and stacking orders to enhance the effective DMI, with the goal of optimizing thin film and multilayer systems for the design of spin-orbitronic devices (8–10, 14) based on chiral spin textures.

Experimentally, most studies on interfacial DMI systems have focused on magnetic layers adjacent to heavy metals in the framework of the Fert-Levy model, such as hafnium (15), tantalum (15–17), tungsten (7, 15, 17, 18), iridium (19–21), platinum (17, 19–21), palladium (22), or ruthenium (23), where large differences of the DMI magnitude among those elements were attributed to the distinct degree of hybridization between 5d and 3d orbitals near the Fermi level (17, 24). Sizable DMI has also been found at certain metal/oxide interfaces, such as Co₉₀Fe₁₀/oxide (25), CoFeB/TaO_x (26), Co/AlO_x, or Co/GdO_x (27). These results point out the correlation between the DMI and the orbital angular momentum (25) and suggest the origin of the voltage-tunable DMI to be the Rashba field at metal/oxide interfaces (26), which was recently predicted (28). In addition, it is fundamentally interesting to explore the effects of elements with a low atomic number on the DMI. For instance, hydrogenation-induced skyrmion formation in Fe/Ir(111) at low temperatures has been reported (29). Furthermore, a large DMI was observed at the Co/graphene interface, which was attributed to the Rashba effect (23, 30). DMI induced by oxygen chemisorption on Fe films, different from the aforementioned oxide systems, has also been theoretically predicted with the DMI mechanism related to the hybridization and charge transfer between atomic oxygen and metal (31). Chemisorbed oxygen on a 3d metal surface is an ideal system to test this picture, as well as the recent theoretical prediction of the relation between the DMI and the electric dipole moment (32), as the presence of atomic oxygen creates a strong internal electric field at the atomic oxygen/metal interface, because of the large difference of electronegativity between oxygen and 3d ferromagnets (oxygen has a Pauling electronegativity of 3.44, and 3d ferromagnets have a Pauling electronegativity of ~1.90), yet such experimental examinations are still missing so far.

Here, we report the direct observation of a large DMI induced at room temperature by chemisorbed oxygen on Ni/Co/Pd/W(110) multilayers, using spin-polarized low-energy electron microscopy (SPLEEM) (33). We first show that the effective DMI in the multilayer stack can be tuned by precisely controlling the Pd spacer layer thickness, d_Pd, which is supported by density functional theory (DFT) calculations. Then, we monitor the oxygen coverage (d_O)–dependent evolution of DW chirality in perpendicularly magnetized Ni/Co films on Pd/W(110). We find that the chemisorbed oxygen can switch the DW chirality when the effective DMI of the bare (oxygen-free) Ni/Co/Pd/W(110) multilayer is Pd-like (left-handed), as a result of a relatively thick Pd spacer layer, but chemisorbed oxygen cannot switch the DW chirality when the Pd spacer layer is thinner and the effective DMI of the bare multilayer is tungsten-like (right-handed). A systematic measurement of the chirality in d_Pd − d_O space allows us to quantify the DMI induced by chemisorbed oxygen. We find that the magnitude of the chemisorbed oxygen–induced DMI is comparable to those induced at ferromagnet/heavy metal interfaces, despite the low atomic number of oxygen. We demonstrate that this oxygen-induced DMI is sufficiently strong to tailor a skyrmion’s winding number as well as its domain wall type at room temperature. The observed large magnitude of the DMI induced by oxygen may be useful for the development of applications in the field of spintronics and magneto-ionics.

RESULTS

A tunable platform for measuring unknown DMI contributions

One of the approaches to quantify the DMI in a layered system is to measure the DW spin texture as a function of layer thickness, where the sign and magnitude of the DMI can be determined by measuring the critical thickness where DW transitions from chiral Néel to achiral Bloch textures (10). This can be done by using SPLEEM (13, 19, 23) or scanning electron microscopy with polarization analysis (34). If the addition of a new interface with unknown DMI to a layered system with calibrated DMI is found to switch the handedness of DWs, then the unknown DMI of the new interface can be quantified by comparison. For example, the observation of right-handed chirality in Co/Ru(0001) and left-handed chirality in graphene/Co/Ru(0001) allowed unambiguous determination of left-handed DMI at the graphene/Co interface (23). The aim to generalize this experimental method motivates the development of DMI-tunable platforms that combine pairs of buried interfaces with opposite DMI (19, 35) to provide magnetic surfaces with either left- or right-handed DW chirality, so that the sign of an unknown DMI at any new interface added to the structure can be unambiguously determined.

In this work, tungsten and palladium are chosen because the growth of Pd on W(110) results in high-quality epitaxial films (fig. S1). The strong LEEM image intensity oscillations associated with the layer-by-layer growth allow a precise determination of the Pd film thickness, which permits fine-tuning of the effective DMI in the Pd/W system. Ni/Co bilayers grown on top provide perpendicular magnetic anisotropy, which allows the observation of DW chirality (19). The compound SPLEEM images (Fig. 1, A, C, and E) show the Pd thickness–dependent switching of the DW Néel chirality in Ni/Co/Pd/W(110) multilayers. The histograms (Fig. 1, B, D, and F) of the angle α calculated from the SPLEEM images show the statistics of DW chirality (19, 23). Note that the DW is aligned along the easy axis of the uniaxial magnetic anisotropy, i.e., the W[001] direction; this alignment is induced by the uniaxial strain in face-centered cubic (fcc) layers on W(110) (18). Therefore, the DW type (Néel, Bloch, or mixed wall) varies on the basis of the DW orientation with respect to the tungsten crystal orientation. While this may result in shifted peaks in the α histogram away from 0° and 180°, the sensitivity of the Néel-component to the interfacial DMI persists (18). The d_Pd-dependent chirality evolution (Fig. 1G) derived from the histograms shows that the change from right-handed (thin d_Pd) to left-handed (thick d_Pd) Néel chirality occurs near d_Pd = 2.5 monolayers (MLs) (Materials and Methods). This chirality switching is attributed to the sign change of the effective DMI, which is supported by DFT calculations (Fig. 1H), where the W-like DMI is right-handed and the Pd-like DMI is left-handed. This tunable DMI, by simply varying the Pd thickness, provides an ideal platform to the quantitative study of the interface-induced DMI.

Fig. 1. Tuning DMI in the Pd/W(110) system.

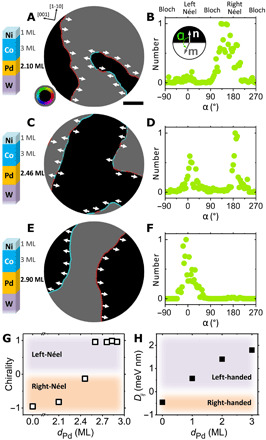
(A, C, and E) Compound SPLEEM images of Ni/Co/Pd/W(110). Scale bar, 2 μm. Gray/black regions represent the down/up magnetization of the perpendicular magnetized domains, respectively, and colored boundaries show the DW magnetization orientation according to the color wheel shown in the inset in (A). White arrows indicate the in-plane magnetization direction in the DW. (B, D, and F) Histograms of angle α between DW magnetization m and DW normal vector n, measured pixel by pixel along the DW centerline, show the evolution of chirality from right-handed Néel-type chirality (B; single peak near 180°), achiral Néel-type chirality (D; two peaks near 0° and 180°), to left-handed Néel-type chirality (F; single peak near 0°). (G) Experimental d_Pd-dependent Néel-type chirality, which is calculated as $\frac{({\displaystyle {\sum }_{-90°}^{90°}}\text{counts}-{\displaystyle {\sum }_{90°}^{270°}}\text{counts})}{({\displaystyle {\sum }_{-90°}^{90°}}\text{counts}+{\displaystyle {\sum }_{90°}^{270°}}\text{counts})}$. (H) Calculated effective DMI strength D_ij in the 1 ML Ni/3 ML Co/0 to 3 ML Pd/W(110) system.

Examining chemisorbed oxygen–induced DW chirality

Ni(111) is an ideal surface to study the role of oxygen on the DMI, as the phase diagram of oxygen chemisorbed on Ni(111) is well understood from literature (36). Two-dimensional O/Ni(111) adsorbate layers can be realized in the range of 0 to 0.5 ML oxygen with respect to the planar atomic density of Ni(111), where oxygen atoms strongly bind to threefold hollow sites on the Ni(111) surface with an oxygen-nickel bond length of 1.88 Å. At room temperature, the oxygen layer remains in a “lattice gas phase” (no long-range order) at a low coverage below 0.21 ML, as the interaction energy between the oxygen adatoms is an order of magnitude smaller than the binding energy (36). A long-range ordered p(2 × 2) structure forms between 0.21 and 0.25 ML, while p(2 × 2) antiphase domains, a ($\sqrt{3}\times \sqrt{3}$)R30° phase, or a mixed phase is present at higher coverage [see sketches of p(2 × 2) and ($\sqrt{3}\times \sqrt{3}$)R30° structures in fig. S2]. In this work, we focus on room temperature oxygen adsorption in the coverage regime up to 0.29 ML, where no formation of NiO is observed (see Materials and Methods) (36).

We find that the presence of adsorbed oxygen on Ni/Co/Pd/W(110) samples favors right-handed chirality. This is unambiguously demonstrated by using the tunability of the DMI in this multilayer, where the chirality of the magnetic layer can be adjusted from left-handed to achiral to right-handed, as a function of the thickness of the Pd spacer. Figure 2 (A to F) shows O coverage–dependent magnetization images at d_Pd = 2.76 ML, where the Néel-type α histogram derived from each image shows that the chirality evolves from left-handed at d_O = 0.12 ML to achiral near d_O = 0.19 ML and to right-handed chirality at d_O = 0.22 ML. This trend can also be seen in samples with other Pd thickness, as summarized in Fig. 2H: For a Pd layer thickness d_Pd = 2.46 ML, the achiral state with essentially vanishing DMI occurs with the pristine Ni(111) surface and, as oxygen coverage is introduced, chirality gradually evolves to right-handedness at d_O = 0.10 ML. The left- to right-handed chirality switch occurs at a progressively larger O coverage as d_Pd is increased, as shown in Fig. 2H for d_Pd = 2.60 ML, 2.76 ML, and 2.83 ML. This is because the effective left-handed DMI increases with the Pd layer thickness (19, 37), and more O coverage is required to provide the balancing right-handed DMI. The role of the chemisorbed oxygen–induced DMI is also examined in systems without heavy metal, where the chirality switching from left-handed chiral Néel wall to achiral Bloch wall is observed in [Co/Ni]₃/Cu(111) with 0.21 ML chemisorbed oxygen (fig. S3). This observation further confirms the large DMI induced at the chemisorbed oxygen/cobalt interface (38).

Fig. 2. Chemisorbed oxygen–dependent chirality evolution.

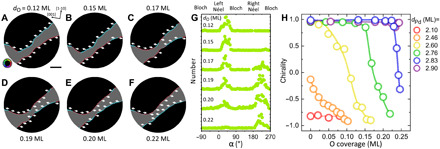
(A to F) Compound SPLEEM images of O/Ni(1 ML)/Co(3 ML)/Pd(2.76 ML)/W(110); oxygen coverages are labeled for each image. Scale bar, 2 μm. White arrows indicate the in-plane magnetization direction in the DW. (G) Oxygen coverage–dependent histogram of angle α between the DW magnetization m and the DW normal vector n, measured from (A) to (F), showing the evolution of chirality from left-handed Néel type to right-handed Néel type. (H) Oxygen coverage–dependent evolution of Néel-type chirality for different Pd thicknesses.

Quantifying chemisorbed oxygen–induced DMI

Summarizing the oxygen coverage–dependent chirality at each Pd thickness in Fig. 2H, we show the phase diagram of magnetic chirality in the d_O-d_Pd space in Fig. 3A, where the achiral state is revealed as the boundary between left-handed Néel DW texture (purple area) and right-handed Néel texture (orange area). Obtaining the slope of the boundary provides an opportunity to compare the Pd thickness d_Pd-dependent DMI and the chemisorbed oxygen coverage d_O-dependent DMI. Noting that the achiral state indicates zero effective DMI, we can, for instance, compare two achiral states at d_Pd = 2.46 ML and d_O = 0 ML and at d_Pd = 2.83 ML and d_O = 0.24 ML (see squares in the phase diagram): This indicates that the magnitude of the DMI change induced by a change in Pd layer thickness of ∆d_Pd = 0.37 ML is effectively balanced by the DMI change induced by a change in oxygen coverage of ∆d_O = 0.24 ML, suggesting that the strength of the DMI induced by oxygen is substantial. The slope of the phase boundary remains roughly constant for an oxygen coverage up to 0.25 ML, suggesting that the effective magnitude of the DMI is proportional to the oxygen coverage. This is expected as the oxygen atoms occupy the same type of binding site (threefold hollow sites on Ni), and the formation of long-range order in the oxygen layer does not affect the chemical environment of oxygen atoms (36).

Fig. 3. Quantification of oxygen chemisorption–induced DMI.

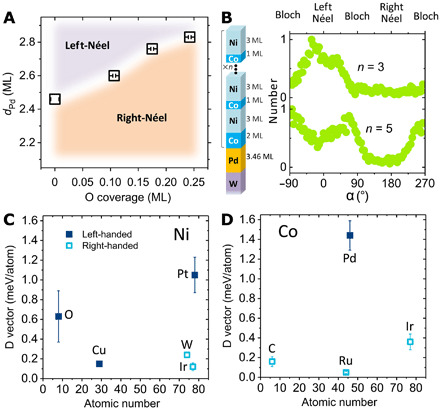
(A) Phase diagram of chirality in d_Pd-d_O space. The dependence of wall texture transition points permits the determination of the oxygen-induced DMI by comparing with Pd thickness–induced DMI variation. (B) Histogram of angle α in the [3Ni/1Co]₂/3Ni/2Co/3.46Pd/W(110) multilayer (upper plot, total Ni/Co stack number n = 3) with a single peak near 0°, and histogram of angle α in the [3Ni/1Co]₄/3Ni/2Co/3.46Pd/W(110) multilayer (lower plot, n = 5) with double peaks at ~−90° and ~+90°. Modeling the film thickness dependence of this chirality transition allows the determination of the DMI strength of the system. (C and D) Summarized magnitude of the DMI vector at the Ni/[nonmagnetic material] interfaces in (C) and Co/[nonmagnetic material] interfaces in (D), all extracted by the same approach used in this work.

In the following, we discuss how the strengths of these DMI contributions can be extracted quantitatively. We start by measuring the DMI in [Ni/Co]_n/Pd/W(110) with d_Pd = 3.46 ML, which is 1 ML thicker than the zero-DMI case of d_Pd = 2.46 ML. This measurement is based on observing DW configurations as a function of the thickness of the magnetic layer. The DMI is extracted by tracking the competition between the interfacial DMI, which favors chiral Néel walls, and the dipolar interaction, which favors Bloch walls. Thus, one can indirectly estimate the DMI strength by calculating the dipolar energy penalty of Néel walls at the experimentally measured thickness of the magnetic film where the Néel/Bloch DW texture transition occurs (10, 19, 23). In [Ni/Co]_n/3.46 ML Pd/W(110) multilayers, we find that this transition occurs between the thicknesses of n = 3 and n = 5 [Ni/Co] repeats, where the DWs are chiral Néel type in the [Ni/Co]₃ multilayer and achiral Bloch type in the [Ni/Co]₅ multilayer (Fig. 3B). Because Co and Ni have an opposite magneto-elastic constant, the Co and Ni layer thicknesses are optimized to suppress the uniaxial anisotropy and its effect on DW (fig. S4) (18). Micromagnetic calculations of the dipolar energy difference between Néel and Bloch DWs at this critical thickness yields an estimate of the effective DMI of 0.41 ± 0.17 meV/atom in [Ni/Co]_n/3.46 ML Pd/W(110) (see Materials and Methods). Note that the effective DMI contribution from the upper [Ni/Co] repeats of the multilayers vanishes due to inversion symmetry (35, 39). Consequently, for sub-monolayer variations of the Pd layer thickness, we can approximate that the DMI varies linearly with Pd thickness. Under this approximation, the DMI change induced by a Pd layer thickness variation of ∆d_Pd = 0.37 ML is about 37% of the DMI change induced by a Pd layer thickness variation of ∆d_Pd = 1 ML, which, as described above, amounts to 0.41 ± 0.17 meV/atom. As our experiments show that the DMI variation induced by ∆d_Pd = 0.37 ML equals that induced by adding 0.24 ML oxygen onto the Ni surface, which is (0.41 ± 0.17) × 0.37 = 0.15 ± 0.06 meV/atom, these measurements allow an estimate of the DMI induced by the chemisorbed oxygen as $(0.41\pm 0.17)\times \frac{0.37}{0.24}=0.63\pm 0.26 \text{meV}/\text{atom}$for 1 ML of oxygen coverage.

It is interesting to compare the extracted oxygen-induced DMI in this system to DMI values in other systems, as summarized in Fig. 3 (C and D). Here, we compare only measurements derived using the experimental approach described in (10, 19, 23) to avoid potential systematic biases due to the use of different methods. Compared to another light element, the DMI at the oxygen/Ni interface is approximately four times larger than that at the graphene/Co interface, where D_graphene/Co = 0.16 ± 0.05 meV/atom (23). The chemisorbed oxygen–induced DMI is also comparable to the DMI induced at interfaces with many transition metals. For selected materials adjacent to the Ni layer (Fig. 3C): D_Ni/Ir = 0.12 ± 0.04 meV/atom (19), D_Ni/W ≈ 0.24 meV/atom (18), D_{Ni/Cu + Fe/Ni} = 0.15 ± 0.02 meV/atom (13), and D_Ni/Pt = 1.05 ± 0.18 meV/atom (19). For selected materials adjacent to the Co layer (Fig. 3D): D_Co/Ir = 0.36 ± 0.08 meV/atom (39), D_Co/Ru = 0.05 ± 0.01 meV/atom (23), and D_Co/Pd = 1.44 ± 0.15 meV/atom as measured in this work (see Materials and Methods).

Tailoring chirality of spin textures via adsorbed oxygen

The large DMI induced by oxygen coverage on magnetic layers opens up new possibilities for designing chiral spin textures without using heavy metals. In the following, we demonstrate experimentally that chemisorbed oxygen can be used to tailor the spin texture of magnetic bubbles. Compound SPLEEM images in Fig. 4 (A to F) highlight DW structures in a down-magnetized magnetic bubble with uniaxial anisotropy at various oxygen coverages in a Ni(1 ML)/Co(3 ML)/Pd(2.6 ML)/W(110) sample, where a complete chirality transition from left-handed (Fig. 4A) to achiral (Fig. 4D) to right-handed (Fig. 4F) is observed. Note that the deformation of the bubble shape is due to the oxygen-induced change of perpendicular magnetic anisotropy. To demonstrate the role of oxygen-induced DMI on regular skyrmions, we also performed experiments on oxygen-assisted skyrmion evolution in the isotropic [Co/Ni]₃/Cu(111) system, without any uniaxial anisotropy. The skyrmion shown in Fig. 4G is a left-handed hedgehog type. With increasing oxygen coverage (0.12 and 0.21 ML oxygen in Fig. 4, H and I, respectively), the skyrmion gradually evolves to the Bloch type. Note that the Bloch-type chirality is not defined by the interfacial DMI; therefore, a bubble with bigger diameter may exhibit achiral Bloch walls at the same oxygen coverage (fig. S3C). These results represent a new approach to tailor the inner structure of magnetic bubbles or skyrmions, which may influence the stability and dynamic properties of the initial bubble domain, due to possible changes of topological number or DW-type–dependent current-induced dynamics (10).

Fig. 4. Oxygen-assisted chirality modification at room temperature.

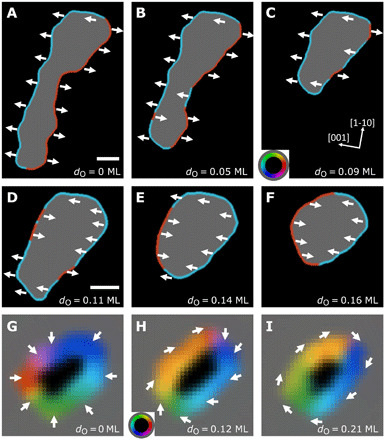
(A to F) Compound SPLEEM images of a magnetic bubble in perpendicularly magnetized Ni(1 ML)/Co(3 ML)/Pd(2.6 ML)/W(110) with increasing oxygen coverage (labeled in each panel), showing a complete chirality transition from left-handed (A) to achiral (D) to right-handed (F). Scale bars, 1 μm (A and D). The change of the bubble shape is due to the weak oxygen-induced magnetic anisotropy. (G) Compound SPLEEM image of a left-handed Néel-type skyrmion in a perpendicularly magnetized [Co/Ni]₃/Cu(111) system. The field of view is 340 nm. Color wheel and white arrows show in-plane magnetization directions. Gray/black regions show out-of-plane components of the magnetization pointing down (−z) or up (+z). (H and I) The Néel-type skyrmion in (G) evolves into a skyrmion with tilted wall and lastly a Bloch-type skyrmion upon oxygen chemisorption [0.12 and 0.21 ML oxygen in (H) and (I), respectively].

DISCUSSION

Note that the DMI of oxygen adsorbed on top of Ni favors right-handed DW textures, which is the same handedness as Pt/Ni and Pd/Ni, suggesting that earth-abundant oxygen could potentially be used as an alternative to replace those rare noble metals in device applications where sizable DMI is needed. The large magnitude of the DMI induced by oxygen may be sufficient to stabilize magnetic chirality in a-few-nanometer-thick magnetic films; for instance, the chirality in typical perpendicular magnetic anisotropy multilayers [Co(1 ML)/Ni(2 ML)]_n might be stabilized up to n = 5 (roughly 3 nm thick). The physical origin of the large magnitude of the oxygen-induced DMI is linked to the electric surface dipole moment induced by charge transfer and related hybridization between p-orbitals of oxygen and d-orbitals of ferromagnets (31). The charge transfer can be explained by the large difference in electronegativity, and therefore, our results provide experimental evidence for the recently predicted relationship between DMI and electronegativity (32). A large work function change (~0.7 eV) is observed for the Ni/Co/Pd/W system upon oxygen chemisorption (fig. S5A), which confirms the oxygen adatom–induced dipole moment (36). This suggests that other adsorbates with strong electronegativity differences may also induce a sizable DMI.

CONCLUSION

In summary, our experiments show that chemisorbed oxygen onto ferromagnet surfaces can induce a large DMI at room temperature, comparable to those induced at typical ferromagnet/transition metal interfaces. The induced DMI can be used to directly tailor the winding number of magnetic skyrmions at room temperature. We anticipate that sizable DMI may also be induced by chemisorbed oxygen on other magnetic surfaces such as chromium (40), manganese (40), iron (41), or cobalt (38). The observation of the large DMI induced by chemisorbed oxygen, along with the possibility of voltage-controlled oxygen migration in multilayer systems (42, 43), may create new possibilities in the field of spintronics and magneto-ionics.

MATERIALS AND METHODS

Sample preparation

The experiments were conducted in the SPLEEM instrument at the National Center for Electron Microscopy of the Lawrence Berkeley National Laboratory. All samples were prepared under ultrahigh vacuum (UHV) conditions in the SPLEEM chamber, with a base pressure lower than 4.0 × 10⁻¹¹ torr. The W(110) substrate was cleaned by flashing to 1950°C in 3.0 × 10⁻⁸ torr O₂ and a final annealing at the same temperature under UHV to remove oxygen. The Cu(111) substrate was cleaned by cycles of Ar⁺ sputtering at 1 keV and annealing at 580°C. Ni, Co, and Pd layers were deposited at room temperature by physical vapor deposition from electron beam evaporators, and the film thicknesses of Ni, Co, and Pd layers were controlled by monitoring the LEEM image intensity oscillations associated with atomic layer-by-layer growth (fig. S1). The thicknesses of Co and Ni in Fig. 3B are optimized to minimize the in-plane uniaxial magnetic anisotropy, which is due to the growth of Co and Ni on the surface of the imperfect fcc(111) lattice of Pd on top of W(110).

Oxygen exposures were done by controlled leaking of high-purity oxygen (99.993%) in pressure ranges of 5 × 10⁻⁹ torr to 1 × 10⁻⁸ torr, and the surface contamination from other residual gases (base pressure < 4 × 10⁻¹¹ torr) is estimated to be at least two orders of magnitude less, which is insufficient to influence the result. The oxygen coverage is estimated based on the kinetics relation reported in (36). Our measurements of the oxygen coverage–dependent work function change show excellent agreement with the previous measurement (fig. S5) (36). The oxygen coverage on the surface of [Co/Ni]₃/Cu(111) is estimated by the oxygen thickness–dependent low-energy electron diffraction (LEED) pattern (fig. S3D, inset), and no formation of CoO is seen due to the absence of additional CoO LEED spots (38).

Magnetic imaging and vector field analysis

The real-space magnetic images were acquired using the SPLEEM instrument at the National Center for Electron Microscopy at the Lawrence Berkeley National Laboratory (33). In each SPLEEM image, the contrast is obtained by calculating the asymmetry of the spin-dependent reflection between spin-polarized beams with up and down spins, which is A = (I_↑ − I_↓)/(I_↑ + I_↓). This asymmetry A represents P ∙ M, where P is the spin polarization vector of the illumination beam and M is the magnetization vector. The Cartesian components M_x, M_y, and M_z of the magnetization were resolved by taking sets of images with the illumination beam spin polarization aligned along the x, y, and z directions, respectively (18, 19). The two in-plane orthogonal directions were chosen to be W[1-10] and W[001]. All images were measured on the samples held at room temperature. The energy of the incident electron beam was set to 5.6 eV for the Ni/Co/Pd/W system to optimize the magnetic contrast. The compound SPLEEM images are converted by combining the set of SPLEEM images (M_x, M_y, and M_z), where the color wheel highlights in-plane magnetization, and gray values represent the perpendicular magnetization component +M_z (black) and −M_z (gray), respectively.

The method to analyze the DW chirality from the SPLEEM images is the same as that described previously (19, 23). The DW normal vector n is determined from out-of-plane SPLEEM images, and the DW magnetization vector m is measured from the asymmetry values of two in-plane SPLEEM images. To highlight the contributions of the Néel component in a DMI system with finite in-plane uniaxial magnetic anisotropy, the angle α–dependent Néel-component counts in the histograms in Figs. 1 and 2 are calculated as total counts ×∣cosα∣ (18).

Estimating the DMI strength

The method to estimate the DMI strength from the film thickness–dependent DW evolution in Fig. 3 is the same as that described previously (19, 23). The strength of the DMI vector can be estimated by calculating the dipolar energy difference in thinner films with Néel walls (lower DMI limit) and thicker films with Bloch walls (upper DMI limit). The dipolar energy constant is ${\mathrm{\mu }}_0{(d_{\text{Co}}{\mathrm{\mu }}_{\text{Co}}+d_{\text{Ni}}{\mathrm{\mu }}_{\text{Ni}})}^2/8\mathrm{\pi }{\mathrm{a}}_{\parallel }^3$, where μ_Co = 1.7 μ_B, μ_Ni = 0.6 μ_B, and $a_{\parallel }=2.51 \mathrm{\AA }$. We numerically calculated the dipolar energy difference of [Ni/Co]_n/Pd/W with various film thicknesses, where cases with n = 3 and n = 5 lead to values of −1.30 meV/atom and −3.20 meV/atom, respectively. Therefore, the DMI vector d is converted based on the hexagonal lattice case (19, 23), which gives 0.41 ± 0.17 meV/atom for [Ni/Co]_n/3.46 ML Pd/W(110). Using the same approach, we further measured the DMI at the Co interface with bulk Pd in the [Ni/Co]_n/Pd(111) system, finding D_Co/Pd = 1.44 ± 0.15 meV/atom (fig. S6). These results show that the bulk Pd–induced DMI is much larger than the DMI variation induced by a small Pd thickness change in the Ni/Co/Pd/W(110) system, similar to the smooth thickness dependence observed in another heavy metal–induced DMI system (37).

DFT calculation of DMI strength

All calculations were based on DFT. Because of the preferred hexagonal growth of Ni, Co, and Pd, we approximated the whole system to follow this pseudomorphic growth. The lattice constant was chosen to be 250 pm. For the stacking order, we followed the preferred bulk ordering for each metal. This results in a reduced C_2v symmetry, in agreement with the real physical system. To most accurately model the W(110), we adjusted the W interlayer distances to obtain the correct experimental bulk volume. Structural relaxations have been performed to determine the remaining interlayer distances using the Vienna ab initio simulation package (44, 45) using the generalized gradient approximation of Perdew-Burke-Ernzerhof (46) for exchange and correlation effects and the projector-augmented wave method (47). The magnetic properties were determined in the local density approximation (48), using the full-potential linearized augmented plane wave method as implemented in the FLEUR code (for the program description, see http://flapw.de). The charge densities of spin spiral states have been converged using a cutoff parameter for the basis functions of k_max = 4.0 a.u.⁻¹ and (32 × 32) k-points in the full two-dimensional Brillouin zone (2DBZ). The DMI was calculated by including spin-orbit coupling in first-order perturbation theory (49) with (64 × 64) k-points in the full 2DBZ on top of a scalar-relativistic spin-spiral calculation, as described in (50, 51).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/33/eaba4924/DC1