Predictive modelling of COVID-19 confirmed cases in Nigeria

Abstract

The coronavirus outbreak is the most notable world crisis since the Second World War. The pandemic that originated from Wuhan, China in late 2019 has affected all the nations of the world and triggered a global economic crisis whose impact will be felt for years to come. This necessitates the need to monitor and predict COVID-19 prevalence for adequate control. The linear regression models are prominent tools in predicting the impact of certain factors on COVID-19 outbreak and taking the necessary measures to respond to this crisis. The data was extracted from the NCDC website and spanned from March 31, 2020 to May 29, 2020. In this study, we adopted the ordinary least squares estimator to measure the impact of travelling history and contacts on the spread of COVID-19 in Nigeria and made a prediction. The model was conducted before and after travel restriction was enforced by the Federal government of Nigeria. The fitted model fitted well to the dataset and was free of any violation based on the diagnostic checks conducted. The results show that the government made a right decision in enforcing travelling restriction because we observed that travelling history and contacts made increases the chances of people being infected with COVID-19 by 85% and 88% respectively. This prediction of COVID-19 shows that the government should ensure that most travelling agency should have better precautions and preparations in place before re-opening.

1. Introduction

COVID19 is a new pandemic triggered by extreme acute respiratory coronavirus syndrome 2 (SARS-CoV-2) and spreads rapidly from person to person (Ceylan, 2020). This pandemic is the most notable world crisis since the Second World War. According to literature, the outbreak originated from Wuhan, China, in late 2019 and has triggered a global economic crisis whose impact will be felt for years to come (Ayinde et al., 2020; WHO, 2020). On January 30, 2020, the World Health Organization (WHO) declared the outbreak as a Public Health Emergency of International concern (International Health Regulations, 2020; World Health Organization 2020). There has been about 8, 061, 550 COVID-19 incidents registered in over 200 republics and regions which had brought about around 440,290 demises as of June 18, 2020 (NCDC Nigeria, 2020). The disease is mainly transmitted through nearby interaction, mostly by tiny beads formed through coughing, sneezing, or speaking (Control and Prevention, 2020; European Centre for Disease Prevention and Control, 2020; World Health Organization, 2020; Centers for Disease). Also, individuals could often turn out to be contaminated through being in contact with an affected exterior (World Health Organization, 2020; Centers for Disease Control and Prevention, 2020).

Nigeria announced the Sub-Sahara Africa’s first confirmed case of COVID-19 disease on Friday January 28, 2020 at around 1 am. This confirmation led to the activation of the country’s National Coronavirus Emergency Operation centre (Adepoju, 2020). According to the Nigeria Centre for Disease Control (NCDC), COVID-19 has presently infected 36 states in Nigeria. As at June 18, 2020 the number of samples tested in Nigeria is 106, 006 out of which 17, 735 of them is confirmed positive, 11, 299 of the individuals are active ones, discharged cases is 5967 and demise is 469 individuals (NCDC Nigeria, 2020; Wikipedia, 2020).

Different models have been used in recent studies to predict incidence, prevalence and mortality rate of COVID-19. Li et al. (2020), for instance, built a method for forecasting the ongoing trend with data-driven analysis and estimating the COVID-19 outburst size in China. Fanelli and Piazza (2020) studied the COVID-19 pandemic temporal dynamics in mainland China, Italy and France. Roda et al. (2020) correlated the standard SIR and SEIR frameworks to model COVID-19 in Wuhan China. Wei et al. (2016) forecast the national and global spread of COVID-19 to determine the impact of the metropolitan-wide isolation of Wuhan and its neighbours. Al-qaness et al. (2020) enhanced the Adaptive Neuro-Fuzzy Inference System (ANFIS) by implementing an Enhanced Flower Pollination Algorithm utilizing the Salp Swarm Algorithm to evaluate the number of confirmed COVID-19 crisis in China. Anastassopoulou et al. (2020) research on the assessment of the severe epidemiological constraints as well as the demonstrating and forecasting the transmission of the COVID-19 pandemic in Hubei, China. Wang et al. (2020) established the Patient Information Based Algorithm for evaluating the demise rate of COVID-19 in real-time by utilizing openly accessible datasets.

Recently, statistical and time series model has also been introduced to model and predict the prevalence of this pandemic. Ayinde et al. (2020) subjected the COVID-19 cumulative confirmed cases in Nigeria to some curve statistical estimation models. Ghosal et al. (2020) employed the linear regression analysis to predict the number of deaths in India due to SARS-CoV-2. Ceylan (2020) applied the auto-regressive integrated moving average (ARIMA) model to predict the prevalence of COVID-19 in Italy, Spain, and France.

This study aims to predict the prevalence of COVID-19 in Nigeria using a linear regression model. Also, to measure the impact of travelling history and contact on COVID-19 confirmed cases.

2. Materials and methods

We consider the general linear regression model:

$$y=X\beta +\epsilon$$ (2.1)

where y is an $n\times 1$vector of response variable, $X$ is a known $n\times p$ full rank matrix of predictor or explanatory variables, $\beta$ is an $p\times 1$ vector of unknown regression parameters, $\epsilon$ is an $n\times 1$vector of errors such that $E(\epsilon )=0$ and $V(\epsilon )={\sigma }^2{I}_n$, $I_n$ is an $n\times n$ identity matrix. The ordinary least squares estimator (OLS) of $\beta$ in (2.1) is defined as:

$$\hat{\beta }={(S)}^{-1}{X}^{\prime }y,$$ (2.2)

where $S=X^{\prime }X$ is the design matrix. The performance of the estimator is best when there is no violation of any of the assumptions of classical linear regression model (Ayinde et al., 2018; Lukman et al., 2019). The assumptions include: non-normality of the error term, uncorrelated error term, orthogonality of the predictor variables and others (Gujarati, 1995). In this study, data was extracted from the NCDC website https://ncdc.gov.ng/. The dataset was collected in an excel file and analysed with the GRETL software. The variables of interest include confirmed cases as the response variable, travelling history and contact as the regressors. The regression model in this study is as follows:

$$y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\epsilon }_i$$ (2.3)

where y represents COVID-19 confirmed cases in Nigeria, X₁ represents the travelling history before and after lockdown and X₂ represents the number of contacts made by a COVID-19 patient. We conducted a correlation analysis to investigate the relationship between the regressors and the response variable.

The results in Table 1 shows that a strong positive relationship exists between the confirmed cases and contact. A low and moderately high positive relationship exists between confirmed cases and travelling history; contact and travelling history, respectively. The descriptive statistics of the variables of interest are available in Table 2. On average, there are 803 contacts made daily by COVID-19 infected patients. Of all the COVID-19 infected patients, about 191 of them have travelling history daily. The minimum and the maximum number of contacts made for the days covered in this study are 18 and 2407, respectively. A regression analysis was carried out to examine the relationship of the response variable (confirmed cases) with the regressors (Travel history and number of contacts). We adopt the Ordinary Least Squares (OLS) estimator in (2.2) to estimate the parameters of the regression model in (2.3). The result of the regression analysis using ordinary least squares estimator is displayed in Table 3.

Table 1.

Correlation matrix of the variables of interest.

confirmed cases	travelling history	contact
confirmed cases	0.4771	0.9955
travelling history		0.5259
Contact

Table 2.

Summary statistics of the variables.

Variable	Mean	Std. Dev	Min	Max
Travel history	191.13	38.564	83	210
Contact	803.30	708.01	18	2407

Table 3.

The multiple regression analysis output after travelling lockdown.

Variable	Coefficient	S.E	t-stat	P-Value	Diagnostic test
Intercept	542.18	158.346	3.424	0.0012	R2	0.9941	Durbin-Watson test	0.5431 (0.0000)
Travel history	−4.8309	0.9036	−5.346	<0.00001	F-test	4771.52 (0.0000)	White test	11.3410 (0.045)
Contact	4.2217	0.0492	85.7753	<0.0001	Jarque Bera-test	1.1261 (0.5695)	VIF	1.382

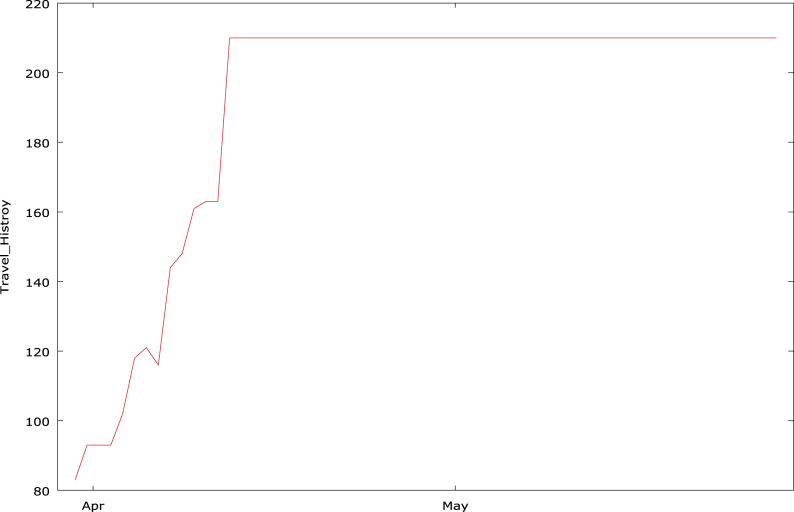
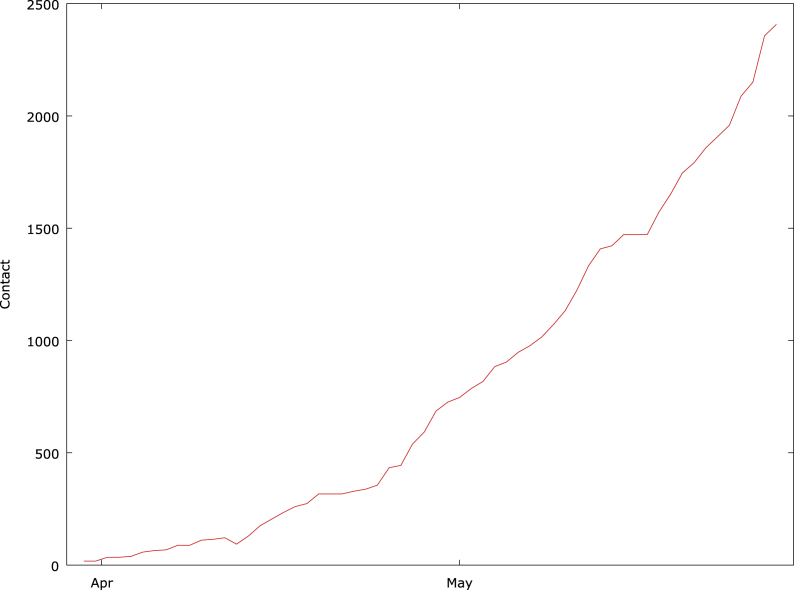
The Jarque-Bera test in Table 3 shows that the error term is normally distributed. From Table 3, we observed that the contact have a positive influence on COVID-19 confirmed cases as expected while travelling history have a negative impact as expected. The introduction of travelling lockdown leads to about 4.8% reduction in the number of COVID-19 cases that could have happened. We observed that the dataset on travelling history became constant from April 14, 2020, when the travelling restriction was placed on both local and international flights by the Federal government of Nigeria. We illustrate this graphically in Fig. 1. Fig. 1 shows that there is a daily rise in travel history up to the point where a ban was placed on all travels which are responsible for the stability seen in travel history over a period. Fig. 2 shows that there is an exponential rise in the number of people contaccting COVID-19 daily. Because the first case of COVID-19 in Nigeria was from an Italian that came into the country on February 25, 2020, this necessitates us to only run a regression model for the dataset from March 31, 2020, to April 13, 2020. The regression model for the reduced data set is available in Table 4.

Fig. 1.

Showing daily effects of travel history on confirmed cases.

Fig. 2.

Showing daily effects of increase in contact rate on confirmed cases.

Table 4.

Multiple regression analysis output before travelling lockdown.

Variable	Coefficient	S.E	t-stat	P-Value	Diagnostic test
Intercept	79.8934	15.2784	5.2292	0.00028	R2	0.9646	Durbin-Watson test	1.5213 (0.0848)
Travel history	0.8542	0.196605	4.3449	0.00117	F-test	150.0757	White test	8.7344 (0.1201)
Contact	0.8762	0.202713	4.3225	0.00121	Jarque Bera-test	0.7836 (0.6758)	VIF	4.262

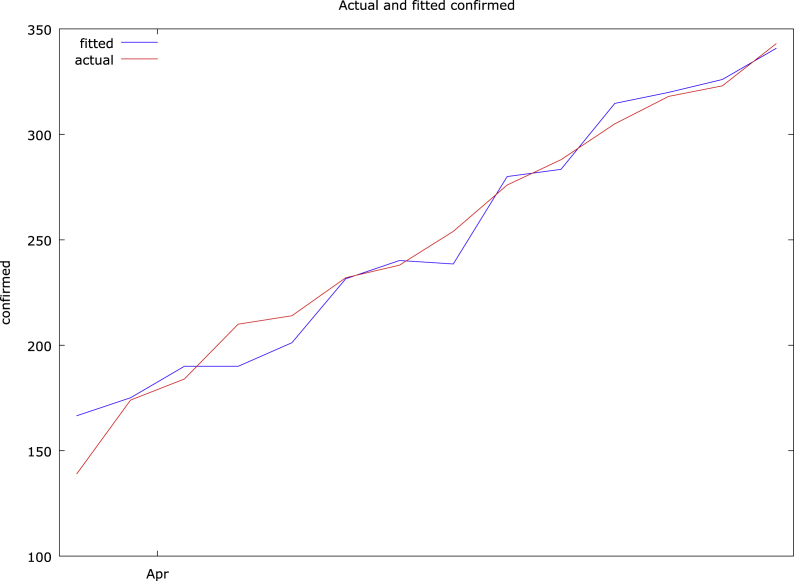
From Table 4, we observed that contact and travelling history have a positive influence on COVID-19 confirmed cases as expected. Travelling history increases the chances of people being infected with COVID-19 by 85% while contacts made by COVID-19 patience increases the tendencies of increasing COVID-19 by about 88%. We conducted a robust diagnosis of the model. The R² shows that these two variables explained about 97% of the factors responsible for COVID-19. The F-test shows that the overall model fits well to the data. According to Lukman et al. (2017), a high R² can signal the presence of multicollinearity. Therefore, we conducted a formal test called variance inflation factor to ascertain if there is multicollinearity problem in the model (Lukman et al., 2020). According to Kibria and Lukman (2020), when the variance inflation factor (VIF) is greater than ten (10) then there is multicollinearity. However, the result in Table 4 shows that the model does not exhibit multicollinearity problem since VIF is less than 10. We further examined if the model has an error term problem. The Jarque-Bera test shows that their error terms come from a normal distribution. The white test and the Durbin-Watson test shows that the error terms are not correlated and possesses constant variance. All these diagnostic checks further strengthen the fact that the performance of OLS estimator in this study is efficient. Fig. 3 shows that the predicted value and the actual values are close. From Table 5, we observed that the actual confirmed cases fall in the prediction interval. The predicted single estimates are also in agreement with the actual values except on few cases.

Fig. 3.

Actual and fitted values of COVID-19 confirmed cases.

Table 5.

The actual values and the prediction.

Date	confirmed	prediction	95% interval
April 5, 2020	232	231.51	202.66–260.37
April 6, 2020	238	240.21	211.35–269.07
April 7, 2020	254	238.57	209.26–267.88
April 8, 2020	276	280.01	250.90–309.12
April 9, 2020	288	283.43	254.35–312.51
April 10, 2020	305	314.69	284.32–345.05
April 11, 2020	318	319.9	289.19–350.61
April 12, 2020	323	326.03	294.35–357.72
April 13, 2020	343	340.77	302.12–379.42

3. Conclusion

Statistical methods and the time series models have been adopted in previous studies to predict epidemic cases. The linear regression model is an essential analytical tool for prediction. In this study, we applied the linear regression model to assess the impact of travelling history and contacts on COVID-19 confirmed cases in Nigeria. The statistical model was conducted before and after the Federal government of Nigeria enforced restriction. The ordinary least squares estimator was used to estimate the parameters of the model. We carry out diagnostic checks and found out the model fitted well to the dataset. We compared the actual values with the predicted values from April 5 to April 13, 2020, and observed the predictions were very close. We found that travelling history and contacts increase people chances of being infected with COVID-19 by 85% and 88% respectively. In conclusion, the government should enforce the right policy for the containment of COVID-19.

Declaration of competing interest

The authors declare that they have no conflict of interest.

Handling editor: Dr. J Wu