On the efficiency of foreign exchange markets in times of the COVID-19 pandemic

Highlights

• •The COVID-19 pandemic has jolted foreign exchange markets within a short time.
• •We measure forex efficiency with multifractal detrended fluctuation analysis.
• •We find varying degrees of forex market efficiency before and during COVID-19.
• •Investors can structure their investment strategies to exploit market inefficiency.
• •Our findings may help policymakers find responses to such forex market upheavals.

Abstract

We employ multifractal detrended fluctuation analysis (MF-DFA) to provide a first look at the efficiency of forex markets during the initial period of the ongoing coronavirus disease 2019 (COVID-19), which has disrupted the global financial markets. We use high-frequency (5-min interval) data of six major currencies traded in forex markets during the period October 1, 2019 to 31 March 31, 2020. Before applying MF-DFA, we examine the inner dynamics of multifractality through seasonal and trend decompositions using loess. Overall, the results confirm the presence of multifractality in forex markets, which demonstrates, in particular, (i) a decline in the efficiency of forex markets during the COVID-19 outbreak and (ii) heterogeneous effects on the strength of multifractality of exchange rate returns under investigation. The largest effect is observed for the Australian dollar, which shows the highest (lowest) efficiency before (during) the COVID-19 pandemic, assessed in terms of low (high) multifractality. The Canadian dollar and the Swiss Franc exhibit the highest efficiency during the COVID-19 outbreak. Our findings may help policymakers shape a comprehensive response to improve forex market efficiency during such a black swan event.

1. Introduction

The COVID-19 pandemic has jolted the global economy within a short span of time. Many countries around the world have been obligated to impose, among others, travel restrictions, border shutdowns, lockdowns, and social distancing in order to control the pandemic. These measures have severe impacts on supply channels, economic activities, and international trade at all scales. In its April 2020 World Economic Outlook, the International Monetary Fund predicted that the global economy might contract by 3% in 2020.1 Financial markets are also witnessing a massive disruption with a very aggressive revaluation and adjustment process across the world amid this global pandemic. For instance, the Dow Jones Industrial Average dropped by 12.9%, and the S&P 500 index lost nearly 12% in a single day, on March 16, 2020. It was the worst percentage drop since the infamous “Black Monday” crash of 1987. Stock markets are in turmoil as the pandemic has severely restricted economic activity due to protection measures and suspension of major events.

It is now well known that sudden “large” shocks, such as the global financial crisis of 2008, cause structural changes in both commodity and financial markets, which can then have potential asymmetric effects on market efficiency, portfolio allocation, and volatility spillovers (e.g., Rapach and Strauss, 2008; Managi and Okimoto, 2013; Mensi et al., 2015). Since the onset of the COVID-19 pandemic, the foreign exchange (forex) market, which is by far the largest financial market,2 has also witnessed unprecedented movements, and is thus subject to close watch by global portfolio investors, market regulators, and policymakers. Most central banks scrambled to adjust the monetary frameworks to address the feedback loop between exchange rate movements and capital outflows in a bid to weather the financial setbacks from the COVID-19 outbreak. Policymakers’ concerns stem from the simultaneous decrease in aggregate and foreign demand, which could put pressure on the currencies with the flow of foreign aid across countries from international donor agencies and financial institutions. Both corporate and institutional investors are worried about the eventual fall of their portfolio investments and seek possible safe havens for their financial assets as the dollar funding cost in the forex market has demonstrated a sharp rise during this turmoil. While the current aggregate volatility levels are atypical, the COVID-19 impact may vary among currencies according to their market standing, risk sensitivities, and the government's policy response. For instance, the Australian dollar (AUD) hit a 17-year low of $0.59215, and the New Zealand dollar an 11-year low of $0.5850 cents. On the other hand, the currencies viewed as safe havens, including the Japanese yen (JPY), traded at 107.42 yen per US$ while the Swiss Franc (CHF) rose to US$ 0.9598 per CHF.

Concerning the COVID-19 impact on forex markets, a critical aspect that needs to be addressed is the efficiency of the forex market. The extant research shows that forex market efficiency is difficult to detect (Katusiime et al., 2015), and the market efficiency of exchange rates changes over time, in particular, during crisis-like situations (Levich et al., 2019). Inefficiency in the forex market generates different puzzling anomalies and delayed overshooting (Li and Miller, 2015). Forex market efficiency is estimated through various approaches such as pairwise co-integration tests (Layton and Tan, 1992), linear unit root tests (Giannellis and Papadopoulos, 2009), correlation functions (Podobnik et al., 2002), network analysis (Jeong et al., 2000), and Pedroni's panel co-integration method (Makovský, 2014). The mainstream literature on financial markets is mainly based on the fundamental assumption that stock prices follow a normal distribution and on Bachelier's (1900) random walk hypothesis (RWH). However, the econophysics literature rejects the RWH hypothesis, arguing that asset prices have different fundamental properties (Mandelbrot, 1967;1971; 1997), including fat tail (Gopikrishnan et al., 2001), long-term correlation (Alvarez-Ramirez et al., 2008), volatility clustering (Kim and Eom, 2008), fractals and multifractals (He et al., 2007), and chaos (Adrangi et al., 2001). Therefore, fractal analysis has widely been applied in the financial market research. By using R/S analysis, Peters (1994) and Edgar (1991) demonstrated monofractal properties in several financial markets. However, monofractals cannot describe the height-height correlation function (Barabási and Vicsek, 1991), while multifractal detrended fluctuation analysis (MF-DFA) can overcome this weakness (Kantelhardt et al., 2002; Alvarez-Ramirez et al., 2008). The MF-DFA method has been employed in finance literature by, among others, Podobnik and Stanley (2008), Wang et al. (2010), Mandelbrot et al. (1997), Kumar and Deo (2009), and Oh et al. (2010).

In the context of forex market efficiency, Ning et al. (2018) investigate the multifractal properties of both British Pound (GBP) and Euro (EUR) exchange rates from 2015 to 2017 through the MF-DFA method. Their results reveal significant nonlinear multifractal properties. Han et al. (2019) show, by examining the exchange rates of four significant currencies (EUR, GBP, CAD and JPY), that their fat-tail distributions and long-range correlation cause their multifractal properties. A recent work (Shahzad et al., 2018) confirms that JPY is a highly efficient currency while GBP is the least efficient. While it is too early to estimate the exact magnitude of economic and financial impacts of the COVID-19 pandemic, this paper provides a first look at the forex market using a sophisticated MF-DFA approach to understand the patterns of large movements in major currencies and the extent of forex market risk due to the pandemic.

This study contributes to the literature in three distinct ways. First, we use five-minute high-frequency exchange rate data for six major currencies (AUD, CAD, CHF, EUR, GBP, and JPY) against the US dollar to draw new and useful conclusions about the impacts of COVID-19 on forex market efficiency. Second, we decompose intraday exchange rate returns by seasonal-trend decomposition using loess (STL). The STL method is advantageous in that it enables us to unearth the inner dynamics of asset returns in addition to improving information reliability and decomposition by removing seasonal components (Laib et al., 2018a). Third, we use the robust multifractal MF-DFA technique for an in-depth comparison of the multifractal behavior of sample currencies before and during the COVID-19 outbreak. The MF-DFA, a generalization of the DFA approach (Kantelhardt et al., 2002), allows estimation of multiple scaling exponents within time series.

Our main findings show evidence of a significant change in the strength of multifractality, pointing to a general decline in forex market efficiency during the COVID-19 period compared to the pre-pandemic level. The efficiency difference might have its roots in how investors perceive currencies—as assets—and in the fundamentals that determine their underlying value. In any case, the price efficiency of any asset is based on the premise that its prices have incorporated all relevant information. Considering various channels through which prices adjust in the forex markets, the difference in the speed of price adjustment may reflect overshooting. Dornbush (1976) shows that an unanticipated change in money supply leads to exchange rate overshooting because consumer prices cannot move immediately to reflect the change in money supply. Therefore, a temporary disequilibrium in forex markets may represent the adjustment of prices based on information received through a relatively faster channel.

The COVID-19 outbreak has led to an immediate response from investors while policymakers’ interventions may take time. Forex markets tend to become inefficient under such volatile conditions. Against this backdrop, our study provides policymakers and regulators with well-coordinated and gradual responses to the turbulent conditions in the forex markets in order to ensure their efficiency and the stability of the respective currencies.

The remainder of the study is organized as follows. Section 2 presents the data and methodology. Section 3 reports and discusses the empirical results. Section 4 provides some concluding remarks.

2. Data and methodology

2.1. Data description

We use high-frequency data (five-minute intervals) to reveal the inner dynamics of forex market efficiency under the COVID-19 impact. The high-frequency data more accurately accounts for long memory and structural changes due to improved continuity in the distribution function. The high-frequency data sample consists of six major currencies traded in forex markets: AUD, CAD, CHF, EUR, GBP, and JPY. All prices are expressed in indirect quotes against US dollars (i.e., amounts of foreign currency per unit of the US dollar). Data from October 1, 2019 to March 31, 2020 are collected from TrueFx and converted to five-minute windows using the “high-frequency” toolkit in R, developed by Boudt et al. (2020).3

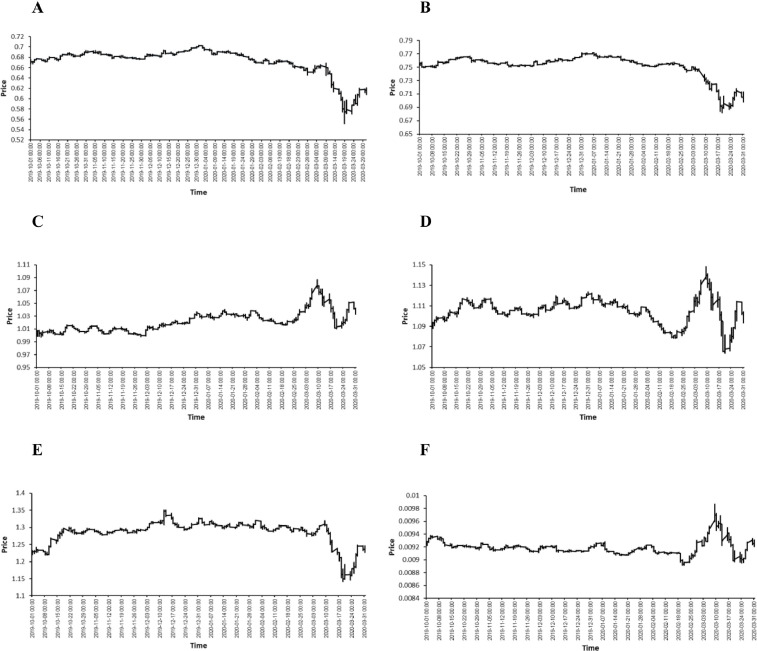
COVID-19 was first reported by Chinese authorities on December 31, 2019 to the World Health Organization (WHO). Based on this date, the intraday exchange rate data are divided into two three-month trading periods (Zhu et al., 2020): October 1, 2019 to December 31, 2019 (before COVID-19) and January 1, 2020 to March 31, 2020 (during COVID-19). The intraday five-minute exchange rate fluctuations are presented in Fig. 1 . We calculate the intraday forex return as in Eq. (1).

$$r_i\left(t\right)=ln{p}_i\left(t\right)-ln{p}_i\left(t-\Delta t\right)$$ (1)

where, p_i(t) denotes the closing price of currency i at time t, Δt is the time interval Δt (five minutes).

Fig. 1.

Time trend of five-minute currency rates from October 1, 2019 to March 31, 2020 (see Table 1 for explanation of the currency codes).

Table 1 shows descriptive statistics of exchange rate returns for the six currencies used in this study. The average five-minute returns are nearly zero before COVID-19. However, the AUD, CAD, EUR, and GBP returns turn negative while the JPY and CHF remain positive during the COVID-19 outbreak. Before COVID-19, the GBP exhibit the highest volatility and fluctuates within a range of 2 to −0.6 basis points, while the AUD return series remains the most volatile during the COVID-19 outbreak fluctuating between 1.1 to −1.6 basis points. All exchange rates were positively skewed before COVID-19, but the AUD, CAD, and GBP have become negative during the pandemic. The kurtosis coefficient of all return series is greater than 3, indicating their fat-tailed behavior. Fig. 1 shows all exchange rate trends before and during COVID-19. A consistent movement with small fluctuations can be noticed before COVID-19, while the first quarter of 2020 exhibits relatively large fluctuations.

Table 1.

List of currencies with summary statistics of their exchange rate returns against the US dollar (5-minute interval).

Currency	Australian dollar-AUD	Canadian dollar-CAD	Swiss Franc-CHF	Euro-EUR	British Pound-GBP	Japanese Yen-JPY
Summary Statistics of Exchange rate returns
2019* (Before COVID-19)
Mean	0.000002	0.000001	0.000002	0.000002	0.000004	0.000000
Std. Dev.	0.000229	0.000164	0.000197	0.000172	0.000379	0.000175
Minimum	−0.003934	−0.004323	−0.003187	−0.003072	−0.006215	−0.002948
Maximum	0.003485	0.005343	0.003490	0.003598	0.020735	0.004551
Skewness	0.408098	0.818122	0.429145	0.792372	9.226872	0.360279
Kurtosis	22.960322	114.113335	26.032817	37.991999	501.914380	53.750461
Observations	18,950	18,950	18,950	18,950	18,950	18,950
2020⁎⁎ (During COVID-19)
Mean	−0.000007	−0.000004	0.000000	−0.000001	−0.000003	0.000001
Variance	0.000720	0.000399	0.000399	0.000393	0.000535	0.000476
Minimum	−0.016646	−0.015399	−0.004651	−0.004142	−0.009830	−0.005915
Maximum	0.011148	0.004472	0.012390	0.007217	0.009860	0.014995
Skewness	−1.367940	−3.624304	1.678191	0.821631	−0.600611	3.188010
Kurtosis	61.144564	143.700572	65.516308	25.499180	35.421532	96.912052
Observations	18,362	18,362	18,362	18,362	18,362	18,362

^⁎2019: October 1, 2019 to December 31, 2019.

^⁎⁎2020: January 1, 2020 to March 31, 2020.

2.2. Methodology

We apply multifractal detrended fluctuation analysis (MF-DFA) to measure the efficiency of exchange rates. Before doing so, we employ the STL method to decompose the time series (Cleveland et al., 1990). Since we use five-minute returns, the STL method helps handle any type of seasonality because it is robust to outliers and flexible enough to allow seasonal component variations over time. In addition to improved reliability and decomposition through removing seasonal components, it also reveals the inner dynamics of asset returns (Laib et al., 2018a). From a technical perspective, the STL method breaks down each exchange rate return time series into a deterministic trend (T_i), a seasonal (S_i) component, and a stochastic remainder (R_i) component (Laib et al., 2018b; Miloş et al., 2020) as follows:

$$r_i\left(t\right)=T_i+S_i+R_i$$ (2)

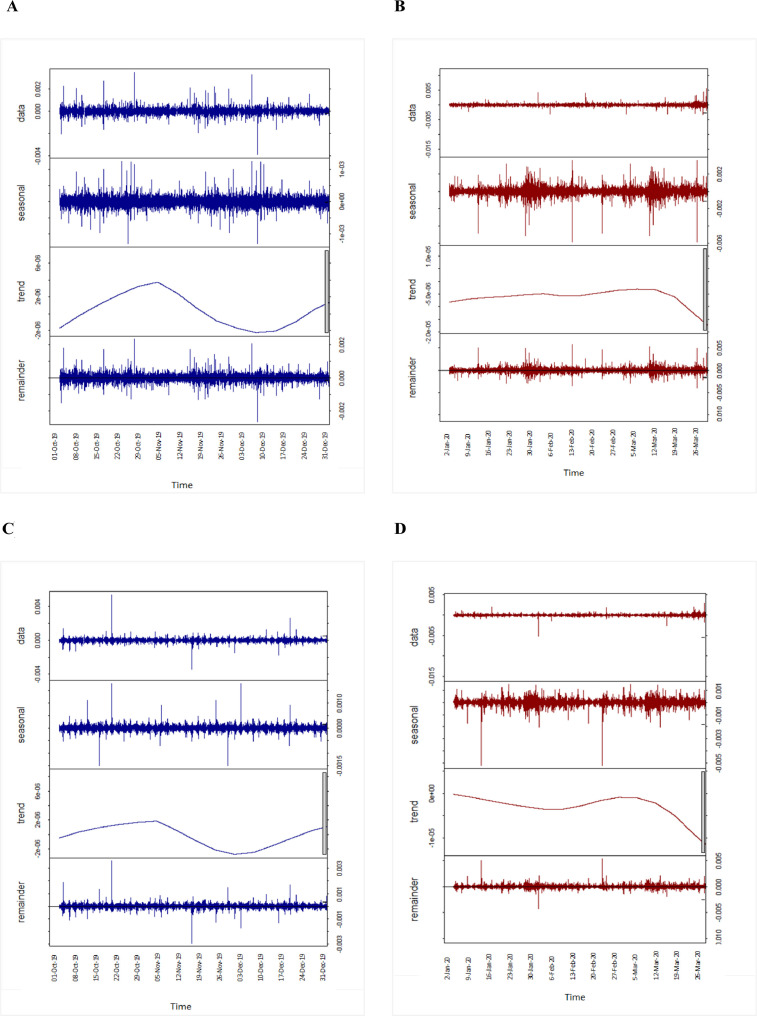
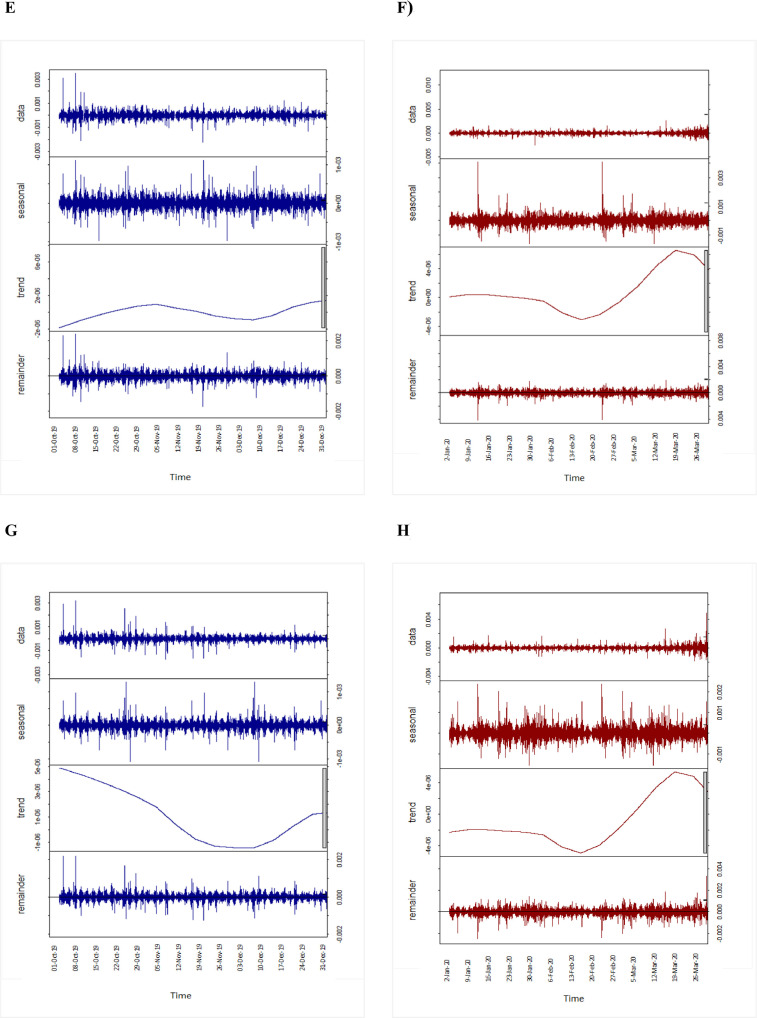
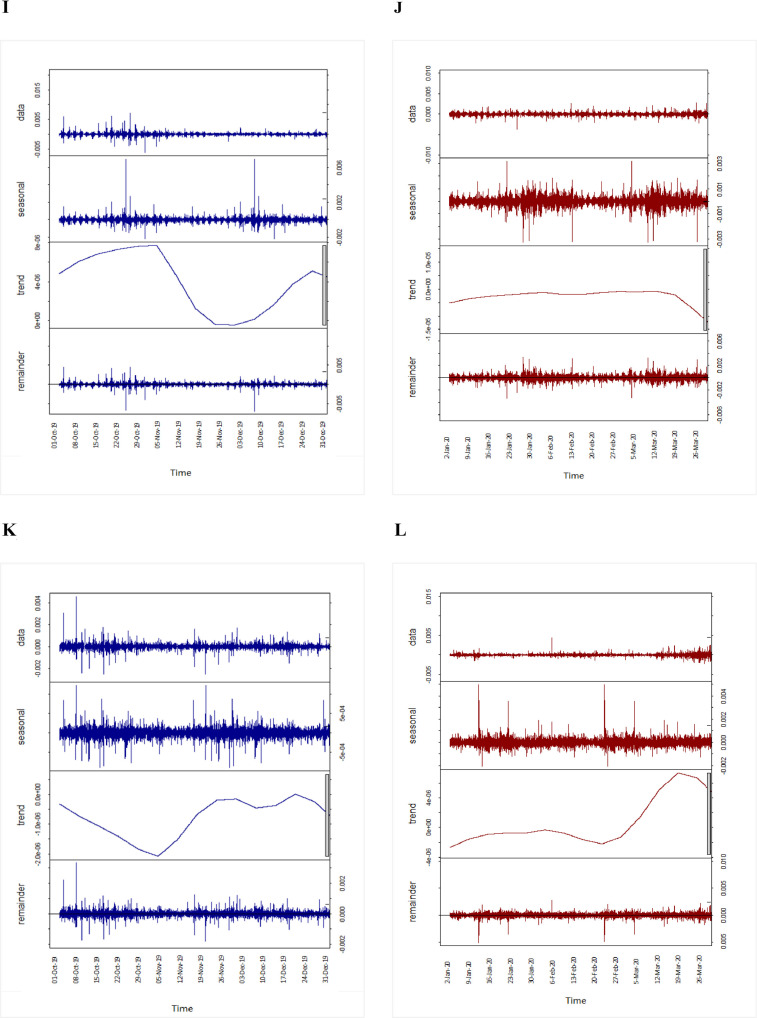
To carry out the STL decomposition, we use the R Stats package (Laib et al., 2018a; Shiskin, 1965; Miloş et al., 2020).4 For our 24-hour trading data with five-minute frequency, we set the span of the loess window for seasonal extraction equal to 288, which is the number of trading prices in one day. The results of the STL decomposition of intraday exchange rates are shown in Fig. 2 . For example, four AUD graphs in panel A present the original time series of daily returns (first row), the seasonal component (second row), the trend component (third row), and the remainder component (fourth row). The AUD exhibits a seasonal pattern consistent with previous findings (De Bondt and Thaler, 1987; Miloş et al., 2020). However, the trend component shows a decline after mid-March 2020. As to the remainder component, it does not follow any specific pattern. The STL decomposition results for other exchange rate returns are reported in Fig. 2, panels B to L.

Fig. 2.

STL decomposition of intraday (five-minute) exchange rate returns for 2019 (blue) and 2020 (red). Row 1: Original five-minute time series; row 2: seasonal component; row 3: trend component; row 4: remainder. STL = seasonal-trend decomposition using loess; see Table 1 for explanation of the currency codes. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.2.1. Multifractal detrended fluctuation analysis

Once STL decompositions are obtained, we apply the MF-DFA technique to compute multifractality in the time series following a five-step procedure. Formally, let $\left\{Z_{t,t=1,\dots \dots ..,N}\right\}$ be a possible non-stationary time series and N the length of the series (number of observations). Then, the MF-DFA method can be summarized as follows:

• Step 1: Construct the profile  X _( k)for MF-DFA estimation as follows:

  $$X_{\left(k\right)}=\sum _{t=1}^k\left(z_t-\overline{z}\right)$$ (3)

where,$k=1,2,3......,N$ and $\overline{z}=\frac{1}{N}\sum _{t=1}^N{z}_{\left(t\right)}$ represents the average of the whole time series.

• Step 2: Divide the profile X _(k) into N_s= $\left[N/s\right]$ non-overlapping boxes of the same length s. While the length N of the series is usually not a multiple of the considered time scale s, it disregards a short part of the profile X _(k) at the end. It is not necessary to disregard this part of the series, and the same procedure will be repeated from the opposite side. Thus, 2N_s segments are obtained in total. Peng et al. (1994) initiated the process with $10<s<Ns/5$.

• Step 3: Calculate the local trend for each of the 2N_s parts by kth-order polynomial fit. After that, the variance is given by

  $$F^2\left(s,m\right)=\frac{1}{s}\sum _{j=1}^s{\left\{X\left[\left(m-1\right)s+j\right]-x_m\left(j\right)\right\}}^2$$ (4)

for the segments between m = 1 and m = N_s and by

$$F^2\left(s,m\right)=\frac{1}{s}\sum _{j=1}^s{\left\{X\left[N-\left(m-N_s\right)s+j\right]-x_m\left(j\right)\right\}}^2$$ (5)

for the segments between $m=N_{s+1}$and $m=2N_s.$

• Step 4: In Eqs. (4) and (5), x _m(j) represents the polynomial fit of the segments. Averaging yields the qth-order fluctuation function, given by

  $$F_{q\left(s\right)}={\left\{\frac{1}{2N_s}\sum _{\rho =1}^{2N_s}{\left[F^2\left(s,m\right)\right]}^{q/2}\right\}}^{1/q}$$ (6)

for any q ≠ 0,  and by

$$F_{0\left(s\right)}=exp\left\{\frac{1}{4N_s}\sum _{\rho =1}^{2N_s}ln\left[F^2\left(s,m\right)\right]\right\}$$ (7)

for $q=0.$

The parameter q allows us to distinguish between segments with large and small fluctuations. Its negative and positive values show small and large fluctuations, respectively. The DFA case is given for q = 2. Note that F _q(s) is the increasing function of s.

• Step 5: Compute the relationship between F _q(s) and s. The task consists of establishing the scaling exponent of the fluctuation function for any fixed q. If F _q(s) is a power law, the time series are in the log-log scale for that particular q.

  $${\mathit{F}}_{\mathit{q}\left(\mathit{s}\right)}\sim {\mathit{S}}^{\mathit{h}\left(\mathit{q}\right)}$$ (8)

Through the least-square fit, the slope of ln F_q(s) is the generalized Hurst exponent h(q), which describes the fractal structure of the time series. An increase in the s scale shows how fast  F_q(s) of local fluctuations grows. If h(q) is constant at different values of q, then the series is monofractal. Otherwise, the series is said to be multifractal. For multifractal series, h(q) describes the scaling behavior of segments with large (small) fluctuations when q is positive (negative). Usually, the multifractal series comes with smaller h(q) at positive q values. The range of h(q), which indicates the level at which the series is multifractal, can be estimated by$\Delta h=h_{\left(qmin\right)}-h_{\left(qmax\right)}$. Specifically, it is called the multifractal spectrum width, which represents the interval between the maximum and minimum probabilities and, thus, measures the degree of the multifractality property. The h(q) value declines as q increases (Zunino et al., 2008), and a higher Δh indicates the presence of higher multifractality in time series (Cajueiro et al., 2009; Anagnostidis et al., 2016). The richer the multifractality, the higher is the degree of market inefficiency because of long-range autocorrelation properties and fat-tail characteristics. Since multifractality is negatively correlated with market efficiency, the higher the width of the multipole spectrum, the lower is the degree of market efficiency (Caraiani, 2012; Domino, 2011). The MF-DFA turns into the DFA at q = 2. More broadly, the Hurst exponent describes the fractal structure of the time series. When h(q) = 0.5, the fluctuation related to q is said to follow a random walk. It is persistent when h(q) > 0.5 and anti-persistent when h(q) < 0.5.

The h(q) value estimated from the MF-DFA can also be presented as a function of Renyi exponent τ(q), as follows:

$$\mathit{\tau }\left(\mathit{q}\right)=\mathit{qh}\left(\mathit{q}\right)-1$$ (9)

The singularity strength h(q) and the singularity spectrum D(q) can be calculated via Legendre transform, or related to h(q), through the following equations:

$$h\left(q\right)=\frac{d\tau \left(q\right)}{dq}=hq-qh{}^{\prime }\left(q\right)$$ (10)

$$D\left(q\right)=qhq-\tau \left(q\right)=1+q\left[\alpha -h\left(q\right)\right]$$ (11)

The multifractal spectrum D(q) describes the fractal dimension of the ensemble formed by all the points that share the same singularity exponent h(q). The width of the multifractal spectrum is the difference between h(q) _max and h(q) _min, representing the maximum and minimum probability, respectively. A wider multipole spectrum potentially indicates a lower efficiency level in the forex market (Domino, 2011; Caraiani, 2012). We use the R package MF-DFA, developed by Laib et al. (2018a) and Laib et al. (2018b), for the MF-DFA analysis.5 We used time scales ranging from 10 to N/5 intraday (five-minute exchange rate) observations.

3. Empirical results and discussions

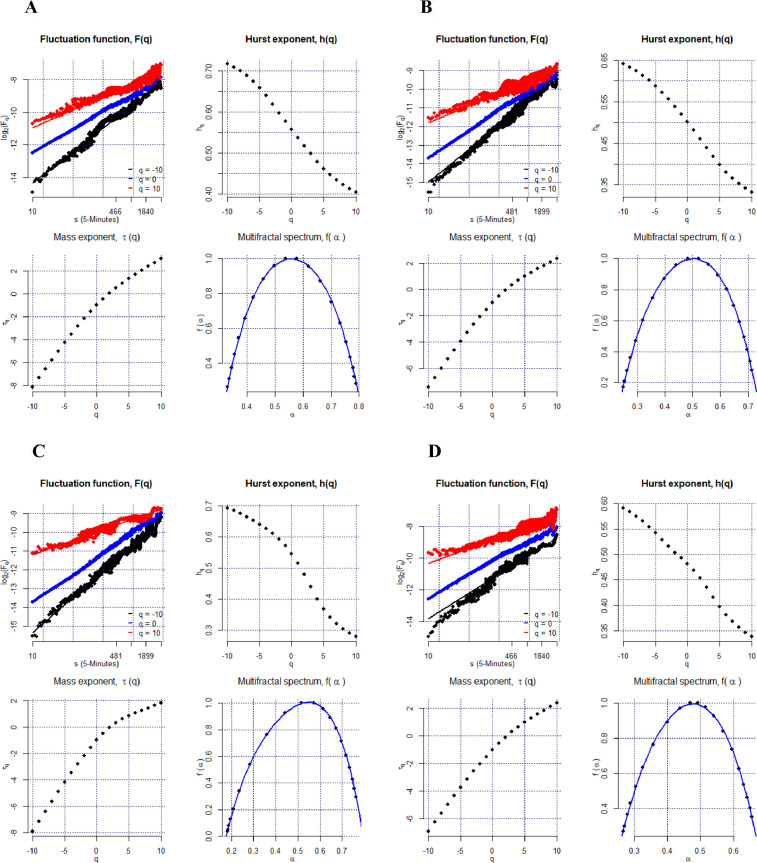
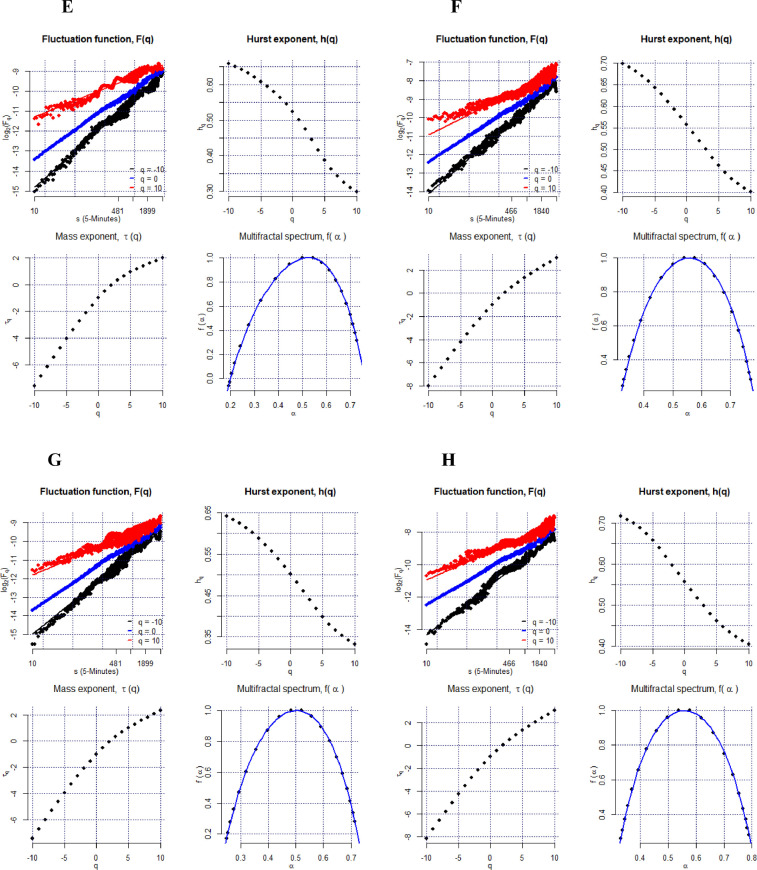
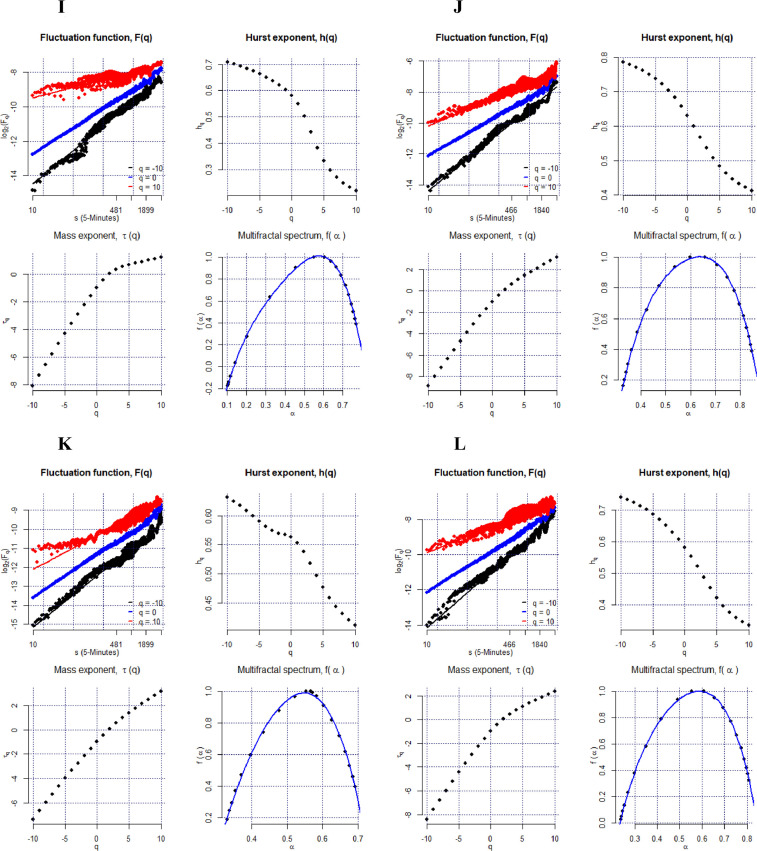
Fig. 3 shows the MF-DFA findings for the remainder component of all exchange rates for 2019 (before COVID-19) and 2020 (during COVID-19) under consideration. It indicates the fluctuation function log₂(F_q(s)) versus log₂(s) plot (q = −10, q = 0, and q = 10), the value of the generalized Hurst exponent h(q) over the range q ∊ [−10, 10], the Renyi exponent τ(q), and the multifractal spectrum f_α.

Fig. 3.

The MF-DFA results of intraday time series of exchange returns. Top left: Fluctuation functions for q=−10, q = 0, q = 10. Top right: Generalized Hurst exponent for each q. Bottom right: Mass exponent, τ(q). Bottom left: Multifractal spectrum. MF-DFA = multifractal detrended fluctuation analysis; see Table 1 for explanation of the currency codes.

For illustration, Fig. 3-A shows the standard MF-DFA findings for the remainder components of AUD for 2019. The top-left panel of Fig. 3-A shows the fluctuation function log₂(F_q) versus log₂(s) plot at q = −10, q = 0, and q = 10, which is well-shaped and appears as a straight line. We calculate the slope of the generalized Hurst exponents for both the short and the long term. The results for 2019 show that h(q) reaches its highest value of 0.58 at q = −10, declines to 0.53 at q = 0, and drops to its lowest value of 0.45 at q = 10. Likewise, from its highest value of 0.71 in 2020, at q = −10, it declines to 0.49 at q = 0 and then to 0.28, its lowest value, at q = 10. This declining trend of the generalized Hurst exponent h(q) confirms its dependence on q, suggesting the existence of multifractality in the time fluctuations of the remainder component for the AUD in 2019. We obtain similar results and patterns for the series of exchange rate returns of the remaining five currencies. Their results are presented in Fig. 3, from 3-B to 3-L.

Furthermore, the Hurst component for 2019 and 2020, h(q) = 0.52 and h(q) = 0.46, respectively, at the q = 2 scaling component (the setting for stationarity of return series) indicates high persistence in 2019 and low persistence in 2020 in the remaining components. Figs. 3-A and 3-B (bottom left) show the Renyi exponent, τ(q), which is nonlinear for multifractal series. In 2019 and 2020, τ(q) exhibits an exponential shape for AUD, indicating multifractality in the exchange rate returns. Finally, in Figs. 3-A and 3-B (bottom right), the multifractal spectrum f_α shows a single-humped shape, confirming the presence of multifractality in the AUD returns series. The exchange rate returns of the other five currencies, displayed in Fig. 3 from 3-B to 3-L, are in line with these results and patterns.

Table 2 reports the width of the generalized Hurst exponent ∆h, which indicates the strength of multifractality, for 2019 (before COVID-19) and 2020 (during COVID-19) over the range q ∊ [−10, 10]. The strength of multiple spectra in Fig. 3 also demonstrates the comparative strength of multifractality across exchange rates before and during the COVID-19 pandemic. The larger the range, the more the multifractality dwells in the series (Kantelhardt et al., 2002). The finding evidences a declining pattern of the Hurst exponent h(q) for all six exchange rates we consider in 2019 and 2020, confirming the time fluctuations of multifractality in the remainder components (Laib et al., 2018a).

Table 2.

Generalized Hurst exponents for six currency exchange rates against the US dollar for 2019 and 2020 and their range over q ∊ [−10, 10].

Order q	AUD-19	CAD-19	CHF-19	EUR-19	GBP-19	JPY-19	AUD-20	CAD-20	CHF-20	EUR-20	GBP-20	JPY-20
−10	0.5825	0.6915	0.6586	0.6410	0.7076	0.6315	0.7065	0.5907	0.6988	0.7164	0.7854	0.7405
−8	0.5695	0.6748	0.6424	0.6238	0.6930	0.6173	0.6921	0.5752	0.6814	0.6990	0.7707	0.7243
−6	0.5542	0.6531	0.6214	0.6012	0.6739	0.5998	0.6732	0.5546	0.6580	0.6743	0.7506	0.7016
−4	0.5397	0.6259	0.5949	0.5724	0.6496	0.5814	0.6493	0.5290	0.6279	0.6397	0.7226	0.6705
−2	0.5311	0.5922	0.5631	0.5387	0.6209	0.5697	0.6183	0.5036	0.5935	0.5976	0.6829	0.6308
0	0.5280	0.5456	0.5243	0.5014	0.5817	0.5632	0.5696	0.4816	0.5577	0.5564	0.6298	0.5825
2	0.5205	0.4787	0.4742	0.4606	0.5032	0.5382	0.4903	0.4541	0.5201	0.5173	0.5676	0.5229
4	0.5025	0.4003	0.4156	0.4182	0.3819	0.4968	0.4026	0.4161	0.4808	0.4793	0.5078	0.4538
6	0.4810	0.3407	0.3632	0.3808	0.2972	0.4589	0.3423	0.3819	0.4462	0.4469	0.4631	0.3972
8	0.4627	0.3035	0.3252	0.3527	0.2492	0.4313	0.3056	0.3570	0.4205	0.4226	0.4331	0.3603
10	0.4485	0.2796	0.2991	0.3325	0.2200	0.4118	0.2821	0.3392	0.4021	0.4048	0.4127	0.3363
∆h	0.1340	0.4119	0.3595	0.3085	0.4876	0.2197	0.4244	0.2515	0.2967	0.3116	0.3727	0.4042

Note: See Table 1 for explanation of the currency codes.

More concretely, the GBP shows the highest multifractality in 2019, with the widest generalized Hurst exponent (∆h = 0.49), followed by the CAD (∆h = 0.41), thus indicating the highest level of unevenness in local fluctuations in the GBP and CAD exchange rate return series. By contrast, the AUD and JPY have the lowest degree of multifractality, with ∆h = 0.13 and ∆h = 0.22 (Hurst exponent width), respectively, corresponding to the highest level of evenness in local fluctuations in the AUD and JPY exchange rate returns. The EUR (∆h = 0.31) and CHF (∆h = 0.36) stay in the middle in terms of multifractality before COVID-19. Among the six intraday exchange rate returns, the GBP and CAD currencies witness the highest degree of multifractality overall, while the AUD and JPY exhibit the lowest degree before COVID-19.

COVID-19 caused significant movements and affected the strength of intraday multifractality in the first three months of 2020 with marked changes in the strength of multifractality of currencies. More specifically, during the COVID-19 period, we observe the highest multifractality for the AUD (∆h = 0.42) followed by the JPY (∆h = 0.40), while the CAD (∆h = 0.25) and CHF (∆h = 0.30) have the lowest multifractality. The multifractal properties are indicative of the financial markets’ efficiency (Anagnostidis et al., 2016). Therefore, based on the multifractal properties observed, the efficiency levels of AUD, JPY, and EUR decreased while those of CAD, CHF, and GBP improved during the COVID-19 period. The AUD showed the most extreme behavior among the six selected currencies; it was the most efficient currency before COVID-19 but became less efficient with the outbreak of the pandemic.

Similarly, in terms of relative efficiency among the six currencies, the JPY was the second-most efficient currency before the COVID-19 period, but was severely affected during the outbreak and became one of the inefficient currencies. Overall, the increase in multifractality confirms that COVID-19 has adversely affected the forex market as it touches a lower level of inefficiency. Our findings are broadly in line with Shahzad et al. (2018).

The persistence of the return series is an important determinant of multifractality. The classical Hurst exponent (q = 2) shows persistent behavior (positive autocorrelation) in 2019 for the JPY (h(q) = 0.54), the AUD (h(q) = 0.52) and the GBP (h(q) = 0.50), which means that positive (negative) values in the previous period would most probably be chased by positive (negative) values in the subsequent period. The remaining three currencies, namely, CAD (h(q)=0.48), CHF (h(q)=0.47), and EUR (h(q)=0.46), exhibit anti-persistent behavior with negative autocorrelation. This evidence implies that any change (positive/negative) in previous time periods would probably be followed by an opposite (negative/positive) change in subsequent times.

The influence of COVID-19 can be noticed in the persistence behavior of forex markets. Three out of six currencies analyzed in the COVID-19 period show changes in their persistence pattern. In 2020, the CHF (h(q) = 0.52) and EUR (h(q) = 0.51) shifted from anti-persistent to persistent behavior. The Hurst exponent (q = 2) for the AUD declined from h(q) = 0.52 in 2019 to h(q) = 0.49 in 2020. We observe no change in the persistence levels for the GBP and the JPY before and during COVID-19. Similarly, the CAD was found to be anti-persistent before and during the COVID-19 period. Overall, the persistence level has increased among these exchange rates.

The AUD and JPY have shown a most peculiar behavior during the COVID-19 pandemic. Both currencies demonstrated a high degree of inefficiency, in relative terms, during the COVID-19 period as opposed to increasing efficiency before. On the other hand, the CAD was at the lowest end in terms of efficiency before COVID-19, but demonstrated the highest degree of efficiency during the pandemic. These differences might have their roots in how these currencies are perceived by investors—as financial assets—and in the fundamentals that determine their underlying value. The AUD is known as a commodity currency because it is sensitive to fluctuations in commodity prices (Lodewijks and Mmnademi, 2017). There is also evidence that it is highly correlated with Chinese economic conditions because of Australia's raw material exports to Chinese industries.6 With the economic slowdown in the Chinese economy, the demand for the AUD currency decreased. Moreover, as COVID-19 cases rose in China and other countries, the AUD depreciated against the USD in the forex market. The decrease in interest rates decided by the Reserve Bank of Australia due to lower inflation expectations will prompt investors to shift to markets offering higher returns.

The recovery of the AUD relative to the USD towards the end of March 2020 represents the risk appetite of investors.7 Our analysis shows that the AUD became more inefficient after the COVID-19 outbreak, which suggests profitable investment opportunities. In the meanwhile, the JPY currency, which generally is considered a safe haven, lost its value amid rising COVID cases in neighboring China.8 For its part, the CAD depreciated against the USD due to COVID-19 outbreak fears, and the Canadian central bank left room for interest rate cuts if required.9 We cautiously explain it as an outcome of the central bank's timely intervention to provide room for economic recovery and stability that, in turn, boosted investor confidence in the Canadian economy and its currency. Thus, we see lower volatility in CAD/USD during COVID-19 compared to the prior period.

In a nutshell, the varying impacts of COVID-19 on the multifractality and efficiency of the forex markets under consideration can be explained by the structure of these markets and the behavior of traders during the COVID-19 pandemic. A significant portion of international news headlines evoked uncertainty, negative sentiments, and fear and sadness (Aslam et al., 2020a). In such a turbulent environment, investors tend to shy away from trading activity to avoid financial losses, which adversely affects the financial markets (Mukerji and Tallon, 2001; Levy and Galili, 2006). COVID-19 affects not only the trading behavior but also the multifractal behavior of financial markets with the considerable uncertainty (Aslam et al., 2020b) and complex issues associated with a low degree of information determinacy. These factors potentially explain the differences in the overall effects of COVID-19 on forex market efficiency, with the heterogeneous expectations of investors and traders about the fundamentals underlying a currency as well as strong trade ties with a severely affected country as with the AUD and reversal of safe haven perception as in the case of the JPY.

Forex market efficiency also depends on the policy response from governments on both fiscal and monetary aspects, which are subject to several factors linked to the prevailing economic and political environment, among others. For example, an unanticipated change in money supply may lead to exchange rate overshooting as consumer prices cannot move immediately to reflect the money supply change (Dornbush, 1976). Building on this analogy, we can argue that a temporary disequilibrium in the forex markets may represent the adjustment of prices to information received through a relatively faster channel. The COVID-19 pandemic emerging from China received a quick response from investors while adjustments by policymakers may take time due to the rather measured interventions such as the recent deployment of central bank dollar swap lines.

Conclusion

This paper provides a first look at forex market efficiency in the context of the COVID-19 pandemic as its economic and social costs are a matter of great concern to the society, policymakers, market operators, and individual investors. For this purpose, we conducted a comparative analysis of the efficiency level of six major currencies traded in forex markets, namely, AUD, CAD, CHF, EUR, GBP, and the JPY. Our study is thus vital as it provides an insightful analysis of fractals in the six major international forex markets. The intraday data of five-minute frequency from October 1, 2019 to March 31, 2020 is divided into before and during the COVID-19 outbreak, with a three-month trading window for each. The robust MF-DFA and STL methods are employed to capture the presence of multifractality in the sample exchange rates against the UD dollar. These methods provide insight into the long-range dependence of these exchange rates in terms of their multifractal structures.

Market efficiency is pivotal in both resource allocation and capital formation, which lead to economic development and stability (Rizvi and Arshad, 2016). The findings of this study show varying degrees of forex market efficiency before and during the COVID-19 outbreak. Investors in the forex market can structure their investment and risk management strategies to exploit market inefficiencies (Dragotă and Ţilică, 2014). In this scheme of things, the estimated Hurst coefficient h(q) provides insight into the dynamics and trending characteristic of forex markets, which are useful for investors in aligning their strategies to market conditions. Against the backdrop of COVID-19, both AUD and CAD exchange rates exhibit anti-persistent behavior (0 < H < 0.5), suggesting mean-reverting characteristics in the two currencies. This implies that, for a time series, a higher financial asset value in the prior periods may decline in the subsequent periods through a mean-reversion process. For the remaining four currencies, a high value of the H exponent (0.5 < H < 1) is indicative of long memory in the time series, where the future value of a series depends partially on its values in prior periods.

In non-technical terms, this evidence suggests a lack of efficiency in the sample currency markets both before and during the COVID-19 pandemic. The AUD and JPY demonstrate the highest degree of efficiency before whereas the CAD and CHF do so during COVID-19. While only three (CAD, CHF, and GBP) of the six major currencies improved their efficiency level during COVID-19, most currency returns generally tend to be more persistent.

Since the COVID-19 pandemic is an ongoing crisis, we believe that no single policy response can be considered successful in the short term. The extant literature suggests minimum intervention in forex markets, while effective management of internal risks in the forex markets (Han et al., 2020) and financial liberalization (Kawakatsu and Morey, 1999) improve market efficiency. The changes in the market efficiency levels of the considered forex markets may be driven by investors’ herd behavior due to the crisis and the fear prevailing in the market regarding the underlying fundamentals of the economy. Such behavior may lead to higher autocorrelation, and hence a decrease in market efficiency. Policymakers may potentially address such behavioral anomalies by ensuring stability in the underlying macroeconomic fundamentals. Market participants would do well to reassess their investment and risk management framework in order to mitigate the new and somewhat higher risk levels of their exposures during the current tumultuous times.

While we acknowledge that the findings of this study should be viewed with caution given the sample period under analysis, it does pave the way for future research regarding the COVID-19 impact on forex markets in the short and long run, the effectiveness of policy responses in maintaining their stability, and volatility transmissions, using larger samples and analysis windows. The changes in investor behavior across two time horizons will potentially transform market linkages and correlations. Thus, the fractal models can be used to further explore the fractal contagion effects caused by the COVID-19 pandemic. Moreover, investigating the primary source of the increase in multifractality to understand the psychological aspects of investment behaviors is potentially an interesting direction for future research.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

CRediT authorship contribution statement

Faheem Aslam: Conceptualization, Methodology, Software, Visualization, Formal analysis, Data curation, Writing - original draft, Writing - review & editing. Saqib Aziz: Conceptualization, Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Duc Khuong Nguyen: Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Khurrum S. Mughal: Conceptualization, Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Maaz Khan: Data curation.

Declaration of Competing Interest

None.

Biographies

Faheem Aslam is Assistant Professor at the Department of Management Sciences, Comsats University Islamabad, Pakistan. He earned his master's and Ph.D. Degrees from Hanyang University Business School, Seoul, South Korea. He deeply invests in creative and innovative research ideas related to financial analytics, data mining, artificial intelligence, and data sciences.

Saqib Aziz is Assistant Professor of Finance in Rennes School of Business in France. He is a PhD in Finance from Rennes 1 University, France. His-primary research interests is in empirical finance, corporate finance, stability of financial institutions - an analysis that cuts across investigating various types of risk and its genesis in mergers and acquisitions led growth strategies, national culture, financial regulations, AI and machine learning in finance, and green firms. His-contributions include various published articles in leading academic journals, book chapters and posts on research blogs.

Duc Khuong Nguyen holds a PhD in Finance from the University of Grenoble Alpes (France) and HDR (Habilitation for Supervising Doctoral Research) in Management Science. He also completed the "Leaders in Development" program at Harvard University, John F. Kennedy School of Government, Executive Education (2013). In 2013, he joined IPAG Business School as Professor of Finance and Deputy Director for Research. Previously, he served in various academic positions at ISC Paris Business School, Grenoble Graduate Institute of Business, at EM Lyon Business School. Dr. Nguyen is also a Non-Resident Research Fellow at the School of Public and Environmental Affairs, Indiana University, and a Visiting Professor at International School, Vietnam National University, Hanoi, Vietnam.

Khurrum S. Mughal is working as a research economist in state bank of Pakistan. He obtained his PhD in Economics from Johannes Kepler University Linz, Austria. He has taught at IQRA University and COMSATS as an Assistant Professor. He completed his Post Doc from Austria. His-research interests include Informal Sector, dynamics of Trade, Exchange rate and Inflation.

Maaz Khan is doing his master's in finance from Comsats University Islamabad. His-research interests include financial modeling, economic analysis and machine learning.