Skip to main content
PMC home page
Infectious Disease Modelling logoLink to Infectious Disease Modelling
. 2020 Aug 15;5:575–579. doi: 10.1016/j.idm.2020.08.002

A simple approach to estimate the instantaneous case fatality ratio: Using the publicly available COVID-19 surveillance data in Canada as an example

Shi Zhao a,b,c,d,∗
PMCID: PMC7428742  PMID: 32835147

Abstract

The case fatality ratio (CFR) is one of the key measurements to evaluate the clinical severity of infectious diseases. The CFR may vary due to change in factors that affect the mortality risk. In this study, we developed a simple likelihood-based framework to estimate the instantaneous CFR of infectious diseases. We used the publicly available COVID-19 surveillance data in Canada for demonstration. We estimated the mean fatality ratio of reported COVID-19 cases (rCFR) in Canada was estimated at 6.9% (95%CI: 4.5–10.6). We emphasize the extensive implementation of the constructed instantaneous CFR that is to identify the key determinants affecting the mortality risk.

Keywords: COVID-19, Case fatality ratio, Epidemic, Modelling, Canada

Introduction

The mortality risk is one of the key measurements to evaluate the clinical severity of diseases. The case fatality ratio (CFR) quantifies the mortality risk of infectious disease when being infected, which is commonly calculated as a constant. However, changes in some external factors may vary the scale of CFR, e.g., pathogenic evolution, health status, changes in treatment strategies or medication (Gautret et al., 2020), the supply of healthcare and critical care resources (He et al., 2018; Zhao, Stone, Gao, Musa, Chong, He, et al.2020), and exposure to the environmental factors (Yao et al., 2020). In such situations, variation in CFR likely occurs. To explore changing dynamics on CFR, the instantaneous, or time-varying, CFR is of importance in understanding the patterns of the mortality risk (Jung et al., 2020; Mizumoto & Chowell, 2020; Wu, Hao, Lau, Wong, Leung, Wu, et al 2020).

Recently, the coronavirus disease 2019 (COVID-19), caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), emerged in Wuhan, China at the end of 2019 (Huang et al., 2020; Li et al., 2020; Lin et al., 2020; Wu, Hao et al, 2020; Wu, Leung, & Leung, 2020; Zhao, Musa, Lin, Ran, Yang, Wang, et al., 2020). The COVID-19 spread to over 200 foreign countries as of July 2020 (Wu et al., 2020; Zhao, Zhuang, Cao Ran, Gao, Lou, et al., 2020). The World Health Organization (WHO) declared the outbreak to be a public health emergency of international concern on January 30, 2020 (World Health Organization, 2020a, 2020b). By the end of June 2020, there were over 13 million COVID-19 confirmed cases globally (World Health Organization, 2020a, 2020b). Previous studies estimated the constant fatality ratio from 0.7% to 1.3% among COVID-19 infections (Russell et al., 2020; Verity et al., 2020), from 1.4% to 2.6% among clinically diagnosable cases (Russell et al., 2020; Verity et al., 2020; Wu, Leung, Bushman, Kishore, Niehus, de Salazar, et al., 2020), from 5.3% to 8.4% among reported cases (Jung et al., 2020; Leung, Wu, Liu, & Leung, 2020; Yang et al., 2020), at 14% among hospitalised cases (Wu, Hao et al., 2020). Although Wu et al. (Wu, Hao et al., 2020) attempted to construct the time-varying fatality ratio among hospitalised (severe) cases, their calculation was based on the crude ratio of the counts of the two terminal events including recovery and death. Estimating instantaneous CFR is essential for uncovering the temporal patterns of the COVID-19 mortality risk.

In this study, we developed a simple likelihood-based framework to estimate the instantaneous case fatality ratio of infectious diseases. We used the publicly available COVID-19 surveillance data in Canada as an example for demonstration.

Methods

For the time interval (denoted by g) between being reported as case and the death (if the death occurs), we use f(∙) to denote the probability distribution function (PDF) of this time interval. For convenience, we denote the time interval between onset and death by s following the PDF of h(s), and the time interval between onset and death by q following the PDF of δ(q). Following the previous study (Jung et al., 2020), the g is modelled as the difference of s minus d, i.e., g = s – q, and we remark that g is not necessarily positive. Then, the PDF of g, i.e., f(g), is formulated as in Eqn (1).

f(g)=∫h(g+q)⋅δ(q)dq. (1)

Thus, if one case is reported at time τ who dies eventually, the value of f(g) is considered as the relative likelihood of death at time (τ + g).

Since each disease-related death is diagnosed as a case at the first place, each individual case is considered as a ‘source’ (or ‘pool’) of the death, i.e., subjects at mortality risk. We consider all reported cases as the ‘pool’ to generate deaths, and we model this candidate pool as a time-varying function denoted by Φ(t) at time t. Then, at time t, the i-th case, who is reported at time τi, contributes f(g = t − τi) to Φ(t). For the contribution from all reported cases, the Φ(t) is summated as in Eqn (2).

Φ(t)=∑if(g=t−τi). (2)

Hence, the reported case fatality ratio (rCFR), i.e., the fatality ratio of reported cases, at time t can be calculated by rCFRt = dt/Φt. Here, the dt is the observed number of deaths at time t, and Φt is the discretised Φ(t) at time t.

To construct the likelihood profile, we model dt as a binomial process with sizes at Φt (rounding to the closest integer) and successful probabilities at rCFRt to be estimated. As such, by fitting to the daily number of deaths time series, dt, the rCFRt can be estimated by using the maximum likelihood estimation approach. The 95% confidence intervals (95%CI) of rCFRt are calculated by using the profile likelihood estimation framework with a cutoff threshold determined by a Chi-square quantile (Fan & Huang, 2005), as well as previously adopted in (Lin et al., 2018; Wang et al., 2020; Zhao, 2020; Zhao et al., 2018, Zhao, Stone et al , 2020, Zhao, Musa et al, 2020).

Demonstration using COVID-19 surveillance data in Canada

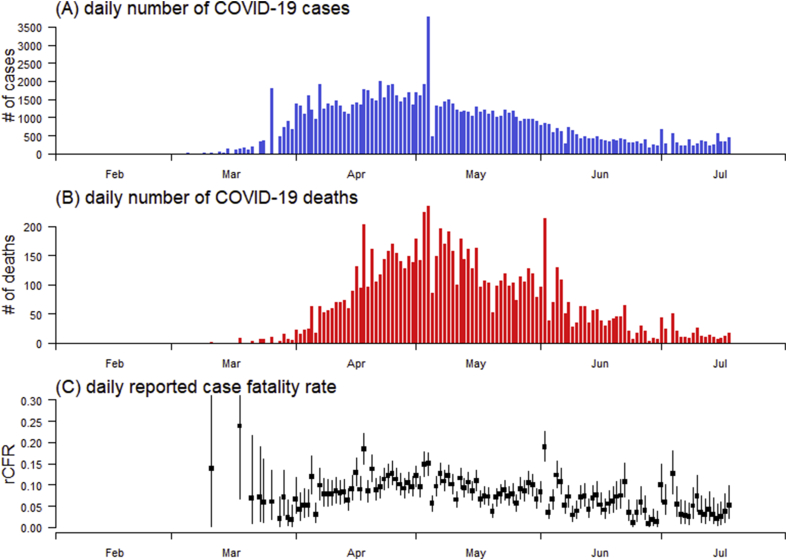
For demonstration, we used the publicly available COVID-19 surveillance data in Canada as an example to construct the instantaneous rCFRt series. The daily reported number of COVID-19 cases and deaths time series were collected from the COVID-19 public surveillance platform released by the WHO, accessed via https://covid19.who.int/region/amro/country/ca. Fig. 1A and B shows the epidemic curve of COVID-19 cases and deaths in Canada from February to July 2020, respectively.

Fig. 1.

Fig. 1

Open in a new tab

The daily number of COVID-19 cases (panel A), deaths (panel B), and estimated reported case fatality ratio (rCFR, panel C) in Canada. In panel C, the squared dots are the points estimates, and the bars are the 95%CIs.

To set up the initial conditions of the model framework in Eqn (Gautret et al., 2020), we set h(s) as a Gamma distribution with mean (±SD) at 20 days (±10) referring to (Verity et al., 2020; Wu, Leung, Bushman et al, 2020), and δ(q) as another Gamma distribution with mean (±SD) at 7 days (±4) referring to (Jung et al., 2020). We remark that slight changes and similar alternative settings in the initial conditions will not affect our main results.

Results and discussion

Since the first COVID-19 death reported on March 11, 2020, we estimated the instantaneous rCFRt ranging from 0% to 23.8%, see Fig. 1C. The mean rCFR of COVID-19 was estimated at 6.9% (95%CI: 4.5–10.6). Our rCFR estimate is largely consistent with previous estimates, e.g., 5.3% in Wuhan, China (Yang et al., 2020), 5.9% in Hubei province, China (Leung, Wu, Liu, and Leung, 2020), and from 5.3% to 8.4% in mainland China (Jung et al., 2020).

Construction of the instantaneous CFR allows one to examine the temporal trends of mortality risk. By using the segmented logistic regression models (Ran et al., 2020), we detected change in the temporal trends, i.e., structural break, of rCFR most likely appeared around May 3, 2020. We found a significant increasing trend in rCFR before May 3 in terms of odds ratio (OR) at 1.08 per week increase (95%CI: 1.03–1.14), but a significant decreasing trend after May 3 in terms of OR at 0.90 per week increase (95%CI: 0.87–0.93).

The data-driven CFR estimate is largely determined by the precision level of the number of COVID-19 cases and deaths. In this study, the reporting efforts in COVID-19 surveillance may largely affect the scale of cases data, whereas the COVID-19 associated deaths are unlikely to be mis-ascertained. Thus, on one hand, the under-ascertainment in COVID-19 number of cases may lead to an outcome that rCFR is larger than the real (unobservable) CFR. On the other hand, if we assume the fatality ratio ranging from 1.4% to 2.6% among clinically diagnosable COVID-19 cases as estimated in previous studies (Russell et al., 2020; Verity et al., 2020; Wu, Leung, Bushman et al., 2020), an average under-ascertainment rate in Canada ranging from 20.3% to 37.7% is calculated backwardly.

Linked to the change in the temporal trends of rCFR, we suspect that the decreasing trends in rCFR after May 3, 2020, might be due to the increase in the ascertainment rate in Canada during the same period. Speculatively, the increasing trends in rCFR before May 3 might be partially associated with insufficient intensive care preparedness during the early phase of the outbreak. However, further studies are warranted to explore evidence for these two speculative hypotheses. This study proposed an analytical approach to construct the instantaneous rCFR that can be adopted to further examine the associations with its potential determinants, e.g., pathogenic evolution, change in the cases ascertainment rate (Nishiura et al., 2020; Wu et al., 2010; Zhao et al., 2020), the supply of critical care resources (He et al., 2018), and exposure to the environmental factors (Yao et al., 2020).

The analytical approach proposed in this study has limitations. First, we presume the real number of disease-induced deaths and the time of each death are correctly reported. This setting is practically reasonable since mortality is considered as a serious clinical outcome, which is under more rigorous surveillance, and thus is unlikely mis-ascertained. Alternatively, an overdispersion setting in the likelihood profile may be incorporated to address the inaccurate ascertainment scenarios. Second, as a data-driven analysis, our estimates are relying on both statistical framework and consistency in the reported COVID-19 cases data. Note that the current framework requires fixed distributions of both the reporting delay, δ(q), and lag between onset and death, h(s), and temporal variation in either of them may undermine the statistical unbiasedness of the rCFR estimates. Nevertheless, our framework can be extended in a more complex context to address this issue. Last, most essentially, merely construct the instantaneous CFR is less important from the public health point of view, but we emphasize its extensive implementation, which is to identify the key determinants affecting the disease mortality risk, e.g., PM2.5 was found positively associated with the crude CFR of COVID-19 (Yao et al., 2020).

Ethics approval and consent to participate

The COVID-19 surveillance data were collected via the public domains, and thus neither ethical approval nor individual consent was applicable.

Availability of materials

All data used in this work were publicly available via https://covid19.who.int/region/amro/country/ca.

Consent for publication

Not applicable.

Funding

This work is not funded.

Disclaimer

The funding agencies had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication.

Author’s contributions

SZ conceived the study, carried out the analysis, drafted the first manuscript, and revised the manuscript.

Declaration of competing interest

The author declares no conflict of interest.

Acknowledgements

None.

Handling editor: Jianhong Wu

Footnotes

Peer review under responsibility of KeAi Communications Co., Ltd.

References

  1. Fan J., Huang T. Profile likelihood inferences on semiparametric varying-coefficient partially linear models. Bernoulli. 2005;11(6):1031–1057. [Google Scholar]
  2. Gautret P., Lagier J.-C., Parola P., Meddeb L., Mailhe M., Doudier B. Hydroxychloroquine and azithromycin as a treatment of COVID-19: Results of an open-label non-randomized clinical trial. International Journal of Antimicrobial Agents. 2020:105949. doi: 10.1016/j.ijantimicag.2020.105949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. He D., Wang X., Gao D., Wang J. Modeling the 2016–2017 Yemen cholera outbreak with the impact of limited medical resources. Journal of Theoretical Biology. 2018;451:80–85. doi: 10.1016/j.jtbi.2018.04.041. [DOI] [PubMed] [Google Scholar]
  4. Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet (London, England) 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Jung S.M., Akhmetzhanov A.R., Hayashi K., Linton N.M., Yang Y., Yuan B. Real-time estimation of the risk of death from novel coronavirus (COVID-19) infection: Inference using exported cases. Journal of Clinical Medicine. 2020;9(2) doi: 10.3390/jcm9020523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Leung K., Wu J.T., Liu D., Leung G.M. First-wave COVID-19 transmissibility and severity in China outside Hubei after control measures, and second-wave scenario planning: A modelling impact assessment. The Lancet. 2020;395(10233):1382–1393. doi: 10.1016/S0140-6736(20)30746-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y. Early transmission dynamics in wuhan, China, of novel coronavirus–infected pneumonia. New England Journal of Medicine. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Lin Q., Chiu A.P., Zhao S., He D. Modeling the spread of Middle East respiratory syndrome coronavirus in Saudi Arabia. Statistical Methods in Medical Research. 2018;27(7):1968–1978. doi: 10.1177/0962280217746442. [DOI] [PubMed] [Google Scholar]
  9. Lin Q., Zhao S., Gao D., Lou Y., Yang S., Musa S.S. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. International Journal of Infectious Diseases. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Mizumoto K., Chowell G. Estimating risk for death from coronavirus disease, China, january–february 2020. Emerging Infectious Diseases. 2020;26(6):1251. doi: 10.3201/eid2606.200233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Nishiura H., Kobayashi T., Yang Y., Hayashi K., Miyama T., Kinoshita R. The rate of underascertainment of novel coronavirus (2019-nCoV) infection: Estimation using Japanese passengers data on evacuation flights. Journal of Clinical Medicine. 2020;9(2) doi: 10.3390/jcm9020419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ran J., Zhao S., Han L., Liao G., Wang K., Wang M.H. A Re-analysis in exploring the association between temperature and COVID-19 transmissibility: An ecological study with 154 Chinese cities. European Respiratory Journal. 2020:2001253. doi: 10.1183/13993003.01253-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Russell T.W., Hellewell J., Jarvis C.I., Van Zandvoort K., Abbott S., Ratnayake R. Estimating the infection and case fatality ratio for coronavirus disease (COVID-19) using age-adjusted data from the outbreak on the Diamond Princess cruise ship. Euro Surveillance. 2020;25(12):2000256. doi: 10.2807/1560-7917.ES.2020.25.12.2000256. February 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Verity R., Okell L.C., Dorigatti I., Winskill P., Whittaker C., Imai N. Estimates of the severity of coronavirus disease 2019: A model-based analysis. The Lancet Infectious Diseases. 2020;20(6):669–677. doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wang K., Zhao S., Liao Y., Zhao T., Wang X., Zhang X. Estimating the serial interval of the novel coronavirus disease (COVID-19) based on the public surveillance data in Shenzhen, China from January 19 to February 22, 2020. Transbound Emerg Dis. 2020 doi: 10.1111/tbed.13647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. World Health Organization . World Health Organization (WHO); 2020. Statement on the second meeting of the International Health Regulations Emergency Committee regarding the outbreak of novel coronavirus (2019-nCoV)https://www.who.int/news-room/detail/30-01-2020-statement-on-the-second-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov) Available from. [Google Scholar]
  17. World Health Organization . World Health Organization (WHO); 2020. Novel Coronavirus (2019-nCoV) situation reports.https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports released by the. Available from. [Google Scholar]
  18. Wu J.T., Cowling B.J., Lau E.H., Ip D.K., Ho L.-M., Tsang T. School closure and mitigation of pandemic (H1N1) 2009, Hong Kong. Emerging Infectious Diseases. 2010;16(3):538. doi: 10.3201/eid1603.091216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in wuhan, China: A modelling study. The Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Wu P., Hao X., Lau E.H., Wong J.Y., Leung K.S., Wu J.T. Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China, as at 22 January 2020. Euro Surveillance. 2020;25(3):2000044. doi: 10.2807/1560-7917.ES.2020.25.3.2000044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Wu J.T., Leung K., Bushman M., Kishore N., Niehus R., de Salazar P.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nature Medicine. 2020;26(4):506–510. doi: 10.1038/s41591-020-0822-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Yang S., Cao P., Du P., Wu Z., Zhuang Z., Yang L. Early estimation of the case fatality rate of COVID-19 in mainland China: A data-driven analysis. Annals of Translational Medicine. 2020;8(4) doi: 10.21037/atm.2020.02.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Yao Y., Pan J., Liu Z., Meng X., Wang W., Kan H. Temporal association between particulate matter pollution and case fatality rate of COVID-19 in wuhan. Environmental Research. 2020:109941. doi: 10.1016/j.envres.2020.109941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zhao S. Estimating the time interval between transmission generations when negative values occur in the serial interval data: Using COVID-19 as an example. Mathematical Biosciences and Engineering. 2020;17(4):3512–3519. doi: 10.3934/mbe.2020198. [DOI] [PubMed] [Google Scholar]
  25. Zhao S., Lin Q., Ran J., Musa S.S., Yang G., Wang W. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. International Journal of Infectious Diseases. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Zhao S., Lou Y., Chiu A.P.Y., He D. Modelling the skip-and-resurgence of Japanese encephalitis epidemics in Hong Kong. Journal of Theoretical Biology. 2018;454:1–10. doi: 10.1016/j.jtbi.2018.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhao S., Musa S.S., Lin Q., Ran J., Yang G., Wang W. Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of january 2020: A data-driven modelling analysis of the early outbreak. Journal of Clinical Medicine. 2020;9(2) doi: 10.3390/jcm9020388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Zhao S., Stone L., Gao D., Musa S.S., Chong M.K.C., He D. Imitation dynamics in the mitigation of the novel coronavirus disease (COVID-19) outbreak in Wuhan, China from 2019 to 2020. Annals of Translational Medicine. 2020;8(7) doi: 10.21037/atm.2020.03.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zhao S., Zhuang Z., Cao P., Ran J., Gao D., Lou Y. Quantifying the association between domestic travel and the exportation of novel coronavirus (2019-nCoV) cases from wuhan, China in 2020: A correlational analysis. Journal of Travel Medicine. 2020;27(2) doi: 10.1093/jtm/taaa022. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Infectious Disease Modelling are provided here courtesy of KeAi Publishing

RESOURCES