Abstract
Purpose:
T1-weighted dynamic contrast-enhanced Magnetic Resonance Imaging (DCE-MRI) is typically quantified by least squares (LS) fitting to a pharmacokinetic (PK) model to yield parameters of microvasculature and perfusion in normal and disease tissues. Such fitting is both time-consuming as well as subject to inaccuracy and instability in parameter estimates. Here, we propose a novel neural network approach to estimate the PK parameters by extracting long and short time-dependent features in DCE-MRI.
Methods:
A Long Short-Term Memory (LSTM) network, widely used for processing sequence data, was employed to map DCE-MRI time-series accompanied with an arterial input function to parameters of the extended Tofts model. Head and neck DCE-MRI from 103 patients were used for training and testing the LSTM model. Arterial input functions (AIFs) from 78 patients were used to generate synthetic DCE-MRI time-series for training, during which data augmentation was used to overcome the limited size of in vivo data. The model was tested on independent synthesized DCE data using AIFs from 25 patients. The LSTM performance was optimized for the numbers of layers and hidden state features. The performance of the LSTM was tested for different temporal resolution, total acquisition time and contrast-to-noise ratio (CNR), and compared to the conventional LS fitting and a CNN-based method.
Results:
Compared to LS fitting, the LSTM model had comparable accuracy in PK parameter estimations from fully temporal-sampled DCE-MRI data (~3s per frame), but much better accuracy for the data with temporally subsampling (4s or greater per frame), total acquisition time truncation by 48%-16%, or low CNR (5 and 10). The LSTM reduced normalized root mean squared error by 40.4%, 46.9% and 53.0% for sampling intervals of 4s, 5s and 6s, respectively, compared to LS fitting. Compared to the CNN model, the LSTM model reduced the error in the parameter estimates up to 55.2%. Also, the LSTM improved the inference time by ~14 times on CPU compared to LS fitting.
Conclusions:
Our study suggests that the LSTM model could achieve improved robustness and computation speed for PK parameter estimation compared to LS fitting and the CNN based network, particularly for suboptimal data.
Keywords: DCE-MRI, machine learning, contrast agent, long-short-term memory, pharmacokinetic model, temporal correlation
1. Introduction
Dynamic contrast-enhanced Magnetic Resonance Imaging (DCE-MRI), an imaging technique where a time-series of T1 weighted images are obtained before, during, and after a bolus administration of a contrast agent (CA), has been widely explored in a wide range of clinical applications for noninvasive cancer detection, characterization, radiation target definition and treatment response assessment1-4. The change in concentrations of CA in images over time can be derived from the MR signal intensity time-series. A parametric pharmacokinetic (PK) model is then typically fit to the CA concentration-time curves to extract quantitative parameters related to vascular permeability, tissue perfusion, and volume of the extravascular extracellular space5.
Practical implementation of DCE-MRI involves a tradeoff of spatial resolution, volume of coverage and temporal resolution. To estimate PK parameters accurately, an adequate temporal resolution of the DCE images is required, which often results in a tradeoff of spatial resolution and/or volume coverage. Several rapid imaging techniques have been introduced to improve both spatial resolution/volume coverage and temporal resolution, e.g., k-space sparse sampling strategies combined with image reconstruction techniques of compressed sensing6 and parallel imaging7,8. After reconstructing image time-series, the PK parameter maps are calculated as a second step, refereed as an indirect method. These methods include nonlinear least-squares (NLLSQ) fitting, which was reported to be sensitive to sampling interval, total acquisition time, and noise9, and requires intensive computation. A more efficient linear least-squares (LLSQ) method10 was developed and showed improved accuracy for signals with signal-to-noise ratio less than 10. More recently, an efficient derivative based LLSQ method with a low-pass filter in time domain11 was introduced. However, for the methods developed so far, obvious degradation of performance with increasing noise level and decreasing temporal resolution is still observed, and the computation time can be further improved. Recently, machine learning methods have been investigated to learn a mapping from fully sampled or subsampled image time-series to the parameter maps utilizing 2D or 3D convolutional neural networks (CNN)12,13. Despite the short inference time, the CNN is not designed to learn long and short-term temporal relationships in the hemodynamics of the CA from the image time-series. Also, the CNN models may suffer from bias in practice since they were trained on similar subject arterial input functions (AIFs). In our experiment, where subject AIFs have diverse shapes, peaks, and time delays, obvious bias can be observed from the estimation from these models13.
Recurrent neural networks (RNN), especially long-short-term memory (LSTM)14, have been successfully applied to learn temporal relationships in sequence data, such as video description and image captioning15. The application of LSTM was also explored in biomedical image analysis. A modified U-net was combined with an LSTM variant to do 3D biomedical volume segmentation16, where the LSTM explored the correlation of slices in the cranial-caudal direction. A pre-trained fine-tuned Visual Geometry Group (VGG) network was used to extract feature maps from DCE-MRI slices, and then the sequence of feature maps was sent into an LSTM to determine whether a breast lesion within a given region of interest (ROI) was benign or malignant17.
Inspired by the recent successes of LSTM and the challenges faced by CNN-based approaches for PK parameter estimation, we propose a LSTM-based approach to learn the mapping of temporal dynamics in single-voxel signals accompanied, with their corresponding AIFs, to the PK parameters in the extended Tofts model18. Our approach is motivated by four factors. First, the signal intensity-time curves of DCE-MRI describe temporal hemodynamics of a CA passing through microvasculature in tissue. The LSTM architecture is able to learn long-term (temporal) dependence of signals15,19 and thus could improve performance of PK parameter estimation compared to the CNN-based approaches using this data. Second, in practice, the AIF varies from patient to patient20. Inclusion of a subject-specific AIF in the estimation process could significantly improve estimation performance. AIFs can be readily incorporated into the input of LSTM as another input dimension, removing the bias observed in the reported CNN-based approaches. Third, by capturing a low-dimensional manifold where the tissue concentration-time curve and AIF reside using LSTM, more robust parameter estimation can be achieved. Fourth, the inference time can be reduced because of the small computational burden of the LSTM as compared to DMF. We compare the results of LSTM with conventional direct model fitting21 as well as a state-of-the-art CNN-based method13, including performances on the DCE-MRI at low contrast-to-noise ratio, low temporal sampling and short total acquisition time.
2. Materials and Methods
Our proposed LSTM-based method treats the PK parameter estimation problem as a mapping from a CA concentration-time curve accompanying with an AIF to the underlying parameters. Here, we investigated our method in the most commonly used extended Tofts model.
2.1. Extended Tofts model.
The extended Tofts model18 has been well described in literature with a few minor variations in implementation. The version of the extended Tofts model and direct model fitting used in this study are described briefly. In our implementation, a contrast bolus arrival time (BAT), τBAT(r) for each tissue voxel is considered for the accurate PK parameter estimation22,23. The implemented extended Tofts model is written as:
| (1) |
where Ct(r, t) is the CA concentration in the tissue voxel, Cb is the CA concentration in the arterial blood (or AIF), Ktrans is the transfer rate constant of the CA that diffuses from the blood vessel to the interstitial space, Kep is the rate constant of the CA efflux from the interstitial space to the blood plasma, and Hct is the small vessel hematocrit. Kep equals to Ktrans/ve, where ve is the fractional interstitial volume.
While equation 1 has been fit using NLLSQ methods10,11 previously, in this investigation we selected a LLSQ method10 that has a better tolerance to low SNR in the DCE data and a more efficient computation speed than NLLSQ fitting, as a benchmark to compare with our proposed LSTM method. In this LLSQ method, Eq [1] can be re-written as:
| (2) |
where Ktrans, Kep, and vp are linearly related to integrals of Ct(r, t) and Cp(t), and Cp(t). For given τBAT(r), Ktrans, Kep, and vp can been rapidly estimated by LLSQ fitting. τBAT(r) can be estimated iteratively with Ktrans, Kep, and vp. The τBAT(r) range can be determined using priori knowledge, e.g., 0-10 seconds for the tissue in head and neck regions. In our implementation, we tested the τBAT(r) between 0 and 10 s with an incremental step 1s, and Hct as 0.459. Hereafter, we refer this implementation of the LLSQ fitting as direct model fitting (DMF).
2.2. PK parameter inference via LSTM.
Formulation.
We estimate the PK parameters by mapping (Ct(r,t), Cp(t)) to the underlying physiological parameters θ = (Ktrans(r), ve(r), vp(r)) using LSTM, which we denote as θ = f((Ct(r, t), Cp(t)))∣Θ), where f(·∣Θ) represents the forward mapping of the LSTM network parameterized by Θ.
Loss function.
Our loss function seeks to reduce the mean squared error (MSE) between the estimated parameters θe and the ground truth parameters θg corresponding to the training signal series. Given a set of N training samples (cti(t), cpi(t), θgi), i = 1, 2, …, N, we train the LSTM network to minimize the following loss function:
| (3) |
LSTM Network Architecture.
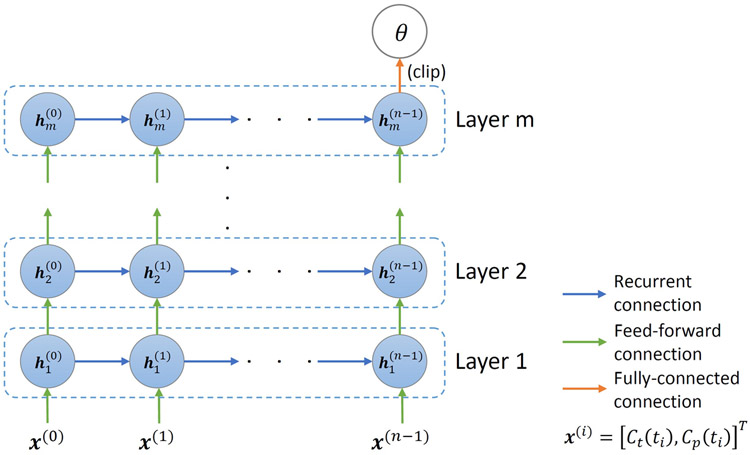
The proposed network (Figure 1) consists of m LSTM layers with n sequentially connected cells in each layer. The network takes an input sequence [Ct, Cp]T, where the AIF is incorporated as another input dimension. The first LSTM layer extracts lower level temporal relationships. The output feature sequence is then passed through the remaining m-1 LSTM layers each to extract higher-order level temporal relationships from the signal and AIF.
Figure 1.
Illustration of the network architecture used for PK parameter estimation from an input of a CA concentration time-series and an AIF as two separate channels. Each layer has n sequentially connected cells.
Each LSTM layer captures the changes in the input sequence by maintaining a hidden state h(t) and a memory cell c(t) by updating them using gating mechanisms when stepping through the input sequence. Specifically, the lth LSTM layer takes a sequence of hidden states , where the superscript and subscript stand for timestep and layer, respectively, and are defined as x(0), x(1),…, x(n−1). The new hidden states are then defined by the equations shown in (4) below
| (4) |
for t ∈ {0,1, …, n − 1} and l ∈ {1,2, … , m}, where σ(·) is the sigmoid function and “∘” denotes the Hadamard product. and control which information to “input” to and “forget” from the memory cell, respectively. The new memory state is then obtained based on the candidate values and the gate values and . Finally, the new hidden state is generated by the candidate values and memory state .
Batch normalization is applied after each LSTM layer except for the last one. A fully connected layer with three features is then applied to find the best combination of features to generate an estimation of the PK parameters. The parameters are clipped to our targeted range, Ktrans ∈ [0, 3](min−1), ve ∈ [0, 0.4], and vp ∈ [0, 0.55], thus confining the parameters to fall within a physiologically realistic range9, to produce the final estimation of the PK parameters.
2.3. Data Preparation.
DCE MR time series for training and testing were synthesized using AIFs from 103 patients with head and neck cancers. As a brief, the DCE MRI images were acquired using a dynamic scanning sequence (TWIST) with an injectionw was approved by the Institutional Review Board of the University of Michigan. The scanning parameters were: flip angle = 10°, echo time (TE) = 0.97ms, repetition time (TR) = 2.73ms, 60 time frames, voxel size = 1.5625×1.5625×2.5mm3, matrix = 192×192. There were small variations in time step of temporal sampling of the dynamic series (median of 3.34 s) and in the numbers of the slices in z-direction between the patients (median of 72). For all cases, the subject-specific AIFs were extracted manually by averaging the signal intensity-time curves of 20 voxels from the carotid artery, which had maximum intensities at the time frame before the enhancement peak24, and then subtracting and dividing by the average pre-contrast signal intensities of the voxels. The targeted parameter maps were estimated using DMF9.
Of 103 patients, 78 cases were randomly selected for training, and 25 for testing. To overcome the limited size of the in vivo DCE-MRI dataset, synthetic data were created for network training and testing. The synthesized data allow us to obtain a reliable and accurate assessment of the performance of the proposed methods by comparing the estimates to the ground truth (the parameters that created the synthetic data). Data augmentation was also applied during training data synthesis. Using equations (1)-(5) of the extended Tofts model, the training signal intensity time-curves were created from different combinations of the AIF, time step (Δt), bolus arrival time (τBAT), and the parameters ( θ = (Ktrans(r), ve(r), vp(r))). Particularly, AIFs and time steps of 78 training cases formed a set of 78 60-dimensional vectors and a set of 78 scalars respectively, defined as Atrain and Ttrain. This yielded a set of 75,678,643 3-dimensional parameter vectors (Ktrans, ve, and vp), which was denoted as Ptrain. For testing, we used the DCE time-series synthesized using the AIFs from the 25 cases in the testing data pool as well as acquired empirical data. Testing with real data can assure that the model is ‘realistic’ enough. The synthesized testing data were generated in the same manner as the training data.
2.4. Experimental setup.
Performances of the LSTM networks on DCE-MRI acquired with different total acquisition times and temporal sampling rates as well as different CNRs were compared with the DMF method and a CNN model13. The LSTM networks were trained with input of fully temporal-sampled signal time-series as well as temporally subsampled time-series.
Training with synthetic data using acquired temporal sampling
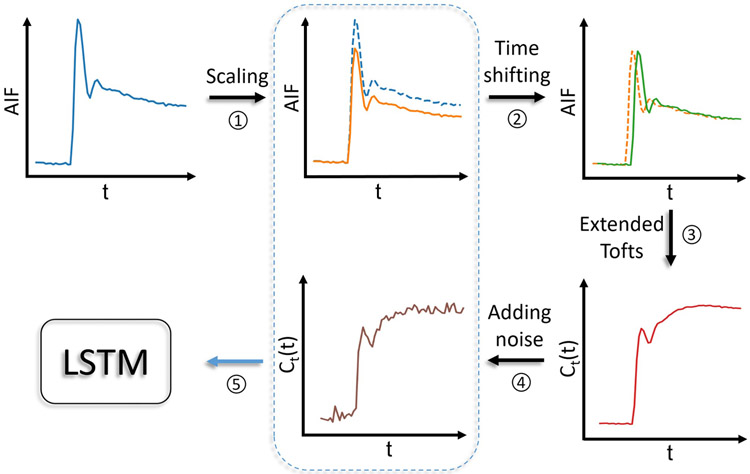
The training data synthesis was executed on-the-fly during the network training and used the data from the training data generation pool consisting of the Ptrain, Atrain, and Ttrain. Figure 2 shows the data generating process during network training. Specifically, at each iteration, 1000 combinations of , AIFs, and time steps , were selected randomly from the aforementioned training data generation pool. For each combination, the AIF was first randomly scaled between 70% and 130% (AIF augmentation)25. The concentration time-curve was then generated by randomly time-shifting the AIF (between 0 and 10 seconds to simulate the delay of CA arrival) using the extended Tofts model, and random Gaussian noise was added to the signal time-series to have contrast-to-noise ratios between 20 and 30. The resultant signal time-series and the corresponding scaled AIF (without time shifting) were concatenated as an input. As a result, this batch data consisted of a vector of dimension 1000×n×2 (where n was the number of time points in the series), and was passed to the network. Each epoch consisted of 1000 batches of training data and 200 batches of validation data. The network was trained with Adam optimizer26 with an initial learning rate of 10−4. The learning rate was reduced by a factor of 0.9 when the validation error was not improved in 30 consecutive epochs. The training was terminated when the validation error was not improved in 75 consecutive epochs.
Figure 2.
Training data generating scheme with BAT simulation and AIF augmentation by random scaling.
To evaluate sufficiency of the size of the training data generation pool on performance of the LSTM model, two other models with the same architecture as that for the initial model (LSTM3) were trained with the same scheme using 60% (LSTM1) and 80% (LSTM2) of the training data generation pool.
Training with temporally subsampled synthetic data
The proposed LSTM network was also trained and tested on temporally subsampled synthetic signal time-curves, where signal time-curves were generated with sampling time steps of Δt: 3, 4, 5 and 6 seconds. Lengths of the time-series were truncated at an integer number of time steps that was close to 168 seconds. The AIF and the PK parameters were drawn from the same data generating pool. The LSTM input size was modified accordingly to match the number of time points of the subsampled signal time-series, while the other processes and parameters were kept the same, including the targeted PK parameters.
Training with truncated data and data with different CNR levels
To examine robustness of the proposed network to signal noise and total acquisition time, the proposed LSTM network was further trained and tested on: (1) truncated synthetic data with the total acquisition times 168s, 141s, 114s, and 87s when keeping the same sampling time step 3 s, and (2) fully temporally sampled synthetic data but with CNR variations at 20-30, 10 and 5.
Performance evaluation and comparison
First, our proposed LSTM network was optimized for the numbers of LSTM layers and hidden state features using fully temporal sampled synthetic data. Particularly, 2, 4, 6 and 8 layers, and 16, 32 and 64 features were trained and tested. Then, the optimal numbers of layers and features were used to train and test the LSTM model, whose performance was compared to both the conventional DMF approach and a CNN model. In testing, both synthetic and actual patient data were used. The synthetic testing data allows us to quantitatively assess the performance of PK parameters estimation by calculating the structural similarity (SSIM) index and normalized root mean squared error (NRMSE) of the estimated parameter maps with respect to the ground truth parameter maps. The NRMSE is defined by for a slice, where NRMSEi, , θij, and N are the NRMSE of the ith parameter, the estimated and ground truth ith parameter for jth voxel, and the number of voxels in the slice. To synthesize the testing signal time-curves, the AIF and the PK parameter maps were from the same patients, for which no cross-combination of the AIF and the PK parameters nor AIF augmentation were used for the training data synthesis. The SSIM and NRMSE were calculated from each of the 2D PK parameter slice maps first, and then averaged over multiple slices and across 25 cases. The proposed LSTM model was further evaluated using the empirical data from the same 25 cases.
The CNN model proposed by Ulas and colleagues13 was implemented for comparison with the LSTM model. The CNN was trained on 1500 3D volumes with ℓ2 loss and validated on 300 3D volumes generated using the same data generation pool as for LSTM training. The model loss term in the original model was dropped since BAT was not considered in the original paper, and enforcing model consistency without BAT correction produced worse results in our experiment. The size effect of the training data generation pool on the performance of the CNN-based method was also investigated by training with 60% (CNN1), 80% (CNN2), and 100% (CNN3) of the training data generation pool.
All codes were implemented using Keras library with Tensorflow backend, and the experiments were performed on an NVIDIA Tesla K40c GPU with 12 GB RAM.
3. Results.
Optimization of the LSTM networks
We investigated the distributions of the PK parameters θ = (Ktransr(r), ve(r), vp(r)) of the 78 patients, which were used as the training data generation pool. The parameter values in the pool covered the whole desired ranges of the parameters (Figure S1).
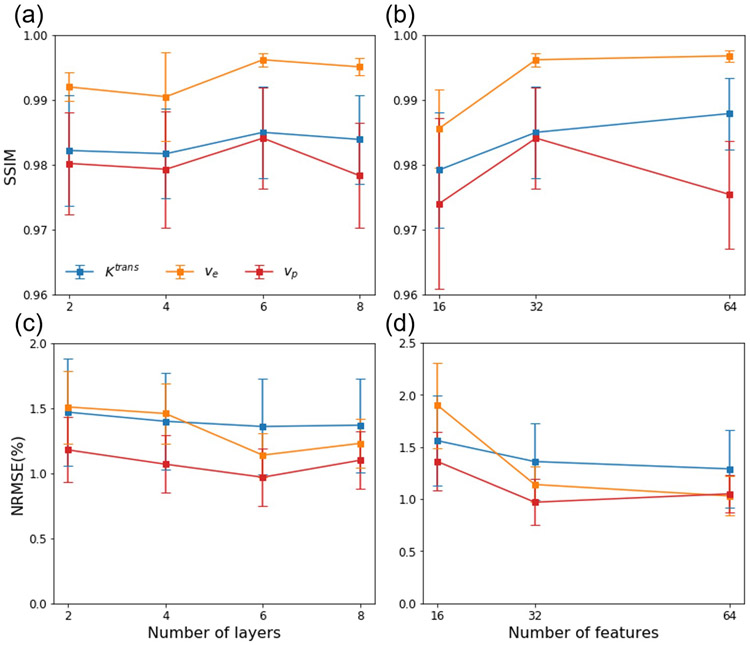
We trained the LSTM networks with 2, 4, 6 and 8 layers and 32 features, and with 16, 32 and 64 features and 6 layers. Figure 3 shows the impact of varying the layers and features on NRMSE% and SSIM. The LSTM network with 6 layers and 32 features had average maximal SSIM, presenting a balance of overfitting and underfitting of the training data and thus this network configuration was used for training under various test conditions.
Figure 3.
SSIM and NRMSE of the parameter map estimation by LSTM networks with (a, c) 2, 4, 6, and 8 LSTM layers with 32 features, and (b, d) 16, 32, and 64 features with 6 layers. Error bar: standard deviation.
Performance of the LSTM networks trained with original temporal-sampling data
The performance of the LSTM networks trained with synthetic data with original temporal-sampling, as well as results using the CNN and DMF models are shown in Table 1. The proposed LSTM network achieved high SSIM and low NRMSE% in the whole field of view as well as in the gross tumor volume (Table 1), comparable to the DMF approach. LSTM3 had < 1% lower SSIMs for Ktrans and vp, higher SSIM for ve, and 13.4%, 19.1%, and 25.4% better NRMSEs for Ktrans, ve and vp, respectively, than the DMF approach. LSTM3 outperformed the CNN-based approach by reducing the NRMSE up to 55.2%. When evaluating the size effect of the data generation pool, the performance of LSTM1, LSTM2 and LSTM3 were similar, and the size effect was insignificant, indicating the training data augmentation is effective. The CNN-based method shows inferior performance compared to the LSTM3 (Table 1). A visual illustration of estimated PK parameters and residuals of the testing data by different methods is given in Figure S2.
Table 1.
Quantitative performance of different methods on test DCE-MRI volumes
| Method | SSIM |
NRMSE (%) |
|||||
|---|---|---|---|---|---|---|---|
| Ktrans | ve | vp | Ktrans | ve | vp | ||
| Whole Range | DMF | 0.9875 ± 0.0052 | 0.9960 ± 0.0010 | 0.9880 ± 0.0046 | 1.57 ± 0.43 | 1.41 ± 0.27 | 1.30 ± 0.38 |
| LSTM1 | 0.9853 ± 0.0068 | 0.9922 ± 0.0027 | 0.9806 ± 0.0159 | 1.47 ± 0.36 | 1.44 ± 0.25 | 1.15 ± 0.24 | |
| LSTM2 | 0.9840 ± 0.0078 | 0.9931 ± 0.0025 | 0.9850 ± 0.0060 | 1.39 ± 0.41 | 1.19 ± 0.14 | 0.97 ± 0.18 | |
| LSTM3 | 0.9850 ± 0.0070 | 0.9962 ± 0.0010 | 0.9841 ± 0.0078 | 1.36 ± 0.37 | 1.14 ± 0.17 | 0.97 ± 0.22 | |
| CNN1 | 0.9547 ± 0.0202 | 0.9534 ± 0.0180 | 0.8946 ± 0.0267 | 3.07 ± 1.32 | 4.04 ± 1.57 | 3.54 ± 1.37 | |
| CNN2 | 0.9629 ± 0.0159 | 0.9594 ± 0.0146 | 0.9323 ± 0.0237 | 2.78 ± 0.99 | 4.17 ± 1.32 | 3.16 ± 1.44 | |
| CNN3 | 0.9627 ± 0.0189 | 0.9556 ± 0.0192 | 0.9302 ± 0.0352 | 2.76 ± 1.10 | 3.95 ± 1.30 | 2.85 ± 0.94 | |
| p | LSTM3 vs DMF | <0.05 | 0.54 | <0.005 | <0.05 | <0.005 | <0.005 |
| p | LSTM3 vs CNN3 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 |
| GTV | DMF | 0.9994 ± 0.0006 | 0.9997 ± 0.0004 | 0.9994 ± 0.0008 | 3.85 ± 2.64 | 0.85 ± 0.35 | 0.74 ± 0.40 |
| LSTM3 | 0.9993 ± 0.0006 | 0.9998 ± 0.0003 | 0.9994 ± 0.0007 | 4.45 ± 2.64 | 0.85 ± 0.21 | 0.71 ± 0.24 | |
| p | 0.38 | <0.05 | 0.63 | <0.05 | 1.00 | 0.45 | |
The LSTM models were trained and tested using synthetic data with original temporal-sampling. The SSIM and NRMSE% (mean + std) with respect to the ground truth parameter maps were obtained in the whole field of view. The bold numbers indicate significant differences (p<0.05) between LSTM and DMF. GTV: gross tumor volume.
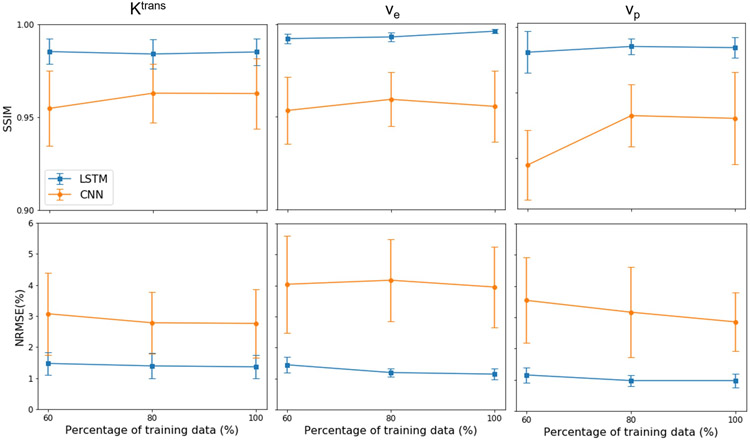
Figure 4 shows the performance of the LSTM and CNN-based methods with different amounts of training data. The performance of CNN-based method changed little with an increase in the size of the training data generation pool, indicating the sufficiency of training data.
Figure 4.
The performance of the LSTM and CNN-based methods under different amounts of training data (60%, 80%, and 100% of the data generation pool).
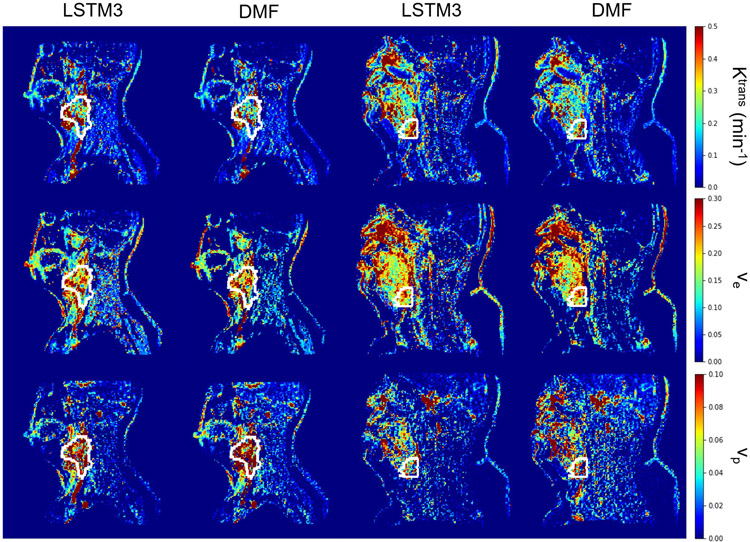
Figure 5 shows examples of the parameter maps generated by the DMF and LSTM methods on the acquired DCE-MRI data from the testing datasets, where the estimations of DMF and LSTM approaches were highly consistent. In most cases, DMF and LSTM approaches fit the signal intensity-time curves similarly well. Examples of fitted signal intensity-time curves are shown in Figure S3. To quantitatively compare the fitting results by LSTM and DMF, the voxel-wise MSE was calculated for both methods. The LSTM approach yielded a lower voxel-wise MSE (0.743 ± 0.130) than the DMF (0.808 ± 0.127). The parameter inference time of LSTM for fully temporal sampled DCE-MRI volumes was ~250s on CPU (~40s on GPU), while DMF approach required ~3600s to generate the PK parameter maps for the same data on the same CPU, representing approximately 14.4 times improvement in computation speed.
Figure 5.
Two exemplary slices (left 2 columns for first slice, right 2 columns for second slice) of PK parameter estimation by DMF and LSTM3 on an in vivo test dataset. The results obtained from DMF and LSTM3 show high similarity in both the tumor volume (depicted by the white contour) and the full FOV.
Performance of the LSTM networks with temporally subsampled data
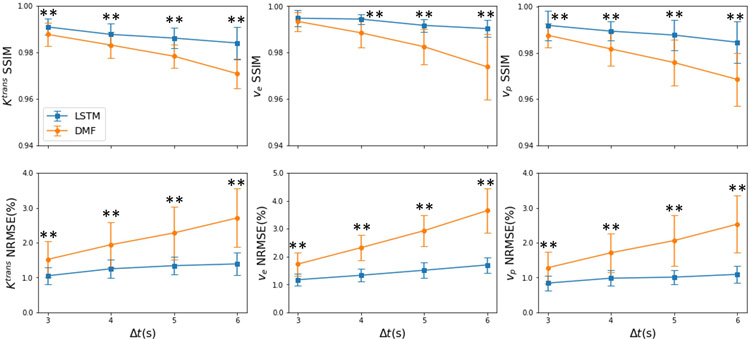
Figure 6 and Table 2 show that the LSTM had significantly better performances for estimating parameters than the DMF method (p<3.2×10−6) when increasing temporal sampling intervals from 3s to 4s, 5s and 6s (Figure S4).
Figure 6.
Quantitative results of the estimated parameters from the 25 synthesized testing datasets with different temporal sampling time intervals (3, 4, 5, and 6s) by the LSTM and DMF approaches. The proposed LSTM shows a more stable performance than the DMF when increasing the sampling interval. Error bar: standard deviation. *: p<0.05; **p<0.005.
Table 2.
Quantitative performance of different methods on temporally subsampled DCE data
| Method | SSIM |
NRMSE (%) |
|||||
|---|---|---|---|---|---|---|---|
| Ktrans | ve | vp | Ktrans | ve | vp | ||
| Δt=3 | DMF | 0.9877 ± 0.0050 | 0.9934 ± 0.0041 | 0.9876 ± 0.0052 | 1.52 ± 0.52 | 1.73 ± 0.41 | 1.28 ± 0.46 |
| LSTM3 | 0.9909 ± 0.0035 | 0.9948 ± 0.0034 | 0.9919 ± 0.0064 | 1.05 ± 0.24 | 1.17 ± 0.21 | 0.84 ± 0.21 | |
| p | <0.005 | 0.12 | <0.005 | <0.005 | <0.005 | <0.005 | |
| Δt=4 | DMF | 0.9831 ± 0.0055 | 0.9885 ± 0.0064 | 0.9817 ± 0.0073 | 1.94 ± 0.64 | 2.32 ± 0.46 | 1.71 ± 0.56 |
| LSTM3 | 0.9877 ± 0.0048 | 0.9944 ± 0.0022 | 0.9894 ± 0.0041 | 1.25 ± 0.27 | 1.33 ± 0.23 | 0.98 ± 0.22 | |
| p | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | |
| Δt=5 | DMF | 0.9783 ± 0.0050 | 0.9825 ± 0.0075 | 0.9758 ± 0.0099 | 2.28 ± 0.76 | 2.93 ± 0.56 | 2.06 ± 0.73 |
| LSTM3 | 0.9861 ± 0.0044 | 0.9917 ± 0.0027 | 0.9877 ± 0.0066 | 1.34 ± 0.26 | 1.51 ± 0.27 | 1.01 ± 0.21 | |
| p | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | |
| Δt=6 | DMF | 0.9708 ± 0.0063 | 0.9738 ± 0.0142 | 0.9685 ± 0.0115 | 2.71 ± 0.84 | 3.65 ± 0.80 | 2.53 ± 0.82 |
| LSTM3 | 0.9840 ± 0.0070 | 0.9903 ± 0.0037 | 0.9846 ± 0.0089 | 1.39 ± 0.33 | 1.70 ± 0.28 | 1.09 ± 0.25 | |
| p | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | |
The SSIM and NRMSE% (mean + std) with respect to the ground truth parameter maps were obtained in the whole field of view. The bold numbers indicate significant differences (p<0.005) between the two methods.
Performance of the LSTM networks with low CNR and reduced total acquisition length
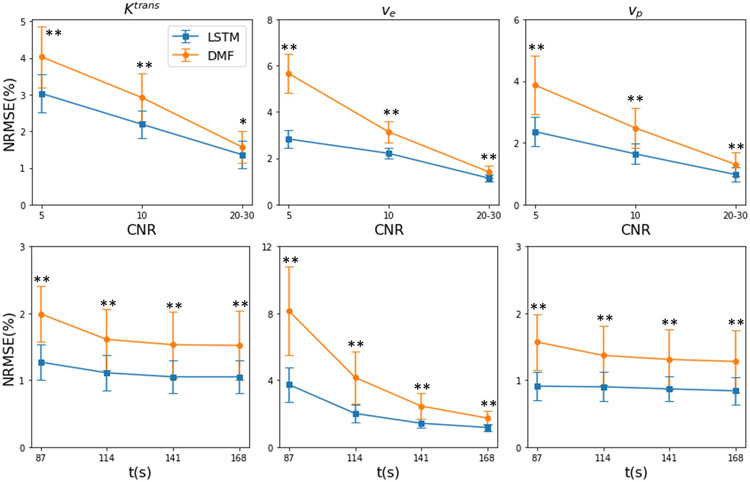
The performance of LSTM on DCE-MRI signals with lower CNRs and reduced total acquisition times is presented in Figure 7 and Table S1. As can be seen, LSTM consistently improved the accuracy for lower CNR levels and reduced total acquisition times from 168s to 87s. ve estimation had the largest improvement when total acquisition time was reduced.
Figure 7.
The performance (NRMSE) of the LSTM and DMF estimations under lower CNRs (first row) with full temporal sampling and reduced total acquisition times t (second row) with Δt=3s and CNR=20-30. Error bar: standard deviation. *: p<0.05; **p<0.005.
4. Discussion
We investigated a novel and potentially powerful LSTM-based network for learning a mapping from a CA concentration-time curve including the corresponding AIF to the underlying PK parameters. The LSTM network is capable of learning long- and short-term dependency of sequence data such as DCE-MRI. We found that the performance of the LSTM on mapping DCE-MRI time-curves to their corresponding PK parameters was superior to a state-of-the-art CNN-based approach, and better than the direct model fitting method in terms of NRMSE. The LSTM was much more robust to temporally subsampled DCE data than the direct PK model fitting, which can be utilized to increase spatial resolution of DCE images. Higher robustness of LSTM to noise and reduced acquisition time is also demonstrated compared with DMF. Our data augmentation strategies, including AIF augmentation and creation of synthetic signal time-curves from the data generation pool, overcame the limited size of the in vivo DCE-MRI training data pool. The LSTM network trained by the synthesized data was also able to perform well on empirical DCE data. This indicates that the synthetic data simulates real signal intensity-time series well and the LSTM network is effectively trained. In addition, our proposed network enables an approximately 90 times of computation time acceleration compared with the direct PK model fitting approach. The LSTM network has the potential to accelerate DCE-MRI acquisition and parameter estimation.
We attribute the superior performance of the LSTM to its capability to learn long- and short-term dependency in sequence data, and to extract dynamic features and temporal correlation in the signal intensity-time series of DCE-MRI. In contrast, the CNN extracts “spatial” features from the DCE-MRI volumes but has a limited capability to exploit the temporal relationships in the DCE data. For example, a 2D CNN model treats the x-y-t data as a 3D volume, in which time-dependent features in the dynamic data could not be effectively extracted27,28. A 3D CNN model12 attempts to address some of the issues of the 2D CNN by leveraging more temporal correlation. Without incorporating an AIF as input in the CNN, the PK parameters could have degeneracy and correspond to multiple signal time-curves, which can lead to a mis-mapping between the PK parameters and DCE curves. The small training and testing patch sizes limited by the high GPU memory demand of the 3D CNN training may further degrade its performance. Our proposed LSTM network structure is straightforward, and there is no PK model information required for LSTM training. Also, the AIF is incorporated into input as a second channel, which allows use of a patient-specific AIF when processing empirical patient DCE data. The proposed network can be easily trained and extended to other PK models, or even other sequence-related medical imaging data, e.g., a high-order diffusion model, with a minimum modification of the network architecture.
We used several strategies to overcome the limited size of the in vivo DCE-MRI data. First, we did not use a fixed triad of the AIF, the PK parameters, and the signal time-curves from the in vivo DCE-MRI dataset, which limits us to a total of 103 patient datasets. We used synthesized signal time-curves that were created by randomly selected and combined PK parameters, AIF (and augmented AIF), and time step from a data pool. In addition, we added random variations of the delay of CA bolus arrival into the signal time-curves. Our evaluation shows that the PK parameters from 78 patients sufficiently cover the parameter ranges of interest. The performance of LSTM2, and LSTM3 indicates that the PK parameters from 60% of the training data could sufficiently cover the ranges of parameter of interest. Our overall strategy of the training data synthesis seems to yield effective training of the LSTM networks, and overcomes the limited size of in vivo datasets. These strategies seem to reasonably mitigate small amount of variation in sampling interval in the in vivo data.
For extraction of PK parameters from signal time curves with different time steps (3-6s), the LSTM models show robust performance compared to the direct PK model fitting, with the latter showing performance degradation with an increase in the time step size. This advantage of the LSTM approach can be utilized to improve the spatial resolution of DCE-MRI when decreasing the temporal resolution of DCE-MRI. For example, a modest increase in the spatial resolution from the currently used 1.6×1.6×2.5 mm3 to 1.4×1.4×1.4 mm3 would prolong the acquisition time of an image volume by a factor of 2. This increase in the temporal resolution from 3s to 6s would result in an increase in NRMSE% of the estimates by 1.7-2.1 times by the DMF but a very small increase by the LSTM model (Figure 6).
This work has several limitations. As we can see from Figure 4 and Table 1, the LSTM performs better than DMF in terms of NRMSE but not as good in terms of SSIM across the whole parameter range. Further analysis of the error distribution reveals that this is mainly due to the minor estimation errors in parameter combinations of zero Ktrans and ve but non-zero vp (mainly in the brain region), which caused by the small portion of these parameter value combinations in the training datasets. Another concern is the accuracy of parameter estimation in the gross tumor volume, which has a different range of the parameters from normal tissue and has a small amount of the data weighting in the training dataset. We note similar SSIM values of DMF and LSTM in the gross tumor volume (Table 1). Further manipulation of the training dataset distribution and/or a modification of the loss function or a weighting training data in different parameter ranges could improve performance of the algorithm. Another path to improvement generalizability is to incorporate temporal sampling intervals into the network input as another channel29. The performance of the current vanilla LSTM architecture could be further improved by using a bidirectional LSTM with attention at the expense of longer training and inference time. A further improved model could use more realistic synthetic data that takes motion artifacts and other factors into account to improve the robustness of performance of the LSTM on in vivo DCE-MRI datasets.
5. Conclusions
In conclusion, our proposed LSTM is a promising approach to estimate PK parameters from DCE-MRI time-series. We demonstrate that the proposed approach provides more accurate PK parameter maps compared to the CNN-based approach, and is comparable to the DMF method with approximately 90 times of computation time reduction. The LSTM networks are more robust to low temporal resolution, lower CNR levels, and reduced total acquisition time than direct PK model fitting. In the future, a similar LSTM network can be applied directly to (k, t) space data to leverage the temporal and spatial sparsity, and thus accelerate both the data acquisition and image reconstruction of DCE-MRI.
Supplementary Material
Figure S1 The distribution of (a) Ktrans, (b) ve, and (c) vp in the training data generation pool.
Figure S2 An exemplary slice of the ground truth parameter maps (column 1), the estimated maps (column 2–4), and the residual maps (last 3 columns) of estimated Ktrans (top row) ve (middle row) and vp (bottom row) by the LSTM3, CNN, and DMF models from a testing case. The white contour depicts the gross tumor volume. GT: ground truth.
Figure S3 Three exemplary in vivo CA concentration-time curve fitting results by DMF and LSTM3 in the tumor region indicated by the white contour shown in the left Ktrans parameter map estimation by DMF. Results from both methods are in reasonable alignment with observed data. (SE = squared error)
Figure S4 An exemplary slice of ground truth of parameter maps (column 1), estimated maps (column 2 and 3), and the residual maps (last 2 columns) by LSTM and DMF using temporal sampling interval Δt = 6s. The tumor volume is depicted by a white contour. GT: ground truth.
Acknowledgements
This work was supported by NIH R01 EB016079
Footnotes
Conflict of Interest
The authors have no conflicts to disclose.
Contributor Information
Jiaren Zou, Department of Radiation Oncology, University of Michigan, Ann Arbor, MI 48109, USA.
James M. Balter, Department of Radiation Oncology, University of Michigan, Ann Arbor, MI 48109, USA; Department of Biomedical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Yue Cao, Department of Radiation Oncology, University of Michigan, Ann Arbor, MI 48109, USA; Department of Radiology, University of Michigan, Ann Arbor, MI 48109, USA; Department of Biomedical Engineering, University of Michigan, Ann Arbor, MI 48109, USA.
References
- 1.Cao Y, Popovtzer A, Li D, et al. Early Prediction of Outcome in Advanced Head-and-Neck Cancer Based on Tumor Blood Volume Alterations During Therapy: A Prospective Study. Int J Radiat Oncol Biol Phys. 2008;72(5):1287–1290. doi: 10.1016/j.ijrobp.2008.08.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gaddikeri S, Gaddikeri RS, Tailor T, Anzai Y. Dynamic contrast-enhanced MR imaging in head and neck cancer: Techniques and clinical applications. Am J Neuroradiol. 2016;37(4):588–595. doi: 10.3174/ajnr.A4458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cao Y, Aryal M, Li P, et al. Predictive Values of MRI and PET Derived Quantitative Parameters for Patterns of Failure in Both p16+ and p16– High Risk Head and Neck Cancer. Front Oncol. 2019;9(November):1–11. doi: 10.3389/fonc.2019.01118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kim MM, Parmar HA, Aryal MP, et al. Developing a Pipeline for Multiparametric MRI-Guided Radiation Therapy: Initial Results from a Phase II Clinical Trial in Newly Diagnosed Glioblastoma. Tomogr (Ann Arbor, Mich). 2019;5(1):118–126. doi: 10.18383/j.tom.2018.00035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Khalifa F, Soliman A, El-Baz A, et al. Models and methods for analyzing DCE-MRI: A review. Med Phys. 2014;41(12):1–32. doi: 10.1118/1.4898202 [DOI] [PubMed] [Google Scholar]
- 6.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391 [DOI] [PubMed] [Google Scholar]
- 7.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952–962. doi: [DOI] [PubMed] [Google Scholar]
- 8.Uecker M, Lai P, Murphy MJ, et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990–1001. doi: 10.1002/mrm.24751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cao Y, Li D, Shen Z, Normolle D. Sensitivity of Quantitative Metrics Derived from DCE MRI and a Pharmacokinetic Model to Image Quality and Acquisition Parameters. Acad Radiol. 2010;17(4):468–478. doi: 10.1016/j.acra.2009.10.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murase K Efficient method for calculating kinetic parameters using T1-weighted dynamic contrast-enhanced magnetic resonance imaging. Magn Reson Med. 2004;51(4):858–862. doi: 10.1002/mrm.20022 [DOI] [PubMed] [Google Scholar]
- 11.Wang C, Yin FF, Chang Z. An efficient calculation method for pharmacokinetic parameters in brain permeability study using dynamic contrast-enhanced MRI. Magn Reson Med. 2016;75(2):739–749. doi: 10.1002/mrm.25659 [DOI] [PubMed] [Google Scholar]
- 12.Ulas C, Tetteh G, Thrippleton MJ, et al. Direct Estimation of Pharmacokinetic Parameters from DCE-MRI using Deep CNN with Forward Physical Model Loss. 2018;11070 LNCS:39–47. doi: 10.1007/978-3-030-00928-1_5 [DOI] [Google Scholar]
- 13.Ulas C, Das D, Thrippleton MJ, et al. Convolutional Neural Networks for Direct Inference of Pharmacokinetic Parameters: Application to Stroke Dynamic Contrast-Enhanced MRI. Front Neurol. 2019;9(January). doi: 10.3389/fneur.2018.01147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hochreiter S, Schmidhuber J. Long Short-Term Memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735 [DOI] [PubMed] [Google Scholar]
- 15.Donahue J, Hendricks LA, Rohrbach M, et al. Long-Term Recurrent Convolutional Networks for Visual Recognition and Description. IEEE Trans Pattern Anal Mach Intell. 2017;39(4):677–691. doi: 10.1109/TPAMI.2016.2599174 [DOI] [PubMed] [Google Scholar]
- 16.Chen J, Yang L, Zhang Y, Alber M, Chen DZ. Combining fully convolutional and recurrent neural networks for 3D biomedical image segmentation. In: Advances in Neural Information Processing Systems. ; 2016:3044–3052. http://arxiv.org/abs/1609.01006. [Google Scholar]
- 17.Antropova N, Huynh B, Li H, Giger ML. Breast lesion classification based on dynamic contrast-enhanced magnetic resonance images sequences with long short-term memory networks. J Med Imaging. 2018;6(01):1. doi: 10.1117/1.jmi.6.1.011002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J Magn Reson Imaging. 1997;7(1):91–101. doi: 10.1002/jmri.1880070113 [DOI] [PubMed] [Google Scholar]
- 19.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
- 20.Paldino MJ, Barboriak DP. Fundamentals of Quantitative Dynamic Contrast-Enhanced MR Imaging. Magn Reson Imaging Clin N Am. 2009;17(2):277–289. doi: 10.1016/j.mric.2009.01.007 [DOI] [PubMed] [Google Scholar]
- 21.Cao Y WE-D-T-6C-03: Development of Image Software Tools for Radiation Therapy Assessment. Med Phys. 2005;32(6Part19):2136–2136. doi: 10.1118/1.1999737 [DOI] [Google Scholar]
- 22.Singh A, Rathore RKS, Haris M, Verma SK, Husain N, Gupta RK. Improved bolus arrival time and arterial input function estimation for tracer kinetic analysis in DCE-MRI. J Magn Reson Imaging. 2009;29(1):166–176. doi: 10.1002/jmri.21624 [DOI] [PubMed] [Google Scholar]
- 23.Bendinger AL, Debus C, Glowa C, Karger CP, Peter J, Storath M. Bolus arrival time estimation in dynamic contrast-enhanced magnetic resonance imaging of small animals based on spline models. Phys Med Biol. 2019;64(4):045003. doi: 10.1088/1361-6560/aafce7 [DOI] [PubMed] [Google Scholar]
- 24.Fritz-Hansen T, Rostrup E, Larsson HBW, Søndergaard L, Ring P, Henriksen O. Measurement of the arterial concentration of Gd-DTPA using MRI: A step toward quantitative perfusion imaging. Magn Reson Med. 1996;36(2):225–231. doi: 10.1002/mrm.1910360209 [DOI] [PubMed] [Google Scholar]
- 25.Robben D, Suetens P. Perfusion parameter estimation using neural networks and data augmentation In: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). Vol 11383 LNCS Springer Verlag; 2019:439–446. doi: 10.1007/978-3-030-11723-8_44 [DOI] [Google Scholar]
- 26.Kingma DP, Ba JL. Adam: A method for stochastic optimization. In: 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings ; 2015. http://arxiv.org/abs/1412.6980. [Google Scholar]
- 27.Arbelle A, Raviv TR. Microscopy cell segmentation via convolutional LSTM networks In: Proceedings - International Symposium on Biomedical Imaging. Vol 2019-April IEEE; 2019:1008–1012. doi: 10.1109/ISBI.2019.8759447 [DOI] [Google Scholar]
- 28.Zhang D, Icke I, Dogdas B, et al. A multi-level convolutional LSTM model for the segmentation of left ventricle myocardium in infarcted porcine cine MR images In: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). Vol 2018-April IEEE; 2018:470–473. doi: 10.1109/ISBI.2018.8363618 [DOI] [Google Scholar]
- 29.Simeth J, Cao Y. GAN and dual-input two-compartment model-based training of a neural network for robust quantification of contrast uptake rate in gadoxetic acid-enhanced MRI. Med Phys. 2020:1–11. doi: 10.1002/mp.14055 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 The distribution of (a) Ktrans, (b) ve, and (c) vp in the training data generation pool.
Figure S2 An exemplary slice of the ground truth parameter maps (column 1), the estimated maps (column 2–4), and the residual maps (last 3 columns) of estimated Ktrans (top row) ve (middle row) and vp (bottom row) by the LSTM3, CNN, and DMF models from a testing case. The white contour depicts the gross tumor volume. GT: ground truth.
Figure S3 Three exemplary in vivo CA concentration-time curve fitting results by DMF and LSTM3 in the tumor region indicated by the white contour shown in the left Ktrans parameter map estimation by DMF. Results from both methods are in reasonable alignment with observed data. (SE = squared error)
Figure S4 An exemplary slice of ground truth of parameter maps (column 1), estimated maps (column 2 and 3), and the residual maps (last 2 columns) by LSTM and DMF using temporal sampling interval Δt = 6s. The tumor volume is depicted by a white contour. GT: ground truth.