GWAS Significance Thresholds for Deep Phenotyping Studies Can Depend Upon Minor Allele Frequencies and Sample Size

Abstract

An important issue affecting Genome-Wide Association Studies (GWAS) with deep phenotyping (multiple correlated phenotypes) is determining the suitable family-wise significance threshold. Straightforward family-wise correction (Bonferroni) of p <0.05 for 4.3 million genotypes and 335 phenotypes would give a threshold of p < 3.46E-11. This would be too conservative because it assumes all tests are independent. The effective number of tests, both phenotypic and genotypic, must be adjusted for the correlations between them.

Spectral decomposition of the phenotype matrix and LD-based correction of the number of tested SNPs, are currently used to determine an effective number of tests. In this paper, we compare these calculated estimates with permutation-determined family-wise significance thresholds. Permutations are performed by shuffling individual IDs of the genotype vector for this dataset, to preserve correlation of phenotypes.

Our results demonstrate that the permutation threshold is influenced by minor allele frequency (MAF) of the SNPs, and by the number of individuals tested. For the more common SNPs (MAF > 0.1), the permutation family-wise threshold was in close agreement with spectral decomposition methods. However, for less common SNPs (0.05<MAF ≤ 0.1) the permutation threshold calculated over all SNPs was off by orders of magnitude. This applies to the number of individuals studied (here 777) but not to very much larger numbers. Based on these findings, we propose that the threshold to find a particular level of family-wise significance may need to be established using separate permutations of the actual data for several minor allele frequency bins.

Introduction

Genome-wide association studies (GWAS) systematically analyze single-nucleotide polymorphisms (SNPs) across the genome for association with a single phenotype of interest such as a clinical diagnosis. In studies with dense phenotyping of multiple correlated phenotypes, an important challenge is to find a significance threshold based on the family-wise error (FWER), i.e. the probability of Type I error in the entire set of tested hypotheses. An inappropriate statistical significance threshold can mask potential true positive signals or incur a false positive signal (1).

The two most common methods to address Multiple Test Correction (MTC) are Bonferroni and Sidak correction. These methods control the experiment wise error rate (α_e) by specifying what point-wise P-value error rate (α_p) should be used for each individual test in order to declare it significant. The Sidak correction gives α_p = 1-(1-α_e)^1/M, and Bonferroni correction is usually obtained as α_p = α_e /M, where M is the number of tests. These two methods each assume that the hypotheses tested are independent, and thus lose power when the tests are correlated(2).

Many algorithms have been proposed to modify these methods in order to account for the correlation structure of phenotypic and genotypic data, through the use of ‘effective number of independent tests’ (3). Effective number of tests (M_eff) -based methods use dimension reduction techniques to filter out the correlation between tests, leaving just the effective number of independent tests, and then apply Bonferroni or Sidak correction by using M_eff instead of M in their respective formulas.

Cheverud (3) was the first to propose a method for calculating M_eff, which was later refined by Nyholt (4). These methods are based on the variance of the eigenvalues derived from a correlation matrix of the phenotypes (in this study), but they were found to be overly conservative for genotypes when there is high linkage disequilibrium (LD) among SNPs (4).

Li and Ji (5) proposed another method for M_eff estimation that showed an improvement in power over Nyholt’s method. Their method partitioned the eigenvalues of a phenotype correlation matrix into integral and non-integral parts, where the integral part of the eigenvalues represents the identical (correlated) tests and the non-integral part represents independent or partly correlated tests. Later, a method similar to Li and Ji (5) was proposed for genotypes that involves dividing the SNPs into different LD blocks and calculating the correlation matrix. Eigenvalue analysis of the correlation matrix for each LD block is then used to calculate the M_eff (6). Gao et al. (2) proposed a principal component analysis (PCA)-based approach named simpleM, which uses composite LD (CLD) correlation to create the correlation matrix and M_eff for a given dataset.

Although the “effective number of tests” procedures do capture the correlation structure, permutation tests are generally considered as the “gold standard” for multiple testing correction (7, 8). For permutation when multiple tests are performed on the same genotypic data set, an empirical adjustment for correlated tests can be made by randomly shuffling the genotype vectors of the individuals, thus preserving the correlation of phenotypes. This generates a distribution of the test statistics for each permuted data set under the null hypothesis (H_o) of no true association (9). The minimum p-values observed for each of the tests are ordered, and the threshold p-value is the percentile in this ordering that corresponds to the point-wise P-value error rate (α_p). Although this method gets cumbersome with the currently huge number of SNPs, because of the large number of random shuffles needed to get reliable genome wide significance levels, and thus substantial computation time, it is less likely to give false positives.

It is claimed that if an effective number of tests exists then the minimum p-value in each permutation should follow a beta distribution with parameters (α=(1), β =(M_E) (10). A Beta distribution is fitted to the minimum P value of permutation replicates by setting the first parameter (α) equal to 1 or by setting both parameters free. Parameter (β) measures the effective number of tests and checks whether the minimum P-value is consistent with the effective number of tests calculated using linear algebra directly on the genotype data (10).

Previous studies have explored the effect of MAF on the probability of obtaining a false positive result (11). These studies have demonstrated that the most common SNPs (MAF between 0.25 and 0.5) had less false positives as compared to the less frequent SNPs (MAF < 0.1). Therefore, it is important to understand if the statistical threshold controlling the false positive rate changes with minor allele frequency using permutation for several minor allele frequency bins.

Several authors have looked at the effect of sample size on the false positive and false negative results to detect true evidence for an association (12, 13). Their work reported that GWAS with larger number of SNPs require a larger sample size to reduce false positives due to MTC. Small sample size can increase the false negative rates and decreases the reliability of results. Hong and Park (12) found that sample size is highly affected by linkage disequilibrium, effect size of the genetic variant and the minor allele frequency of the variants, and confirmed that lower sample size is required for testing more common SNPs (MAF of 0.3) then for testing SNPs with MAF of 0.05. It is therefore important to check family-wise permutation p-values as a function of MAF and sample size.

To overcome the computational burden, permutation approximation-based methods have been proposed for SNPs, among which the SLIDE program (Sliding-window method for Locally Inter-correlated markers with asymptotic Distribution Errors corrected) showed the best performance on a genome-wide scale(14). SLIDE is a parametric method that relies on sliding-window strategy to account for the linkage disequilibrium (LD) among the SNPs. It uses a Monte-Carlo approach to approximate the multivariate normal (MVN) distribution and scales the MVN to correct for the inaccuracies in the tails of the true null distribution.

Here we report comparative estimations of genome-wide and family-wise significance thresholds applied to data from the Bipolar-Schizophrenia Network for Intermediate Phenotypes (B-SNIP), a multi-phenotype project (15). For permutation, we calculate the empirical genome-wide significance threshold based on the minimum P values distribution of the permuted data-sets tested with GWAS using the program PLINK (16). For comparison with permutation results, we present several combined multiple testing correction strategies, where we correct for the multiple correlated phenotypes and multiple correlated genotypes using the data reduction techniques and MVN method described above, and calculate the family-wise GWAS significance thresholds. We propose a permutation threshold for multiple correlated phenotypes, and observe that the permutation thresholds vary widely with the common and less common variants, and that these effects are present at moderate but not large numbers of individuals studied.

Methods

Datasets, individuals, genotyping

We performed permutation and other null hypothesis analyses of probabilities on 335 Magnetic Resonance Imaging data (MRI) structural brain imaging phenotypes determined by Freesurfer6 (17). Data from the Bipolar-Schizophrenia Network for Intermediate Phenotypes (B-SNIP) (15, 18) were available for 777 patients with Schizophrenia, Schizoaffective disorder, psychotic Bipolar Disorder, and Healthy Controls (HC), who were unrelated to each other (we removed individuals with 3^rd degree or closer kinship by PREST-plus and KING analysis) (19, 20). Of these 777 individuals, 483 were cases (169 Bipolar, 127 Schizoaffective and 187 Schizophrenia) and 294 were HC. There were 32.18 % individuals self-reported as African Americans, 62.16 % individuals as Caucasians and 5.66 % other ethnicities (includes Asian, American Indian, multiracial and unknown). Genotyping was performed at the Broad Institute, using the Illumina Infinium Psych Array (PsychChip), which contains 588,454 SNP markers including 50,000 specific genetic markers for neuropsychiatric disorder (21). PsychChip genotype calls were processed at the Broad institute using a custom pipeline designed to merge calls from three different algorithms (GenCall, Birdseed and zCall) in order to enhance reliability. To reduce the genotyping errors in LD estimation, SNPs were included in the analysis with call rate > 98%, HWE P-value > 1E-06 in controls, Inbreeding Coefficient (-0.2 > F_Het > 0.2) and Minor Allele Frequency (MAF) 0.05. Later, genotypes were imputed to the 1000 Genomes project multiethnic reference panel using HAPI-UR for pre-phasing and IMPUTE (22, 23). After imputation, around 30 Million variants were obtained which were reduced to 4,322,238 by filtering for <0.05 missingness by marker, <0.02 missingness by individual sample and MAF > 0.05.

Permutation

We permuted 4.3 million imputed common genotypes (MAF >=0.05) on the phenotype vector for 777 individuals. In each permutation shuffle, we swapped labels of 777 unrelated individuals and generated a new dataset under the null hypothesis of no association, assuming that the individuals are interchangeable. For each permuted sample, we tested association of the SNPs with 335 phenotypes (whose correlations were preserved by permuting genotypes), in a linear regression model using PLINK software (16). Permutation tests also may give inaccurate significance thresholds in the presence of population stratification that results when both risk of phenotype and the allele frequency of the genetic marker differ across subpopulations (24, 25). To avoid the population stratification issue in our permutation procedure, we included as covariates the top two eigenvectors from the principal component analysis of SNP data as summary measures of ancestry (26), and also used age, sex and intracranial volume as other covariates. The role of these covariates was maintained in each permuted dataset even though the associations between genotypes and phenotypes were broken.

The minimum P-values across all phenotype of each permutation (P_min) were recorded and arranged in ascending order. The 100(α) percentile of the P_min was the empirical genome-wide significance threshold for the overall (family-wise) significance level of α =0.05 (9). Whatever threshold is used for significance; it is a fundamental assumption that null p-values follow a uniform distribution. If this assumption is not met the efforts to establish a threshold of significance may produce incorrect results (27). We confirmed that the null p-values follow a uniform distribution on a SNP set of 4.3 million genotypes (including imputation) permuted 60 times. Each SNP was then tested for association to the phenotype data and the distribution of the resulting p-values displayed as a histogram (Supplementary Fig. S1).

To understand the relationship between the statistical significance threshold and MAFs of the variants, we plotted the permutation P-values against the MAF (Fig. 1). We found that as the MAF of the variants decreases, thresholds become more stringent. To further explore this, we divided the SNPs into two bins, one with MAF < 0.1 and other as MAF > 0.1 and calculated the permutation threshold. For testing the effects of sample size, we made one hundred copies of the genotypic data set, and shuffled the existing individual phenotype sets among them. This produced a 100x larger sample with the same phenotypic correlations.

Fig. 1.

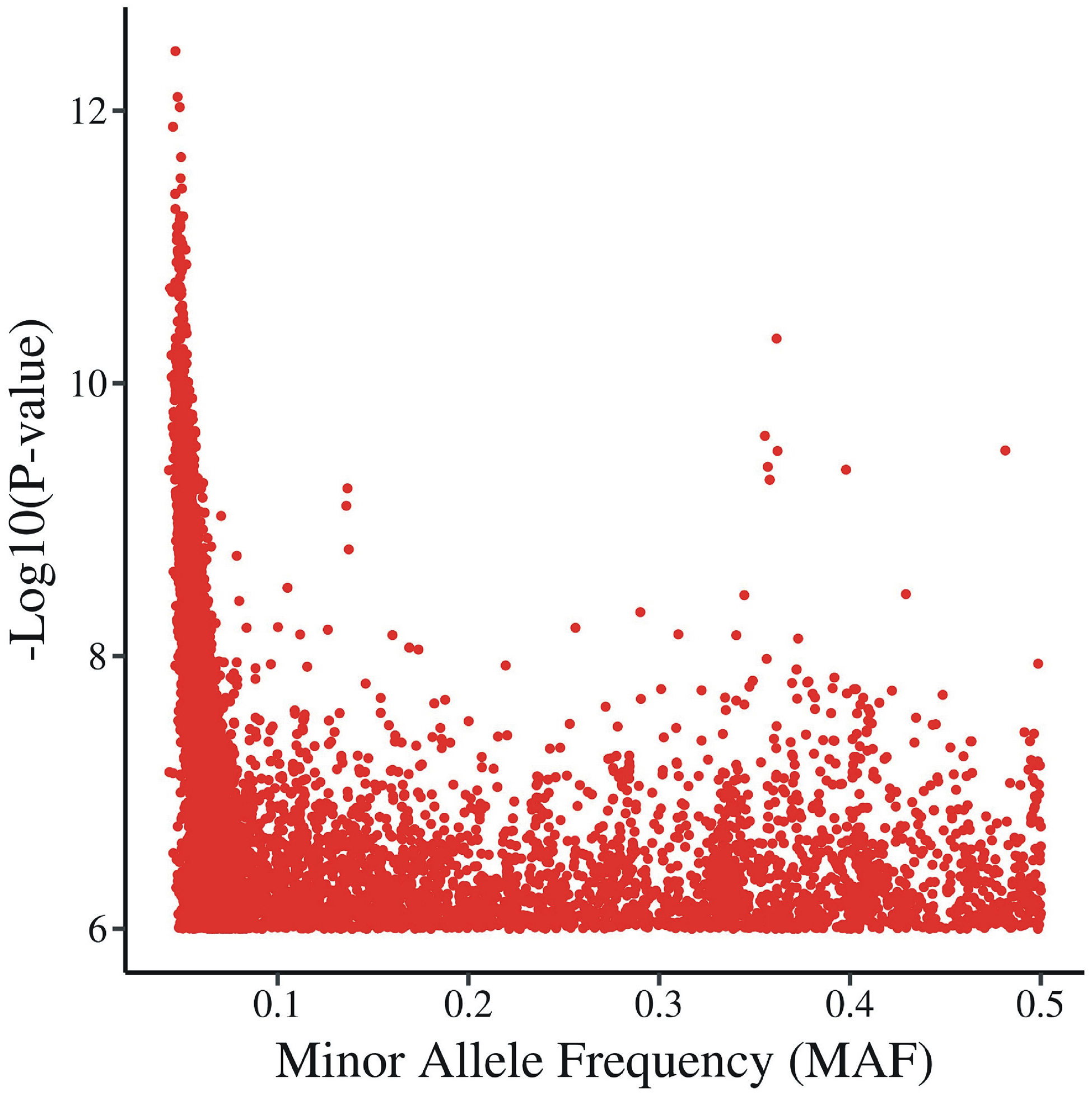
Observed permutation p-values as a function of minor allele frequency in 777 individuals and 335 correlated phenotypes. SNPs with P value ≤ 1.0E-06 are extracted from permuted genotype data and plotted against their minor allele frequency (MAF). Each red dot represents a P value of one SNP.

Permutation tests were performed on a computer cluster of the Psychiatry and Behavioral Neuroscience Department at the University of Chicago.

Multiple testing correction for correlated phenotypes

Effective number of tests (M_eff) estimation

Nyholt method (4).

We estimated the phenotype correlation matrix using the cor() function in R. We use this correlation matrix as an input to calculate the M_eff. For Nyholt effective number of tests (M_{eff_Nyholt}) we used equation 1 where M is equal to total number of phenotypes (M= 335) and Var(λ) is the variance of observed eigenvalues.

$${\text{M}}_{\text{eff\_Nyholt}}=1+\left(\text{M}-1\right)\left(1-\text{Var}(\lambda )/\text{M}\right)$$ (1)

Li and Ji method (5).

To estimate Li and Ji effective number of tests (M_{eff_Li-and-Ji}) we use [Li and Ji’s] equation 2

$${\text{M}}_{\text{eff\_Li-and-Ji }}={\sum }_{i=1}^{M}f\left(\left|\lambda \right|\right)$$ (2)

where

f(λ_i) = I(x ≥ 1) + (x − ⌊x⌋), x ≥ 0

Here I(x ≥ 1) is the indicator function, which gives 1 where x ≥ 1 and 0 otherwise, and ⌊x⌋ is the floor function which gives the largest integer less than or equal to x.

Multivariate normal distribution-based (MVN) approximation test (14)

To implement the MVN based approximation to permutation test we used SLIDE software (14). SLIDE relies on the assumption that association statistics over multiple markers asymptotically follow a multivariate normal distribution (MVN). In our analysis, we used a window size of 100 markers using the quantitative trait option and 10,000 samplings.

Li et al method (6)

To correct for LD between the SNPs, we performed eigenvalue analysis of the SNPs correlation matrix and calculated effective number of LD-independent SNPs and genome wide significant threshold using Genetic type I Error Calculator (GEC) version 0.2 (6).

Gao et al method (2)

We used Gao et al’s method (equation 3) to measure the composite LD (CLD) correlation between the SNPs and calculated the M_eff using the number of principal components that contribute to 99.5% of variation in the SNPs.

$${\sum }_{i=1}^x\lambda i/{\sum }_{i=1}^M\lambda i>\text{C}$$ (3)

where C is the percentage cutoff and we use Gao’s recommendation of 0.995.

Beta Distribution (10)

We fitted the Beta distribution to the observed minimum p-values from the permutation tests for each GWAS dataset and estimated the two beta parameters, once with the first parameter set to 1 and again with both parameters free using the method of moments. The Quantile-Quantile plot comparing the observed minimum P-distributions against the expected quantiles of the β(0.7, 0.76E06) distribution showed that the minimum p-values follow the beta distribution and β is close to the effective number of tests calculated by using spectral decomposition methods (Supplementary Fig. S2).

Results

Table 1 shows the results of several spectral decomposition methods on 335 correlated phenotypes (Supplementary Fig. S3). The correction based on the Nyholt method determined 286 effective phenotype tests, while that of Li and Ji estimated 122 effective phenotypes. The genome-wide significance threshold to control the family-wise type I error rate at 0.05 is estimated based on these corrections. The corrections using Nyholt effective phenotypes were more conservative than the ones made by using Li and Ji effective phenotypes.

Table 1.

Estimated effective number of independent phenotypes

Methods	Total number of phenotypes	Effective number of phenotypes	References
Bonferroni	335	335	(Bonferroni, 1936)
Nyholt spectral decomposition method	335	286	(Nyholt, 2004)
Li and Ji method (2005)	335	122	(Li and Ji, 2005)

We further adjusted for the interdependence of SNPs in linkage disequilibrium (LD). The standard Bonferroni correction (simply using the total number of SNPs) in our BSNIP1 data gave a threshold of 1.16E-08 for one phenotype. We estimated the number of effective SNPs using several dimension reduction methods and determined the genome-wide significance threshold. The effective number of SNPs using Gao et al, Li et al and SLIDE methods were 1.22M, 0.90M, and 1.75M respectively, which showed marked reductions from the total 4.3M directly measured SNPs (Table 2). The Bonferroni correction using these effective number of SNPs gave 4.08E-08, 5.54E-08 and 2.86E-08 significance thresholds corresponding to overall genome-wide significance level of α = 0.05 for one phenotype (Table 3).

Table 2.

Estimated effective number of independent SNPs

Methods	Total number of SNPs	Effective number of SNPs	References
Bonferroni	4.3M	4.3M	(Bonferroni, 1936)
Gao et al’s method (MGao) (Composite LD correlation between the SNPs)	4.3M	1.22M	(Gao et al., 2008)
Li et al’s method (MLi) (Block wise LD of genotypes)	4.3M	0.90M	(Li et al., 2012)
Han et al’s method (LD in sliding window of genotypes) (MHan)	4.3M	1.75M	(Han et al., 2009)

Table 3.

GWAS significance thresholds for correlated genotypes and phenotypes in this data set

Methods	GWAS threshold for one phenotype	Effective number of phenotypic tests	Family-wise threshold (alpha=0.05)
Bonferroni correction	1.16E-08	335	3.46E-11
Nyholt method for phenotypes with Bonferroni correction of genotypes	1.16E-08	286	4.06E-11
Li and Ji method for phenotypes with Bonferroni correction of genotypes	1.16E-08	122	9.51E-11
Han et al (LD in sliding window of genotypes, Li and Ji for phenotypes)	2.86E-08	122	2.34E-10
Li et al (Block wise LD of genotypes, Li and Ji for phenotypes)	5.54E-08	122	4.54E-10
Gao et al (LD of genotypes, Li and Ji for phenotypes)	4.08E-08	122	3.34E-10
Permutation of genotype (subject indices) all allele frequencies	5.29E-08	NA	8.39E-13
Permutation of genotype (subject indices) (MAF > 0.1)	5.29E-08	NA	1.93E-10
Permutation of genotype (subject indices) (SNPs with MAF ≤ 0.1)	1.51E-08	NA	8.39E-13

Next, we used the combined correlation correction strategy to obtain the thresholds that are adjusted both for corrected numbers of genotypes and phenotypes. We adjusted the thresholds obtained using genotype multiple testing corrections with the effective phenotypes obtained by Li and Ji and Nyholt method (Table 3, Supplementary Table 1 and 2).

Then, we computed significance thresholds based on permutation. We found the permutation threshold for a single phenotype as ~5E-08 which is similar to the one previously reported (based on an estimated multiple testing burden in GWAS of individuals of European ancestry after adjusting for ~1 million independent tests. (28, 29).

We calculated the 5^th percentile genome-wide permutation threshold for multiple correlated phenotypes (as discussed in the Methods section) as 1.93E-10 for common SNPs with MAF > 0.1. This is in the same range as the threshold calculated using spectral decomposition methods. A histogram of minimum p-values used to derive this threshold is plotted in Supplementary Fig. S4. The distribution is skewed as is typical for distribution of extreme values, but it does fit the Beta distribution.

To evaluate the relationship between the P-value threshold and the allele frequency spectrum, we extracted all SNPs with P value ≤ 1.0E-06 from the permuted data and plotted the P-values against the minor allele frequency (MAF). We found that as the minimum MAF of the variants decreases, more stringent thresholds are observed, possibly due to a decrease in the number of actual calculations, leading to greater variation in the results (Fig. 1). To further evaluate this findings, based on the observed distribution of P-values, we split the SNPs into two bins, one with MAF < 0.1 and other with MAF > 0.1. We found that for the variants with MAF > 0.1, the P-value threshold is comparable to the that calculated by spectral decomposition, i.e. 1.93E-10. However, as the minimum MAF of the variants decreases (variants with MAF < 0.1), the threshold gets very stringent i.e. 8.39E-13 (Table 3). These findings are true both for single and multiple correlated phenotypes (Table 3).

To check if significance threshold changes with MAF are a function of this study’s sample size, we duplicated the genotype matrix of the studied individuals 100 times, to generate 77,700 individuals for permutation of genotypes and phenotypes, and calculated significance thresholds at different allele frequencies. We observed that the change in significance threshold with MAF was either absent or nearly absent in the large sample (Fig. 2).

Fig. 2: Family-wise Permutation p-values as a function of minor allele frequency (MAF) and sample sizes.

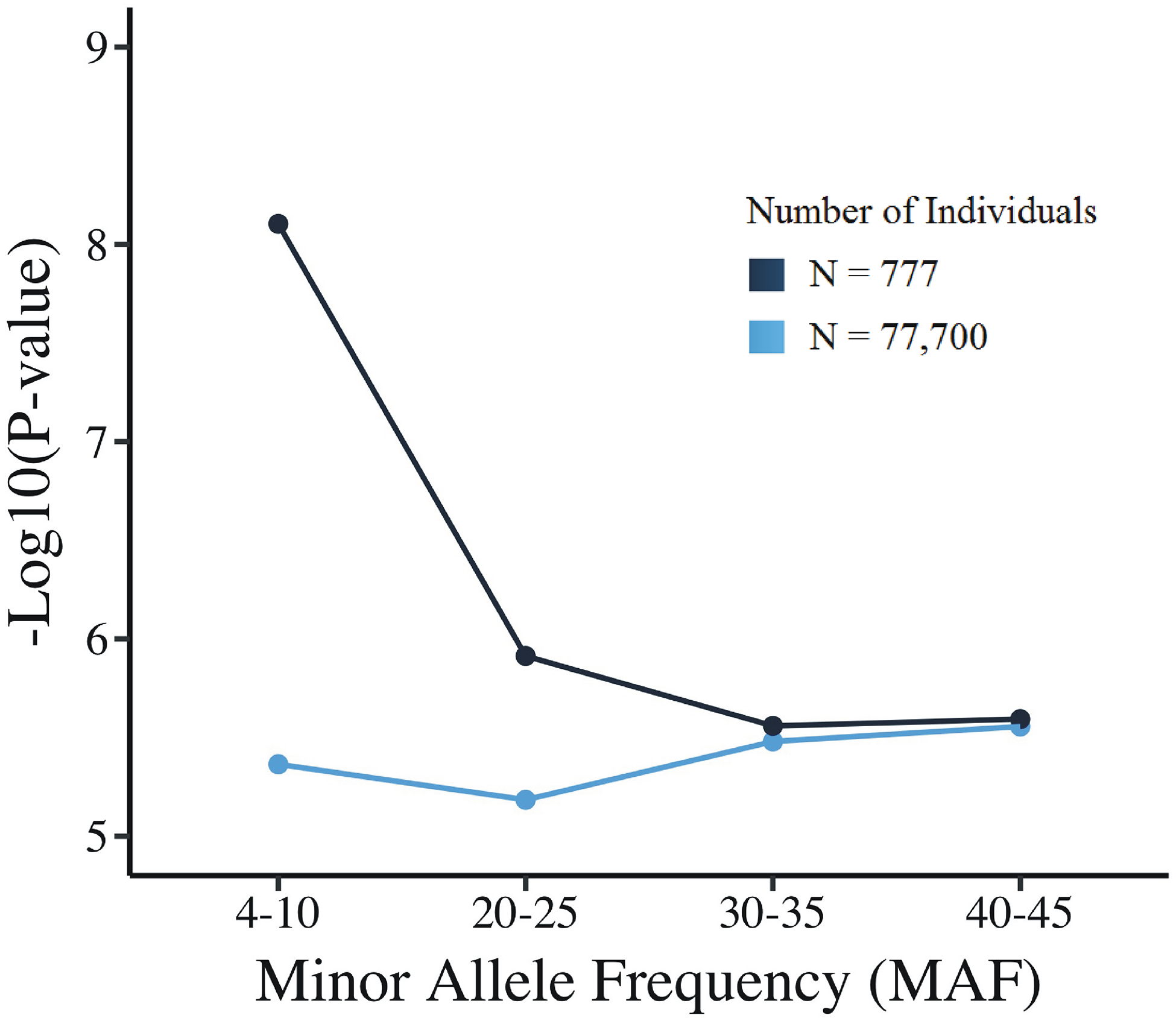
We selected SNPs each at MAFs of 4–10%, 20–25%, 30–35% and 40–45% and examine the threshold for different sample sizes (N=777 and N= 77700). The effect of minor allele frequency is attenuated in the larger sample size.

Discussion

Using permutation of the entire set of genotypes and phenotypes, to simultaneously take into account correlation of the multiple genotypes and structural MRI phenotypes, while preserving the correlations within genotypes and within phenotypes, we find a genome-wide significance threshold of 1.93E-10 for a 5% family-wise error for common SNPs with MAF > 0.1 in these data. This threshold is comparable to the thresholds calculated by combining spectral decomposition and other methods to account separately for inter-phenotypic and inter-genotypic correlations.

However, when we plotted the P-values against the MAF (Fig. 1), we observed that beginning with MAFs <0.1, permutation p-value thresholds are more stringent (8.39E-13). Our findings are consistent with a previous analysis that relied on effective SNPs approach and obtained different genome and exome-wide association P-value thresholds in different allele frequency ranges, based on pruning SNPs based on an LD threshold (30). However, our permutation based approach does not discard any SNPs from the analysis, and may prove to be more sensitive.

We have based our calculations on 60 permutations that give 60 minimum p-values, because the data size is huge for our available computational resources; each permutation is based on ~ 86 billion association tests. However, even with this number of permutations, the observed p-values give a smooth continuous curve (Figure S4), suggesting that the large number of computations gives stable family-wise p-values.

We examined the permutation threshold for different sample sizes to find its effect at different allele frequencies. We found that as we increase the sample size from 777 to 77,700 individuals, the effect of minor allele frequency is so reduced as to be ignorable. We observed clear evidence that a single overall p-value threshold calculated using a small sample size (N = 777) may not be reliable for the entire range of common MAFs, and may not be the same as thresholds calculated for a larger sample (N= 77,700). A previous report makes a similar point on threshold change with changing sample size, variant frequency, and genetic ancestry differences, but that paper did not address deep phenotyping and quantitative phenotypes (31).

Initially we considered how the Bonferroni method can be made less stringent by computing the effective number of tests. Among the three methods used for LD adjusted Bonferroni corrected P-value thresholds for genotypes, SLIDE gave most stringent threshold but it was still much less conservative than the standard Bonferroni method. The Gao et al and Li et al methods are both based on block-wise LD correction strategy. Earlier findings reported that with a large number of SNPs, Gao et al’s method underestimates the number of independent SNPs and is less efficient (32), while Li et al is more robust to variable LD and is capable of handling large datasets. Family-wise type I error rates obtained by the Li et al method was found comparable to permutation (33). Consistent with their results, we observed that the GWAS threshold for one phenotype using Li et al method was similar to what we found using permuted genotype data with one phenotype. In contrast to these methods, SLIDE uses the sliding window LD correction strategy. SLIDE takes care of the inter-block correlations while Gao et al’s and Li et al’s methods only account for the correlations within the LD blocks and ignores the correlation between disjoint marker blocks. The effective number of SNPs calculated by these methods allows less violation of the assumption of independence as compared to the standard Bonferroni correction.

For the two methods used to calculate the number of effective phenotypes, we found the Nyholt method to be overly conservative. Previously Salyakina et al suggested that Nyholt’s estimate of effective tests is highly conservative, especially when there are large number of strongly correlated tests (34). We had similar findings using the strongly correlated phenotypes in this dataset.

Since our proposed thresholds are based on the effective number of tests (SNPs and phenotypes) derived from this dataset, we do not propose a general threshold for multiple phenotypes GWAS data. We do provide support for permutation of genotypes and phenotypes for datasets that contain large numbers of intercorrelated variables, as opposed to formulas based on separate approaches to phenotypes and genotypes, and for caution in interpreting significance of associations with SNPs that are in the lower range of “common.”

Supplementary Material

1

Supplementary Fig. S1: Null P-values follow a uniform distribution. To check whether the null P-values follow a uniform distribution, the genotypes were permuted 60 times. These permuted datasets were then tested for association to the 335 phenotypes. For this histogram, we extracted all p-values from one phenotype results (4.3M SNPs × 60 shuffles × one phenotype = 259,334,280 tests). As the null P values follow a uniform distribution, this confirms that data is randomized fairly and is unbiased.

Supplementary Fig. S2: Quantile-Quantile plots of the observed minimum P-distributions against the expected quantiles of the β(0.7, 0.76E06) distribution. The fit appeared to be good suggesting that the minimum p-values from permutation follow the beta distribution.

Supplementary Fig. S3: Correlation matrix of 335 BSNIP phenotypes. Positive and negative correlations are represented by red and blue color respectively.

Supplementary Fig. S4: Histogram of minimum P-values obtained from 60 random genotype permutations 4.3 million genotypes were permuted and then tested for association with 335 multiple correlated phenotypes (whose correlations were preserved by permuting genotypes). Minimum P-values were extracted for each of the permutations (~ 86 billion association tests). The distribution of these resulting minimum p-values is displayed as a histogram.