Deficits in auditory predictive coding in individuals with the psychosis risk syndrome: Prediction of conversion to psychosis

Abstract

The mismatch negativity (MMN) event-related potential (ERP) component is increasingly viewed as a prediction error signal elicited when a deviant sound violates the prediction that a frequent “standard” sound will repeat. Support for this predictive coding framework emerged with the identification of the repetition positivity (RP), a standard stimulus ERP component that increases with standard repetition and is thought to reflect strengthening of the standard’s memory trace and associated predictive code. Using electroencephalographic recordings, we examined the RP elicited by repeating standard tones presented during a traditional “constant standard” MMN paradigm in individuals with the psychosis risk syndrome (PRS; n=579) and healthy controls (HC; n=241). Clinical follow-up assessments identified PRS participants who converted to a psychotic disorder (n=77) and PRS non-converters who were followed for the entire 24-month clinical follow-up period and either remained symptomatic (n=144) or remitted from the PRS (n=94). In HC, RP linearly increased from early- to late-appearing standards within local trains of repeating standards (p<.0001), consistent with auditory predictive code/memory trace strengthening. Relative to HC, PRS participants showed a reduced RP across standards (p=0.0056). PRS converters showed a relatively small RP deficit for early appearing standards relative to HC (p=.0.0107), and a more prominent deficit for late-appearing standards (p=0.0006) relative to both HC and PRS-remitted groups. Moreover, greater RP deficits predicted shorter time to conversion in a subsample of unmedicated PRS individuals (p=.02). Thus, auditory predictive coding/memory trace deficits precede psychosis onset and predict future psychosis risk in PRS individuals.

General Scientific Summary:

This study examines a neurophysiological measure of how the brain builds a memory for repeating sounds in order to predict the sounds that are likely to be encountered next, and shows that this measure is compromised in individuals at risk for developing psychotic disorders like schizophrenia. Moreover, the greater the deficit in this neurophysiological measure, the sooner individuals are likely to transition from an at-risk state to full psychosis.

Introduction

Electrophysiological signals relevant to predictive coding include the mismatch negativity (MMN), an auditory event-related potential (ERP) component elicited by infrequent “deviant” auditory stimuli randomly interspersed among frequent “standard” stimuli (Näätänen et al. 2012; Näätänen, Gaillard, and Mäntysalo 1978). The deviant stimulus elicits a negative voltage deflection in the stimulus-locked ERP at ~100–200 ms that is maximal at frontocentral sites (Näätänen, Teder, Alho, & Lavikainen, 1992; Näätänen et al. 2012). In order to detect deviance, the auditory system maintains a representation of the recent auditory stream, leading to early interpretations that MMN reflected sensory echoic memory (Näätänen et al., 2012). From the more recently developed predictive coding framework, MMN is a prediction error signal triggered when an improbable deviant stimulus violates the prediction that recent, frequent stimuli will recur (Friston, 2005; Garrido, Kilner, Stephan, & Friston, 2009). Thus, the earlier perspective that stimulus repetition strengthens a memory trace for the repeated stimulus is complemented by the emerging view that this memory trace subserves predictive coding, by providing a prediction for what will occur next in the auditory stream.

It has long been observed that MMN has a larger (more negative) amplitude when a greater number of standard repetitions precede the deviant (Imada, Hari, Loveless, McEvoy, & Sams, 1993; Javitt, Grochowski, Shelley, & Ritter, 1998; Näätänen, Teder, Alho, & Lavikainen, 1992; Sams, Alho, & Näätänen, 1983). This, along with observations that MMN is larger when elicited by deviants presented later relative to earlier in the recording, suggested that longer term memory processes may contribute to MMN (Cheour et al., 1998; Näätänen, Schröger, Karakas, Tervaniemi, & Paavilainen, 1993; Ritter, Gomes, Cowan, Sussman, & Vaughan, 1998; Winkler, Cowan, Csépe, Czigler, & Näätänen, 1996). Specifically, these observations provided indirect evidence that the memory trace for the standards strengthens with standard repetitions, since MMN is enhanced when the standard’s memory trace has presumably been strengthened by repetition (Näätänen, 1992). More direct evidence for this strengthening memory trace in the standard stimulus ERP was not described in traditional MMN studies, which predominantly used “constant standard” paradigms involving presentation of the same high probability standard throughout the stimulus sequence. MMN studies that examined the ERP to the standard as a function of recording time report that standards presented late in the recording session elicited an increased positivity coinciding with P1 - P2 ERP components (50–150 ms) relative to standards presented early in the session, possibly reflecting strengthening of the standard’s memory trace over time (Baldeweg, Williams, & Gruzelier, 1999; Näätänen et al., 1993). However, direct evidence for memory trace strengthening with standard stimulus repetition did not emerge until ERPs to standards were examined in “roving standard” MMN paradigms (Baldeweg, Klugman, Gruzelier, & Hirsch, 2004; Haenschel, Vernon, Dwivedi, Gruzelier, & Baldeweg, 2005).

Roving Standard vs. Constant Standard MMN Paradigms and the Repetition Positivity

In roving standard paradigms, a standard stimulus repeats until a new stimulus appears (Cowan, Winkler, Teder, & Näätänen, 1993). The first appearance of the new stimulus constitutes a deviant and elicits a MMN, but this stimulus is repeated, becoming the new standard. Each stimulus change in a roving standard paradigm evokes an MMN, with subsequent repetitions of the stimulus inducing the formation and strengthening of a new standard memory trace. Baldeweg et al. (2004) analyzed ERPs to standards and deviants from a roving standard paradigm, as a function of the number of standard repetitions preceding a deviant, in addition to the traditional MMN based on the deviant-standard difference wave. Similar to prior work, the MMN and corresponding negativity to the deviant (referred to as the “deviant negativity”) increased in amplitude (larger negativity) when deviants were preceded by a greater number of standard repetitions (Baldeweg et al., 2004). However, by analyzing standard stimuli binned according to their sequential position in each local train of repeating standards, a frontocentral positivity was also observed that was larger for standards that repeated multiple times relative to standards that repeated fewer times (i.e., comparison of the ERPs from the 2^nd, 6^th, 18^th, and 36^th consecutive standard). Baldeweg et al. referred to this as the “repetition positivity” (RP), and while it was broadly evident from 50–250 ms post-stimulus onset, it was maximal at the peak latency of the P2 component (~180 ms). Because the RP time window overlapped with the MMN time window, this finding highlighted the fact that the traditional MMN derived from the deviant-standard difference wave incorporated two distinct electrophysiological signals: the deviant negativity and the standard RP. Moreover, these distinct signals both showed memory trace effects (i.e., increasing in amplitude as a function of the number of preceding standard repetitions). From a predictive coding framework (Baldeweg, 2006, 2007; Baldeweg et al., 2004; Baldeweg, Wong, & Stephan, 2006; Haenschel et al., 2005), the RP memory trace effect reflects strengthening of the memory trace for the standard stimulus and the prediction that it will repeat.

Prior studies of the RP have predominantly used roving standard paradigms (Baldeweg et al., 2004, 2006; Costa-Faidella, Baldeweg, Grimm, & Escera, 2011; Haenschel et al., 2005). In fact, it was assumed that the RP memory trace effect would not be evident in ERPs from constant standard paradigms because, traditional paradigms do not require de novo encoding of novel stimulus features each time a deviant stimulus repeats and becomes the new standard (Baldeweg et al., 2004; Baldeweg, 2006). This assumption remained untested until Cooper et al. examined memory trace effects on the RP and MMN from a roving standard and constant standard paradigm (Cooper, Atkinson, Clark, & Michie, 2013). These authors observed a RP memory trace effect in the ERPs to standards binned according to their sequential position within local trains of repeating standard (16^th > 8^th > 4^th standard) in both the roving standard and the constant standard paradigms at mastoid electrodes. This RP effect was also evident at Fz, but only for the roving standard paradigm.

Predictive Coding Deficits in Schizophrenia and the Psychosis Risk Syndrome

Predictive coding dysfunction has been proposed as a mechanism underlying symptoms in schizophrenia, particularly positive symptoms (Fletcher & Frith, 2009; Stephan, Friston, & Frith, 2009; Sterzer et al., 2018). To the extent that MMN reductions in schizophrenia are interpreted as attenuated prediction error signaling, they provide strong support for accounts of disrupted predictive coding in schizophrenia. Despite the growing momentum of predictive coding to explain core symptoms, and an extensive literature supporting reduced MMN in SZ (Avissar et al., 2018; Erickson, Ruffle, & Gold, 2016; Javitt, Doneshka, Zylberman, Ritter, & Vaughan, 1993; Light et al., 2015; Shelley et al., 1991; Umbricht & Krljes, 2005), the formation and strengthening of the predictive code for the standard stimulus, as reflected by the RP, has rarely been studied in schizophrenia. The RP was first described in a roving standard MMN study of schizophrenia that observed RP deficits (i.e., attenuated positivity) for late, relative to early, appearing standards within local trains of repeating standards, consistent with deficient predictive code formation and strengthening (Baldeweg et al., 2004). However, a more recent roving standard MMN study (McCleery et al., 2019) reported an intact RP memory trace effect, but a deficient deviant negativity memory trace effect, in schizophrenia patients. In light of these conflicting findings and the paucity of studies to date, it remains unclear whether the RP is intact or deficient in schizophrenia.

Given their theoretical role in generating psychotic symptoms (Fletcher & Frith, 2009; Stephan, Friston, & Frith, 2009; Sterzer et al., 2018), predictive coding abnormalities are expected in individuals meeting criteria for the psychosis risk syndrome (PRS) prior to psychosis onset. However, despite prior MMN studies in PRS (Bodatsch, Brockhaus-Dumke, Klosterkötter, & Ruhrmann, 2015; Erickson, Ruffle, & Gold, 2016), the RP has not been examined in PRS individuals. Accordingly, the current study examined auditory predictive code formation, as indexed by the RP memory trace effect to repeating standards in PRS and healthy control (HC) individuals followed in the North American Prodrome Longitudinal Study-2 (NAPLS-2). NAPLS-2 is a multisite consortium focused on identifying predictors of transition to full-blown psychosis in individuals meeting PRS criteria followed longitudinally for two years (Addington et al., 2012).

As noted above, only one prior study (Cooper et al., 2013) has shown an RP memory trace effect in a constant standard paradigm, and this effect had previously been thought to require a roving standard paradigm (Baldeweg, Klugman, Gruzelier, & Hirsch, 2004). Thus, given that the current study used a constant standard paradigm, the first hypothesis tested was that an RP memory trace effect would be evident in local trains of standard repetitions in HCs. Second, based on a theoretical perspective that posits short-term neuroplasticity and predictive coding deficits as a core pathophysiological mechanism preceding psychosis onset, we hypothesized that the RP and its memory trace effect would be deficient in PRS individuals relative to HC. Third, we hypothesized that greater RP memory trace deficits would predict conversion to psychosis, as well as the imminence of conversion, in PRS individuals. Further analyses parsed PRS non-converters into sub-groups that did or did not remit symptomatically to assess whether the RP was predictive of more granular clinical outcomes after 24 months.

Methods

Participants

Participants were recruited from eight sites (University of California, San Diego, University of California, Los Angeles, Emory University, Harvard University, Zucker Hillside Hospital, University of North Carolina at Chapel Hill, University of Calgary, and Yale University). Participants were 579 individuals meeting criteria for PRS and 241 demographically similar HC individuals. PRS participants met Criteria of Psychosis-risk Syndromes (COPS) based on the Structured Interview for Psychosis-risk Syndromes (SIPS) (McGlashan, Walsh, & Woods, 2010; Miller et al., 2002), meeting criteria for at least one of three sub-syndromes: attenuated positive symptom state (APSS), brief intermittent psychotic state (BIPS), and/or genetic risk and deterioration state (GRDS). Participants were 12–35 years, and were excluded for current or lifetime psychotic disorders, IQ below 70, and/or any significant central nervous system disorder. HC individuals were additionally excluded if they had a first-degree relative with a past or current psychotic disorder. Recruitment procedures and inclusion/exclusion criteria have been described in detail (Addington et al., 2012, 2015). The study was approved by the Institutional Review Board at each study site, and participants provided written informed consent (with guardian consent/minor assent for minor participants). After completing clinical assessments and EEG recording, participants completed clinical assessments every six months, and were followed for 24 months or until they transitioned to psychosis: 77 PRS individuals converted to a psychotic disorder (i.e., met Presence of Psychotic Symptoms (POPS) criteria; Miller et al., 2003) (PRS-C; n = 77), while 238 did not convert and were followed for the full 24-month follow-up period (PRS-NC; n = 238). PRS-NC were further classified by clinical outcomes at 24 months, based on SIPS assessment. Clinical outcomes included non-converter remission (PRS-NC-Remission; n = 94) and non-converter symptomatic (PRS-NC-Symptomatic; n = 144; based on continuing to meet COPS criteria or experiencing attenuated positive symptoms in the prior month) Addington et al. (2015).

MMN Paradigm

Auditory stimuli comprised a pseudorandom sequence of 85% standard tones (633 Hz, 50 ms), 5% duration deviant tones (633 Hz,100 ms), 5% frequency deviant tones (1000 Hz, 50 ms), and 5% frequency+duration double-deviant tones (1000 Hz, 100 ms) delivered at 75 dB using Presentation software (Neurobehavioral Systems, Albany, CA). 1794 stimuli were presented over 3 blocks. Tones were presented with 5 ms rise and fall and a 500 ms stimulus onset asynchrony. To minimize attentional confounds, participants were instructed to ignore auditory stimuli while performing a visual oddball target detection task. Visual stimuli presentation was jittered to avoid co-occurring visual oddball and MMN signals. The current analysis focuses on the ERPs elicited by the auditory standards to assess the RP; analysis of the MMN to auditory deviants is presented elsewhere (Mathalon et al., in preparation).

EEG Collection and Preprocessing

Data Acquisition

All sites used BioSemi EEG acquisition systems (www.biosemi.com, Amsterdam, Netherlands). EEG was digitized at 1024 Hz using a 32-channel (Emory, Hillside, UCSD, Calgary) or 64-channel (UCLA, Harvard, UNC, Yale) electrode cap. Additional electrodes were placed 1) above and below the right eye to assess the vertical electro-oculogram (VEOG) 2) at the outer canthi of both eyes to assess the horizontal electro-oculogram (HEOG), 3) at the mastoids as the primary reference, and 4) at the nose tip as an alternative reference. All electrodes were re-referenced offline to the average mastoid.

Pre-processing

Continuous EEG data were high-pass filtered at 1 Hz offline before segmentation into 1000 ms epochs (−500 to 500 ms). Blinks and eye movement artifacts in the EEG were corrected using VEOG and HEOG channels in a regression-based correction algorithm (Gratton, Coles, and Donchin 1983). Following baseline correction (−100 to 0 ms), outlier electrodes were interpolated within single trial epochs (Nolan, Whelan, & Reilly, 2010). A spherical spline interpolation (Delorme & Makeig, 2004) was applied to any electrode that was determined to be a statistical outlier (|z| > 3) on one or more of four parameters: variance to detect additive noise, median gradient to detect high-frequency activity, amplitude range to detect pop-offs, and deviation of the mean amplitude from the common average to detect electrical drift. Epochs with amplitudes greater than ±100 μV in any of the following electrodes were rejected: AF3, AF4, F3, Fz, F4, FC1, FC2, FC5, FC6, C3, Cz, C4.

RP Measurement

Standard tones were divided into roughly equal sized bins based on their sequential position within each local series of repeating standards following a deviant tone. Standards were assigned to one of six bins based on appearing second (s2, n = 235), third (s3, n = 216), fourth or fifth (s4–5, n = 312), sixth or seventh (s6–7, n = 187), eighth through tenth (s8–10, n = 161), and eleventh or greater (s11+, n = 142; range 11–23) in sequential position following a deviant. Standard tones immediately following a deviant (s1, n = 272) were not analyzed because of expected baseline contamination from the preceding deviant.

ERP averages for all standard bins were determined using sorted averaging (Rahne, von Specht, & Mühler, 2008). This method reduces noise in task waveforms by averaging over the subset of trials that optimizes the estimated signal to noise ratio (eSNR) for each subject. Single-epoch root mean squared (RMS) amplitude values for each trial were calculated at each of the 12 artifact rejection electrodes, averaged across electrode, and sorted in ascending order for each standard bin. The subset of sorted trials selected for ERP averaging were associated with the largest eSNR, which is the ratio of the number of trials to the variance of the RMS amplitude across trials. Next, ERPs were 30 Hz low-pass filtered. Given that the RP is superimposed on the N1 and P2 components in the standard ERP, identification and measurement of the RP was facilitated by subtracting the s2 ERP waveform (where the RP was expected to be the smallest) from all other standard repetition ERPs, yielding five standard repetition difference waves (s3 – s2, s4–5 – s2, s6–7 – s2, s8–10 – s2, s11+ – s2) for each participant. Subsequently, the most positive peak between 50 and 200 ms was identified at electrode Fz (Baldeweg et al., 2004; Costa-Faidella et al., 2011; Haenschel et al., 2005) for each standard repetition ERP difference wave, and the mean amplitude ±25 ms centered on the peak was used to quantify the RP amplitude.

Statistical Plan

Clinical Data

Groups were compared on demographic and clinical continuous variables using analysis of variance (ANOVA), and on categorical variables using chi-square tests (Table 1).

Table 1.

Participant demographic characteristics for baseline and clinical outcome analyses.

2-Group Baseline Analysis
Healthy Controls				Psychosis Risk Syndrome
				Unmedicated sub-sample¶		Full Sample
n	241			449		579
*Age (years)	20.33 ± 4.74			19.36 ± 4.51		19.34 ± 4.48
Gender (% male)	52.70%			56.12%		57.30%
4-Group 24-Month Clinical Outcome Analysis
Group:	Healthy Controls (HC)	Psychosis Risk Syndrome - Remission (PRS-NC-R)		Psychosis Risk Syndrome - Symptomatic (PRS-NC-S)		Psychosis Risk Syndrome - Conversion (PRS-C)
		Unmedica ted sub-sample¶	Full Sample	Unmedica ted sub-sample¶	Full Sample	Unmedica ted sub-sample¶	Full Sample
n	241	78	94	112	144	54	77
*Age (years)	20.33 ± 4.74	18.61 ± 4.58	18.65 ± 4.43	20.08 ± 4.75	19.97 ± 4.16	18.94 ± 3.57	18.64 ± 3.63
Gender (% male)	52.70%	47.40%	50%	58.00%	58.30%	63.00%	62.30%

^¶Excludes PRS individuals on antipsychotic medication at time of EEG recording

^*Age: HC vs. PRS-baseline, Full Sample F(1,818) = 10.42, p=.001; HC vs. PRS-Baseline, Unmedicated Sub-sample F(1, 688) = 7.33, p=.007

^*Age: 4-Group Clinical Follow-up Sample, Full Sample F (3,552) = 4.87, p = .002

Tukey-Kramer HSD post-hoc tests HC>PRS-C, p=.02; HC>PRS-NC-R, p=.01

^*Age: 4-Group Clinical Follow-up Sample, Unmedicated Sub-sample F (3,481) = 3.56, p = .01

Tukey-Kramer HSD post-hoc tests HC>PRS-NC-R, p=.02

Healthy Control Repetition Positivity Analysis: Modeling Age and Site

Analyses were conducted in the HC group to establish the expected RP memory trace effect and inform subsequent group analyses. Using SAS v9.4, a mixed effects model treated Site (8 levels) as a fixed between-subjects factor and Standard Repetition (5 levels) as a fixed within-subjects factor, Age as a covariate, and Subject nested within Site as a random factor. An Age X Standard Repetition interaction term was included to assess for differences in the age-RP relationship as a function of standard repetition. Both unstructured and compound symmetry covariance matrices were evaluated using Schwarz’s Bayesian Information Criterion (BIC) to assess model fit (Sakamoto, Ishiguro, & Kitagawa, 1986; Schwarz, 1978). Significant standard repetition effects were followed up using orthogonal linear and quadratic contrasts as well as one-sample t-tests of each standard repetition RP effect (relative to s2) and corresponding Cohen’s d effect size estimates.

Statistical Correction for Normal Aging and NAPLS Site Effects

To adjust for the effects of normal aging (i.e., normal brain maturation) and site, mean RP amplitude difference scores (relative to s2) from electrode Fz, averaged across the 5 standard repetitions, was regressed on Age and Site within the HC group. The resulting regression equation was used to calculate age- and site-corrected RP z-scores for all individuals, regardless of group membership, separately for the RP difference score associated with each standard bin (relative to s2). This was done by subtracting the predicted RP amplitude difference score based on a subject’s age and site from the observed RP amplitude difference score, and then dividing this difference by the standard error of the HC regression model. The resulting z-scores are age- and site-adjusted, reflecting deviations from the value expected for a healthy individual of a specific age tested at a specific NAPLS site. We have used this approach in prior studies (e.g., Perez et al, 2014). This approach is preferable to using analysis of covariance (ANCOVA) because i) only normal age effects are removed, while retaining pathological aging effects, and ii) it avoids re-estimating fixed effects of site in secondary (i.e., correlation) or clinical follow-up analyses that do not include healthy controls and that may involve small sub-groups of PRS individuals (e.g., PRS-C).

Mixed Models Comparing Repetition Positivity z-scores between Groups

Three additional mixed effects models were applied. First, a two-group model specified Group (HC, n=241; PRS, n=579) as a fixed between-subjects factor, Standard Repetition (5 levels) as a fixed within-subjects factor, and Subject nested within Group as a random factor in order to compare RP standard repetition effects in HC with those in the entire PRS sample irrespective of their clinical outcome. Next, a three-group model incorporated clinical outcome data and included only the PRS individuals who converted to psychosis or were followed for 24 months without converting. This model specified Group as a fixed between-subjects factor comprising HC (n=241) and PRS sub-groups who converted (PRS-C, n=77) or did not convert (PRS-NC, n=238) based on 24-month clinical status, Standard Repetition (5 positions) as a fixed within-subjects factor, and Subject nested within Group as a random factor. Lastly, a four-group model was run to further parse non-converting PRS individuals by clinical outcome status. This model specified Group as a fixed between-subjects factor comprising HC (n=241) and 3 PRS sub-groups based on 24-month clinical status (PRS-NC-R, n=94; PRS-NC-S, n=144; PRS-C, n=77), Standard Repetition (5 positions) as a fixed within-subjects factor, and Subject nested within Group as a random factor. For all models, in addition to assessing main effects of Group, a significant Group X Standard Repetition interaction effect was parsed by i) comparing the Standard Repetition linear and quadratic trends across standard positions between the groups, with follow-up Bonferroni-corrected (p<.05) pairwise group comparisons, and ii) assessing the Group effect at each of the five Standard Repetition positions, with follow-up pairwise group differences assessed using Tukey HSD tests.

Cox Proportional Hazards Model Predicting Time to Conversion

Cox regression was performed to model the relationship between RP difference z-scores and time to psychosis onset (i.e., “survival time”) among PRS participants. All PRS individuals with at least one follow-up assessment were included, with censoring of those who either did not convert to psychosis or dropped out before reaching the 24-month follow-up.

Clinical Symptom Correlations

To assess correlations between RP and symptom severity, the Scale of Psychosis-Risk Symptoms (SOPS) Positive, Negative, Disorganization, and General Symptom subscales, as well as two SOPS items, P1 (Unusual Thought Content) and P2 (Suspiciousness), previously found to be the strongest clinical predictors of conversion to psychosis (Cannon et al., 2008; Perkins et al., 2015), were regressed on RP z-scores. All correlation tests were Bonferroni corrected (p<.05).

Results

Healthy Control Analysis

The comparison of BIC from mixed models of Standard Repetition, Site, and Age on RP amplitude raw difference scores indicated that a compound-symmetry covariance structure provided the best fit. The initial model including an Age X Standard Repetition interaction showed no significant interaction effect (F (4,956) = 1.15, p = 0.3337). Accordingly, this interaction term was dropped, imposing a common slope for the age relationships across Standard Repetition positions. In the final, reduced model, there was a significant effect of Age (F(1, 232) = 4.44, p = .036; partial r= −.15) but not Site (F(7, 232) = 0.14, p = 0.995), indicating that RP amplitude modestly decreased with age.

Importantly, there was a significant Standard Repetition effect on the RP (F(4,960) = 7.25, p <.0001). Polynomial follow-up tests revealed a significant positive linear trend (t(960) = 4.65, p <.0001), but not a quadratic trend (t(232) = −0.049, p = 0.8300), with RP amplitudes increasing with more standard repetitions. Follow-up tests of the RP difference scores at each standard repetition position (relative to s2) were all significant (p <.0001), with effect sizes ranging from medium to large and the strongest effect at s11+ (Cohen’s d: s3 = 0.745, s4–5 = 0.710, s5–6 = 0.948, s8–10 = 0.899, s11+ = 0.989). Figure 1 shows grand average plots of HC RP difference waves.

Figure 1.

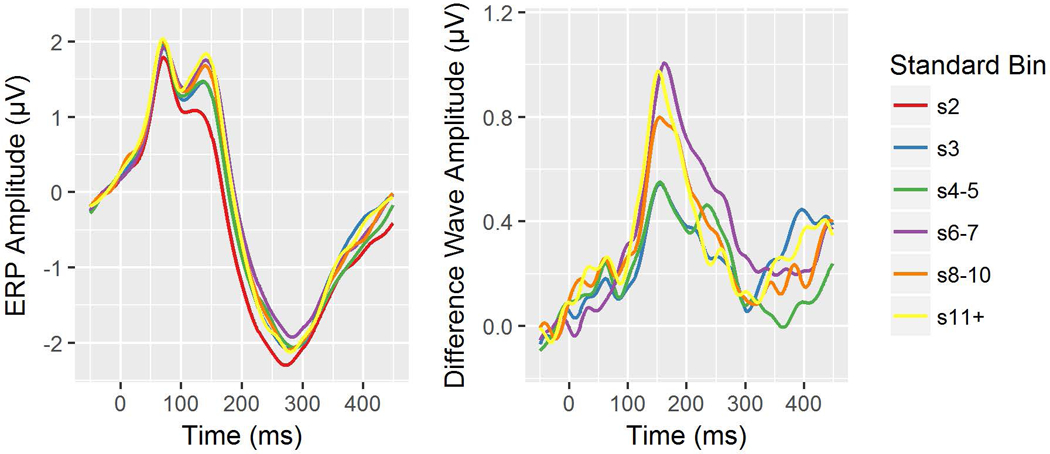
Healthy Control (HC) group event-related potential (ERP) waveforms from electrode Fz by standard repetition position (left) and ERP difference waves for each standard repetition position minus the s2 position (right).

Statistical Correction for Normal Aging and NAPLS Site Effects

Given the absence of a significant Age X Standard Repetition interaction effect on RP in the HC, RP amplitudes were averaged across all 5 standard repetition positions before being regressed on Age and Site. Age and site-specific beta coefficients were used to calculate age- and site-specific RP z-scores for each standard repetition position, as described in the methods. The resulting z-scores express, in standard units, the deviation of the RP amplitude from the average RP value expected across standard repetition positions for a healthy individual of a given age at a specific site.

RP z-scores Group Comparisons

All mixed models comparing groups used compound-symmetry covariance matrices for consistency with the HC model. Tables 2 and 3 report complete test statistics, with significant effects involving Group. In the two-group model (HC vs. PRS), there was a significant main effect of Group due to reduced RP z-scores in PRS relative to HC (p = 0.0056) across standard repetitions, with a non-significant Group X Standard Repetition interaction (Figure 2).

Table 2.

Test statistics comparing Repetition Positivity (RP) amplitudes across conversion status groups.

							C.I. (95%)
	Estimate	SE	DF	t or F Value	p-value	p-value,adjusted	Lower	Upper
Group X Standard Position Omnibus*	-	-	2212	(F) 2.11	0.0317	-	-	-
Group X Standard position linear	-	-	2212	(F) 1.76	0.1719	-	-	-
Group X Standard position quadratic*	-	-	2212	(F) 4.79	0.0084	-	-	-
quadratic RP effect (within HC)	−0.0242	0.1696	2212	−0.14	0.8868	-	−0.3568	0.3084
quadratic RP effect (within PRS-NC)*	−0.3551	0.1707	2212	−2.08	0.0376	-	−0.6898	−0.0204
quadratic RP effect (within PRS-C)*	−1.0849	0.3001	2212	−3.62	0.0003	-	−1.6734	−0.4965
quadratic RP effect HC vs. PRS-NC	0.3309	0.2406	2212	1.38	0.1692	0.5076	−0.1409	0.8028
quadratic RP effect HC vs. PRS-C*	1.0608	0.3447	2212	3.08	0.0021	0.0063	0.3849	1.7367
quadratic RP effect PRS-NC vs. PRS-C	0.7299	0.3452	2212	2.11	0.0346	0.1038	0.0529	1.4068
Between-Group Comparisons: At Each Standard Position
main effect of group at s3*	-	-	2212	(F) 4.31	0.0136	-	-	-
HC vs. PRS-NC	0.1289	0.0885	2212	1.46	0.1453	0.3121	−0.0446	0.3025
HC vs. PRS-C*	0.3670	0.1268	2212	2.89	0.0038	0.0107	0.1184	0.6156
PRS-NC vs. PRS-C	0.2381	0.1270	2212	1.87	0.0609	0.1462	−0.0109	0.4871
main effect of group s4–5	-	-	2212	(F) 0.44	0.6434	-	-	-
main effect of group s6–7	-	-	2212	(F) 0.45	0.6398	-	-	-
main effect of group s8–10*	-	-	2212	(F) 4.09	0.0168	-	-	-
HC vs. PRS-NC	0.1825	0.0885	2212	2.06	0.0394	0.0982	0.0089	0.356
HC vs. PRS-C*	0.3266	0.1268	2212	2.58	0.0101	0.0272	0.0780	0.5753
PRS-NC vs. PRS-C	0.1442	0.1270	2212	1.14	0.2564	0.4924	−0.1049	0.3932
main effect of group s11+*	-	-	2212	(F) 7.28	0.0007	-	-	-
HC vs. PRS-NC	0.1837	0.0885	2212	2.07	0.0381	0.0953	0.0101	0.3572
HC vs. PRS-C*	0.4722	0.1268	2212	3.72	0.0002	0.0006	0.2236	0.7208
PRS-NC vs. PRS-C	0.2885	0.1270	2212	2.27	0.0232	0.0599	0.0395	0.5376

^*p<.05; SE = standard error; DF = degrees of freedom; C.I. = confidence interval

p-value adjusted = Bonferroni-corrected (for polynomial contrasts) or Tukey HSD-corrected (for pairwise group comparisons within positions)

Table 3.

Test statistics comparing Repetition Positivity (RP) amplitudes across clinical outcome groups.

							C.I. (95%)
	Estimate	SE	DF	t or F Value	p-value	p-value, adjusted	Lower	Upper
Group X Standard Position Omnibus			2208	(F) 1.74	0.0522	-	-	-
Group X Standard position linear			2208	(F) 1.70	0.1648	-	-	-
Group X Standard position quadratic*			2208	(F) 3.77	0.0103	-	-	-
quadratic RP effect (within HC)	−0.0242	0.1696	2208	−0.14	0.8868	-	−0.3568	0.3084
quadratic RP effect (within PRS-NC-R)	−0.0775	0.2716	2208	−0.29	0.7754	-	−0.6100	0.4551
quadratic RP effect (within PRS-NC-S)*	−0.5363	0.2194	2208	−2.44	0.0146	-	−0.9666	−0.1060
quadratic RP effect (within PRS-C)*	−1.0849	0.3001	2208	−3.62	0.0003	-	−0.1673	−0.4965
quadratic RP effect HC vs. PRS-NC-R	0.0533	0.3202	2208	0.17	0.8677	1.0000	−0.5745	0.6812
quadratic RP effect HC vs. PRS-NC-S	0.5121	0.2773	2208	1.85	0.0649	0.3894	−0.0317	1.0560
quadratic RP effect HC vs. PRS-C*	1.0608	0.3447	2208	3.08	0.0021	0.0126	0.3849	1.7367
quadratic RP effect PRS-NC-R vs. PRS-NC-S	0.4588	0.3491	2208	1.31	0.1889	1.0000	−0.2259	1.1434
quadratic RP effect PRS-NC-R vs. PRS-C	1.0075	0.4047	2208	2.49	0.0129	0.0774	0.2138	1.8011
quadratic RP effect PRS-NC-S vs. PRS-C	0.5487	0.3717	2208	1.48	0.1401	0.8406	−0.1803	1.2776
Group Effect At Each Standard Position
main effect of Group at s3*			2208	(F) 2.88	0.0349	-	-	-
HC vs. PRS-NC-R	0.1172	0.1178	2208	0.99	0.3200	0.7524	−0.1138	0.3483
HC vs. PRS-NC-S	0.1366	0.1021	2208	1.34	0.1808	0.5383	−0.0635	0.3367
HC vs. PRS-C*	0.3670	0.1268	2208	2.89	0.0038	0.0201	0.1183	0.6157
PRS-NC-R vs. PRS-NC-S	0.0194	0.1285	2208	0.15	0.8800	0.9988	−0.2326	0.2713
PRS-NC-R vs. PRS-C	0.2498	0.1489	2208	1.68	0.0936	0.3359	−0.0422	0.5419
PRS-NC-S vs. PRS-C	0.2304	0.1368	2208	1.68	0.0922	0.3321	−0.0378	0.4987
main effect of Group s4–5			2208	(F) 0.30	0.8274	-	-	-
main effect of Group s6–7			2208	(F) 0.30	0.8271	-	-	-
main effect of Group s8–10*			2208	(F) 2.73	0.0426	-	-	-
HC vs. PRS-NC-R	0.1872	0.1178	2208	1.59	0.1122	0.3851	−0.0438	0.4183
HC vs. PRS-NC-S	0.1794	0.1021	2208	1.76	0.0789	0.2942	−0.0208	0.3795
HC vs. PRS-C*	0.3266	0.1268	2208	2.58	0.0101	0.0494	0.0779	0.5754
PRS-NC-R vs. PRS-NC-S	−0.0078	0.1285	2208	−0.06	0.9514	0.9999	−0.2598	0.2441
PRS-NC-R vs. PRS-C	0.1394	0.1489	2208	0.94	0.3493	0.7854	−0.1526	0.4315
PRS-NC-S vs. PRS-C	0.1472	0.1368	2208	1.08	0.2818	0.7040	−0.1210	0.4155
main effect of Group s11+*			2208	(F) 5.79	0.0006	-	-	-
HC vs. PRS-NC-R	0.0535	0.1178	2208	0.45	0.6499	0.9689	−0.1776	0.2845
HC vs. PRS-NC-S*	0.2686	0.1021	2208	2.63	0.0085	0.0424	0.0685	0.4688
HC vs PRS-C*	0.4722	0.1268	2208	3.72	0.0002	0.0012	0.2235	0.7209
PRS-NC-R vs. PRS-NC-S	0.2151	0.1285	2208	1.67	0.0942	0.1884	−0.0368	0.4671
PRS-NC-R vs. PRS-C*	0.4187	0.1489	2208	2.81	0.0050	0.0256	0.1267	0.7108
PRS-NC-S vs. PRS-C	0.2036	0.1368	2208	1.49	0.1368	0.4448	−0.0647	0.4718

^*p<.05; SE = standard error; DF = degrees of freedom; C.I. = confidence interval

p-value adjusted = Bonferroni-corrected (for polynomial contrasts) or Tukey HSD-corrected (for pairwise group comparisons within positions)

Figure 2.

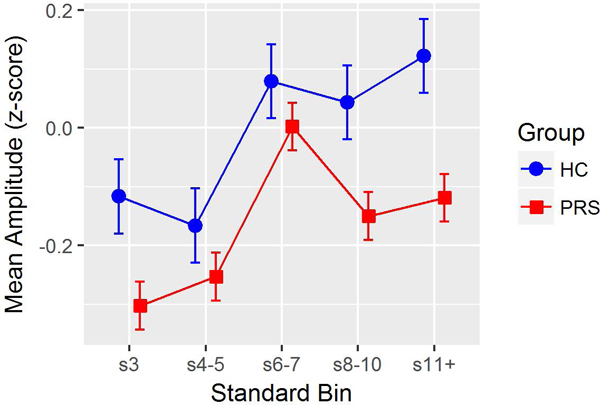
Age- and site-adjusted repetition positivity (RP) amplitude z-scores at each standard repetition position (difference scores from s2 RP), by Baseline Group (Healthy Controls, HC; Psychosis Risk Syndrome (PRS). Line plots illustrate a main effect of group, with PRS showing less RP amplitude across all standard repetition positions.

In the three-group model (HC vs. PRS-NC vs. PRS-C), the Group X Standard Repetition interaction was significant (p = 0.0317). Analyses were then conducted to follow-up the significant interaction effect: i) Polynomial contrast analyses indicated no significant Group X Linear effect (p=.1719), but a significant Group X Quadratic effect (p=.0084). The quadratic Group effect was mainly driven by a significant quadratic effect in PRC-C (p=.0003) that was much stronger (p=.0063, adjusted) than in HC (who showed no quadratic effect, p=.8868) and somewhat more prominent (p=.1038, adjusted) than in PRS-NC (who showed a small but significant quadratic effect, p=.0376). The PRS-C quadratic effect reflected RP amplitude deficits to both early- and late-appearing standards within local trains of repeating standards, but intact RP amplitudes for mid-train standards; ii) Group effects were then assessed at each Standard Repetition position, with significant effects emerging for positions s3 (p=0.0136), s8–10 (p= 0.0168) and s11+ (p=0.0007) but not s4–5 and s6–7 (p>0.6463). Pairwise Tukey follow-up tests of the significant Group effects indicated that PRS-C had significantly lower RP z-scores than HC for standard positions s3 (p= 0.0107), s8–10 (p= 0.0272), and, most prominently, s11+ (p= 0.0006), as well as a trend toward lower RP z-scores than PRS-NC for s11+ (p=.0599). No other pairwise group comparisons were significant after adjusting for multiple comparisons.

In the four-group model (HC vs. PRS-NC-R vs. PRS-NC-S vs. PRS-C), the Group X Standard Repetition interaction was nearly significant (p = 0.0522), motivating follow-up testing. Polynomial contrast analyses indicated no significant Group X Linear effect (p=.1648), but a significant Group X Quadratic effect (p=.0103). The quadratic group effect was explained by a significant difference between HC and PRC-C (p=.0126, adjusted) resulting from the same quadratic pattern in PRS-C already described above, as well as a similar but less pronounced quadratic pattern in PRS-NC-S (p=.0146) that also tended to differ from the HC pattern (p=.0774, adjusted), with no other groups differing. Main effects of Group were then assessed at each Standard Repetition position, with significant Group effects emerging for positions s3 (p= 0.0349), s8–10 (p= 0.0426) and s11+ (p=0.0006) but not s4–5 and s6–7 (p>0.8271). Pairwise Tukey follow-ups tests indicated that the PRS-C had significantly lower RP z-scores than HC for standard repetition positions s3 (p= 0.0201), s8–10 (p= 0.0494), and s11+ (0.0012) as described above, as well as additional findings indicating that at s11+, PRS-NC-S had significantly lower RP amplitudes than HC (p=0.0424), and PRS-C had significantly lower RP amplitudes than PRS-NC-R (p=0.0256). No other pairwise comparisons were significant after adjusting for multiple comparisons (Figure 3).

Figure 3.

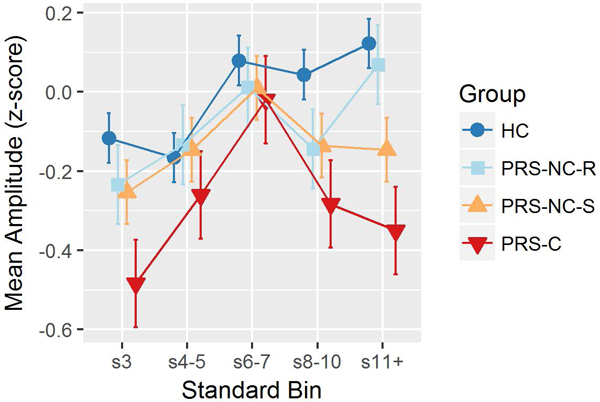
Age- and site-adjusted Repetition Positivity (RP) amplitude z-scores at each standard repetition position (difference scores from s2 RP), by Clinical Outcome Group (Healthy Controls, HC; Psychosis Risk Syndrome-Conversion, PRS-C; Psychosis Risk Syndrome-Remission, PRS-NC-R; Psychosis Risk Syndrome-Symptomatic, PRS-NC-S). Line plots illustrate a Group X Standard Repetition interaction effect, with PRS-C showing smaller RP amplitudes at the s3, s8-10, and s11+ positions.

Removing PRS participants who were taking antipsychotic medication at the time of EEG testing from the two-group (n=130), three-group (n=71), or four-group (n=71) models did not change the pattern of results. In addition, RP z-scores at each standard repetition position did not significantly differ between PRS non-converters who were followed for a full 24-months and those who dropped out earlier.

Given that significant group effects were only observed for standard repetition positions s3, s8–10, and s11+, we averaged the RP z-scores across these three positions for use in subsequent Cox regression and correlational analyses.

Cox Proportional Hazards Model of Time to Conversion

The Cox regression model predicting the time from ERP assessment to psychosis conversion in the entire PRS group indicated that more deficient mean RP amplitude z-scores showed a tendency to predict a shorter time to psychosis onset (χ² = 3.17, p = .0751, Exp(β) = .760, p = .0771). Removing PRS individuals on antipsychotic medication at the time of EEG testing improved the predictive model (χ² = 5.26, p = .0218, Exp(β) = .660, p = .0223), and the resulting hazard ratio indicated that a one-unit decrease in RP z-score (i.e., 1 standard deviation smaller RP) is associated with a 1.51-fold (i.e., 51%) increase in risk for conversion to psychosis. This effect is illustrated in Figure 4 for the unmedicated PRS sub-sample.

Figure 4.

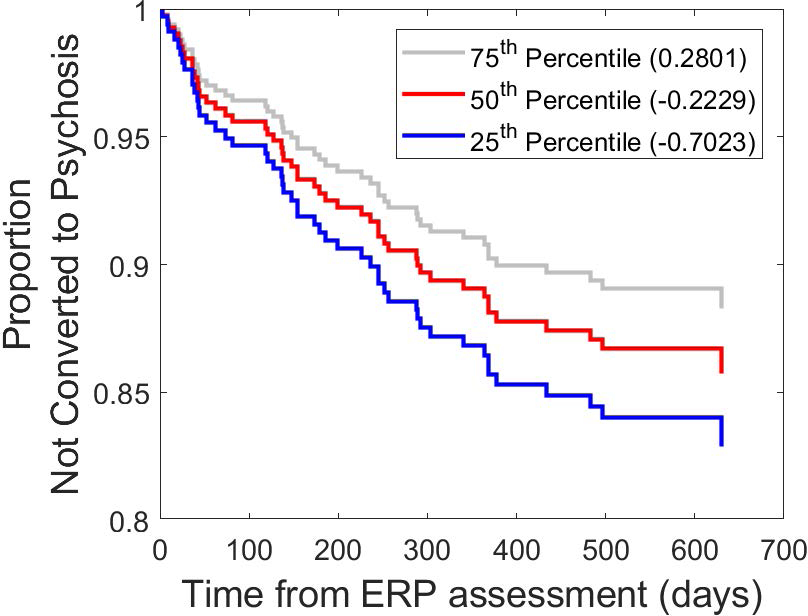
Predicting time to transition to psychosis. Cox regression-based estimated cumulative survival functions, indicating the probability of not converting to psychosis, for repetition positivity (RP) z-scores corresponding to the 25^th, 50^th, and 75^th percentiles within the psychosis risk syndrome sample (unmedicated sub-sample). Survival curves showing the estimated risk of transitioning to psychosis over time for baseline RP amplitudes at the 75^th percentile (grey), 50^th percentile (red) and 25^th percentile (blue), illustrating significant (p=.022) predictive relationship between smaller RP amplitudes at baseline and an earlier transition to psychosis.

Correlations between Repetition Positivity Amplitude and SOPS Clinical Ratings

There were no significant (all uncorrected p>.05) associations between mean RP z-scores and SOPS Positive, Negative, Disorganization or General Symptom sub-scales, or for the Unusual Thought Content (P1) and Suspiciousness (P2) items.

Discussion

In a large sample of HC, we observed an approximately linear increase in RP amplitude over successive standards within local trains of repeating standards following deviant stimuli. The largest RP amplitude was elicited by standards preceded by the greatest number of repetitions, consistent with the standard’s memory trace and associated predictive code strengthening with repetition. Relative to HC, PRS individuals had reduced RP amplitudes across standard repetition positions; further, RP amplitudes for early- and late-appearing standards, but not mid-train standards, were significantly reduced in PRS individuals who subsequently converted to psychosis (PRS-C), relative to HC. Moreover, the greater this RP amplitude deficit (averaged over s3, s8–10, s11+ positions), the shorter the time to psychosis onset in PRS individuals. In contrast to the linear increase in RP to repeating standards exhibited by HCs, the RP memory trace effect in PRS-C individuals showed an inverted U pattern. This was reflected by deficient RP amplitude in PRS-C, relative to HC, to early standards (s3), which then normalized for mid-range positions, with a deficiency re-emerging for late-appearing standards at s8–10, and particularly for position s11+, when the memory trace should be strongest. The effect sizes for these comparisons indicate that the latest appearing standards elicit the largest deficit (Cohen’s d, unmedicated sample = 0.23 for s3; 0.25 for s8–10; 0.38 for s11+). We interpret this pattern to suggest that PRS-C individuals show deficits at both the earliest stages of memory trace formation, as well as a more prominent deficit in sustaining memory traces when the local repetition train exceeds a certain length, though a mechanistic understanding of this finding awaits further study.

Repetition Positivity Memory Trace Effect using a Constant Standard MMN Paradigm

The significant linear RP effect we observed in HCs provides further evidence that the RP builds with repetition of the frequent standard stimulus, consistent with predictive coding accounts of sensory memory trace formation (Baldeweg et al., 2004; Costa-Faidella et al., 2011; Garrido, Kilner, Kiebel, et al., 2009; Haenschel et al., 2005). The fact that we observed this RP memory trace effect using a constant standard paradigm has important implications for the interpretation of the RP. Prior studies documenting the RP memory trace effect used a roving standard MMN paradigm (Baldeweg et al., 2004, 2006; Costa-Faidella et al., 2011; Haenschel et al., 2005; McCleery et al., 2019), reflecting an assumption that RP memory trace effects require de novo encoding of stimulus features each time a deviant is repeated and becomes the new local standard (Baldeweg et al., 2004; Baldeweg, 2006). However, Cooper et al. showed RP memory trace effects at mastoids for both constant standard and roving standard paradigms, with only the roving standard paradigm producing RP effects at frontal sites (Cooper et al., 2013). Cooper et al. speculated that frontal sources may retain a longer-term representation of the recent auditory stream than temporal sources, making further build-up of the standard memory trace in frontal regions unnecessary during constant standard paradigms. In contrast, we observe RP memory trace effects at frontal sites using a traditional constant standard MMN paradigm, possibly owing to our larger sample affording more power than the Cooper et al. study. Further, our results indicate that the RP memory trace effect does not depend on the encoding of novel features of a new standard; rather, there may be a local rebuilding of the predictive code for the standard following each deviant, despite the constant standard. Thus, short-term plasticity in the auditory system putatively indexed by the RP strengthens the representation of the standard as a function of recent stimulus history, providing a mechanism for adaptive adjustment of the perceptual model for the standard stimulus (Näätänen & Winkler, 1999) and dynamic updating of prediction strength based on local stimulus context (Garrido, Kilner, Kiebel, et al., 2009).

Consistent with pathophysiological models of schizophrenia posing neuroplasticity and predictive coding deficits (Fletcher & Frith, 2009; Stephan et al., 2009; Sterzer et al., 2018), as well as a prior report showing a deficient RP memory trace in schizophrenia (Baldeweg et al., 2004) (though see McCleery et al., 2019), we found that the PRS group as a whole exhibited smaller RP amplitudes regardless of standard repetition. However, when the PRS group was sub-divided according to clinical outcome after 24 months, a more complex picture emerged wherein group differences in the RP significantly depended on the standard’s position within the local series of repetitions. In particular, when considering the standards preceded by the greatest number of repetitions (s11+), where the RP memory trace effect was strongest in HCs, PRS-C showed a significantly reduced RP memory trace when compared to both PRS non-converters (PRS-NC-S + PRS-NC-R) and HC. The pattern of results across standard repetition positions (Figure 3) indicates that all groups, including PRS-C, showed a memory trace strengthening for standard repetitions 3–7 (relative to s2), but the PRS-C group failed to further strengthen, or even maintain, the RP memory trace for late appearing standards, relative to the other groups. This suggests that in PRS individuals at greatest risk for conversion to psychosis, deficient strengthening of the predictive code for repeating standards is most evident after 10 consecutive standards, precisely when the standard’s memory trace and associated predictive code were the strongest in HCs. This deficit not only predicted conversion to psychosis among PRS individuals, it also predicted an earlier onset of psychosis for the PRS sub-group not taking antipsychotic medication at the time of the EEG assessment. Given that other major results did not change when PRS individuals on antipsychotics were excluded, RP deficits are unlikely to result from antipsychotic medication. Thus, our findings indicate that deficient RP memory trace effects predate the onset of psychosis and are most prominent in PRS individuals at greatest risk for transitioning to full-blown psychosis.

While our results showing a deficient RP memory trace effect in PRS-C individuals are similar to Baldeweg et al. (2004) study of patients with schizophrenia using a roving standard MMN paradigm, a recent study examining the RP using a roving standard MMN paradigm reported a normal RP memory trace in schizophrenia, but a deficient deviant negativity and MMN memory trace (McCleery et al., 2019). Thus few prior studies have examined the RP memory trace in schizophrenia, warranting more research on this topic, including possible moderation of effects by paradigm and illness stage of the patients studied.

Mechanistic Models of the Repetition Positivity Memory Trace Effect

From the traditional perspective of MMN as a reflection of sensory echoic memory, the RP memory trace effect can be viewed as a short-term auditory plasticity effect reflecting repetition-dependent strengthening of stimulus representation in sensory echoic memory. A mnemonic interpretation of the RP as memory trace formation was supported by evidence of acetylcholinergic modulation, with nicotine administration augmenting the RP and its memory trace effect without affecting the negativity elicited by the deviant stimulus (Baldeweg et al., 2006). Other neural phenomena associated with stimulus repetition, including stimulus specific adaptation (SSA) (Farley, Quirk, Doherty, & Christian, 2010; Nelken & Ulanovsky, 2007; Netser, Zahar, & Gutfreund, 2011) and repetition suppression (Garrido, Kilner, Kiebel, et al., 2009) may underlie the RP and its increase with repetition. Proponents of predictive coding (Baldeweg, 2006; Friston, 2005; Garrido, Kilner, Stephan, et al., 2009) argue that this framework is able to fully account for mnemonic, adaptation, and repetition suppression perspectives of MMN and RP. Predictive coding involves interactions between hierarchically organized cortical levels, with top-down feedforward connections from higher cortical areas to lower sensory areas that convey predictions about impending sensory events based on recent stimulus history, and subsequent feedback from sensory areas to higher-order cortical areas conveying prediction errors when sensory predictions are violated, ultimately leading to updated predictions (Friston, 2005). In this framework, the negativity elicited by the deviant stimulus in a MMN paradigm is considered a prediction error, whereas the RP reflects top-down suppression of this signal (possibly relating to SSA and repetition suppression neural phenomena), with the suppression increasing with stimulus repetition. The stronger this suppression, the stronger the prediction that a standard stimulus will recur (Garrido, Kilner, Kiebel, et al., 2009).

While MMN is well-known to be modulated by glutamate transmission at NMDA receptors (Javitt, Steinschneider, Schroeder, & Arezzo, 1996; Rosburg & Kreitschmann-Andermahr, 2016) it remains unclear whether the RP is also NMDA-modulated. A rodent study of repeating standard tones interspersed with infrequent deviants found that SSA in auditory cortical neurons was not modulated by NMDA receptor activity (Farley, Quirk, Doherty, & Christian, 2010). However, this does not necessarily generalize to predictive coding accounts of the RP, which may involve frontal lobe generators (Cooper et al., 2013; Haenschel et al., 2005). Higher cortical areas involved in predictive code formation “backward connect” to lower sensory areas involved in bottom-up processing with predictions mediated by NMDA receptors, while forward connections carrying sensory information to higher cortical areas are thought to be mediated by AMPA and GABAA receptors (Friston, 2005). Empirically, one human study has shown RP amplitude is diminished by ketamine administration, consistent with NMDA receptor involvement (Rosch, Auksztulewicz, Leung, Friston, & Baldeweg, 2018).

Limitations and Conclusions

The current study had several limitations. First, no clinical symptom correlations with the RP were detected, despite being well-powered. Many factors make the detection of symptom correlations in schizophrenia challenging (Mathalon & Ford, 2012), and in the PRS population, the restricted range of attenuated psychotic symptoms may further obscure relationships. Second, more research is needed to further elucidate the functional significance of the RP. One of the many questions of interest is whether enhanced RP to repeating standards happens globally across the entire sequence of standards and deviants that are presented over the course of the recording session, in addition to the local stimulus history effects examined in this study. Third, while we observed RP memory trace effects using a constant standard paradigm, it is possible that a roving standard paradigm would yield RP measures that are more sensitive to memory trace formation and clinical deficits. Fourth, although our PRS sample was relatively large at baseline (n= 579), a sizeable sub-group did not complete the full 24 months of follow-up (~50%). This limitation is partially mitigated by analyses demonstrating no RP differences between completers and non-completers.

Despite these limitations, we demonstrated RP deficits in a large PRS sample at baseline, and RP deficits in PRS-C both for early appearing standards, when the memory trace is initially developing, and more prominently for the late-appearing standards when the memory trace and predictive code for standard stimuli should be the strongest. These data: i) suggest that the RP may be worth consideration as a candidate biomarker of psychosis risk and transition in its own right and ii) offer important nuance to the larger MMN literature by demonstrating that deficits in predictive code formation may be relevant for understanding pathophysiology of auditory processing in schizophrenia, and therefore must be considered along with deviation-specific signals in interpreting the composite (i.e., deviant minus standard) MMN effect. At a broader level, these findings support models that implicate deficits in neuroplasticity and predictive coding in schizophrenia (Stephan et al., 2009), and demonstrate that an EEG-based measure of these deficits is sensitive to psychosis risk and transition.