High-resolution atmospheric inversion of urban CO₂ emissions during the dormant season of the Indianapolis Flux Experiment (INFLUX)

Abstract

Based on a uniquely dense network of surface towers measuring continuously the atmospheric concentrations of greenhouse gases (GHGs), we developed the first comprehensive monitoring systems of CO₂ emissions at high resolution over the city of Indianapolis. The urban inversion evaluated over the 2012–2013 dormant season showed a statistically significant increase of about 20% (from 4.5 to 5.7 MtC ± 0.23 MtC) compared to the Hestia CO₂ emission estimate, a state-of-the-art building-level emission product. Spatial structures in prior emission errors, mostly undetermined, appeared to affect the spatial pattern in the inverse solution and the total carbon budget over the entire area by up to 15%, while the inverse solution remains fairly insensitive to the CO₂ boundary inflow and to the different prior emissions (i.e., ODIAC). Preceding the surface emission optimization, we improved the atmospheric simulations using a meteorological data assimilation system also informing our Bayesian inversion system through updated observations error variances. Finally, we estimated the uncertainties associated with undetermined parameters using an ensemble of inversions. The total CO₂ emissions based on the ensemble mean and quartiles (5.26–5.91 MtC) were statistically different compared to the prior total emissions (4.1 to 4.5 MtC). Considering the relatively small sensitivity to the different parameters, we conclude that atmospheric inversions are potentially able to constrain the carbon budget of the city, assuming sufficient data to measure the inflow of GHG over the city, but additional information on prior emission error structures are required to determine the spatial structures of urban emissions at high resolution.

1. Introduction

The increase in the atmospheric concentration of carbon dioxide (CO₂) reached the fastest decadal rate over the period 2002–2011 with 2 ± 0.1 ppm/yr. Consequently, CO₂ remains the largest single contributor to the increase in the anthropogenic radiative forcing [Intergovernmental Panel on Climate Change, 2014], with 80% of the emissions originating from fossil fuel combustion and industrial processes. Quantification of anthropogenic CO₂ emissions is typically accomplished via bottom-up accounting or inventory methods at global [e.g., Marland et al., 1985; Andres et al., 1996, 2012; Asefi-Najafabady et al., 2014] and regional scales [Gurney et al., 2009, 2012]. These inventories remain affected by large uncertainties [Andres et al., 2014] which increases at higher spatial and temporal resolutions [e.g., Turnbull et al., 2011]. As legislation to regulate greenhouse gas (GHG) emissions becomes increasingly likely, independent verification of inventory-based anthropogenic emissions becomes an emerging need [NRC, 2010].

Urban CO₂ emissions represent about 70% of the global emissions and will likely increase as large metropolitan areas are projected to grow twice as fast as the world population in the coming 15 years [United Nations Department of Economic and Social Affairs Population Division, 2014]. Monitoring urban emissions using independent approaches is therefore a critical need for current and future regulation policies with atmospheric inversion techniques being a potential candidate to provide a robust and complementary approach to current reporting activities [Nisbet and Weiss, 2010]. However, a better understanding of the underlying human activities remains critical for policy decisions and mitigation strategies [Hutyra et al., 2014], which implies the use of process-oriented systems, highly resolved in both space and time [Gurney et al., 2012]. Current atmospheric inversion systems remain too coarse spatially and are limited to constraining the emissions rather than the underlying processes. Therefore, higher resolution inverse systems are needed to better understand and quantify the emissions by sector (e.g., manufacturing sources, power generation sources, and mobile sources) in support of future policies.

This lack of well-established methods for quantifying spatially and temporally resolved GHG emissions applies to urban areas. Recent studies have provided high-resolution emission products separated by sector [Gurney et al., 2012] but are difficult to assemble and very likely prone to systematic errors [Gurney, 2014]. Atmospheric methods offer a unique angle on urban emissions by capturing the accumulated atmospheric signals emitted from all sectors of activity [Turnbull et al., 2011]. But these methods are also limited by various sources of errors, mostly due to the atmospheric transport models [Gerbig et al., 2003; Diaz-Isaac et al., 2014] and the incorrect characterization of prior flux errors [Koohkan and Bocquet, 2012], as well as by the number of atmospheric measurements available over the region of interests. At moderate resolutions (10–40 km), atmospheric inversions using regional atmospheric transport models [Lauvaux et al., 2012; Schuh et al., 2013] have the potential to provide spatially and temporally resolved GHG surface fluxes [Ogle et al., 2015]. At higher resolutions, several studies have shown the potential of atmospheric systems to detect emissions [McKain et al., 2012; Kort et al., 2012; Bréon et al., 2015].

The inversion of large point sources and well-defined emitting areas are particularly sensitive to the transport model and the representation of plume structures over flat or complex terrain, especially for observations within the urban domain [Bréon et al., 2015]. Large spatial and temporal gradients in urban emissions generate large gradients in atmospheric mixing ratios. Therefore, the development of accurate atmospheric modeling systems able to simulate these gradients is a prerequisite to the detection and quantification of emissions over highly contrasted urban environment. High-density observations combined with high-resolution atmospheric modeling have the potential to yield such resolution over small domains. At the mechanistic level, processes from specific sectors of the economy shape the spatial pattern of GHG emissions across urban centers. But atmospheric inversions have not yet been used to separate the contributions from individual sectors of the economy [Djuricin et al., 2012] or to separate biogenic and anthropogenic sources [Djuricin et al., 2010]. Expanding the atmospheric inversion systems to include multiple trace gases, including isotopic tracers such as ¹⁴CO₂ [e.g., Kuc, 1986; Newman et al., 2008], offers the capability to measure the fraction of the signals related to fossil fuel consumption and perhaps sectoral emissions. However, discrete isotopic measurements and the lack of proper characterization of background conditions [Turnbull et al., 2015; Vardag et al., 2015] limit the use of isotopic tracers to quantify the fluxes from highly managed vegetated areas. In order to build a first comprehensive atmospheric system at the urban scale, the dormant season simplifies the inverse problem with decreased biogenic signals, contributing to only 5% of the total city plume over Indianapolis [Turnbull et al., 2015].

The Indianapolis Flux Experiment (INFLUX) is exploring the technical limits of atmospheric methods for inferring highly resolved anthropogenic GHG emissions estimates. Here we present the first atmospheric inversion system producing high-resolution GHG emissions of CO₂ at the urban scale, assimilating both atmospheric mixing ratios of greenhouse gases and meteorological measurements. The inverse modeling system is able to derive spatially and temporally resolved urban CO₂ emissions within a large urban area, starting with a high-resolution emission product, Hestia [Gurney et al., 2012]. First, we developed an atmospheric four-dimensional data assimilation (FDDA) modeling system at 1 km spatial resolution assimilating continuously meteorological measurements to improve the representation of the local atmospheric dynamics. Transport errors associated with the atmospheric modeling system are then quantified as a function of the accuracy of different meteorological variables. Second, we demonstrate the current inversion system ability to monitor GHG emissions using a high-density spatially distributed atmospheric observing network of instrumented towers, using two existing high-resolution CO₂ emissions products. Finally, we construct an ensemble of inverse solutions to represent additional sources of errors in the current inversion system and quantify the uncertainties associated with parameters in the system.

2. Methods

2.1. Atmospheric Modeling System

2.1.1. Atmospheric Four-Dimensional Data Assimilation (FDDA) Modeling System

The core of our real-time modeling system Deng et al. [2012a] used in this research is the Weather Research and Forecasting model coupled with Chemistry (WRF-Chem) [Grell et al., 2005] modified for passive tracers as in Lauvaux et al. [2012]. The WRF configuration for the model physics used here was based on previous numerical modeling studies [e.g., Gaudet et al., 2009; Rogers et al., 2013; Deng et al., 2012b] using (1) the single-moment three-class simple ice scheme for microphysical processes, (2) the Kain-Fritsch scheme for cumulus parameterization on the 9 km grid, (3) the Rapid Radiative Transfer Model for longwave atmospheric radiation and the Dudhia scheme for shortwave atmospheric radiation, (4) the turbulent kinetic energy (TKE)-predicting Mellor-Yamada-Nakanishi-Niino (MYNN) Level 2.5 turbulent closure scheme for the turbulence parameterization in the planetary boundary layer (PBL), and (5) the five-layer thermal diffusion scheme for representation of the interaction between the land surface and the atmospheric surface layer [Skamarock et al., 2008].

The WRF modeling system used in this study has FDDA capabilities to allow the meteorological observations to be continuously assimilated into the model. The FDDA technique used in this study was originally developed for MM5 [Stauffer and Seaman, 1994] and recently implemented into WRF [Deng et al., 2009] and has been used in several studies [e.g., Rogers et al., 2013; Lauvaux et al., 2013]. Nudging of the wind field is applied through all model layers, but nudging of the mass fields (temperature and moisture) is only allowed above the model-simulated PBL so that the PBL structure produced by the model is dominated by the model physics. More recent studies have assimilated mass fields within the PBL [Reen and Stauffer, 2010], but the sensitivity of the model depends on the stability conditions, becoming numerically unstable in nonconvective PBL by disrupting the energy balance. For these reasons, we excluded the innovations of mass fields within the PBL. In this specific application, the World Meteorological Organization (WMO) observations were assimilated into the WRF-Chem system to produce a dynamic analysis, blending the model simulations and the observations to produce the most accurate meteorological conditions possible to simulate the atmospheric CO₂ concentrations in space and time throughout the Indianapolis region.

The WRF model grid configuration used for this demonstration is comprised of three grids: 9 km, 3 km, and 1 km (cf. Figure 1 for the 3 km and 1 km grids), all of which are cocentered at Indianapolis, Indiana. The 9 km grid, with a mesh of 100×100 grid points, contains the eastern part of the U.S. Midwest. The 3 km grid, with a mesh of 99×99 grid points, contains the southern part of the state of Indiana. The 1 km grid, with a mesh of 87×87, covers the metropolitan area of Indianapolis and the eight counties surrounding Marion county. Fifty-nine vertical terrain-following layers are used, with the center point of the lowest model layer located ~6 m above ground level (AGL). The thickness of the layers increases gradually with height, with 25 layers below 850 hPa (~1550 m AGL).

Figure 1.

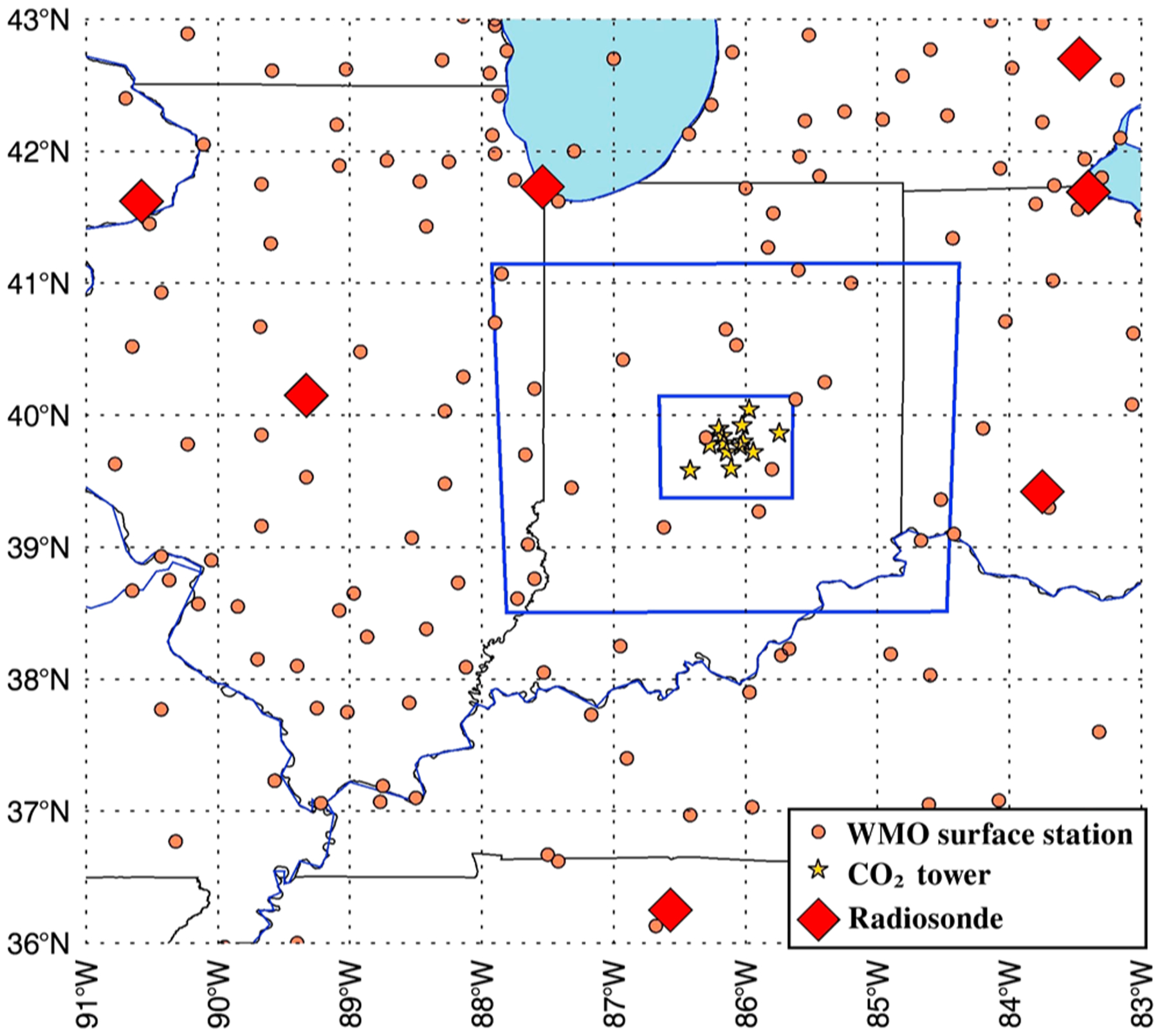
Surface meteorological observation distribution including surface meteorological stations (red circles) and rawinsondes (red diamonds) from the WMO database used in the WRF-FDDA modeling system, and CO₂ tower locations (gold stars) in the 1 km simulation domain (blue square). Indianapolis is located at the center of the domains.

The FDDA parameters used in this application can be found in Deng et al. [2012a]. For this application, 3-D analysis nudging and surface analysis nudging were applied on the 9 km grid with reduced nudging strength compared to observation nudging, and observation nudging was applied on all grids with the same nudging strength. No mass fields (temperature and moisture) observations are assimilated within the WRF-predicted PBL. The meteorological observations assimilated into the WRF system are based on the WMO observations distributed by the National Weather Service (NWS) and include both 12-hourly upper air rawinsondes and hourly surface observations. Figure 1 shows the WMO surface observation distributions, indicating a significant number of observations over the region. The gridded meteorological data used to initialize the WRF-Chem real-time system were the National Centers for Environmental Prediction (NCEP) North American Regional Reanalysis (NARR) available every 3 h.

2.1.2. Lagrangian Particle Dispersion Modeling

The Lagrangian Particle Dispersion Model (LPDM) described by Uliasz [1994] is used as the adjoint model of the WRF-FDDA modeling system. Particles are released from the receptors in a backward in time mode with the wind fields and the turbulence generated by the Eulerian model WRF-FDDA. In a backward in time mode, particles are released from the measurement locations and travel to the surface and the boundaries. Compared to a forward mode where particles are released from the entire surface of the simulation domain, the particles in backward mode are released only from the observation locations with all of them being used to estimate fluxes, which reduces the computational cost of the simulation. Every 20 s, 35 particles are released at the position of the towers, which corresponds to 6300 particles per hour per measurement site (or receptor). At high spatial resolutions, the particle locations have to be stored at a much higher frequency compared to regional applications. As a first estimation, a particle would fly over a 1 km pixel in about 3 min (assuming a horizontal mean wind speed of 5 m/s). To avoid any gaps in the particle trajectories, particle positions were recorded every minute. At the opposite, because the domain is small (87 km wide), the integration time, i.e., the time window during which the air masses are influenced by the local surface emissions, is limited to few hours. Here particles were integrated over 12 h to ensure that particles traverse the entire domain in any meteorological situations.

The dynamical fields in LPDM are forced by mean horizontal winds (u, v, w), potential temperature and turbulent kinetic energy (TKE) from WRF-FDDA. At this resolution (1 km), turbulent motion corresponds to the closure of the energy budget at each time step. This scalar is used to quantify turbulent motion of particles as a pseudo random velocity. Based on the TKE, wind, and potential temperature, the Lagrangian model diagnoses turbulent vertical velocity and dissipation of turbulent energy. The off-line coupling between an Eulerian and a Lagrangian model solves most of the problems of nonlinearity in the advection term at the mesoscale. Most of the nonlinear processes resolved by the atmospheric model are attributed to a scalar representing the velocity of the particles. At each time step (here 20 s), particles move with a velocity interpolated from the dynamical fields of the WRF-FDDA simulation stored every 20 min. The time step depends on the TKE, following the discretization scheme described in Thomson [1987].

The formalism for inferring source-receptor relationships from particle distributions is described by Seibert and Frank [2004]. At each time step, the fraction of particles (released from one receptor at one time) within some volume gives the influence of that volume on the receptor. If the volume includes the surface this will yield the influence of surface sources. If the volume includes the boundary (sides or top) it yields the influence of that part of the boundary.

2.2. The INFLUX CO₂ Observation Tower Network

Indianapolis, Indiana, has a population of about 900,000 and a metropolitan area of about 1.7 million people, including Marion County and its eight surrounding counties. The city presents a relatively small urban center but extends over a wide area of about 40 km by 50 km mostly covered by low density suburban areas of less than 3000 people per square mile. The flat terrain offers better modeling performances and the absence of large cities in a radius of 200 km limits the potential variability in GHG boundary inflow. The full measurement network of the INFLUX project includes 12 sites fully deployed and operational by July 2013. For the time period of this study, only nine of them were measuring CO₂ continuously. We used the hourly averaged CO₂ mixing ratios during daytime (17–22 UTC) between September 2012 and April 2013.

The sites (1, 2, 3, 4, 5, 7, 9, 10, and 12) are presented in Figure 2. Their respective sampling heights are 121 m, 136 m, 54 m, 60 m, 125 m, 58 m, 130 m, 40 m, and 40 m. The Cavity Ring Down Spectrometer instruments [Crosson, 2008] measured the atmospheric CO₂ mixing ratios continuously over the period, at the sampling heights described above. Instruments were deployed in temperature-controlled environment using existing tower infrastructures. The minimum sampling height is 40 m high at Site 10 and the maximum is 136 m high at Site 2. The instruments were calibrated using the protocol described in Richardson et al. [2011], with a drift of less than 0.2 ppm per year across the sites, and a noise of 0.1 ppm on daily daytime averages.

Figure 2.

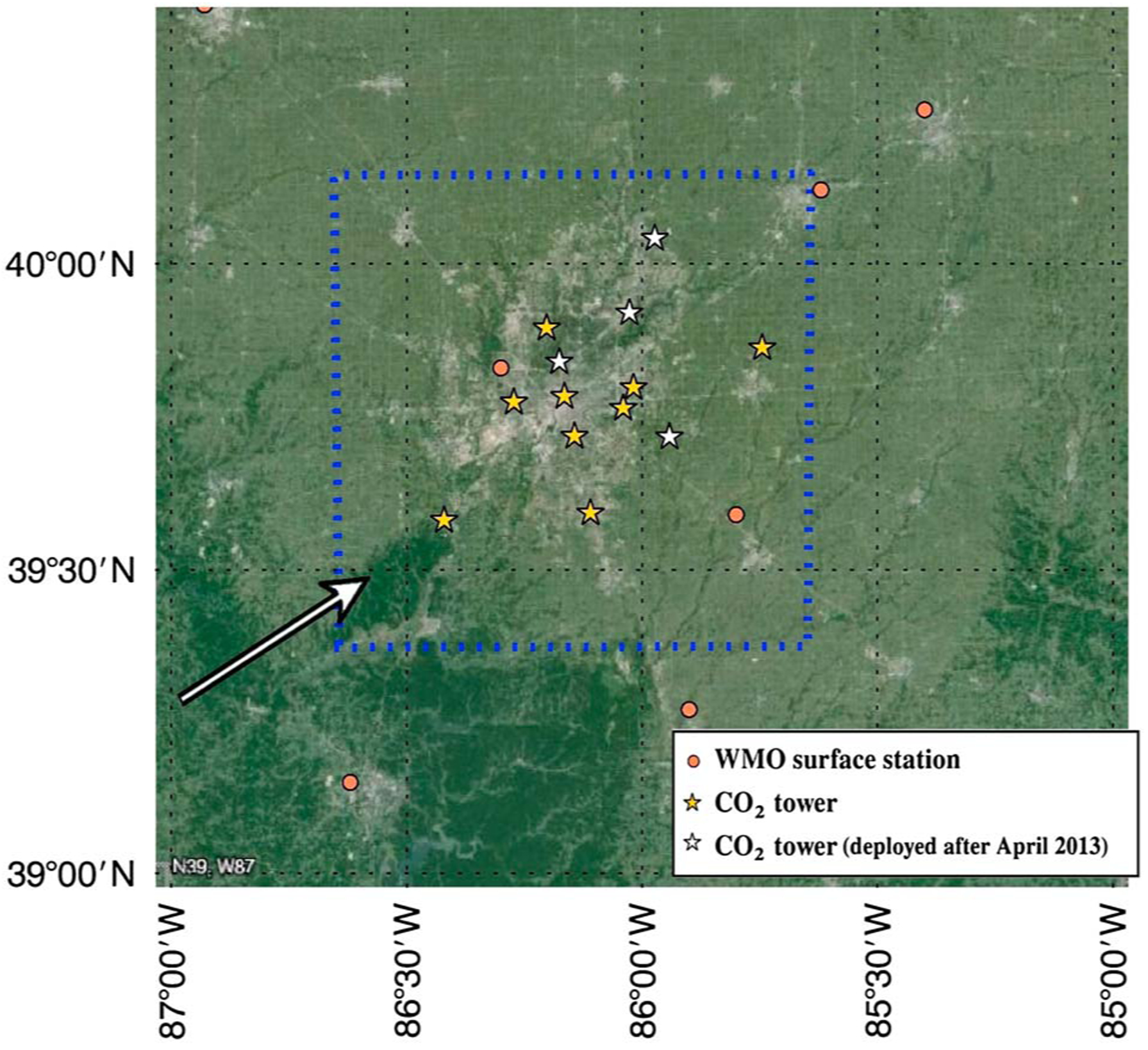
CO₂ tower locations (gold stars) in the 1 km simulation domain (blue square), with additional towers not available for the study period (white stars), and surface meteorological stations (red circles) from the WMO database used in the WRF-FDDA modeling system. Indianapolis is located at the center of the domains.

2.3. Prior Fluxes for CO₂

2.3.1. High-Resolution Emissions: The Hestia Product

The Hestia CO₂ emission product [Gurney et al., 2012] was coupled to the WRF-FDDA model to simulate the CO₂ atmospheric mixing ratios over and around Indianapolis. The Hestia product combines observations and modeling to produce CO₂ emissions from the combustion of fossil fuels and is considered here as a “bottom-up” approach. A wide range of data sources are used to quantify emissions at the scale of individual buildings and road segments, including local traffic monitoring, property tax assessor data, power plant emissions monitoring, and air quality pollution reporting. The data product includes some spatial and temporal proxies to attain hourly emissions at fine spatial scales for Marion County and the eight counties that surround Marion County. The space and time patterns are generated for the year 2011. Emissions for 2012 and 2013 reflect the application of scale factors derived from the Department of Energy (DOE) Energy Information Administration (EIA) fuel statistics specific to sector and fuel type. Hence, the magnitude of emissions change over the 2011–2013 time period but the subcounty spatial structure remains fixed. Furthermore, the submonthly time structure in all sectors other than power production are represented by fixed time cycles derived from multiple years of monitoring data. For example, the onroad CO₂ emissions reflect a spatially explicit use of a mean weekly cycle (7 day cycle within a given month) and mean diurnal cycle (24 h cycle within a given week). The emissions available for each of the eight economic sectors (cf. Table 1) for the years 2012 and 2013 were aggregated from the initial building-level product down to 0.002 degree resolution. The 0.002 gridded product was then aggregated further at 1 km resolution over the WRF grid, covering Marion County and the eight surrounding counties. Figure 3 (left) shows the CO₂ emissions in ktC km⁻² from Hestia with the nine instrumented towers that were operational during the inversion period. The 1 km WRF grid was designed to cover the area corresponding to the nine counties, except for a minor fraction extending beyond the rectangular domain. The total CO₂ emissions for the nine counties around Indianapolis are 6.84 MtC for the year 2012 and 7.17 MtC for 2013. The 8 month total emissions over the inversion domain, representing most of the nine counties slightly cropped following the WRF simulation domain, are 4.56 MtC for September 2012 to April 2013.

Table 1.

Sectoral Contributions (in %) in the Simulated Tower Mixing Ratios Averaged Over the Network of Nine Towers Compared to the Surface CO₂ Emissions (Hestia)

Emission Sector	Commercial	Industrial	Road	Nonroad	Residential	Utility
Atmospheric signals	6%	13%	45%	5%	9%	20%
Surface emission	6%	9%	44%	6%	8%	20%

Figure 3.

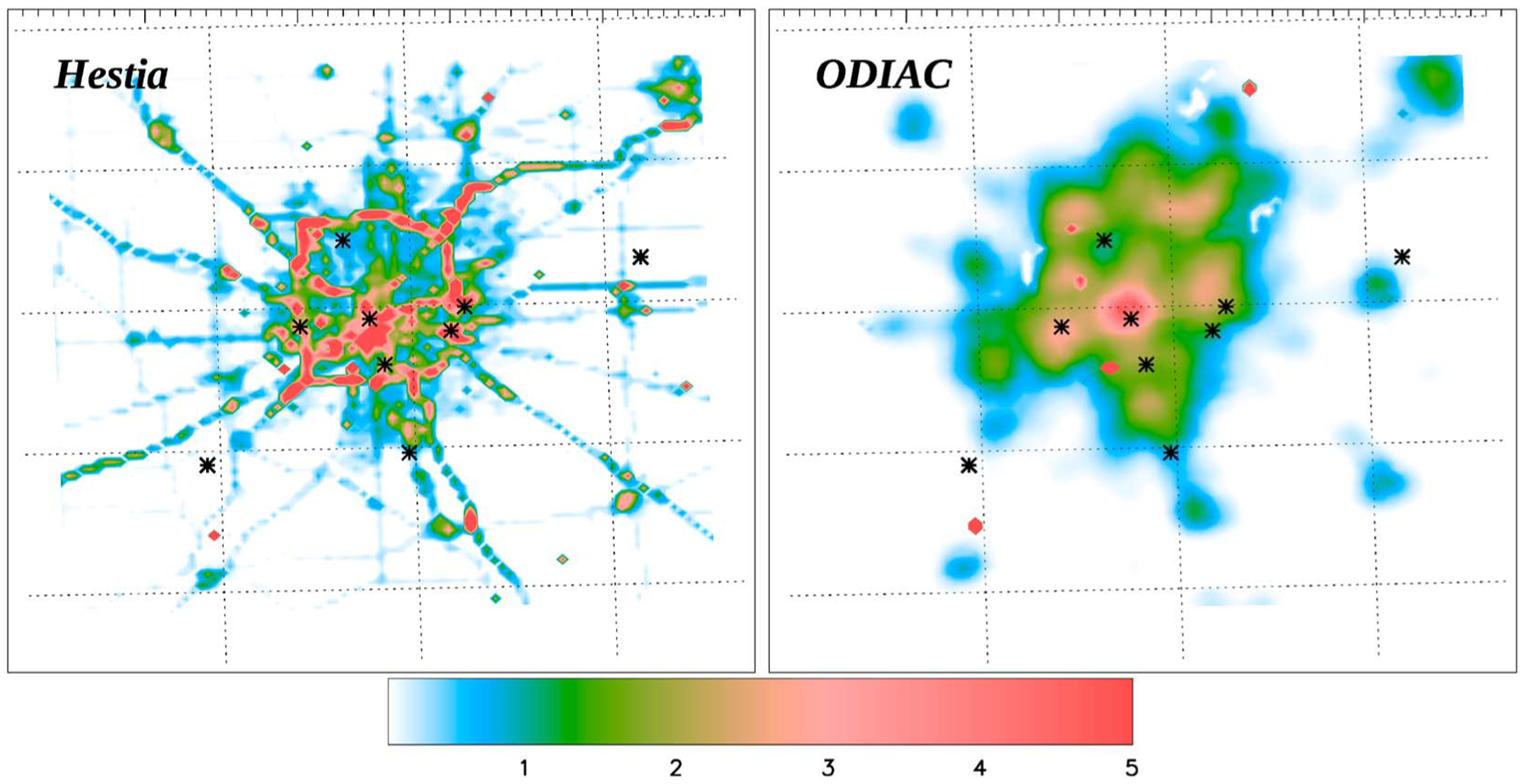
CO₂ a priori emissions (in ktC km⁻² over 5 days) using (left) the Hestia product aggregated at 1 km resolution and (right) the space-based emissions from ODIAC downscaled at 1 km resolution.

2.3.2. The Open-Source Data Inventory for Anthropogenic CO₂ (ODIAC) Emission Data

We used the Open-Source Data Inventory for Anthropogenic CO₂ (ODIAC) emission data [Oda and Maksyutov, 2011] as an alternative prior for inversion. While Hestia clearly prevails over ODIAC for Indianapolis, we want to evaluate here the value of ODIAC, globally available, assuming that CO₂ emission products of similar quality can be produced anywhere over the globe. The version of the ODIAC emission data used in this study is based on emission estimates updated using the Carbon Dioxide Information Analysis Center (CDIAC) global and national fossil fuel emission estimates (http://cdiac.ornl.gov/trends/emis/meth_reg.html; last access 27 March 2015) and the year 2013 edition of BP statistical review of world energy (http://www.bp.com/en/global/corporate/about-bp/energy-economics/statistical-review-of-world-energy/statistical-review-downloads.html; last access 27 March 2015). The emission spatial distributions were estimated at 1 × 1 km resolution using the same method presented in Oda and Maksyutov [2011]. The emissions from power plants are mapped using the geolocation reported in the Carbon Monitoring and Action (CARMA) global power plant database (www.carma.org; last access 27 March 2015) and the rest of the emissions (nonpoint source emissions) are distributed using the satellite observed nightlight data. The nightlight data used in this version of ODIAC emission data were developed using a new algorithm, improving the representation of suburban areas compared to the original version Oda et al. [2010]. ODIAC emission data only indicate monthly emissions (based on CDIAC monthly emission data) and do not have diurnal and weekly cycles. Further details of the ODIAC are described in Oda and Maksyutov [2011].

2.4. Inversion Methodology

The inversion system solves for a 5 day averaged emission vector of 87×87 unknowns as described in Tarantola [2004] by minimizing a cost function and following the equation:

$$x=x_0+B{H}^T{\left(HB{H}^{\top }+R\right)}^{-1}\left(y-H{x}_0\right),$$ (1)

where x are the unknown CO₂ emissions, x₀ the a priori emission estimate, y the CO₂ mixing ratio observations, H the influence functions, and R and B the uncertainty covariance matrices of the observations and the prior emissions, respectively. We can define the posterior error covariance A for sources given by the following expression A⁻¹ = B⁻¹ + H^T R⁻¹H.

The number of observations over the 5 day periods vary from 185- to 270-hourly measurements per time period, with an average of about 245. No diurnal cycle has been considered here as the advection of air masses across the domain takes less than 5 h. With the first observation time being 17 UTC (12 P.M./1 P.M. local time), the correction of the emissions applies only to daytime emissions (7 A.M./8 A.M.). In other terms, nighttime emissions cannot be constrained using daytime observations for such a small domain. For the total emissions presented in this study, the posterior emissions correspond to the inverse results for the period 12–22 UTC, combined with the prior emissions (Hestia) for the period 23–11 UTC. We performed a second case using a slightly different time window, i.e., 20 to 23 UTC, due to the lack of a precise definition of the afternoon, corresponding in theory to the well-mixed conditions in the PBL. We followed the optimal time window defined in Bakwin et al. [1998] to evaluate the sensitivity of the inverse emissions to the observation time window (cf. section 3.6).

2.5. Prior Emission Errors

The complexity of the underlying model used to generate the Hestia emission product at very high resolution (i.e., building scale) limits our ability to rigorously quantify the associated errors, including their spatial and temporal structures. As a simplified approach, we defined the error variances as a percentage of the net emissions for all the economical sectors, except for the utility sector for which the emissions are better constrained. Hourly energy production statistics and direct measurements provide more accurate hourly emissions for energy production (i.e., utility sector). Therefore, we defined the standard deviations as 60% of the net emissions at 1 km resolution in the reference case for all the sectors except the utility sector. Overall, the aggregated error variance is about 25% of the total emissions over the entire domain for each 5 day periods, assuming no temporal error correlation between two periods. When performing inversions over 10 day time windows, similar inverse emissions were produced, which gives us confidence in our assumption. The optimal time window of 5 days was defined based on footprint analyses (not shown here) which corresponds to different synoptic wind conditions. By assimilating over 4 days or longer, the tower footprints cover a larger area with varying wind directions. We performed a second test with much larger prior errors (i.e., 100% of the net emissions) to evaluate the convergence of the inverse emissions in a very underconstrained system (cf. section 4.4). In this configuration, the inverse solutions can be negative, but the scaling of the variances to the net prior emissions limits the occurrence of negative values to very few isolated cases (≪1%). For the spatial error structures, we used a similar approach to Lauvaux et al. [2012], i.e., correlations exponentially decaying with the distance, applied among urban pixels only (based on the National Land Cover Database 2010). The distance-based correlation matrix (C_L) is created first and then combined with land cover types for each land cover type assuming no correlation between urban and nonurban pixels (C_urb). The combined matrix is created assuming equal weights from both correlation matrices, using $C_f=\sqrt{C_L}\cdot \sqrt{C_{\text{urb}}}$. For the definition of the correlation length L, we tested the impact on the posterior emissions using varying distances, i.e., no correlation, L = 4 km and L = 12 km. The use and the definition of correlation length in prior emission errors is discussed in section 4.4 and considered as an additional contribution to the overall uncertainties, mainly associated with the definition of the correlation length, in section 4.4.

The length of the inversion window was defined by the averaged length of synoptic and mesoscale events over the area. Typically, wind directions change with the passage of weather systems, which results in incomplete surface coverage in terms of tower footprints if the inversion time window is too short. The minimum of 5 days corresponds to two synoptic conditions on average and represents the minimum length to constrain the whole area. As we invert for 5 day emissions, temporal correlations are considered negligible between two inversion windows. This assumption is conservative but may underestimate the error correlation in the input data used to construct prior CO₂ emission fields at various temporal scales (e.g., fuel statistics aggregated monthly with superimposed daily variations). To evaluate this assumption, we performed a similar inversion using 10 day periods and compare the results in section 3.6.

2.6. Observation Errors

2.6.1. Observation Error Variances

For the transport model errors, we propagated the errors of the WRF-FDDA system into the inversion system through the error variances. The propagation of errors was performed in three steps: (1) we scaled the error variances using the normalized distance of a χ² distribution λ over each 5 day period. This first step provides an average variance for the period; (2) we adjust the variances for every hour using WRF-FDDA model performances for wind speed and direction; and (3) we readjust the variances by computing the normalized distance of a χ² distribution for the second time λ′. In the second step, we quantified the WRF-FDDA model performances (mean absolute errors (MAE)) for both wind speed and direction using the available surface WMO stations. This technique removes singular time steps during which the transport model performed poorly.

During the first step, the balance between prior error statistics and observation errors was evaluated using the χ² normalized distance λ, defined by

$$\lambda =\frac{1}{n}[{(y-H{x}_0)}^T{(HB{H}^{\top }+R)}^{-1}(y-H{x}_0)]$$ (2)

similar to Kaminski et al. [2001].

For the second step, the hourly daytime MAE averaged over the domain, ε, for the wind speed and direction were used to define the hourly transport errors. Because these measurements were assimilated in the WRF-FDDA simulation, the true MAE is most likely underestimated. However, we use these model-data residuals as a representation of the relative performances of the WRF-FDDA model at the hourly time scale. In principle, meteorological errors cannot directly be diagnosed from modeled CO₂ mixing ratios to describe the CO₂ variances in the inversion. Indeed, both flux and transport errors affect the simulated CO₂ mixing ratios. Instead, we only diagnosed transport errors from meteorological errors, which were then transformed into hourly scaling factors applied to hourly CO₂ variances. To quantify these scaling factors, an error model was created to generate transport errors for the CO₂ mixing ratios depending on both errors, i.e., in wind speed and direction. An adjustment coefficient defined as the ratio between the hourly MAE and the median of the MAE over the 5 day period was computed for both variables. The maximum of the two ratios define the hourly adjustment coefficient. To avoid using the time steps during which the model is inaccurate, the hourly errors were used to scale the variances ${\epsilon }_{i,j}^2$ for an observation (i) (i.e., the diagonal terms in R) using the following relationship:

$${\epsilon }_i^2=\text{max}\left(\frac{{\epsilon }_{\text{spd}}}{{\mu }_{\text{spd}}},\frac{{\epsilon }_{\text{dir}}}{{\mu }_{\text{dir}}}\right)\cdot {\epsilon }_{\text{init}}^2$$ (3)

with ε_spd and ε_dir the hourly mean errors, μ the median of the 5 day errors, and ${\epsilon }_{\text{init}}^2$ the initial variance from step 1. We propagated the hourly transport model errors by using a multiplicative factor scaled with the performances of the modeled wind speed and direction. Over the inversion period (September 2012 to April 2013), the median of the wind speed MAE is about 0.8 m s⁻¹ and 12° for the wind direction. These two terms μ_dir and μ_spd were used to provide a ratio between the averaged MAE and the hourly errors. A similar analysis was performed on the wind direction. On an hourly basis, the ratio between the median and the hourly MAE would define the adjustment of the initial error, e.g., multiplied by 2 for a wind speed MAE between 0.8 and 1.6 m s⁻¹, or by 3 between 1.6 to 2.4 m s⁻¹, with no limit applied to the ratio. As described in equation (3), the maximum of the two variables (wind speed and direction) was used to define the final multiplicative factor applied to the initial CO₂ variance to adjust for incorrect wind direction or speed at any given time step, as described in equation (3). In section 3.6, we compared this method to using a constant ε_i,j over time with no hourly adjustment based on the MAE.

The adjustment of the variances is computed from a χ² test (cf. section 2.4) using the normalized distance λ over each 5 day periods [Tarantola, 2004]. For nondiagonal matrices, as described in the next section, the normalized distance λ correction cannot be applied directly to the variances and covariances; otherwise, the correction would be applied multiple times through the covariances and therefore overestimate the total errors. To compensate for the overestimation by the error covariances, we applied the square root of the scaling factor $\left(\sqrt{\lambda }.{\epsilon }_{i,j}^2\right)$ which assumes a linear relationship between variances and covariances (cov_x,y = corr_x,y.σ_x.σ_y). This technique was tested over multiple 5 day segments and produced a systematically better normalized distance λ (i.e., closer to one).

2.6.2. Observation Error Correlations

At high resolutions, spatial and temporal correlations in transport model errors become increasingly important. Past studies have approached the problem at coarser resolutions [e.g., Gerbig et al., 2003; Lauvaux et al., 2009a] and found that error covariances are significant when the distance between observation locations is low. Using a diffusion equation model with an ensemble of transport simulations at 8 km resolution, Lauvaux et al. [2009a] estimated the average correlation length in transport model errors at about 30–40 km. Between the INFLUX towers, the average distance is about 40 km, which suggests that spatial error correlations may be significant. However, the correlation length may vary in space and time and is likely to depend on model resolution and physics. To evaluate the sensitivity of the inverse emissions to spatial error correlations, we assumed a relatively small correlation length and an exponentially decaying model for the distance, with L_obs =10 km, following the equation:

$$C_{\text{obs}}^{i,j}={\text{exp}}^{-\frac{d_{i,j}^2}{L_{\text{obs}}^2}}$$ (4)

with $C_{\text{obs}}^{i,j}$ the correlation coefficient between two tower locations i and j and d_i,j the distance between the towers i and j. The observation error correlation matrix C_obs has to be symetric, positive semidefinite, with the diagonal terms equal to one. Further investigations of C_obs showed that a small number of eigenvalues were negative and required some modifications of the initial matrix before inversion. Following Brissette et al. [2007], we used an iterative process to filter negative eigenvalues. The negative values were replaced by slightly positive eigenvalues, and the correlation matrix was regenerated using the original eigenvectors. The matrix was slightly modified to be symmetric and with positive correlations only. The iterative process converged for all the inversion periods, modifying the correlation by less than 10%.

Temporal error correlations at high frequency (i.e., hourly) can also affect the simulated atmospheric mixing ratios [Lauvaux et al., 2009a]. However, the batch inversion system as defined here is less affected by the impact of hourly error correlations, as the atmospheric data are assimilated in a single block. Spatially, emission corrections may still vary, but the overall city-wide emissions are unlikely to be affected. Further investigations of temporal error correlations in the observations are needed to better quantify their impact on the inverse solution. Here no temporal correlation was introduced in the errors. We quantified the impact of spatial error correlations by performing a sensitivity study, comparing the impact of error correlation, i.e., nondiagonal terms in R to the reference configuration in section 2.6.2. Further investigation is required to define more completely the spatial and temporal error correlations in high-resolution transport simulations and their impact on the inverse emissions, similar to Lauvaux et al. [2009a] at coarser resolution.

2.7. Boundary Inflow: Data Selection

The constant flow of air through the boundaries of a limited-domain atmospheric simulation represents a significant amount of carbon compared to the local emissions and therefore is a critical quantity that has to be characterized in the inversion system [Göckede et al., 2010; Lauvaux et al., 2012]. Several studies have suggested to simply measure this quantity upwind of the metropolitan area [Kort et al., 2012; McKain et al., 2012] similar to aircraft mass balance techniques [Cambaliza et al., 2014; Karion et al., 2015]. However, background measurements can be affected by local fluxes and/or the local atmospheric dynamics which would impair its spatial representativity as a background measurement. The inflow of air follows primarily the wind direction and its variability in time and space, directly affecting our ability to measure the upwind conditions in any meteorological situations. Therefore, no measured background concentration would remain constant as the air moves across the domain. Advection-diffusion and vertical mixing modify the mixing ratios as air masses move over the city, increasing the representation errors associated with upwind measurements.

To measure the background air, the initial design of the Influx network included two sites covering the two major wind directions in the area, i.e., Site 1 for the northwesterly through westerly flows and Site 9 for northerly through easterly winds. We compared several sites of the network (i.e., Sites 1, 4, 5, and 9) by computing the fraction of days corresponding to low atmospheric concentrations for each site. This analysis assumes that cleaner air should be measured at the background sites. The results indicate that Site 1 shows the lowest concentrations on average over time, whereas Site 9 is systematically higher by a couple tenths of a ppm. Sites 4 and 5 are clearly influenced by local emissions and should not be used as background sites.

We selected Sites 1 and 9 as our least biased background sites for our analysis and defined the background concentration for each hourly measurement over Indianapolis following different scenarios. These scenarios correspond to the definition of the upwind concentrations at a given time, or under specific conditions. To evaluate the impact of the definition of the boundary conditions on the inverse emissions, we produced several inverse emissions using different selection methods. First, we used a fixed site for the entire inversion period, using the hourly concentrations at the exact hour. This scenario is the simplest option for limited networks of towers. Second, we used an upwind model, selecting the sites based on the hourly surface wind direction in the center of Indianapolis. The upwind model selected Site 1 when the wind was between 135° and 315° and Site 9 for 315° to 135° (cf. Figure 4). Third, we used a daily minimum measured across the network to evaluate the importance of hourly changes. The results are presented in section 3.5. Additional errors could still affect the background sites such as local biogenic signals from soil respiration which are nonnegligible even in wintertime in midlatitudes [cf. Pataki et al., 2007]. A third background tower is being deployed in a different area to address more carefully the possible local biogenic fluxes mixed with large-scale gradients in atmospheric mixing ratios advected over the city.

Figure 4.

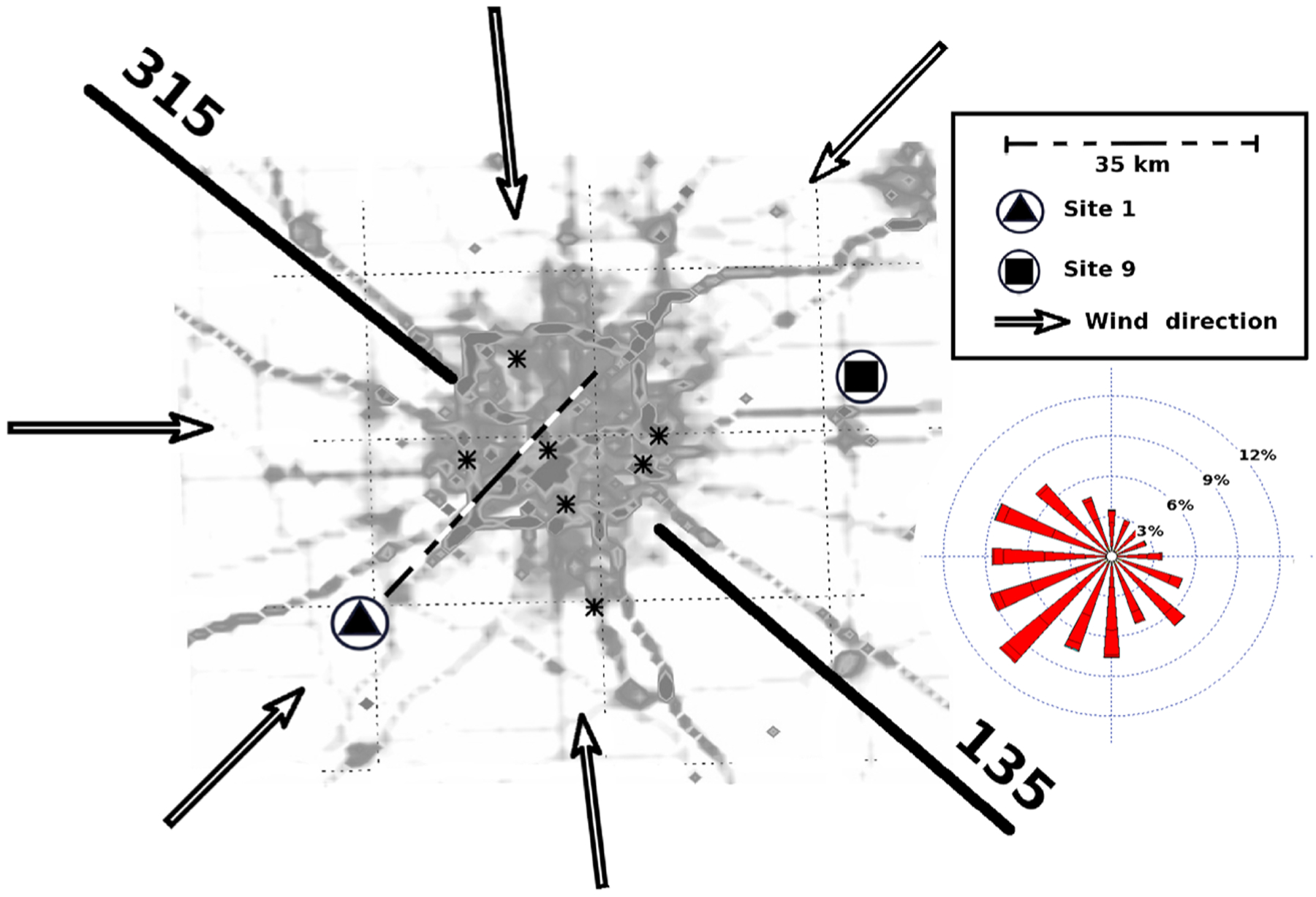
Selection of the background site to determine the upwind concentrations of CO₂ over Indianapolis, using two semicircles (135° and 315°) and hourly modeled wind directions from the WRF-FDDA system at three locations across the city. The emitting area defined by Hestia is represented in gray. The distance between Site 1 and Site 9 (about 35 km) corresponds to an advection time of about 2 h. The wind climatology for the month of December at the Indianapolis airport (IND station) is shown under the legend (in red).

3. Results

3.1. Sectoral Contributions From Hestia

We show in Figure 5 the sectoral contributions at each tower locations based on Hestia 2012 emissions combined with the WRF-FDDA-LPDM footprints for the month of October 2012. The simulated CO₂ mixing ratios correspond to the 1 km surface footprints combined with the aggregated 1 km Hestia emissions, at the hourly time scale, averaged over the month of October 2012 for the hours 17–22 UTC. The atmospheric mixing ratios have not been corrected for the impact of lower sampling heights on the magnitude of the atmospheric signals. This effect is simulated by the Eulerian and the Lagrangian models later in this study. The two sites with two lowest sampling heights (at 40 m high) are the sites 10 and 12. Atmospheric enhancement at Site 12 is low despite the low sampling height. However, the enhancements at Sites 10 and 3 are large, mostly because of the presence of two power plants. The mobility sector, (i.e., traffic emissions) is the largest contributor to the atmospheric enhancements (45% of the total enhancements) at the nine tower locations, similar to the emission ratios for the same sector (44%). This result is explained by the presence of sector emissions in almost every single urban pixel of the domain. Economical sectors overlap almost systematically across the city, which explains the similar distribution of sector contributions between the atmospheric signals and the emissions. The second contributor is the utility sector, with two towers showing very large contributions (about 50%), and most the towers between 10 and 20% (except Site 9 with only 2% of the signals). In terms of emissions, the utility sector represents 20% of the emissions over the nine counties. This sector is clearly underrepresented by most towers, overrepresented at two sites (3 and 10), and absent at Site 9. The nonuniform distribution is explained by the locations of the power plants, i.e., with only few large point sources over the domain. Atmospheric signals from the industry sector represents about 13% on average, similar to its associated emission contribution of about 9%. The commercial and residential sectors represent respectively 6% and 9% of the atmospheric enhancements, compared to 6% and 7% of the emissions. Finally, the airport and the railroad sectors represent less than 2% each of the total signals, similar to the emission contribution.

Figure 5.

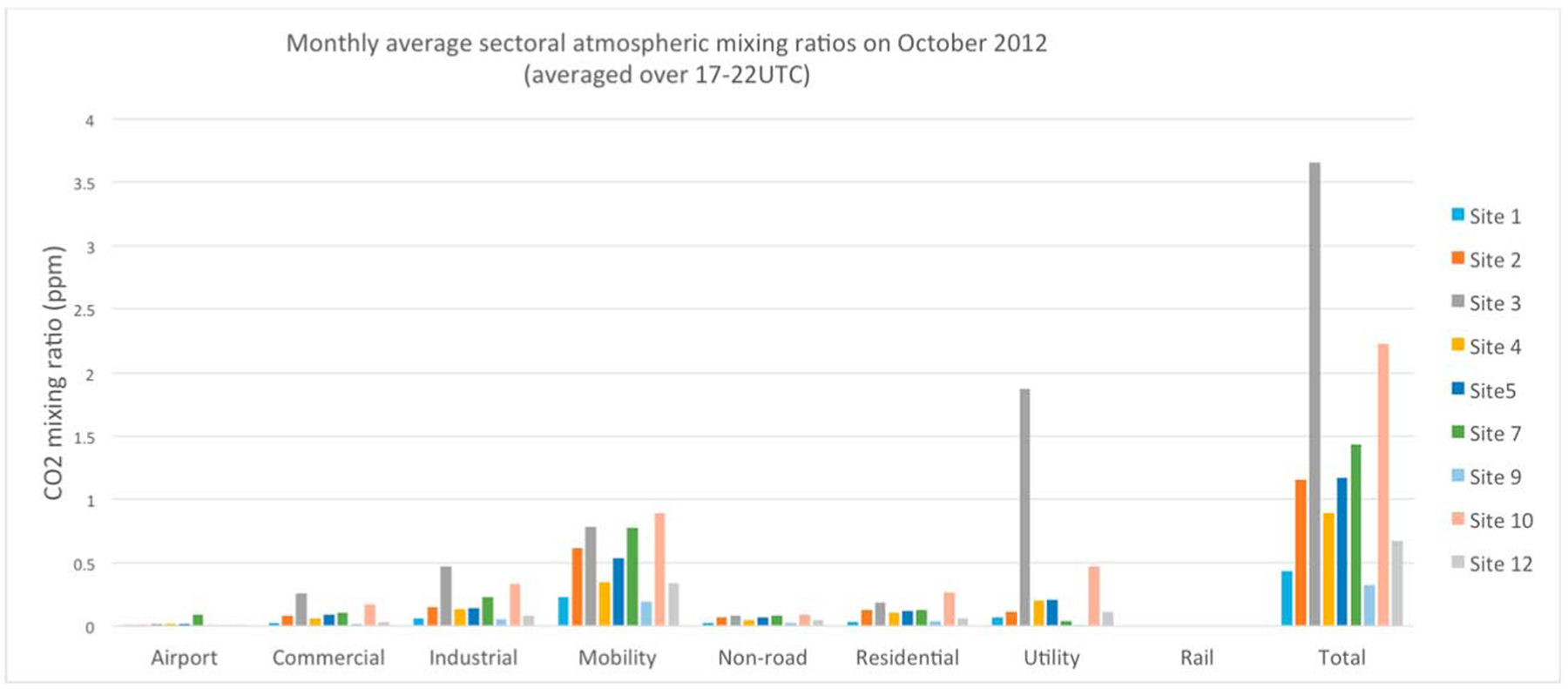
Sectoral contributions (in ppm) using the WRF-FDDA-LPDM footprints at 1 km resolution combined with the Hestia sectoral CO₂ emissions for October 2012, except for the Railroad and the airport sectors representing about 2% of the emissions and the atmospheric enhancements.

3.2. CO₂ Inverse Emissions Over Indianapolis (Reference Configuration)

We present here the results for the reference configuration of the inversion system. Some of the assumptions made in this inversion are discussed later as additional unknowns. Here the a priori emissions correspond to the Hestia emissions aggregated at 1 km resolution. The prior error standard deviations were defined as 60% of the net emissions, including an urban correlation length of 4 km to define the spatial error structures as described in section 2.5. The background mixing ratios were defined by the observed mixing ratios at Site 1 (SW of Indianapolis). We present the time series of the prior and posterior atmospheric mixing ratios (minus the background) in Figure 6 for the month of January 2013. The initial mismatch between the prior and the observations is about −0.52 ppm (median) and is further reduced to −0.11 ppm after inversion. Over the 8 month period, the prior mismatch of about −0.68 ppm is reduced to −0.19 ppm (median values). We present the corresponding statistical distributions of the mixing ratios for January 2013 (cf. Figure 7). About 5% of the observed values are negative, which indicate potential discrepancies between the upwind and downwind sites. The mixing ratios from WRF-Hestia (a priori) show a large number of near-zero values that are not observed, as well as a short tail distribution (most values under 3 ppm) compared to the observations (up to 8 ppm). After inversion, the number of near-zero values has significantly decreased (between 18 to 24% for the 0. to 1.2 ppm bins) while the tail has extended to 5 ppm values, in better agreement with the observations.

Figure 6.

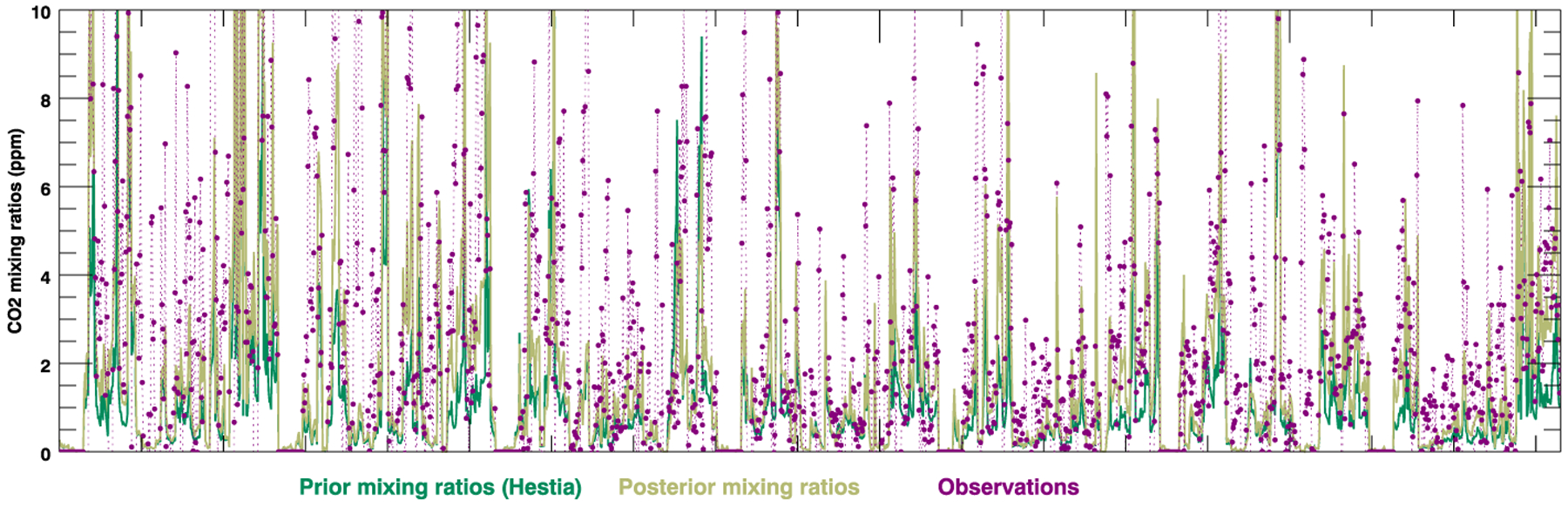
CO₂ atmospheric mixing ratios from WRF-LPDM footprints coupled to the Hestia prior emissions (in green), the posterior emissions (in brown), and the observations at all the surface towers available for that period (in purple) for the month of January 2013.

Figure 7.

Distribution of the CO₂ atmospheric mixing ratios from WRF-LPDM footprints coupled to the Hestia prior emissions (in green) and to the posterior emissions (in brown), compared to the observations at all the surface towers available for that period (in purple) for the month of January 2013.

Figure 8 shows the CO₂ emissions time series averaged over 5 day periods from Hestia (top, in red) and the corresponding posterior emissions (top, in blue) from September 2012 through April 2013. The errors for each 5 day estimate are significantly reduced after inversion, from about 25% to around 9% on average. Over the 8 month period, the inverse emissions remain relatively similar to the a priori Hestia emissions, with some additional high frequency variability. The emissions increased during the first few months (September to mid-November). The total aggregated emissions are about 20% higher than the Hestia emissions over the period (5.5 MtC versus 4.56 MtC). The emission corrections are shown in Figure 9 (bottom left) with an overall increase following the beltway and the residential and commercial areas. The error reduction (top left) is about 30% in the urban area, with larger values in the southern part of town, where the tower density is higher (cf. Figure 2). Due to significant transport errors in nonconvective stability conditions, the inversion system constrains emissions only between the time of the first atmospheric observation (17 UTC) minus the advection time of the air over the city (about 4 to 5 h). The innovation (adjustment of the emissions after inversion) corresponds to an adjustment of the daytime emissions (i.e., 12–22 UTC) while the nighttime emissions remain unchanged. Daytime emissions being larger, the 12–22 UTC emissions still represent more than nighttime emissions, or about 60% of the total over the period. However, the innovation (emission correction) could be potentially larger if the inversion system was able to assimilate the entire atmospheric data set.

Figure 8.

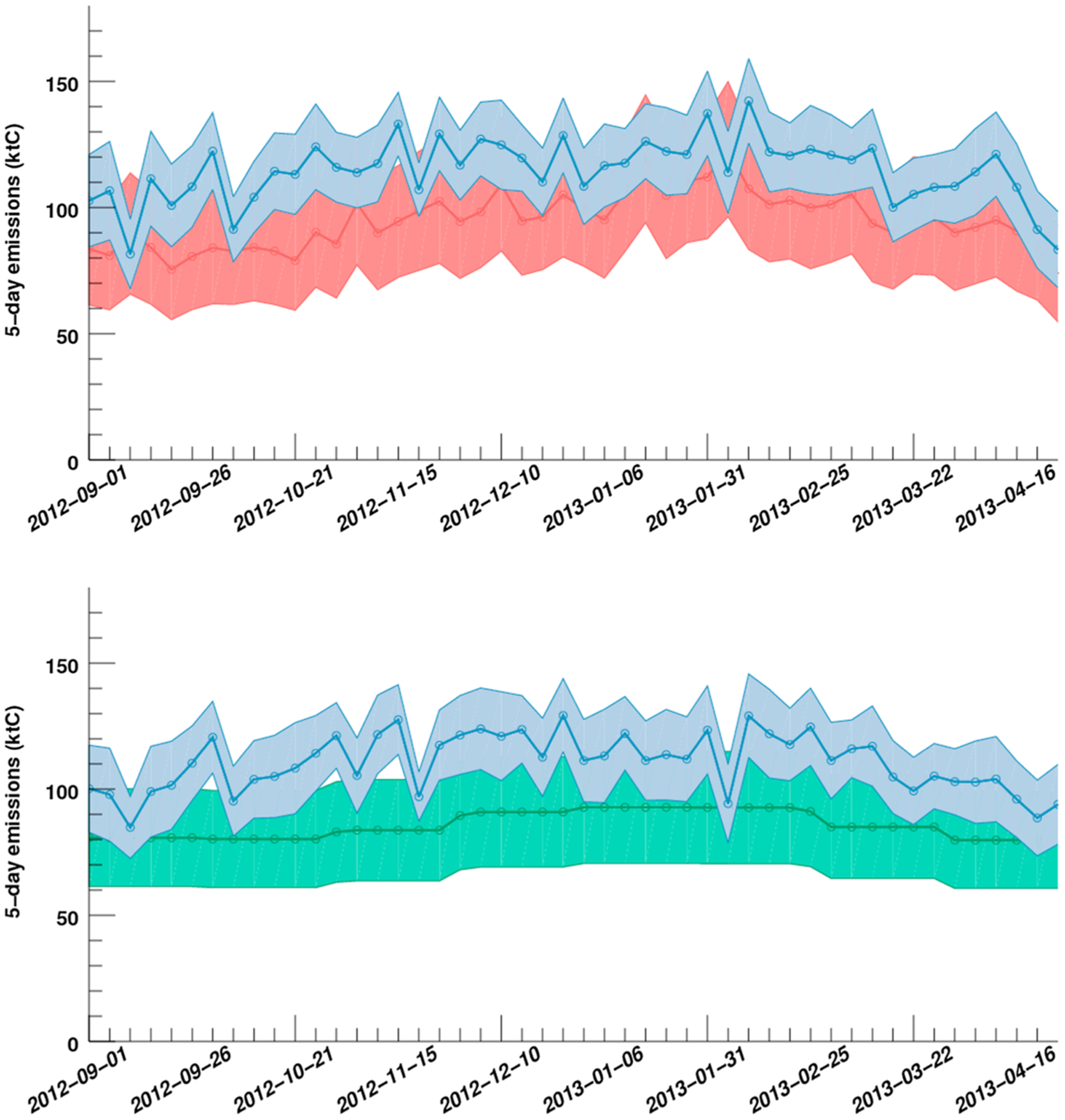
The 5 day inverse emission estimates in ktC for (top) Hestia (in red), (bottom) ODIAC (in green), and their respective inverse emissions (in blue) for the period September 2012–April 2013.

Figure 9.

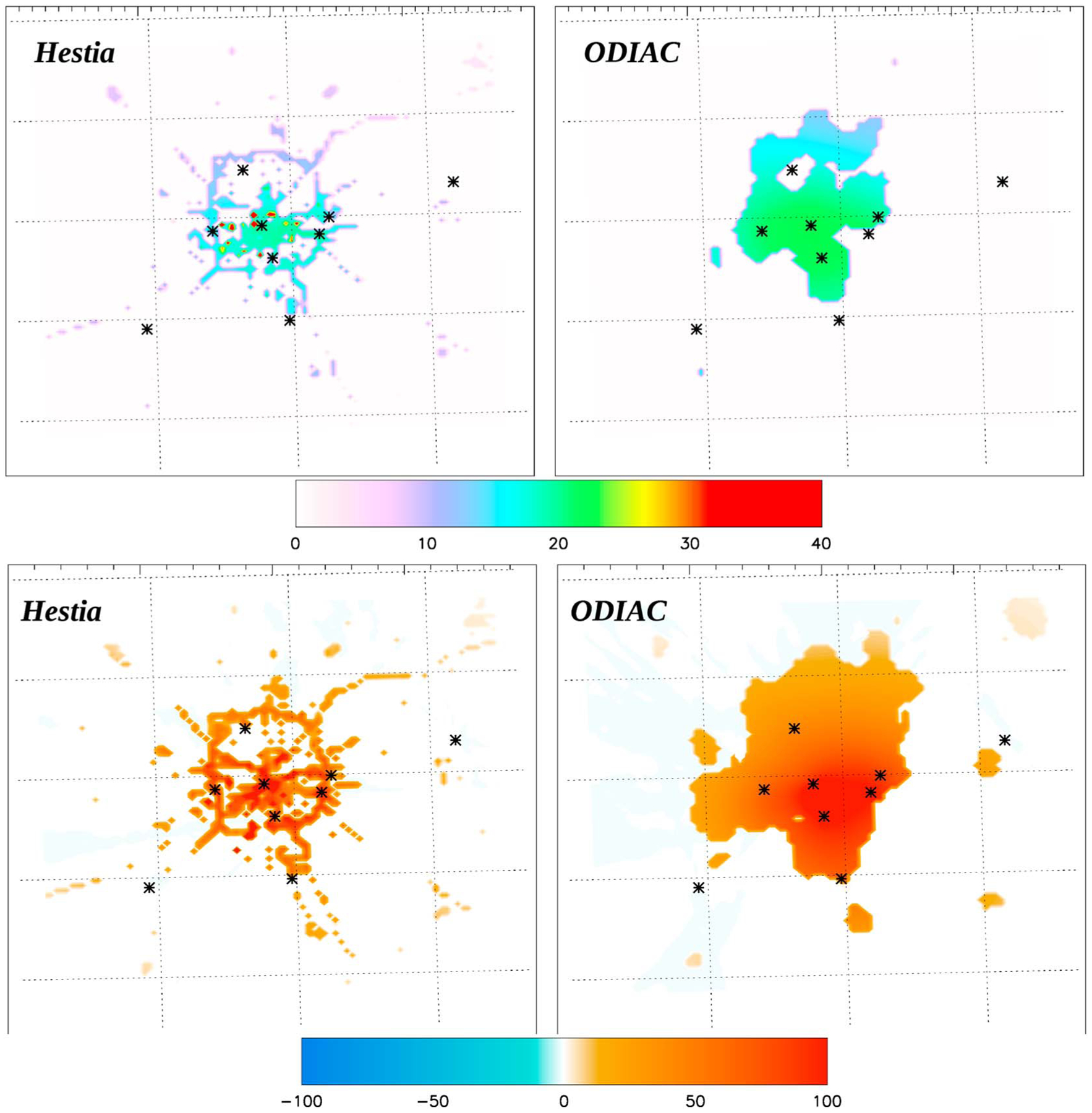
(top row) Error reduction (in %) and relative change in emissions after inversion (in %), i.e., (bottom row) differences between the prior and the posterior emissions, using the Hestia product (left) and ODIAC (right) as prior emissions.

3.3. Impact of a Priori Emissions (ODIAC)

The ODIAC CO₂ emissions were used as a priori emissions for another inversion scenario. Similar to the reference configuration, the a priori errors for this scenario are a function of the a priori mean emissions. In addition, a larger error was used for ODIAC, i.e., 100% at the 1 km pixel level. Figure 8 shows the 5 day emissions from ODIAC (bottom, in green) and the corresponding inverse emissions (bottom, in blue). The temporal variability in the inverse emissions shows some differences compared to the reference case, which suggests that the spatial distribution of the prior emissions and their associated errors can impact the temporal variability of the inverse solution. However, the variability remains similar to the reference case, with lower emissions around the end of 2012 and early 2013. The error reduction presented in Figure 9 (top right) shows a reduction of about 30%, driven primarily by the homogeneous variances and the spatial error correlations, and covering a larger surface extent than the Hestia-based inversion estimate. The emission corrections (bottom right) are similar to the error reduction spatial distribution as would be expected. We present three other cases in section 4.4 and discuss the current limitations due to the absence of well-characterized error structures in the prior emissions. The total emissions are indicated in Table 2 with an a prior total of 4.14 MtC, slightly lower than Hestia, and an inverse estimate of 5.4 MtC, less than inverse estimates using Hestia. The assumptions in the prior errors drive to a large extent the larger emission correction when using ODIAC, considering that ODIAC errors are larger than Hestia.

Table 2.

Prior and Posterior Emissions From the Various Inversion Configurations Referred as the Reference Inversion Case (L = 4 km), a Decrease of 40% in the A Priori Traffic Emissions (Low Traffic), a Decrease of 40% in Emissions From the A Priori Energy Production Sector (Low Utility), Using Large Prior Emission Variances (Large ${\sigma }_B^2$), Using ODIAC as Prior Emissions (ODIAC), Assimilating Only Four Sites Out of Nine (Four Sites (A) and Four Sites (B)), Assimilating Only Four Sites Out of Nine With a Lower Correlation Length of L = 4 km (Four Sites A (L = 4 km) and Four Sites B (L = 4 km)), Varying the Correlation Length L in the Prior Emissions Errors (L = 0 km and L = 4 km), Varying the Definition of the Background Conditions Using the Wind Direction (Wind Model) or the Minimum of the Day (Daily Min), Assimilating Over a 10 Day Time Window Instead of 5 Days (10 Days), Filtering Hourly Observations Using Wind Model Errors (λ.ε), and Varying the Afternoon Window for Observations (20–23 UTC)

Case	L = 12 km	Low Traffic	Low Utility	Large ${\sigma }_B^2$	ODIAC	L = 4 km (RE
Prior	4.56	4.15	4.2	4.56	4.14	4.56
Posterior	5.79	5.16	5.24	6.13	5.35	5.5
Case	Wind model	Daily Min	10 days	λ.ε (& L = 12 km)	20–23 UTC	L = 0 km
Prior	4.56	4.56	4.56	4.56	4.56	4.56
Posterior	5.53	6.	5.88	5.73	5.69	4.73
Case	Four Sites (A)	Four Sites (B)	Four Sites A (L = 4 km)	Four Sites B (L = 4 km)
Prior	4.56	4.56	4.56	4.56
Posterior	5.36	5.52	5.13	5.17

3.4. Transport Model Errors: Scaling of Variances

The atmospheric simulations using the WRF-FDDA modeling system were evaluated using three meteorological surface stations in the Indianapolis area for both the horizontal mean wind speed and direction. The PBL depth evaluation over two months (September–October 2013) was used to select the model physics configuration and quantify the impact of the meteorological assimilation system [Deng et al., 2016]. Over a 2 month period, the simulated PBL depths were compared to observations from a HALO Photonics Doppler lidar (http://www.esrl.noaa.gov/csd/projects/influx/). HALO measures high-resolution vertical velocity variance and aerosol backscatter signal strength profiles that can be used to measure the mixing depth. The systematic model-data mismatch (mean error) is 105 m over the two months, and the mean absolute error is 275 m. These mismatches are relatively small over the 2 month period corresponding to less than 7% of the PBL depth. Considering model performances at higher frequencies (hourly to daily variability), we used surface 10 m wind measurements to quantify the hourly variances as a first-order assessment of model errors. The PBL depth was not used to estimate model errors at the hourly time scale. In urban environments, the spatial gradients in emissions are extremely large compared to natural ecosystems. Therefore, wind errors can affect significantly the spatial distribution of the inverse emissions if a large source is attributed to a near-zero emission area. In this particular case, wind direction and speed are the two most relevant meteorological variables related to transport model errors. We used both of them as proxies in order to propagate model errors into the inversion and avoid source attribution errors.

Wind speed and direction model-data differences were used to scale the hourly errors (i.e., the variances in the observation error covariance matrix R) associated with the modeled mixing ratios. The monthly statistics for both variables are shown in Figure 10 with the quartiles of the mean error, and the median of the mean absolute errors over each month. Whereas the hourly variability (represented by the 25% and 75% quartiles) is large, the monthly medians are low (about 12.2° for wind direction and 0.8 m s⁻¹ for wind speed over the entire period). These results suggest that whereas monthly systematic transport errors are small, the hourly errors can be large. The simulated meteorological conditions can be off by 45° or more for a specific observations. We corrected for hourly errors by introducing the hourly wind errors in R (diagonal elements) as explained in section 2.6.1. When using the scaling of the variances of the observations based on model transport errors, the inverse emissions aggregated over the period decrease slightly compared to a similar configuration using a constant variance and a correlation length L = 12 km with 5.73 MtC instead of 5.79 MtC (cf. Table 2).

Figure 10.

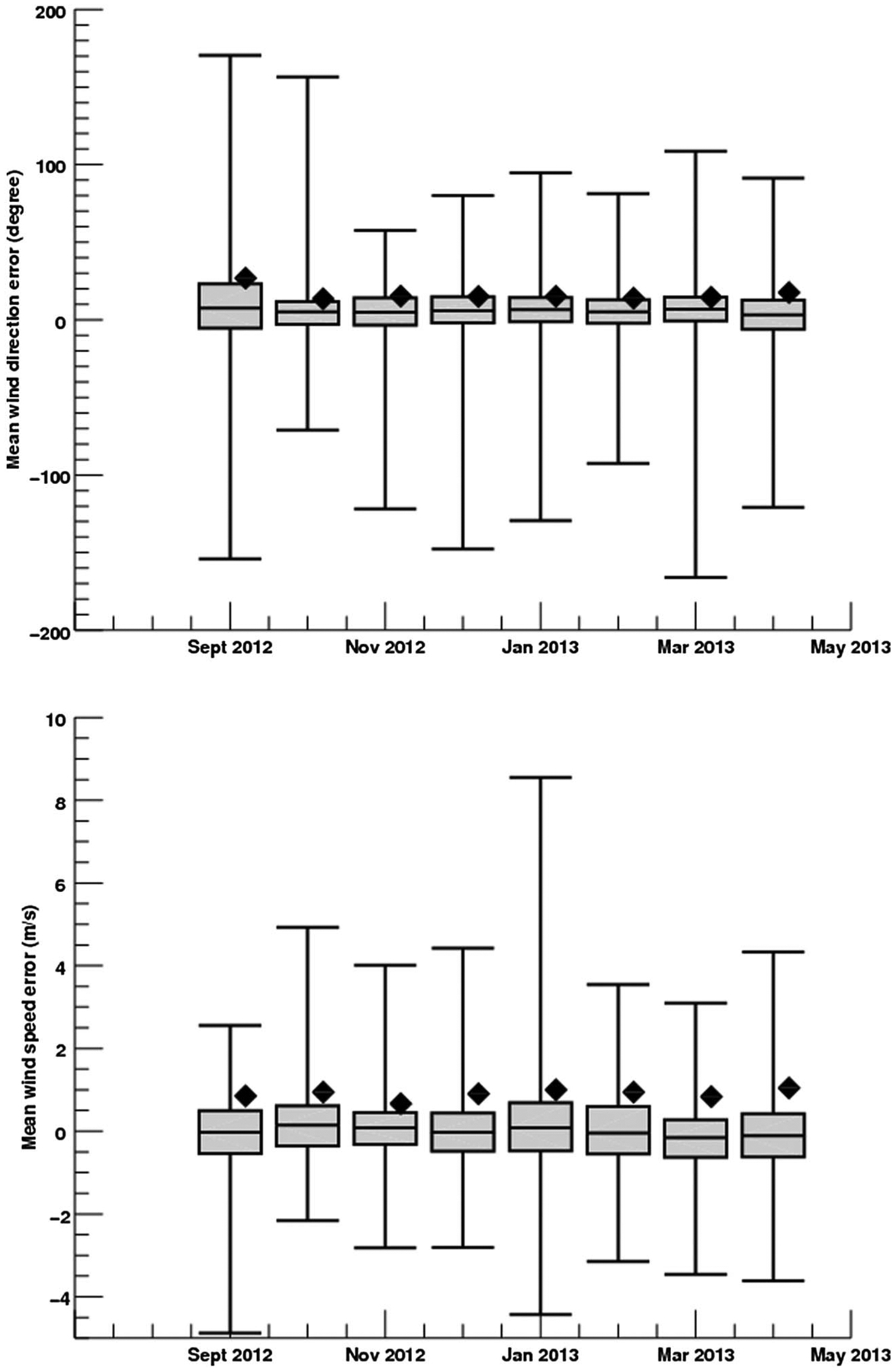
Quartiles of the hourly mean error and mean absolute errors (black diamond) for the (top) horizontal mean wind direction and (bottom) speed at 1 km resolution using measurements from WMO surface stations. Mean wind direction errors were calculated by comparing every available hourly average WMO observation to the WRF-assimilated hourly average wind direction for the corresponding time. The black diamond indicates the average absolute value of this error while the box plot shows the distribution of all of these errors (i.e., 25th and 75th quartiles and range).

Overall, the WRF-FDDA system improves significantly the averaged performance of the WRF atmospheric model compared to the historical mode (i.e., no assimilation of meteorological data), as shown in Rogers et al. [2013]. For this second step, i.e., propagating hourly variances into the inversion system, which is equivalent to filtering the transport model results, the impact is less significant over the entire time periods. Errors associated with specific meteorological events have been considerably reduced by removing specific days. But over the 8 month time period, no bias has been associated with the hourly transport errors. This analysis suggests that long-term model improvements are more important than propagating short-term model deficiencies to avoid misattribution of hourly signals. However, localized biases in wind direction near large point sources could have a significant impact on the modeled mixing ratios for specific towers. We only considered the long-term average over the city and ignored local effects which would require high-resolution modeling of local plumes.

3.5. Sensitivity to the Background Concentrations

We present here the results of the different strategies used to define the background concentrations. Compared to previous regional inversion studies [e.g., Göckede et al., 2010; Lauvaux et al., 2012], the boundary conditions were directly sampled upwind of the tower network, which provides accurate measurements but is potentially less representative than spatially resolved modeled concentrations. However, considering the magnitude of the city enhancement (i.e., about 3 ppm at the downtown site), current regional models would fail to provide sufficient accuracy over the city, as shown by Bréon et al. [2015]. At larger scales (i.e., 10 km), Lauvaux et al. [2012] estimated that the long-term bias from the model atmospheric mole fractions of CarbonTracker [Peters et al., 2007] was around 0.5 ppm, with daily errors from 1 to 7 ppm depending on the season. Here the first strategy defines the background concentrations by using the concentrations at Site 1 at the exact time of the observations. Site 1 is the climatological background site located upwind about 60% of the time (cf. Figure 4). The second strategy uses the optimal site location based on the wind direction (upwind model), as described earlier. Sites 1 and 9 are the two options depending on the wind direction. When one site is not operational, the other is used even if the wind direction is not optimal. Over the 8 month period, Site 1 was operational about 65% of the time, while Site 9 was measuring more than 90% of the time. The last strategy uses the daily minimum at the upwind site, similar to the second strategy. This last option offset potential temporal variations observed in the early afternoon. The risk of sampling low concentrations at later times is not negligible. This strategy is the least likely option for realistically sampling the background. Table 2 shows that the two first strategies produce very similar inverse total emissions with 5.53 MtC (wind model) and 5.5 MtC (L = 4 km), whereas the third strategy increases the total emissions significantly (6 MtC). The daily minimums are selected over the time window 17–22 UTC, with the lowest values being usually observed between 20 and 22 UTC. This technique introduces a positive bias in the inverse solution by selecting late afternoon mixing ratios at the upwind site (i.e., lower concentrations), artificially increasing the emissions over the city. This last method is the least realistic because the lowest concentrations are often observed at the end of the day, which is inconsistent with the advection time of air masses across the city. The first two strategies represent the difference between Site 1 and a combination of Sites 1 and 9 depending on the wind direction. If Site 1 is contaminated by any local signals, the current analysis would not diagnose its impact. An additional site measuring background concentrations will be deployed to test the potential impact of upwind sources.

3.6. Uncertainty Assessment: Ensemble Approach of Inverse Estimates

An ensemble approach of inversion configurations was designed to quantify systematic errors due to the various assumptions made in the urban inversion system. The ensemble consists of two sets of results, the first representing prior-related cases, such as varying the spatial error structures in prior emission errors, and the second set of results related to the observations and their associated uncertainties. The first set of results, presented in Figure 11 (light gray), shows three different correlation lengths L (as described in section 2.5) and a different prior (ODIAC). The impact of various L is clearly the main contributor to the changes in total emissions, even if the fully uncorrelated prior emission scenario seems very unlikely considering the use of data and model parameters in the Hestia and ODIAC products. We discuss the impact of L on the spatial distribution and the total emissions in section 4.4. The use of ODIAC is also important with noticeable differences in the spatial distribution. The second set of results, in gray, includes different assumptions related to the time window for the observations (20–23 UTC instead of 17–22 UTC). We defined the well-mixed conditions based on the temporal variability in the CO₂ mixing ratios and found that the period 20–23 UTC would be more appropriate to avoid a late morning transition in the PBL depth. The results are presented in Table 2. The difference with the reference case remains small which may suggest that the WRF-FDDA model is able to simulate the late PBL growth in the early afternoon. The ensemble includes several other configurations including the use of hourly transport errors based on hourly wind error statistics, and the definition of the background concentrations. The two sets were used to define the quartiles of the ensemble, noted ensemble spread in Figure 11. The ensemble mean is about 5.66 MtC, the second and third quartiles at 0.23 MtC from the mean, the first and fourth quartiles at 0.85 MtC from the mean. The inverse emission using Hestia and ODIAC are statistically different from the 50–75% of the ensemble mean. However, the definition of the correlation length seems to encompass both prior and posterior solutions, especially between no correlation in prior emission errors and the case L = 4 km. We discuss the sensitivity to the prior error structures in section 4.4. The third set of results exploring network design cases and sectoral emissions, in Figure 11 (dark gray), was not included in the ensemble and are discussed later in section 4.3.

Figure 11.

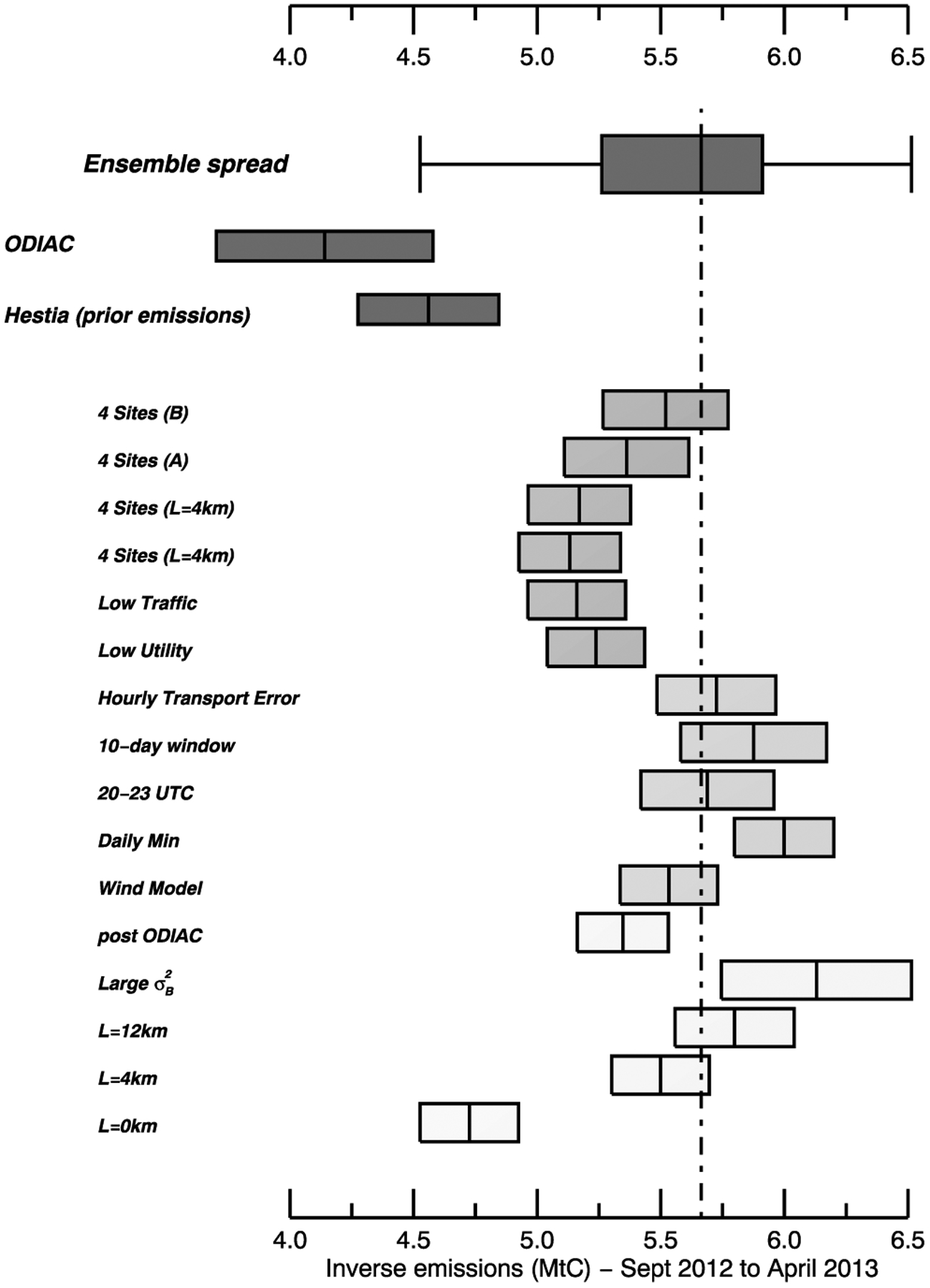
Whole-city inverse emission estimates in MtC over September 2012–April 2013 using the different inverse system configurations and prior emissions.

The time series presented in Figure 12 was created by the same two subsets of configurations (excluding the top six cases presented in Figure 11 in dark gray). In Figure 12, the dark gray zone represents the ensemble spread, whereas the light gray zone includes the ensemble spread and the posterior uncertainties of the cases. Across the ensemble, inverse emissions remain higher than Hestia, similar to the time series of the posterior emissions in the reference configuration (cf. section 3.2). The emissions are significantly larger than the Hestia prior (dashed line) during the first 3 months of the period but more similar to Hestia at the end of December and in early January 2013. An overall agreement is observed in the first months of 2013. Some short-term variations are consistent across the different configurations, e.g., the large increase in late October 2012. The seasonal variations agree between Hestia and the inverse emissions, with a maximum in early February.

Figure 12.

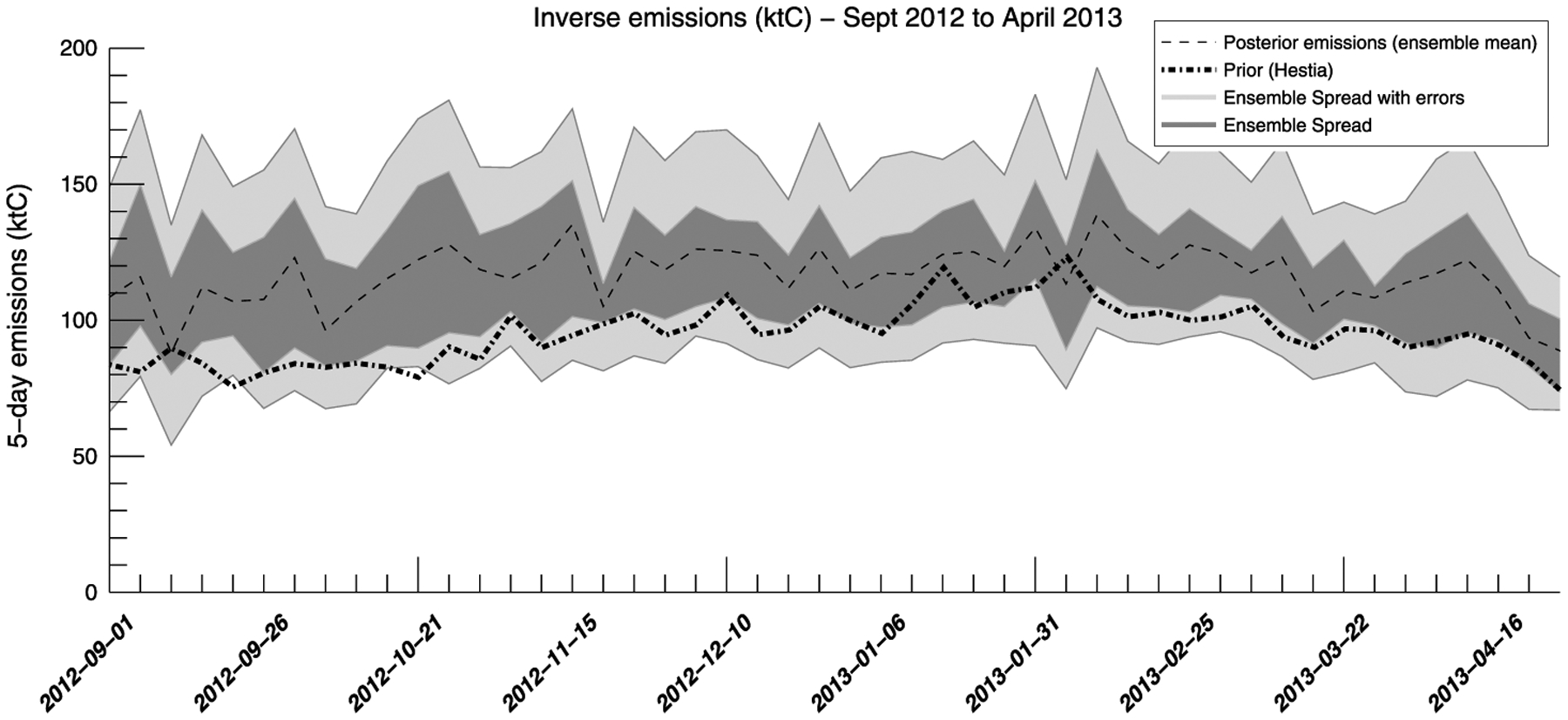
Ensemble of 5 day inverse emission estimates in ktC using multiple configurations, i.e., varying the prior error correlation length, the background definition, or the transport model errors, from September 2012 to April 2013.

4. Discussion

4.1. Impact of Transport Errors at High Resolution

Atmospheric inversion methods able to quantify urban emissions are likely to require the development of high-resolution modeling systems as the scale is potentially reaching the physical limits of the numerical scheme assumptions in mesoscale models, such as the turbulence closure scheme in the PBL. Considering the different numerical schemes used here, the risk of violating the parameterized subgrid scale processes is significant, e.g., the turbulence assumption in stable and neutral conditions with turbulent eddies smaller than the model resolution. At short distances, the plume structures centered on isolated sources would not match the well-mixed assumptions of the model. For this reason, we have avoided the nighttime periods, which implies that we have almost no observations to constrain the nighttime emissions. More accurate representation of the high-resolution atmospheric dynamics is required when trying to constrain nocturnal emissions. This limitation suggests that additional corrections may have further modified the prior emissions. Large Eddy Simulation mode may provide more realistic physical parameterizations to represent nocturnal small-scale motions near the surface. In addition to physical limits of the schemes, the local atmospheric dynamics is influenced by large spatial gradients in the surface energy fluxes. Under these conditions, sources of systematic errors in the transport model are numerous and difficult to overcome. The use of a meteorological assimilation system, i.e., WRF-FDDA, improves the model performances [Rogers et al., 2013] but large discrepancies can still affect the wind direction and speed (cf. Figure 10). Additional evaluation of the near-field atmospheric dynamics is still required to quantify the modeling performance and the representation of fine-scale structures, mostly visible around the major sources at short distances. Especially under low wind speed conditions, representation errors could significantly impair our ability to constrain the urban emissions, introducing biases in our source estimates. Future studies of the transport of near-field emissions will provide critical information to filter out data or inflate errors under various stability conditions. Here we improved our initial WRF modeling system with the FDDA methodology and propagated errors into the inversion scheme. We evaluated the impact of the spatial structures in the transport model errors through the use of correlation lengths, similar to Lauvaux et al. [2009b] who diagnosed structures from a small ensemble of perturbed simulations.

In this study, the correlation length scale was applied to the observation error covariance matrix with an exponentially decaying model. Considering the use of our high-resolution WRF-FDDA simulation over a highly heterogeneous landscape, we reduced the length scale from 30 km (in the original study) to 10 km to represent the potentially smaller spatial structures in transport errors. When introducing these covariances, the posterior emissions end up at 4.93 MtC, with a smaller correction to the prior emissions compared to the reference inversion, as expected when increasing the errors associated with observations. This inversion shows the importance of potential error structures at fine scales. No temporal correlation was introduced due to the lack of information at these scales.

4.2. Network Design: Impact of Tower Locations and Heights

4.2.1. Network Design of Surface Towers

The deployment of tower networks for emission monitoring highly depends on the objectives of the study. We propose here to discuss the monitoring of the emissions from the entire urban area and the mapping of emissions at higher resolutions. For the first objective, we compare two subnetworks, presented in Table 2 as networks A and B, which correspond to two optimal network configurations with one upwind site, one downwind site, and three centrally located towers. We also used two different correlation lengths (L = 4 km and L = 12 km) in the prior error statistics as this parameter can significantly impact the inverse solution (cf. section 4.4). By assuming a larger correlation length (L = 12 km), the two networks produce fairly different total emissions with 5.36 MtC and 5.52 MtC, which are further decreased with lower L (respectively 5.13 MtC and 5.17 MtC). Figure 13 shows that the main difference between the two networks (left column compared to the right column) originates from the magnitude of the correction in the center of the city and a short section of the beltway (SW and N sections) which shifted from a negative correction (lower left panel) to a positive correction (lower right panel). The impact of the correlation length (4 km versus 12 km) is similar to the results using the entire network (cf. Figure 15), confirming that prior emission error structures do not only alter the total emissions but also the location of the sources, as discussed in section 4.4. Overall, the tower deployment is highly dependent on the assumptions made in the prior emission errors. If large correlations are to be true, a network of five towers would suffice to constrain the urban emissions. But this assumption is highly uncertain, meaning that network design will require a better understanding and a better quantification of prior error structures before any robust conclusions can be made.

Figure 13.

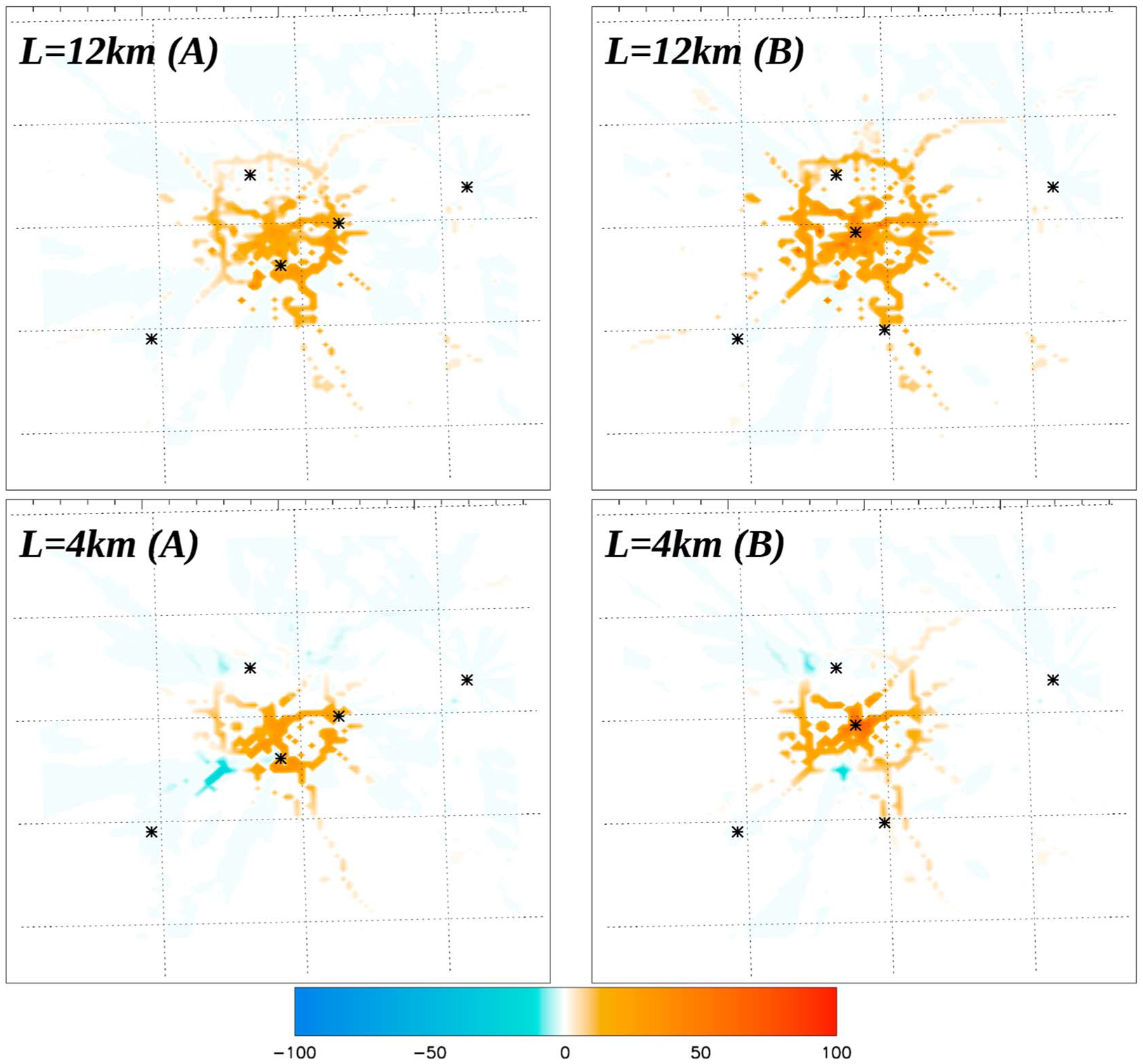
Emission correction (in %), corresponding to the ratio of emission change between the prior and the posterior emissions, for two different subnetworks. Both networks include four tower locations selected for both maximum enhancements over the city and background sampling. Both inversions were performed over the period September 2012–April 2013, using the reference configuration.

Figure 15.

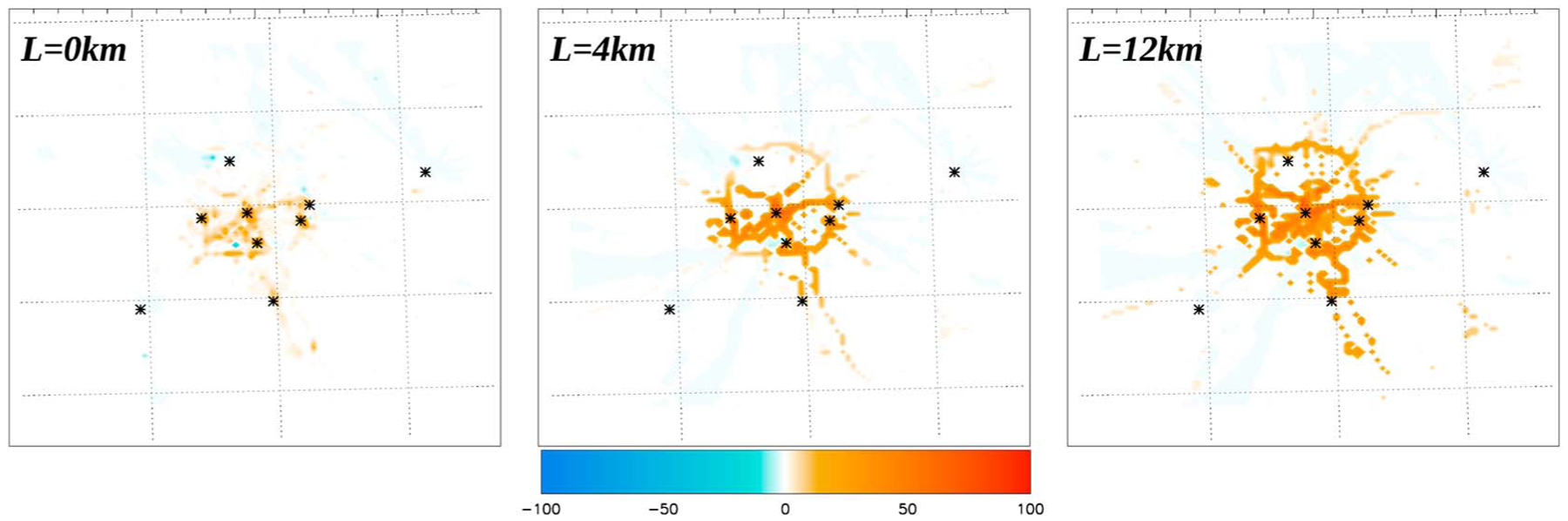
Relative change in emissions after inversion (in %) using no correlation length (left), a correlation length of 4km within the urban area (middle), and 12km within the urban area (right) in the prior emission error covariances

4.2.2. Sampling Heights: Sensitivity to Surface Emissions

The various GHG analyzers deployed around the Indianapolis area are all on tower structures, with four instruments at 120 m or more, four on 60–90 m towers, and four at about 40 m high. The sampling height remains a critical parameter in the mesoscale models, with large vertical gradients in stable to neutral stability conditions that are difficult to simulate correctly. In well-mixed conditions, 40 m towers may still be affected by vertical gradients in the surface atmospheric layer and very likely to suffer from large model errors. The atmospheric surface layer (ASL) is not explicitly simulated in mesoscale systems suggesting that even higher vertical resolution is unlikely to improve the vertical mixing near the surface. In Figure 14, we show the influence functions for the nine towers used in this study. Towers 1 and 9, located outside of the city to the west and the east of the network respectively, have a smaller impact on the surface emissions. These two towers are the tallest structures instrumented for the experiment, at 136 m and 121 m high. The WRF-LPDM footprints represent the increased sensitivity to the surface when the stability conditions are not convective. Because the inversion period covers winter, observations in the afternoon are still affected by vertical gradients in CO₂ despite selecting the period of maximum solar radiation. At these low elevations above ground level, vertical gradients can be observed. Further studies are needed to estimate the capability of mesoscale models to simulate correctly the vertical gradients in the ASL during well-mixed, stable, and neutral periods.

Figure 14.

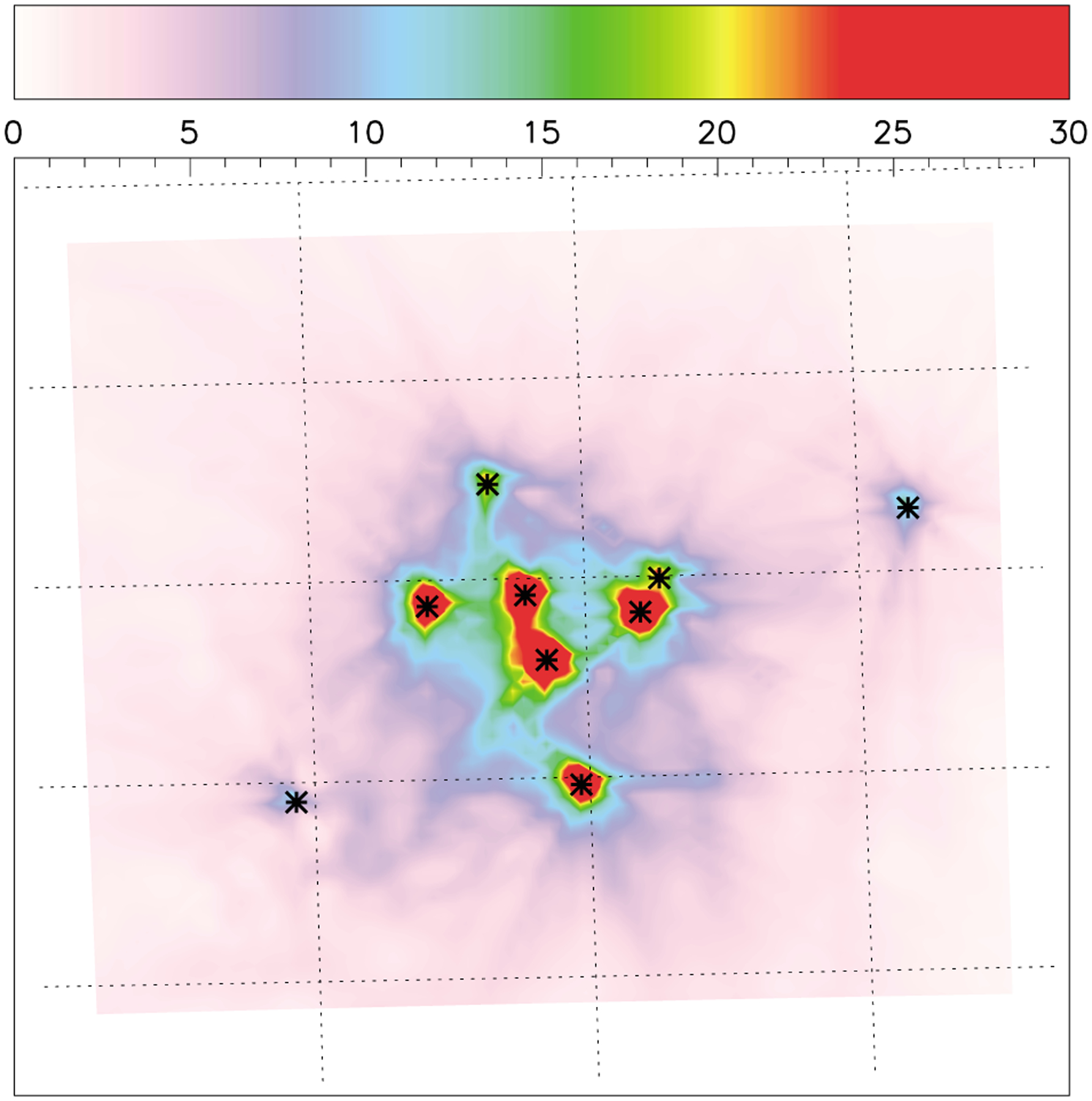
Influence functions in ppm/(gC m⁻² h⁻¹) for the nine instrumented INFLUX towers aggregated over the 8-month period. Sites 1 and 9 show the lowest sensitivity to the surface primarily due to higher sampling heights under low vertical mixing conditions. Additional effects on shorter tower sensitivity due to the proximity of the sources is not considered here.

4.3. Biogenic and Sectoral Emission Detection and Quantification

In the current study, the emissions over Indianapolis metropolitan area were inverted using the total CO₂ concentrations, i.e., without any consideration for the underlying emission processes. In section 3.1, the sectoral contribution is presented in the simulated mixing ratios, using the forward simulations from the WRF model. To investigate the potential of detection of the major economical sectors in the inversion, i.e., traffic and energy production, we performed two additional inversions decreasing the emissions from these two sectors, by 40% for the utility sector and by 20% for the traffic sector. These values are significantly larger than any reasonable change in emissions over a year. This sensitivity test represents a long-term change, e.g., decadal, which would require the implementation of major emission mitigation policies. We retrieved the total CO₂ emissions but the attribution of the innovations to the different sectors is not possible with the current system. Only the total inverse CO₂ emissions are produced by the inversion. When applying these changes, the total prior emissions decreased from 4.56 MtC originally to 4.2 MtC and 4.15 MtC (cf. Table 2), respectively. The inversion is able to retrieve most of the artificial decrease in both sectors, ending at 5.24 MtC and 5.16 MtC, respectively. The partial recovery of the initial sector decrease is also limited by the scaling of the variances. The net emissions in the prior have decreased significantly and their associated prior errors as well by construction. For the utility sector, the inverse solution distributed the correction according to the spatial structures in prior emission errors (not shown here), failing to identify precisely where the power plants were located. When assuming no spatial correlation in prior emission errors, the main emission correction was located in the southwest quadrant of town, around the main major power plant (Harding Street) which reinforces the idea that the inversion could detect major changes across the city. For the low traffic scenario, the spatial pattern of the emission correction matches the beltway, but this spatial pattern may be primarily constrained by the prescribed variances associated with high traffic emissions. This first-order assessment of emission detection suggests that the inversion system is able to retrieve major changes in sector emissions assuming well-known prior errors. Additional investigations are needed to define the exact potential of the system for both trend detection in specific sectors and spatial variability. The contribution from biogenic fluxes was avoided in this study by inverting for the emissions during the dormant season. Soil respiration and other biogenic sources are expected to contribute to about 5% of the total emissions over that period, as shown in Turnbull et al. [2015]. The inversion system presented here lacks a biogenic flux prior and the ability to assimilate flask measurements which could help produce year-round emission estimates, separating biogenic fluxes from fossil fuel emissions. Future studies will need to address the possible contamination of background sites due to the presence of vegetation and the advection of the background air over the city while affected by horizontal and vertical diffusion. In this study, we limit our analyses and conclusions to the wintertime only to provide a first estimate of total CO₂ urban emissions in the absence of any significant natural sinks.

4.4. Impact of Prior Error Statistics on Inverse Emissions

The definition of the prior emission errors remains subjective at this point, with no existing rigorous quantification of emission errors at high resolutions. We used the difference between several existing emission products (i.e., Hestia and ODIAC) at the pixel level to define the prior error variances, equivalent to 25% of the net emissions aggregated over the domain. At the pixel level, this corresponds to an uncorrelated error of about 60% for Hestia. We increased this error to 200% to generate a purely data-driven solution, with a low correlation length of 4 km. The inverse emissions aggregated over the domain are equal to 5.57 MtC compared to 5.5 MtC over the same time period for the reference case. The two solutions remain similar despite the very large prior emissions error. This result confirms that the total prior errors do not overconstrain the inverse solution. But solving for spatial structures across the area requires additional information related to the spatial structures of the prior emissions errors Saide et al. [2011]. Methodologies to define the error structures exist [e.g., Wu et al., 2013], assuming that simple parameters can be optimized, such as a correlation length in an exponentially decaying scenario. Here the use of correlation length over the urban area increases the complexity of such a model. But this approach was assumed to better represent the spatial coherence of incorrect emission factors for the mobility sector or any systematic errors affecting the underlying models used in the Hestia emission product. A simpler model would ignore the urban area and potentially propagate corrections to nonurban areas. In Figure 15, we show the difference between the inverse emissions and the prior, using three different correlation lengths, i.e., L = 0 km (left), L = 4 km (middle), and L=12 km (right).The spatial distributions vary from localized adjustments around the sites (for L = 0 km), to an overall adjustment of the road emissions when assuming large correlations (L = 12 km). Clearly, the spatial distribution of the flux corrections is driven by the prior emission error structures. In addition, the total emissions vary from a minor correction (4.73 MtC with L = 0 km), to more important corrections (5.5 MtC and 5.79 MtC with L = 4 km and L = 12 km) due to the increase in the prior errors through the increase of the error covariances. Therefore, the quantification of prior emission errors and their associated structures is a critical component of the information. The correlation length impacts the total inverse solution and the spatial distribution of the solution, which relates to the sectoral attribution problem, as the structures dictate the distribution over different areas of the city. One could argue that no correlation in the prior emission errors may be an extreme case, considering that the underlying models used in the emission products such as Hestia combine emission factors with their input data. Therefore, spatial correlations would be likely to affect the emissions for specific combustion processes but not across the city as whole. Knowing that CO₂ emissions combine several sectors of activity which are unrelated for the most part, spatial structures in emission errors may be spatially limited once combined into total CO₂ prior emissions. For these reasons, future studies will need to address careful this key parameter in the inversion system. Similar work has been accomplished at the regional scales, using optimization methods such as Wu et al. [2013].

5. Conclusions

This study presents a high-resolution inversion system based on a Four-Dimensional Data Assimilation meteorological system to simulate the atmospheric dynamics at 1 km resolution over the city of Indianapolis. The inverse emissions were evaluated over 8 months (i.e., September 2012 to April 2013) using two different a priori emissions, Hestia, a state-of-the-art building-level emission product and ODIAC, a space-based emission product. The reference inversion produced whole city inverse emissions of 5.5 MtC, about 20% higher than the prior emissions from Hestia (4.6 MtC). Total CO₂ emissions for the Indianapolis urban area based on the ensemble mean and quartiles are 5.26–5.91 MtC, i.e., a statistically significant difference compared to the two prior total emissions of 4.1 to 4.5 MtC. Biogenic fluxes due to soil respiration which are not accounted for in the prior CO₂ emissions could represent about 5% of the total city signals based on Δ¹⁴CO₂ measurements, or about a quarter of the corrections by the inversion. Single configurations of the inversion system produced lower posterior uncertainties than the ensemble spread, reflecting the uncertainties associated with the various assumptions. Transport model errors were estimated from the WRF-FDDA system and introduced in the inversion system through the use of hourly variances adjusted according to the hourly model performances. The upwind conditions were prescribed by using two towers located at about 20 to 30 km from the city, with an hourly site selection based on wind observations. However, several parameters of the inverse system remain underconstrained, at the origin of the ensemble variability. In particular, spatial structures in prior emission errors, mostly undetermined, affect significantly the spatial pattern in the inverse solution, as well as the carbon budget over the urban area. We therefore conclude that atmospheric inversions are able to constrain the carbon budget of the whole city to an absolute uncertainty of about 25%, but additional information on prior emissions and more specifically about their associated error structures are required if atmospheric inversion systems are built to determine the spatial structures of urban greenhouse gas emissions at high resolutions.

Key Points:

• High resolution bottom-up and top-down fossil fuel emissions agree within 20% at the city scale

• Inverse urban emissions and GHG boundary inflow are well constrained by dense tower observation network

• Undefined error structures in prior emissions impact significantly the source attribution capability at high resolution