Net primary productivity estimates and environmental variables in the Arctic Ocean: An assessment of coupled physical-biogeochemical models

Abstract

The relative skill of 21 regional and global biogeochemical models was assessed in terms of how well the models reproduced observed net primary productivity (NPP) and environmental variables such as nitrate concentration (NO₃), mixed layer depth (MLD), euphotic layer depth (Z_eu), and sea ice concentration, by comparing results against a newly updated, quality-controlled in situ NPP database for the Arctic Ocean (1959–2011). The models broadly captured the spatial features of integrated NPP (iNPP) on a pan-Arctic scale. Most models underestimated iNPP by varying degrees in spite of overestimating surface NO₃, MLD, and Z_eu throughout the regions. Among the models, iNPP exhibited little difference over sea ice condition (ice-free versus ice-influenced) and bottom depth (shelf versus deep ocean). The models performed relatively well for the most recent decade and toward the end of Arctic summer. In the Barents and Greenland Seas, regional model skill of surface NO₃ was best associated with how well MLD was reproduced. Regionally, iNPP was relatively well simulated in the Beaufort Sea and the central Arctic Basin, where in situ NPP is low and nutrients are mostly depleted. Models performed less well at simulating iNPP in the Greenland and Chukchi Seas, despite the higher model skill in MLD and sea ice concentration, respectively. iNPP model skill was constrained by different factors in different Arctic Ocean regions. Our study suggests that better parameterization of biological and ecological microbial rates (phytoplankton growth and zooplankton grazing) are needed for improved Arctic Ocean biogeochemical modeling.

1. Introduction

Primary production provides the energy that fuels the Arctic Ocean ecosystem. However, given the regional heterogeneity, the dramatic seasonal changes, and the limited access due to harsh environments, it is difficult to obtain a comprehensive picture of the Arctic Ocean’s in situ primary production regime. Models of biogeochemical carbon cycling at various spatial/temporal scales also rely on quantification of the first level of the marine food chain—phytoplankton, their biomass, and production. Current projected changes in future climate and responses of the Arctic Ocean may indicate either (i) an increase in net primary production (NPP) due to enhanced light availability as a direct result of sea ice and snow cover loss as well as increased nutrient fluxes from sub-Arctic waters, bottom water by vertical mixing and greater upwelling as sea ice extent decreases, as well as nutrient input by Arctic rivers and terrestrial ecosystems as temperature rises [Slagstad et al., 2015], or (ii) a decrease of NPP due to nutrient limited conditions with enhanced stratification (due to ice melt, freshwater inflow, and thermal warming), increased denitrification, and decreased light availability (due to more clouds and higher water turbidity from permafrost melt, beach erosion, riverine input, and wind-driven resuspension) [Wassmann and Reigstad, 2011]. But, not all drivers listed above are commonly incorporated in numerical models that are widely used for evaluating future changes in NPP over the entire Arctic region today and under a changing climate.

There are two main types of numerical models that have been applied to estimate NPP in the Arctic Ocean: satellite-based diagnostic models (reviewed in Babin et al. [2015] and International Ocean Colour Coordinating Group (IOCCG) [2015], and assessed in Lee et al. [2015]) and process-based coupled dynamic physical-biological models run in either retrospective or predictive modes. This latter class of models has been applied to improve our understanding of the Arctic Ocean carbon sinks and sources using regional [e.g., Deal et al., 2011; Manizza et al., 2013; Slagstad et al., 2015; Zhang et al., 2010c,2015] to global [e.g., Popova et al., 2010; Vancoppenolle et al., 2013] ice-ocean-atmosphere carbon cycle simulations. In general, the magnitude, vertical extent, and seasonal evolution of NPP are simulated largely as a function of temperature, light, nutrient availability, and physical forcing (advection, mixing, and stratification) as well as associated planktonic and sea ice food web processes. The complexity of the models differs not only in the number of processes/drivers included in model simulations but also in their degree of interactive coupling among oceanic, sea ice, atmospheric, and/or hydrologic processes as well as in their biogeochemical component and spatial resolution; on one end, this allows for year-round simulations in ice-free and ice-covered waters and for detailed comparisons with satellite-derived observations at certain times and places. At the other end, certain models will lack ecosystem, biogeochemical and physical (i.e., freshwater inputs, sea ice concentration/extent/thickness, and stratification) parameterizations and feedbacks important to the Arctic Ocean, which in turn impact controls on NPP. For instance, regional models may have more flexibility to include processes that are specific to the Arctic Ocean, but are limited by the boundary conditions. Global models, on the other hand, are independent of the boundary conditions, but are often lacking in regional complexity in representation of Arctic processes.

Previous primary production intercomparison exercises matched in situ carbon uptake rates with NPP estimated mostly from ocean color models (OCMs) [e.g., Balch et al., 1992; Campbell et al., 2002; Saba et al., 2011] and, more recently, from some coupled biogeochemical ocean general circulation models (BOGCMs) [Carr et al., 2006; Friedrichs et al., 2009; Saba et al., 2010] in various regions of the ocean except the Arctic Ocean. Popova et al. [2012] and Vancoppenolle et al. [2013] reported the results from various BOGCMs and Earth System Models (ESMs) that were compared for the Arctic domain against satellite-derived NPP albeit with known issues. These latter two studies found reasonable agreement on the main features of pan-Arctic annual NPP and highlighted the disagreement among the models with respect to nutrient availability and source, as well as which factor, light or nutrients, controls the present-day and future Arctic Ocean NPP. Furthermore, recent individual model studies emphasized the need to accurately parameterize specific processes to adequately represent NPP within the Arctic Ocean system, such as sea ice physics and biogeochemistry [e.g., Jin et al., 2012, 2016; Tedesco and Vichi, 2014], circulation patterns [e.g., Popova et al., 2013], and secondary production [Slagstad et al., 2015].

Models that estimate Arctic Ocean NPP have previously been assessed using annual mean and seasonal variations in surface nutrients from the World Ocean Atlas and, as indicated above, ocean color-derived NPP. Babin et al. [2015] and IOCCG [2015] extensively review the strengths (pan-Arctic, weekly, or monthly regular coverage) and limitations (time and space composite imagery; sea ice, cloud/fog; seasonal darkness; bio-optical and physiological considerations; mostly surface observations) of remotely sensed data in this seasonally dark and ice-covered region. More recently, Lee et al. [2015] assessed the skill of 32 OCMs to reproduce the observed NPP across the Arctic Ocean. Overall, OCMs were most sensitive to uncertainties in surface chlorophyll-a concentration (hereafter, chlorophyll), generally performing better with in situ chlorophyll than with ocean color-derived values. Regardless of type or complexity, most OCMs were not able to fully reproduce the variability of in situ NPP, whereas some of them exhibited almost no bias. As a group, OCMs overestimated mean NPP, however, this was partly offset by some models underestimating NPP when a subsurface chlorophyll maximum was present. OCMs performed better reproducing NPP values when using Arctic-relevant parameter values.

Sampling difficulties and the resulting biogeochemical data scarcity in the Arctic Ocean affect vertical, horizontal, and temporal interpolations frequently used for BOGCM and ESM validation and skill assessment, such that only basin-wide, temporally averaged (i.e., annual) data are often used to evaluate their NPP estimates. While sampling irregularity in the Arctic Ocean, even in summer, has a strong effect on the spatio-temporal distribution of in situ biogeochemical data, it is the increasing availability of such data in recent years that currently makes the assessment of BOGCM and ESM simulated NPP at smaller and shorter scales in the Arctic Ocean possible. We have assembled a pan-Arctic, multidecadal data set of in situ NPP and nitrate (NO₃) vertical profiles as well as associated biophysical parameters that allow model skill to be assessed, especially at regional scales.

NPP observations are herein compared against an available ensemble of physical-biological simulations presently being applied for a range of global and Arctic-specific carbon and ecosystem questions (Table 1). While model performance of multiple models should ideally be assessed using simulations generated with identical forcing, initialization, and boundary conditions, such restrictions would severely limit the number of models considered and fail to sample the variety of present modeling systems. Thus in this study, in an opportunistic approach, 21 model simulations were analyzed within the Arctic domain, without forcing the participants to use the same setup, with the aim of elucidating large-scale similarities and contrasts in NPP and associated drivers. Model skill of existing simulations was quantified by assessing modeled integrated NPP (hereafter, iNPP), vertical profiles of NPP and NO₃, euphotic layer depth (Z_eu; defined here as the depth at which photosynthetically available radiation (PAR) is 1% of the surface value), mixed layer depth (MLD), and sea ice concentration against in situ or climatological (only MLD) data. The participating BOGCMs and ESMs include biogeochemical and ecosystem modules of varying complexity that may or may not have been optimized for the Arctic Ocean. Only Models 9 and 14 include an ice algae component, but ice algal production was not included in NPP for this study. Spatial resolution also varies among the participating models. Despite these caveats, BOGCMs and ESMs are the only tools that account for complex processes of land-ocean-atmosphere-sea ice responses to future climate change in the Arctic Ocean. Their steady improvement requires a regular assessment of their skill to reproduce observations. Here, we report the first intercomparison study of NPP in the Arctic Ocean, based on 21 simulations from various BOGCMs and ESMs, against in situ measurements. It is a companion study to our earlier assessment of NPP estimates derived from OCMs [Lee et al., 2015].

Table 1.

A Brief Description of Participating Models and Output Variables

												Sea Ice Biology/River		Model Output Variables
Model	Name	Domain/Type	Horizontal Resolution (km)	Vertical Levels	Vertical Mixing	Atmospheric Forcing	Sea Ice	Nutrients	# of Phyto plankton Classes	# of Zooplankton Classes	# of Detritus	Nutrients/Pelagic-Benthic Coupling	Simulation Period	Integrated NPP	NPP (0–100 m)	no3 (0–100 m)	Zeu (1%)	Sea Ice	MLD
1	HYCOM-NORWECOM	Regional	10–16.5	28	GISS	ERA-Interim reanalysis	Hunke and Dukowicz [1997]	N, P, Si	2	2	3	N/Y/N	1997–2011	•	•	•	•	•	•
2	NEMO-PISCES	Global	10–16	75	TKE	ERA-Interim reanalysis	LIM2	N, P, Si, Fe	2	2	3	N/Y/Y	1998–2014	•	•	•	•	•
3	PlankTOM5.3	Global	0.13–192	30	TKE	NCEP reanalysis	LIM2	N, Si, Fe	3	2	7	N/Y/N	1956–2013	•	•	•		•
4	PlankTOMIO	Global	0.13–192	30	TKE	NCEP reanalysis	LIM2	N, P, Si, Fe	6	3	7	N/Y/N	1948–2013	•	•	•		•
5	MOM-SIS-COBALT	Global	25–111	50	KPP	CORE2	GFDL-SIS	N, P, Si, Fe	3	3	1	N/Y/Y	1948–2007	•	•	•			•
6	MOM-S IS-TOPAZ	Global	25–111	50	KPP	CORE2	GFDL-SIS	N, P, Si, Fe, NH4	3	1	7	N/Y/Y	1948–2007	•	•	•	•	•	•
7	SINMOD	Regional	20	25	Based on the Richardson Number	ERA-1 nterim reanalysis	Hibler [197]; Hunke and Dukowicz [1997]	N, Si	2	2	2	N/Y/Y	1979–2014	•	•	•	•	•	•
8	NorESM-OC	Global	18–65	53	TKE	CORE2	CICE4	N, P, Si, Fe	1	1	3	N/N//N	1850–2012	•	•	•		•	•
9	BIOMAS	Regional	3–70	30	KPP	NCEP reanalysis	Thickness and enthalpy distribution	N, Si	2	3	2	Y/N/N	1971–2015	•	•	•		•	•
10	NEMO-MEDUSA	Global	6.8–15.4	64	TKE	DFS4.1 reanalysis	LIM2	N, Si, Fe	2	2	1	N/N/N	1988–2006	•	•	•		•	•
11	NEMO-ERSEM (xhonp)	Global	25–68	75	TKE	CORE2	CICE	N, P, Si, Fe	4	3	6	N/N/Y	1890–2007	•	•	•	•	•	•
12	NEMO-ERSEM (xhonc)	Global	25–68	75	TKE	CORE2	CICE	N, P, Si, Fe	4	3	6	N/N/Y	1890–2007	•	•	•	•	•	•
13	PELAGOS	Global	120–160	30	TKE	ERA-Interim reanalysis	LIM2	N, P, Si, Fe	3	3	1	N/Y/N	1988–2010	•	•	•	•	•	•
14	IARC POP-CICE	Global	30–45	40	KPP	CORE2	CICE 5.0	N, P, Si, Fe	3	1	1	Y/N/N	1958–2009	•	•	•		•	•
15	NEMO/PISCES	Global	63–131	31	TKE	DFS5.2 reanalysis	LIM2	N, P, Si, Fe	2	2	2	N/Y/Y	1979–2010	•	•		•	•
16	NEMO/PISCES	Global	32	46	TKE	CORE2 + NCEP/DOE AMIP-II	LIM3	N, P, Si, Fe	2	2	2	N/Y/N	2002–2011	•	•			•
17	NEMO-GELATO-PISCES	Global	40–70	42	TKE	NCEP reanalysis	GELAT05	N, P, Si, Fe	2	2	2	N/Y/Y	1948–2013	•	•	•	•	•	•
18	MITgcm	Regional	18	50	KPP	JRA25 reanalysis	Hibler [1979]	N	2	2	2	N/Y/N	1979–2012	•	•	•		•	•
19	NorESM	Global/ESM	18–65	53	TKE	CMIP5 + RCP8.5	CICE4	N, P, Si, Fe	1	1	3	N/N/N	1850–2012	•	•	•		•	•
20	GISS-E2-R-CC	Global/ESM	100–125	32	KPP	20th century climate forcing	Sea ice modelE2	N, Si, Fe	4	1	3	N/N/N	1850–2010	•		•		•	•
21	MPI-ESM (MPIOM-HAMOCC)	Global/ESM	15–65	40	Pacanowski and Philander [1981] +wind mixing	CMIP5 + RCP4.5	Notz et al. [2013]	N, P, Si, Fe	1	1	3	N/N/Y	1850–2012	•

2. Participating Models

A total of 21 models (Table 1) participated in this exercise: 18 of these were coupled ocean-ice-ecosystem models (4 Arctic regional and 14 global) and 3 were ESMs. The participating models have a horizontal resolution between 0.1 and 200 km with 25–75 vertical levels; they used various vertical mixing schemes, atmospheric forcing, and sea ice physics (Table 1). Only Model 9 assimilated sea ice concentration and sea surface temperature. In terms of biogeochemistry, each model has between one and six phytoplankton and zooplankton groups. Models use nitrogen (N) or carbon (C) as currency in their simulations, while phosphorus (P), silica (Si), and/or iron (Fe) are included as state variables in some cases as well. Some models additionally include sea ice biology, riverine nutrients, and/or benthic-pelagic coupling. A brief description of the models can be found in Appendix A.

3. Data and Methods

3.1. In Situ Net Primary Productivity (NPP; 1959–2011)

We built a quality-controlled in situ NPP (mgC m⁻³ d⁻¹) database over five decades (1959–2011) that were sampled mostly in the Chukchi, Beaufort, and Barents Seas as well as the Canadian Archipelago (Figure 1). This database consisted of the ARCSS-PP data set [Matrai et al., 2013], available at NOAA/National Oceanographic Data Center (NODC) (http://www.nodc.noaa.gov/cgi-bin/OAS/prd/accession/details/63065), and more recent international polar research activities such as CASES (2004) [Brugel et al., 2009; Tremblay et al., 2011], ArcticNet (2005–2008 and 2010–2011) (M. Gosselin, personal communication, 2014), K-PORT (2007, 2008, and 2010) (S. H. Lee, personal communication, 2014), CFL (2008) [Mundy et al., 2009; Sallon et al., 2011], ICE-CHASER (2008) [Charalampopoulou et al., 2011], JOIS (2009) [Yun et al., 2012], RUSALCA (2009) (S. H. Lee, personal communication, 2014), JAMSTEC (2009–2010; http://www.godac.jamstec.go.jp/darwin/e), Malina (2009; http://malina.obs-vlfr.fr/), and ICESCAPE (2010–2011; http://seabass.gsfc.nasa.gov/) [Arrigo et al., 2014]. These recent data were primarily collected in the Pacific-sector of the Arctic Ocean (Figure 1c). The in situ sampling stations were selected such that discrete NPP measurements, using ¹³C or ¹⁴C-labeled compounds, were available for at least four discrete depths at each station where the minimum depth of in situ NPP was between 0 and 5 m in the surface layer. Most of the in situ NPP using a ¹⁴C-labeled compound were measured after 24 ± 2 h in situ or simulated in situ incubations (N = 480) and the rest of the ¹⁴C samples were measured after less than a 12 h incubation or an unknown time period (N = 397). In situ carbon uptake rates were also measured using ¹³C-labeled compounds (N = 90) after 3–6 h on-deck incubations [Lee and Whitledge, 2005; Lee et al., 2010]. A good agreement between estimates of ¹³C and ¹⁴C productivity was previously described [Cota et al., 1996]. Most of the NPP data were reported as daily values, but, if hourly in situ production rates were reported, they were converted to daily production rates by multiplying with a calculated day length [Forsythe et al., 1995], based on the date and location of the sampling stations. Note that we did not assess ice algal production in this study due to the scarcity of in situ measurements, although sea ice algae may contribute significantly to NPP early in the growth season and in certain localities [Fernández-Méndez et al., 2015; Leu et al., 2015].

Figure 1.

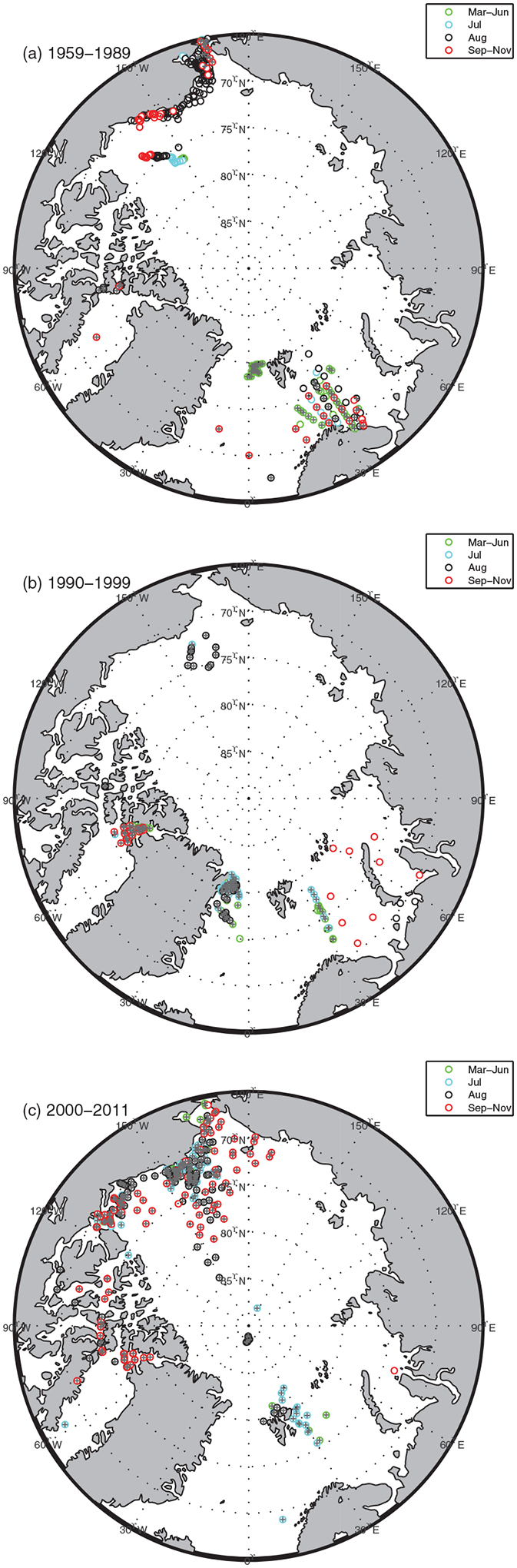
The sampling stations where in situ NPP (open circle, N = 928, 1959–2011) and nitrate (1, N = 663, 1979–2011) weremeasured during the periods of (a) 1959–1989, (b) 1990–1999, and (c) 2000–2011. In each plot, the stations were also grouped by seasons: March–June (green), July (blue), August (black), and September–November (red).

Prior to any integration, minimum NPP was set to 0.25 mgC m⁻³ d⁻¹ due to reported methodological precision [Richardson, 1991]. If the NPP value at the surface (0 m, Z₀) was not measured, it was assumed to be the same as the closest measurement taken from the uppermost 5 m (Z_min) of the water column. In addition, if the maximum sampling depth (Z_max) was shallower than 100 m (or bottom depth, Z_bot), NPP was extrapolated from Z_max to 100 m (or Z_bot) by assuming NPP decreased exponentially. Using the multiple segment trapezoidal rule, NPP was integrated from Z₀ to 100 m depth as well as, alternatively, over the euphotic layer that was determined during the incubation or calculated from available light penetration data; but, in situ Z_eu was reported at approximately half of the NPP sampling stations (N = 519): ice-influenced or ice-free. In order to maximize the number of stations available for skill assessment, iNPP down to 100 m (or Z_bot) was used for analysis since it exhibited only a small difference when compared to iNPP down to Z_eu (r = 0.99, p < 0.01).

Although all the available in situ iNPP ranged between 5.45 and 18,200 mgC m⁻² d⁻¹ at 967 stations, outliers (N = 39; 4%) at a confidence level of 95% were removed prior to any analysis due to accuracy issues with in situ NPP measurements. The remaining in situ iNPP data (N = 928; Figure 2) were between 15.7 and 5,260 mgC m⁻² d⁻¹ (Table 2) with a median value of 246 mgC m⁻² d⁻¹. These iNPP data were log-transformed (base 10) throughout the analysis, with a mean of 2.42 and a standard deviation of 0.60 (Table 2); they exhibited a log-normal distribution (Figure 2a) that was confirmed with the Kolmogorov-Smirnov (K-S) test. The majority of available NPP data in the Arctic Ocean was measured after 1975 (Figure 2b) and collected in the region between 70 and 80°N (Figure 2c), mainly from June to September (Figure 2d).

Figure 2.

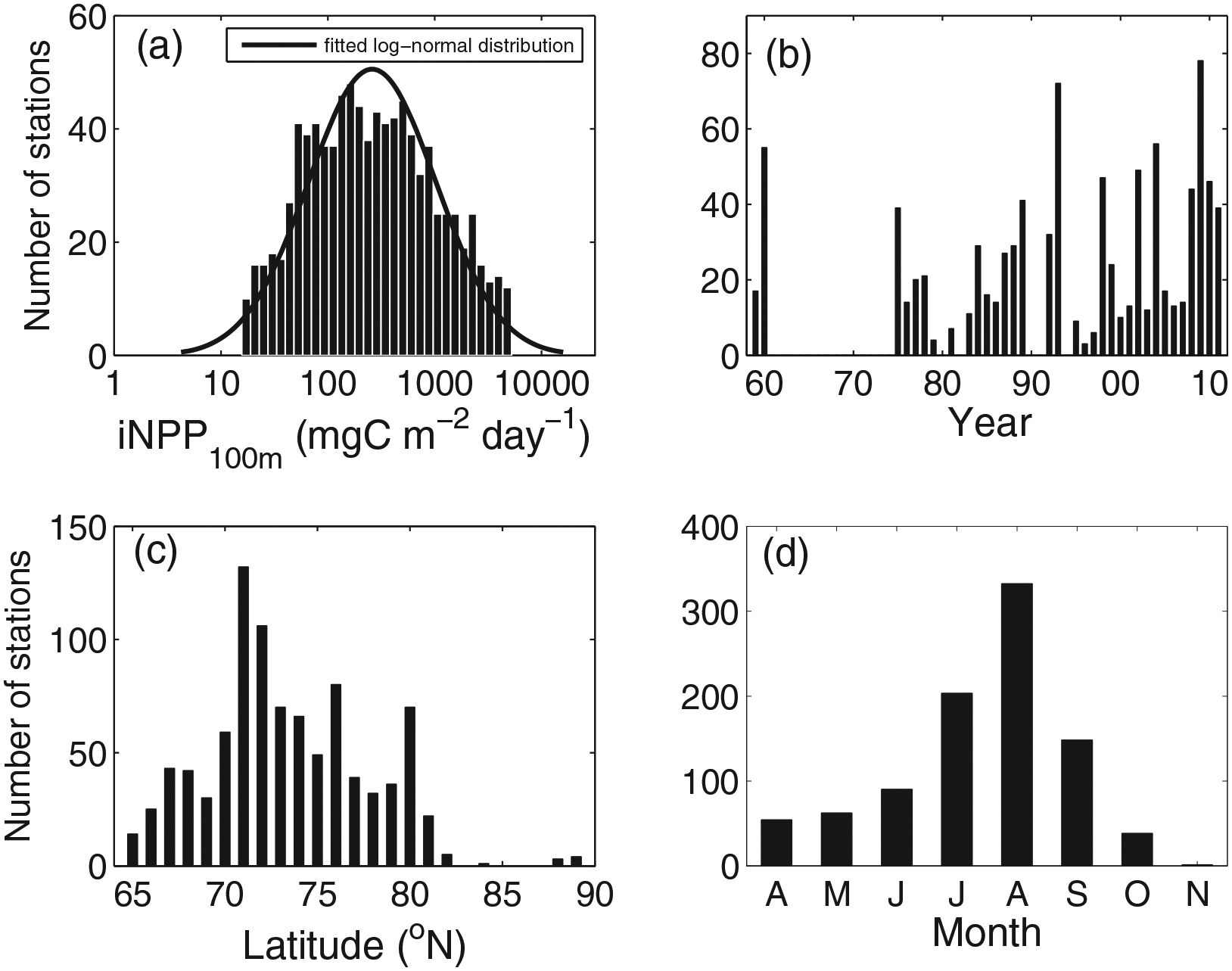
(a) The log-transformed distribution of in situ iNPP (mgC m⁻² d⁻¹) down to 100 m (N = 927). (b), (c), and (d) show when and where those in situ NPP were measured in terms of years, latitude, and month, respectively.

Table 2.

Mean (μ) and Standard Deviation (r) of In Situ Log-Transformed iNPP (1959–2011; N = 928) and Depth-Averaged NO₃ (1979–2011; N = 663) in Different Regions (Except for Sea Ice Condition During the Period of 1979–2011), Periods (Except for NO₃ During the Period of 1979–2011), and Months (Except for March and November)

		log(iNPP)		iNPP (mgC m−2 d−1)		Depth-Averaged NO3 (mmol m−3)
		N	μ ± σ	10μ	Range	N	μ ± σ
Regions	Sea ice-free	349	2.42 ± 0.58	263	18.1–5260	273	3.90 ± 3.05
	Sea ice-influenced	413	2.47 ± 0.63	295	15.7–5210	390	3.76 ± 2.77
	Shelf	432	2.51 ± 0.60	321	18.1–5080	244	3.47 ± 2.91
	Deep	496	2.34 ± 0.58	217	15.7–5260	419	4.03 ± 2.86
Periods	Year 1959–1989	344	2.50 ± 0.58	316	19.4–5260	284	5.09 ± 3.10
	Year 1990–1999	193	2.61 ± 0.55	404	17.4–5080
	Year 2000–2011	391	2.25 ± 0.59	177	15.7–4460	379	2.87 ± 2.30
Months	April-June	201	2.64 ± 0.59	436	24.0–5260	176	5.89 ± 3.32
	July	203	2.61 ± 0.52	408	24.9–4420	160	3.27 ± 2.23
	August	332	2.39 ± 0.60	244	16.0–5080	182	2.86 ± 2.28
	September–October	186	2.03 ± 0.45	108	15.7–1570	139	2.86 ± 1.96
	All	928	2.42 ± 0.60	260	15.7–5260	663	3.82 ± 2.89

3.2. In Situ Nitrate (1979–2011)

Vertical profiles (0–100 m) of in situ NO₃ were extracted from the NOAA/NODC ArcNut database [Codispoti et al., 2013] (http://www.nodc.noaa.gov/archive/arc0034/0072133/) as well as additional polar research cruises at the stations where NPP was measured. However, in situ NO₃ profiles were available only at 663 stations (Figure 1). Note that, if only combined values of in situ NO₃ and nitrite concentration (hereafter, NO₂) were available, those were assumed to be the same as NO₃ because NO₂ in the Arctic Ocean is extremely low [Codispoti et al., 2013]. Vertical profiles were sorted by layers (0–10, 10–20, 20–30, 30–50, and 50–100 m); the deepest layer varied depending on station bottom depth, and in most cases (approximately 70%) was measured between 50 and 100 m.

3.3. Sea Ice Concentration (1979–2011)

Monthly sea ice concentrations (%) at the corresponding location and date of each NPP station were determined at the nearest grid cell (25 km × 25 km polar stereographic projection), using NOAA/National Snow and Ice Data Center (NSIDC) Climate Data Record of Passive Microwave Sea Ice Concentration, Version 2 (ftp://sidads.colorado.edu/pub/DATASETS/NOAA/G02202_v2/north/monthly/) [Meier et al., 2013, updated 2015; Peng et al., 2013]. These data files include not only monthly sea ice concentration from July 1987 to the present, but also the merged Goddard Space Flight Center NASA Team [Cavalieri et al., 1984] and Bootstrap [Comiso, 1986] sea ice concentrations from late 1978 to mid-1987, as an ancillary data set. Sea ice concentration was used to distinguish ice-free (sea ice concentration <10% which is the NSIDC threshold cutoff for sea ice edge detection in Meier et al. [2013, updated 2015]) and ice-influenced (sea ice concentration ≥10%) regions. Roughly 46% of the NPP stations were located in ice-free waters (N = 349, Table 2). Among the ice-influenced stations (N = 413), 75% were in marginal ice zones (N = 175 where sea ice concentration was 10–50%; N = 136 where sea ice concentration was 50–80%) and the rest (N = 102) were in ice-covered regions (sea ice concentration ≥80%).

3.4. Mixed Layer Depth (MLD)

Because temperature and salinity profile data were often missing or unavailable at the in situ NPP stations (i.e., separate files archived at different locations), monthly climatological salinity, and temperature from the Polar Science Center Hydrographic Climatology (http://psc.apl.washington.edu/nonwp_projects/PHC/Climatology.html) [Steele et al., 2001] were used to estimate MLD. After linearly interpolating the climatological temperature and salinity data in the vertical, the monthly climatological MLD was determined at the nearest grid cell (1° × 1° resolution) for each NPP station by using a threshold criterion of Δσ_θ = 0.1 kg m⁻³ [Peralta-Ferriz and Woodgate, 2015], where Δσ_θ = σ_θ (z) − σ_θ (5 m); σ_θ(z) and σ_θ(5 m) are the potential density anomaly (σ_θ = ρ_θ − 1000 kg m⁻³, with ρ_θ being potential density) at a given depth (z) and 5 m, respectively.

3.5. Model Output

Location (latitude and longitude) and date of the in situ NPP station data were provided to all modeling teams. Each modeling team was then asked to generate monthly mean estimates for vertical profiles (0–100 m) of NPP and NO_3, iNPP, MLD, Z_eu, and sea ice concentration. Note that a minimum value for model NPP was set to 0.25 mgC m⁻³ d⁻¹, similar to the minimum in situ NPP. Five models (two global and three regional) provided daily mean iNPP as well (Models 1, 2, 3, 7, and 9). Unlike iNPP, other output variables were provided by fewer models due to their model setup and configuration (Table 1). For instance, Z_eu was only available in nine participating models. Moreover, because the simulation period differed among the participating models, the number of stations used for model-data comparisons varied between N = 853 and N = 353 (Figure 3). Regardless of the number of in situ stations represented by each model, the corresponding in situ iNPP were log-normally distributed whereas model estimates were not, based on a single sample K-S test, except for Models 2, 6, 10, and 17 (not shown). Note that the minimum value for model iNPP was set similar to the minimum in situ value of 5.45 mgC m⁻² d⁻¹, instead of removing extremely low or negative values. Then, analogous to the in situ iNPP approach, statistical outliers at a confidence level of 95% were discarded in each set of model iNPP output (i.e., 0–10% of model results).

Figure 3.

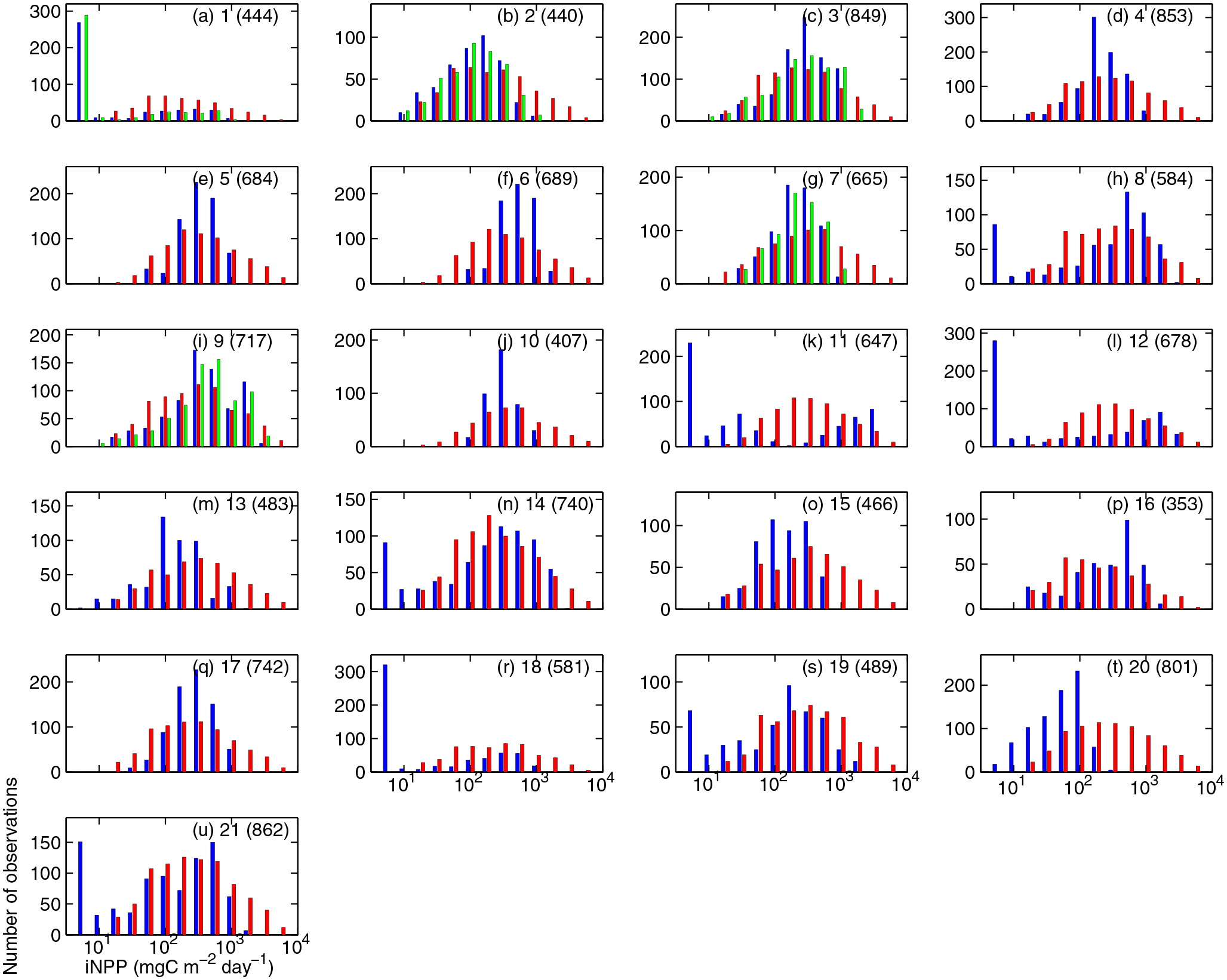
(a–u) Histogram of simulated (blue, monthly mean; green, daily mean) and in situ iNPP (red; mgC m⁻² d⁻¹). Indicated are model numbers in the upper right with the number of sampling stations in parenthesis, which varies due to different simulation periods.

3.6. Model Skill Assessment

A model-data intercomparison of NPP (log-transformed) and NO₃ was carried out by assessing the root-mean-square difference (RMSD) from 21 participating models using Target [Jolliff et al., 2009] and Taylor [Taylor, 2001] diagrams, where N is the number of observations in each variable:

$$RMS{D}^2=\frac{{\sum }_{i=1}^N{\left(X_{\mathit{\text{model}}}^i-X_{\text{in situ}}^i\right)}^2}{N}=bia{s}^2+\mathit{\text{uRMS}}{D}^2$$

$$\mathit{\text{bias}}=\overline{X_{\mathit{\text{model}}}}-\overline{X_{\text{in\hspace{0.17em}situ}}}$$

$$\mathit{\text{uRMSD}}=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\left[\left(X_{\mathit{\text{model}}}^i-\overline{X_{\mathit{\text{model}}}}\right)-\left(X_{\text{in situ}}^i-\overline{X_{\text{in\hspace{0.17em}situ}}}\right)\right]}^2}$$

Bias represents the difference between the means of in situ measurement and model output, and uRMSD represents the difference in the variability between in situ data and model results. Hence, bias and uRMSD provide measures of how well mean and variability are reproduced, respectively.

To visualize bias and uRMSD on a single plot, a Target diagram [Jolliff et al., 2009] is used after normalizing by the standard deviation (σ) of in situ data, i.e., normalized bias (bias*) is defined as:

$$\mathit{\text{bias}}*=\mathit{\text{bias}}/{\sigma }_{\text{in situ}}$$

Although uRMSD is a positive quantity mathematically, normalized uRMSD (uRMSD*) is also defined in Target diagram as:

$$\begin{gathered} \mathit{\text{uRMS}}{D}^{*}=\mathit{\text{uRMSD}}/{\sigma }_{\text{in situ }}(\mathit{\text{when }}{\sigma }_{\mathit{\text{model}}}>{\sigma }_{\text{in situ}}) \\ =-\mathit{\text{uRMSD}}/{\sigma }_{\text{in situ}}(\mathit{\text{when }}{\sigma }_{\mathit{\text{model}}}<{\sigma }_{\text{in situ}}) \end{gathered}$$

where σ_model is the standard deviation of X_model. If uRMSD* is positive (negative), the model overestimates (underestimates) the variability of the in situ data. In this diagram, the closer to the observational reference (the origin), the higher the skill of the model.

The Taylor diagram [Taylor, 2001] illustrates a different set of statistics in terms of uRMSD* that is comprised of standard deviation (σ) of the model output and in situ data as well as the Pearson’s correlation coefficient (r) between model estimates and in situ measurements:

$$\mathit{\text{uRMS}}{D}^{*}=\sqrt{1+\frac{{\sigma }_{\mathit{\text{model}}}{}^2}{{\sigma }_{\text{in situ}}{}^2}-2\cdot \frac{{\sigma }_{\mathit{\text{model}}}}{{\sigma }_{\text{in situ}}}\cdot r}$$

Note that, unlike the Target diagram, bias is not illustrated in the Taylor diagram.

In addition, the Willmott skill (WS) scores [Willmott, 1981] were used to quantify an overall regional agreement between multimodel mean (i.e., iNPP, NO₃, Z_eu, sea ice concentration, and MLD) and observations, and computed as:

$$WS=1-\frac{N\cdot RMS{D}^2}{{\sum }_{i=1}^N{\left[\left(X_{\mathit{\text{model }}}^i-\overline{X_{\text{in situ}}}\right)-\left(X_{\text{in situ}}^i-\overline{X_{\text{in situ}}}\right)\right]}^2}$$

The highest value, WS =1, means perfect agreement between model and observation, while the lowest value, WS =0, indicates disagreement. In this study, WS is used to quantify model performance in simulating different parameters from various model runs at regional scales. However, WS may not be useful when in situ data have extremely low variability and zero mean, i.e., when nutrients are depleted, because ${\sum }_{i=1}^N{\left[\left(X_{\mathit{\text{model }}}^i-\overline{X_{\text{in situ}}}\right)-\left(X_{\text{in situ}}^i-\overline{X_{\text{in situ}}}\right)\right]}^2$ becomes close to N · RMSD². Moreover, since WS is often criticized for producing high skill values for entirely uncorrelated signals [Ralston et al., 2010], we provide the modeling efficiency (ME) as an alternative validation metric which determines the relative magnitude of the residual variance compared to the measured data variance [Nash and Sutcliffe, 1970]. ME indicates how well the plot of observed versus simulated regionally averaged data fits the 1:1 line [Moriasi et al., 2007], but it can be sensitive to a number of factors such as sample size, outliers, and magnitude bias [McCuen et al., 2006].

$$ME=1-\frac{RMS{D}^2}{{\sigma }_{\text{in situ}}^2}$$

The range of ME lies between 1.0 (perfect fit) and −∞ [Stow et al., 2009]. If ME is zero, the model estimates are as accurate as the mean of the observed data, whereas an efficiency less than zero (−∞ < ME < 0) indicates that the observed mean is a better predictor than the model. ME can also be illustrated by drawing a circle with a radius equal to one, i.e., ME = 0, from the origin on the Target diagram. For example, ME is negative (positive) when a model symbol appears outside (inside) the circle with a radius of one.

4. Results

The models broadly captured the spatial features of iNPP on a pan-Arctic scale. A majority of the models underestimated iNPP by varying degrees in spite of overestimating surface NO₃, MLD, and Z_eu throughout the regions. Model skill of iNPP exhibited little difference over sea ice condition and bottom depth. The models performed equally well on daily versus monthly scales and relatively well for the most recent decade and toward the end of Arctic summer. Much complexity can be seen from the high and sometimes opposing interaction between iNPP and selected physical variables, as shown by the variable degree of skill provided by the different participating models.

4.1. Comparison Between Simulated Daily and Monthly Mean iNPP

Most of the models in this intercomparison were only able to provide monthly mean rather than daily mean iNPP. In order to determine how the results of this analysis would be affected by using monthly mean model output instead of simulated daily iNPP, those five models that provided both daily and monthly estimates (Models 1, 2, 3, 7, and 9) were compared to each other. The distributions of simulated daily and monthly mean iNPP were very similar in each model (Figures 3a–3c, 3f, and 3h) and they were strongly correlated (r = 0.83 to 0.91, p < 0.01). On average, the maximum simulated iNPP was up to 6% higher when computed from daily mean values compared to the monthly mean estimates (log-transformed). The standard deviation was higher (4–23%) when computed from the daily mean iNPP estimates, except Model 1. However, the simulated mean iNPP from those five models computed from the monthly averaged output was almost equal or slightly higher (up to 7%) than that computed from the daily mean estimates. This demonstrates that, as expected, the monthly averaging smoothed the daily variability while the mean value exhibited little change. Hence, results based on the simulated monthly mean iNPP are representative of higher temporal resolution data. Although the simulated daily mean iNPP exhibited little difference over monthly averaging, the simulated monthly mean iNPP could miss details of the dynamics of NPP on daily time scales. For example, no highest estimate from the bloom peak should be shown in model monthly mean output, relative to in situ data.

4.2. Model Skill Assessment of iNPP and Depth-Averaged NO₃

iNPP was underestimated by most models on a station-by-station basis though not consistently. Log-mean values of simulated iNPP were mostly negatively biased (Table 3) because the log-distribution of iNPP from many models was negatively skewed with a longer tail on the left, toward low values. While the bias was small for some models, it was very large, i.e., a factor of 10 for others. Thirteen out of 21 models reproduced iNPP up to 1500 mgC m⁻² d⁻¹ and five others estimated iNPP up to 3000 mgC m⁻² d⁻¹; the remaining three models simulated iNPP up to 4300 mgC m⁻² d−¹ (see Figure 3) while the maximum in situ value was 5255 mgC m⁻² d⁻¹ (Table 2). Generally, models with large uRMSD, i.e., overestimated variability of iNPP or depth-averaged NO₃, exhibited high standard deviation due to underestimating iNPP (Figure 3) or overestimating depth-averaged NO₃ (not shown), respectively. Unlike iNPP, depth-averaged NO₃ was positively biased in most of the models, indicating those models overestimated the mean NO₃ in the top 100 m, and their correlation coefficients were relatively high compared to those of iNPP (Table 3). However, no evident relationship was found that better model skill in estimating NO₃ effected better reproduction of iNPP, or vice versa, in terms of RMSD (i.e., combining mean and variability).

Table 3.

Mean (μ) and Standard Deviation (σ) of Estimated iNPP (Log-Transformed) and Depth-Averaged NO₃ (mmol m⁻³)^a

	log(iNPP)									Depth-Averaged NO3
		μ		σ							μ		σ
Model	N	In Situ	Modeled	In Situ	Modeled	RMSD	Bias	uRMSD	r	N	In Situ Modeled		In Situ Modeled		RMSD	Bias	uRMSD	r
1	444	2.27	1.30	0.59	0.76	1.32	20.98	0.89	0.16	439	3.21	4.05	2.63	1.71	2.64	0.86	2.50	0.39
2	440	2.31	2.02	0.60	0.44	0.67	20.29	0.60	0.37	445	3.22	5.23	2.65	2.28	3.26	2.02	2.56	0.46
3	849	2.40	2.43	0.58	0.42	0.59	0.03	0.59	0.34	663	3.82	5.43	2.89	2.29	4.03	1.61	3.70	20.01
4	853	2.40	2.32	0.58	0.36	0.63	20.08	0.62	0.20	663	3.82	6.04	2.89	3.96	4.75	2.23	4.19	0.28
5	684	2.53	2.51	0.54	0.29	0.59	20.01	0.59	0.10	461	4.22	3.67	3.09	3.47	2.70	20.54	2.65	0.68
6	689	2.52	2.71	0.54	0.27	0.59	0.19	0.56	0.16	461	4.22	0.41	3.09	0.41	4.73	23.80	2.82	0.66
7	665	2.47	2.31	0.60	0.34	0.59	20.16	0.57	0.37	621	3.89	5.60	2.90	2.76	3.27	1.72	2.78	0.52
8	584	2.42	2.31	0.59	0.83	0.92	20.11	0.92	0.20	436	3.92	9.79	3.03	3.20	7.37	5.87	4.46	20.02
9	717	2.44	2.57	0.60	0.51	0.68	0.13	0.67	0.27	663	3.82	5.01	2.89	4.88	5.67	1.20	5.54	0.05
10	407	2.58	2.50	0.53	0.22	0.55	20.08	0.55	0.12	392	4.11	3.78	3.09	2.97	3.06	20.33	3.04	0.49
11	647	2.50	1.81	0.54	1.08	1.43	20.69	1.25	20.09	448	4.26	6.53	3.07	2.09	3.93	2.27	3.21	0.27
12	678	2.51	1.82	0.55	1.07	1.42	20.69	1.24	20.06	461	4.22	9.33	3.09	3.18	6.36	5.12	3.77	0.28
13	483	2.45	2.13	0.60	0.47	0.71	20.32	0.63	0.32	493	3.69	1.93	2.93	1.74	2.96	21.74	2.39	0.57
14	740	2.36	2.18	0.58	0.78	0.88	20.18	0.86	0.22	578	3.92	6.86	2.96	3.05	4.61	2.95	3.54	0.30
15	466	2.44	2.13	0.61	0.36	0.68	20.31	0.61	0.28	-	-	-	-	-	-	-	-	-
16	353	2.26	2.39	0.59	0.50	0.60	0.14	0.59	0.44	-	-	-	-	-	-	-	-	-
17	742	2.39	2.43	0.58	0.31	0.60	0.03	0.60	0.23	550	3.82	7.29	3.00	2.86	4.62	3.48	3.04	0.46
18	581	2.37	1.42	0.60	0.83	1.45	20.94	1.10	20.17	548	3.21	5.82	2.45	2.77	4.06	2.62	3.10	0.30
19	489	2.47	1.98	0.58	0.72	0.99	20.49	0.86	0.13	436	3.92	12.51	3.03	2.45	9.38	8.59	3.78	0.06
20	730	2.39	1.23	0.60	0.39	1.37	21.16	0.72	20.03	585	3.81	0.66	2.78	0.83	3.97	23.15	2.42	0.56
21	862	2.40	1.96	0.59	0.76	0.98	20.44	0.87	0.18	-	-	-	-	-	-	-	-	-

^aRMSD, bias, uRMSD, and Pearson’s correlation coefficient (r) are computed between each model estimate and in situ measurement (see Appendix A for details). The number of stations (N) varies mainly due to different model simulation periods and in situ data availability. Note that Models 15, 16, and 21 did not provide model estimates of NO₃, which is indicated by a dash (−).

4.3. Model Skill Assessment of iNPP as a Function of Ice Cover, Depth, Decade, and Season

Based on Table 3, model skill of estimating iNPP was not a function of model domain, type, or complexity in terms of RMSD on a pan-Arctic scale. Hence, the model skill was examined spatially as a function of sea ice presence, defined from satellite measurements (see section 3.3), and bottom depth as well as temporally by seasons and simulation periods (Figure 4). While more individual models overestimated mean iNPP (Figure 4a) and exhibited a higher correlation coefficient (Figure 4b) in ice-free regions than in ice-influenced regions, most models performed nearly equally well in terms of standard deviation between ice-influenced and ice-free regions. Indeed, as a group, model performance was similar regardless of sea ice presence or absence in terms of both bias and variability, i.e., RMSD. Similarly, in the case of bottom depth (Z_bot) (shelf, Z_bot < 200 m versus deep ocean, Z_bot > 200 m), little difference in model skill was exhibited in terms of bias (Figure 4c) and variability (Figure 4d). Therefore, based on the K-S test at a 5% level of significance, model performance was not significantly different between spatially defined regions (i.e., ice-free versus ice-influenced and shelf versus deep ocean) in terms of RMSD (not shown).

Figure 4.

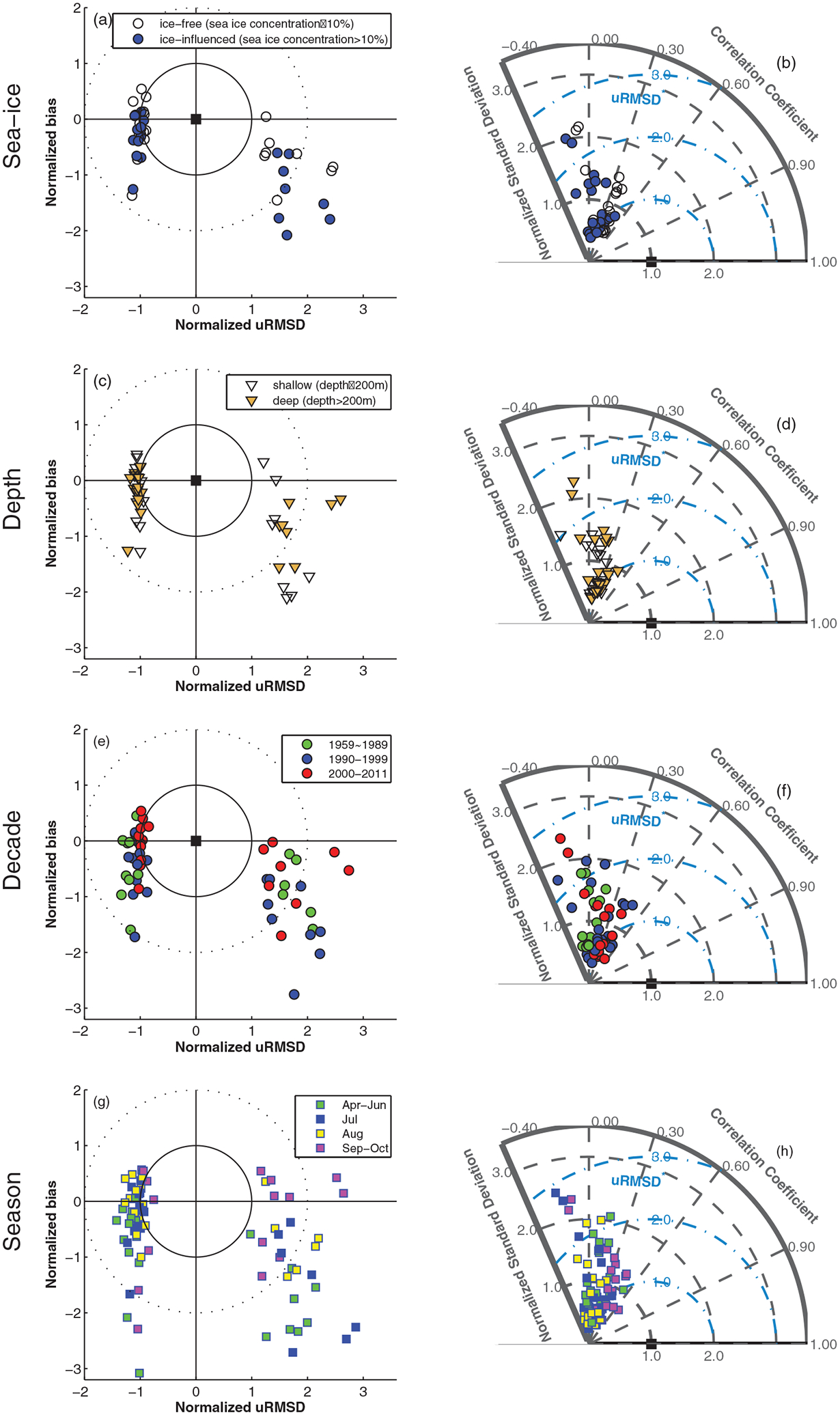
(a, c, e, and g) Target and (b, d, f, and h) Taylor diagrams illustrating relative model performance in reproducing iNPP as a function of (Figures 4a and 4b) sea ice condition: ice-free region (sea ice concentration ≤15%) versus ice-influenced region (sea ice concentration >15%), (Figures 4c and 4d) depth: shelf (≤200 m) versus deep (>200 m), (e and f) simulation period (1959–1989, 1990–1999, and 2000–2011), and (g and h) month (April–June, July, August, and September–October).

With respect to temporal scales, the performance of models was significantly different between two simulation periods: 1959–1989 and 2000–2011. Overall, the models performed better in the most recent decade (2000–2011) in terms of RMSD whereas most of them significantly underperformed in terms of correlation coefficient during the earliest decade (r = −0.24 to 0.24) compared to the latter period (r = −0.19 to 0.53) (Figure 4f). However, no significant difference was found between the two periods in terms of bias only (Figure 4e) based on the K-S test for 5% significance. This may be partly due to the fact that more in situ measurements have become available in recent years when ice-free conditions have become more pronounced. On the other hand, seasonally estimated iNPP was more negatively biased in the growth period (mean bias of −1.12 in April–June) compared to other seasons (mean bias of −0.72 in July, −0.24 in August, and −0.23 in September–October), but the models performance was not significantly different between seasons in terms of variability (Figures 4g and 4h). This is probably because the models have a seasonal cycle that, although slightly shifted early in phase for the Arctic Ocean, is still within a reasonable range. In addition, the models include a range of approaches to estimating the vertical distribution of irradiance (i.e., light transmission through sea ice). Some models simply scale down shortwave radiation by sea ice concentration, whereas others include radiation transmission as a fully coupled and bidirectional formulation (e.g., CICE-based models). Still other models compute light transmission through sea ice as a function of sea ice physics and biogeochemistry. For example, the Pelagic Interaction Scheme for Carbon and Ecosystem Studies (PISCES)-based models have a complex formulation of the vertical penetration of PAR through the water column, which takes into account incoming radiation, wavelength, chlorophyll-dependent attenuation coefficients assigned to distinct phytoplankton groups represented in the model [e.g., Aumont et al., 2015] and thus result in differing Z_eu for the same incoming PAR. These differences may account for the early negative bias in the participating model runs, but do not (yet) point to either phytoplankton bloom physiology or phenology processes being preferentially affected.

4.4. Model Skill Assessment of Vertical Profiles of NPP and NO₃

On a pan-Arctic scale, the models had a strong tendency to underestimate the observed mean NPP at various depths; eight out of 19 models had negative bias at all depth layers (Figure 5a). Note that not all the models provided vertical profiles of NPP and NO₃ (see Table 1). When the model standard deviation was smaller than the observed one (−uRMSD*), mean NPP was mostly underestimated (Figure 5a). But, when the model standard deviation was larger than the observed one (+uRMSD*), mean NPP was mostly underestimated only between 0 and 20 m and overestimated between 30 and 100 m (Figure 5a). Deep NPP (50–100 m; mean RMSD of 1.27) was better estimated than surface NPP (0–10 m; mean RMSD of 1.48) in terms of RMSD since both bias and uRMSD became less at depth.

Figure 5.

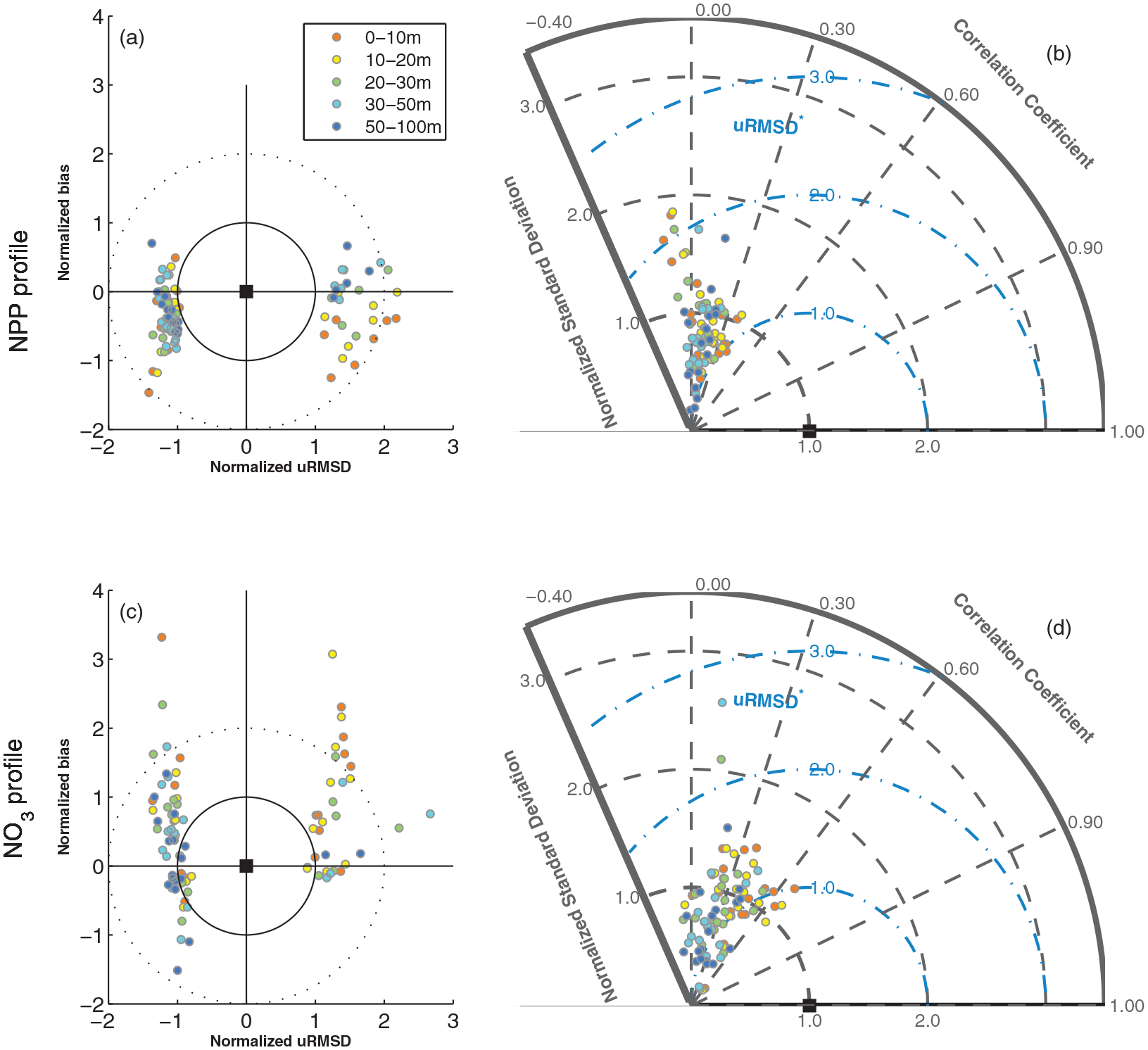
(a and c) Target and (b and d) Taylor diagrams of vertical profiles in (Figures 5a and 5b) NPP (mgC m⁻³ d⁻¹) and (Figures 5c and 5d) (NO3) (mmol m⁻³), which were grouped at given depth layers: 0–10 m, 10–20 m, 20–30 m, 30–50 m, and 50–100 m.

Unlike NPP, nine of 19 models overestimated mean NO₃ at all depth layers while four models (Models 5, 10, 13, and 20) underestimated mean NO₃, except at the deepest layer (50–100 m) (Figure 5c). Model bias was lowest at depth such that mean NO₃ concentration in the deep layer was better reproduced than in the surface layer (mean bias of 0.29 and 1.31, respectively), while the correlation coefficient was slightly higher at the surface (Figure 5d). Furthermore, the range of model bias for NO₃ became wider (i.e., more scattered both in negative and positive y axis) when the model standard deviations were smaller than the observed one (−uRMSD*). However, no significant difference in terms of uRMSD was exhibited between the depth layers (K-S test at a 5% level of significance). Overall performance of the models for NPP and NO₃ was not significantly different within each depth layer, although correlation coefficients were higher for NO₃ (Figures 5b and 5d). In general, the models performed better in reproducing NO₃ and NPP in the deepest layer (50–100 m) than at the surface (0–10 m).

4.5. Regional iNPP and NO₃ Climatologies

To illustrate climatological spatial patterns and compare with regional iNPP estimated from each model, available in situ iNPP was projected onto the Equal-Area Scalable Earth Grid (EASE-Grid) map (100 km spatial resolution) by averaging data within each grid cell (Figure 6a). EASE-Gridded model iNPP was then averaged across all models in each grid cell and compared to in situ climatological iNPP in six different regions of the Arctic Ocean where NPP was frequently measured between 1959 and 2011 (Figures 6b–6g). In situ and model iNPP exhibited no significant linear relationship on 10,000 km² basis (Figures 6c and 6f) and, regionally, the lowest WS (Table 4) in the Chukchi and Greenland Seas; both are influenced by inflow from subpolar latitudes. In addition, mean iNPP was most underestimated in the Canadian Archipelago and the Greenland Sea (Figures 6d and 6f) where ME was lowest (Table 4). Hence, iNPP was least reproduced regionally in the Greenland Sea in terms of intermodel mean (i.e., bias) as well as variability (i.e., WS and ME). As a group, the models performed best in the interior regions of the Arctic Ocean, such as the Beaufort Sea and the central Arctic Basin (Figures 6b and 6e) where NPP is relatively low (Figure 6a) and surface nutrients are depleted toward the end of the growing season [Codispoti et al., 2013]. At the larger pan-Arctic scale, model skill for iNPP was higher than for most individual regions, except where iNPP was best estimated, i.e., the Beaufort Sea (WS and ME) and the Central Arctic Basin (WS, Table 4).

Figure 6.

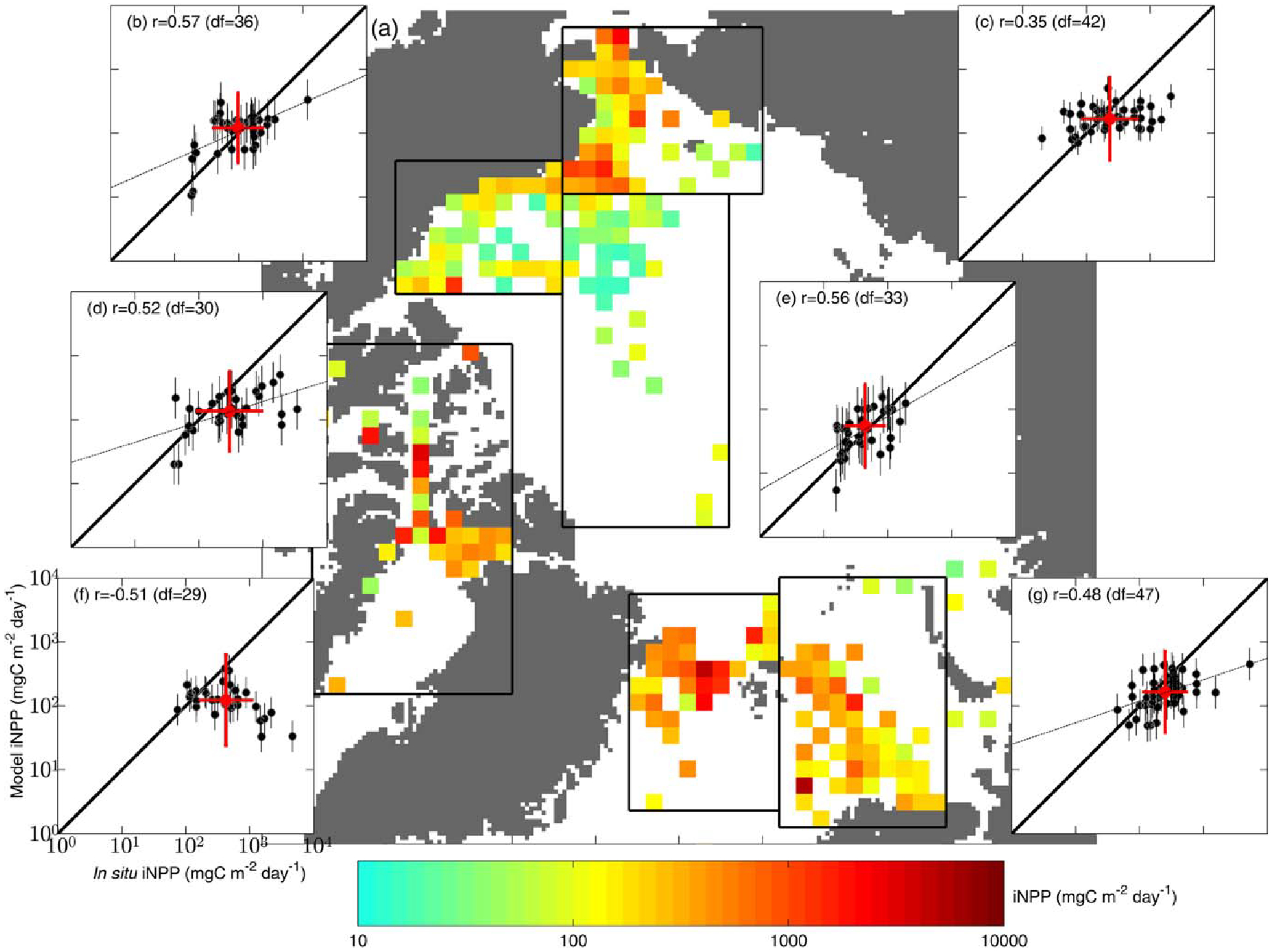
(a) In situ iNPP (mgC m⁻² d⁻¹) projected on the EASE-Grid map is shown. (b–g) Average model estimates with an error bar (±1 standard deviation from the multimodel mean) in each grid cell were regionally compared to in situ values in Figure 6b the Beaufort Sea, 6c the Chukchi Sea, 6d Canadian Archipelago, 6e the central Arctic Basin, 6f the Greenland Sea, and 6g the Barents Sea; all inserts have the same axis units as in Figure 6f. In each plot, the solid-line shows a slope of 1.0 and the dashed line is a linear regression fit if significant (p<0.05). The correlation coefficient (r) with degrees of freedom (df = number of grid cells–2) are shown in the upper left. A red circle with error bars indicates the regional average of in situ (x axis) and modeled (y axis) iNPP.

Table 4.

Willmott Skill (WS) Score Ranging Between 0 and 1 for a Perfect Model, and Modeling Efficiency (ME) Between −∞ and 1 for a Perfect Model of Multimodel Mean iNPP, Surface, and Deep NO₃, Z_eu, Sea Ice Concentration, and MLD in Six Regions of the Arctic Ocean

		Variables
Regions	Model Skill	iNPP	Surface NO3	Deep NO3	Zeu	Sea ice	MLD
Chukchi	WS	0.49	0.46	0.33	0.67	0.90	0.08
	ME	20.06	23.65	−0.27	−0.55	0.72	−264
Canadian Archipelago	WS	0.61	0.49	0.59	0.31	0.54	0.46
	ME	20.32	22.31	0.30	−12.8	−0.04	−4.49
Beaufort	WS	0.77	0.09	0.51	0.65	0.85	0.25
	ME	0.36	−135	0.15	0.01	0.64	−7.64
Central	WS	0.75	0.13	0.46	0.45	0.67	0.34
Arctic Basin	ME	0.09	−38.3	0.15	0.01	0.39	−2.25
Barents	WS	0.63	0.80	0.25	0.63	0.72	0.93
	ME	20.10	0.42	−0.14	−0.38	0.15	0.79
Greenland	WS	0.33	0.74	0.74	0.27	0.40	0.90
	ME	22.84	0.09	0.41	−24.7	−0.19	0.62
Pan–Arctic	WS	0.67	0.63	0.47	0.67	0.80	0.92
	ME	0.12	−0.84	0.07	−0.25	0.50	0.74

Analogously, in situ and modeled NO₃ were also processed onto the EASE-Grid map in the deep layer (50–100 m; Figure 7a) as well as at the surface (0–10 m; Figure 8a). Again, the models better reproduced the regional mean NO₃ at the deepest layer overall (Figures 7b–7g). However, models notably underestimated deep NO₃ variability in the inflow Chukchi (Figure 7c) and Barents (Figure 7g) Seas (r= −0.08 and r = 0.23, respectively) (see Table 4). On the contrary, at the surface, the models exhibited a tendency to overestimate mean NO₃ (Figures 8b–8g). This bias was smaller in the Greenland and Barents Seas (Figures 8f and 8g, respectively) and highest in the interior regions of the Arctic Ocean (Figures 8b and 8e) where in situ surface NO₃ is depleted at the end of summer and NPP is relatively low compared to that in other regions (Figures 8a and 6a, respectively) [Codispoti et al., 2013]. Model skill scores (Table 4) indicate that the regions where the models have the best skill in reproducing iNPP are also the ones where they exhibited the least skill in reproducing mean surface NO₃, i.e., the Beaufort Sea and central Arctic Basin.

Figure 7.

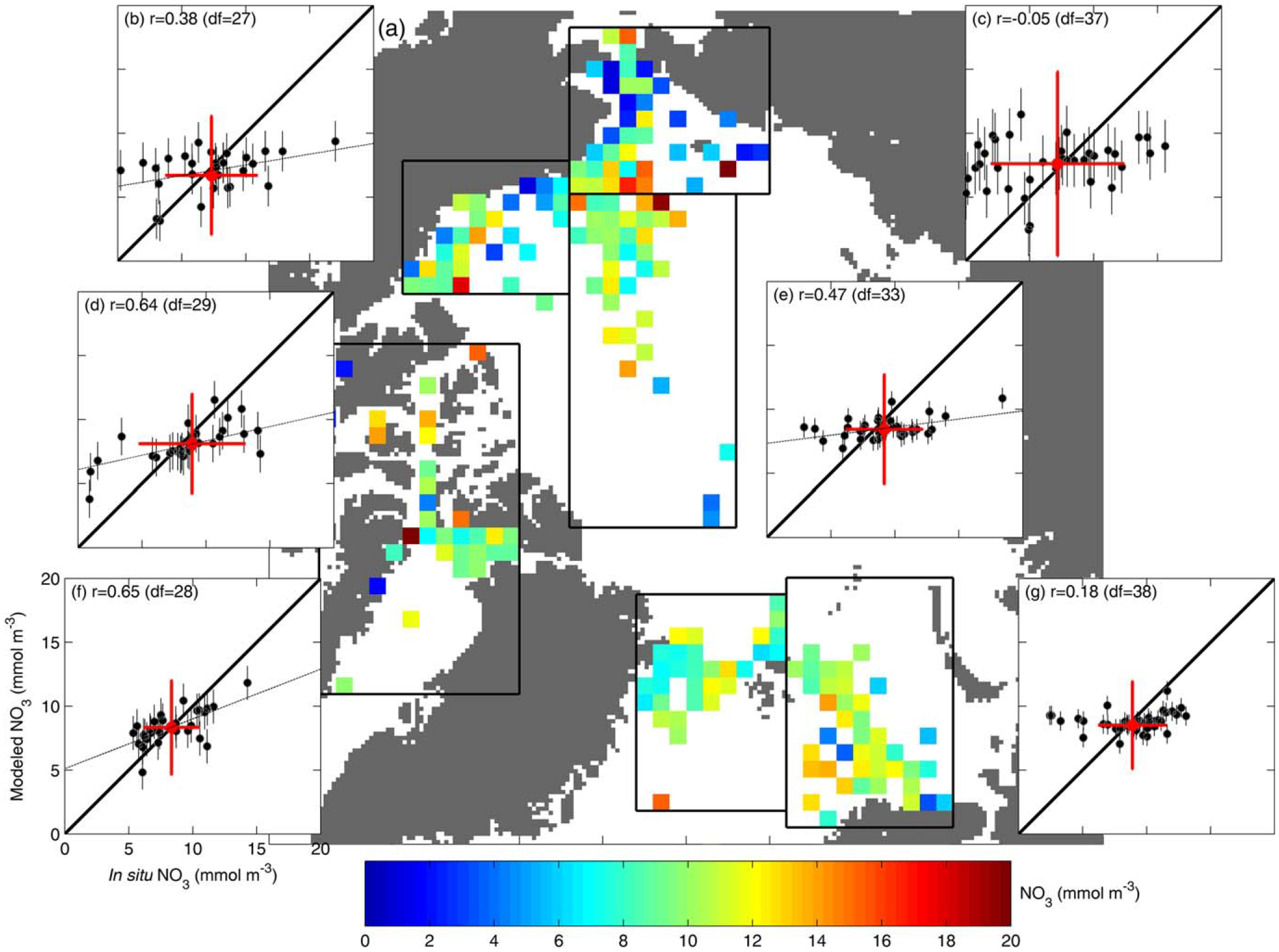
Same as Fig. 6, but for NO₃ (mmol m⁻³) in the deep layer (50–100 m).

Figure 8.

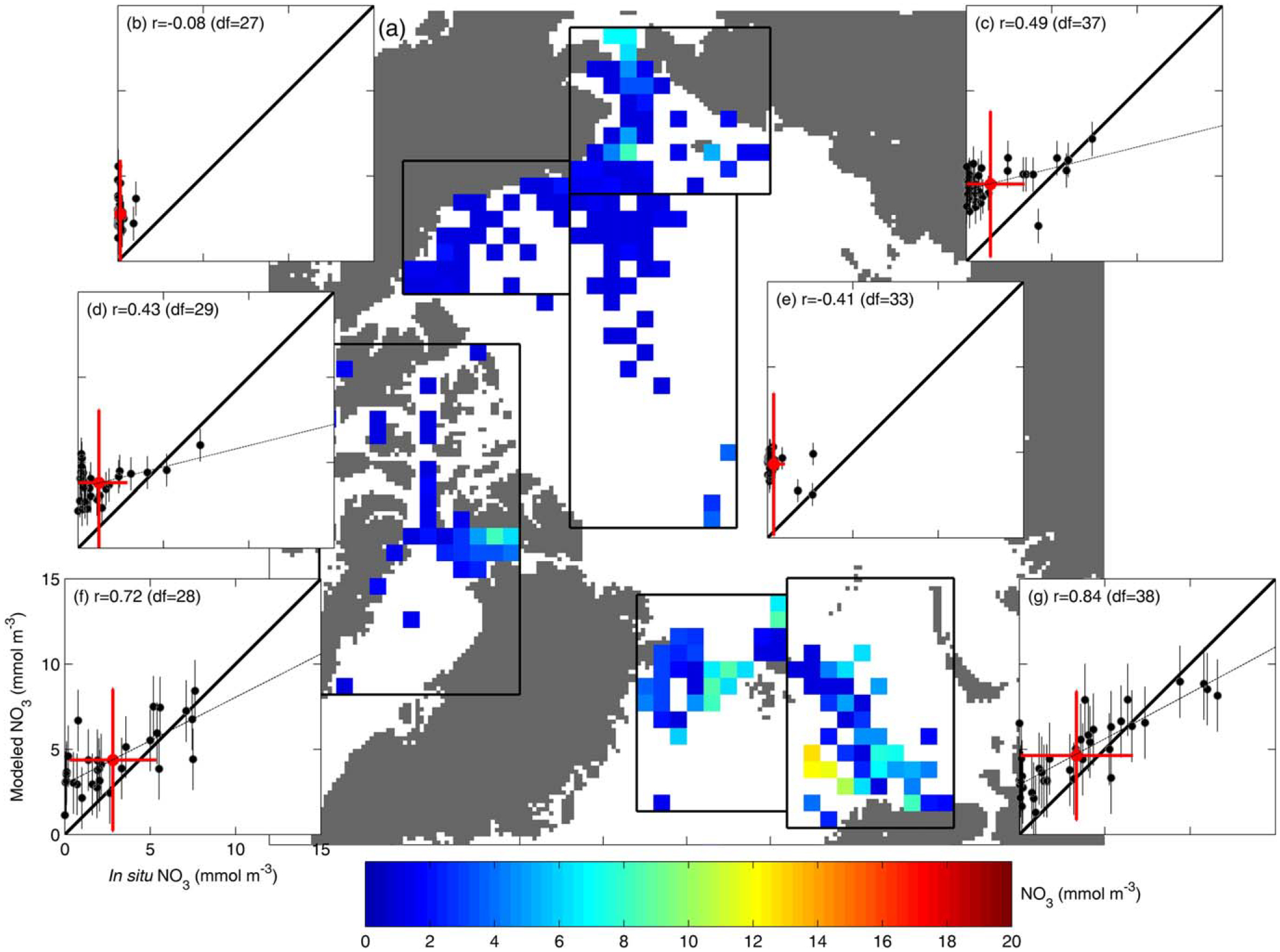
Same as Fig. 6, but for NO₃ (mmol m⁻³) in the surface layer (0–10 m).

4.6. Regional MLD, Z_eu, and Sea Ice Concentration Climatologies

Using the same approach as in section 4.5, the regional, mean MLD was relatively better estimated in the Barents and Greenland Seas (i.e., highest WS and ME in Table 4) and least reproduced in the Chukchi Sea where MLD was consistently overestimated (Figure 9a). Moreover, the highest regional model skills in surface NO₃ were also calculated in the Barents and Greenland Seas. But they do not necessarily appear to influence iNPP estimates, i.e., poorly simulated iNPP, especially in those regions. Compared to the variables previously analyzed, Z_eu had the least amount of field data, especially in the Barents and Greenland Seas, and its mean was largely overestimated (Figure 9b); indeed, incoming PAR onto the surface ocean will be very different in open waters versus snow and ice-covered waters in the same latitude and season. In the absence of additional biological light-relevant parameters, the assessment of model estimates of Z_eu provides a limited understanding of phytoplankton light utilization, as it does not take into account that model phytoplankton will differ in their response to the same light field. Sea ice concentration is a logical next factor to consider; its model skill response is different from region to region, and is mostly underestimated in the Greenland Sea and overestimated in the Barents Sea (Figure 9c). In the Chukchi Sea, mean sea ice concentration was best estimated, but iNPP was still rather poorly estimated when compared to other regions (Table 4), as indicated earlier. While more high WS and ME model skill scores were shown for MLD and sea ice concentration among the different regions, no single environmental factor showed consistently high model skill for all regions; indeed, correlation analysis (not shown) between iNPP and any one environmental factor ME skill suggests a possible robust relationship with Z_eu instead, despite individual lower skill scores. Hence, iNPP model skill was constrained by different factors in different Arctic Ocean regions. Pan-Arctic averaging did not necessarily improve model skill for iNPP and associated variables over regional (Table 4) and subregional (Figure 6) scales.

Figure 9.

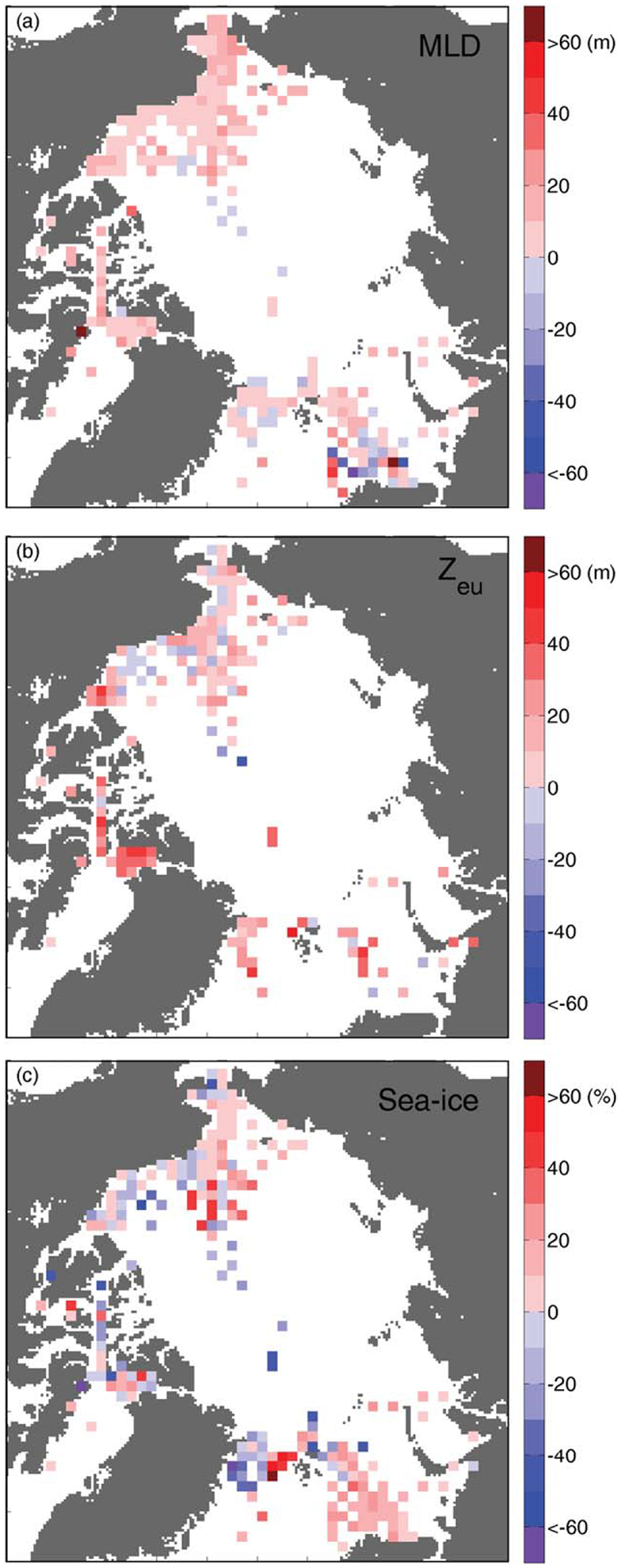
Modeled MLD, Z_eu, and sea ice concentration bias: (a) MLD bias between 15 model mean and monthly climatological MLD (m), (b) Z_eu bias between 9 model mean and in situ Z_eu (m), and (c) sea ice concentration bias between 19 model mean and satellite-derived values (%).

5. Discussion

It has long been known that marine primary production is controlled by the interplay of the bottom-up factors of light and nutrients, whose availability is a function of physical and/or biological processes. Earlier intercomparison studies for the Arctic Ocean emphasized the importance of a realistic representation of ocean physics [Popova et al. 2012], in particular vertical mixing and nutrient concentration, for accurate Arctic Ocean ecosystem modeling. Five BOGCMs manifested similar levels of light limitation owing to a general agreement on the simulated sea ice distribution [Popova et al. 2012]. On the other hand, the ESMs participating in the Vancoppenolle et al. [2013] study showed that Arctic phytoplankton growth was more limited by light related to sea ice than by nutrient availability for the period of 1980–1999. Furthermore, with the large uncertainties on present-day nitrate in the sea ice zone, ESMs used in the framework of the CMIP5 exercise were inconsistent in their future projections of primary production and oligotrophic condition in the Arctic Ocean [Vancoppenolle et al., 2013]. The need to quantify the relative role of environmental and ecological controls on NPP in the heterogeneous, seasonally ice-covered Arctic Ocean remains.

In our study, iNPP model skill was linked to different environmental variables in the various Arctic Ocean regions. The models exhibited relatively lower skill in reproducing iNPP in high to very high production Arctic Ocean regions [in the sense of Codispoti et al., 2013] (i.e., the Chukchi and Greenland Seas in Table 4 and Figure 6), despite higher model skill in physical parameters such as sea ice concentration or MLD, respectively. Model performance in estimating iNPP was also more related to the model skill of sea ice conditions (and Z_eu) than NO₃ (and MLD) in the extremely low production regions [in the sense of Codispoti et al., 2013] (i.e., the Beaufort Sea and central Arctic Basin in Table 4 and Figure 8), where in situ NO₃ is virtually depleted (i.e., almost no variability in the in situ data). Field studies in the Arctic Ocean have failed to demonstrate any statistical relationship between phytoplankton biomass or productivity and ambient nutrient concentrations or nutrient utilization rates in eastern Arctic waters [Harrison and Platt, 1986; Harrison and Cota, 1991], while phytoplankton biomass and productivity were significantly related to incident radiation [Harrison and Cota, 1991; but see Tremblay et al., 2015]. Hence, simulated iNPP was close to in situ values in such low production regions because light fields were likely better reproduced, even though surface NO₃ was systematically biased (Figures 8b and 8e).

Our study also showed that simulations of surface NO₃ (nutrient) and Z_eu (light) associated with MLD (controlling the depth horizon where phytoplankton cells are) exhibited low model skill in most of the regions (Table 4), being lowest in the interior of the Arctic Ocean. This observation is not necessarily new [Popova et al., 2012; Vancoppenolle et al., 2013], but one should be cautious when interpreting this result because these three simulated parameters were positively biased (i.e., means usually overestimated) (Figures 8 and 9). For example, the simulated, mean surface NO₃ was vastly overestimated, especially in the low-productivity, nutrient-depleted interior regions of the Arctic Ocean, i.e., the Beaufort Sea and the central Arctic Basin where model and in situ iNPP agreed best (Figures 6b and 6e; Table 4). At least on a regional scale, the overestimation of surface NO₃ possibly stems from spurious vertical mixing between the upper mixed layer and deeper water in the model simulations, resulting in excessive nutrient supply into the surface layer. For example, except in the Greenland and Barents Seas, MLD mean and variability were poorly estimated (Table 4) and mostly overestimated (Figure 9a) by as much as twofold, possibly resulting in higher nutrients at the surface. Alternatively, a physiological perspective may be examined, based on the most common model parameterization of phytoplankton growth (i.e., a combination of a nutrient term, a light term, a temperature-dependent growth term, and a maximum growth rate over a daily period). Then, the overestimated NO₃ may be caused by insufficient phytoplankton nutrient uptake (i.e., too low a rate for Arctic waters) since NPP was overall underestimated by most of the models. Phytoplankton nitrate uptake is strongly dependent on both temperature (i.e., less at colder temperatures) [Lomas and Glibert, 1999] and irradiance (i.e., photoinhibited at higher levels) [Hu and Smith, 1998] and becomes more dependent on their combined effect in the simultaneously cold and dark Arctic waters during the transition to spring conditions [Tremblay et al., 2006]. It is likely that several of the models have globally relevant phytoplankton physiological parameter values that are too high and may thus not correspond to the lower and narrower ranges required by Arctic (or polar) phytoplankton. Some Arctic phytoplankton species are shade-acclimated, especially in spring, though most available data are for summer, light-adjusted phytoplankton [Sakshaug, 2004; Harrison et al., 1982]. Arctic phytoplankton community structure appears to change toward smaller cells in response to warming both in the field and in experiments [Li et al., 2009; Tremblay et al., 2009; Coello-Camba et al., 2014, 2015] that may have different nutrient uptake kinetics [Lovejoy et al., 2007], while individual phytoplankton species may have narrower temperature ranges for optimal growth, usually in combination with light requirements [Harrison and Platt, 1986; Vernet et al., 2012]. These phenological changes will require the inclusion of multiple phytoplankton size classes in models and/or different physiological rates.

The distribution of NO₃—hence, its potential availability for NPP—differed by depth (Figure 5c) as well as region (Table 4). A less ecological and more pragmatic explanation for the overestimation of surface NO₃ may be that the models are incapable of reproducing the vertical mixing dynamics required (as shown by the ubiquitous MLD overestimation; Figure 9a); no evident relationship was found between vertical resolution and skill in surface NO₃ among the participating models (not shown). Indeed, the future Arctic Ocean may produce less NPP per unit area due to less surface NO₃ [e.g., Vancoppenolle et al., 2013] resulting from enhanced freshening [Coupel et al., 2015], as also hypothesized by McLaughlin and Carmack [2010]. Unlike surface NO₃, deep NO₃ was more realistically reproduced pan-Arctic wide in terms of the multimodel ensemble mean values at 100 km grid scales (average symbols in Figure 7). Indeed, deep NO₃ and sea ice concentration (i.e., measured as ME) were relatively well explained by the multimodel ensemble in at least four regions (Table 4). Still, deep NO₃ (50–100 m) was relatively poorly estimated in the inflow Barents and Chukchi Seas in terms of correlation coefficients (Figures 7c and 7g) and regional means (WS in Table 4). Those two regions are strongly influenced by horizontal advection of sub-Arctic inflow waters which contribute to the nutrient supply into the Arctic Ocean via the Bering Strait and Fram Strait/Barents Sea openings [e.g., Carmack and Wassmann, 2006; Wassmann et al., 2015]. Torres-Valdé et al. [2013] estimated the volume and NO₃ transports into the Arctic Ocean based on a combination of modeled and in situ velocity fields and nutrient sections: total volume and NO₃ transport into the Arctic Ocean at depth corresponded to 20% and 80% through the Bering Strait and the Barents Sea opening, respectively (i.e., a significant contribution). Smith et al. [2011] also showed the greater relative importance of this advective nutrient input compared to vertical mixing in the Arctic Ocean.

Involvement of a light-driven component of the simulation of NPP is provided by the fact that Z_eu was generally overestimated in all Arctic regions by most of the nine models that provided this field (Figure 9b). The simulated Z_eu (9 model mean of 56 m), compared to the mean in situ Z_eu (37 m), was deeper than MLD (18 model mean of 23 m and climatological mean of 16 m). Possible explanations for the Z_eu overestimation may include the prescription of lower turbidity levels than the typical values in the Arctic Ocean. In addition (or instead), the parametrization of light extinction in the water column may be associated with sea ice conditions, i.e., the Z_eu overestimation, coupled with underestimation of sea ice concentration, may result in light being able to penetrate deeper into the water column during a simulation. From a biophysical perspective, the self-shading effect caused by the presence of phytoplankton is considered in many of the participating models already. Although we focused on model skill in estimating NPP, not phytoplankton biomass, the self-shading effect has been reported as negligible for high latitudes in sensitivity analyses [Manizza et al., 2005]. Yet, other biogeochemical species like colored dissolved organic matter that could reduce the light penetration into the water column are not represented in the models used in this study [Granskog et al., 2012; Dutkiewicz et al., 2015; Kim et al., 2015]. Nonetheless, NPP was still underestimated despite apparent light availability, emphasizing a physiological coupling between light availability and light requirements by phytoplankton; alternatively, it suggests that low NPP would generate low phytoplankton biomass which would result in a deeper Z_eu simply due to lack of light absorption.

Given that the models overestimated surface NO₃ and Z_eu, the simulated phytoplankton populations would experience more nutrient and light availability, which should have led to higher iNPP. However, the simulated NPP was mostly underestimated in all regions of the Arctic Ocean, clearly indicating that surface nutrients were not the primary limiting factor for the underestimated iNPP in these model simulations. Because the regions with higher model skill at estimating iNPP coincided with better model skill in Z_eu and sea ice concentration, especially in low production regions, the amount of shortwave radiation or PAR transmitted through sea ice could account partly for underestimating iNPP [Babin et al., 2015]. Our findings further suggest that biological processes (i.e., phytoplankton growth and photosynthesis) were possibly misrepresented by the model configurations run for this Arctic Ocean exercise. A previous model intercomparison study for lower latitudes pointed out that an improved understanding of the temperature effect on photosynthesis and a better parameterization of the maximum photosynthetic rate are required [Carr et al., 2006]. Hence, one might argue that phytoplankton growth functions were not adequately parameterized especially for colder high latitudes in many models, resulting in lesser utilization of surface nutrients. This is debatable in the Beaufort Sea where the effect of temperature on photosynthetic parameters over the in situ range observed (−2 to 8°C) was found not significant [Huot et al., 2013]. Furthermore, a large variability in photosynthetic parameters and half-saturation constants exists in Arctic ecosystem models, as recently reviewed by Babin et al. [2015]; during a model sensitivity exercise, they showed that temperature was not as strong a limiting factor for phytoplankton growth as others (i.e., light and nitrate). Although it could be that nutrients, light and temperature relationships need to be adjusted to improve model skill in the Arctic Ocean, such a regional tuning is, however, not possible for global BOGCMs and ESMs.

Simulated NPP may be low due to not only limiting factors, but also because of too little biomass, e.g., through excessive loss of carbon from or in the upper water column. Vertical export of organic matter is parameterized in all models. The organic carbon to organic nitrogen stoichiometric ratio in sinking particulate matter has been shown not to be constant in Arctic waters [Tamelander et al., 2013; Michel et al., 2006], as assumed in most models. Arctic phytoplankton are also known to have large exudation levels during certain phases of their growth cycle [Vernet et al., 1998; Laroche et al., 1999] which promotes the formation of sinking aggregates, resulting in significant carbon export from the surface layer when large phytoplankton cells dominate [Reigstad et al., 2011; Wassmann et al., 2006]. Changes in phytoplankton species composition and bloom phenology in Arctic waters are also being reported. These changes include shifts toward smaller cells, possibly with different physiology, especially in the freshening Beaufort Sea and Canadian Arctic Archipelago [Li et al., 2009; Tremblay et al., 2009], which will again affect vertical export fluxes. Changes in bloom phenology have been described as lengthening bloom periods or even the presence of fall blooms (reviewed by Babin et al. [2015]; Michel et al. [2006, 2015]). However, these changes are fairly recent and likely not yet simulated by models nor captured by the in situ data used for our exercise, despite covering five decades back (i.e., diminishing the likelihood of an effect in our field data set).

If bottom-up factors were not the main or sole controls on phytoplankton productivity, grazing could be: not only may grazers reduce NPP but they also regulate vertical flux. If simulated grazing rates were too high, then the resulting nutrient concentrations would be much higher than the values of the high saturation constants used. This scenario was ruled out for high latitudes by a PISCES-based model simulation in which bottom-up controls did dominate [Aumont et al., 2015]. On the other hand, the northward advective inflow of sub-Arctic water has been reported to also carry significant zooplankton biomass [Wassmann et al., 2015]. Hence, it is possible that the Arctic Ocean primary production in model simulations might be reduced under increased grazing pressure from such sub-Arctic (expatriate) zooplankton. Such a hypothetical extension of sub-Arctic grazing influence to the interior regions of the Arctic Ocean is not currently supported by observations [Kosobokova and Hopcroft, 2010]. Much is changing with respect to trophic structure in the Arctic Ocean, including grazer community composition and biodiversity [Bluhm et al., 2015], all of which may or may not be simulated by the models, with consequences for estimating iNPP. However, we currently lack a comprehensive review and climatology for in situ micro, meso, and macrozooplankton growth and grazing rates in the Arctic Ocean to broadly assess model relative skill.

Our use of an in situ NPP database allowed the assessment of model skill in ice-influenced as well as in ice-free waters, overcoming a limitation encountered by previous model intercomparison exercises for the Arctic Ocean [e.g., Popova et al., 2012; Vancopenolle et al., 2013] that depended on satellite-derived NPP, which is not available for ice-covered regions. Regardless of whether sea ice was present or not, the mean and variance of in situ iNPP were almost identical, confirming that the ice-influenced regions could be as productive as the ice-free regions (Table 2). It should be noted that the similarity could be due to biased seasonal coverage by field studies in ice-free waters, introducing more measurements collected in late summer and fall (i.e., September), thus lowering the ice-free iNPP average (not shown). Alternatively, the similarity in simulated iNPP values in ice-free and ice-influenced areas could result from the averaging of regional differences previously observed in field and satellite-derived NPP data [e.g., Arrigo et al., 2012; Hill et al., 2013; Ardyna et al., 2013] as well as in model simulations [e.g., Zhang et al., 2015]. Recently, Jin et al. [2016] showed that simulated under-ice production is also regionally different (i.e., higher in the Arctic shelves, possibly due to enhanced nutrient supply) [Zhang et al., 2015], but not necessarily related to the recent decrease in sea ice concentration, especially in marginal ice zones. Regardless of whether NPP was measured in deep versus shallow areas or ice-influenced versus open water regions, model skill for iNPP differed little on such spatial scales.

Time did make a difference, however. Model skill varied from decade to decade, and higher model skill was found for the most recent decade (Figures 4e and 4f) when in situ iNPP and NO₃ were lower (Table 2), since the models performed better with low iNPP. For example, on a pan-Arctic scale, in situ carbon uptake rates decreased to 177 mg C m⁻² d⁻¹ (N = 344; 2000–2011) compared to 316 mg C m⁻² d⁻¹ in the earlier decades (N = 391; 1959–1989). Similarly, in situ depth-averaged NO₃ decreased from 5.1 mmol m⁻³ (N = 284; 1979–1999) to 2.9 mmol m⁻³ (N = 379; 2000–2011). These decreases likely resulted from differences in geographical sampling distribution between decades (Figure 1). For example, during 2000–2011, more data were available from the large Canadian and International Polar Year programs in low production regions, such as the Beaufort Sea and the central Arctic Basin (Figure 1c). Not all of the participating models captured these decreasing changes in simulated iNPP and NO₃ (not shown). However, regardless of whether model iNPP estimates increased or decreased over the most recent decade, simulated iNPP values became more comparable to in situ values on a pan-Arctic scale, such that model skill was seen to be improved in more recent years (Figures 4e and 4f). On a seasonal time-scale, the models generally performed poorly in the beginning of the growing season (April–June) compared to later months (Figures 4g and 4h). For some models, this could be due to insufficient penetration of winter mixing, as the main mechanism controlling basin-scale patterns of nutrient supply [e.g., Popova et al., 2012]; though, as stated earlier, MLD was overestimated overall (Figure 9a). Also occurring at this time is the critical balance between the onset and phenology of sea ice melting, ice algal bloom, and/or phytoplankton bloom; small mismatches in timing among them resulted in a large variability of simulated phytoplankton availability, especially at the Arctic marginal seas [Ji et al., 2013].

Model quantification of biogeochemical processes is highly dependent on how accurately physical fields are simulated [Friedrichs et al., 2006; Popova et al., 2012]. Submesoscale physical features are especially important to biogeochemical processes affecting the horizontal and vertical distribution of nutrients and phytoplankton biomass [Watanabe et al., 2014]. Most of the participating models are developed on global scales and only four of them are regional models of the order of 10 km resolution (Table 1). The Rossby radius of deformation is dramatically reduced with increasing latitude and it becomes less than 10 km in the Arctic Ocean. Hence, those models with resolution of the order of 10–100 km may not adequately resolve submesoscale physical features at the surface layer that are likely critical for Arctic biogeochemical processes—in particular—regionally [Timmermans et al., 2012], rather than larger-scale physical processes determining the response of the pan-Arctic marine ecosystem. High spatial resolution models or more Arctic-appropriate parameterizations and closures are necessary to capture small-scale physical processes, such as eddies, tides, fronts, internal waves as well as interactions between shelf and open ocean or sea and ice processes, that can influence phytoplankton growth, especially in high-productivity, coastal shelf regions adjacent to sub-Arctic waters. Indeed, regionally, model skill patterns are contradictory, such that the Greenland Sea has a very closely simulated surface and deep NO₃ and MLD (Table 4) but the least skill in simulated sea ice concentration (Figure 9c); yet it has the lowest skill in iNPP, underestimating it (Figure 6f). Conversely, the Beaufort Sea shows medium skill in deep NO₃, least skill in surface NO₃ (overestimating concentrations) and yet the best skill in iNPP (Table 4)—still underestimating iNPP and its variability (Figure 6b), though less than other Arctic Ocean subregions. Assuming improved parameterization of nutrient, light, and temperature relationships of phytoplankton growth, a higher spatial resolution model could potentially produce significant subregional features [e.g., Yool et al., 2015], as mesoscale and submesoscale processes have been shown to stimulate biological productivity in lower latitudes [McGillicuddy et al., 1998; Oschlies and Garcon, 1998; Lévy et al., 2001]. Finally, coastal regions, characterized by elevated primary productivity are also not properly resolved by a coarse model grid, in general [Aumont et al., 2015]. Higher resolution in ecosystem complexity has already been shown to lead to improved realism of BOGCM high latitude simulations, with the addition of slow growing macrozooplankton leading to the successful representation of the different bloom dynamics in the Southern Ocean [Le Quéré et al., 2016]. Much effort is now being applied in the modeling community to introduce high-resolution strategies into BOGCMs, especially those regionally focused on the Arctic Ocean [Interagency Arctic Research Policy Committee, 2013], with the hope that reproducing meso and submesoscale processes and features will improve their predictive skill for iNPP and other biogeochemical properties in the Arctic Ocean.

6. Summary and Recommendation

Using in situ, satellite-derived, and climatological data, we have analyzed model estimates of iNPP and NO₃ associated with physical variables such as MLD, Z_eu, and sea ice concentration from 21 BOGCMs and ESMs during the period of 1959–2011, although the time span of simulation as well as the initialization and forcing were different among the participating models. No models fully reproduced the variability of in situ measurements, whereas some of them exhibited almost no bias. Generally, the models captured the spatial features of the iNPP distribution: lower iNPP in the interior regions and higher iNPP in the inflow regions. The models exhibited different regional characteristics in estimating iNPP since each model’s skill was a function of environmental factors with distinctive sensitivity in one region versus another. For example, MLD and NO₃ were reproduced well in the Atlantic-side inflow and outflow regions, Z_eu had greater skill in the interior regions, and sea ice concentration was reasonably well estimated everywhere, except in the Greenland Sea. Most of the models generally underestimated mean iNPP, in spite of overestimating Z_eu and surface NO₃, especially in the Chukchi and Greenland Seas where mean in situ iNPP is high. Regionally, model iNPP was best estimated in the regions where simulated surface NO₃ was most overestimated relative to in situ values and where both sea ice concentration and Z_eu were reproduced well, such as the Beaufort Sea and the central Arctic Basin. By contrast, iNPP exhibited the largest model-data disagreement in the Greenland Sea where the simulated surface NO₃ and MLD had greater model skill, but sea ice concentration had lower model skill.

The Arctic Ocean appears to be experiencing a fundamental shift from a polar to a temperate mode, which is likely to alter its marine ecosystem [Yool et al., 2015; Wassmann et al., 2015]. Under a changing climate, sea ice loss, shifts in composition and distribution of phytoplankton functional types, and bloom phenology changes already play a role in the Arctic Ocean marine ecosystem [e.g., Li et al., 2009; Ardyna et al., 2014]. Globally, changes in nutrient and light availability have emerged as the most important determinants in models for alterations in simulated growth rates, with light generally playing a lesser role, except for the very high latitudes, particularly the Arctic Ocean [Laufkötter et al., 2015]. At these high latitudes, temperature does not appear to play a physiological role but could well play an ecological role of controlling phytoplankton bloom composition and phenology [Babin et al., 2015]. Thus, ecosystem processes and algal physiology in models need to be carefully parameterized for the Arctic Ocean in order to better quantify uncertainties in estimating primary production, including under-ice primary production and ice algae production [Leu et al., 2015; Jin et al., 2016]; enhanced functional types for all levels of the marine food web [Babin et al., 2015]; and, the role of horizontal advection of planktonic organisms versus their vertical export [Wassmann et al., 2015]. Furthermore, it is necessary to resolve submesoscale physical processes to decide the apparently contradictory bottom-up controls of NPP and the resulting biogeochemical cycles in the various subregions of the Arctic Ocean, with the hope that BOGCMs and ESMs perform within the uncertainty due to natural variability. Last but not least, models will continue to improve their skill when additional validating data sets and climatologies are gathered and openly shared for relevant biogeochemical, physiological, and ecological variables in the Arctic Ocean.

Key Points:

• Arctic models underestimated net primary productivity (NPP) but overestimated nitrate, mixed layer depth, and euphotic depth

• Arctic NPP model skill was greatest in low production regions

• Arctic NPP model skill was constrained by different environmental factors in different Arctic Ocean regions

Appendix A: Brief Description of Participating Models

A1. Model 1

HYCOM-NORWECOM [Samuelsen et al., 2015] is a regional coupled physical-biogeochemical model with 11 compartments in the biogeochemical model. The physical model is the Hybrid Coordinate Ocean Model (HYCOM) [Bleck, 2002] adapted to the North Atlantic and Arctic Ocean [Bertino and Lisaeter, 2008]. The model encompasses the entire North Atlantic and has open lateral boundaries at the Bering Strait in the Pacific Ocean and near the equator between 3°S and 16°S in the Atlantic Ocean; the model is relaxed toward climatological values at the lateral boundaries. The model is forced by ERA-Interim [Dee et al., 2011], hydrological forcing from TRIP [Oki and Sud, 1998], but does not include tidal forcing. The sea ice model uses an elastic-viscous-plastic (EVP) rheology [Hunke and Dukowicz, 1997] while thermodynamics are described in Drange and Simonsen [1996]. NORWEgian ECOlogical Model (NORWECOM) [Aksnes et al., 1995; Skogen and Søiland, 1998] is coupled online to HYCOM and uses HYCOM facility for advection of tracers and has the same time-step as the physical model. The current model version includes two classes of phytoplankton (diatom and flagellates), two classes of zooplankton (meso and microzooplankton) derived with the same formulation from the model ECOHAM4 [Pätsch et al., 2009], three types of nutrients (N, P, and Si) and detritus (N and P), biogenic Si, and oxygen (O₂). Additionally, riverine nutrient loads are based on the results from the Global-NEWS model [Seitzinger et al., 2005]. The model assumes a constant element ratio (i.e., Redfield) as well as constant chlorophyll:N ratio in phytoplankton. In the model, light does not propagate through sea ice; therefore, the model is not expected to yield realistic primary production and nutrients in areas with thin ice cover where light actually is available for primary production.

A2. Model 2

This global biogeochemical model (1998–2014) uses the PISCES formulation on the horizontal curvilinear grid ORCA025 and 75 vertical levels. It is forced offline by daily fields of an ocean circulation simulation: Nucleus for European Modelling of the Ocean (NEMO)-Océan PArallélisé (OPA) (version 3.1) [Madec, 2008]. Atmospheric forcings are 3 hourly ERA-Interim reanalysis product with the CORE bulk formulation. There is no assimilation of physical data. The sea ice model is the Louvain la Neuve sea Ice Model version 2 (LIM2) with EVP rheology [Fichefet and Morales Maqueda, 1997]. PISCES (volume 2) [Aumont et al., 2015] is a model of intermediate complexity designed for global ocean applications and is a component of the NEMO modeling system. It has 24 prognostic variables and simulates biogeochemical cycles of O₂, C, and the main nutrients controlling phytoplankton growth (NO₃, ammonium (NH₄), phosphate (PO₄), silicate (SiO₄), and Fe). The model distinguishes four plankton functional types based on size: two phytoplankton groups (nanophytoplankton and diatoms) and two zooplankton groups (micro and mesozooplankton). PISCES traces three nonliving pools for small and big particulate organic carbon (POC), and semilabile dissolved organic carbon (DOC). Version 3.5 of NEMO-PISCES with default parameter set is used here. The configuration is described and assessed in the Product User Manual and Quality Information Document (http://marine.copernicus.eu/documents/PUM/CMEMS-GLO-PUM-001-018.pdf and http://marine.copernicus.eu/documents/QUID/CMEMS-GLO-QUID-001-018.pdf). Daily and monthly mean outputs are available on Copernicus Marine Service website (http://marine.copernicus.eu).

A3. Model 3

This model is the Plankton Types Ocean Model 5.3 (PlankTOM5.3) biogeochemical model coupled to the NEMO (version 2.3) global ocean circulation model and sea ice model (LIM2). The biological model is a 26 component marine pelagic ecosystem model, including three phytoplankton components (diatoms, coccolithophores, and mixed phytoplankton), two zooplankton components (micro and mesozooplankton), DOC, small and large detrital POC and particulate organic Fe, detrital particulate Si and calcite, and dissolved NO₃, SiO₄, and Fe [Buitenhuis et al., 2013]. Each phytoplankton functional type has C, chlorophyll, and Fe components, linked with a dynamic photosynthesis model [Buitenhuis and Geider, 2010]. The standard simulation was spun up from 1920 to 1955, and for the purpose of this paper the optimized simulation was run from 1956 to 2013 [Buitenhuis et al., 2013].

A4. Model 4

This model is the Plankton Types Ocean Model 10 (PlankTOM10) biogeochemical model coupled to the NEMO (version 3.1)-LIM2 ocean circulation and sea ice model. The biological model is a 37 component marine pelagic ecosystem model, including six phytoplankton components (diatoms, coccolithophores, picophytoplankton, N₂-fixers, phaeocystis, and mixed phytoplankton), three zooplankton components (micro, meso, and macrozooplankton), bacteria, DOC, small and large detrital POC and particulate organic Fe, detrital particulate Si and calcite, and dissolved NO₃, SiO₄, and Fe [Le Quéré et al., 2016]. PlankTOM10 has the same dynamic photosynthesis model as PlankTOM5.3 (Model 3). In addition, it has an improved representation of the difference between the high latitude Northern and Southern Hemisphere phytoplankton blooms through the representation of slow growing macrozooplankton. The different physical settings result in different overwintering macrozooplankton populations, in turn leading to different trophic cascades and more realistic phytoplankton blooms [Le Quéré et al., 2016].

A5. Model 5

The Carbon, Ocean Biogeochemistry, and Lower Trophics (COBALT) version 1.0 marine ecosystem model uses 33 state variables to resolve global-scale cycles of C, N, P, Si, Fe, calcium carbonate (CaCO₃), O₂, and lithogenic material [Stock et al., 2014a]. COBALT derives many elements of its biogeochemical formulation from the TOPAZ model (see Model 6). However, COBALT enhances the resolution of planktonic food web dynamics to better understand the climate impacts on the flow of energy from phytoplankton to fish [Stock et al., 2014b]. The model includes three phytoplankton groups (small, large, and diazotrophs) and uses the variable chlorophyll:C formulation of Geider et al., [1997] to estimate NPP. Results contributed to this study were conducted with the Modular Ocean Model (MOM) version 4p1 [Griffies, 2012] with sea ice dynamics as described in Winton [2000]. The model was run on a global domain with a nominal spatial resolution of 18 and a tripolar Arctic grid. The model uses 50 vertical layers with a nominal resolution of 10 m over the top 200 m. Simulations are forced with the Coordinated Ocean-ice Reference Experiment version 2 (CORE2) data set [Large and Yeager, 2009]. The 60 year forcing period was looped twice and results from the second loop provided for this study. Surface salinity is relaxed to observations with 2 month relaxation time-scale in order to avoid salinity drifts characteristic of long integrations of ocean-ice simulations without fully coupled atmosphere dynamics [Griffies et al., 2009]. Complete details of the simulation and model validation can be found in Stock et al. [2014a].

A6. Model 6

Tracers of Ocean Phytoplankton with Allometric Zooplankton version 2.0 (TOPAZ2) is an ocean biogeochemical and ecological model developed at NOAA’s Geophysical Fluid Dynamics Laboratory for global Earth System Model simulations contributed to the 5th assessment report of the Intergovernmental Panel on Climate Change [Dunne et al., 2012b,2013]. TOPAZ2 includes 30 tracers to describe the cycles of C, N, P, Si, Fe, O₂, alkalinity, and lithogenic material as well as surface sediment calcite dynamics [Dunne et al., 2012a]. TOPAZ2 considers three explicit phytoplankton groups (small, large, and diazotrophs) that utilize a modified growth physiology after Geider et al. [1997] with Eppley [1972] temperature functionality and iron colimitation with luxury uptake after Sunda and Huntsman [1997]. CO₂:NO₃:O₂ stoichiometry is 106:16:150 after Anderson [1995]. N:P is based on optimal allocation after Klausmeier et al. [2004]. Complete technical details are available in the supplementary information of Dunne et al. [2013]. Results contributed to this study were conducted with the MOM (version 4p1) [Griffies, 2012] with sea ice dynamics as described in Winton [2000]. The model was run on a global domain with a nominal spatial resolution of 18 and a tripolar Arctic grid. The model uses 50 vertical layers with a nominal resolution of 10 m over the top 200 m. Simulations are forced with the CORE2 data set [Large and Yeager, 2009]. The 60 year forcing period was looped twice and results from the second loop provided for this study. Surface salinity is relaxed to observations with 2 month relaxation time-scale in order to avoid salinity drifts characteristic of long integrations of ocean-ice simulations without fully coupled atmosphere dynamics [Griffies et al., 2009].

A7. Model 7

SINMOD is a model system that has been continuously developed over 30 years and includes a hydrodynamic and a sea ice module [Slagstad and McClimans, 2005], an ecosystem module [Wassmann et al., 2006], and stage resolved zooplankton models [Slagstad and Tande, 2007]. The hydrodynamic model is based on the primitive Navier-Stokes equations and is established on a Z-grid [Slagstad and McClimans, 2005]. The ice model is similar to that of Hibler [1979] and has two state variables: ice thickness and ice concentration. The ice momentum equation is solved together with an equation for the ice internal stress, using the EVP dynamical model of Hunke and Dukowicz [1997]. The ecosystem model includes nutrients (NO₃, NH₄, and SiO₄), phytoplankton (diatoms and flagellates), bacteria, heterotrophic nanoflagellates, microzooplankton, and two mesozooplankters: the Atlantic Calanus finmarchicus and the arctic C. glacialis, two compartments for fast and slow sinking detritus, DOC, and sediments. The model uses constant stoichiometry with a C:N ratio equal 7.6, based upon average data from the Barents Sea [Reigstad et al., 2002]. In the present study, SINMOD data are from a pan-Arctic configuration with 20 km horizontal grid resolution and with 25 vertical layers. Forcing fields includes atmospheric forcing from the ERA-Interim reanalysis (http://www.ecmwf.int) [Dee et al., 2011], tides from TPXO 6.2 model prescribed at open boundaries, and freshwater run-off from R-ArcticNet (http://www.r-arcticnet.sr.unh.edu/). More details of the recent updates of SINMOD and the model setup may be found in Slagstad et al. [2015].

A8. Model 8

The NorESM-OC is the ocean component of the Norwegian Earth System Model (NorESM). It is a coupled BOGCM, which comprises the Miami Isopycnic Coordinate Ocean Model (MICOM) coupled with the Hamburg Oceanic Carbon Cycle (HAMOCC)−5 model [Schwinger et al., 2016]. HAMOCC consist of a Nutrient-Phytoplankton-Detritus-Zooplankton (NPDZ)-type ecosystem model, where the primary production is formulated as a function of phytoplankton growth and nutrient concentration within the euphotic layer (fixed at 100 m). In addition to multinutrients (i.e., NO₃, PO₄, and dissolved Fe) colimitation, the phytoplankton growth is regulated by light availability and temperature. The model adopts a generic single class phytoplankton and zooplankton compartment. The particulate materials (i.e., POC, biogenic opal, and CaCO₃) produced at the surface sink with constant velocities and are remineralized at depth. The production of surface opal and CaCO₃ is determined by the SiO₄ availability at the surface. Nonremineralized particles reaching the seafloor undergo chemical reactions with sediment pore waters, bioturbation, and vertical advection within the sediment module. For the simulation produced in this study, the NorESM-OC was forced by the CORE2 atmospheric reanalysis data.

A9. Model 9

This model is the Biology/Ice/Ocean Modeling and Assimilation System (BIOMAS), a coupled biophysical model [Zhang et al., 2010a] with four model elements: an ocean circulation model, a sea ice model, a pelagic biological model, and a sea ice algae model. The ocean circulation model is based on the Parallel Ocean Program (POP), developed at Los Alamos National Laboratory [Smith et al., 1992] and modified by Zhang and Steele [2007] so that open boundary conditions can be specified. The POP ocean model is further modified by Zhang et al. [2010b] to incorporate tidal forcing from eight primary constituents [Gill, 1982]. The sea ice model is a thickness and enthalpy distribution (TED) sea ice model [Zhang and Rothrock, 2003; Hibler, 1980], with eight categories each for ice thickness, ice enthalpy, and snow depth. It is adopted from the Pan-arctic Ice/Ocean Modeling and Assimilation System (PIOMAS) [Zhang and Rothrock, 2003] and capable of assimilating satellite observations of sea ice concentration [Lindsay and Zhang, 2006] and sea surface temperature [Manda et al., 2005; Schweiger et al., 2011]. The pelagic biological model is an 11 component marine pelagic ecosystem model, including two phytoplankton components (diatoms and flagellates), three zooplankton components (microzooplankton, copepods, and predatory zooplankton), dissolved organic nitrogen (DON), detrital particulate organic nitrogen (PON), particulate organic Si, NO₃, NH₄, and SiO₄ (see Figure 3 in Zhang et al. [2014]; also see Kishi et al. [2007]). Values for key biological parameters used in the model are listed in Zhang et al. [2010a]. The sea ice algal component of BIOMAS represents colonies in a 2 cm layer at the bottom of each of eight sea ice thickness categories, coupled to the pelagic model through nutrient and biotic fluxes. The sea ice algae model has two ice algae components (diatoms and flagellates), with NO₃, NH₄, and SiO₄ as limiting nutrients for ice algal growth. Nutrient and biotic exchange at the sea ice and water interface is based on Jin et al. [2006].

A10. Model 10

This model is NEMO (version 3.2)-MEDUSA, a coupled biophysics model comprised of an ocean general circulation model (OGCM), a sea ice model, and a representation of marine biogeochemistry [Popova et al., 2010, 2012]. Ocean circulation is modeled using OPA version 9 (OPA9) [Madec, 2008], a primitive equation model configured at global-scale, with a horizontal resolution of approximately 0.25° and 64 grid levels in the vertical [Popova et al., 2010]. The model grid is tripolar with cell sizes ranging approximately 6.8–15.4 km horizontally, and increasing in thickness from 6 m at the surface to approximately 250 m at abyssal depths. OPA9 includes partial level thicknesses at the seafloor to improve bottom circulation, and a parameterized turbulent kinetic energy scheme for vertical mixing [Gaspar et al., 1990; Madec, 2008]. The model is forced at the surface using bulk formulae [Large and Yeager, 2004] fed using DFS4.1 climatology fields of atmospheric properties and downward heat and freshwater fluxes [DRAKKAR Group, 2007]. Sea ice is represented with LIM2 [Timmermann et al., 2005], based on a viscous-plastic ice rheology [Hibler, 1979] with three layer (two ice and one snow) thermodynamics [Semtner, 1976]. LIM2 is coupled to OPA9 every five ocean time steps through a nonlinear quadratic drag law of ocean-ice shear [Timmermann et al., 2005], and represents detailed heat and freshwater fluxes [Fichefet and Morales Maqueda, 1997]. OPA9 and LIM2 are combined as the NEMO physical model [Madec, 2008]. Marine biogeochemistry is represented using the Model of Ecosystem Dynamics, nutrient Utilization, Sequestration, and Acidification (MEDUSA) [Yool et al., 2011]. This includes the N, Si, and Fe cycles in a model of the pelagic ecosystem that resolves nanophytoplankton, diatoms, and micro and mesozooplankton, as well as size-resolved (small and large) detrital material, including biomineral ballasting [Armstrong et al., 2002]. MEDUSA has simplified seafloor remineralization of organic material and does not explicitly include sea ice algae.

A11. Model 11 and 12

NEMO (version 3.2)-European Regional Seas Ecosystem Model (ERSEM) is a global ocean model that includes the NEMO ocean circulation model, the ERSEM marine biogeochemistry model, and the Los Alamos sea ice model (CICE). NEMO (version 3.2) is a framework of ocean related engines, ocean dynamics, thermodynamics, sinks and sources, and transport [Madec, 2008]. The CICE model [Hunke et al., 2013] has several interacting components: a thermodynamic submodel, an ice dynamics submodel, a vertical and a horizontal transport submodel. ERSEM is a lower trophic level biogeochemical cycling, carbon-based process model that uses the functional-group approach [Blackford et al., 2004; Butenschön et al., 2016]. The C, N, P, Si, and Fe cycles are explicitly resolved with variable stoichiometry. The pelagic ERSEM model simulates four phytoplankton functional types, three zooplankton functional types, one bacterial functional type, and six detritus size classes. The benthic ERSEM is a simple parameterization of remineralization where sedimented organic matter is recycled to the water column in inorganic form. The simulations were run as part of the iMarNet project: an intercomparison project of six UK biogeochemical models [Kwiatkowski et al., 2014]. The simulation of Model 12 (xhonc) uses an updated configuration of the ERSEM model, with a new iron model, updated food web, and reduced detrital sinking rate relative to the simulation of Model 11 (xhonp).

A12. Model 13

PELAgic biogeochemistry for Global Ocean Simulations (PELAGOS) [Vichi et al., 2007a,2007b] is a global ocean biogeochemical model that consists of the coupling between the NEMO (version 3.4) [Madec, 2008] and the Biogeochemical Flux Model (BFM, version 5.1, http://bfm-community.eu) [Vichi et al., 2015a]. The ocean model is computed on the ORCA2 grid that has a nominal resolution of 2° with a refinement of the latitudinal grid size toward the equator down to 0.5°, with 30 vertical levels and partial step parameterization to increase the resolution of bottom gradients. The physical parameterizations are as in Vichi et al. [2007b]. The sea ice model is LIM2 and the BFM model can directly be coupled with NEMO [Vichi et al., 2015b]. The BFM is based on a biomass continuum description of the lower trophic levels of the marine system [Vichi et al., 2015b]. The model implements a set of biomass-based differential equations that solve the fluxes of C, N, P, Si, and Fe among selected biological functional groups representing the major components of the lower trophic levels. The functional groups in the pelagic environment are represented by unicellular planktonic autotrophs (pico and nanophytoplankton and diatoms), zooplankton (nano, micro, and mesozooplankton) and heterotrophic oxic and anoxic bacterioplankton. The model also simulates the dynamics of NO₃, NH₄, PO₄, biogenic Si, Fe, O₂, and it has an explicit parameterization of the biochemical cycling of dissolved/particulate nonliving organic matter. Another peculiarity of the model is that the nutrient stoichiometry is not fixed and therefore the ratios of C to N, P, and Si can vary within the living functional groups as well as the chlorophyll:C ratio in phytoplankton. This simulation includes nutrient river inputs from Cotrim da Cunha et al. [2007] but no benthic remineralization.

A13. Model 14

A marine biogeochemical (mBGC) module [Moore et al., 2004; Jin et al., 2012, 2016] is incorporated in a global version of the POP-CICE model developed at Los Alamos National Laboratory. A subgrid-scale ocean mixing scheme [Jin et al., 2012] was added to reduce model errors in simulated mixed layer depth, salinity, and nutrients in the Arctic Ocean. The pelagic component of mBGC includes 26 state variables of multiple nutrients, phytoplankton, zooplankton, and detritus. The ice algal component of mBGC represents colonies in a 3 cm layer at the bottom of each sea ice thickness category, coupled to the pelagic model through nutrient and biotic fluxes. This submodel was based on biophysical ice core data collected in land-fast ice offshore from Barrow, Alaska [Jin et al., 2006] and coupled with a pelagic ecosystem model in vertically 1-D models [Jin et al., 2007] and global POP-CICE model settings [Deal et al., 2011; Jin et al., 2012, 2016].

A14. Model 15

This model is based on the ocean circulation model OPA, the dynamical component of NEMO (version 3.5). It solves the primitive equations on the Arakawa C-grid, with a second-order centered finite difference scheme [Madec, 2008]. It assumes the Boussinesq and hydrostatic approximations, the incompressibility hypothesis, and uses a free-surface formulation [Roullet and Madec, 2000]. The density is computed from potential temperature, salinity, and pressure using the Jacket and Mcdougall [1995] equation of state. Vertical mixing is computed from a turbulence closure scheme based on a prognostic vertical turbulent kinetic equation, which performs well in the tropics [Blanke and Delecluse, 1993]. Partial step formulation of bottom topography is used instead of a full step one [Bernard et al., 2006]. LIM2 is a two-level thermodynamic-dynamic sea ice model in which sensible heat storage and vertical heat conduction within snow and ice are determined by a three-layer model (one layer for snow and two layers for ice) [Fichefet and Morales Maqueda, 1997; Bouillon et al., 2009]. PISCES is the biogeochemical component of NEMO and it simulates the lower trophic levels of marine ecosystem and the biogeochemical cycles of carbon and of the main nutrients (P, N, Fe, and Si) [Aumont and Bopp, 2006]. There are 24 prognostic variables including two phytoplankton compartments (diatoms and nanophytoplankton), two zooplankton size-classes (micro and mesozooplankton) and a description of the carbonate chemistry. Formulations in PISCES are based on a mixed Monod-Quota formalism: on one hand, stoichiometry of C, N, and P is fixed and growth rate of phytoplankton is limited by the external availability in N, P, and Si. On the other hand, the Fe and Si quotas are variable and growth rate of phytoplankton is limited by the internal availability in Fe. There are three nonliving compartments: semilabile-dissolved organic matter, small and big sinking particles.

A15. Model 16

This simulation is based on the global ocean biogeochemical model NEMO-PISCES. NEMO (version 3.4) was run with horizontal resolution of up to 1° by 1° (globally 362 longitude × 292 latitude grid points) and with 46 vertical levels. The model results are available for 2002–2011. For those years, external ocean-surface forcing was specified from the CORE2 (2002–2007) and NCEP/DOE AMIP-II Reanalysis (Reanalysis-2) data (2008–2011). The ocean circulation model is based on the hydrostatic, primitive equation model OPA [Madec et al., 1998], and is a finite difference OGCM with a free sea surface. OPA uses a global tripolar orthogonal curvilinear grid to avoid singularity points inside the computational domain and attain the ratio of anisotropy of nearly one [Madec and Imbard, 1996]. The variables are distributed on a 3-D Arakawa-C type grid. The sea ice model (LIM3) is a C-grid dynamic-thermodynamic model, including the representation of the subgrid-scale distributions of five-category sea ice thickness, enthalpy, salinity, and age distributions. The representation of sea ice is done through a velocity vector and a series of ice state variables described in Vancoppenolle et al. [2009a]. Brine entrapment and drainage as well as brine impact on ice thermodynamics and a snow ice formation scheme are explicitly included [Vancoppenolle et al., 2009a, 2009b]. The biogeochemical model used is PISCES (volume 2) [Aumont et al., 2015]. It has 24 prognostic variables and simulates the lower trophic levels of marine ecosystems and the biogeochemical cycles of O₂, C, and the main nutrients (P, N, Fe, and Si). The model distinguishes four plankton functional types based on size: two phytoplankton groups (nanophytoplankton and diatoms) and two zooplankton groups (micro and mesozooplankton). Prognostic phytoplankton variables are total biomass in C, Fe, Si (for diatoms) and chlorophyll and hence the Fe:C, Si:C, chlorophyll:C ratios are fully predicted by the model. For zooplankton, all O, C, N, and P ratios are kept constant and total biomass in C is the only prognostic variable. The bacterial pool is not modeled explicitly.

A16. Model 17

This simulation is based on the NEMO-PISCES model. The ocean component uses NEMO (version 3.2) [Madec, 2008] in the ORCA1 configuration with horizontal resolution from 1° in polar regions to 1/3° near the equator and 42 vertical levels. This configuration includes an improved Turbulent Kinetic Energy (TKE) closure scheme based on Blanke and Delecluse [1993]. The ocean radiative scheme is represented by three-wave-band scheme of Lengaigne et al. [2007], which accounts for influence of phytoplankton chlorophyll. The sea ice model is GELATO5 [Salas Mélia, 2002], which considers four ice thickness categories (0–0.3 m, 0.3–0.8 m, 0.8–3 m, and over 3 m). Each category has 10 vertical layers with enhanced resolution near the top of the slab. The sea ice dynamics is represented by the EVP rheology [Hunke and Dukowicz, 1997]. The biogeochemical model PISCES [Aumont and Bopp, 2006] simulates the biogeochemical cycles of O₂, C, and the main nutrients: NO₃, NH₄, PO₄, SiO₄, Fe, two sizes of phytoplankton, two sizes of zooplankton, semilabile-dissolved organic matter, and small and big sinking particles. Three different sources supply nutrients: atmospheric dust deposition [Tegen and Fung, 1995; Jickells and Spokes, 2001; Moore et al., 2004], rivers [Ludwig et al., 1996], and sediment mobilization [Johnson et al., 1999; de Baar and de Jong, 2001]. The model input of riverine-dissolved inorganic carbon (DIC) and DOC is taken from the annual estimates of the Global Erosion Model [Ludwig et al., 1996]. The DOC from rivers is assumed to be labile and is directly converted to DIC upon its delivery to the ocean. Inputs of dissolved Fe, NO₃, PO₄, and SiO₄ are computed from the sum of DIC and DOC river input using a constant set of ratios for C:N:P:Si:Fe as computed from Meybeck [1982] for C:N, from Takahashi et al. [1985] for N:P, from de Baar and de Jong [2001] for Fe:C, and from Tréguer et al. [1995] for Si:C. More complete descriptions of the whole ocean-sea ice and marine biogeochemistry component are provided by Voldoire et al. [2013] and Séférian et al. [2013], respectively.

A17. Model 18

This model is the MIT general circulation model (MITgcm) [Marshall et al., 1997] coupled with a sea ice model and with a pelagic biogeochemical model. The coupled model is configured on a “cubed-sphere” grid encompassing the Arctic domain with open boundaries at around 55°N in the Atlantic and Pacific sectors. Prescribed boundary conditions for potential temperature, salinity, flow, and sea surface elevation are provided from previous integrations of a global configuration of the same model [Menemenlis et al., 2005]. The sea ice component follows the viscous-plastic rheology formulation of Hibler [1979] with momentum equations solved implicitly on a C-grid [Arakawa and Lamb, 1977] using a procedure based on Zhang and Hibler [1997]. The biogeochemical component, improved from previous applications in Arctic waters [Le Fouest et al., 2011, 2013], has 10 state variables [see Le Fouest et al., 2015, Figure 1]. Equations and biological parameters are listed in Le Fouest et al. [2005]. It includes NO₃, NH₄, 2 size-fractionated phytoplankton and zooplankton, DON, PON, bacteria, and riverine DON (RDON) that couples the marine and terrestrial cycling of N. The RDON flux is based on the approach developed by Manizza et al. [2009] using seasonally explicit regression relationships quantifying the covariation between freshwater discharge and measured RDON.

A18. Model 19

The NorESM is a fully coupled climate-biogeochemical model [Tjiputra et al., 2013]. It is the fully coupled version of Model 8 described above. In this configuration, the NorESM-OC is coupled with atmospheric general circulation (modified from Community Atmospheric Model, CAM4), land (Community Land Model, CLM4), and sea ice (CICE version 4). For the simulation performed in this study, we apply the standard Coupled Model Intercomparison Project phase 5 (CMIP5) protocol for the historical and future high CO₂ (RCP8.5) scenario.

A19. Model 20

The GISS-E2-R-CC is a coupled atmosphere-land-ocean-ice model with ocean biogeochemistry explicitly simulated [Romanou et al., 2013, 2014]. GISS-E2 is the GISS atmospheric model within the coupled climate model, which was submitted in the CMIP5 [Schmidt et al., 2014], and which employs a very accurate and nondiffusive quadratic upstream differencing scheme for the advection of tracers such as CO₂. The GISS-E2-R ocean model [Russell et al., 1995; Hansen et al., 2007] is a non-Boussinesq mass-conserving ocean model with a free surface and natural surface boundary fluxes of freshwater and heat. It uses the Gent and Mcwilliams [1990] scheme for isopycnal eddy fluxes and isopycnal thickness diffusion and the K-Profile Parameterization (KPP) [Large et al., 1994] for vertical mixing, with nonlocal mixing effects included. The GISS-E2 sea ice model includes improvements from earlier model versions mostly in the formulation of temperature profiles in the sea ice, which greatly improved Arctic sea ice distributions. Salinity is treated as thermodynamically passive in the sea ice, though it does impact basal ice formation/melt and heat diffusion through a new glacial-melt and melt-pond fraction [Schmidt et al., 2004]. The interactive ocean carbon cycle model consists of the NASA Ocean Biogeochemistry Model (NOBM) [Gregg and Casey, 2007], a gas exchange parameterization for the computation of the CO₂ flux between the ocean and the atmosphere and radiative coupling between the atmosphere and the ocean biology. NOBM utilizes ocean temperature and salinity, MLD, ocean circulation fields and the horizontal advection and vertical mixing schemes from the host ocean model as well as shortwave radiation (direct and diffuse) and surface wind speed obtained from the atmospheric model to produce horizontal and vertical distributions of several biogeochemical constituents. There are four phytoplankton groups (diatoms, chlorophytes, cyanobacteria, and coccolithophores), with distinct maximum growth rates, sinking rates, nutrient requirements, and optical properties, and four nutrients (NO₃, NH, SiO₄, and Fe), three detrital pools (for NO₃:C, SiO₄, and Fe) and a single herbivore component.

A20: Model 21

The HAMOCC [Ilyina et al., 2013] is the global ocean biogeochemical model, which is part of the Max Planck Institute’s Earth System Model (MPI-ESM) [Giorgetta et al., 2013]. The model HAMOCC is coupled to the MPIESM’s ocean general circulation model MPI-OM [Junglcaus et al., 2013] with an embedded sea ice submodel [Notz et al., 2013]. The ocean physics, biogeochemistry, and sea ice are thus resolved on the same spatial grid. In this study, the low-resolution configuration of MPI-ESM from the CMIP5 was used with a nominal resolution of 1.5°. The grid has a bipolar structure with one pole located over Greenland and another one over Antarctica. In the Arctic Ocean, the model resolution varies between 15 and 65 km depending on the proximity to the pole. The model has 40 levels with varying thicknesses increasing toward the bottom. HAMOCC represents the biogeochemical cycles of carbon and nutrients in the water column and in the upper sediments (represented by an interactive sediment module) [Heinze et al., 1999]. The biological part of HAMOCC is based on the NPZD approach (extended by dissolved organic matter) [Six and Maier-Reimer, 1996] so that the concentrations of phytoplankton and zooplankton (both represented by 1 tracer) are functions of, solar radiation, temperature, and colimiting nutrients (NO₃, PO₄, SiO₄, and Fe). The model separates detrital material into POC, CaCO₃, and opal, each exported from the euphotic layer with individually distinct sinking speeds. Phytoplankton growth and air-sea exchange of CO₂ are modulated by the presence of sea ice; no air-sea exchange takes place through sea ice. In this model configuration biogeochemistry in sea ice has not been considered. Zero concentrations of nutrients, DIC, and total alkalinity in riverine fluxes are assumed. The model considers globally uniform weathering fluxes of CaCO₃ and SiO₄.