Three-Dimensional Single-Molecule Localization Microscopy in Whole-Cell and Tissue Specimens

Abstract

Super-resolution microscopy techniques are versatile and powerful tools for visualizing organelle structures, interactions, and protein functions in biomedical research. However, whole-cell and tissue specimens challenge the achievable resolution and depth of nanoscopy methods. We focus on three-dimensional single-molecule localization microscopy and review some of the major roadblocks and developing solutions to resolving thick volumes of cells and tissues at the nanoscale in three dimensions. These challenges include background fluorescence, system- and sample-induced aberrations, and information carried by photons, as well as drift correction, volume reconstruction, and photobleaching mitigation. We also highlight examples of innovations that have demonstrated significant breakthroughs in addressing the abovementioned challenges together with their core concepts as well as their trade-offs.

INTRODUCTION

Far-field fluorescence microscopy is a powerful tool in biological and biomedical research for studying organelle structures, interactions, and protein functions due to its compatibility with live cells and its molecular specificity (1). A major hurdle during the past 100 years has been the limited resolution of far-field fluorescence microscopy (2). Modern super-resolution microscopy or nanoscopy techniques, such as structured illumination microscopy (SIM), stimulated emission depletion microscopy, and single-molecule localization microscopy (SMLM), have made it possible to overcome this fundamental barrier by improving the resolution of fluorescence microscopy (i.e., 250 to 700 nm) by a factor of ten (2).

In particular, SMLM (3–7) uses a stochastic approach to allow a small subset of isolated fluorescent molecules to be switched on at a particular moment while the majority remain in a non-fluorescent, or dark, off state. The fluorescent signal emitted by these single fluorescent probes are captured by a camera, forming individual emission patterns whose centers can then be pinpointed with high precision (8). An SMLM image is reconstructed by localizing thousands to millions of such single-molecule emission events. This imaging strategy was initially applied to two-dimensional (2-D) imaging and later extended to three dimensions (9–13). Three-dimensional (3-D) SMLM images routinely achieve 20–40 nm resolution in the focal plane (i.e., lateral, x–y) and 50 to 80 nm in the axial direction.

The key to 3-D SMLM can be summarized as the encoding and decoding of the 3-D molecular position in the form of a single-molecule emission pattern, known as a point spread function (PSF). Hardware modifications made to the detection path of the imaging system [e.g., by using a cylindrical lens (10), phase mask (11), or multifocal planes (9)] encode the axial position of single molecules in the form of axially varying, nondegenerate 3-D emission patterns (i.e., 3-D PSFs). During the decoding process, the detected emission patterns originating from individual fluorescent molecules in a biological specimen are used to infer their molecular positions in three dimensions based on previously calibrated feature maps or a relevant PSF model (8). While 3-D SMLM can be routinely carried out for thin specimens and cellular structures that lie flat on the coverslip surface, whole-cell and tissue specimens remain challenging for single-molecule super-resolution imaging, thus limiting its achievable resolution and depth.

Here, we review some of the major challenges to 3-D SMLM of thick specimens. We begin by discussing the background fluorescence that is often encountered in whole-cell and tissue imaging. We then discuss the effects of system- and sample-induced aberrations on single-molecule localization and potential strategies to address these issues, both computational and instrumental. Further, we compare strategies to encode 2-D and 3-D molecular positions and their information content in terms of achievable localization precision in both the lateral and axial dimensions. We also discuss drift correction methods, volumetric reconstruction approaches, and photobleaching mitigation strategies, which are critical to achieving high-resolution, large 3-D volumes in whole cells and tissues.

BACKGROUND FLUORESCENCE

Tissue-slice and cell specimens are packed with intra- or extracellular constituents, or both, such as water, proteins, lipids, and nucleic acids. During single-molecule super-resolution imaging, excitation laser intensity ranges from 1 kW/cm² to 15 kW/cm² (14–16), making autofluorescence (i.e., the spontaneous emission of light by these constituents upon excitation) a major contributor to the fluorescence background. On the one hand, the average background level determines the overall feasibility of single-molecule detection and localization precision (17). On the other hand, pixel-to-pixel variation introduces localization biases that could be difficult to detect or eliminate (17). In this section, we discuss major sources of fluorescence background in SMLM, their influences on single-molecule detection and localization, and the methods used to mitigate these effects.

Sources and Types of Fluorescence Background

When imaging through a whole cell, a noticeable autofluorescence in the wavelength range between 500 and 600 nm (18) comes from the cell nucleus where DNA molecules are tightly packed within a volume, typically 5 × 5 × 5 μm³. This is generally problematic, especially when the stained cellular targets are located next to the nucleus (e.g., Golgi-associated proteins) (19). However, the intrinsic absorption and emission from the polynucleotides have been further exploited for super-resolution imaging to resolve chromosomes in a label-free manner (Figure 1a,b) (18).

Figure 1.

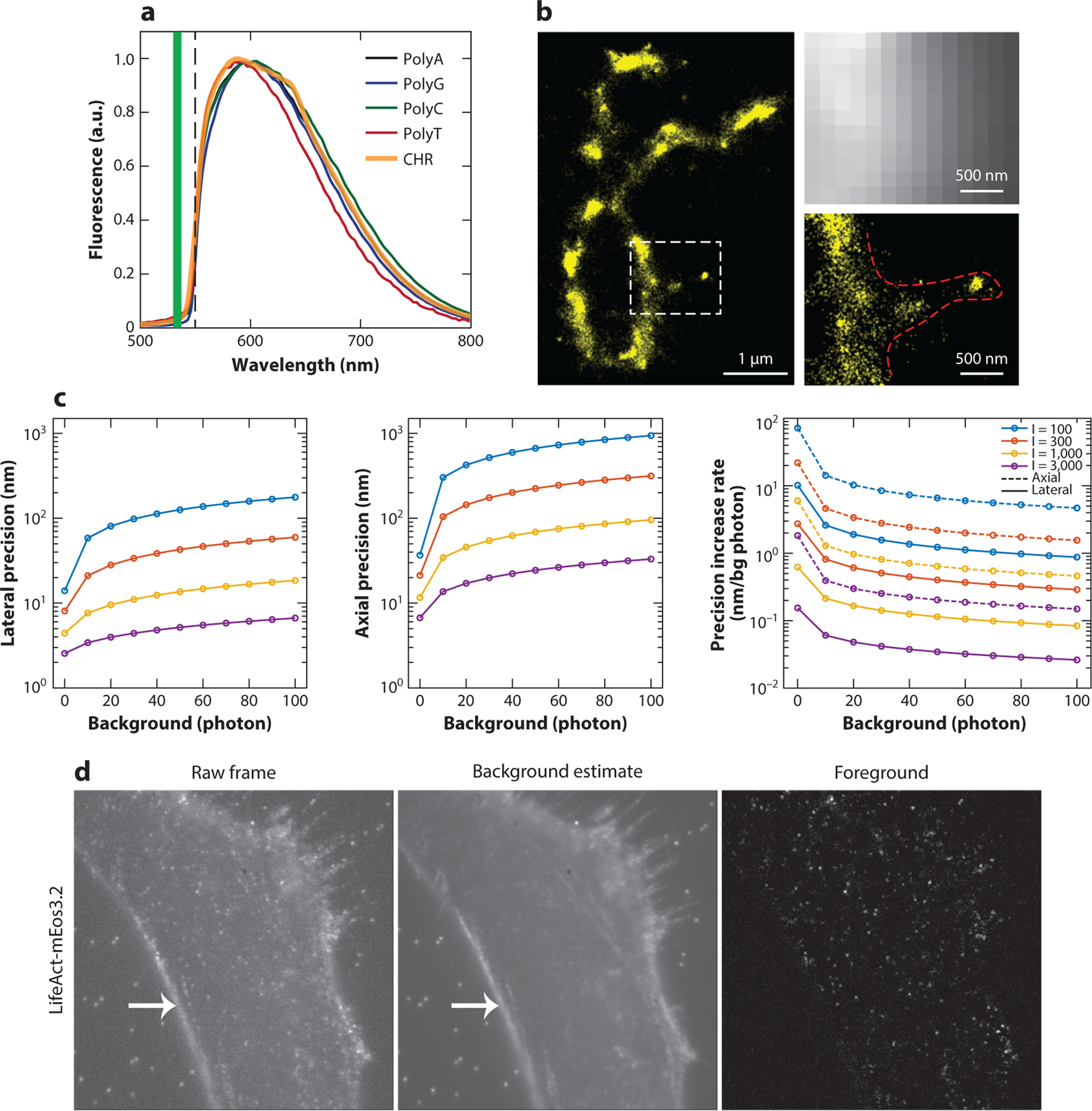
Examples of background fluorescence, its effect on localization precision, and super-resolution microscopy methods based on autofluorescence from polynucleotides. (a) Fluorescence spectra of the polynucleotides PolyA, -G, -C, and -T and an isolated chromosome (CHR) sample. Abbreviation: a.u., arbitrary unit. Panel a adapted from Reference 18 with permission. (b) (Left) Single-molecule photon localization microscopy (PLM) image of DNA with x-shaped chromosomes separated from HeLa cells. (Right) Wide-field fluorescence and DNA-PLM images of the squared region on the left image show additional fine features that are not resolvable in a wide-field image. Panel b adapted from Reference 18 with permission. (c) The lower bounds of localization precision and their deterioration rates at various photon and background levels. Precision lower bounds were calculated from the Cramér–Rao lower bound (CRLB) given a point spread function (PSF) model without aberration (lateral) or with astigmatism aberration (axial; aberration amplitude = 1.5 λ/2π), assuming that detected photoelectrons follow a Poisson distribution. The background (bg) level is the bg photon per pixel. The emitted photon (I) equals the sum of all pixel intensity after bg subtraction. The simulation parameters include the numerical aperture (1.49), emission wavelength (0.69 μm), pixel size (50 nm), and PSF subregion size (64 × 64 pixels). Lateral precision was calculated at an in-focus position (z = 0), and the axial precisions were calculated by averaging across an axial range from −400 nm to 400 nm. (d) (Left) Raw camera frame of a single-molecule data set with the actin cytoskeleton marker LifeAct-mEos3.2. Middle) Background fluorescence estimated using a temporal median filter. (Right) Foreground shown after background subtraction. The fiducial beads that are visible in the raw frame and background image are no longer apparent in the foreground image, nor is the ridge at the cell boundary (arrow). Panel d adapted from Reference 17 with permission.

Proteins provide another major source of autofluorescence in both cells and tissues. The autofluorescence from cellular organelles is predominant at the short wavelength range, from 400 to 550 nm (20), making blue-, green-, and yellow-emitting organic dyes or fluorescent proteins less favorable for cell imaging than red probes. For mammalian tissues, the fluorescent pigment lipofuscin, which accumulates with age in the cytoplasm of cells, has been shown to be a major source of autofluorescence in tissue slices used for confocal microscopy (20).

Another major source of background fluorescence comes from unbound or out-of-focus fluorescent probes. Careful and repeated cycles of washing and incubation usually allow for a reduction in the amount of diffusing fluorescent tags during immunostaining. However, in some cases these unbound probes are required during single-molecule imaging using, for example, DNA-based points accumulation for imaging in nanoscale topography (known as DNA-PAINT) (21, 22) or binding-activated localization microscopy (known as BALM) (23). Therefore, it is preferable to combine these dynamic in situ labeling strategies with confined excitation schemes (24). Additionally, out-of-focus fluorescent probes that are attached to the cellular target generate background fluorescence that increases with the extent of the axial distribution of the stained cellular structure. These probes not only increase the overall level of background fluorescence but also may give rise to spatially varying background patterns on top of the isolated single-molecule emission patterns.

Localization Bias and Precision in the Presence of Background Fluorescence

The background photon counts, from either autofluorescence or out-of-focus probes, follow the same Poisson statistics as the photons emitted by a single molecule. Therefore, an increase in background fluorescence will also increase the detected photon fluctuation, both temporally across frames in a single pixel and spatially across neighboring pixels in a single frame. An elevated background level can effectively mask single-molecule emission events with low photon counts by making them indistinguishable from noisy fluctuations, thus effectively reducing the possibility of detecting single molecules in a specimen.

Given an emission pattern detected from a single molecule, a high background fluorescence level reduces the localization precision. When quantified from the theoretical information limit using the Cramér–Rao lower bound (CRLB), the deterioration rate of localization precision per background photon varies with respect to the average background level and the emitter intensity (25, 26). Given an example of a single-molecule emission pattern with 300 emitted photons, the deterioration rate ranges from as low as 0.3 nm/photon to as high as 3 nm/photon in the lateral direction (Figure 1c), varying according to the background level. In general, localization precision degrades faster as the background photon level gets lower and vice versa (Figure 1c). This rate also depends on the emitter intensity: The more photons are emitted from a single emitter, the slower the deterioration of localization precision with background fluorescence (Figure 1c). Notably, under the condition of low-photon single emitters (e.g., 300 total emitted photons and a 3-photon background level), such as typically occurs when imaging fluorescent protein in live-cell super-resolution experiments, an additional single background photon will decrease the achievable lateral resolution by 2 nm. In contrast, in the case of high-photon single emitters (e.g., 3,000 total emitted photons and a 10-photon background level), typically encountered when imaging bright organic dyes or using labeling methods such as DNA-PAINT, an additional single background photon reduces the achievable lateral resolution by just 0.06 nm (Figure 1c).

Inhomogeneous backgrounds, in which background levels vary from pixel to pixel within an isolated single-molecule subregion, can have significant effects on the accuracy of single-molecule localization (i.e., localization bias). The arbitrariness of these background patterns—due to the local cell or tissue context—makes it difficult to incorporate them into regression-based localization algorithms or even into deep neural networks that are not trained with the whole spectrum of such background patterns (27). In the special case that occurs when inhomogeneous backgrounds can be modeled as a 1-D or 2-D gradient distribution, including an analytical expression of the background profile can restore the optimal accuracy of single-molecule localization. Notably, the use of a temporal median filter, which takes advantage of the spatial and temporal sparsity of single-molecule data sets, has been demonstrated to be an effective method for subtracting inhomogeneous backgrounds (17) (Figure 1d).

Methods of Reducing Background Fluorescence

To reduce background fluorescence, optical sectioning techniques, such as confocal scanning, temporal focusing, and light-sheet illumination, have been combined with SMLM to increase the signal-to-noise ratio of single-molecule detections.

Confocal-based excitation and detection.

In comparison with wide-field illumination and detection methods, SMLM employing spinning-disc confocal illumination and detection methods along with DNA-PAINT (28) has been used to reject out-of-focus background photons. However, to effectively reject background fluorescence while minimizing the blocking of fluorescence signal from the in-focus sample plane, confocal approaches require a small pinhole size (usually ∼1 Airy unit) (29). This pinhole size, which allows only a small portion of the sample to be imaged at each time point, results in slow imaging speed. A line-scanning confocal imaging system has been developed for SMLM to achieve an imaging speed of 33 frames/s (30) (Figure 2a). Furthermore, scanning with a laterally confined, highly inclined and laminated optical sheet (HILO) beam paired with a synchronized rolling-shutter readout of a complementary metal oxide–semiconductor sensor, increases the signal integration time for single-molecule detection when compared with line-scanning and spinning-disc confocal methods, and it also increases the signal-to-background ratio by 2.6 times when compared with wide-field HILO illumination (31) (Figure 2c).

Figure 2.

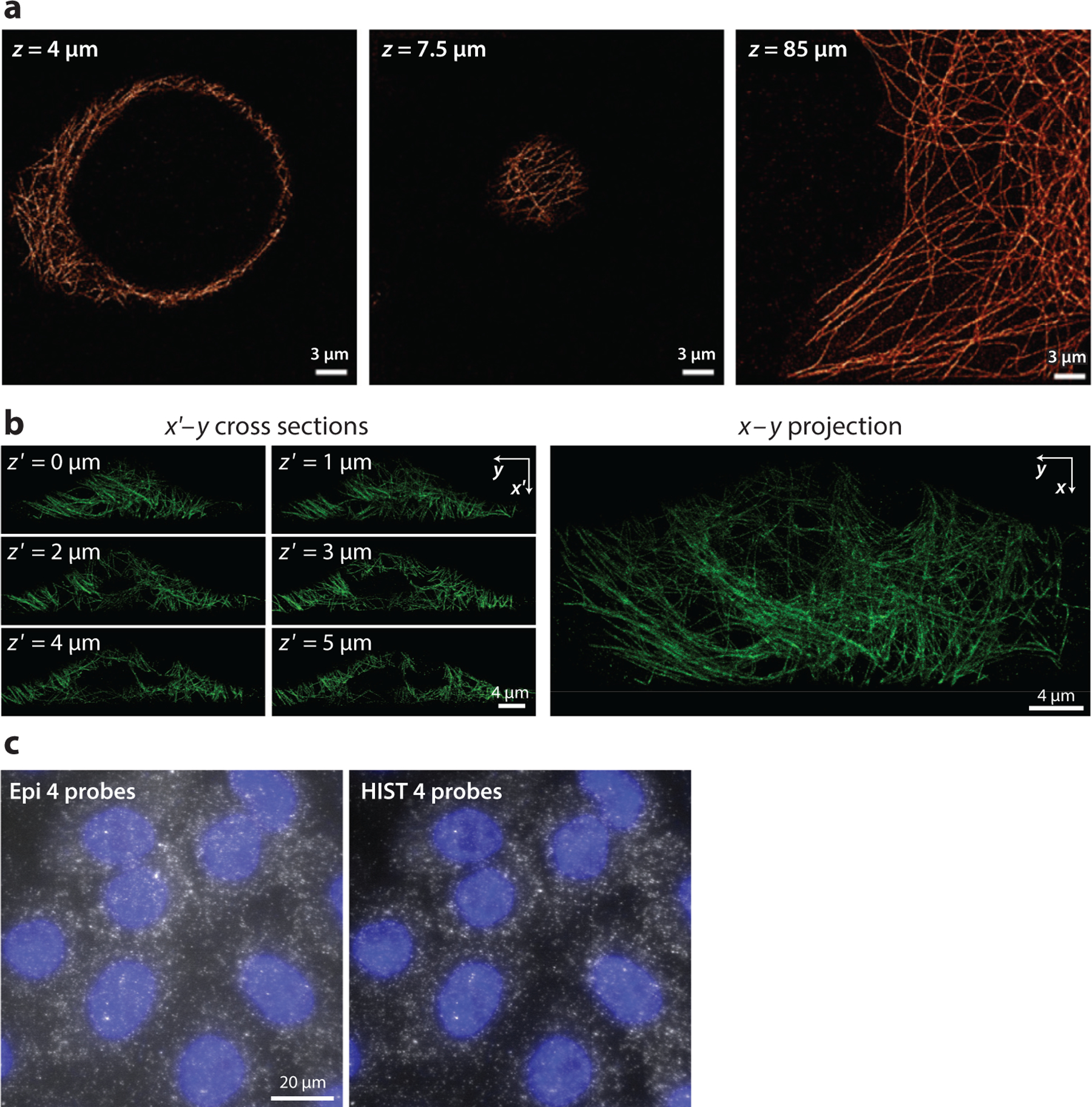
Examples of methods developed to reduce background fluorescence. (a) Super-resolution images of microtubules at depths of 4 μm, 7.5 μm, and 85 μm made using a single-molecule imaging system based on line-scanning confocal microscopy. Panel a adapted from Reference 30 with permission. (b) Super-resolution images of six adjacent oblique planes and the x–y plane projection obtained using epi-illumination selective plane illumination microscopy (or eSPIM) system. Panel b adapted from Reference 52 with permission. (c) Single-molecule fluorescence in situ hybridization images of eukaryotic translation elongation factor 2 on A549 cells using epi-illumination and highly inclined swept tile (HIST) microscopy. Panel c adapted from Reference 31 with permission.

Temporal focusing.

Temporal focusing accomplishes axially confined excitation by harnessing the ultrafast pulse width in the time domain (32, 33). In the typical implementation of temporal focusing, the ultrafast pulse beam is scattered by a diffraction grating and is recombined at the sample plane through telescope-based image-relay optics. The diffraction grating angularly separates the constituent wavelengths of the incoming pulse, thus broadening the temporal pulse width in its propagation space except at the sample plane, where all of the wavelengths reconstitute the original pulse. Therefore, two-photon absorption efficiency is optimal only near the sample plane, where the peak pulse intensity is the highest. Although temporal focusing alone can provide 2-D wide-field illumination sheets with ∼2 μm depth of focus (34), spatial beam shaping and 1-D fast scanning (e.g., line scanning) can be combined with temporal focusing to offer optical sectioning performance that is almost identical to that of point-scanning two-photon microscopy in the wide-field illumination mode (35–39). Temporal focusing has been used for whole-cell super-resolution imaging by axially confining the activation of photoactivatable (PA) fluorescent proteins, such as Dronpa and PA-mCherry (34, 35). One remarkable property of temporal focusing is that it can reliably deliver any spatial pattern of light, even deep into highly scattering turbid media, without much distortion (40, 41). This attribute, combined with the spatial light modulator (SLM)–based beam shaping technique, has been used in neuroscience and optogenetics research for photostimulation inside tissue (42). It is exciting to speculate on the new avenues that combine temporal focusing–based excitation and 3-D SMLM.

Light-sheet illumination.

Light-sheet fluorescence microscopy (LSFM) is another powerful technique for reducing background fluorescence and photobleaching in thick biological samples. When imaging living specimens, it also reduces phototoxicity (43–48). However, its application to SMLM has been limited due to the low numerical aperture (NA) objectives commonly employed in most LSFM systems, in which the geometrical positioning of two separate detection and illumination objectives must be considered.

Single-molecule imaging with multiobjective light-sheet systems.

In one type of multiobjective LSFM configuration, the objectives are positioned in close proximity, either orthogonally or non-orthogonally, with no additional optical element between illumination and detection. For systems using orthogonal arrangements, such as selective plane illumination microscopy (SPIM) (43), multidirectional SPIM (mSPIM) (49), inverted SPIM (iSPIM) (44), dual-view iSPIM (DiSPIM) (45), individual molecule localization SPIM (IML-SPIM) (46), and lattice light-sheet microscopy (LLSM) (47), the uses of detection NA up to 1.1 were demonstrated. The limitation of these arrangements is that an increase in the detection NA usually comes with a sacrifice in the illumination NA. As was demonstrated with IML-SPIM (46), a detection NA of 1.1 and an illumination NA of 0.3 were used for single-molecule localization microscopy. Similarly, a demonstration of lattice light-sheet microscopy used a detection NA of 1.1 and a custom-designed illumination objective of NA 0.65 for SMLM (24, 47) (Figure 3d). This restriction on the NA value is mainly due to the bulky size of commercial high-NA objectives. Custom-designed objectives, while lessening such constraints, however, are not readily accessible. Three-objective SPIM (TriSPIM) (50), a theoretical study using a design with three orthogonally arranged objectives of NA 0.8, suggested that a 1.1 detection NA can be achieved by taking advantage of structured illumination. In non-orthogonal arrangements, such as that used in πSPIM (51), the use of a detection NA of up to 1.1 has been demonstrated. In πSPIM, two objectives were positioned in an obtuse angle, which alleviated the restriction on the NA and allowed for both the detection and illumination NAs to be >1. πSPIM offers high spatial resolution imaging (with a 1.1 detection NA) as well as excellent optical sectioning capability (with a 1.49 illumination NA). This unique design makes it a promising candidate for 3-D SMLM imaging. We note that currently it restricts the detection objective to a water dipping lens, for which the highest NA, commonly accessible, is 1.1.

Figure 3.

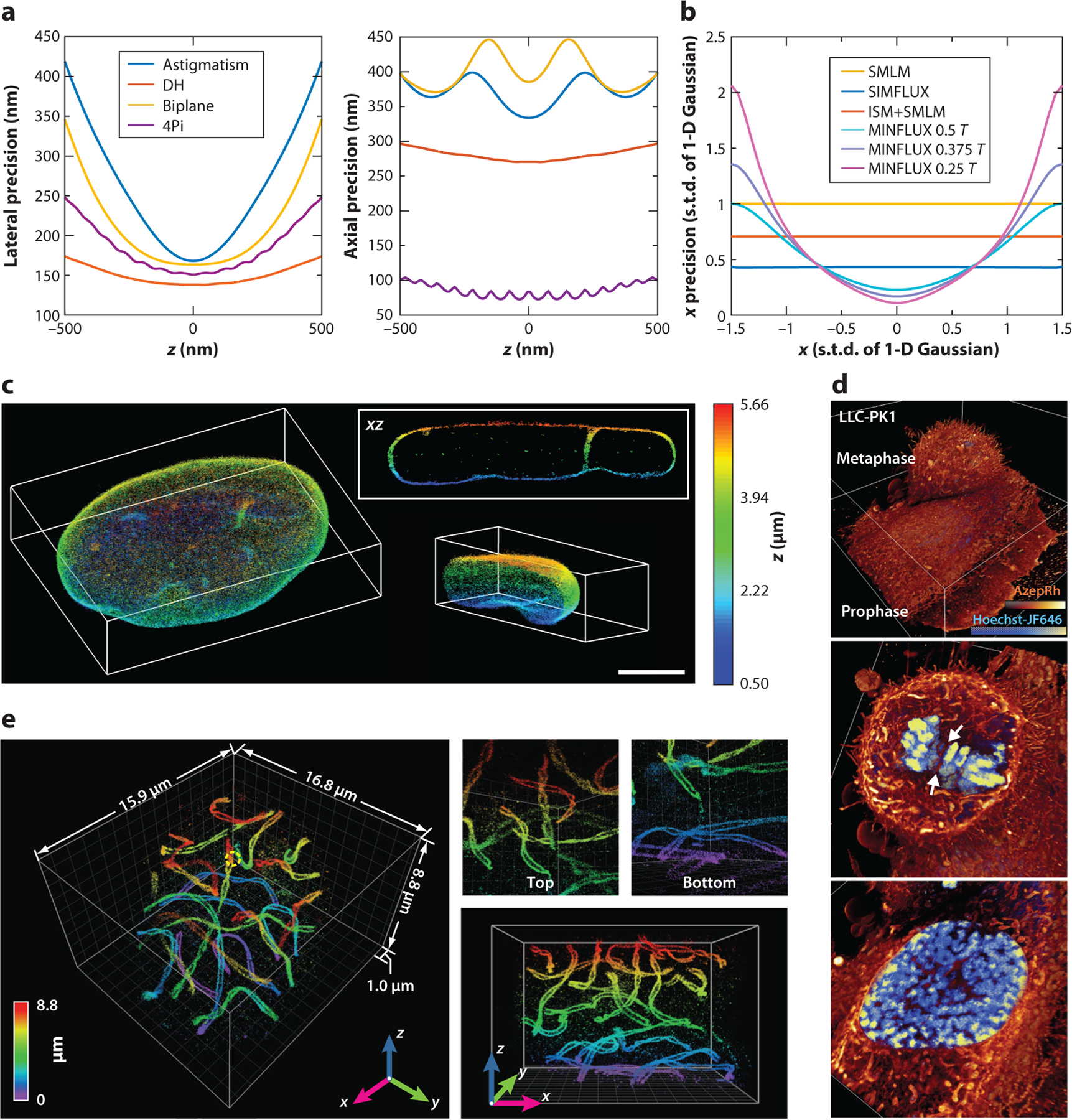
(a) Lower bounds of lateral and axial localization precision when using different three-dimensional (3-D) single-molecule localization microscopy (SMLM) modalities with a single emitted photon and near zero background (10⁻⁶). Precision values were calculated from Cramér–Rao lower bounds and assume a Poisson distribution for detected photoelectrons. Double-helix (DH) point spread functions (PSFs) were generated from Gaussian–Laguerre modes and efficiency optimized for pupil function. Astigmatism PSFs were generated from the fifth Zernike polynomial (Wyant order) with an amplitude of 1.5 (λ/2π), and biplane PSFs used ideal PSFs (i.e., with no aberration) for each plane, with an optimized plane distance of 305 nm. 4Pi (interferometric) PSFs were generated based on coherent pupil functions, with an astigmatism aberration of 1.5 (λ/2π) that had perfect coherence and zero transmission loss. To avoid computational instabilities, we used a background of 10⁻⁶ photons per pixel for single-plane PSF models (astigmatism and DH), 10⁻⁶/2 for biplane PSFs, and 10⁻⁶/4 for 4Pi PSFs. For each PSF model, to evaluate the precision achieved by one expected photon count, the sum of all pixel values after background subtraction is one. DH PSFs give the lowest lateral precision with the least increase over z, partially benefiting from the side lobes of the shape-invariant PSFs. 4Pi PSFs give the lowest axial precision, taking advantage of coherent detection of single molecules. Other simulation parameters include the numerical aperture (1.49), emission wavelength (0.69 μm), pixel size (50 nm), and PSF subregion size (64 × 64 pixels). (b) Lower bounds of 1-D localization precision when using different patterned excitation SMLM methods. A 1-D Gaussian model with a width of one pixel was used for both the emission PSF and the excitation PSF in image-scanning microscopy (ISM). A 1-D sinusoid pattern with a period of 3 pixels (T = 3 pixels) was used for both the structured illumination (SIM) and the minimal emission fluxes (MINFLUX). Here, precision was calculated at one photon in total and zero background. Abbreviation: s.t.d., standard deviation. (c) 3-D SMLM reconstructions of the entire nuclear lamina (lamin B1) of a HeLa cell made using tilted light-sheet microscopy with 3-D PSFs (TILT3D). Scale bar: 5 μm. Panel c adapted from Reference 55 with permission. (d) Volume rendering of two dividing LLC-PK1 cells in prophase (bottom) and metaphase (top) labeled with Hoechst-JF646 and AzepRh to visualize DNA and intracellular membranes, seen using 3-D lattice light-sheet illuminated 3-D SMLM. Panel d adapted from Reference 24 with permission. (e) 3-D super-resolution volumes of synaptonemal complexes in a whole-mouse spermatocyte obtained by 4Pi (interferometric)-based single-molecule detection and localization assisted by adaptive optics. Panel e adapted from Reference 92 with permission.

Other multiobjective configurations have been developed to circumvent the problem of space constraints, with either the illumination or detection path being redirected by additional optics. One method utilizes remote detection. In epi-illumination SPIM (eSPIM) (52), a water immersion objective (NA, 1.27) was used for both illumination and detection. With an oblique light sheet generated by the water immersion objective, an intermediate image of the illuminated plane was formed by an air objective (NA, 0.9), and then by positioning a water dipping objective (NA, 1.0) such that its focal plane overlapped with the intermediate image plane, the full oblique illumination area at the sample was detected on the camera. Although similar to eSPIM, oblique plane stochastic optical reconstruction microscopy (obSTORM) (53) uses a tilted mirror, instead of a third objective, to form a secondary intermediate image plane that coincides with the focal plane of the remote objective through which the final image is formed on the camera. Both methods are able to take advantage of high NA (≥1.2) water immersion objectives to assist with single-molecule localization as well as to simplify the sample mounting procedure so that it is the same as that used for a conventional inverted microscope.

Another type of system focuses on modifying the illumination scheme. In one approach, termed reflected light-sheet microscopy (RLSM) (54), a thin light sheet generated from an upright objective was reflected at 90° by a small mirror positioned just above the coverslip, and an inverted objective with a high NA (1.35 or 1.4) was used for detection. This technique has enabled the implementation of oil immersion objectives in LSFM and enhanced its capability to detect ultralow fluorescence signals. However, RLSM introduces a 2-μm gap above the coverslip that is not accessible to the reflected light sheet. Another approach, named tilted light-sheet microscopy with 3-D PSFs (TILT3D) (55) (Figure 3c), uses a thin light sheet reflected at an oblique angle (10°) to the coverslip rather than being parallel; this removes the illumination gap. However, the light sheet position is coupled with one lateral translation of the sample chamber and, therefore, requires beam readjustments when translating the specimen in the coupled direction. Hu et al. (56) developed an alternative to reflection-based approaches, termed light-sheet Bayesian microscopy (LSBM), in which a light sheet is refracted into a plane parallel to the detection objective focal plane by positioning a prism next to the illumination object. The refracted light sheet delivers exceptional optical sectioning beyond the limit of the illumination NA. However, the detection NA of this approach remains limited by that of the water dipping objective.

Single-molecule imaging with single-objective light-sheet illumination.

Light-sheet generation and fluorescence detection can be accomplished by using a single objective. HILO (57) is a relatively straightforward technique that uses a single objective, and a detection NA of up to 1.49 has been demonstrated. For effective background-reduction performance, the field of view (FOV) in both dimensions is usually limited to 5 to 10 μm, and it typically requires a total internal reflection–compatible objective lens (NA ≥ 1.45) to achieve reliable performance. However, because index-mismatch aberration occurs between the immersion oil and whole-cell or tissue specimens and rapidly increases with imaging depth, this technique is typically limited to thin specimens.

Galland et al. (58) and Meddens et al. (59) proposed, respectively, single-objective SPIM (soSPIM) and single-objective light-sheet microscopy (SO-LSM), and in both cases, a thin light sheet from the objective was reflected by a reflective surface inside a specially designed microfluidic channel. These methods can potentially be adapted to any water or oil immersion objective. However, when using a single objective, the axial translation of the light sheet is coupled with the axial scanning of the sample, and this requires additional scanning of the light sheet in order to align the light sheet with the focal plane (58, 59). Another notable drawback of these approaches is that, similar to RLSM, the reflected light sheet will be distorted near the coverslip unless a specially designed chamber (58) raises the sample away from it.

Nondiffracting light-sheet illumination.

High-NA objectives, although benefiting light-sheet confinement as well as single-molecule detection and localization, are susceptible to sample-induced aberrations that often arise from light scattering or inhomogeneous refractive indices inside the specimen. Low-NA light-sheet illumination is less prone to these aberrations (48) because of its ability to generate nondiverging sheet illumination over a large distance. Therefore, explorations of nondiffracting beams (e.g., an Airy beam or Bessel beam) used along with high-NA detection have been a new emphasis in LSFM techniques. The nondiffracting beam (60, 61) is formed by a wave field whose transverse intensity profile remains unchanged in free-space propagation, and thus is termed propagation invariant (62). These wave fields feature the remarkable property of regenerating their intensity profile, even after disturbance by an object or in turbid media, and this property is often referred to as self-healing or self-reconstruction (61). Bessel beams, well-investigated nondiffracting beams, have been shown to possess greater resistance to scattering media and to have a greater penetration depth than Gaussian beams (63–66). However, these nondiffracting profiles come with bright side lobes, which are a corollary of the self-healing property but can greatly deteriorate the optical sectioning performance of a light sheet at the same time. Strategies to balance this trade-off between the extent of a nondiffracting center beam and the side lobe intensities have been developed to make nondiffracting beams a useful tool in LSFM. By combining a Bessel beam with structured illumination or two-photon excitation techniques (67, 68), the side lobes of the Bessel beam can be sufficiently suppressed, and an isotropic resolution can be achieved while maintaining a large FOV (up to 60 μm). In the case of an Airy beam, image artifacts introduced by the side lobe can be effectively reduced by deconvolution (69, 70), and a substantially extended FOV (up to 160 μm) as well as improved resolution over Bessel-beam and Gaussian-beam illumination have been demonstrated (70).

ABERRATIONS IN SINGLE-MOLECULE LOCALIZATION MICROSCOPY

Photons emitted from single molecules travel through the specimen and microscope before being detected by the camera. Due to the inhomogeneous refractive indices of cellular and extracellular structures, their wavefronts, passing through different parts of the cell and through tissue structures, travel at different speeds and, therefore, are curved or distorted according to the path through the specimen. Optical system imperfections may also introduce significant wavefront distortions (71). Left unattended, these distortions lower the information of molecular position carried per photon. The discrepancy between the actual distorted or blurred PSF and the assumed or measured PSF model further causes localization bias. Taken together, aberrations—induced by either the optical instrument or the specimen—degrade the achievable resolution and introduce localization artifacts in single-molecule imaging, and these effects are especially significant in the axial direction. In this section, we discuss the major types of aberrations encountered in SMLM, examine their influences on the precision and accuracy of single-molecule localization, and introduce the methods used to optically correct or numerically mitigate aberrations during single-molecule imaging.

System- and Sample-Induced Aberrations

Aberrations in microscopy systems can mainly be categorized into two types: One is systematic aberrations, which are caused by the instrument itself, and the other is the sample-induced aberrations caused by the inhomogeneous refractive indices of extra- and intracellular constituents in cells and tissues. Systematic aberrations vary between microscopes. They are frequently observed in both custom-built and commercial single-molecule imaging systems. Here, we discuss several major aberration types caused by either misalignment or defects of optical components in a microscope.

Spherical aberration.

Spherical aberration is the only primary monochromatic aberration that exists if the object is on the optical axis (72), and it leads to an asymmetry of PSFs along the optical axis (Figure 4a). A common source of spherical aberration is a camera positioned incorrectly along the optical axis (73). A commercial objective is optimized at a designated focal plane, and, therefore, the camera must be positioned such that the sample plane is coincident with the designed focal plane in order to minimize spherical aberration. This phenomenon is especially prevalent on remote-focusing microscope systems (52, 53, 74), for which careful alignment is required to ensure the coincidence of the two focal planes of the two objectives.

Figure 4.

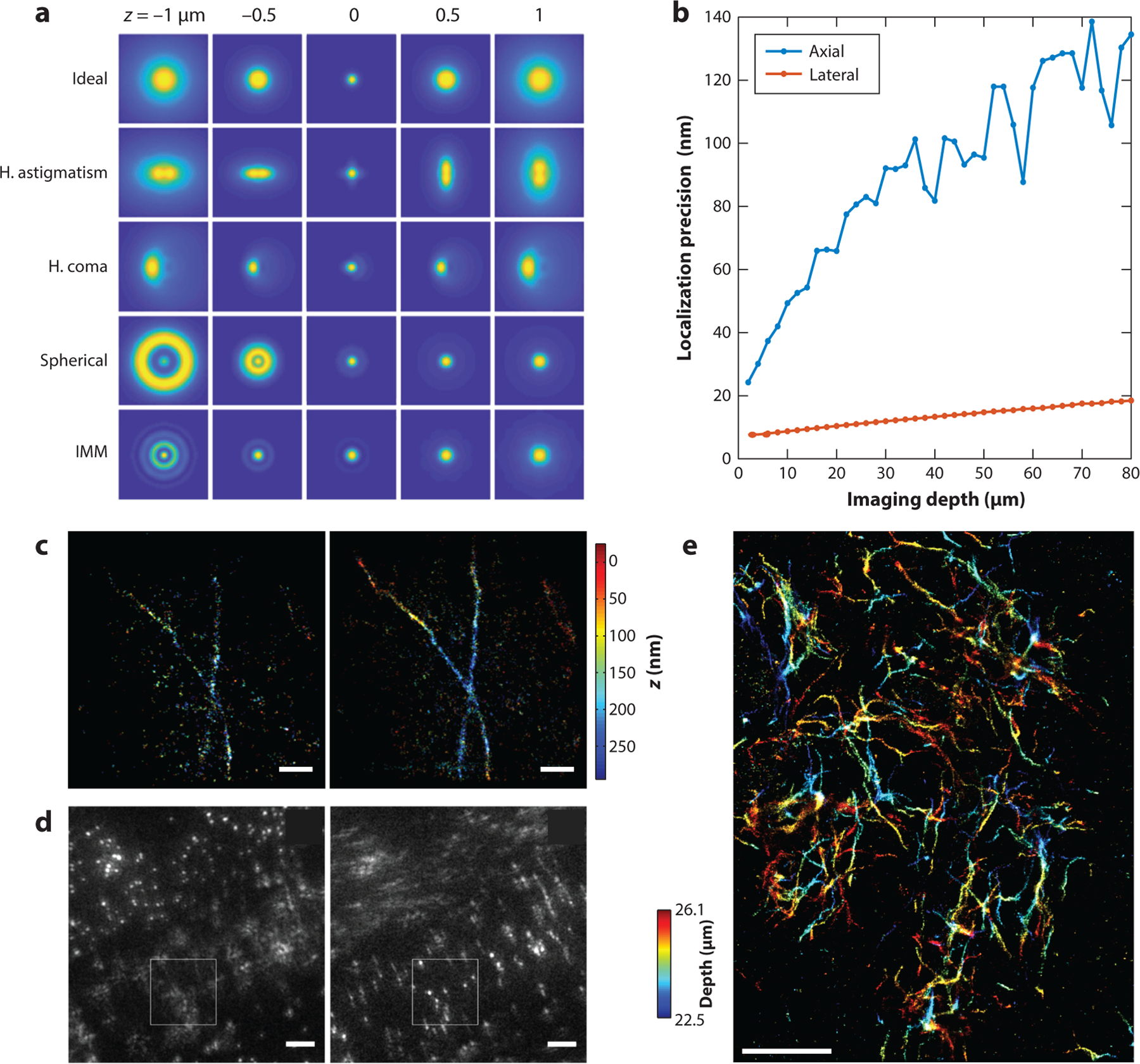
(a) Examples of three-dimensional (3-D) point spread functions (PSFs) based on a high–numerical aperture (NA) imaging system, showing various aberrations, including horizontal astigmatism (H. astigmatism), horizontal coma (H. coma), spherical, and index mismatch aberration (IMM). Ideal PSFs were also generated for comparison. The simulation parameters include the NA (1.49), emission wavelength (0.69 μm), pixel size (50 nm), and PSF subregion size (64 × 64 pixels). For astigmatism, coma, and spherical aberration, the amplitudes of the corresponding Zernike polynomials (fifth, seventh, and ninth; Wyant order) are, respectively, 1.5, 1.5, and −1.5 (units, λ/2π). For IMM, the imaging depth (stage position) was set to 10 μm, and the refractive indices of the immersion and the sample media are, respectively, 1.52 and 1.33. (b) Lower bounds of lateral and axial localization precision at different imaging depths were calculated using biplane detection when considering refractive IMM. The parameters used in the simulation include the NA (1.4), the refractive index of the objective immersion medium (1.52), the refractive index of the sample immersion medium (1.33), wavelength (0.7 μm), number of emitted photons per single molecule (1,000), and background fluorescence per pixel (10). The precision values at image depths from 2 to 80 μm are shown. At each depth, 101 PSFs at z positions uniformly distributed from −600 nm to 600 nm relative to the apparent focal position were simulated. The average precision in the lateral and axial directions are reported at each depth. (c) 3-D single-molecule localization microscopy (SMLM) images of immune-labeled α-tubulin in COS-7 cells, with (left) the adaptive optics (AO) set to correct for instrumental aberrations only and (right) the AO set to correct for instrumental- and specimen-induced aberrations. Scale bars: 1 μm. Panel c adapted from Reference 107 with permission. (d) Correction of aberration induced by Caenorhabditis elegans using a sensorless AO driven by a genetic algorithm. Scale bars: 5 μm. Panel d adapted from Reference 108 with permission. (e) 3-D SMLM image of an amyloid-β plaque in a 30-μm brain slice from a mouse model of Alzheimer’s disease. Image made using adaptive PSF shaping and sensorless AO driven by the Nelder–Mead simplex algorithm. Scale bar: 5 μm. Panel e adapted from Reference 80 with permission.

Coma.

Coma is a type of off-axis aberration, and it results in radial asymmetry of PSFs in the lateral dimension (75) (Figure 4a). Because it is an off-axis aberration, it usually occurs at the edge of the FOV. However, if the system is misaligned, it may also be observed in the middle of the FOV. Coma is commonly observed in microscopy systems using a water (76) or a silicon oil objective lens. Because of the index mismatch between the cover glass and the immersion medium, even a slight tilt of the cover glass (i.e., away from the angle orthogonal to the optical axis) can cause significant coma. The tilting and decentering of optical lenses can also cause coma.

Astigmatism.

Astigmatism is another type of off-axis aberration; in this case, PSFs appear to be elongated in different directions above and below the focal plane (75) (Figure 4a). Similar to coma, astigmatism is more noticeable near the edge of the FOV, particularly in systems consisting only of radial symmetrical lenses. One common reason for the occurrence of astigmatism in the middle of the FOV is that an optical element is deformed into a cylindrical curvature. This usually appears in multichannel systems, in which a slight bending of the beam splitter or dichroic mirror can cause astigmatism in the reflection channel. Therefore, a thick beam-splitting element is preferred in these systems. Additionally, the tilting and decentering of optical lenses can also cause astigmatism.

Chromatic aberration.

Chromatic aberration is caused by the phenomenon of different wavelengths being focused at different axial or lateral positions. Many commercial objectives and optical lenses are achromatic (72) to ensure minimum chromatic aberration. However, the effect of chromatic aberration can be more significant (77, 78) for microscopy systems that have a dispersion element, such as a prism or a grating, since the spectral dimension is spread over one lateral dimension of the image plane.

Other system-induced aberrations.

For microscopy systems equipped with a wavefront control element, such as a deformable mirror (DM) or SLM, misalignment of this component can cause various aberrations (79). Siemons et al. (79) examined the major aberrations caused by misalignment of the SLM in microscopy systems, including field-dependent aberration, which is caused by axial misalignment, and observable lateral shift of the PSFs with a defocus wavefront applied by the SLM, which is caused by lateral misalignment. These aberrations can also occur in systems employing a DM. Since the active area of the DM is usually much smaller than that of the SLM, the lateral misalignment can further cause beam clipping, which is easily observable from the defocused PSFs (80). A clipping edge present in an out-of-focus PSF indicates that partial marginal rays of the emitter are missed by the DM. Similar effects can also be observed when a lens or a mirror is significantly decentered or its size is smaller than the incident beam size.

Sample-induced aberration.

One type of sample-induced aberration that has been extensively studied is the aberration caused by refractive index mismatch between the sample medium and the immersion medium of the objective (73, 81–83) (Figure 4a). A water immersion objective is less susceptible to the index mismatch aberration since most sample media are aqueous, with a refractive index close to that of water. For high-NA oil immersion objectives, as are commonly employed in single-molecule super-resolution imaging, the index mismatch aberration will worsen rapidly with imaging depth. Although its influence on the shapes of the PSF looks similar to that of spherical aberration, the exact wavefront shape differs from that of spherical aberration. In terms of Zernike polynomials (84), the wavefront of an index mismatch aberration can be expressed by a linear combination of defocus and spherical aberrations of various orders (82). In terms of single-molecule localization, the index mismatch aberration has much stronger effects on deteriorating the achievable precision in the axial direction than in the lateral direction (Figure 4b).

Silicone oil immersion objectives have been recently developed to accommodate the need for thick specimen imaging; the refractive index of silicone oil (∼1.4) makes it less susceptible to the index mismatch aberration while it is still possible to maintain a high NA (∼1.3), and thus it is suitable for 3-D SMLM of tissue specimens (80). Water dipping objectives, however, require the refractive index of the sample medium to closely match that of water; otherwise its long working distance (1 to 2 mm) may turn even a small refractive index mismatch into a large deviation of optical path difference from the designed condition.

Another type of aberration is induced by the biological specimen itself. These aberrations and their corresponding wavefront distortions are highly specific to the local constituents of cells and tissues, and, therefore, there exist neither generally applicable mathematical models nor quick remedies for such types of aberrations. As a result, the distorted emission patterns of single fluorescent probes cannot be modeled or measured a priori. Such sample-induced aberration is more pronounced when imaging tissue specimens, and it has been extensively reported in two-photon microscopy (85).

3-D Single-Molecule Imaging in the Presence of Aberrations

3-D SMLM relies on encoding and decoding the axial positions of single molecules in the form of their 3-D response functions (i.e., 3-D PSF). Multiple PSF-engineering approaches have been developed to tackle the single-molecule imaging tasks for thick specimens. One of the areas of attention aims to achieve an extended axial localization range. Perhaps one of the first attempts was the invention of double-helix PSF (DH-PSF) (11), engineered from propagation-invariant wave fields (62, 86). The DH-PSF consists of two main lobes that rotate along the propagation direction. With this property, DH-PSFs give a nearly uniform localization precision in an axial range of 2 μm. Self-bending PSFs (87) take advantage of a nondiffracting Airy beam, extending the axial localization range to 3 μm. Further, Shechtman et al. (88) have proposed a PSF optimization method to determine the PSF shape that yields optimal average localization precision along any given axial range by minimizing the theoretical precision limit obtained from the CRLB. As a result, the saddle-point PSF (88) was generated by optimizing the 3-μm axial range, whereas the tetrapod PSF (89) was later developed to enable single-particle tracking in an axial range of 6 μm without scanning. We note that saddle-point and tetrapod PSFs require moderate isolation between emitters, making sparsely labeled specimens their preferred applications. However, the lateral dimension of the engineered PSFs tends to increase along with the designed axial range, which may make them more sensitive to aberrations and noise (79).

Another area of emphasis is optimizing the performance of axial resolution by improving the localization precision (and, therefore, the resolution) given a limited emitter intensity and background level. This is beneficial for thick specimen imaging in cases in which the signal-to-noise ratio is relatively low. 3-D imaging modalities, such as biplane (9), astigmatism (10), and phase ramp (90), have been widely adapted in 3-D SMLM systems, which achieve a 10- to 20-fold improvement in resolution when compared with confocal microscopy. By using two opposing objective lenses (i.e., 4Pi detection geometry), the detection efficiency of single molecules can be doubled, which in turn leads to an ∼1.4-fold improvement in localization precision in all three dimensions (91). Furthermore, when the fluorescence signals from the two objective lenses are combined coherently and, therefore, are allowed to interfere, the resulting PSF features significantly increase the achievable axial resolution (12, 13, 92). The center intensity of the 4Pi (interferometric) PSF is modulated with respect to the axial position of the emitter, with a period of ∼300 nm. By extracting the phase of the PSFs according to the center intensity, a 10-nm axial resolution can be achieved with 600 photons/objective (93). A recent study switched the emphasis of PSF engineering toward mitigating the influence of optical aberrations on PSF shape. This method, termed self-interference microscopy (SELFI) (94), proposed a new type of PSF that is generated through self-interference by way of a diffraction grating placed close to an intermediate image plane in the detection path. The diffraction grating was able to encode the curvature information of a focusing wavefront into the PSF patterns, with a demonstrated imaging depth of 40 μm (94).

Multifocus microscopy (78) has been developed to acquire extended imaging depths without scanning. The system simultaneously forms images on 9 to 25 equally spaced planes along the axial direction and instantly captures a 3-D volume of the biological structure within an imaging depth of 4 to 8 μm (95–97). Therefore, all planes can be imaged at the same time without the delay caused by scanning in the axial direction. However, multifocus microscopy techniques suffer from low photon efficiency: Only 5% of all total photons were received by each plane in a nine-plane configuration; as a consequence, a longer exposure time of 30 to 50 ms is required (95, 97).

Single-Molecule Localization in Aberrated Point Spread Functions

To achieve accurate (low bias) and precise localization of single molecules in the presence of aberrations, there are mainly two approaches: accurate modeling of the PSF and correcting aberrations.

Phase-retrieval methods.

During single-molecule localization, one needs to infer the lateral and axial positions of individual fluorescent probes from the shape and location of their detected emission patterns. Therefore, when inferring single-molecule positions in the presence of observable aberrations, the resulting PSF distortions must be incorporated into the PSF model in order to achieve high localization accuracy (i.e., low localization bias).

One way to incorporate such distortion is by using a phase-retrieved PSF (PR-PSF) as described by pupil function. The pupil function describes the electric wave field at the pupil plane in the detection path of an imaging system. When retrieved from a set of experimentally recorded PSFs at different axial positions, the pupil function describes the wavefront distortion as well as the transmission amplitude of the light wave and is related to the PSF in the imaging plane through the Fourier transform. Hanser et al. (98, 99) demonstrated that PR-PSFs retrieved using the Gerchberg–Saxton (GS) algorithm closely match experimental PSFs in microscopy systems with a high-NA objective. This GS-based phase retrieval algorithm was further applied to SMLM to improve localization accuracy in the case of various engineered PSFs (81, 83, 100). To increase the computational speed, an analytical PSF model can be obtained by expanding the retrieved pupil function in terms of Zernike polynomials when the optical aberrations are relatively small (81). However, in the presence of significant wavefront distortions (peak–valley >1 λ), discontinuities arise in the pupil phase due to extensive phase wrapping, which results in inaccurate estimations when using Zernike expanded pupil functions (27). Additionally, GS-based PR algorithms do not take into account the photon statistics of the recorded PSFs; therefore, this leads to inaccurate results when retrieving pupil functions from PSFs with low signal-to-noise ratios. Maximum likelihood estimator (MLE)–based phase retrieval algorithms (101, 102) were developed to address these difficulties. MLE phase retrieval methods estimate a set of Zernike polynomial amplitudes by maximizing a likelihood function that represents the similarity between the PR-PSFs and the experimental PSFs. By directly estimating the Zernike amplitudes, MLE phase retrieval successfully avoids phase wrapping and has been demonstrated to be applicable to large wavefront distortions. Furthermore, by incorporating photon statistics in the likelihood function, MLE phase retrieval is less susceptible to noise (101).

Interpolation-based methods.

An analytical PSF model can also be built through cubic interpolation of a set of recorded PSFs. With the cubic spline method, one can skip the complicated phase retrieval process—which often requires a user’s knowledge of the microscopy system—to generate an equally accurate PSF model (103). A recent implementation of the cubic spline method on a graphics processing unit achieved a localization speed of >10⁵ emitters/s, with precision approaching the theoretical information limit calculated by the CRLB (104). However, the cubic spline method requires a set of recorded PSFs at finely sampled axial positions with intervals of 10 to 50 nm (104), which increases the acquisition time and makes this method more sensitive to sample drift. Additionally, noise in the recorded PSFs can substantially affect the accuracy of the spline PSF model, thus requiring averaging of multiple recorded PSF stacks that are well aligned in both the lateral and axial directions (104).

Measuring and Correcting Aberrations Using Adaptive Optics

By employing the algorithms mentioned above, localization bias can be reduced, given an accurate numerical or analytical model of the PSF distorted by the optical system. However, the information loss introduced by aberrations from the microscopy system or the specimen causes a permanent reduction in localization precision, and this precision loss is not recoverable using computational methods.

For example, a theoretical limit on axial precision increases (i.e., worsens) by fivefold at an imaging depth of 50 μm for a common configuration of SMLM (Figure 4b). While advanced algorithms can be developed to perform unbiased single-molecule localizations that approach this theoretical precision bound, any further decrease in localization uncertainty requires a physical element that corrects the distorted wavefront of single-molecule emissions prior to its detection on the camera.

To optically correct wavefront distortions, two types of wavefront modifying devices are commonly used: a DM or an SLM. A DM usually consists of a reflective membrane surface, either continuous or segmented, with electrostatic or electromagnetic actuators controlling the curvature of the mirror. Therefore, light reflected from the DM is modified in its optical path length by twice the mirror deformation distance (71). The same optical path length modification occurs in spite of the wavelength and polarization state of the light. SLMs control the incident light wavefront by locally changing the refractive index at a pixel of the liquid crystal–based device. However, the introduced modulation of the refractive index depends on the polarization of the incident light and its propagation direction (105). This characteristic of SLMs makes them less suitable for wavefront control in SMLM in which unpolarized emissions are expected from fluorescent probes. Despite this disadvantage, SLMs usually consist of a large number of pixels and, therefore, can generate significantly more complex wavefront shapes than can DMs.

In astronomy and ophthalmology, wavefront distortions are often measured using devices such as Shack–Hartmann wavefront sensors (106). By inserting a microlens array into the pupil plane of an imaging system, the wavefront generated by a bright and stationary point source (also known as a guide star) can be dissected into small pieces that each contain, by approximation, the tip and tilt of the local wavefront. The amount of tip and tilt of each wavefront segment is then translated into lateral shifts on the focal plane by the microlenses and measured by a camera. However, the prerequisite of providing a bright, stationary point source remains the limiting factor in implementing this method for SMLM.

Sensorless adaptive optics (AO), however, do not require a guide star (71). In general, this approach optimizes the induced wavefront shape using an adaptive element, typically a DM or an SLM. It iteratively determines the amplitudes of individual Zernike modes—encoded by the DM or SLM—that maximize a predefined metric, such as image sharpness or peak intensity, quantified from the captured image. For SMLM, both iterative and non-iterative sensorless AO methods have been developed using optimization approaches such as coordinate search (Figure 4c) (107), genetic algorithms (Figure 4d) (108), particle swarm optimization (109), and the Nelder–Mead simplex algorithm (Figure 4e) (80). Although sensorless AO is relatively straightforward to implement, the multiple cycles of DM update and image acquisition that are typically required limit the response time, and, therefore, its application has been focused on correcting static wavefront distortions in fixed-cell and tissue specimens.

An SMLM data set usually contains thousands of emission patterns generated by single fluorescent probes within a typical imaging volume of 30 × 30 × 1 μm³. The numerous photons emitted by these point sources are likely to experience a similar wavefront distortion induced by the specimen. In principle, it may be possible to simultaneously estimate both the molecular positions and the common wavefront distortions (e.g., in terms of Zernike amplitude) from raw, blinking SMLM data themselves. However, such regression could be considered intangible due to the high dimensionality of the parameter space and the associated local minimums preventing the regression algorithms from finding the global minimum solution.

In contrast to regression, deep learning extracts information-carrying features from the training data set while ignoring irrelevant features. Single-molecule deep neural networks (smNets) based on residue and bottleneck architectures have been shown to retrieve the common wavefront distortion shared by all of the single-molecule emission events detected in a biplane configuration (27). We note that the accuracy of smNet-based inference depends on careful consideration of the imaging system during the training process (27). Further developments using smNet’s wavefront estimation capability could potentially allow deep learning to actively drive the DM in real time.

INFORMATION CONTENT IN 3-D POINT SPREAD FUNCTIONS

Information Carried Per Photon

Here, we examine the amount of molecular position information carried per photon in several 3-D imaging modalities in terms of the theoretical precision bounds in the lateral and axial dimensions. For an unbiased estimator, the lower bound of a parameter’s estimation variance can be calculated by using the CRLB (25, 110):

$$\mathrm{var}\left({\theta }_i\right)\ge {\left[F{\left(\theta \right)}^{-\text{1}}\right]}_{ii},$$ 1.

where F is the Fisher information matrix, θ is a vector of estimation parameters, and i denotes the index of each parameter. Intuitively, this definition indicates that the estimation precision of a certain parameter can be improved by increasing the information associated with that parameter.

Assuming that the detected photon counts of each pixel follow a Poisson distribution and the stochastic counting process is independent between different pixels, the elements of the Fisher information matrix can be derived as

$$F_{ij}=\sum _q\frac{1}{{\mu }_q}\frac{\partial {\mu }_q}{\partial {\theta }_i}\frac{\partial {\mu }_q}{\partial {\theta }_j},$$ 2.

with q being the pixel index and μ_q representing the intensity of a single-molecule emission pattern at pixel q. μ can be written as

$$\mu \left(x,y,z\right)=I{\mu }_0\left(x,y,z\right)+bg,$$ 3.

where μ₀ is a normalized PSF with its integration equal to one, I is the total photon count of the single emitter, and bg is a uniform background photon count at each pixel. For the imaging systems containing multiple views of the same emitter, such as biplane and 4Pi single-molecule switching nanoscopy (4Pi-SMSN) systems, the Fisher information matrix is given by (81)

$$F_{ij}=\sum _m\sum _q\frac{1}{{\mu }_{mq}}\frac{\partial {\mu }_{mq}}{\partial {\theta }_{mi}}\frac{\partial {\mu }_{mq}}{\partial {\theta }_{mj}},$$ 4.

with m being the index of each imaging view. From Equations 2 to 4, it can be observed that a high total photon count (I) and low background photon count will increase F_ij, resulting in more information (for simplicity, one could imagine the task of estimating one parameter such that the Fisher information matrix becomes a single value). To obtain a consistent comparison, we calculated the theoretical precision limit from the Fisher information per photon at zero background to quantify various imaging modalities, similar to an approach by Backlund et al. (111) (Figure 3a).

According to Equations 2 to 4, to improve the estimation precision of single-molecule positions, one could modify the PSF shape μ₀, as in Equation 3, to increase the Fisher information. Based on this principle and focusing on improving the precision of axial localization, DH (11), self-bending (87), saddle-point (88), and tetrapod PSFs (89, 101, 112) allow for improvements in the precision of axial localization over an extended axial range (Figure 3a). Through the coherent detection of single molecules using two opposing objective lenses, 4Pi-SMSN can be considered to be another type of PSF that provides significantly increased axial information and is capable of further improving localization precision in all three dimensions (12, 13, 92) (Figure 3a,e).

Increasing Fisher Information Through Excitation

In addition to PSF engineering, which focuses on optimizing the PSF shape (i.e., μ₀ in Equation 3) with respect to its axial positions, one may also modulate the intensity of the PSF according to the position in order to achieve increased Fisher information (i.e., I in Equation 3). The recently developed nanometer resolution imaging with minimal emission fluxes (MINFLUX) (113) and SIMFLUX (where SIM stands for structured illumination microscopy) (114) systems are based on this principle. In both cases, the total photon count I in Equation 3 becomes a function of the emitter’s lateral position [i.e., I (x, y)]. To achieve this, structured excitation profiles are scanned around the single molecule multiple times in lateral or axial directions (115). To ensure consistent comparisons, we used as the comparison metric a precision limit from the Fisher information matrix per photon at zero background, with the total expected photon flux over one scan cycle normalized to one.

Specifically, in SIMFLUX (114), a single molecule is excited and imaged with a sinusoidal illumination pattern at multiple phase positions that are uniformly distributed in a 2π range. Figure 3b shows a simulation result in a 1-D case, given ${\sum }_k{I}_k=1$ and k is the index of each phase position. SIMFLUX allows for further increases in the theoretical Fisher information and, therefore, improves localization precision when compared with SMLM under uniform illumination (Figure 3b). In MINFLUX, single molecules within a subdiffraction-limited area are scanned by a donut beam at multiple positions (113). The key idea of MINFLUX is to scan the molecule near the local minimum of the illumination pattern, inducing a near-zero excitation intensity of a single molecule such that the term 1/μ_q in Equation 2 can be greatly increased when the background photon count is near zero. To demonstrate such a principle, we calculated the information gain for the 1-D case when a single molecule is scanned only in the valley of a 1-D sinusoidal excitation pattern. In contrast to SIMFLUX, in which molecules are scanned by the full modulation period of the illumination pattern, MINFLUX achieves better precision when the scanning range becomes smaller, especially for molecules near the local minimum of the sinusoidal pattern. Also, as the scanning range decreases, the variation in localization precision across the lateral diffraction-limited area increases rapidly. Assuming a modulation period of 300 nm (i.e., the valley-to-valley distance), MINFLUX achieves better localization precision than SIMFLUX in an imaging area of ∼100 nm. Theoretically, the lowest achievable resolution for MINFLUX becomes infinitesimal, and it requires the local minimum of the excitation pattern to be zero. In addition, instead of relying on the emission pattern from single molecules to pinpoint the molecular center, MINFLUX relies on knowledge of the excitation intensity profile to pinpoint the molecular center. System- and sample-induced aberrations may affect both the condition of the zero-intensity center as well as the exact intensity profile near the center minimum required for optimal resolution.

In addition to MINFLUX and SIMFLUX, we also examined the case of applying image-scanning microscopy (ISM) in single-molecule localization. In ISM, a focused laser spot (usually modeled as a 2-D Gaussian illumination pattern) raster scans across the FOV, which is typically much larger than the laser spot. Therefore, each molecule will be probed by the entire size of the laser spot. Figure 3b shows the simulation results for 1-D ISM imaging using a 1-D Gaussian illumination pattern. Similar to SIMFLUX, combining ISM and SMLM increases the information obtained and, therefore, reduces the achievable precision limit when compared with SMLM using uniform illumination (Figure 3b).

SAMPLE DRIFT, VOLUME ALIGNMENT, AND PHOTOBLEACHING

To acquire an entire cellular or tissue volume using SMLM, samples need to be scanned in the axial direction (9, 10). Depending on the 3-D modality used in SMLM, the thickness of each optical section ranges from as thin as 250 nm up to 3 μm (13, 87). Multiple optical sections are needed to reconstruct a whole-cell or tissue volume. Correcting or numerically compensating for drift in each optical section imaged between multiple cycles as well as stitching super-resolved and axially shifted volumes are critical in maintaining the resolution achieved in each optical section. Moreover, for illumination modalities such as wide-field and HILO, in which the illumination profile is several times or significantly thicker than the optical section, certain single molecules that are excited may be out of focus for localization. When a large volume is acquired, this introduces inhomogeneous photobleaching that may result in reduced localization density at the optical sections that are imaged later compared with those imaged earlier. Here, we discuss these considerations in drift correction methods, optical section alignment, and photobleaching mitigation.

Drift Correction

Fiducial marker–based drift correction was used for general time-lapse microscopy before the introduction of SMLM. Fluorescent beads or gold nanoparticles adsorbed onto the coverslip surface have served as the simplest form of fiducial marker for tracking and correcting sample drift, through either postprocessing (116–118) or real-time active feedback compensation (119, 120). This approach suffers from a number of drawbacks. First, there should be at least one fiducial marker inside the camera FOV being imaged. However, too many fiducial markers will interfere with the actual single-molecule signals in cases in which the fluorescence or photoluminescence signal of the markers is detected in the same image. But it is a practical challenge to achieve the optimal concentration of fiducial markers in a consistent way using nano- or microbeads. Additionally, the brightness difference between fiducial markers and single-molecule fluorescence signals often forces data to be acquired under suboptimal imaging conditions in terms of sensitivity and the dynamic range of the detector. Furthermore, potential optical and physical degradation or the motion of fiducial markers relative to the sample over time can make drift correction less reliable. These issues have been addressed to some extent by imprinting regular array patterns of fiducial markers on coverslips using electron beams (121) or soft lithography (122, 123) and also by separating the detection of fiducial markers from the single-molecule imaging channel [e.g., as in bright-field imaging (119, 122–124) or back-focal-plane laser detection (121) of fiducial markers]. Remarkably, using the fiducial marker–based method in combination with back-focal-plane interferometry one can achieve real-time 3-D drift correction with subnanometer precision (121).

3-D imaging of thick samples, such as a whole cell, imposes additional challenges to drift correction. Primarily, the fiducial beads on the coverslip surface may be out of focus when the focal plane is set high above the coverslip for imaging thick volumes, and this issue is more significant for high-NA objectives and their shallow depth of focus. Therefore, the popular fluorescent nano- and microbeads may not be suitable fiducial markers for imaging thick samples in a conventional setting. One approach is to image the two focal planes together (i.e., one for the sample and the other for the fiducial beads), either by switching the axial position of the sample stage between the two focal planes between imaging cycles (125) or by optically separating the two focal planes and projecting them onto different areas of the camera (126). Another approach is to use bright-field images of the cellular structure itself as fiducial markers (127, 128). By employing transillumination light that is spectrally distinct from the fluorescence of excitation or emission, as well as a separate camera for the bright-field imaging, this method of drift correction can be operated independently of fluorescence imaging. Recently, tetrapod PSFs with a tunable axial depth range of up to 20 μm have been used as fiducial markers, allowing for 3-D super-resolution reconstruction of an entire nuclear lamina in a HeLa cell (55).

The use of correlation-based drift correction methods during postprocessing has been demonstrated in both 2-D and 3-D SMLM (92, 129, 130). These methods rely on finding the decentered peak within a cross-correlation volume obtained from the same optical section but at a different time point. The correlation peak—whose height and width depend on the localization density as well as the achieved resolution in each volume—can be precisely localized to track sample drift when the 3-D resolved volume contains high-resolution and well-defined ultrastructures. Furthermore, by incorporating redundancy within the set of the pairwise shifts between volumes at all time points, the estimation fidelity of independent lateral and axial shifts between temporally adjacent volumes can be significantly increased (92, 130, 131).

Multiple Optical Section Imaging and Alignment

A common strategy when imaging large volumes of 3-D SMLM data is to perform multicycle imaging in which each cycle goes through the entire volume. This strategy, however, gives significantly lower localization density per optical section acquired at each cycle when compared with imaging the entire volume in a single cycle. Therefore, the benefit of having evenly distributed localization density across the imaging volume (despite photobleaching) comes with the challenges of later segment alignment as well as axial drift across the cycles. For imaging volumes with large axial depth, the time interval between the two adjacent scan cycles may be exceedingly large (e.g., 30 min to 1 h), and, therefore, the potential axial drift of a microscopy system during such a long interval could be as large as the axial dimension of the optical section itself. This could make correlation-based drift correction inapplicable, as supposedly the same two optical sections obtained in two adjacent cycles might contain completely different cellular or tissue structures. In this case, fiducial marker– or transmission image–based axial position correction will be crucial to keep the FOV in place between imaging cycles. Alternatively, a subset of the entire volume containing axially adjacent optical sections can be imaged at each cycle while moving this subset through the entire volume (80). This could help to reduce the axial drift between cycles, as the time delay between imaging cycles can be significantly shortened.

Alignment of the sequentially obtained optical sections is critical in maintaining the high resolution achieved in each section. Misalignment could result in the deterioration of resolution in the reconstructed volume in both the lateral and axial directions. Stacking optical sections with a fixed theoretical axial shift has been demonstrated in relatively small volumes and at shallow depths (10). For cell and tissue specimens, 3-D correlation-based optical section alignment has been developed in which the partially overlapping volumes between adjacent optical sections are used to find both lateral and axial shifts between the sections (92). To increase the accuracy of alignment, this correlation-based approach also allows for the incorporation of redundancy into the correlation measurements when multiple (i.e., more than two) axially shifted optical sections share partially overlapping volumes.

Photobleaching Mitigation

It cannot be overstated how pivotal are the roles that the tailored, novel photophysics of fluorophores play in the SMLM field, and, therefore, the topic of SMLM fluorescent probes and their photophysics has been extensively reviewed previously (132–134). SMLM requires stochastic photoswitching and almost negligible photobleaching, if possible. Mitigating photobleaching is particularly critical to 3-D SMLM of whole cells or tissues due to the extended imaging time. The primary method for inhibiting photobleaching has been to remove oxygen in the imaging buffer using enzymatic oxygen scavenger systems combined with photostabilizers, either those in the class of triplet-state quenchers [e.g., Trolox (Hoffmann-LaRoche), 1,3,5,7-cyclooctatetraene, or nitrobenzyl alcohol] or those in the class of reduction–oxidation systems (e.g., methyl viologen, ascorbic acid). It was reported that the combined use of photostabilizer additives synergistically improved the photostability of the cyanine and Alexa fluorophores (135). The recently developed concept of a self-healing approach (136) is based on covalently bonding photostabilizers to organic fluorescent probes to facilitate photostabilizer function in the most efficient manner without the need for additives in the buffer solution (Figure 5a). The self-healing concept was further extended to fluorescence resonance energy transfer (or FRET) conjugates (137) in which the acceptor plays a role similar to that of a photostabilizer for the donor, with the additional energy transfer channel effectively suppressing pathways to the intermediate dark states that eventually lead to the photobleaching (Figure 5b). Another notable recent study combined photoswitching and fluxionality to develop a fluorescent probe (138) that can be used for time-lapse, live, whole-cell 4-D SMLM with minimal toxicity and no apparent photobleaching (Figure 5c). Once fluorophores are photoactivated by a 405-nm pulse, the fluorophores exhibit a ground-state equilibrium between a fluorescent and a dark species, resulting in spontaneous blinking that allows for single-molecule localization at a low excitation intensity. The unique feasibility of SMLM at a low excitation intensity could contribute to the minimization of dye photobleaching and cell toxicity and may also be applied to significantly reduce background fluorescence when tissue specimens are imaged.

Figure 5.

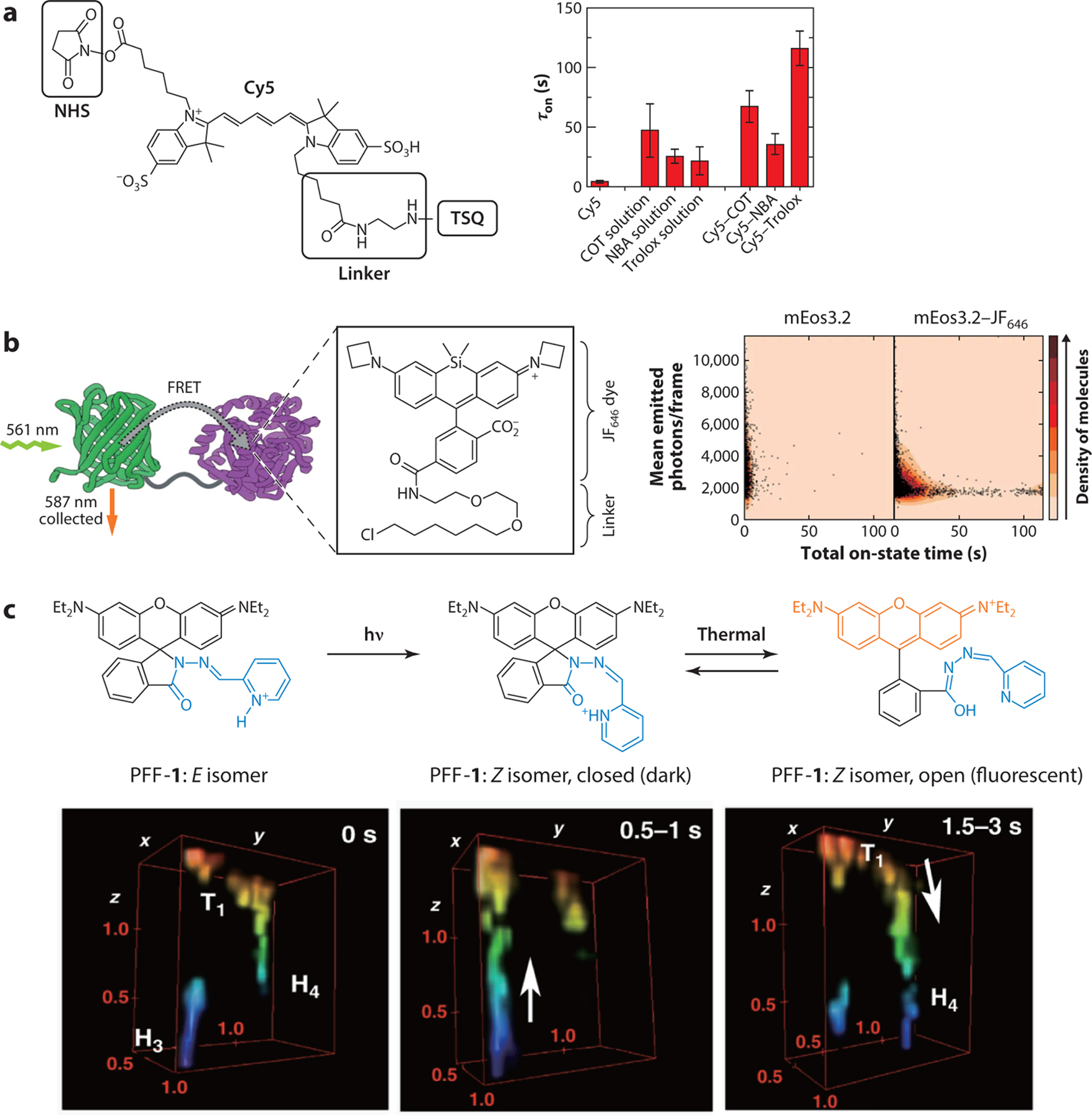
(a) TSQ-conjugated Cy5 (left) and average photobleaching times (τ_on) with individual TSQs in solution or directly conjugated to Cy5 (right). Shown are error bars and standard deviations (n ≥ 6 movies from at least two independent experiments). (b) JF₆₄₆-linked mEos3.2 (left) and 2-D histogram of total on-state time (i.e., individual track length), and total number of switching events per molecule when performing SMLM using either mEos3.2 or the mEos3.2–JF₆₄₆ FRET pair. (c) Mechanism of the photoregulated fluxional fluorophore PFF-1 (top) and 3-D live-cell SMLM imaging of vesicle movement at a synapse, displaying a vesicle moving from hotspot H₃ to H₄ through track T₁ (bottom). The volumes are colored according to the axial direction. The dimension of ROI is 1.5 μm × 1.5 μm × 1.5 μm. Panels a, b, and c adapted with permission from References 136, 137, and 138, respectively. Abbreviations: COT, 1,3,5,7-cyclooctatetraene; FRET, fluorescence resonance energy transfer; NBA, nitrobenzyl alcohol; NHS, N-hydroxysuccinimidyl ester; ROI, region of interest; SMLM, single-molecule localization microscopy; TSQ, triplet-state quencher.

CONCLUSIONS

Whole-cell and tissue specimens challenge the achievable resolution and depth of 3-D SMLM. Instead of relying on one specific solution, the practically achievable resolution, depth, and fidelity of 3-D SMLM in thick specimens rely on careful consideration of multiple aspects of the process, including excitation and detection design, specimen preparation, and localization algorithms, as well as postprocessing of the super-resolved volumes.

Here, we reviewed a selection of these considerations, some innovative solutions, and the consequent trade-offs. Innovations that target to reduce background fluorescence (e.g., light sheet illumination; see Table 1), to correct or compensate for system- and sample-induced aberrations, and to optimize volume reconstruction and the photophysics of single fluorescent probes, as well as to improve information carried by the emitted photons, are discussed. During the past several years, the pace of these developments and their demonstrated breakthroughs have been staggering. When combined, these methods could expand the routine applicability of ultrahigh-resolution 3-D imaging from cellular targets that lie close to the coverslip surface to intra- and extracellular constituents in tissues and cells.

Table 1.

Examples of confined illumination strategies

Light-sheet fluorescence microscopy	Detection numerical aperture	Example specimen type	Single-molecule localization microscopy	Reference
Multidirectional SPIM (mSPIM)	Not available	Zebrafish embryo	No	49
Airy beam	0.4	Juvenile amphioxus	No	70
Inverted SPIM (iSPIM)	0.8	C. elegans embryo	No	44
Dual-view iSPIM (DiSPIM)	0.8	C. elegans embryo, cell	No	45
Three-objective SPIM (TriSPIM)	0.8	Theoretical	No	50
Axially swept light-sheet microscopy (ASLM)	0.8	Cell	No	144
Tiling light-sheet SPIM (TLS-SPIM)	0.8	C. elegans embryo	No	145
	0.8	C. elegans embryo	No	146
Swept confocally aligned planar excitation (SCAPE)	0.95	Mouse, Drosophila larva	No	147
Oblique plane microscopy (OPM)	1.35	Pollen grain	No	148
Digital scanned laser light-sheet fluorescence microscopy (DLSM)	0.075–1.0	Zebrafish embryo	No	149
Selective plane illumination microscopy (SPIM)	0.25–0.8	Medaka embryo, Drosophila embryo	No	43
Light-sheet Bayesian microscopy (LSBM)	1.0	Cell	Yes	56
Individual molecule localization SPIM (IML-SPIM)	0.8 and 1.1	Spheroid	Yes	46
πSPIM	1.1	Cell	No	51
Lattice light-sheet microscopy (LLSM)	1.1	Cell, C. elegans embryo, Drosophila embryo	Yes	47
Bessel beam	0.8	Cell	No	67
	1.1	Cell, C. elegans embryo and larva, Drosophila embryo and adult brain	No	68
Lateral interference tilted excitation (LITE)	≥1.2	Cell, C. elegans embryo, Drosophila embryo	No	150
Single-objective light-sheet microscopy (SO-LSM)	1.2	Cell	Yes	151
Oblique plane stochastic optical reconstruction microscopy (obSTORM)	1.2	Cell, C. elegans, Drosophila larval brain, mouse retina and brain sections	Yes	53
Axial plane optical microscopy (APOM)	1.4	Pollen grain, mouse brain section	No	74
Epi-illumination SPIM (eSPIM)	1.27	Cell	Yes	52
Reflected light-sheet microscopy (RLSM)	1.35 and 1.4	Cell	Yes	54
Single-objective SPIM (soSPIM)	0.3–1.4	Cell, Drosophila embryo	Yes	58
Tilted light-sheet microscopy with 3-D PSFs (TILT3D)	1.4	Cell	Yes	55
Highly inclined swept tile (HIST)	1.45	Cell	No	31
Highly inclined and laminated optical sheet (HILO)	1.49	Cell	No	57

We also expect that by combining 3-D SMLM with recently developed tissue clearing and expansion techniques (139–141) and multiplexed labeling methods (22, 142, 143), resolution and imaging depth may be further extended in the pursuit of ultrahigh-resolution imaging (1 to 5 nm) that is capable of revealing the architecture and arrangement of multiple protein species at the molecular scale deep inside a large tissue volume.