An experimental and computational framework for modeling multi-muscle responses to transcranial magnetic stimulation of the human motor cortex

Abstract

Current knowledge of coordinated motor control of multiple muscles is derived primarily from invasive stimulation-recording techniques in animal models. Similar studies are not generally feasible in humans, so a modeling framework is needed to facilitate knowledge transfer from animal studies. We describe such a framework that uses a deep neural network model to map finite element simulation of transcranial magnetic stimulation induced electric fields (E-fields) in motor cortex to recordings of multi-muscle activation. Critically, we show that model generalization is improved when we incorporate empirically derived physiological models for E-field to neuron firing rate and low-dimensional control via muscle synergies.

I. INTRODUCTION

How the human brain controls multiple muscles to produce coordinated movement remains an essential, but still unresolved, question in neuroscience. It is a classic structure-function biology problem. To date our understanding of this control comes primarily from animal models using a variety of elegant methods including tract tracing [1], neural recording [2], and intracortical microstimulation [3]. These techniques have suggested the presence of motor control for individual muscles as well as coordinated control of coherent muscle groups [4]. Empirical evidence suggests that these coherent muscle groups can be represented as low dimensional bases (known as muscle synergies), and that synergistic motor output can be represented as a linear combination of the these bases notwithstanding known neural circuit non-linearities [5]. However, without availability of results from such highly invasive methods, translation of these insights to humans has been slow and uncertain.

Transcranial magnetic stimulation (TMS) is a non-invasive stimulation modality that has shown promise to bridge this gap. For example, TMS studies of human motor control have shown that evoked hand movements can be well-described by a low dimensional representation of postural synergies [6]. However, the use of TMS as a tool to investigate motor neurophysiology has been limited by our poor understanding of how TMS-induced electric fields (E-fields) are dispersed in the motor cortex (M1) and how resulting directional current densities produce multi-muscle responses.

Here we propose an experimental and mathematical framework for a forward model to predict TMS-evoked multi-muscle activation based on stimulus parameters and anatomical imaging. The full framework incorporates a sequence of input-output models as follows:

• A finite element (FE) model that maps TMS parameters (coil geometry/position/orientation, magnetic pulse characterization) to a volumetric E-field on a subject-specific multi-tissue mesh.

• A deep neural network (DNN) model that provides a lower-dimensional representation of the E-fields.

• A second DNN model that maps stimuli (E-fields or firing rates) to muscle activations.

We used this framework to test two empirically derived physiological phenomena. We tested whether the incorporation of a nonlinear function (derived from macaque studies) that maps local E-fields to expected neural ensemble firing rates improved generalization performance compared to a model that uses E-fields directly. We also tested whether the incorporation of low dimensional bases (derived from human data), representing muscle synergies (Fig. 1, blue dashed lines), improved generalization performance compared to a model of direct cortical-to-muscle connections (Fig. 1, red dashed lines). Additionally, we trained direct cortical-to-muscle connections on the residual information unexplained by synergies to test for further improvements in model performance.

Fig. 1.

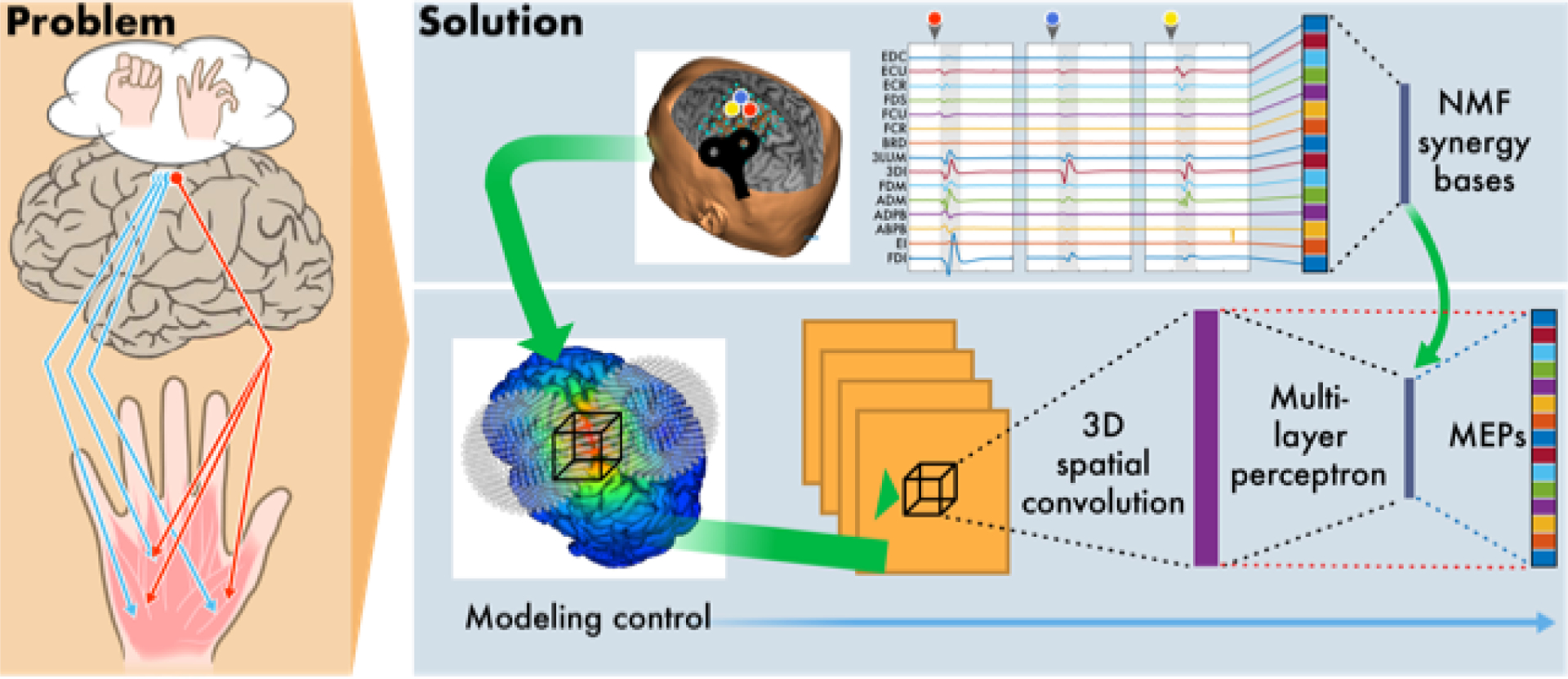
Conceptual overview of the experimental and computational framework for modeling multi-muscle responses to TMS of the human motor cortex.

II. EXPERIMENTAL METHODS

A 35 year old, right-handed, healthy male, eligible for TMS [7], participated in the study following informed consent. The subject was seated, with forearms supported. Surface EMG (Trigno, Delsys, 2kHz) was recorded from 15 hand-arm muscles during TMS: 1st dorsal interosseus (FDI), 3rd dorsal interosseous (3DI), 3rd lumbrical (3Lum), extensor indicus (EI), abductor pollicis brevis (AbPB), adductor pollicis brevis (AdPB), abductor digiti minimi (ADM), flexor digiti minimi (FDM), flexor carpi radialis (FCR), flexor carpi ulnaris (FCU), flexor digitorum superficialis (FDS), extensor digitorum (EDC), and extensor carpi radialis (ECR), extensor carpi ulnaris (ECU), Brachioradialis (BRD). A previously-acquired T1-weighted image (TI=1100ms, TE=2.63ms, TR=2000ms, FOV=256×192mm, 256×192×160 acquisition matrix, 1mm³ voxels) was used for neuronavigation (Brainsight, Rogue Research) and FE Modeling. The TMS coil (Magstim 200, 70mm figure-8) was held tangential to the scalp with the handle posterior and 45° to midline. The right FDI hotspot was found via a coarse map of the hand knob area. Peak-to-peak EMG amplitude 20–50msec after the TMS pulse (motor evoked potential, MEP) was measured (Matlab, The Mathworks). TMS intensity was set at 120% of resting motor threshold, the minimum intensity required to elicit MEPs >50 μV on 3/6 consecutive trials.

TMS maps consisted of 300 stimuli (4sec ISI) delivered on a 7cm² square grid centered on the hotspot. One stimulus was delivered to each of 49 equidistant grid points, followed by delivery of the remaining stimuli based on real-time feedback from neuronavigated MEPs, focusing on excitable and border regions rather than distant, non-responsive, ones [8].

III. MODEL FRAMEWORK

A. Finite Element (FE) Model Component

FE computation was carried out per established procedures [9]: tissue segmentation (scalp, skull, cerebrospinal fluid, gray and white matter) of the subject’s high resolution structural MRI (using Freesurfer, Seg3D), using a hexahedral mesh, assignment of isotropic conductivity values [10] to each mesh element based on tissue type, and simulation of TMS using a quasi-static FE framework (BrainStimulator, SCIRun) [9], [11]. TMS coil output was approximated as the magnetic vector potential from small magnetic dipoles distributed across the coil [12], [13]. The E-field distribution in the cortex was calculated for each coil position, spatially resampled, and used as input for the next stage of the model.

B. Nonlinear E-field to Neural Firing Rate Component

A nonlinear mapping that predicts neural ensemble firing rates for volumetric units in M1, given local E-field values, was developed using nonhuman primate experimental data based on previous studies with concurrent TMS and single neuron recording in alert macaques [14], [15]. Spikes within a few ms of TMS stimulus artifact were recorded with a custom TMS coil that fit around a chamber as a microdrive advanced an electrode into the E-field in M1 and adjacent premotor areas from 243 neurons in two macaques. To classify the neurons, action potential waveforms were fit using a Gaussian mixture model technique [16] resulting in clusters of putative axons, excitatory neurons, and inhibitory neurons. The main effect of TMS in all three clusters was a dose-dependent, short-latency burst of activity followed, in most cases, by an extended pause. As TMS intensity increased, the short-latency burst approached motor threshold (approx. .8 V/m in these macaques). The middle panel of Fig. 2 shows the dose-response curve for putative excitatory neurons in the sample, representing how TMS dose translated to induction of spiking activity in neurons that may project to spinal circuits.

Fig. 2.

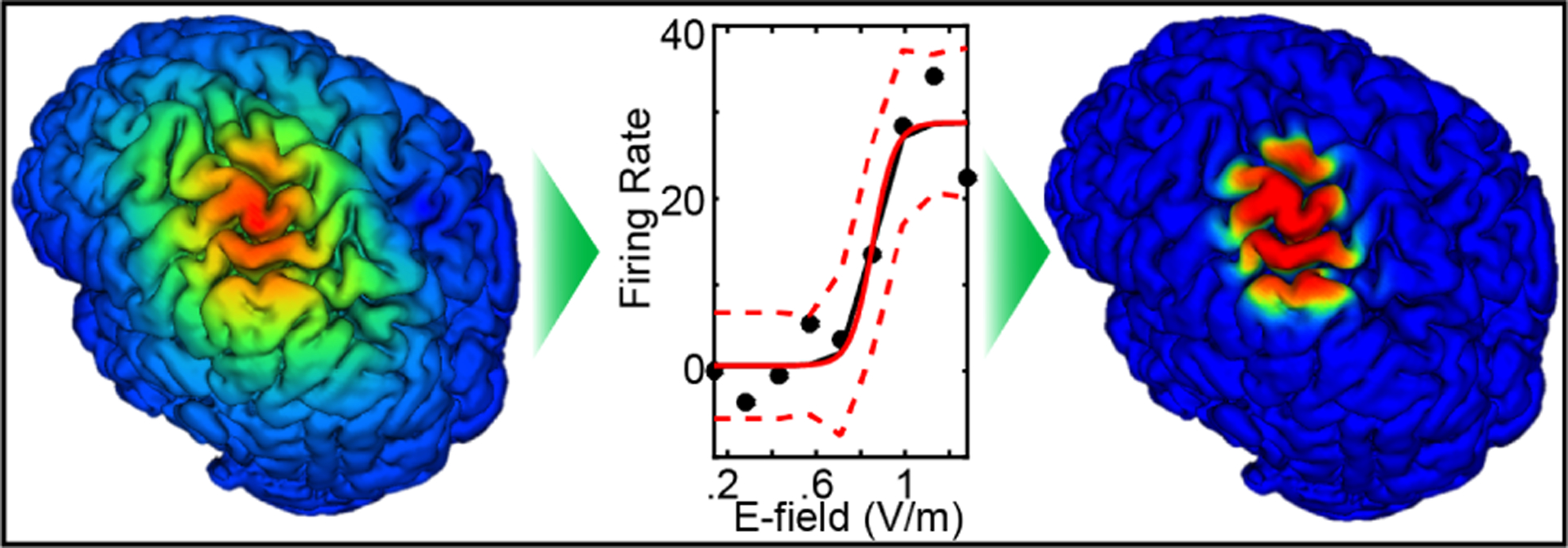
Left-to-Right: FE model of the TMS-induced E-field in human; transfer function from E-field to neural firing rate based on macaque M1 recordings; resulting estimation of TMS-induced firing rates used as inputs to a refined DNN.

C. Deep Neural Net Model Components

The spatial E-field distribution (with / without refinements from estimated ensemble neural firing rate) was processed with feedforward multilayer perceptron (MLP) DNN models. A convolutional autoencoder was employed to build a lower dimensional representation of the brain stimulation map after resampling the E-field to a uniform 3D grid (80×80×80 with 1mm³ voxels), with a field-of-view containing M1. The encoder was trained with mean squared error as the cost function and Adagrad as the optimizer [17] and output a 10×10×10 intermediate spatial representation using a combination of convolution, pooling, and exponential linear activation functions. Convolutional neural networks (CNNs) were used to extract texture features characterizations of spatial fluctuations in input field, followed by a fully connected MLP layer to project high dimensional spatial convolution features onto the lower dimensional target variables [18]. CNN models using spatially localized feature extraction in a hierarchical/multiscale fashion were chosen since we know from physiology that M1 is spatially organized. We used statistical model order selection procedures to prevent over-fitting to calibration data; in addition the CNN structure also has the benefit that repeated use of identical convolution modules specifically controls model complexity [19].

D. Linear Low Dimensional Component (Muscle Synergies)

A low dimensional linear structure, representing muscle synergies, was extracted using non-negative matrix factorization (NMF) [20], [21] applied on TMS-induced MEPs. NMF solutions can be understood as constrained maximum likelihood estimates for a statistical generative model of observed EMG features: m_t = Sa_t + w_t where m_t ≽ 0, t ∈ {1,…,T} are the 15-dimensional measured non-negative EMG features per trial (T = 300 TMS trials; S is the unknown 15 × R synergy basis matrix, where each column s_r; r ∈ {1, … ,R} indicates the relative activation level of each muscle in each synergy basis, a_t is the unknown activation vector that linearly combines synergy bases, and ${\mathbf{\text{w}}}_t~\mathcal{N}\left(0,{\sigma }^2\mathbf{\text{I}}\right)$ is spatiotemporal white additive Gaussian noise. Under this model, maximum likelihood parameter estimation reduces to:

$$\begin{gathered} \underset{\left\{\dots ,{\mathbf{\text{a}}}_t,\dots \right\},\mathbf{\text{S}}}{\text{minimize}}\frac{1}{2}{\sum _n\Vert m_t-S{a}_t\Vert }_2^2\text{\hspace{1em}subject}\text{to} \\ {a}_t\succcurlyeq 0\forall t\text{\hspace{1em}and\hspace{1em}}S\succcurlyeq 0\text{\hspace{1em}and\hspace{1em}}{S}^{\text{T}}1=1 \end{gathered}$$ (1)

An iterative algorithm was used to estimate optimal model parameters with the stopping criterion based on relative reduction in squared error [21]. The choice of rank (R ∈ {1,…,15}) controls model complexity. As is typical in the literature, we chose R as the minimum rank needed to describe 90% of the overall ”variance accounted for”, (R²), where R² = 1 - RSS/SST, RSS is the residual sum of squares, and SST is the total sum of squares [22].

IV. RESULTS & DISCUSSION

The autoencoder output was used as an input to a fully connected 3-layer MLP, and both the MLP layers and the encoder parameters were further optimized using binary cross-entropy loss and weight decay regularization (assuming a zero-mean Gaussian prior for MLP model parameters) to estimate muscle activity directly (Fig. 1, thick red dashed lines), through activations of NMF synergy matrices (Fig. 1, thick blue dashed lines), or with a combination of both. The muscle activity data was normalized to the unit interval [0, 1]; therefore, we used sigmoid non-linearities σ(.) in the final layer. Specifically, given the input E-field ε_t to the model, the output layer of the MLP took one of three forms to produce muscle activity estimates ${\widehat{\mathbf{\text{m}}}}_t$ from the input x_t = f(ε_t) to this final layer: (Directly) ${\widehat{\mathbf{\text{m}}}}_t=\sigma \left({\mathbf{\text{W}}}_d{\mathbf{\text{x}}}_{\text{t}}\right)$; (Via synergy activation) ${\widehat{\mathbf{\text{m}}}}_t=\sigma \left({\mathbf{\text{SW}}}_a{\mathbf{\text{x}}}_{\text{t}}\right)$; (Accounting for residuals from synergy activations) ${\widehat{\mathbf{\text{m}}}}_t=\sigma \left({\mathbf{\text{W}}}_r\text{+}{\mathbf{\text{SW}}}_a{\mathbf{\text{x}}}_t\right)$.

The three model variations were trained using 10-fold cross-validation using the E-field or neuron firing rate (see Fig. 2) as inputs. The performance of all six models is compared quantitatively and visually in Fig. 3, which provides a quantitative comparison of all model outputs with the ground truth. To quantify model performance (Fig. 3D), we computed accuracy of model alignment using dot products between model outputs and ground truth; we report alignment accuracy by the cosine of the angle between them and accuracy of model magnitude, using the amplitude scale factor (closer to 1 indicates better match for both measures). Error bars in panel D show 90% confidence intervals computed based on the jackknife estimation procedure [23].

Fig. 3.

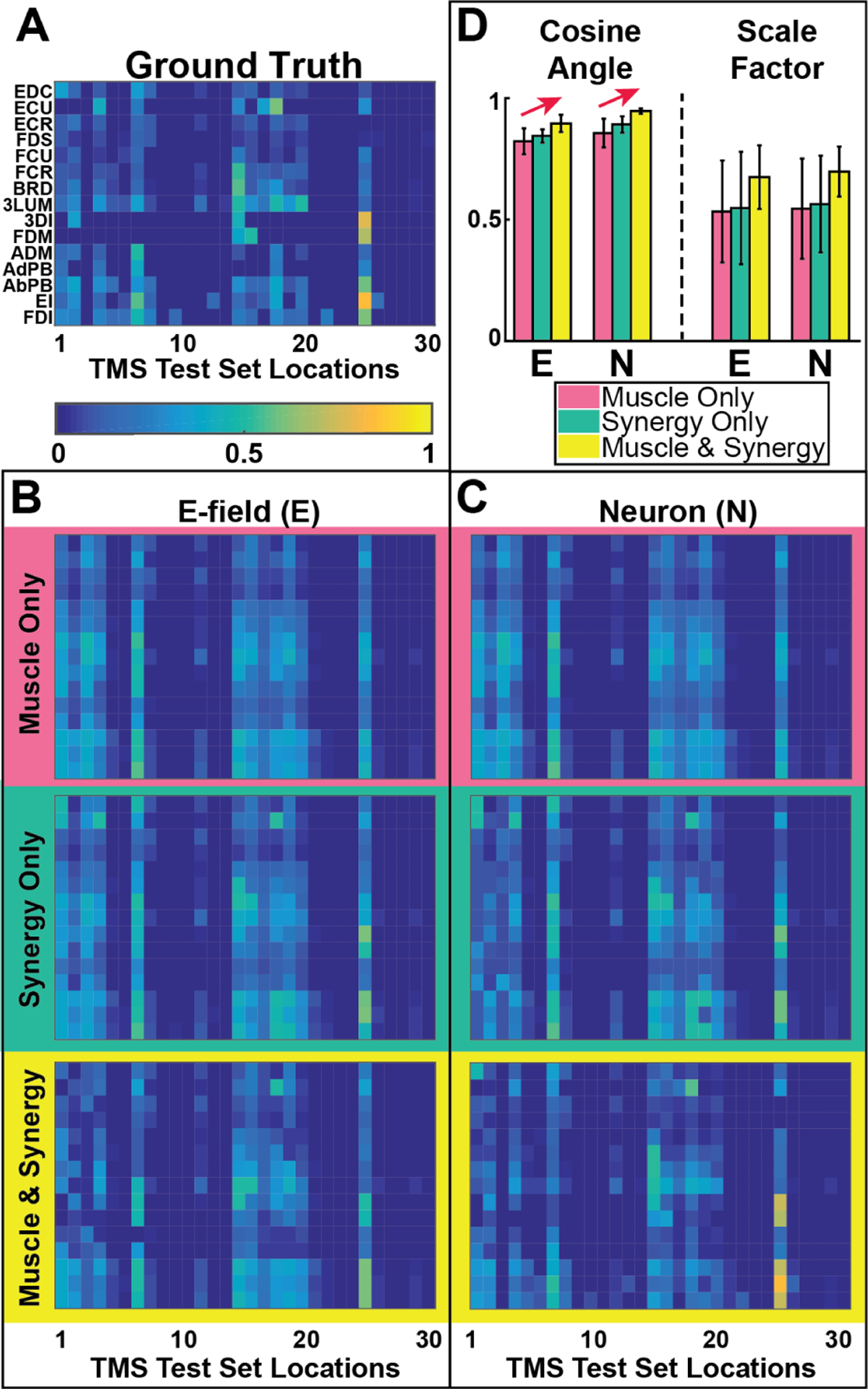
Forward model comparisons: (A)-(C) Map of response of muscles (rows) vs stimulus location (columns): (A) Measured MEPs for 30 TMS locations. (B) MEP estimates using E-field distributions as inputs to DNNs; direct-to-muscle (top), via synergy (middle), and combined (bottom) output layer connections in the model. (C) MEP estimates as in panel B using neuron firing rate distributions (obtained by passing E-field values in each voxel through the firing rate transfer function. See Fig. 2 for E-field-to-Neuron transfer function effects on modeled activation. (D) Summary comparison of result using metrics of alignment (Cosine Angle) and magnitude (Scale Factor) as described in the text.

Results of NMF applied to TMS-induced multi-muscle MEPs, and rank determination as describe above, indicated that 9 synergies accounted for >90% of the variance. Incorporation of synergies (Fig. 3B,C middle/green rows and Fig. 3D middle/green bars) and training of direct connections to account for information poorly characterized by synergies (Fig. 3B,C bottom/yellow rows and Fig. 3D right/yellow bars) each led to improvement in model prediction. This is in accordance with current theories of motor control that predict reduced redundancy and control complexity is provided by synergies and supplemented via direct cortico-motor connections for fractionated non-synergistic control [24].

Use of neural firing rates as inputs improved generalization in all models. In the E-field models error accumulated due to weak E-fields at the periphery of the stimulation, which in a neurophysiological sense are unlikely to result in cortical activation. Previous investigations which have used FE modeling of E-fields to depict an activated region in response to TMS used arbitrary thresholds to bound the E-field zone. Our pilot data suggest that using an experimentally derived transfer function from E-field to neural firing rate significantly improved model accuracy.

V. CONCLUSIONS

We believe that this kind of systematic application of modeling techniques will improve interpretation of TMS data and has the promise to yield meaningful insights into human corticospinal organization. These insights have the potential for clinical translation by improving presurgical mapping, tracking of reorganization with pathology and rehabilitation, prescription of synergy-based interventions, and neuroprosthetic control.