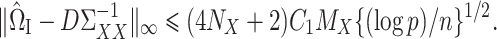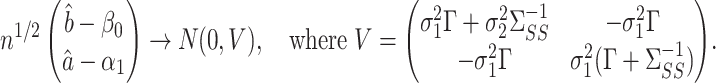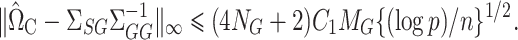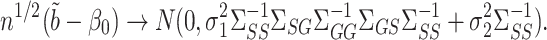Summary
Mediation analysis is difficult when the number of potential mediators is larger than the sample size. In this paper we propose new inference procedures for the indirect effect in the presence of high-dimensional mediators for linear mediation models. We develop methods for both incomplete mediation, where a direct effect may exist, and complete mediation, where the direct effect is known to be absent. We prove consistency and asymptotic normality of our indirect effect estimators. Under complete mediation, where the indirect effect is equivalent to the total effect, we further prove that our approach gives a more powerful test compared to directly testing for the total effect. We confirm our theoretical results in simulations, as well as in an integrative analysis of gene expression and genotype data from a pharmacogenomic study of drug response. We present a novel analysis of gene sets to understand the molecular mechanisms of drug response, and also identify a genome-wide significant noncoding genetic variant that cannot be detected using standard analysis methods.
Keywords: High-dimensional inference, Integrative genomics, Mediation analysis
1. Introduction
Mediation analysis is of great interest in many areas of research, such as psychology, epidemiology and genomics (MacKinnon, 2008; Hayes, 2013; Huang et al., 2014). A major goal is to understand the direct and indirect effects of an exposure variable on an outcome variable, potentially mediated through several intervening variables. Statistical methods for estimating and testing direct and indirect effects are well-developed when the number of mediator variables is relatively small (Hayes, 2013; VanderWeele & Vansteelandt, 2014; VanderWeele, 2015), but problems arise when the number of potential mediators exceeds the sample size. This high-dimensional scenario is common in genomics applications. For example, the effects of genetic variants may be mediated through the regulation of gene expression, but it is usually not known a priori which genes are regulated, so the total number of potential mediators can be very large.
General methods for high-dimensional inference are currently the subject of intense research. Techniques based on debiasing penalized regression estimators have been shown to provide asymptotically normal and unbiased estimators for certain parametric sparse regression models (Javanmard & Montanari, 2014, 2018; Van de Geer et al., 2014; Zhang & Zhang, 2014). The sparsity level of the regression parameter is not typically known. Cai & Guo (2017) discussed the construction of confidence intervals that can adapt to this unknown sparsity, and Zhu & Bradic (2018) proposed a test that avoids the sparsity requirement by instead assuming that the precision matrix is known or has certain sparsity properties. While these methods can be used for testing direct effects, they cannot be directly applied to perform inference on indirect effects. One approach is to use them to extend low-dimensional mediation analysis methods such as VanderWeele & Vansteelandt (2014), but it may be difficult to achieve valid inference for reasons that will be explained in § 2.1.
Several semiparametric high-dimensional methods have recently been proposed in the causal inference literature for peforming inference on causal effects in the presence of high-dimensional controls (Belloni et al., 2017; Athey et al., 2018). In particular, the procedure of Athey et al. (2018) is closely related to the method proposed here, and is discussed in detail in § 2.5. However, these approaches do not directly apply to estimating indirect effects in high-dimensional mediation models. Chen et al. (2015) and Huang & Pan (2016) use principal components analysis to reduce the dimensionality of the mediators, and employ the bootstrap for inference. Hanson et al. (2016) and Zhang et al. (2016) first screen the mediators according to their marginal correlations with the response.
In this paper we propose and provide asymptotic guarantees for two new inferential procedures for the indirect effect in high-dimensional linear mediation analysis models. We first consider the incomplete mediation setting, where both direct and indirect effects might exist. This is a common scenario, for example in genome-wide methylation studies that investigate whether environmental exposures exert their effects on phenotype by altering DNA methylation patterns. The exposures may also act through a nonmethylation pathway, giving rise to potential direct effects. We illustrate another application in § 6, where we identify gene sets that may mediate the effect of a gene of interest on a drug response phenotype.
We then consider the complete mediation setting when it is known that a direct effect does not exist. This setting is common when studying genetic variants located in noncoding regions of the genome, which typically can only exert their effects on a phenotype by regulating gene expression. Recent work has shown that in the low-dimensional case, testing for the indirect effect can be much more powerful than directly testing the total effect, even though both are equal under complete mediation (Kenny & Judd, 2014; Zhao et al., 2014b; Loeys et al., 2015). We show theoretically and in simulations that this is also true for our proposed high-dimensional method. Our work can thus be useful in genome-wide association studies where powerful tests are required to detect important variants. In an analysis of the genetics of drug response in § 6, our method was able to identify a genome-wide significant noncoding genetic variant that could not be detected by the standard approach.
2. Proposed methods
2.1. Mediation model and notation
For the  th subject,
th subject,  , let
, let 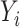 be the outcome,
be the outcome, 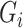 be a vector of
be a vector of  mediators and
mediators and 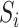 be a vector of
be a vector of  exposures. We allow
exposures. We allow  to be larger than the sample size
to be larger than the sample size  , but we assume that
, but we assume that 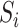 is low-dimensional. Finally, assume that the
is low-dimensional. Finally, assume that the 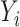 ,
, 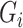 and
and 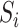 have all been centred to have zero mean. We consider the following linear mediation model:
have all been centred to have zero mean. We consider the following linear mediation model:
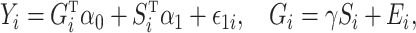 |
(1) |
where 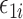 are mean-zero random variables and
are mean-zero random variables and 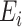 are mean-zero random vectors that are independent of
are mean-zero random vectors that are independent of 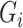 and
and 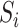 . Model (1) implies that
. Model (1) implies that 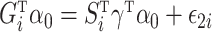 , where
, where 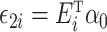 . Let
. Let 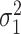 denote the variance of
denote the variance of 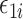 , and
, and 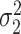 denote the variance of
denote the variance of  .
.
We are interested in performing inference on the indirect effect
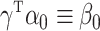 |
(2) |
of 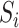 on
on 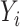 when the dimension of
when the dimension of  exceeds the sample size. We will describe separate methods for the incomplete mediation setting, where
exceeds the sample size. We will describe separate methods for the incomplete mediation setting, where  may have a direct effect on
may have a direct effect on 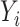 through
through 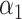 , and the complete mediation setting, where
, and the complete mediation setting, where 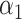 is assumed to equal zero. We will assume throughout that
is assumed to equal zero. We will assume throughout that 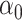 is sparse, so that only a small number of variables mediate the effect of
is sparse, so that only a small number of variables mediate the effect of 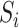 on
on 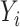 .
.
Assuming that model (1) is correctly specified with no unmeasured confounders,  and the direct effect
and the direct effect 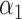 admit causal interpretations under a counterfactual framework, analogous to low-dimensional mediation models (Huang et al., 2014; VanderWeele & Vansteelandt, 2014). See the Supplementary Material for a detailed discussion. Our method can also accommodate measured confounders or covariates. If
admit causal interpretations under a counterfactual framework, analogous to low-dimensional mediation models (Huang et al., 2014; VanderWeele & Vansteelandt, 2014). See the Supplementary Material for a detailed discussion. Our method can also accommodate measured confounders or covariates. If 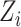 is a low-dimensional vector of potential confounders, we could write
is a low-dimensional vector of potential confounders, we could write
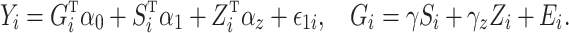 |
For example, in our data analysis in § 6 we let 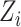 be a set of principal components to adjust for population stratification; in the Supplementary Material we describe how our proposed procedures can be modified for this setting. In this paper we do not consider more complicated models, such as interactions between the
be a set of principal components to adjust for population stratification; in the Supplementary Material we describe how our proposed procedures can be modified for this setting. In this paper we do not consider more complicated models, such as interactions between the 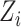 and
and 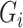 or between
or between 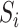 and
and 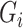 . These may require additional methodological development, which we leave for future work.
. These may require additional methodological development, which we leave for future work.
The remainder of the paper will use the following notation. Let 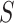 be an
be an 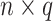 matrix of the
matrix of the 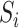 ,
, 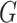 be an
be an  matrix of the
matrix of the 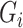 ,
,  be an
be an 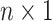 vector of the
vector of the 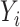 ,
, 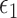 be an
be an 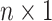 vector of the
vector of the 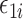 , and
, and 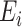 be an
be an 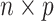 matrix of the
matrix of the 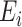 . Define the vector
. Define the vector 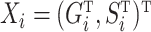 . Also define the sample matrices
. Also define the sample matrices  ,
, 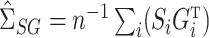 ,
,  ,
, 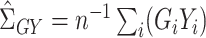 ,
, 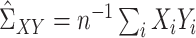 , and
, and 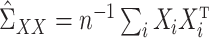 , as well as their population-level versions
, as well as their population-level versions  ,
, 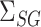 ,
, 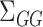 ,
, 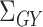 ,
, 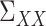 and
and 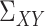 . Finally, for any matrix
. Finally, for any matrix 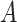 , let
, let 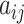 denote the
denote the 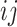 th entry and let
th entry and let 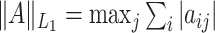 ,
,  denote the elementwise
denote the elementwise 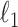 norm, and
norm, and 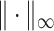 denote the elementwise
denote the elementwise 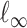 norm of either a vector or a matrix.
norm of either a vector or a matrix.
2.2. Intuitions
This section provides an intuitive description of the challenges of performing inference on the indirect effect 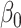 (2) with high-dimensional mediators. For simplicity, in this subsection we assume that the direct effect
(2) with high-dimensional mediators. For simplicity, in this subsection we assume that the direct effect 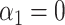 . In the low-dimensional problem when
. In the low-dimensional problem when  ,
, 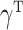 and
and 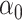 can be estimated using the ordinary least squares estimates
can be estimated using the ordinary least squares estimates 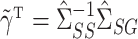 and
and 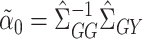 , respectively. Then
, respectively. Then  can be estimated using
can be estimated using  . Inference is straightforward because this product estimator typically has an asymptotically normal distribution (Sobel, 1982; Zhao et al., 2014b), though see the last paragraph of § 3.1. In high dimensions, when
. Inference is straightforward because this product estimator typically has an asymptotically normal distribution (Sobel, 1982; Zhao et al., 2014b), though see the last paragraph of § 3.1. In high dimensions, when 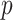 exceeds
exceeds 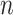 , the challenge is that the ordinary least squares estimator of
, the challenge is that the ordinary least squares estimator of 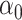 does not exist. Since
does not exist. Since 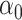 is sparse, one solution would be to use penalized regression, such as the lasso, to estimate
is sparse, one solution would be to use penalized regression, such as the lasso, to estimate 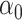 . However, these do not have tractable limiting distributions, so inference on
. However, these do not have tractable limiting distributions, so inference on 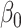 using this approach is difficult.
using this approach is difficult.
An alternative might be to instead use a debiased lasso estimator 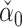 of
of  , whose components do have nice asymptotic distributions (Javanmard & Montanari, 2014; Van de Geer et al., 2014; Zhang & Zhang, 2014). We first briefly introduce
, whose components do have nice asymptotic distributions (Javanmard & Montanari, 2014; Van de Geer et al., 2014; Zhang & Zhang, 2014). We first briefly introduce 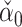 following Javanmard & Montanari (2014). In high dimensions, the ordinary least squares estimator
following Javanmard & Montanari (2014). In high dimensions, the ordinary least squares estimator  is not feasible because
is not feasible because 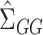 is no longer invertible, but we can still consider estimators of the form
is no longer invertible, but we can still consider estimators of the form 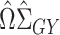 for a different data-dependent matrix
for a different data-dependent matrix 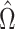 . By model (1),
. By model (1),
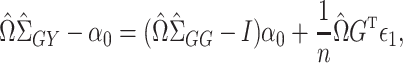 |
(3) |
where 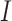 is the
is the 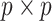 identity matrix. In general,
identity matrix. In general, 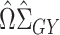 will therefore be a biased estimator, with bias equal to
will therefore be a biased estimator, with bias equal to 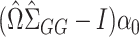 . When
. When 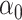 is sparse, it turns out that this bias can be well-estimated by
is sparse, it turns out that this bias can be well-estimated by 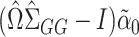 , if we carefully construct
, if we carefully construct 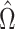 so that
so that 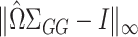 is small and
is small and 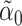 is a lasso estimate of
is a lasso estimate of 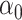 so that
so that 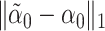 is small; for more details see Javanmard & Montanari (2014). The debiased lasso estimator is then constructed by subtracting the estimated bias from
is small; for more details see Javanmard & Montanari (2014). The debiased lasso estimator is then constructed by subtracting the estimated bias from 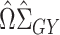 :
:
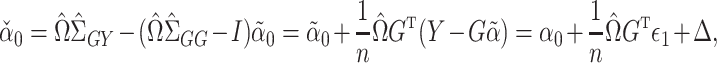 |
(4) |
where 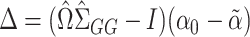 . It can be shown for suitably constructed
. It can be shown for suitably constructed 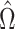 that each component of
that each component of 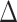 is
is 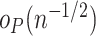 , so that each component of
, so that each component of 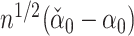 is asymptotically normal. Javanmard & Montanari (2014) chose
is asymptotically normal. Javanmard & Montanari (2014) chose 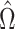 to minimize the variance of
to minimize the variance of 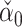 , while Van de Geer et al. (2014) and Zhang & Zhang (2014) chose
, while Van de Geer et al. (2014) and Zhang & Zhang (2014) chose 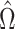 to estimate the precision matrix
to estimate the precision matrix 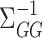 .
.
Despite these encouraging properties, inference using the corresponding estimator 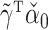 for
for 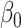 is still not always possible. Using (4),
is still not always possible. Using (4),
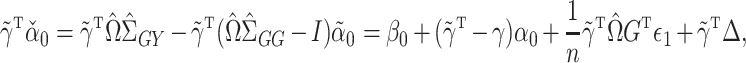 |
which can be interpreted as a debiased version of 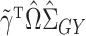 for
for 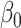 . However, the error
. However, the error 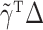 is no longer negligible: even though each component of
is no longer negligible: even though each component of 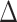 is
is 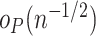 , the linear combination
, the linear combination 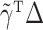 may not be, so
may not be, so 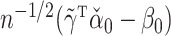 may not have an easily characterized asymptotic distribution. We argue in the Supplementary Material that we would need to at least assume either that
may not have an easily characterized asymptotic distribution. We argue in the Supplementary Material that we would need to at least assume either that 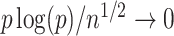 or that
or that 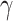 is sparse in order for
is sparse in order for 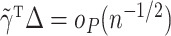 . However, these conditions are restrictive.
. However, these conditions are restrictive.
In this paper we propose an estimate of 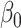 under the weaker assumption that
under the weaker assumption that 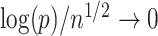 , and without assumptions on the sparsity of
, and without assumptions on the sparsity of 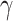 . Our central idea is to develop a debiased estimator not of
. Our central idea is to develop a debiased estimator not of 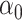 or
or 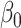 , but of
, but of 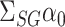 . We will show that the bias of our initial estimator for this quantity can be estimated sufficiently accurately as long as we construct the matrix
. We will show that the bias of our initial estimator for this quantity can be estimated sufficiently accurately as long as we construct the matrix 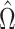 appropriately. By premultiplying our debiased estimate of
appropriately. By premultiplying our debiased estimate of 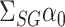 by the low-dimensional quantity
by the low-dimensional quantity 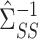 , we will obtain an asymptotically normal estimate of
, we will obtain an asymptotically normal estimate of 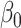 .
.
2.3. Inference for the indirect effect under incomplete mediation
We first estimate the indirect effect 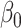 (2) under incomplete mediation, where
(2) under incomplete mediation, where 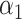 is allowed to be nonzero. Let
is allowed to be nonzero. Let 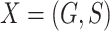 be the
be the 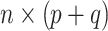 design matrix and
design matrix and 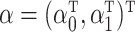 . As described in § 2.2, our strategy is to first obtain a debiased estimator for
. As described in § 2.2, our strategy is to first obtain a debiased estimator for 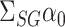 , which we will then premultiply by
, which we will then premultiply by 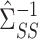 . First, define
. First, define
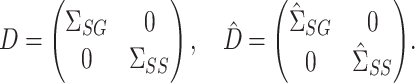 |
(5) |
Following (3), we first consider estimators of the form 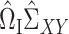 , for a matrix
, for a matrix 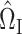 that we will construct later. By model (1),
that we will construct later. By model (1),
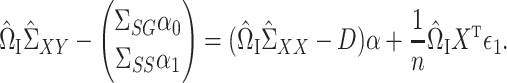 |
Since 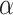 is sparse, we can estimate the bias term using
is sparse, we can estimate the bias term using 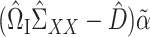 as in (3), using a carefully constructed
as in (3), using a carefully constructed 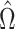 and where
and where  is a lasso estimate of
is a lasso estimate of  . We will use the scaled lasso of Sun & Zhang (2012) because it also provides a consistent estimate of the variance of the
. We will use the scaled lasso of Sun & Zhang (2012) because it also provides a consistent estimate of the variance of the 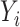 , which will be useful later. We may also leave
, which will be useful later. We may also leave 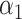 unpenalized, which is further discussed in § 7.
unpenalized, which is further discussed in § 7.
We can therefore construct a debiased estimate of 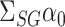 by subtracting the estimated bias from
by subtracting the estimated bias from 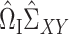 , analogous to (4). We then premultiply the debiased estimator by
, analogous to (4). We then premultiply the debiased estimator by 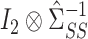 , where
, where 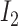 denotes the
denotes the 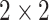 identity matrix and
identity matrix and 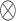 denotes the Kronecker product. This gives our proposed estimator
denotes the Kronecker product. This gives our proposed estimator 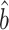 for the indirect effect
for the indirect effect 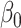 under incomplete mediation, as well as an estimate
under incomplete mediation, as well as an estimate 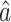 of the direct effect
of the direct effect 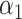 :
:
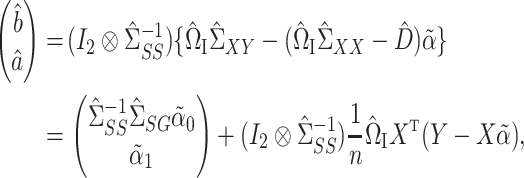 |
(6) |
where 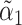 is the component of
is the component of 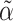 that estimates
that estimates 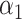 .
.
Analogous to (4), it remains to find a suitable matrix 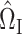 so that
so that 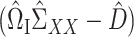 is small. We propose to choose
is small. We propose to choose 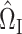 to estimate the matrix
to estimate the matrix 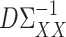 , for
, for 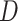 defined in (5) and
defined in (5) and 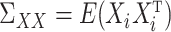 . Our estimator is based on constrained
. Our estimator is based on constrained 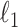 optimization, similar to the precision matrix estimation procedure of Cai et al. (2011):
optimization, similar to the precision matrix estimation procedure of Cai et al. (2011):
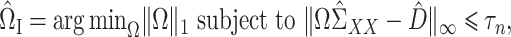 |
(7) |
where 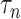 is a tuning parameter. We will show in § 3 that
is a tuning parameter. We will show in § 3 that 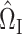 will converge to
will converge to 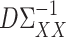 under the condition that
under the condition that 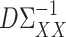 is sparse.
is sparse.
We show in § 3 that under certain conditions, 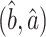 is asymptotically normal and centred at the true
is asymptotically normal and centred at the true 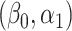 . We also provide estimates of the asymptotic variance of
. We also provide estimates of the asymptotic variance of 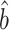 , which will allow us to construct confidence intervals and conduct Wald tests for the indirect effects. Though this paper focuses on the indirect effect, (6) also gives an estimate
, which will allow us to construct confidence intervals and conduct Wald tests for the indirect effects. Though this paper focuses on the indirect effect, (6) also gives an estimate 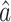 for the direct effect. As pointed out by a referee, the direct effect could also be estimated by subtracting
for the direct effect. As pointed out by a referee, the direct effect could also be estimated by subtracting 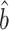 from the ordinary least squares estimate of the total effect of
from the ordinary least squares estimate of the total effect of 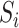 on
on 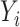 . We show in § 4.3 in the Supplementary Material that these two approaches are asymptotically equivalent.
. We show in § 4.3 in the Supplementary Material that these two approaches are asymptotically equivalent.
2.4. Inference for the indirect effect under complete mediation
In some applications, for example in the analysis of noncoding genetic variants, it may be known that exposure does not act directly on the outcome, and only acts through mediators. We can make use of the extra information that 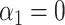 to develop a more efficient procedure for estimating the indirect effect
to develop a more efficient procedure for estimating the indirect effect 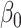 (2). As above, we first obtain a debiased estimator for
(2). As above, we first obtain a debiased estimator for 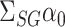 and then premultiply by
and then premultiply by 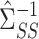 . We again first consider estimators of the form
. We again first consider estimators of the form 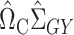 , which by model (1) satisfy
, which by model (1) satisfy
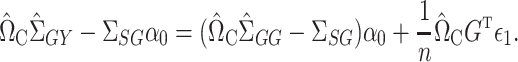 |
We construct 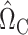 to estimate
to estimate 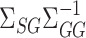 , analogous to
, analogous to 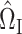 (7) above:
(7) above:
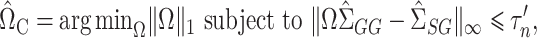 |
(8) |
where 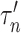 is a tuning parameter. We show in § 3 that
is a tuning parameter. We show in § 3 that 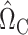 will converge to
will converge to 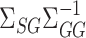 if the latter is sparse. If
if the latter is sparse. If 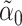 is the scaled lasso estimate of
is the scaled lasso estimate of 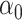 , we can estimate the bias of
, we can estimate the bias of 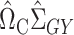 using
using 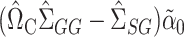 . Subtracting this from
. Subtracting this from 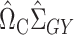 and premultiplying by
and premultiplying by 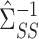 gives our proposed estimate of
gives our proposed estimate of 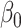 under complete mediation:
under complete mediation:
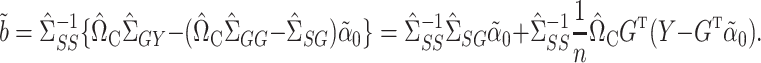 |
(9) |
We show in § 3 that 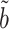 is asymptotically normal and centred at the true
is asymptotically normal and centred at the true 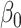 , and provide estimates for its asymptotic variance.
, and provide estimates for its asymptotic variance.
This estimator has an interesting efficiency property. Under complete mediation, 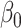 can also be estimated by directly regressing
can also be estimated by directly regressing 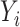 on
on 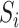 and ignoring the mediating gene expression information. We will show that the asymptotic variance of the ordinary least squares estimator of
and ignoring the mediating gene expression information. We will show that the asymptotic variance of the ordinary least squares estimator of 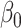 is always greater than or equal to the variance of our
is always greater than or equal to the variance of our 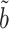 . The same phenomenon has been observed in a low-dimensional mediation model (Kenny & Judd, 2014; Zhao et al., 2014b; Loeys et al., 2015). Intuitively, our procedure achieves this efficiency gain by denoising the outcome
. The same phenomenon has been observed in a low-dimensional mediation model (Kenny & Judd, 2014; Zhao et al., 2014b; Loeys et al., 2015). Intuitively, our procedure achieves this efficiency gain by denoising the outcome 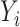 , replacing it with an estimate
, replacing it with an estimate 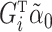 of its conditional expectation
of its conditional expectation 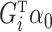 and thus removing much of the variation from the error term
and thus removing much of the variation from the error term 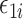 .
.
2.5. Connections to existing work
Estimating the indirect effect in high dimensions is challenging because 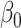 (2) is a linear combination of the high-dimensional vector
(2) is a linear combination of the high-dimensional vector 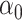 . Athey et al. (2018) encountered a similar issue studying inference for a causal effect in the presence of high-dimensional controls, and also took a debiasing approach. Both of our approaches can be viewed as debiasing a pilot estimator by subtracting a weighted sum of the residuals from a fitted penalized regression model for
. Athey et al. (2018) encountered a similar issue studying inference for a causal effect in the presence of high-dimensional controls, and also took a debiasing approach. Both of our approaches can be viewed as debiasing a pilot estimator by subtracting a weighted sum of the residuals from a fitted penalized regression model for 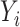 . Athey et al. (2018) chose the weights in this weighted sum to minimize the estimation error of the desired linear combination, while our weights are equal to
. Athey et al. (2018) chose the weights in this weighted sum to minimize the estimation error of the desired linear combination, while our weights are equal to 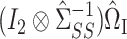 in (6) and
in (6) and 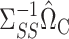 in (9). The coefficients of the desired linear combination are known in the setting of Athey et al. (2018), while in our approach they are equal to
in (9). The coefficients of the desired linear combination are known in the setting of Athey et al. (2018), while in our approach they are equal to 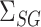 and must be estimated, so the method of Athey et al. (2018) is not directly applicable here. It would be interesting to apply their strategy to our mediation framework in the future.
and must be estimated, so the method of Athey et al. (2018) is not directly applicable here. It would be interesting to apply their strategy to our mediation framework in the future.
There are alternative approaches to constructing the matrices 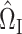 (7) and
(7) and 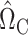 (8). One method might be to choose them to minimize the variances of the resulting estimators
(8). One method might be to choose them to minimize the variances of the resulting estimators 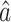 ,
, 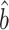 and
and 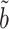 while controlling their biases. In the standard linear regression setting with high-dimensional covariates, Javanmard & Montanari (2014) showed that this strategy can give asymptotically optimal inference without requiring the precision matrix of the covariates to be sparse. As pointed out by a referee, applying this strategy to the present mediation setting may obviate the need to assume sparsity of
while controlling their biases. In the standard linear regression setting with high-dimensional covariates, Javanmard & Montanari (2014) showed that this strategy can give asymptotically optimal inference without requiring the precision matrix of the covariates to be sparse. As pointed out by a referee, applying this strategy to the present mediation setting may obviate the need to assume sparsity of 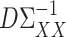 and
and 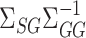 . This is an important direction for future work, and the Supplementary Material contains a detailed discussion and simulation study exploring the robustness of our procedure to the accuracy of estimating
. This is an important direction for future work, and the Supplementary Material contains a detailed discussion and simulation study exploring the robustness of our procedure to the accuracy of estimating 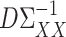 and
and 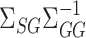 . On the other hand, our current strategy of choosing
. On the other hand, our current strategy of choosing 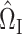 and
and 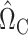 to estimate
to estimate 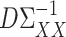 and
and 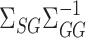 allows us to characterize the asymptotic variances of our proposed estimators in terms of population-level quantities, as well as to construct consistent estimates of those variances. Hirshberg & Wager (2019) studied a similar approach for a more general class of debiased estimators.
allows us to characterize the asymptotic variances of our proposed estimators in terms of population-level quantities, as well as to construct consistent estimates of those variances. Hirshberg & Wager (2019) studied a similar approach for a more general class of debiased estimators.
3. Theoretical results
3.1. Incomplete mediation
This section presents the theoretical properties of our proposed indirect effect inference procedure under incomplete mediation. We first require 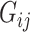 ,
, 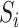 and residual error
and residual error 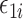 to have exponential-type tails and make several sparsity assumptions.
to have exponential-type tails and make several sparsity assumptions.
Assumption 1.
For each
,
has mean zero and
for some constant
and all
, where
and
. The same tail conditions hold for
and
.
Assumption 2.
For
defined in (5), there exist constants
and
such that
and
. Furthermore, if
denotes the
th entry of
, then
for some
and
.
The quantity 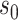 in Assumption 2 measures the degree of sparsity of
in Assumption 2 measures the degree of sparsity of 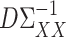 . The condition on
. The condition on 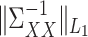 requires that none of the rows contain too many large entries. This is reasonable, as precision matrices are frequently used to model conditional dependencies between genes in a gene network (Danaher et al., 2014; Zhao et al., 2014a), and gene networks are typically thought to be sparse. The condition on
requires that none of the rows contain too many large entries. This is reasonable, as precision matrices are frequently used to model conditional dependencies between genes in a gene network (Danaher et al., 2014; Zhao et al., 2014a), and gene networks are typically thought to be sparse. The condition on 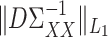 is related to the irrepresentable condition of Zhao & Yu (2006), and is similar to requiring that
is related to the irrepresentable condition of Zhao & Yu (2006), and is similar to requiring that 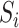 cannot be completely explained by
cannot be completely explained by 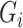 .
.
Theorem 1.
Let
solve (7) with tuning parameter
for
, where
and
are from Assumption 2 and
. Then, under Assumptions 1 and 2, with probability greater than
and with
defined in (5),
Theorem 1 shows that our 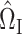 (7) is a consistent estimate of the population-level matrix
(7) is a consistent estimate of the population-level matrix 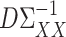 . As discussed in § 2.3, in the standard linear regression setting Javanmard & Montanari (2014) proposed a method for high-dimensional inference that does not require consistent estimation of precision matrices. In the Supplementary Material we discuss whether their approach can be applied here as well, which would avoid the need for the sparsity conditions in Assumption 2.
. As discussed in § 2.3, in the standard linear regression setting Javanmard & Montanari (2014) proposed a method for high-dimensional inference that does not require consistent estimation of precision matrices. In the Supplementary Material we discuss whether their approach can be applied here as well, which would avoid the need for the sparsity conditions in Assumption 2.
We can now characterize the asymptotic behaviour of our incomplete mediation estimators 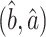 (6). We require additional assumptions necessary for the good performance of the scaled lasso of Sun & Zhang (2012).
(6). We require additional assumptions necessary for the good performance of the scaled lasso of Sun & Zhang (2012).
Theorem 2.
Let
and
be calculated such that both tuning parameters
and
are
. Assume the model for
(1) satisfies the conditions of Theorem 2 of Sun & Zhang (2012) and that
has at most
nonzero components. Under Assumptions 1 and 2, if
, and
and
are not both zero, and if
converges to a positive-definite matrix, then
The ultra-sparsity assumption on 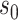 in Theorem 2 is standard in the debiased lasso literature (Javanmard & Montanari, 2014; Van de Geer et al., 2014; Zhang & Zhang, 2014). The choice of
in Theorem 2 is standard in the debiased lasso literature (Javanmard & Montanari, 2014; Van de Geer et al., 2014; Zhang & Zhang, 2014). The choice of 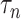 controls the coherence parameter
controls the coherence parameter 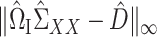 at rate
at rate 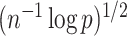 , which is necessary for showing that the bias of our proposed estimator goes to 0 when
, which is necessary for showing that the bias of our proposed estimator goes to 0 when 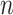 and
and 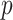 go to infinity. The proof of Theorem 2 shows that the asymptotic variance
go to infinity. The proof of Theorem 2 shows that the asymptotic variance 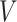 can be consistently estimated using
can be consistently estimated using
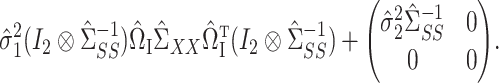 |
Consistency of 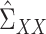 and
and 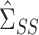 is standard, and consistency of
is standard, and consistency of 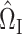 is given by Theorem 1. Estimation of
is given by Theorem 1. Estimation of 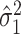 and
and 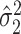 is discussed in § 4.
is discussed in § 4.
We caution that Theorem 2 does not cover the setting where both 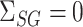 and
and 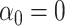 . This would cause
. This would cause 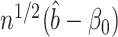 to asymptotically equal zero, rather than be normally distributed. A related issue arises even for standard low-dimensional Wald-type tests for the indirect effect, such as Sobel’s test (Sobel, 1982; Hayes, 2013; Barfield et al., 2017). In practice, these tests can be conservative when the exposure, the mediator and the outcome are only weakly associated. In this case, the true finite-sample distribution of the Wald test statistic has higher kurtosis than a normal distribution, so that critical values calculated assuming a normal distribution lead to a conservative test (Barfield et al., 2017). This setting is different from the weak instrumental variable problem, which we discuss in the Supplemetary Material.
to asymptotically equal zero, rather than be normally distributed. A related issue arises even for standard low-dimensional Wald-type tests for the indirect effect, such as Sobel’s test (Sobel, 1982; Hayes, 2013; Barfield et al., 2017). In practice, these tests can be conservative when the exposure, the mediator and the outcome are only weakly associated. In this case, the true finite-sample distribution of the Wald test statistic has higher kurtosis than a normal distribution, so that critical values calculated assuming a normal distribution lead to a conservative test (Barfield et al., 2017). This setting is different from the weak instrumental variable problem, which we discuss in the Supplemetary Material.
3.2. Complete mediation
We now present the theoretical properties of our indirect effect inference procedure under complete mediation. Similar to Assumption 2, we first make several sparsity assumptions, under which we can show that 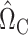 (8) is a consistent estimate of
(8) is a consistent estimate of 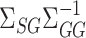 .
.
Assumption 3.
There exist constants
and
such that
and
. Furthermore, if
denotes the
th entry of
, then
for some
and
.
Theorem 3.
Let
solve (8) with tuning parameter
. Then, under Assumptions 1 and 3, with probability greater than
, and with
and
as in Theorem 1,
We can now characterize the asymptotic behaviour of our complete mediation indirect effect estimator 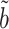 (9). The proof of Theorem 4 indicates that the asymptotic variance of
(9). The proof of Theorem 4 indicates that the asymptotic variance of 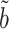 can be consistently estimated by
can be consistently estimated by 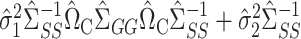 . As with incomplete mediation case, the requirement that
. As with incomplete mediation case, the requirement that 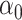 and
and 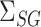 are not both zero arises here as well.
are not both zero arises here as well.
Theorem 4.
Let
be calculated such that both tuning parameters
and
are of order
. Assume the model for
in mediation model (1) has
but otherwise satisfies the conditions of Theorem 2 of Sun & Zhang (2012), and that
has at most
nonzero components. Under Assumptions 1 and 3, if
,
and
are not both zero, and if
converges to a positive-definite matrix, then
As mentioned in § 2.4, under complete mediation the indirect effect 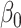 can also be consistently estimated by directly regressing
can also be consistently estimated by directly regressing 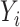 on
on 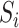 . The expression for the asymptotic variance of
. The expression for the asymptotic variance of 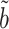 from Theorem 4 now allows us to analytically compare our estimator with the ordinary least squares estimate of
from Theorem 4 now allows us to analytically compare our estimator with the ordinary least squares estimate of 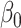 .
.
Proposition 1.
In model (1), assume that
, so that
is a consistent estimator of
. Then, under the conditions of Theorem 4,
converges to a positive semidefinite matrix.
Proposition 1 shows that our 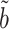 always has equal or lower asymptotic variance compared to the ordinary least squares estimator, even when the mediators are high-dimensional. This extends similar findings in low dimensions (Kenny & Judd, 2014; Zhao et al., 2014b; Loeys et al., 2015). In fact, we show in the Supplementary Material that for any fixed
always has equal or lower asymptotic variance compared to the ordinary least squares estimator, even when the mediators are high-dimensional. This extends similar findings in low dimensions (Kenny & Judd, 2014; Zhao et al., 2014b; Loeys et al., 2015). In fact, we show in the Supplementary Material that for any fixed 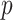 , our estimator
, our estimator 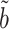 achieves the minimum asymptotic variance among all asymptotically unbiased estimators of
achieves the minimum asymptotic variance among all asymptotically unbiased estimators of  with the same convergence rate. Tests based on
with the same convergence rate. Tests based on 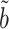 will thus have higher power to detect nonzero
will thus have higher power to detect nonzero 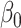 than tests based on
than tests based on 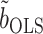 , as confirmed by simulations in § 5.3. In practice, the Wald test based on
, as confirmed by simulations in § 5.3. In practice, the Wald test based on 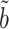 can still be conservative when
can still be conservative when 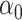 and
and 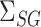 are close to zero, for reasons discussed in § 3.1, but simulations show that our proposed
are close to zero, for reasons discussed in § 3.1, but simulations show that our proposed 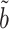 can still have significant power gains over the majority of the parameter space.
can still have significant power gains over the majority of the parameter space.
In a closely related setting, Athey et al. (2020) found that when estimating the causal effect of a treatment on a long-term outcome, leveraging intermediate outcomes can increase efficiency. In the Supplementary Material we provide a detailed comparison. Together, these results converge on a common principle, and provide theoretical justification for recent work in genomics showing that data integration using mediation analysis can increase the power to detect important biological signals (Wang et al., 2012; Huang et al., 2015).
The improved efficiency guaranteed by Proposition 1 requires strong scientific or expert knowledge to justify the absence of the direct effect. Furthermore, it also depends on the correct specification of both stages of the linear mediation model (1). In low dimensions, this has been pointed out by Loeys et al. (2015). This is in contrast to the usual ordinary least squares estimator, which requires fewer modelling assumptions. We illustrate the effect of model misspecification on our proposed estimator in the Supplementary Material.
Our estimator 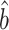 (6), proposed in § 2.3 under incomplete mediation, could also be used to estimate the indirect effect under complete mediation. Proposition 2 shows that under complete mediation,
(6), proposed in § 2.3 under incomplete mediation, could also be used to estimate the indirect effect under complete mediation. Proposition 2 shows that under complete mediation, 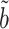 is asymptotically more efficient.
is asymptotically more efficient.
Proposition 2.
In model (1), assume that
. Under the conditions of Theorems 2 and 4,
converges to a positive semidefinite matrix.
4. Implementation
We first centre the 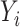 ,
, 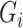 and
and 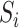 . To apply the scaled lasso, we standardize all covariates to have unit variance and then choose the tuning parameter
. To apply the scaled lasso, we standardize all covariates to have unit variance and then choose the tuning parameter 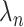 using the quantile-based penalty procedure in the R package scalreg (R Development Core Team, 2020).
using the quantile-based penalty procedure in the R package scalreg (R Development Core Team, 2020).
To estimate the asymptotic variances of our estimators, given in Theorems 2 and 4, we need estimates of the residual variances 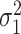 and
and 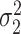 from our mediation model (1). Sun & Zhang (2012) showed that the scaled lasso can provide a consistent estimate
from our mediation model (1). Sun & Zhang (2012) showed that the scaled lasso can provide a consistent estimate 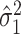 for
for 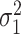 . Since model (1) implies that
. Since model (1) implies that 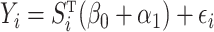 where
where 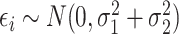 , we can estimate
, we can estimate 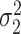 by first regressing
by first regressing 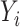 on
on 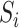 to obtain the ordinary least squares residual variance estimator
to obtain the ordinary least squares residual variance estimator 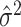 , and using
, and using 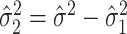 . In practice,
. In practice, 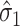 may sometimes be larger than
may sometimes be larger than 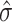 , in which case we estimate
, in which case we estimate 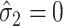 . This is sensible because
. This is sensible because 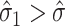 likely occurs when no mediators are associated with the outcome, i.e.,
likely occurs when no mediators are associated with the outcome, i.e., 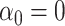 , in which case
, in which case 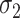 indeed equals zero.
indeed equals zero.
We construct the matrices 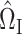 (7) and
(7) and 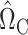 (8) by setting the tuning parameters
(8) by setting the tuning parameters 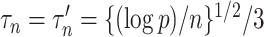 . This choice is guided by Theorems 1 and 3. We also tried choosing the tuning parameters by minimizing an ad hoc information criterion-type measure, but this resulted in confidence intervals with poor coverage in some cases. Finding a more data-adaptive tuning procedure is an important direction for future research.
. This choice is guided by Theorems 1 and 3. We also tried choosing the tuning parameters by minimizing an ad hoc information criterion-type measure, but this resulted in confidence intervals with poor coverage in some cases. Finding a more data-adaptive tuning procedure is an important direction for future research.
The time-consuming part of our method is the constrained 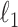 optimization, in (7) and (8), which we implement using fast algorithms from the flare package. For
optimization, in (7) and (8), which we implement using fast algorithms from the flare package. For 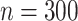 subjects,
subjects, 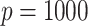 mediators and
mediators and 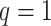 exposure, our procedure with tuning parameter
exposure, our procedure with tuning parameter 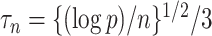 takes 66 seconds on a single core of an Intel Xeon X5675 processor at 3.07 GHz and with 8 GB of RAM, and larger
takes 66 seconds on a single core of an Intel Xeon X5675 processor at 3.07 GHz and with 8 GB of RAM, and larger 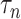 results in shorter computation time: our procedure with
results in shorter computation time: our procedure with 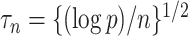 takes 5 seconds. Our procedure is available in the R package freebird, available at https://github.com/rzhou14/freebird.
takes 5 seconds. Our procedure is available in the R package freebird, available at https://github.com/rzhou14/freebird.
5. Numerical results
5.1. Comparison of methods
We compared our methods to a naive nondebiased remax method, discussed in § 2.2. This estimates  using
using 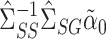 , where
, where 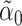 is a standard lasso estimate of
is a standard lasso estimate of 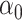 implemented using the R package glmnet. There is no tractable limiting distribution for this estimate of
implemented using the R package glmnet. There is no tractable limiting distribution for this estimate of  , so we used the bootstrap to obtain percentile confidence intervals, and obtained average power and coverages based on those intervals. Bootstrapping the lasso is not theoretically justified (Dezeure et al., 2015), but this at least allows us to have a comparable baseline method.
, so we used the bootstrap to obtain percentile confidence intervals, and obtained average power and coverages based on those intervals. Bootstrapping the lasso is not theoretically justified (Dezeure et al., 2015), but this at least allows us to have a comparable baseline method.
We also compared our procedures to the high-dimensional mediation analysis method of Zhang et al. (2016), using their R package HIMA. The method first uses marginal screening on mediators to reduce dimensionality. It then regresses the outcome on the retained mediators using penalized regression with the minimax concave penalty (Zhang, 2010). Using only the selected mediators, it uses ordinary least squares to compute a pair of 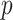 -values for each mediator, for its associations with the outcome and the exposure. These
-values for each mediator, for its associations with the outcome and the exposure. These 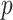 -values are Bonferroni-corrected for the number of selected mediators, and Zhang et al. (2016) identify a mediator as significant if both of its adjusted
-values are Bonferroni-corrected for the number of selected mediators, and Zhang et al. (2016) identify a mediator as significant if both of its adjusted 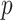 -values are less than the desired significance level. However, this testing approach based on the maximum of two
-values are less than the desired significance level. However, this testing approach based on the maximum of two 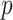 -values does not provide confidence intervals.
-values does not provide confidence intervals.
Under complete mediation, the indirect effect is equal to the total effect, which can be tested directly using ordinary least squares. In this setting we therefore also compared our complete mediation method to ordinary least squares.
5.2. Simulations under incomplete mediation
We first studied our estimators under incomplete mediation. Following model (1), for samples 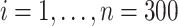 we generated
we generated 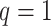 exposure
exposure  and
and 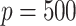 potential mediators
potential mediators 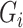 following
following 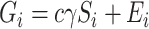 , where
, where 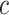 was a scalar,
was a scalar, 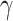 was a
was a 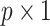 coefficient vector and
coefficient vector and 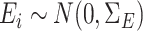 . We generated
. We generated 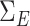 following procedures in Danaher et al. (2014) such that
following procedures in Danaher et al. (2014) such that 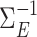 was sparse in the sense of Assumption 2 and had diagonal entries equal to 1. Finally, we generated the outcome according to
was sparse in the sense of Assumption 2 and had diagonal entries equal to 1. Finally, we generated the outcome according to 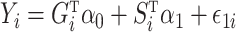 , where
, where 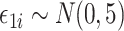 . In the Supplementary Material we show that our simulation results were similar even when
. In the Supplementary Material we show that our simulation results were similar even when 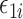 was not normally distributed. We let
was not normally distributed. We let 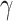 have 15 nonzero components randomly generated between
have 15 nonzero components randomly generated between 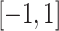 , fixing
, fixing 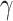 across replications, and let
across replications, and let 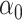 have 15 nonzero components equal to one. We chose either one or five of these nonzero components to correspond to variables whose entries in
have 15 nonzero components equal to one. We chose either one or five of these nonzero components to correspond to variables whose entries in 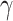 were also nonzero; these were the true mediators. Here we set the direct effect
were also nonzero; these were the true mediators. Here we set the direct effect 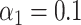 , and in the Supplementary Material we present results when
, and in the Supplementary Material we present results when 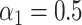 . In this simulation scheme the indirect effect
. In this simulation scheme the indirect effect 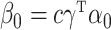 , and we varied
, and we varied 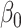 by varying the constant
by varying the constant 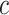 .
.
When there was only one true mediator, we used all three competing methods to test 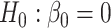 at the
at the 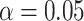 significance level, and used our proposed method and naive method to calculate 95% confidence intervals for different values of
significance level, and used our proposed method and naive method to calculate 95% confidence intervals for different values of 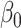 . When there were five true mediators, we did not apply the method of Zhang et al. (2016) because it considers each mediator separately and does not provide inference for the overall indirect effect. The existence of multiple significant mediators does not imply that the indirect effect is nonzero because the effects of the different mediators may cancel each other out, a phenomenon known as inconsistent mediation.
. When there were five true mediators, we did not apply the method of Zhang et al. (2016) because it considers each mediator separately and does not provide inference for the overall indirect effect. The existence of multiple significant mediators does not imply that the indirect effect is nonzero because the effects of the different mediators may cancel each other out, a phenomenon known as inconsistent mediation.
Figure 1 reports average coverage probabilities and power curves over 200 replications. The naive method had worse coverage than our approach, and though it had excellent power, it was not theoretically justified, as mentioned in § 5.1. The method of Zhang et al. (2016) had counter-intuitive behaviour when  was large, and surprisingly high power when
was large, and surprisingly high power when 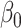 was small. Its power was poor for large
was small. Its power was poor for large 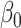 because its model selection step performed poorly: larger
because its model selection step performed poorly: larger 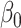 corresponded to larger
corresponded to larger 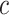 , and therefore to increased collinearity between
, and therefore to increased collinearity between 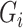 and
and 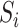 in the regression for
in the regression for 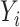 , making consistent model selection difficult. Its power was surprisingly high for small
, making consistent model selection difficult. Its power was surprisingly high for small 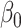 because it did not appropriately account for the variability of its model selection step. In the Supplementary Material we describe a slightly modified version of their approach that gives confidence intervals and show that it has poor coverage, and also construct a setting where it fails to maintain Type I error because of its improper post-model selection inference.
because it did not appropriately account for the variability of its model selection step. In the Supplementary Material we describe a slightly modified version of their approach that gives confidence intervals and show that it has poor coverage, and also construct a setting where it fails to maintain Type I error because of its improper post-model selection inference.
Fig. 1.
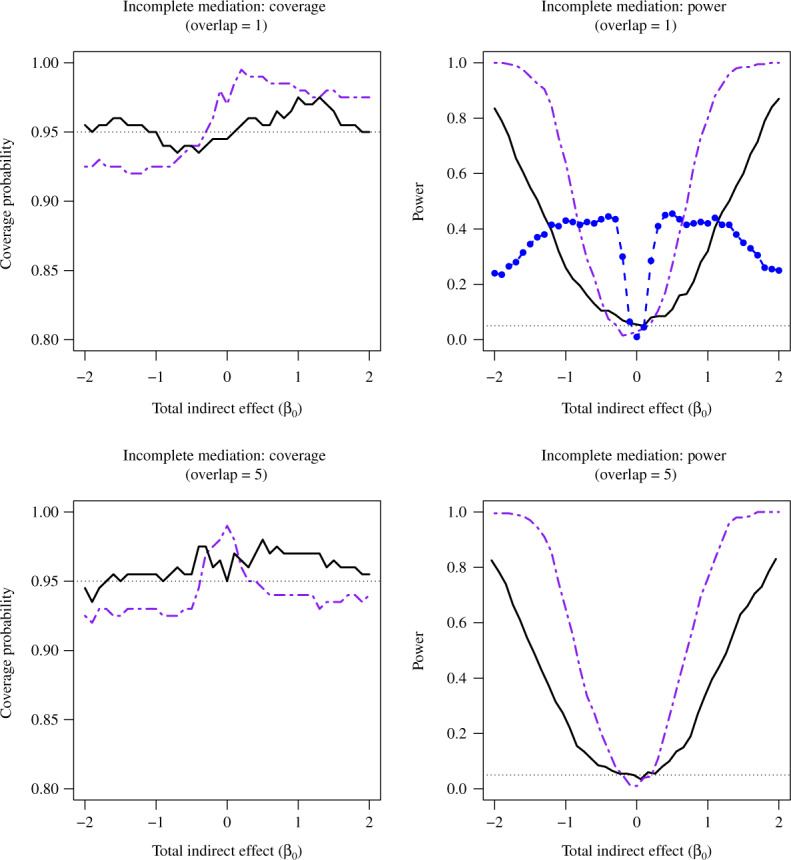
Average coverage probabilities of 95% confidence intervals (left panels) and average power curves at significance level  (right panels) for estimating and testing the indirect effect under incomplete mediation, over 200 replications. The direct effect was
(right panels) for estimating and testing the indirect effect under incomplete mediation, over 200 replications. The direct effect was  . The number of true mediators was 1 in the upper panels and 5 in the lower panels. Proposed (solid):
. The number of true mediators was 1 in the upper panels and 5 in the lower panels. Proposed (solid):  from (6); Naive (dot-dash): the naive method discussed in § 5.1; Zhang (large dot-dash): method of Zhang et al. (2016).
from (6); Naive (dot-dash): the naive method discussed in § 5.1; Zhang (large dot-dash): method of Zhang et al. (2016).
5.3. Simulations under complete mediation
We next studied the performance of our indirect effect estimator under complete mediation. We considered four simulation settings based on the same data generation scheme used above, but with 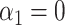 . We generated
. We generated 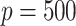 potential mediators with either one or five true mediators, and in the Supplementary Material we present results for
potential mediators with either one or five true mediators, and in the Supplementary Material we present results for  .
.
Figure 2 reports average coverage probabilities and power curves over 200 replications. Our method was always able to maintain the nominal coverage probability and significance level, and in every case had higher power than ordinary least squares and the naive method for sufficiently large 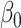 , consistent with Proposition 1. The average lengths of 95% confidence intervals were also smaller for our method compared to ordinary least squares; see the Supplementary Material. Similar to the incomplete mediation setting, the method of Zhang et al. (2016) had high power when
, consistent with Proposition 1. The average lengths of 95% confidence intervals were also smaller for our method compared to ordinary least squares; see the Supplementary Material. Similar to the incomplete mediation setting, the method of Zhang et al. (2016) had high power when 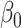 was small and counter-intuitive behaviour when
was small and counter-intuitive behaviour when 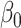 was large. Our test was slightly conservative for
was large. Our test was slightly conservative for 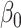 close to zero because the normal approximation to the distribution of our Wald-type test statistic is poor under weak mediation, as discussed in § 3.1.
close to zero because the normal approximation to the distribution of our Wald-type test statistic is poor under weak mediation, as discussed in § 3.1.
Fig. 2.
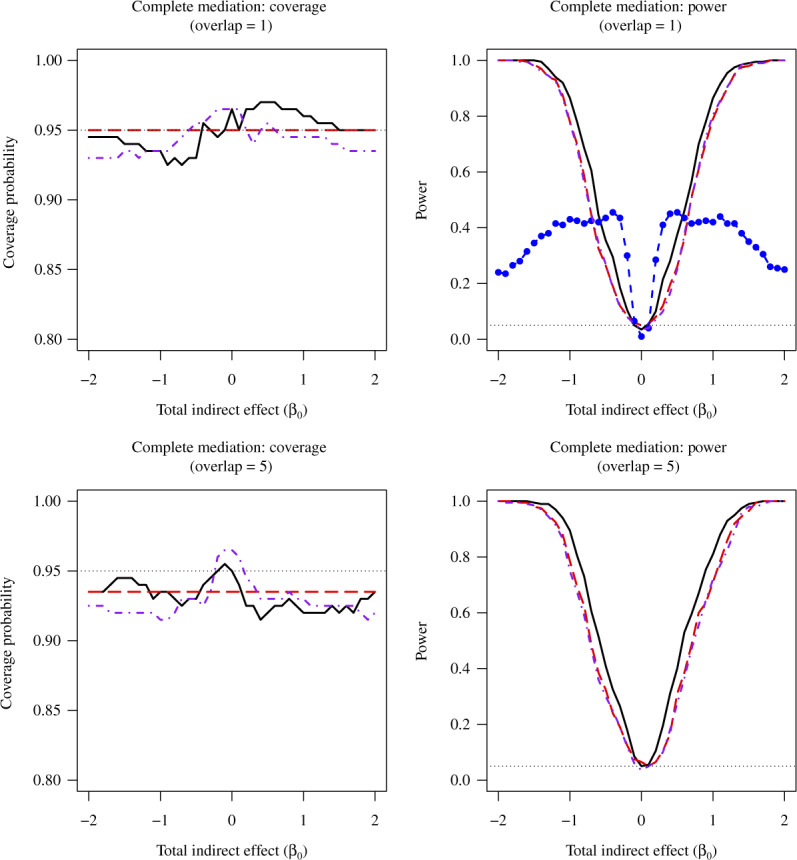
Average coverage probabilities of 95% confidence intervals (left panels) and average power curves at significance level 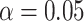 (right panels) for estimating and testing the indirect effect under complete mediation, over 200 replications. The number of true mediators was 1 in the upper panels and 5 in the lower panels, with 500 potential mediators. Proposed (solid):
(right panels) for estimating and testing the indirect effect under complete mediation, over 200 replications. The number of true mediators was 1 in the upper panels and 5 in the lower panels, with 500 potential mediators. Proposed (solid): 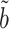 from (9); Naive (dot-dash): the naive method discussed in § 5.1; OLS (log dash): ordinary least squares estimate; Zhang (large dot-dash): the method of Zhang et al. (2016).
from (9); Naive (dot-dash): the naive method discussed in § 5.1; OLS (log dash): ordinary least squares estimate; Zhang (large dot-dash): the method of Zhang et al. (2016).
6. Data analysis
6.1. Data description
Understanding the mechanisms behind individual variation in drug response is an important step in the development of personalized medicine. We applied our proposed methods to pharmacogenetic studies of the response to the cancer drug docetaxel in human lymphoblastoid cell line (Niu et al., 2012; Hanson et al., 2016). The data consists of genotype data on 1 362 849 single nucleotide polymorphisms and expression data on 54 613 probes, after pre-processing, from cell lines from 95 Han-Chinese, 96 Caucasian and 93 African-American individuals. These data are available from the Gene Expression Omnibus under accession number GSE24277. Niu et al. (2012) exposed these cells to docetaxel and quantified their responses using 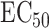 , the concentration at which a drug reduces the population of cells by half (Hanson et al., 2016).
, the concentration at which a drug reduces the population of cells by half (Hanson et al., 2016).
6.2. Gene set analysis
It is common in gene expression profiling experiments to identify genes that are significantly associated with the phenotype being studied. A natural next step is to identify gene sets, representing biological pathways, through which these significant genes may act. This is a difficult analysis problem because the intervening pathways may contain a large number of genes, resulting in a high-dimensional mediation analysis problem. This is different from standard gene set enrichment analysis (Subramanian et al., 2005), as the latter does not allow for direct testing of mediation by the gene set.
We applied our proposed procedures to test whether a candidate gene set mediates the indirect effect of a given gene of interest on the phenotype. We used our incomplete mediation estimator 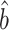 (6), because the gene of interest may have a direct effect on the phenotype that does not proceed through the candidate gene set. As in our simulations, we set the tuning parameter
(6), because the gene of interest may have a direct effect on the phenotype that does not proceed through the candidate gene set. As in our simulations, we set the tuning parameter 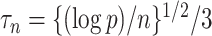 when estimating
when estimating 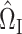 (7). As an illustration, we studied the indirect effects of TMED10, a transmembrane trafficking protein whose corresponding gene was the most significantly associated with docetaxel response in our data. We retrieved biological process Gene Ontology gene sets with at least 50 genes from the Molecular Signatures Database (Subramanian et al., 2005; Liberzon et al., 2011), then applied our proposed approach to test the indirect effect of TMED10 through each of the 4436 candidates. Of these, 420 gene sets contained more genes than there were samples, making our high-dimensional approach indispensable.
(7). As an illustration, we studied the indirect effects of TMED10, a transmembrane trafficking protein whose corresponding gene was the most significantly associated with docetaxel response in our data. We retrieved biological process Gene Ontology gene sets with at least 50 genes from the Molecular Signatures Database (Subramanian et al., 2005; Liberzon et al., 2011), then applied our proposed approach to test the indirect effect of TMED10 through each of the 4436 candidates. Of these, 420 gene sets contained more genes than there were samples, making our high-dimensional approach indispensable.
Our procedure found 257 gene sets with significant indirect effects that passed Bonferroni correction. One reason for the large number of significant findings is that many gene sets are subgroups of larger sets. Table 1 reports the top ten most significant ones, as ranked by their indirect effect 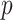 -values. Many of these are involved in transmembrane transport, which suggests that the role of TMED10 in the response to docetaxel may be to move small molecules into and out of cells. Our proposed method can thus generate useful exploratory results for further downstream analysis. We also implemented the method of Zhang et al. (2016), which found no significant gene sets.
-values. Many of these are involved in transmembrane transport, which suggests that the role of TMED10 in the response to docetaxel may be to move small molecules into and out of cells. Our proposed method can thus generate useful exploratory results for further downstream analysis. We also implemented the method of Zhang et al. (2016), which found no significant gene sets.
Table 1.
Top ten most significant gene sets through which the TMED10 gene may act on drug response
| Gene set |
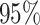 CI CI |
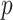 -value -value |
|---|---|---|
| Regulation of heart rate |
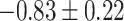
|
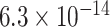
|
| Synaptic vesicle cycle |
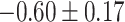
|
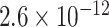
|
| Regulation of vasoconstriction |
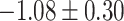
|
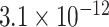
|
| Negative regulation of transporter activity |
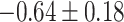
|
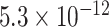
|
| Negative regulation of cation transmembrane transport |
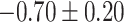
|
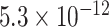
|
| Positive regulation of blood circulation |
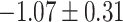
|
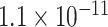
|
| Negative regulation of transmembrane transport |
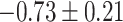
|
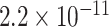
|
| Regulation of cardiac muscle contraction |
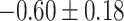
|
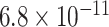
|
| Neurotransmitter transport |
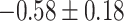
|
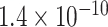
|
| Regulation of oxidoreductase activity |
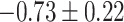
|
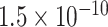
|
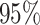 CI, confidence intervals obtained from the proposed method under incomplete mediation (6);
CI, confidence intervals obtained from the proposed method under incomplete mediation (6); 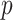 -value, raw
-value, raw 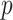 -values obtained from the proposed procedure.
-values obtained from the proposed procedure.
6.3. Noncoding variants analysis
We next studied the effects of noncoding genetic variants on the response to docetaxel. We first performed a standard genome-wide association study and regressed docetaxel 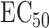 on each variant separately, controlling for the first five principal components of the genotype data in order to control for population stratification (Price et al., 2006). This approach did not identify any significant variants after multiple testing correction. We were then interested in whether a high-dimensional mediation analysis method could provide more power. We chose the top 1000 expression probes with the largest variances as potential mediators and controlled for the first five principal components. We first applied the method of Zhang et al. (2016), but it did not detect any significant variants that passed Bonferroni correction.
on each variant separately, controlling for the first five principal components of the genotype data in order to control for population stratification (Price et al., 2006). This approach did not identify any significant variants after multiple testing correction. We were then interested in whether a high-dimensional mediation analysis method could provide more power. We chose the top 1000 expression probes with the largest variances as potential mediators and controlled for the first five principal components. We first applied the method of Zhang et al. (2016), but it did not detect any significant variants that passed Bonferroni correction.
It is known that noncoding variants likely do not have a direct effect on the phenotype. This justifies application of our complete mediation estimator 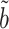 (9) to test for noncoding variances associated with
(9) to test for noncoding variances associated with 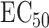 . We use
. We use 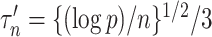 when estimating
when estimating 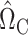 (8), and controlled for the first five principal components in all of our analyses. Our new procedure was indeed able to identify one significant variant that passed Bonferroni correction for all noncoding variants: the single nucleotide polymorphism rs11578000, with an estimated indirect effect of
(8), and controlled for the first five principal components in all of our analyses. Our new procedure was indeed able to identify one significant variant that passed Bonferroni correction for all noncoding variants: the single nucleotide polymorphism rs11578000, with an estimated indirect effect of 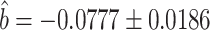 and a
and a 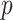 -value of
-value of 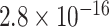 . Interestingly, the Genotype Tissue Expression Project (Lonsdale et al., 2013) found that in heart and muscle tissue, rs11578000 regulated the expression of the gene SUSD4, which has been found to inhibit the complement system (Holmquist et al., 2013), a system of proteins involved in innate immunity that may be involved in the response to epirubicin/docetaxel treatment in breast cancer patients (Michlmayr et al., 2010). Our
. Interestingly, the Genotype Tissue Expression Project (Lonsdale et al., 2013) found that in heart and muscle tissue, rs11578000 regulated the expression of the gene SUSD4, which has been found to inhibit the complement system (Holmquist et al., 2013), a system of proteins involved in innate immunity that may be involved in the response to epirubicin/docetaxel treatment in breast cancer patients (Michlmayr et al., 2010). Our  provides novel findings that could not have been detected using standard approaches.
provides novel findings that could not have been detected using standard approaches.
7. Discussion
Our methods require that the directions of causality in mediation model (1) be correctly specified. In practice this causal pathway may be complex, as some genes react to the outcome, rather than cause the outcome. Our method’s findings should thus be further analysed to verify that the causal directions are indeed of interest. One potential solution to this issue is to use recently developed methods for high-dimensional causal inference (Bühlmann et al., 2014) to first screen out reactive genes before applying our proposed procedures.
Though we focused on testing the indirect effect in this paper, our incomplete mediation method also provides 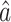 , a natural estimate of the direct effect, as discussed in § 2.3. We explored using
, a natural estimate of the direct effect, as discussed in § 2.3. We explored using 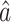 to test for the presence of a direct effect, and similar to Kenny & Judd (2014), we found that the power was relatively low. This may be because when calculating our estimators we penalize the direct effect parameter
to test for the presence of a direct effect, and similar to Kenny & Judd (2014), we found that the power was relatively low. This may be because when calculating our estimators we penalize the direct effect parameter 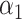 when we fit the scaled lasso. This makes sense if the direct effect is expected to be zero, which is sensible in our integrative genomics applications, but an alternative is to leave
when we fit the scaled lasso. This makes sense if the direct effect is expected to be zero, which is sensible in our integrative genomics applications, but an alternative is to leave 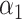 unpenalized. This may give a more powerful test for the direct effect, and more work is required to derive the asymptotic distribution of the resulting estimator. Inference for the direct effect in high dimensions could also be achieved by applying debiased lasso methods to test
unpenalized. This may give a more powerful test for the direct effect, and more work is required to derive the asymptotic distribution of the resulting estimator. Inference for the direct effect in high dimensions could also be achieved by applying debiased lasso methods to test  in the regression of
in the regression of 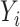 on
on 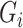 and
and 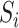 in our model (1). Based on some simulations, we found that our estimator
in our model (1). Based on some simulations, we found that our estimator 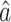 is always smaller in absolute value, and usually had smaller variance, compared to the debiased estimator of Van de Geer et al. (2014).
is always smaller in absolute value, and usually had smaller variance, compared to the debiased estimator of Van de Geer et al. (2014).
Finally, we have so far only considered linear mediation models for continuous outcomes. It is possible to extend our methods to generalized linear models for the outcome 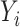 in mediation model (1). However, the causal interpretation of these nonlinear models requires special care (VanderWeele & Vansteelandt, 2010; VanderWeele, 2015). Also, we have so far assumed that the residual errors
in mediation model (1). However, the causal interpretation of these nonlinear models requires special care (VanderWeele & Vansteelandt, 2010; VanderWeele, 2015). Also, we have so far assumed that the residual errors 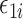 and
and 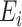 are independent of the exposure
are independent of the exposure 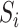 and mediator
and mediator 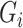 in model (1). Under heteroscedasticity, if the errors are dependent on either
in model (1). Under heteroscedasticity, if the errors are dependent on either 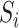 or
or 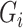 , our theoretical results will likely not hold, and extending our approach to this setting is an important research direction.
, our theoretical results will likely not hold, and extending our approach to this setting is an important research direction.
Supplementary Material
Acknowledgement
The authors thank the reviewers and the associate editor for their extremely useful comments, as well as Casey Hanson for his help with data processing. This work was funded in part by the Mayo Clinic-UIUC Alliance and by the trans-NIH Big Data to Knowledge initiative. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Zhao was funded in part by the National Science Foundation and is also affiliated with the Carl R. Woese Institute for Genomic Biology at the University of Illinois.
Supplementary material
Supplementary material available at Biometrika online contains further comparisons, additional simulation results and proofs of theorems and propositions.
References
- Athey, S., Chetty, R., Imbens, G. & Kang, H. (2020). Estimating treatment effects using multiple surrogates: The role of the surrogate score and the surrogate index. arXiv:1603.09326v3. [Google Scholar]
- Athey, S., Imbens, G. W. & Wager, S. (2018). Approximate residual balancing: Debiased inference of average treatment effects in high dimensions. J. R. Statist. Soc. B 80, 597–623. [Google Scholar]
- Barfield, R., Shen, J., Just, A. C., Vokonas, P. S., Schwartz, J., Baccarelli, A. A., VanderWeele, T. J. & Lin, X. (2017). Testing for the indirect effect under the null for genome-wide mediation analyses. Genet. Epidem. 41, 824–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belloni, A., Chernozhukov, V., Fernández-Val, I. & Hansen, C. (2017). Program evaluation and causal inference with high-dimensional data. Econometrica 85, 233–98. [Google Scholar]
- Bühlmann, P., Kalisch, M. & Meier, L. (2014). High-dimensional statistics with a view toward applications in biology. Ann. Rev. Statist. Appl. 1, 255–78. [Google Scholar]
-
Cai, T., Liu, W. & Luo, X. (2011). A constrained
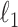 minimization approach to sparse precision matrix estimation. J. Am. Statist. Assoc. 106, 594–607. [Google Scholar]
minimization approach to sparse precision matrix estimation. J. Am. Statist. Assoc. 106, 594–607. [Google Scholar] - Cai, T. T. & Guo, Z. (2017). Confidence intervals for high-dimensional linear regression: Minimax rates and adaptivity. Ann. Statist. 45, 615–46. [Google Scholar]
- Chen, O. Y., Crainiceanu, C., Ogburn, E. L., Caffo, B. S., Wager, T. D. & Lindquist, M. A. (2015). High-dimensional multivariate mediation with application to neuroimaging data. Biostatistics 19, 121–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danaher, P., Wang, P. & Witten, D. M. (2014). The joint graphical lasso for inverse covariance estimation across multiple classes. J. R. Statist. Soc. B 76, 373–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Dezeure, R., Bühlmann, P., Meier, L. & Meinshausen, N. (2015). High-dimensional inference: Confidence intervals,
 -values and R-software HDI. Statist. Sci. 30, 533–58. [Google Scholar]
-values and R-software HDI. Statist. Sci. 30, 533–58. [Google Scholar] - Hanson, C., Cairns, J., Wang, L. & Sinha, S. (2016). Computational discovery of transcription factors associated with drug response. Pharmacogenomics J. 16, 573–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes, A. F. (2013). Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. New York: Guilford Press. [Google Scholar]
- Hirshberg, D. A. & Wager, S. (2019). Augmented minimax linear estimation. arXiv:1712.00038v5. [Google Scholar]
- Holmquist, E., Okroj, M., Nodin, B., Jirström, K. & Blom, A. M. (2013). Sushi domain-containing protein 4 (SUSD4) inhibits complement by disrupting the formation of the classical C3 convertase. FASEB J. 27, 2355–66. [DOI] [PubMed] [Google Scholar]
- Huang, Y.-T., Liang, L., Moffatt, M. F., Cookson, W. O. & Lin, X. (2015). IGWAS: Integrative genome-wide association studies of genetic and genomic data for disease susceptibility using mediation analysis. Genet. Epidem. 39, 347–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, Y.-T. & Pan, W.-C. (2016). Hypothesis test of mediation effect in causal mediation model with high-dimensional continuous mediators. Biometrics 72, 402–13. [DOI] [PubMed] [Google Scholar]
- Huang, Y.-T., VanderWeele, T. J. & Lin, X. (2014). Joint analysis of SNP and gene expression data in genetic association studies of complex diseases. Ann. Appl. Statist. 8, 352–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Javanmard, A. & Montanari, A. (2014). Confidence intervals and hypothesis testing for high-dimensional regression. J. Mach. Learn. Res. 15, 2869–909. [Google Scholar]
- Javanmard, A. & Montanari, A. (2018). Debiasing the lasso: Optimal sample size for Gaussian designs. Ann. Statist. 46, 2593–622. [Google Scholar]
- Kenny, D. A. & Judd, C. M. (2014). Power anomalies in testing mediation. Psychol. Sci. 25, 334–9. [DOI] [PubMed] [Google Scholar]
- Liberzon, A., Subramanian, A., Pinchback, R., Thorvaldsdóttir, H., Tamayo, P. & Mesirov, J. P. (2011). Molecular signatures database (MSIGDB) 3.0. Bioinformatics 27, 1739–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeys, T., Moerkerke, B. & Vansteelandt, S. (2015). A cautionary note on the power of the test for the indirect effect in mediation analysis. Front. Psychol. 5, 1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lonsdale, J., Thomas, J., Salvatore, M., Phillips, R., Lo, E., Shad, S., Hasz, R., Walters, G., Garcia, F., Young, N.. et al. (2013). The genotype-tissue expression (GTEx) project. Nature Gene. 45, 580–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon, D. P. (2008). Introduction to Statistical Mediation Analysis. London: Routledge. [Google Scholar]
- Michlmayr, A., Bachleitner-Hofmann, T., Baumann, S., Marchetti-Deschmann, M., Rechweichselbraun, I., Burghuber, C., Pluschnig, U., Bartsch, R., Graf, A., Greil, R.. et al. (2010). Modulation of plasma complement by the initial dose of epirubicin/docetaxel therapy in breast cancer and its predictive value. Br. J. Cancer 103, 1201–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu, N., Schaid, D. J., Abo, R. P., Kalari, K., Fridley, B. L., Feng, Q., Jenkins, G., Batzler, A., Brisbin, A. G., Cunningham, J. M.. et al. (2012). Genetic association with overall survival of taxane-treated lung cancer patients: A genome-wide association study in human lymphoblastoid cell lines followed by a clinical association study. BMC Cancer 12, 422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A. & Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Gene. 38, 904–9. [DOI] [PubMed] [Google Scholar]
- R Development Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. http://www.R-project.org.
- Sobel, M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. Sociol. Methodol. 13, 290–312. [Google Scholar]
- Subramanian, A., Tamayo, P., Mootha, V. K., Mukherjee, S., Ebert, B. L., Gillette, M. A., Paulovich, A., Pomeroy, S. L., Golub, T. R., Lander, E. S.. et al. (2005). Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc. Nat. Acad. Sci. 102, 15545–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, T. & Zhang, C.-H. (2012). Scaled sparse linear regression. Biometrika 99, 879–98. [Google Scholar]
- Van de Geer, S., Bühlmann, P., Ritov, Y. & Dezeure, R. (2014). On asymptotically optimal confidence regions and tests for high-dimensional models. Ann. Statist. 42, 1166–202. [Google Scholar]
- VanderWeele, T. J. (2015). Explanation in Causal Inference: Methods for Mediation and Interaction. Oxford: Oxford University Press. [Google Scholar]
- VanderWeele, T. J. & Vansteelandt, S. (2010). Odds ratios for mediation analysis for a dichotomous outcome. Am. J. Epidemiol. 172, 1339–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele, T. J. & Vansteelandt, S. (2014). Mediation analysis with multiple mediators. Epidemiol. Meth. 2, 95–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, W., Baladandayuthapani, V., Morris, J. S., Broom, B. M., Manyam, G. & Do, K.-A. (2012). iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 29, 149–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, C.-H. (2010). Nearly unbiased variable selection under minimax concave penalty. Ann. Statist. 38, 894–942. [Google Scholar]
- Zhang, C.-H. & Zhang, S. S. (2014). Confidence intervals for low dimensional parameters in high dimensional linear models. J. R. Statist. Soc. B 76, 217–42. [Google Scholar]
- Zhang, H., Zheng, Y., Zhang, Z., Gao, T., Joyce, B., Yoon, G., Zhang, W., Schwartz, J., Just, A., Colicino, E.. et al. (2016). Estimating and testing high-dimensional mediation effects in epigenetic studies. Bioinformatics 32, 3150–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, P. & Yu, B. (2006). On model selection consistency of lasso. J. Mach. Learn. Res. 7, 2541–63. [Google Scholar]
- Zhao, S. D., Cai, T. T. & Li, H. (2014a). Direct estimation of differential networks. Biometrika 101, 253–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, S. D., Cai, T. T. & Li, H. (2014b). More powerful genetic association testing via a new statistical framework for integrative genomics. Biometrics 70, 881–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, Y. & Bradic, J. (2018). Linear hypothesis testing in dense high-dimensional linear models. J. Am. Statist. Assoc. 113, 1583–600. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.