Flow-accelerated platelet biogenesis is due to an elasto-hydrodynamic instability

Significance

To maintain the high number of blood platelets in mammalian blood, an exceptionally efficient process for platelet biogenesis is required. While recent in vitro experiments demonstrate blood flow as a key factor accelerating biogenesis, the biophysical mechanism behind this acceleration remains unclear. Here we use computer simulations to show how fluid flow can indeed strongly increase biogenesis. The key aspect of our work is that we introduce a physical mechanism, akin to the well-known Rayleigh–Plateau instability of a liquid jet, as the likely origin of accelerated platelet production. Our findings can lead to a more efficient design of microfluidic bioreactors for platelet production, but also explain the exceptionally strong coupling of fluid flow and platelet biogenesis in vivo.

Abstract

Blood platelets are formed by fragmentation of long membrane extensions from bone marrow megakaryocytes in the blood flow. Using lattice-Boltzmann/immersed boundary simulations we propose a biological Rayleigh–Plateau instability as the biophysical mechanism behind this fragmentation process. This instability is akin to the surface tension-induced breakup of a liquid jet but is driven by active cortical processes including actomyosin contractility and microtubule sliding. Our fully three-dimensional simulations highlight the crucial role of actomyosin contractility, which is required to trigger the instability, and illustrate how the wavelength of the instability determines the size of the final platelets. The elasto-hydrodynamic origin of the fragmentation explains the strong acceleration of platelet biogenesis in the presence of an external flow, which we observe in agreement with experiments. Our simulations then allow us to disentangle the influence of specific flow conditions: While a homogeneous flow with uniform velocity leads to the strongest acceleration, a shear flow with a linear velocity gradient can cause fusion events of two developing platelet-sized swellings during fragmentation. A fusion event may lead to the release of larger structures which are observable as preplatelets in experiments. Together, our findings strongly indicate a mainly physical origin of fragmentation and regulation of platelet size in flow-accelerated platelet biogenesis.

Blood platelets are the second most abundant cell type in blood and are responsible for a quick stop of bleeding after an injury (1). Due to their short life span of only 7 to 10 d, platelets need to be constantly produced and global platelet number kinetics have been studied using mathematical models for quite some time (2–6). On a single-cell level, the highly efficient process of platelet biogenesis starts from megakaryocytes (MKs) residing extravascularly in the bone marrow. Mature MKs first grow long tubular extensions, termed proplatelets, which reach into the adjacent sinusoidal blood vessels. The extended proplatelets then form periodic swellings and fragment into smaller pieces that eventually mature into functional platelets (7, 8). Recently, intensive efforts have been under way toward the in vitro production of platelets (9–19) in various kinds of bioreactors. In those microfluidic devices, MKs are either attached to pillars (17) and exposed to an approximately homogeneous flow or trapped in structures resembling the vascular endothelium (15, 16) and exposed to parabolic Poiseuille flow during the process of proplatelet growth and fragmentation. In both cases, the flow strength to which proplatelets are subjected can easily be tuned externally. Interestingly, a dramatic acceleration of platelet biogenesis up to 20 times caused by fluid flow has been consistently reported in various bioreactor geometries (7, 12, 15–17, 19). The mechanisms behind this fascinating example of an active biological process directly interacting with its surrounding hydrodynamic environment have so far not been elucidated.

Here, to explain these findings, we propose an elasto-hydrodynamic instability akin to the Rayleigh–Plateau instability of a water jet leading to breakup into droplets as the key biophysical mechanism behind platelet biogenesis. To back up this hypothesis, we use our recently developed simulation method (20) which computes the forces created by the cortical actomyosin system and microtubules and the resulting dynamic deformation of the proplatelet membrane as well as the important two-way coupling to the flowing hydrodynamic environment in a fully three-dimensional (3D) situation. Motivated by experimental observations on the importance of actomyosin (9, 21–29), we show how cortical actomyosin contractility creates periodic swellings along the proplatelet in a similar, yet not identical, way as surface tension triggers the breakup of a water jet exiting from a faucet into a series of droplets in the classic Rayleigh–Plateau scenario. Indeed, we find that experimentally observed platelet sizes are in good agreement with predictions for this mechanism. That such a “biological Rayleigh–Plateau instability” may exist different from platelet biogenesis has been hypothesized before in axisymmetric situations for active (30, 31) as well as passive (32–34) vesicles and membranes. Here, specifically focusing on cell biogenesis in fully 3D, hydrodynamic flows, we go one step farther and fully take into account the flowing environment present both in sinusoidal blood vessels in vivo and in microfluidic devices in vitro. Consistent with experimental findings, we report a strong acceleration of the fragmentation process in the presence of hydrodynamic flow. We then uncover the specific effects of different flow patterns: Shear, i.e., velocity gradients, as present in parabolic Poiseuille flow through microchannels or blood vessels leads to the fusion of neighboring swellings. We hypothesize this to be the mechanism behind the formation of larger structures, called preplatelets, frequently observed in the bloodstream (35). In contrast, homogeneous flow with constant velocity, as approximately present in some bioreactor systems (17), leads to a systematic and strong acceleration without fusion events, which highlights its potential role for efficient in vitro production of monodisperse platelets. We report a robust size of the released platelets which is determined by the dominant wavelength of the instability and is largely independent of fluid flow in agreement with experimental findings. Our model thus strongly indicates that a simple physical mechanism determines both platelet size and accelerated platelet biogenesis in flow without the need of specific biochemical regulation. Furthermore, our findings highlight in general the strong influence of external flow on activity-driven cell deformation and thus may be relevant for other processes such as cell division and in vitro cell reproduction.

Computational Model for Platelet Biogenesis

In the following, we introduce our computational model for platelet biogenesis. Platelet biogenesis can be divided into two key steps: proplatelet extension and proplatelet fragmentation, which itself consists of formation of platelet-like swellings and their release as premature platelets. The first step, proplatelet extension, has been shown to rely on sliding of microtubule filaments driven by dynein (16). In the second step, once the proplatelet is extended, characteristic swellings form along the proplatelet shaft as we show in Fig. 1 A–C by experiments using a bioreactor, which are described in Materials and Methods. After swelling formation, the proplatelet ruptures, releasing the swellings as separate premature platelets into the bloodstream. In this work we focus specifically on the second step, i.e., the fragmentation mechanism of already extended proplatelets. Key ingredients of our model are the proplatelet’s active cell cortex including actomyosin and microtubules, its elastic membrane, and external fluid flow.

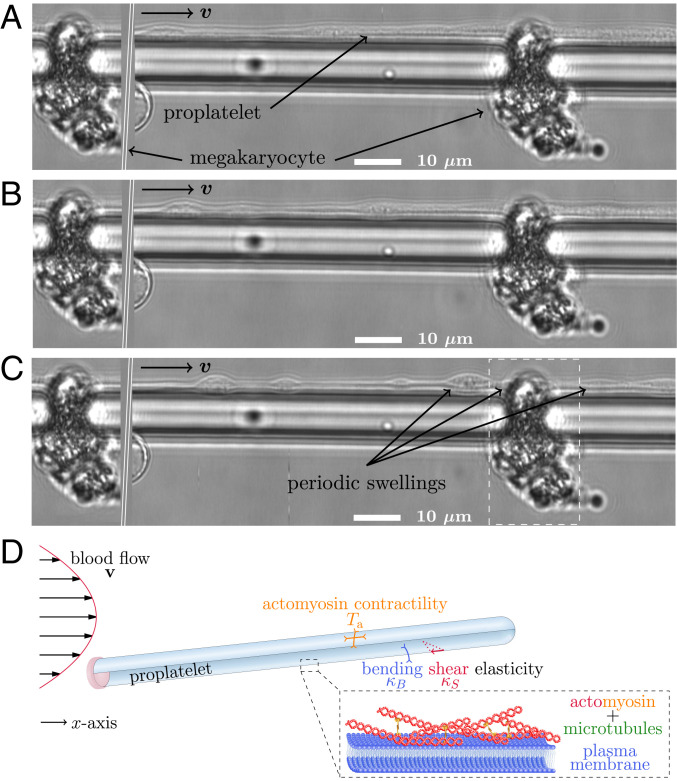
Fig. 1.

Experiments and setup illustration. (A) MKs imaged in vitro grow long tubular extensions (proplatelets) which after some time form periodic swellings along their shaft as shown in B and C. MKs are trapped in the bottom part of a microfluidic bioreactor by small gaps (15, 16) and remain fixed during proplatelet extension and fragmentation. To illustrate the periodic arrangement of MKs as shown in SI Appendix, Fig. S21, the marked area on the right-hand side has been copied and reinserted on the left of the image. Fluid flows with a maximum velocity of 2.2 mm/s and the complete width of the experimental image is $137.5\hspace{0.17em}\mathrm{\mu }$m. (D) Illustration of the computational model for the proplatelet membrane. Plasma membrane and cortex (Inset) are treated together as an active, elastic thin shell. The shell is endowed with bending and shear elasticity as well as actomyosin contractility in concert with microtubule sliding. We model the proplatelet as an initially cylindrical membrane with one fixed end and one free end according to the experimental situation. The proplatelet is subject to external flow.

A sketch of our simulation setup is shown in Fig. 1D. We model the extended proplatelet as a cylindrical membrane of finite length and radius $R_0=1.5\hspace{0.17em}\mathrm{\mu }$m (17) terminated by a spherical cap on the right and attached to a solid wall on the left. Attachment is achieved by an overlap of the proplatelet end with the wall and mimics the large and spatially fixed MK as seen in experiments, e.g., in Fig. 1A. In our simulations we use 90 times the radius as typical length of a proplatelet. The proplatelet is immersed in blood plasma.

The overall picture that has emerged from a series of recent studies (9, 21–29) highlights the key role of the cortical actomyosin system for swelling formation. Actin filaments have been shown by electron micrographs to be confined mostly to the thin cell cortex of the proplatelet (36, 37) where they form a disordered but homogeneous network (38). Such actomyosin networks are known to be contractile (39–47) in an isotropic fashion (39). In addition to the actomyosin, microtubule sliding has been shown to extend the proplatelet (16), which we therefore consider as being extensile mainly along the axis. These observations motivate us to use an active thin shell formulation; i.e., we treat the cortex together with the plasma membrane as an infinitely thin two-dimensional shell. The theoretical framework for active membranes has recently been established (48) based on active gel theory, which is a well-established tool for the continuum description of active dynamics in cytoskeletal assemblies (49, 50) and has been successfully utilized for the investigation of mechanisms regulating the cell shape in general (51, 52), in cell division (53, 54), and for cell motility (55). For the computational realization, we use our recently developed method for active membranes in 3D fluid flows (20), which is based on the lattice-Boltzmann/immersed boundary method (56) and is further detailed in SI Appendix, section S1. This method covers both the influence of the cell on the surrounding fluid flow and the forces acting on the cell due to external flow. Taken together, we consider an anisotropic active stress which accounts for the combination of microtubule extension and actomyosin contractility. The active part of the in-plane surface stress tensor (20) therefore takes the form

$$t_{\mathrm{a}\alpha }^{\hspace{0.17em}\beta }=\left(\begin{array}{cc}\hfill T_{\mathrm{a}}^z\hspace{1em}\hfill & \hfill 0\hfill \\ \hfill 0\hspace{1em}\hfill & \hfill T_{\mathrm{a}}^{\varphi }\hfill \end{array}\right)$$ [1]

with $T_{\mathrm{a}}^z<T_{\mathrm{a}}^{\varphi }$ due to microtubule extension acting against actomyosin contractility in the axial direction. We choose a ratio of $T_{\mathrm{a}}^z/T_{\mathrm{a}}^{\varphi }=0.75$ and the value $T_{\mathrm{a}}^{\varphi }=2.5\times 10^{-5}$ N/m, which is close to what has been predicted as the cortical tension of human blood platelets (36). This value is somewhat below, but in the same range as, the contractile stress of activated platelets where 3D stresses of ${\sigma }_0=150$ kPa have been reported in adhered platelets with a thickness of h=10 to 100 nm (57, 58) leading to a membrane stress of around ${\sigma }_{0}h=1.5\cdot 10^{-3}$ N/m. Direct measurements of the active stress in MKs or extended proplatelets have thus far not been carried out. We show in SI Appendix, Fig. S11, however, that our results do not critically depend on the precise value of the active stress. Similarly, SI Appendix, section S3 shows that our results are not qualitatively altered if an isotropic contractility ($T_{\mathrm{a}}^z/T_{\mathrm{a}}^{\varphi }=1$) is assumed.

To cover the passive elasticity of the plasma membrane and cortical cytoskeletal network, we furthermore assign shear and bending resistance to the proplatelet membrane. Shear elasticity stems from the continuous spectrin network in the proplatelet (59) and is considered using the common Skalak model which has been established for numerical simulations of red blood cells (60). Bending elasticity stems from the properties of the plasma membrane and is modeled using the Helfrich model (60, 61). We use a resistance to shear of ${\kappa }_{\mathrm{S}}=5\times 10^{-6}$ N/m and a resistance to bending of ${\kappa }_{\mathrm{B}}=2\times 10^{-19}$ Nm as they are reported for red blood cells (60). Proplatelets are immersed into a flowing liquid with the properties of blood plasma having a density $\rho =\mathrm{1,000}$ g/L and a viscosity $\eta =1.2\times 10^{-3}$ Pa$\cdot$s. The proplatelet interior is filled with a liquid of the same properties, except in SI Appendix, Fig. S13 where we increase the viscosity contrast. The channel diameter is chosen to be about eight times the proplatelet diameter. Our simulations in general do not consider thermal fluctuations. Including them, however, does not significantly affect the results as shown in SI Appendix, Fig. S12.

Results

In the following three subsections, we investigate proplatelet fragmentation first in a quiescent fluid such as a petri dish followed by fragmentation in parabolic Poiseuille flow for two different geometries. In the first geometry, the flow is loosely confined between two parallel plates with a channel height of 23.5 $\mathrm{\mu }$m corresponding to microchannel bioreactors as well as to typical sinusoidal capillaries in the bone marrow (62). The second geometry is a narrow cylinder with a diameter of 9 $\mathrm{\mu }$m and thus only slightly larger than the proplatelet itself corresponding to small and intermediate capillaries in the bone marrow (62). Finally, we consider a homogeneous flow with constant velocity, which can be utilized for efficient platelet biogenesis in micropillar bioreactors.

Proplatelet Fragmentation without Flow by a Biological Rayleigh–Plateau Instability.

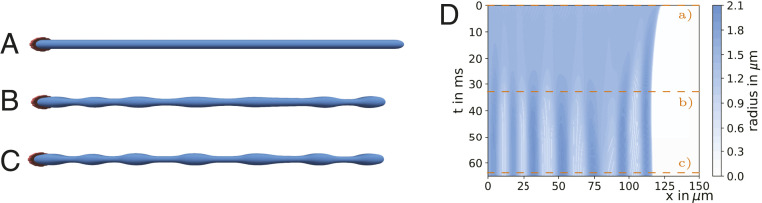
We start by considering a proplatelet immersed in a quiescent fluid subject to actomyosin contractility in concert with microtubule sliding. Fig. 2 A–C shows the dynamic evolution of the proplatelet shape for different times. Initially, in Fig. 2A the proplatelet is attached to a pillar on the left-hand side. As the simulation starts, the free end of the proplatelet on the right starts contracting and a spherical tip forms as seen in Fig. 2B. The initially cylindrical shaft starts to deform and a periodic, equidistant arrangement of platelet-sized swellings develops. These swellings are connected by small membrane strings, as shown in Fig. 2C. Once the membrane strings become too thin to be properly resolved numerically, the simulation is stopped and fragmentation is considered complete. The entire process is shown in Movie S1.

Fig. 2.

Proplatelet fragmentation by a biological Rayleigh–Plateau instability without flow. (A) The initially cylindrical proplatelet is subject to microtubule sliding and actomyosin contractility. (B) The proplatelet starts contracting and periodic swellings develop. (C) Eventually the proplatelet consists of a series of platelet-sized swellings. (D) A kymograph illustrates the dynamics of swelling formation with the color coding for the local proplatelet radius. Time steps for the corresponding proplatelet shapes in A–C are indicated by the orange lines.

The numerically obtained proplatelet dynamics in Fig. 2 A–C can be compared to our experimental images in Fig. 1 A–C and SI Appendix, Fig. S21. For the complete, experimental time series we refer to SI Appendix, Fig. S20. The simulations resemble the experimental proplatelet shapes very well: The initially cylindrical proplatelet (shown in Fig. 2A) first exhibits small undulations (shown in Fig. 2B) which eventually grow to swellings connected by membrane strings in Fig. 2C. This agreement demonstrates that our computational model is able to reproduce well the experimentally observed proplatelet fragmentation process.

A complete illustration of proplatelet fragmentation is given by the kymograph in Fig. 2D. Here, the color code corresponds to the local proplatelet radius shown with respect to position along the proplatelet axis and time. At the beginning of the simulation, contraction at the proplatelet’s free tip is visible by the dark blue band developing at the top right. With increasing time a periodic pattern of vertical stripes develops. These stripes correspond to the swellings visible in Fig. 2 B and C. We note that fragmentation in our simulations happens on shorter time scales than in corresponding in vitro experiments (e.g., figure S3 of ref. 17) which we attribute to the low viscosity that we use and the omitted viscoelasticity for the proplatelet interior. Indeed, simulations presented in SI Appendix, Fig. S13 indicate a strong increase in fragmentation time with an increase in internal viscosity. After the swellings are established, the periodic pattern along the shaft remains without any movement of the individual swellings.

The observed fragmentation in Fig. 2 is visually strikingly similar to the fragmentation of a liquid jet, e.g., water issuing from a tap, by the classic Rayleigh–Plateau instability (63) as shown in figure 2 of ref. 64. To further quantify our hypothesis that indeed a biological equivalent of the Rayleigh–Plateau instability is the key mechanism behind proplatelet fragmentation we investigate the wavelength of the periodic swellings along the proplatelet. To ensure a one-to-one correspondence of the two mechanisms, we consider first the results for isotropic actomyosin contractility in SI Appendix, Fig. S7, where we observe a wavelength of about $\lambda =14.3\hspace{0.17em}\mathrm{\mu }$m. Taken relative to the cylinder radius this leads to $\frac{2\pi }{\lambda }{R}_0\approx 0.66$ which is very close to the classic Rayleigh–Plateau value of 0.69 for the most unstable wavelength. The value for anisotropic contractility of 0.74 is close to the theory, as well. Furthermore, from experimentally measured proplatelet diameters of 2 to 4 $\mathrm{\mu }$m (8) we can estimate, based on the classic Rayleigh–Plateau criterion, a range for the platelet-sized swelling volume of about 28.6 to 229 $\mathrm{\mu }{\mathrm{m}}^3$. This compares well with observations in refs. 65 and 66 who found volumes of matured platelets in the range 8.377 to 50 $\mathrm{\mu }{\mathrm{m}}^3$ [for volume calculation we use diameter and height reported for platelets (65, 66) assuming an oblate ellipsoid].

The Rayleigh–Plateau instability of a liquid jet is driven by the surface tension $\gamma$ of a liquid–gas interface. At the interface the surface tension enters as an in-plane surface stress

$$t_{\hspace{1em}\alpha }^{\text{Jet}\hspace{0.17em}\beta }=\left(\begin{array}{cc}\hfill \gamma \hspace{1em}\hfill & \hfill 0\hfill \\ \hfill 0\hspace{1em}\hfill & \hfill \gamma \hfill \end{array}\right)$$ [2]

in mathematically the same way as the actomyosin/microtubule system in terms of an active stress $T_{\mathrm{a}}$ given in Eq. 1 does in the case of the proplatelet membrane. An important difference is that the proplatelet membrane is subject to anisotropic stresses due to microtubule extension along the axis. Thus, it becomes clear that the actomyosin contractility during proplatelet fragmentation plays essentially the same role as surface tension in the case of a liquid jet. The contractility triggers a biological Rayleigh–Plateau instability with a wavelength not depending on the absolute value of the contractility (SI Appendix, Fig. S11), in a similar way as the dominant wavelength of the classic Rayleigh–Plateau instability does not depend on the value of the surface tension coefficient (63). The biological Rayleigh–Plateau instability directly sets in with tip contraction and does not depend on thermal fluctuations (as shown in SI Appendix, Fig. S12). Our simulations thus suggest a physical mechanism regulating platelet size during the formation process: The dominant wavelength of the biological Rayleigh–Plateau instability determines platelet size.

Platelet Biogenesis In Vivo and in Microchannels: Parabolic Poiseuille Flow.

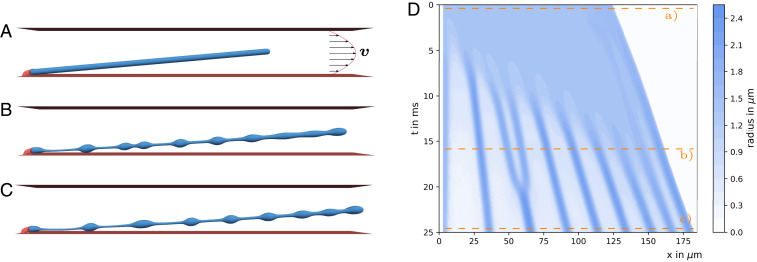
Motivated by the fact that in vivo platelet biogenesis occurs in the flowing bloodstream and that in vitro experiments have demonstrated a massive acceleration of platelet biogenesis due to flow in bioreactors (7, 12, 15–17, 19), we now go one step farther and investigate the role of various nonaxisymmetric flow fields. We first consider a channel bounded on top and bottom by a flat wall mimicking a typical bioreactor geometry or an in vivo sinusoidal blood vessel. Below we compare this to a narrow cylindrical channel corresponding closely to the geometry of a narrow capillary. The geometry in Fig. 3 leads to the well-known parabolic Poiseuille velocity profile far away from the cell. The simulations include the realistic alteration of the flow field due to the presence of the proplatelet by the two-way coupling between fluid and membrane (20). The channel height of 23.5 $\mathrm{\mu }$m and the flow velocities are chosen in the range reported by experiments (62) on sinusoidal blood vessels. The bioreactor used in Fig. 1 A–C and used in refs. 15 and 16 with approximately twice the diameter has the same order of magnitude. As shown in Fig. 3A, we then attach a proplatelet to one of the walls which, corresponding to proplatelet extension into sinusoidal blood vessels in the bone marrow and in the bioreactor as shown in SI Appendix, Fig. S21, is tilted in the flow direction (in SI Appendix, Fig. S15 we show a minor influence of a change in the tilting angle). Due to actomyosin contractility the proplatelet undergoes a biological Rayleigh–Plateau instability and platelet-sized swellings develop along its shaft similar to that in a quiescent fluid in Proplatelet Fragmentation without Flow by a Biological Rayleigh–Plateau Instability above. Proplatelet shapes after swelling formation are shown in Fig. 3 B and C for a flow velocity of $v=3.33$ mm/s. In contrast to a quiescent fluid, the action of the flow suppresses the contraction at the proplatelet free tip and the proplatelet undergoes a net extension. Furthermore, the proplatelet is tilted downward by the flow and eventually the proplatelet tip nearly aligns in the flow direction. Again, a close similarity between the predicted proplatelet shape in Fig. 3C and the experimental image in Fig. 1C is observed. The complete simulation is shown in Movie S2.

Fig. 3.

Blood platelet biogenesis in Poiseuille flow. Shown is blood platelet biogenesis in a parabolic Poiseuille flow with maximum velocity of $v=3.33$ mm/s. (A) A proplatelet is subject to Poiseuille flow with a parabolic velocity profile far away from the cell confined between two walls. (B) Due to the action of the flow the proplatelet extends and swellings form. (C) The final platelet-sized swellings move at nonuniform distance along the proplatelet shaft. (D) The corresponding kymograph shows the dynamics of swelling formation and the motion of the final swellings. Compared to the case without external flow in Fig. 2, swellings form at earlier times. Furthermore, swellings move along the proplatelet shaft with different velocity, resulting in nonuniform distances between neighboring swellings. Two initially separated platelet-sized swellings fuse at around 20 ms.

To investigate the dynamics of the fragmentation process in Poiseuille flow in more detail, we show in Fig. 3D the temporal evolution of the membrane shape in the corresponding kymograph. At the top, i.e., at very short times, membrane dynamics directly set in and the proplatelet swelling at the tip forms; however, it does not contract. The fluid flow rather leads to proplatelet extension. After 5 ms formation of the three leftmost platelet-sized swellings sets in. The other swellings form after 6 to 11 ms. In contrast to the quiescent fluid, the Poiseuille flow leads to nonsimultaneous formation, which may be triggered by locally different forces on the membrane caused by fluid flow. The nonsimultaneous formation is in good agreement with the experimental observations in Fig. 1A where the leftmost swelling is visible before the others form.

In contrast to Fig. 2D, the presence of flow disturbs the periodic arrangement of swellings with uniform distance. The negative slope of the bands in the kymograph clearly demonstrates the movement of the swellings with different velocities along the extending proplatelet. The different velocity of the individual swellings is due to the different location relative to the curved velocity profile of the external flow: Swellings close to the channel center are advected faster than swellings near the wall. While the swellings move in the flow direction, the contraction at the tip opposes the flow and leads to slower tip movement. Most remarkably, swellings two and three from the left first form and are clearly separate, but fuse afterward at around 20 ms. While the two swellings at first move with nearly constant velocity (according to the slope of the corresponding band in the kymograph in Fig. 3D), swelling three slows down. As a consequence both swellings approach each other, come into contact, and due to contractility eventually fuse. This points to a realignment in flow direction due to external shear through velocity gradients as the origin of swelling fusion. As the swelling shapes in Fig. 3 B and C illustrate, the fusion of two swellings leads to larger spherical structures, which eventually can be released into the bloodstream.

To bring out more clearly this apparent connection between fluid shear and swelling fusion, we consider a proplatelet immersed in pure shear flow as shown in SI Appendix, Fig. S2A and Movie S3. The channel geometry is the same as in Fig. 3A, but the flow now possesses a linear shear rather than a parabolic profile. Proplatelet fragmentation and swelling dynamics are shown in SI Appendix, Fig. S2 A–C. Comparing the simulation snapshots in SI Appendix, Fig. S2 B and C shows clear fusion events: one between swellings two and three and two more events for swellings farther to the right. These rich dynamics, swelling movement and fusion, are also reflected in the corresponding kymograph in SI Appendix, Fig. S2D, where a heterogeneous movement of the individual swellings, the fusions of swellings two and three and the neighboring ones at around 20 ms, and another at around 27 ms are clearly visible. Such fusion events could explain the release of larger structures called preplatelets into the circulatory system (35), as discussed in more detail in Discussion. In summary, we conclude that swelling fusion is triggered by fluid shear via a realignment of the proplatelet during swelling formation.

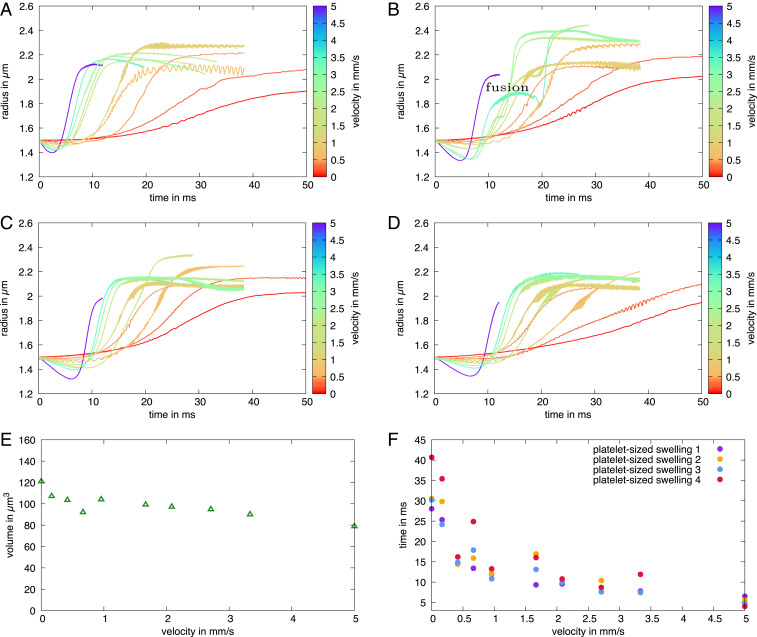
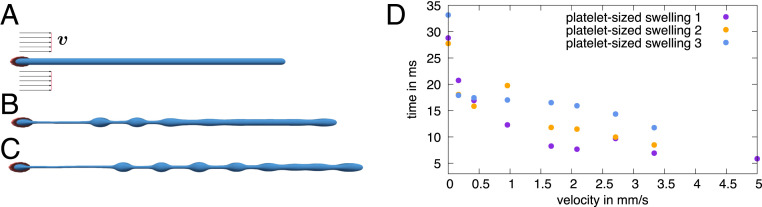
As a next step we investigate the influence of the external flow more systematically by varying the flow velocity. For this, we track the formation of the individual swellings over time as described in SI Appendix, section S1. We do so for the first to the fourth swellings, which are clearly separated in Fig. 3B. In Fig. 4 A–D we show the local proplatelet radius following the position of an individual swelling while forming. Starting from the initially homogeneous proplatelet radius, the radius at the position of a swelling increases and finally reaches a plateau, which indicates completion of swelling formation. Color coding of the curves indicates the systematic variation of the external flow velocity. With increasing external flow velocity the formation process takes place at earlier times (SI Appendix, Fig. S17) and the slope between the initial and the final plateau becomes steeper. This clearly demonstrates an acceleration of swelling formation with increasing velocity.

Fig. 4.

Acceleration of swelling formation in flow. (A–D) Time course of platelet-sized swelling formation in Poiseuille flow for (A) first, (B) second, (C) third, and (D) fourth swelling at varying external flow velocity. With increasing velocity, swelling formation shifts toward earlier times and the slope in the profile becomes steeper, which indicates acceleration of proplatelet fragmentation. At large velocity the second swelling shows a fusion event, which manifests itself in an additional transient plateau (fusion). (E) Swelling volume stays nearly constant over the whole range of velocities. (F) With increasing flow velocity the duration time of the biological Rayleigh–Plateau instability / of swelling formation strongly accelerates.

Despite the acceleration of swelling formation by flow, the final swelling radius varies only by about 10% and swelling volume (shown in Fig. 4E) stays nearly constant over the entire range of velocities. The small variation can be understood by the fact that the proplatelet extends with larger velocity and thus also the swellings and the membrane strings in between are stretched. To quantify the acceleration, we analyze the duration of swelling formation. We fix the time when the local proplatelet deformation reaches 2% as the beginning and the time when the plateau is reached as the end; the time difference serves as a measure for formation duration. Remarkably, for all swellings a significant acceleration occurs, demonstrating that fluid flow strongly influences the dynamics of proplatelet fragmentation. SI Appendix, Fig. S3 confirms that an acceleration of proplatelet fragmentation is also present in pure shear flow, but less pronounced compared to Poiseuille flow.

The above results correspond to the flow situation occurring in typical platelet bioreactor geometries (15, 16) as well as sinusoidal blood vessels in vivo (62). We now modify the geometry and consider a proplatelet in cylindrical confinement mimicking a narrow capillary of the bone marrow (62). The proplatelet undergoes a biological Rayleigh–Plateau instability as illustrated in SI Appendix, Fig. S4. Importantly, we again observe a strong acceleration of the swelling formation in SI Appendix, Fig. S5D with increasing flow speed. No fusion events are observed. This indicates that the biological Rayleigh–Plateau instability is the key mechanism behind accelerated platelet biogenesis also under narrowly confined in vivo flow conditions.

All in all, the predictions from our model are in full agreement with experimental observations where the size distribution of the produced platelets was largely independent of the applied flow velocity, but the production rate increased dramatically (16, 17). Our modeling efforts allow us to trace back this remarkable observation to the elasto-hydrodynamic origin of platelet biogenesis by a biological Rayleigh–Plateau instability.

Efficient Acceleration in Bioreactors with Homogeneous Flow.

As a next step we consider a homogeneous flow with uniform velocity approximating the flow pattern in microfluidic bioreactors, where megakaryocytes are attached to pillars (17). Studying the simple homogeneous flow geometry will further clarify the role of pulling (as opposed to shearing) by fluid forces as the origin of the accelerated swelling formation.

In Fig. 5A we show a proplatelet immersed in a homogeneous flow. The complete simulation is shown in Movie S4. Under the action of the homogeneous flow the proplatelet strongly extends in Fig. 5B while three swellings form. Fig. 5C shows the formation of additional swellings. In Fig. 5D, we show that homogeneous flow leads to a strong acceleration of proplatelet fragmentation with increasing flow velocity.

Fig. 5.

Blood platelet biogenesis in homogeneous flow. (A) A proplatelet is immersed in a homogeneous flow with constant velocity $v=2.0$ mm/s and attached to a wall on the left-hand side. (B and C) The proplatelet undergoes a biological Rayleigh–Plateau instability while being extended by the homogeneous flow. (D) Systematic variation of the external flow velocity shows a strong and systematic acceleration of the duration of swelling formation.

By comparing the kymograph for Poiseuille flow in Fig. 3D and that for homogeneous flow in SI Appendix, Fig. S6A, we discover a more pronounced successive formation of swellings in homogeneous flow. We further observe that, in contrast to Poiseuille and shear flow, in homogeneous flow no swelling fusion events occur. All swellings move with the same velocity as seen by the same slope of the bands in the kymograph, because they all experience the same external flow. Consequently, swellings show a more uniform distribution. In accordance with the argument above, fusion does not occur due to the absence of flow-induced realignment.

In SI Appendix, Fig. S6 B–E we again trace the swelling radius during formation. Here, for all three completely separated swellings we observe a shift of the curves toward shorter times and a strong change in slope when increasing the flow velocity. The final swelling radius does not vary for the first swelling. Swellings two and three show a certain variation in the final radius which is due to a pronounced stretching against proplatelet tip contraction at large velocities. In SI Appendix, Fig. S6F we show that swelling volume hardly varies with flow velocity despite the accelerated fragmentation in agreement with experimental observations.

Discussion

In this work, we provide a physical computational model for platelet biogenesis. We explicitly consider a single proplatelet and focus on its mechanical behavior under the influence of an external flow. Previous mathematical models (2, 3) account for the regulation of global platelet counts and are based on empirical differential equations describing macroscopic platelet number kinetics. Such an approach has been utilized to investigate pathological cyclic oscillations in platelet number (4) and the influence of chemotherapy (5, 6). In contrast to these empirical kinetic models, our computational model provides a mechanistic insight and unravels the biophysical mechanism of platelet biogenesis in external flows on the single-cell level.

The key ingredient of our proposed mechanism and trigger of the instability is actomyosin contractility. Indeed, it has been shown that extended proplatelets lack formed swellings when actin activity is disturbed (9, 22, 28, 29), e.g., by usage of drugs (9) or gene knockout (22, 28, 29). Our findings propose an explanation for these observations: If filamentous actin is absent (22), no contractility can arise in the proplatelet cortex and thus in turn no biological Rayleigh–Plateau instability occurs; i.e., the proplatelet does not fragment. Microtubule extension along the axis reduces the importance of the (stabilizing) axial contractility relative to the (destabilizing) actomyosin-induced azimuthal contractility and thus further amplifies the instability. Our findings suggest that the biological Rayleigh–Plateau instability may be a generic mechanism and that a similar instability may play a role also for other cells subject to actomyosin contractility such as axons of neurons. We note that our model does not incorporate biochemical effects such as the reported up-regulation of myosin contractility by induced stresses (27). Most likely an additional up-regulation would even enhance the acceleration in presence of flow. Our model can be the basis to include these biochemical regulation effects in the future, which would require a refined constitutive law for the active stress based on future experimental insights into proplatelet mechanics. Our simulations nevertheless show that biochemical regulation per se is not required for accelerated proplatelet fragmentation in flow.

In Poiseuille as well as in pure shear flow we report motion of swellings along the proplatelet shaft. Most importantly, this motion leads to fusion events of adjacent swellings as can be seen, e.g., in Fig. 3D. This is in agreement with observations in the experimental videos of ref. 17 (video S2 of ref. 17 at 6:44 min left above the pillar and at 12:36 min right above the pillar). Leading to considerably larger fragments, fusion events can explain the release of preplatelets. These fragments, which typically are about twice as large as an individual platelet, are frequently observed in the circulatory system (35) and have been demonstrated to represent an intermediate stage of platelet biogenesis (8). In the circulatory system these preplatelets undergo a transition to barbell-shaped proplatelets, which eventually fission into two platelets (35). In line with the reported failure of preplatelet to barbell-shaped proplatelet transition for inhibited myosin (27), an interplay of microtubule extension and actomyosin contractility is argued to drive the transition of preplatelets to barbell-shaped proplatelets (23). Our findings suggest a more precise physical role of actomyosin similar to proplatelet fragmentation: After extension of the spherical preplatelet by microtubules the actomyosin triggers a biological Rayleigh–Plateau instability. This in turn leads to the conversion to barbell-shaped proplatelets that eventually fission into platelets (as shown in SI Appendix, Fig. S19). Based on our simulations, we predict that preplatelets should to a much lesser extent occur in quiescent or homogeneous flow situations. Indeed, this prediction is supported by a reduced occurrence of preplatelets during platelet biogenesis in quiescent situations (16). Thus, a homogeneous flow velocity in vitro not only should lead to efficient, accelerated platelet production but also is expected to show a more monodisperse distribution of platelet size. In contrast, shear gradients in microfluidic devices would favor the fusion of swellings and thus the release of larger structures.

The teardrop-like structure of the free end of the proplatelet in Fig. 3C resembles the tip shape of proplatelets quite remarkably, as can be seen by comparing figures 3C and 4B of ref. 15. In our simulations, the proplatelet tip contracts due to actomyosin contractility in line with the so-called retraction phases (16, 17). As in our simulations, tip retraction has been found to be suppressed at higher flow velocities (16, 17). Thus, our simulations explain the transition between retraction phase (16) for no flow and pure extension in presence of flow (16, 17) by the hydrodynamic drag acting against actomyosin contractility.

Different from platelet biogenesis, theoretical studies predicted the existence of a Rayleigh–Plateau instability for membranes by an energy argument with an incorporated surface tension term (30) or by considering the force balance of an axisymmetric membrane including isotropic active stresses (31). For passive vesicle membranes, lacking the actomyosin, a Rayleigh–Plateau instability can occur due to external stimuli, as shown in the experiments (32) due to laser-induced tension, in a theoretical study (33), or in simulations for vesicles in extensional flow (34). An elastocapillary instability has also been suggested for mitochondrial fission (67).

In summary, our simulations reproduce the experimentally observed acceleration of platelet biogenesis in external flows. Our work strongly indicates that flow-accelerated proplatelet fragmentation into (pre)platelets can be understood as a mainly physical, accelerated elasto-hydrodynamic instability which is not triggered by biochemical sensing of external flow. We have identified actomyosin contractility in the cortex of an extended proplatelet as the essential ingredient required for this instability. Going further, the 3D simulations allow us to disentangle the different roles played by the different flow patterns. The observation that proplatelet fragmentation is strongly accelerated in homogeneous and parabolic flows, but to a much lesser extent in shear flows, leads us to conclude that the pulling of the flow at the proplatelet, rather than shear forces, is chiefly responsible for the accelerated fragmentation. Shear flows, on the other hand, are predicted to lead to more heterogeneous platelet size distributions due to fusion of platelet-sized swellings during the fragmentation process. These findings can serve as guidelines for the design of future bioreactors: It may indeed be desirable to employ geometries that produce relatively homogeneous flow components while at the same time avoiding shear components.

Our present simulations not only strongly indicate a biological Rayleigh–Plateau instability as a mechanism of platelet biogenesis, but also highlight in a general fashion the strong influence of external flow. Accordingly, we speculate that interaction with flow may also significantly affect the dynamics of other activity-driven processes in flowing environments.

Materials and Methods

Experimental Methodology.

Fetal liver cells of embryos at days 13.5 to 14.5 were cultured in medium (Dulbecco’s Modified Eagle’s Medium, 10% fetal calf serum, and 1% penicillin/streptomycin) containing 50 ng/mL thrombopoietin (68). On day 3, MKs were enriched by gradient density filtration with 1.5 and 3% bovine serum albumin. Day 4 MKs were infused at 12.5 $\mathrm{\mu }$L/h into a microfluidic bioreactor (15) (only bovine serum albumin coated) and proplatelet formation was observed with a Zeiss Observer Z1 microscope.

Data Availability.

All data discussed in this paper are available in the main text and SI Appendix.