When possible, report a Fisher-exact P value and display its underlying null randomization distribution

Significance

Statistical analyses of randomized experiments often rely on asymptotic P values instead of using the actual randomization procedure that led to the observed data. Fisher-exact and asymptotic P values can differ dramatically: The former should be preferred because it is calculated using the exact null randomization distribution, which, in small samples, can substantially differ from its approximating Student’s t distribution. Moreover, we may learn something scientifically interesting from examining the shape of the null randomization distribution.

Abstract

In randomized experiments, Fisher-exact P values are available and should be used to help evaluate results rather than the more commonly reported asymptotic P values. One reason is that using the latter can effectively alter the question being addressed by including irrelevant distributional assumptions. The Fisherian statistical framework, proposed in 1925, calculates a P value in a randomized experiment by using the actual randomization procedure that led to the observed data. Here, we illustrate this Fisherian framework in a crossover randomized experiment. First, we consider the first period of the experiment and analyze its data as a completely randomized experiment, ignoring the second period; then, we consider both periods. For each analysis, we focus on 10 outcomes that illustrate important differences between the asymptotic and Fisher tests for the null hypothesis of no ozone effect. For some outcomes, the traditional P value based on the approximating asymptotic Student’s t distribution substantially subceeded the minimum attainable Fisher-exact P value. For the other outcomes, the Fisher-exact null randomization distribution substantially differed from the bell-shaped one assumed by the asymptotic t test. Our conclusions: When researchers choose to report P values in randomized experiments, 1) Fisher-exact P values should be used, especially in studies with small sample sizes, and 2) the shape of the actual null randomization distribution should be examined for the recondite scientific insights it may reveal.

Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.

John W. Tukey

This famous sentence from John W. Tukey (ref. 1, p. 13) clearly affirms our position that calculating Fisher-exact P values is superior to the current more common practice of calculating approximating asymptotic (i.e., large sample) P values. We believe using the exact null randomization distribution generally addresses the right question, whereas using its approximating asymptotic distribution generally does not.

Although randomized experimental studies support the calculation of Fisher-exact P values for sharp null hypotheses, many published analyses report potentially deceptive P values based on assumed asymptotic distributions of statistics. Our attitude with randomized experiments is to eschew asymptotic P values, used decades ago because of the lack of modern computing equipment, and instead examine the actual null randomization distributions, which are generated by the randomized procedure that was used to collect the data, as proposed since R. A. Fisher (2).

Here, we illustrate the general statistical framework to assess Fisherian sharp null hypotheses using data from an epigenetic randomized experiment. The sharp null hypothesis, which was investigated in this experiment, is that exposure to ozone has the identical effect on the participant’s outcome as exposure to clean air.

1. Simple Experiment with a Completely Randomized Assignment Mechanism

1.1. Fisher-Exact Hypothesis Test.

Consider the simplest situation with N participants indexed by i, some exposed to active treatment, indicated by W_i = 1, and some exposed to control treatment, indicated by W_i = 0. Let $W$ denote the N-component vector of randomized exposures with ith component W_i. After each assigned exposure, an outcome measurement, generically called Y_i, is observed for participant i, where we denote by Y_i(W_i = 0) and Y_i(W_i = 1), the two potential outcomes that would have been observed had participant i been exposed to W_i = 0 and W_i = 1. Only one potential outcome, Y_i(W_i = 0) or Y_i(W_i = 1), can actually be observed. The Fisher sharp null hypothesis (H₀) states that, for each participant, $Y_i\left(W_i=0\right)=Y_i\left(W_i=1\right)$. To implement the test itself, we need to define its test statistic.

1.1.1. Test statistic.

Choosing a good statistic is an issue to be guided by scientific and statistical considerations, such as statistical power—see, for example, a nonstandard choice in the context of a cloud-seeding experiment (3). A common test statistic to compare two groups is the Welch test statistic:

$$T_{\mathrm{Welch}}=\frac{\frac{1}{N_t}{\displaystyle {\sum }_{i:W_i=1}{Y}_i\left(W_i=1\right)}-\frac{1}{N_c}{\displaystyle {\sum }_{i:W_i=0}{Y}_i\left(W_i=0\right)}}{\sqrt{\frac{s_t^2}{N_t}+\frac{s_c^2}{N_c}}},$$

where $s_t^2$ and $s_c^2$ are the sample variances of the outcome variable among the $N_t$ units assigned to active exposure and the $N_c$ units to control exposure, respectively. As in this example, any test statistic is a function of the observed potential outcomes, and consequently is a function of potential outcomes and the W_i, which indicates which potential outcomes are observed.

1.1.2. Construction of the null randomization distribution.

Assuming the Fisher sharp null hypothesis of absolutely no difference between treatment and control exposures, we calculate the value of the test statistic that would be observed for all possible random allocations, $W=\left(W_1,\dots ,W_N\right)$, to obtain the Fisher-exact null randomization distribution, or more succinctly, the “null randomization distribution” of the test statistic.

1.1.3 Fisher-exact P value.

We compare the observed value of the test statistic to the null randomization distribution constructed in section 1.1.2. The Fisher-exact P value corresponds to the proportion of values of the test statistic that are as extreme (i.e., as unusual) or more extreme than the observed value of that test statistic. The minimum attainable Fisher-exact P value, P value_min, that can be achieved is 1/N_{randomizations}.

1.2. Standard Student’s t Test Approximation.

Because of limited computing power, among other reasons, even in the late 20th century, researchers have retreated to using asymptotic Student’s t tests rather than Fisher-exact hypothesis tests. Thus, instead of locating $T_{\text{Welch}}^{\text{obs}}$ within its null randomization distribution and calculating its associated Fisher-exact P value, a Student’s t test capitalizing on the asymptotic null distribution of $T_{\text{Welch}}$ was used, i.e., a Student’s t distribution with degrees of freedom as follows:

$$\text{df}\approx \frac{{\left(\frac{s_t^2}{N_t}+\frac{s_c^2}{N_c}\right)}^2}{\frac{s_t^4}{N_t^2\left(N_t-1\right)}+\frac{s_c^4}{N_c^2\left(N_c-1\right)}}.$$

1.3. Illustration in a Human Epigenetic Study.

1.3.1. Description of the simple version of the experiment and notations.

A randomized epigenetic study was conducted in which N = 17 blinded participants were exposed for 2 h, either to 0.3 ppm ozone or to clean air. The study is described by Devlin et al. (4) and registered on ClinicalTrials.gov (NCT01492517).

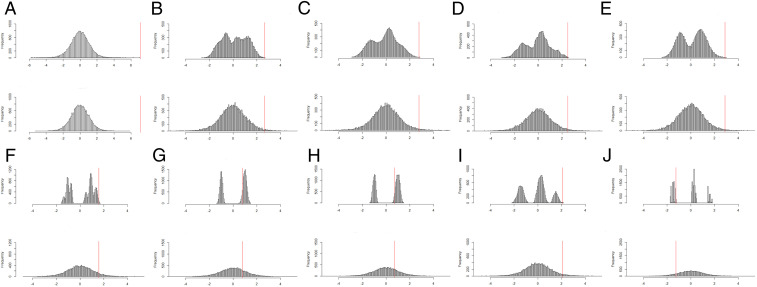
We denote clean air exposure by W_i = 0 and ozone exposure by W_i = 1. After the exposure, DNA methylation (denoted by Y) was measured at 484,531 genomic locations where a cytosine nucleotide is followed by a guanine nucleotide, which are called 5′-C-phosphate-G-3′ (CpG) sites. Here, we focus on the calculation of Fisher-exact P values for 10 illustrative CpG sites. Even these tests convey an important point that we do not find articulated in previous literature, which can succinctly be summarized as follows: If two hypotheses have the same Fisher-exact P value, the randomization-based evidence against their sharp null hypotheses is the same, even if their asymptotic P values are dramatically different, which can happen as illustrated in section 3.1.1.

1.3.2. Assignment mechanism.

We first analyze the data from this study as a simple completely randomized experiment; that is, we assume that the exposure was completely randomized with $N_t=10$; i.e., for each unit i, $P\left(W_i=1\right)=\frac{N_t}{N}=\frac{10}{17}$ and $P\left(W=\hspace{0.17em}w\right)=\frac{1}{\left(\begin{array}{c}N\\ N_t\end{array}\right)}=\frac{1}{\left(\begin{array}{c}17\\ 10\end{array}\right)}=\frac{1}{\mathrm{19,448}}$ if $\sum _{i=1}^N{w}_i=N_t$ and 0 otherwise, and N_{randomizations} = 19,448.

1.3.3. Sharp null hypothesis test.

We used T_Welch to assess the sharp null hypothesis of no effect of ozone vs. clean air for any participant on DNA methylation measured at 10 CpG sites. We contrast 1) the statistical conclusions concerning the plausibility of the Fisher sharp null hypothesis obtained using the actual randomization procedure that was used, to those obtained 2) using the approximating asymptotic Student’s t distribution. Specifically, we present in Table 1:

$$•\hspace{0.17em}\text{max}\left({\text{ratio}}_1,{\text{ratio}}_2\right)\underset{¯}{\underset{¯}{\mathrm{def}}}\hspace{0.17em}\text{max}\left(\frac{\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}}{\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}}\hspace{0.17em},\frac{\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}}{\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}}\right),$$

$$•\hspace{0.17em}\text{max}\left({\text{diff}}_1,{\text{diff}}_2\right)\underset{¯}{\underset{¯}{\mathrm{def}}}\hspace{0.17em}\text{max}\left(\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}\hspace{0.17em}\mathrm{-}\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value},\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}-\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}\right),$$

Table 1.

Comparison of the Fisher-exact and asymptotic P values

Simple completely randomized experiment (TWelch)
CpG site (Fig. 1)	Fisher-exact P value	Asymptotic P value (df)	Max ratio*	Max diff†
cg09008103 (Fig. 1A)	1/19,448 = 0.0000514	0.0000034 (13.4)	15.0	<0.001
cg19264123 (Fig. 1B)	1/19,448 = 0.0000514	0.0126364 (9.1)	245.8	0.013
cg14354270 (Fig. 1C)	2/19,448 = 0.0001028	0.0154687 (6.3)	150.4	0.015
cg00876272 (Fig. 1D)	6/19,448 = 0.0003085	0.0208069 (7.1)	67.4	0.020
cg24928995 (Fig. 1E)	2/19,448 = 0.0001028	0.0071438 (11.5)	69.5	0.007
cg18988170 (Fig. 1F)	36/19,448 = 0.0018511	0.0735370 (9.1)	39.7	0.072
cg06818710 (Fig. 1G)	10,335/19,448 = 0.5324455	0.2246968 (9.2)	2.4	0.308
cg06255955 (Fig. 1H)	10,911/19,448 = 0.5610346	0.24447612 (9.3)	2.3	0.316
cg00004771 (Fig. 1I)	6/19,448 = 0.0003085	0.0407666 (6.0)	132.1	0.040
cg21036194 (Fig. 1J)	13,546/19,448 = 0.6965241	0.8808444 (9.4)	1.3	0.184

^*$\text{Max}\hspace{0.17em}\text{ratio}=\text{max}\left({\text{ratio}}_1,{\text{ratio}}_2\right)=\text{max}(\frac{\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}}{\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}},\frac{\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}}{\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}})$.

^†$\text{Max}\hspace{0.17em}\text{diff}=\text{max}\left({\text{diff}}_1,{\text{diff}}_2\right)=\text{max}\left(\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}-\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value},\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}-\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}\right)$.

and then visually compare the null randomization distributions to the approximated null distributions based on a Student’s t distribution.

1.3.4. Results.

As seen in Table 1, the Fisher-exact P values substantially differ from the asymptotic P values, either on the multiplicative (e.g., ratio greater than 245) or on the additive scale (e.g., difference greater than 0.3). Comparing the univariate Fisher-exact P values to a significance level adjusted for multiple testing is not relevant to the message of this paper. However, this high-dimensional example gives us the opportunity to display interesting results (in section 3) from Fisher-exact and asymptotic P values, where the latter can be unrealistically small.

For CpG sites cg09008103 and cg19264123, the Fisher-exact P values achieve the minimum attainable Fisher-exact P value; Fig. 1 A and B display their null distributions. For the cg09008103 site, we notice a serious problem with the P value based on the asymptotic approximation: it subceeds the minimum attainable Fisher-exact P value, $1/\mathrm{19,448}$. Although the null randomization distribution of T_Welch for this site follows an approximate t distribution, as assumed by the asymptotic approach, it is not the case for the nine other CpG sites, whose null randomization distributions are multimodal (Fig. 1 B–J), and sometimes not even symmetric (e.g., Fig. 1 B–D), leading to large discrepancies between the Fisher-exact and asymptotic P values.

Fig. 1.

Exact (Upper) and approximating (Lower) null randomization distributions for 10 epigenetic outcome variables, labeled A, B, C, D, E, F, G, H, I, J, as explicated by the rows of Table 1; the test statistic being used is T_Welch, where for each variable the vertical red line indicates the actual observed value of T_Welch.

We postpone the discussion of these results until we present the results of the next section because some of our comments are best articulated by contrasting the more complex conclusions that can be reached with the more complex data structures of the full experiment.

2. Randomized Crossover Experiment

2.1. Description of the Experiment.

The data that were analyzed in the previous section actually arose from the first period of a randomized crossover experiment, in which two exposure sessions were separated by a minimum of 13 days in an attempt to avoid carry over effects from the first exposure. Here, each participant has two outcome values observed, one under ozone and one under clean air. The difference between the values estimates the effect of ozone vs. clean air for that participant under simple specific assumptions. We again focus on 10 illustrative CpG sites and assess the Fisher sharp null hypothesis of no differential effect of ozone vs. clean air on DNA methylation for any participant.

2.2. Fisher-Exact Hypothesis Test.

Let W now be an N×2 matrix with ith row W_i = (W_i,j=1, W_i,j=2), where we index by j = 1, 2 the two visits for participant i. In the epigenetic experiment, for clean air exposure followed by ozone exposure, W_i = (W_i,j=1,W_i,j=2) = (0,1), and for ozone exposure followed by clean air exposure W_i = (W_i,j=1,W_i,j=2) = (1,0). The randomness of the exposure assignment mechanism resides in the order to which each participant is exposed, i.e., W_i,j=1 is randomized and W_i,j=2 is 1 − W_i,j=1. After each assigned exposure, either Y_i,j=1 or Y_i,j=2 is observed. For participant i, the four potential outcomes are Y_i,j=1(W_i,j=1 = 0), Y_i,j=1(W_i,j=1 = 1), Y_i,j=2(W_i,j=1 = 1, W_i,j=2 = 0), and Y_i,j=2(W_i,j=1 = 0, W_i,j=2 = 1). In a crossover experiment, the Fisher sharp null hypothesis (H₀₀) states that for each participant i, $Y_{i,j=1}\left(W_{i,j=1}=0\right)=Y_{i,j=1}\left(W_{i,j=1}=1\right)$ and $Y_{i,j=2}\left(W_{i,j=1}=1,W_{i,j=2}=0\right)=Y_{i,j=2}\left(W_{i,j=1}=0,W_{i,j=2}=1\right)$. For each participant i and each visit j, only one potential-outcome value can be observed.

A natural test statistic for assessing H₀₀ is the traditional paired statistic (T_paired), a scaled version of the average observed difference across all participants between outcome when exposed to ozone and when exposed to clean air:

$$T_{\mathrm{paired}}=\frac{\frac{1}{17}{\displaystyle {\sum }_{i=1}^{17}{d}_i}}{\frac{s_D}{\sqrt{17}}},$$

where

• • d_i denotes the observed participant difference when exposed to ozone vs. exposed to clean air:

•   ◦d_i = Y_i,j=2(W_i,j=2 = 1) − Y_i,j=1(W_i,j=1 = 0) for participants exposed to clean air first (i: 1, …, N_c-t), and
• ◦d_i = Y_i,j=1(W_i,j=1 = 1) – Y_i,j=2(W_i,j=2 = 0) for participants exposed to ozone first (i: 1, …, N_t-c),

•  •N_c-t and N_t-c are the number of participants who were first exposed to clean air and first exposed to ozone, respectively.
•  •$s_D^2=\left[{\sum }_{i=1:17},{\left(d_i-\left(1/17\right){\sum }_{i=1:17}{d}_i\right)}^2\right]/16.$

2.3. Paired Student’s t Test.

Similarly as in section 1.2, a paired Student’s t test assumes the asymptotic distribution of $T_{\text{paired}}$ under the null hypothesis, i.e., a Student’s t distribution with N − 1 degrees of freedom.

2.4. Illustration in the Same Human Epigenomic Study.

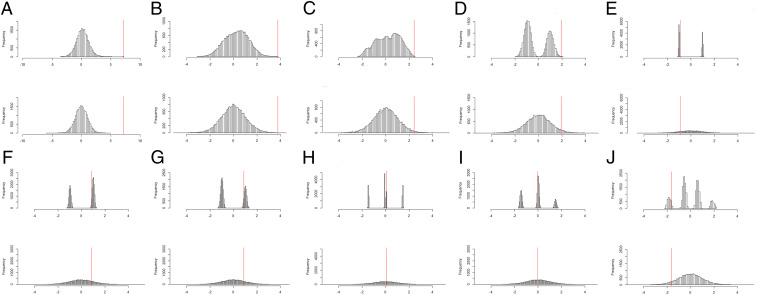
Similarly as in section 1.3.4, the Fisher-exact P values substantially differ from the asymptotic approximate P values, either on the multiplicative (e.g., ratio $\approx 450$) or on the additive scale (e.g., difference $\approx 0.4$) (Table 2). For the CpG sites cg00605859 and cg20129242, the Fisher-exact P values achieve the minimum possible exact P value; see Fig. 2 A and B for the null randomization distributions. For the site cg00605859, we again observe that the P value based on the asymptotic approximation subceeds the minimum exact P value, 1/19,448. For the eight other CpG sites, the null randomization distributions of T_paired for them deviate from the approximating asymptotic Student’s t distribution (Fig. 2 C–J).

Table 2.

Comparison of the Fisher-exact and asymptotic P values

Crossover randomized experiment (Tpaired)
CpG site (Fig. 2)	Fisher-exact P value	Asymptotic P value	Max ratio*	Max diff†
cg00605859 (Fig. 2A)	1/19,448 = 0.0000514	0.0000011	467.3	<0.001
cg20129242 (Fig. 2B)	1/19,448 = 0.0000514	0.0008217	1.6	<0.001
cg19150029 (Fig. 2C)	6/19,448 = 0.0003085	0.0142026	46.0	0.014
cg24274662 (Fig. 2D)	7/19,448 = 0.0003599	0.0351475	97.7	0.035
cg10484990 (Fig. 2E)	8,028/19,448 = 0.4127931	0.8131226	2.0	0.400
cg05907976 (Fig. 2F)	11,105/19,448 = 0.5710099	0.2009453	2.8	0.370
cg17324941 (Fig. 2G)	7,230/19,448 = 0.3717606	0.1957607	1.9	0.176
cg24869172 (Fig. 2H)	5,894/19,448 = 0.5710099	0.4718175	1.2	0.099
cg19611616 (Fig. 2I)	11,769/19,448 = 0.6051522	0.5242950	1.2	0.081
cg21036194 (Fig. 2J)	16,767/19,448 = 0.8621452	0.9402809	1.1	0.078

^*$\text{Max ratio}=\text{max}\left({\text{ratio}}_1,{\text{ratio}}_2\right)=\text{max}(\frac{\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}}{\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}},\frac{\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}}{\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}})$.

^†$\text{Max}\hspace{0.17em}\text{diff}=\text{max}\left({\text{diff}}_1,{\text{diff}}_2\right)=\text{max}\left(\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}\hspace{0.17em}–\hspace{0.17em}\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value},\text{Asymptotic}\hspace{0.17em}P\hspace{0.17em}\text{value}\hspace{0.17em}–\hspace{0.17em}\text{Fisher-exact}\hspace{0.17em}P\hspace{0.17em}\text{value}\right)$.

Fig. 2.

Exact (Upper) and approximating (Lower) null randomization distributions for 10 epigenetic outcome variables, labeled A, B, C, D, E, F, G, H, I, J, as explicated by the rows of Table 2; the test statistic being used is T_paired, where for each variable the vertical red line indicates the actual observed value of T_paired.

3. Discussion

3.1. Discussion of the Results from the Examples.

3.1.1. When possible, why not report Fisher-exact P values?

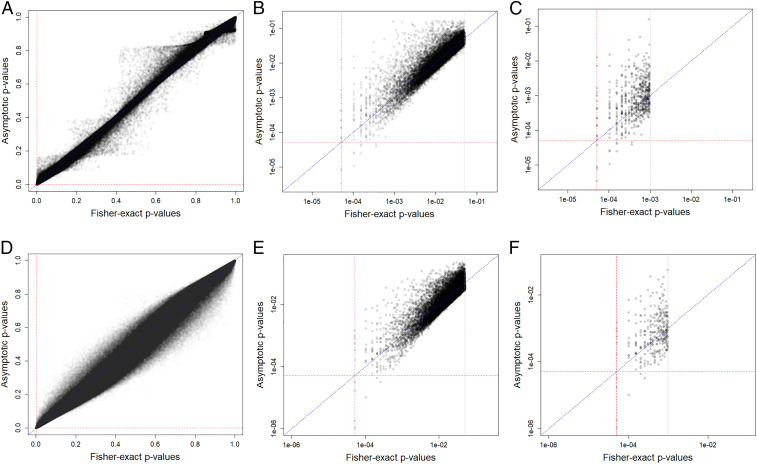
Here, we have illustrated the Fisherian inferential framework to assess 20 sharp null hypotheses of no ozone vs. clean air effect on epigenetic outcomes in a randomized crossover experiment, thereby highlighting how simple and interpretable randomization-based inference can be implemented using current computers. For the chosen CpG sites, the asymptotic t statistic P values did not track the Fisher-exact P values, and even more troubling, revealed that some asymptotic P values were below P value_min. Across all 484,531 CpG sites, the Fisher-exact P values also differ from the asymptotic P values in both the first period analysis and the crossover analysis. For the first period analysis, the asymptotic P values subceed the Fisher-exact P values over 50% of the time (Fig. 3A), 60% of the time when the Fisher-exact P values are below 0.05 (Fig. 3B), and over 35% of the time when the Fisher-exact P values are below 0.001 (Fig. 3C). For the crossover analysis, the asymptotic P values subceed the Fisher-exact P values over 60% of the time (Fig. 3D), nearly 70% of the time when the Fisher-exact P values are below 0.05 (Fig. 3E), and close to 40% of the time when the Fisher-exact P values are below 0.001 (Fig. 3F). In the lower range of P values, one might think that relying on asymptotic approximation is “safe” to use because it is “statistically conservative.” However, statistically conservative does not imply, for example, medically conservative (e.g., in studies of negative side effects). Again, tests that share the same Fisher-exact P value have the same randomization-based evidence against their sharp null hypotheses. Attributing different levels of plausibility to these hypotheses may be misleading, since in many cases their Fisher-exact P values are identical (see Fig. 3 A and B where 19 Fisher-exact tests generated P value_min = 0.0000514, but their asymptotic P values ranged from 0.0000034 to 0.0126364, a ratio from 0.07 to almost 250 and Fig. 3 E and F where 10 Fisher-exact tests generated P value_min, but their asymptotic P values ranged from 0.0000011 to 0.0015192, a ratio from 0.02 to almost 30). Although the scientist may often think about this issue as, how far is the approximation (or estimate) from the correct answer (i.e., the bias of the estimate), the practitioner possibly is more likely to think about, how far is my convenient P value from the, albeit, tediously calculated, correct answer? Of course, these are “two sides of the same coin,” but the different attitudes do lead to different ways of expressing conclusions.

Fig. 3.

Asymptotic P values vs. Fisher-exact P values in the epigenomic study (484,531 CpG sites). Legend: (Top, A–C) First period; (Bottom, D–F) Crossover experiment. Left, range = [0,1]; Middle, Fisher-exact P values < 0.05; Right, Fisher-exact P values < 0.001. Red line: P value = P value_min. Blue line: 45° line. (A) Range of asymptotic P values: [0.0000034; 0.9999996]; range of Fisher-exact P values: [1/19,448 = 0.0000514; 1]; 52% of the asymptotic P values are less than the Fisher-exact P values. (B) Range of asymptotic P values: [0.0000034; 0.1653300]; range of Fisher-exact P values: [1/19,448 = 0.0000514; 0.0499794]; 60% of the asymptotic P values are less than the Fisher-exact P values. (C) Range of asymptotic P values: [0.0000034; 0.1598584]; range of Fisher-exact P values: [1/19,448 = 0.0000514; 0.0009770]; 36% of the asymptotic P values are less than the Fisher-exact P values. (D) Range of asymptotic P values: [0.0000011; 0.9999806]; range of Fisher-exact P values: [1/19,448 = 0.0000514; 1]; 63% of the asymptotic P values are less than the Fisher-exact P values. (E) Range of asymptotic P values: [0.0000011; 0.2311926]; range of Fisher-exact P values: [1/19,448 = 0.0000514; 0.0499794]; 68% of the asymptotic P values are less than the Fisher-exact P values. (F) Range of asymptotic P values: [0.0000011; 0.0551901]; range of Fisher-exact P values: [1/19,448 = 0.0000514; 0.0009770]; 38% of the asymptotic P values are less than the Fisher-exact P values.

A major appeal of Fisherian inference is that any statistic can be used. However, when the P value is small enough so that sharp null hypothesis is doubtful, all of its implied assumptions, implicit as well as explicit, are suspect, such as the assumptions of “no carryover” and “no time” effects commonly made in crossover experiments; thus, the researcher needs to consider whether H₀₀ was deemed doubtful because of possible carryover or time effects, or whether the exposure had an effect on the outcome.

Moreover, regarding the null distribution of T_Welch and T_paired, the Student’s t test assumes a Student’s t distribution, which is symmetric about 0. When we assume a Bernoulli assignment mechanism with P = 1/2, the null randomization distributions of T_Welch and T_paired are symmetric about 0, but not when a completely randomized assignment mechanism with $N_t\ne N_c$.

3.1.2. Display null randomization distributions.

For the CpG sites (e.g., cg00605859 and cg20129242) with Fisher-exact P value equal to P value_min, we learned that ozone increased DNA methylation for all participants. However, there may be more to learn from this analysis! In particular, notice that we can also learn something scientifically interesting from the shape of the null randomization distribution, knowledge that is not adequately summarized by the location of the observed test statistic in that distribution. This fact is also illustrated when the Fisher-exact tests led to multimodal null randomization distributions, for which we can infer varying individual estimated effects by examining which sets of randomized allocations comprised the various modes. For the CpG site cg24274662, the null randomization distribution is bimodal (Fig. 2D) because only one participant substantially “responded” to ozone (i.e., the participant’s DNA methylation increased by 0.06 in contrast to the other 16 whose increase was negligible), leading to an asymptotic P value of ∼0.035 in contrast to the Fisher-exact P value of ∼0.00036. The nonnormality of the null randomization distribution itself carries information, although somewhat recondite, about these results of the study: The nonunimodality of the null randomization distribution arises from the hypothetical randomized allocations of the “responder.” The first mode displayed in Fig. 2D comprises the 11,440 values of T_paired (under H₀₀), for which the hypothetical randomizations for the responder were the opposite from the observed w_i, and vice versa (i.e., same as observed) for the second mode. For the CpG site cg21036194, the null randomization distribution is multimodal (Fig. 2J) because three participants “responded” to ozone, and thus the actual null randomization distribution of T_paired substantially differed from its approximating asymptotic null distribution. The first mode displayed in Fig. 2J comprises the 3,003 values of T_paired (under H₀), for which the hypothetical randomizations for the three responders were the same as their observed w_i values. Similarly, the second, third, and fourth modes correspond to values of T_paired, for which the hypothetical randomizations for two, one, or none of the three responders were the same as the observed w_i values, respectively.

These discrepancies highlight the importance of principled Fisherian inference when relying on P values in randomized experiments, especially in those with small sample sizes or effect heterogeneity across participants. The topic of heterogeneous causal effects has been discussed in the statistical literature, e.g., researchers have asked whether it is better to conduct “a larger, more heterogeneous study [or] a smaller, less heterogeneous study” (5). However, this topic, although interesting, is well beyond the scope of this article. Here, we identified ozone “responders” and the question is: what to do next? Should future ozone experiments include only “responders” in order to avoid averaging “responders” and “nonresponders,” or should future investigations study the individual characteristics creating differential ozone responses? Given a priori knowledge of heterogeneity, we could test potentially more interesting sharp null hypotheses stating that, for example, for each responder unit defined by Y_i,j=1(w_i,j=1 = 1) − Y_i,j=1(w_i,j=1 = 0) = 0.5 and for each nonresponder unit Y_i,j=1(w_i,j=1 = 1) − Y_i,j=1(w_i,j=1 = 0) = 0. Again, an in-depth discussion is well beyond the scope of this article, but this observation does point to the utility of examining the null randomization distribution in revealing this issue.

3.1.3. Computational time considerations and software implementation.

In our first set of analyses of the first period of the crossover randomized study, obtaining a Fisher-exact P value (recall, based on N_{randomizations} = 19,448) using a fairly powerful personal computer required about 5 min for each CpG site, which would mean years for all 484,531 CpG sites using one such computer. We ran the computations in this paper on the Faculty of Arts and Sciences (FAS) Research Computing Cannon cluster supported by the FAS Division of Science Research Computing Group at Harvard University, capitalizing on parallel calculations. Had the number of participants been larger and/or had the test statistic been more complex to compute, the computing time would have obviously grown and exceeded local current computing capacity. In this case, we advise approximating the randomization null distribution using randomly selected allocations. We believe that this strategy is superior to the asymptotic approximation, thereby resonating with the quote by Tukey that initiated our article.

In the crossover analysis, we use the fact that the denominator of T_paired was invariant for each randomized allocation. To obtain the Fisher-exact P value for each CpG site, we efficiently constructed the null randomization distribution of the numerator of T_paired by multiplying the 19,448 × 34 matrix of all random allocations with each 34 × 1 CpG outcome vector. Calculating the Fisher-exact P value for each CpG only required about 0.036 s using the same personal computer, and less than 5 h for all 484,531 Fisher-exact P values. When possible, we recommend to vectorize the code and avoid loops. We believe that the calculations of Fisher-exact P values in settings with large sample sizes and the development of software implementing these calculations will involve collaborations between classically trained statisticians and computer scientists. Moreover, we recommend using off-the-shelf “exact inference” software only if confident that the assignment mechanism assumed by the software corresponds to the actual one that led to the data or if one can upload the matrix of all, or a random sample of, the randomized allocations.

3.2. Recommendation for Small Randomized Studies.

Although it is generally difficult to advise and assess the computational feasibility for moderate and large studies in the future, in part due to the facts that computing power evolves quickly and some test statistics (e.g., posterior estimates found by Markov chain Monte Carlo) can now take hours or days to calculate, we have strong recommendations for studies with small sample sizes similar to the illustrative study we used here: We believe that Fisher-exact P values should always be reported instead of approximating asymptotic P values. Common statistical analyses of randomized experiments in the current literature mostly rely on asymptotic P values, which is especially problematic in small randomized studies.

For an explicit example, Zhong et al. (6) conducted a crossover experiment with 10 participants, in which, among other hypotheses, they tested the effect of exposure to particulate matter less than 2.5 µm vs. clean air on DNA methylation. The authors not only reported P values based on the asymptotic approximation but also chose a “suggestive threshold” of 1/10,000 to indicate statistical significance, which was below the minimum attainable P value of 1/1,024 if we assume a Bernoulli assignment mechanism with probability 1/2, which is doubtful to have been the actual randomization. Although randomization-based tests can be computationally intensive, they can often be implemented exactly, or to great accuracy, with modern computing power. For N = 10 as in Zhong et al., the number of possible randomizations is only 1,024!

3.3. Sensitivity Analyses for the Assumed Assignment Mechanism.

In sections 1 and 2, we assumed a completely randomized assignment for period 1 and therefore conditioned on the statistic N_t-c = 10 when conducting the Fisher-exact test. Because of the crossover structure, the period 1 assignments determined the period 2 assignments. However, this apparently was not the actual assignment mechanism. Of course, we advise knowing the actual assignment mechanism, but not necessarily following it to conduct randomization-based inference; the reason is that many statisticians recommend conditioning on ancillary statistics [see Ghosh et al. (7) for discussion]. However, in our setting, why not condition on N_t-c ∈ {7, 8, 9, 10}, each of which would had led to equal or more balanced designs than the observed one? In practice, the exact randomization may be unknown, as in the epigenetic experiment, in which case, you could, and some would argue you should, conduct sensitivity analyses, rather than condition on the ancillary sample sizes.

Our statistical conclusions are based on N_{randomizations} = 19,448 due to conditioning on N_t-c = 10. However, what would have been the conclusions, had we instead assumed a Bernoulli assignment mechanism with probability $P=1/2$, that is, each participant has probability 1/2 of being assigned to ozone exposure first [i.e., $P\left(W_{i,j=1}=1\right)=1/2$], and N_{randomizations} = 2¹⁷ = 131,072? We provide these alternative conclusions in Table 3. For simplicity, because T_Welch is easily defined for Bernoulli allocations that have at least two participants in each group, we consider only allocations where N_t and N_c ≥ 2 (i.e., N_{randomizations} = 131,036), when we calculate the Fisher-exact P values for the first period. In the crossover experiment, for the site cg00605859, the Fisher-exact P value was $1/\mathrm{19,448}$ when we assumed a completely randomized assignment, but when we assumed Bernoulli with $P=1/2$, it was $1/\mathrm{131,072}$, the minimum attainable Fisher-exact P value in a randomized experiment with n = 17. In practice, the assumed assignment mechanisms could lead to different statistical conclusions, in which case further investigations are needed. Other randomized designs could have been examined, e.g., a completely randomized design within blocks of males and females, or Bernoulli with unit-level probabilities that depend on covariates, a design that bridges to the next section.

Table 3.

Sensitivity analysis of the Fisher-exact P values assuming different assignment mechanisms in the epigenomic study

First period (TWelch)			Crossover randomized experiment (Tpaired)
CpG site (Fig. 1)	Completely randomized	Bernoulli with probability P = 1/2	CpG site (Fig. 2)	Completely randomized	Bernoulli with probability P = 1/2
cg09008103 (Fig. 1A)	1/19,448 = 0.0000514	2/131,036 = 0.0000153	cg00605859 (Fig. 2A)	1/19,448 = 0.0000514	1/217 = 0.0000076
cg19264123 (Fig. 1B)	1/19,448 = 0.0000514	7/131,036 = 0.0000534	cg20129242 (Fig. 2B)	1/19,448 = 0.0000514	1/217 = 0.0000076
cg14354270 (Fig. 1C)	2/19,448 = 0.0001028	65/131,036 = 0.0004960	cg19150029 (Fig. 2C)	6/19,448 = 0.0003085	18/217 = 0.0001373
cg00876272 (Fig. 1D)	6/19,448 = 0.0003085	398/131,036 = 0.0030373	cg24274662 (Fig. 2D)	7/19,448 = 0.0003599	23/217 = 0.0001755
cg24928995 (Fig. 1E)	2/19,448 = 0.0001028	36/131,036 = 0.0002747	cg10484990 (Fig. 2E)	8,028/19,448 = 0.4127931	66,391/217 = 0.5065231
cg18988170 (Fig. 1F)	36/19,448 = 0.0018511	297/131,036 = 0.0022666	cg05907976 (Fig. 2F)	11,105/19,448 = 0.5710099	62,108/217 = 0.4738464
cg06818710 (Fig. 1G)	10,335/19,448 = 0.5324455	60,470/131,036 = 0.4614762	cg17324941 (Fig. 2G)	7,230/19,448 = 0.3717606	57,278/217 = 0.4369965
cg06255955 (Fig. 1H)	10,911/19,448 = 0.5610346	62,954/131,036 = 0.4804329	cg24869172 (Fig. 2H)	5,894/19,448 = 0.5710099	42,722/217 = 0.3259430
cg00004771 (Fig. 1I)	6/19,448 = 0.0003085	114/131,036 = 0.0008700	cg19611616 (Fig. 2I)	11,769/19,448 = 0.6051522	85,407/217 = 0.6516037
cg21036194 (Fig. 1J)	13,546/19,448 = 0.6965241	100,373/131,036 = 0.7659956	cg21036194 (Fig. 2J)	16,767/19,448 = 0.8621452	115,933/217 = 0.8844986

3.4. Observational Studies.

Even in nonrandomized studies, if researchers choose to address their causal question with hypothesis testing and associated P values, we believe that Fisher-exact P values should replace asymptotic ones. To do so, we recommend reconstructing a plausible hypothetical randomized exposure assignment mechanism as suggested by Freedman (8, 9), Rubin (10, 11), or more explicitly by Bind and Rubin (12). Because this embedding carries a much stronger assumption about the assignment mechanism, we also recommend conducting associated sensitivity analyses, in which scenarios deviate from the assumed assignment mechanism. One commonly used assignment mechanism is one that depends only on the matrix of observed covariates, $X_{j=1}^{\mathrm{obs}}$. In other words, the assignment mechanism is assumed to be unconfounded (13) given $X_{j=1}^{\mathrm{obs}}$, i.e.,

$$P\left(W{}_{j=1}=w_{j=1}|Y_{i,j=1}\left(W_{j=1}=0\right),Y_{i,j=1}\left(W_{j=1}=1\right),X_{j=1}^{\mathrm{obs}},X_{j=1}^{\mathrm{unobs}}\right)=P\left(W{}_{j=1}=w_{j=1}|X_{j=1}^{\mathrm{obs}}\right),\hspace{0.17em}\mathrm{in}\hspace{0.17em}\mathrm{an}\hspace{0.17em}\mathrm{obvious}\hspace{0.17em}\mathrm{notation}.$$

Let us assume that the observational study is embedded in a Bernoulli trial, so that:

$$P\left(W_{j=1}=w_{j=1}|X_{j=1}^{\mathrm{obs}}\right)=\prod _{i=1}^{N}P{\left(W_{i,j=1}=1|X_{i,j=1}^{\mathrm{obs}}\right)}^{W_{i,j=1}}{\left(1-P\left(W_{i,j=1}=1|X_{i,j=1}^{\mathrm{obs}}\right)\right)}^{1-W_{i,j=1}}.$$

The probability distribution $P\left(W_{i,j=1}=1|X_{i,j=1}^{\mathrm{obs}}\right)$ is known as the “propensity score” model (14), which has been described as the “naïve” model (5) for modeling observational data because it does not consider any unobserved covariates, $X_{j=1}^{\mathrm{unobs}}$. In this naïve setting, the $w_{j=1}$ values are not necessarily equiprobable, and the Fisher-exact P value, which we denote by $p_{\text{Naïve}}$ to use Rosenbaum’s terminology (5), is as follows:

$$\begin{array}{l}{p}_{\mathrm{Naïve}}=\sum _{w_{j=1}\in W^{+}}\delta \left(T\left(W_{j=1}=w_{j=1}\right)\ge T_{}^{\mathrm{obs}}\right)P\left(W_{j=1}=w_{j=1}|X_{j=1}^{\mathrm{obs}}\right)\\ =\sum _{w_{j=1}:T\left(W_{j=1}=w_{j=1}\right)\ge T_{}^{\mathrm{obs}}}P\left(W_{j=1}=w_{j=1}|X_{j=1}^{\mathrm{obs}}\right),\end{array}$$

where $W^{+}$ is the set of all possible random assignments of $W_{j=1}$.

Another, less commonly used strategy, also introduced by Rosenbaum (5), assumes that the unit-level assignment mechanism depends on the observed and unobserved covariates, i.e., $P\left(W_{i,j=1}=1|X_{i,j=1}^{\mathrm{obs}},X_{i,j=1}^{\mathrm{unobs}}\right)\ne P\left(W_{i,j=1}=1|X_{i,j=1}^{obs}\right)$. Rosenbaum’s sensitivity analysis model considers deviations from the naïve model $P\left(W_{i,j=1}\hspace{0.17em}=1|X_{i,j=1}^{\mathrm{obs}}\right)$. In a setting where the assignment mechanism depends on the observed and unobserved covariates, the $W_{j=1}$ values are also not necessarily equiprobable and the Fisher-exact P value that we denote by $p_{\text{Sensitivity}}$ using Rosenbaum’s terminology (5) would depend on $X_{j=1}^{\mathrm{obs}}$ and $X_{j=1}^{\mathrm{unobs}}$:

$$p_{\mathrm{Sensitivity}}=\sum _{w_{j=1}:T\left(W_{j=1}=w_{j=1}\right)\ge T_{}^{\mathrm{obs}}}P\left(W_{j=1}=w_{j=1}|X_{j=1}^{\mathrm{obs}},X_{j=1}^{\mathrm{unobs}}\right).$$

We provide some insights on how the Fisher-exact P values would have changed had the human epigenetic experiment not been randomized. In our illustrative crossover example, for the sites cg00605859 and cg20129242, $w_{j=1}^{\mathrm{obs}}$ was associated with the most extreme value of $T_{paired}\left(W_{j=1}=w_{j=1}\right)$, $T_{paired}^{\mathrm{obs}}$, not only when we assume a completely randomized assignment, but also when we assume a Bernoulli assignment mechanism with probability 1/2; thus, $p_{\mathrm{Naïve}}=P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}}\right)$ and $p_{\mathrm{Sensitivity}}=P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}},X_{j=1}^{\mathrm{unobs}}\right)$. In the analysis of the first period, for the site cg09008103, when we assume a completely randomized assignment, $w_{j=1}^{\mathrm{obs}}={\left(0,0,0,1,1,0,0,1,0,1,1,0,1,1,1,1,1\right)}^T$ was the only exposure allocation such that $T_{Welch}\left(W_{j=1}=w_{j=1}\right)\ge T_{Welch}^{\mathrm{obs}}$. More importantly, when we assume a Bernoulli assignment with P = 1/2, $w_{j=1}^{\ast }={\left(0,0,0,1,1,0,0,1,1,1,1,0,1,1,1,1,1\right)}^T$ was the only exposure allocation such that $T_{Welch}\left(W_{j=1}=w_{j=1}\right)>T_{Welch}^{\mathrm{obs}}$. In this case, $p_{\mathrm{Naïve}}=P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}}\right)+P\left(W_{j=1}=w_{j=1}^{\ast }|X_{j=1}^{\mathrm{obs}}\right)$ and $p_{\mathrm{Sensitivity}}=P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}},\hspace{0.17em}{X}_{j=1}^{\mathrm{unobs}}\right)+P\left(W_{j=1}=w_{j=1}^{\ast }|X_{j=1}^{\mathrm{obs}},X_{j=1}^{\mathrm{unobs}}\right)$.

Subject-matter knowledge should motivate the plausible range of $P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}}\right)$, $P\left(W_{j=1}=w_{j=1}^{\ast }|X_{j=1}^{\mathrm{obs}}\right)$, $P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}},\hspace{0.17em}{X}_{j=1}^{\mathrm{unobs}}\right)$, and $P\left(W_{j=1}=w_{j=1}^{\ast }|X_{j=1}^{\mathrm{obs}},X_{j=1}^{\mathrm{unobs}}\right)$. Researchers could present how their conclusions vary as plausible deviations of the assumed hypothetical assignment mechanism in observational studies are considered. Scientifically, why would we anticipate $P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}}\right)$ to differ from $P\left(W_{j=1}=w_{j=1}^{\ast }|X_{j=1}^{\mathrm{obs}}\right)$, from $P\left(W_{j=1}=w_{j=1}^{\mathrm{obs}}|X_{j=1}^{\mathrm{obs}},\hspace{0.17em}{X}_{j=1}^{\mathrm{unobs}}\right)$, and from $P\left(W_{j=1}=w_{j=1}^{\ast }|X_{j=1}^{\mathrm{obs}},X_{j=1}^{\mathrm{unobs}}\right)$? These are questions that should be addressed by the researcher and used as the basis for a constructive debate, e.g., as argued by Rosenbaum in section 3.4 of his textbook (5).

4. Conclusion

Recently, there has been some debate within the academic community regarding banning P values in scientific articles. We certainly agree that the use of P values has been abused for decades in many fields and that the associated “replicability crisis” remains concerning. However, we believe that Fisher-exact P values and their underlying null randomization distributions can be helpful when appropriately used, because of their flexibility and limited underlying assumptions. If researchers choose to examine scientific questions with hypothesis tests, they should use the actual randomization procedure to compute Fisher-exact P values, rather than the asymptotic P values, and they should examine the shape of the actual null randomization distribution. In sum, we should not lose sight of Tukey’s edict, which should inform future generations of data analysts.

Data Availability Statement.

All data discussed in the paper will be made available to readers. The epigenetic data are accessible on a GitHub public repository, https://github.com/abele41/Human-epigenetic-study.