Polygenic inheritance, GWAS, polygenic risk scores, and the search for functional variants

Abstract

The reconciliation between Mendelian inheritance of discrete traits and the genetically based correlation between relatives for quantitative traits was Fisher’s infinitesimal model of a large number of genetic variants, each with very small effects, whose causal effects could not be individually identified. The development of genome-wide genetic association studies (GWAS) raised the hope that it would be possible to identify single polymorphic variants with identifiable functional effects on complex traits. It soon became clear that, with larger and larger GWAS on more and more complex traits, most of the significant associations had such small effects, that identifying their individual functional effects was essentially hopeless. Polygenic risk scores that provide an overall estimate of the genetic propensity to a trait at the individual level have been developed using GWAS data. These provide useful identification of groups of individuals with substantially increased risks, which can lead to recommendations of medical treatments or behavioral modifications to reduce risks. However, each such claim will require extensive investigation to justify its practical application. The challenge now is to use limited genetic association studies to find individually identifiable variants of significant functional effect that can help to understand the molecular basis of complex diseases and traits, and so lead to improved disease prevention and treatment. This can best be achieved by 1) the study of rare variants, often chosen by careful candidate assessment, and 2) the careful choice of phenotypes, often extremes of a quantitative variable, or traits with relatively high heritability.

The key to Mendel’s successful demonstration of the discrete nature of inheritance, without which it would not be possible to maintain the genetic variability required by Darwinian evolution by natural selection, was his careful choice of clearly dichotomous phenotypes for study. Only in this way could he have observed the simple ratios that defined his laws. That is why we refer to clearly inherited, often extreme, differences that are obviously familial, as “Mendelian.”

The ultimate reconciliation between Mendelian discrete inheritance and the correlation between relatives for continuously inherited traits, such as height or weight, which had been clearly observed by Francis Galton and his biometrician followers and which implied inherited tendencies for such traits, was provided by R. A. Fisher (1) in his seminal 1918 paper. This was entitled “The correlation between relatives on the supposition of Mendelian inheritance.” He showed that the observed correlations could be explained by a model in which a large number of discrete inherited differences were each inherited according to Mendel’s laws and where each had a small effect on the quantitative trait in question. The cumulative effect of such variants at many loci could be assumed to lead to a normal distribution, and it was in this paper that Fisher introduced the term variance as we now know it and the concept of the analysis of variance. This “infinitesimal model” is commonly considered to be the founding principle of quantitative genetics. It explains observed correlations between relatives based on Mendelian genetics but does not attempt to identify the causal effects of particular genetic variants on the quantitative trait being studied. Fisher returned only once to the analysis of quantitative inheritance using the infinitesimal model, and this was in the context of plant breeding (2). Here, his aim was to show how statistical approaches based on analyzing the quantitative distribution of a trait could be useful even, as he put it, “when individual factors cannot be recognized….”

At that time, Fisher had become very interested in the serological techniques then being developed by Charles Todd, which were the basis for the later recognition of red cell blood groups. Fisher suggested in a letter to Todd, with remarkable foresight, that these techniques might be able to detect “the direct products of individual genes rather than (those that) have secondary reactions.” In this correspondence with Todd, Fisher later said that he believed that such “work is going to lead to a greater advance, both theoretical and practical, in the problems of human genetics than can be expected from any further work on biometrical or genealogical lines.” Here, he was foreseeing the possibility of identifying biochemically the products of genes whose variants determine a given human trait, and so identifying the effects of a given variant on the trait at the molecular level.

The transition from the “work on biometrical or genealogical lines” to the wish to identify the direct products of genes epitomizes the prevailing conflict in studying the genetics of complex traits. This conflict is in the contrast between analyses that do not aim to identify the contributions of individual genetic variants and those that aim to understand the underlying molecular basis of the trait variation through the identification of specific variants, in genes with defined functions, that have clearly defined effects on the trait. The concept of a gene in the context we are discussing, is any defined mapped DNA sequence in the genome that can have some functional effect and so within which a variant sequence may have some detectable differential effect on a given phenotype. It is this dichotomy of approaches between not identifying the contribution of individual variants, and understanding their molecular function, which we analyze in this paper.

Polygenic Inheritance and the Location of Polygenes

The first use of polygenic in the context of quantitative inheritance was by Mather (3) in 1941. He talked of polygenic characters and polygenic variation and postulated that this type of inheritance, following Fisher’s infinitesimal model, was controlled by a different category of genes that he called “polygenes.” He accepted that “it is possible that if some organism could be grown in a constant environment and rendered homozygous for all but one of the genes affecting a quantitative character, this one gene might be observed to segregate and give sharply distinct classes just as a qualitative gene does.” He also pointed out that although “stature, for example, is usually a quantitative character,” there were “qualitative” genes, for example, for dwarfism that could affect this character in addition to the polygenes.

It was Thoday (4), a former pupil of Mather’s, who showed in a paper entitled “Location of polygenes” how it was possible to locate polygenes by, for example, mapping regions of the Drosophila genome that had a statistically significant large effect on bristle number in Drosophila, his model quantitative trait. Jinks, a Mather disciple and a distinguished and influential British geneticist, took the opposite view to its extremes and would not accept, for example, that for certain diseases, including diabetes, that could be interpreted through a threshold model (5) as quantitative traits, it could be possible to find specific genetic variants at defined genes with recognizably large effects on the chance of getting diabetes.

HLA and Disease Associations

While there were claims of associations between ABO types and certain diseases starting in the early 1950s, it was the really striking associations of HLA types with autoimmune diseases, notably HLA-B*27 with ankylosing spondylitis (6), that changed the whole field of studying multifactorial inheritance by looking for associations between phenotypes and specific, possibly causal, genetic variants. The first suggestion that linkage disequilibrium (LD) with an unobserved causal variant could account for associations between a genetic variant and a disease was made by Bodmer (7), based on early data on Hodgkin’s disease and this idea was further developed in the context of autoimmune diseases by McDevitt and Bodmer (8). The role of HLA in the control of the immune response provided a clear rationale for testing these associations. Early examples of the use of LD with common HLA polymorphic alleles for identifying causal variants in novel closely linked genes are the discovery of the key role of an HLA-DQ allele in susceptibility to type I diabetes through the initial disease association with HLA-B*8,15 and then HLA-DR*3,4 (9, 10), and the discovery of HFE gene variants as the main underlying cause of hereditary hemochromatosis through its association with HLA-A*3 (11).

Genome-Wide Association Studies

It was an obvious possibility to extend the HLA and disease association studies to looking for the association between any marker and a disease on the assumption that this could lead, by LD, to the discovery of the functionally relevant variant in the vicinity of the gene carrying the associated variant (12). Thus, the interpretation of the reason for an observed association between a given identified variant and a given phenotype is that either there is a direct effect of the variant on the phenotype or that the association is due to the effect of one or more as-yet-not-identified variants all in strong LD with observed associated variant, and collectively with a larger effect on the phenotype being studied than the originally associated variant.

Many initial studies looking for such disease associations in genes chosen as likely functionally relevant candidates proved difficult to repeat. This was, presumably, because of a combination of inadequately sized studies and the inevitable difficulty in choosing the right candidates. The development of DNA technologies for working with very large numbers of polymorphic variants (defined usually by a minor allele frequency of greater than 5%) then provided the basis for genome-wide association studies (GWAS) as we now know them, that did not make any assumptions about possible candidates. This, however, raised the problem of correcting for multiple comparisons, the need for which had already been realized for the HLA and disease studies, but now was required on a hugely larger scale. Very large-scale studies became necessary for reaching significant P values that needed to be about a million times smaller than the conventional 5% or 1% levels when testing for association with 500,000 to 1 million SNPs (single-nucleotide polymorphisms).

Clearly, the larger the effect, the higher the chance of finding a significant association for a given size of study and given allele frequency. It soon became clear, however, that the chance of finding effects with an odds ratio (OR) (from 2 × 2 associations between a given marker and a particular disease) even of ∼1.5 was quite small. Even at this level, proving that a variant truly has a functional effect on a trait is very challenging. In the hope of finding variants with larger effects, the suggestion was made that these might be found at lower frequencies, of say 1% or less, in carefully chosen candidate genes, for example, those in which obviously deleterious mutations had large effects on a trait [see Frayling et al. (13), Bodmer (14), and, for more historical detail, Bodmer and Bonilla (15)]. While contributing to the possible understanding of the functional basis of a trait, as determined by variants in genes with known functions, the approach of looking for rare variants did not necessarily aim to explain a large proportion of the overall genetic variance in the studied traits.

Some large effects found by early GWAS were previously well established by linkage or candidate gene association studies (16), for example, NOD2 in Crohn’s disease (17, 18) and INS in type 1 diabetes (19). However, two of the early studies showed quite strong effects of common variants on myocardial infarction (20) (ORs 1.5 to 1.8) and age-related macular degeneration (21) (OR ∼ 7.5), which pointed to relatively unexpected biological mechanisms due to being located in genes that probably would not have been chosen as candidates a priori. Later, GWAS of Crohn’s disease (22) and type 1 diabetes (23) yielded a handful of additional relatively large effects, which later became a pattern across autoimmune diseases.

The record of GWAS in driving the discovery of biological causes of phenotypes has, however, in general been disappointing. Advocates point to the discovery of the effect of FTO variation on obesity and body mass index (24) and of C4 genes on schizophrenia (25) as examples of GWAS generating novel biological hypotheses that have then gone on to be tested experimentally (26). The FTO effect on obesity is notable for being large relative to other GWAS hits not previously discovered by candidate gene approaches, with an OR of 1.67 for the effect of the homozygote risk genotype (rs9939609 A/A) (27). Experimental work has verified that the C4 genes that are differentially expressed between schizophrenia cases and controls, are expressed in relevant regions of the human brain and influence the extent of synaptic pruning in mice (25), but it remains unclear whether these phenomena are causally connected with schizophrenia development in humans. There have also been studies suggesting that genetically supported targets for drug development chosen from disease GWAS could improve the eventual drug approval rates, although it is not clear how this would be applied in practice, or how great the improvement would be (28, 29). More recently, GWAS significant associations (or “hits”) with common diseases have conformed overwhelmingly to a standard pattern of many small “polygenic” effect variants (OR < 1.2) at moderately or highly polymorphic SNP loci (minor allele frequency > 1%) (26), and similar results are found for continuous phenotypes such as height and IQ (30, 31).

In the attempt to bridge the gap between the finding of genetic variants with well-defined functional effects on a trait, and those that collectively account for a significant proportion of the genetic variance of a trait, larger and larger GWAS, including large replicates, are being carried out. These very large-scale studies naturally also increase the problem of spurious associations due to population stratification, more especially so if the effect sizes are small, although sophisticated methods have been developed for attempting to correct these biases (32).

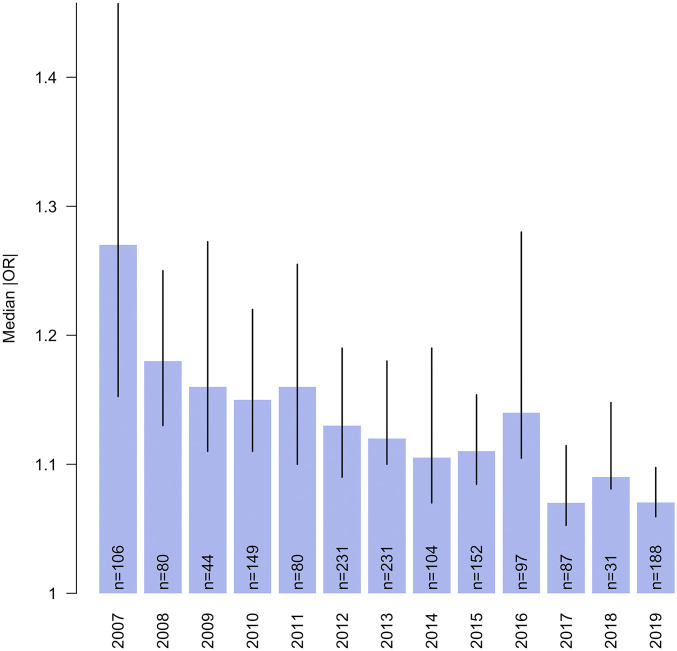
Fig. 1 shows the median sizes of ORs for new GWAS hits obtained each year, for the seven diseases originally studied by the Wellcome Trust Case Control Consortium (16). ORs were obtained from the National Human Genome Research Institute (NHGRI)/European Bioinformatics Institute (EBI) GWAS Catalogue (33), which collates results of all GWAS hits with combined discovery and replication P values less than 1 × 10⁻⁵. We restricted the analysis to studies where replication of initial associations was reported.

Fig. 1.

Decrease in GWAS hits’ effect sizes from the NHGRI-EBI GWAS catalog, for seven diseases initially studied as part of the Wellcome Trust Case Control Consortium between 2007 and 2019. Interquartile ranges are shown, along with the number of hits published in each year. The diseases are rheumatoid arthritis, Crohn’s disease, type 1 diabetes, type 2 diabetes, coronary artery disease, hypertension, and bipolar disorder.

The increase in the sizes of GWAS has led to a gradual decrease, with time, in the median size of genome-wide significant ORs, so that now a high proportion of the variants assumed to be relevant have ORs well under 1.1.

Establishing the role of small effect variants is extremely difficult. These are likely to exert their influences on phenotypes through very indirect mechanisms, far downstream from their proximal functions, giving rise to a large number of potential candidate functions to investigate. Although much progress has been made to improve fine-mapping methods (34, 35), establishing which variants are causal, among an associated set in LD, remains challenging when their effects on the phenotype are so small. Thus, at the level of effect sizes with ORs mostly well under 1.1, it is virtually impossible to identify unequivocally a particular variant’s functional effect on the trait being studied.

The situation is now approaching Fisher’s infinitesimal model, with individual variants whose specific contribution to the function of a trait is not identifiable. Perhaps these are really the polygenes postulated by Mather and his colleagues. However, the question arises, notwithstanding these small individual effects of variants, whether the pattern of variants associated with a given trait can nevertheless provide some useful overall indication of biologically relevant functions.

In the absence of a small number of variants with large or moderately large effect sizes that can be followed up for their individual functional effects, it is possible to assess whether, out of a large number of phenotypically associated SNP variants, there is a disproportionate number belonging to certain biological categories, for example being expressed in a specific tissue or acting in a particular enzyme pathway. Thus, under the polygenic model, where there are large numbers of hits with small effect sizes, the functional annotations of hits can be inspected to establish whether, for a given trait, there is such overrepresentation in particular pathways or gene ontology categories.

For example, in a large-scale GWAS of major depression (36), gene set analysis based on mRNA expression data in different tissues showed that only brain samples showed significant enrichment. Within this, the association was with neuronal gene expression rather than other cell types in the brain. There was an indication that the brain regions most associated were those that might be expected for major depression. While this information gives some general clues to functional effects of SNPs associated with major depression, the study only explained a minor fraction of the likely total genetic variation affecting major depression, and the ORs of the significant SNPs only ranged from 0.95 to 1.04. Similar results have been obtained, for example, for studies on neuroticism (37) and IQ (38).

The EA3 study on educational attainment, a highly polygenic trait, is another notable recent example of this type of analysis (39). A very large number of category enrichment analyses was performed on 1,271 independent genome-wide significant signals detected in a GWAS of 1.1 million individuals with educational attainment data. The authors highlight two broad findings. First, the most significantly prioritized genes that were implicated as causal show trajectories of expression in the brain that are increased before the late prenatal stage of development and decline thereafter. Weaker, newly discovered, associations showed no such trajectory. This suggests a modestly disproportionate influence of brain development relative to active brain functioning in determining differences between individual abilities underlying educational attainment, which is perhaps not surprising. Second, genes expressed in glial cells are relatively weakly enriched for educational attainment SNPs compared to those expressed in neurons. Thus, the enrichment effects reported for glial cells are 1.08 for astrocytes and 1.09 for oligodendrocytes, in contrast with 1.33 for neurons. The extent to which such studies make a definitive contribution to the functional genetic understanding of such complex traits is surely questionable.

In any large-scale GWAS, while the cutoff point for including SNPs of interest is based on some chosen upper threshold P value, after allowing for multiple comparisons, it remains possible that with large enough sample sizes there could eventually be a very long tail of SNPs with very small ORs. This notion has been extended by Boyle et al. (40) to what they call the “omnigenic” model. They base this on two key issues: 1) that a very long tail of SNPs with very small effects could account for a high proportion of the population genetic variance in a complex trait, and 2) that a high proportion of genes is involved in two or more pathways that might seem unrelated, such as the brain and the immune system, or contribute to basic functions common to many cell types, such as replication or protein processing. GWAS, such as those we have quoted above, suggest that, in many cases, subsets of genes with notably higher ORs, although still quite low, can be found that do focus broadly on certain tissues, notably the brain. This, of course, does not rule out the possibility that most of the population heritability for a trait could be explained by the very long tail of very low OR SNPs. In a further development of the omnigenic model, Liu et al. (41) find evidence that there are SNPs in “core” genes that contribute more or less directly to a trait and the rest that contribute what they refer to as peripherally, namely indirectly via effects on the levels of gene expression of the core genes. Thus, they propose a dichotomization of SNPs, effectively by their effect sizes, as in the studies mentioned above. It is not clear, however, in what way this contributes to a better understanding of the genetic control of quantitative traits at a functional level. The omnigenic model simply seems to make the case for a greater contribution to potential functional understanding of genetic contributions to a quantitative trait from what they call the core genes, namely those with the highest ORs that fit into defined functional categories, relative to the much larger tail of very low OR SNPs, which nevertheless may contribute most to the trait heritability.

Many GWAS disease associations are cis-expression quantitative trait loci, influencing the mRNA expression levels of nearby genes due to their locations in regulatory elements, and colocalization analysis often confirms that the same association signal is responsible for both expression level changes and effects on disease risk (42). Although this implies that, in these cases, changes to the expression levels of specific genes have causal effects on disease, these genes are likely to be separated from the key disease-influencing molecules by several steps in a molecular pathway, and will be linked to many other molecules by similar degrees of separation. Thus, although it may be possible to establish the proximal function responsible for a GWAS signal, this does not change the fact that, when variants’ phenotypic effects are small, these will have little relevance to disease etiology.

Polygenic Risk Scores

The obvious question that arises from our discussion so far is, what use can be made of GWAS results that do not give useful insights as to the functional effects of specific genetic variants. This is the question that Fisher et al. (2) addressed: “When individual factors cannot be recognized the analytic method of genetic study cannot even be commenced, and the question arises as to whether genetics as a science has any further resource to offer.” Fisher emphasized that in plant and animal breeding, the extent of genetic variance in a character would determine the scope for response to selection for a quantitative trait and this could be calculated without knowledge of the individual genetic factors involved. The larger the number of such factors, the greater the opportunity for continued success in selective breeding.

Goddard and his colleagues (43, 44) have been the pioneers of the application of SNP data to selective plant and animal breeding. They introduced the concept of an individual’s breeding value based on a weighted sum of the effects of a number of SNPs on a given quantitative trait, where the weights are based on the effect sizes of the SNPs estimated from a GWAS of the trait in question. This approach to selection based on breeding values has had an enormous effect on the efficacy of selection, completely bypassing the need for progeny testing.

An equivalent to the breeding value in human applications has been called the polygenic risk score (PRS) and provides an estimate of the genetic propensity to a trait at the individual level. This is calculated by computing, for each individual, the sum of the effects of risk alleles corresponding to a phenotype of interest, with each allele weighted by its effect size estimated from an independent GWAS on the phenotype. If the phenotype is, for example, breast cancer, then the PRS should give the genetic risk of an individual getting breast cancer based on their particular combination of at-risk alleles. The application of this information could then be, for example, to give women with a PRS above some chosen level more frequent breast cancer screens or start their screening at a younger age. The benefit would only come if these criteria for screening were more stringent than those generally applied. The general aim of the application of a PRS is to situations where individuals with a high PRS could benefit from particular treatments or behavioral modifications, for example with respect to diet or exercise, or by taking an appropriate medicine.

Calculating PRSs has now become a popular application of GWAS datasets to a wide variety of phenotypes, from height and body weight to cardiovascular disease and rheumatoid arthritis. Thresholds can be applied to determine the optimum number of SNPs to include, with filtering, for example, based on each SNPs’ GWAS P value (e.g., a threshold of 1 would include all SNPs, and a threshold of 5 × 10⁻⁸ would include only those considered to be genome-wide significant hits) (45, 46). For many phenotypes, models that use a large number of SNPs with effects too small to be individually significant outperform those using a smaller number of confirmed associations, in line with the trend toward decreasing sizes of effects for GWAS hits and with the evidence that much of the overall genetic variance for such a trait probably lies in the long tail of very low-level effect SNPs (47, 48). However, recent work using thousands of whole-genome sequenced individuals with height and BMI measurements strongly suggests that, at least for these phenotypes, rare variants that are poorly LD-tagged by common variants can explain the remaining genetic variation (49). Although the distribution of effect sizes among these variants is still unknown, it is quite possible that many will have quite large effects, which would be identifiable via DNA sequencing but are not detected by conventional GWAS using only markers with minor allele frequencies >1%.

The predictive performance of PRSs is in many cases quite good. For example, individuals with a cardiovascular PRS in the top 8% were found to have relative risk (RR) of 3 for developing the condition when compared to the rest of the population, with somewhat lower percentages of individuals meeting this level of risk when applying the same approach to arterial fibrillation, inflammatory bowel disease, breast cancer, and type 2 diabetes (50). In a separate dataset, individuals in the top 20% of cardiovascular disease PRSs had a hazard ratio of 4.17 when compared to the bottom 20% (51). These levels of effects may be sufficient to justify the use of PRSs for clinical screening of individuals to detect those in the extreme tail who may be invited for preemptive treatment or monitoring. However, it is not clear that it would be ethical to exclude individuals from such a screening process on the basis that their PRS is low, as they may nevertheless be at some significant risk. Preventative medicine often comprises lifestyle advice such as eating less or not smoking, and it could be argued that everyone should be encouraged to follow such advice regardless of their genetic predisposition. If the advice is to take a medicine, such as statins, the issue is whether to take it at all or to change the dosage. It is not clear, however, whether if, say, a PRS were calculated for heart disease at an early age one could give any other advice concerning diet and smoking than that which should be given to everybody whatever their PRS level.

It is important to realize that PRS scores may be significantly different in different populations, even though the populations may share common relatively large effect SNPs (52, 53). There are three key reasons for this. In most cases, disease-associated alleles will not be causal. As the LD between causal and associated alleles is likely to differ between the population the PRS is trained on and the one it is applied to, the estimates of allelic effect sizes will often be biased for the latter. Second, even when LD is similar in each population, if there is less allelic variation at the associated SNPs in the application population, this will lead to lower predictive power in the PRS. Third, predictions will be affected by the presence of admixture from the application population in the training population dataset. Widespread application of PRSs may, therefore, eventually require quite long-term, large-scale population-specific studies to justify their application in any given situation (54).

Search for Functional Variants

Genetic mapping to inform the molecular basis of any phenotype eventually depends on the molecular and functional understanding of the effects of variants with sufficiently large and individually identifiable effects on the phenotype. For clearly Mendelian traits segregating in families, positional cloning to identify the genes that explain the trait segregation, and through that the underlying function, has become relatively straightforward.

It is important to recognize that most large-effect variants will not lead to a clustering of extreme phenotypes within families. This is because the penetrance of rare variants, even if they have relatively large effects, is likely to be fairly low and certainly well below 50%. Most matings involving a rare dominant risk variant, D, will be Dd × dd. It can be shown, for example, that even for a penetrance of 20%, which is high for a variant with an OR of 3, only 5.2% of families with four offspring will include more than one affected offspring. Only when penetrances are well above 50% does one approach a familial concentration that begins to look like a standard Mendelian segregation. This means that for genetic effects that are not associated with a very high Mendelian-level penetrance, family studies will be of little use, at least in the average Western society (15). The question now is, what are the best approaches to finding specific functional variants with well-defined effects on multifactorial and quantitative traits that do not obviously show Mendelian segregation in families.

The early discoveries of remarkably strong associations between particular HLA types and diseases were the first clear examples of the use of population-marker association studies to gain insight into the functional basis of a disease [see Tomlinson and Bodmer (55) for a historical perspective]. These studies established the rationale for GWAS and raised the hope that many more sufficiently strong marker–disease associations that threw light on disease causality would be found. The reality, however, has been that such strong associations are quite uncommon and seem mostly to involve polymorphisms that have been associated with strong effects of natural selection. In addition to the HLA associations connected with immune functions, other examples include the well-known associations of the hemoglobin gene and G6PD polymorphisms with malaria and the more recently described association of certain APOL1 variants prevalent in certain West African populations with kidney disease and resistance to Trypanosoma brucei-caused African sleeping sickness (56).

In these examples, the relevant polymorphisms are maintained by some sort of balancing selection, sometimes frequency dependent, as in the case of HLA, or simple overdominance, as in the case of the hemoglobinopathies. High-frequency polymorphisms due to prior positive selection may just remain in a large population for very long periods of time even after the selection that established them has stopped, so long as there is then no counterselection. This, for example, is likely to be the case for past epidemics that led to selection for new resistant genetic variants.

It seems unlikely that many, if any, further large-effect common variants for complex multifactorial phenotypes will be found by more GWAS performed in the standard way, since so many have already been conducted at extremely well-powered levels for detection of quite small effects.

Many GWAS have been done on specific infectious diseases, including HIV [see e.g., Newport and Finan (57) and Klebanov (58)], revealing some interesting possible candidate functional genes other than those associated with the HLA and related systems. In addition, early GWAS on type 1 diabetes by Todd et al. (23) revealed suggestive functional effects of non-HLA variants involved in immune functions. Another interesting application of GWAS is to the study of severe allergies and drug responses, where very strong associations with particular HLA types, and with no other variants, genome-wide, have shown that those associated HLA types are the only significant determinants of the idiosyncratic reaction [see, e.g., Hung et al. (59) and Daly et al. (60)].

These results emphasize that one reason for the low success rate of many GWAS in finding variants with relatively large ORs is due to the complex mixture and variation in expression of the phenotypes studied. This suggests that there is still scope for the discovery of functionally meaningful individual variants in the study of more narrowly defined phenotypes.

Rare Variants with Large Effects

Conventional GWAS have not included rare variants with frequencies substantially lower than 1% mainly because it was assumed that good statistical power to detect variants whose effect sizes were as low as ORs of around 1.2 or less would require unrealistically large sample sizes to achieve significance. Although it is possible to impute genotypes at rare variants based on LD information from sequencing reference panels, together with GWAS SNP data, accuracy will typically be low for those with less than around 0.5% frequency. Common variants cannot associate with disease by tagging an unobserved rare, large-effect disease-causing variant, due to insufficient levels of LD. For example, r² = 0.02 is the highest possible correlation coefficient that can be observed for LD association between 0.05 and 0.001 frequency variants.

Some studies incorporating whole-exome or whole-genome sequencing have begun to find statistically significant associations of very-low-frequency, large-effect variants on common phenotypes. To do this, associated variants are filtered to consider only those with frequencies <0.1%, and to use a variety of criteria, such as whether the variants are nonsense, splice influencing or missense, in a way that is likely to affect protein function, so that only variants with likely functional effects are included for analysis. This helps to increase the effective power of a study by reducing the extent of correction for multiple comparisons (61–64).

Particular success in the search for rare variants has been achieved in psychiatric diseases including, for example, schizophrenia where several studies of family and unrelated samples have found a number of examples of relatively large-effect, low-frequency variants (65–68).

Like any genetic mapping association, rare variant associations cannot be assumed to be causal without, first, analysis of associations between the phenotype with all available haplotypes formed by the focal variant, and physically proximal variants in LD (i.e., fine mapping). Second, causality can only be unequivocally established via functional experimental work.

Rare Variants in Candidate Genes

Another approach to finding rare variants of presumed functional effects is to look for them in candidate genes, as described by Bodmer and Bonilla (15). Candidates may be chosen by two criteria: 1) genes in which obviously severe disruption of function gives rise to an extreme, usually clearly familial, abnormal version of the phenotype being studied, and 2) genes unequivocally known to be involved in the biology of the phenotype based on biochemical and physiological studies. Specific variants of functionally relevant effect are then sought by genome sequencing of the chosen candidate genes in individuals with the relevant phenotype. The frequencies of putative variants found in this way in individuals with the phenotype under study are then compared with those in controls, just as in a GWAS. This strategy involves a much-reduced constraint on power because the multiple-comparison correction need only take into account the number of candidates chosen for the study. The initial stimulus for the suggestion that rare variants could be found in appropriately chosen candidate genes came from the observation of missense variants in the APC gene, whose severe mutations cause familial polyposis coli, which were associated with a much milder form of polyposis (13, 69). The idea was then confirmed by additional studies on colorectal adenomas (70) and high-density lipoprotein cholesterol levels (71). For more recent discussions on approaches to rare variant analysis, see Lee et al. (72) and Povysil et al. (73).

As the number of candidate genes may be relatively large, and there are very large numbers of rare variants present in even a single gene, it is likely that such studies will benefit from going beyond the standard statistical approach of testing each variant independently and Bonferroni correcting P values, for example using gene-based rare-variant burden tests (74, 75).

Choice of Phenotypes: Distribution Extremes

As Mendel taught us, the choice of phenotype is the key to finding clear-cut patterns of inherited variation. This is reflected in the fact that larger variant effect sizes are obtained by GWAS for more narrowly defined disease such as type I diabetes, specific infectious diseases, adverse drug reactions, and severe specific allergies, as already discussed, rather than for broader categories such as mental or heart disease. Clearly, the more narrowly a disease can be defined using medical and biological criteria, generally reducing the heterogeneity of causal mechanisms, the greater the chance of finding specific functionally relevant genetic variants. It is also important to mention that there is a variety of types of genetic disease heterogeneity. Different variants in the same gene may have different effects, variants in different genes may have similar effects, and different combinations of genes may have similar effects.

For quantitative traits, it is likely to be the upper and lower extreme tails of a distribution that will yield the most biologically homogeneous individuals best suited for the search for specific relatively large-effect variants. In that case, looking for rare variants in the tails would suggest that these should be overrepresented in any sampling design. A further possibility is to use genomic data, or for humans, where available, twin data, to choose quantities with relatively high heritability. This is how we have identified specific large-effect genetic variants for particular recognizably different facial features (76).

Regression Analysis of Quantitative Phenotypes and Thresholds for Effect Size

The standard approach to a GWAS of a quantitative trait is, for each SNP, to regress the measurements for the three genotypes for the SNP allele pair against the number of minor frequency alleles carried, namely 2, 1, and 0. The slope of this regression is then a measure of the quantitative effect size and the P value is that for the difference of the slope from 0. To standardize comparisons between SNPs, the actual effect size is taken to be the linear regression coefficient divided by the SD of the phenotype. Just as for a discrete dichotomized phenotype, the steeper this normalized slope, the greater is the SNP effect on the quantitative trait measure and so the more likely it is that the effect can be interpreted at the functional level either due to the SNP variant itself, if it is in a functional part of the genome, or by a variant in a nearby functional region in strong LD with the “discovery” SNP.

To compare effect sizes measured in this way with ORs from 2 × 2 contingency tables obtained for discrete “all-or-none” variables, such as diseases, it is necessary to dichotomize the continuous variable by choice of a threshold, such that one category is defined to be all values above the threshold and the other those values below the threshold. The resulting 2 × 2 contingency table can also be used to test for the significance of the SNPs’ association with the quantitative trait, but usually with some loss of power. However, it is the OR from this 2 × 2 table that provides the most important impression of effect size, namely how likely is it that variant-carriers fall into the group with differential biological features relative to noncarriers. This is because any experimental follow-up of variants associated with continuous phenotypes, as for binary phenotypes, would usually require designation of samples to “case” and “control” groups.

Under reasonable assumptions, there is a one-to-one mathematical relationship between continuous and categorical effect sizes. It can be shown (SI Appendix) that when samples are dichotomized into those that are phenotypically extreme and nonextreme using a threshold, the RR relating genotype to extreme status is approximately the following:

$$\ln \text{RR}\approx \frac{\beta }{\left(1-p\right)s}\left(0.8+0.68\frac{t}{s}+0.064\frac{t^2}{s^2}\right)-\frac{{\beta }^2}{{\left(1-p\right)}^2{s}^2}\left(0.34+0.064\frac{t}{s}-0.0128\frac{t^2}{s^2}\right),$$ [1]

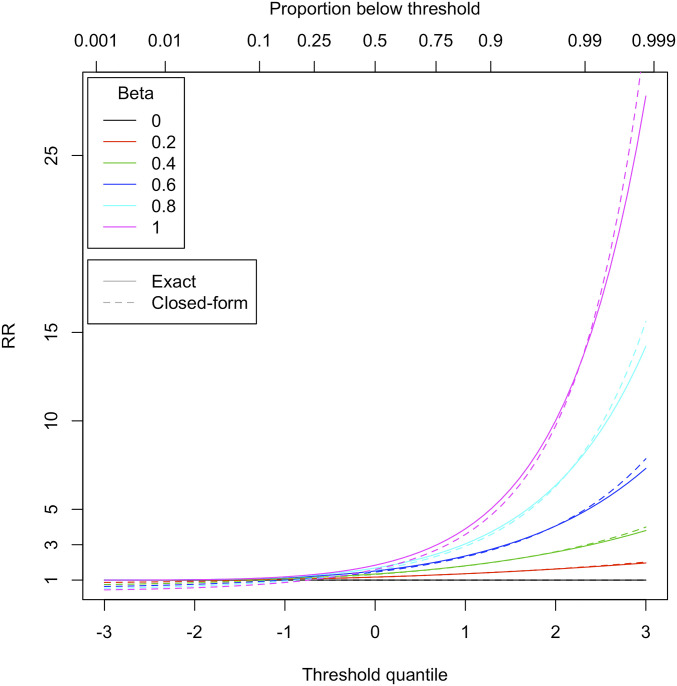
where β is the regression coefficient on risk allele number, p is the allele frequency, s is the SD of the phenotype within genotype groups, and t is the number of SDs (for a standard normal variable) taken as the threshold for extreme status. The approximation of Eq. 1 can be used to relate RRs obtained for categorical phenotypes, often for example disease status, to the equivalent effect sizes for continuous traits, as shown in Fig. 2 (an exact calculation produced using normal density and cumulative distribution functions is also shown). The RR is similar to the OR when the trait in question, in this case extreme status defined as lying above the threshold, is fairly rare.

Fig. 2.

Exact and closed-form calculations of relative risks (RRs), similar to ORs, for association of a binary variable produced by thresholding of a continuous characteristic with mean zero and SD of 1 (details in SI Appendix). Phenotypic threshold is represented by the x-axis, with units in standard deviations of the continuous phenotype. Proportions of individuals falling below various thresholds are shown above the plot. The different colored lines refer to different regression coefficients for the continuous phenotype on allele count. The phenotype is modeled as a mixture of two normal distributions, with individuals coming from the higher mean distribution if they possess a dominant genotype. The allele frequency is 5%.

The figure shows that as the threshold for the choice of extreme phenotype (t) increases, the corresponding effect size (RR) increases exponentially, provided that it is greater than zero. Increasing the threshold stringency clearly increases the probability of the risk variant being found in the upper extreme group. However, there is in another sense a diminishing return from doing this because it reduces the size of the target population for finding the risk variant. Note that even for β = 0.2, the RR hardly rises above 1.5 for a 1% upper threshold, while most GWAS hits reported for quantitative traits have β well below 0.2 or even 0.02.

In a “biobank” type of study design, where individuals are not selected but sampled randomly with respect to their phenotype, as we have already mentioned use of the continuous phenotypes will usually provide more statistical power than the dichotomized phenotypes for rejecting the null hypothesis of zero effect. The exception is when the number of phenotyped individuals is relatively small, and there is a large number of unphenotyped individuals to potentially use as controls. In this situation, using phenotypic extremes as cases will often provide more power. Furthermore, given limited resources, there is an argument for oversampling the extreme category for genotyping whenever this is feasible, to counterbalance any possible loss of power, since it is always likely that there will be an excess of unphenotyped controls and using these will have a minimal effect on an association study since the phenotype extremes will be a small proportion of such controls. However significant departures from the null hypothesis of zero effect are evaluated, we advocate the use of dichotomized phenotypes for assessment of effect sizes, as 1) the resulting ORs permit comparisons with ORs for categorical phenotypes, usually diseases, that are widely used, and 2) continuous phenotypes are best used as a guide for identifying subsets of individuals that are likely to be homogeneous for specific biological features.

Effect Size Versus Statistical Significance

Many GWAS and sequencing studies have failed to detect associations with rare, large-effect variants that pass stringent genome-wide corrections for multiple comparisons based only on P values (26). Given the greater biological insight that is provided by large-effect variants, it may be reasonable to accept them as significantly associated at a higher false-positive rate than that used for small-effect variants. This approach is commonly taken in gene expression studies, where “volcano plots” of effect size versus significance are used to select variables that have a satisfactory combination of both (76, 77). Empirical Bayesian shrinkage methods (78) may be the best approaches for selecting large-effect variants for follow-up, allowing accurate assessments of posterior distributions of variants’ effect sizes without resorting to subjective fully Bayesian inference. From this information, it is straightforward to compute the probability that a variant has an effect size greater than some minimum effect size of interest.

Conclusions

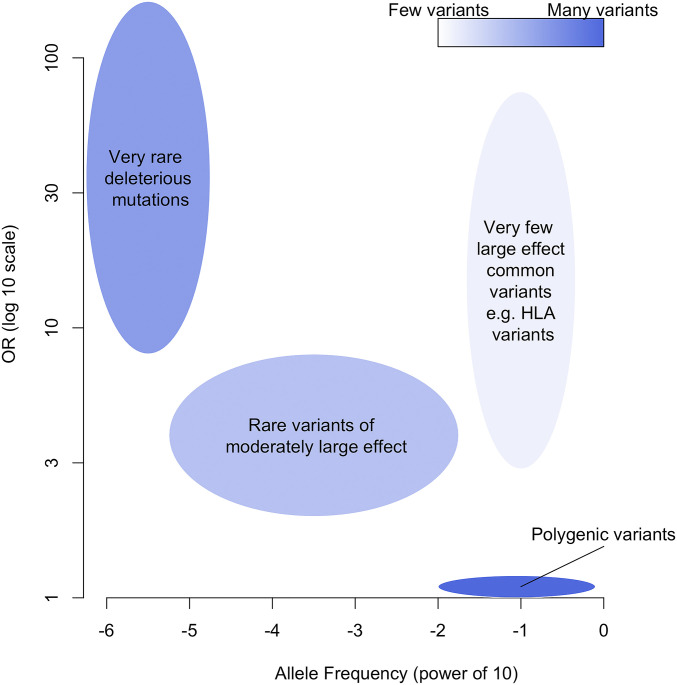
A schematic distribution of the relationships between variant frequency, effect size, and abundance that we have discussed in this analysis is given in Fig. 3. The largest category is the polymorphic polygenic variants discovered by large-scale GWAS from which it is not possible to obtain useful functional information on single variants. These variants can, however, be used to estimate individual overall genetically based risks (PRS), which may be a basis for recommendations of medical treatments or behavioral modifications to help reduce the risks. Each such claim will, however, need very careful investigation on a population-by-population basis before its practical use can be justified.

Fig. 3.

Schematic distribution of the relationship between variant frequency, effect size, and abundance.

The challenge now is to use limited genetic association studies to find individually identifiable variants of significant functional effect. This can best be achieved by 1) the study of rare variants, often chosen by careful candidate assessment, and 2) the careful choice of phenotypes, often extremes of a quantitative variable, or traits with relatively high heritability.

It is, therefore, the rare variants of moderately large effect that will be the main basis for finding individually identifiable functional variants that can help to understand the molecular basis of complex diseases and traits, and so lead to improved disease prevention and treatment.