Thinner biological tissues induce leaflet flutter in aortic heart valve replacements

Significance

Percutaneous valve replacement procedures enable the deployment of bioprosthetic heart valves through a catheter, which offers a minimally invasive option to treat valvular heart disease. Although these bioprostheses typically employ thinner leaflet tissues to accommodate the collapsed valve dimensions, the impact of using such tissues remains poorly understood. This study used high-fidelity computational methods to model realistic aortic valve implants and analyze the behavior of thinner tissues in the valvular system. The results from this investigation provide essential knowledge about a previously understudied phenomenon and indicate that thinner, more flexible biological tissues induce significant leaflet flutter during the cardiac cycle. This observed response introduces blood flow disturbances and leaflet irregularities that can lead to cardiovascular dysfunction and reduced valve durability.

Abstract

Valvular heart disease has recently become an increasing public health concern due to the high prevalence of valve degeneration in aging populations. For patients with severely impacted aortic valves that require replacement, catheter-based bioprosthetic valve deployment offers a minimally invasive treatment option that eliminates many of the risks associated with surgical valve replacement. Although recent percutaneous device advancements have incorporated thinner, more flexible biological tissues to streamline safer deployment through catheters, the impact of such tissues in the complex, mechanically demanding, and highly dynamic valvular system remains poorly understood. The present work utilized a validated computational fluid–structure interaction approach to isolate the behavior of thinner, more compliant aortic valve tissues in a physiologically realistic system. This computational study identified and quantified significant leaflet flutter induced by the use of thinner tissues that initiated blood flow disturbances and oscillatory leaflet strains. The aortic flow and valvular dynamics associated with these thinner valvular tissues have not been previously identified and provide essential information that can significantly advance fundamental knowledge about the cardiac system and support future medical device innovation. Considering the risks associated with such observed flutter phenomena, including blood damage and accelerated leaflet deterioration, this study demonstrates the potentially serious impact of introducing thinner, more flexible tissues into the cardiac system.

Heart valves play a critical role in regulating the direction of blood flow through different chambers of the heart. The aortic valve specifically allows blood to flow from the left ventricle to the aorta during the contraction of the heart (systole) and prevents blood from flowing back into the ventricle when the heart relaxes (diastole). Various heart valve pathologies can induce remodeling and deterioration of the leaflet tissues that comprise the aortic valve, which may inhibit proper dynamic valvular function and accelerate disease progression. Valve calcification and structural degeneration are the primary causes of aortic valve failure and contribute to stenosis and regurgitation, which further disrupt blood flow and may lead to irreversible cardiac dysfunction. Currently, as there exists no proven therapy for halting the progression of these conditions, replacement with a prosthetic device remains one of the only options for treating aortic valve diseases. Additionally, the increased incidence of such diseases in aging populations has substantially expanded the need for replacement valve systems and devices (1).

A variety of prosthetic implant technologies exist to replace diseased valves, the most common of which are bioprosthetic heart valves fabricated from xenograft biomaterials (2). These bioprostheses are typically constructed using glutaraldehyde-fixed porcine valves or bovine pericardial tissues and are largely intended to emulate the behavior of the native valve (3). Despite numerous design advancements in replacement technologies, devices that incorporate exogenously cross-linked biological tissues continue to face substantial limitations in long-term durability due to tissue deterioration. This is evident through leaflet tearing (4, 5) and calcification of the pericardial tissue (6, 7). The overall lack of leaflet structural integrity over time can often lead to additional surgical procedures to replace the bioprosthesis after 10 to 15 years (7–9). Recently developed microstructurally based models of the initial stages of pericardial leaflet degeneration have demonstrated several important structural-remodeling mechanisms in the first 50 million cycles of operation (10, 11). However, there are a number of factors that may further accelerate leaflet deterioration and reduce the tissue durability over the bioprosthetic valve lifetime. One such factor is leaflet flutter, a phenomenon that has been observed in human and prosthetic heart valve tissues (12–15) and has been previously associated with increased calcification, tearing, and early fatigue failure over the valve lifetime (16–20). Consequently, studies aimed at characterizing valve functionality have identified fluttering of the leaflets in the blood flow as a crucial quality criterion in prosthetic valve designs that incorporate biological tissues (21).

In recent years, clinical practice has increasingly employed lower-risk heart valve implantations that are performed using percutaneous devices that require only minimally invasive procedures instead of open-heart surgery (22, 23). Percutaneous replacements, such as transcatheter aortic valve replacement, more commonly known as “TAVR,” offer many advantages for patients, including decreased postoperative pain and faster rehabilitation times (24). Percutaneous devices have also made heart valve replacement more accessible for patients who cannot undergo high-risk surgical operations. The replacement procedure includes crimping the bioprosthesis into a catheter and deploying and implanting the valve, typically through the femoral artery (transfemoral implantation) or the left-ventricular apex (transapical implantation) (25). Recent developments have advanced these percutaneous technologies toward implantation systems with smaller crimping diameters that offer fewer procedural complications compared with systems that require larger catheters for deployment (26). One straightforward and typical design approach for achieving such compact collapsed dimensions is to construct the valve leaflets from tissues that are sufficiently thin to accommodate the cross-sectional requirements of smaller catheters through a reduced leaflet volume (26).

While percutaneous valves offer patients numerous advantages over their surgical counterparts, the impact of using thinner biological tissues, which are intrinsically more compliant because of the associated reduction in flexural and in-plane stiffness, is not well understood. Due to the complex function of replacement heart valves over the cardiac cycle (2), a change to one component can have adverse effects on many other functional aspects. For example, an experimental study that investigated the onset of turbulent flow using varying inflow conditions for different aortic valve materials briefly noted that reduced leaflet rigidity may lead to increased fluttering, which can contribute to leaflet fatigue and tissue deterioration over time (19). Turbulent flow, which may be further amplified by leaflet flutter (27), has also been linked to blood damage, including platelet activation, thrombosis, and hemolysis (28, 29). A recent analytical study proposed a mathematical model to predict the critical flow speed of flutter onset as a function of valve properties, including tissue thickness (30). In terms of quantifying leaflet flutter, recent experimental work has proposed different methods to track the leaflet free-edge motion with varying levels of accuracy (21, 31, 32). While these previous investigations have made some efforts to examine and quantify leaflet flutter, the existing studies are limited in number and have been restricted by current experimental approaches that are challenging to perform, especially for individual valve variables, and measurement techniques that provide limited information about the flutter characteristics.

In this work, we utilize a validated computational methodology to fully isolate the impact of heart valve tissue thickness on the presence, nature, and extent of leaflet flutter. This high-fidelity computational approach provides comprehensive and highly detailed information about the flow characteristics, leaflet dynamics, and valvular mechanics throughout the cardiac cycle. To the best of our knowledge, such a study has not been previously performed. The present work captures the flutter behavior of a physiologically realistic aortic valve model, including an elastic wall, physiological boundary conditions, and nonlinear leaflet materials, using computational fluid–structure interaction (FSI) based on immersogeometric analysis (IMGA) (33, 34). For this study, a dataset of varying leaflet thicknesses is generated and examined through simulation to determine the influence of tissue thickness on leaflet flutter. The comprehensive FSI-based flutter-quantification methodology is used to evaluate the flutter behavior over the entire valve and in localized regions of the leaflets. The computational simulation and analysis approaches used in this work are summarized schematically in Fig. 1 and detailed in Materials and Methods. Through the identification and analysis of leaflet flutter in thinner pericardial tissues, this computational study provides in-depth insight about the valvular dynamics and the behavior of the cardiac system. This work identifies a direct connection between leaflet flutter of thinner tissues and a number of important quantities of interest that are linked to various negative cardiovascular outcomes over the lifetime of a bioprosthetic valve implant.

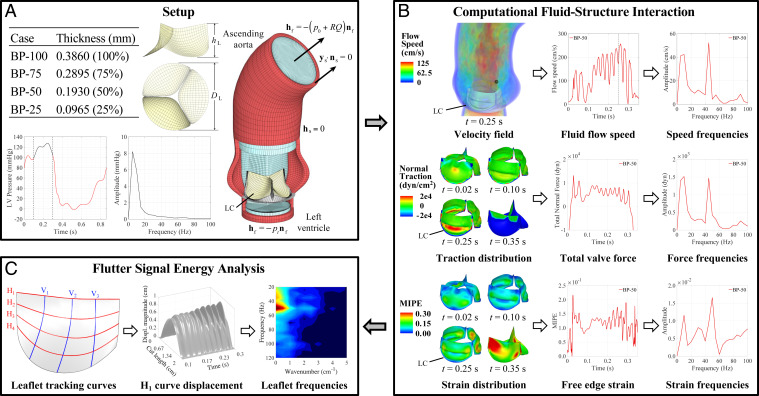
Fig. 1.

Overall schematic of the FSI-simulation and flutter-quantification methodologies. All results and analyses show the BP-50 case. The left coronary leaflet (LC) is indicated on each geometry. Further details can be found in Materials and Methods. (A) Valve thicknesses, ventricular pressure waveform, and problem setup for the computational simulation of the aorta and valve geometry. (B) FSI results and signal analysis procedure for the velocity field, leaflet normal tractions, and leaflet strains. The time signals of each quantity are analyzed using DFT operations. (C) Flutter-analysis methodology for the leaflet displacement. The tracking curves on the leaflet indicate the horizontal and vertical locations along which the flutter behavior is quantified. High-resolution version of this figure is available in the SI Appendix.

Results

Leaflet-Thickness Cases.

The full set of leaflet thicknesses considered in this work are shown in Fig. 1A. The baseline leaflet thickness of 0.386 mm is defined as a representative value for adult bovine pericardial (BP) tissue (26, 33, 35). The other cases are defined with respect to this baseline model, with the 75% thickness and 50% thickness cases falling within or near a representative range for adolescent and fetal bovine pericardial tissue, respectively (26). Considering potential future advancements in tissue engineering, one additional extreme case at 25% of the baseline thickness is also considered. The case names (BP-100, BP-75, BP-50, or BP-25) indicate a bovine pericardium valve at a certain percentage of the baseline thickness. FSI simulations are conducted for the four different leaflet thickness cases with all other aspects of the simulation remaining unchanged. Based on the left-ventricular pressure data shown in Fig. 1A for a single cardiac cycle, three consecutive cardiac cycles are analyzed, and the flutter behavior is quantified for each case. Representative solutions from a single cardiac cycle are shown in the following sections.

FSI-Simulation Results.

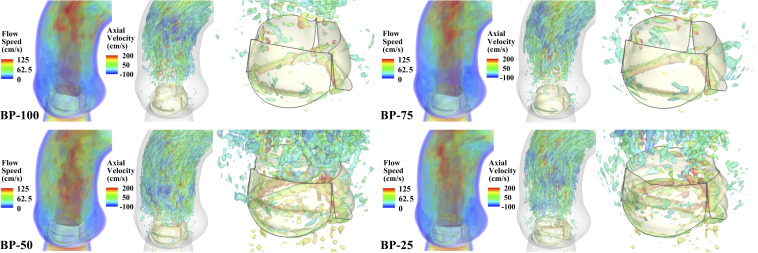
The vorticity isosurfaces, colored by the axial (normal to the aortic annulus) velocity, are shown in Movie S1 for the full cardiac cycle. The frames of the flow speed and vorticity isosurfaces at peak systole are shown in Fig. 2. As observed from these results, the flow patterns in the BP-50 and BP-25 cases are significantly affected by the change in the leaflet motion due to the thinner tissues. In the BP-100 and BP-75 cases, there is a large section of high-speed flow in the ascending aorta before the flow reaches a more chaotic state further away from the valve. The vortical structures observed downstream are created only by the shear between the high-speed jet and surrounding low-speed fluids. In the BP-50 and BP-25 cases, as illustrated in Movie S1, the thinner tissues induce leaflet flutter that disrupts the flow, causing a chaotic flow state adjacent to the leaflets. Comparing the vorticity isosurfaces between different time instances, it is clear that the vortices near the free edge of the thinner valves are only generated after 0.1 s. Based on these results, we conclude that the induced flutter causes vortex shedding from the free edge and is responsible for the immediate disturbance in the downstream flow.

Fig. 2.

FSI-simulation results for each valve thickness case. Volume-rendering visualization of the velocity field, colored by the flow speed, and vorticity isosurfaces, colored by the axial (normal to the aortic annulus) velocity, at peak opening ($t=0.25$ s) are shown for each case. High-resolution version of this figure is available in the SI Appendix.

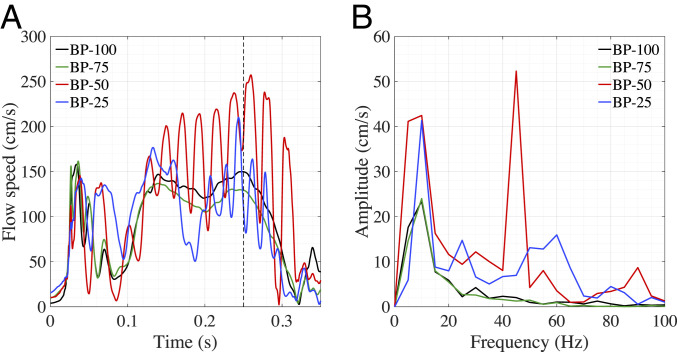
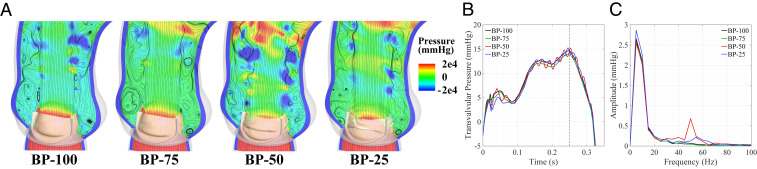
The flutter motion of the thinner leaflets also initiates temporal flow fluctuations. Regardless of whether the flow is laminar or turbulent, frequency analysis of the fluid velocity can provide a quantitative assessment of the disrupted flow behavior that is observed in the aorta (36). Since the flutter-induced disturbances are most prominent near the free edge, we record the history of flow speed passing a monitor point in the vicinity downstream of the noncoronary leaflet, as illustrated by the black point in Fig. 1B. The magnitude of the three-dimensional (3D) unsteady flow at the monitor point is plotted in Fig. 3A for each case. To specifically examine the prominent high-frequency flow fluctuations that are limited to the time interval of $t=$ 0.1 to 0.3 s, we isolate this section of the opening period for further frequency analysis of the flow disturbances. Fig. 3B shows a temporal frequency domain representation of the flow speed in the $t=$ 0.1- to 0.3-s time interval, which indicates a significant low-frequency peak for each valve. Based on observations of the BP-100 valve and frequency analysis of the ventricular pressure data (Fig. 1A) for the same time interval, the corresponding low frequency is observed in both the flow speed and pressure waveform. Due to the limited flutter in the BP-100 case and the matching frequencies between the flow speed and the pressure waveform, we conclude that these low frequencies result from the opening and closure of the valve within the analyzed time interval. In addition to this component of the typical valve behavior, the frequency analysis also captures the significant high-frequency fluctuation in the BP-50 case that is induced by the leaflet flutter.

Fig. 3.

Flow-speed results for each valve thickness case. (A) The speed is evaluated for each valve at the point indicated in Fig. 1B. (B) Frequency domain from the DFT operations for $t=0.1$ to 0.3 s of the flow speed.

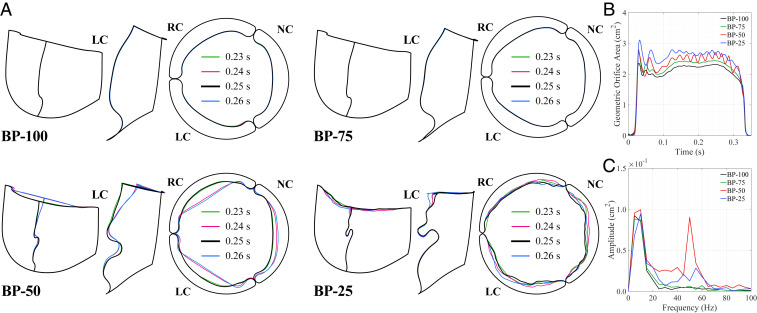
To better visualize the temporal and spatial oscillations in the valve, we plot the outline of each leaflet at the free edge, ${\mathrm{H}}_1$, and the central vertical tracking curve, ${\mathrm{V}}_2$, indicated in Fig. 1C. For these curves, we evaluate four time instances from $t=$ 0.23 to 0.26 s at the peak opening of the valve, as shown in Fig. 4A. These results exhibit the smooth, uniform leaflet shape at the free edge and in the belly region for the BP-100 and BP-75 cases. During the 0.23- to 0.26-s time interval, there is no visible change in the leaflet motion along the tracking curves on these valves, and the leaflet shape appears to be radially symmetric. In the BP-50 and BP-25 cases, the effects of leaflet thickness on the flutter behavior are visually apparent. Specifically, both temporal and spatial leaflet oscillations are observed. In the top view of the valve edge in Fig. 4A, the asymmetry between leaflets is also visible for the thinner valves, particularly in the noncoronary leaflet of the BP-50 case. This behavior is particularly noticeable in Movie S2, which reveals that the BP-50 noncoronary leaflet motion is out of phase with the left and right coronary leaflets. Such asymmetry may generate additional fluid forces that further amplify the leaflet oscillation.

Fig. 4.

Leaflet shapes at selected time instances for each valve thickness case. (A) Side and top views of the shape at the free edge (${\mathrm{H}}_1$) and at the central vertical tracking curve (${\mathrm{V}}_2$). The top view shows the orientation of the right coronary leaflet (RC) and noncoronary leaflet (NC) relative to the left coronary leaflet (LC). (B) Projected geometric orifice area computed for each valve. (C) Frequency domain from the DFT operations for $t=0.1$ to 0.3 s of the geometric orifice area.

As shown in Fig. 4B, we also evaluate the geometric orifice area (GOA) to assess the temporal leaflet flutter. The relative magnitude of the GOAs indicate that the thinner, more compliant tissues create larger opening areas than the thicker tissues. These solutions also show that the leaflet flutter appears around $t=$ 0.1 s and subsides after $t=$ 0.3 s, which confirms previous observations about the flow field during this period of the cardiac cycle. Frequency analysis of this period reveals the same low-frequency peaks that were observed from the flow analysis and identifies the high-frequency oscillation in the BP-50 and BP-25 cases. In these thinner cases, there are multiple frequency peaks between 30 and 60 Hz that indicate the higher temporal frequencies of the valve flutter.

The pressure data are shown in Fig. 5 and reflect the oscillatory leaflet behavior of the thinner valves. The pressure contours and velocity streamlines, shown in Fig. 5A, indicate that the flow is more disturbed near the valve, which is also consistent with the velocity results (Fig. 2). This disrupted flow generates lower-pressure regions in the aorta that are more pronounced near the valve in the cases that experience flutter. While there is some flow circulation in each case, the additional low-pressure areas in the cases with flutter generate more disturbances in the region directly above the sinuses. With the increased orifice area of the thinner cases (Fig. 4B), the thinner valves are expected to have lower transvalvular pressure gradients. As shown in Fig. 5B, the expected pressure gradient decrease is noticeable between the BP-100 and BP-75 cases, but the appearance of leaflet flutter in the BP-50 and BP-25 cases disrupts this expected pressure behavior. This is consistent with the accelerated velocity in the flutter cases shown in Fig. 3A. The discrete frequency analysis of the transvalvular pressure, shown in Fig. 5C, indicates that the flutter introduces a high-frequency component in the pressure that is particularly noticeable in the BP-50 case.

Fig. 5.

Pressure field and transvalvular pressure gradient. (A) Pressure contours superimposed with streamlines at peak opening ($t=0.25$ s). The transvalvular pressure gradient is evaluated for each case as the difference between the left-ventricular pressure (0.1 cm below the annulus) and the aortic pressure (1.3 cm above the annulus) at the indicated points on each side of the valve. (B) Transvalvular pressure gradient across each valve. (C) Frequency domain from the DFT operations for $t=0.1$ to 0.3 s of the transvalvular pressure. High-resolution version of this figure is available in the SI Appendix.

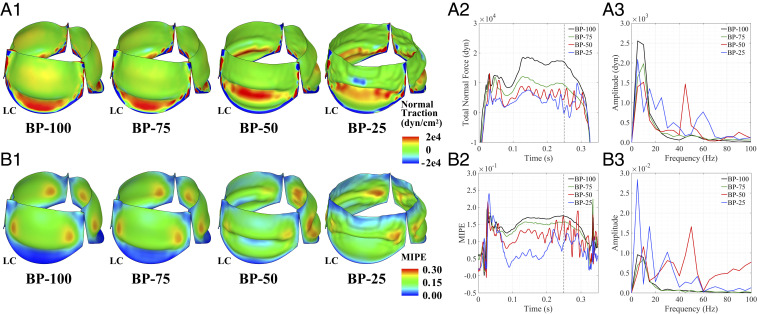
To analyze the connection between the valve dynamics and the blood flow, the FSI force on the valve is collected during the simulation and analyzed for each thickness case. The traction normal to each leaflet, which is associated with the fluid pressure and viscous forces, directly reveals the interaction between the valve and the flow. These FSI traction data are plotted on the leaflet, as shown in Fig. 6A1. The tractions on the BP-100 and BP-75 valves exhibit higher magnitudes due to the smooth, curved region below the free edge that experiences a higher normal traction in both cases. In comparison, the BP-50 and BP-25 cases exhibit much more irregular motion in this region and significantly lower traction magnitudes. We also note that the change in tissue thickness makes the thinner leaflets much more compliant and easier to open, requiring less force for an increased orifice area (Fig. 4B). The normal traction is integrated over the left coronary leaflet and the temporal frequencies are analyzed, as shown in Fig. 6 A2 and A3, respectively. Here, we again note the same low-frequency peaks due to the natural motion of each valve. In the thinner cases, we observe significant high-frequency temporal oscillations in the forces shown in Fig. 6A2 that are captured through the frequency analysis. Prominent high-frequency peaks due to the valve flutter are observed around 45 Hz for the BP-50 valve and around 60 Hz for the BP-25 valve. In the BP-100 and BP-75 cases, no prominent frequency peaks are observed in the high-frequency range.

Fig. 6.

Frequency analysis of force and strain information on the leaflets. (A1) Leaflet normal traction at peak opening ($t=0.25$ s). (A2) Integrated normal traction on the left coronary leaflet (LC). (A3) Frequency domain from the DFT operations for $t=0.1$ to 0.3 s of the integrated traction force. (B1) Leaflet maximum in-plane principal Green–Lagrange strain (MIPE) at peak opening ($t=0.25$ s) evaluated on the aortic side of the leaflets. (B2) MIPE at the center of the free edge on the left coronary leaflet. (B3) Frequency domain from the DFT operations for $t=0.1$ to 0.3 s of the MIPE. High-resolution version of this figure is available in the SI Appendix.

Fig. 6B1 illustrates the strain distribution on each valve at peak systole. While the BP-100 and BP-75 valves exhibit similar strain distributions and magnitudes, the BP-50 and BP-25 valves show significantly altered strain behavior due to the thinner tissues. Near the attachment edges of the thinner leaflets, where significant bending appears, the strain magnitudes increase noticeably compared with the BP-100 and BP-75 leaflets. The strain distributions also reflect the asymmetry between the noncoronary leaflet and the other two leaflets of the BP-50 valve. To highlight the temporal strain behavior, the strain at the center point of the free edge is evaluated over the opening period of the cardiac cycle and the temporal frequency behavior is analyzed, as shown in Fig. 6 B2 and B3, respectively. The computed quantities again demonstrate the oscillatory motion of the leaflets in time and display frequencies that are similar to the high frequencies that were observed in the GOA and leaflet forces.

Flutter Analysis.

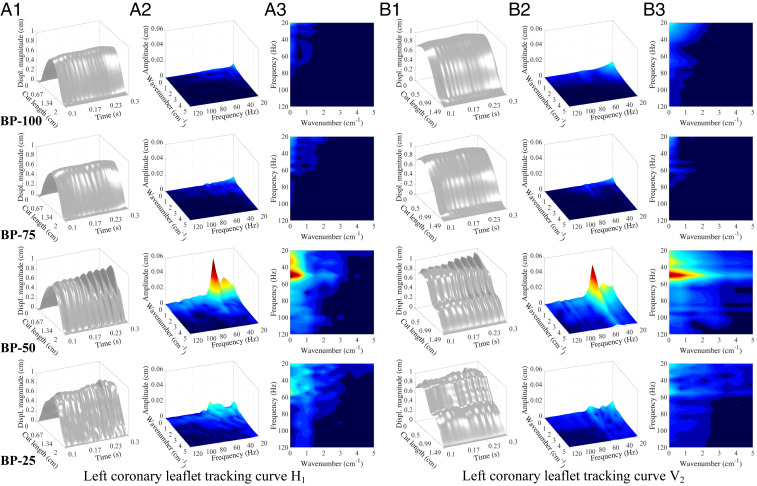
To further analyze and quantify the flutter behavior of each valve, we track the displacement of the leaflet free edge throughout the $t=$ 0.1- to 0.3-s period of the opening cycle. The displacement plots for ${\mathrm{H}}_1$ in Fig. 7A1 show a generally parabolic shape along the free edge, which results from the natural motion of the leaflets during the opening cycle; each leaflet is attached to the rigid stent at both ends of the free edge, so the valve geometry inherently experiences larger displacements near the center of each leaflet. The two-dimensional (2D) signal data from the free-edge displacement are analyzed and quantified using the frequency spectrum analysis operations outlined in Materials and Methods. These 3D computational data from the free edge provide information that is similar to the 2D data that can be measured using experimental methods (21, 32); however, the full 3D FSI simulation provides significantly more detailed information on the valve. Additional tracking curves along different directions of each leaflet can also be analyzed to comprehensively capture the flutter behavior over the entire valve.

Fig. 7.

Frequency analysis of the leaflet displacement. Data are tracked on horizontal tracking curve ${\mathrm{H}}_1$ (A1–A3) and vertical tracking curve ${\mathrm{V}}_2$ (B1–B3) on the left coronary leaflet, as shown in Fig. 1C. A1 and B1 show the displacement magnitude visualization of the leaflet tracking curves throughout the $t=0.1$- to 0.3-s portion of the valve-opening period. Cut length denotes the length of each tracking curve. A2–A3 and B2–B3 show the 3D view and 2D top view of the frequency domain visualization from the DFT operations for $t=0.1$ to 0.3 s of the displacement magnitude data, respectively. The data below 20 Hz are excluded for the computation of the flutter signal energy. High-resolution version of this figure is available in the SI Appendix.

Fig. 7A1 demonstrates the significant increase in the flutter behavior of the thinner valves that is evident in the displacement plots along the free edge of the leaflets. To quantify the energy and spectral distribution of the flutter displacement signal, we isolate the high-frequency responses of the valve from the inherent low-frequency motion. As shown in Fig. 7 A2 and A3, there are no prominent high frequencies in the BP-100 and BP-75 spectra since they do not experience flutter. We observe multiple high-frequency peaks for the BP-50 and BP-25 cases at low wavenumbers that reflect broad amplitude modulations of the flutter across the leaflet. The BP-50 valve shows a prominent narrow frequency band around 50 Hz, which reflects the sinusoidal flutter behavior across the leaflet. The BP-25 case exhibits a wide frequency band around 20 to 60 Hz, which reflects the more chaotic flutter behavior. The flutter amplitude also diminishes near the stent attachments for both cases.

The oscillatory flutter motion in the thinner cases that was observed at the free edge (${\mathrm{H}}_1$) is also evident across larger areas of the leaflet, as observed from Fig. 4A and Movies S2 and S3. Fig. 7B1 shows the displacement plots for the vertical tracking curve along the center of each leaflet, ${\mathrm{V}}_2$, which exhibits the largest displacements at the free edge and smaller displacements near the stent attachment. This central region of the leaflet exhibits more varied motion and visible flutter displacements in the BP-50 and BP-25 cases. The results for ${\mathrm{V}}_2$ display similar spectral characteristic as the results from ${\mathrm{H}}_1$, with the BP-50 case showing a strong, narrow frequency band near 50 Hz.

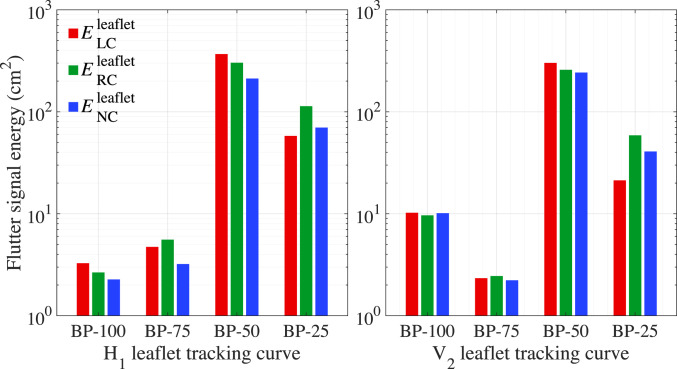
Fig. 8 summarizes the results from the frequency analysis and flutter-quantification calculation for tracking curves ${\mathrm{H}}_1$ and ${\mathrm{V}}_2$ on each leaflet for a single cardiac cycle. SI Appendix, Table S1 shows the values corresponding to the flutter results from Fig. 7, and SI Appendix, Tables S2 and S3 show the quantified values of the flutter signal energy for each leaflet and cycle. The flutter signal energy of each leaflet is averaged over each cycle and shown in SI Appendix, Fig. S1. As summarized in SI Appendix, Table S4, the valve averages are also computed from the flutter results of each leaflet and cycle. As expected, these values indicate an overall inverse relationship between flutter and thickness. In the BP-50 case, the flutter signal energy is at least an order of magnitude larger on the left coronary leaflet and over the entire valve compared with the BP-100 case, demonstrating the significant correlation between tissue thickness and the initiation of flutter. It is also notable that the flutter displacement is unevenly distributed over the three leaflets. Based on the observation of different flutter patterns among leaflets in Fig. 4A and Movie S2 and the frequency analysis of tracking curve ${\mathrm{H}}_1$ in Fig. 8, the noncoronary leaflet contributes the lowest flutter signal energy in the BP-50 case. This asymmetry is consistent over three cycles, as indicated in SI Appendix, Fig. S1, and is reflected by the corresponding averaged valve quantities shown in SI Appendix, Table S4. The quantified flutter values also indicate that the BP-25 valve experiences less flutter than the BP-50 case. In this thinnest case, the flutter motion may be inhibited by the folding behavior of the BP-25 valve that is observed from Fig. 4A and Movie S3.

Fig. 8.

Quantified results of the flutter signal energy for tracking curves H₁ (Left) and V₂ (Right). $E_{\hspace{0.17em}\text{LC}}^{\hspace{0.17em}\text{leaflet}}$ indicates the signal energy on the left coronary leaflet for a single cardiac cycle. $E_{\hspace{0.17em}\text{RC}}^{\hspace{0.17em}\text{leaflet}}$ and $E_{\hspace{0.17em}\text{NC}}^{\hspace{0.17em}\text{leaflet}}$ indicate the signal energy on the right coronary and noncoronary leaflets, respectively. ${\mathrm{H}}_1$ and ${\mathrm{V}}_2$ indicate the free edge and the central vertical tracking curve on the leaflets, respectively, as shown in Fig. 1C.

To capture the flutter behavior in other regions of the valve, we analyze the leaflets using three additional tracking curves, ${\mathrm{H}}_2$, ${\mathrm{H}}_3$, and ${\mathrm{H}}_4$, along the horizontal direction, and two additional tracking curves, ${\mathrm{V}}_1$, ${\mathrm{V}}_3$, along the vertical direction. These computational results provide insight about the 3D leaflet motion that would be significantly more challenging to collect using experimental approaches. As shown in SI Appendix, Figs. S2–S8 and Table S4, each additional tracking curve is analyzed using the same flutter-quantification methods, and similar conclusions can be drawn from the results.

Discussion

The present study employed computational FSI to model and simulate four bioprosthetic heart valve configurations and analyzed their flutter behavior throughout the opening period of the cardiac cycle. Analysis of leaflet quantities, including GOA, leaflet forces, and strains, reveals irregular, oscillatory valve behavior due to the induced flutter motion of the thinner leaflets. These irregularities, particularly the strain distributions on the thinner valve, pose a number of potential issues for the thin biological tissue’s structural performance. Due to the inherent cyclic loading associated with the cardiac cycle, fatigue is already a commonly observed issue in bioprosthetic valves that do not experience flutter (37). The additional cyclic-strain behavior that is observed at the free edge of the BP-50 and BP-25 cases will lead to an associated cyclic stress on the leaflets. Similar cyclic flexural loading has also been previously associated with decreased flexural rigidity and increased fatigue damage in other bioprosthetic valve tissues (38, 39). Over the lifetime of a valve that experiences significant flutter, this additional induced cyclic loading may contribute to nonuniform or accelerated leaflet fatigue and deterioration.

For the cases that experience flutter, the FSI results exhibit disturbed flow and pressure through the ascending aorta and induced vortices near the leaflet free edges. The results of the frequency and flutter-quantification analyses indicate significant increases in the leaflet flutter signal energy of at least an order of magnitude between the BP-100 and BP-50 valves. This type of flutter behavior in the thinner valves may be caused by a flow-induced instability that excites the valve bending vibrations. As suggested by the analysis of flag-flutter phenomena (40), for a thin, flexible plate in fluid, there is a critical flow velocity above which flutter can be induced. Specifically, the critical velocity is proportional to $h^{3/2}$, where $h$ is the thickness of the structure. During the time period of $t=$ 0.1 to 0.3 s, similar magnitudes of flow speed are observed with all four leaflet thicknesses. It seems that this velocity falls between the critical velocities needed for BP-75 and BP-50 cases, which may explain the appearance of leaflet flutter in the BP-50 and thinner cases.

Velocity analysis and visualization of the flow indicate an increasingly chaotic flow field associated with the flutter of the thinner leaflets. These flutter-induced flow disturbances raise concerns about potential blood damage that may result in valve thrombosis or other thromboembolic complications (27, 41). Numerous studies have associated local alterations in the blood flow patterns with thrombus formation (41–43). Mechanical heart valves, for example, are highly thrombogenic and require life-long anticoagulant therapy (44). The intensified vortex formation and boundary-layer separation are believed to be responsible for the high incidence of thrombi after mechanical valve replacement, as these flow features may induce platelet activation. Since bioprosthetic valves are more compliant and structurally similar to native heart valves, the postsurgery hemodynamics better resemble that of the native cardiac system. As a result, bioprosthetic valves have a reportedly lower risk of thrombosis and are often only treated with anticoagulants during the first three months after replacement (45). However, highly disturbed flow patterns, as observed in the thinner leaflet cases especially around the valve orifice, are likely to increase the risk of thrombosis. In the BP-25 and BP-50 cases, the high-frequency transverse motion of the free edge could dramatically increase the rate of shear stress. The risk of platelet activation, aggregation, and decomposition is enhanced by such flow conditions, which in turn cause dramatic morphological and biomechanical changes to platelets that lead to thrombus formation (46, 47).

The additional vortices induced by the leaflet flutter may play a role in increasing the flow-energy loss. However, the thinner, more compliant tissues allow blood to flow more easily through the valve region during systole, which may also result in reduced energy loss. The overall flow-energy performance is determined by the trade-off between these two effects. Energy efficiency, $\eta$, defined as the ratio between the energy fluxes out of and into the system (48), is a useful measure to quantify the valve performance. To calculate the energy efficiencies shown in SI Appendix, Table S5, we integrate the energy fluxes on the inlet and outlet of the aorta over a complete cardiac cycle. The increase in energy efficiency from the BP-100 to BP-75 case is purely the effect of the increased orifice area due to the thinner leaflet tissues, as fluttering is absent in these two cases. Without leaflet flutter, we would expect a consistently increasing efficiency trend in the thinner cases. However, the BP-50 case demonstrates a drop in efficiency due to the viscous dissipation that is introduced by the leaflet flutter. Interestingly, the BP-25 valve achieves an increased efficiency compared with the BP-100 valve. This can be explained by the assumption that the efficiency drop due to fluttering is smaller than the efficiency increase due to the larger orifice area for the BP-25 case, which is consistent with its smaller flutter signal energy compared with the BP-50 case. We note that the differences among the energy efficiencies of all four cases are within 1%, which suggests that leaflet flutter does not noticeably increase the heart afterload. Thus, the potential adverse effects on the structural integrity and blood flow seem to be the primary concern when using thinner valve tissues.

While this study provides distinct evidence that thinner biological tissues induce heart valve leaflet flutter, there are many avenues to extend this work. The presented results from the simulation of a physiologically realistic cardiac system consider only the specified conditions and do not account for uncertainty or variation in any of the experimentally based parameters or quantities, such as the ventricular pressure waveform. Subsequent studies on the impact of thinner tissues could include investigations of these uncertainties for specific relevant input conditions. Analysis and future studies of other system quantities, such as turbulence kinetic energy or material fatigue life, could also contribute to an improved understanding of the impact of flutter on long-term heart function, biological tissue durability, and valvular degeneration. Although this paper focuses on the identification and quantification of flutter behavior due to thinner biological tissues, we do not explore possible mechanisms for the initial onset of leaflet flutter. In addition to investigating the phenomena responsible for initiating flutter, expanded studies of heart valve leaflet flutter could explore other relevant system parameters, such as flow speed and valve size, that may induce or reduce flutter. Finally, future study and quantification of flutter for other valve configurations and input flow conditions could also provide a baseline for a simulation-based empirical model of heart valve leaflet flutter. Such analyses might determine whether certain thinner valves could perform better over their lifetime, despite increases in leaflet flutter.

The present investigation concretely demonstrates that a major reduction in valve material thickness can induce leaflet flutter, and the results exhibit the impact that a single parameter can have on both the structural performance of the tissue and the blood flow behavior throughout the cardiac cycle. In addition to the notable results on the impact of thinner biological tissues, this work also highlights the benefits of computational analysis and quantification. Compared with experimental approaches, the methods employed here provide more detailed information about the cardiac system, which enables rigorous quantification of the leaflet flutter. Realistic computational simulations, such as those performed in this study, can be used to develop inverse models to understand material behaviors in intact devices rather than in isolated materials testing. The computational adaptability and cost-effective repeatability of IMGA for valvular FSI supports the application of these methods to other types of valves and geometric configurations. These advantages offer significant potential for improving future valves through iterative design using parameter sweeps or heuristic optimization methods that incorporate standards to reduce leaflet flutter and satisfy the requirements of minimally invasive valve replacements. Considering the increasing prevalence of percutaneous valves, the present findings underscore the important role of detailed valvular analysis in improving long-term implant performance and mitigating potentially damaging mechanism in the cardiac system. Given the risks associated with observed flutter phenomena, including blood damage and accelerated leaflet deterioration, this study demonstrates the potentially serious impact of introducing thinner, more flexible tissues into the cardiac system.

Materials and Methods

Numerical Methodology.

The simulations in this work are carried out using the IMGA FSI framework (33, 34, 49–55). IMGA is a geometrically flexible numerical technique for solving FSI problems involving large, complex structural deformation and change of fluid-domain topology (e.g., due to structural contact). The method makes direct use of the computer-aided design boundary representation (B-rep) of a complex design structure by immersing it into a non–boundary-fitted discretization of the surrounding fluid domain (56–60). The computational FSI system for heart valves includes the dynamics of blood flow, the artery wall, and the valve leaflets. The IMGA framework models all of these subproblems and accounts for the necessary couplings between them. The key components of the framework for heart valve FSI simulations are briefly summarized here.

The blood flow in a deforming artery is governed by the Navier–Stokes equations of incompressible flows. The equations are numerically solved using the variational multiscale (VMS) (61) formulation on an arbitrary Lagrangian–Eulerian (ALE) frame (62). The ALE formulation is a widely used approach for vascular blood-flow simulations on moving domains. The VMS formulation accounts for the potential turbulent flow regime near the valve using a residual-based large-eddy simulation turbulence model. The structures in the FSI system, namely the artery wall and the valve leaflets, are modeled using two different approaches. The artery wall is modeled using a large-deformation hyperelastic solid written in the Lagrangian frame (63). The leaflets, on the other hand, are modeled as thin-shell structures. The anisotropic hyperelastic Kirchhoff–Love shell formulation (54, 64) is employed in this work.

The discretizations of the blood-flow domain and artery wall are defined such that they are conforming. This allows the kinematic- and traction-compatibility conditions to be satisfied automatically and the FSI coupling to be handled using a monolithic formulation (63). However, this approach is not practical for the coupling of blood flow and heart valves because much larger displacements and contact are present in the motion of leaflet structures. To avoid the challenges associated with mesh deformation in a traditional boundary-fitted ALE approach, we immerse the leaflet into a non–boundary-fitted discretization of the background fluid domain and directly analyze the spline representation of the thin-shell structure using the IMGA approach. A semi-implicit numerical method, which we refer to as the Dynamic Augmented Lagrangian approach (34), is used for weakly enforcing constraints at the immersed fluid–structure interface in time-dependent immersogeometric FSI problems. When the valve closes during diastole, a penalty-based approach is used for imposing contact conditions between the shell structures. Finally, all these numerical ingredients are combined into the coherent IMGA framework and discretized in time using the generalized-$\alpha$ method (63). For the detailed formulations of the immersogeometric FSI methodology, readers are referred to the aforementioned references. Additional validation results for the immersogeometric FSI framework applied to a bioprosthetic heart valve problem are provided in SI Appendix, Validation Study.

Problem Setup.

A 23-mm-diameter annulus aorta geometry, including the blood-flow domain and the artery wall, is constructed based on the adult aorta size statistics obtained from 2D echocardiographic images and coupled to a typical 23-mm valve geometry with leaflet diameter $D_L=21.9$ mm and leaflet height $h_L=11.1$ mm, as shown in Fig. 1A. The parameterization, dimensions, and computational domain are detailed by Wu et al. (section 3.3 in ref. 65). Quadratic trivariate nonuniform rational B-spline elements are used to discretize the entire domain, with 8,640 elements in the artery wall and 88,560 elements in the fluid domain. The 23-mm bioprosthetic valve is modeled using cubic B-spline surfaces. The stent consists of 1,380 B-spline elements, and each leaflet consists of 351 B-spline elements. This mesh resolution is similar to that used in the computations of Xu et al. (53), which show that the quantities of interest are converged at this mesh refinement level. The geometric model of the aorta, computational meshes, and boundary conditions used in the FSI simulation are shown in Fig. 1A. We refer to the “inlet” as the left ventricular end of the aorta and the “outlet” as the end of the tubular ascending aorta.

Based on the previous valvular FSI simulations (33, 49, 50), the blood is modeled as an incompressible flow with a density and viscosity of 1.0 g/${\mathrm{c}\mathrm{m}}^3$ and $3\times 10^{-2}$ g/(cm s), respectively. A physiologically realistic left-ventricular pressure waveform from Yap et al. (66) is applied at the inlet, as shown in Fig. 1A. An idealized approximation of the same pressure waveform is also examined in the SI Appendix, Pressure Waveform Study. The cardiac cycle has a period of 0.86 s, and a time step size of $1.0\times 10^{-4}$ s is used to advance the simulation in time. A traction of $-\left(p_0+RQ\right){\mathbf{n}}_{\text{f}}$ is applied at the outlet as the resistance boundary condition (67), where $p_0=80$ mmHg is a constant physiological pressure level, ${\mathbf{n}}_{\text{f}}$ is the outward-facing normal of the fluid domain, and $R=70$ (dyn s)/${\mathrm{c}\mathrm{m}}^5$ is a resistance coefficient. A backflow stabilization (68) is applied at both ends of the computational domain for numerical stability. The applied boundary conditions produce a reasonable outlet pressure and permit an average peak flow rate of $Q=472.6$ mL/s for the BP-100 case over three cardiac cycles, which is within the normal physiological range (69). This setup also generates physiological outputs for a typical patient, including an average stroke volume of 102.7 mL per beat and average cardiac output of 7.17 L/min over three cardiac cycles. For adults at a resting heart rate, typical stroke volumes are observed in the 65- to 120-mL range, which leads to cardiac outputs around 4.5 to 8.5 L/min (70). For the sake of consistency, we assume that the cardiac function does not change due to the change in leaflet thickness and apply the same boundary conditions to each thickness case. We note that while the use of a resistance boundary condition at the outlet generates reasonable cardiac performance, it does not account for the phase lag between the pressure and flow. A more sophisticated model at the outlet, such as an impedance or Windkessel boundary condition (67, 71), should be considered to capture this physiological phenomenon. This type of model is expected to alter the relative start of the valve-opening period within the cardiac cycle, but it is not expected to dramatically impact the flutter behavior of the valve and the flow phenomena.

The neo-Hookean material model is used for the artery wall tissue, in which the Young’s modulus and Poisson’s ratio are set to $10^7$ dyn/${\mathrm{c}\mathrm{m}}^2$ and 0.45, respectively. The density of the arterial wall is 1.0 g/${\mathrm{c}\mathrm{m}}^3$, and a mass-proportional damping with coefficient $1.0\times 10^4\hspace{0.17em}{\mathrm{s}}^{-1}$ is added to the motion of the wall to model the interaction of the artery with the surrounding tissues and interstitial fluid. A zero-traction boundary condition is applied on the outer wall of the artery. The inlet and outlet cross-sections are free to slide in their tangential planes and deform radially, but they are constrained not to move in the normal directions (72). For the bioprosthetic valve, the stent is assumed to be rigid and stationary due to its large stiffness relative to the leaflets and the artery wall. Each leaflet is clamped to the stent at the attachment edge. The valve is immersed into the sinus section of the aorta, with the stent cut into the interior of the artery domain. The solid elements in the artery wall that are intersected by the stent are fixed in space and time. The transversely isotropic Lee–Sacks material model (54) is used for the leaflets. A ${\mathrm{45}}^{○}$ fiber orientation that approximates the collagen fiber alignment of typical pericardial tissue is considered. The material coefficients reported by Wu et al. (54), obtained from fitting the equibiaxial experimental data of a glutaraldehyde-treated bovine pericardium specimen (73), is adopted. The density of the leaflets is 1.0 g/${\mathrm{c}\mathrm{m}}^3$, and the leaflet thicknesses considered in this study are summarized in Fig. 1A.

GOA Calculation.

The GOA, which is also known as the aortic valve area or the anatomical orifice area, is typically measured for patient valves by computed tomographic, magnetic resonance, or echocardiographic planimetry (74). These clinical methods of calculating the GOA implement image-processing procedures to evaluate the maximum opening of the leaflet free edges at each time instance during the cardiac cycle. The present study implements a projection-based approach to compute the valve GOA from the FSI solutions. Using this procedure, the GOA is calculated by projecting the opening area of the valve leaflets along the axial (normal to the aortic annulus) direction. This quantity is computed every $5.0\times 10^{-4}$ s to obtain the area signal during the opening period of the cardiac cycle, as shown in Fig. 4B.

Flutter-Quantification Formulation.

For experimental analysis, as described in the works of Condurache et al. (21) and Avelar et al. (32), a video-based approach is generally implemented to capture valve motion and flutter behavior by tracking the leaflet edges frame by frame. Different methods are used to track the free edge and calculate various flutter measures, but each approach relies on the potentially limited accuracy associated with free-edge tracking and the pixelated representation of the free edge in the video data, which is a considerable source of uncertainty. Additionally, the temporal fidelity of the video data is inherently limited by the video-acquisition technology, another potential source of uncertainty and complexity.

This study implements a flutter-quantification approach that takes advantage of the IMGA-based computational FSI framework to track the motion of the different tracking curves along the leaflet with high spatial and temporal resolutions. Each leaflet tracking curve, as indicated in Fig. 1C, is monitored with 150 uniformly distributed tracking points. Note that the selected number of tracking points is flexible due to the high-order smoothness provided by the B-spline functions. Throughout the FSI analysis, the magnitude of the 3D displacement from the reference configuration is computed for each tracking point every $1.0\times 10^{-4}$ s. The full set of displacement magnitude values throughout time form a 2D space–time signal from which a 2D discrete Fourier transform (DFT) (75) can be computed using a fast Fourier transform algorithm.

As demonstrated by the frequency analysis in Fig. 1A, the pressure signal in the $t=0.1$- to 0.3-s range has a low-frequency component. In order to isolate the contribution of the leaflet flutter to the signal energy, the low-frequency components are excluded from the quantification of the flutter signal energy. The DC component (75) is also removed from the displacement magnitude by subtracting the mean amplitude of the 2D signal. For each case, only frequencies within the relevant flutter domain, which is empirically defined as the frequencies at and above 20 Hz, are considered in the calculation of the flutter signal energy. The resulting measure of the flutter motion captures only the contributions of the high-frequency leaflet flutter, and the signal energy of the displacement magnitude is computed based on Parseval’s Theorem (75) as:

$$E^{\text{leaflet}}=\frac{1}{N_1{N}_2}\sum _{r_1=0}^{N_1-1}\sum _{r_2=0}^{N_2-1}{\left|X\left(r_1,r_2\right)\right|}^2,$$

where $X\left(r_1,r_2\right)$ is the $r_1$, $r_2$ element of the DFT matrix with the low-frequency components removed, and $N_1$ and $N_2$ are the sizes of the spatial and temporal domains, respectively. In this work, $N_1$ represents the number of tracking points along the leaflet tracking curves, and $N_2$ represents the number of time steps. This formulation quantifies flutter using the total high-frequency energy content of the displacement signal per leaflet, which may be further combined as a sum or an average to obtain a measure of the total valve flutter.

Data Availability.

The data that support the findings of this study are available from the corresponding authors upon reasonable request.